An Innovative Approach to Nonlinear Fractional Shock Wave Equations Using Two Numerical Methods

Abstract

In this research, we propose a combined approach to solving nonlinear fractional shock wave equations using an Elzaki transform, the homotopy perturbation method, and the Adomian decomposition method. The nonlinear fractional shock wave equation is first transformed into an equivalent integral equation using the Elzaki transform. The homotopy perturbation method and Adomian decomposition method are then utilized to approximate the solution of the integral equation. To evaluate the effectiveness of the proposed method, we conduct several numerical experiments and compare the results with existing methods. The numerical results show that the combined method provides accurate and efficient solutions for nonlinear fractional shock wave equations. Overall, this research contributes to the development of a powerful tool for solving nonlinear fractional shock wave equations, which has potential applications in many fields of science and engineering. This study presents a solution approach for nonlinear fractional shock wave equations using a combination of an Elzaki transform, the homotopy perturbation method, and the Adomian decomposition method. The Elzaki transform is utilized to transform the nonlinear fractional shock wave equation into an equivalent integral equation. The homotopy perturbation method and Adomian decomposition method are then employed to approximate the solution of the integral equation. The effectiveness of the combined method is demonstrated through several numerical examples and compared with other existing methods. The results show that the proposed method provides accurate and efficient solutions for nonlinear fractional shock wave equations.

1. Introduction

Fractional differential equations (FDEs) provide a mathematical framework for modeling systems that exhibit nonlinear or complex dynamics. Unlike traditional differential equations, FDEs utilize fractional derivatives, which capture the rate of change in these systems. FDEs have found widespread applications in fields such as physics, engineering, finance, and biology, where they have been used to model phenomena such as anomalous diffusion, viscoelastic materials, and fractional control systems [1,2,3,4,5].

Fractional derivatives are a generalization of classical integer derivatives and can be defined in various ways, including the Riemann–Liouville, Caputo, and Grunwald–Letnikov derivatives. Various numerical methods, such as the finite difference, boundary element, and variational methods, can be used to solve FDEs. The study of FDEs has a rich history dating back to the 17th century, when mathematician John Wallis first introduced the concept of fractional calculus [6,7,8]. In recent years, FDEs have gained significant attention and become increasingly popular due to their ability to model complex systems and their broad range of applications [9,10,11,12,13].

The nonlinear shock wave equation, also known as Burgers’ equation, is a fundamental equation in fluid dynamics and nonlinear physics. Its history can be traced back to the early 20th century, with important contributions by several mathematicians and physicists. In the following decades, mathematicians and physicists made significant contributions to the understanding of Burgers’ equation and its properties. In the 1950s, the Russian mathematician Andrei Kolmogorov studied the behavior of solutions to the equation in the limit of high Reynolds numbers. He showed that the solutions exhibit self-similarity and developed a theory of turbulence based on this observation [14,15]. In the 1960s, the American mathematician Richard Courant and his collaborators developed numerical methods for solving Burgers’ equation, which played a key role in the development of computational fluid dynamics. In the 1970s and 1980s, the equation was studied extensively in the context of nonlinear wave propagation and shock waves [16,17,18,19]. Today, Burgers’ equation continues to be an active area of research in mathematics, physics, and engineering. It has applications in fields such as fluid mechanics, nonlinear optics, and plasma physics [20,21,22,23,24].

The nonlinear shock wave equation is a mathematical model that describes the behavior of shock waves, which are sudden changes in the pressure and density of a fluid that propagates through it. Unlike linear shock wave equations, the nonlinear shock wave equation takes into account the nonlinear effects that occur when the fluid pressure exceeds a critical value [25,26]. These nonlinear effects cause the shock wave to become distorted and the velocity of the fluid to change rapidly, leading to complex and diverse behaviors. The nonlinear shock wave equation plays an important role in many areas of science and engineering, including fluid dynamics, combustion, and blast waves [27,28,29].

The fractional nonlinear shock wave equation is a mathematical tool extensively employed to describe the intricate behavior of shock waves in different engineering and physical applications. Due to the nonlinear nature of shock waves, their behavior can be complicated and unpredictable. This equation incorporates the nonlinear effects, allowing for an accurate representation of the shock wave’s dynamics over time. Moreover, the use of fractional derivatives in this equation provides a more precise description of shock wave behavior. The application of this equation is particularly valuable in fluid dynamics research, where it is used to model shock waves in fluids with complex properties such as viscoelastic fluids. Additionally, the equation finds its applications in material science, where it can be employed to simulate the behavior of shock waves in solids, including their responses to stress and deformation [30,31,32].

The highly nonlinear nature of the fractional nonlinear shock wave equation implies that the solution is dependent on the initial conditions and underlying physical laws. Due to this nonlinearity, there are diverse shock wave behaviors, such as propagating waves, standing waves, and bifurcation points. These behaviors can exhibit multiple distinct characteristics. Despite its complexity, the fractional nonlinear shock wave equation is a crucial tool in comprehending shock wave behavior, leading to a more accurate and thorough understanding of these complex physical phenomena. Continued research and development of this equation is promising, and it is expected to offer new insights into a wide range of scientific and engineering disciplines. Its implications will be essential in several areas of research and development [33,34].

The homotopy perturbation method (HPM) and Elzaki transform are two mathematical techniques that are widely used to solve nonlinear and linear partial differential equations (PDEs) [35,36]. The HPM is a numerical method that is based on the concept of homotopy and is used to approximate solutions to nonlinear problems. On the other hand, the Elzaki transform is a mathematical tool that is used to transform linear problems into nonlinear ones, making them easier to solve. Both the HPM and Elzaki transform have been extensively researched and applied in various fields, including engineering, physics, and mathematics [37,38].

The Adomian decomposition method (ADM) has been widely used for solving various types of nonlinear differential equations. This method is based on the decomposition of the nonlinear term into a series of polynomials and then using this series to find the solution. However, the convergence of the ADM series is slow, which makes it unsuitable for some applications. To overcome this limitation, various researchers have proposed combining the ADM with other mathematical techniques to improve its efficiency and accuracy. One of these techniques is the Elzaki transform (ET), which has been used to solve linear and nonlinear partial differential equations [39,40]. The combination of the ADM and ET has been applied to solve various types of nonlinear differential equations, including nonlinear partial differential equations, nonlinear integro-differential equations, and nonlinear differential-difference equations (Elzaki and Mustafa, 2011; Khodaei et al., 2015; Mahmoud, 2018). The results obtained from these studies demonstrate the efficiency and accuracy of the combined method in solving nonlinear differential equations [39,40].

The following is the rest of this study. Section 2 compiles some basic definitions. Section 3 introduces the concept of the HPTM, whereas Section 4 introduces the concept of the ETDM. The proposed methods’ convergence analysis is provided in Section 5. In Section 6, various approximative solutions to the fractional nonlinear wave equation are derived by using the form of the initial value, and the structure of the solutions is displayed using graphs and tables. In Section 6, the work’s conclusion is examined.

2. Basic Definitions

 Definition 1.

The fractional derivative $D^{ß}$ in the Abel–Riemann sense, having an order ß, is given as follows [41,42]:

$$D^{ß}\theta \left(\mu \right)=\left\{\begin{array}{c}\frac{d^{\kappa }}{d{\mu }^{\kappa }}\theta \left(\mu \right),ß=\kappa ,\hfill \\ \frac{1}{\Gamma (\kappa -ß)}\frac{d}{d{\mu }^{\kappa }}{\int }_0^{\mu }\frac{\theta \left(\mu \right)}{{(\mu -\varphi )}^{ß-\kappa +1}}d\varphi ,\kappa -1<ß<\kappa ,\hfill \end{array}\right.$$

where $\kappa \in Z^{+}$, $ß\in R^{+}$ and

$$D^{-ß}\theta \left(\mu \right)=\frac{1}{\Gamma (ß)}{\int }_0^{\mu }{(\mu -\varphi )}^{ß-1}\theta \left(\varphi \right)d\varphi ,0<ß\le 1.$$

 Definition 2.

The fractional integration operator ${\kappa }^{\varphi }$ in the Abel–Riemann sense is defined as [41,42]

$${\kappa }^{ß}\theta \left(\mu \right)=\frac{1}{\Gamma (ß)}{\int }_0^{\mu }{(\mu -\varphi )}^{ß-1}\theta \left(\mu \right)d\mu ,\mu >0,ß>0.$$

having the properties

$$\begin{array}{c}\hfill {\kappa }^{ß}{\mu }^{\kappa }=\frac{\Gamma (\kappa +1)}{\Gamma (\kappa +ß+1)}{\mu }^{\kappa +\varphi },\\ \hfill D^{ß}{\mu }^{\kappa }=\frac{\Gamma (\kappa +1)}{\Gamma (\kappa -ß+1)}{\mu }^{\kappa -\varphi }.\end{array}$$

 Definition 3.

The Caputo derivative $D^{ß}$ of the fractional order ß is given by [41,42]

$${}^C{D}^{ß}\theta \left(\mu \right)=\left\{\begin{array}{c}\frac{1}{\Gamma (\kappa -ß)}{\int }_0^{\mu }\frac{{\theta }^{\kappa }\left(\varphi \right)}{{(\mu -\varphi )}^{ß-\kappa +1}}d\varphi ,\kappa -1<ß<\kappa ,\hfill \\ \frac{d^{\kappa }}{d{\mu }^{\kappa }}\theta \left(\mu \right),\kappa =ß.\hfill \end{array}\right.$$

(1)

 Definition 4.

$$\begin{array}{cc}\hfill {\kappa }_{\mu }^{ß}{D}_{\mu }^{ß}\theta \left(\mu \right)& =\theta \left(\mu \right)-\sum _{k=0}^m{\theta }^k\left(0^{+}\right)\frac{{\mu }^k}{k!},for\mu >0,and\kappa -1<ß\le \kappa ,\kappa \in N.\hfill \\ \hfill D_{\mu }^{ß}{\kappa }_{\mu }^{ß}\theta \left(\mu \right)& =\theta \left(\mu \right).\hfill \end{array}$$

(2)

 Definition 5.

The Caputo operator in terms of the Elzaki transform is given by [41,42]

$$\mathit{E}[D_{\mu }^{ß}\theta \left(\mu \right)]=s^{-ß}E\left[\theta \left(\mu \right)\right]-\sum _{k=0}^{\kappa -1}{s}^{2-ß+k}{\theta }^{\left(k\right)}\left(0\right),where\kappa -1<ß<\kappa .$$

3. General Methodology of the HPTM

This section focuses on the core method used by the HPTM to find solutions for the general partial differential equation

$$D_{\vartheta }^{ß}\mathit{V}(\wp ,\vartheta )={\mathcal{P}}_1[\wp ]\mathit{V}(\wp ,\vartheta )+{\mathcal{Q}}_1[\wp ]\mathit{V}(\wp ,\vartheta ),1<ß\le 2,$$

(3)

subjected to the initial conditions

$$\mathit{V}(\wp ,0)=\xi (\wp ),\frac{\partial }{\partial \vartheta }\mathit{V}(\wp ,0)=\zeta (\wp ).$$

Here, $D_{\vartheta }^{ß}=\frac{{\partial }^{ß}}{\partial {\vartheta }^{ß}}$ is the fractional Caputo derivative and ${\mathcal{P}}_1[\wp ]$ and ${\mathcal{Q}}_1[\wp ]$ are the linear and nonlinear operators, respectively.

By utilizing the Elzaki transformation in Equation (3), we achieve

$$\mathit{E}[D_{\vartheta }^{ß}\mathit{V}(\wp ,\vartheta )]=\mathit{E}[{\mathcal{P}}_1[\wp ]\mathit{V}(\wp ,\vartheta )+{\mathcal{Q}}_1[\wp ]\mathit{V}(\wp ,\vartheta )],$$

(4)

$$\frac{1}{u^{ß}}\{\mathit{V}(\wp ,\vartheta )-u\mathit{V}\left(0\right)-u^2{\mathit{V}}^{\prime }\left(0\right)\}=\mathit{E}[{\mathcal{P}}_1[\wp ]\mathit{V}(\wp ,\vartheta )+{\mathcal{Q}}_1[\wp ]\mathit{V}(\wp ,\vartheta )].$$

(5)

After simplifying, the result is obtained:

$$\mathit{V}(\wp ,\vartheta )=u\mathit{V}\left(0\right)+u^2{\mathit{V}}^{\prime }\left(0\right)+u^{ß}\mathit{E}[{\mathcal{P}}_1[\wp ]\mathit{V}(\wp ,\vartheta )+{\mathcal{Q}}_1[\wp ]\mathit{V}(\wp ,\vartheta )].$$

(6)

By applying the inverse Elzaki transform to both sides, we obtain

$$\mathit{V}(\wp ,\vartheta )=\mathit{V}\left(0\right)+{\mathit{V}}^{\prime }\left(0\right)+{\mathit{E}}^{-1}[u^{ß}\mathit{E}[{\mathcal{P}}_1[\wp ]\mathit{V}(\wp ,\vartheta )+{\mathcal{Q}}_1[\wp ]\mathit{V}(\wp ,\vartheta )]].$$

(7)

Now, by using the HPM, we have

$$\mathit{V}(\wp ,\vartheta )=\sum _{k=0}^{\infty }{ϵ}^k{\mathit{V}}_k(\wp ,\vartheta ).$$

(8)

The decomposition of the nonlinear terms can be expressed as follows. With the perturbation parameter $ϵ\in [0,1]$, we have

$${\mathcal{Q}}_1[\wp ]\mathit{V}(\wp ,\vartheta )=\sum _{k=0}^{\infty }{ϵ}^k{H}_n\left(\mathit{V}\right).$$

(9)

He’s polynomials, designated as $H_k\left(\mathit{V}\right)$, are expressed by

$$H_n({\mathit{V}}_0,{\mathit{V}}_1,...,{\mathit{V}}_n)=\frac{1}{\Gamma (n+1)}{D}_{ϵ}^k{\left[{\mathcal{Q}}_1\left(\sum _{k=0}^{\infty }{ϵ}^i{\mathit{V}}_i\right)\right]}_{ϵ=0}.$$

(10)

where $D_{ϵ}^k=\frac{{\partial }^k}{\partial {ϵ}^k}.$

By incorporating the sources in Equations (8) and (9) into Equation (7), we arrive at a conclusion:

$$\sum _{k=0}^{\infty }{ϵ}^k{\mathit{V}}_k(\wp ,\vartheta )=\mathit{V}\left(0\right)+{\mathit{V}}^{\prime }\left(0\right)+ϵ\times \left({\mathit{E}}^{-1}\left[u^{ß}\mathit{E}\{{\mathcal{P}}_1\sum _{k=0}^{\infty }{ϵ}^k{\mathit{V}}_k(\wp ,\vartheta )+\sum _{k=0}^{\infty }{ϵ}^k{H}_k\left(\mathit{V}\right)\}\right]\right).$$

(11)

Upon evaluating the $ϵ$ coefficient, we obtain

$$\begin{array}{cc}\hfill & {ϵ}^0:{\mathit{V}}_0(\wp ,\vartheta )=\mathit{V}\left(0\right)+{\mathit{V}}^{\prime }\left(0\right),\hfill \\ \hfill & {ϵ}^1:{\mathit{V}}_1(\wp ,\vartheta )={\mathit{E}}^{-1}\left[u^{ß}\mathit{E}({\mathcal{P}}_1[\wp ]{\mathit{V}}_0(\wp ,\vartheta )+H_0\left(\mathit{V}\right))\right],\hfill \\ \hfill & {ϵ}^2:{\mathit{V}}_2(\wp ,\vartheta )={\mathit{E}}^{-1}\left[u^{ß}\mathit{E}({\mathcal{P}}_1[\wp ]{\mathit{V}}_1(\wp ,\vartheta )+H_1\left(\mathit{V}\right))\right],\hfill \\ \hfill & ⋮\hfill \\ \hfill & {ϵ}^k:{\mathit{V}}_k(\wp ,\vartheta )={\mathit{E}}^{-1}\left[u^{ß}\mathit{E}({\mathcal{P}}_1[\wp ]{\mathit{V}}_{k-1}(\wp ,\vartheta )+H_{k-1}\left(\mathit{V}\right))\right],k>0,k\in N.\hfill \end{array}$$

(12)

Finally, we employ truncated series to estimate the analytical solution ${\mathit{V}}_k(\wp ,\vartheta )$:

$$\mathit{V}(\wp ,\vartheta )=\underset{M\to \infty }{lim}\sum _{k=1}^M{\mathit{V}}_k(\wp ,\vartheta ).$$

(13)

The solutions to this series tend to reach stability rapidly.

4. General Methodology of the YTDM

This section focuses on the core procedure for resolving partial differential equations of any arbitrary order through the utilization of the ETDM:

$$D_{\vartheta }^{ß}\mathit{V}(\wp ,\vartheta )={\mathcal{P}}_1(\wp ,\vartheta )+{\mathcal{Q}}_1(\wp ,\vartheta ),0<ß\le 1,$$

(14)

subjected to initial conditions

$$\mathit{V}(\wp ,0)=\xi (\wp ),\frac{\partial }{\partial \vartheta }\mathit{V}(\wp ,0)=\zeta (\wp ).$$

By utilizing the Elzaki transformation, it is possible to express the fractional Caputo derivative $D_{\vartheta }^{ß}$ as the fractional derivative with respect to ${\vartheta }^{ß}$. Additionally, ${\mathcal{P}}_1$ and ${\mathcal{Q}}_1$ are linear and nonlinear operators, respectively:

$$\mathit{E}[D_{\vartheta }^{ß}\mathit{V}(\wp ,\vartheta )]=\mathit{E}[{\mathcal{P}}_1(\wp ,\vartheta )+{\mathcal{Q}}_1(\wp ,\vartheta )].$$

(15)

By utilizing the characteristic of the Elzaki transform that distinguishes it, we can deduce that

$$\frac{1}{u^{ß}}\{M\left(u\right)-u\mathit{V}\left(0\right)-u^2{\mathit{V}}^{\prime }\left(0\right)\}=\mathit{E}[{\mathcal{P}}_1(\wp ,\vartheta )+{\mathcal{Q}}_1(\wp ,\vartheta )].$$

(16)

Regarding simplification, we obtain

$$M\left(\mathit{V}\right)=u\mathit{V}\left(0\right)+u^2{\mathit{V}}^{\prime }\left(0\right)+u^{ß}\mathit{E}[{\mathcal{P}}_1(\wp ,\vartheta )+{\mathcal{Q}}_1(\wp ,\vartheta )].$$

(17)

By applying the inverse Elzaki transformation to both sides, we obtain

$$\mathit{V}(\wp ,\vartheta )=\mathit{V}\left(0\right)+{\mathit{V}}^{\prime }\left(0\right)+{\mathit{E}}^{-1}[u^{ß}\mathit{E}[{\mathcal{P}}_1(\wp ,\vartheta )+{\mathcal{Q}}_1(\wp ,\vartheta )].$$

(18)

By utilizing the ETDM, the solution to the infinite series of $\mathit{V}(\wp ,\vartheta )$ is obtained:

$$\mathit{V}(\wp ,\vartheta )=\sum _{m=0}^{\infty }{\mathit{V}}_m(\wp ,\vartheta ).$$

(19)

The Adomian polynomials for nonlinear terms ${\mathcal{Q}}_1$ can be expressed by

$${\mathcal{Q}}_1(\wp ,\vartheta )=\sum _{m=0}^{\infty }{\mathcal{A}}_m.$$

(20)

where

$${\mathcal{A}}_m=\frac{1}{m!}{\left[\frac{{\partial }^m}{\partial {\ell }^m}\left\{{\mathcal{Q}}_1\left(\sum _{k=0}^{\infty }{\ell }^k{\wp }_k,\sum _{k=0}^{\infty }{\ell }^k{\vartheta }_k\right)\right\}\right]}_{\ell =0}.$$

(21)

By combining Equations (21) and (19) into Equation (18), we arrive at a new expression:

$$\sum _{m=0}^{\infty }{\mathit{V}}_m(\wp ,\vartheta )=\mathit{V}\left(0\right)+{\mathit{V}}^{\prime }\left(0\right)+{\mathit{E}}^{-1}{u}^{ß}\left[\mathit{E}\left\{{\mathcal{P}}_1(\sum _{m=0}^{\infty }{\wp }_m,\sum _{m=0}^{\infty }{\vartheta }_m)+\sum _{m=0}^{\infty }{\mathcal{A}}_m\right\}\right].$$

(22)

The following terms will be explained:

$${\mathit{V}}_0(\wp ,\vartheta )=\mathit{V}\left(0\right)+\vartheta {\mathit{V}}^{\prime }\left(0\right),$$

(23)

$${\mathit{V}}_1(\wp ,\vartheta )={\mathit{E}}^{-1}\left[u^{ß}{\mathit{E}}^{+}\{{\mathcal{P}}_1({\wp }_0,{\vartheta }_0)+{\mathcal{A}}_0\}\right].$$

In general, when $m\ge 1$, it can be stated that

$${\mathit{V}}_{m+1}(\wp ,\vartheta )={\mathit{E}}^{-1}\left[u^{ß}{\mathit{E}}^{+}\{{\mathcal{P}}_1({\wp }_m,{\vartheta }_m)+{\mathcal{A}}_m\}\right].$$

5. Applications

 Example 1.

Consider the fractional shock wave equation, given by

$$\frac{{\partial }^{ß}\mathit{V}}{\partial {\vartheta }^{ß}}+\left(\frac{1}{c_0}-\frac{\mathrm{{\rm Y}}+1}{2}\frac{\mathit{V}}{c_0^2}\right)\frac{\partial \mathit{V}}{\partial \wp }=0,0<ß\le 1,$$

(24)

with the initial condition

$$\mathit{V}(\wp ,0)=exp\left(-\frac{{\wp }^2}{2}\right).$$

We utilized the Elzaki transform and set the constant values of $c_0$ to 2 and Υ to 1.5, which correspond to the flow of air:

$$\mathit{E}\left(\frac{{\partial }^{ß}\mathit{V}}{\partial {\vartheta }^{ß}}\right)=-\mathit{E}\left[\left(\frac{1}{c_0}-\frac{\mathrm{{\rm Y}}+1}{2}\frac{\mathit{V}}{c_0^2}\right)\frac{\partial \mathit{V}}{\partial \wp }\right].$$

(25)

By utilizing the differentiation property of the Elzaki transform, it can be shown that

$$\frac{1}{u^{ß}}\{M\left(u\right)-u\mathit{V}\left(0\right)\}=-\mathit{E}\left[\left(\frac{1}{c_0}-\frac{\mathrm{{\rm Y}}+1}{2}\frac{\mathit{V}}{c_0^2}\right)\frac{\partial \mathit{V}}{\partial \wp }\right],$$

(26)

$$M\left(u\right)=u\mathit{V}\left(0\right)-u^{ß}\mathit{E}\left[\left(\frac{1}{c_0}-\frac{\mathrm{{\rm Y}}+1}{2}\frac{\mathit{V}}{c_0^2}\right)\frac{\partial \mathit{V}}{\partial \wp }\right].$$

(27)

Using the inverse Elzaki transformation, we obtain

$$\begin{array}{cc}\hfill & \mathit{V}(\wp ,\vartheta )=\mathit{V}\left(0\right)-{\mathit{E}}^{-1}\left[u^{ß}\left\{\mathit{E}\left[\left(\frac{1}{c_0}-\frac{\mathrm{{\rm Y}}+1}{2}\frac{\mathit{V}}{c_0^2}\right)\frac{\partial \mathit{V}}{\partial \wp }\right]\right\}\right],\hfill \\ \hfill & \mathit{V}(\wp ,\vartheta )=exp\left(-\frac{{\wp }^2}{2}\right)-{\mathit{E}}^{-1}\left[u^{ß}\left\{\mathit{E}\left[\left(\frac{1}{c_0}-\frac{\mathrm{{\rm Y}}+1}{2}\frac{\mathit{V}}{c_0^2}\right)\frac{\partial \mathit{V}}{\partial \wp }\right]\right\}\right].\hfill \end{array}$$

(28)

Now, by applying the HPM, we achieve

$$\sum _{k=0}^{\infty }{ϵ}^k{\mathit{V}}_k(\wp ,\vartheta )=\gamma +ϵ\left({\mathit{E}}^{-1}\left[u^{ß}\mathit{E}\left[\frac{1}{c_0}\frac{\partial \mathit{V}}{\partial \wp }\left(\sum _{k=0}^{\infty }{ϵ}^k{\mathit{V}}_k(\wp ,\vartheta )\right)-\frac{\mathrm{{\rm Y}}+1}{2}\frac{1}{c_0^2}\left(\sum _{k=0}^{\infty }{ϵ}^k{H}_k\left(\mathit{V}\right)\right)\right]\right]\right).$$

(29)

where the nonlinear terms shown by He’s polynomial $H_k\left(\mathit{V}\right)$, represented by

$$\sum _{k=0}^{\infty }{ϵ}^k{H}_k\left(\mathit{V}\right)=\mathit{V}\frac{\partial \mathit{V}}{\partial \wp }.$$

(30)

A few components of He’s polynomial are determined as follows:

$$H_0\left(\mathit{V}\right)={\mathit{V}}_0\frac{\partial {\mathit{V}}_0}{\partial \wp },H_1\left(\mathit{V}\right)={\mathit{V}}_0\frac{\partial {\mathit{V}}_1}{\partial \wp }+{\mathit{V}}_1\frac{\partial {\mathit{V}}_0}{\partial \wp }$$

By comparing both sides’ coefficients of ϵ, we achieve

$$\begin{array}{cc}\hfill & {ϵ}^0:{\mathit{V}}_0(\wp ,\vartheta )=exp\left(-\frac{{\wp }^2}{2}\right),\hfill \\ \hfill & {ϵ}^1:{\mathit{V}}_1(\wp ,\vartheta )={\mathit{E}}^{-1}\left(u^{ß}\mathit{E}\left[\frac{1}{c_0}\frac{\partial {\mathit{V}}_0}{\partial \wp }-\frac{\mathrm{{\rm Y}}+1}{2}\frac{1}{c_0^2}{H}_0\left(\mathit{V}\right)\right]\right)=-\left[\frac{1}{c_0}-\frac{\mathrm{{\rm Y}}+1}{2c_0^2}exp\left(-\frac{{\wp }^2}{2}\right)\right]\wp exp\left(-\frac{{\wp }^2}{2}\right)\frac{{\vartheta }^{ß}}{\Gamma (ß+1)},\hfill \\ \hfill & {ϵ}^2:{\mathit{V}}_2(\wp ,\vartheta )={\mathit{E}}^{-1}\left(u^{ß}\mathit{E}\left[\frac{1}{c_0}\frac{\partial {\mathit{V}}_1}{\partial \wp }-\frac{\mathrm{{\rm Y}}+1}{2}\frac{1}{c_0^2}{H}_1\left(\mathit{V}\right)\right]\right)=exp\left(-\frac{{\wp }^2}{2}\right)[-\frac{1}{c_0^2}+\frac{{\wp }^2}{c_0^2}-\frac{\mathrm{{\rm Y}}+1}{c_0^3}exp\left(-\frac{{\wp }^2}{2}\right)\hfill \\ \hfill & -\frac{2(\mathrm{{\rm Y}}+1)}{c_0^3}{\wp }^{2}exp\left(-\frac{{\wp }^2}{2}\right)-\frac{{(\mathrm{{\rm Y}}+1)}^2}{4c_0^4}exp(-{\wp }^2)+\frac{3{(\mathrm{{\rm Y}}+1)}^2}{4c_0^4}{\wp }^{2}exp(-{\wp }^2)]\frac{{\vartheta }^{2ß}}{\Gamma (2ß+1)},\hfill \\ \hfill ⋮\end{array}$$

Some element of the HPTM result can be obtained:

$$\begin{array}{cc}\hfill & \mathit{V}(\wp ,\vartheta )=exp\left(-\frac{{\wp }^2}{2}\right)-\left[\frac{1}{c_0}-\frac{\mathrm{{\rm Y}}+1}{2c_0^2}exp\left(-\frac{{\wp }^2}{2}\right)\right]\wp exp\left(-\frac{{\wp }^2}{2}\right)\frac{{\vartheta }^{ß}}{\Gamma (ß+1)}+exp\left(-\frac{{\wp }^2}{2}\right)\hfill \\ \hfill & [-\frac{1}{c_0^2}+\frac{{\wp }^2}{c_0^2}-\frac{\mathrm{{\rm Y}}+1}{c_0^3}exp\left(-\frac{{\wp }^2}{2}\right)-\frac{2(\mathrm{{\rm Y}}+1)}{c_0^3}{\wp }^{2}exp\left(-\frac{{\wp }^2}{2}\right)-\frac{{(\mathrm{{\rm Y}}+1)}^2}{4c_0^4}exp(-{\wp }^2)+\hfill \\ \hfill & \frac{3{(\mathrm{{\rm Y}}+1)}^2}{4c_0^4}{\wp }^{2}exp(-{\wp }^2)]\frac{{\vartheta }^{2ß}}{\Gamma (2ß+1)}+\cdots .\hfill \end{array}$$

Now, We Use the ETDM

The Elzaki decomposition method is a mathematical technique used to decompose a given function into a set of simpler functions. The Elzaki decomposition method involves expressing the original function as a sum of the auxiliary functions, each of which satisfies a simpler differential equation. The auxiliary functions used in the Elzaki decomposition method are chosen so that they form a complete set, meaning that any function can be expressed as a linear combination of these functions. Once the auxiliary functions have been determined, the coefficients of the linear combination can be found by applying the boundary conditions or initial conditions to the original function.

By applying the Elzaki transformation in Equation (24), we obtain

$$\mathit{E}\left\{\frac{{\partial }^{ß}\mathit{V}}{\partial {\vartheta }^{ß}}\right\}=-\mathit{E}\left[\left(\frac{1}{c_0}-\frac{\mathrm{{\rm Y}}+1}{2}\frac{\mathit{V}}{c_0^2}\right)\frac{\partial \mathit{V}}{\partial \wp }\right].$$

(31)

By applying the Elzaki transformation differentiation property, we have

$$\frac{1}{u^{ß}}\{M\left(u\right)-u\mathit{V}\left(0\right)\}=-\mathit{E}\left[\left(\frac{1}{c_0}-\frac{\mathrm{{\rm Y}}+1}{2}\frac{\mathit{V}}{c_0^2}\right)\frac{\partial \mathit{V}}{\partial \wp }\right],$$

(32)

$$M\left(u\right)=u\mathit{V}\left(0\right)+u^{ß}\mathit{E}\left[\left(\frac{1}{c_0}-\frac{\mathrm{{\rm Y}}+1}{2}\frac{\mathit{V}}{c_0^2}\right)\frac{\partial \mathit{V}}{\partial \wp }\right].$$

(33)

By applying the inverse Elzaki transformation, we achieve

$$\begin{array}{cc}\hfill & \mathit{V}(\wp ,\vartheta )=\mathit{V}\left(0\right)-{\mathit{E}}^{-1}\left[u^{ß}\left\{\mathit{E}\left[\left(\frac{1}{c_0}-\frac{\mathrm{{\rm Y}}+1}{2}\frac{\mathit{V}}{c_0^2}\right)\frac{\partial \mathit{V}}{\partial \wp }\right]\right\}\right],\hfill \\ \hfill & \mathit{V}(\wp ,\vartheta )=exp\left(-\frac{{\wp }^2}{2}\right)-{\mathit{E}}^{-1}\left[u^{ß}\left\{\mathit{E}\left[\left(\frac{1}{c_0}-\frac{\mathrm{{\rm Y}}+1}{2}\frac{\mathit{V}}{c_0^2}\right)\frac{\partial \mathit{V}}{\partial \wp }\right]\right\}\right].\hfill \end{array}$$

(34)

The series form solution of $\mathit{V}(\wp ,\vartheta )$ is given by

$$\mathit{V}(\wp ,\vartheta )=\sum _{m=0}^{\infty }{\mathit{V}}_m(\wp ,\vartheta ).$$

(35)

The nonlinear functions found with the help of the Adomian polynomials of $\mathit{V}\frac{\partial \mathit{V}}{\partial \wp }={\sum }_{m=0}^{\infty }{\mathcal{A}}_m$ are given by

$$\begin{array}{cc}\hfill & \sum _{m=0}^{\infty }{\mathit{V}}_m(\wp ,\vartheta )=\mathit{V}(\wp ,0)-{\mathit{E}}^{-1}\left[u^{ß}\left\{\mathit{E}\left[\left(\frac{1}{c_0}\frac{\partial \mathit{V}}{\partial \wp }-\frac{\mathrm{{\rm Y}}+1}{2c_0^2}\sum _{m=0}^{\infty }{\mathcal{A}}_m\right)\right]\right\}\right],\hfill \\ \hfill & \sum _{m=0}^{\infty }{\mathit{V}}_m(\wp ,\vartheta )=exp\left(-\frac{{\wp }^2}{2}\right)-{\mathit{E}}^{-1}\left[u^{ß}\left\{\mathit{E}\left[\left(\frac{1}{c_0}\frac{\partial \mathit{V}}{\partial \wp }-\frac{\mathrm{{\rm Y}}+1}{2c_0^2}\sum _{m=0}^{\infty }{\mathcal{A}}_m\right)\right]\right\}\right].\hfill \end{array}$$

(36)

In same technique, the nonlinear terms are expressed as follows:

$${\mathcal{A}}_0={\mathit{V}}_0\frac{\partial {\mathit{V}}_0}{\partial \wp },{\mathcal{A}}_1={\mathit{V}}_0\frac{\partial {\mathit{V}}_1}{\partial \wp }+{\mathit{V}}_1\frac{\partial {\mathit{V}}_0}{\partial \wp }.$$

When comparing both sides, we obtain

$${\mathit{V}}_0(\wp ,\vartheta )=exp\left(-\frac{{\wp }^2}{2}\right),$$

For $m=0$, we have

$${\mathit{V}}_1(\wp ,\vartheta )=-\left[\frac{1}{c_0}-\frac{\mathrm{{\rm Y}}+1}{2c_0^2}exp\left(-\frac{{\wp }^2}{2}\right)\right]\wp exp\left(-\frac{{\wp }^2}{2}\right)\frac{{\vartheta }^{ß}}{\Gamma (ß+1)}.$$

For $m=1$, we have

$$\begin{array}{cc}\hfill & {\mathit{V}}_2(\wp ,\vartheta )=exp\left(-\frac{{\wp }^2}{2}\right)[-\frac{1}{c_0^2}+\frac{{\wp }^2}{c_0^2}-\frac{\mathrm{{\rm Y}}+1}{c_0^3}exp\left(-\frac{{\wp }^2}{2}\right)-\frac{2(\mathrm{{\rm Y}}+1)}{c_0^3}{\wp }^{2}exp\left(-\frac{{\wp }^2}{2}\right)-\hfill \\ \hfill & \frac{{(\mathrm{{\rm Y}}+1)}^2}{4c_0^4}exp(-{\wp }^2)+\frac{3{(\mathrm{{\rm Y}}+1)}^2}{4c_0^4}{\wp }^{2}exp(-{\wp }^2)]\frac{{\vartheta }^{2ß}}{\Gamma (2ß+1)}.\hfill \end{array}$$

The remaining steps of ${ß}_m$ for the ETDM for $(m\ge 2)$ are simple to obtain. Hence, we write the series type result as follows:

$$\mathit{V}(\wp ,\vartheta )=\sum _{m=0}^{\infty }{\mathit{V}}_m(\wp ,\vartheta )={\mathit{V}}_0(\wp ,\vartheta )+{\mathit{V}}_1(\wp ,\vartheta )+{\mathit{V}}_2(\wp ,\vartheta )+\cdots .$$

$$\begin{array}{cc}\hfill & \mathit{V}(\wp ,\vartheta )=exp\left(-\frac{{\wp }^2}{2}\right)-\left[\frac{1}{c_0}-\frac{\mathrm{{\rm Y}}+1}{2c_0^2}exp\left(-\frac{{\wp }^2}{2}\right)\right]\wp exp\left(-\frac{{\wp }^2}{2}\right)\frac{{\vartheta }^{ß}}{\Gamma (ß+1)}+exp\left(-\frac{{\wp }^2}{2}\right)\hfill \\ \hfill & [-\frac{1}{c_0^2}+\frac{{\wp }^2}{c_0^2}-\frac{\mathrm{{\rm Y}}+1}{c_0^3}exp\left(-\frac{{\wp }^2}{2}\right)-\frac{2(\mathrm{{\rm Y}}+1)}{c_0^3}{\wp }^{2}exp\left(-\frac{{\wp }^2}{2}\right)-\frac{{(\mathrm{{\rm Y}}+1)}^2}{4c_0^4}exp(-{\wp }^2)+\hfill \\ \hfill & \frac{3{(\mathrm{{\rm Y}}+1)}^2}{4c_0^4}{\wp }^{2}exp(-{\wp }^2)]\frac{{\vartheta }^{2ß}}{\Gamma (2ß+1)}+\cdots .\hfill \end{array}$$

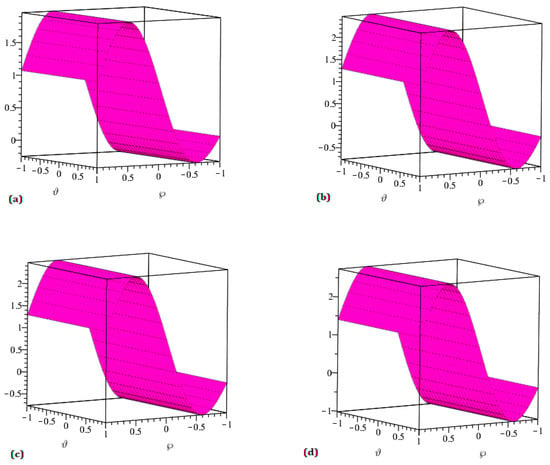
In Figure 1, The solutions for the $\mathit{V}(\wp ,\vartheta )$ surface with regard to ℘ and ϑ are explored for various values of ß. (a) The surface solution of the function $\mathit{V}(\wp ,\vartheta )$ at the value of $ß=0.25$, (b) $ß=0.50$, (c) $ß=0.75$, and (d) $ß=1$. Each of these solutions provides insight into how the surface of $\mathit{V}(\wp ,\vartheta )$ changes as the value of ß is altered.

Figure 1. The solutions for the $\mathit{V}(\wp ,\vartheta )$ surface with regard to ℘ and $\vartheta$ are explored for various values of ß. (a) The surface solution of the function $\mathit{V}(\wp ,\vartheta )$ at the value of $ß=0.25$, (b) $ß=0.50$, (c) $ß=0.75$, and (d) $ß=1$. Each of these solutions provides insight into how the surface of $\mathit{V}(\wp ,\vartheta )$ changes as the value of ß is altered.

Example

Consider the fractional shock wave equation, given by

$$\frac{{\partial }^{ß}\mathit{V}}{\partial {\vartheta }^{ß}}+\mathit{V}\frac{\partial \mathit{V}}{\partial \wp }-\frac{\partial }{\partial \vartheta }\frac{\partial {\mathit{V}}^2}{\partial {\wp }^2}=0,0<ß\le 1,$$

(37)

with the initial condition

$$\mathit{V}(\wp ,0)=3{\sec \mathrm{h}}^2\left(\frac{\wp -15}{2}\right).$$

By using the Elzaki transformation, we obtain

$$\mathit{E}\left(\frac{{\partial }^{ß}\mathit{V}}{\partial {\vartheta }^{ß}}\right)=\mathit{E}\left(\frac{\partial }{\partial \vartheta }\frac{\partial {\mathit{V}}^2}{\partial {\wp }^2}-\mathit{V}\frac{\partial \mathit{V}}{\partial \wp }\right).$$

(38)

By applying the Elzaki transformation differentiation property, we obtain

$$\frac{1}{u^{ß}}\{M\left(u\right)-u\mathit{V}\left(0\right)\}=\mathit{E}\left(\frac{\partial }{\partial \vartheta }\frac{\partial {\mathit{V}}^2}{\partial {\wp }^2}-\mathit{V}\frac{\partial \mathit{V}}{\partial \wp }\right),$$

(39)

$$M\left(u\right)=u\mathit{V}\left(0\right)+u^{ß}\mathit{E}\left(\frac{\partial }{\partial \vartheta }\frac{\partial {\mathit{V}}^2}{\partial {\wp }^2}-\mathit{V}\frac{\partial \mathit{V}}{\partial \wp }\right).$$

(40)

By performing the inverse Elzaki transformation, we obtain

$$\begin{array}{cc}\hfill & \mathit{V}(\wp ,\vartheta )=\mathit{V}\left(0\right)+{\mathit{E}}^{-1}\left[u^{ß}\left\{\mathit{E}\frac{\partial }{\partial \vartheta }\frac{\partial {\mathit{V}}^2}{\partial {\wp }^2}-\mathit{V}\frac{\partial \mathit{V}}{\partial \wp }\right\}\right],\hfill \\ \hfill & \mathit{V}(\wp ,\vartheta )=3{\sec \mathrm{h}}^2\left(\frac{\wp -15}{2}\right)+{\mathit{E}}^{-1}\left[u^{ß}\left\{\mathit{E}\left(\frac{\partial }{\partial \vartheta }\frac{\partial {\mathit{V}}^2}{\partial {\wp }^2}-\mathit{V}\frac{\partial \mathit{V}}{\partial \wp }\right)\right\}\right].\hfill \end{array}$$

(41)

Using the HPM, we now gain access to

$$\sum _{k=0}^{\infty }{ϵ}^k{\mathit{V}}_k(\wp ,\vartheta )=3{\sec \mathrm{h}}^2\left(\frac{\wp -15}{2}\right)+ϵ\left({\mathit{E}}^{-1}\left[u^{ß}\mathit{E}\left[{\left(\sum _{k=0}^{\infty }{ϵ}^k{\mathit{V}}_k(\wp ,\vartheta )\right)}_{\wp \wp \vartheta }-\left(\sum _{k=0}^{\infty }{ϵ}^k{H}_k\left(\mathit{V}\right)\right)\right]\right]\right).$$

(42)

In the representation of nonlinear terms, He’s polynomial $H_k\left(\mathit{V}\right)$ is used. This equation states that the nonlinear terms can be expressed through He’s polynomial:

$$\sum _{k=0}^{\infty }{ϵ}^k{H}_k\left(\mathit{V}\right)=\mathit{V}\frac{\partial \mathit{V}}{\partial \wp }.$$

(43)

The calculation of certain components of He’s polynomials can be performed as follows:

$$H_0\left(\mathit{V}\right)={\mathit{V}}_0\frac{\partial {\mathit{V}}_0}{\partial \wp },H_1\left(\mathit{V}\right)={\mathit{V}}_0\frac{\partial {\mathit{V}}_1}{\partial \wp }+{\mathit{V}}_1\frac{\partial {\mathit{V}}_0}{\partial \wp }.$$

By comparing the value of the $ϵ$ coefficient, we are able to deduce the following:

$$\begin{array}{cc}\hfill & {ϵ}^0:{\mathit{V}}_0(\wp ,\vartheta )=3{\sec \mathrm{h}}^2\left(\frac{\wp -15}{2}\right),\hfill \\ \hfill & {ϵ}^1:{\mathit{V}}_1(\wp ,\vartheta )={\mathit{E}}^{-1}\left(u^{ß}\mathit{E}\left[\frac{\partial }{\partial \vartheta }\frac{\partial {\mathit{V}}_0^2}{\partial {\wp }^2}-H_0\left(\mathit{V}\right)\right]\right)=9{\sec \mathrm{h}}^4\left(\frac{\wp -15}{2}\right)tanh\left(\frac{\wp -15}{2}\right)\frac{{\vartheta }^{ß}}{\Gamma (ß+1)},\hfill \\ \hfill & {ϵ}^2:{\mathit{V}}_2(\wp ,\vartheta )={\mathit{E}}^{-1}\left(u^{ß}\mathit{E}\left[\frac{\partial }{\partial \vartheta }\frac{\partial {\mathit{V}}_1^2}{\partial {\wp }^2}-H_1\left(\mathit{V}\right)\right]\right)=[\frac{189}{2}{\sec \mathrm{h}}^6\left(\frac{\wp -15}{2}\right){tanh}^2\left(\frac{\wp -15}{2}\right)-\frac{27}{2}\hfill \\ \hfill & {\sec \mathrm{h}}^6\left(\frac{\wp -15}{2}\right)]\frac{{\vartheta }^{2ß}}{\Gamma (2ß+1)}+\left[\frac{135}{2}{\sec \mathrm{h}}^4\left(\frac{\wp -15}{2}\right){tanh}^3\left(\frac{\wp -15}{2}\right)-\frac{63}{2}{\sec \mathrm{h}}^4\left(\frac{\wp -15}{2}tanh\left(\frac{\wp -15}{2}\right)\right)\right]\hfill \\ \hfill & \frac{\Gamma (ß+1){\vartheta }^{2ß-1}}{\Gamma (2ß)},\hfill \\ \hfill & ⋮\hfill \end{array}$$

To fully implement the HPTM solution, we need to persist in our approach:

$$\begin{array}{cc}\hfill & \mathit{V}(\wp ,\vartheta )=3{\sec \mathrm{h}}^2\left(\frac{\wp -15}{2}\right)+9{\sec \mathrm{h}}^4\left(\frac{\wp -15}{2}\right)tanh\left(\frac{\wp -15}{2}\right)\frac{{\vartheta }^{ß}}{\Gamma (ß+1)}+[\frac{189}{2}{\sec \mathrm{h}}^6\left(\frac{\wp -15}{2}\right)\hfill \\ \hfill & {tanh}^2\left(\frac{\wp -15}{2}\right)-\frac{27}{2}{\sec \mathrm{h}}^6\left(\frac{\wp -15}{2}\right)]\frac{{\vartheta }^{2ß}}{\Gamma (2ß+1)}+[\frac{135}{2}{\sec \mathrm{h}}^4\left(\frac{\wp -15}{2}\right){tanh}^3\left(\frac{\wp -15}{2}\right)-\hfill \\ \hfill & \frac{63}{2}{\sec \mathrm{h}}^4\left(\frac{\wp -15}{2}tanh\left(\frac{\wp -15}{2}\right)\right)]\frac{\Gamma (ß+1){\vartheta }^{2ß-1}}{\Gamma (2ß)}+\cdots .\hfill \end{array}$$

Now, We Use the ETDM

By utilizing the Elzaki transformation method, we obtain

$$\mathit{E}\left\{\frac{{\partial }^{ß}\mathit{V}}{\partial {\vartheta }^{ß}}\right\}=\mathit{E}\left(\frac{\partial }{\partial \vartheta }\frac{\partial {\mathit{V}}^2}{\partial {\wp }^2}-\mathit{V}\frac{\partial \mathit{V}}{\partial \wp }\right).$$

(44)

By utilizing the differentiation property of the Elzaki transform, it is possible to obtain

$$\frac{1}{u^{ß}}\{M\left(u\right)-u\mathit{V}\left(0\right)\}=\mathit{E}\left(\frac{\partial }{\partial \vartheta }\frac{\partial {\mathit{V}}^2}{\partial {\wp }^2}-\mathit{V}\frac{\partial \mathit{V}}{\partial \wp }\right),$$

(45)

$$M\left(u\right)=u\mathit{V}\left(0\right)+u^{ß}\mathit{E}\left(\frac{\partial }{\partial \vartheta }\frac{\partial {\mathit{V}}^2}{\partial {\wp }^2}-\mathit{V}\frac{\partial \mathit{V}}{\partial \wp }\right).$$

(46)

By applying the inverse Elzaki transform to both sides, we obtain

$$\begin{array}{cc}\hfill & \mathit{V}(\wp ,\vartheta )=\mathit{V}\left(0\right)+{\mathit{E}}^{-1}\left[u^{ß}\left\{\mathit{E}\left(\frac{\partial }{\partial \vartheta }\frac{\partial {\mathit{V}}^2}{\partial {\wp }^2}-\mathit{V}\frac{\partial \mathit{V}}{\partial \wp }\right)\right\}\right],\hfill \\ \hfill & \mathit{V}(\wp ,\vartheta )=\frac{1}{{(1+{exp}^{\wp })}^2}+{\mathit{E}}^{-1}\left[u^{ß}\left\{\mathit{E}\left(\frac{\partial }{\partial \vartheta }\frac{\partial {\mathit{V}}^2}{\partial {\wp }^2}-\mathit{V}\frac{\partial \mathit{V}}{\partial \wp }\right)\right\}\right].\hfill \end{array}$$

(47)

With the use of the ETDM, an infinite series solution for $\mathit{V}(\wp ,\vartheta )$ can be obtained:

$$\mathit{V}(\wp ,\vartheta )=\sum _{m=0}^{\infty }{\mathit{V}}_m(\wp ,\vartheta ).$$

(48)

Using the Adomian polynomials, the nonlinear terms are obtained through $\mathit{V}\frac{\partial \mathit{V}}{\partial \wp }={\sum }_{m=0}^{\infty }{\mathcal{A}}_m$:

$$\begin{array}{cc}\hfill & \sum _{m=0}^{\infty }{\mathit{V}}_m(\wp ,\vartheta )=\mathit{V}(\wp ,0)+{\mathit{E}}^{-1}\left[u^{ß}\mathit{E}\left[\frac{\partial }{\partial \vartheta }\frac{\partial {\mathit{V}}^2}{\partial {\wp }^2}-\sum _{m=0}^{\infty }{\mathcal{A}}_m\right]\right],\hfill \\ \hfill & \sum _{m=0}^{\infty }{\mathit{V}}_m(\wp ,\vartheta )=\frac{1}{{(1+{exp}^{\wp })}^2}+{\mathit{E}}^{-1}\left[u^{ß}\mathit{E}\left[\frac{\partial }{\partial \vartheta }\frac{\partial {\mathit{V}}^2}{\partial {\wp }^2}-\sum _{m=0}^{\infty }{\mathcal{A}}_m\right]\right].\hfill \end{array}$$

(49)

The nonlinear terms are determined as follows:

$${\mathcal{A}}_0={\mathit{V}}_0\frac{\partial {\mathit{V}}_0}{\partial \wp },{\mathcal{A}}_1={\mathit{V}}_0\frac{\partial {\mathit{V}}_1}{\partial \wp }+{\mathit{V}}_1\frac{\partial {\mathit{V}}_0}{\partial \wp }.$$

When comparing both sides, we obtain

$${\mathit{V}}_0(\wp ,\vartheta )=3{\sec \mathrm{h}}^2\left(\frac{\wp -15}{2}\right),$$

For $m=0$, we have

$${\mathit{V}}_1(\wp ,\vartheta )=9{\sec \mathrm{h}}^4\left(\frac{\wp -15}{2}\right)tanh\left(\frac{\wp -15}{2}\right)\frac{{\vartheta }^{ß}}{\Gamma (ß+1)}.$$

For $m=1$, we have

$$\begin{array}{cc}\hfill & {\mathit{V}}_2(\wp ,\vartheta )=\left[\frac{189}{2}{\sec \mathrm{h}}^6\left(\frac{\wp -15}{2}\right){tanh}^2\left(\frac{\wp -15}{2}\right)-\frac{27}{2}{\sec \mathrm{h}}^6\left(\frac{\wp -15}{2}\right)\right]\frac{{\vartheta }^{2ß}}{\Gamma (2ß+1)}+[\frac{135}{2}{\sec \mathrm{h}}^4\left(\frac{\wp -15}{2}\right)\hfill \\ \hfill & {tanh}^3\left(\frac{\wp -15}{2}\right)-\frac{63}{2}{\sec \mathrm{h}}^4\left(\frac{\wp -15}{2}tanh\left(\frac{\wp -15}{2}\right)\right)]\frac{\Gamma (ß+1){\vartheta }^{2ß-1}}{\Gamma (2ß)}.\hfill \end{array}$$

As a result, finding the remaining elements ${ß}_m$ of the ETDM for values of $m\ge 3$ is straightforward. Therefore, we can express the solution in series form:

$$\mathit{V}(\wp ,\vartheta )=\sum _{m=0}^{\infty }{\mathit{V}}_m(\wp ,\vartheta )={\mathit{V}}_0(\wp ,\vartheta )+{\mathit{V}}_1(\wp ,\vartheta )+\cdots$$

$$\begin{array}{cc}\hfill & \mathit{V}(\wp ,\vartheta )=3{\sec \mathrm{h}}^2\left(\frac{\wp -15}{2}\right)+9{\sec \mathrm{h}}^4\left(\frac{\wp -15}{2}\right)tanh\left(\frac{\wp -15}{2}\right)\frac{{\vartheta }^{ß}}{\Gamma (ß+1)}+[\frac{189}{2}{\sec \mathrm{h}}^6\left(\frac{\wp -15}{2}\right)\hfill \\ \hfill & {tanh}^2\left(\frac{\wp -15}{2}\right)-\frac{27}{2}{\sec \mathrm{h}}^6\left(\frac{\wp -15}{2}\right)]\frac{{\vartheta }^{2ß}}{\Gamma (2ß+1)}+[\frac{135}{2}{\sec \mathrm{h}}^4\left(\frac{\wp -15}{2}\right){tanh}^3\left(\frac{\wp -15}{2}\right)-\hfill \\ \hfill & \frac{63}{2}{\sec \mathrm{h}}^4\left(\frac{\wp -15}{2}tanh\left(\frac{\wp -15}{2}\right)\right)]\frac{\Gamma (ß+1){\vartheta }^{2ß-1}}{\Gamma (2ß)}+\cdots .\hfill \end{array}$$

At $ß=1$, we find as the closed type the exact result:

$$\mathit{V}(\wp ,\vartheta )=3{\sec \mathrm{h}}^2\left(\frac{\wp -15-\vartheta }{2}\right).$$

(50)

In Figure 2, The solutions for the $\mathit{V}(\wp ,\vartheta )$ surface with regard to ℘ and $\vartheta$ are explored for various values of ß. (a) The surface solution of the function $\mathit{V}(\wp ,\vartheta )$ at the values of $ß=0.25$, (b) $ß=0.50$, (c) $ß=0.75$, and (d) $ß=1$. In Table 1, the exact ETDM and HPTM results of $\mathit{V}(\wp ,\vartheta )$ for problem 1 at various fractional orders of ß having different values of ℘ and $\vartheta$.

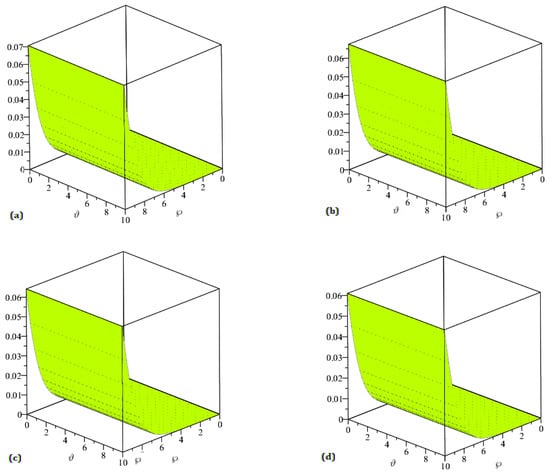
Figure 2. The solutions for the $\mathit{V}(\wp ,\vartheta )$ surface with regard to ℘ and $\vartheta$ are explored for various values of ß. (a) The surface solution of the function $\mathit{V}(\wp ,\vartheta )$ at the values of $ß=0.25$, (b) $ß=0.50$, (c) $ß=0.75$, and (d) $ß=1$.

Table 1. The exact $ETDM$ and $HPTM$ results of $\mathit{V}(\wp ,\vartheta )$ for problem 1 at various fractional orders of ß having different values of ℘ and $\vartheta$.

$\mathit{\vartheta }$	℘	$ß=0.6$	$ß=0.8$	$ß=1\left(\mathit{Approx}\right)$	$ß=1\left(\mathit{Approx}\right)$	$ß=1\left(\mathit{Exact}\right)$
	0.2	0.000004490	0.000004487	0.000004483	0.000004483	0.000004479
	0.4	0.000005481	0.000005479	0.000005476	0.000005476	0.000005470
0.01	0.6	0.000006693	0.000006691	0.000006688	0.000006688	0.000006681
	0.8	0.000008171	0.000008171	0.000008169	0.000008169	0.000008161
	1	0.000009982	0.000009980	0.000009978	0.000009978	0.000009968
	0.2	0.000004490	0.000004487	0.000004483	0.000004483	0.000004474
	0.4	0.000005482	0.000005478	0.000005476	0.000005476	0.000005465
0.02	0.6	0.000006693	0.000006690	0.000006688	0.000006688	0.000006675
	0.8	0.000008177	0.000008172	0.000008169	0.000008169	0.000008153
	1	0.000009987	0.000009982	0.000009978	0.000009978	0.000009958
	0.2	0.000004489	0.000004485	0.000004483	0.000004483	0.000004470
	0.4	0.000005489	0.00000583	0.000005476	0.000005476	0.000005459
0.03	0.6	0.000006693	0.000006690	0.000006688	0.000006688	0.000006668
	0.8	0.000008179	0.000008174	0.000008169	0.000008169	0.000008145
	1	0.000009989	0.000009982	0.000009978	0.000009978	0.000009948
	0.2	0.000004492	0.000004487	0.000004483	0.000004483	0.000004465
	0.4	0.000005487	0.000005481	0.000005476	0.000005476	0.000005454
0.04	0.6	0.000006699	0.000006691	0.000006688	0.000006688	0.000006661
	0.8	0.000008183	0.000008177	0.000008169	0.000008169	0.000008136
	1	0.000009999	0.000009983	0.000009978	0.000009978	0.000009938
	0.2	0.000004497	0.000004489	0.000004483	0.000004483	0.000004461
	0.4	0.000005490	0.000005479	0.000005476	0.000005476	0.000005448
0.05	0.6	0.000006697	0.000006691	0.000006688	0.000006688	0.000006655
	0.8	0.000008191	0.000008185	0.000008169	0.000008169	0.000008128
	1	0.000009997	0.000009988	0.000009978	0.000009978	0.000009928

6. Conclusions

In this study, an effective solution approach is presented for solving nonlinear fractional shock wave equations. The proposed method combines the Elzaki transform, homotopy perturbation method, and Adomian decomposition method. The Elzaki transform is employed to convert the nonlinear fractional shock wave equation into an equivalent integral equation. Then, the homotopy perturbation method and Adomian decomposition method are used to approximate the solution of the integral equation. Numerical examples were included to demonstrate the effectiveness of the proposed approach, and the obtained results were compared with those obtained by other existing methods. The findings reveal that the combined method yielded accurate and efficient solutions for nonlinear fractional shock wave equations. In summary, the proposed approach can be a promising technique for solving nonlinear fractional shock wave equations and can be used in various scientific and engineering applications.