Structural Topology Optimization with Local Finite-Life Fatigue Constraints
Abstract
1. Introduction
2. Optimization Model
2.1. Fatigue Failure Analysis
2.2. Fatigue Constraint
2.3. Sensitivity Analysis
3. Augmented Lagrangian Method
4. Results and Discussion
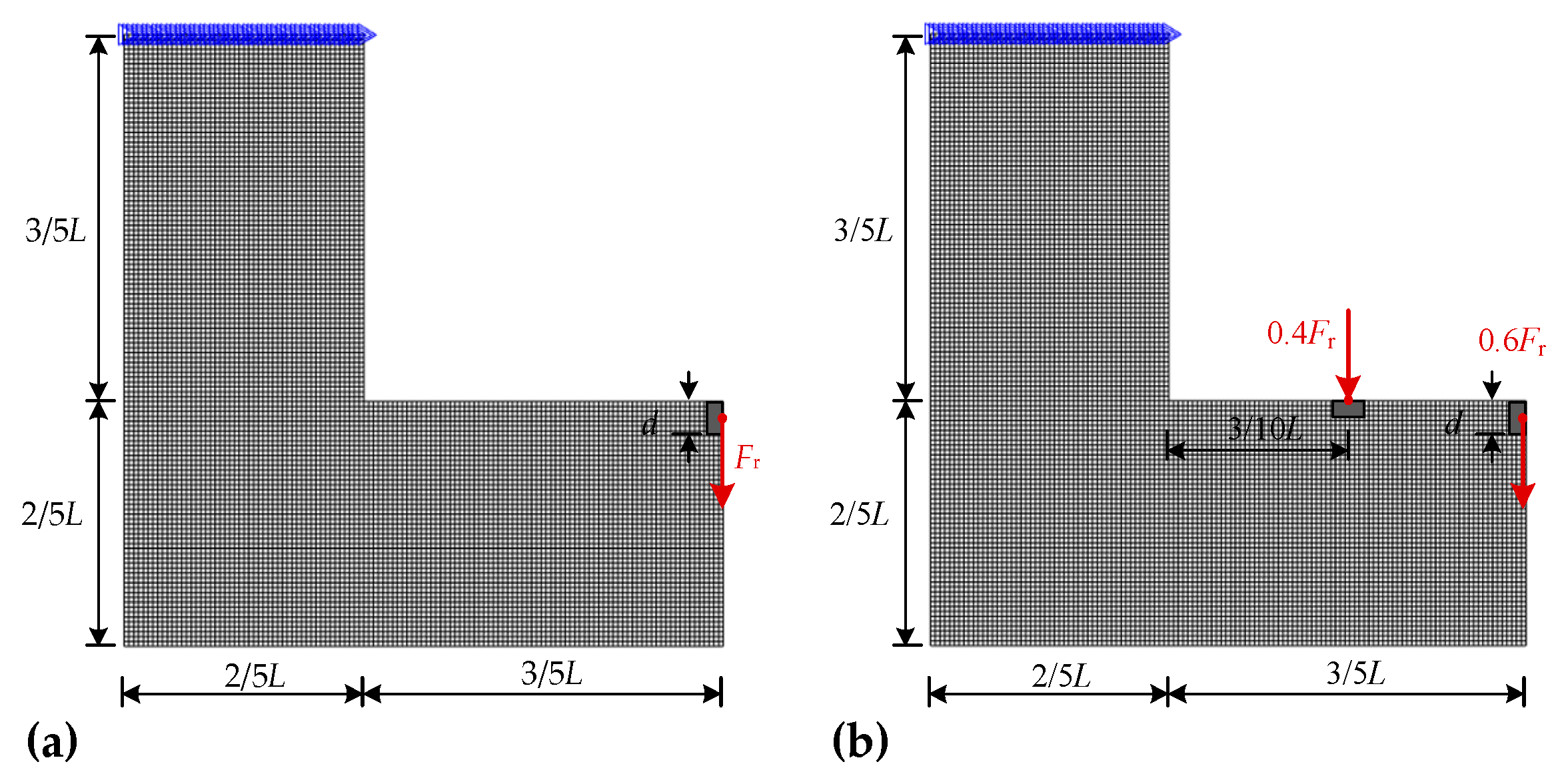
4.1. L-Bracket
4.2. Antenna Bracket
4.3. Portal Frame
4.4. Rectangular Plate with Round Hole
4.5. Curved Plate with Circular Holes
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Zhu, J.; Zhou, H.; Wang, C.; Zhou, L.; Yuan, S.; Zhang, W. A review of topology optimization for additive manufacturing: Status and challenges. Chin. J. Aeronaut. 2021, 34, 91–110. [Google Scholar] [CrossRef]
- Lian, Y.; Wang, P.; Gao, J.; Liu, J.; Li, Q.; Liu, C.; Heng, X.; Gao, L.; Li, H.; Lei, H.; et al. Fundamental mechanics problems in metal additive manufacturing: A state-of-art review. Adv. Mech. 2021, 51, 648–701. [Google Scholar]
- Holmberg, E.; Torstenfelt, B.; Klarbring, A. Fatigue constrained topology optimization. Struct. Multidiscip. Optim. 2014, 50, 207–219. [Google Scholar] [CrossRef]
- Verbart, A.; Langelaar, M.; Keulen, F.V. Damage approach: A new method for topology optimization with local stress constraints. Struct. Multidiscip. Optim. 2015, 53, 1081–1098. [Google Scholar] [CrossRef]
- Zhan, J. Topological design of compliant mechanisms with maximum stress constraint. J. Mech. Eng. 2018, 54, 32–38. [Google Scholar] [CrossRef]
- Wang, X.; Liu, H.; Long, K.; Yang, D.; Hu, P. Stress-constrained topology optimization based on improved bi-directional evolutionary optimization method. Chin. J. Theor. Appl. Mech. 2018, 50, 385–394. [Google Scholar]
- Silva, G.A.; Beck, A.T.; Sigmund, O. Topology optimization of compliant mechanisms with stress constraints and manufacturing error robustness. Comput. Method Appl. Eng. 2019, 354, 397–421. [Google Scholar] [CrossRef]
- Silva, G.A.; Beck, A.T.; Sigmund, O. Stress-constrained topology optimization considering uniform manufacturing uncertainties. Comput. Method Appl. Eng. 2019, 344, 512–537. [Google Scholar] [CrossRef]
- Emmendoerfer, H.J.R.; Silva, E.C.N.; Fancello, E.A. Stress-constrained level set topology optimization for design-dependent pressure load problems. Comput. Method Appl. Eng. 2019, 344, 569–601. [Google Scholar] [CrossRef]
- Oliver, G.L.; Glaucio, H.P. PolyStress: A Matlab implementation for local stress-constrained topology optimization using the augmented Lagrangian method. Struct. Multidiscip. Optim. 2021, 63, 2065–2097. [Google Scholar]
- Talischi, C.; Paulino, G.H.; Pereira, A.; Menezes, I.F.M. Polytop: A Matlab implementation of a general topology optimization framework using unstructured polygonal finite element meshes. Struct. Multidiscip. Optim. 2012, 45, 329–357. [Google Scholar] [CrossRef]
- Pokkalla, D.K.; Wang, Z.P.; Poh, L.H.; Quek, S.T. Isogeometric shape optimization of smoothed petal auxetics with prescribed nonlinear deformation. Comput. Method Appl. Eng. 2019, 356, 16–43. [Google Scholar] [CrossRef]
- Pokkalla, D.K.; Poh, L.H.; Quek, S.T. Isogeometric shape optimization of missing rib auxetics with prescribed negative Poisson’s ratio over large strains using genetic algorithm. Int. J. Mech. Sci. 2021, 193, 106169. [Google Scholar] [CrossRef]
- Wang, Z.P.; Kumar, D. On the numerical implementation of continuous adjoint sensitivity for transient heat conduction problems using an isogeometric approach. Struct. Multidiscip. Optim. 2017, 56, 487–500. [Google Scholar] [CrossRef]
- Oest, J.; Lund, E. Topology optimization with finite-life fatigue constraints. Struct. Multidiscip. Optim. 2017, 56, 1045–1059. [Google Scholar] [CrossRef]
- Ye, H.; Su, P.; Wang, W.; Sui, Y. Continuum topology optimization with fatigue life constraints. J. Beijing Univ. Technol. 2020, 46, 236–244. [Google Scholar]
- Chen, Z.; Long, K.; Wen, P.; Nouman, S. Fatigue-resistance topology optimization of continuum structure by penalizing the cumulative fatigue damage. Adv. Eng. Softw. 2020, 150, 102924. [Google Scholar] [CrossRef]
- Nabaki, K.; Shen, J.; Huang, X. Evolutionary topology optimization of continuum structures considering fatigue failure. Mater. Design 2019, 166, 107586. [Google Scholar] [CrossRef]
- Zhan, J.; Liu, T.; Liu, M.; Zhu, B. Topological design of compliant mechanisms considering fatigue constraints. J. Mech. Eng. 2021, 57, 59–68. [Google Scholar]
- Hou, J.; Zhu, J.; Wang, C.; Wang, J.; Zhang, W. Topology optimization of the multi-fasteners jointed structure considering joint load constraint and fatigue constraints. Sci. China Press 2019, 64, 79–86. [Google Scholar] [CrossRef]
- Gao, X.; Caivano, R.; Tridello, A.; Chiandussi, G.; Berto, F. Innovative formulation for topological fatigue optimisation based on material defects distribution and TopFat algorithm. Int. J. Fatigue 2021, 147, 106176. [Google Scholar] [CrossRef]
- Zhang, S.; Le, C.; Gain, A.L.; Norato, J.A. Fatigue-based topology optimization with non-proportional loads. Comput. Method Appl. Eng. 2019, 345, 805–825. [Google Scholar] [CrossRef]
- Suresh, S.; Lindstrm, S.B.; Thore, C.J.; Bo, T.; Klarbring, A. Topology optimization using a continuous-time high-cycle fatigue model. Struct. Multidiscip. Optim. 2020, 61, 1011–1025. [Google Scholar] [CrossRef]
- Jeong, S.H.; Choi, D.H.; Yoon, G.H. Fatigue and static failure considerations using a topology optimization method. Appl. Math. Model 2015, 39, 1137–1162. [Google Scholar] [CrossRef]
- Lee, J.W.; Yoon, G.H.; Jeong, S.H. Topology optimization considering fatigue life in the frequency domain. Comput. Math. Appl. 2015, 70, 1852–1877. [Google Scholar] [CrossRef]
- Zhao, L.; Xu, B.; Han, Y.; Xue, J.; Rong, J. Structural topological optimization with dynamic fatigue constraints subject to dynamic random loads. Eng. Struct. 2020, 205, 110089. [Google Scholar] [CrossRef]
- He, X.; Yu, D. Fatigue design of auxiliary frame of an agitator truck based on ESLs structural optimization method. J. Vib. Shock 2013, 32, 64–69. [Google Scholar]
- Jeong, S.H.; Lee, J.W.; Yoon, G.H.; Dong, H.C. Topology optimization considering the fatigue constraint of variable amplitude load based on the equivalent static load approach. Appl. Math. Model 2018, 56, 626–647. [Google Scholar] [CrossRef]
- Wang, F.; Lazarov, B.S.; Sigmund, O. On projection methods, convergence and robust formulations in topology optimization. Struct. Multidiscip. Optim. 2011, 43, 767–784. [Google Scholar] [CrossRef]
- Bourdin, B. Filters in topology optimization. Comput. Method Appl. Eng. 2001, 50, 2143–2158. [Google Scholar] [CrossRef]
- Senhora, F.V.; Giraldo-Londoo, O.; Menezes, I.F.M.; Paulino, G.H. Topology optimization with local stress constraints: A stress aggregation-free approach. Struct. Multidiscip. Optim. 2020, 62, 1639–1668. [Google Scholar] [CrossRef]
- Nguyen, N.V.; Nguyen-Xuan, H.; Lee, J. Polygonal composite elements for stress-constrained topology optimization of nearly incompressible materials. Eur. J. Mech. A-Solid 2022, 94, 104548. [Google Scholar] [CrossRef]
- Stephens, R.I.; Fatemi, A.; Stephens, R.R.; Fuchs, H.O. Metal Fatigue in Engineering, 2nd ed.; John Wiley & Sons: New York, NY, USA, 2000. [Google Scholar]
- Kiyono, C.Y.; Vatanabe, S.L.; Silva, E.C.N.; Reddy, J.N. A new multi-p-norm formulation approach for stress-based topology optimization design. Compos. Struct. 2016, 156, 10–19. [Google Scholar] [CrossRef]
- Giraldo-Londono, O.; Paulino, G.H. A unified approach for topology optimization with local stress constraints considering various failure criteria: Von Mises, Drucker–Prager, Tresca, Mohr-Coulomb, Bresler-Pister, and William-Warnke. Proc. R. Soc. A 2020, 476, 20190861. [Google Scholar] [CrossRef] [PubMed]
- Svanberg, K. A class of globally convergent optimization methods based on conservative convex separable approximations. SIAM J. Optimiz. 2002, 12, 555–573. [Google Scholar] [CrossRef]









Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Teng, X.; Wang, C.; Jiang, X.; Chen, X. Structural Topology Optimization with Local Finite-Life Fatigue Constraints. Mathematics 2023, 11, 1220. https://doi.org/10.3390/math11051220
Teng X, Wang C, Jiang X, Chen X. Structural Topology Optimization with Local Finite-Life Fatigue Constraints. Mathematics. 2023; 11(5):1220. https://doi.org/10.3390/math11051220
Chicago/Turabian StyleTeng, Xiaoyan, Can Wang, Xudong Jiang, and Xiangyang Chen. 2023. "Structural Topology Optimization with Local Finite-Life Fatigue Constraints" Mathematics 11, no. 5: 1220. https://doi.org/10.3390/math11051220
APA StyleTeng, X., Wang, C., Jiang, X., & Chen, X. (2023). Structural Topology Optimization with Local Finite-Life Fatigue Constraints. Mathematics, 11(5), 1220. https://doi.org/10.3390/math11051220




