Role of Nanofluid and Hybrid Nanofluid for Enhancing Thermal Conductivity towards Exponentially Stretching Curve with Modified Fourier Law Inspired by Melting Heat Effect

Abstract

The intensive of this study is to examine the melting heat and second-order slip (SoS) effect at the boundary in nanofluid and hybrid nanofluid (HN) ethylene–glycol (EG) based fluid through a curved surface using the Modified Fourier Law (MFL) and dust particles. Considering similarity transformation, the PDEs are converted to ODEs and then solved numerically by using the finite element method (FEM). The effects of solid volume fraction (SVF), melting heat factor, curvature factor, first and second-order slip factor, fluid particle concentration factor, and mass concentration factor on the velocity field, dust phase velocity (DPV), temperature field, dust phase temperature (DPT), and the Ski Friction (SF) are investigated through graphs and tables. The thermophysical properties of nanofluid and HN are depicted in tables. The novelty of the present work is to investigate the dusty- and dusty-hybrid nanoliquids over the curved surface with a melting heat effect and MFL which has not yet been studied. In the limiting case, the present work is compared with the published work and a good correlation is found. The confirmation of the mathematical model error estimations has been computed.

1. Introduction

Nanofluid technology development is a very important study in mathematics, manufacturing, physics, and materials science. Architects and researchers strive to effectively convey an adequate understanding of the heat transfer process in nanofluid for many applications of practical interest. Nanofluid is critical in a wide range of applications, including chips, refrigerators, hybrid-powered motors, food improvement, heat exchangers, and more. Choi et al. [1] first introduced the concept of nanofluid. This method tries to improve thermal conductivity by integrating a base liquid like water with a solitary kind of nanosized molecule, such as copper, aluminum, carbon nanotubes, etc. Buongiorno [2] gave a mathematical form of the nanoparticles. Subsequently, mathematicians and researchers have widely used nanofluids to examine practical problems like industrial applications [3,4], biomedical engineering [5], solar thermal applications [6], and numerous other production fields applied for different physical problems [7,8,9].

Several current studies [10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26] concentrate on various nanoparticle characteristics utilized for various applications. Although traditional fluids have a broad range of applications, many researchers discovered it challenging to attain good thermal performance. Scientists have been pushed by this problem to create a new class of nanomaterials that significantly increases heat transfer in base fluids. Compared to convectional fluids, the hybrid nanofluid method has greater thermodynamic conductivity. Solar energy, refrigeration, heating, heavy machinery, compound cycles, ventilation, and refrigeration are just a few of the uses for hybrid nanofluids.

Hybrid nanoliquid development has grown significantly in recent years to address the most pressing practical difficulties in a number of industries, including heat absorption and electrical equipment [27], and in several domains to improve the pace of heat transfer and thermal efficiency. Zeeshan et al. [28] examined the stability analysis of nanofluid past a horizontal channel with heat source and thermal. The squeezed HN flow between two walls with identical centers and different thermal conduction was examined by Riasat et al. [29]. Several authors discussed the mathematical characterization of a hybrid nanofluid [30,31,32,33] over a stretched permeable sheet of MHD thin-film movement that comprises Cu and Al₂O₃ distributed in ethylene glycol. A few pertinent studies on the HN movement have recently been reported [34,35,36,37,38].

According to physics laws, heat transfer happens due to temperature differences between dissimilar or similar bodies. It is interesting to note that Fourier Law (FL) is considered as a standard for heat diffusion, but later it was exposed that this is not valid in many cases due to the initial disturbance that overcomes during the practice. Cattaneo [39] determined this matter by signifying the addition of the thermal relaxation factor in the Fourier model. This was scrutinized by Christov [40], who recommended Oldroyd Upper Convective Derivative (OUCD) with respect to time. This is known as the C-C heat flux model [41]. Hayat et al. [42] investigated the Maxwell model flow over a stretchable sheet using C–C heat flux and enclosing the slip effect by using the HAM approach. Abbas et al. [43] examined the C–C heat flux model over a stretched sheet with changing thickness. Similarly, Li et al. [44] used the same idea and considered the Oldroyd-8 model. The velocity of a non-Newtonian viscous fluid with the MHD effect was examined over a vertically stretched sheet using C–C heat flux by Kumar et al. [45]. Recently, Amjad et al. [46] studied the numerical solution of MHD Williamson nanofluid over a stretchable sheet with variable viscosity. The double diffusion heat flux model with temperature-dependent viscosity passed through an extendable sheet was investigated by Amjad et al. [47]. Ahmed et al. [48] gave a mathematical model for magnetized Williamson nanofluid on a stretching surface. Similarly, Atashafrooz et al. [49] investigated the radioactive heat effect in nanofluid movement considering the influence of a magnetic field over the open trapezoidal enclosure. In his recent paper, the effect of Lorentz force on the hydrothermal behavior of NF over the trapezoidal recess enclosing the second law of thermodynamics has been examined [50]. Rasool et al. [51] examined the numerical analysis of EMHD nanofluid movements’ through a convectively heated pattern situated horizontally in a porous medium. Nehad [52] investigated the second-grade thermodynamic activity past a vertical sheet. Raju et al. [53] explored the ternary HN flow with various shapes and varying densities over contracting permeable walls. Shah et al. [54] studied some inventive changes to the TFF of NF.

Based on the given literature, the present study aims to investigate the HN flow enclosing dust particles over a stretched curved surface with heat and mass transfer analysis. Nanoparticles such as Cu and CuO are suspended in EG to boost the thermal conductivity of the base fluid. The melting heat and second-order slip effect at the boundary are also encountered in the appearance of MFL. The basic flow equations are transformed into PDEs. The similarity transformation is applied to convert PDEs to ODEs. For the numerical solution, the new variables are introduced in order to get first-order differential equations. The numerical solutions are obtained via the RK4 method. The numerous characterizing factors for the stream phenomena and their features are deliberated via graphs. Additionally, for the validation of the present work [46], a comparison is done with the published work, and excellent agreement is found.

We will attempt to answer the following question through this research:

(i)

How does the curving surface’s curvature affect the dust stage movement?

(ii)

What role does the solid volume part play in the dust and flowing phases?

(iii)

How does the thermal relaxation factor affect the fluid temperature?

(iv)

What is the effect of the slippage?

(v)

How liquidity, speed, and heat are impacted by the curvature of the sheet?

(vi)

Which type of nanofluid is most dominant?

(vii)

How does fluid velocity connect to the molten heat phenomenon?

2. Mathematical Modulation

The 2D (two-dimensional) flow of nanofluid and HN flow over a curved surface is considered in the current analysis. More generally, the study of first and second-order slippage and melting heat at the boundary have many applications in engineering, wire/fiber coating, nuclear waste disposal, etc. Due to the current investigation, we consider HN over the curved surface with dust particles enclosing the slippage effect of first and second order and melting heat at the boundary-based Ethylene Glycol fluid. Assuming the coordinate system $\left(r, s\right)$ which is the arc lengths taken at the direction of the flow of the curved surface and at any point on the surface normal to the tangential vector as shown in Figure 1 in which R is the radius of the curve. The curve is stretched with velocity $u=a_1{e}^{\frac{S}{l}}$ $(a_1, l>1)$ along s direction in which $a_1$ is the initial starched and $l$ is the length. The MFL is used for this analysis to analyze the heat mechanism.

The model equations for nanofluid and dust nanofluid are [46].

2.1. For Nanoliquid

For the nanofluid flow, the basic equations are

$$\frac{\partial }{\partial r}\left\{\left(R+r\right)v\right\}+R\frac{\partial u}{\partial s}=0,$$

(1)

$$\frac{u^2}{r+R}=\frac{1}{\rho hnf}\frac{\partial p}{\partial r}$$

(2)

$$v\frac{\partial u}{\partial r}+\left(\frac{Ru}{r+R}\right)\frac{\partial u}{\partial s}+\frac{uv}{r+R}=-\left(\frac{1}{\rho hnf}\frac{R}{r+R}\right)\frac{\partial p}{\partial s}+\frac{\mu hnf}{\rho hnf} (\frac{{\partial }^{2}u}{\partial r^2}+\frac{1}{r+R}\frac{\partial u}{\partial r} -\frac{u}{{\left(r+R\right)}^2})-\frac{KS}{{\rho }_{hnf}} \left(u_p-u\right),$$

(3)

$${\left(\rho C_p\right)}_{hnf}(v\frac{\partial T}{\partial r}+\frac{Ru}{r+R}\frac{\partial T}{\partial s})=-\nabla .q+\frac{{\rho }_{p{C}_{pf}}}{{\tau }_T} \left(T_p-T\right)+\frac{{\rho }_{p{C}_p}}{{\tau }_v}{\left(u_p–u\right)}^2,$$

(4)

Subsequent Cattaneo-Christov hypothesis [46], we have:

$$q+{ƛ}_{\pounds }\left(V.\nabla q-q.\nabla V+\left(\nabla .V\right)q\right)=-K^{°}\nabla T$$

(5)

Here $K^{°}$ and ${ƛ}_{\pounds }$ address thermal characteristics and the relaxation time.

For constant density liquid [46]:

$$\nabla .V=0$$

(6)

Equation (5) becomes:

$$q+{ƛ}_{\pounds }\left(V.\nabla q-q.\nabla V\right)=-K^{°}\nabla T$$

(7)

In this way, the temperature field takes the structure:

$$\begin{gathered} v\frac{\partial T}{\partial r}+\frac{Ru}{r+R}\frac{\partial T}{\partial s}=\frac{K^{°}}{(\left(\rho C_p\right)hnf}[\frac{{\partial }^{2}T}{\partial r^2}+\frac{1}{r+R}\frac{\partial T}{\partial r}+{\left(\frac{R}{r+R}\right)}^2\frac{{\partial }^{2}T}{\partial s^2})-{ƛ}_{\pounds }\left(u^2{\left(\frac{R}{r+R}\right)}^2\frac{{\partial }^{2}T}{\partial s^2}\right)+v^2\frac{{\partial }^{2}T}{\partial r^2}+\left(v\frac{\partial v}{\partial r}+u \frac{\partial v}{\partial s}+\frac{R}{r+R}\right) \frac{\partial T}{\partial r}+ \\ \frac{R}{r+R}v\frac{\partial u}{\partial s}(u \frac{\partial u}{\partial s} {\left(\frac{R}{r+R}\right)}^2\frac{\partial u}{\partial s}+\left(\frac{R}{r+R}\right)v\frac{\partial u}{\partial s}) \frac{\partial T}{\partial s}+2v\frac{R}{r+R}v\frac{{\partial }^{2}T}{\partial r\partial s}\left)\right]+\frac{{\rho }_{p{C}_{pf}}}{{\left(\rho C_p\right)}_{hnf} {\tau }_T} \left(T_p-T\right)+\frac{{\rho }_{p{C}_{pf}}}{{\left(\rho C_p\right)}_{hnf}{\tau }_v}{\left(u_p-u\right)}^2, \end{gathered}$$

(8)

2.2. For Dusty Liquid

For the dusty liquid the above equations will be

$$\frac{\partial }{\partial r}\left\{\left(R+r\right)v_p\right\}+R\frac{\partial u_p}{\partial s}=0,$$

(9)

$$v_p\frac{\partial u_p}{\partial r}+\frac{R{u}_p}{r+R}\frac{\partial u_p}{\partial s}+\frac{u_p{v}_p}{r+R}=\frac{KS}{{\rho }_p}\left(u_p-u\right),$$

(10)

$$v_p\frac{\partial T_p}{\partial r}+\frac{R{u}_p}{r+R}\frac{\partial T_p}{\partial s}=\frac{C_p}{C_m{\tau }_T}\left(T_p-T\right),$$

(11)

With the relevant conditions are [46]:

$${u|}_{r=0}=a_1{e}^{\frac{S}{l}}+{ƛ}_1 \left(\frac{u}{r+R}-{\frac{\partial u}{\partial r}|}_{r=0} \right)+\left({ƛ}_2 {\frac{{\partial }^{2}u}{\partial r^2}|}_{r=0}- \frac{u}{{\left(r+R\right)}^2}+\frac{1}{r+R}{\frac{\partial u}{\partial r}|}_{r=0}\right),$$

(12)

$${T|}_{r=0} =T_m, k_{hnf}{\frac{\partial T}{\partial r}|}_{r=0}={\rho }_{hnf}\left(ƛ+C_S\right) \left(T_m-T_0\right))v \left(s,0\right),$$

$${u|}_{r\to \infty }\to 0,{u_p|}_{r\to \infty }\to 0,{v_p|}_{r\to \infty }\to v,{\frac{\partial u}{\partial r}|}_{r\to \infty }\to 0,{T|}_{r\to \infty }\to T_{\infty }.$$

(13)

The mathematical properties of Cu, Cu O, & Ethylene glycol are expressed in

Table 1. Thermo characteristics are given below [46].

Base Fluid/Nanomaterial	${\mathit{C}}_{\mathit{p}}$(J/kg K)	$\mathit{\rho } (Kg/m^3$)z	K (W/mK)
C2H6O2	2430	1115	0.253
CuO	531.8	6320.0	76.5
Cu	385	8933	401

.

The thermos-actual qualities for nanoliquid are known as:

$${\mu }_{nf}=\frac{{\mu }_f}{{\left(1-\varnothing \right)}^{2.5}}{a}_{1nf}=\frac{k_{nf}}{(\rho C_{p)}{}_{nf}},$$

(14)

$${\rho }_{nf= }{\left(1-\varphi \right)}_{ }{\rho }_f+\varphi {\rho }_S,{\left(\rho C_p\right)}_{nf}=\left(1-\varphi \right){\left(\rho C_p\right)}_f+\varphi {\left(\rho C_p\right)}_S,$$

(15)

$$\frac{k_{nf}}{k_f}=\frac{\left({\mathrm{k}}_s+2{\mathrm{k}}_f\right)-2\varphi \left({\mathrm{k}}_f-{ \mathrm{k}}_s\right)}{\left({\mathrm{k}}_s+2{\mathrm{k}}_f \right)+2\varphi \left({\mathrm{k}}_f-{ \mathrm{k}}_s\right)}$$

(16)

For the hybrid nanofluid, the thermo physical characteristics [51] are given as:

$${\mu }_{nf}={\mu }_{f } {\left(1-{\varphi }_1\right)}^{-2.5}{\left(1-{\varphi }_2\right)}^{-2.5}$$

(17)

$$D_{4=}{(\rho C_P)}_{hnf}={(\rho C_P)}_{S_{2}hnf}{\varphi }_2-\left({\varphi }_2-1\right)\{\left(1-{\varphi }_1\right){(\rho C_P)}_f+{(\rho C_P)}_{S_1}{\varphi }_1\}.$$

(18)

$${\rho }_{hnf}=\left(1-{\varphi }_2\right)\left\{\left(1-{\varphi }_1\right){\rho }_f+{\varphi }_1{\rho }_{s1}\right\}+{\rho }_{s2}{\varphi }_{2,}$$

(19)

$$\frac{k_{hnf}}{K_f}=\frac{{\mathrm{k}}_{bf} \left(\mathrm{n} -1\right)+{ \mathrm{k}}_{s2}-\left(\mathrm{n} -1\right)\left[{\mathrm{k}}_{bf}-{ \mathrm{k}}_{s2} \right]{\varphi }_2}{{\mathrm{k}}_{bf}\left(\mathrm{n} -1\right)+{\mathrm{k}}_{s2}+\left[{\mathrm{k}}_{bf}-{ \mathrm{k}}_{s2} \right]{\varphi }_2},$$

$$\frac{k_{bf}}{k_f}=\frac{{\mathrm{k}}_{s1}+\left(\mathrm{n} -1\right)k_f-\left(\mathrm{n} -1\right)\left[k_f-k_{s1} \right]{\varphi }_1}{k_{s1}+\left(n-1\right)k_f+\left[k_f-k_{s1}\right]{\varphi }_1}$$

(20)

3. Introducing the Similarity Transformation

The corresponding PDEs for dusty-nanofluid and dusty hybrid nanofluid is transformed to ODEs by introducing the following transformation:

$$\eta =\sqrt{\frac{a_1}{2lvf}}r{e}^{s/2l}, p={\rho }_f{a}_1^2{e}^{\frac{2s}{l}}P\left(\eta \right), \theta \left(\eta \right)=\frac{T-T_m}{T_{\infty -T_m}}, {\theta }_p\left(\eta \right)=\frac{T_p-T_m}{T_{\infty -T_m}}$$

$$u=a_1{e}^{s|l}{f}^{\prime }\left(\eta \right), v=-\frac{R}{r+R}\sqrt{\frac{a_1{v}_f}{2l}}{e}^{s|2l} (f^{\prime }\left(\eta \right)+\eta f^{\prime }\left(\eta \right),$$

$$u_p=a_1{e}^{s/l}{f}^{\prime }\left(\eta \right),v=-\frac{R}{r+R}\sqrt{\frac{a_1{v}_f}{2l}}{e}^{\frac{s}{2l}}\left(f^{\prime }\left(\eta \right)+\eta f^{\prime }\left(\eta \right)\right)$$

(21)

Here, prime indicates derivative with respect to $\eta$. The transformation defined in Equation (21) satisfies the continuity automatically while the fluid stream and the dust fluid take the form:

3.1. For Nanoparticles Fluid

After using the Equation (21), the basic equation for the nanofluid will become as

$$\frac{{\rho }_f}{{\rho }_{hnf}}{P}^{\prime }=\frac{f{\prime }^2}{\eta +K_p}$$

(22)

$$\frac{{\rho }_f}{{\rho }_{hnf}}\frac{2k}{\mathsf{\eta }+\mathrm{k}}P=\frac{{\mu }_{hnf}/{\mu }_f}{{\rho }_{hnf}/{\rho }_f}\left(f^{‴}-\frac{f^{\prime }}{{\left(K_p+\eta \right)}^2}+\frac{f^{″}}{\eta +K_p}\right)-\frac{K_p{f^{\prime }}^2}{\eta +K_p}+\frac{K_{p}f{f}^{″}}{K_p+\eta }+\frac{K_{p}f{f}^{\prime }}{{\left(K_p+\eta \right)}^2}+\frac{l_m{B}_v}{{\rho }_{hnf}}\left(F^{\prime }-f^{\prime }\right)$$

(23)

$$\frac{1}{Pr}\frac{k_{hnf}}{K_p} \left({\theta }^{″}+\frac{1}{\eta +K_p}{\theta }^{\prime }\right)+D_4\left[\frac{K_p}{\eta +K_p}f{\theta }^{\prime }-{\epsilon }_{Ther}\left(\frac{K_p^2}{{\left(\eta +K_p\right)}^2}\left(f{{\theta }^{\prime }}^{\prime }+f{f}^{\prime }{\theta }^{\prime }\right)-K_p^2{f}^2{\theta }^{\prime }\right)\right]+M_d{B}_T\left({\theta }_P-\theta \right)+M_d{B}_v{E}_C\left(F^{\prime }-f^{\prime }\right)=0,$$

(24)

3.2. For Dusty Fluid Flow

Similarly, using Equation (21), the basic equations for the dusty fluid will become as

$$\frac{K_p}{K_p+\eta }F{F}^{″}\frac{K_p}{\eta +K_p}{F}^{\prime 2}+\frac{K_p}{{\left(K_p+\eta \right)}^2}{F}^{\prime }F+B_v\left(f^{\prime }-F^{\prime }\right)=0$$

(25)

$$\frac{K_p}{\eta +K_p}\mathrm{F}{\theta }_P^{\prime }-\mathsf{\gamma }{B}_T\left({\theta }_P-\mathsf{\theta }\right)=0,$$

(26)

With the transformed boundary conditions:

$$\begin{gathered} D_{2}Prf\left(0\right)+\frac{k_{hnf}}{k}M{\theta }^{\prime }\left(0\right)=0, f^{\prime }\left(0\right)-1-L_0\left(f^{″}\left(0\right)-\frac{f^{\prime }\left(0\right)}{K_p}\right)-L_1\left(f^{‴}\left(0\right)-\frac{f^{″}\left(0\right)}{\eta +K_p}-f^{″}\left(0\right)-\frac{f^{\prime }\left(0\right)}{{\left(\eta +K_p\right)}^2}\right) \\ =0, \theta \left(0\right)=1, \theta \left(\eta \right)\to 0, {\theta }_P\left(\eta \right)\to 0,as \eta \to \infty . \end{gathered}$$

(27)

Involved parameters are expressed as

$$K_P=R\sqrt{\frac{a}{2v_{fl}}}, B_v=\frac{1}{a_1{\tau }_v}, Pr=\frac{vf}{{\alpha }_f},B_T=\frac{1}{a_1{\tau }_T}, {\epsilon }_{Ther}=a_1{ƛ}_{E,}$$

(28)

$$E_C=\frac{a_1^2{e}^{2s/l}2l}{C_P\left(T_{\infty }-T_m\right)}, M_d=\frac{mS}{{\mathsf{\rho }}_P},Sc=\frac{v_f}{D}, L_0={ƛ}_1\sqrt{\frac{a_1}{2v_{f}l},} L_1={ƛ}_2\sqrt{\frac{a_1}{2v_{f}l}}, M=\frac{C_P\left(T_m-T_0\right)}{ƛ+C_s\left(T_m-T_0\right)}.$$

Eliminating the pressure term from Equations (22) and (23) by differentiating the Equation (21) with respect to $\eta$ and then, using in Equation (23), we obtain as

$$\begin{gathered} f^{iv}+\frac{2f^{‴}}{\eta +K_p}-\frac{f^{″}}{{\left(\eta +K_p\right)}^2}+\frac{f^{\prime }}{{\left(\eta +K_p\right)}^3}+D_1{D}_2\left\{\frac{K_p}{{\left(\eta +K_p\right)}^2}\left({f^{\prime }}^2-f{f}^{″}\right)-\frac{K_p}{\left(\eta +K_p\right)}\left(f^{\prime }{f}^{″}-f{f}^{‴}\right)-\frac{K_p}{{\left(\eta +K_p\right)}^3}f{f}^{\prime }\right\} \\ +D_1{M}_d{B}_v\left(F^{″}-f^{″}\right)+D_1{M}_d{B}_v\frac{1}{\left(\eta +K_p\right)}\left(F^{\prime }-f^{\prime }\right)=0, \end{gathered}$$

(29)

The surface drag force ($C_f)$,

$$C_f=\frac{{\tau }_{rx}}{\frac{1}{2}\rho q_w^2}.$$

(30)

Here, ${\mathsf{\tau }}_{rx}$signify the wall shear stress, $q_w$shows the wall heat flux, and is determined as below:

$${\mathsf{\tau }}_{rx}={\mu }_{nf}{\left(\frac{\partial u}{\partial r}-\frac{u}{r+R}\right)}_{r=0}.$$

(31)

After simplification we get:

$$C_f\sqrt{R{e}_s} = \frac{1}{D_1} \left(f^{″}\left(0\right)-\frac{f^{\prime }\left(0\right)}{K_p}\right)$$

(32)

Here, $R{e}_s$ verifies the local Reynolds Number (LRN).

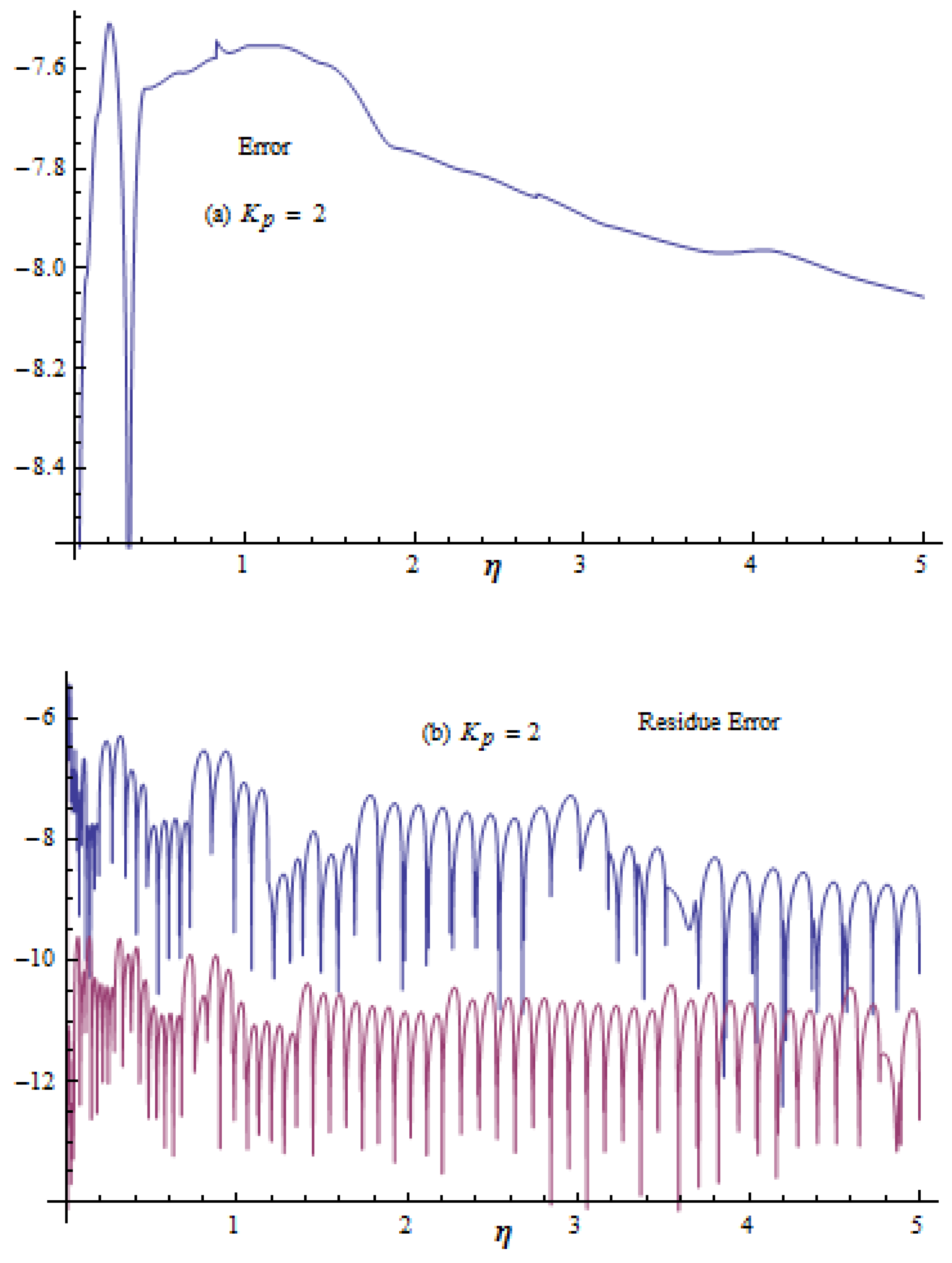
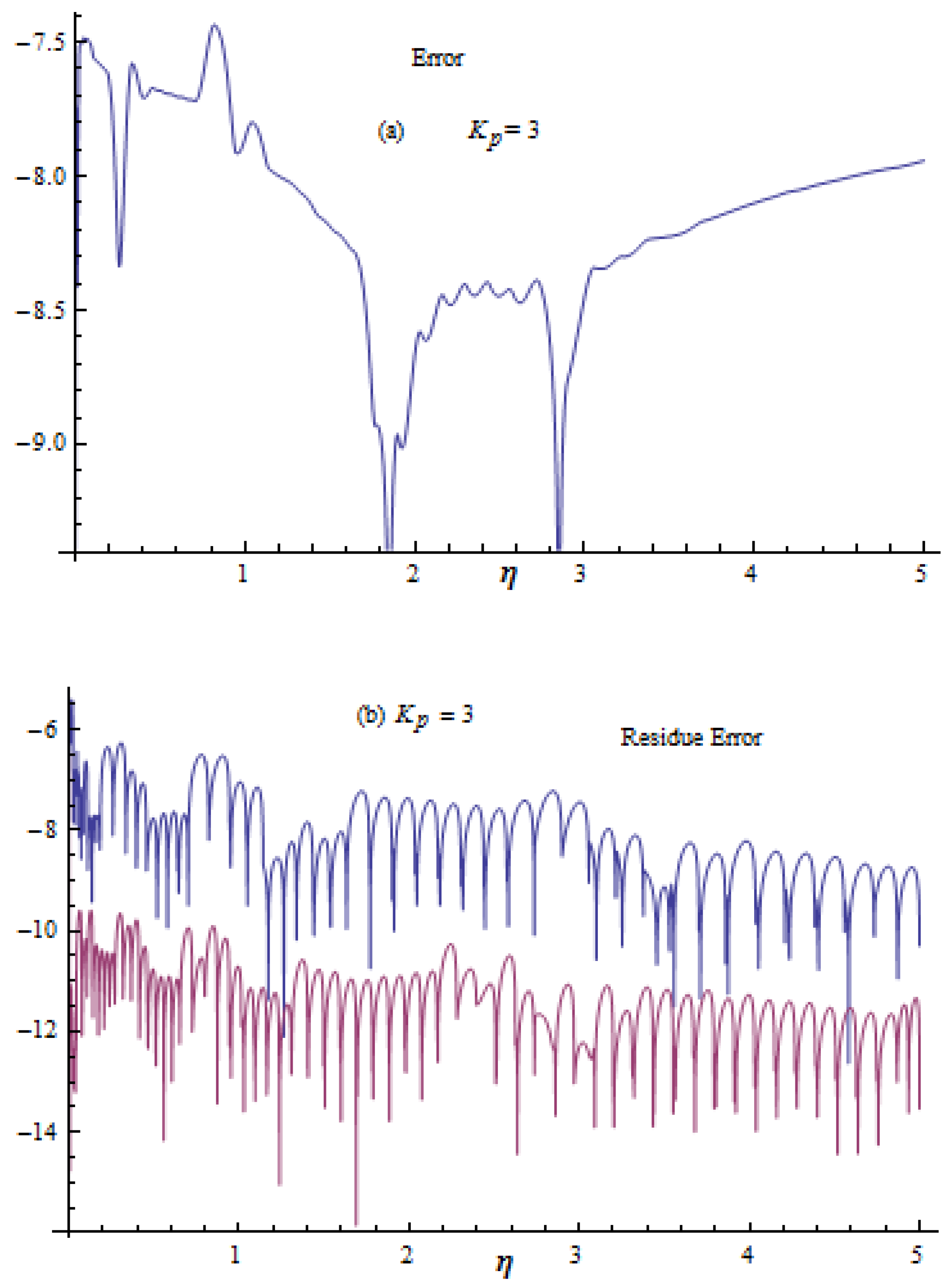
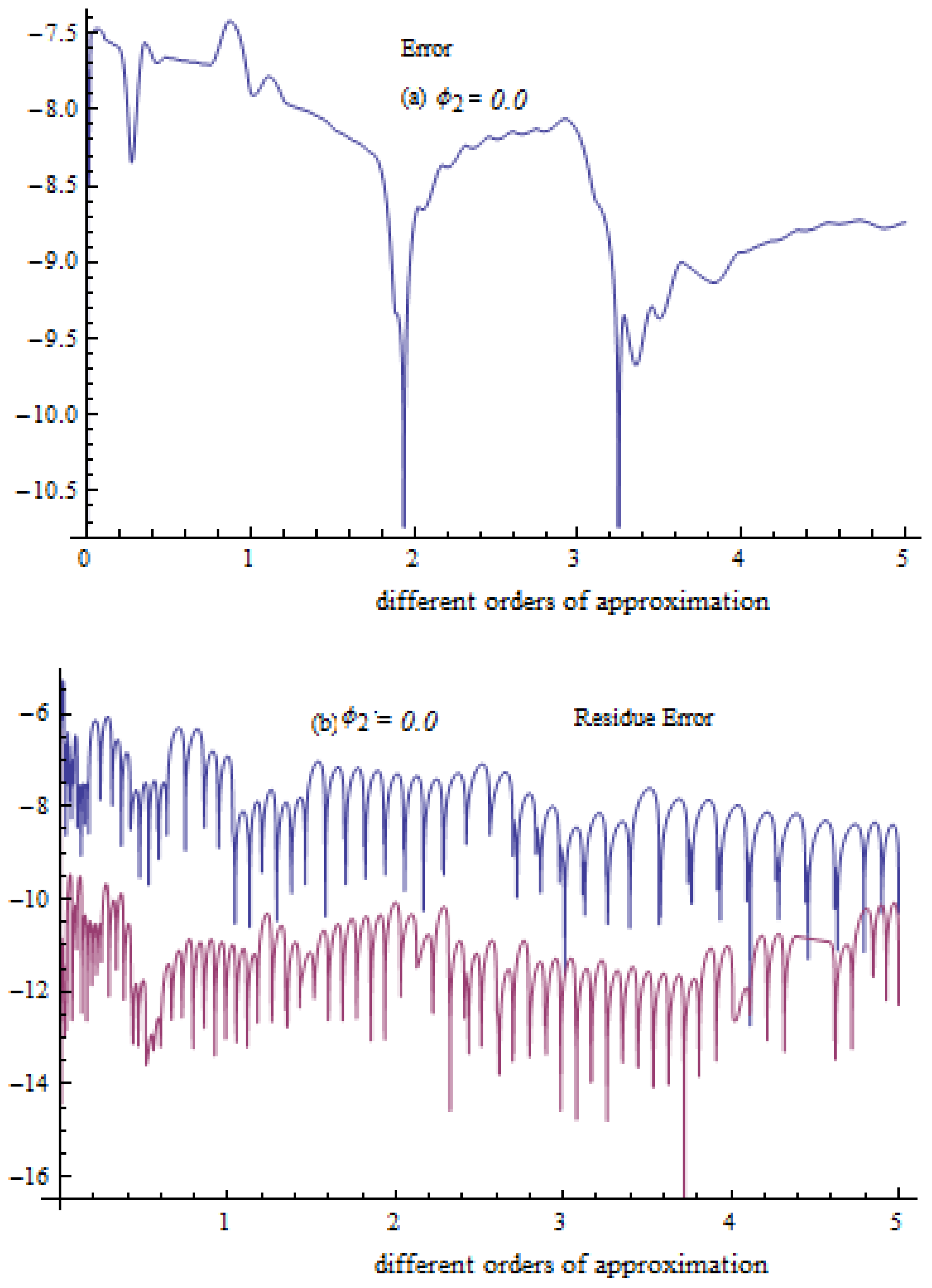
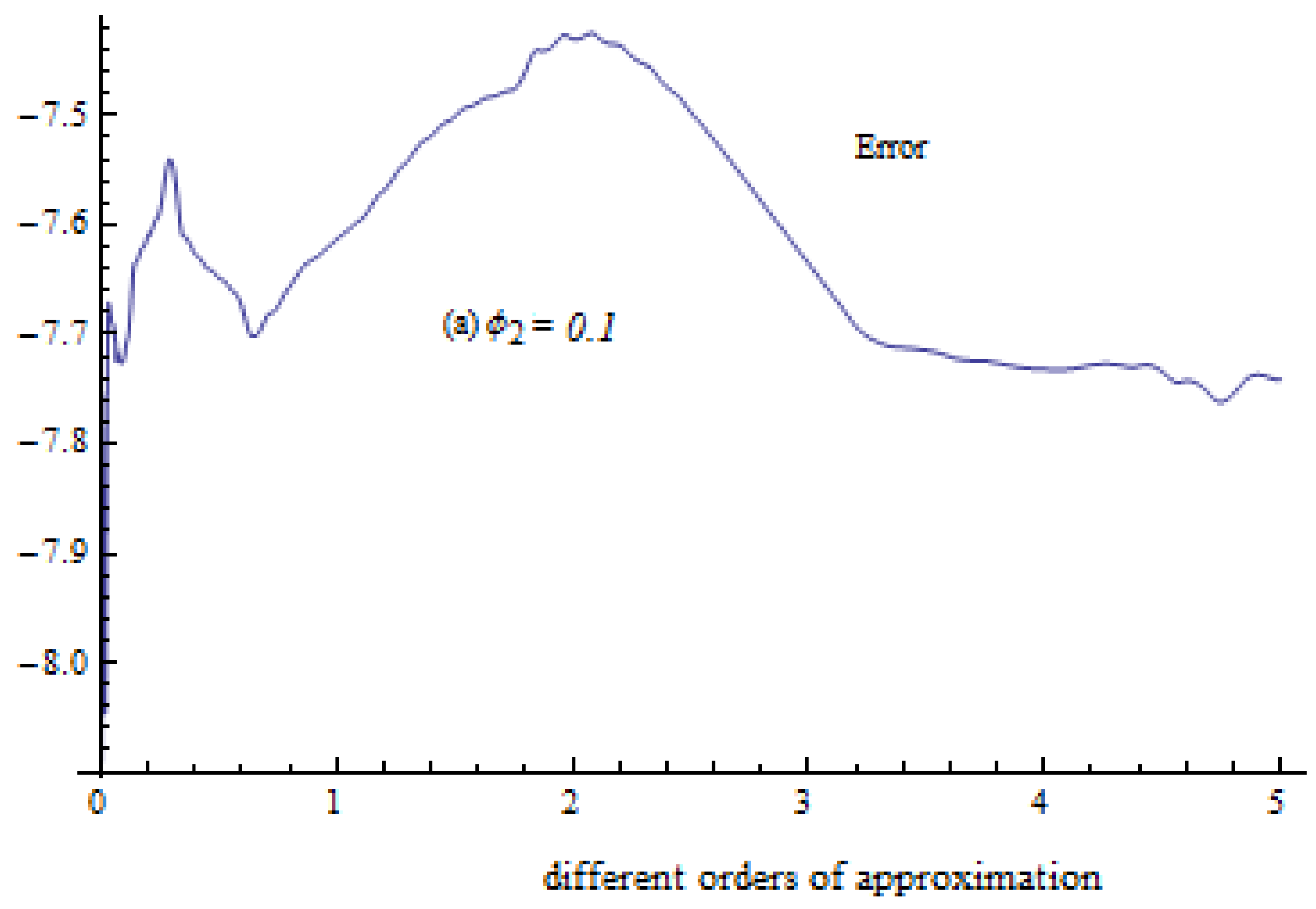
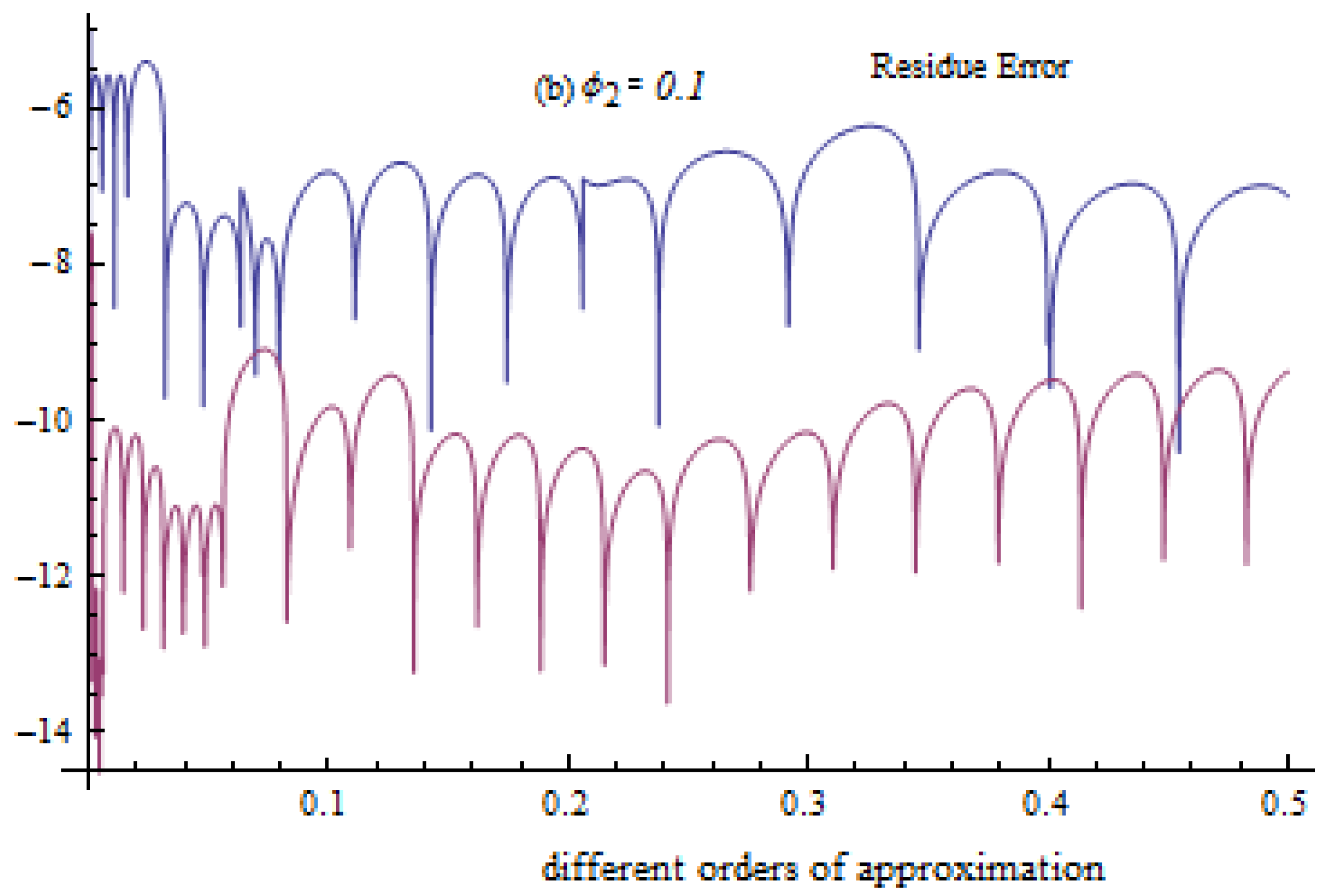
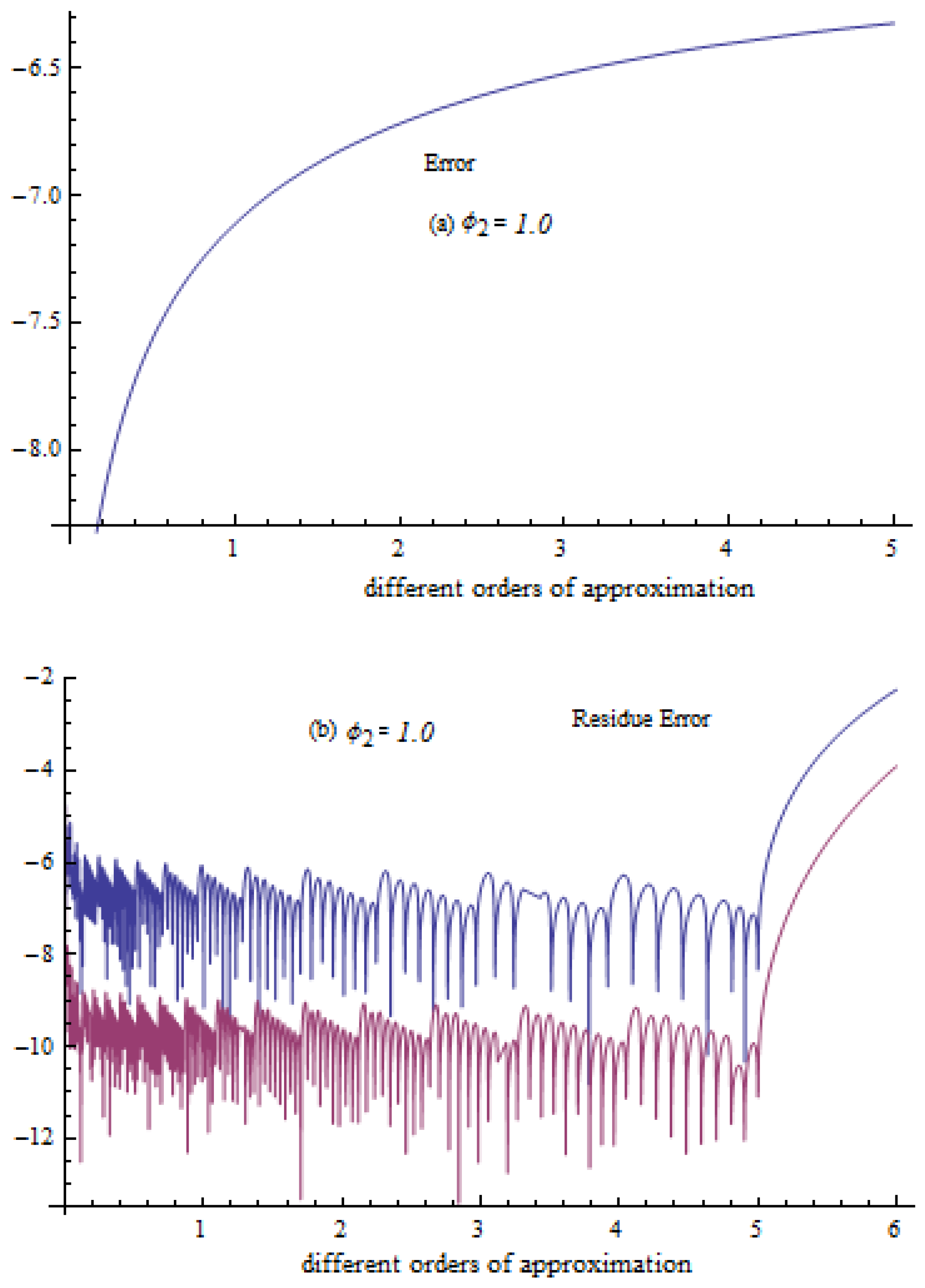
4. Error Explanation

For utmost differential equations, the outcomes given by FEM are relatively accurate. Nevertheless, because its outcomes are established on numerical sampling and error estimates, there can rarely be significant errors. Linking a solution computed with a work precision higher than the default Machine Precision (MP) is often a convenient way to check consequences. the HAM method was used with the default work precision to compute the solution of the problem and then we used the same method with working precision-22 to compute the error solution. Subsequently, errors are frequently quite small; it is beneficial to interpret them on a logarithmic scale.

In the following graphs, we computed the error solutions for different physical parameters involved in the model.

Before making physical estimations, we performed an error analysis to verify the method’s credibility. Figure 2, Figure 3, Figure 4, Figure 5, Figure 6, Figure 7 and Figure 8 are designed specifically for this goal. In the FEM procedure, the minimal error of 10⁻³⁰ is fixed throughout the computations. The Mathematica module FEM to minimize total average squared residual error was used. To observe inaccuracy for various orders of approximation, multiple examples were studied for altering Kp, Pi and placing $L_0=1.4, L_1=1.4,B_v=1.2, M=0.2,$ and $M_d=1.2$. Figure 2, Figure 3 and Figure 4 show the highest average squared residual error for various values of $K_p$ using various approximation orders. It is witnessed that the selected values of $K_p$ to show the influence on DPV and DPT are significant. In Figure 5, when ${\varphi }_2=0.2,$ the TASRE and ASRE drop as the order of approximation increases, but when ${\varphi }_2=0$, the error is dramatically reduced as compared with the case for ${\varphi }_2=0.2$, as seen in Figure 5. Consequently, when ${\varphi }_2=1$, the error is higher as compared to ${\varphi }_2=0.2$ as shown in Figure 8.

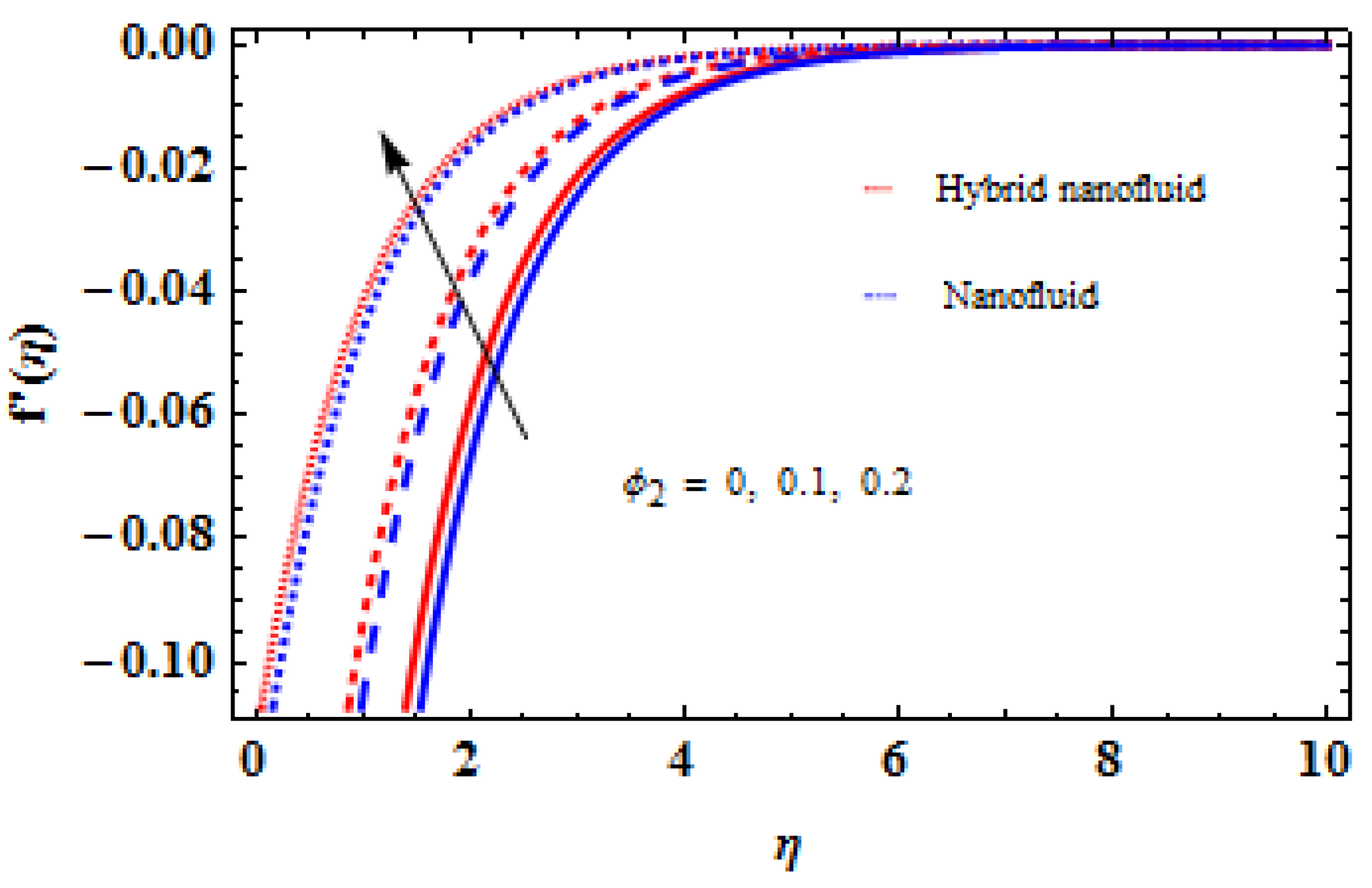
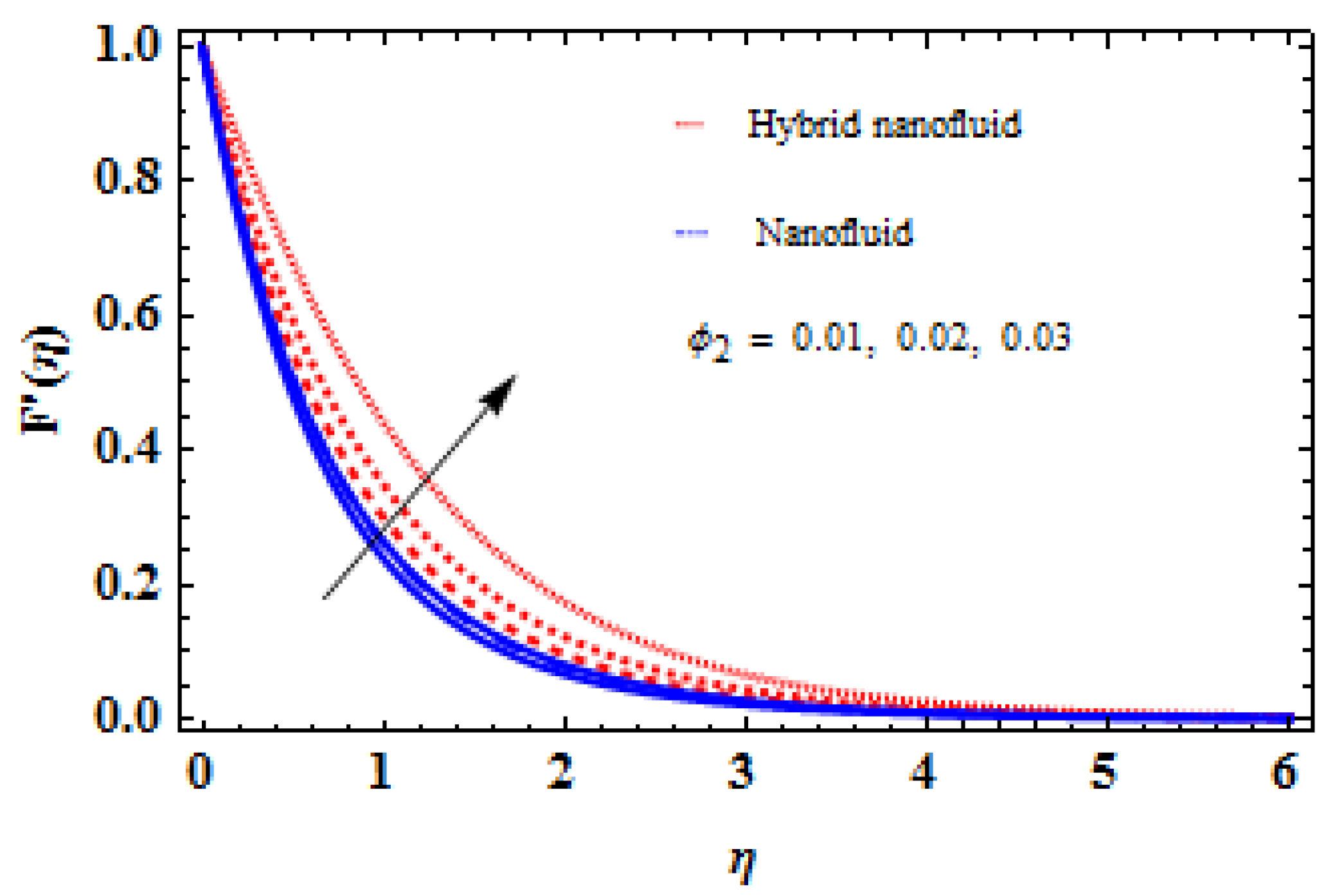
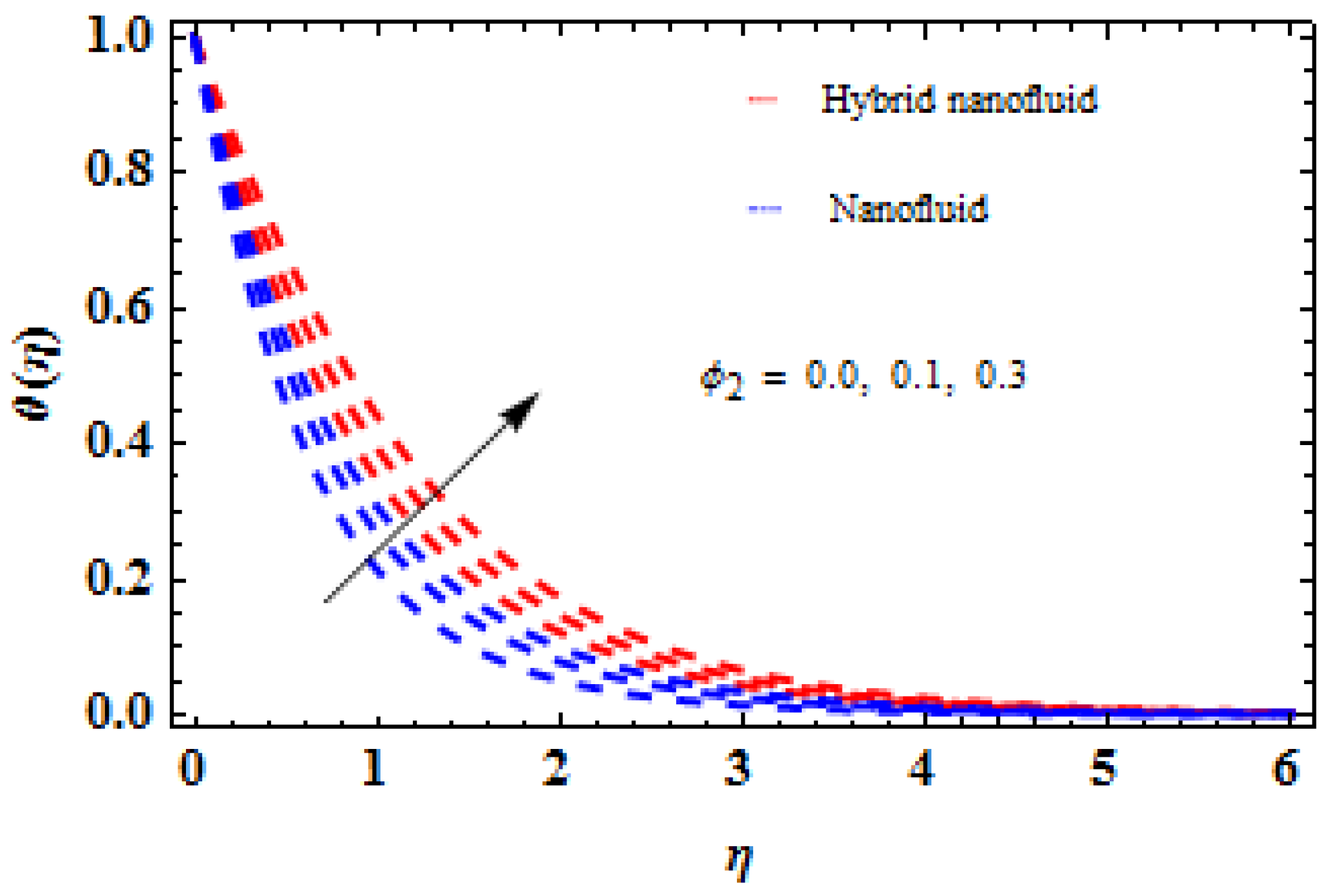
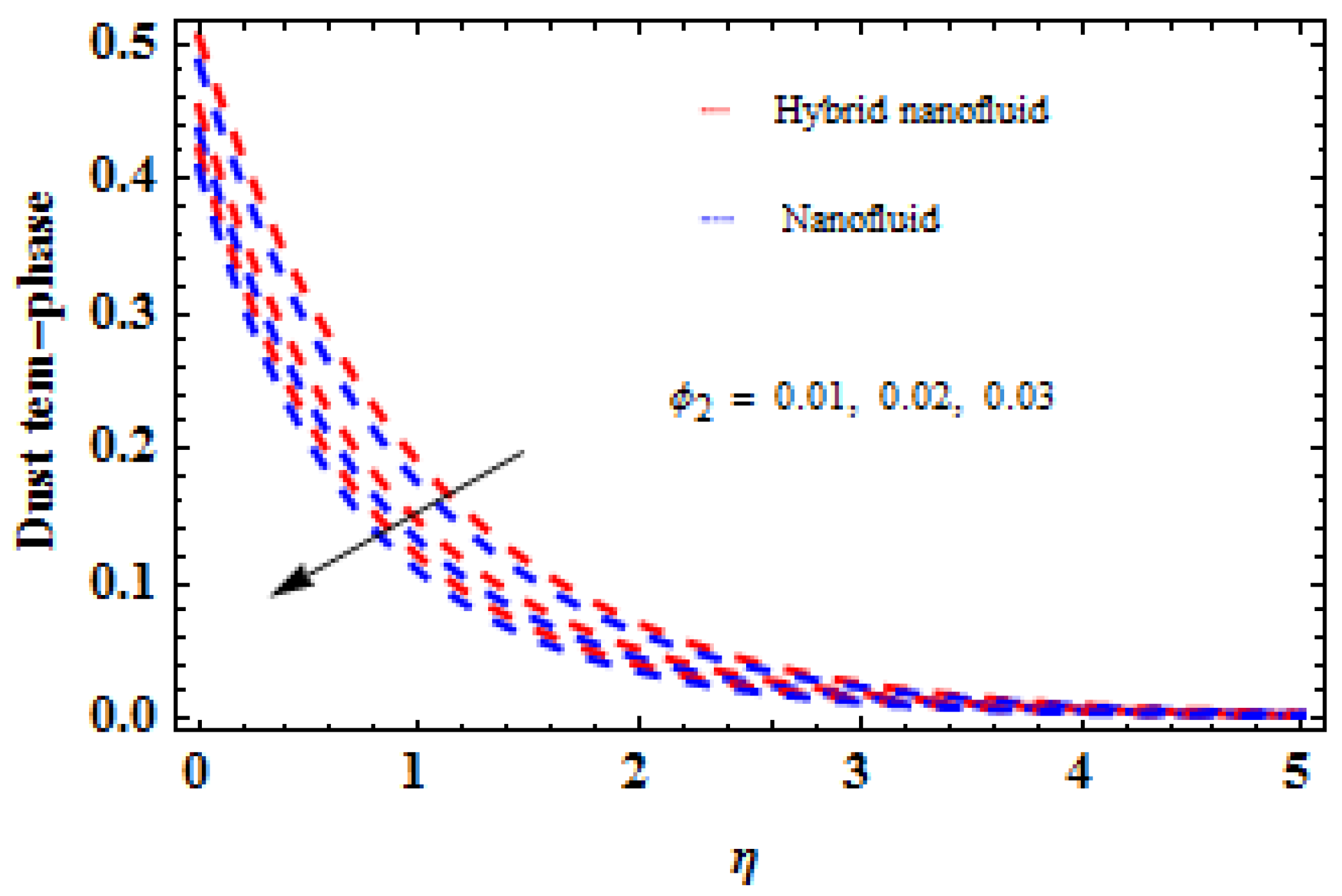
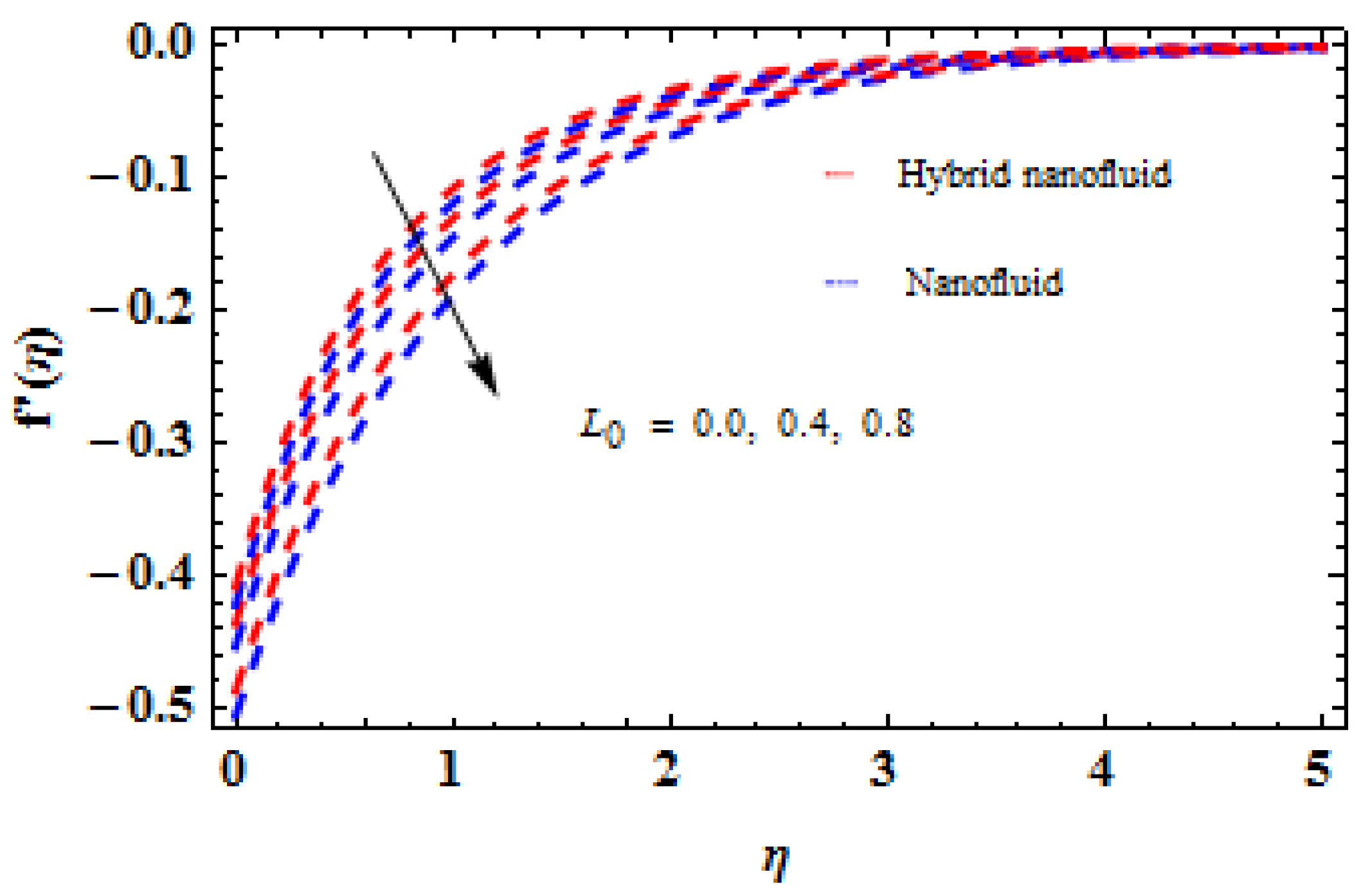
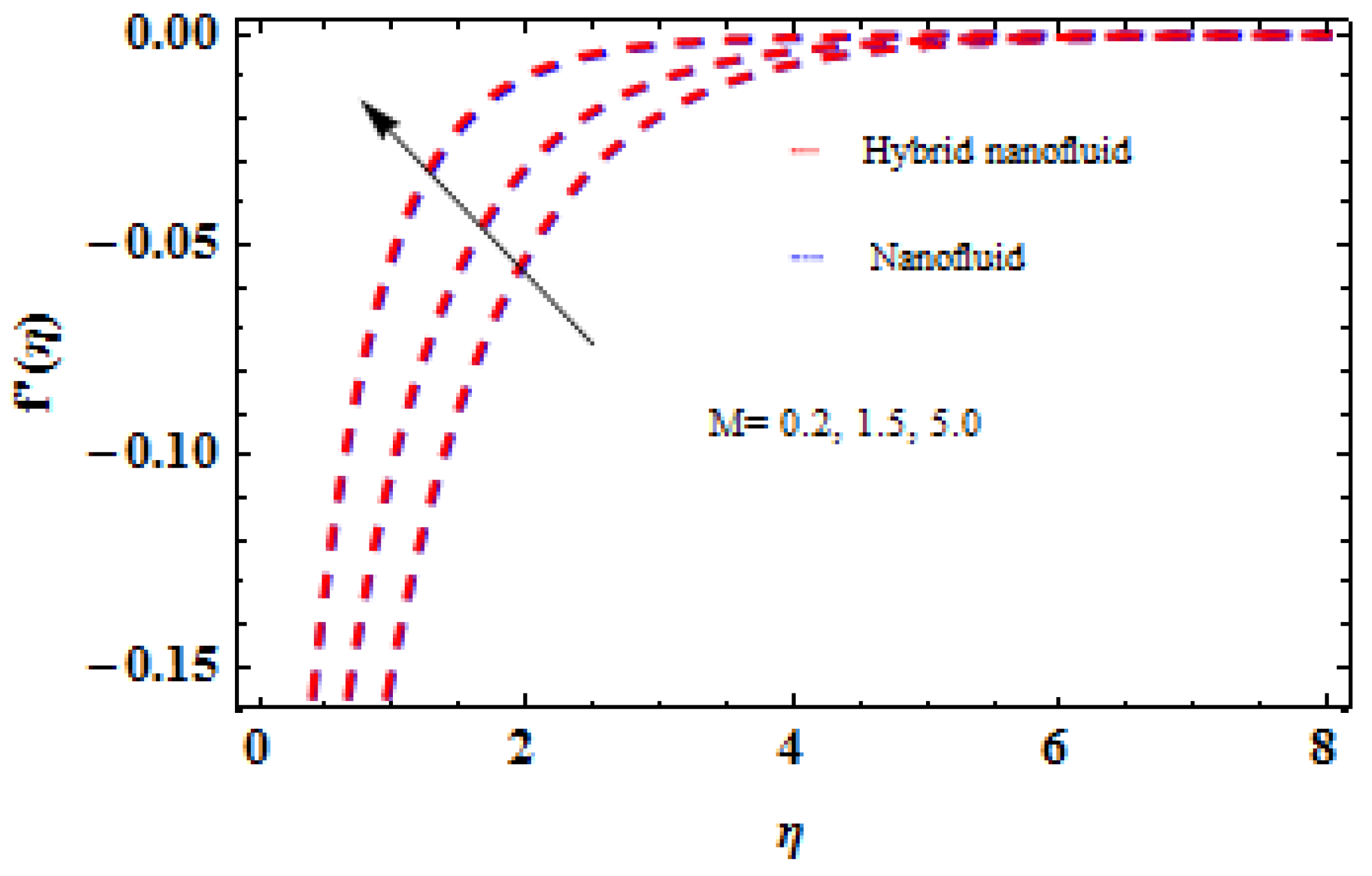
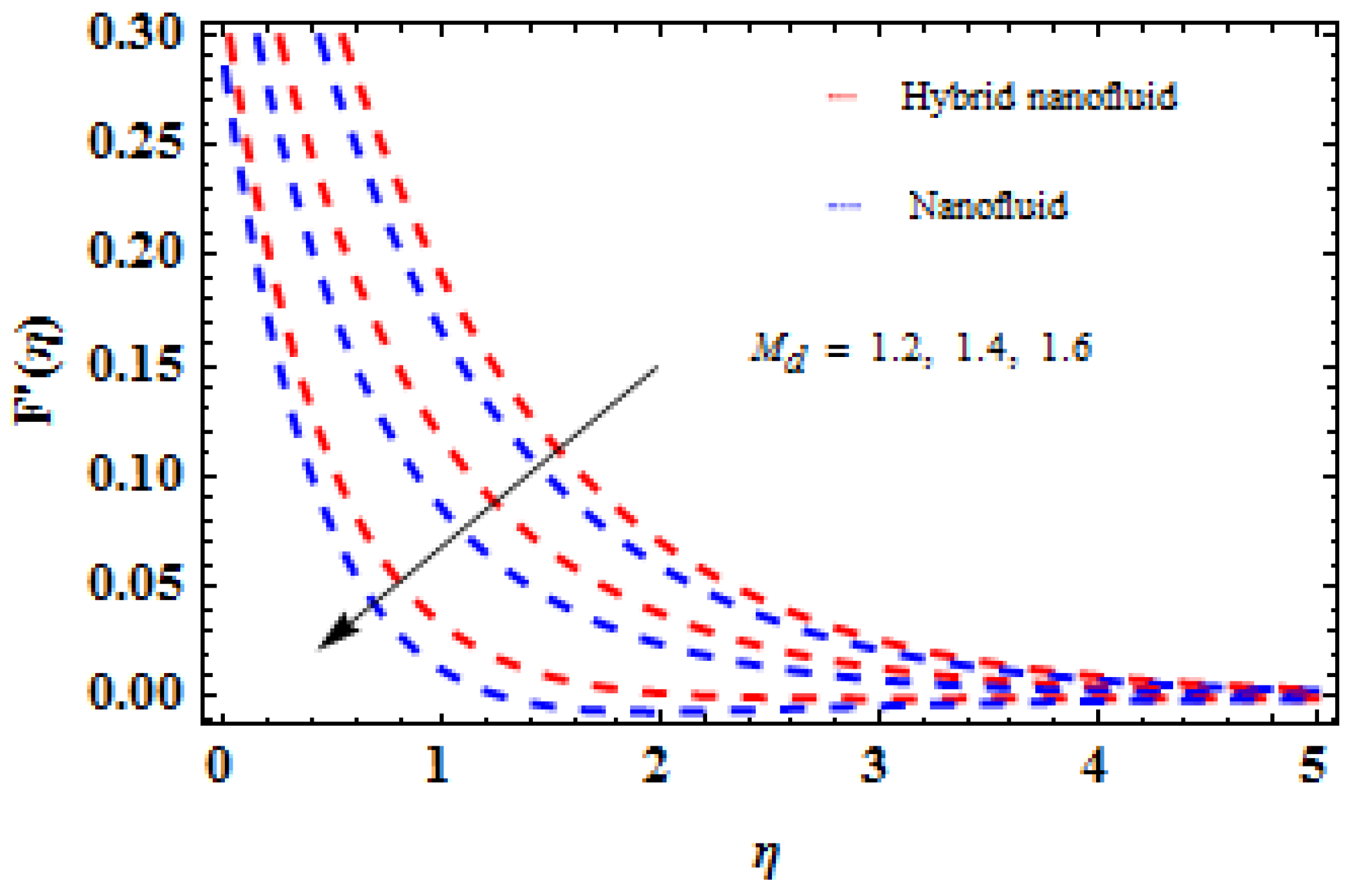
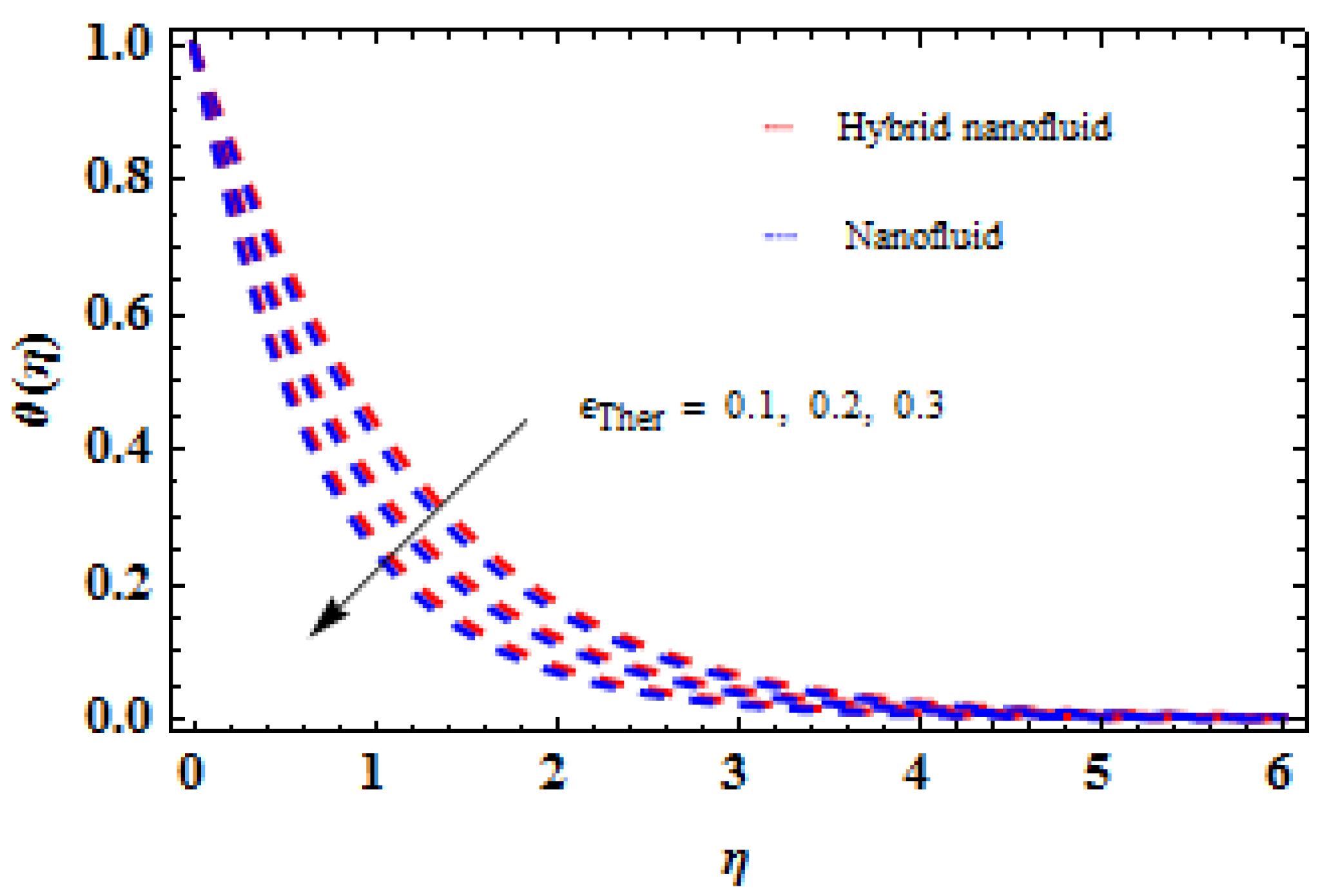
5. Analysis and Results

In this analysis, we examine the nanofluid and hybrid nanofluid over an exponentially curved surface in the presence of dust particles showing the impact of melting heat and second-order slip at the boundary. The modeled PDEs are converted to convectional ODEs through similarity transformation and then solved numerically by using FEM with MATHEMATICA SOFTWARE. This impact of various dimensionless factors on the velocity field, dust phase velocity (DPV), temperature field, dust phase temperature (DPT), and the physical quantities of interest such as Skin Friction (SF) is analyzed through graphs and tables. The confirmation of the present work with the previous one is also given.

Figure 9 is depicted to examine the relationship between the DPV of the fluid with the curvature of the curved surface (CCS). It is noted here that the DPV of the fluid is enhanced once the CCS is increased. Consequently, diminishing curved sheet radii come across a minor interaction surface region, and ultimately fluid experiences the smallest resistance. Due to small resistance, the fluid velocity is enhanced. Conversely, Figure 10 describes a differing tendency in the circumstance of the DPV. The frequency of heat transmission inside the liquid through the sheet is moderately more leisurely than a flow in CCS. As a result, a decline in the DPT is perceived. It is importance to know that the results on account of hybrid nanoliquid are stronger than the nanoliquid stream. Figure 11 and Figure 12 are designed to inspect the solid volume fraction ${\varphi }_2$ on velocity field $f^{\prime }\left(\eta \right)$ and the DPV $F^{\prime }\left(\eta \right)$. It is observed that the liquid velocity $f^{\prime }\left(\eta \right)$ displays rising performance close to the sheet and, away from the boundary, it shows diminishing performance for higher assessment of ${\varphi }_2$. Likewise, enhancing phenomena are noticed for dusty liquid $F^{\prime }\left(\eta \right)$ (Figure 12). Here, again the strength of the hybrid nanofluid is witnessed. The nanosized particle thermal conductivity enlarges for advanced approximations of ${\varphi }_2$ which upsurges the heat transmission as a consequence of fluid temperature augments (Figure 13) for both HN and nanofluid.

Figure 14 reveals the fluid DPT performance for distinguishing values of the solid volumetric fraction. It is perceived that the fluid DPT declines. Furthermore, it was observed that the ethylene-glycol nanofluid was slightest affected by the immersion of ${\varphi }_2$ relative to (Cu−CuO)-hybrid nanofluid due to the decreased density guesses of the copper-based ethylene glycol nanofluid.

Figure 15 and Figure 16 disclose the variation in $f^{\prime }\left(\eta \right)$ for numerous values of factors $L_0$ (first) and $L_1$ (second). From this analysis, it is examined that augmentations in $L_0$, indicate a descent in velocity magnitude $f^{\prime }\left(\eta \right)$ and a boost in $L_1$ fluid velocity for both situations increase. Figure 17 shows the impact of melting heat factor $M$ on fluid velocity. Obviously, the amount of liquid molecule with the dust speed of liquid ascends toward the bigger $M$. This is because of the more grounded sub-atomic movement that ultimately helps the liquid speed. For hybrid nanoliquid, attributes are significant. The variation of numerous values of $B_v$ and $M_d$ on $F^{\prime }\left(\eta \right)$ is visible in Figure 18 and Figure 19, respectively. It is investigated that the dust phase stream is the decreasing function of $B_v$ and $M_d.$ For various values of ${\epsilon }_{Ther}$ (thermal relaxation time) on the temperature field $\theta \left(\eta \right),$ Figure 20 is designed. A development in ${\epsilon }_{Ther}$ estimations designates a lesser temperature. The bigger approximations of ${\epsilon }_{Ther}$ indicate that the sequestered type is substantial and is responsible for the reduction in the liquid temperature.

The motivation of factor$\gamma$ on DPT is notable in Figure 21. For rising values of $\gamma$, the temperature of the fluid is enhanced. Figure 22 shows the Eckert number’s ($Ec)$ impact on the temperature field both for nanofluid and hybrid nanofluid. With an increasing Ec, an enormous heat modification is recognized. This heat escalation is due to frictional heating by an upgrade in Ec.

The stability of the present outcomes is described in

Table 2. Validation of the present work to the published work for Skin Friction (SF) $C_f\sqrt{R{e}_s}$ by varying $a_1$ when $Bv=L_0=0=L_1=M={\varphi }_1={\varphi }_2=0$.

${\mathit{K}}_{\mathit{p}}$	Present Work	Published Work [45]	Relative Error (%)
5	1.418911	1.418910	0.2 $\times$ 10−5
10	1.346602	1.346600	0.6 $\times$ 107
20	1.313613	1.313610	1.1 $\times$ 10−9
30	1.302801	1.302800	3.02 $\times$ 10−11
50	1.297512	1.297510	5.2 $\times$ 10−13
15	1.294402	1.294410	1.7 $\times$ 10−16
20	1.288104	1.288100	0.9 $\times$ 10−21

and is an admirable settlement with the published result reported by Kumar et al. [45].

Table 3. Evaluations of SF for numerous values taking Pr = 5, Bv = 0.5, M_d = 10 fixed.

Skin Friction
$L_0$	Nanofluid	Hybrid nanofluid
0.1	0.62711	0.68294
0.3	0.68324	0.74782
0.5	0.75485	0.83164
Skin Friction
${\varphi }_2$	Nanofluid	Hybrid nanofluid
0.1	0.53744	0.58389
0.3	0.56885	0.61826
0.5	0.59326	0.65572
Skin Friction
$L_1$	Nanofluid	Hybrid nanofluid
0.2	1.29731	1.49161
0.4	0.79299	0.87499
0.8	0.5344	0.58389
Skin Friction
$K_p$	Nanofluid	Hybrid nanofluid
1	0.79558	0.89749
2	0.93826	0.91633
3	0.93799	0.99629
Skin Friction
$M$	Nanofluid	Hybrid nanofluid
2	0.45851	0.49471
4	0.42724	0.43335
6	0.42638	0.42775

portrays the disparity in Skin Friction (SF) for the statistical estimates of various factors. It is perceived that SF enlarges for rising assessments of ${\varphi }_2$, $L_0$, and $K_p$. Conversely, an opposing tendency is countersigned in the situation of $L_1$, and M in the occasion of HN and nanofluid simulations.

6. Concluding Remarks

In this review, a correlation of the Cu/EG (nanofluid) and Cu-CuO/EG (Hybrid nanofluid) enclosing dust particles has been introduced towards MFL through a curved surface with a second-order slip effect. The mathematical problem is solved numerically using FEM [54] and the effects of various factors are explained diagrammatically against related profiles and in an organized structure. For the confirmation of the mathematical model the present work is compared with the previous and by error analysis. The key points of the present study are:

• It is observed that the dust-phase velocity $F^{\prime }\left(\eta \right)$ is improved when $K_p$ is augmented.
• It is examined that the velocity profile is increased with the increasing values of ${\varphi }_2,$while the phase-density velocity declines with growing values of ${\varphi }_2$.
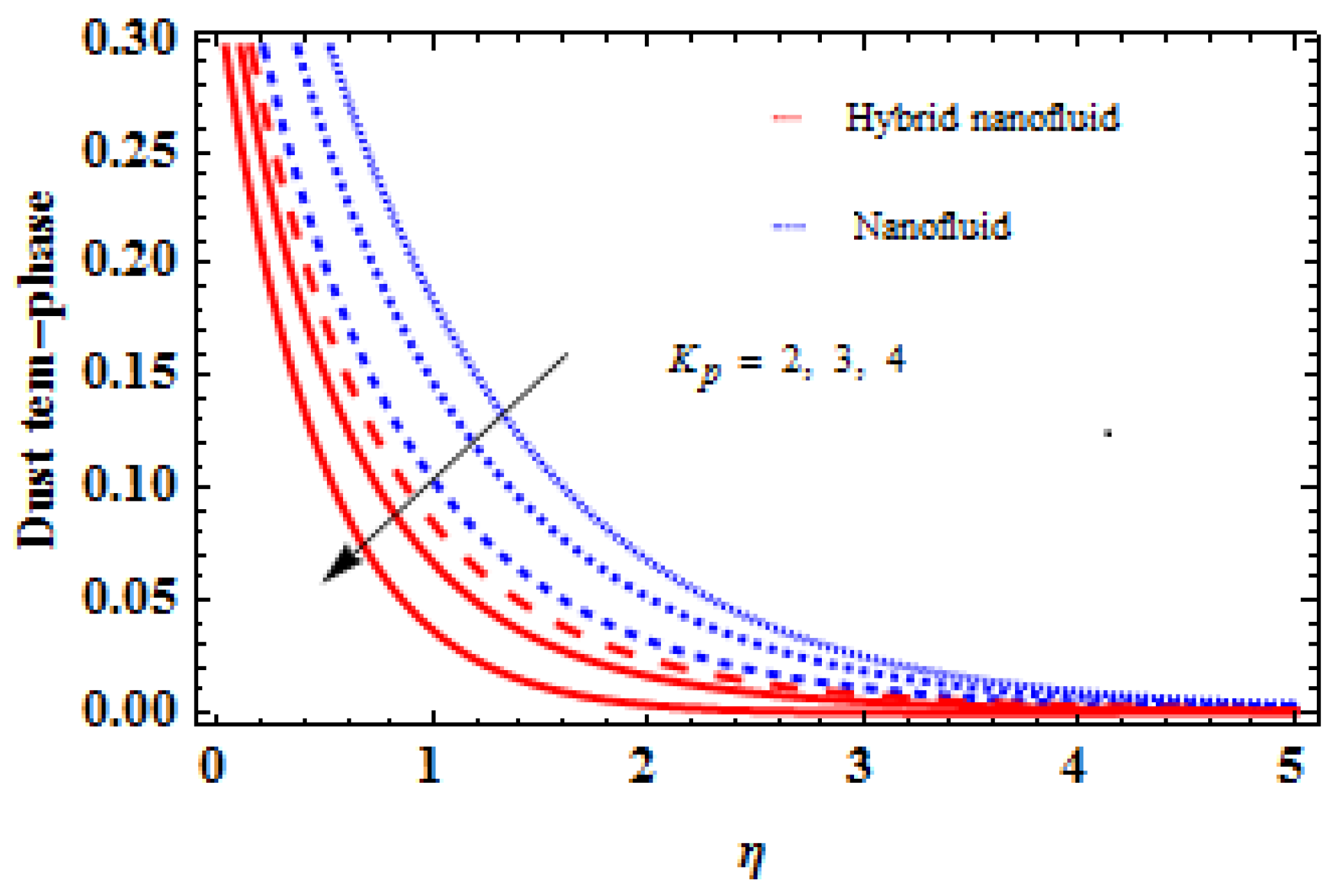
• When compared to the thermal relaxation factor, the temperature of the liquid decreases.
• Similarly, for each of the liquid and dusty phases, rising and diminishing tendencies can be detected in the motion and thermal profiles against the curvature factor.
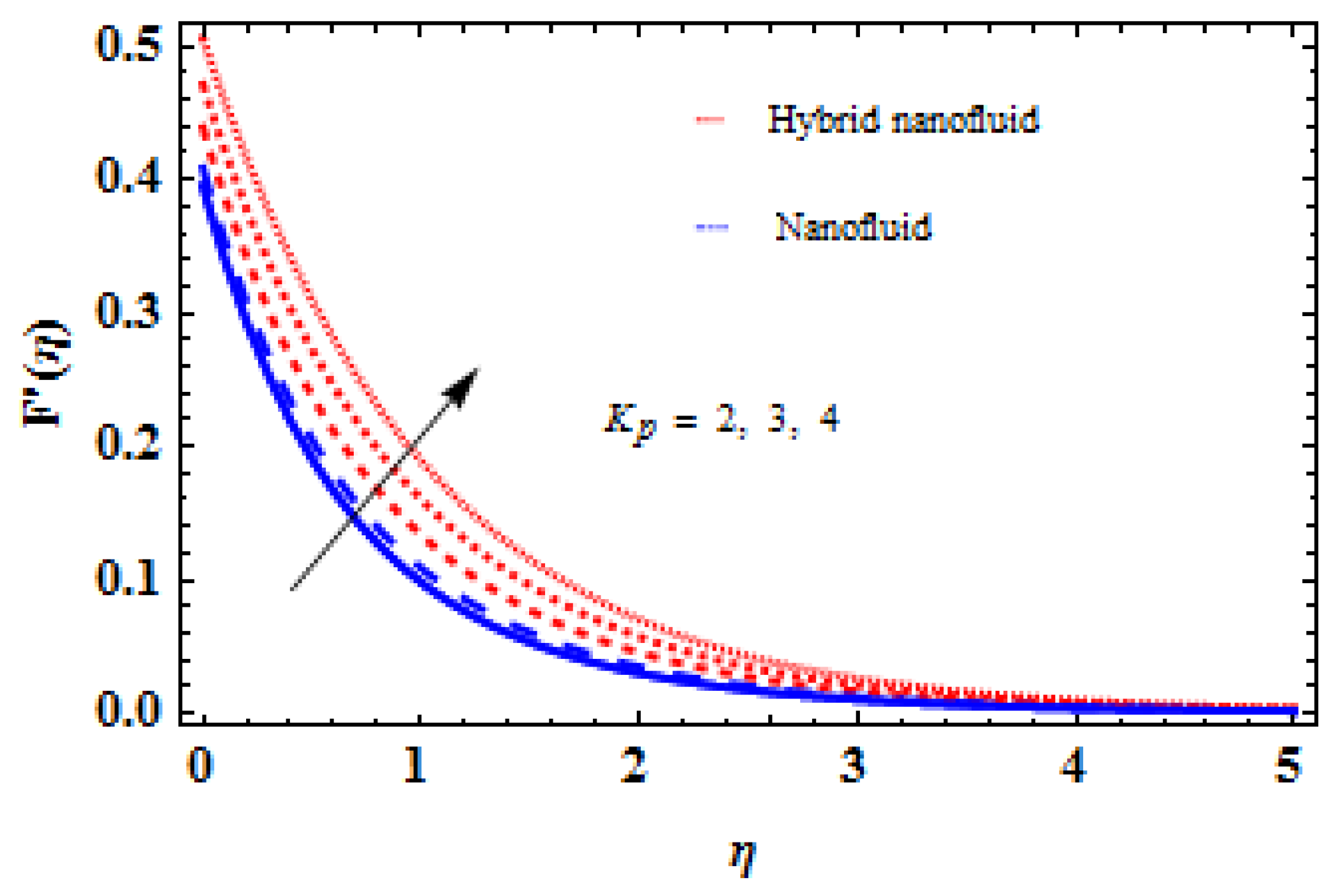
• The efficiency of the hybrid nanofluid is much better than that of the conventional nanofluid.
• The first-order slip factor, the curved factor, and the dragging force component all have increasing effects on the velocity field DPV, temperature field, and DPT. However, it decreases for the second-order slippage factor.