Low-Rank Matrix Completion via QR-Based Retraction on Manifolds
Abstract
1. Introduction
2. Preliminary
3. Algorithms
| Algorithm 1 Initialization |
| Input: data M and rank r Output: initialization
|
| Algorithm 2 Steepest descent (SD) direction of the function in (9) with orthogonality of Q |
| Input: Data M, iterate , rank r, and metric constant . Output: SD direction
|
| Algorithm 3 Conjugate descent (CD) direction of the function in (9) |
| Input: Last conjugate direction (Set ), conjugate direction . Output: Conjugate direction .
|
| Algorithm 4 Exact line search |
| Input: Data M, iterate , Conjugate direction . Output: Step size s.
|
| Algorithm 5 Inexact line search |
| Input: Data M, iterate x, constant , times limitation , parameter , SD direction , and CD direction . Output: Stepsize s.
|
| Algorithm 6 Retraction with QR factorization |
| Input: Iteration , direction , stepsize and parameter . Output: Next iterate .
|
| Algorithm 7 Modified Gram–Schmidt algorithm |
| Input: with . Output: and .
|
| Algorithm 8 QR Riemannian gradient descent (QRRGD) |
| Input: Function (see (9)), initial point (generated by Algorithm 1), tolerance parameter Output:
|
| Algorithm 9 QR Riemannian conjugate gradient (QRRCG) |
| Input: Function (see (9)), initial point , tolerance parameter p Output:
|
4. Analysis
4.1. Convergence
4.2. Computational Cost
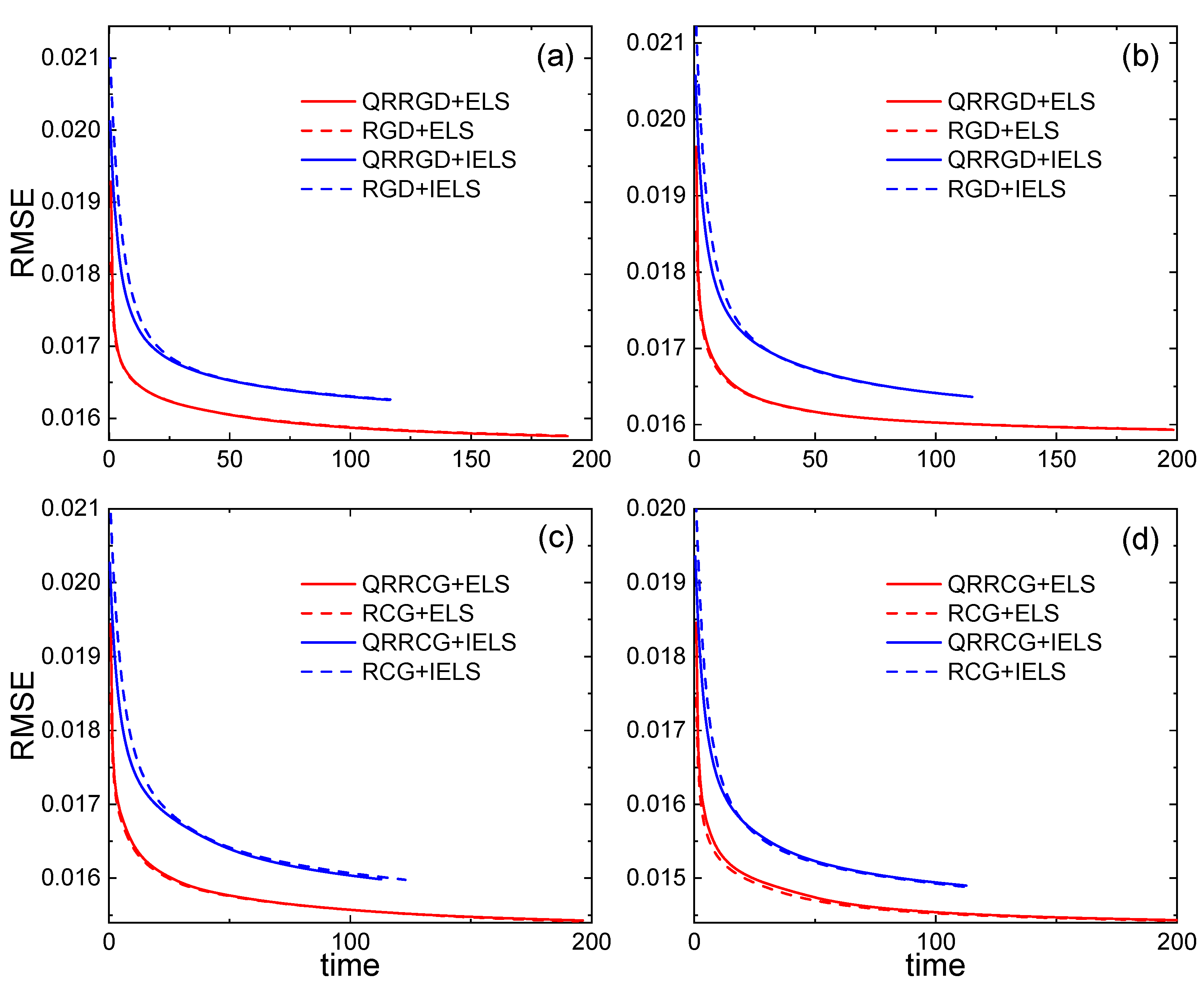
5. Numerical Experiments
5.1. Synthetic Data
5.2. Empirical Data
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Candes, E.J.; Plan, Y. Matrix Completion With Noise. Proc. IEEE 2010, 98, 925–936. [Google Scholar] [CrossRef]
- Xu, Y.; Yin, W.; Wen, Z.; Zhang, Y. An alternating direction algorithm for matrix completion with nonnegative factors. Front. Math. China 2012, 7, 365–384. [Google Scholar] [CrossRef]
- Markovsky, I.; Usevich, K. Structured Low-Rank Approximation with Missing Data. SIAM J. Matrix Anal. Appl. 2013, 34, 814–830. [Google Scholar] [CrossRef]
- Markovsky, I. Recent progress on variable projection methods for structured low-rank approximation. Signal Process. 2014, 96, 406–419. [Google Scholar] [CrossRef]
- Usevich, K.; Comon, P. Hankel Low-Rank Matrix Completion: Performance of the Nuclear Norm Relaxation. IEEE J. Sel. Top. Signal Process. 2016, 10, 637–646. [Google Scholar] [CrossRef]
- Davenport, M. An overview of low-rank matrix recovery from incomplete observations. IEEE J. Sel. Top. Signal Process. 2016, 10, 608–622. [Google Scholar] [CrossRef]
- Chi, Y. Low-rank matrix completion [lecture notes]. IEEE Signal Process. Mag. 2018, 35, 178–181. [Google Scholar] [CrossRef]
- Ding, Y.; Krislock, N.; Qian, J.; Wolkowicz, H. Sensor Network Localization, Euclidean Distance Matrix completions, and graph realization. Optim. Eng. 2010, 11, 45–66. [Google Scholar] [CrossRef]
- Liu, Z.; Vandenberghe, L. Interior-Point Method for Nuclear Norm Approximation with Application to System Identification. SIAM J. Matrix Anal. Appl. 2010, 31, 1235–1256. [Google Scholar] [CrossRef]
- Jacob, M.; Mani, M.P.; Ye, J.C. Structured Low-Rank Algorithms: Theory, Magnetic Resonance Applications, and Links to Machine Learning. IEEE Signal Process. Mag. 2020, 37, 54–68. [Google Scholar] [CrossRef]
- Jawanpuria, P.; Mishra, B. Structured low-rank matrix learning: Algorithms and applications. arXiv 2017, arXiv:1704.07352. [Google Scholar]
- Lu, S.; Ren, X.; Liu, F. Depth Enhancement via Low-rank Matrix Completion. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Columbus, OH, USA, 23–28 June 2014; pp. 3390–3397. [Google Scholar]
- Nguyen, L.T.; Kim, J.; Shim, B. Low-rank matrix completion: A contemporary survey. IEEE Access 2019, 7, 94215–94237. [Google Scholar] [CrossRef]
- Vandereycken, B. Low-rank matrix completion by Riemannian optimization. SIAM J. Optim. 2013, 23, 1214–1236. [Google Scholar] [CrossRef]
- Wang, H.; Zhao, R.; Cen, Y.; Liang, L.; He, Q.; Zhang, F.; Zeng, M. Low-rank matrix recovery via smooth rank function and its application in image restoration. Int. J. Mach. Learn. Cybern. 2018, 9, 1565–1576. [Google Scholar] [CrossRef]
- Candès, E.J.; Recht, B. Exact matrix completion via convex optimization. Found. Comput. Math. 2009, 9, 717–772. [Google Scholar] [CrossRef]
- Cai, J.F.; Candès, E.J.; Shen, Z. A singular value thresholding algorithm for matrix completion. SIAM J. Optim. 2010, 20, 1956–1982. [Google Scholar] [CrossRef]
- Lee, K.; Bresler, Y. Admira: Atomic decomposition for minimum rank approximation. IEEE Trans. Inf. Theory 2010, 56, 4402–4416. [Google Scholar] [CrossRef]
- Jain, P.; Netrapalli, P.; Sanghavi, S. Low-rank matrix completion using alternating minimization. In Proceedings of the 45th Annual ACM Symposium on Theory of Computing, Palo Alto, CA, USA, 1–4 June 2013; pp. 665–674. [Google Scholar]
- Tanner, J.; Wei, K. Low rank matrix completion by alternating steepest descent methods. Appl. Comput. Harmon. Anal. 2016, 40, 417–429. [Google Scholar] [CrossRef]
- Absil, P.A.; Mahony, R.; Sepulchre, R. Optimization Algorithms on Matrix Manifolds; Princeton University Press: Princeton, NJ, USA, 2009. [Google Scholar]
- Boumal, N. An Introduction to Optimization on Smooth Manifolds; Cambridge University Press: Cambridge, UK, 2023. [Google Scholar]
- Guglielmi, N.; Scalone, C. An efficient method for non-negative low-rank completion. Adv. Comput. Math. 2020, 46, 31. [Google Scholar] [CrossRef]
- Mishra, B.; Meyer, G.; Bonnabel, S.; Sepulchre, R. Fixed-rank matrix factorizations and Riemannian low-rank optimization. Comput. Stat. 2014, 29, 591–621. [Google Scholar] [CrossRef]
- Cambier, L.; Absil, P.A. Robust low-rank matrix completion by Riemannian optimization. SIAM J. Sci. Comput. 2016, 38, S440–S460. [Google Scholar] [CrossRef]
- Dong, S.; Absil, P.A.; Gallivan, K. Riemannian gradient descent methods for graph-regularized matrix completion. Linear Algebra Its Appl. 2021, 623, 193–235. [Google Scholar] [CrossRef]
- Zhu, X. A Riemannian conjugate gradient method for optimization on the Stiefel manifold. Comput. Optim. Appl. 2017, 67, 73–110. [Google Scholar] [CrossRef]
- Sato, H.; Aihara, K. Cholesky QR-based retraction on the generalized Stiefel manifold. Comput. Optim. Appl. 2019, 72, 293–308. [Google Scholar] [CrossRef]
- Golub, G.H.; Van Loan, C.F. Matrix Computations; JHU Press: Baltimore, MD, USA, 2013. [Google Scholar]
- Keshavan, R.H.; Montanari, A.; Oh, S. Matrix completion from noisy entries. J. Mach. Learn. Res. 2010, 11, 2057–2078. [Google Scholar]
- Dai, Y.H.; Yuan, Y. A nonlinear conjugate gradient method with a strong global convergence property. SIAM J. Optim. 1999, 10, 177–182. [Google Scholar] [CrossRef]
- Armijo, L. Minimization of functions having Lipschitz continuous first partial derivatives. Pac. J. Math. 1966, 16, 1–3. [Google Scholar] [CrossRef]
- Björck, Å.; Paige, C.C. Loss and recapture of orthogonality in the modified Gram–Schmidt algorithm. SIAM J. Matrix Anal. Appl. 1992, 13, 176–190. [Google Scholar] [CrossRef]
- O’Searcoid, M. Metric Spaces; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2006. [Google Scholar]
- Boyd, S.; Boyd, S.P.; Vandenberghe, L. Convex optimization; Cambridge University Press: Cambridge, UK, 2004. [Google Scholar]
- Nesterov, Y. Introductory Lectures on Convex Optimization: A Basic Course; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2003. [Google Scholar]
- Dua, D.; Graff, C. UCI Machine Learning Repository. 2017. Available online: http://archive.ics.uci.edu/ml (accessed on 10 February 2019).
- Liu, J.; Feng, Y.; Zou, L. Some three-term conjugate gradient methods with the inexact line search condition. Calcolo 2018, 55, 1–16. [Google Scholar] [CrossRef]
- Zhou, G.; Huang, W.; Gallivan, K.A.; Van Dooren, P.; Absil, P.A. A Riemannian rank-adaptive method for low-rank optimization. Neurocomputing 2016, 192, 72–80. [Google Scholar] [CrossRef]
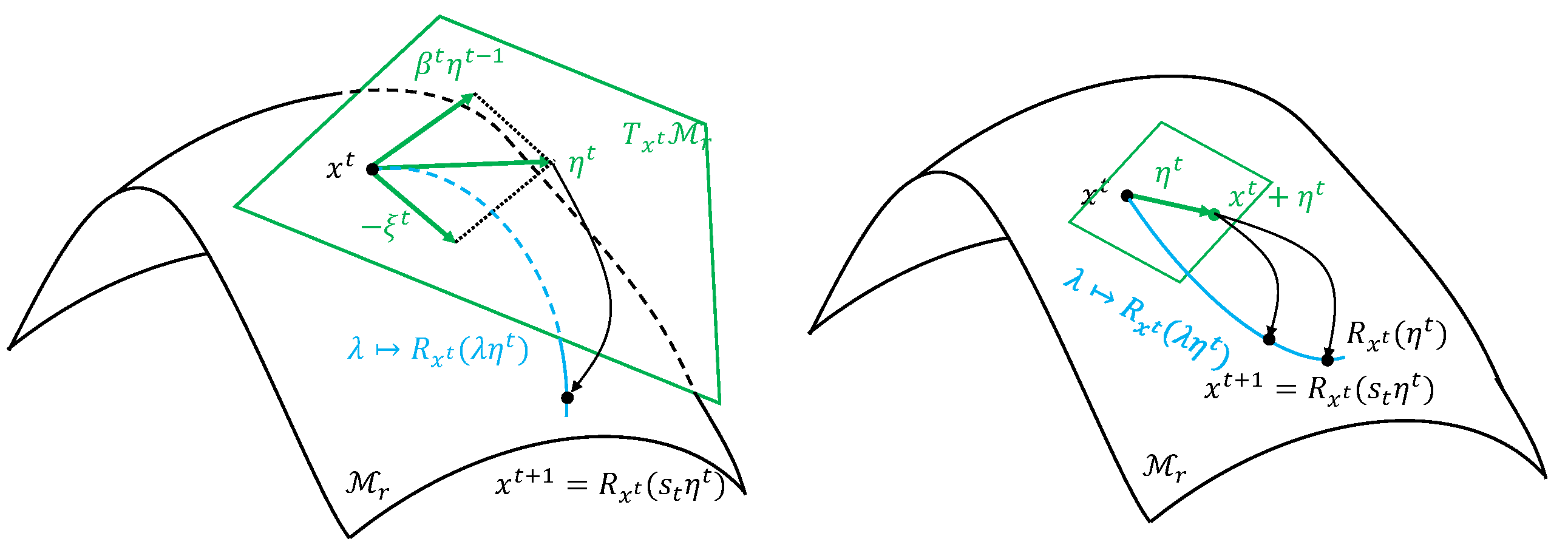

| Computation | Cost |
|---|---|
| Computation | Cost |
|---|---|
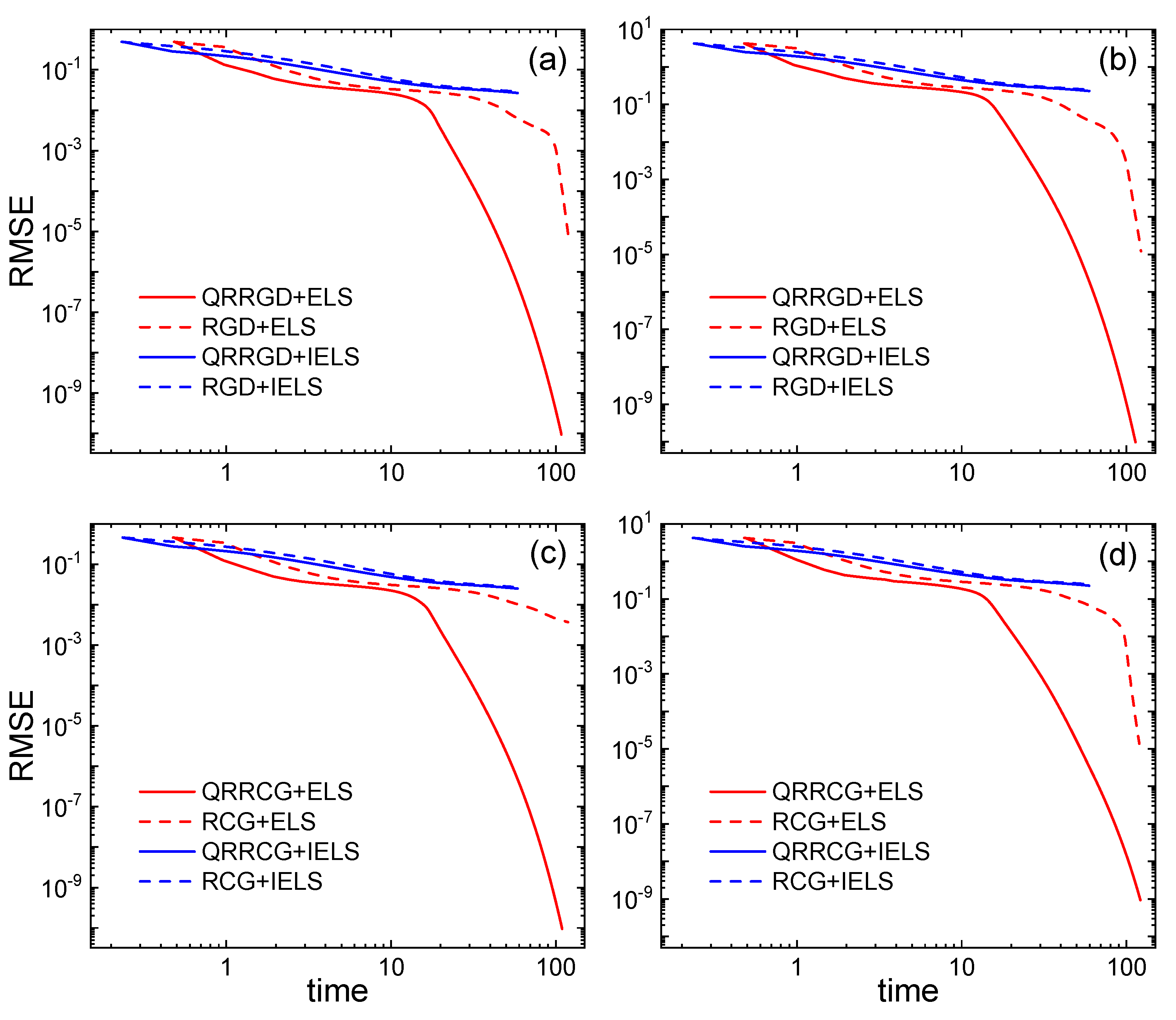
| Subfigure | Method | Time | RMSE | Iteration |
|---|---|---|---|---|
| (a) | QRRGD+ELS | 108.282 | 223 | |
| RGD+ELS | 120.644 | 250 | ||
| QRRGD+IELS | 58.763 | 250 | ||
| RGD+IELS | 57.905 | 250 | ||
| (b) | QRRGD+ELS | 113.655 | 237 | |
| RGD+ELS | 122.815 | 250 | ||
| QRRGD+IELS | 59.640 | 250 | ||
| RGD+IELS | 59.400 | 250 | ||
| (c) | QRRCG+ELS | 109.363 | 227 | |
| RCG+ELS | 118.726 | 250 | ||
| QRRCG+IELS | 58.677 | 250 | ||
| RCG+IELS | 59.849 | 250 | ||
| (d) | QRRCG+ELS | 121.740 | 250 | |
| RCG+ELS | 119.905 | 250 | ||
| QRRCG+IELS | 59.449 | 250 | ||
| RCG+IELS | 58.432 | 250 |
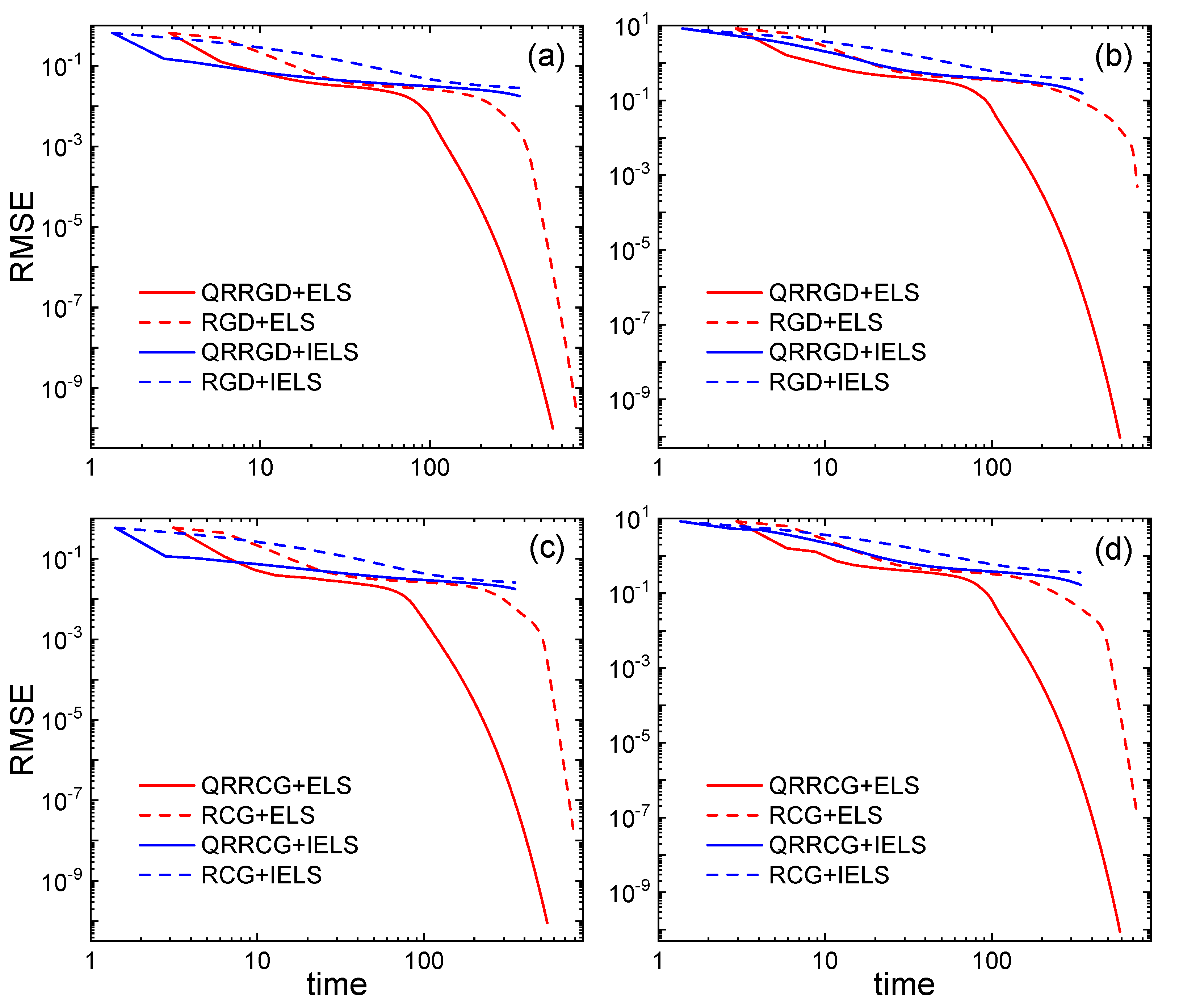
| Subfigure | Method | Time | RMSE | Iteration |
|---|---|---|---|---|
| (a) | QRRGD+ELS | 529.851 | 181 | |
| RGD+ELS | 733.993 | 250 | ||
| QRRGD+IELS | 337.730 | 250 | ||
| RGD+IELS | 335.950 | 250 | ||
| (b) | QRRGD+ELS | 586.522 | 201 | |
| RGD+ELS | 745.970 | 250 | ||
| QRRGD+IELS | 349.708 | 250 | ||
| RGD+IELS | 348.213 | 250 | ||
| (c) | QRRCG+ELS | 547.370 | 173 | |
| RCG+ELS | 782.545 | 250 | ||
| QRRCG+IELS | 351.655 | 250 | ||
| RCG+IELS | 350.344 | 250 | ||
| (d) | QRRCG+ELS | 586.297 | 199 | |
| RCG+ELS | 738.357 | 250 | ||
| QRRCG+IELS | 341.237 | 250 | ||
| RCG+IELS | 338.835 | 250 |
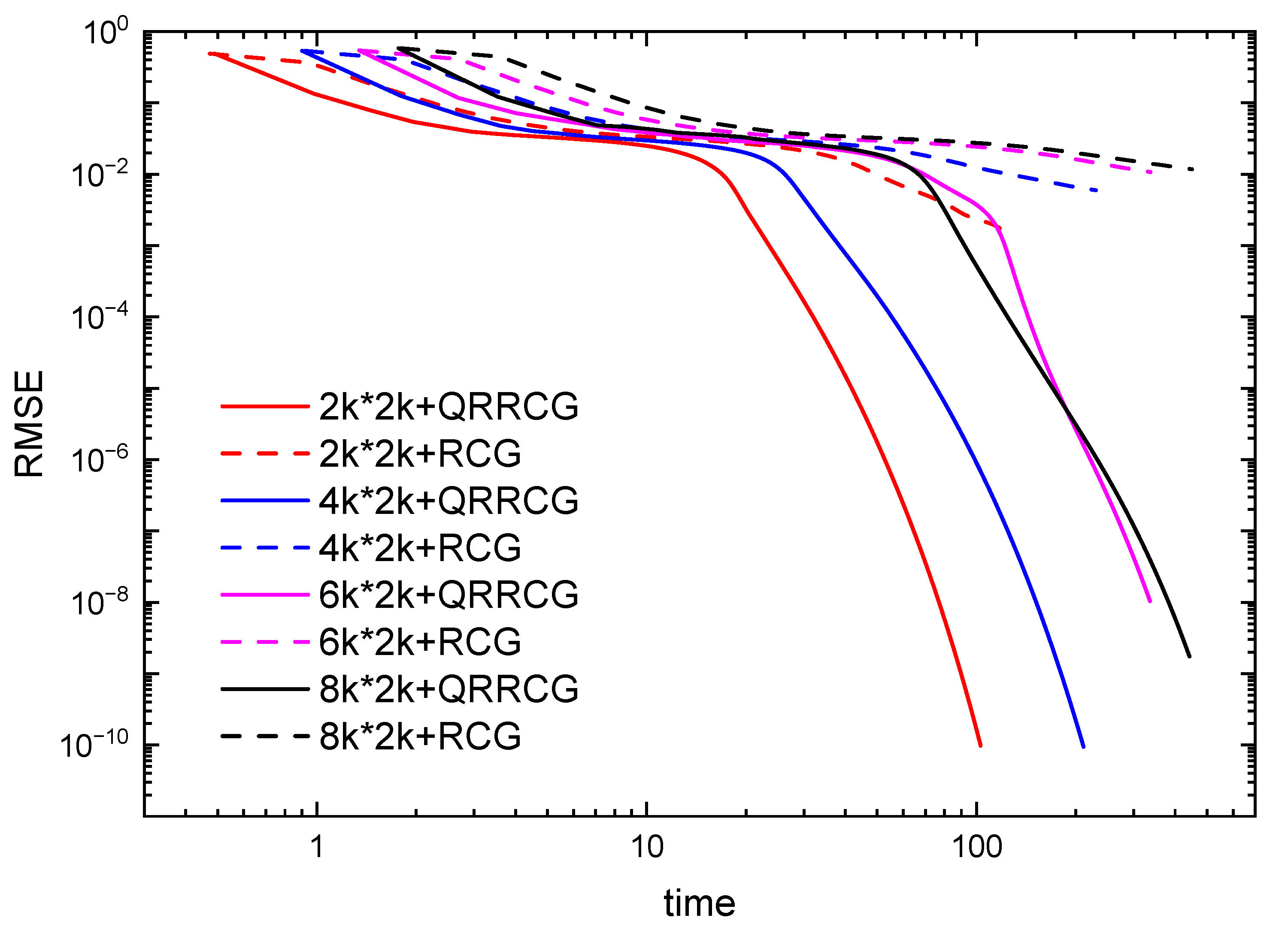
| r,OSF | Size | Method | Time | RMSE | Iteration |
|---|---|---|---|---|---|
| 18,2.79 | QRRCG | 102.939 | 210 | ||
| RCG | 118.397 | 250 | |||
| 24,2.79 | QRRCG | 211.122 | 234 | ||
| RCG | 230.015 | 250 | |||
| 27,2.79 | QRRCG | 335.745 | 250 | ||
| RCG | 336.917 | 250 | |||
| 29,2.77 | QRRCG | 442.133 | 250 | ||
| RCG | 449.752 | 250 |
| Subfigure | Method | Time | RMSE | Iteration |
|---|---|---|---|---|
| (a) | QRG+ELS | 189.945 | 250 | |
| RGD+ELS | 192.104 | 250 | ||
| QRRGD+IELS | 116.213 | 250 | ||
| RGD+IELS | 116.576 | 250 | ||
| (b) | QRRGD+ELS | 198.433 | 250 | |
| RGD+ELS | 196.615 | 250 | ||
| QRRGD+IELS | 115.070 | 250 | ||
| RGD+IELS | 113.418 | 250 | ||
| (c) | QRRCG+ELS | 196.291 | 250 | |
| RCG+ELS | 194.373 | 250 | ||
| QRRCG+IELS | 112.798 | 250 | ||
| RCG+IELS | 122.820 | 250 | ||
| (d) | QRRCG+ELS | 201.373 | 250 | |
| RCG+ELS | 196.029 | 250 | ||
| QRRCG+IELS | 112.663 | 250 | ||
| RCG+IELS | 112.358 | 250 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, K.; Chen, Z.; Ying, S.; Xu, X. Low-Rank Matrix Completion via QR-Based Retraction on Manifolds. Mathematics 2023, 11, 1155. https://doi.org/10.3390/math11051155
Wang K, Chen Z, Ying S, Xu X. Low-Rank Matrix Completion via QR-Based Retraction on Manifolds. Mathematics. 2023; 11(5):1155. https://doi.org/10.3390/math11051155
Chicago/Turabian StyleWang, Ke, Zhuo Chen, Shihui Ying, and Xinjian Xu. 2023. "Low-Rank Matrix Completion via QR-Based Retraction on Manifolds" Mathematics 11, no. 5: 1155. https://doi.org/10.3390/math11051155
APA StyleWang, K., Chen, Z., Ying, S., & Xu, X. (2023). Low-Rank Matrix Completion via QR-Based Retraction on Manifolds. Mathematics, 11(5), 1155. https://doi.org/10.3390/math11051155








