Insights into the 3D Slip Dynamics of Jeffrey Fluid Due to a Rotating Disk with Exponential Space-Dependent Heat Generation: A Case Involving a Non-Fourier Heat Flux Model
Abstract
1. Introduction
- What influence do the Deborah number, Hall effect, and magnetic field have on the hydrodynamics of the Jeffrey fluid surface layer under first-order slip conditions?
- How do CCTFM characteristics affect heat transport features under thermal slip conditions?
- What effect do the ERTS and TRTS parameters have on the temperature and the Nusselt number?
- What effect does the Deborah number have on the friction factors?
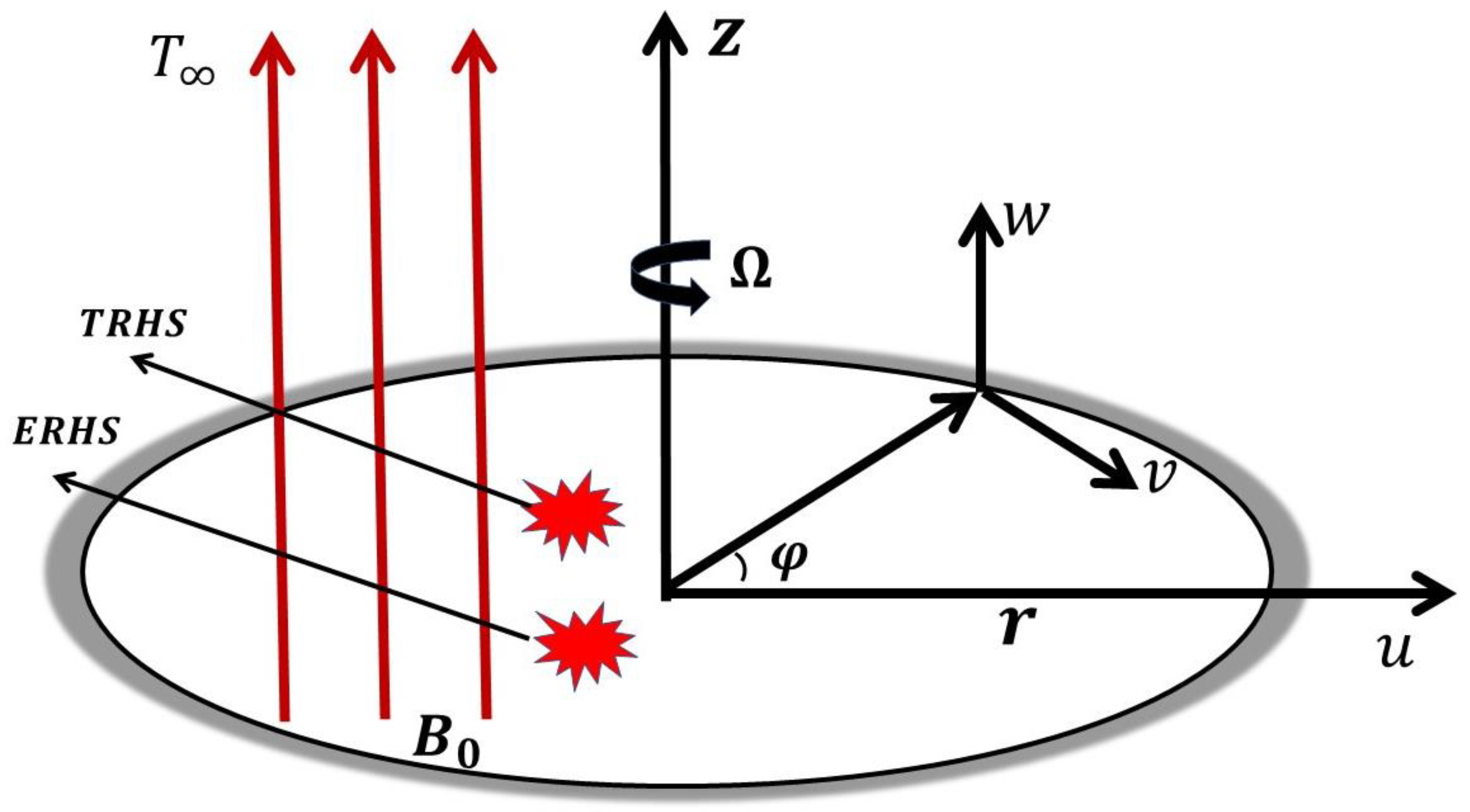
2. Formulation of the Problem
- The flow is laminar, steady, and axisymmetric.
- The fluid is incompressible, meaning that the density of the fluid is taken to be constant.
- Fluid properties are kept constant.
- The first-order velocity slip and temperature jump conditions are incorporated on the disk surface, whereas the velocity and temperature are kept constant in an ambient state.
- The Cattaneo–Christov heat flux (CCHF) model for temperature is used.
- The electric field, ion slip, and polarization effects are ignored.
3. Numerical Approach
4. Results and Discussion



5. Concluding Remarks
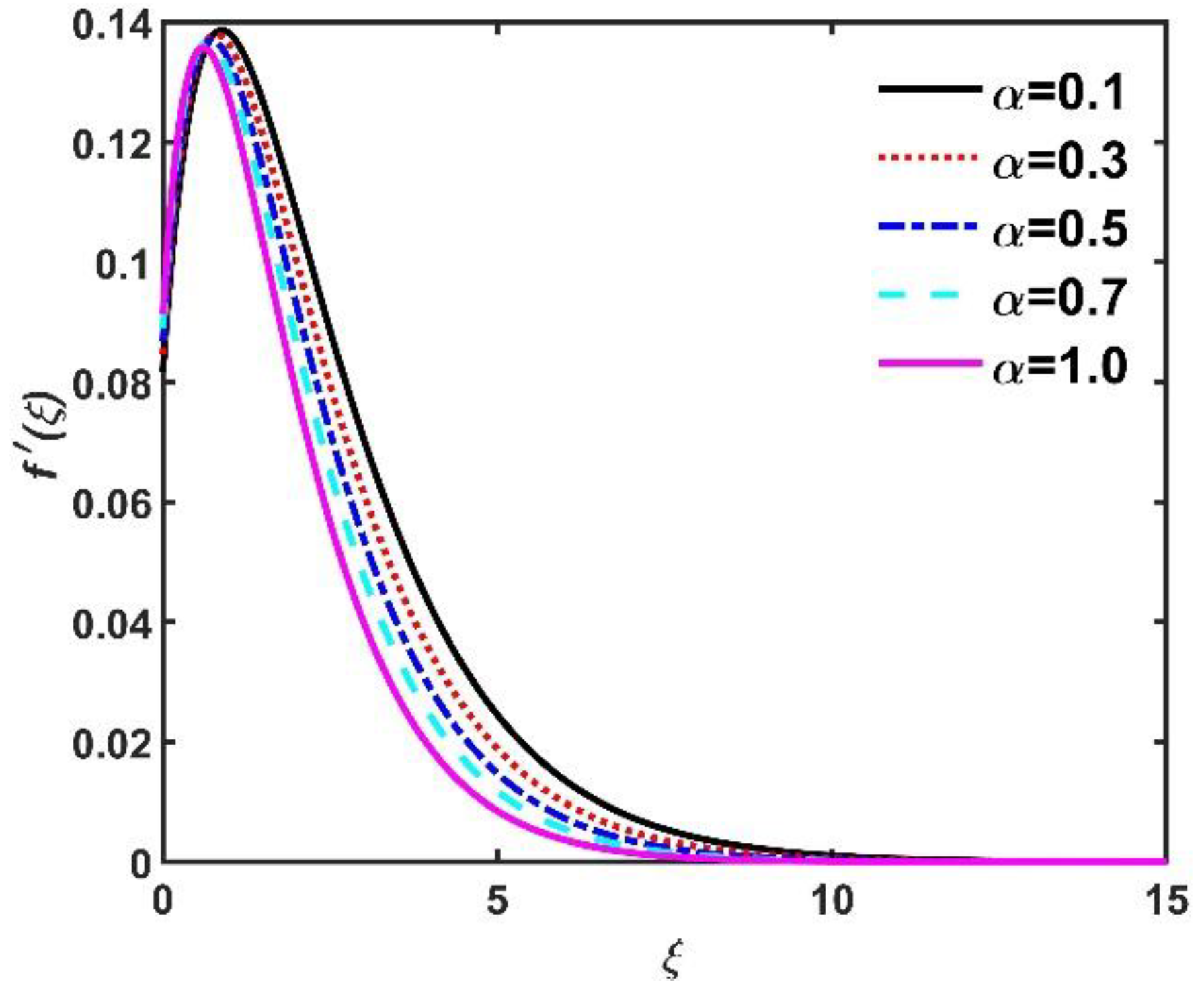
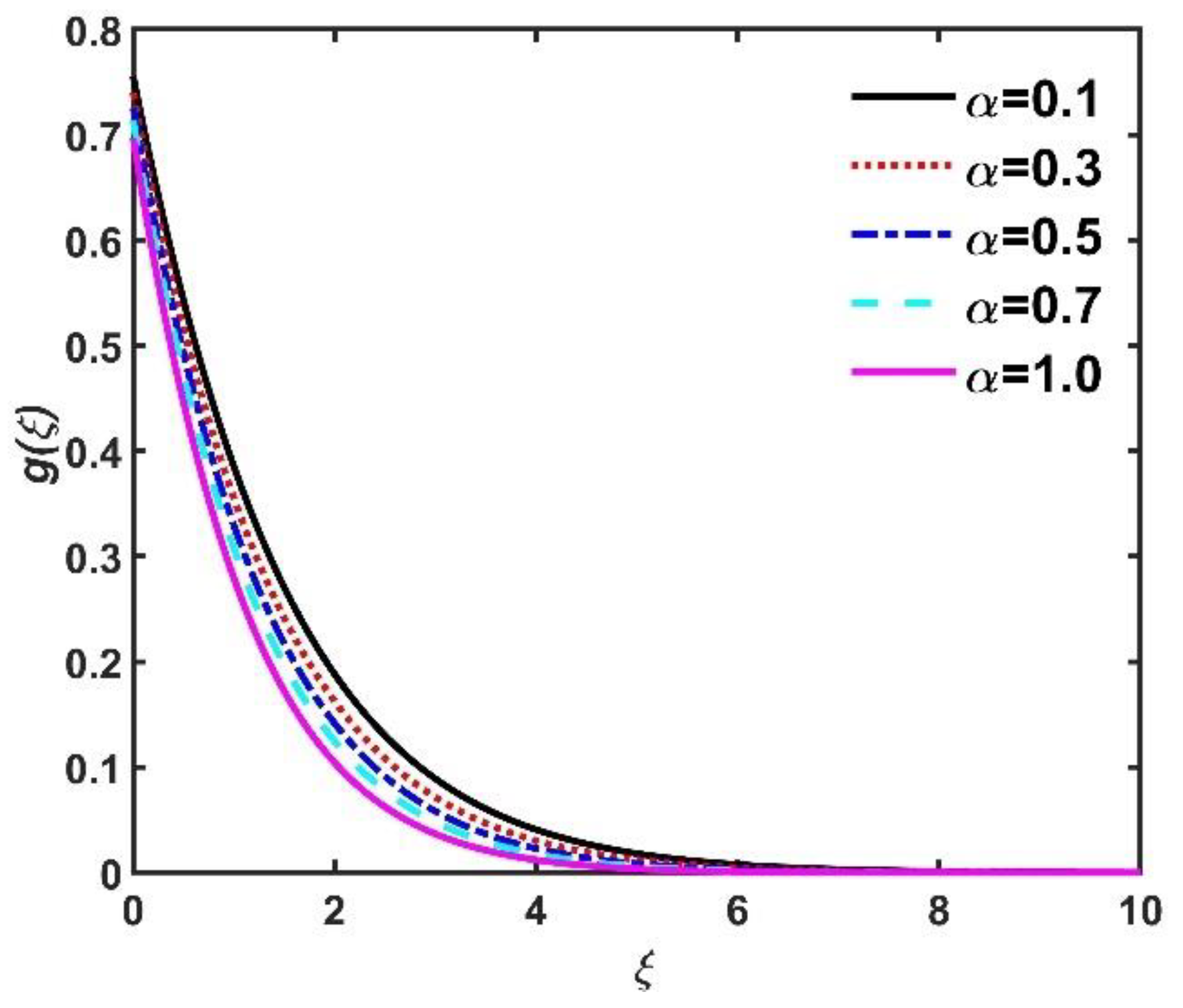
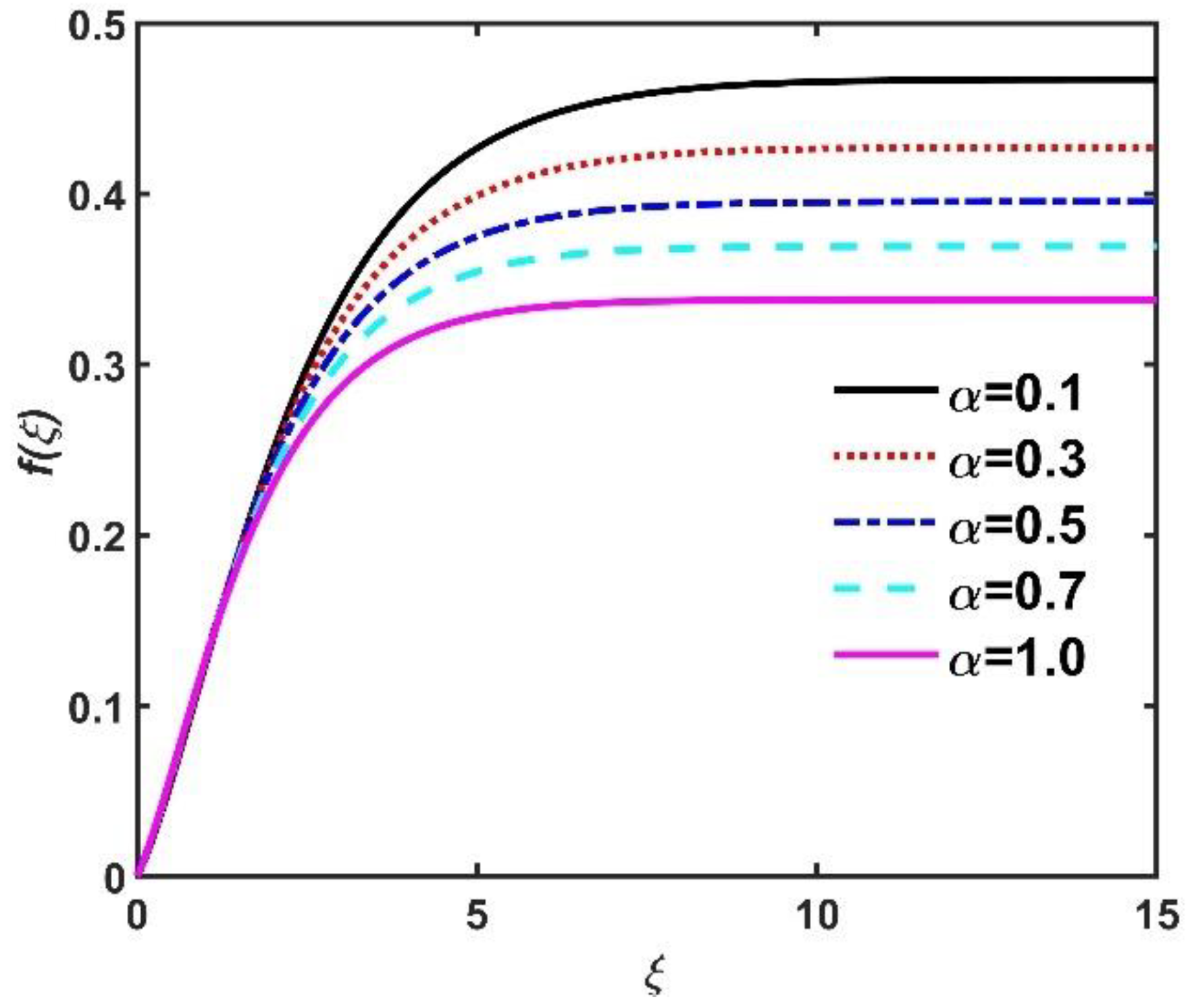
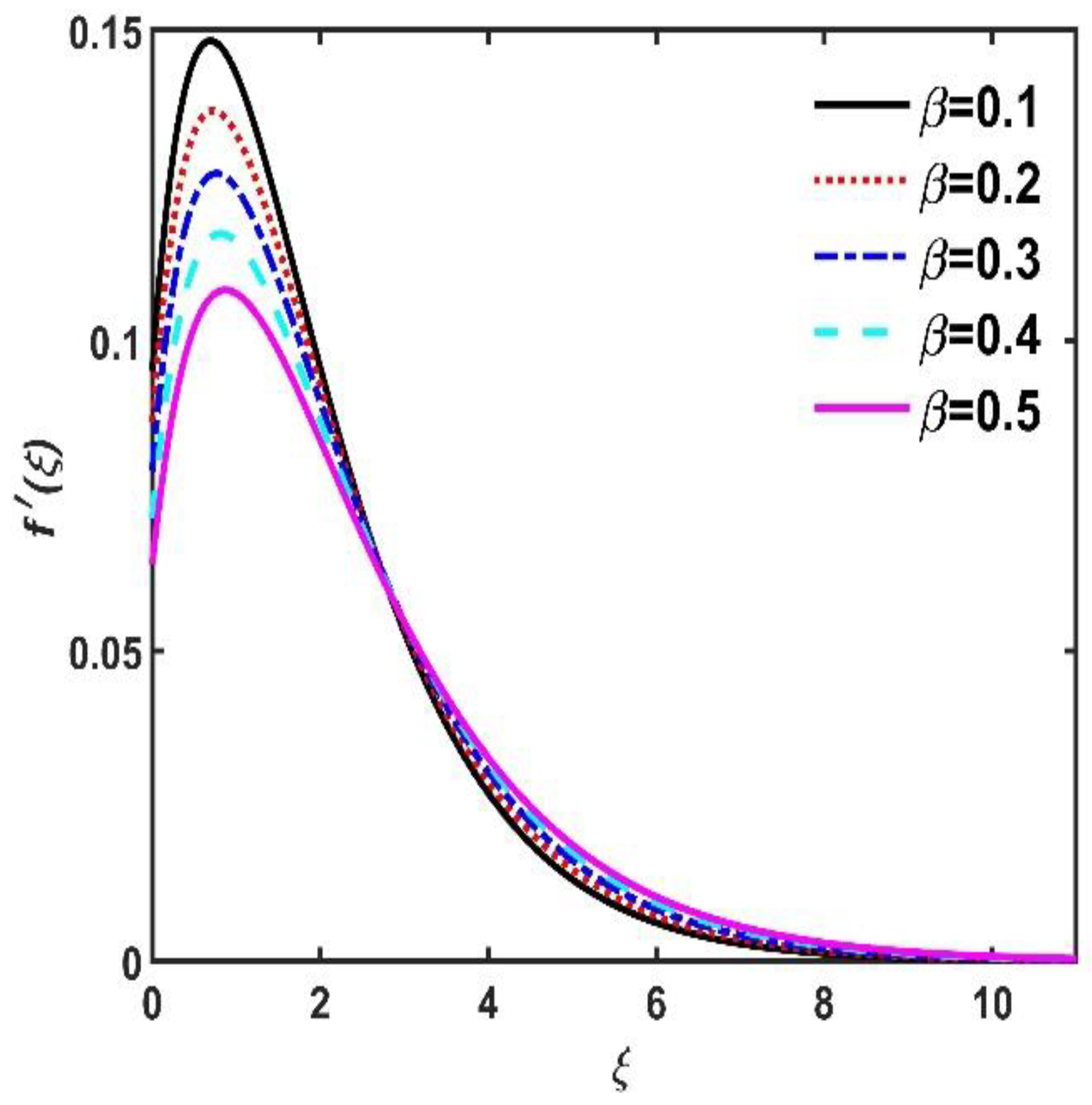
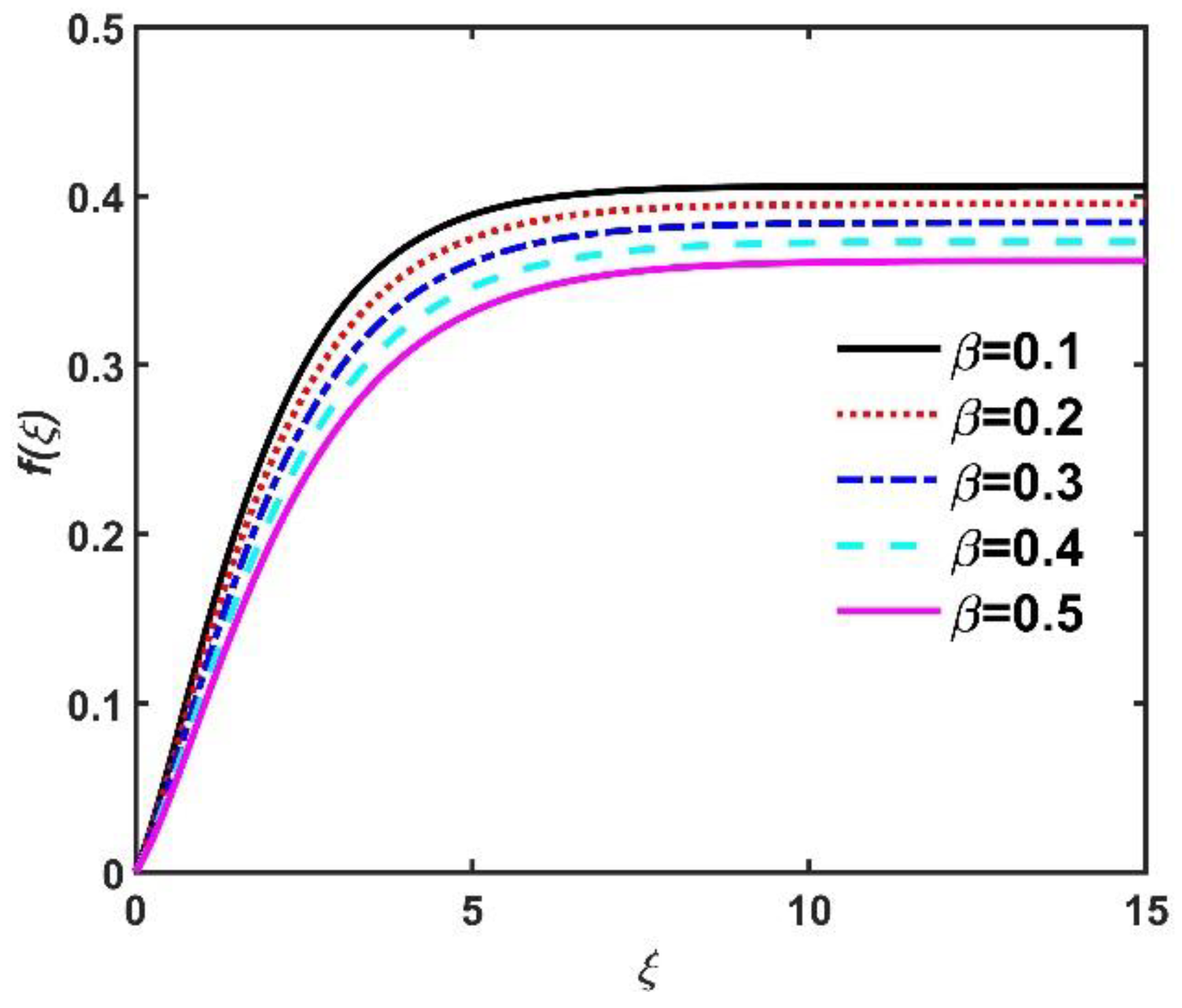
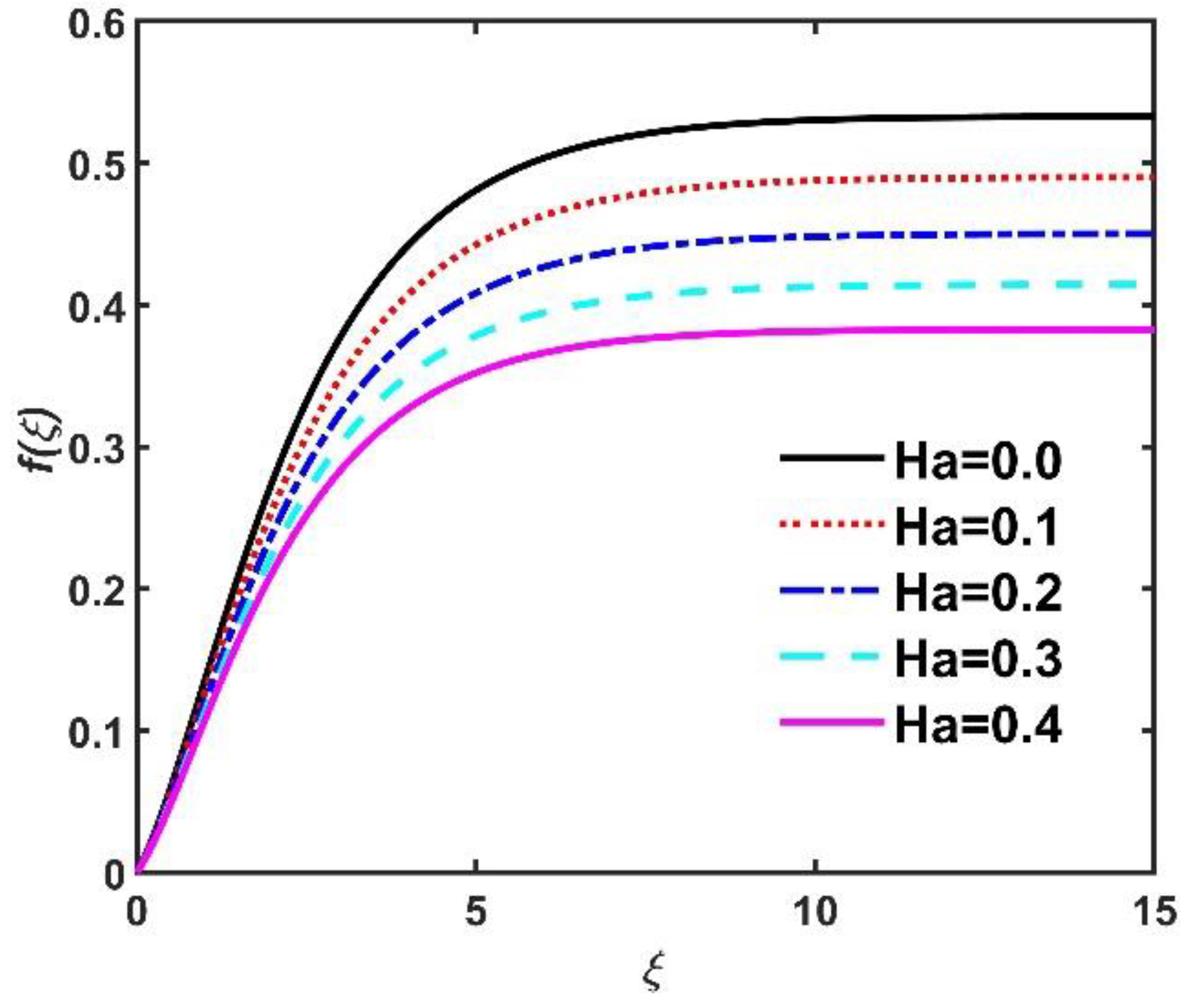
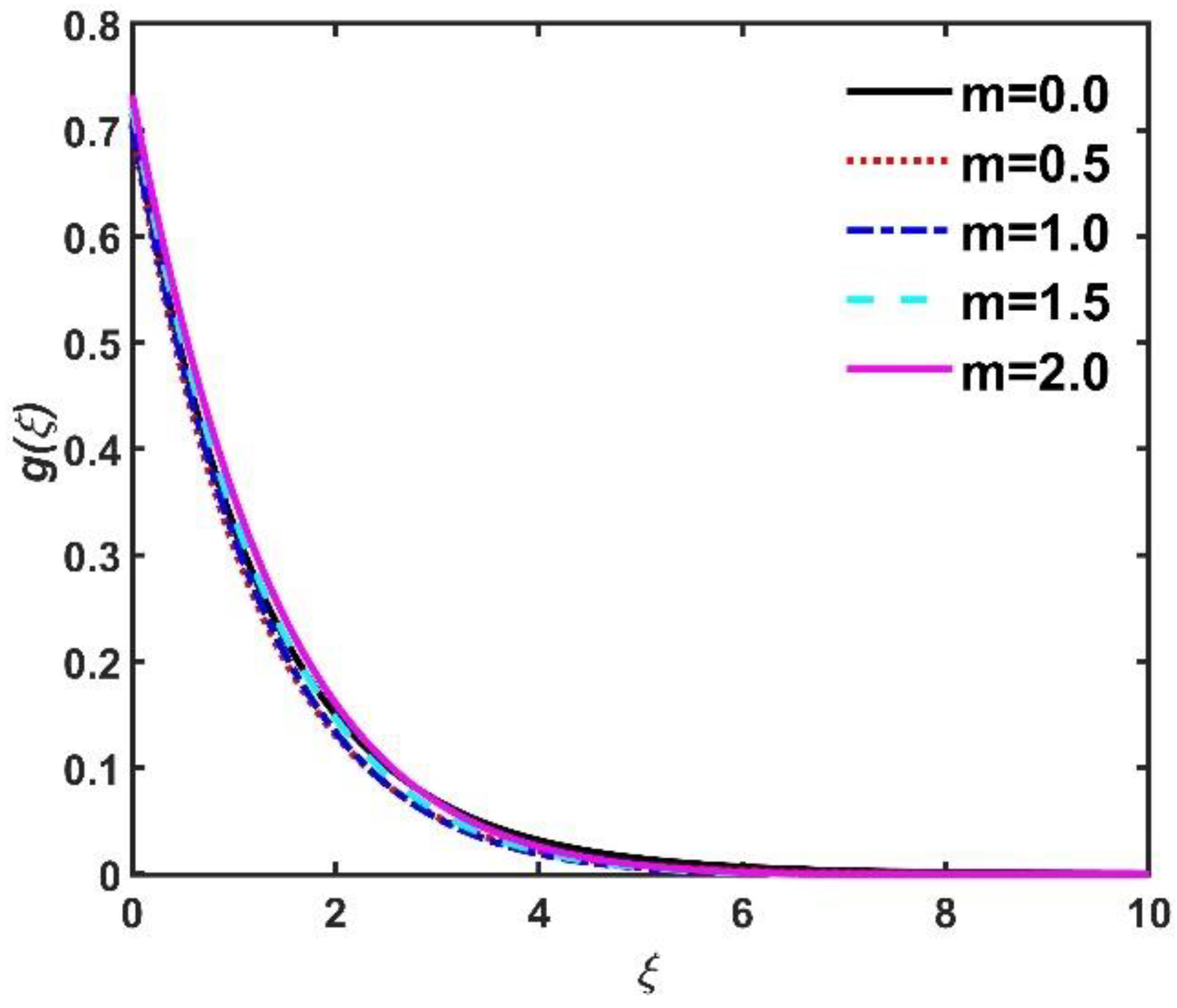
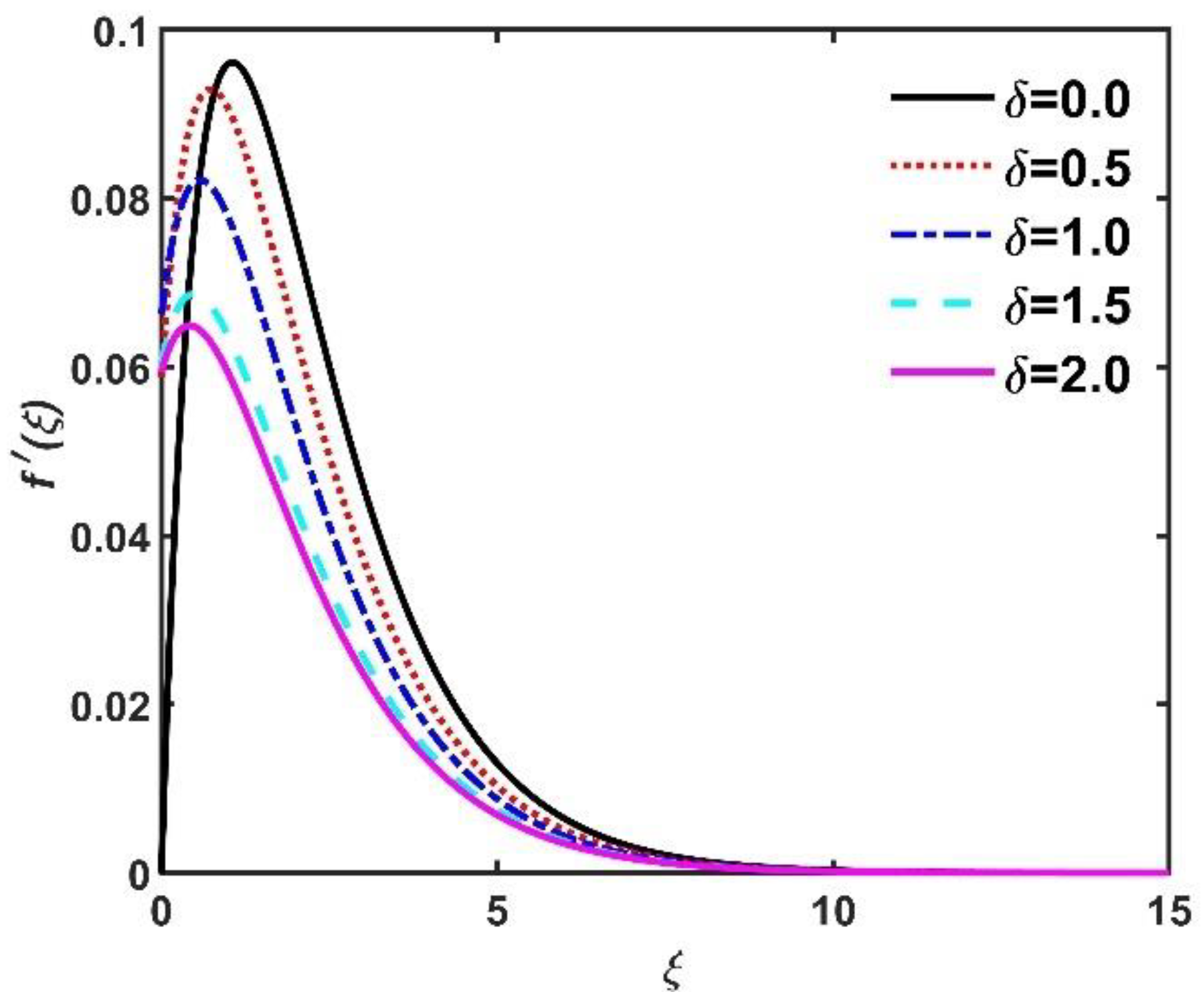
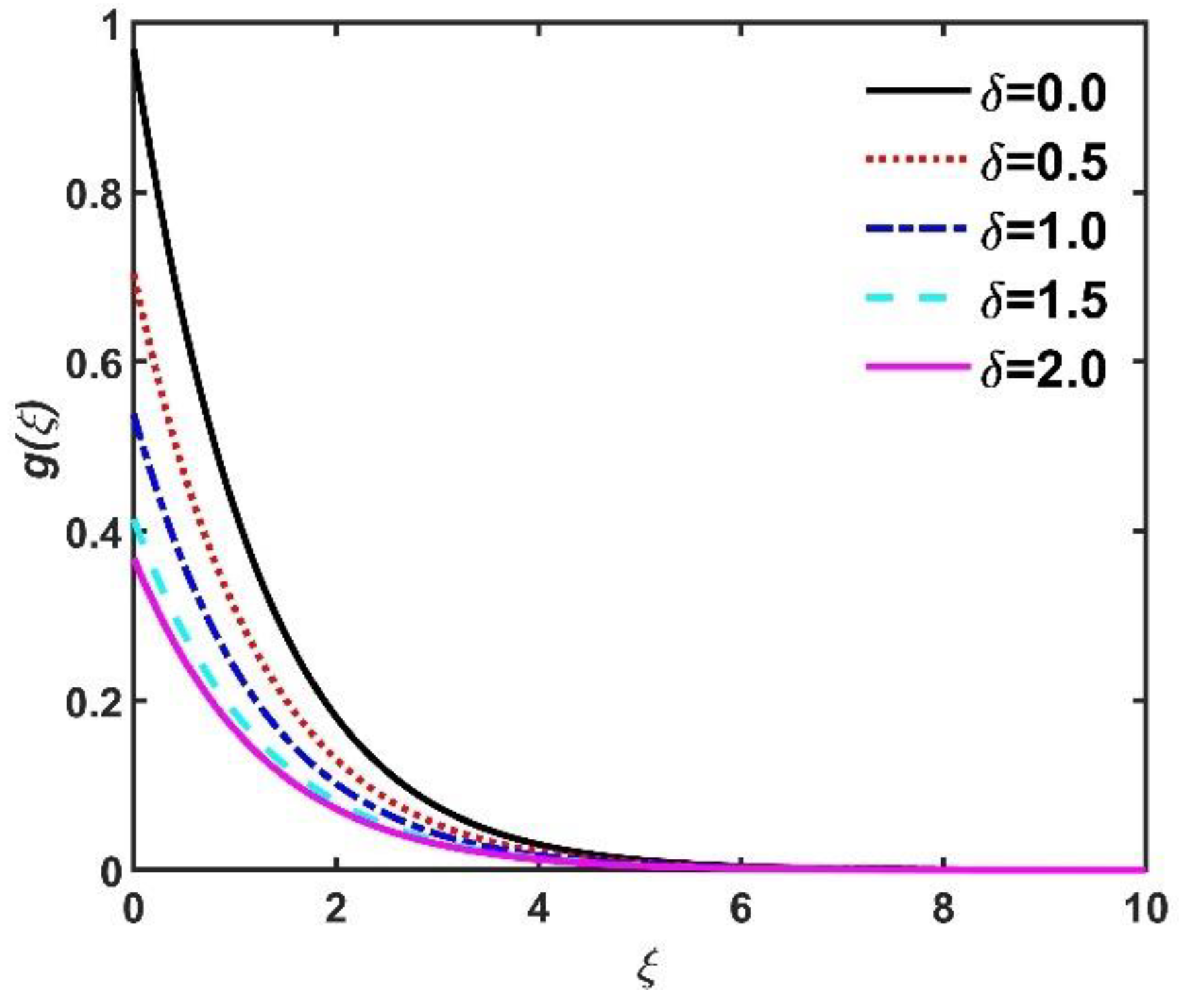
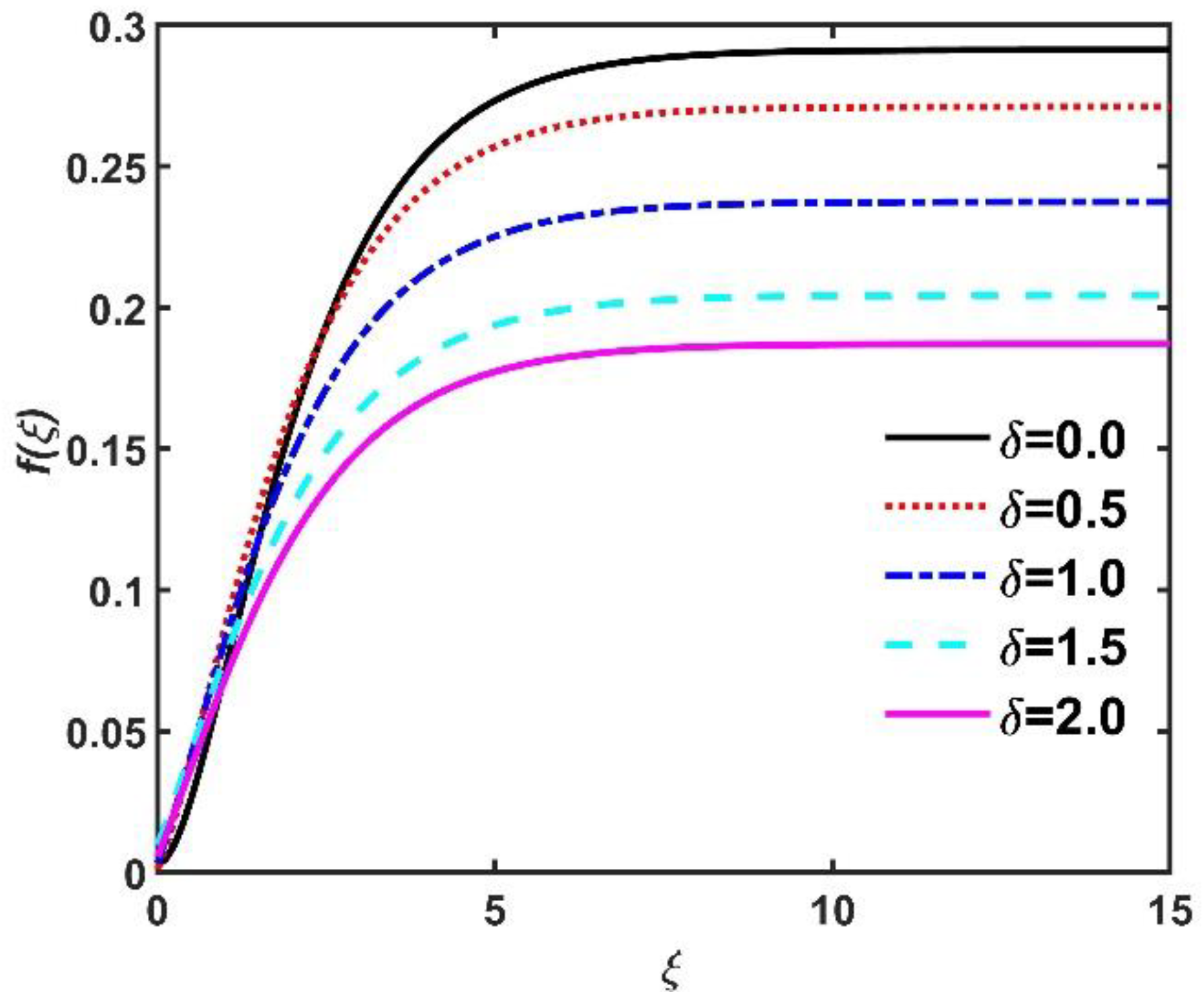
- Non-dimensional radial velocity , azimuth velocity , and tangential velocity components diminished when values increased but improved due to the Hall current.
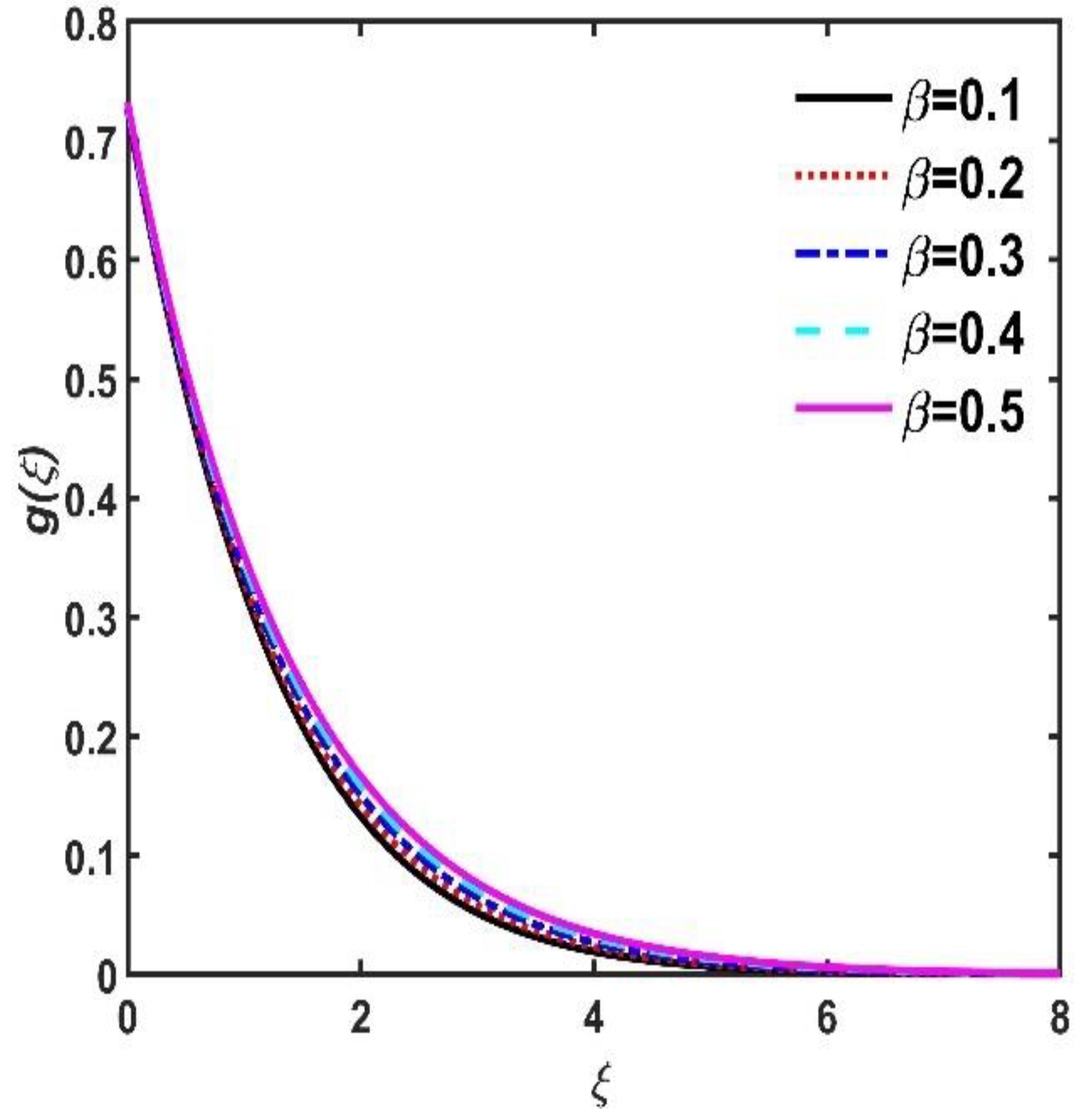
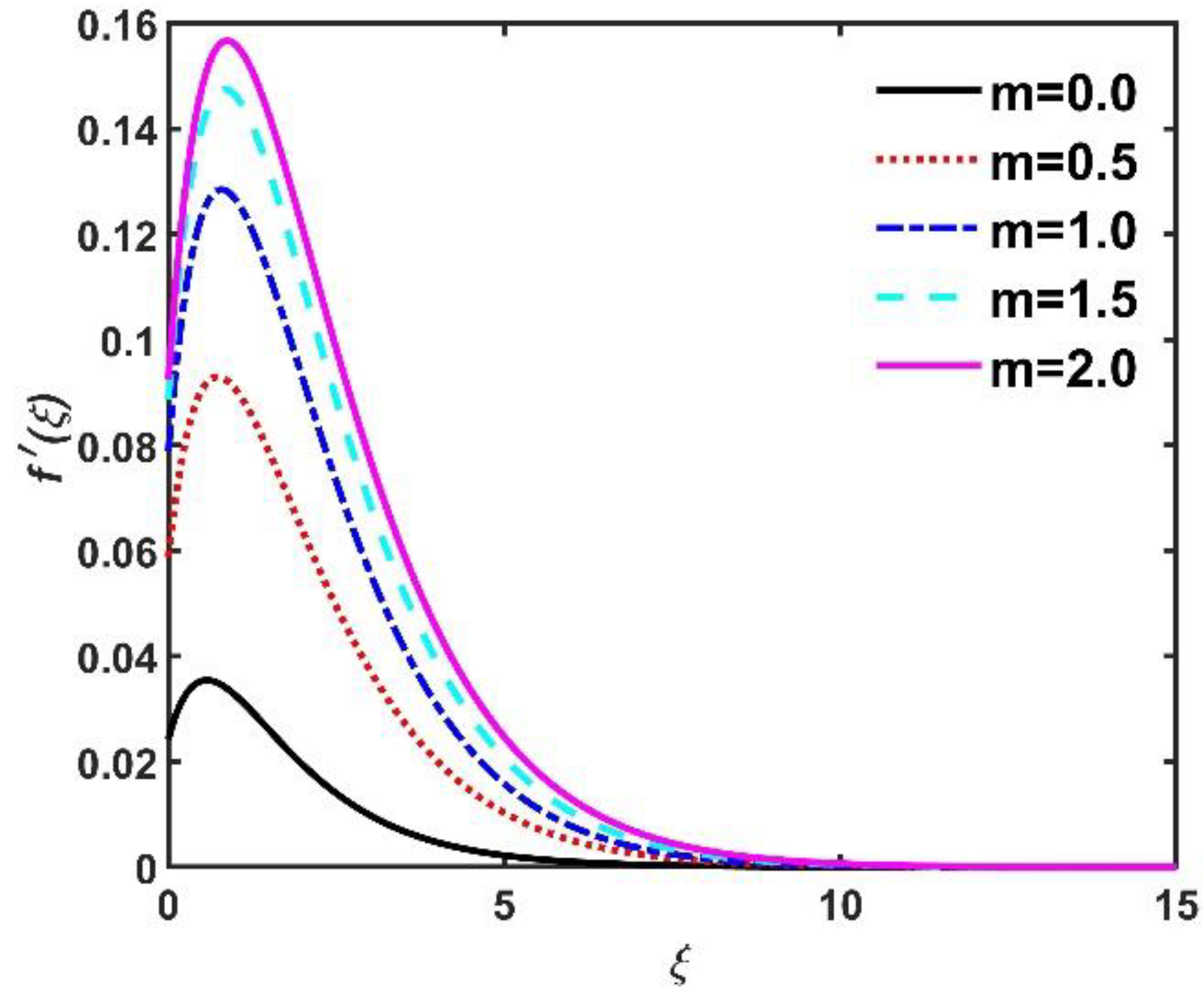
- Dimensionless azimuth velocity improved because of a larger .
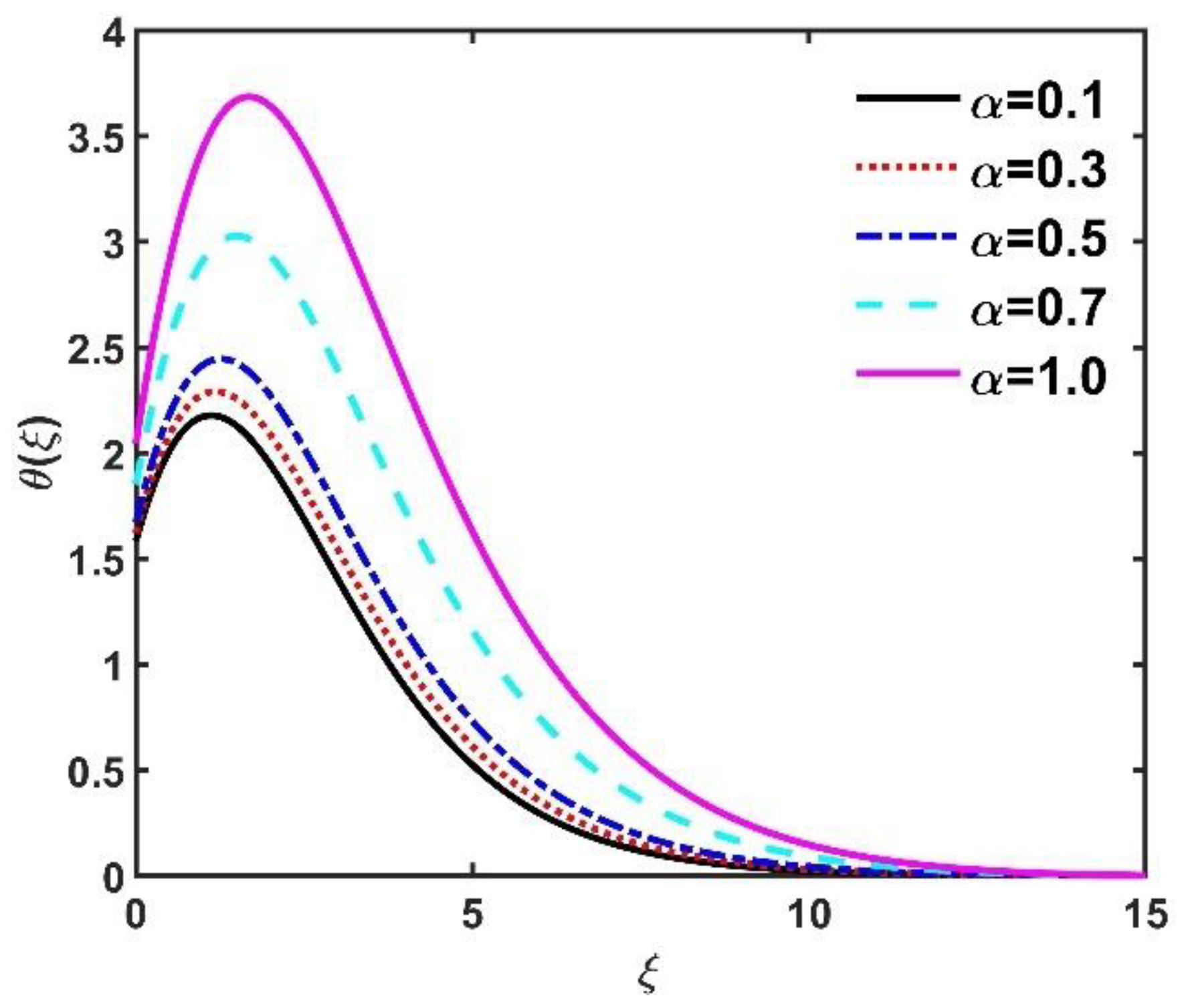
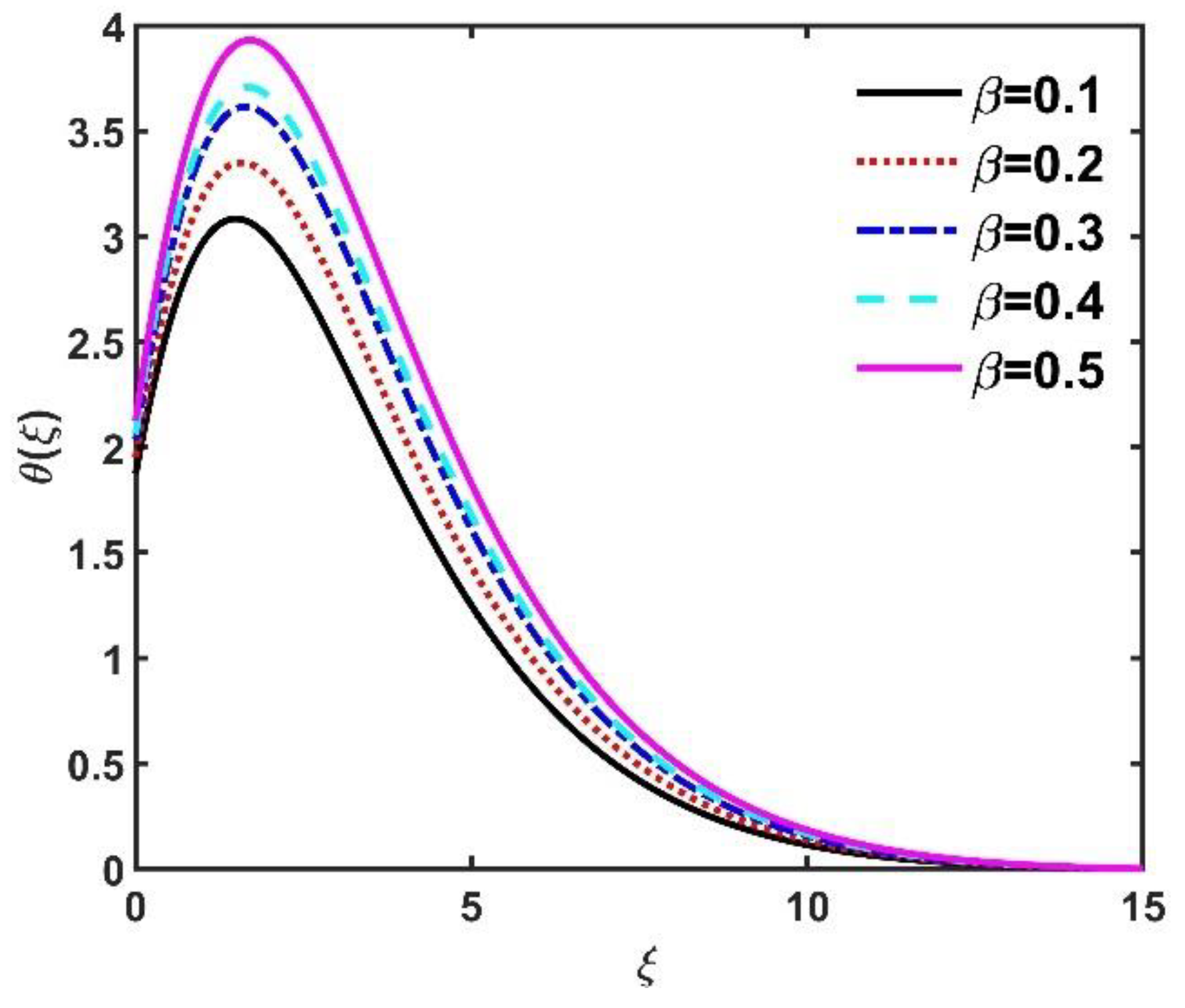
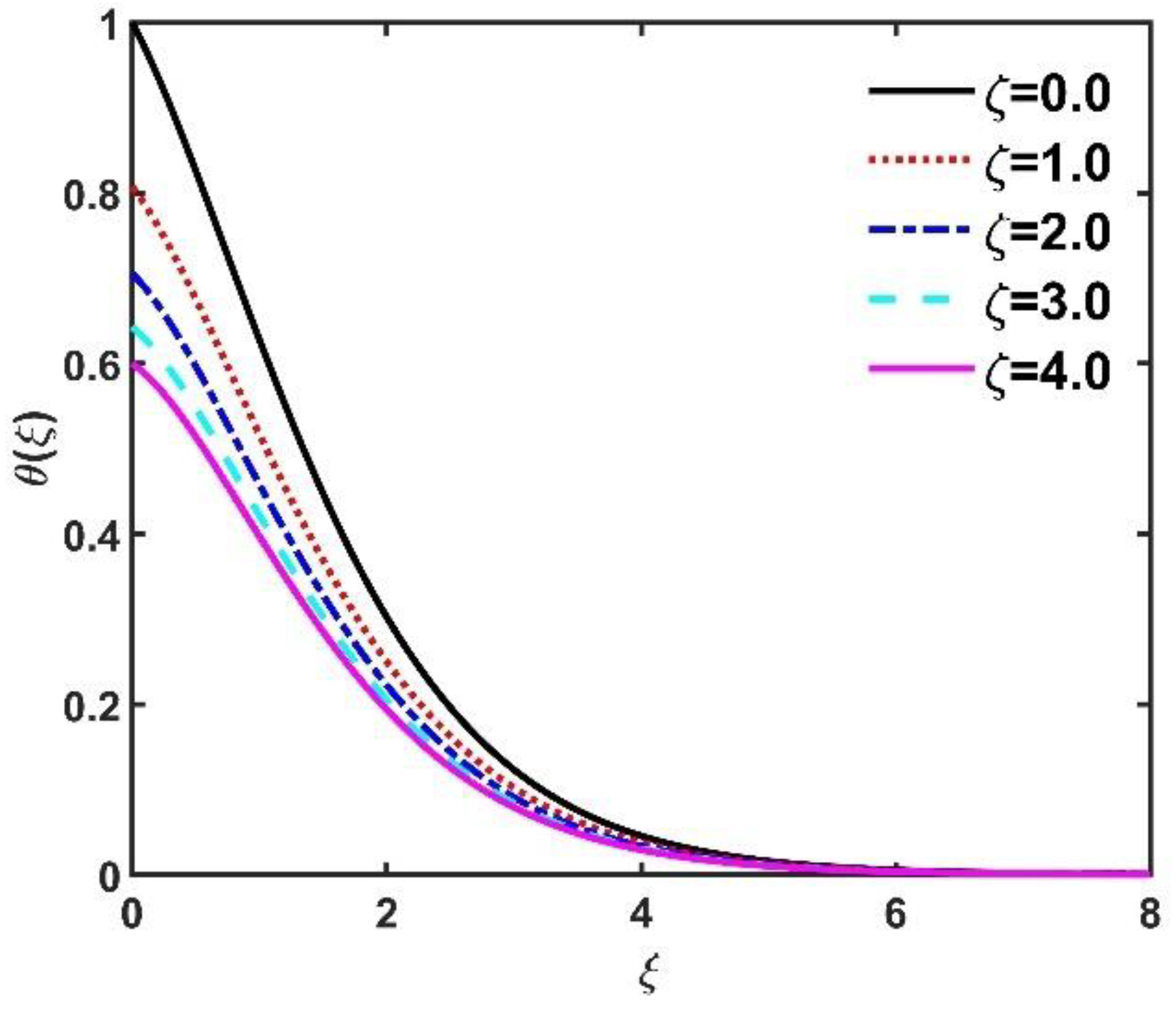
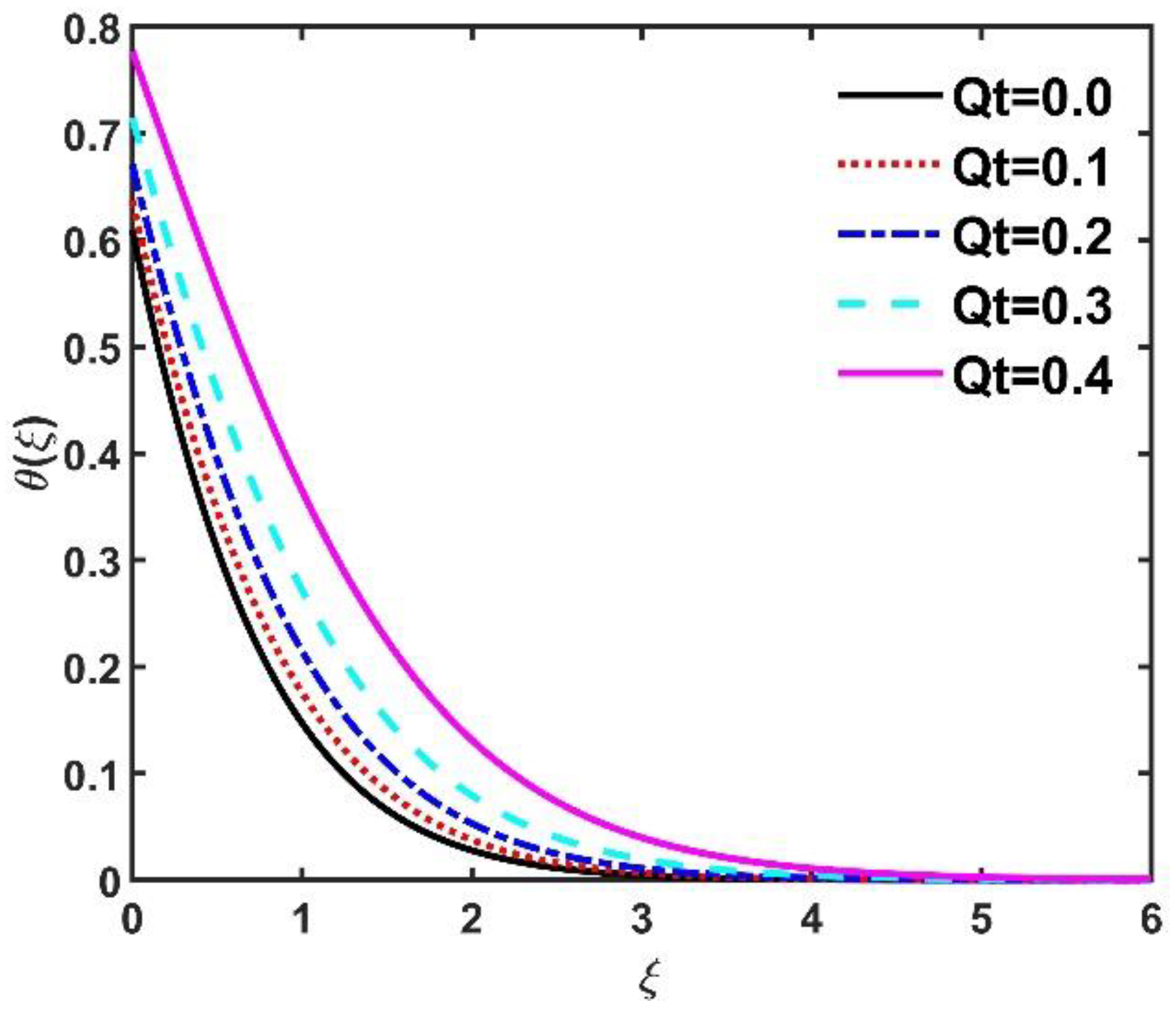
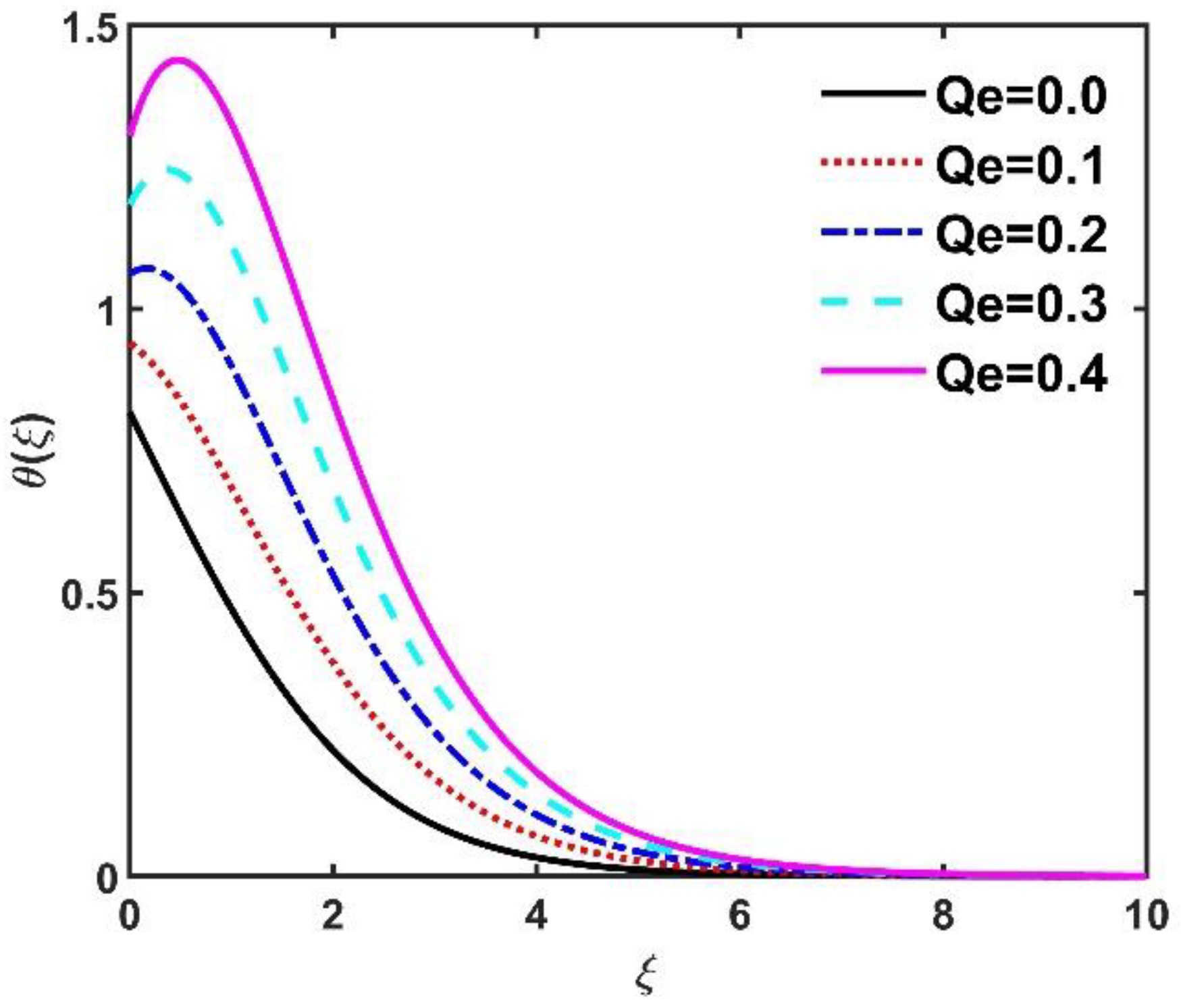
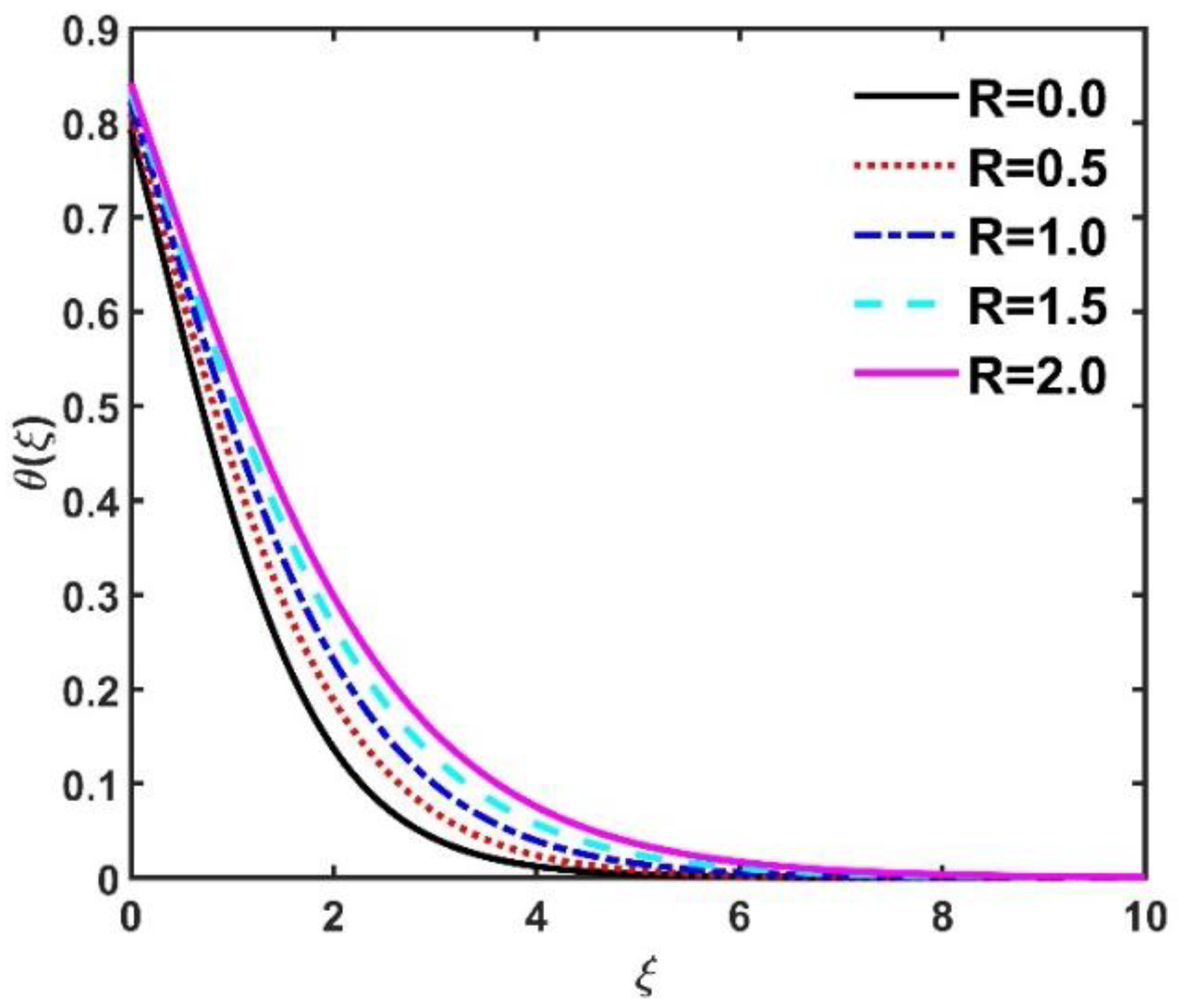
- The temperature field improved when and were elevated.
- The number had a constructive impact on the temperature field .
- Multiple slip conditions diminished the radial velocity , azimuth velocity , radial velocity and temperature .
- Compared to TRHS, ERHS had a more pronounced effect on temperature .
- Dimensionless , , and diminished when increased, but this did not happen when increased.
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Kármán, T.V. Über laminare und turbulente Reibung. Z. Angew. Math. Mech. 1921, 1, 233–252. [Google Scholar] [CrossRef]
- Brady, J.F.; Durlofsky, L. On rotating disk flow. J. Fluid Mech. 1987, 175, 363–394. [Google Scholar] [CrossRef]
- Cobb, E.C.; Saunders, O.A. Heat transfer from a rotating disk. Proc. R. Soc. Lond. Series A. Math. Phys. Sci. 1956, 236, 343–351. [Google Scholar]
- Benton, E.R. On the flow due to a rotating disk. J. Fluid Mech. 1966, 24, 781–800. [Google Scholar] [CrossRef]
- Tribollet, B.; Newman, J. The Modulated Flow at a Rotating Disk Electrode. J. Electrochem. Soc. 1983, 130, 2016–2026. [Google Scholar] [CrossRef]
- Turkyilmazoglu, M. Nanofluid flow and heat transfer due to a rotating disk. Comput. Fluids 2014, 94, 139–146. [Google Scholar] [CrossRef]
- Ellahi, R.; Tariq, M.H.; Hassan, M.; Vafai, K. On boundary layer nano-ferroliquid flow under the influence of low oscillating stretchable rotating disk. J. Mol. Liq. 2017, 229, 339–345. [Google Scholar] [CrossRef]
- Hayat, T.; Muhammad, T.; Shehzad, S.A.; Alsaedi, A. On magnetohydrodynamic flow of nanofluid due to a rotating disk with slip effect: A numerical study. Comput. Methods Appl. Mech. Eng. 2016, 315, 467–477. [Google Scholar] [CrossRef]
- Aziz, A.; Alsaedi, A.; Muhammad, T.; Hayat, T. Numerical study for heat generation/absorption in flow of nanofluid by a rotating disk. Results Phys. 2018, 8, 785–792. [Google Scholar] [CrossRef]
- Mahanthesh, B.; Lorenzini, G.; Oudina, F.M.; Animasaun, I.L. Significance of exponential space-and ther-mal-dependent heat source effects on nanofluid flow due to radially elongated disk with Coriolis and Lorentz forces. J. Therm. Anal. Calorim. 2020, 141, 37–44. [Google Scholar] [CrossRef]
- Cowling, T.G. Magnetohydrodynamics; Wiley Inter Science: New York, NY, USA, 1957. [Google Scholar]
- Aboul-Hassan, A.L.; Attia, H.A. Flow due to a rotating disk with Hall effect. Phys. Lett. A 1997, 228, 286–290. [Google Scholar] [CrossRef]
- Acharya, N.; Bag, R.; Kundu, P.K. Influence of Hall current on radiative nanofluid flow over a spinning disk: A hybrid approach. Phys. E: Low-Dimens. Syst. Nanostructures 2019, 111, 103–112. [Google Scholar] [CrossRef]
- Maleque, K.A.; Sattar, M.A. The effects of variable properties and Hall current on steady MHD laminar convective fluid flow due to a porous rotating disk. Int. J. Heat Mass Transf. 2005, 48, 4963–4972. [Google Scholar] [CrossRef]
- Abdel-Wahed, M.; Akl, M. Effect of hall current on MHD flow of a nanofluid with variable properties due to a rotating disk with viscous dissipation and nonlinear thermal radiation. AIP Adv. 2016, 6, 095308. [Google Scholar] [CrossRef]
- Shaheen, N.; Ramzan, M.; Alaoui, M.K. Impact of Hall current on a 3D Casson nanofluid flow past a rotating de-formable disk with variable characteristics. Arab. J. Sci. Eng. 2021, 46, 12653–12666. [Google Scholar] [CrossRef]
- Shehzad, S.; Abbas, Z.; Rauf, A.; Mushtaq, T. Effectiveness of Hall current and thermophysical properties in compressible flow of viscous fluid thorough spinning oscillatory disk. Int. Commun. Heat Mass Transf. 2020, 116, 104678. [Google Scholar] [CrossRef]
- Hayat, T.; Ellahi, R.; Asghar, S. Hall effects on unsteady flow due to non-coaxially rotating disk and a fluid at in-finity. Chem. Eng. Commun. 2008, 195, 958–976. [Google Scholar] [CrossRef]
- Maleque, K.A. Effects of combined temperature- and depth-dependent viscosity and hall current on an unsteady mhd laminar convective flow due to a rotating DISK. Chem. Eng. Commun. 2009, 197, 506–521. [Google Scholar] [CrossRef]
- Turkyilmazoglu, M. Exact solutions for the incompressible viscous magnetohydrodynamic fluid of a porous rotating disk flow with Hall current. Int. J. Mech. Sci. 2012, 56, 86–95. [Google Scholar] [CrossRef]
- Ramzan, M.; Riasat, S.; Zhang, Y.; Nisar, K.S.; Badruddin, I.A.; Ahammad, N.A.; Ghazwani, H.A.S. Significance low oscillating magnetic field and Hall current in the nano-ferrofluid flow past a rotating stretchable disk. Sci. Rep. 2021, 11, 23204. [Google Scholar] [CrossRef] [PubMed]
- Barnoon, P.; Toghraie, D.; Salarnia, M.; Karimipour, A. Mixed thermomagnetic convection of ferrofluid in a porous cavity equipped with rotating cylinders: LTE and LTNE models. J. Therm. Anal. Calorim. 2020, 146, 187–226. [Google Scholar] [CrossRef]
- Cai, W.; Toghraie, D.; Shahsavar, A.; Barnoon, P.; Khan, A.; Beni, M.H.; Jam, J.E. Eulerian-Lagrangian investigation of nanoparticle migration in the heat sink by considering different block shape effects. Appl. Therm. Eng. 2021, 199, 117593. [Google Scholar] [CrossRef]
- Barnoon, P.; Toghraie, D.; Karimipour, A. Application of rotating circular obstacles in improving ferrofluid heat transfer in an enclosure saturated with porous medium subjected to a magnetic field. J. Therm. Anal. Calorim. 2020, 145, 3301–3323. [Google Scholar] [CrossRef]
- Basavarajappa, M.; Bhatta, D. Heat and mass transfer of a molten polymer conveying nanoparticles in a wire coating process with temperature-dependent fluid properties: Optimization using Response surface method. Int. Commun. Heat Mass Transf. 2022, 133, 105941. [Google Scholar] [CrossRef]
- Xiao, C.; Nourbakhsh, M.; Alizadeh, A.; Toghraie, D.; Barnoon, P.; Khan, A. Investigation of thermal behavior and performance of different microchannels: A case study for traditional and Manifold Microchannels. Case Stud. Therm. Eng. 2022, 39, 102393. [Google Scholar] [CrossRef]
- Basavarajappa, M.; Bhatta, D. Unsteady nonlinear convective flow of a nanofluid over a vertical plate due to impulsive motion: Optimization and sensitivity analysis. Int. Commun. Heat Mass Transf. 2022, 134, 106036. [Google Scholar] [CrossRef]
- Miansari, M.; Darvishi, M.R.; Toghraie, D.; Barnoon, P.; Shirzad, M.; Alizadeh, A. Numerical investigation of grooves effects on the thermal performance of helically grooved shell and coil tube heat exchanger. Chin. J. Chem. Eng. 2021, 44, 424–434. [Google Scholar] [CrossRef]
- Akram, S.; Athar, M.; Saeed, K.; Razia, A.; Muhammad, T.; Alghamdi, H.A. Mathematical simulation of double diffusion convection on peristaltic pumping of Ellis nanofluid due to induced magnetic field in a non-uniform channel: Applications of magnetic nanoparticles in biomedical engineering. J. Magn. Magn. Mater. 2023, 569, 170408. [Google Scholar] [CrossRef]
- Akram, S.; Athar, M.; Saeed, K.; Razia, A.; Muhammad, T.; Hussain, A. Hybrid double-diffusivity convection and induced magnetic field effects on peristaltic waves of Oldroyd 4-constant nanofluids in non-uniform channel. Alex. Eng. J. 2023, 65, 785–796. [Google Scholar] [CrossRef]
- Qasim, M. Heat and mass transfer in a Jeffrey fluid over a stretching sheet with heat source/sink. Alex. Eng. J. 2013, 52, 571–575. [Google Scholar] [CrossRef]
- Reddy, M.G.; Makinde, O.D. Magnetohydrodynamic peristaltic transport of Jeffrey nanofluid in an asymmetric channel. J. Mol. Liq. 2016, 223, 1242–1248. [Google Scholar] [CrossRef]
- Sandeep, N.; Sulochana, C.; Animasaun, I.L. Stagnation-Point Flow of a Jeffrey Nanofluid over a Stretching Surface with Induced Magnetic Field and Chemical Reaction. Int. J. Eng. Res. Afr. 2015, 20, 93–111. [Google Scholar] [CrossRef]
- Mehmood, R.; Nadeem, S.; Saleem, S.; Akbar, N.S. Flow and heat transfer analysis of Jeffery nano fluid impinging obliquely over a stretched plate. J. Taiwan Inst. Chem. Eng. 2017, 74, 49–58. [Google Scholar] [CrossRef]
- Saleem, S.; Al-Qarni, M.M.; Nadeem, S.; Sandeep, N. Convective Heat and Mass Transfer in Magneto Jeffrey Fluid Flow on a Rotating Cone with Heat Source and Chemical Reaction. Commun. Theor. Phys. 2018, 70, 534. [Google Scholar] [CrossRef]
- Khan, N.A.; Khan, S.; Riaz, F. Analytic Approximate Solutions and Numerical Results for Stagnation Point Flow of Jeffrey Fluid Towards an Off-Centered Rotating Disk. J. Mech. 2014, 31, 201–215. [Google Scholar] [CrossRef]
- Farooq, M.; Gull, N.; Alsaedi, A.; Hayat, T. MHD Flow of a Jeffrey Fluid with Newtonian Heating. J. Mech. 2015, 31, 319–329. [Google Scholar] [CrossRef]
- Hayat, T.; Qayyum, S.; Imtiaz, M.; Alsaedi, A. Homogeneous-heterogeneous reactions in nonlinear radiative flow of Jeffrey fluid between two stretchable rotating disks. Results Phys. 2017, 7, 2557–2567. [Google Scholar] [CrossRef]
- Reddy, G.B.; Sreenadh, S.; Reddy, R.H.; Kavitha, A. Flow of a Jeffrey fluid between torsionally oscillating disks. Ain Shams Eng. J. 2015, 6, 355–362. [Google Scholar] [CrossRef]
- Hayat, T.; Abbas, T.; Ayub, M.; Muhammad, T.; Alsaedi, A. On Squeezed Flow of Jeffrey Nanofluid between Two Parallel Disks. Appl. Sci. 2016, 6, 346. [Google Scholar] [CrossRef]
- Hayat, T.; Farooq, S.; Ahmad, B.; Alsaedi, A. Effectiveness of entropy generation and energy transfer on peristaltic flow of Jeffrey material with Darcy resistance. Int. J. Heat Mass Transf. 2017, 106, 244–252. [Google Scholar] [CrossRef]
- Muhammad, T.; Hayat, T.; Alsaedi, A.; Qayyum, A. Hydromagnetic unsteady squeezing flow of Jeffrey fluid between two parallel plates. Chin. J. Phys. 2017, 55, 1511–1522. [Google Scholar] [CrossRef]
- Kumar, P.M.; Kavitha, A. Three-dimensional flow of Jeffrey fluid between a rotating and stationary disks with suction. Ain Shams Eng. J. 2018, 9, 2351–2356. [Google Scholar] [CrossRef]
- Hayat, T.; Nawaz, M.; Awais, M.; Obaidat, S. Axisymmetric magnetohydrodynamic flow of Jeffrey fluid over a rotating disk. Int. J. Numer. Methods Fluids 2011, 70, 764–774. [Google Scholar] [CrossRef]
- Siddiqui, A.M.; Farooq, A.A.; Haroon, T.; Babcock, B.S. A variant of the classical von Karman flow for a Jeffrey fluid. Appl. Math. Sci. 2013, 7, 983–991. [Google Scholar] [CrossRef]
- Qasim, M.; Afridi, M.I.; Wakif, A.; Saleem, S. Influence of Variable Transport Properties on Nonlinear Radioactive Jeffrey Fluid Flow Over a Disk: Utilization of Generalized Differential Quadrature Method. Arab. J. Sci. Eng. 2019, 44, 5987–5996. [Google Scholar] [CrossRef]
- Sadiq, M.N.; Sajid, M.; Fahim, M.; Javed, T.; Ali, N. Swirling Flow of Jeffrey Fluid by a Spiraling Disk. Iran. J. Sci. Technol. Trans. A: Sci. 2020, 44, 821–831. [Google Scholar] [CrossRef]
- Imtiaz, M.; Shahid, F.; Hayat, T.; Alsaedi, A. Chemical reactive flow of Jeffrey fluid due to a rotating disk with non-Fourier heat flux theory. J. Therm. Anal. Calorim. 2019, 140, 2461–2470. [Google Scholar] [CrossRef]
- Sadiq, M.; Sajid, M.; Javed, T.; Ali, N. Modeling and simulation for estimating thin film lubrication effects on flow of Jeffrey liquid by a spiraling disk. Eur. J. Mech.—B/Fluids 2021, 91, 167–176. [Google Scholar] [CrossRef]
- Fourier, J. Théorie Analytique de Chaleur; Chez firmin didot, pere et fils; Libraries pour les Mathématiques: Paris, France, 1822. [Google Scholar]
- Cattaneo, C. Sulla conduzione del calore. Atti Sem. Mat. Fis. Univ. Modena 1948, 3, 83–101. [Google Scholar]
- Christov, C. On frame indifferent formulation of the Maxwell–Cattaneo model of finite-speed heat conduction. Mech. Res. Commun. 2008, 36, 481–486. [Google Scholar] [CrossRef]
- Bissell, J.J. Thermal convection in a magnetized conducting fluid with the Cattaneo–Christov heat-flow model. Proc. R. Soc. A: Math. Phys. Eng. Sci. 2016, 472, 20160649. [Google Scholar] [CrossRef] [PubMed]
- Layek, G.; Pati, N. Bifurcations and chaos in convection taking non-Fourier heat-flux. Phys. Lett. A 2017, 381, 3568–3575. [Google Scholar] [CrossRef]
- Mehmood, R.; Rana, S.; Anwar Bég, O.; Kadir, A. Numerical study of chemical reaction effects in magnetohydro-dynamic Oldroyd-B: Oblique stagnation flow with a non-Fourier heat flux model. J. Braz. Soc. Mech. Sci. Eng. 2018, 40, 526. [Google Scholar] [CrossRef]
- Shamshuddin, M.D.; Mishra, S.R.; Bég, O.A.; Kadir, A. Numerical study of heat transfer and viscous flow in a dual rotating extendable disk system with a non-Fourier heat flux model. Heat Transf. 2018, 48, 435–459. [Google Scholar] [CrossRef]
- Mabood, F.; Mackolil, J.; Mahanthesh, B.; Rauf, A.; Shehzad, S.A. Dynamics of Sutterby fluid flow due to a spinning stretching disk with non-Fourier/Fick heat and mass flux models. Appl. Math. Mech. 2021, 42, 1247–1258. [Google Scholar] [CrossRef]
- Kumar, P.B.S.; Mahanthesh, B.; Gireesha, B.J.; Shehzad, S.A. Quadratic convective flow of radiated nano-Jeffrey liquid subject to multiple convective conditions and Cattaneo-Christov double diffusion. Appl. Math. Mech. 2018, 39, 1311–1326. [Google Scholar] [CrossRef]
- Hayat, T.; Javed, M.; Imtiaz, M.; Alsaedi, A. Effect of Cattaneo-Christov heat flux on Jeffrey fluid flow with variable thermal conductivity. Results Phys. 2017, 8, 341–351. [Google Scholar] [CrossRef]
| Ha | Hayat et al. [44] | Present Results | ||
|---|---|---|---|---|
| 0 | 1.01735 | −1.27135 | 1.017349 | −1.271352 |
| 1.0 | −0.01336 | −1.09247 | −0.013357 | −1.092468 |
| 2.0 | −0.72170 | −1.00951 | −0.721704 | −1.009513 |
| 2.5 | −0.98025 | −0.99714 | −0.980251 | −0.997145 |
| Ha | Non-Magnetic Jeffrey Fluid | ||||
|---|---|---|---|---|---|
| 0.1 | 0.2 | −0.06125664 | −0.39446355 | −1.17901854 | |
| 0.2 | 0.2 | −0.06008768 | −0.37373903 | −1.17861751 | |
| 0.3 | 0.2 | −0.05897289 | −0.35550976 | −1.17834275 | |
| 0.4 | 0.2 | −0.05790908 | −0.33932084 | −1.17817031 | |
| 0.0 | 0.5 | 0.2 | −0.05689318 | −0.32482506 | −1.17808173 |
| 0.2 | 0.1 | 0.05340656 | −0.35924537 | −1.15292255 | |
| 0.2 | 0.2 | −0.06008768 | −0.37373903 | −1.17861751 | |
| 0.2 | 0.3 | −0.17308504 | −0.38369116 | −1.18436835 | |
| 0.2 | 0.4 | −0.28369392 | −0.39065929 | −1.18990441 | |
| 0.2 | 0.5 | −0.39113367 | −0.39493977 | −1.19520976 | |
| Ha | Magnetic Jeffrey Fluid | ||||
|---|---|---|---|---|---|
| 0.1 | 0.2 | −0.20719834 | −0.54699975 | −1.21448688 | |
| 0.2 | 0.2 | −0.19735447 | −0.51658603 | −1.21487245 | |
| 0.3 | 0.2 | −0.18864641 | −0.48992375 | −1.21530051 | |
| 0.4 | 0.2 | −0.18087120 | −0.46631856 | −1.21575914 | |
| 0.5 | 0.5 | 0.2 | −0.17387347 | −0.4452424 | −1.21623946 |
| 0.2 | 0.1 | −0.03462087 | −0.50858416 | −1.18607258 | |
| 0.2 | 0.2 | −0.19735447 | −0.51658603 | −1.21487245 | |
| 0.2 | 0.3 | −0.35766588 | −0.51886684 | −1.22226033 | |
| 0.2 | 0.4 | −0.51393502 | −0.5172768 | −1.22949732 | |
| 0.2 | 0.5 | −0.66511655 | −0.51213728 | −1.23656366 | |
| Ha | m | |||
|---|---|---|---|---|
| 0 | 0 | −0.06008768 | −0.37373903 | −1.17861751 |
| 0.1 | −0.08426340 | −0.38368352 | −1.18984404 | |
| 0.2 | −0.10745435 | −0.39453821 | −1.20053417 | |
| 0 | 5 | −0.06008768 | −0.37373903 | −1.17861751 |
| 0.1 | −0.06146400 | −0.3789904 | −1.17769753 | |
| 0.2 | −0.06279512 | −0.38411897 | −1.17681152 | |
| 0 | 10 | −0.06008768 | −0.37373903 | −1.17861751 |
| 0.1 | −0.06056089 | −0.37636651 | −1.17802761 | |
| 0.2 | −0.06102613 | −0.37896354 | −1.17744919 | |
| 0 | 100 | −0.06008768 | −0.37373903 | −1.17861751 |
| 0.1 | −0.06011372 | −0.37399731 | −1.17854714 | |
| 0.2 | −0.06013971 | −0.37425529 | −1.1784769 |
| n | ζ | |||
|---|---|---|---|---|
| Qt = Qe = 0.2 | Qt = Qe = 0 | |||
| 0.1 | 0.5 | 0.5 | −1.41850538 | −1.16647540 |
| 0.2 | −1.36654000 | −1.16647540 | ||
| 0.3 | −1.32706867 | −1.16647540 | ||
| 0.4 | −1.29593067 | −1.16647540 | ||
| 1 | 0.1 | 0.5 | −1.41494968 | −1.41884553 |
| 0.2 | −1.34453339 | −1.34604109 | ||
| 0.3 | −1.28525897 | −1.28034291 | ||
| 0.4 | −1.23467631 | −1.22075960 | ||
| 1 | 0.5 | 0.1 | −0.86416390 | −0.82476824 |
| 0.2 | −0.94531928 | −0.90931794 | ||
| 0.3 | −1.02685975 | −0.99449018 | ||
| 1 | 0.5 | 0.4 | −1.10876180 | −1.08022592 |
| Qt | Qe | ||
|---|---|---|---|
| Γ = 0 | Γ = 0.1 | ||
| 0 | 0.2 | −1.48401825 | −1.48133282 |
| −0.1 | −1.30346759 | −1.30280458 | |
| −0.2 | −1.19102030 | −1.19080604 | |
| −0.3 | −1.11064431 | −1.11056507 | |
| −0.2 | 0 | −0.98769763 | −0.98736978 |
| 0.1 | −1.08935897 | −1.08908791 | |
| 0.2 | −1.19102030 | −1.19080604 | |
| −0.2 | 0.3 | −1.29268164 | −1.29252360 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Alshomrani, A.S. Insights into the 3D Slip Dynamics of Jeffrey Fluid Due to a Rotating Disk with Exponential Space-Dependent Heat Generation: A Case Involving a Non-Fourier Heat Flux Model. Mathematics 2023, 11, 1096. https://doi.org/10.3390/math11051096
Alshomrani AS. Insights into the 3D Slip Dynamics of Jeffrey Fluid Due to a Rotating Disk with Exponential Space-Dependent Heat Generation: A Case Involving a Non-Fourier Heat Flux Model. Mathematics. 2023; 11(5):1096. https://doi.org/10.3390/math11051096
Chicago/Turabian StyleAlshomrani, Ali Saleh. 2023. "Insights into the 3D Slip Dynamics of Jeffrey Fluid Due to a Rotating Disk with Exponential Space-Dependent Heat Generation: A Case Involving a Non-Fourier Heat Flux Model" Mathematics 11, no. 5: 1096. https://doi.org/10.3390/math11051096
APA StyleAlshomrani, A. S. (2023). Insights into the 3D Slip Dynamics of Jeffrey Fluid Due to a Rotating Disk with Exponential Space-Dependent Heat Generation: A Case Involving a Non-Fourier Heat Flux Model. Mathematics, 11(5), 1096. https://doi.org/10.3390/math11051096





