A Numerical Framework for Entropy Generation Using Second-Order Nanofluid Thin Film Flow over an Expanding Sheet: Error Estimation and Stability Analysis
Abstract
1. Introduction
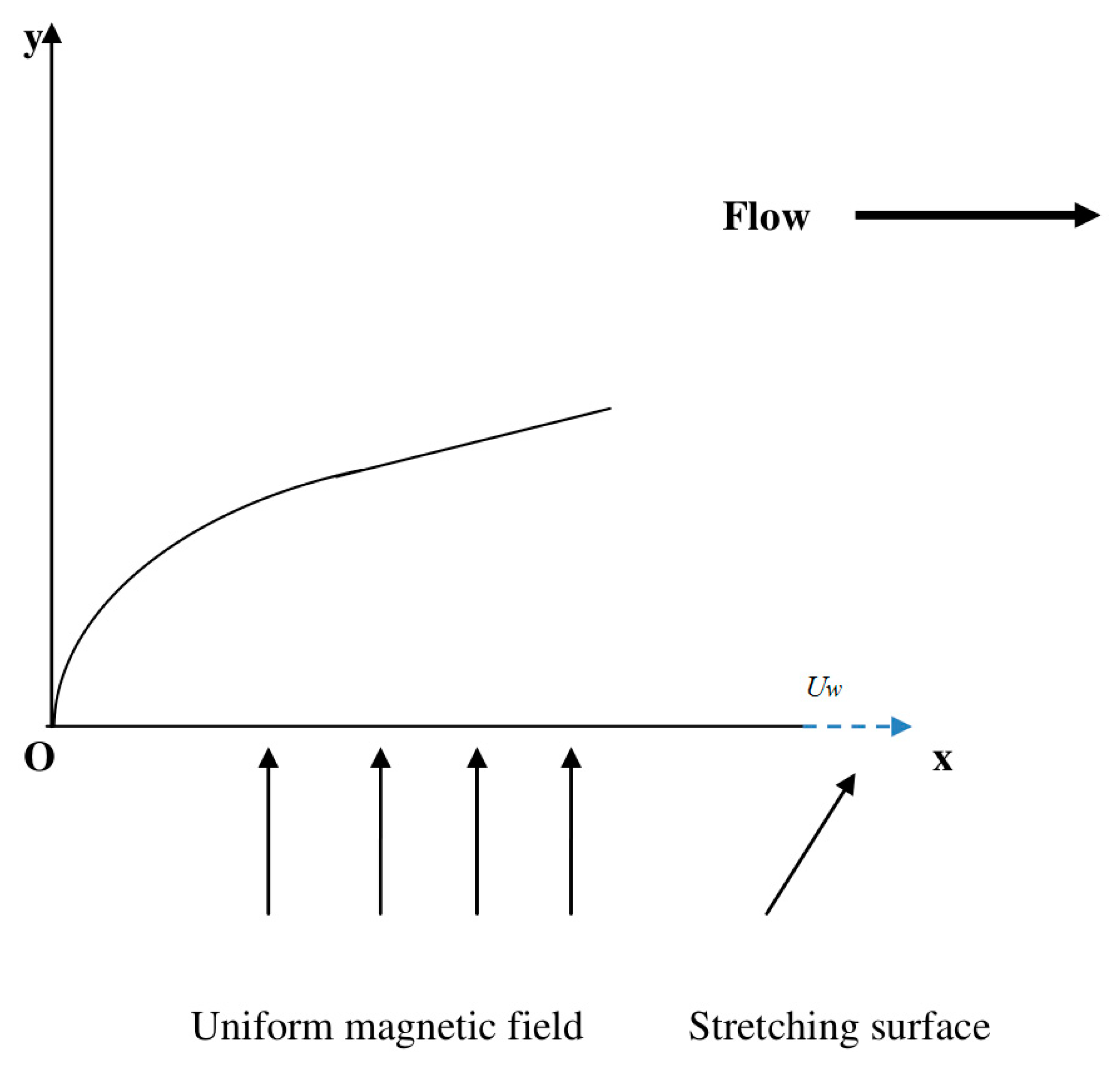
2. Mathematical Modeling
3. The Governing Equations
4. Physical Parameters of Interest
4.1. Skin Friction
4.2. Nusselt Number
4.3. Sherwood Number
5. Mathematical Expression for Entropy Generation
6. Numerical Procedure and Stability Analysis
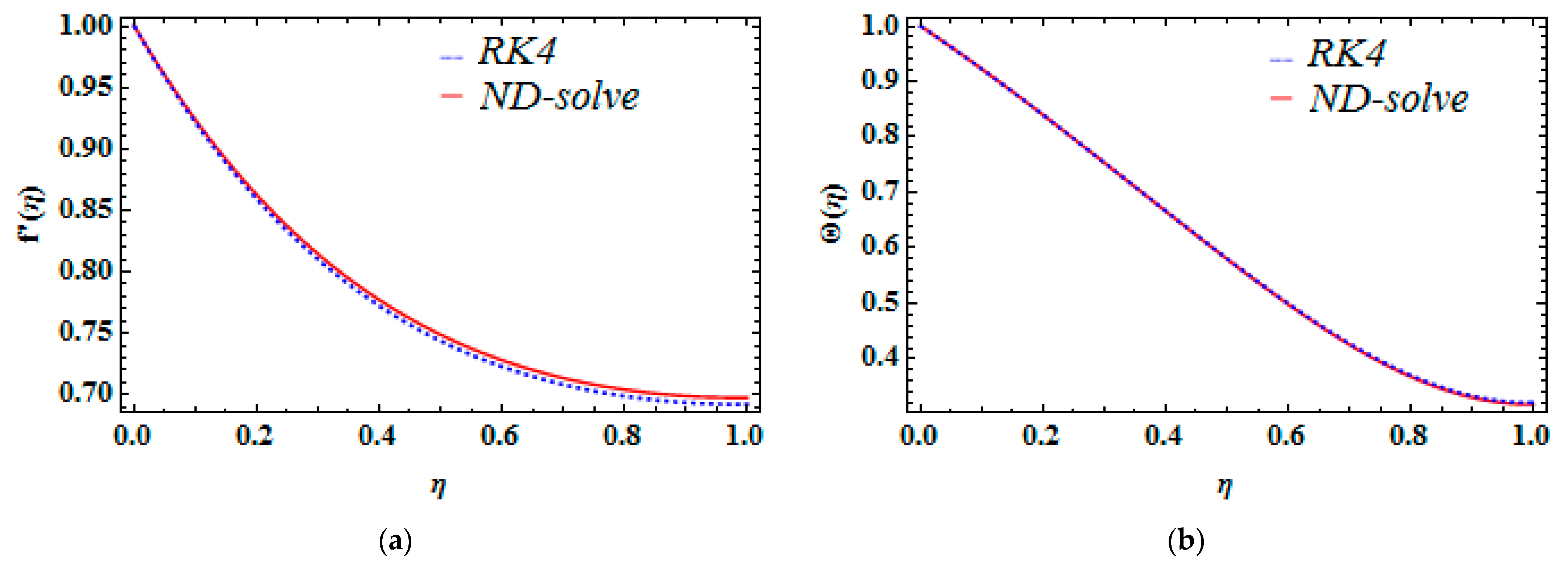
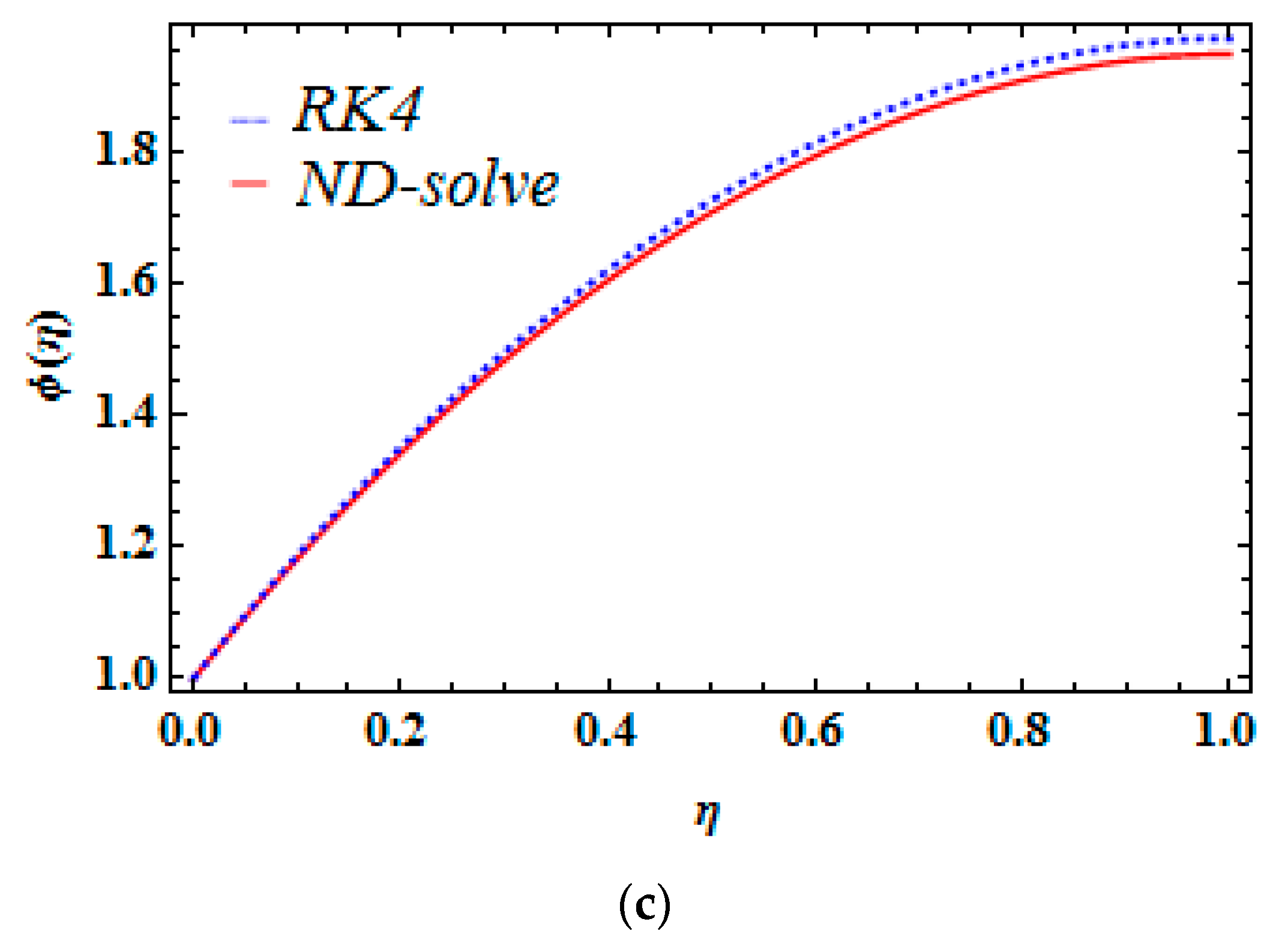
7. Error Analysis and Confirmation of the RK4 Method
8. Table Discussion
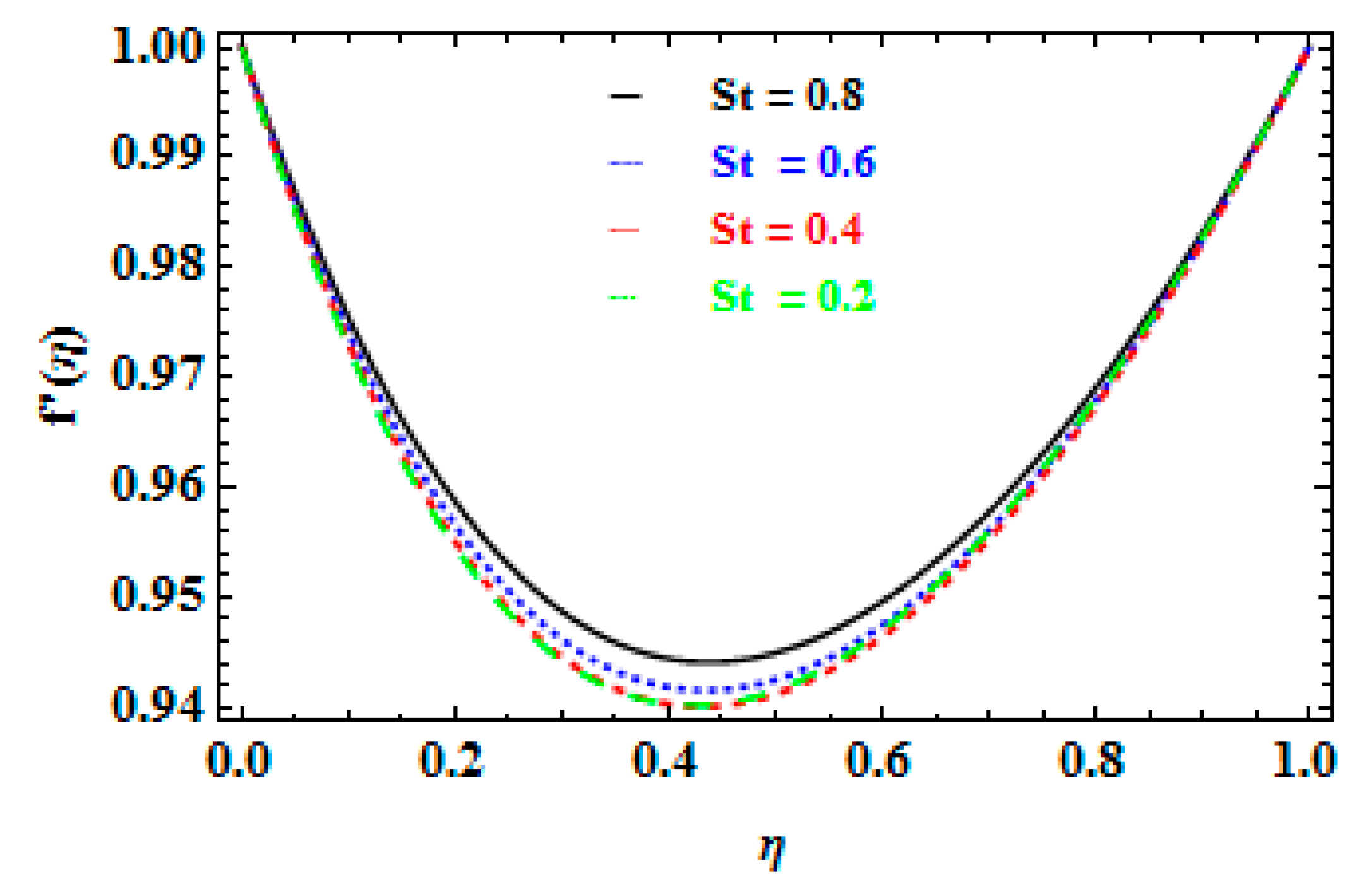
9. Results and Discussion
10. Conclusions
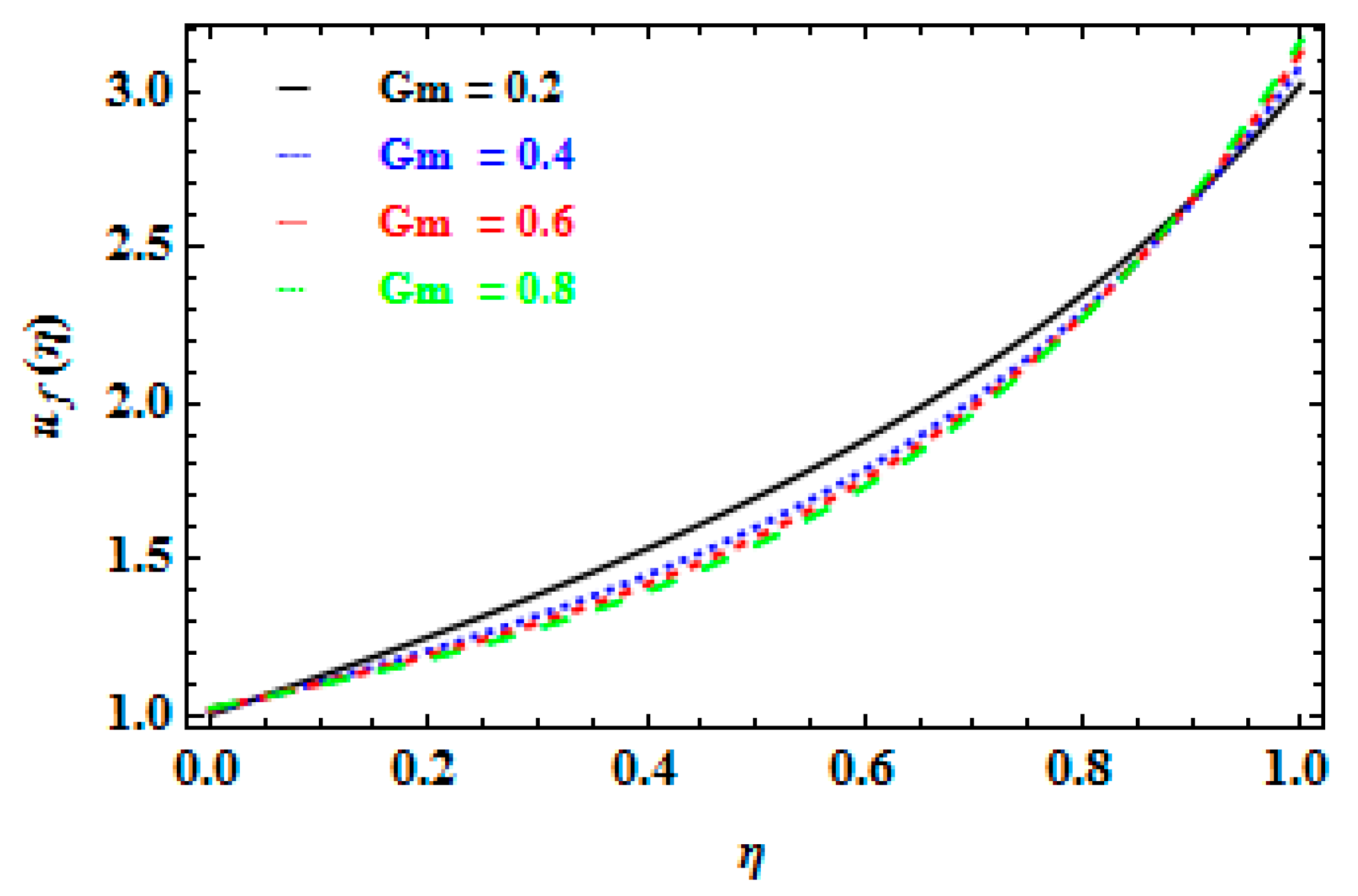
- The velocity field of the nanoparticle’s fluid film upsurges when the unsteadiness factor is enhanced, but the velocity profile of the nanofluid film decreases due to increases in the magnetic factor.
- The coefficient of skin friction significantly develops when and are increased; however, the coefficient of skin friction reduces as the stretching and thickness parameters are increased.
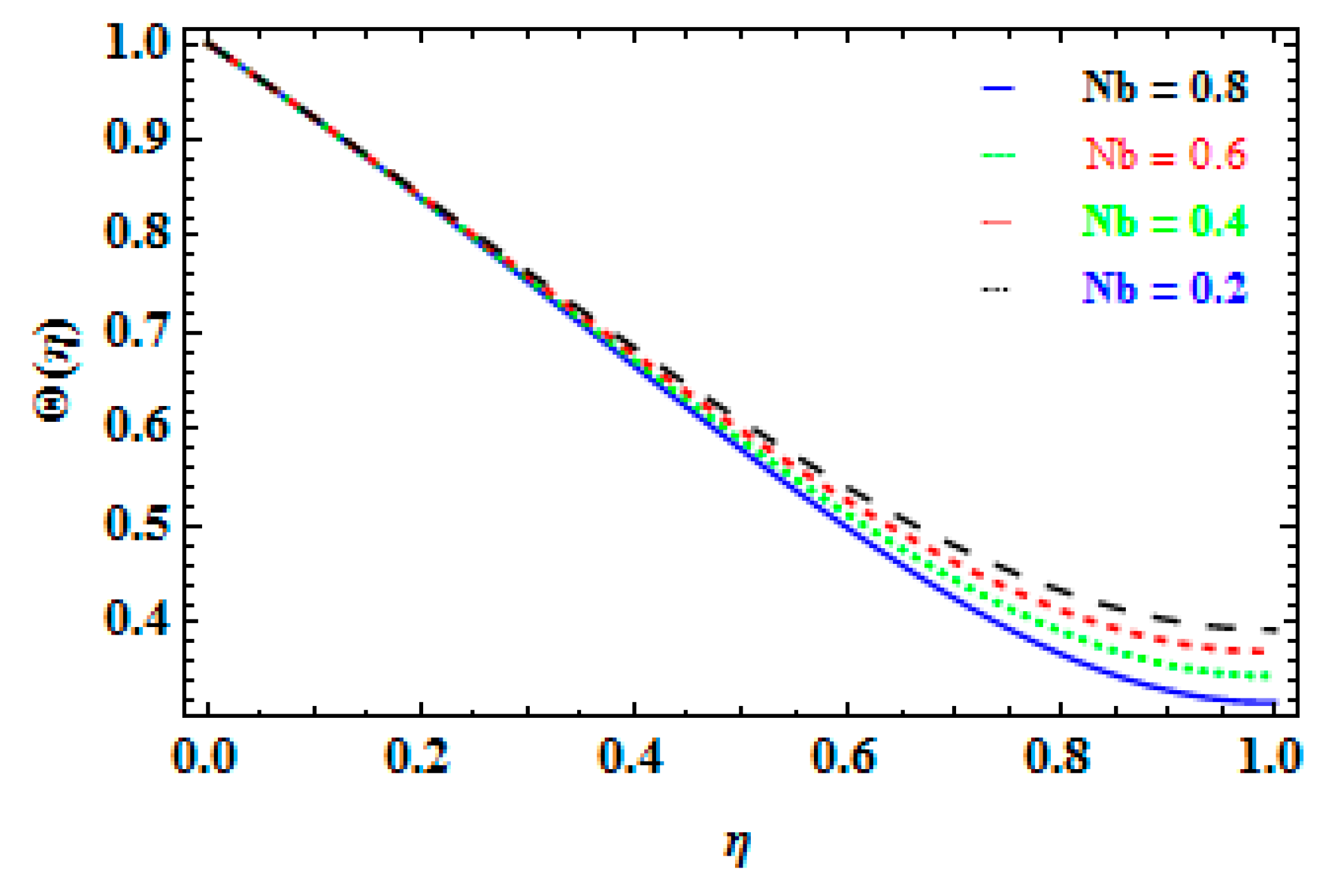
- The Brownian factor has a direct impact on the temperature profile.
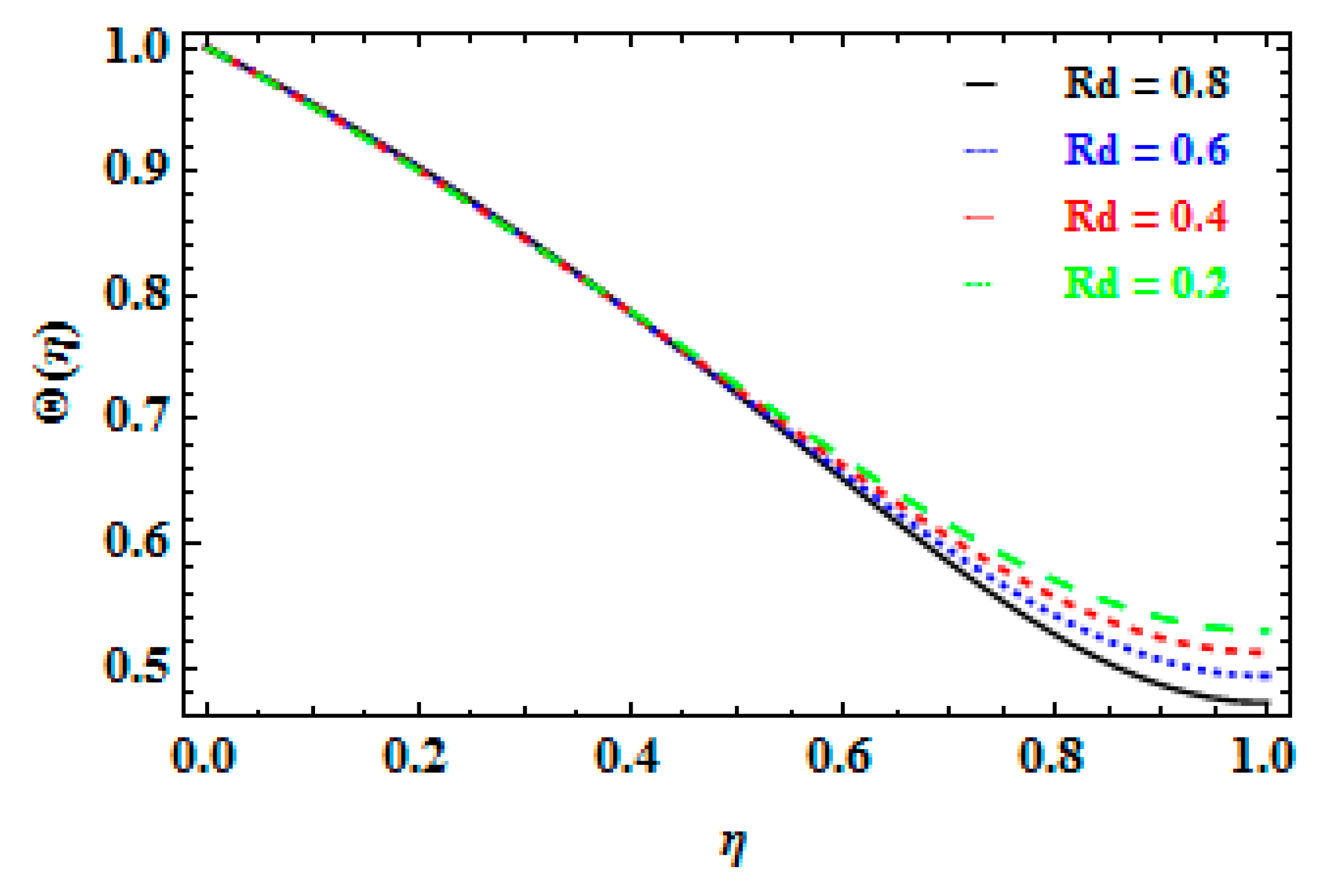
- With rising values of the and , the Nusseltnnumber, the thermal boundary-layer thickness reduces.
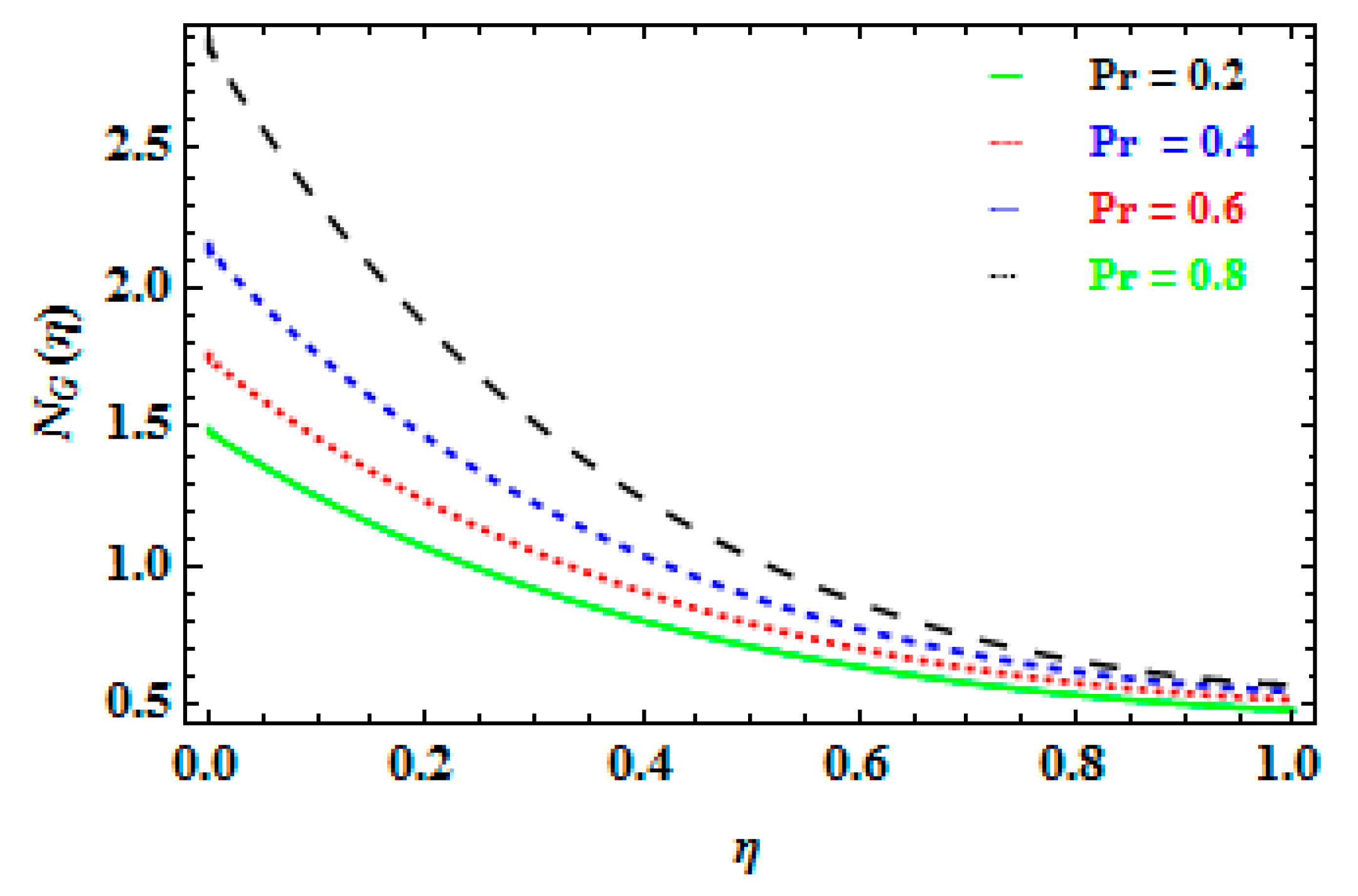
- With higher Prandtl numbers, the fluid’s surface temperature rises, but for higher values , the temperature field has a reverse effect.
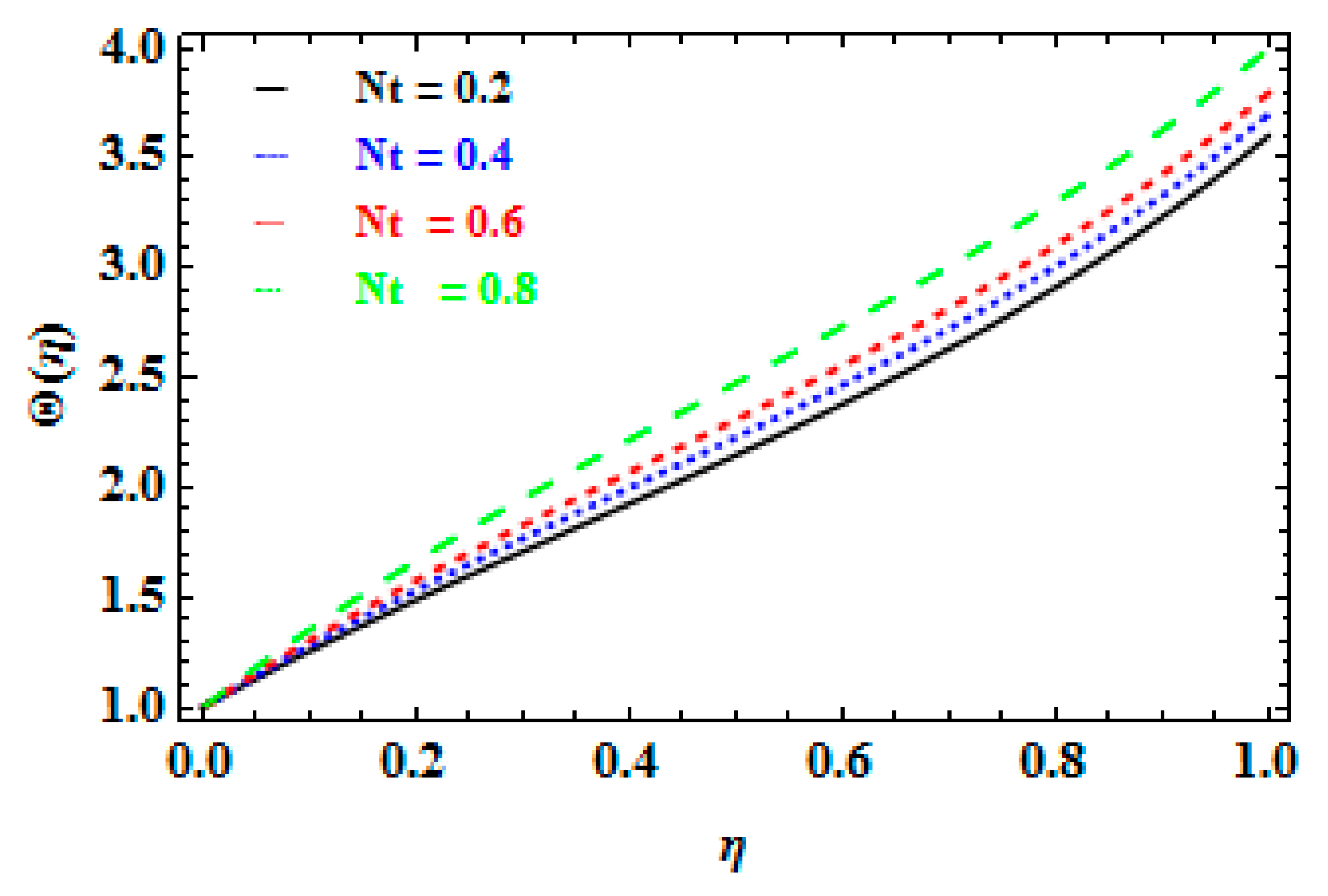
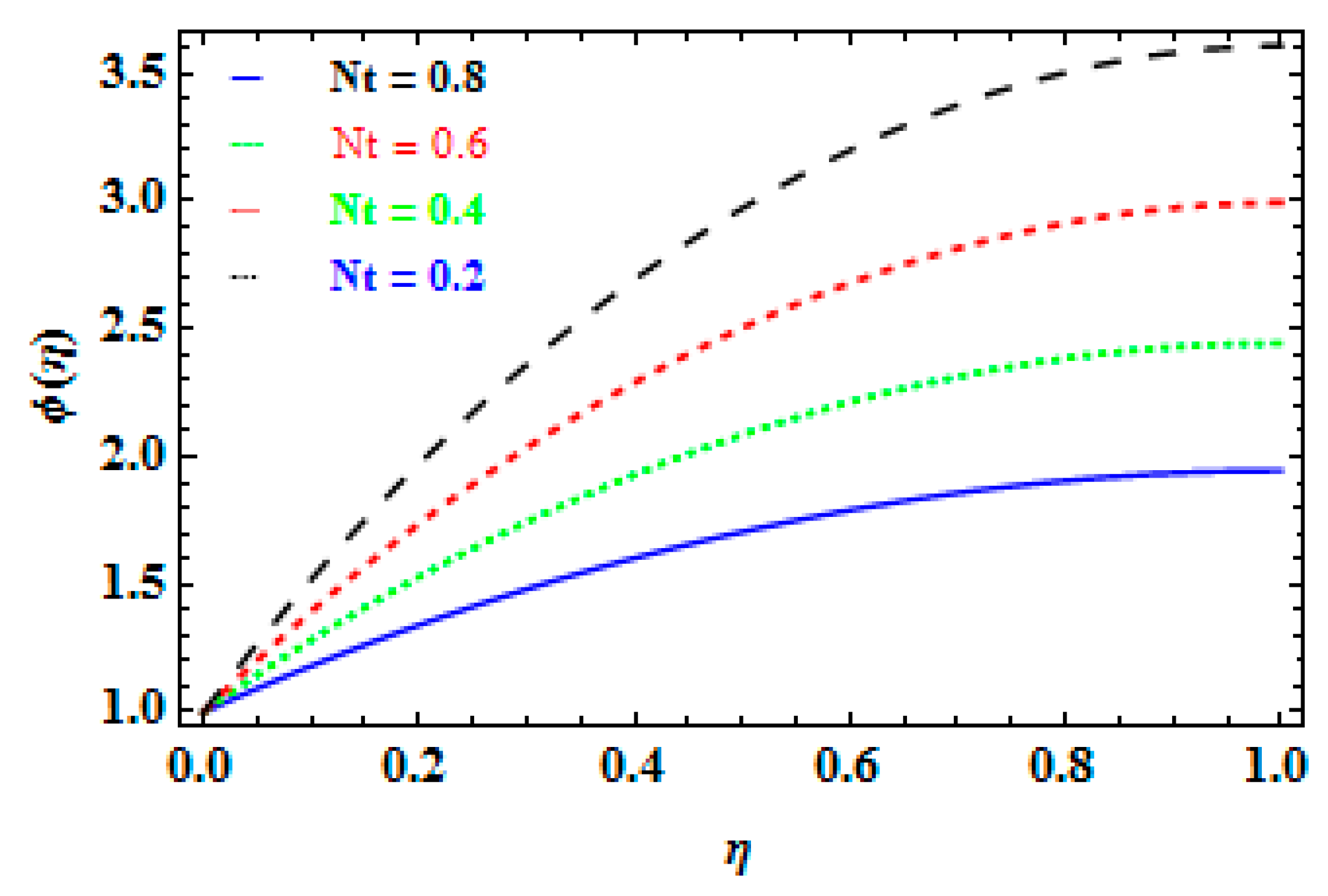
- Observing the impact of the thermophoresis parameter, a similar consequence is observed for the temperature profile.
- The mass flow rate decreases when the Brownian factor is increased, but the thermophoretic factor displays the reverse tendency.
- For the validation of the numerical approach, the implemented technique convergence is quantitatively illustrated. Moreover, the present is compared with the published work reported by Nehad et al. [20], and a good agreement is established.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Myers, T. Application of non-Newtonian models to thin film flow. Phys. Rev. E 2005, 72, 066302. [Google Scholar] [CrossRef] [PubMed]
- Marinca, V.; Herişanu, N.; Nemeş, I. Optimal homotopy asymptotic method with application to thin film flow. Open Phys. 2008, 6, 648–653. [Google Scholar] [CrossRef]
- Sandeep, N.; Malvandi, A. Enhanced heat transfer in liquid thin film flow of non-Newtonian nanofluids embedded with graphene nanoparticles. Adv. Powder Technol. 2016, 27, 2448–2456. [Google Scholar] [CrossRef]
- Wang, C. Liquid film on an unsteady stretching surface. Q. Appl. Math. 1990, 48, 601–610. [Google Scholar] [CrossRef]
- Usha, R.; Sridharan, R. On the motion of a liquid film on an unsteady stretching surface. ASME Fluids Eng. 1993, 150, 43–48. [Google Scholar] [CrossRef]
- Liu, I.C.; Andersson, H.I. Heat transfer in a liquid film on an unsteady stretching sheet. Int. J. Therm. Sci. 2008, 47, 766–772. [Google Scholar] [CrossRef]
- Aziz, R.C.; Hashim, I.; Alomari, A. Thin film flow and heat transfer on an unsteady stretching sheet with internal heating. Meccanica 2011, 46, 349–357. [Google Scholar] [CrossRef]
- Tawade, L.; Abel, M.; Metri, P.G.; Koti, A. Thin film flow and heat transfer over an unsteady stretching sheetwith thermal radiation, internal heating in presence of external magnetic field. Int. J. Adv. Appl. Math. Mech. 2016, 3, e40. [Google Scholar]
- Andersson, H.I.; Aarseth, J.B.; Dandapat, B.S. Heat transfer in a liquid film on an unsteady stretching surface. Int. J. Heat Mass Transf. 2000, 43, 69–74. [Google Scholar] [CrossRef]
- Chen, C.H. Heat transfer in a power-law fluid film over a unsteady stretching sheet. Heat Mass Transf. 2003, 39, 791–796. [Google Scholar] [CrossRef]
- Chen, C.H. Effect of viscous dissipation on heat transfer in a non-Newtonian liquid film over an unsteady stretching sheet. J. Non-Newton. Fluid Mech. 2006, 135, 128–135. [Google Scholar] [CrossRef]
- Ishaq, M.; Ali, G.; Shah, S.I.A.; Shah, Z.; Muhammad, S.; Hussain, S.A. Nanofluid Film Flow of Eyring Powell Fluid with Magneto Hydrodynamic Effect on Unsteady Porous Stretching Sheet. J. Math. 2019, 51, 131–153. [Google Scholar]
- Shah, Z.; Bonyah, E.; Islam, S.; Gul, T. Impact of thermal radiation on electrical MHD rotating flow of Carbon nanotubes over a stretching sheet. AIP Adv. 2019, 9, 015115. [Google Scholar] [CrossRef]
- Khan, A.; Nie, Y.; Shah, Z.; Dawar, A.; Khan, W.; Islam, S. Three-dimensional nanofluid flow with heat and mass transfer analysis over a linear stretching surface with convective boundary conditions. Appl. Sci. 2018, 8, 2244. [Google Scholar] [CrossRef]
- Shah, Z.; Bonyah, E.; Islam, S.; Khan, W.; Ishaq, M. Radiative MHD thin film flow of Williamson fluid over an unsteady permeable stretching sheet. Heliyon 2018, 4, e00825. [Google Scholar] [CrossRef] [PubMed]
- Rasheed, H.U.; Zeeshan; Islam, S.; Abbas, T.; Yassen, M.F. Analytical evaluation of magnetized nanofluid flow in a stagnation point with chemical reaction and nonlinear radiation effect configured by an extended surface. J. Appl. Math. Mech. 2022, 103, e202200234. [Google Scholar] [CrossRef]
- Zeeshan; Jan, A.U.; El-Zahar, E.R.; Shah, N.A.; Shah, R. Computation of magnetized Couette–Poiseuille thermal flow of couple stress between two analogous plate with variable viscosity suspending the hafnium particles. Int. Commun. Heat Mass Transf. 2022, 134, 106042. [Google Scholar] [CrossRef]
- Zeeshan; Shah, R.; Khan, W.; El-Zahar, E.R.; Yook, S.-J.; Shah, N.A. Mathematical Simulation of Heat Transfer in Thermally Magnetised Oldroyd-B Fluid in Sakiadis Rheology with a Heat Reservoir. Mathematics 2022, 10, 1775. [Google Scholar] [CrossRef]
- Rasool, G.; Shah, N.A.; El-Zahar, E.R.; Wakif, A. Numerical investigation of EMHD nanofluid flows over a convectively heated riga pattern positioned horizontally in a Darcy-Forchheimer porous medium: Application of passive control strategy and generalized transfer laws. Waves Random Complex Media 2022, 1–20. [Google Scholar] [CrossRef]
- Nehad, A.S.; Abderrahim, W.; Essam, R.E.; Thirupathi, T.; Se-Jin, Y.; Ashwinkumar, G.P. Heat transfers Thermodynamic activity of a second-grade ternary nanofluid flow over a vertical plate with Atangana-Baleanu Time-Fractional integral. Alex. Eng. J. 2022, 12, 10045–10053. [Google Scholar]
- Raju, C.S.K.; Ameer, N.A.; Kiran, S.; Nehad, A.S.; Se-jin, Y.; Dinesh, M.K. Nonlinear linear movements of axisymmetric ternary hybrid nanofluids in a thermally radiated expanding or contracting permeable Darcy Walls with different shapes and densities: Simple linear regression. Int. Commun. Heat Mass Transf. 2022, 135, 106110. [Google Scholar] [CrossRef]
- Shah, Z.; Dawar, A.; Islam, S.; Khan, I.; Ching, D.L.C. Darcy-Forchheimer flow of radiative carbon nanotubes with microstructure and inertial characteristics in the rotating frame. Case Stud. Therm. Eng. 2018, 12, 823–832. [Google Scholar]
- Khan, N.S.; Gul, T.; Islam, S.; Khan, A.; Shah, Z. Brownian motion and thermophoresis effects on MHD mixed convective thin film second-grade nanofluid flow with Hall effect and heat transfer past a stretching sheet. J. Nanofluids 2017, 6, 812–829. [Google Scholar] [CrossRef]
- Tahir, F.; Gul, T.; Islam, S.; Shah, Z.; Khan, A.; Khan, W.; Ali, L. Flow of a nano-liquid film of Maxwell fluid with thermal radiation and magneto hydrodynamic properties on an unstable stretching sheet. J. Nanofluids 2017, 6, 1021–1030. [Google Scholar] [CrossRef]
- Chu, R.C.; Simons, R. Recent development of computer cooling technology. In Proceedings of the International Symposium on Transport Phenomena in Thermal Engineering, Seoul, Republic of Korea, 9–13 May 1993; pp. 17–25. [Google Scholar]
- Dixit, T.; Ghosh, I. Review of micro-and mini-channel heat sinks and heat exchangers for single phase fluids. Renew. Sustain. Energy Rev. 2015, 41, 1298–1311. [Google Scholar] [CrossRef]
- Xie, X.; Liu, Z.; He, Y.; Tao, W. Numerical study of laminar heat transfer and pressure drop characteristics in a water-cooled minichannel heat sink. Appl. Therm. Eng. 2009, 29, 64–74. [Google Scholar] [CrossRef]
- Srivastava, L.; Srivastava, V.; Sinha, S. Peristaltic transport of a physiological fluid. Biorheology 1983, 20, 153–166. [Google Scholar] [CrossRef]
- Abbasi, F.M.; Hayat, T.; Shehzad, S.A.; Alsaadi, F.; Altoaibi, N. Hydromagnetic peristaltic transport of copper–water nanofluid with temperature-dependent effective viscosity. Particuology 2016, 27, 133–140. [Google Scholar] [CrossRef]
- Abolbashari, M.H.; Freidoonimehr, N.; Nazari, F.; Rashidi, M.M. Analytical modeling of entropy generation for Casson nano-fluid flow induced by a stretching surface. Adv. Powder Technol. 2015, 26, 542–552. [Google Scholar] [CrossRef]
- Hayat, T.; Muhammad, T.; Shehzad, S.; Alsaedi, A. Three-dimensional boundary layer flow of Maxwell nanofluid: Mathematical model. Appl. Math. Mech. 2015, 36, 747–762. [Google Scholar] [CrossRef]
- Malik, M.; Khan, I.; Hussain, A.; Salahuddin, T. Mixed convection flow of MHD Eyring-Powell nanofluid over a stretching sheet: A numerical study. AIP Adv. 2015, 5, 117118. [Google Scholar] [CrossRef]
- Nadeem, S.; Haq, R.U.; Khan, Z. Numerical study of MHD boundary layer flow of a Maxwell fluid past a stretching sheet in the presence of nanoparticles. J. Taiwan Inst. Chem. Eng. 2014, 45, 121–126. [Google Scholar] [CrossRef]
- Raju, C.; Sandeep, N.; Malvandi, A. Free convective heat and mass transfer of MHD non-Newtonian nanofluids over a cone in the presence of non-uniform heat source/sink. J. Mol. Liq. 2016, 221, 108–115. [Google Scholar] [CrossRef]
- Rokni, H.B.; Alsaad, D.M.; Valipour, P. Electrohydrodynamic nanofluid flow and heat transfer between two plates. J. Mol. Liq. 2016, 216, 583–589. [Google Scholar] [CrossRef]
- Nadeem, S.; Haq, R.U.; Khan, Z. Numerical solution of non-Newtonian nanofluid flow over a stretching sheet. Appl. Nanosci. 2014, 4, 625–631. [Google Scholar] [CrossRef]
- Shehzad, S.; Hayat, T.; Alsaedi, A. MHD flow of Jeffrey nanofluid with convective boundary conditions. J. Braz. Soc. Mech. Sci. Eng. 2015, 37, 873–883. [Google Scholar] [CrossRef]
- Sheikholeslami, M.; Hatami, M.; Ganji, D. Nanofluid flow and heat transfer in a rotating system in the presence of a magnetic field. J. Mol. Liq. 2014, 190, 112–120. [Google Scholar] [CrossRef]
- Sheikholeslami, M.; Shah, Z.; Shafee, A.; Khan, I.; Tlili, I. Uniform magnetic force impact on water based nanofluid thermal behavior in a porous enclosure with ellipse shaped obstacle. Sci. Rep. 2019, 9, 1196. [Google Scholar] [CrossRef]
- Mahmoodi, M.; Kandelousi, S. Kerosene-alumina nanofluid flow and heat transfer for cooling application. J. Cent. South Univ. 2016, 23, 983–990. [Google Scholar] [CrossRef]
- Shah, Z.; Gul, T.; Islam, S.; Khan, M.A.; Bonyah, E.; Hussain, F.; Mukhtar, S.; Ullah, M. Three dimensional third grade nanofluid flow in a rotating system between parallel plates with Brownian motion and thermophoresis effects. Results Phys. 2018, 10, 36–45. [Google Scholar] [CrossRef]
- Shah, Z.; Gul, T.; Khan, A.; Ali, I.; Islam, S.; Husain, F. Effects of hall current on steady three dimensional non-newtonian nanofluid in a rotating frame with brownian motion and thermophoresis effects. J. Eng. Technol. 2017, 6, e296. [Google Scholar]
- Shah, Z.; Dawar, A.; Kumam, P.; Khan, W.; Islam, S. Impact of Nonlinear Thermal Radiation on MHD Nanofluid Thin Film Flow over a Horizontally Rotating Disk. Appl. Sci. 2019, 9, 1533. [Google Scholar] [CrossRef]
- Saeed, A.; Islam, S.; Dawar, A.; Shah, Z.; Kumam, P.; Khan, W. Influence of Cattaneo–Christov Heat Flux on MHD Jeffrey, Maxwell, and Oldroyd-B Nanofluids with Homogeneous-Heterogeneous Reaction. Symmetry 2019, 11, 439. [Google Scholar] [CrossRef]
- Kumam, P.; Shah, Z.; Dawar, A.; Rasheed, H.U.; Islam, S. Entropy Generation in MHD Radiative Flow of CNTs Casson Nanofluid in Rotating Channels with Heat Source/Sink. Math. Probl. Eng. 2019, 2019, 9158093. [Google Scholar] [CrossRef]
- Koriko, O.K.; Adegbie, K.S.; Shah, N.A.; Animasaun, I.L.; Olotu, M.A. Numerical solutions of the partial differential equations for investigating the significance of partial slip due to lateral velocity and viscous dissipation: The case of blood-gold Carreau nanofluid and dusty fluid. Numer. Methods Part. Differ. Equ. 2021, 7, 1–15. [Google Scholar] [CrossRef]
- Eswaramoorthi, S.; Loganathan, K.; Faisal, M.; Botmart, T.; Shah, N.A. Analytical and numerical investigation of Darcy-Forchheimer flow of a nonlinear-radiative non-Newtonian fluid over a Riga plate with entropy optimization. Ain Shams Eng. J. 2023, 14, 101887. [Google Scholar] [CrossRef]
- Ragupathi, P.; Ahammad, N.A.; Wakif, A.; Shah, N.A.; Jeon, Y. Exploration of Multiple Transfer Phenomena within Viscous Fluid Flows over a Curved Stretching Sheet in the Co-Existence of Gyrotactic Micro-Organisms and Tiny Particles. Mathematics 2022, 10, 4133. [Google Scholar] [CrossRef]
- Saeed, A.; Shah, Z.; Islam, S.; Jawad, M.; Ullah, A.; Gul, T.; Kumam, P. Three-Dimensional Casson Nanofluid Thin Film Flow over an Inclined Rotating Disk with the Impact of Heat Generation/Consumption and Thermal Radiation. Coatings 2019, 9, 248. [Google Scholar] [CrossRef]
- Sheikholeslami, M.; Bhatti, M. Forced convection of nanofluid in presence of constant magnetic field considering shape effects of nanoparticles. Int. J. Heat Mass Transf. 2017, 111, 1039–1049. [Google Scholar] [CrossRef]
- Sheikholeslami, M. CuO-water nanofluid flow due to magnetic field inside a porous media considering Brownian motion. J. Mol. Liq. 2018, 249, 921–929. [Google Scholar] [CrossRef]
- Sheikholeslami, M.; Shamlooei, M.; Moradi, R. Fe3O4-Ethylene glycol nanofluid forced convection inside a porous enclosure in existence of Coulomb force. J. Mol. Liq. 2018, 249, 429–437. [Google Scholar] [CrossRef]
- Munkhbayar, B.; Tanshen, M.R.; Jeoun, J.; Chung, H.; Jeong, H. Surfactant-free dispersion of silver nanoparticles into MWCNT-aqueous nanofluids prepared by one-step technique and their thermal characteristics. Ceram. Int. 2013, 39, 6415–6425. [Google Scholar] [CrossRef]
- Esfe, M.H.; Wongwises, S.; Naderi, A.; Asadi, A.; Safaei, M.R.; Rostamian, H.; Dahari, M.; Karimipour, A. Thermal conductivity of Cu/TiO2–water/EG hybrid nanofluid: Experimental data and modeling using artificial neural network and correlation. Int. Commun. Heat Mass Transf. 2015, 66, 100–104. [Google Scholar] [CrossRef]
- Akhgar, A.; Toghraie, D. An experimental study on the stability and thermal conductivity of water-ethylene glycol/TiO2-MWCNTs hybrid nanofluid: Developing a new correlation. Powder Technol. 2018, 338, 806–818. [Google Scholar] [CrossRef]
- Keyvani, M.; Afrand, M.; Toghraie, D.; Reiszadeh, M. An experimental study on the thermal conductivity of cerium oxide/ethylene glycol nanofluid: Developing a new correlation. J. Mol. Liq. 2018, 266, 211–217. [Google Scholar] [CrossRef]
- Ranjbarzadeh, R.; Meghdadi, A.H.; Hojaji, M. The analysis of experimental process of production, stabilizing and measurement of the thermal conductivity coefficient of water/graphene oxide as a cooling nanofluid in machining. J. Mod. Process. Manuf. Prod. 2016, 5, 43–53. [Google Scholar]
- Carreau, P.; Kee, D.D.; Daroux, M. An analysis of the viscous behaviour of polymeric solutions. Can. J. Chem. Eng. 1979, 57, 135–140. [Google Scholar] [CrossRef]
- Kefayati, G.R.; Tang, H. MHD thermosolutal natural convection and entropy generation of Carreau fluid in a heated enclosure with two inner circular cold cylinders, using LBM. Int. J. Heat Mass Transf. 2018, 126, 508–530. [Google Scholar] [CrossRef]
- Olajuwon, B.I. Convection heat and mass transfer in a hydromagnetic Carreau fluid past a vertical porous plate in presence of thermal radiation and thermal diffusion. Therm. Sci. 2011, 15, S241–S252. [Google Scholar] [CrossRef]
- Hayat, T.; Asad, S.; Mustafa, M.; Alsaedi, A. Boundary layer flow of Carreau fluid over a convectively heated stretching sheet. Appl. Math. Comput. 2014, 246, 12–22. [Google Scholar] [CrossRef]
- Alsarraf, J.; Moradikazerouni, A.; Shahsavar, A.; Afrand, M.; Salehipour, H.; Tran, M.D. Hydrothermal analysis of turbulent boehmite alumina nanofluid flow with different nanoparticle shapes in a minichannel heat exchanger using two-phase mixture model. Phys. A Stat. Mech. Its Appl. 2019, 520, 275–288. [Google Scholar] [CrossRef]
- Azari, A.; Kalbasi, M.; Rahimi, M. CFD and experimental investigation on the heat transfer characteristics of alumina nanofluids under the laminar flow regime. Braz. J. Chem. Eng. 2014, 31, 469–481. [Google Scholar] [CrossRef]
- Munir, A.; Shahzad, A.; Khan, M. Convective flow of Sisko fluid over a bidirectional stretching surface. PLoS ONE 2015, 10, e0130342. [Google Scholar] [CrossRef]
- Olanrewaju, P.; Adigun, A.; Fenwa, O.; Oke, A.; Funmi, A. Unsteady free convective flow of sisko fluid with radiative heat transfer past a flat plate moving through a binary mixture. Therm. Energy Power Eng. 2013, 2, 109–117. [Google Scholar]
- Weigand, B.; Birkefeld, A. Similarity solutions of the entropy transport equation. Int. J. Therm. Sci. 2009, 48, 1863–1869. [Google Scholar] [CrossRef]
- Makinde, O.D. Second law analysis for variable viscosity hydromagnetic boundary layer flow with thermal radiation and Newtonian heating. Entropy 2011, 13, 1446–1464. [Google Scholar] [CrossRef]
- Hayat, T.; Khan, M.I.; Khan, T.A.; Khan, M.I.; Ahmad, S.; Alsaedi, A. Entropy generation in Darcy-Forchheimer bidirectional flow of water-based carbon nanotubes with convective boundary conditions. J. Mol. Liq. 2018, 265, 629–638. [Google Scholar] [CrossRef]
- Makinde, O. Thermodynamic second law analysis for a gravity-driven variable viscosity liquid film along an inclined heated plate with convective cooling. J. Mech. Sci. Technol. 2010, 24, 899–908. [Google Scholar] [CrossRef]
- Esmaeilpour, M.; Abdollahzadeh, M. Free convection and entropy generation of nanofluid inside an enclosure with different patterns of vertical wavy walls. Int. J. Therm. Sci. 2012, 52, 127–136. [Google Scholar] [CrossRef]
- Paoletti, S.; Rispoli, F.; Sciubba, E. Calculation of exergetic losses in compact heat exchanger passages. Asme Aes. 1989, 10, 21–29. [Google Scholar]
- Zarastvand, M.R.; Asadijafari, M.H.; Talebitooti, R. Acoustic wave transmission characteristics of stiffened composite shell systems with double curvature. Compo. Struct. 2022, 292, 115688. [Google Scholar] [CrossRef]
- Seilsepour, H.; Zarastvand, M.R.; Talebitooti, R. Acoustic insulation characteristics of sandwich composite shell systems with double curvature: The effect of nature of viscoelastic core. J. Vib. Control. 2022. [Google Scholar] [CrossRef]












| Order | |||
|---|---|---|---|
| 1 | −0.050000 | −1.218600 | 0.064860 |
| 2 | −0.215767 | −0.218600 | 0.1967944 |
| 4 | −0.226793 | −0.217991 | 0.1946782 |
| 6 | −0.229531 | −0.217928 | 0.1966267 |
| 8 | −0.229191 | −0.217919 | 0.1196998 |
| 10 | −0.229372 | −0.217917 | 0.1972274 |
| 12 | −0.229414 | −0.217918 | 0.1972568 |
| 14 | −0.229424 | −0.217917 | 0.1972641 |
| 16 | −0.229426 | −0.217917 | 0.1972659 |
| 18 | −0.229427 | −0.217917 | 0.1972663 |
| 22 | −0.229427 | −0.217917 | 0.1972665 |
| 24 | −0.229427 | −0.217917 | 0.1972665 |
| M | Gr | St | Nehad et al. [20] | ||
|---|---|---|---|---|---|
| 0.2 | 0.4 | 0.1 | 1.4 | −0.2819 | −0.2815 |
| 0.4 | −0.3145 | −0.3142 | |||
| 1.2 | −0.3571 | −0.3570 | |||
| 1.8 | 0.2 | −0.2887 | −0.2881 | ||
| 0.4 | −0.2819 | −0.2812 | |||
| 1.2 | −0.2819 | −0.2813 | |||
| 1.7 | 0.2 | −0.4545 | −0.4548 | ||
| 0.4 | −0.8574 | −0.8570 | |||
| 1.2 | −7.9971 | −7.9973 | |||
| 1.7 | 0.2 | −2.9783 | −2.9787 | ||
| 0.4 | −0.3328 | −0.3329 | |||
| 1.2 | −0.2431 | −0.2435 |
| M | St | Pr | Nu | Nehad et al. [20] | |
|---|---|---|---|---|---|
| 0.2 | 0.2 | 1.4 | 1.5 | 0.4634 | 0.4636 |
| 0.4 | 0.4632 | 0.4637 | |||
| 1.2 | 0.4629 | 0.4623 | |||
| 1.8 | 0.2 | 0.4634 | 0.4630 | ||
| 0.4 | 2.6256 | 2.6252 | |||
| 1.2 | 2.3727 | 2.3725 | |||
| 1.7 | 0.2 | 2.7359 | 2.7353 | ||
| 0.4 | 0.3395 | 0.3390 | |||
| 1.2 | 0.3915 | 0.3913 | |||
| 1.7 | 1.2 | 0.4634 | 0.4638 | ||
| 1.8 | 0.4354 | 0.4350 | |||
| 4.0 | 0.4198 | 0.4197 | |||
| 6.0 | 0.4123 | 0.4122 |
| Nb | Nt | Sc | St | Pr | Nehad et al. [20] | |
|---|---|---|---|---|---|---|
| 0.2 | 0.4 | 0.2 | 1.4 | 1.4 | −2.4693 | −2.4693 |
| 0.4 | −0.3499 | −0.3492 | ||||
| 1.2 | −0.1988 | −0.1983 | ||||
| 1.7 | 0.2 | −0.1334 | −0.1338 | |||
| 0.4 | −2.4693 | −2.4690 | ||||
| 1.2 | −3.8648 | −3.8642 | ||||
| 1.7 | 0.2 | −5.2566 | −5.2566 | |||
| 0.4 | −4.9778 | −4.9772 | ||||
| 1.2 | −4.8564 | −4.8566 | ||||
| 1.7 | 0.2 | −2.9216 | −2.9214 | |||
| 0.4 | −3.4169 | −3.4160 | ||||
| 1.2 | −3.9294 | −3.9290 | ||||
| 1.7 | 1.4 | −4.6374 | −4.6372 | |||
| 2.5 | −6.7241 | −6.7244 | ||||
| 4.0 | −7.8817 | −7.8812 | ||||
| 6.0 | −8.4434 | −8.4438 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zeeshan; Attaullah; Ahammad, N.A.; Shah, N.A.; Chung, J.D. A Numerical Framework for Entropy Generation Using Second-Order Nanofluid Thin Film Flow over an Expanding Sheet: Error Estimation and Stability Analysis. Mathematics 2023, 11, 1078. https://doi.org/10.3390/math11051078
Zeeshan, Attaullah, Ahammad NA, Shah NA, Chung JD. A Numerical Framework for Entropy Generation Using Second-Order Nanofluid Thin Film Flow over an Expanding Sheet: Error Estimation and Stability Analysis. Mathematics. 2023; 11(5):1078. https://doi.org/10.3390/math11051078
Chicago/Turabian StyleZeeshan, Attaullah, N. Ameer Ahammad, Nehad Ali Shah, and Jae Dong Chung. 2023. "A Numerical Framework for Entropy Generation Using Second-Order Nanofluid Thin Film Flow over an Expanding Sheet: Error Estimation and Stability Analysis" Mathematics 11, no. 5: 1078. https://doi.org/10.3390/math11051078
APA StyleZeeshan, Attaullah, Ahammad, N. A., Shah, N. A., & Chung, J. D. (2023). A Numerical Framework for Entropy Generation Using Second-Order Nanofluid Thin Film Flow over an Expanding Sheet: Error Estimation and Stability Analysis. Mathematics, 11(5), 1078. https://doi.org/10.3390/math11051078





