A New Reciprocal Weibull Extension for Modeling Extreme Values with Risk Analysis under Insurance Data
Abstract
:1. Introduction and Motivation
2. Properties
3. KRIs
3.1. VAR Indicator
3.2. TVAR Risk Indicator
3.3. TV Risk Indicator
3.4. TMV Risk Indicator
- the TMV TV ,
- for , TMV TVAR ,
- for , TMV TVAR TV
4. Modeling
4.1. Comparing the Competitive Extensions under the Stress Data
4.2. Comparing the Competitive Extensions under the Glass Fiber Data
4.3. Comparing the Competitive Extensions under the Relief Times Data
5. Risk Analysis
5.1. Artificial Risk Analysis
- The (), and increase when q increases for all estimation methods.
- The and decrease when q increases for all estimation methods.
- The three tables’ results enable us to verify that all approaches are valid and that it is impossible to categorically recommend one approach over another. Given this fundamental finding, we are obliged to develop an application based on real data in the hopes that it would enable us to select one strategy over another and identify the best and most appropriate methods. In other words, even though the results from the five ways to risk assessment were equivalent, the simulation research did not help us decide how to balance the methodologies. These convergent findings comfort us that, when modelling actuarial data and evaluating risk, all methodologies function satisfactorily and within allowable limits.
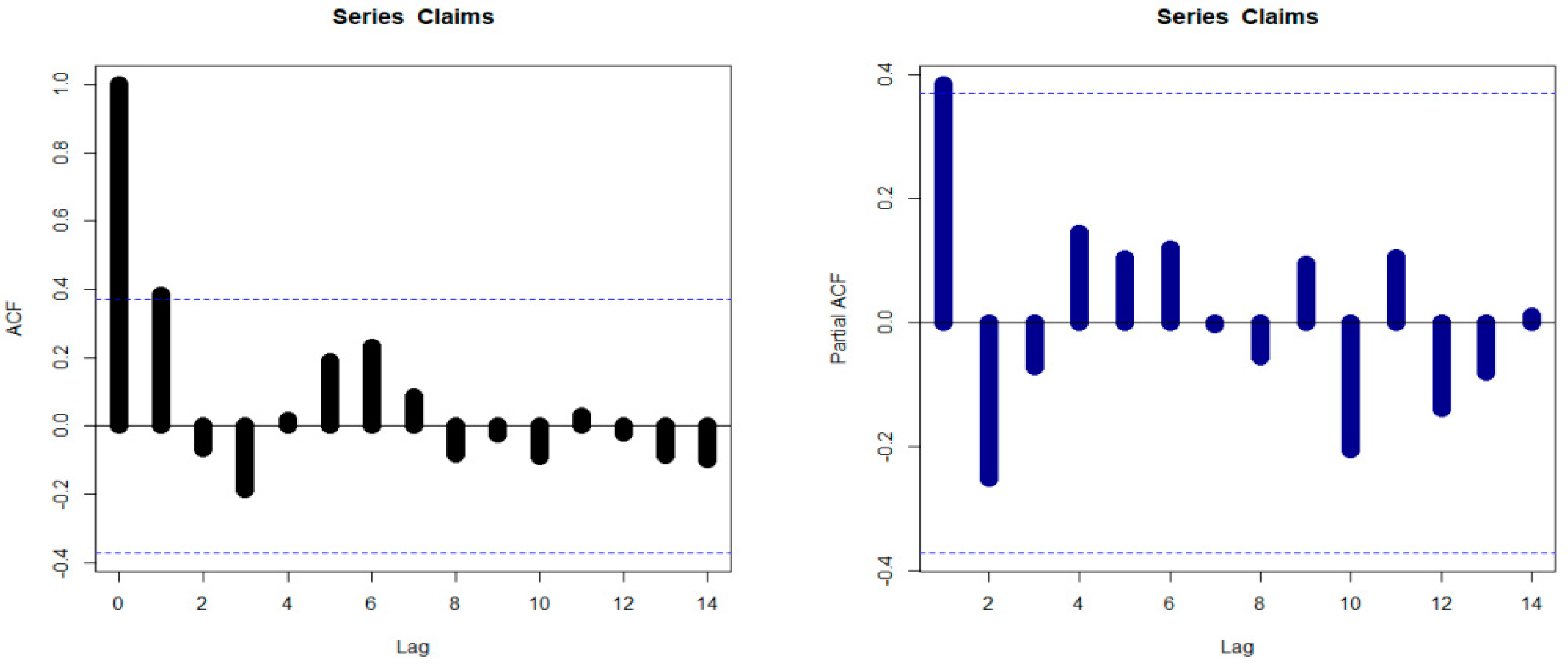
5.2. Insurance Data for Risk Analysis
- For all risk assessment methods |:
- For all risk assessment methods |:
- For Most risk assessment methods |:
- For all risk assessment methods |:
- For all risk assessment methods |:
- Under the GGR-RW model and the MLE method, the VAR() is monotonically increasing indicator starting with 2519.589871 and ending with 9747.670085, the TVAR() is a monotonically increasing indicator starting with 4267.691033 and ending with 12,352.578196. However, the TV(), the TMV() and the EL() are decreasing functions. Under the RW model and the MLE method, the VAR() is a monotonically increasing indicator starting with 1986.487789 and ending with 58,937.60432, the TVAR() is a monotonically increasing indicator starting with 11,961.555933 and ending with 270,450.59761, the TV(), the TMV() and the EL() are decreasing function indicators.
- Under the GGR-RW model and the LSE method, the VAR() is a monotonically increasing indicator starting with 2428.50708 and ending with 13,665.84114, the TVAR() is a monotonically increasing indicator starting with 4865.81245 and ending with 18,627.28911. However, the TV(), the TV() and the TMV () are decreasing functions. Under the RW model and the OLSQ method, the VAR() is a monotonically increasing indicator starting with 2226.27121 and ending with 44,780.28947, the TVAR() is a monotonically increasing indicator starting with 9174.03623 and ending with 151,748.59629. Also, the TV (), the TMV () and the EL() are decreasing functions.
- Under the GGR-RW model and the WLSQ method, the VAR() is a monotonically increasing indicator starting with 2356.17122 and ending with 9514.1782, the TVAR() is a monotonically increasing indicator starting with 4108.2022 and ending with 12,042.68509. However, the TV(), the TMV() and the EL() are decreasing functions. Under the RW model and the WLSQ method, the VAR() is a monotonically increasing indicator starting with 1964.20669 and ending with 19,161.39616, the TVAR() is a monotonically increasing indicator starting with 4830.43197 and ending with 41,550.35309. However, the TV(), the TMV(), and the EL() are decreasing functions.
- Under the GGR-RW model and the CVM method, the VAR() is a monotonically increasing indicator starting with 2440.48715 and ending with 12,431.24689, the TVAR() in monotonically increasing indicator starting with 4680.62835 and ending with 16,642.80352. However, the TV(), the TMV(), and the EL() are decreasing function. Under the RW model and the AE method, the VAR() is a monotonically increasing indicator starting with 2229.99377 and ending with 38,705.15155, the TVAR() is a monotonically increasing indicator starting with 8126.51599 and ending with 118,195.6688, the TV(), the TMV(Z ) and the EL() are decreasing functions.
6. Concluding Remarks
- For all risk assessment methods |:
- For all risk assessment methods |:
- For Most risk assessment methods |:
- For all risk assessment methods |:
- For all risk assessment methods |:
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Artzner, P. Application of Coherent Risk Measures to Capital Requirements in Insurance. N. Am. Actuar. J. 1999, 3, 11–25. [Google Scholar] [CrossRef]
- Wirch, J. Raising Value at Risk. N. Am. Actuar. J. 1999, 3, 106–115. [Google Scholar] [CrossRef]
- Tasche, D. Expected Shortfall and Beyond. J. Bank. Financ. 2002, 26, 1519–1533. [Google Scholar] [CrossRef]
- Acerbi, C.; Tasche, D. On the coherence of expected shortfall. J. Bank. Financ. 2002, 26, 1487–1503. [Google Scholar] [CrossRef]
- Furman, E.; Landsman, Z. Tail variance premium with applications for elliptical portfolio of risks. ASTIN Bull. 2006, 36, 433–462. [Google Scholar] [CrossRef]
- Landsman, Z. On the tail mean—Variance optimal portfolio selection. Insur. Math. Econ. 2010, 46, 547–553. [Google Scholar] [CrossRef]
- Fréchet, M. Sur la loi de probabilité de lécart maximum. Ann. Soc. Pol. Math. 1927, 6, 93–116. [Google Scholar]
- Nadarajah, S.; Kotz, S. The exponentiated Fréchet distribution. Interstate Electron. J. 2003, 14, 1–7. [Google Scholar]
- Krishna, E.; Jose, K.K.; Alice, T.; Risti, M.M. The Marshall-Olkin Fréchet distribution. Commun. Stat. Theory Methods 2013, 42, 4091–4107. [Google Scholar] [CrossRef]
- Nichols, M.D.; Padgett, W.J. A bootstrap control chart for Weibull percentiles. Qual. Reliab. Eng. Int. 2006, 22, 141–151. [Google Scholar] [CrossRef]
- Smith, R.L.; Naylor, J. A comparison of maximum likelihood and Bayesian estimators for the three-parameter Weibull distribution. J. R. Stat. Soc. Ser. C Appl. Stat. 1987, 36, 358–369. [Google Scholar] [CrossRef]
- Mohamed, H.S.; Cordeiro, G.M.; Minkah, R.; Yousof, H.M.; Ibrahim, M. A size-of-loss model for the negatively skewed insurance claims data: Applications, risk analysis using different methods and statistical forecasting. J. Appl. Stat. 2022, 1–22. [Google Scholar] [CrossRef]
- Hamed, M.S.; Cordeiro, G.M.; Yousof, H.M. A New Compound Lomax Model: Properties, Copulas, Modeling and Risk Analysis Utilizing the Negatively Skewed Insurance Claims Data. Pak. J. Stat. Oper. Res. 2022, 18, 601–631. [Google Scholar] [CrossRef]
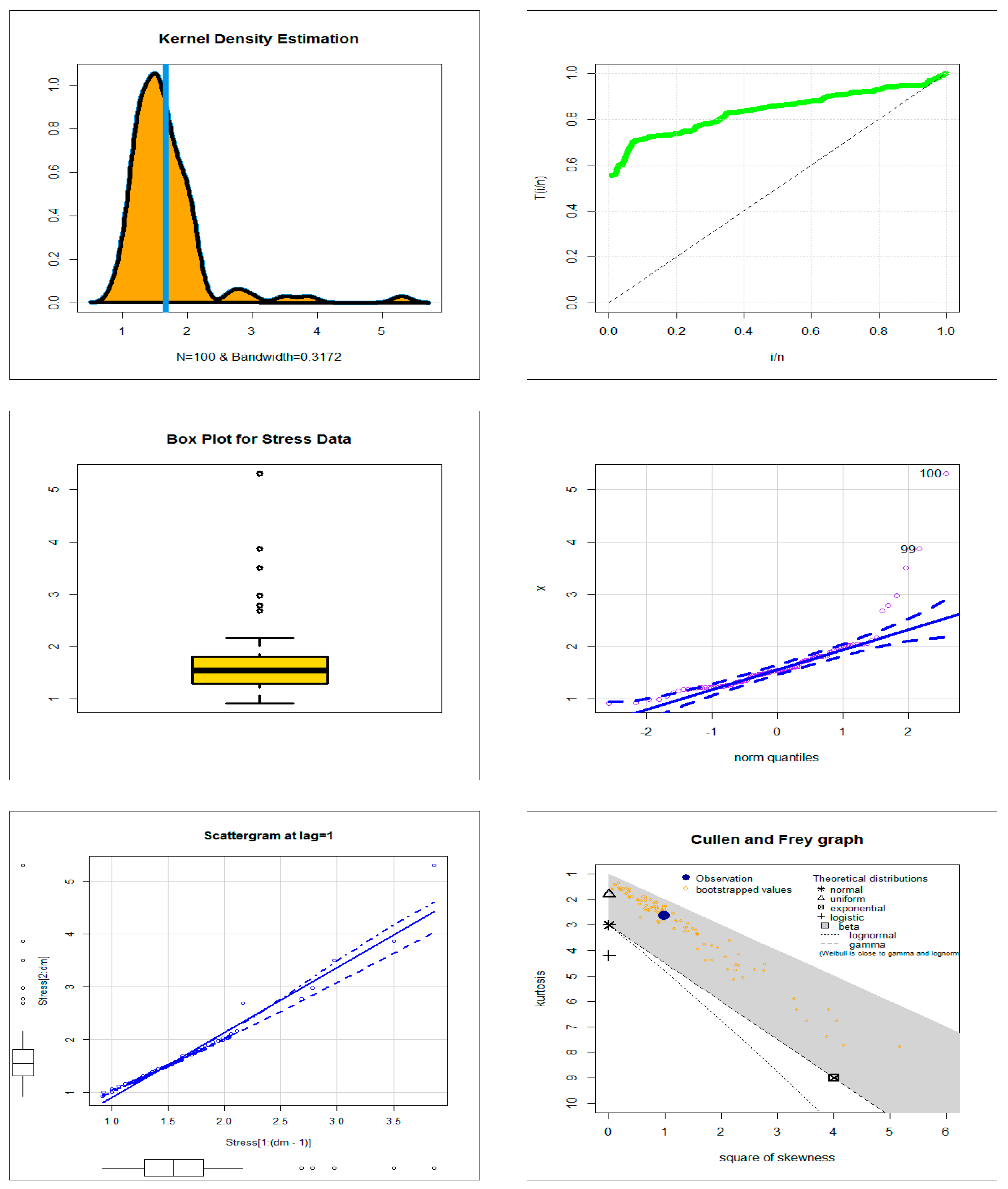
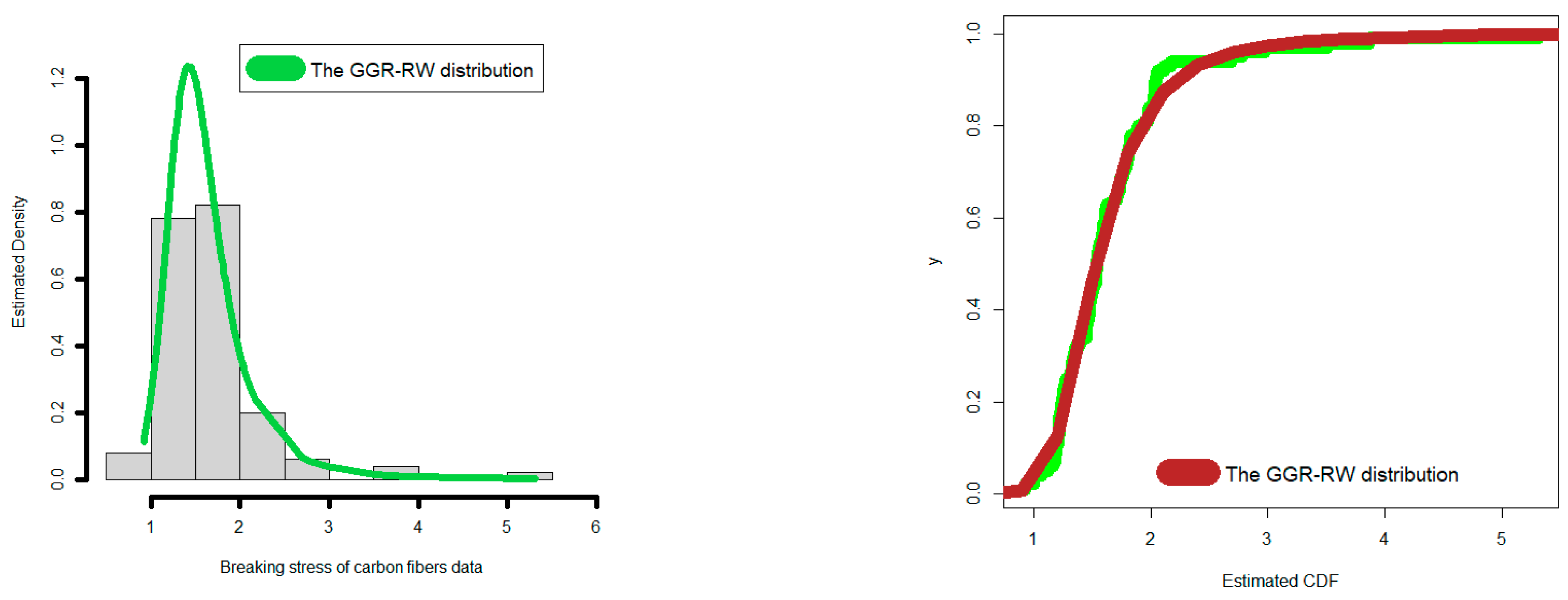
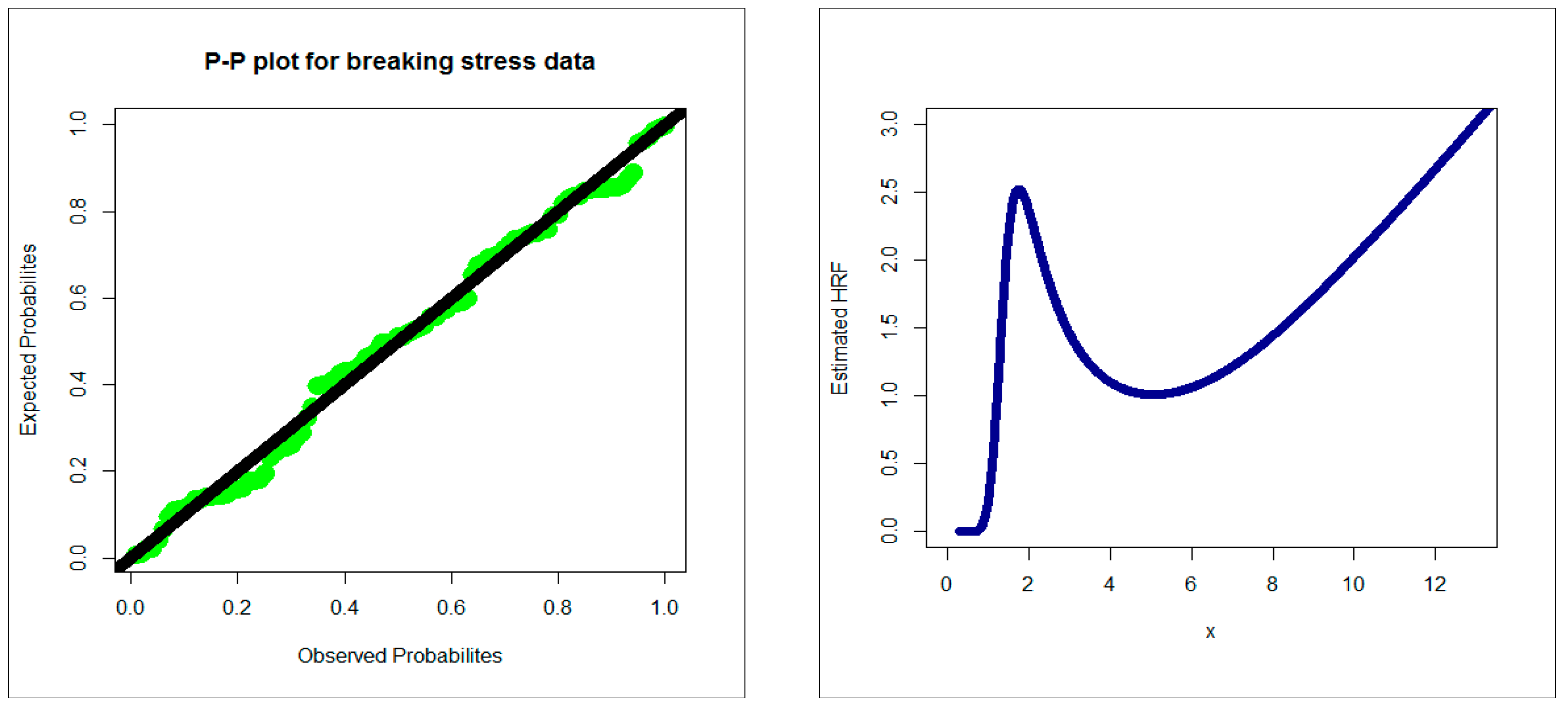
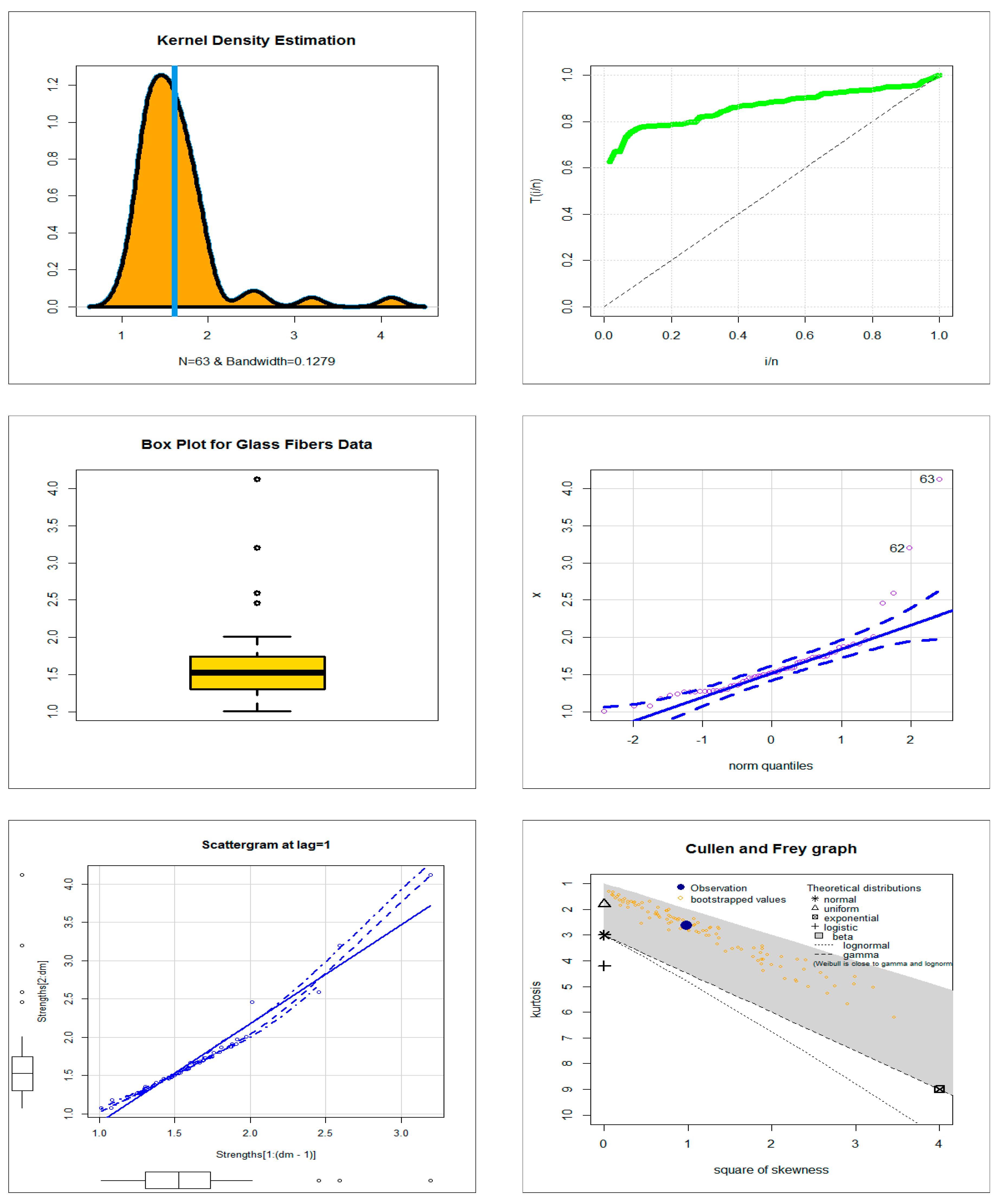
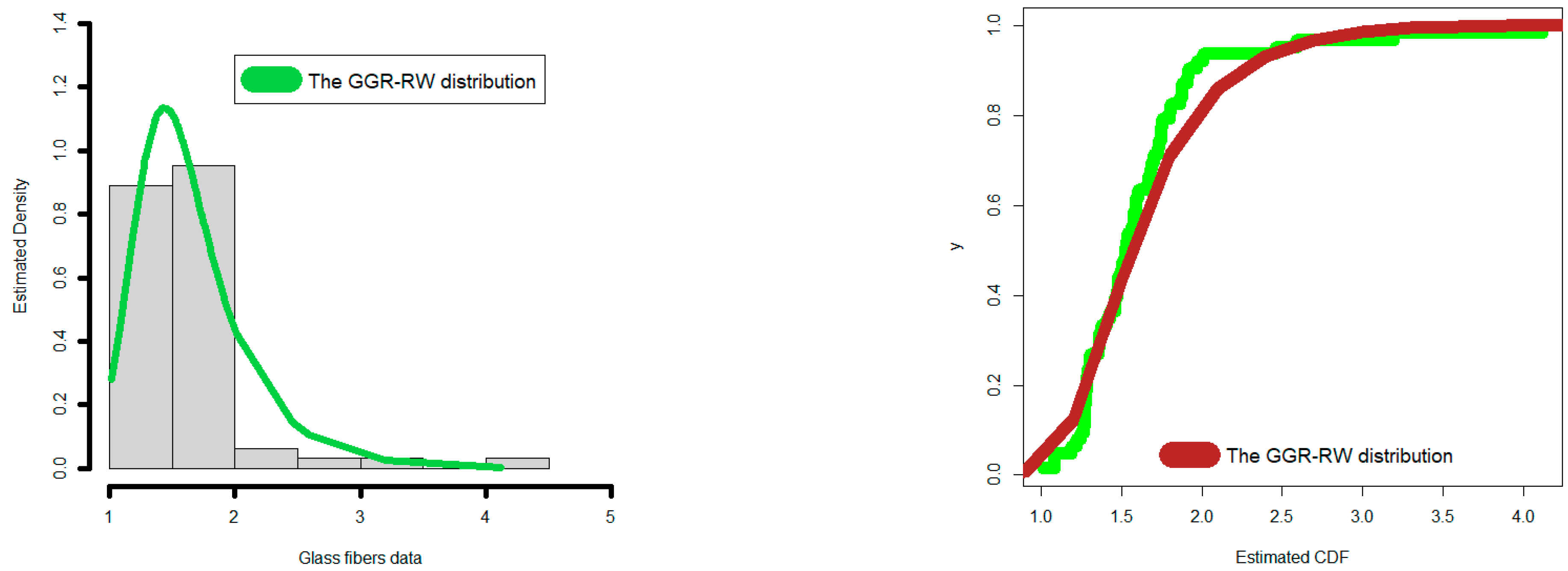
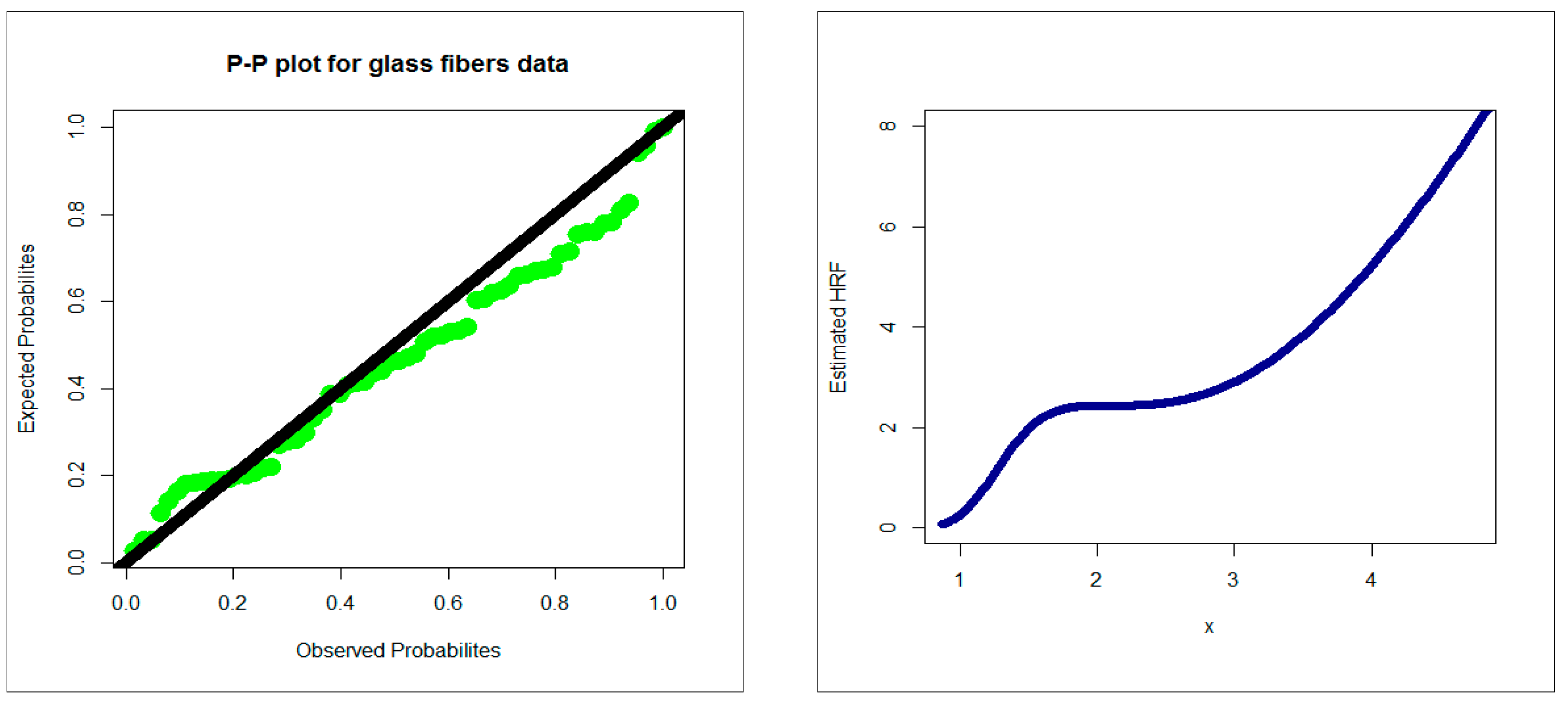
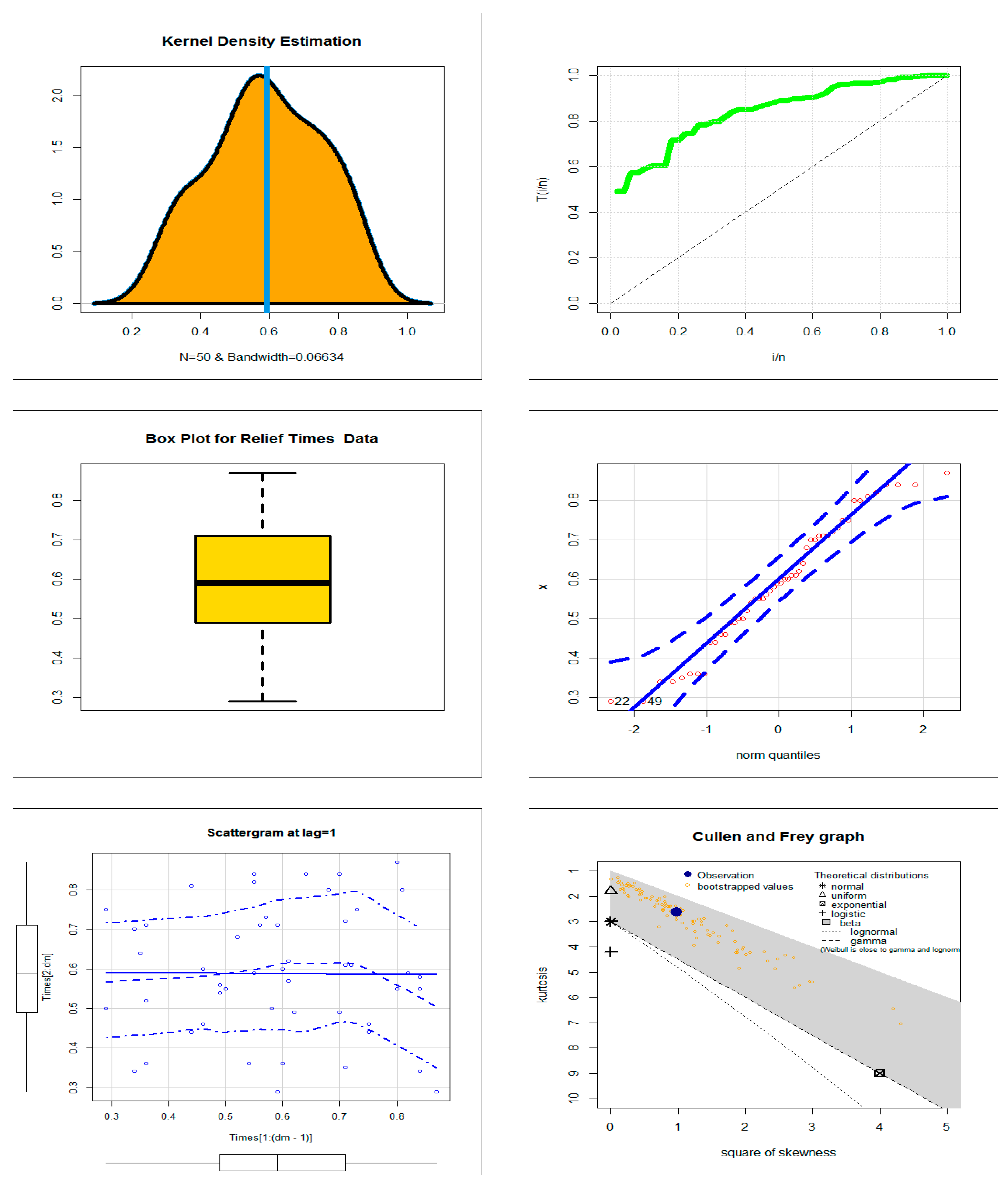
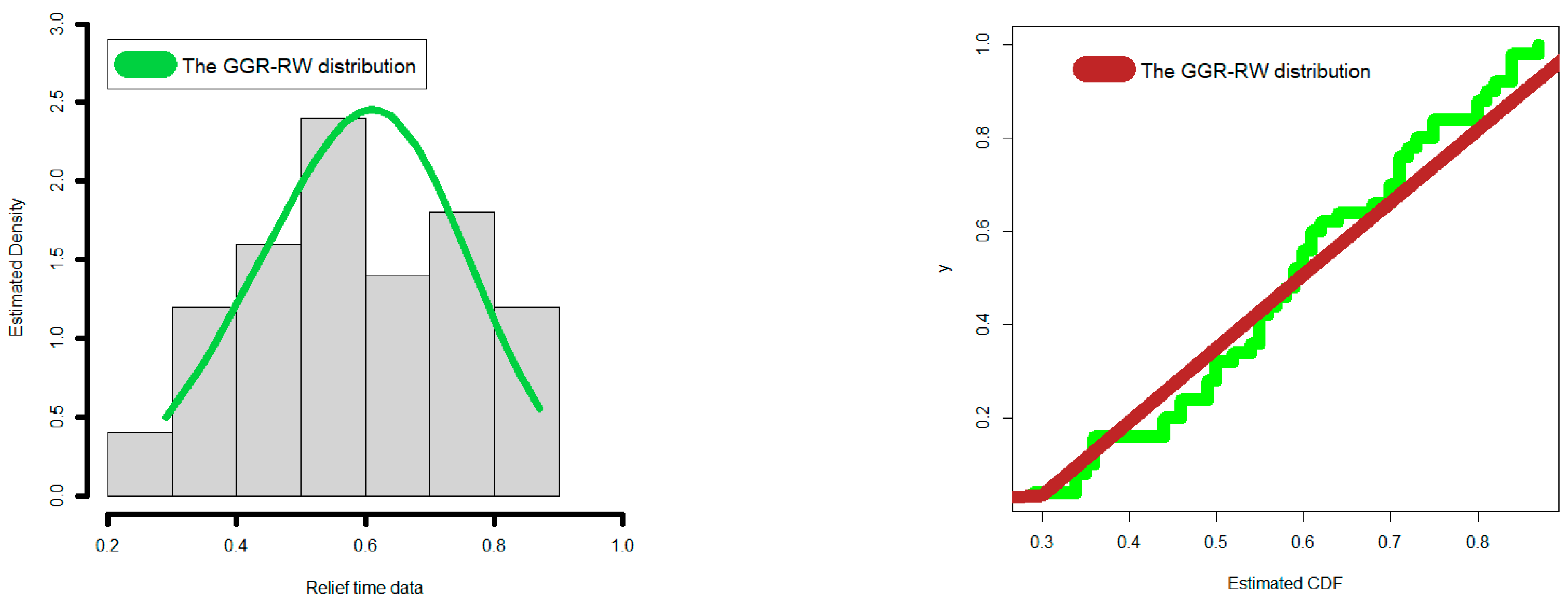
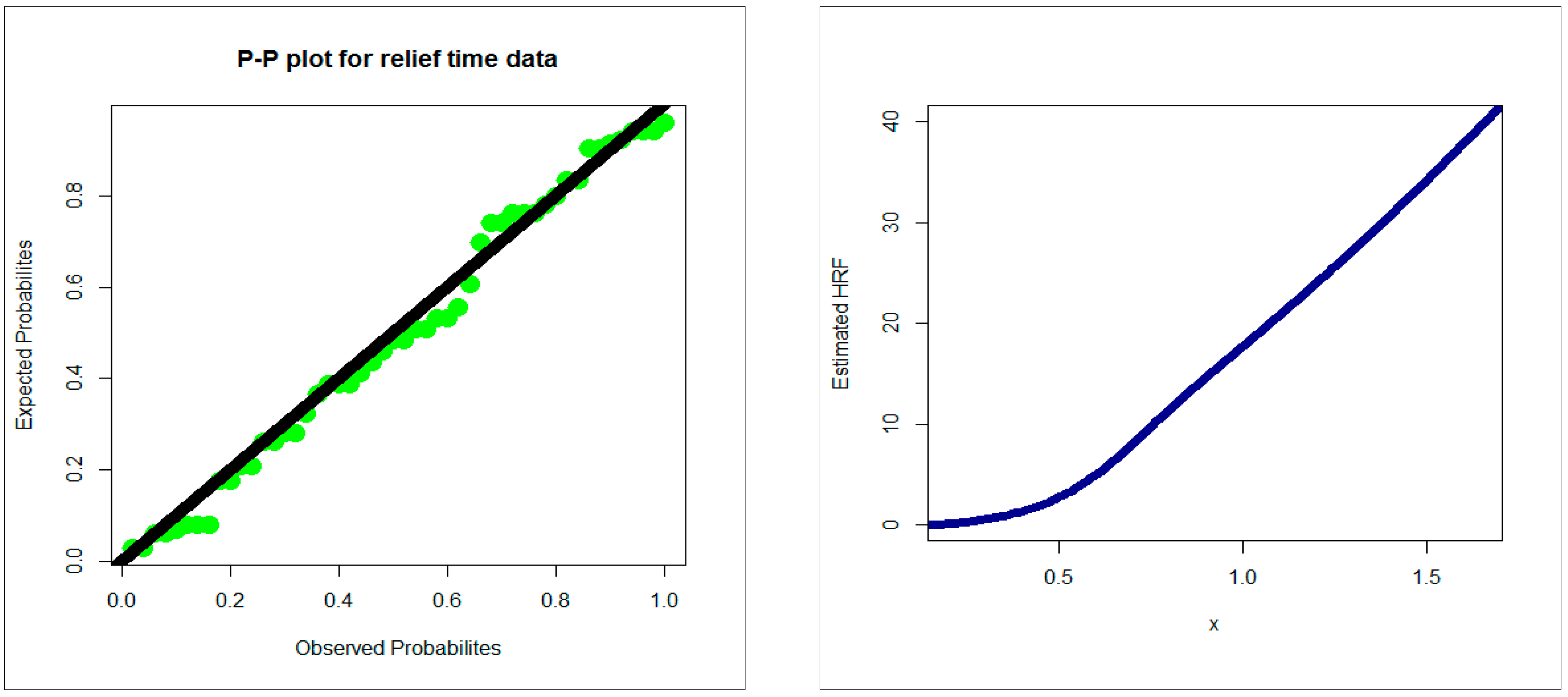
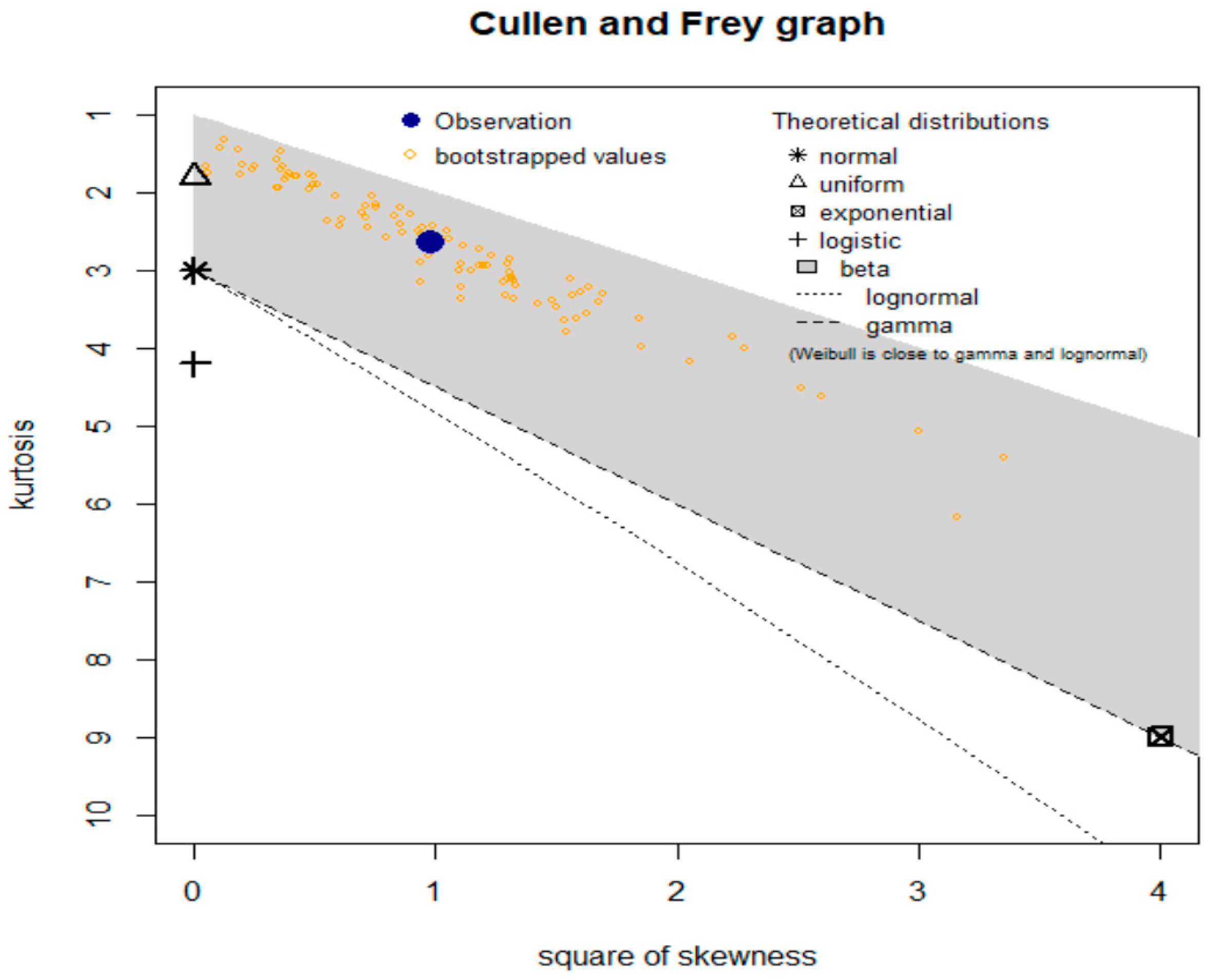
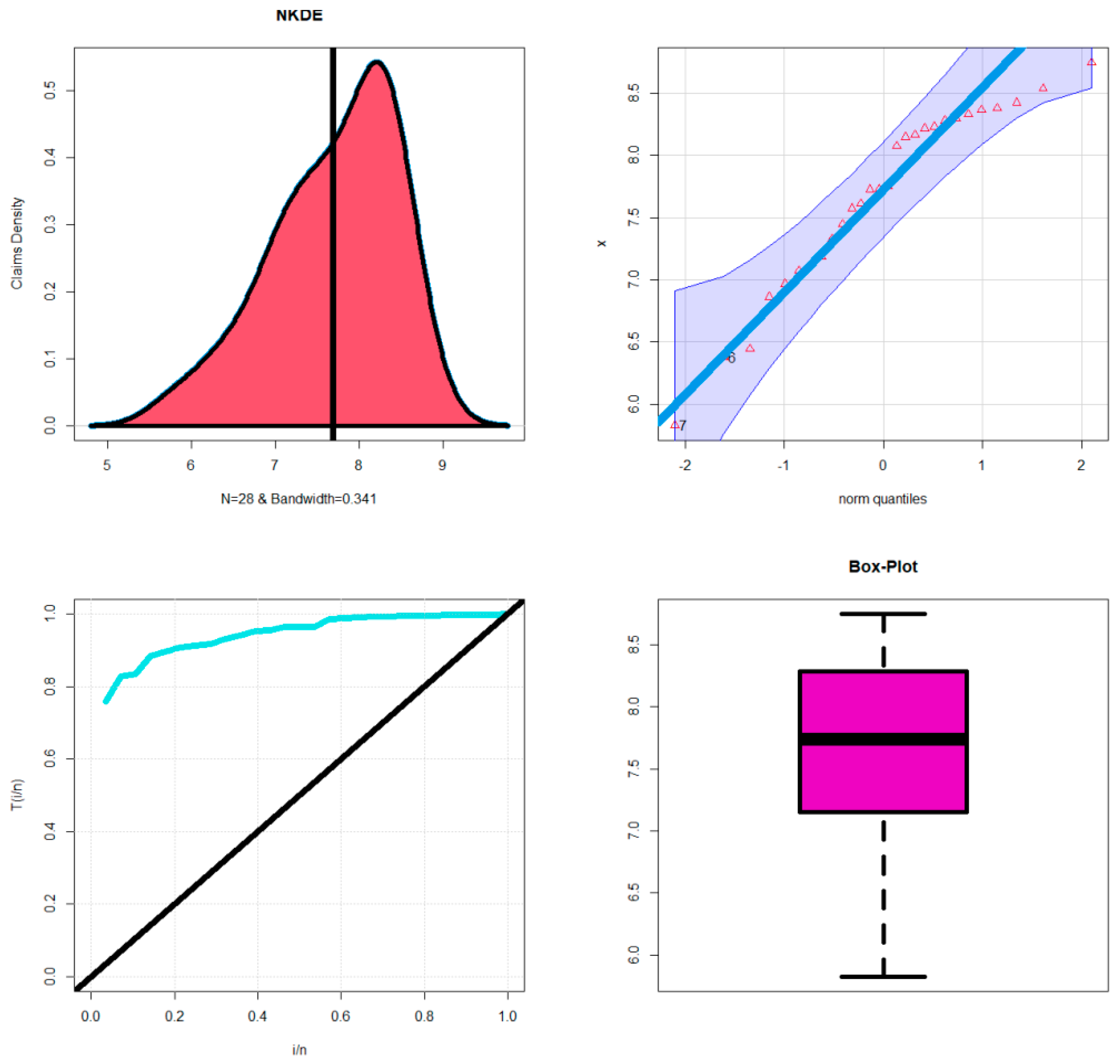
| Competitive Models (Author(s)) | Abbreviation |
|---|---|
| reciprocal Weibull | RW |
| exponentiated reciprocal Weibull | E-RW |
| Beta reciprocal Weibull model | Beta-RW |
| Marshal-Olkin reciprocal Weibull | MO-RW |
| transmuted reciprocal Weibull model | T-RW |
| Kumaraswamy reciprocal Weibull | Kum-RW |
| McDonald reciprocal Weibull | Mc-RW |
| odd log-logistic reciprocal Rayleigh | OLL-RR |
| odd log-logistic exponentiated reciprocal Weibull | OLLE-RW |
| odd log-logistic exponentiated reciprocal Rayleigh | OLLE-RR |
| generalized odd log-logistic reciprocal Rayleigh | GOLL-RR |
| Goodness of Fit Criteria | |||
|---|---|---|---|
| AD | CVM | ||
| GGR-RW | 0.44671 | 0.0612 | 0.05887 (0.8789) |
| OLLE-RW | 0.96404 | 0.1204 | 0.5561 () |
| Mc-RW | 1.0608 | 0.1333 | 0.0807 (0.53323) |
| OLLE-RR | 1.2120 | 0.1553 | 0.6550 () |
| Beta-RW | 0.6207 | 0.0809 | 0.0757 (0.61472) |
| Kum-RW | 0.6217 | 0.0812 | 0.07596 (0.6118) |
| RW | 0.7657 | 0.1090 | 0.08746 (0.4282) |
| E-RW | 0.7658 | 0.1093 | 0.0875 (0.428667) |
| MO-RW | 0.6142 | 0.0886 | 0.07629 (0.51677) |
| OB-RW | 0.4717 | 0.0662 | 0.06310 (0.82202) |
| OLL-RR | 1.2120 | 0.1553 | 0.6550 () |
| T-RW | 0.6209 | 0.0873 | 0.07821 (0.573443) |
| Estimates | |||||
|---|---|---|---|---|---|
| GGR-RW | 250.2153 (393.532) | 0.029866 (0.01752) | 74.12585 (68.9231) | 1.1729339 (0.222893) | |
| GGR-RW | 5.195441 (0.00123) | 0.59904 (0.0323) | 1.040482 (0.0444) | 1.232432 (0.003323) | |
| OLLE-RW | 0.135122 (0.011223) | 3.72164 (0.00343) | 0.92963 (0.0034) | 21.31942 (0.00363) | |
| OLLE-RR | 0.4946375 (0.04143) | 0.067433 (0.71955) | 1.742628 (9.30073) | ||
| OLL-RR | 0.494583 (0.04139) | 0.452423 (0.03877) | |||
| RW | 1.39688 (0.0336) | 4.37255 (0.3278) | |||
| Kum-RW | 0.84892 (16.083) | 1.62393 (0.6979) | 1.63413 (9.0492) | 3.42083 (0.7639) | |
| E-RW | 0.93951 (3.5434) | 1.41693 (2.56832) | 0.9391 (0.3273) | ||
| Beta-RW | 0.73463 (1.5290) | 1.58383 (0.7137) | 1.66844 (0.7662) | 3.51126 (0.9680) | |
| T-RW | 0.71663 (0.26162) | 1.265642 (0.0571) | 4.71219 (0.36590) | ||
| MO-RW | 0.003349 (0.00092) | 6.23965 (1.01348) | 1.241982 (0.1180) | ||
| Mc-RW | 0.85035 (0.13537) | 44.42332 (25.1324) | 19.8591 (6.7066) | 0.02039 (0.00683) | 46.9745 (21.8735) |
| Goodness of Fit Criteria | |||
|---|---|---|---|
| AD | CVM | ||
| GGR-RW | 0.89752 | 0.11304 | 0.12348 (0.269121) |
| OLLE-RR | 1.14697 | 0.15025 | 0.67949 () |
| OLLE-RW | 0.83253 | 0.10487 | 0.55196 () |
| OLL-RR | 1.14697 | 0.15023 | 0.67951 () |
| Estimates | |||||
|---|---|---|---|---|---|
| GGR-RW | 14.89942 (6.22644) | 0.005742 (0.00093) | 53.55753 (11.9332) | 1.594772 (0.09712) | |
| OLLE-RW | 0.144922 (0.01294) | 0.008792 (0.00021) | 1.299724 (0.00006) | 24.87832 (0.00025) | |
| OLLE-RR | 0.502541 (0.05292) | 0.071613 (1.13065) | 1.704832 (13.4744) | ||
| OLL-RR | 0.502512 0.052946 | 0.4559913 0.0486522 | |||
| Goodness of Fit Criteria | |||
|---|---|---|---|
| AD | CVM | ||
| GGR-RW | 0.4014 | 0.0485 | 0.081911 (0.8906) |
| RW | 2.0301 | 0.3233 | 0.150622 (0.2066) |
| GOLL-RR | 1.3498 | 0.1955 | 0.110083 (0.5797) |
| OB-RW | 0.4208 | 0.0490 | 0.091243 (0.7994) |
| OLLE-RW | 1.0988 | 0.1577 | 0.53498 () |
| Beta-RW | 2.5133 | 0.3613 | 0.143345 (0.3601) |
| E-RW | 2.0304 | 0.3233 | 0.150619 (0.2064) |
| T-RW | 1.81528 | 0.2823 | 0.137013 (0.3045) |
| Estimates | |||||
|---|---|---|---|---|---|
| GGR-RW | 0.377621 (0.6077) | 0.008394 (0.00151) | 21.01783 (21.46851) | 1.212893 (0.45608) | |
| OB-RW | 17.79132 (0.00014) | 6.996212 (4.03633) | 0.126862 (0.00023) | 0.178433 (0.00044) | |
| GOLL-RR | 1.961322 (0.23402) | 0.111237 (0.00146) | 1.412323 (0.00534) | ||
| OLLE-RW | 0.066923 (0.00762) | 0.00464 (0.0028) | 0.35583 (0.0047) | 32.5611 (0.0063) | |
| RW | 0.485933 (0.02272) | 3.20785 (0.3263) | |||
| E-RW | 0.90474 (18.7863) | 0.50134 (3.24444) | 3.20774 (0.3265) | ||
| Beta-RW | 4.01545 (0.11153) | 1.334933 (0.1476) | 2.00223 (0.32134) | 0.87017 (0.00333) | |
| T-RW | 0.58161 (0.27873) | 0.440232 (0.0293) | 3.49742 (0.3527) | ||
| MLE | 0.0381111 | 0.1486531 | 0.0233400 | 0.1603231 | 0.1105419 | |
| 0.0541547 | 0.1744053 | 0.0258538 | 0.1873322 | 0.1202507 | ||
| 0.0782740 | 0.2107700 | 0.0291661 | 0.225353 | 0.1324959 | ||
| 0.1189146 | 0.2678643 | 0.033902 | 0.2848153 | 0.1489497 | ||
| 0.2057473 | 0.3801243 | 0.0419915 | 0.4011201 | 0.174377 | ||
| 0.3123655 | 0.5088242 | 0.0499369 | 0.5337926 | 0.1964587 | ||
| 0.6217416 | 0.8601832 | 0.0678638 | 0.8941151 | 0.2384416 | ||
| LS | 0.0374667 | 0.1490600 | 0.0241590 | 0.1611395 | 0.1115933 | |
| 0.0535004 | 0.1750774 | 0.0268089 | 0.1884819 | 0.121577 | ||
| 0.0776905 | 0.2118756 | 0.0303126 | 0.2270319 | 0.1341851 | ||
| 0.1185895 | 0.2697621 | 0.0353475 | 0.2874358 | 0.1511726 | ||
| 0.2063194 | 0.3838971 | 0.0440212 | 0.4059077 | 0.1775778 | ||
| 0.3144706 | 0.5151746 | 0.0526295 | 0.5414893 | 0.200704 | ||
| 0.6301761 | 0.8753958 | 0.0723317 | 0.9115617 | 0.2452197 | ||
| WLS | 0.0342739 | 0.1376783 | 0.0210272 | 0.1481916 | 0.1034040 | |
| 0.0489822 | 0.1618043 | 0.0233691 | 0.1734889 | 0.1128222 | ||
| 0.0712356 | 0.1959845 | 0.026472 | 0.2092206 | 0.1247489 | ||
| 0.1090019 | 0.2498647 | 0.0309402 | 0.2653348 | 0.1408628 | ||
| 0.1904255 | 0.3563898 | 0.0386510 | 0.3757153 | 0.1659643 | ||
| 0.2912627 | 0.4792157 | 0.0463079 | 0.5023696 | 0.187953 | ||
| 0.5868431 | 0.8170242 | 0.0638199 | 0.8489342 | 0.2301812 | ||
| CVM | 0.0373757 | 0.1483838 | 0.0239460 | 0.1603568 | 0.1110082 | |
| 0.0532972 | 0.1742681 | 0.0265773 | 0.1875568 | 0.1209709 | ||
| 0.077324 | 0.2108897 | 0.0300559 | 0.2259176 | 0.1335657 | ||
| 0.1179792 | 0.2685231 | 0.0350509 | 0.2860486 | 0.1505439 | ||
| 0.2053027 | 0.3822116 | 0.0436372 | 0.4040302 | 0.176909 | ||
| 0.3130633 | 0.5129930 | 0.0521284 | 0.5390572 | 0.1999297 | ||
| 0.6276448 | 0.8716274 | 0.0714515 | 0.9073532 | 0.2439827 |
| MLE | 0.0373339 | 0.1457556 | 0.0222846 | 0.1568979 | 0.1084217 | |
| 0.053175 | 0.1710013 | 0.0246639 | 0.1833332 | 0.1178263 | ||
| 0.0769553 | 0.2066087 | 0.027798 | 0.2205076 | 0.1296533 | ||
| 0.1169123 | 0.2624301 | 0.0322832 | 0.2785717 | 0.1455178 | ||
| 0.2019247 | 0.371995 | 0.0399747 | 0.3919824 | 0.1700704 | ||
| 0.3059526 | 0.497478 | 0.0475827 | 0.5212694 | 0.1915254 | ||
| 0.6074063 | 0.8402381 | 0.0649493 | 0.8727127 | 0.2328318 | ||
| LS | 0.0368937 | 0.1454241 | 0.0225629 | 0.1567055 | 0.1085304 | |
| 0.0526345 | 0.1707094 | 0.0250017 | 0.1832103 | 0.1180749 | ||
| 0.0763185 | 0.2064162 | 0.0282203 | 0.2205263 | 0.1300977 | ||
| 0.1162205 | 0.2624769 | 0.0328365 | 0.2788952 | 0.1462565 | ||
| 0.2014086 | 0.3727327 | 0.0407754 | 0.3931204 | 0.1713242 | ||
| 0.3059839 | 0.4992581 | 0.0486494 | 0.5235828 | 0.1932743 | ||
| 0.6100726 | 0.8456811 | 0.0666786 | 0.8790204 | 0.2356086 | ||
| WLS | 0.0364107 | 0.1431778 | 0.0217920 | 0.1540738 | 0.1067671 | |
| 0.0519162 | 0.1680499 | 0.0241419 | 0.1801208 | 0.1161336 | ||
| 0.0752356 | 0.2031654 | 0.0272418 | 0.2167863 | 0.1279298 | ||
| 0.1145055 | 0.2582839 | 0.0316851 | 0.2741264 | 0.1437783 | ||
| 0.1982991 | 0.3666467 | 0.0393191 | 0.3863063 | 0.1683476 | ||
| 0.3011073 | 0.4909484 | 0.0468821 | 0.5143894 | 0.189841 | ||
| 0.5998334 | 0.8310739 | 0.064172 | 0.8631599 | 0.2312405 | ||
| CVM | 0.0371846 | 0.1459834 | 0.0225801 | 0.1572735 | 0.1087988 | |
| 0.0530105 | 0.1713256 | 0.0250089 | 0.1838300 | 0.1183151 | ||
| 0.0768006 | 0.2070954 | 0.0282116 | 0.2212012 | 0.1302948 | ||
| 0.116839 | 0.2632221 | 0.0328008 | 0.2796225 | 0.1463831 | ||
| 0.2022038 | 0.3735195 | 0.0406832 | 0.3938610 | 0.1713156 | ||
| 0.3068647 | 0.4999904 | 0.0484911 | 0.5242360 | 0.1931258 | ||
| 0.6107723 | 0.8459199 | 0.0663415 | 0.8790906 | 0.2351476 |
| MLE | 0.0370309 | 0.14445380 | 0.02182030 | 0.155364 | 0.1074229 | |
| 60% | 0.0527590 | 0.1694630 | 0.0241430 | 0.1815345 | 0.1167039 | |
| 0.0763570 | 0.2047240 | 0.0272020 | 0.2183249 | 0.128367 | ||
| 0.1159737 | 0.2599773 | 0.0315796 | 0.2757671 | 0.1440036 | ||
| 0.2001615 | 0.3683678 | 0.0390906 | 0.3879131 | 0.1682064 | ||
| 0.3030780 | 0.492457 | 0.0465288 | 0.5157214 | 0.189379 | ||
| 0.6011336 | 0.8313712 | 0.0635422 | 0.8631423 | 0.2302376 | ||
| LS | 0.0368989 | 0.1445928 | 0.0220315 | 0.1556085 | 0.1076939 | |
| 0.0526166 | 0.1696712 | 0.0243896 | 0.1818660 | 0.1170547 | ||
| 0.0762228 | 0.2050486 | 0.0274979 | 0.2187975 | 0.1288258 | ||
| 0.1158991 | 0.2605198 | 0.0319508 | 0.2764952 | 0.1446207 | ||
| 0.2003359 | 0.3694332 | 0.0396026 | 0.3892345 | 0.1690973 | ||
| 0.3036975 | 0.4942325 | 0.0471918 | 0.5178284 | 0.1905351 | ||
| 0.6035121 | 0.8354713 | 0.0645834 | 0.867763 | 0.2319592 | ||
| WLS | 0.0373859 | 0.1456207 | 0.0221189 | 0.1566801 | 0.1082348 | |
| 0.0532489 | 0.1708169 | 0.0244691 | 0.1830515 | 0.117568 | ||
| 0.0770415 | 0.2063356 | 0.0275636 | 0.2201174 | 0.1292942 | ||
| 0.1169704 | 0.2619815 | 0.0319904 | 0.2779767 | 0.1450112 | ||
| 0.2017831 | 0.3711118 | 0.0395819 | 0.3909027 | 0.1693287 | ||
| 0.3054192 | 0.4960116 | 0.0470956 | 0.5195594 | 0.1905925 | ||
| 0.6054054 | 0.8370118 | 0.0642700 | 0.8691468 | 0.2316064 | ||
| CVM | 0.0370433 | 0.1448759 | 0.0220367 | 0.1558943 | 0.1078326 | |
| 0.0528079 | 0.1699834 | 0.0243888 | 0.1821778 | 0.1171755 | ||
| 0.0764724 | 0.2053916 | 0.027488 | 0.2191356 | 0.1289192 | ||
| 0.1162215 | 0.2608921 | 0.0319261 | 0.2768551 | 0.1446705 | ||
| 0.2007439 | 0.3698128 | 0.0395488 | 0.3895872 | 0.1690689 | ||
| 0.3041334 | 0.4945666 | 0.0471064 | 0.5181198 | 0.1904333 | ||
| 0.6038073 | 0.8355222 | 0.0644203 | 0.8677323 | 0.2317149 |
| MLE | 2519.589871 | 4267.691033 | 3,540,150.406026 | 1,774,342.894046 | 1748.101162 | |
| 2925.721995 | 4653.938764 | 3,669,072.521249 | 1,839,190.199388 | 1728.216769 | ||
| 3413.601872 | 5152.008492 | 3,909,892.629211 | 1,960,098.323098 | 1738.40662 | ||
| 4075.783589 | 5868.385465 | 4,288,227.900333 | 2,149,982.335632 | 1792.601877 | ||
| 5218.837237 | 7158.545734 | 4,934,867.46325 | 2,474,592.277359 | 1939.708497 | ||
| 6438.143819 | 8557.764414 | 6,119,681.689183 | 3,068,398.609005 | 2119.620595 | ||
| 9747.670085 | 12,352.578196 | 8,779,151.168388 | 4,401,928.162391 | 2604.908111 | ||
| OLSQ | 2428.50708 | 4865.81245 | 9,023,336.47326 | 4,516,534.04908 | 2437.30537 | |
| 2932.40857 | 5433.64085 | 9,547,186.93457 | 4,779,027.10814 | 2501.23228 | ||
| 3564.63797 | 6167.11262 | 11,189,826.32321 | 5,601,080.27423 | 2602.47465 | ||
| 4465.10947 | 7244.54736 | 12,380,274.28873 | 6,197,381.69173 | 2779.4379 | ||
| 6120.70566 | 9336.0422 | 16,098,692.10948 | 8,058,682.09694 | 3215.33654 | ||
| 8009.94191 | 11,695.34684 | 21,542,109.96081 | 10,782,750.32724 | 3685.40493 | ||
| 13,665.84114 | 18,627.28911 | 36,958,017.28968 | 18,497,635.93395 | 4961.44797 | ||
| WLSQ | 2356.17122 | 4108.2022 | 3,439,375.14482 | 1,723,795.77462 | 1752.03099 | |
| 2767.2538 | 4495.98899 | 3,543,850.04098 | 1,776,421.00948 | 1728.73519 | ||
| 3260.32173 | 4993.20737 | 3,729,494.08495 | 1,869,740.24984 | 1732.88564 | ||
| 3927.39086 | 5703.45655 | 4,062,565.44978 | 2,036,986.18143 | 1776.06568 | ||
| 5071.69421 | 6976.10477 | 4,779,635.04769 | 2,396,793.62862 | 1904.41056 | ||
| 6281.71599 | 8352.06028 | 5,653,941.85453 | 2,835,322.98755 | 2070.34429 | ||
| 9514.1782 | 12,042.68509 | 8,239,930.80908 | 4,132,008.08963 | 2528.50689 | ||
| CVME | 2440.48715 | 4680.62835 | 6,934,737.28581 | 3,472,049.27125 | 2240.1412 | |
| 2918.03280 | 5186.36109 | 7,534,972.10069 | 3,772,672.41143 | 2268.32829 | ||
| 3510.16653 | 5847.41837 | 8,012,409.48002 | 4,012,052.15838 | 2337.25184 | ||
| 4342.45308 | 6818.48345 | 9,433,643.36101 | 4,723,640.16395 | 2476.03037 | ||
| 5846.10485 | 8654.84099 | 12,514,954.3509 | 6,266,132.01648 | 2808.73614 | ||
| 7529.80733 | 10,735.92128 | 16,138,733.3737 | 8,080,102.60813 | 3206.11394 | ||
| 12,431.2469 | 16,642.80352 | 25,779,255.9529 | 12,906,270.7800 | 4211.55663 |
| Methods | ||||
|---|---|---|---|---|
| MLE | 0.00109 | 0.43439 | 2.71691 | 0.16504 |
| LS | 0.00065 | 0.32104 | 2.54461 | 0.12257 |
| WLS | 0.00459 | 0.76214 | 2.04483 | 0.18936 |
| CVM | 0.00084 | 0.37663 | 2.39879 | 0.13348 |
| MLE | 1986.487789 | 11,961.555933 | 174,419,897,519.9525 | 87,209,960,721.53221 | 9975.068144 | |
| 2536.462153 | 14,390.782535 | 217,997,610,644.2704 | 108,998,819,712.9177 | 11,854.320382 | ||
| 3381.788446 | 18,212.884768 | 290,611,198,248.8563 | 145,305,617,337.3129 | 14,831.096322 | ||
| 4923.241114 | 25,288.557461 | 435,793,880,982.5539 | 217,896,965,779.8344 | 20,365.316347 | ||
| 8978.892448 | 44,037.774889 | 870,728,145,024.2504 | 435,364,116,549.9001 | 35,058.882441 | ||
| 15,979.12723 | 76,311.911159 | 1,739,359,709,696.955 | 869,679,931,160.3890 | 60,332.783923 | ||
| 58,937.60432 | 270,450.59761 | 8,648,937,166,516.464 | 4,324,468,853,708.830 | 211,512.99328 | ||
| LS | 2226.27121 | 9174.03623 | 35,221,234,657.96799 | 17,610,626,503.02022 | 6947.76502 | |
| 2764.08554 | 10,847.551 | 44,014,544,061.32928 | 22,007,282,878.21564 | 8083.46547 | ||
| 3565.72511 | 13,418.65557 | 58,664,352,289.24406 | 29,332,189,563.2776 | 9852.93045 | ||
| 4972.24847 | 18,032.50003 | 87,948,130,492.44542 | 43,974,083,278.72273 | 13,060.25156 | ||
| 8464.56169 | 29,681.73496 | 175,453,235,244.5421 | 87,726,647,304.00603 | 21,217.17327 | ||
| 14,100.50824 | 48,626.87171 | 350,184,932,240.5994 | 175,092,514,747.1714 | 34,526.36347 | ||
| 44,780.28947 | 151,748.59629 | 1,737,405,220,156.72 | 868,702,761,826.9589 | 106,968.30682 | ||
| WLS | 1964.20669 | 4830.43197 | 353,521,360.01739 | 176,765,510.44066 | 2866.22528 | |
| 2314.75014 | 5505.26712 | 439,620,494.28391 | 219,815,752.40908 | 3190.51699 | ||
| 2808.25355 | 6491.97705 | 582,260,408.85219 | 291,136,696.40314 | 3683.7235 | ||
| 3614.31526 | 8152.00969 | 865,097,200.4972 | 432,556,752.25829 | 4537.69443 | ||
| 5412.18198 | 11,944.5794 | 1,701,168,649.8689 | 850,596,269.51388 | 6532.39742 | ||
| 7972.02825 | 17,419.4644 | 3,341,868,718.7883 | 1,670,951,778.8585 | 9447.43615 | ||
| 19,161.39616 | 41,550.35309 | 15,948,264,082.767 | 7,974,173,591.7366 | 22,388.9569 | ||
| CVM | 2229.99377 | 8126.51599 | 16,383,249,373.39099 | 8,191,632,813.21149 | 5896.52223 | |
| 2739.42855 | 9540.45443 | 20,470,957,007.79706 | 10,235,488,044.35295 | 6801.02588 | ||
| 3489.97698 | 11,691.68313 | 27,278,563,176.74898 | 13,639,293,280.05762 | 8201.70615 | ||
| 4787.7631 | 15,503.20904 | 40,882,367,103.10032 | 20,441,199,054.7592 | 10,715.44594 | ||
| 7940.21618 | 24,938.28648 | 81,425,453,617.80911 | 40,712,751,747.19104 | 16,998.0703 | ||
| 12,899.51936 | 39,927.04311 | 162,397,882,831.5135 | 81,198,981,342.79988 | 27,027.52374 | ||
| 38,705.15155 | 118,195.6688 | 804,158,697,120.1825 | 402,079,466,755.7600 | 79,490.51725 |
| Methods | ||
|---|---|---|
| MLE | 1481.24152 | 1.24882 |
| LS | 1716.84523 | 1.41054 |
| WLS | 1612.67569 | 1.85864 |
| CVM | 1741.81127 | 1.48342 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yousof, H.M.; Tashkandy, Y.; Emam, W.; Ali, M.M.; Ibrahim, M. A New Reciprocal Weibull Extension for Modeling Extreme Values with Risk Analysis under Insurance Data. Mathematics 2023, 11, 966. https://doi.org/10.3390/math11040966
Yousof HM, Tashkandy Y, Emam W, Ali MM, Ibrahim M. A New Reciprocal Weibull Extension for Modeling Extreme Values with Risk Analysis under Insurance Data. Mathematics. 2023; 11(4):966. https://doi.org/10.3390/math11040966
Chicago/Turabian StyleYousof, Haitham M., Yusra Tashkandy, Walid Emam, M. Masoom Ali, and Mohamed Ibrahim. 2023. "A New Reciprocal Weibull Extension for Modeling Extreme Values with Risk Analysis under Insurance Data" Mathematics 11, no. 4: 966. https://doi.org/10.3390/math11040966
APA StyleYousof, H. M., Tashkandy, Y., Emam, W., Ali, M. M., & Ibrahim, M. (2023). A New Reciprocal Weibull Extension for Modeling Extreme Values with Risk Analysis under Insurance Data. Mathematics, 11(4), 966. https://doi.org/10.3390/math11040966






_Masoom_Ali.png)


