Exact and Numerical Analysis of the Pantograph Delay Differential Equation via the Homotopy Perturbation Method
Abstract
1. Introduction
2. The first Canonical Form: PSS
3. The Second Canonical Form: EPS
4. Characteristics of the Components and a Unified Formula for
4.1. Characteristics of the Components
- involves two terms and can be written aswhere
- consists of three terms in the form:where
- contains four terms and we can writewhere
- Similarly, can be evaluated from (26) and is given bywhere
- In view of (31), (34), (38), and (44), takes the form . Moreover, the initial component where . Based on the above characteristics, unified formulas for the coefficients and, hence, the -order component will be determined. This is the issue of the next section.
4.2. Unified Formula for
5. Closed-Form Solution via Quantum Calculus
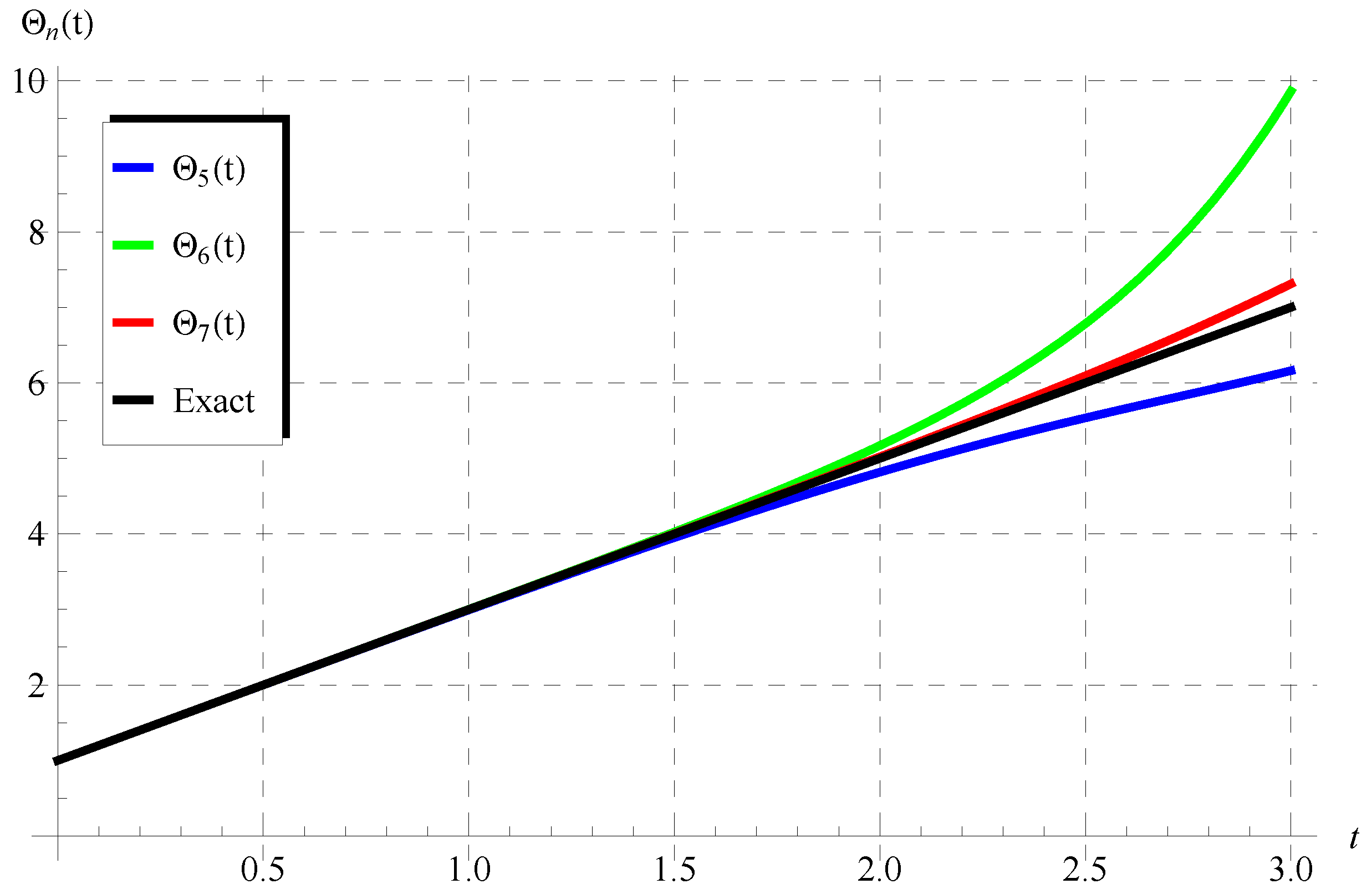
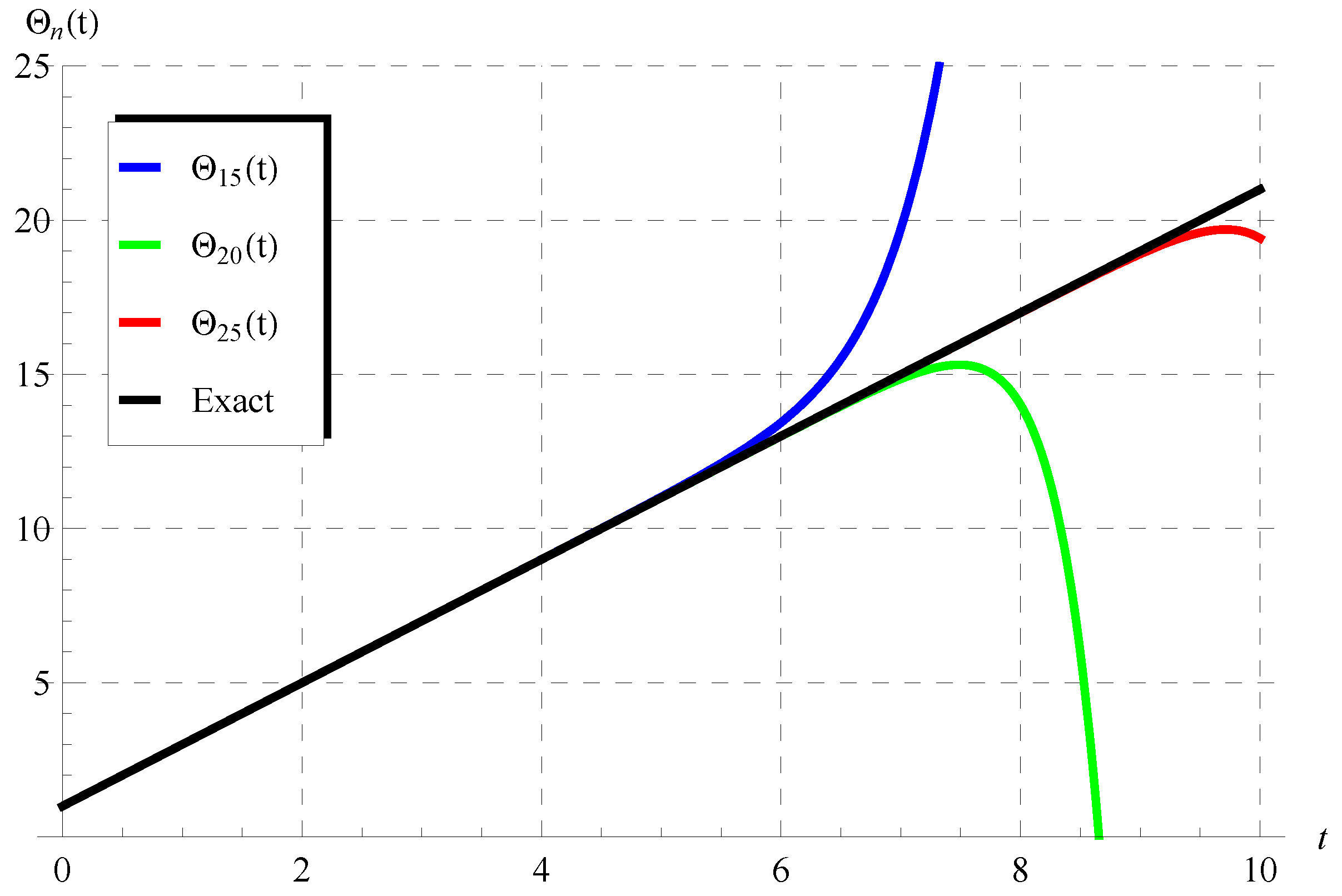
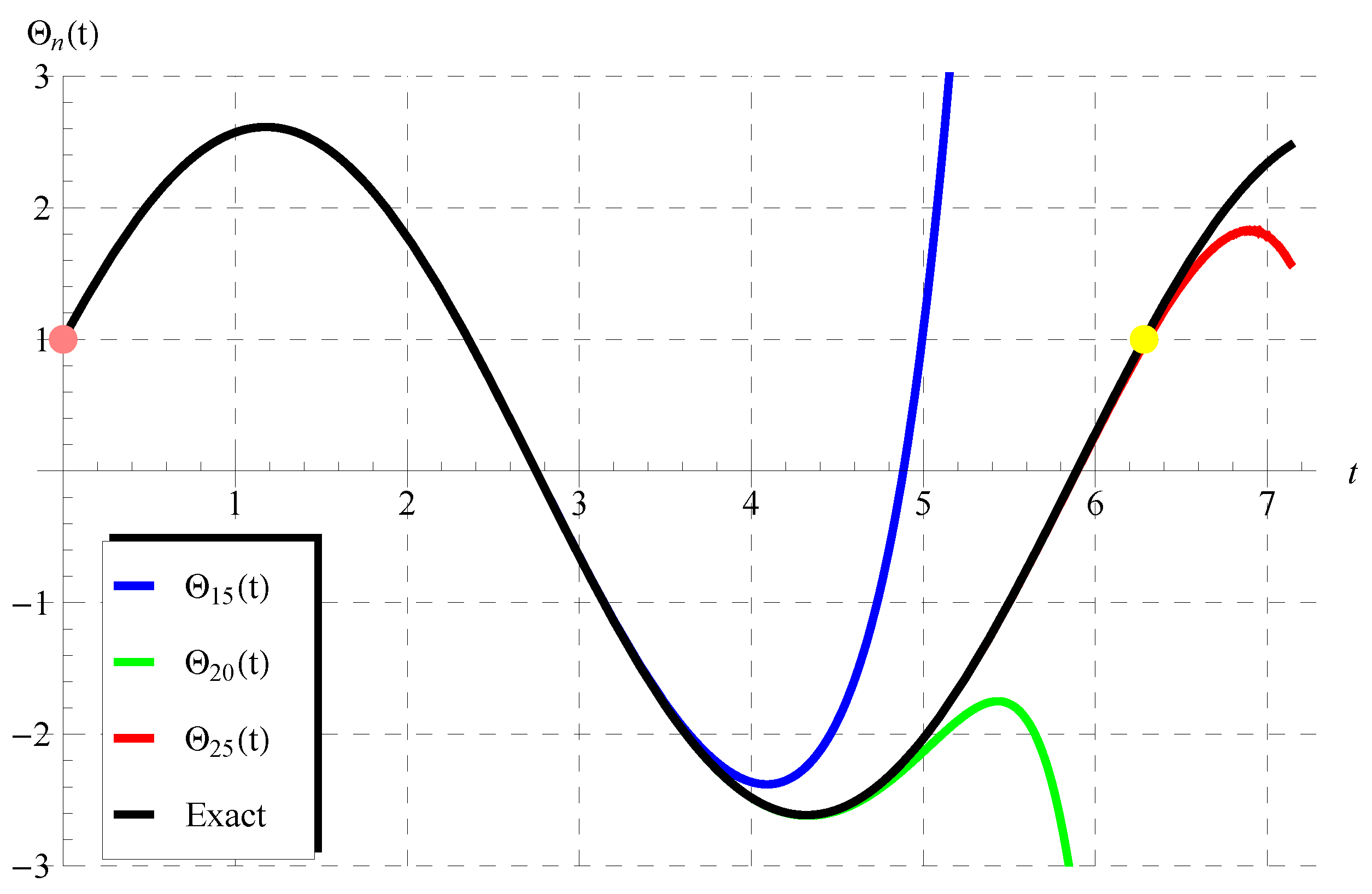
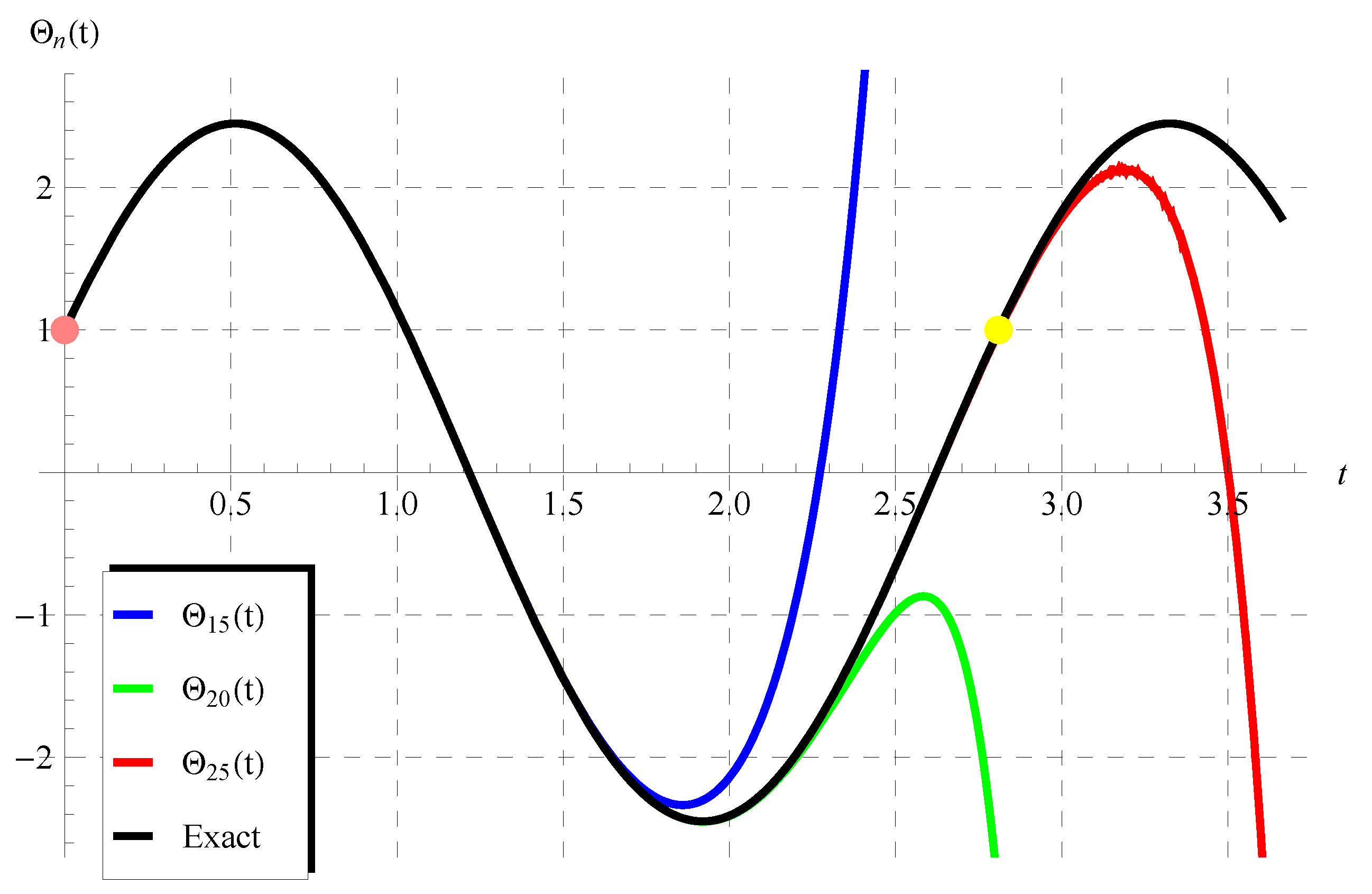
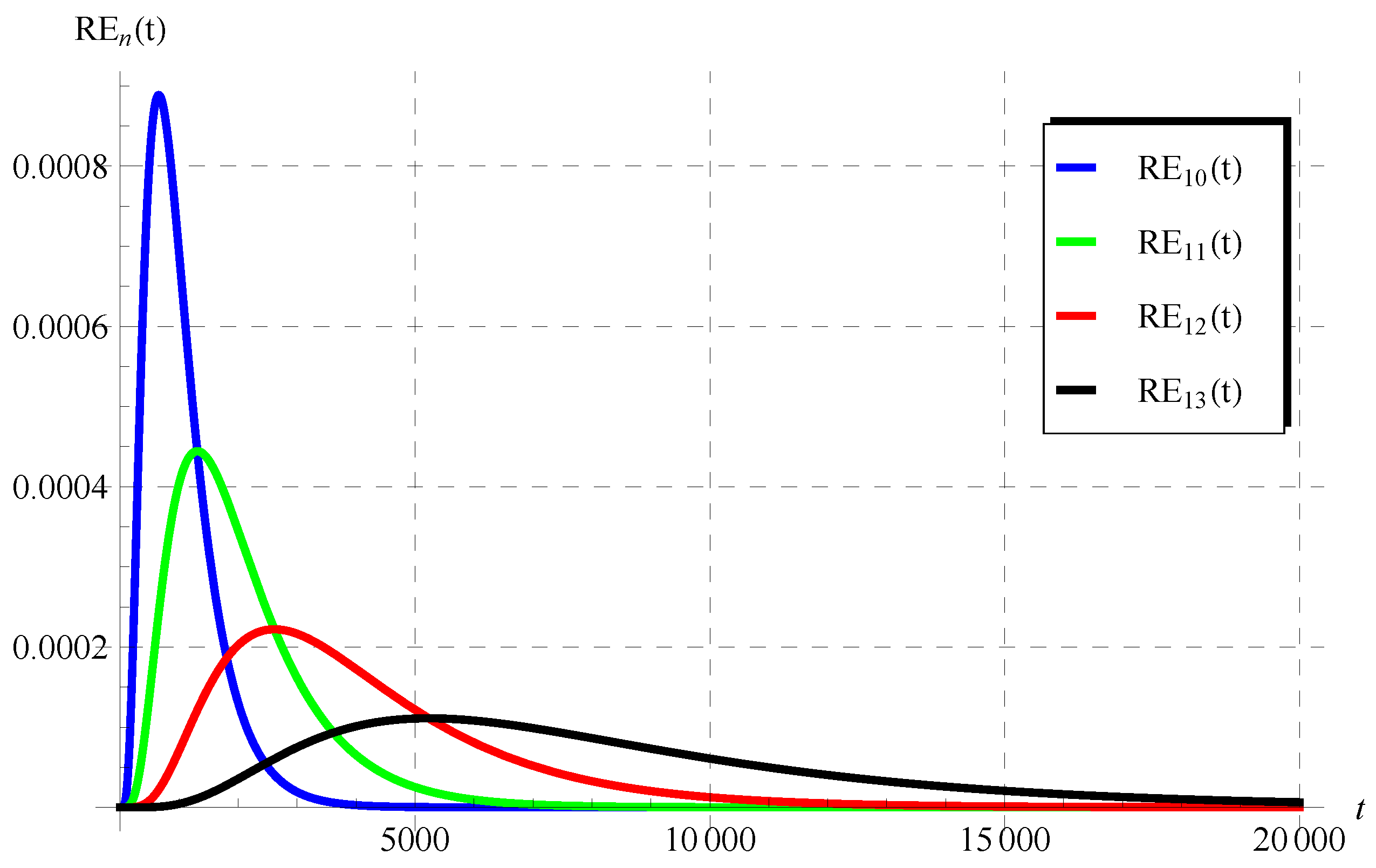
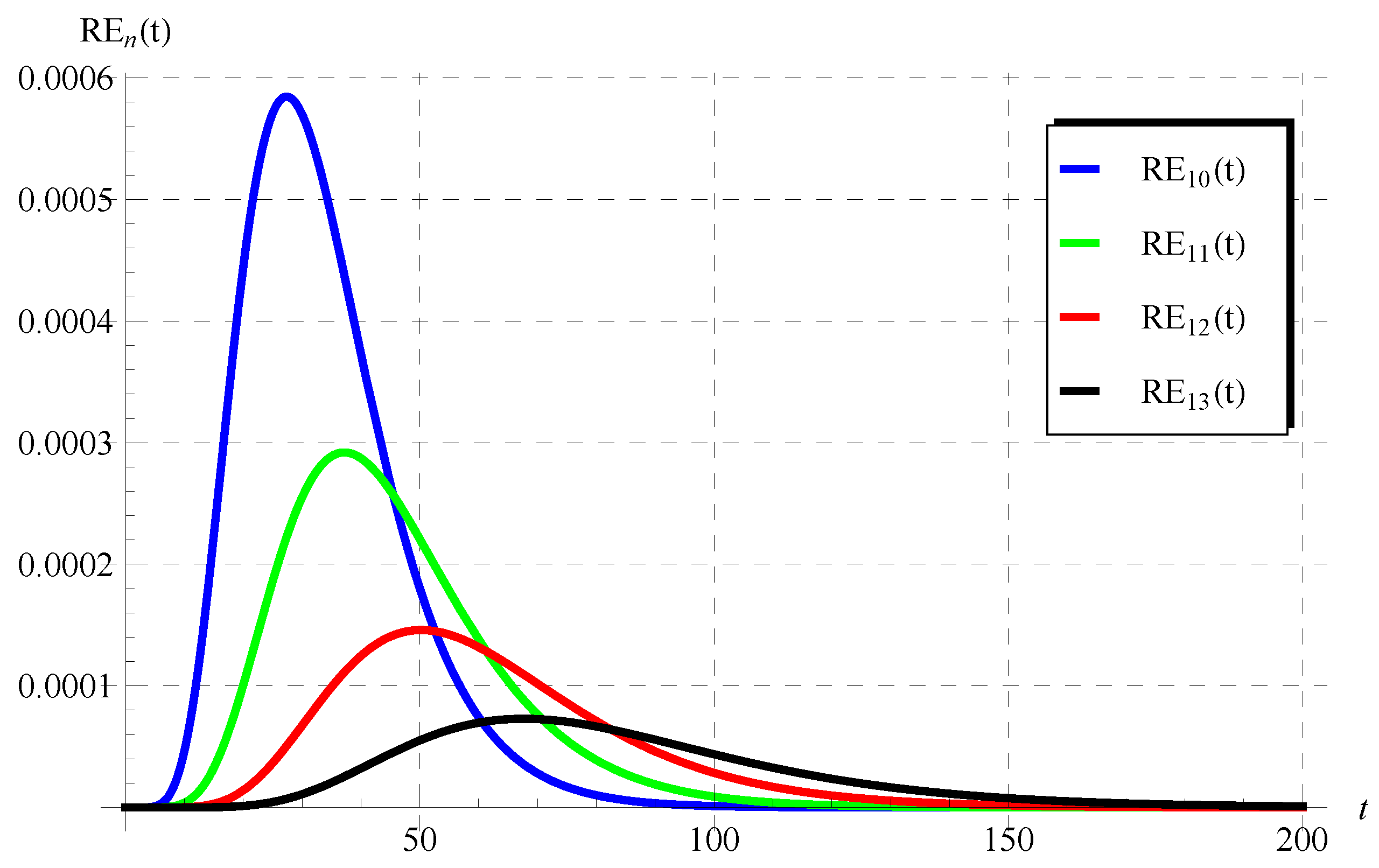
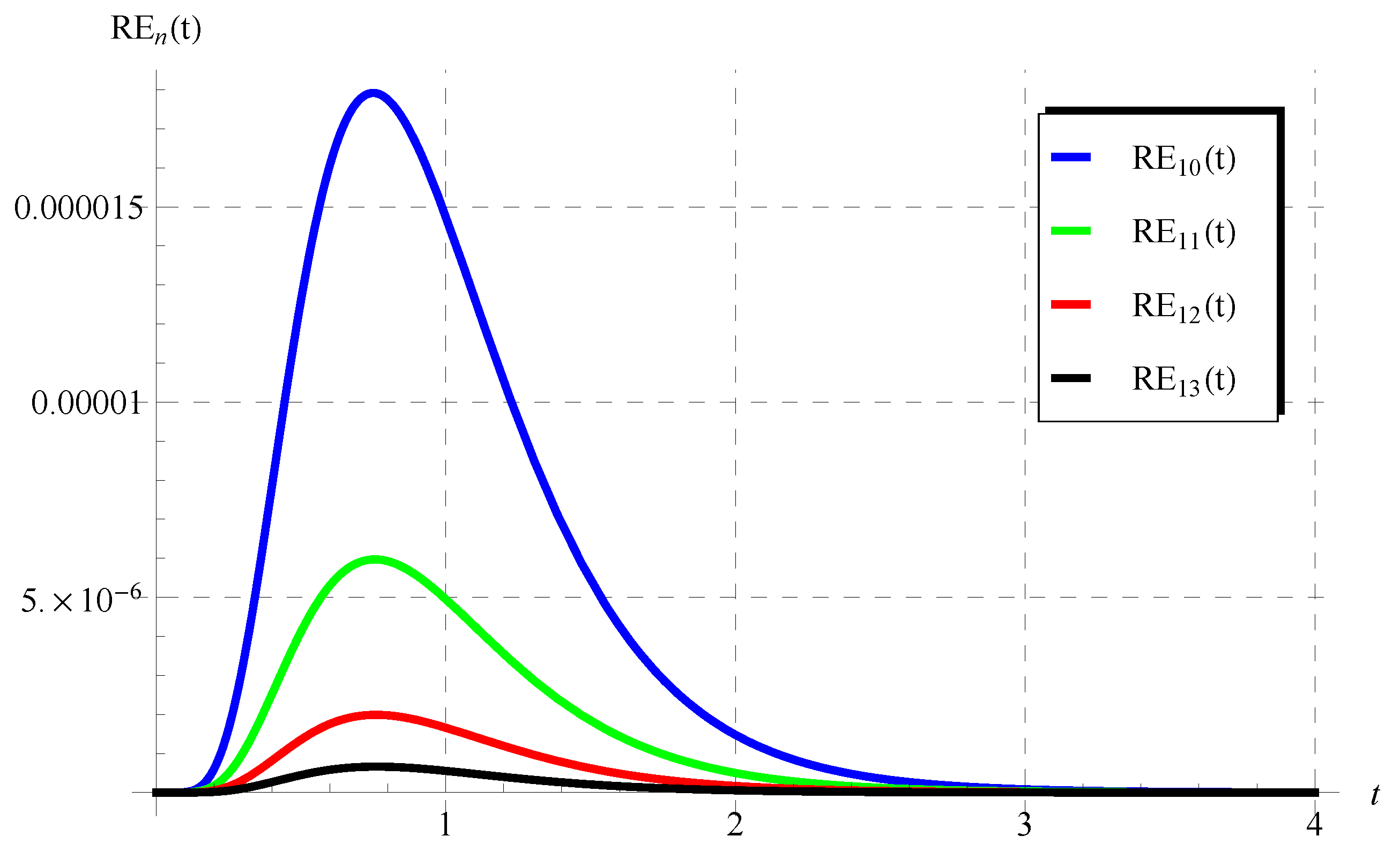
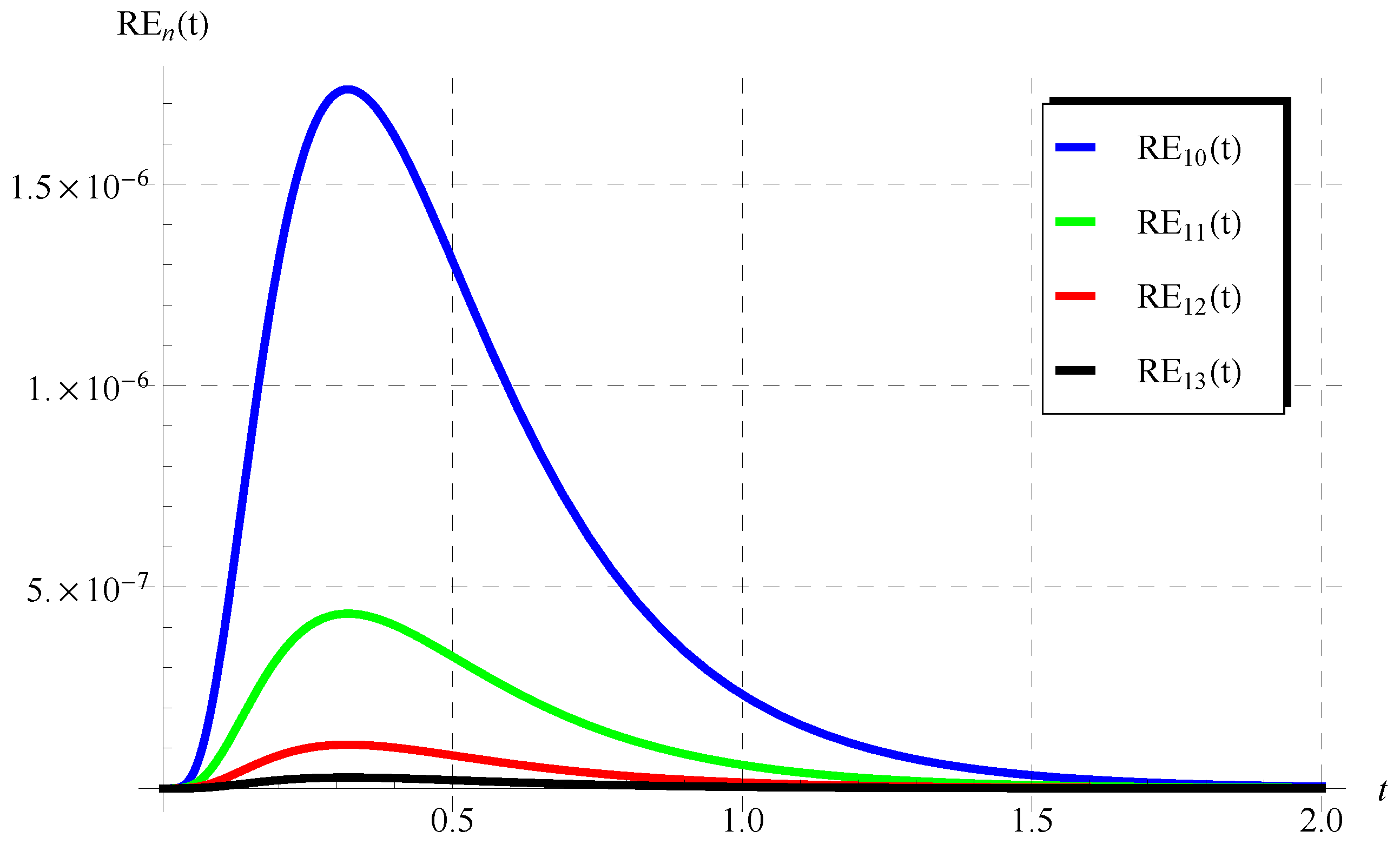
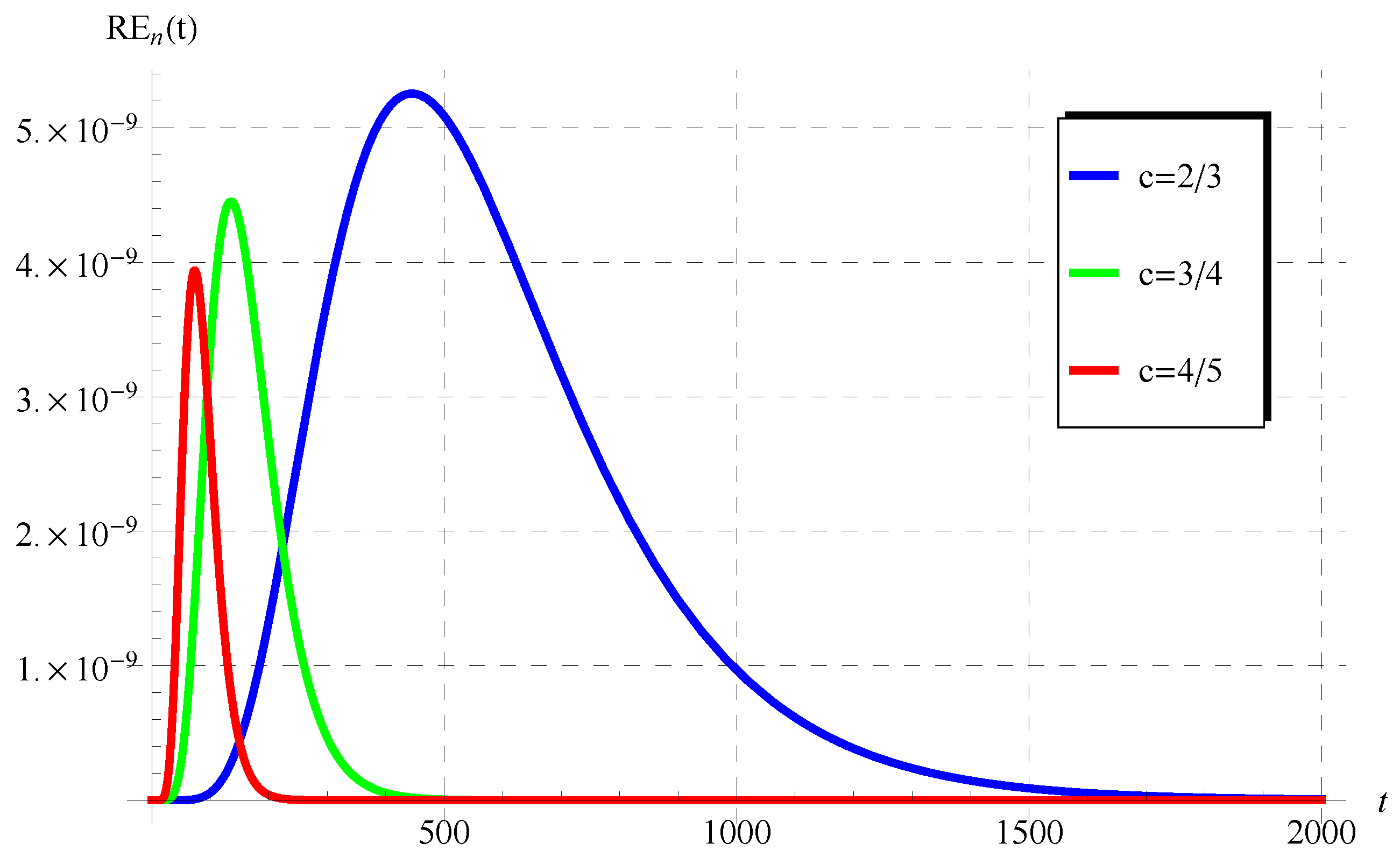
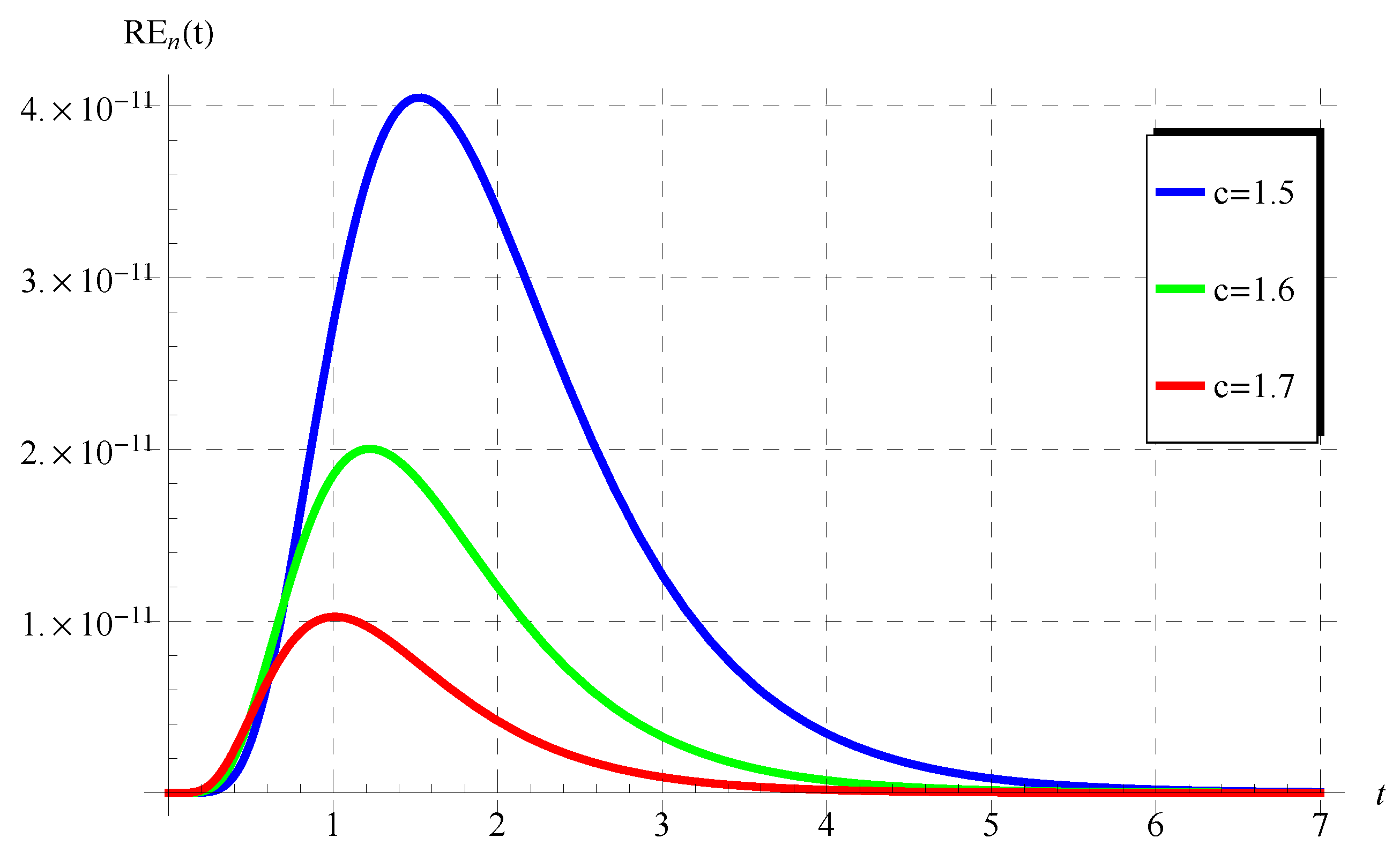
6. Discussion
7. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Andrews, H.I. Third paper: Calculating the behaviour of an overhead catenary system for railway electrification. Proc. Inst. Mech. Eng. 1964, 179, 809–846. [Google Scholar] [CrossRef]
- Abbott, M.R. Numerical method for calculating the dynamic behaviour of a trolley wire overhead contact system for electric railways. Comput. J. 1970, 13, 363–368. [Google Scholar] [CrossRef]
- Gilbert, G.; Davtcs, H.E.H. Pantograph motion on a nearly uniform railway overhead line. Proc. Inst. Electr. Eng. 1966, 113, 485–492. [Google Scholar] [CrossRef]
- Caine, P.M.; Scott, P.R. Single-wire railway overhead system. Proc. Inst. Electr. Eng. 1969, 116, 1217–1221. [Google Scholar] [CrossRef]
- Ockendon, J.; Tayler, A.B. The dynamics of a current collection system for an electric locomotive. Proc. R. Soc. Lond. A Math. Phys. Eng. Sci. 1971, 322, 447–468. [Google Scholar]
- Kato, T.; McLeod, J.B. The functional-differential equation y′(x) = ay(λx) + by(x). Bull. Am. Math. Soc. 1971, 77, 891–935. [Google Scholar]
- Iserles, A. On the generalized pantograph functional-differential equation. Eur. J. Appl. Math. 1993, 4, 1–38. [Google Scholar] [CrossRef]
- Derfel, G.; Iserles, A. The pantograph equation in the complex plane. J. Math. Anal. Appl. 1997, 213, 117–132. [Google Scholar] [CrossRef]
- Patade, J.; Bhalekar, S. Analytical Solution of Pantograph Equation with Incommensurate Delay. Phys. Sci. Rev. 2017, 2. [Google Scholar] [CrossRef]
- Fox, L.; Mayers, D.; Ockendon, J.R.; Tayler, A.B. On a functional differential equation. IMA J. Appl. Math. 1971, 8, 271–307. [Google Scholar] [CrossRef]
- Alenazy, A.H.S.; Ebaid, A.; Algehyne, E.A.; Al-Jeaid, H.K. Advanced Study on the Delay Differential Equation y′(t) = ay(t) + by(ct). Mathematics 2022, 10, 4302. [Google Scholar] [CrossRef]
- Ambartsumian, V.A. On the fluctuation of the brightness of the milky way. Dokl. Akad Nauk. USSR 1994, 44, 223–226. [Google Scholar]
- Patade, J.; Bhalekar, S. On Analytical Solution of Ambartsumian Equation. Natl. Acad. Sci. Lett. 2017, 40, 291–293. [Google Scholar] [CrossRef]
- Alharbi, F.M.; Ebaid, A. New Analytic Solution for Ambartsumian Equation. J. Math. Syst. Sci. 2018, 8, 182–186. [Google Scholar] [CrossRef]
- Bakodah, H.O.; Ebaid, A. Exact solution of Ambartsumian delay differential equation and comparison with Daftardar-Gejji and Jafari approximate method. Mathematics 2018, 6, 331. [Google Scholar] [CrossRef]
- Ebaid, A.; Al-Enazi, A.; Albalawi, B.Z.; Aljoufi, M.D. Accurate Approximate Solution of Ambartsumian Delay Differential Equation via Decomposition Method. Math. Comput. Appl. 2019, 24, 7. [Google Scholar] [CrossRef]
- Khaled, S.M.; El-Zahar, E.R.; Ebaid, A. Solution of Ambartsumian delay differential equation with conformable derivative. Mathematics 2019, 7, 425. [Google Scholar] [CrossRef]
- Kumar, D.; Singh, J.; Baleanu, D.; Rathore, S. Analysis of a fractional model of the Ambartsumian equation. Eur. Phys. J. Plus 2018, 133, 133–259. [Google Scholar] [CrossRef]
- Ebaid, A.; Al-Jeaid, H.K. On the exact solution of the functional differential equation y′(t) = ay(t) + by(−t). Adv. Differ. Equ. Control Process. 2022, 26, 39–49. [Google Scholar] [CrossRef]
- Adomian, G. Solving Frontier Problems of Physics: The Decomposition Method; Kluwer Academic Publishers: Boston, MA, USA, 1994. [Google Scholar]
- Duan, J.S.; Rach, R. A new modification of the Adomian decomposition method for solving boundary value problems for higher order nonlinear differential equations. Appl. Math. Comput. 2011, 218, 4090–4118. [Google Scholar] [CrossRef]
- Bhalekar, S.; Patade, J. An analytical solution of fishers equation using decomposition Method. Am. J. Comput. Appl. Math. 2016, 6, 123–127. [Google Scholar]
- Diblík, J.; Kúdelcíková, M. Two classes of positive solutions of first order functional differential equations of delayed type. Nonlinear Anal. 2012, 75, 4807–4820. [Google Scholar] [CrossRef]
- Abbaoui, K.; Cherruault, Y. Convergence of Adomian’s method applied to nonlinear equations. Math. Comput. Model. 1994, 20, 69–73. [Google Scholar] [CrossRef]
- Cherruault, Y.; Adomian, G. Decomposition Methods: A new proof of convergence. Math. Comput. Model. 1993, 18, 103–106. [Google Scholar] [CrossRef]
- Rach, R. A bibliography of the theory and applications of the Adomian decomposition method, 1961–2011. Kybernetes 2012, 41, 1087–1148. [Google Scholar] [CrossRef]
- Alshaery, A.; Ebaid, A. Accurate analytical periodic solution of the elliptical Kepler equation using the Adomian decomposition method. Acta Astronaut. 2017, 140, 27–33. [Google Scholar] [CrossRef]
- Ebaid, A. Remarks on the homotopy perturbation method for the peristaltic flow of Jeffrey fluid with nano-particles in an asymmetric channel. Comput. Math. Appl. 2014, 68, 77–85. [Google Scholar] [CrossRef]
- Ayati, Z.; Biazar, J. On the convergence of Homotopy perturbation method. J. Egypt. Math. Soc. 2015, 23, 424–428. [Google Scholar] [CrossRef]
- Pasha, S.A.; Nawaz, Y.; Arif, M.S. The modified homotopy perturbation method with an auxiliary term for the nonlinear oscillator with discontinuity. J. Low Freq. Noise Vib. Act. Control 2019, 38, 1363–1373. [Google Scholar] [CrossRef]
- Bayat, M.; Pakar, I.; Bayat, M. Approximate analytical solution of nonlinear systems using homotopy perturbation method. Proc. Inst. Mech. Eng. Part E J. Process Mech. Eng. 2016, 230, 10–17. [Google Scholar] [CrossRef]
- Ahmad, S.; Ullah, A.; Akgül, A.; De la Sen, M. A novel homotopy perturbation method with applications to nonlinear fractional order KdV and Burger equation with exponential-decay kernel. J. Funct. Spaces 2021, 2021, 8770488. [Google Scholar] [CrossRef]
- He, J.-H.; El-Dib, Y.O.; Mady, A.A. Homotopy perturbation method for the fractal Toda oscillator. Fractal Fract. 2021, 5, 93. [Google Scholar] [CrossRef]
- Obeya, P.O.; Akinlabi, G.O. Application of the regular perturbation method for the solution of first-order initial value problems. J. Phys. Conf. Ser. 2021, 1734, 012021. [Google Scholar] [CrossRef]
- Kac, V.G.; Cheung, P. Quantum Calculus; Springer: New York, NY, USA, 2002. [Google Scholar]
- Sezer, M.; Akyuz-Dascıoglu, A. A Taylor method for the numerical solution of generalized pantograph equations with linear functional argument. J. Comput. Appl. Math. 2007, 200, 217–225. [Google Scholar] [CrossRef]
- Yüzbası, S.; Sezer, M. An exponential approximation for solutions of generalized pantograph-delay differential equations. Appl. Math. Model. 2013, 37, 9160–9173. [Google Scholar] [CrossRef]
- Rihan, F.A.; Rihan, A.F. An Analysis of the Theta-Method for Pantograph Type Delay Differential Equations. Complexity 2022, 2022, 8961352. [Google Scholar] [CrossRef]
- Rihan, F.A. Delay Differential Equations and Applications to Biology (Forum for Interdisciplinary Mathematics), 1st ed.; 2021 Edition; Springer: New York, NY, USA, 2021. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Albidah, A.B.; Kanaan, N.E.; Ebaid, A.; Al-Jeaid, H.K. Exact and Numerical Analysis of the Pantograph Delay Differential Equation via the Homotopy Perturbation Method. Mathematics 2023, 11, 944. https://doi.org/10.3390/math11040944
Albidah AB, Kanaan NE, Ebaid A, Al-Jeaid HK. Exact and Numerical Analysis of the Pantograph Delay Differential Equation via the Homotopy Perturbation Method. Mathematics. 2023; 11(4):944. https://doi.org/10.3390/math11040944
Chicago/Turabian StyleAlbidah, Abdulrahman B., Nourah E. Kanaan, Abdelhalim Ebaid, and Hind K. Al-Jeaid. 2023. "Exact and Numerical Analysis of the Pantograph Delay Differential Equation via the Homotopy Perturbation Method" Mathematics 11, no. 4: 944. https://doi.org/10.3390/math11040944
APA StyleAlbidah, A. B., Kanaan, N. E., Ebaid, A., & Al-Jeaid, H. K. (2023). Exact and Numerical Analysis of the Pantograph Delay Differential Equation via the Homotopy Perturbation Method. Mathematics, 11(4), 944. https://doi.org/10.3390/math11040944






