Abstract
Atrial fibrillation (AF) is the most common form of cardiac arrhythmia. Despite the frequency of the disease, the treatment strategies for AF are inefficient. We developed a cost-effectiveness model to evaluate potential improvements in the application of cardiac ablations to treat AF. These are surgical procedures to terminate the arrhythmia and restore Sinus Rhythm. A Markov Model with a time horizon of five years was built to represent the management of patients in AF. A Montecarlo simulation was developed as a sensitivity analysis when the effectiveness increases the estimate of the potential impact of an improvement on the efficacy of cardiac ablation. The result of the analysis showed 44% of patients were untreated in any way. The base case ends up with 45% of patients having sinus rhythm restored after five years. The Montecarlo simulation estimates that in 58% of cases, the alternative of increasing ablation effectiveness by 25% would be cost-effective. If the number of performed ablations is doubled, the robustness increases to 86%. In conclusion, the model of management of AF highlights the importance of not only increasing effectiveness, but also treating more patients. Our study shows that investing in new screening technology to increase the effectiveness of ablations would be cost-effective.
MSC:
60J20
1. Introduction
Atrial fibrillation (AF) is a heart condition that causes an irregular and often abnormally fast heart rate. The major risk of AF is the consequences of these irregular rhythms: blood can coagulate and double the possibility of suffering a stroke, major bleeds, and heart failure. In fact, AF doubles the risk of any complication, causes brain injuries, and worsens the quality of life [1,2]. It also causes a dramatic reduction in life expectancy (doubled mortality and increased risk of embolic stroke, heart failure, and dementia).
More than 43.6 million people worldwide suffer from AF, the most common cardiac arrhythmia [3]. This is reflected in the amount of time that the clinicians invest in it since it accounts for the highest number of medical consultations and days of hospitalization than any other cardiac arrhythmia [4].
Antiarrhythmic drugs (AAD) are the first line of treatment, but these have limited efficacy (<40%) [5]. In patients not controlled with AAD, the most effective treatment is an interventional cardiac ablation (CA). CA is a surgical intervention that restores the heart rhythm by burning or destroying the heart tissue that is the driver of the irregularity of the heart frequency, using a catheter [3].
There are different techniques that have the objective of stopping arrhythmia using CA. The most common technique is pulmonary vein isolation. This only focuses on isolating the electrical conduction between the pulmonary veins and the cardiac tissue to avoid initiation or maintenance of the arrhythmia. There are also more complex techniques that personalize the search for drivers, the mechanisms that may give rise to arrhythmia [6,7]. The effectiveness of these personalized treatments has been shown to be higher although more expensive and dependent on the complexity of AF in each patient.
Unfortunately, even these invasive interventions have a low success rate: around 50% of patients relapse in their arrhythmia during the 48 months following the intervention [5]. The effectiveness of the CA depends on the technique and the precision of the diagnosis. Proper identification of the underlying mechanisms that sustain an arrhythmia is crucial for successful patient stratification and treatment. Only by accurately identifying these mechanisms can patients be treated with the highest likelihood of success.
The effective management of AF patients is crucial not only for improving public health, but also for reducing healthcare costs. In European countries, it is estimated that AF accounts for up to 2% of total annual healthcare expenditure, or approximately 13,500 million Euros per year [8]. One of the major contributors to the overall cost of managing AF is the use of medical procedures and inpatient care [9,10]. This is mainly due to aging populations and the intensification of complications [11] and according to the Guidelines, there is a need for measures to reduce hospitalizations [3]. One of the major findings by Guo et al. [12] was that AF ablation is associated with a reduction in all-cause hospitalization by nearly one-half. Research has also shown that healthcare costs are significantly higher for patients who require repeat ablations for AF compared to those who only require a single procedure. This highlights the economic benefit of successful AF ablation in reducing the need for repeat procedures and lowering healthcare costs.
In addition to interventional CA, there are other options for treating patients with AF. Some therapies focus on preventing complications without restoring sinus rhythm (SR), and are referred to as Rate Control (RC) therapies. Other therapies, such as AAD and CA, can restore normal SR and are known as Rhythm Control therapies. The classification is based on the European Society of Cardiology Official Guidelines 2020 [3]. The “ABC” pathway is the integrated pathway for AF management [13], standing for: ‘A’—Anticoagulation or Avoid stroke; ‘B’—Better symptom management; and ‘C’—Cardiovascular and Comorbidity optimization. The A is related to the use of anticoagulant medications. The B is based on RC, whereas the C step is focused on Rhythm Control.
The principal reason for the low treatment efficacy is the lack of tools to identify the patients that would benefit from ablation. A key message extracted from the 2020 ESC Guidelines [3] for management of AF, is that novel tools for screening and detecting AF substantially improve the diagnostic opportunities in patients at risk. Nevertheless, the management pathways including such tools are still to be defined. The personalization of the treatment is not possible without identifying the mechanisms of AF initiation and perpetuation in each patient.
Several studies have compared the effectiveness of different treatments for AF. The literature suggests that radiofrequency interventional CA has higher overall effectiveness rates and lower rates of complications compared to AAD therapy [14]. These findings suggest that CA may be a more effective treatment option for AF compared to AAD therapy. Some studies have found that RC and Rhythm Control therapies have similar effects on preventing death, despite the lower effectiveness of RC therapies. This suggests that both approaches may be effective in certain situations, but that rhythm control therapies may be more effective overall [15]. However, there is evidence that CA greater reduces mortality (and also the recurrence of AF) compared to drug therapy [5]. The exact percentages of that study were 23.8% for Rhythm Control group and 21.3% for RC.
Many studies have compared the cost-effectiveness of complex surgical procedures for the treatment of AF, but few have considered the overall impact on the healthcare system. This can make it difficult to fully assess the value of these treatments Studies that aim to improve the diagnosis of AF often rely on simple devices like smartphones or hand-held devices for mass screening in untreated populations. However, there is currently a lack of research on the most effective treatments for AF and which approach would be most cost-effective in the long term. [14,16].
Given the lack of research on the diagnosis and management of AF, this study aims to fill this gap and provide new insights into the effective management of AF. It builds upon existing studies by considering factors such as cost-effectiveness and the overall impact on the healthcare system. There is significant variation in the use of interventional CA for AF among different countries. For example, in Spain, only 5000 ablations [17] are performed per year, while in Germany, which has twice the population, more than 40,000 ablations are performed annually [5]. However, more than 90% of AF patients are unable to access the most effective treatments, such as CA, due to limited clinical resources [6].
In this study, we evaluated the potential impact of novel technologies on the diagnosis and treatment of AF. These technologies aim to (a) identify patients who would benefit from CA and (b) increase the efficacy of the procedure by guiding the ablation intervention. The use of a novel device to improve the efficacy of interventional CA for AF could overcome the current limitations in treating AF patients. In addition to examining the impact on the effectiveness of the surgical procedure, it is also important to consider the number of ablations performed and the investment required. This study aims to evaluate the extent to which increasing the number of patients treated and the resources invested can improve the management of AF.
For this purpose, this study will use a cost-effectiveness model to evaluate the potential benefits of a novel technology that improves the accuracy of interventional CA for AF. Specifically, we aim to estimate the improvement in effectiveness and cost savings that this technology could achieve in Spain and Europe. By examining the impact of this technology on CA outcomes and healthcare costs, we hope to provide insights into the value of investing in such innovations for the management of AF.
2. Materials and Methods
A Markov Model was developed to evaluate different scenarios for the management of AF. The Markov Model is a discrete stochastic model used to model pseudo-randomly changing systems. The simplest type of Markov Model is a Markov chain. Essentially, it is a discrete process in which a random variable Xn changes over time between different states. These chains have the property that the probability of Xn = j only depends on the state immediately before the system: Xn−1. When in a chain the probabilities do not depend on the time they are considered, n, it is called a homogeneous chain, that is, the probabilities are constant at every step. In this study, an analysis of the base case was performed with invariable probabilities and a further sensitivity analysis with the variations of the probabilities within a statistical distribution.
MATLAB ver. R2021a was used for modeling and simulating the model.
2.1. Description of the Model
The model was designed to represent the current healthcare situation considered in this study for patients in AF. The temporal horizon is set at five years and each cycle is three months long, based on similar studies from the literature [7]. The initial patient cohort establishes a population of older than 65 years diagnosed with AF. This age is the lower boundary provided by the ESC Official Guidelines of 2020 [3].
The effectiveness of treatment was measured as patients with SR restored. In total, eight states were included to faithfully represent the real situation of AF. They include the available treatments for AF, the different health states in which a patient can be, and the most common complications derived from an arrhythmia.
X1 AF: The initial state for all patients diagnosed with any of the types of AF (paroxysmal, persistent, permanent). RC, i.e., anticoagulants, is the treatment applied by default to any patient with the disease and risk for strokes. From this state, a patient may continue with RC treatment or receive one of the rhythm control treatment strategies (such as AAD) or interventional CA, or experience one of the considered complications.
X2 AAD: Used to treat abnormal heart rhythms, but their success rates are often low. They include, for example, Class I sodium-channel and III Potassium-channel blockers, which can restore SR with lower effectiveness.
X3 CA: This state covers the procedures which include catheter ablation to isolate pulmonary veins.
X4 SR: The patient has the normal rhythm restored after successful treatment. This can result in the maintenance of SR, a recurrence of AF, or death
X5 Post Heart Failure: This is the state that is reached when one of the most common complications of AF, heart failure, occurs. Heart failure is a condition in which the heart is unable to pump enough blood to meet the body’s needs, resulting in symptoms such as shortness of breath, fatigue, and swelling in the legs.
X6 Post Stroke: Stroke occurs when there is a clot blocking a cerebral artery due to AF. This can result in brain damage, which can cause a range of symptoms depending on the area of the brain affected.
X7 Post Major Bleed: A major bleed is a serious and potentially life-threatening complication that can occur due to AF. The most severe types of major bleeds include intracranial hemorrhage (bleeding in the brain) and pericardial hemorrhage (bleeding in the area around the heart).
X8 Death: Absorbent situation in which, based on the mortality rates, the individuals end up if they suffer any complications.
In Figure 1 the transitions between the states in the model are shown.
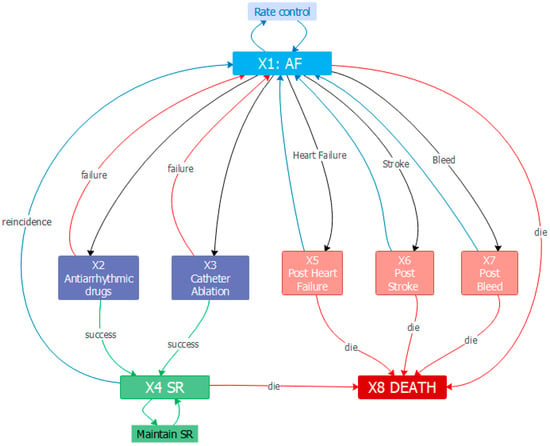
Figure 1.
Model state diagram. States and transitions. Source: prepared by the authors.
The following notation is introduced in a homogeneous finite chain with eight possible states:
where i, j = 1, 2, …, 8. If pij > 0, then the state Xi can communicate with Xj. The communication can be also mutual if pij > 0. For each i fixed, the values {pij} are transition probabilities since in any step they can satisfy the condition
for every i = 1, 2, …, 8. All these values are combined to build a transition matrix T of size 8 × 8 where
pij = P(Xn = j|Xn−1 = i),
It can be observed that every row i of the matrix is a probability distribution, i.e., .
An important probability is that of reaching Xj after n steps { given a probability distribution {. It is observed that { is the probability that the system initially occupies the state Xi, so as .
If is what is called the probability of reaching Xj in one step, then, based on the total probability theorem
This can also be expressed as a vector shape: with and the row vectors of the probability given by and , where is the initial probability distribution and is the probability of reaching any of the states X1, …, X8 after a step. With this notation, it can be expressed
where T is the transition matrix. In this model the transition matrix is expressed as follows:
2.2. Transformation of Time Horizon of Probability
It is commonly seen indicated in the literature that the transition probabilities refer to a natural year period of 12 months. Nevertheless, when the fixed cycles for transitions are shorter than a year, these probabilities should be adapted to the period studied. It is assumed that the event probability does not rely on the time period, and therefore can be modeled as a Poisson distribution with a constant r ratio [18]. Therefore, the probability distribution follows a negative exponential such that . The annual probabilities were transformed into 3-month-length periods with the exponential distribution.
2.3. Input Data
The model was completed by populating it with real-world evidence data. Different sources from the literature were contrasted, and cardiology experts were consulted. Although models using Randomized clinical trials (RCTs) data are widely accepted, nowadays the attention on the use of real-world evidence (RWE) to populate effectiveness data in this type of model is increasing [19]. It is also essential to avoid a particular study in the literature for model population, as sometimes there is not enough attention paid to the representatives of the assumptions [20].
The costs associated with each state are expressed in Euros (EUR) and refer to 2020, with a discount rate of 3%. The discount rate is the annual fixed value to equalize monetary units between different temporal moments. Most of the costs were obtained from the Public Taxes Law [21] and Hospital Costs were provided by the Spanish Ministry of Health [22]. The full fee for hospital processes is based on Diagnosis-Related Groups, which are standardized categories that reflect the expected costs of treating specific medical conditions.
In Table 1 the annual probabilities of the model are listed. They are identified with the corresponding transition probability in the model. It may be important to note that, as not all patients are able to opt for a treatment, the model included a percentage of them who would maintain AF. This is referred to in the table as Distribution to RC. Beta-blockers and anticoagulants are administered to prevent further complications, but will never restore SR.

Table 1.
Transition probabilities of the model.
Effectiveness refers to the success rate of the treatments: CA and AAD. Distribution means the proportion of patients undergoing each treatment: CA, AAD, or RC. The distribution for RC is equivalent to the proportion of the population who remain in the AF state. Recurrence is of AF after SR has been restored. The probability of occurrence of the different complications and the mortality rates of each event are included.
In Table 2 the costs for each state are indicated. At every period the costs are multiplied to update their values based on the proportion of the population that falls into each state.

Table 2.
Costs of the states of the model.
2.4. Scenarios
For the current study, different scenarios were considered, with the base case as the current situation for managing AF patients. We performed an analysis of potential scenarios to choose the most appropriate for the cost-effectiveness plane. We considered the scenario with an increase of effectiveness of CA of 25% due to the use of the novel technology. In addition, we took into account extreme scenarios varying the distribution of patients: 0% of patients under treatment, 100% of patients under AAD, and 100% of patients under CA. By examining these scenarios, we were able to gain a better understanding of the model and its potential impact on patient outcomes and healthcare costs.
In the final analysis, we selected two optimal scenarios for the cost-effectiveness plane based on two different cases. The first scenario compares the base case (current treatment approach) to a scenario where the effectiveness of interventional CA is increased by 25% due to the use of a novel technology. The second scenario compares the base case to a scenario where the effectiveness of CA is increased by 25% and the number of ablations performed is doubled (10% of patients receive CA). These two scenarios will be described and analyzed in more detail in the following sections.
2.5. Probabilistic Sensitivity Analysis
The above-mentioned data was substituted in the model in a static way. In a second part of the analysis, the limitations and the potential of the system were analyzed.
Firstly, a graphic representation of the patient distribution in the system was made. The proportion of patients undergoing the different treatments varied: RC, AAD, and CA. For each scenario, we calculated the potential number of patients in SR and the cost per patient in the system.
After creating this representation, we selected a scenario to be included in the sensitivity analysis to evaluate the potential benefits. This method was applied twice: first, using the current effectiveness of interventional CA in clinical practice (57%), and second, using an increased effectiveness of CA by 25% due to the use of a novel technology. By comparing these two scenarios, we were able to understand the potential impact of the technology on patient outcomes and costs.
The sensitivity analysis was performed to identify how random changes in parameters in the model influence the outputs, using Monte Carlo simulations to assess the uncertainty [21]. To develop a probabilistic sensitivity analysis, it is important to define the probability distributions followed by the parameters of the model. To select the distributions of these parameters others studies in the literature were checked [7,25]. The selected distribution for the transition probabilities was the beta distribution, which is used for modeling a continuous probability distribution for probabilities. Finally, for the random variation of costs, the statistical distribution log-normal was applied. Each cost obtained from the literature was the mean of the distribution, and the standard deviation was computed for a plausible range of 20%, which determines the limits for the uncertainty.
3. Results
3.1. Validation of the Model
The first representation (Figure 2) shows the current situation of the system for treating AF and shows the evolution of AF population for five years. The trend is for a significant increment of patients that restore SR during the first two years (24 months). After that, the proportion of patients in SR remains relatively stable for the next three years, gradually increasing until the final percentage of patients in SR reaches 45.06% after 60 months. This figure illustrates the current effectiveness of AF treatment and the potential for improvement.
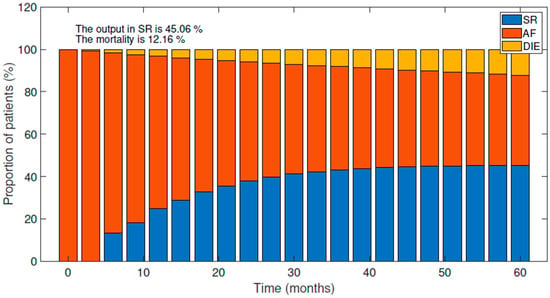
Figure 2.
Evolution of the current situation of the AF population after five years. Variations between SR, AF, and Death.
Mortality progressively increases up to 12.11% for the five years considered. These values are consistent with those observed in clinical trials [5,35] and other cost-effectiveness studies, which have reported mortality rates ranging from 8% to 15% after five years. In addition, other cost-effectiveness studies [7] have shown that the final proportion of patients in SR after five years is around 49%. These findings suggest that the model is realistic and can provide valuable insights into the management of AF.
Another important aspect to extract from the model is the cost of the management of the AF patient in the system. The model shows that, on average, the system spends 10,543 EUR per AF patient after five years. This value is similar to those reported in the literature [9]. In that European study from the Euro Heart Survey, the annual cost per patient in Spain was 11,575 EURin 2006.
3.2. Predictions of the Model: Evaluation of Potential Scenarios
The design of potential scenarios that could overcome the current situation and improve the effectiveness of treatments was done by varying different parameters of the model, such as the effectiveness or the number of ablations performed. The comparison between the different situations will be based on the total costs of the system and the final percentage of patients in SR.
The first approach was focused on the distribution of patients among the available procedures and therapies. In Figure 3, three different plots can be observed. Point A represents the current management of AF patients, while points B, C, and D are extreme scenarios described in the next section. Point E represents a potential scenario that will be further analyzed in subsequent sections.
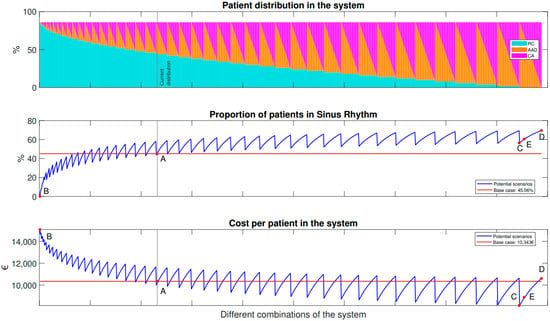
Figure 3.
Representation of potential situations with their total costs and final percentage of patients in SR.
In Figure 3, the top graph shows the variation between different therapies: RC, AAD, and CA. Along the X-axis, the different combinations of the proportion of patients undergoing different treatments are shown. This starts on the left with all patients under RC, varying until the last one on the right, which represents all patients undergoing ablation. The combinations vary from 0% of total patients in each option to 86%. It was supposed that there is a percentage (14%) that will always have a risk of suffering any of the complications (HF, ST, or BL), which is why the maximum percentage is 86%. Furthermore, the gray vertical line denoted as ‘Current situation’ represents the current combination of the present scenario: specifically, 44% of patients in RC, 35% with AAD, and 4.8% undergoing a CA. These values are taken from the literature [10], respectively.
In Figure 3, the two graphs at the bottom show the main outcomes of the model, while the plot in the middle represents the final percentage of patients in SR. The final plot shows the total costs of the AF system’s management after five years. The values of the base case are denoted with the letter A. The current situation shows that the final outcome of patients in SR is 45.06% and the total cost per patient after five years is 10,343 EUR.
The horizontal red line serves as a reference for the current variables of the system: the final number of patients in SR and the total costs of the system.
The blue line in each graph corresponds to the potential situations described in the upper graph: the distribution of patients between RC, AAD, and CA. The saw-tooth shape of the blue line in the top graph is due to the fact that as the percentage of patients receiving RC is fixed (represented by the light blue columns), the remaining percentage is distributed between AAD and CA.
The saw-tooth shape of the blue line in the top graph is a result of calculating all possible combinations of AAD and CA, starting with 0% in CA (magenta) and the maximum in AAD (orange). The minimum point in terms of costs and patients in SR corresponds to AAD, as these medications have lower costs and lower effectiveness compared to CA. The maximum point is reached when 0% of patients receive AAD and the maximum percentage receive CA, resulting in higher effectiveness but also higher costs compared to AAD. Scenarios that have lower costs and higher outcomes compared to the base case (represented by the red line) are considered cost-effective and represent improvements over the current situation. Based on the current situation, there are several potential scenarios that can be considered to improve effectiveness and reduce costs. One observation is that increasing the number of patients receiving rhythm control therapies (i.e., AAD or CA) would improve efficacy and lower costs. Similarly, a higher number of cardiac ablations would increase effectiveness, although at the cost of higher expenses compared to AAD treatment.
The results indicate that rhythm control therapies (i.e., AAD or CA) are more effective at restoring SR compared to RC therapy both in terms of costs and reduced mortality. To better understand the impact of distributing patients among the different therapies, illustrative scenarios with extreme values are presented in detail in Table 3. These scenarios provide insight into how varying the number of patients among the therapies affects the effectiveness and total costs.

Table 3.
Key values of hypothetical situations after 5 years: RC treatment, AAD and CA.
Scenario B represents the worst-case scenario, in which it is assumed that the arrhythmia cannot be terminated, and all patients receive only RC therapy. This results in all patients maintaining AF. Despite not undergoing any treatment, the total cost for the system is highest in this scenario due to the negative effects of the arrhythmia. Additionally, the mortality rate in scenario B reaches 21.73%, nearly double that of the base case. The treatment with AAD, as seen in scenario C, results in a decrease in total costs and an increase in the number of patients with restored SR. While this is a cost-effective solution compared to the base case, it is clear that the use of CA, as demonstrated in scenario D, has even greater potential for success in terms of restoring SR and reducing costs. In scenario D, all AF patients undergo ablation. In this extreme case, the lowest overall mortality is achieved (7.62%), as well as the most effective restoration of SR (69.55%). Notice that despite requiring 20 times more ablations than in the current situation, the total cost per patient for the system only increases from 10,343 EURto 10,696 EUR.
Finally, scenario E represents one of the possible optimal scenarios with a higher efficacy, lower mortality, and lower cost that the base case. To select this optimal scenario, the constraint was set to achieve a cost like that of treating all patients with AAD (8264 EUR). Specifically, by increasing the number of ablations performed by four times, the efficacy increases from 45.06% to 60.58%, the five-year mortality decreases from 12.16% to 8.64%, and the cost per patient decreases by 15%, from 10,343 EUR to 8890 EUR.
3.3. Evaluation of Potential Scenarios with a More Effective Ablation Strategy
In this part of the analysis, the potential impact of a technology that increases CA efficacy by 25% (from 57% assumed in the current situation [36] to 82%) is evaluated.
Several novel technologies are being developed in an effort to increase the efficacy of AF treatment, such as technology that guides ablation based on driver ablation, technology that prevents reconnections of pulmonary vein isolations [6,37,38,39] and technology that screens patients who would benefit from ablation [36,39]. While these technologies hold great promise, their economic impact has not yet been systematically evaluated.
In Figure 4, we can see a comparison between the current situation and a scenario in which the effectiveness of catheter ablation (CA) has increased by 25%. The graph is organized in the same way as Figure 3, with different combinations of patient distribution between different therapies plotted along the x-axis. In this case, an additional line has been added to represent the situation where the effectiveness of CA is 82%. Key values from the different scenarios are also marked on the graph and summarized in Table 4.
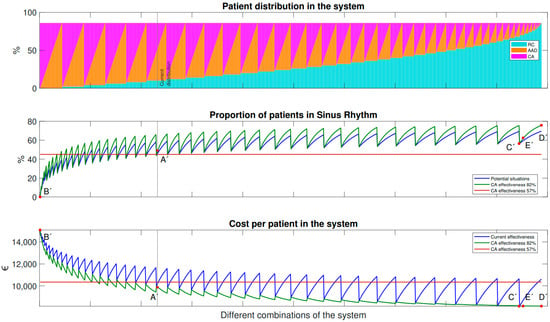
Figure 4.
Variation of the distribution between the treatments with an increase of CA effectiveness of 25%.

Table 4.
Key values of potential situations after 5 years with the increase of effectiveness during CA due to the novel device.
Figure 4 illustrates the relationship between the proportion of patients undergoing treatment and the cost-effectiveness of ablation therapy in the case of increased effectiveness (top line). As long as the proportion of patients receiving treatment is equal to or greater than the current situation, ablation therapy is always cost-effective with an increase in effectiveness. Even if the number of treated patients is lower than the current situation (left side of A’), the therapy remains cost-effective with an increase in effectiveness. The same situations as previously discussed (points A’ to E’) are also depicted in the graph.
In Figure 4, Point A’ shows the current distribution among the available therapies (i.e., RC, AAD, and CA) and how it is affected by the increase of effectiveness of CA by 25%. Note that in this basal scenario, A, the percentage of patients that receive ablation is 4.80%. An increase in the efficacy of the CA leads to a 4.55% reduction in total cost, a 4% increase in overall effectiveness, and a 0.42% decrease in mortality.
Scenarios B’ (where all patients are maintained in AF and only RC treatments are applied) and C’ (where all patients are treated with AAD) are not affected by the increase in the efficacy of CA and the results are the same as for B and C in the previous scenarios.
In scenario D’, all patients receive optimized CA treatment. This scenario involves a 15-fold increase in the number of ablations performed. As a result, total efficacy increases by 30%, while costs and mortality are reduced by 21% and 56.5% respectively compared to the base case. The total costs per patient after five years would be even lower than the cost of AAD.
Finally, point E’ represents a potential scenario in which the number of ablation procedures is three times the current rate. With the increase of CA effectiveness, the cost is even less than with AAD, and effectiveness and mortality are better than in the situation shown in the previous scenario, E. To achieve the optimal results shown in point E’, it would be necessary to perform three times more ablations than currently, rather than four times as in situation E. This is because the increase in the effectiveness of CA by 25% allows for the same cost and effectiveness to be achieved with a lower number of ablations, as seen when compared to Figure 3.
3.4. Probabilistic Sensitivity Analysis
The cost-effectiveness planes show the variation of two improved situations with respect to the base case. In both cases, the effectiveness of CA has been increased by 25%. However, as we have observed that the number of CAs performed expands the limitations of the model, we will also consider the case where more CAs are carried out. To further understand the model’s behavior and the improvements relative to the current situation, we also consider a scenario where the number of CAs is doubled. This scenario was chosen as it represents a feasible increase in the number of ablations.
On the one hand, the current situation is compared to the situation in which the novel technology increases the effectiveness of CA by 25% (Figure 5a). Here, the AF patients are distributed as: 4.80% in CA, 34.60 % in AAD and 44.00 % in RC. This situation is cost-effective with a robustness of 59.70%. The mean increase (blue point in Figure 5) is 2.31 % more patients having restored SR after five years and saving 363.73EUR per patient. This is observed in Figure 5a.
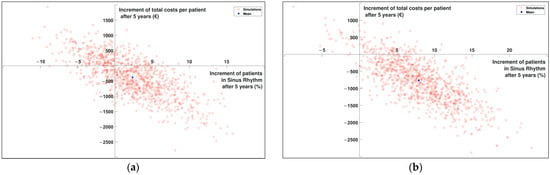
Figure 5.
Cost-effectiveness plane (a) Comparison of current situation with an increase of 25% in effectiveness of CA. (b) Comparison of current situation with an increase of 25% in effectiveness of CA and an increase of 5% in patients undergoing CA.
On the other hand, the second plane shows the impact of the increase in effectiveness when doubling the number of CAs performed (Figure 5b). In this case, 5% more patients in the model undergo a CA, maintaining the 25% increase in effectiveness. The AF patients are distributed as: 9.60 % in CA, 34.60 % in AAD, and 39.20 % in RC. In this case, the robustness increases to 89.80%, with a mean of 8.06 % more patients having restored SR after five years and 827.41 EUR saved per patient. The representation is plotted in Figure 5 b, where the movement of the cloud of points to the right is noticeable.
The mean savings per patient is used as an estimation of how much we can increase the expenditure per patient. In this case, we have around 365 EUR without doubling CAs and 827 EUR by doubling CAs. This would mean that there is even more margin for the increase in the cost of CA: around 1000 EUR for situation (a) and 1300 EUR for situation (b).
3.5. Impact on Costs in Europe
This section estimates the cost impact of using new technology that increases the effectiveness of ablations compared to current technology.
In Europe, there is a prevalence of AF in approximately of 900/100,000 individuals [3] (around 6,750,000 people have AF in Europe) and an ablation rate of 378/1,000,000 inhabitants [37], which implies 283,500 ablations every year.
Table 5 illustrates the potential impact of increasing the number of ablations on the management of AF patients, including annual savings and effects on effectiveness. Based on the results in Table 5, the increase in the number of ablations per year leads to a greater annual savings and an increase in the number of patients in SR after five years. The base case, where the number of ablations remains unchanged, results in an annual savings of 250 million euros and an increase of 155,000 patients in SR after five years.

Table 5.
Key values of the impact of the increase of ablations in Europe after five years with 25% more effectiveness of CA and including the price of the device.
When the number of ablations is doubled, the annual savings increase to 348 million EUR and the number of patients in SR increases to 573,500. Finally, when the number of ablations is quadrupled, the annual savings reach 600 million EUR and the number of patients in SR increases to 1,000,000. These results suggest that increasing the number of ablations can lead to significant improvements in the management of AF patients, both in terms of cost and effectiveness.
4. Discussion
This is the first study in which a cost-effectiveness study has been conducted with a focus on the broad management of AF patients. A novel Cost-Effectiveness Mathematical Model for the Management of AF has been presented. This model demonstrated that an increase in ablation rates together with better stratification and ablation effectiveness would be cost-effective.
The model designed has shown results coherent with those observed in the literature. The values obtained from the base case were similar to those observed in other sources in the literature, which [35] gives a mortality of approximately 12% after three years. In other cost-effectiveness studies representing CA and medical management of AF patients, 49% of patients ended up in SR after five years [7]. These numbers validate the performance of the proposed model.
CA treatment has been shown to be more cost-effective than AAD treatment, in addition to the fact that the latter carries an appreciably higher risk of complications, and aggressively decreases the quality of life [40].
It is well-recognized in the literature that ablation is a cost-effective solution. It provides better results than medication (i.e., AAD) and can maintain the SR in more patients with fewer complications. When considering the literature, most of the cost-effectiveness studies related to AF are focused on studying novel complex procedures: the effectiveness of novel complex ablations [7] or comparison between different medications [19]. However, the results of this project have highlighted another point of view to be considered. A more sophisticated patient selection process or ablation procedure with higher efficacy could have a significant effect on the final management of AF. The increase in the effectiveness of CA is the key, as resources would be optimized if clinicians were able to restore SR at a first attempt with CA, without having to undergo a second CA procedure [41]. This would increase the savings in Europe by 500 million per year and the efficacy of treatment in 135,000 patients, as well as the sustainability of the system.
A meticulous and wide-ranging review of the literature has been carried out and, using the input data, a model has been built to extract insights into the situation of AF patients. In the literature, there are reviews and comparisons of the situation of AF between different countries or types of AF [9,42], but not many are aimed at looking for novel opportunities regarding the diagnosis and treatment of these patients.
Regarding the clinical implications, the key insight is the lack of patients under treatment, i.e., rhythm control. The current situation for AF patient management is far from optimal. There is a potential benefit in patients restoring SR and in decreasing mortality. To do so, the model points out that an investment and an increase in the number of ablations would be cost-effective. The increase of patients treated with AAD to end arrhythmia could restore SR in a higher number of patients, but this potential is limited by the potential of CA. When doubling the number of ablations, the novel technology considered could increase the number of patients in SR after five years by 573,500 in Europe. This is the same increase as if all patients were under AAD, which highlights the limited potential of the latter treatment and how the CA can further improve. It is important to highlight that the sensitivity analysis relies on the base probabilities from the literature plus an uncertainty range of 20% within the selected distributions. These parameters might vary from one country to another, and it would be interesting to study how the increases are affected by tuning them.
Additionally, with respect to the economic implications, this study highlights the potential savings obtained by reconsidering the management of patients in AF. As well as the clinical implications, the economic situation of the current management of AF patients is not optimal. The investment needed to increase the number of patients under treatment is justified by the benefit that could be achieved. A situation has been identified as cost-effective. This is when the number of ablations is doubled, and the additional cost of the novel device has been added to the model. The benefit is 348 million Euros in Europe per year and the ability to restore SR in 573,500 more AF patients after five years. The previous values mean that the use of a novel technology to improve the effectiveness of CA and the increase of patients undergoing rhythm control is a cost-effective situation. This benefit is sufficient to cover the investment needed for the increase of treatments.
5. Conclusions
Principally, a profitable opportunity has been found when the novel technology, which improves the effectiveness of the ablations, is incorporated and, in addition, the number of surgical procedures increased. An increment in the effectiveness of the ablations due to the incorporation of novel technology influences the efficiency of the system, but the magnitude of the savings increases to 78.80% when more people are treated.
This represents an opportunity to improve the treatment of AF, as it allows the number of patients in SR to be greater (8%) and mortality to be reduced by 10%. In addition, the effect on the increase in effectiveness and savings is greater as the number of CAs increases.
The extrapolation of the quantities in the model to real values shows significant savings and a greater final number of patients in SR in Europe. If the number of patients treated with CA is increased by 10%, the annual net benefit of incorporating the device would reach 348 million EUR in Europe.
Therefore, the incorporation of novel, patient-personalized treatments is justified since the savings that would be obtained by increasing the efficiency of the ablations would compensate for the investment necessary to increase the number of ablations.
This would cover the personnel, necessary equipment, and places. The margin after subtracting the costs of the device is still quite wide. Increased efficacy must be followed by the expansion of therapy to more patients.
Author Contributions
Conceptualization, D.V.-C. and A.M.C.; methodology, D.V.-C., J.D.-C. and I.B.-M.; software, I.S.-P. and J.D.-C.; validation J.D.-C.; formal analysis, I.S.-P.; investigation, D.V.-C. and A.M.C.; resources, D.V.-C.; data curation, I.S.-P.; writing—original draft preparation, I.S.-P. and I.B.-M.; writing—review I.B.-M.; visualization, J.D.-C., I.S.-P. and I.B.-M.; supervision, D.V.-C. and A.M.C.; project administration, I.B.-M.; funding acquisition, A.M.C. and I.S.-P. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported by Spanish Agencia Estatal de Investigación (AEI) (PID2020-119364RB-I00 and RYC2018-024346-I) and the EIT Health (SAVE-COR Activity code 220385, EIT Health is supported by EIT, a body of the European Union).
Acknowledgments
We would also like to thank John Wright for his help in editing the English.
Conflicts of Interest
A.M.C. is the cofounder and receives a salary from Corify Care SL. I.S.P. received a grant from Corify Care SL.
References
- Ball, J.; Carrington, M.J.; McMurray, J.J.V.; Stewart, S. Atrial Fibrillation: Profile and Burden of an Evolving Epidemic in the 21st Century. Int. J. Cardiol. 2013, 167, 1807–1824. [Google Scholar] [CrossRef]
- Chugh, S.S.; Havmoeller, R.; Narayanan, K.; Singh, D.; Rienstra, M.; Benjamin, E.J.; Gillum, R.F.; Kim, Y.H.; McAnulty, J.H.; Zheng, Z.J.; et al. Worldwide Epidemiology of Atrial Fibrillation: A Global Burden of Disease 2010 Study. Circulation 2014, 129, 837–847. [Google Scholar] [CrossRef] [PubMed]
- Hindricks, G.; Potpara, T.; Dagres, N.; Arbelo, E.; Bax, J.J.; Blomström-Lundqvist, C.; Boriani, G.; Castella, M.; Dan, G.A.; Dilaveris, P.E.; et al. 2020 ESC Guidelines for the Diagnosis and Management of Atrial Fibrillation Developed in Collaboration with the European Association for Cardio-Thoracic Surgery (EACTS). Eur. Heart J. 2021, 42, 373–498. [Google Scholar] [CrossRef]
- Fibrilación Auricular. Síntomas y Causas. Mayo Clinic. Available online: https://www.mayoclinic.org/es-es/diseases-conditions/atrial-fibrillation/symptoms-causes/syc-20350624 (accessed on 18 April 2021).
- Mark, D.B.; Anstrom, K.J.; Sheng, S.; Piccini, J.P.; Baloch, K.N.; Monahan, K.H.; Daniels, M.R.; Bahnson, T.D.; Poole, J.E.; Rosenberg, Y.; et al. Effect of Catheter Ablation vs Medical Therapy on Quality of Life among Patients with Atrial Fibrillation: The CABANA Randomized Clinical Trial. JAMA 2019, 321, 1275–1285. [Google Scholar] [CrossRef] [PubMed]
- Willems, S.; Verma, A.; Betts, T.R.; Murray, S.; Neuzil, P.; Ince, H.; Steven, D.; Sultan, A.; Heck, P.M.; Hall, M.C.; et al. Targeting Nonpulmonary Vein Sources in Persistent Atrial Fibrillation Identified by Noncontact Charge Density Mapping: UNCOVER AF Trial. Circ. Arrhythm. Electrophysiol. 2019, 12, e007233. [Google Scholar] [CrossRef]
- Anderson, L.H.; Black, E.J.; Civello, K.C.; Martinson, M.S.; Kress, D.C. Cost-Effectiveness of the Convergent Procedure and Catheter Ablation for Non-Paroxysmal Atrial Fibrillation. J. Med. Econ. 2014, 17, 481–491. [Google Scholar] [CrossRef] [PubMed]
- Velleca, M.; Costa, G.; Goldstein, L.; Bishara, M.; Ming Boo, L. A Review of the Burden of Atrial Fibrillation: Understanding the Impact of the New Millennium Epidemic across Europe. EMJ Cardiol. 2019, 7, 110–118. [Google Scholar] [CrossRef]
- Ringborg, A.; Nieuwlaat, R.; Lindgren, P.; Jönsson, B.; Fidan, D.; Maggioni, A.P.; Lopez-Sendon, J.; Stepinska, J.; Cokkinos, D.V.; Crijns, H.J.G.M. Costs of Atrial Fibrillation in Five European Countries: Results from the Euro Heart Survey on Atrial Fibrillation. EP Eur. 2008, 10, 403–411. [Google Scholar] [CrossRef] [PubMed]
- Arbelo, E.; Brugada, J.; Hindricks, G.; Maggioni, A.P.; Tavazzi, L.; Vardas, P.; Laroche, C.; Anselme, F.; Inama, G.; Jais, P.; et al. The Atrial Fibrillation Ablation Pilot Study: An European Survey on Methodology and Results of Catheter Ablation for Atrial Fibrillation Conducted by the European Heart Rhythm Association. Eur. Heart J. 2014, 35, 1466–1478. [Google Scholar] [CrossRef]
- Wolowacz, S.E.; Samuel, M.; Brennan, V.K.; Jasso-Mosqueda, J.G.; Van Gelder, I.C. The Cost of Illness of Atrial Fibrillation: A Systematic Review of the Recent Literature. Europace 2011, 13, 1375–1385. [Google Scholar] [CrossRef]
- Guo, J.; Nayak, H.M.; Besser, S.A.; Beaser, A.; Aziz, Z.; Broman, M.; Ozcan, C.; Tung, R.; Upadhyay, G.A. Impact of Atrial Fibrillation Ablation on Recurrent Hospitalization: A Nationwide Cohort Study. JACC Clin. Electrophysiol. 2019, 5, 330–339. [Google Scholar] [CrossRef] [PubMed]
- Lip, G.Y.H. The ABC Pathway: An Integrated Approach to Improve AF Management. Nat. Rev. Cardiol. 2017, 14, 627–628. [Google Scholar] [CrossRef] [PubMed]
- Mairesse, G.H.; Moran, P.; Van Gelder, I.C.; Elsner, C.; Rosenqvist, M.; Mant, J.; Banerjee, A.; Gorenek, B.; Brachmann, J.; Varma, N.; et al. Screening for Atrial Fibrillation: A European Heart Rhythm Association (EHRA) Consensus Document Endorsed by the Heart Rhythm Society (HRS), Asia Pacific Heart Rhythm Society (APHRS), and Sociedad Latinoamericana de Estimulación Cardíaca y Electrofisiolog. Europace 2017, 19, 1589–1623. [Google Scholar] [CrossRef]
- A Comparison of Rate Control and Rhythm Control in Patients with Atrial Fibrillation. N. Engl. J. Med. 2002, 347, 1825–1833. [CrossRef] [PubMed]
- Jacobs, M.S.; Kaasenbrood, F.; Postma, M.J.; Van Hulst, M.; Tieleman, R.G. Cost-Effectiveness of Screening for Atrial Fibrillation in Primary Care with a Handheld, Single-Lead Electrocardiogram Device in the Netherlands. Europace 2018, 20, 12–18. [Google Scholar] [CrossRef]
- Quesada, A.; Cózar, R.; Anguera, I. Registro Español de Ablación Con Catéter: XIX Informe Oficial de La Asociación Del Ritmo Cardiaco de La Sociedad Española de Cardiología (2019). Rev. Española Cardiol. 2020, 73, 1049–1060. [Google Scholar] [CrossRef]
- Sociedad Española de Salud Pública y Administración Sanitaria; Rodríguez Bezos, D.; Rodríguez Barrios, J.M. Gaceta Sanitaria; Sociedad Española de Salud Pública y Administración Sanitaria: Barcelona, Spain, 2010; Volume 24. [Google Scholar]
- Bowrin, K.; Briere, J.-B.; Levy, P.; Millier, A.; Tardu, J.; Toumi, M. Real-World Cost-Effectiveness of Rivaroxaban and Apixaban vs VKA in Stroke Prevention in Non-Valvular Atrial Fibrillation in the UK. J. Mark. Access Health Policy 2020, 8, 1782164. [Google Scholar] [CrossRef]
- Wodchis, W.P.; Bhatia, R.S.; Leblanc, K.; Meshkat, N.; Morra, D. A Review of the Cost of Atrial Fibrillation. Value Health 2012, 15, 240–248. [Google Scholar] [CrossRef]
- Ley de Tasas 20/2017, de 28 de Diciembre de La Generalitat Valenciana [2017/12159] [DOGV núm. 8202 de 30.12.2017]. Regional ACT. 2017, p. 258. Available online: https://dogv.gva.es/es/eli/es-vc/l/2017/12/28/20/ (accessed on 1 January 2023).
- Ministerio de Sanidad, Consumo y Bienestar Social. Portal Estadístico Del SNS. Estadisticas y Estudios. Informes y Recopilaciones. Available online: https://www.mscbs.gob.es/estadEstudios/estadisticas/inforRecopilaciones/anaDesarrolloGDR.htm (accessed on 8 July 2021).
- Calkins, H.; Reynolds, M.R.; Spector, P.; Sondhi, M.; Xu, Y.; Martin, A.; Williams, C.J.; Sledge, I. Treatment of Atrial Fibrillation With Antiarrhythmic Drugs or Radiofrequency Ablation. Circ. Arrhythmia Electrophysiol. 2009, 2, 349–361. [Google Scholar] [CrossRef]
- Meiltz, A.; Zimmermann, M.; Urban, P.; Bloch, A.; on behalf of the Association of Cardiologists of the Canton of Geneva. Atrial Fibrillation Management by Practice Cardiologists: A Prospective Survey on the Adherence to Guidelines in the Real World. EP Eur. 2008, 10, 674–680. [Google Scholar] [CrossRef]
- Kim, D.; Yang, P.-S.; Sung, J.-H.; Jang, E.; Yu, H.T.; Kim, T.-H.; Uhm, J.-S.; Kim, J.-Y.; Pak, H.-N.; Lee, M.-H.; et al. Less Dementia after Catheter Ablation for Atrial Fibrillation: A Nationwide Cohort Study. Eur. Heart J. 2020, 41, 4483–4493. [Google Scholar] [CrossRef] [PubMed]
- Biffi, M.; Boriani, G.; Bartolotti, M.; Reggiani, L.B.; Zannoli, R.; Branzi, A. Atrial Fibrillation Recurrence after Internal Cardioversion: Prognostic Importance of Electrophysiological Parameters. Heart 2002, 87, 443–448. [Google Scholar] [CrossRef] [PubMed]
- Nieuwlaat, R.; Prins, M.H.; Le Heuzey, J.-Y.; Vardas, P.E.; Aliot, E.; Santini, M.; Cobbe, S.M.; Widdershoven, J.W.M.G.; Baur, L.H.; Lévy, S.; et al. Prognosis, Disease Progression, and Treatment of Atrial Fibrillation Patients during 1 Year: Follow-up of the Euro Heart Survey on Atrial Fibrillation. Eur. Heart J. 2008, 29, 1181–1189. [Google Scholar] [CrossRef]
- Gage, B.F.; Yan, Y.; Milligan, P.E.; Waterman, A.D.; Culverhouse, R.; Rich, M.W.; Radford, M.J. Clinical Classification Schemes for Predicting Hemorrhage: Results from the National Registry of Atrial Fibrillation (NRAF). Am. Heart J. 2006, 151, 713–719. [Google Scholar] [CrossRef] [PubMed]
- Instituto Nacional de Estadística (INE)/Lista Completa de Operaciones. Available online: https://www.ine.es/dyngs/INEbase/listaoperaciones.htm (accessed on 28 January 2021).
- Levy, D.; Kenchaiah, S.; Larson, M.G.; Benjamin, E.J.; Kupka, M.J.; Ho, K.K.L.; Murabito, J.M.; Vasan, R.S. Long-Term Trends in the Incidence of and Survival with Heart Failure. N. Engl. J. Med. 2002, 347, 1397–1402. [Google Scholar] [CrossRef] [PubMed]
- Lakshminarayan, K.; Schissel, C.; Anderson, D.C.; Vazquez, G.; Jacobs, D.R.; Ezzeddine, M.; Luepker, R.V.; Virnig, B.A. Five-Year Rehospitalization Outcomes in a Cohort of Medicare Linkage Study. Stroke 2011, 42, 1556–1562. [Google Scholar] [CrossRef] [PubMed]
- Amlani, S.; Nadarajah, T.; Afzal, R.; Pal-Sayal, R.; Eikelboom, J.W.; Natarajan, M.K. Mortality and Morbidity Following a Major Bleed in a Registry Population with Acute ST Elevation Myocardial Infarction. J. Thromb. Thrombolysis 2010, 30, 434–440. [Google Scholar] [CrossRef]
- Vademecum. Es-Su Fuente de Conocimiento Farmacológico. Available online: https://www.vademecum.es/ (accessed on 26 April 2021).
- Ministerio de Sanidad, Consumo y Bienestar Social. Portal Estadístico Del SNS. Pesos de Los GRDs Del Sistema Nacional de Salud. Años Anteriores. Available online: https://www.mscbs.gob.es/estadEstudios/estadisticas/inforRecopilaciones/anaDesarrolloGDRanteriores.htm (accessed on 9 July 2021).
- Packer, D.L.; Mark, D.B.; Robb, R.A.; Monahan, K.H.; Bahnson, T.D.; Poole, J.E.; Noseworthy, P.A.; Rosenberg, Y.D.; Jeffries, N.; Mitchell, L.B.; et al. Effect of Catheter Ablation vs Antiarrhythmic Drug Therapy on Mortality, Stroke, Bleeding, and Cardiac Arrest among Patients with Atrial Fibrillation: The CABANA Randomized Clinical Trial. JAMA 2019, 321, 1261–1274. [Google Scholar] [CrossRef]
- Rodrigo, M.; Climent, A.M.; Hernández-Romero, I.; Liberos, A.; Baykaner, T.; Rogers, A.J.; Alhusseini, M.; Wang, P.J.; Fernández-Avilés, F.; Guillem, M.S.; et al. Noninvasive Assessment of Complexity of Atrial Fibrillation: Correlation with Contact Mapping and Impact of Ablation. Circ. Arrhythmia Electrophysiol. 2020, 13, e007700. [Google Scholar] [CrossRef]
- Qin, M.; Jiang, W.F.; Wu, S.H.; Xu, K.; Liu, X. Electrogram Dispersion-Guided Driver Ablation Adjunctive to High-Quality Pulmonary Vein Isolation in Atrial Fibrillation of Varying Durations. J. Cardiovasc. Electrophysiol. 2020, 31, 48–60. [Google Scholar] [CrossRef]
- Narayan, S.M.; Baykaner, T.; Krummen, D.; Shivkumar, K.; Clopton, P.; Miller, J. Firm Ablation at Rotors and Focal Sources Has Similarly High Efficacy for Paroxysmal and Persistent Atrial Fibrillation. J. Am. Coll. Cardiol. 2013, 61, E328. [Google Scholar] [CrossRef]
- Molero, R.; Soler Torro, J.M.; Martínez Alzamora, N.; Climent, M.A.; Guillem, M.S. Higher Reproducibility of Phase Derived Metrics from Electrocardiographic Imaging during Atrial Fibrillation in Patients Remaining in Sinus Rhythm after Pulmonary Vein Isolation. Comput. Biol. Med. 2021, 139, 104934. [Google Scholar] [CrossRef]
- Humphries, K.H.; Kerr, C.R.; Steinbuch, M.; Dorian, P. Limitations to Antiarrhythmic Drug Use in Patients with Atrial Fibrillation. CMAJ 2004, 171, 741–745. [Google Scholar] [CrossRef] [PubMed]
- Mansour, M.; Karst, E.; Heist, E.K.; Dalal, N.; Wasfy, J.H.; Packer, D.L.; Calkins, H.; Ruskin, J.N.; Mahapatra, S. The Impact of First Procedure Success Rate on the Economics of Atrial Fibrillation Ablation. JACC Clin. Electrophysiol. 2017, 3, 129–138. [Google Scholar] [CrossRef] [PubMed]
- Luik, A.; Radzewitz, A.; Kieser, M.; Walter, M.; Bramlage, P.; Hörmann, P.; Schmidt, K.; Horn, N.; Brinkmeier-Theofanopoulou, M.; Kunzmann, K.; et al. Cryoballoon versus Open Irrigated Radiofrequency Ablation in Patients with Paroxysmal Atrial Fibrillation. Circulation 2015, 132, 1311–1319. [Google Scholar] [CrossRef] [PubMed]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).