Local Correlation Integral Approach for Anomaly Detection Using Functional Data

Abstract

The present work develops a methodology for the detection of outliers in functional data, taking into account both their shape and magnitude. Specifically, the multivariate method of anomaly detection called Local Correlation Integral (LOCI) has been extended and adapted to be applied to the particular case of functional data, using the calculation of distances in Hilbert spaces. This methodology has been validated with a simulation study and its application to real data. The simulation study has taken into account scenarios with functional data or curves with different degrees of dependence, as is usual in cases of continuously monitored data versus time. The results of the simulation study show that the functional approach of the LOCI method performs well in scenarios with inter-curve dependence, especially when the outliers are due to the magnitude of the curves. These results are supported by applying the present procedure to the meteorological database of the Alternative Energy and Environment Group in Ecuador, specifically to the humidity curves, presenting better performance than other competitive methods.

1. Introduction

The present work is framed in the thematic related to the detection of anomalies or outliers, in terms of the purpose and, with respect to, the statistical methodology in the area of Functional Data Analysis (FDA). In fact, FDA is a branch of statistics of growing importance in recent years [1], and although it is a relatively new field of study (compared to multivariate data analysis), it has a great scientific activity, with high production in many different fields of science. Thus, in the last 5 years, more than 5000 documents have been published in the Web of Science (core collection, SCI-EXPANDED, SCI, and AHCI) that include, in either their title or keywords, the terms “Functional Data Analysis” or FDA. These documents belong to very diverse scientific areas including health sciences, chemistry, engineering, and of course, statistics, among many others. The field of anomaly detection is even more productive, with more than 5700 papers published in the last 5 years (in the WoS core collection, SCI-EXPANDED, SCI, and AHCI, containing the words “Anomaly detection” or “Outlier detection” in keywords or title), mainly in areas related to engineering and computer science. In both FDA and anomaly detection, the number of publications is growing year by year, as is the number of citations (more than 37,000 in FDA and more than 47,000 in the anomaly detection domain, corresponding to articles published in the last 5 years), which is an indicator of the growing impact and visibility of the two domains.

In this work, we propose a new extension of a multivariate outlier detection method to the specific case of functional data, increasingly common due to recent advances in sensing and IoT [2]. The ever-increasing computational capacity to take and handle this type of data has promoted the current development of the FDA. Using FDA, we can perform descriptive statistics [3,4], classification [5,6,7,8,9], and regression modeling [10,11,12,13,14], also including techniques to develop an analysis of variance [15,16], time series modeling [17,18], process control [19,20,21], or outlier detection methods [22,23,24,25] that allow us to work with time or frequency dependent curves or surfaces [25,26,27]. The seminal works of Ramsay and Silverman [25] and Ferraty and Vieu [26], among others, have significantly helped to popularize FDA to solve problems in many different domains apart from the statistics area. In this way, FDA is currently applied in domains ranging from material science, chemometrics [16,28,29], and engineering [20,21,30,31] to geosciences [32], medicine [33,34], genetics [35], or environmental sciences [20,36,37,38], among others.

In the last years, new monographs have appeared that have significantly enriched the FDA field with new knowledge and methods. Of particular note, in the methodological domain, are the works by Horváth and Kokoszka [39] and Hsing and Eubank [40], while of particular relevance for presenting and defining the new approach to Elastic Functional Data Analysis is the monograph developed by Srivastava and Klassen [41]. Most of the FDA literature is focused on the $L^2$ norm, but there are some concerns about its application in all possible scenarios. Namely, the distances under the $L^2$ metric could be larger than they should be, i.e., a possible misalignment between curves or phase variability can be incorrectly interpreted as actual variability in terms of amplitude [42]. Therefore, the functional means and other statistics calculated under the $L^2$ norm could be not representative in these cases defined by phase variation between curves, leading to the subsequent error in tasks such as outlier detection, classification, regression, or analysis of variance, among others. This can be amended by applying elastic registration of curves [43] that takes into account both the vertical and horizontal variability ($L^2$ registration only considers vertical variability). In this regard, we can also highlight the work of Kurtek et al. [44] and Marron et al. [45]. Based on the above works, anomaly detection methods based on elastic distance have been proposed in recent years. In fact, Xie et al. [46] proposed a box plot based on elastic distance, while Harris et al. [47] defined a method to detect anomalous curves, considering their shape, from an elastic depth (itself based on elastic distance). In the present work, our proposal is compared with the latter method based on elastic depth; moreover, this elastic depth is also incorporated in the present methodology by replacing the $L^2$ metric. In addition to the elastic FDA approach, the monographs by Mateu and Giraldo [48], which combines the current state of the art in temporal and spatial dependence, as well as the monograph by Moretin et al. [49] dedicated to the application of wavelets in FDA, are also worth mentioning. Because of this intense activity, there are a very large number of libraries of functions, implemented in R software, that present these techniques to a broad number of possible users. To mention one example, we refer to the fda.usc [50] package.

On the other hand, the automatic detection of outliers and anomalies are increasingly demanded tasks in the context of digitization and Industry 4.0 since they help in predictive maintenance and continuous improvement of services and processes [51]. Moreover, their application is essential at the beginning of any data analysis since the existence of outliers can significantly condition the results and lead to erroneous conclusions [51]. In this work, outliers are defined as extreme values with respect to a set, while anomalies are data generated with a different distribution (another process) than the one that generates the rest of the observations. In the specific case of FDA, several methods have emerged to detect outliers using functional data, most of them being based on the concept of functional depth [23,52,53]. An example of these methodologies is the proposal by Sun and Genton [4] for the construction of a boxplot using functional data, by means of which outliers can be identified in a similar way to the classical boxplots, relying on depth bands and the calculation of functional quantiles. Procedures based on bootstrap resampling, such as the one proposed by Febrero et al. [23], are also very popular. There are also the alternatives of control charts for functional data for outlier and anomaly detection, such as the one proposed by Flores et al. [21], which include a Phase I control chart based on the calculation of data depth, in addition to a nonparametric Phase II chart based on the calculation of ranges. It is important to note that, at present, outlier detection methods based on functional depth are usually not specifically designed to find outliers based on their shape [54], making outliers more difficult to detect. In this regard, Kuhnt and Rehage [54], on the one hand, and Arias-Gil and Romo [55], on the other hand, propose two alternatives for outlier detection due to changes in the shape of the data. In addition, outlier detection can also be approached from the calculation of distances between curves and the application of bootstrap procedures to estimate their distribution, a procedure used in interlaboratory studies [56]. The works of Yu et al. [57] and Lei et al. [58] also present alternative methods that are not based on functional depth.

This study provides a new FDA alternative for the identification of outliers not only in magnitude but also attending to the shape of the data. Specifically, a new approach of the Local Correlation Integral (LOCI) method is proposed for the case of functional data, supported by the good performance of the LOCI procedure with multivariate data (in terms of computational efficiency and speed), which has made it a very popular alternative in the area of artificial intelligence [53,59]. Therefore, a different and novel approach for outlier detection from functional data is proposed, including a complete study of its performance with the design of different simulation scenarios (including the analysis of the influence of the dependence between curves, either positive or negative) and its validation through its application on real meteorological data, specifically ambient humidity level curves.

Next, we summarize the main innovations and contributions of the proposed methodology:

• Extension of the multivariate anomaly detection LOCI method to the context of functional data. This method allows the detection of anomalous curves (functional data) by applying the LOCI method, where all statistics are estimated in a functional way and using the $L^2$ distance.
• The present algorithm provides a method to detect anomalies both in terms of magnitude and shape.
• A comprehensive simulation study is provided, from which we propose values of LOCI parameters, such as $r$ and $\theta$, in order to optimize the results of classification between anomalies and normal observations.
• In addition, the present Bootstrap-LOCI proposal is a competitive method (in terms of accuracy, sensitivity, and specificity) with respect to benchmark functional anomaly detection procedures such as those based on data depth.
• It is a flexible methodology that allows us to incorporate alternative metrics to $L^2$, such as the benchmarking elastic distance, suitable for the detection of shape anomalies.
• It is also important to note that this method could be easily combined with visualization tools, from the fact of its simplicity (similar to the concept of control charts) in addition to its implementation in R statistical software, one of the more flexible software to display data.
• We would like also to stress that the motivation for this work breaks from the necessity, in the academy, industry, and companies, such as those that provide and manage IoT platforms fed by highly dependent continuously monitored data, i.e., functional data.

This work is structured as follows. Section 2 presents the concepts, definitions, and characteristics of this new methodology, as well as the description of the LOCI algorithm applicable to functional data. Section 3 measures the performance of the new method using Monte Carlo simulation, considering different scenarios defined by different sample sizes and different levels of dependence between functional data. Section 4 evaluates the performance of the functional LOCI method from its application to a real data set, specifically to average ambient humidity curves, while Section 5 presents the main conclusions of the present study.

2. Methodology

A functional random variable is defined as a variable X(t) taking values in the Hilbert space $L^2\left(\mathrm{T}\right)$, where $\mathrm{T}=\left[\mathrm{a},\mathrm{b}\right]\subset \mathrm{R}$, while functional data would be realizations of this variable [11]. One can also consider functional data as trajectories of stochastic processes defined in a given infinite dimensional space [60]. These ideas allow us to extend the concepts of the LOCI algorithm [59,61], starting from the definition of distance in a Hilbert space (let $\mathrm{d}\left(·\right)$ be such a distance [62]) to define neighborhoods in the functional space, aiming to obtain a density measure with the Multigranular Deviation Factor ($\widetilde{\mathrm{MDEF}}$) from which we can label outliers. With this scheme in mind, the adaptation of the LOCI method to be applied to functional data is presented below. More information about the LOCI method for multivariate data can be found in the work of Papadimitriou et al. [59]. The present FDA approach is based on the aforementioned LOCI version for multivariate data.

Let $\tilde{\mathrm{P}}=\left\{{\mathrm{x}}_1\left(\mathrm{t}\right),\dots .,{\mathrm{x}}_{\mathrm{n}}\left(\mathrm{t}\right);\mathrm{t}\in \mathrm{T}\right\}$ be one sample of functional data and $\mathrm{r}\in \mathrm{R}$ be a radius. Thus, we can define a neighborhood of each functional datum ${\mathrm{x}}_{\mathrm{i}}\left(\mathrm{t}\right)\in \tilde{\mathrm{P}}$ by:

$$\widetilde{ℳ}\left(x_i\left(t\right),r\right)=\left\{x\left(t\right)\in \tilde{\mathbb{P}}:d\left(x_i\left(t\right),x\left(t\right)\right)<r\right\}$$

which cardinality is given by:

$$\widetilde{𝓂}\left(x_i\left(t\right),r\right)=\left|\widetilde{ℳ}\left(x_i\left(t\right),r\right)\right|.$$

The building of the sub-neighborhoods can be carried out using the definition of the parameter $\theta \in \left(0,1\right]$, as a function of $\widetilde{ℳ}\left(x\left(t\right),\widehat{r}\right),$ with $\widehat{r}=\theta ·r$ for $x\left(t\right)\in \widetilde{ℳ}\left(x_i\left(t\right),r\right)$.

The mean $\widetilde{mean}\left(x_i\left(t\right),r,\theta \right)$, standard deviation $\tilde{\sigma }\left(x_i\left(t\right),r,\theta \right)$, $\widetilde{MDEF}$, and normalized standard deviation $\widetilde{{\sigma }_{nor}}\left(x_i\left(t\right),r,\theta \right)$ are defined following the schemes of the LOCI methods for multivariate data [59,61]. Therefore, the mean is defined as the sum of observations within each sub-neighborhood $\widetilde{ℳ}\left(x\left(t\right),\widehat{r}\right)$ in $\widetilde{𝓂}\left(x_i\left(t\right),r\right)$, as shown in:

$$\widetilde{mean}\left(x_i\left(t\right),r,\theta \right)=\frac{{\mathsf{\Sigma }}_{x\left(t\right)\in \widetilde{ℳ}\left(x_i\left(t\right),r\right)} \widetilde{𝓂}\left(x\left(t\right),\widehat{r}\right)}{\widetilde{𝓂}\left(x_i\left(t\right),r\right)},$$

whereas the standard deviation is defined by the expression:

$$\tilde{\sigma }\left(x_i\left(t\right),r,\theta \right)=\sqrt{\frac{{\mathsf{\Sigma }}_{x\left(t\right)\in \widetilde{ℳ}\left(x_i\left(t\right),r\right)} {\left(\widetilde{𝓂}\left(x\left(t\right),\widehat{r}\right)-\widetilde{mean}\left(x_i\left(t\right),r,\theta \right)\right)}^2}{\widetilde{𝓂}\left(x_i\left(t\right),r\right)}}$$

Moreover, the $\widetilde{MDEF}$ and the normalized standard deviation are given, respectively, by:

$$\widetilde{MDEF}\left(x_i\left(t\right),r,\theta \right)=1-\frac{\widetilde{𝓂}\left(x_i\left(t\right),r\right)}{\widetilde{mean}\left(x_i\left(t\right),r,\theta \right)}$$

and:

$$\widetilde{{\sigma }_{nor}}\left(x_i\left(t\right),r,\theta \right)=\frac{\tilde{\sigma }\left(x_i\left(t\right),r,\theta \right)}{\widetilde{mean}\left(x_i\left(t\right),r,\theta \right)}$$

More information of LOCI parameters can be retrieved from Papadimitriou et al. [59].

The radius varies from a minimum value ($r_{min}$), defined as containing at least 20 observations, and a maximum value ($r_{max}$), containing the whole sample [61]. Finally, a functional data $x_i\in \tilde{\mathbb{P}}$ is classified as an anomaly if for any $r\in \left[r_{min},r_{max}\right]$, the value of $\widetilde{MDEF}$ is large enough, that is,

$$\widetilde{MDEF}>k\widetilde{{\sigma }_{nor}}\left(x_i\left(t\right),r,\theta \right),$$

with $k>0$. To perform the classifications, $k=3$ is usually set taking into account the Chevyshev inequality, defined by:

$$\widetilde{P(MDEF}>k\widetilde{{\sigma }_{nor}}\left(x_i\left(t\right),r,\theta \right))\le \widetilde{P(|MDEF}| >k\widetilde{{\sigma }_{nor}}\left(x_i\left(t\right),r,\theta \right))$$

$$\le \frac{\widetilde{{\sigma }_{nor}}{\left(x_i\left(t\right),r,\theta \right)}^2}{{\left[k\widetilde{{\sigma }_{nor}}\left(x_i\left(t\right),r,\theta \right)\right]}^2}=\frac{1}{k^2}.$$

There is no single perspective for the application of the LOCI algorithm; in fact, all the different possibilities are detailed in Papadimitriou et al. [59]. Specifically, in this work, we explore the alternative in which practitioners choose to use a single value for the radius or, failing that, to handle a limited range of them. Therefore, given the sample $\tilde{\mathbb{P}}$ and a radius r, for each $x_i\left(t\right)\in \tilde{\mathbb{P}}$, the Functional Data–Local Correlation Integral (FD-LOCI) algorithm is defined as follows:

• Select $\theta \in \left(0,1\right]$.
• Develop the neighborhoods $\widetilde{ℳ}\left(x_i\left(t\right),r\right)$ and sub-neighborhoods $\widetilde{ℳ}\left(x\left(t\right),\widehat{r}\right).$
• Calculate $\widetilde{mean}\left(x_i\left(t\right),r,\theta \right)$ and $\widetilde{MDEF}\left(x_i\left(t\right),r,\theta \right)$.
• If $\widetilde{MDEF}>3·\widetilde{{\sigma }_{nor}}\left(x_i\left(t\right),r,\theta \right)$, identify $x_i\left(t\right)$ as an outlier.

The performance of the FD-LOCI method is also compared with new benchmark alternatives both in the simulation scenarios and in the real dataset, in order to assess its scope and usability. Specifically, the following anomaly detection procedures have been compared:

• FD-LOCI method implementing the $L^2$ distance (our original proposal).
• FD-LOCI method but replacing the $L^2$ distance with the so-called elastic distance [47].
• Elastic Depth Method [47], specifically designed to better detect anomalies taking into account their shape.
• Outlier detection method based on data depth as defined by Febrero et al. [23].

The first option is the present proposal, whereas the second is our proposal where the $L^2$ distance is replaced with the elastic distance defined in Harris et al. (2021). This type of distance has demonstrated the best performance in the cases in which there are phase variations in original data; thus, this distance and the corresponding depth definitions are now a reference to differentiate curves and shapes in terms of shape. Namely, Harris et al. [47] developed a recent anomaly detection method based on the concept of elastic depth (specially defined for detecting anomalies due to their different shape), which is also applied in the present study (third method). Finally, the application of a traditional outlier detection method based on functional data depth is also included [23].

The performance of the anomaly detection methods is assessed with the calculation of $accuracy=\frac{TP+TN}{TP+FN+TN+FP}$, $sensitivity=\frac{TP}{TP+FN}$, $specificity=\frac{TN}{TN+FP}$, and kappa index $\kappa =\frac{2\times \left(TP\times TN-FN\times FP\right)}{\left(TP+FP\right)\times \left(FP+TN\right)+\left(TP+FN\right)\times \left(FN+TN\right)}$. Whereby FN accounts for the number of false negatives, TP the true positives, FP the false positives, and TN the true negatives in the framework of a confusion matrix of two classes. The closer to 1 the indices are, the better the classification performance.

3. Simulation Study

In this section, the performance of the new methodology is studied by estimating the Type I error ($\alpha$) and the power ($1-\beta$), where $\beta$ is the Type II error, using a simulation performed with the Monte Carlo procedure. The different scenarios are defined by varying the values of the different parameters of the FD-LOCI algorithm in addition to the degree of dependence between curves. For the simulation of curves, the study of Febrero et al. [23] is taken as a basis in which $x_1\left(t\right),\dots , x_n\left(t\right)$ functional data are considered, which are realizations of a stochastic process in the $t\in T=\left[0,1\right]$ interval. The assumed stochastic process is Gaussian, following the $\mathsf{{\rm X}}\left(t\right)=30t{\left(1-t\right)}^{\raisebox{1ex}{$3$}\!\left/ \!\raisebox{-1ex}{$2$}\right.}+\sigma \left(t\right)·ϵ\left(t\right)$ model, with $\sigma \left(t\right)=0.5$, whereas $ϵ\left(t\right)$ is also Gaussian process distributed, $ϵ\left(t\right)~GP\left(0,\mathsf{\Sigma }\right)$, with zero mean and a variance–covariance matrix defined by $\mathsf{\Sigma }=E\left[ϵ\left(t_i\right)\times ϵ\left(t_j\right)\right]=0.3\exp \left\{-\frac{\left|t_i-t_j\right|}{0.3}\right\}$. In addition, an alternative model is used to generate the outlier curves, defined by the mean equal to $\mu \left(t\right)=E\left[\mathsf{{\rm X}}\left(t\right)\right]=30t^{\raisebox{1ex}{$3$}\!\left/ \!\raisebox{-1ex}{$2$}\right.}\left(1-t\right)$.

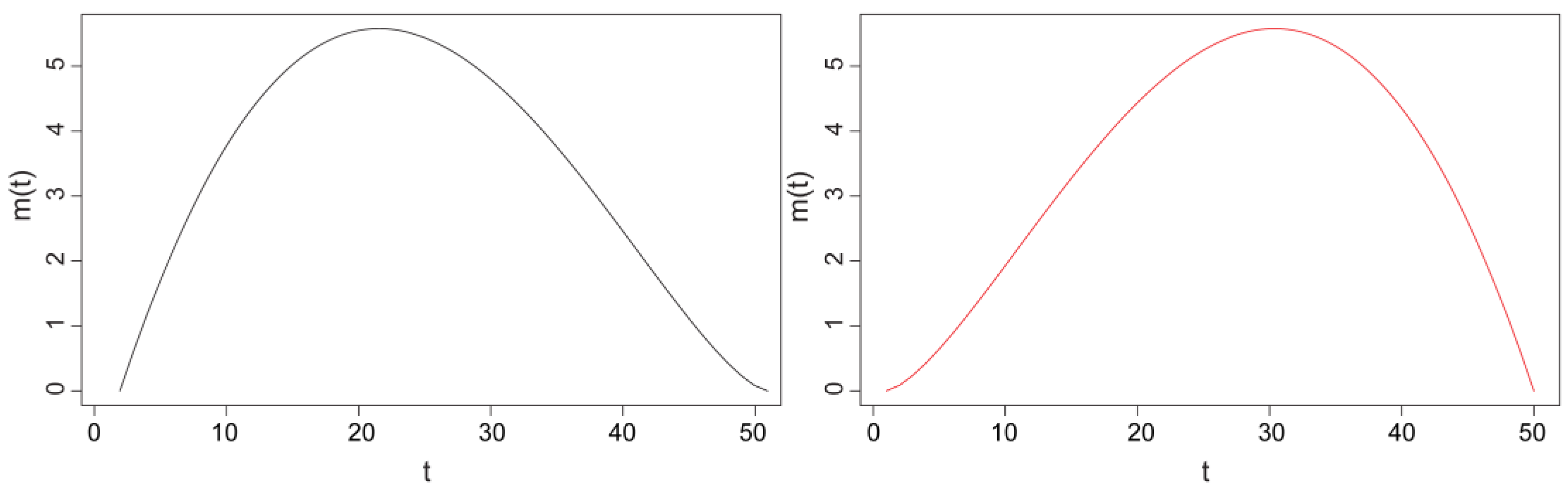
Figure 1 shows the functional means for each of the two processes. The black line is the functional mean corresponding to the data generated with the first model, without considering outlier data, while the red one accounts for the functional mean for the process that generates the anomalous functional data.

On the other hand, in order to detect outliers that differ from the common data either in shape or in magnitude, the following cases are proposed, following the guide shown in Flores et al. [21]:

(a)

Variation in shape: We will use a model whose mean is:

$$\mu \left(t\right)=E\left[\mathsf{{\rm X}}\left(t\right)\right]=\left(1-\eta \right)·30t{\left(1-t\right)}^{\raisebox{1ex}{$3$}\!\left/ \!\raisebox{-1ex}{$2$}\right.}+\eta ·30t^{\raisebox{1ex}{$3$}\!\left/ \!\raisebox{-1ex}{$2$}\right.}\left(1-t\right),$$

varying the $\eta$ parameter from 0.2 to 1 using steps of 0.2 units.

(b)

Variation in magnitude: We will use a model whose mean is:

$$\mu \left(t\right)=E\left[\mathsf{{\rm X}}\left(t\right)\right]=30t{\left(1-t\right)}^{\raisebox{1ex}{$3$}\!\left/ \!\raisebox{-1ex}{$2$}\right.}+\delta ,$$

with $\delta$ on a grid defined between 0.4 and 2 with a step of 0.4 units.

Figure 2 shows cases (a) and (b), with the black line defining the process without outliers, while the green and blue lines represent cases (a) and (b), respectively. The blue curve for case (a) corresponds to $\eta =0.4$, while the green line for case (b) was obtained by setting $\delta =0.8$. For more information, a complete taxonomy of anomalous functional data, from which different simulation scenarios can be defined, can be found in Hubert and Rousseeuw [63].

The Gaussian stochastic process considered to generate the functional data assumes that the curves are independent of each other. However, in the framework of continuously monitored data with respect to time, numerous examples defined by functional time series can be observed, in which there is a strong dependence between the curves, as is the case of the demand and price time series in the electricity market [64]. To simulate scenarios defined by curves dependent on each other, the model $Y\left(t\right)=\mu \left(t\right)+\sigma \left(t\right)·\widetilde{ϵ}\left(t\right)$ will be followed, with $\widetilde{ϵ}\left(t\right)=\rho ·{\widetilde{ϵ}}_{i-1}\left(t\right)+\left(1-\rho \right)·{ϵ}_i\left(t\right)$, where $\rho$ is the measure of dependence between the curves and $\sigma \left(t\right)=0.5$, with $\widetilde{ϵ}$ and $ϵ$ being Gaussian processes.

To define the structure of the simulation study, different radii will be used, according to whether 50%, 70%, or 90% of the observations are covered; hereafter, they will be denoted as $n_0$. On the other hand, the parameter θ will vary between ($0,1]$, taking the values 0.1, 0.4, 0.7, and 1. In addition, different scenarios defined by different sample sizes will be taken into account, being $n=50, 100$ curves. For each different value of the sample size, $n$, scenarios defined by different combinations of $n_0$ and $\theta$ will be defined. For the Type I error estimation, each scenario is replicated 1000 times, previously setting $\alpha =5\%$, obtaining as a result the mean percentage of false alarms. In order to estimate the power of the FD-LOCI method, a similar study is performed. For each scenario, we will generate a curve within the alternative hypothesis (variation in shape or magnitude). This last procedure will be performed 1000 times. Those scenarios, with different degrees of dependence between curves, will be defined by different values of the parameter $\rho$.

3.1. Simulation Scenarios with Independent Curves

In the first instance, the Type I error estimation yielded that the mean percentage of values detected as false alarms is close to the 5% nominal value when $0.7\le \theta \le 1$. As expected, it is observed that the approximation improves as $n$ grows. On the other hand, in the simulation scenarios defined by $\theta <0.7$, the FD-LOCI method tends to underestimate the nominal value of 5%, i.e., the method turns out to be overly conservative, not detecting even 1% of the curves as anomalies. Therefore, in order not to present very extensive tables and considering the lower value of $\theta$ in the interval $\theta \in \left[0.7,1\right]$, which resulted in a better approximation of the Type I error, the value of $\theta =0.78$ is recommended. The reason for using a value of $\theta$ equal to 0.78 is based on the fact that the corresponding power is very similar to that corresponding to higher theta. In fact, it could be said that $\theta =0.78$ is the lowest value of theta to which corresponds a practically maximum power. The reason for not using a higher theta is that, in this way, we increase the number of neighbors that have to be taken into account in the algorithm, which can slow it down noticeably. In

Table 1. Proportion of false alarms (Type I error) for various scenarios in which independence between curves has been assumed, defined also by different values of $n$, $n_0$, and $\theta =0.78$.

	$\mathit{n}$
${\mathit{n}}_0 (\mathbf{\%})$	50	100
50	0.011	0.014
70	0.028	0.032
90	0.041	0.043

, the proportion of false alarms (Type I error), for different simulation scenarios are presented. In fact, the estimates of Type I error (proportion of false alarms) are closer to the theoretical $\alpha$ value the higher the values of $n$ and $n_0$ are, coinciding practically when the radius contains 70% or 90% of the sample ($n_0=35.45$ or $n_0=70.90$). The estimates of $\alpha$ have an approximate value of between 1% and 3% when the radius contains 50% of the sample observations ($n_0=25$ or $n_0=50$).

Table 2. Results of power estimates (1-Type II error) for variation in shape (η) and magnitude (δ), in the case of independence between curves and considering $\theta =0.78$.

		η					δ
n	${\mathit{n}}_0 (\mathbf{\%})$	0.2	0.4	0.6	0.8	1	0.4	0.8	1.2	1.6	2
50	50	0.037	0.187	0.601	0.917	0.995	0.046	0.253	0.684	0.927	0.994
	70	0.083	0.296	0.726	0.96	0.995	0.114	0.409	0.817	0.972	1
	90	0.088	0.319	0.714	0.963	0.997	0.159	0.499	0.866	0.981	1
100	50	0.035	0.262	0.704	0.957	0.998	0.068	0.346	0.727	0.969	0.998
	70	0.07	0.342	0.786	0.977	0.999	0.134	0.478	0.83	0.989	0.999
	90	0.086	0.34	0.776	0.974	0.999	0.16	0.534	0.865	0.993	1

shows the results of the different simulation scenarios considering $\theta =0.78$ and the same values of the parameters $n_0$ and $\theta$ as those shown in Table 1. The results of the power calculation evidence that the FD-LOCI algorithm is all the more capable of detecting changes in shape or magnitude as the values of the parameters $\delta$ and $\eta$ increase, having a very similar performance for detecting the two types of outliers. Specifically, significantly high power is observed to detect changes in magnitude corresponding to η > 0.6, almost for any value of $\mathrm{n}$ and ${\mathrm{n}}_0$, fixing $\theta =0.78$. The power will be higher the higher $\theta$, $\mathrm{n}$, and ${\mathrm{n}}_0$ are. Regarding shape, also the power of FD-LOCI tends to be higher with larger $\theta$, $\mathrm{n}$, and ${\mathrm{n}}_0$, being relatively high to detect changes corresponding to $\delta \ge 1.2$ for almost any value of $\mathrm{n}$ and ${\mathrm{n}}_0$.

3.2. Simulation Scenarios with Dependent Curves

In the IoT framework, functional data resulting from continuous monitoring performed with sensors usually present autocorrelation [21]; thus, the study of the role of dependence between curves is important to see the real applicability of method. Consequently, in this simulation study, the dependence factor $\rho$ is also considered, varying in the $\left[-0.7,0.7\right]$ interval. Specifically, different values for $\rho$ are fixed in order to define scenarios with different degrees of dependence, from weak to strong and from negative to positive: ${\rho }_1=-0.7$, ${\rho }_2=-0.3$, ${\rho }_3=0.3$ and ${\rho }_4=0.7$.

Table 3. Type I error estimation results for the case of dependent curves and $\theta =0.78$.

n	50				100
${\mathit{n}}_0 (\mathbf{\%})$	${\mathit{\rho }}_1$	${\mathit{\rho }}_2$	${\mathit{\rho }}_3$	${\mathit{\rho }}_4$	${\mathit{\rho }}_1$	${\mathit{\rho }}_2$	${\mathit{\rho }}_3$	${\mathit{\rho }}_4$
50	0.012	0.015	0.015	0.010	0.017	0.019	0.019	0.016
70	0.029	0.033	0.033	0.028	0.034	0.037	0.036	0.034
90	0.044	0.046	0.047	0.043	0.046	0.047	0.047	0.046

shows that the estimates of $\alpha$ (proportion of false alarms) are closer to the theoretical value equal to 0.05 the higher the values of the parameters $\theta$, $n$, and $n_0$, although good estimates are obtained with $\theta =0.78$, even though the sample is relatively small, $n=50$, and $n_0$ is relatively high, $n_0=45$, accounting for the 90% of the data. It is important to note that the performance of the FD-LOCI method is little affected by the level of dependence between curves, either negative or positive. While it is true that the estimation results are slightly better (for lower values of $n_0$) under low dependence conditions (${\rho }_2$ and ${\rho }_3$).

We can also observe that there are slight differences in the power estimation of the FD-LOCI method depending on whether the dependence between curves is negative. Specifically,

Table 4. Results of power estimates (1-Type II error) for variation in shape (η) and magnitude (δ) for the case of inter-curve dependence (ρ = −0.7), considering $\theta =0.78$.

		η					δ
n	${\mathit{n}}_{0 }(\mathbf{\%})$	0.2	0.4	0.6	0.8	1	0.4	0.8	1.2	1.6	2
50	50	0.027	0.051	0.179	0.416	0.704	0.018	0.087	0.275	0.495	0.741
	70	0.052	0.119	0.28	0.544	0.813	0.04	0.161	0.418	0.657	0.86
	90	0.065	0.132	0.289	0.541	0.808	0.064	0.23	0.489	0.713	0.897
100	50	0.031	0.099	0.265	0.534	0.793	0.038	0.107	0.325	0.592	0.814
	70	0.051	0.142	0.364	0.637	0.853	0.075	0.192	0.435	0.707	0.893
	90	0.052	0.144	0.351	0.627	0.822	0.1	0.234	0.499	0.756	0.922

,

Table 5. Results of power estimates (1-Type II error) for variation in shape (η) and magnitude (δ) for the case of inter-curve dependence (${\rho }_3=-0.3$), considering $\theta =0.78$.

		η					δ
n	${\mathit{n}}_0 (\mathbf{\%})$	0.2	0.4	0.6	0.8	1	0.4	0.8	1.2	1.6	2
50	50	0.023	0.128	0.413	0.764	0.952	0.033	0.163	0.49	0.801	0.965
	70	0.056	0.222	0.559	0.864	0.981	0.073	0.301	0.644	0.895	0.989
	90	0.082	0.225	0.561	0.866	0.971	0.108	0.358	0.719	0.92	0.996
100	50	0.032	0.165	0.523	0.87	0.984	0.059	0.227	0.548	0.873	0.974
	70	0.061	0.25	0.619	0.908	0.995	0.096	0.355	0.682	0.936	0.992
	90	0.074	0.248	0.603	0.889	0.991	0.127	0.41	0.753	0.948	0.994

,

Table 6. Results of power estimates (1-Type II error) for variation in shape (η) and magnitude (δ) for the case of inter-curve dependence (${\rho }_3=0.3$), considering $\theta =0.78$.

		η					δ
n	${\mathit{n}}_0(\mathbf{\%})$	0.2	0.4	0.6	0.8	1	0.4	0.8	1.2	1.6	2
50	50	0.059	0.333	0.783	0.988	1	0.087	0.412	0.821	0.991	1
	70	0.116	0.482	0.88	0.997	1	0.168	0.582	0.908	0.999	1
	90	0.116	0.471	0.878	0.995	1	0.213	0.661	0.936	0.999	1
100	50	0.094	0.408	0.848	0.996	1	0.094	0.488	0.886	0.995	1
	70	0.137	0.509	0.906	0.999	1	0.164	0.612	0.94	0.998	1
	90	0.151	0.495	0.885	0.996	1	0.208	0.685	0.953	0.999	1

and

Table 7. Results of power estimates (1-Type II error) for variation in shape (η) and magnitude (δ) for the case of inter-curve dependence ($\rho =0.7$), considering $\theta =0.78$.

		η				δ
n	${\mathit{n}}_0(\mathbf{\%})$	0.2	0.4	0.6	0.8	0.4	0.8	1.2	1.6	2
50	50	0.14	0.692	0.986	1	0.201	0.734	0.991	0.999	1
	70	0.22	0.801	0.994	1	0.31	0.852	1	1	1
	90	0.23	0.797	0.996	1	0.36	0.893	1	1	1
100	50	0.18	0.763	0.994	1	0.217	0.796	0.992	1	1
	70	0.24	0.829	0.996	1	0.303	0.875	0.996	1	1
	90	0.24	0.797	0.994	1	0.353	0.91	0.996	1	1

show that when η (anomalies by different magnitude) and δ (shape anomalies) increase, the power growth tends to be faster for cases with positive dependence, as is the case for the comparison between the powers of the scenarios defined by ${\rho }_1=-0.7$ (Table 4) and ${\rho }_4=0.7$ (Table 7). When there is positive dependence, the power curves are of a similar level and growth rate to those corresponding to scenarios with independent curves.

In order to simplify the analysis and to compare our methodology under adverse conditions (with respect to reference methods just under such conditions), two scenarios have been chosen. Both are defined by the existence of shape anomalies (more difficult to identify with traditional methods based on the $L^2$ norm). For this purpose, a parameter $\eta$ (which establishes the difference in shape with respect to the original curves) equal to 1 has been defined. In the first scenario, independence between curves is assumed, while in the second scenario, strong positive dependence is assumed (defined by $\rho =0.7$). The curve simulation procedure is the same as that proposed in Harris et al. [47], i.e., 100 curves are simulated of which 10 are anomalous, for which performance measures (proportion of correct classification, kappa) are calculated. This procedure is performed 1000 times, then plotting the performance indices using boxplots.

It is very important to note that we decided to show the performance of our method in very unfavorable starting scenarios (shape anomalies, horizontal variability more important than vertical variability). In addition, we have chosen to compare the present methodology with reference tools and proven performance in these scenarios, such as the elastic depth method developed by Harris et al. [47] and, also, the method based on the measurement of data depth proposed by Febrero et al. [23]. In order to correct this disadvantage (to be observed in simulation scenarios), a modification of our FD-LOCI methodology has been proposed (see Figure 3). In fact, the use of the $L^2$ distance has been replaced with the elastic distance application [41,43,47]. As a tentative approach, its amplitude component [47] has been used, but not the phase component, which is expected to be incorporated in future work and whose potential is promising for cases where the differences between anomalies are larger in the horizontal than in the vertical direction.

In general terms, the limitations of the FD-LOCI method for detecting shape anomalous curves are noted. However, its performance is greatly increased when replacing the $L^2$ distance with the elastic distance (amplitude). Its performance can also be improved by modifying parameters of the FD-LOCI algorithm such as the k parameter. Figure 3 shows the correct classification ratio (accuracy) of the LOCI-L2 and LOCI_EP methods, assuming dependence between curves. It is observed that the LOCI_EP method performs better in this scenario, for any value of k, being optimal for $k>2$. The LOCI-L2 method has a moderate median accuracy (0.75) for $k=3$. Therefore, the usefulness of incorporating the elastic distance into the FD-LOCI method when trying to detect shape anomalies has been demonstrated.

The next step is to compare our proposed methodology (using different metrics) with those benchmark alternatives to detect shape anomalies, such as e.depth (using the amplitude component), and other traditional and contrasted methods, such as fdqcs.depth (see Figure 4).

Consequently, Figure 4 shows the accuracy and kappa indices corresponding to the scenarios with independent curves (A,B) and with dependent curves (C,D). The FD-LOCI alternatives were performed by fixing $k=2$. The methods that incorporate the elastic depth provide more or less the same performance working with dependent or independent curves. The e.depth and fdqcs.depth provide higher accuracies, but that corresponding to LOCI_ED (that also incorporates the elastic distance) is also high and similar. The four methods are defined by relatively low kappa indices. In addition, considering the accuracy values, this means that the methods have difficulties identifying the anomalies correctly. Regarding kappa indices, the best performance in the independence framework is provided by the fdqcs.depth, whereas the LOCI_ED procedure is the better method to detect the anomalies in the scenario with dependence. In all the cases, the LOCI_L2 does not have a good performance. This is partly due to the fact that $k=2$ has been chosen (it performs better for $k=3$) and that it presents more difficulties in detecting anomalies when the differences are set more horizontally than vertically. It is also important to note that the benchmark e.depth method has a kappa index of about 0.75 and an accuracy close to 1 when the phase component of the elastic distance is used instead the amplitude, i.e., this method is able to correctly identify almost all the curves. This supports incorporating the phase component in the FD-LOCI in the future.

4. Case Study

In order to illustrate the performance of the algorithm described above, we proceed to apply it to a time series composed of hourly average humidity data (24 h) obtained at the Tixán meteorological station (Chimborazo, Ecuador), monitored by the Alternative Energies and Environment Group (GEAA) of the Escuela Superior Politécnica de Chimborazo (ESPOCH), located in Riobamba (Ecuador). The database contains information in the interval between 2014 and 2019, with overall 52,560 records (hours) corresponding to 2190 days (curves).

Figure 5 shows that the mean hourly humidity variable has a functional nature, considering its behavior over the course of a day. Since the data are collected in a discrete manner, with hourly observations, smoothing methods are applied in order to process the daily mean humidity curves as observations of a functional variable. For this purpose, each day is considered as a function obtained from 24 measurements corresponding to the value of the mean humidity in each hour. Because of the high possibility of periodicity in the data, the smoothing is performed using Fourier basis fitting, as shown in Figure 5. This plot corresponds to the curve for 1 January 2014. On the other hand, it is important to highlight that the anomalous daily humidity curves have been previously identified by experts of the GEAA group, in a total of 57 days, thus working with a controlled sample that allows the evaluation and comparison of different anomaly detection methods.

In order to be able to apply the FD-LOCI algorithm, its parameters must be previously defined. In Section 3, it was observed that the use of a radius that collects 50% of the observations is sufficient to provide good results both for the Type I error estimation and for the power of the test. Therefore, in this particular case, for the identification of anomalies, attending to the results of the simulation study, a radius comprising 50% of the observations ($n_0=1095$) and a value of $\theta =0.78$ is taken. Taking into account the labeling of the anomalous curves, the performance of the FD-LOCI method is evaluated by constructing the confusion matrix, in which the class corresponding to non-anomalous curves is labeled with 0 and those corresponding to anomalies with 1 (see

Table 8. Confusion matrix corresponding to the FD-LOCI application, assuming $\theta =0.78$ and a sampling radius that accounts for 50% of the observations (neighbors), $n_0=1095$ observations.

	0	1
0	2120	22
1	13	35

).

In order to evaluate the FD-LOCI approach, its performance has been compared with that of two competitive methods within the FDA that are based on the calculation of the depth of each functional data. Specifically, a Functional Boxplot (F. Boxplot) has been constructed, using the functions available in the fda package, using the modified band depth (MBD) method [65]. In addition, the Phase I control chart for functional data described in Flores et al. [21] has been applied, based on the procedure defined by Febrero et al. [23] and implemented using the fdqcs.depth function of the qcr package [66] for the 2190 average moisture curves. The results provided by each of the methods, including the present proposal, the FD-LOCI ($\theta =0.78$ and $n_0=1095$), expressed in terms of the number of detected outliers (D.A.) and correctly detected anomalies (C.D.A.), in addition to other goodness-of-classification measures such as the proportion of correct classification (accuracy), sensitivity (ability to detect anomalies), specificity (ability to detect non-anomalies), and the kappa index, can be seen in

Table 9. Performance measures of the methods used to detect anomalies (57 actual anomalies detected by a group of experts). The proportion of correct classification (accuracy), the kappa index, the specificity, the sensibility, and the number of true alarms detected are included.

Method	k Parameter	D.A.	C.D.A.	Accuracy	Kappa	Specificity	Sensitivity
FD-LOCI ($L^2$)	3	47	36	0.9854	0.6849	0.9948	0.6316
	4	129	42	0.9534	0.4311	0.9592	0.7368
	4.5	35	28	0.9836	0.6008	0.9967	0.4912
FD-LOCI (elastic distance)	3	325	41	0.863	0.1783	0.8669	0.7193
	4	32	17	0.9749	0.3702	0.993	0.2982
	4.5	18	12	0.9767	0.3114	0.9972	0.2105
fdqcs.depth		76	35	0.9712	0.5118	0.9808	0.614
F. Boxplot		2	2	0.9749	0.0661	1	0.03509
Elastic Depth		40	24	0.9776	0.4838	0.9925	0.4211

. Following Landis and Koch [67], in absolute terms, the kappa corresponding to the FD-LOCI method indicates that the rating is substantially good (negative values account for no agreement in the rating, 0–0.20 slight, 0.21–0.40 fair, 0.41–0.60 moderate, 0.61–0.80 substantial, and 0.81–1 means almost perfect agreement). If the Fleiss criterion is followed, the classification obtained is fair to good (0.4–0.75). Considering the accuracy index, the best classification is obtained with the FD-LOCI using the $L^2$ metric with $k=3$. Comparable values are obtained with the FD-LOCI (with elastic depth and $k=4$), the F. Boxplot, Elastic Depth, and fdqcs.depth methods. In terms of specificity (ability to detect non-anomalies), all the methods have a very high and similar performance. Regarding the sensibility (ability to detect anomalies), the best method is FD-LOCI ($L^2$) with $k=4$ and FD-LOCI (elastic depth) with $k=3$. In the case of kappa, the highest values are obtained for FD-LOCI ($L^2$). Thus, the method with a best balance to detect anomalies and non-anomalies in this specific case is the proposed FD-LOCI ($L^2$) procedure.

Figure 6 shows all the daily humidity curves belonging to the Tixán meteorological station database. In gray are shown the curves that present a normal behavior (N), while in black are shown those curves correctly identified as anomalies (C.D.A.) and in green are shown those anomalous curves that were not identified as detected anomalies (N.D.A.) using the FD-LOCI method. It is observed that the curves marked in green are in fact similar in shape and magnitude to the common non-anomalous curves, which is the reason why they are not detected using the model.

5. Conclusions

The FD-LOCI algorithm proposes a new methodology for the detection of outliers or anomalies by applying it to functional data. This method is a functional approximation of the LOCI algorithm, in which the distances are calculated in the functional space or Hilbert space, and the classification is performed according to a variable or score obtained from the Multigranular Deviation Factor and the normalized standard deviation.

Simulation studies indicate that the FD-LOCI method performs well in terms of Type I error (proportion of false anomalies) and Type II error (model power) with moderate sample sizes (n $\in \left[50, 100\right]$), moderate to high values for $\theta$ (greater than or equal to 0.78) and radii covering around 70% of the data onwards (being also acceptable with 50% coverages). It is also important to note that the FD-LOCI method has similar power to detect outliers both due to their magnitude and also due to their different shape. Specifically, significantly high power is observed to detect changes in magnitude corresponding to $\eta >0.6$ and of $\delta \ge 1.2$ in shape, for almost any value of $n$ and $n_0$.

The simulation study also shows that the FD-LOCI method is robust against the existence of autocorrelation between the various functional data (dependence between curves), a very common situation in data continuously monitored with respect to time, whether this dependence is negative or positive. In any case, the estimates of the false alarm ratio and the power are slightly better (for lower values of $n_0$) under low dependence conditions. The power of the FD-LOCI model tends to be higher in scenarios with positive dependence than in scenarios defined by negative dependence. It is also noteworthy that the power curves when there is positive dependence are of a similar level and speed of growth to those corresponding to scenarios with independent curves.

In order to improve the performance of the FD-LOCI method in those scenarios defined by shape anomalous curves, the $L^2$ distance is replaced with the elastic distance. The use of FD-LOCI (using elastic distance) improves the performance of the FD-LOCI method to detect anomalies depending on the shape, as the benchmark methods based on the elastic distance such as that labeled as e.depth.

Regarding the application to real data, it is observed that the FD-LOCI algorithm is a very useful tool for the detection of outliers and may present advantages in terms of the number of true anomalies detected, number of false alarms, accuracy, specificity, and sensitivity with respect to other FDA methods of outlier detection based on the calculation of data depth. In fact, we observe that the highest values for accuracy, kappa, sensitivity, and specificity are obtained using the LOCI_L2 method, providing a very good performance. Thus, we can see that there are scenarios where this present approach presents better performance than the other benchmark methodologies.