Abstract
In order to obtain the numerical results of 3D convection-diffusion-reaction problems with variable coefficients efficiently, we select the improved element-free Galerkin (IEFG) method instead of the traditional element-free Galerkin (EFG) method by using the improved moving least-squares (MLS) approximation to obtain the shape function. For the governing equation of 3D convection-diffusion-reaction problems, we can derive the corresponding equivalent functional; then, the essential boundary conditions are imposed by applying the penalty method; thus, the equivalent integral weak form is obtained. By introducing the IMLS approximation, we can derive the final solved linear equations of the convection-diffusion-reaction problem. In numerical examples, the scale parameter and the penalty factor of the IEFG method for such problems are discussed, the convergence is proved numerically, and the calculation efficiency of the IEFG method are verified by four numerical examples.
MSC:
65N22
1. Introduction
The convection-diffusion-reaction equation has been widely used in economics, chemistry, physics, and fluid mechanics fields. Because of the complexity of some problems with various coefficients, exact solutions are usually limited to only a few simplified cases. Therefore, how to obtain the numerical solutions of 3D convection-diffusion-reaction problems [1,2,3,4] with higher computational accuracy and computational speed is an important direction in the research of numerical methods.
As an important numerical method, the finite element method has been widely applied in many science and engineering fields, but the mesh distortion is not avoided when solving large deformation and crack propagation problems. As we know, meshless methods [5,6,7,8,9,10] are based on the scattered point approximation, which can avoid the mesh reconstruction, and, thus, a higher accuracy of the numerical solutions can be obtained.
In recent years, several meshless methods have been used to analyze convection-diffusion-reaction problems, such as the Galerkin and least squares method [11], variational multiscale element-free Galerkin methods [12,13,14], meshfree local Petrov Galerkin methods [15,16], Hermite method [17], and local knot method [18].
As an important meshless method, the element-free Galerkin (EFG) method [19] was invented by Belytschko et al., which uses the moving least-squares (MLS) approximation [20] to construct the shape function. This approximation is based on the ordinary least-squares method, which is the best approximation in mathematics [21], and it has been applied in engineering fields widely [22,23,24]. However, the singular function cannot be avoided and the calculation speed is slower. Afterward, the IMLS approximation [25] was proposed to improve the calculation speed of the MLS approximation by using the orthogonal basis function. Thus, the IEFG method [26,27,28,29,30] was presented for some partial differential equations and mechanics problems, and the higher computational efficiency of the IEFG method was proved.
Generally, we use the penalty method or the Lagrange multiplier method to impose the essential boundary conditions when studying the EFG and the IEFG methods. In order to impose the essential boundary conditions directly, the interpolating MLS approximation based on the singular weight function was inverted [20]. Afterward, the improved interpolating MLS approximation [31] and the improved interpolating EFG method [32,33,34,35] were proposed. Qin et al. [36] studied the interpolating smoothed particle method.
Wang et al. [37] proposed another interpolating MLS method by employing the nonsingular weight function instead of the singular weight function; thus, the corresponding interpolating EFG method [8] was presented by using this improved approximate function. Liu et al. used this interpolating EFG method to solve some large deformation problems [38,39,40].
Combining the complex theory with the MLS approximation, Cheng et al. [41] studied the complex variable moving least-squares (CVMLS) approximation. Based on the conjugate basis function, Bai et al. [42] proposed the improved complex variable moving least-squares (ICVMLS) approximation to obtain the shape functions, which can enhance the efficiency of the MLS approximation. Using the ICVMLS approximation to construct the shape function, the improved complex variable element-free Galerkin (ICVEFG) method was presented for elasticity [42] and wave propagation [43] problems. However, the ICVEFG method cannot be applied to 3D problems, due to the complication of the complex variable shape function.
In this paper, the IEFG method is selected to solve 3D convection-diffusion-reaction problems with variable coefficients. For the governing equation of such problems, we can derive the corresponding equivalent functional; then, the essential boundary conditions are imposed by applying the penalty method; thus, the equivalent integral weak form is obtained. By introducing the IMLS approximation, we can derive the final solved linear equations of convection-diffusion-reaction problems.
In numerical examples, the influence of the scale parameter, penalty factor, and the nodes distribution on numerical accuracy are discussed, the convergence is demonstrated numerically, and the correctness and the efficiency of the IEFG method are verified by four numerical examples. Additionally, it can avoid singular matrices that often exist in the EFG method.
2. The IMLS Approximation
The approximation of a function is
where is the basis function vector, is the basis function number, and
is the coefficient vector of .
In general,
The local approximation is
Define
where is a weighting function, and () are the nodes with influence domains covering the point .
Equation (6) can be written as
where
and
From
we have
where
Equation (12) sometimes forms a singular or ill-conditional matrix. In order to make up for this deficiency, for basis functions
using the Gram–Schmidt process, we can obtain
and
Then, from Equation (12), can be obtained as
where
Substituting Equation (18) into Equation (5), we have
where
is the shape function.
This is the IMLS approximation [25], in which the shape function can be obtained more easily than the MLS approximation. Moreover, the IMLS approximation can also avoid the singular matrix. Thus, it can enhance the computational efficiency of the MLS approximation.
3. The IEFG Method for 3D Steady Convection-Diffusion-Reaction Problems
The equation of 3D steady convection-diffusion-reaction problems is considered as follows:
the boundary conditions are
where and are the given values; is the source term; , ; is the convection velocity in direction ; is the diffusion efficient in the direction ; is the reaction coefficient; is the unit outward normal to boundary in the direction .
For 3D convection-diffusion-reaction equations, the equivalent functional is
The penalty method is selected to impose the essential boundary conditions, using α to refer to the penalty factor; thus, the modified functional is
Let
and the equivalent integral weak form is
where
We select nodes in the 3D domain ; therefore, the corresponding function value is
Thus, we have
where
Substituting Equations (31) and (33) into Equation (28), we have
All integral terms of Equation (36) are analyzed as follows:
where
Substituting Equations (37)–(45) into Equation (36), we have
Let
Because is arbitrary, Equation (55) can be transformed as
This is the IEFG method for 3D convection-diffusion-reaction problems.
4. Numerical Examples
We compute the relative error of the IEFG method for 3D convection-diffusion-reaction problems; thus, the formula is given as
The IEFG and the EFG methods are used to solve these numerical examples. We select regularly distributed nodes, 3 × 3 × 3 Gaussian points are selected in each integral cell, and the linear basis function is selected. The relative error and calculation efficiency of the IEFG and the EFG methods are compared.
The first example is
and the problem domain is Ω = [0,0.5] × [0,0.5] × [0,0.5].
The boundary conditions are
The theoretical result is
In this paper, we should discuss the scale parameter, penalty factor, and convergence.
First, different values of dmax will influence the relative error of the numerical solution. In addition, 11 × 11 × 11 regular nodes, 10 × 10 × 10 integral cells, and the cubic spline function are used, and α = 7.0 × 103. Figure 1 shows the relationship between dmax and the relative error. We can see that if dmax = 1.4~1.5, the relative error is smaller.
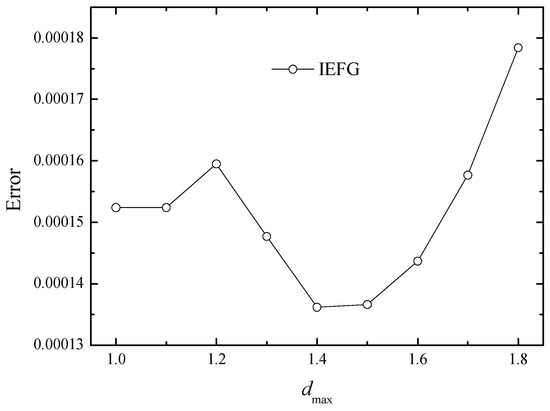
Figure 1.
The relationship between dmax and the relative error.
Secondly, different values of α will influence the relative error of the numerical solution. In addition, 11 × 11 × 11 regular nodes, 10 × 10 × 10 integral cells, and the cubic spline function are used, and dmax = 1.44. Figure 2 shows the relationship between α and the relative error. We can see that when α = 5.0 × 103~1.0 × 104, the relative error is smaller.
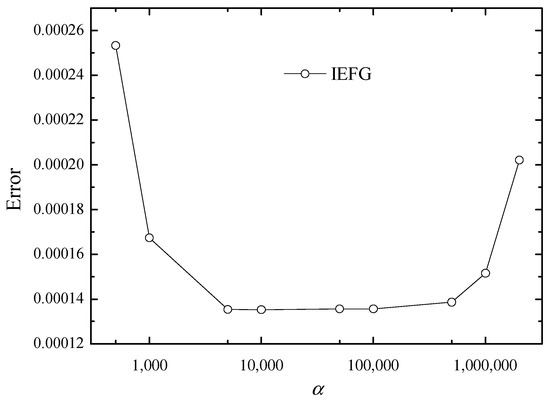
Figure 2.
The relationship between α and the relative error.
In order to demonstrate the convergence of the IEFG method, the distribution of nodes must be discussed. dmax = 1.44, α = 7.0 × 103, and the cubic spline function is used. Table 1 shows the relationship between the node distribution and the relative errors. It is easy to see that with increase in nodes, the relative error shows a decreasing trend. Figure 3 shows the contour plot of nodes, numerical solutions, and the relative errors.

Table 1.
The relative errors and CPU times of the IEFG and the EFG methods with the increase in node distribution.
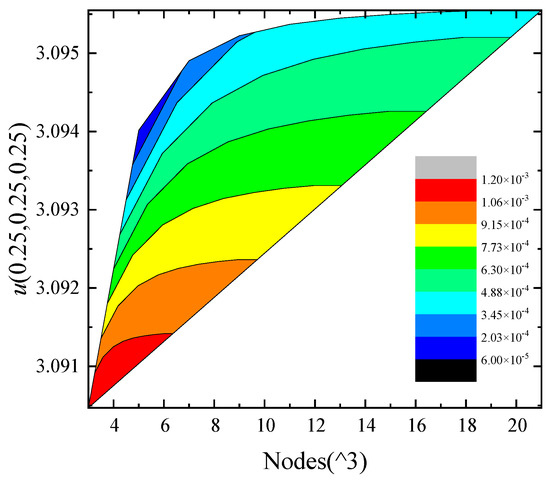
Figure 3.
The contour plot of nodes, numerical solutions, and the relative errors.
In this example, we select 11 × 11 × 11 regular nodes, 10 × 10 × 10 integral cells, and the cubic spline function. In order to obtain the numerical results with smaller relative errors by using the IEFG and the EFG methods, we should select the appropriate parameters in MATLAB codes, dmax = 1.44 and α = 7.0 × 103; thus, the smaller relative errors of the IEFG and the EFG methods are equal to 0.0135%, and the corresponding CPU times are 61.7 s and 64.7 s, respectively.
Figure 4, Figure 5 and Figure 6 and Table 2, Table 3 and Table 4 show the comparison of the numerical solutions of two methods and the analytical ones. We can see that the numerical solutions of both methods are in good agreement with the analytical one.
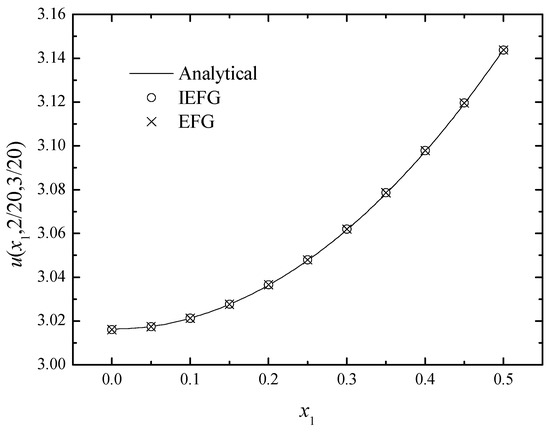
Figure 4.
The comparison of numerical and exact solutions along x1-axis.
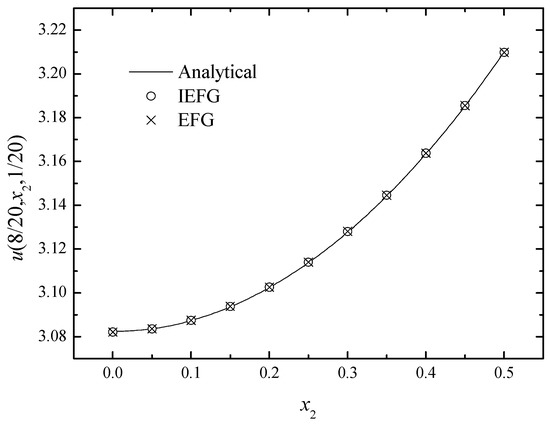
Figure 5.
The comparison of numerical and exact solutions along x2-axis.
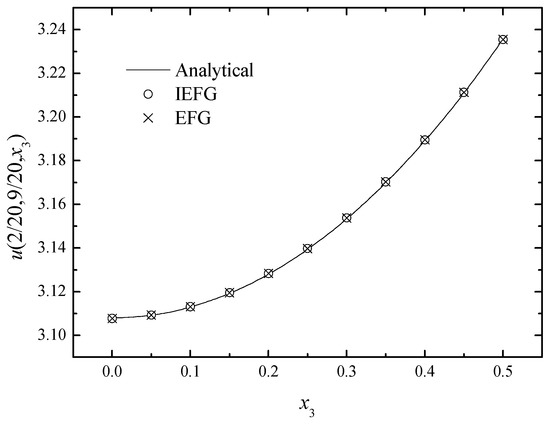
Figure 6.
The comparison of numerical and exact solutions along x3-axis.

Table 2.
The analytical and numerical solutions of u(x1, 2/20, 3/20).

Table 3.
The exact and numerical solutions of u(8/20, x2, 1/20).

Table 4.
The exact and numerical solutions of u(2/20, 9/20, x3).
When using the IEFG method to solve it, calculation resources can be saved although similar relative errors are obtained.
In addition, singular matrices can be avoided if the IEFG method is selected. When the EFG method is used, we select dmax = 1.0; thus, the singular matrices appear. If the IEFG method is selected, α = 7.0 × 103, dmax = 1.0, and the relative error is 0.0152%. The numerical solutions and analytical ones are compared in Figure 7. We can see that numerical solutions are in good agreement with the analytical one.
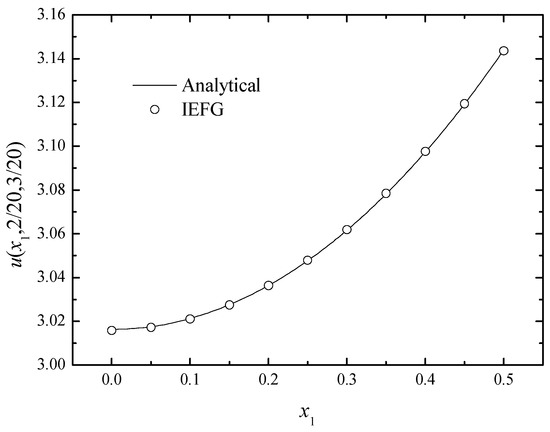
Figure 7.
The comparison of numerical and exact solutions along x1-axis.
The second example [11] is
and the problem domain is Ω = [0,1] × [0,1] × [0,1].
The boundary conditions are
The theoretical result is
In this example, we select 11 × 11 × 11 regular nodes, 10 × 10 × 10 integral cells, and the cubic spline function. In order to obtain the numerical results with smaller relative errors by using the IEFG and the EFG methods, we should select the appropriate parameters in MATLAB codes, α = 7.0 × 102, dmax = 1.21; thus, the smaller relative errors of the IEFG and the EFG methods are equal to 0.0892%, and the corresponding CPU times are 52.8 s and 55.8 s.
Figure 8, Figure 9 and Figure 10 show the comparison of the numerical solutions of two methods and the analytical ones. We can see that the numerical solutions of both methods are in good agreement with the analytical one.
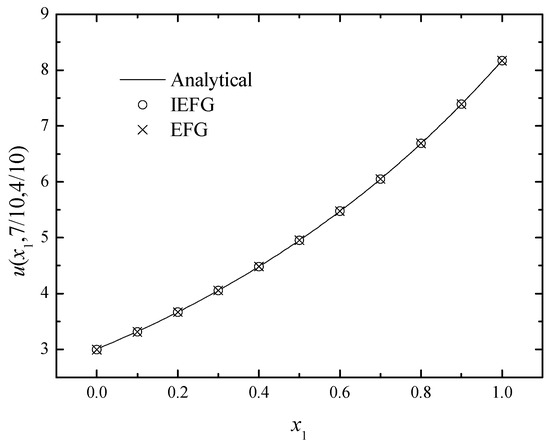
Figure 8.
The comparison of numerical and exact solutions along x1-axis.
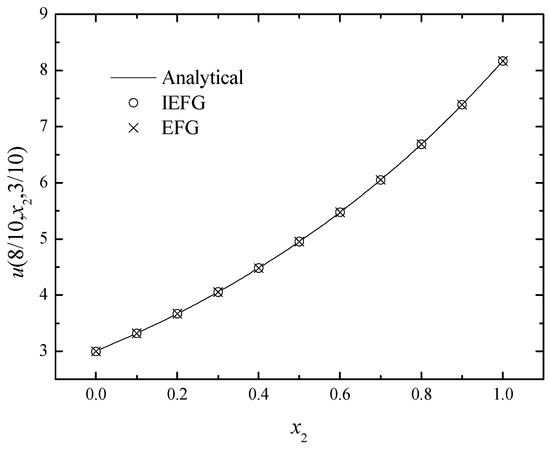
Figure 9.
The comparison of numerical and exact solutions along x2-axis.
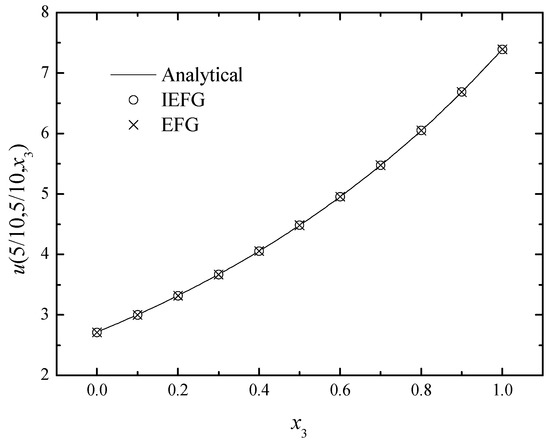
Figure 10.
The comparison of numerical and exact solutions along x3-axis.
From this example, we can see that, under the condition of similar calculation precision, the IEFG method can solve 3D convection-diffusion-reaction problems successfully with less calculation resources.
In addition, singular matrices can be avoided if the IEFG method is selected. When the EFG method is used, we select dmax = 1.0; thus, the singular matrices appear. If the IEFG method is selected, α = 7.0 × 102, dmax = 1.0, and the relative error is 0.0922%. The numerical solutions and analytical ones are compared in Figure 11. We can see that numerical solutions are in good agreement with the analytical one.
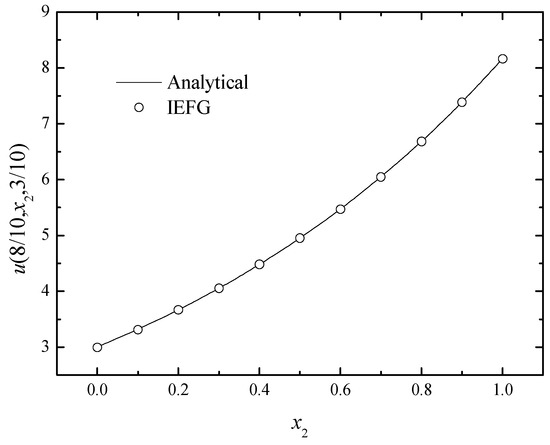
Figure 11.
The comparison of numerical and exact solutions along x2-axis.
The third example [44,45,46] is
where
and the problem domain is Ω = [0,0.5] × [0,0.5] × [0,0.5].
The boundary conditions are
The theoretical result is
In this example, we select Re = 100, 19 × 19 × 19 regular nodes, 18 × 18 × 18 integral cells, and the cubic spline function. In order to obtain the numerical results with smaller relative errors by using the IEFG and the EFG methods, we should select the appropriate parameters in MATLAB codes, dmax = 1.29, α = 1.6 × 103; thus, the smaller relative errors of the IEFG and the EFG methods are equal to 0.2646%, and the corresponding CPU times are 497.7 s and 525.8 s.
Figure 12, Figure 13 and Figure 14 show the comparison of the numerical solutions of two methods and the analytical ones. We can see that the numerical solutions of both methods are in good agreement with the analytical one.
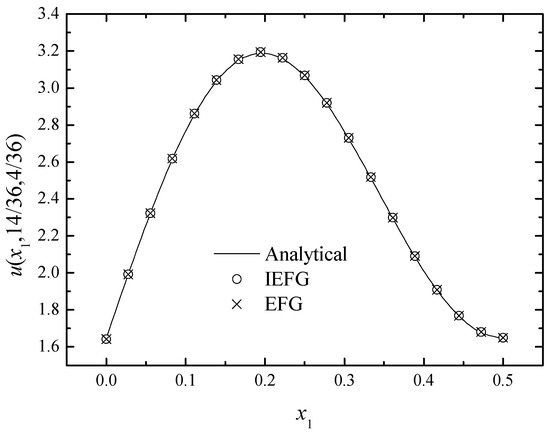
Figure 12.
The comparison of numerical and exact solutions along x1-axis.
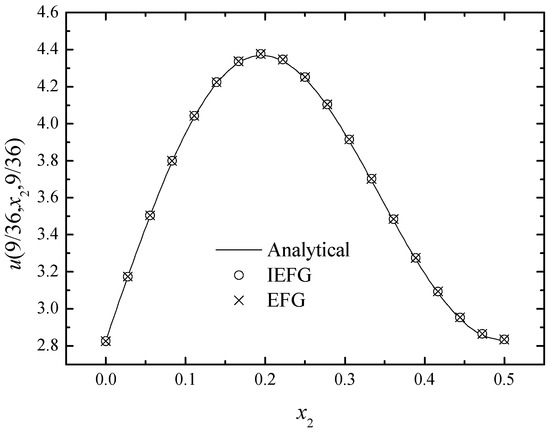
Figure 13.
The comparison of numerical and exact solutions along x2-axis.
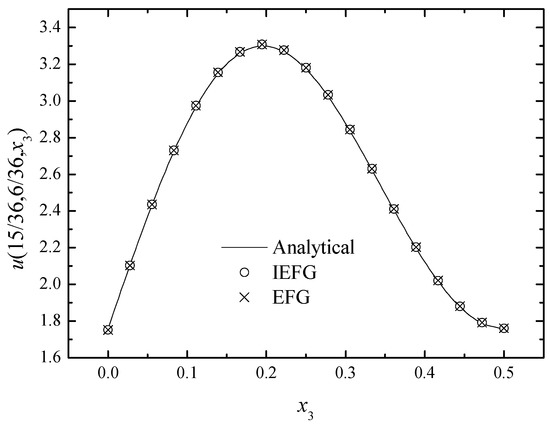
Figure 14.
The comparison of numerical and exact solutions along x3-axis.
From this example, we can see that, under the condition of similar calculation precision, the IEFG method can solve 3D convection-diffusion-reaction problems successfully with less calculation resources.
In addition, singular matrices can be avoided if the IEFG method is selected. When the EFG method is used, we select dmax = 1.0; thus, the singular matrices appear. If the IEFG method is selected, α = 1.6 × 103, dmax = 1.0, and the relative error is 0.2659%. The numerical solutions and analytical ones are compared in Figure 15. We can see that numerical solutions are in good agreement with the analytical one.
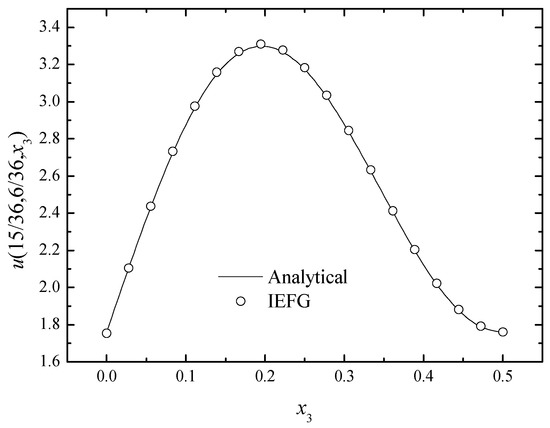
Figure 15.
The comparison of numerical and exact solutions along x3-axis.
The fourth example [46] is
and the problem domain is Ω = [0,1] × [0,1] × [0,1].
The boundary conditions are
The theoretical result is
In this example, we select 15 × 15 × 15 regular nodes, 14 × 14 × 14 integral cells, and the cubic spline function. In order to obtain the numerical results with smaller relative errors by using the IEFG and the EFG methods, we should select the appropriate parameters in MATLAB codes, dmax = 1.21, α = 2.9 × 104; thus, the smaller relative errors of the IEFG and the EFG methods are equal to 0.5147%, and the corresponding CPU times are 111.2 s and 118.3 s.
Figure 16, Figure 17 and Figure 18 show the comparison of the numerical solutions of the two methods and the analytical ones. We can see that the numerical solutions of both methods are in good agreement with the analytical one.
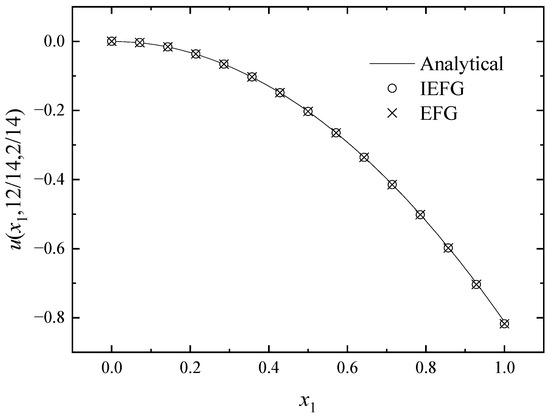
Figure 16.
The comparison of numerical and exact solutions along x1-axis.
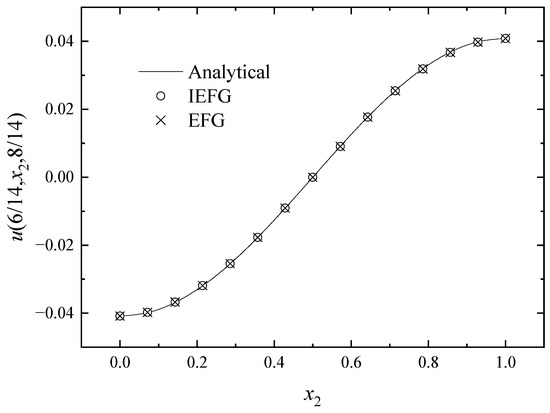
Figure 17.
The comparison of numerical and exact solutions along x2-axis.
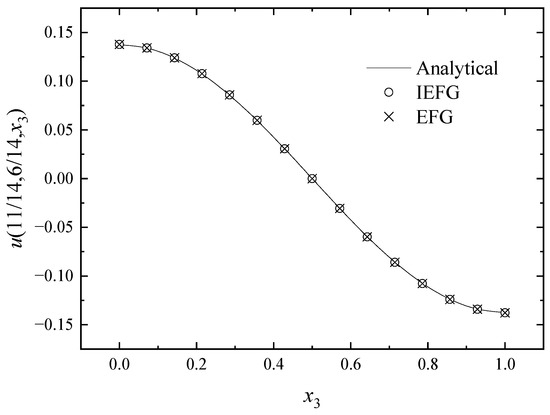
Figure 18.
The comparison of numerical and exact solutions along x3-axis.
We can see that the calculation efficiency can be improved when using the IEFG method to analyze it.
In addition, singular matrices can be avoided if the IEFG method is selected. When the EFG method is used, we select dmax = 1.0; thus, the singular matrices appear. If the IEFG method is selected, α = 2.9 × 104, dmax = 1.0, and the relative error is 0.5346%. The numerical solutions and analytical ones are compared in Figure 19. We can see that numerical solutions are in good agreement with the analytical one.
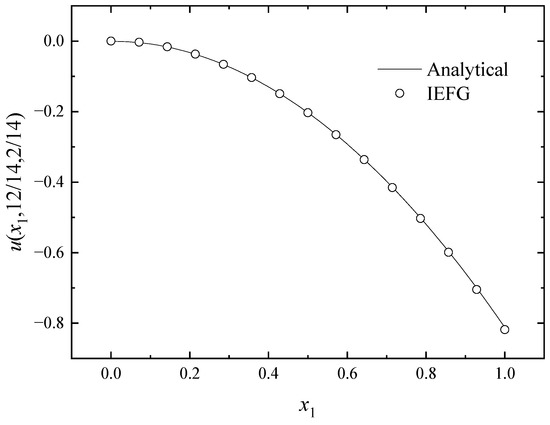
Figure 19.
The comparison of numerical and exact solutions along x1-axis.
5. Conclusions
In this paper, we select the IEFG method instead of the traditional EFG method to solve 3D convection-diffusion-reaction problems with variable coefficients.
The convergence is demonstrated numerically from numerical examples, the correctness of the IEFG method is verified, and we can see that the IEFG method can improve the calculation speed of the EFG method without losing calculation accuracy. Additionally, the IEFG method can avoid singular matrices that often exist in the EFG method.
Our study can extend the scope of application of the IEFG method in science and engineering fields.
Author Contributions
Conceptualization, H.C.; methodology, H.C.; software, H.C.; writing—original draft preparation, H.C.; writing—review and editing, Z.X. and Y.L.; visualization, Z.X.; supervision, H.C.; funding acquisition, H.C. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported by the Natural Science Foundation of Shanxi Province (Grant No. 20210302124388).
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Hidayat, M. Meshless finite difference method with B-splines for numerical solution of coupled advection-diffusion-reaction problems. Int. J. Therm. Sci. 2021, 165, 106933. [Google Scholar] [CrossRef]
- Abdulle, A.; Souza, G. A local adaptive discontinuous Galerkin method for convection-diffusion-reaction equations. J. Comput. Phys. 2022, 451, 110894. [Google Scholar] [CrossRef]
- Mesgarani, H.; Kermani, M.; Abbaszadeh, M. Application of SPD-RBF method of lines for solving nonlinear advection-diffusion-reaction equation with variable coefficients. Int. J. Numer. Methods Heat Fluid Flow 2022, 32, 850–886. [Google Scholar] [CrossRef]
- Al-Bayati, S.A.; Wrobel, L.C. Numerical modelling of convection-diffusion problems with first-order chemical reaction using the dual reciprocity boundary element method. Int. J. Numer. Methods Heat Fluid Flow 2022, 32, 1793–1823. [Google Scholar] [CrossRef]
- Chen, L.; Cheng, Y.M. Reproducing kernel particle method with complex variables for elasticity. Acta Phys. Sin. 2008, 57, 1–10. [Google Scholar] [CrossRef]
- Dai, B.D.; Cheng, Y.M. Local boundary integral equation method based on radial basis functions for potential problems. Acta Phys. Sin. 2007, 56, 597–603. [Google Scholar]
- Cheng, H.; Peng, M.J.; Cheng, Y.M. A hybrid improved complex variable element-free Galerkin method for three-dimensional advection-diffusion problems. Eng. Anal. Bound. Elem. 2018, 97, 39–54. [Google Scholar] [CrossRef]
- Sun, F.X.; Wang, J.F.; Cheng, Y.M. An improved interpolating element-free Galerkin method for elastoplasticity via nonsingular weight functions. Int. J. Appl. Mech. 2016, 8, 1650096. [Google Scholar] [CrossRef]
- Wu, Q.; Peng, M.J.; Cheng, Y.M. The interpolating dimension splitting element-free Galerkin method for 3D potential problems. Eng. Comput. 2022, 38, 2703–2717. [Google Scholar] [CrossRef]
- Peng, P.P.; Cheng, Y.M. Analyzing three-dimensional wave propagation with the hybrid reproducing kernel particle method based on the dimension splitting method. Eng. Comput. 2022, 38, 1131–1147. [Google Scholar] [CrossRef]
- Romão, E.C.; de Moura, L.F.M. Galerkin and Least Squares Methods to Solve a 3D Convection-Diffusion-Reaction Equation with Variable Coefficients. Numer. Heat Transf. Part A Appl. 2012, 61, 669–698. [Google Scholar] [CrossRef]
- Zhang, X.H.; Xiang, H. Variational multiscale element free Galerkin method for convection-diffusion-reaction equation with small diffusion. Eng. Anal. Bound. Elem. 2014, 46, 85–92. [Google Scholar] [CrossRef]
- Zhang, T.; Li, X.L. A variational multiscale interpolating element-free Galerkin method for convection-diffusion and Stokes problems. Eng. Anal. Bound. Elem. 2017, 82, 185–193. [Google Scholar] [CrossRef]
- Cao, X.T.; Zhang, X.H.; Shi, X.T. An adaptive variational multiscale element free Galerkin method based on the residual-based a posteriori error estimators for convection-diffusion-reaction problems. Eng. Anal. Bound. Elem. 2022, 136, 238–251. [Google Scholar] [CrossRef]
- Li, J.W.; Qiao, Y.Y.; Zhai, S.Y.; Feng, X.L. Meshless local Petrov Galerkin method for 2D/3D nonlinear convection-diffusion equations based on LS-RBF-PUM. Numer. Heat Transf. Part B Fundam. 2018, 74, 450–464. [Google Scholar] [CrossRef]
- Li, J.W.; Feng, X.L.; He, Y.N. RBF-based meshless local Petrov Galerkin method for the multi-dimensional convection-diffusion-reaction equation. Eng. Anal. Bound. Elem. 2019, 98, 46–53. [Google Scholar] [CrossRef]
- Chang, J.Y.; Chen, R.Y.; Tsai, C.C. Hermite method of approximate particular solutions for solving time-dependent convection-diffusion-reaction problems. Mathematics 2022, 10, 188. [Google Scholar] [CrossRef]
- Wang, F.J.; Wang, C.; Chen, Z.T. Local knot method for 2D and 3D convection-diffusion-reaction equations in arbitrary domains. Appl. Math. Lett. 2020, 105, 106308. [Google Scholar] [CrossRef]
- Belytschko, T.; Lu, Y.Y.; Gu, L. Element-free Galerkin Methods. Int. J. Numer. Methods Eng. 1994, 37, 229–256. [Google Scholar] [CrossRef]
- Lancaster, P.; Salkauskas, K. Surfaces generated by moving least squares methods. Math. Comput. 1981, 37, 141–158. [Google Scholar] [CrossRef]
- Cheng, J. Mathematical models and data analysis of residential land leasing behavior of district governments of Beijing in China. Mathematics 2021, 9, 2314. [Google Scholar] [CrossRef]
- Cheng, J.; Xie, Y.; Zhang, J. Industry structure optimization via the complex network of industry space: A case study of Jiangxi Province in China. J. Clean. Prod. 2022, 338, 130602. [Google Scholar] [CrossRef]
- Cheng, J.; Luo, X.W. Analyzing the land leasing behavior of the government of Beijing, China, via the multinomial logit model. Land 2022, 11, 376. [Google Scholar] [CrossRef]
- Cheng, J. Residential land leasing and price under public land ownership. J. Urban Plan. Dev. 2021, 147, 0502100. [Google Scholar] [CrossRef]
- Cheng, Y.M.; Chen, M.J. A boundary element-free method for linear elasticity. Acta Mech. Sin. 2003, 35, 181–186. [Google Scholar]
- Zhang, Z.; Zhao, P.; Liew, K.M. Analyzing three-dimensional potential problems with the improved element-free Galerkin method. Comput. Mech. 2009, 44, 273–284. [Google Scholar] [CrossRef]
- Yu, S.Y.; Peng, M.J.; Cheng, H.; Cheng, Y.M. The improved element-free Galerkin method for three-dimensional elastoplasticity problems. Eng. Anal. Bound. Elem. 2019, 104, 215–224. [Google Scholar] [CrossRef]
- Zheng, G.D.; Cheng, Y.M. The improved element-free Galerkin method for diffusional drug release problems. Int. J. Appl. Mech. 2020, 12, 2050096. [Google Scholar] [CrossRef]
- Cheng, H.; Zheng, G.D. Analyzing 3D advection-diffusion problems by using the improved element-free Galerkin method. Math. Probl. Eng. 2020, 2020, 4317538. [Google Scholar] [CrossRef]
- Cheng, H.; Peng, M.J. The improved element-free Galerkin method for 3D Helmholtz equations. Mathematics 2022, 10, 14. [Google Scholar] [CrossRef]
- Ren, H.P.; Cheng, Y.M.; Zhang, W. Researches on the improved interpolating moving least-squares method. Chin. J. Eng. Math. 2010, 27, 1021–1029. [Google Scholar]
- Ren, H.P.; Cheng, Y.M. The interpolating element-free Galerkin (IEFG) method for two-dimensional elasticity problems. Int. J. Appl. Mech. 2011, 3, 735–758. [Google Scholar] [CrossRef]
- Liu, D.; Cheng, Y.M. The interpolating element-free Galerkin method for three-dimensional transient heat conduction problems. Results Phys. 2020, 19, 103477. [Google Scholar] [CrossRef]
- Wu, Q.; Liu, F.B.; Cheng, Y.M. The interpolating element-free Galerkin method for three-dimensional elastoplasticity problems. Eng. Anal. Bound. Elem. 2020, 115, 156–167. [Google Scholar] [CrossRef]
- Wu, Q.; Peng, P.P.; Cheng, Y.M. The interpolating element-free Galerkin method for elastic large deformation problems. Sci. China Technol. Sci. 2021, 64, 364–374. [Google Scholar] [CrossRef]
- Qin, Y.X.; Li, Q.Y.; Du, H.X. Interpolating smoothed particle method for elastic axisymmetrical problem. Int. J. Appl. Mech. 2017, 9, 1750022. [Google Scholar] [CrossRef]
- Wang, J.F.; Sun, F.X.; Cheng, Y.M. An improved interpolating element-free Galerkin method with nonsingular weight function for two-dimensional potential problems. Chin. Phys. B 2012, 21, 090204. [Google Scholar] [CrossRef]
- Liu, F.B.; Cheng, Y.M. The improved element-free Galerkin method based on the nonsingular weight functions for elastic large deformation problems. Int. J. Comput. Mater. Sci. Eng. 2018, 7, 1850023. [Google Scholar] [CrossRef]
- Liu, F.B.; Wu, Q.; Cheng, Y.M. A meshless method based on the nonsingular weight functions for elastoplastic large deformation problems. Int. J. Appl. Mech. 2019, 11, 1950006. [Google Scholar] [CrossRef]
- Liu, F.B.; Cheng, Y.M. The improved element-free Galerkin method based on the nonsingular weight functions for inhomogeneous swelling of polymer gels. Int. J. Appl. Mech. 2018, 10, 1850047. [Google Scholar] [CrossRef]
- Cheng, Y.M.; Peng, M.J.; Li, J.H. The complex variable moving least-square approximation and its application. Acta Mech. Sin. 2005, 37, 719–723. [Google Scholar]
- Bai, F.N.; Li, D.M.; Wang, J.F.; Cheng, Y.M. An improved complex variable element-free Galerkin method for two-dimensional elasticity problems. Chin. Phys. B 2012, 21, 020204. [Google Scholar] [CrossRef]
- Cheng, H.; Peng, M.J.; Cheng, Y.M. Analyzing wave propagation problems with the improved complex variable element-free Galerkin method. Eng. Anal. Bound. Elem. 2019, 100, 80–87. [Google Scholar] [CrossRef]
- Lin, J.; Reutskiy, S. A cubic B-spline semi-analytical algorithm for simulation of 3D steady-state convection-diffusion-reaction problems. Appl. Math. Comput. 2020, 371, 124944. [Google Scholar] [CrossRef]
- Mohanty, R.K.; Setia, N. A new high order compact off-step discretization for the system of 3D quasi-linear elliptic partial differential equations. Appl. Math. Model. 2013, 37, 6870–6883. [Google Scholar] [CrossRef]
- Aziz, I.; Asif, M. Haar wavelet collocation method for three-dimensional elliptic partial differential equations. Comput. Math. Appl. 2017, 73, 2023–2034. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).