A Chaotic Image Encryption Method Based on the Artificial Fish Swarms Algorithm and the DNA Coding

Abstract

Aiming at the problems of small key space and weak resistance to differential attacks in existing encryption algorithms, we proposed a chaotic digital image encryption scheme based on an optimized artificial fish swarm algorithm and DNA coding. First, the key is associated with the ordinary image pixel through the MD5 hash operation, and the hash value generated by the ordinary image is used as the initial value of the hyper-chaotic system to increase the sensitivity of the key. Next, the artificial fish school algorithm is used to scramble the positions of pixels in the block. In addition, scrambling operation between blocks is proposed to increase the scrambling effect. In the diffusion stage, operations are performed based on DNA encoding, obfuscation, and decoding technologies to obtain encrypted images. The research results show that the optimized artificial fish swarm algorithm has good convergence and can obtain the global optimal solution to the greatest extent. In addition, simulation experiments and security analysis show that compared with other encryption schemes, the scheme proposed in this paper has a larger key space and better resistance to differential attacks, indicating that the proposed algorithm has better encryption performance and higher security.

1. Introduction

The popularity of the network and the wide application of information technology have made us more aware of the importance of safe data transmission. As an important carrier of information transmission, digital images can be classified into two ways to ensure their information security: information hiding [1,2,3,4,5,6] and encryption. Image encryption originated from the early classical encryption theory [7,8,9,10], but because digital images and texts have different storage methods and their inherent characteristics, such as high correlation, high redundancy and a large amount of data between adjacent pixels [11], classic encryption methods such as DES and RSA are no longer applicable [12,13]. Therefore, many scholars have proposed many encryption schemes [14,15,16,17]. These technologies mainly rely on DNA computing [18,19,20] cellular automata [21,22,23], chaotic systems [24,25,26], wavelet compression [27,28], and other methods.

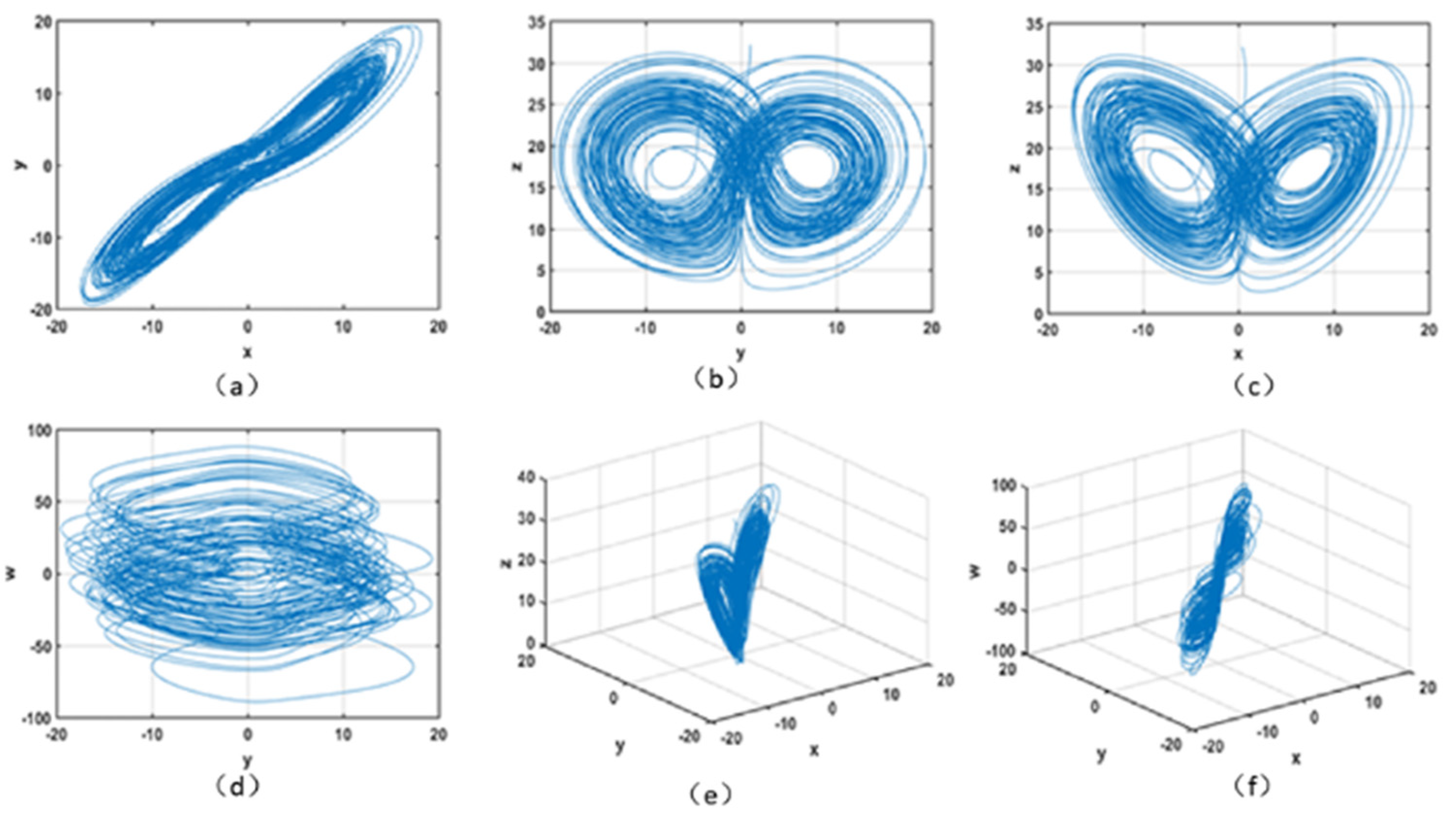
Chaos research has made great progress in many aspects [29,30,31,32,33,34,35,36,37,38,39,40,41,42,43]. Due to the characteristics of chaos, such as high sensitivity to initial conditions and control parameters, and inherent randomness, chaos meets the requirements of image encryption. Generally, this kind of encryption scheme includes two important steps: scrambling and diffusion. Since Matthews et al. [44] proposed that one-dimensional chaotic maps can be used as a time pad for encrypting messages, they proposed various image encryption algorithms based on chaotic systems. For example, Fuh GwoJeng et al. [45] and others proposed an image encryption scheme based on a hype-chaos, aiming at the security loopholes in the scheme proposed by Gao He Chen [46] and Rhouma and Belghith [47]. Liu et al. [48] showed image encryption based on one-time key and two powerful chaotic maps. Wang et al. [49] proposed a high-dimensional chaotic image encryption system with a perceptron model. Complex chaotic systems such as high-dimensional chaotic systems or hyper-chaotic systems can generate chaotic sequences with better randomness, which increases the security of encryption schemes.

In recent years, due to its outstanding performance in parallelism, robustness, evolution, and other aspects, the bionic swarm intelligence optimization algorithm has in-depth research in human intelligence such as perception, recognition, and associative memory [50,51,52]. It has also attracted the attention of many scholars in the field of image encryption. For example, Wang et al. [53] proposed an optimization algorithm for an image encryption scheme combined with DNA coding. They selected the key sequence through PSO and used DNA mask and plaintext DNA coding of quick shuffle to operate, and formed an encryption system. Enayatifar R et al. [54] proposed an image encryption algorithm based on a DNA chaos map and genetic algorithm (GA). By improving the quality of the DNA mask, the best mask compatible with pure images was obtained. Wang, J, et al. [55] proposed a new framework using the population-based particle swarm optimization algorithm to improve the speed of encryption. However, because the correlation between the scrambling phase key and the plaintext image is not close, the encryption scheme can’t resist the differential attack well, the scheme can’t well resist the differential attack. In the above algorithms, a common problem is that the encryption scheme does not have enough key space, and the generated data has low pseudo-randomness and ergodicity, leading to insufficient security performance of the scheme. In addition, the traditional swarm intelligence algorithm is trapped in local optimization due to premature convergence and parameter selection.

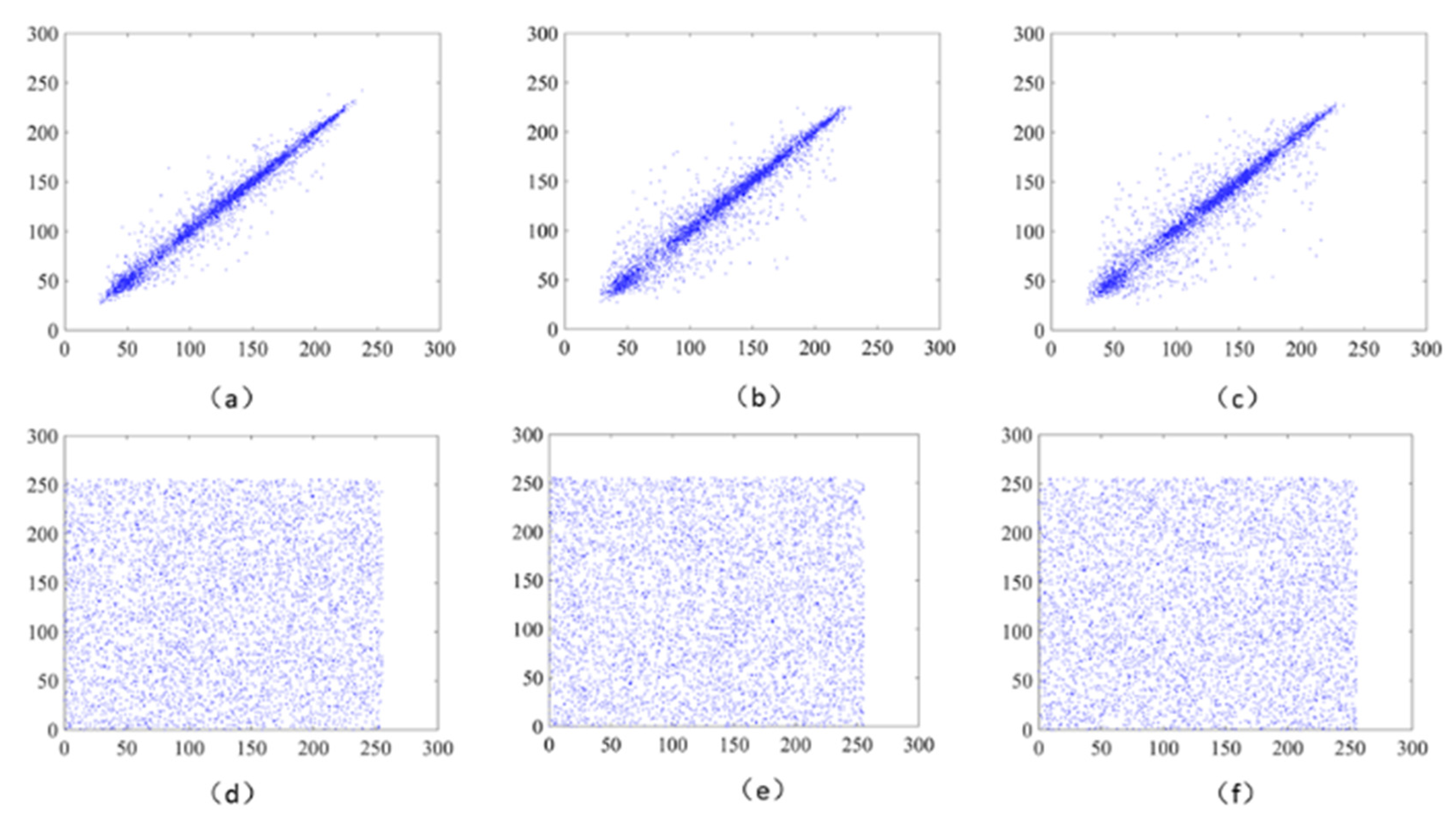
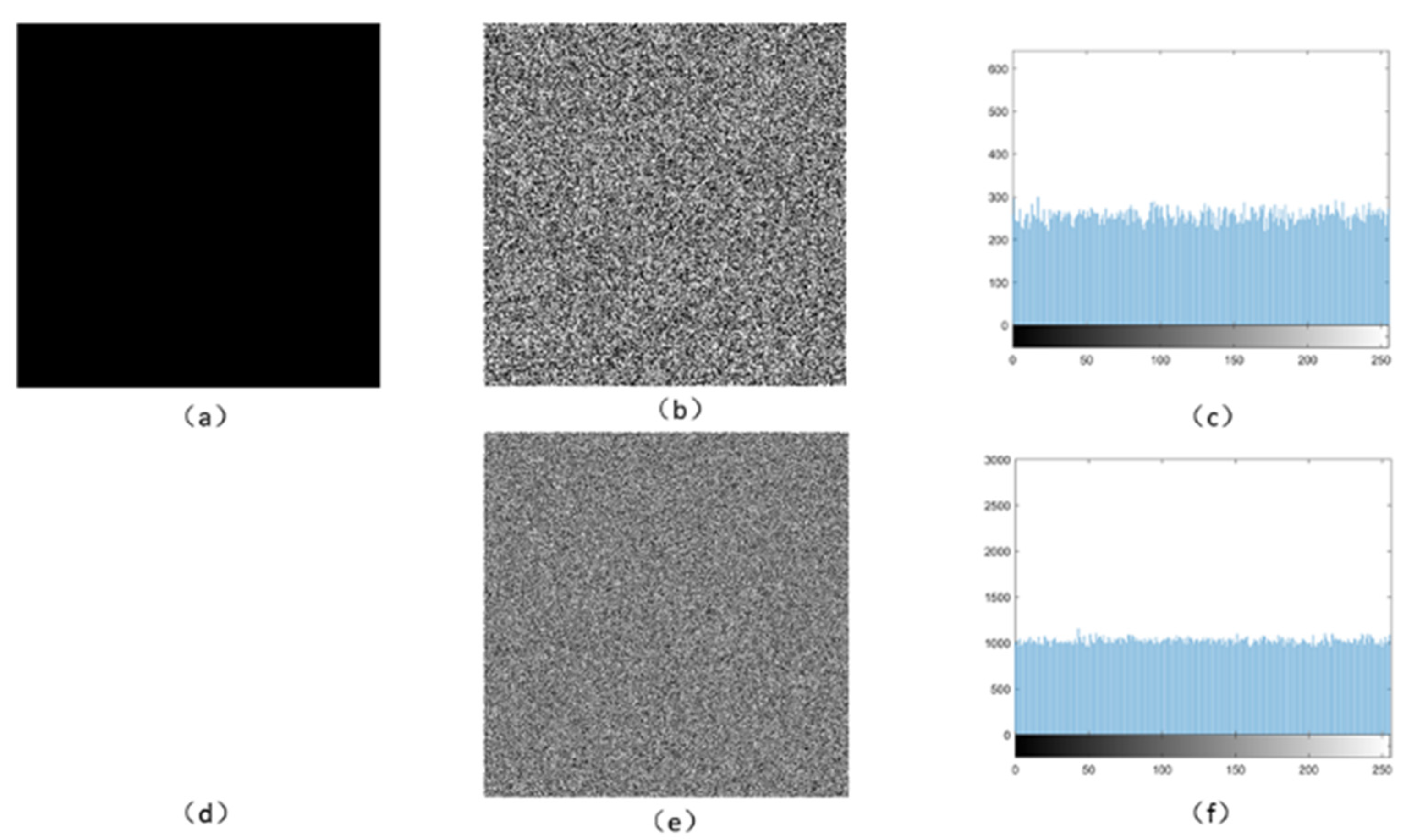
For the purpose of overcoming the above problems, we propose a digital chaotic image encryption scheme based on an optimized artificial fish swarm algorithm and DNA coding. First, the image is scrambled by the artificial fish school algorithm, and then Chen’s hyper-chaos system is used to obtain the initial key sequence through iteration, which is diffused by DNA XOR operation, and finally, the image encryption is completed Therefore, the proposed scheme can not only change the histogram of the image, but also break the high correlation between adjacent pixels. At the same time, associating the initial parameters of Chen chaotic system with plaintext images helps to obtain the unique key stream of each image, which ensures that the encryption scheme proposed in this paper is sufficiently sensitive to plaintext, and have the advantages of effectively resisting plaintext attacks and selecting plaintext attacks. The extensive experimental results of a histogram, adjacent pixel correlation, entropy, sensitivity, key space, robustness, randomness, known and selected plaintext attacks, etc. show that the scheme meets the security requirements of the encryption algorithm, and the encryption effect is satisfactory.

The rest of the study is arranged as follows. In the Section 2, we introduce the Chen hyper-chaos system, and evaluate its dynamic behavior through the Lyapunov exponent, artificial fish swarm algorithm, and relevant knowledge of DNA coding technology. The Section 3 introduces the recommended encryption scheme. Section 4 introduces the simulation results and security analysis of the image. Section 5 discusses the defects of the algorithm. Finally, in the Section 6, the research content is summarized.

2. Relevant Knowledge

2.1. Chen’s Hyper-Chaotic System

Compared with a chaotic system, a hyper-chaotic system has multiple positive Lyapunov exponents, so the motion behavior is more difficult to predict, has more abundant dynamic behavior, and meets the requirements of digital image encryption. Therefore, Chen’s hyper-chaotic system is selected in our algorithm [56]. The dynamic equation of the system is shown in Equation (1).

$$\{\begin{array}{c}\dot{x}=a\left(x-y\right)+w,\hfill \\ \dot{y}=bx+cy-xz,\hfill \\ \dot{z}=xy-dz,\hfill \\ \dot{w}=yz+rw,\hfill \end{array}$$

(1)

where $a=35, b=3, c=10, d=7, 0.1085\le r\le 0.1798$, the system is in hyper-chaotic state. The initial condition is set as (0.3838, 0.9876, 32.1234, 0.6565), and the time step of iteration is 0.001, Figure 1 shows the phase the diagram of the system.

Figure 1. The phase diagram of the proposed hyper-chaotic system: (a) x–y phase diagram; (b) x–z phase diagram; (c) y–z phase diagram; (d) y–w phase diagram; (e) x–y–z phase diagram; (f) x–y–w phase diagram.

2.2. Artificial Fish Swarm Algorithm

The artificial fish swarm algorithm (AFSA) is a new swarm intelligence algorithm proposed by Li Xiaolei in 2002. It mainly simulates the foraging, grouping, and rear-end behavior of fish swarms by constructing artificial fish swarms, and adopts a bottom-up optimization mode to start from the underlying behavior of constructing individuals, so as to find the behavior of the maximum food density in space.

The external perception of artificial fish is achieved by relying on vision, and the following methods are used in this model to achieve a virtual vision of artificial fish:

$$X_v=X+Visuanl\times Rand(),$$

(2)

$$X_{next}=X+X_V-X\parallel X_V-X\parallel \times Step\times Rand().$$

(3)

where $Rand()$ is a random function used to generate random numbers between 0 and 1, and Step is a step size. Figure 2 shows a hypothetical artificial fish with a continuous field of view. The area it can see is a circular area with a certain distance as the radius and the current position $X_i$ as the center. The location $X_j$ is the point of view it patrols at one time. If there is more food in this place than in the previous place, it is decided that the random number of advance steps to this place will reach the location $X_{next}$. In addition, the AFSA has five basic parameters: the moving step of artificial fish, the visual field of artificial fish visual, the maximum number of attempts of artificial fish for each try-number, and the crowding factor $\mathsf{\delta }$ of artificial fish. The following briefly describes the four behaviors of artificial fish.

Figure 2. Continuous visual field of artificial fish.

• Foraging behavior: It is generally believed that fish sense food or food concentration in water through vision or taste to choose the direction of action. Set the state of the current artificial fish, and randomly select another state within its visual range. If the objective function of the obtained state is larger than the current state, it will move one step closer to the latter state; otherwise, it will reselect the new state.
  Algorithm description: Equation (4) describes that the artificial fish $X_i$ randomly selects a state $X_j$ in its field of view.

  $$X_j=X_i+Visuanl\times Rand(),$$

  (4)
  Calculate the objective function values $Y_i$ and $Y_j$ of $X_i$ and $X_j$ respectively. If $Y_j$ is found to be better than $Y_i$, $X_i$ moves one step in the direction of $X_j$:

  $$X_i^{t+1}=X_i^t+\frac{X_j-X_i^t}{||X_j-X_i^t||}\times Step\times Rand(),$$

  (5)

  otherwise, $X_i$ will continue to select the state $X_j$ in its field of view, judge whether the advance condition is met, and if the advance condition is still not met after repeated attempts of try_number, execute a random behavior. Algorithm 1 shows the pseudo-code snippets for the foraging behavior.

  Algorithm 1 Foraging behavior Pseudo-code.

  for    i = 1:N

  for j = 1:Try_number

  Xj = x(i) + Visual × rand();

  If f(X(j)) < f(x(i))

  X_next = x(i) + rand()× step ×(Xj − x(i))/norm(Xj − x(i));

  break;

  else

  X_next = x(i) + step × rand();

  end

  end

  end

• Group behavior: the artificial fish explores the number of partners in the current neighborhood, calculates the central position of the partners, and then compares the newly obtained objective function of the central position with the objective function of the current position. If the objective function of the central position is better than the objective function of the current position and is not very crowded, the current position moves one step toward the central position, otherwise, the foraging behavior is executed.
  Three rules must be observed when fish flock together: first, try to move towards the center of the neighboring partners; second, avoid overcrowding; and third, try to be consistent with the average direction of the neighboring partners.
  Algorithm description: the artificial fish $X_i$ searches for the number of partners nf and the center position $X_c$ in the current field of view $\left(d_{ij}<visual\right)$, if $\raisebox{1ex}{$Y_C$}\!\left/ \!\raisebox{-1ex}{$nf$}\right.<\delta \times Y_i$ (where $Y_C$ and $Y_i$ are the fitness values of $X_c$ and $X_i$, respectively), it indicates that the partner’s central location is better and less crowded, and $X_i$ moves one step toward the partner’s central location:

  $$X_i^{t+1}=X_i^t+\frac{X_j-X_i^t}{||X_j-X_i^t||}\times Step\times Rand(),$$

  (6)
  Otherwise, the foraging behavior will be executed. Algorithm 2 shows the pseudo-code snippets for the group behavior.

  Algorithm 2 Group behavior Pseudo-code.

  nf = 0; X_inside = 0;

  for    i = 1:N

  for j = 1:N

  if norm(x(j) − x(i)) < Visual

  nf = nf + 1;

  X_inside = X_inside + x(j);

  end

  X_inside = X_inside − x(i);

  nf = nf − 1;

  Xc = X_inside/nf;

  if    f(Xc)/nf < δ× f(x(i))

  x_next = x(i) + rand * Step * (Xc − x(i))/norm(Xc − x(i)); else Execute foraging behavior;

  end

  end

  end

• Rear-end behavior: It refers to the behavior of a fish moving in the optimal direction within its field of view. The artificial fish $X_i$ searches for the individual $X_j$ with the highest fitness in its field of view ($d_{ij}<visual$), and its fitness value is $Y_j$, and explores the number of partners nf in the field of view of the artificial fish $X_i$, if $\raisebox{1ex}{$Y_j$}\!\left/ \!\raisebox{-1ex}{$nf$}\right.<\delta \times Y_i$, indicating that $X_j$ is in a better state and is not too crowded, $X_i$ moves one step toward $X_j$, otherwise it executes foraging behavior. Algorithm 3 shows the pseudo-code snippets for the Rear-end behavior.

  Algorithm 3 Rear-end behavior Pseudo-code.

  Y_max = inf; nf = 0;

  for i = 1:N

  for j = 1:N

  if norm(x(j) − x(i)) < Visual && f(x(j)) < Y_max

  X_max = x(j);

  Y_max = f(x(j));

  end

  end

  for j = 1:N

  if(norm(x(j) − X_max) < Visual)

  nf = nf + 1;

  end

  end

  nf = nf − 1;

  if Y_max/nf < delta × f(x(i))

  x_next = x(I,:) + rand × Step. × (temp_maxX − x(i,:)) ./ norm(temp_maxX − x(i,:));

  else

  Execute foraging behavior;

  end

  end

• Random behavior: it is the default behavior of foraging behavior, which refers to the random movement of artificial fish in the field of vision. When food is found, it will move rapidly in the direction of gradually increasing food. This is to find food points or partners in a wider range.

  $$X_i^{t+1}=X_i^t+Visuanl\times Rand(),$$

  (7)

2.3. DNA Coding and Decoding Rules

A DNA sequence consists of four nucleic acid bases: A(adenine), C(cytosine), G(guanine), and T(thymine). ‘A’ and ‘T’ as well as ‘G’ and ‘C’ are complementary. As ‘0’ and ‘1’ are complementary in the binary system, ‘00’ and ‘11’ are complementary. In addition, ‘01’ and ‘10’ are also complementary. There are 24 types of encoding rules using the four nucleic acid bases (A, C, G, and T) to encode ‘00’, ‘01’, ‘10’, and ‘11’. However, only 8 of them satisfy the Watson-Crick complementary rule as shown in Table 1 [57]. Note that DNA decoding rule is the reverse operation of the DNA encoding rule.

Table 1. DNA encoding and decoding rules.

Rules	1	2	3	4	5	6	7	8
A	00	00	01	01	10	10	11	11
T	11	11	10	10	01	01	00	00
C	01	10	00	11	00	11	01	10
G	10	01	11	00	11	00	10	01

For example, the greyscale value of a pixel is ‘126’, and the corresponding binary number is ‘01111110’. The DNA sequence ‘GTTC’ is obtained using DNA encoding rule 2. Inversely, if the DNA sequence is ‘TGCA’, the binary number can be obtained by rule 8 (the decoding rule is 8), that is ‘00011011’, the decimal number is ‘78’, and this is the decoding process of the DNA sequence.

DNA XOR Algebraic Operation

In this study, DNA XOR operation is used for image diffusion. DNA XOR operation is the same as binary XOR operation. An example of a DNA XOR operation is provided. Using Table 2, the XOR result of DNA sequences “AGCT” and “TGAC” is “TACG”.

Table 2. DNA XOR operation rules.

XOR	A	G	C	T
A	A	G	C	T
G	G	A	T	C
C	C	T	A	G
T	T	C	G	A

3. Encryption and Decryption Process

We assume the size of the plain image A is $\left(\mathrm{M}\times \mathrm{N}\right)$, and divide it into $\left(\mathrm{M}\times \mathrm{N}\right)/\left(\mathrm{m}\times \mathrm{n}\right)$ blocks by $\left(\mathrm{m}\times \mathrm{n}\right)$. Figure 3 gives the flow chart of our proposed encryption scheme.

Figure 3. The flow chart of the scheme.

3.1. The Generation of Initial Values of the Hyper-Chaotic System

No matter what the size of the input ordinary image is, a 128-bit summary will be obtained after the MD5 hash. Even if there is only a one-bit difference, the generated summary will be completely different. Therefore, this step is to associate the key of the algorithm with the plaintext image, which can increase the security of the algorithm. Divide the 128-bit summary into 8 blocks by Equation (8).

$$\mathrm{K}=k_1,k_2\dots k_7,k_8,$$

(8)

According to the following calculation method, four initial values of Chen’s hyper-chaotic system are obtained. Among them, $x_0,y_0,z_0,w_0$ are the given initial value, $\oplus$ is for operation.

$$\{\begin{array}{c}{x}_0^{\prime }=x_0+\frac{k_1\oplus k_2}{256},\hfill \\ y_0^{\prime }=y_0+\frac{k_3\oplus k_4}{256},\hfill \\ z_0^{\prime }=z_0+\frac{k_5\oplus k_{60}}{256}, \hfill \\ w_0^{\prime }=w_0+\frac{k_7\oplus k_8}{256},\hfill \end{array}$$

(9)

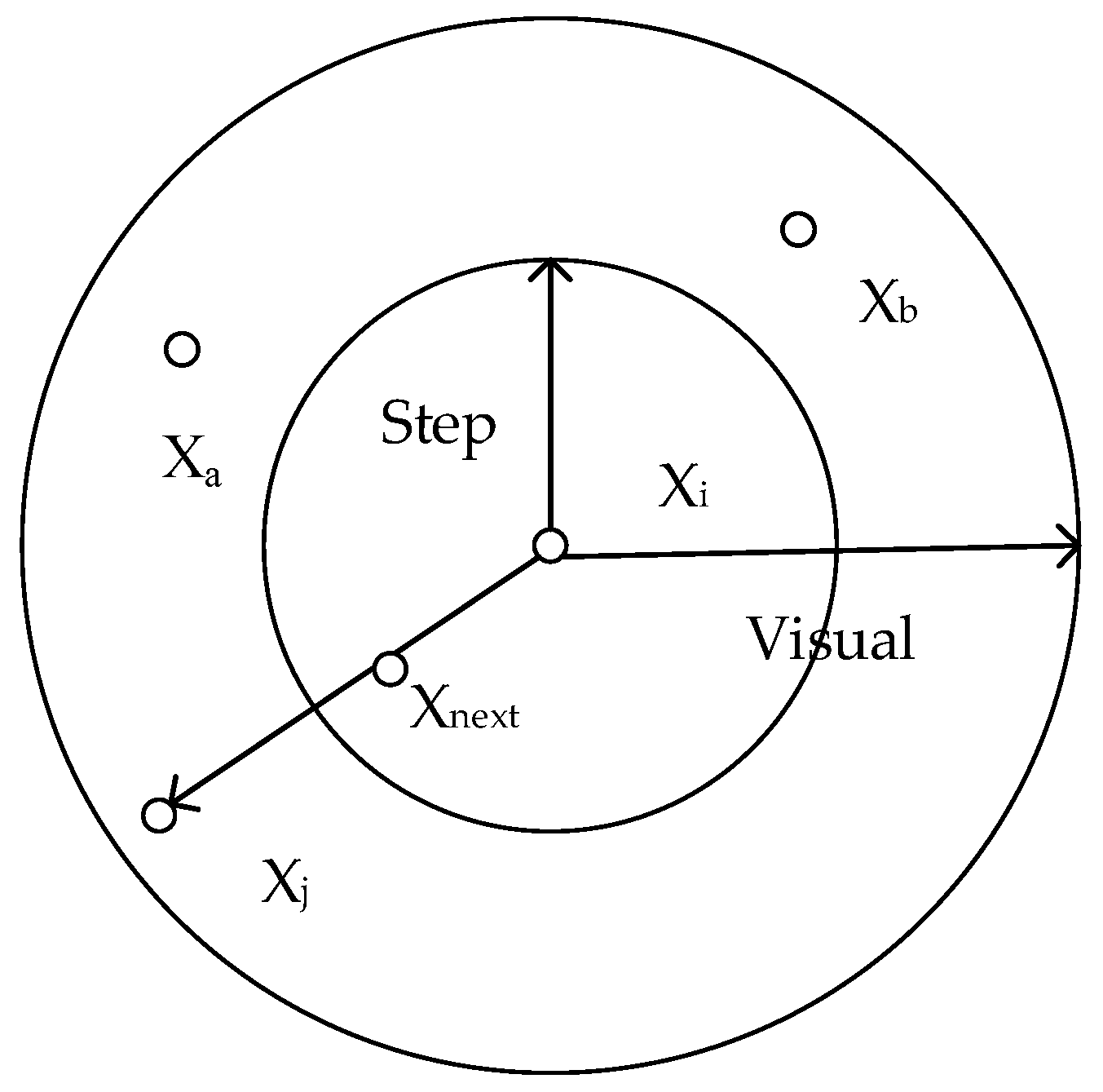
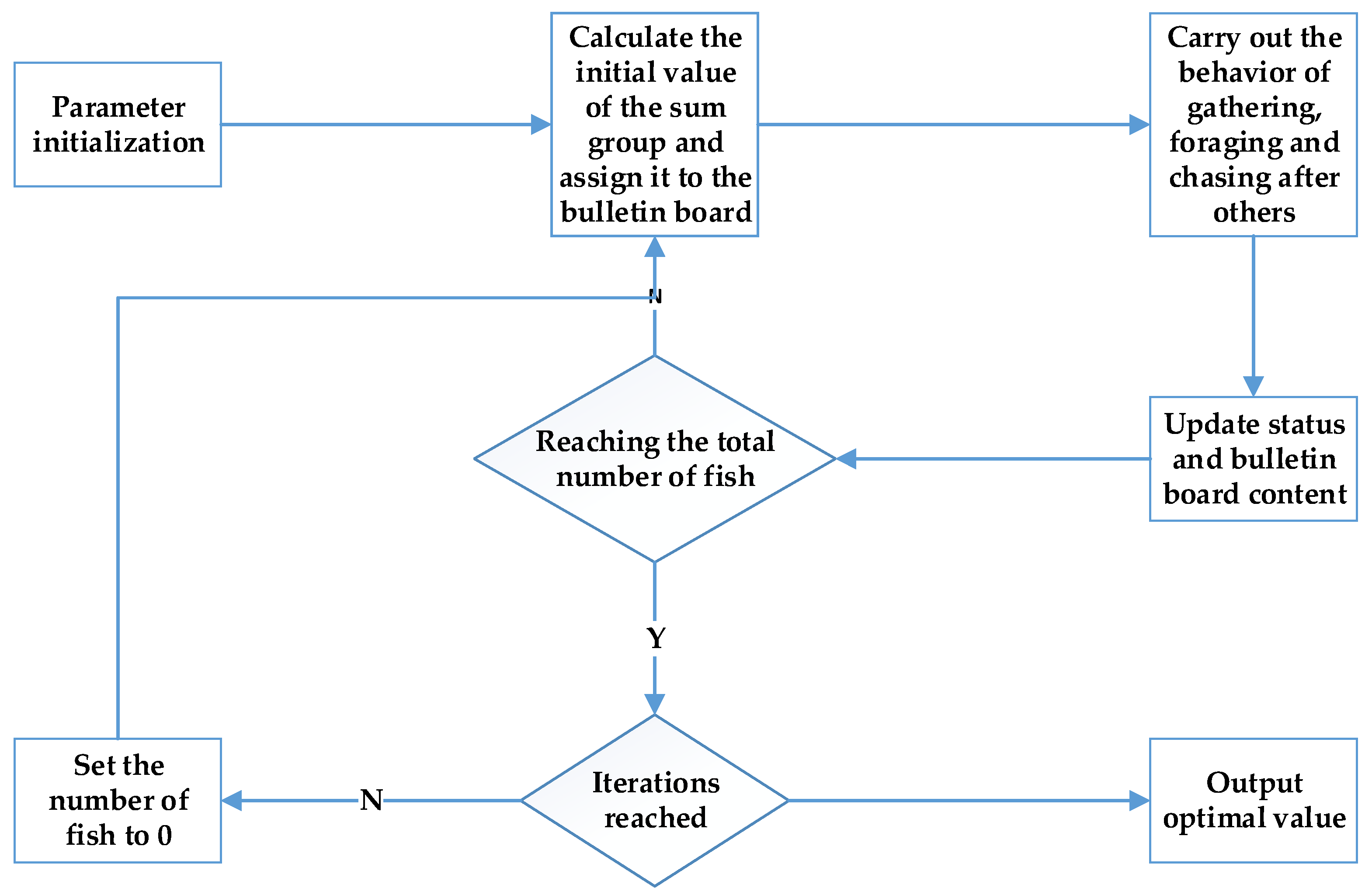
3.2. Artificial Fish Swarm Algorithm

The artificial fish swarm algorithm has good robustness and insensitivity to initial parameters. Figure 4 shows the flow of the artificial fish swarm algorithm.

Figure 4. AFSA Flow Char.

Step 1: Initialization settings, including the number of artificial fish, initial position, artificial fish field of vision, step size, crowding factor, bulletin board, and iteration times, where the initial position is generated by Chen chaotic system iteration.

Step 2: Evaluate each individual and choose the behaviors they want to perform, including foraging Prey, gathering Swarm, tailgating Follow, and evaluation behavior bullet; Refer to Section 2.2 for specific selection rules.

Step 3: Execute the behavior of artificial fish, update yourself, and generate a new school of fish.

Step 4: Evaluate all individuals. If an individual is superior to the bulletin board, the bulletin board will be updated to the individual.

Step 5: Determine whether the termination conditions are met. If it is satisfied, the algorithm is over; otherwise, go to step 2.

3.3. Substitution

Considering that in the digital image, the closer the pixel is, the greater the influence is, and the image block processing can better process each pixel and obtain more details. In this paper, the image is block processed. If the size of the plaintext image is $\left(M\times N\right)$, it will be divided into $\left(M\times N\right)/\left(m\times n\right)$ sub blocks. In principle, M should be an integral multiple of $m,N$ should be an integer multiple of $\mathrm{n}$. Otherwise, the missing part will be automatically filled in black, so the encryption algorithm proposed in this paper will not have the limitation of picture size.

3.3.1. Intra Block Permutation

Based on the filling position of each sub block image pixel obtained in Section 3.2, the specific operation of block built-in transformation is described in Algorithm 4.

Algorithm 4 Pseudo code of built-in commutation in sub image block.

Input: TB matrix A, sub block image B

Output: displacement sub block B’

1.    convert A and B into one-dimensional sequences

2.    for i = 1: $\left(M\times N\right) / \left(m\times n\right)$

3.        for j = 1:m × n

4.              $B_i^{\prime }\leftarrow B_i^{\prime }\left(j\right)=B_i\left(A\left(j\right)\right)$

5.        end

6.    end

3.3.2. Inter Block Permutation

After the block in the conversion of each sub block, the pixels of each image block are replaced with the pixels of other image blocks. The specific operation of inter block replacement is shown in Algorithm 5.

Algorithm 5 Pseudocode for permutation between sub image blocks.

Input: permutation image block B’, chaotic sequence w

Output: displacement image D

1.  $\mathrm{W}\leftarrow \mathrm{floor}\left(\mathrm{w} \times {10}^{13}\right)$

2.    $\mathrm{for} \mathrm{i}$= 1:$\left(\mathrm{M}\times \mathrm{N}\right) / \left(\mathrm{m}\times \mathrm{n}\right)$

3.        $\mathrm{for} \mathrm{j}=$1: $\mathrm{m}\times \mathrm{n}$

4.          $\mathrm{k}\leftarrow (\mathrm{W} \mathrm{mod}\left(\frac{\mathrm{M} \times \mathrm{N}}{\mathrm{m}\times \mathrm{n}}-\mathrm{i}\right)+1$

5.            exchange $B_{i^{\prime }}^{\prime }\left(j\right) and B_i^{\prime }\left(j\right)$

6.        end

7.        end

8.    Reconstruct the $\left(\mathrm{M}\times \mathrm{N}\right) / \left(\mathrm{m}\times \mathrm{n}\right)$ sub block int an D

3.4. Spread

The diffusion process can greatly enhance the ability of encryption schemes to resist statistical attacks and differential attacks. In order to obtain a better diffusion effect, we choose DNA coding technology with strong parallel computing ability, low energy consumption, and high information density for diffusion operation. The specific operations are as follows:

Step 1: Chen hyper-chaotic system iterates $N_0+M\times N$ times to obtain sequences $X_1, Y_1, Z_1, W_1,$ and then discards the first $N_0$ value to eliminate the transient effect of the chaotic system.

Step 2: Calculate each element of $X_1, Y_1, Z_1,$ and $W_1$ according to Equations (10)–(13) to obtain four vectors $R_i, R_y, R_z,$ and $R$.

$$R_x\left(i\right)=mod\left(floor\left(X_1\left(i\right)\times {10}^{14}\right),8\right)+1,$$

(10)

$$R_y\left(i\right)=mod\left(floor\left(Y_1\left(i\right)\times {10}^{14}\right),8\right)+1,$$

(11)

$$R_z\left(i\right)=mod\left(floor\left(Z_1\left(i\right)\times {10}^{14}\right),8\right)+1$$

(12)

$$\mathrm{R}\left(i\right)=mod\left(floor\left(W_1\left(i\right)\times {10}^{14}\right),256\right),$$

(13)

where $X_1\left(i\right), Y_1\left(i\right), Z_1\left(i\right),$ and $W_1\left(i\right)$ represent the ith element of $X_1, Y_1, Z_1,$ and $W_1$, $\mathrm{i}\in \left[1,M\times N\right]$, floor(a) is the rounding down of a. The result of mod (a, b) is the remainder of a divided by b.

Step 3: Expand the scrambled matrix $\mathrm{P}1$ into a vector $\mathrm{E}\left(\mathrm{i}\right)$, $\mathrm{i}\in \left[1,M\times N\right]$. Define variables temp and i, where the initial value of temp is shown in Equation (14), and the initial value of i is 1.

$$temp=mod\left({\sum }_{i=1}^{M\times N}P1,256\right),$$

(14)

Step 4: According to the DNA coding rules corresponding to $R_z\left(i\right)$, conduct DNA coding on $\mathrm{R}\left(i\right)$ to obtain $\mathrm{DNA}\_\mathrm{R}\left(i\right)$, at the same time, according to the DNA coding rules corresponding to $R_y$, DNA code $\mathrm{E}\left(\mathrm{i}\right)$ to obtain $\mathrm{DNA}\_\mathrm{E}\left(i\right)$, Then calculate the XOR of $\mathrm{DNA}\_\mathrm{R}\left(i\right)$ and $\mathrm{DNA}\_\mathrm{E}\left(i\right)$ to get $\mathrm{New}\_\mathrm{E}\left(\mathrm{i}\right)$.

Step 5: Decode $\mathrm{New}\_\mathrm{E}\left(\mathrm{i}\right)$ to get $\mathrm{de}\_\mathrm{New}\_\mathrm{E}\left(\mathrm{i}\right)$ according to the DNA coding rules corresponding to $R_x\left(i\right).$ Calculation the XOR of $\mathrm{de}\_\mathrm{New}\_\mathrm{E}\left(\mathrm{i}\right)$ and temp to obtain $\mathrm{C}\_\mathrm{New}\_\mathrm{E}\left(\mathrm{i}\right)$. At the same time, change the value of the variable temp to $C\_New\_E\left(i\right)$ and the value of variable $\mathrm{i}$ is $i+1$.

Step 6: Repeat steps 4 and 5. When $i=M\times N+1$, convert the resulting vector into a matrix of $M\times N$, that is, encrypt the resulting image.

3.5. Decryption Process

The decryption process is the reverse of the encryption process. In the process of encryption, we first scramble the image and then spread it. Therefore, in the decryption stage, it is necessary to perform diffusion decryption first, and then scrambling decryption. It is worth noting that before decryption, we need to obtain the parameter value and initial value of the hyper-chaotic system to generate a sequence before decryption.

4. Simulation Results and Security Analysis

4.1. Simulation Results

The digital images used for the test are lean $\left(512\times 512\right)$, butterfly $\left(512\times 768\right)$, terrace $\left(1200\times 256\right)$, and color image bridge $\left(\mathrm{color} \mathrm{image} 256\times 256\right)$. Figure 5 shows the encryption and decryption results of this scheme. Obviously, it can be seen that the plaintext image and the decrypted image are the same. In addition, since the size of the tested image is different, this scheme is not limited by the image size.

Figure 5. Encryption and decryption results: (a) plain images; (b) cipher images; (c) decrypted images.

In the following simulation experiments, the experimental environment is windows10 and MATLAB R2017a, and the test image is Lena $\left(512\times 512\right)$, with an 8-bit gray scale. The security analysis is as follows.

4.2. Key Space Analysis

In image encryption, key space analysis refers to the problem of key quantity. The size of the key space is usually described by the bit length occupied by the key. In this scheme, the key consists of two parts: the initial values of the hyper-chaotic system and the hash value of the plaintext image. For its initial value, because it is double precision, its space is ${10}^{16}{}^8={10}^{128}\approx 2^{384}.$ The space of the 128-bit hash value of the image is $2^{64}.$ Therefore, the key space of the whole scheme is $2^{384}\times 2^{64}=2^{448}.$ The research shows that for the security scheme, the key space is larger than $2^{100}.$ Obviously, Table 3 shows that compared with other schemes, our scheme has a larger key space, and has stronger resistance to exhaustive attacks.

Table 3. Key space comparison.

Schemes	Ours	Ref. [55]	Ref. [58]	Ref. [59]	Ref. [60]
Key space	2448	1084	2448	10322	5.12 × 1066

4.3. Key Sensitivity Analysis

Key sensitivity means that in the process of encryption and decryption, due to the small change of the initial key, the key generated after a series of actions changes greatly, so that the encrypted and decrypted image changes greatly. In this paper, setting $X_0=0.3838, Y_0=0.9876, Z_0=32.1234,W_0=0.6565$ as the initial value of the key, and setting $X_0=0.3838+{10}^{-10},Y_0=0.9876, Z_0=32.1234, W_0=0.6565$ as the modified initial value. The Lena image is encrypted with the original key and the modified key respectively. Figure 6b shows the cipher-text image encrypted with the original key. Figure 6c is to encrypt the plaintext image with the modified key and obtains another cipher-text image. Figure 6d shows the difference between the two cipher-texts. Obviously, the cipher-texts between the two images are very different. In the decryption process, the plaintext image can be recovered with the original key, but the plaintext image cannot be recovered with the modified key, as shown in Figure 6e.

Figure 6. Encryption secret key sensitivity test: (a) ordinary image; (b) original key encrypted image; (c) modified key encrypted image; (d) differences between the two cipher-texts; (e) use the modified key to solve the cipher-text image encrypted by the original key.

4.4. Statistical Attack Analysis

The attack scheme against statistical law is called a statistical analysis attack, which means that the attacker decodes the password by analyzing the statistical law between cipher-text and plaintext and extracting the transformation relationship between the plaintext image and cipher-text image. The ability of the scheme to resist statistical attacks can be analyzed from the following aspects.

4.4.1. Histogram Analysis

Histogram can intuitively reflect the distribution of each gray value in the image. In an ideal cipher-text image, each gray value should have an equal probability distribution. Taking Lena (512 × 512) as an example, the gray histogram before and after encryption is intuitively displayed in Figure 7.

Figure 7. (a) horizontal of plain image; (b) vertical of plain image; (c) diagonal of plain image; (d) horizontal of cipher image; (e) vertical of cipher image; (f) diagonal of cipher image.

4.4.2. Information Entropy Analysis

Information entropy can be used to measure whether the gray value distribution is uniform. The greater the information entropy of the image, the more balanced the gray value distribution, and the greater the possibility of resisting an entropy attack. Use the following formula to calculate the information entropy of each image before and after encryption.

$$\mathrm{H}={\displaystyle \sum }_{i=0}^{255}{P}_{ij}log{P}_{ij}$$

(15)

$$P_{ij}=\raisebox{1ex}{$f\left(i,j\right)$}\!\left/ \!\raisebox{-1ex}{$N^2$}\right.,$$

(16)

where $f\left(i,j\right)$ is the frequency of the characteristic binary $\left(i,j\right)$, and N is the scale of the image.

Table 4 shows the comparison results of information entropy of encrypted images between our scheme and other schemes. The experimental results show that the gray value in the ciphertext image is close to the unimodal distribution, and the ciphertext information entropy is close to the ideal value of 8, that is, our scheme can effectively resist low-frequency analysis attacks.

Table 4. Information entropy analysis result of encrypted image.

Image	Ours	Ref. [55]	Ref. [58]	Ref. [60]
Lena	7.9993	7.9978	7.9993	--
Butterfly	7.9996	7.994	--	--
Terrace	7.9998	--	--	--
Bridge (color image)	7.9992	--	--	7.9896

4.4.3. Correlation Coefficient Analysis

Due to the high correlation between adjacent pixels of an image, a pixel often divulges the information of its surrounding pixels. The calculation formula of the correlation coefficient in horizontal, vertical, and diagonal directions is as follows:

$$R_{xy}=\frac{cov\left(x,y\right)}{\sqrt{D\left(x\right)}\times \sqrt{D\left(y\right)}},$$

(17)

$$E\left(x\right)=\frac{1}{N}{\displaystyle \sum }_{i=1}^N{x}_i,$$

(18)

$$D\left(x\right)=\frac{1}{N}{{\displaystyle \sum }}_{i=1}^N(x_i-E{\left(x\right)}^2,$$

(19)

$$\mathrm{cov}\left(x,y\right)=\frac{1}{N}{{\displaystyle \sum }}_{i=1}^N\left(x_i-E\left(x\right)\right)\left(y_i-E\left(y\right)\right),$$

(20)

where y is the sum of the adjacent pixels of x, and n is the selected pixels, Cov (x, y) is the covariance at two pixels x and y, $\sqrt{D\left(x\right)}$ is the standard deviation, D(x) is the variance, and E(x) is the mean. Generally, the correlation of adjacent pixels in plaintext images is close to 1, while the correlation of adjacent pixels in ciphertext images should be close to 0.

The correlation distribution of ordinary images and encrypted images in three directions is shown in Figure 7.

By comparing the correlation coefficients between domain pixels of ordinary images and encrypted images, as shown in Table 5, it can be concluded that the correlation between domain pixels of encrypted images is low, so our scheme has a good ability to resist statistical analysis attacks.

Table 5. Correlation coefficient.

	Level		Vertical		Diagonal
Image	Plain Image	CIPHER-TEXT	Plain Image	Cipher-Text	Plain Image	Cipher-Text
lean	0.9738	−0.0024	0.9547	−0.0054	0.9277	−0.0129
bridge	0.9717	0.0036	0.9650	0.0471	0.9589	0.0105
terrace	0.9783	−0.0248	0.9733	0.0016	0.9535	0.0057
butterfly	0.9456	−0.0135	0.9509	−0.0090	0.9164	−0.0089

4.5. Differential Attack Analysis

Differential attack is an important analysis method to test the sensitivity of algorithms to plaintext. If the cipher-text image obtained by the slight change of plaintext is very different from the cipher-text obtained by the original plaintext, the algorithm is sensitive to plaintext. Two parameters (Pixel Rate of Change (NPCR) and Uniform Average Intensity of Change (UACI)) are used to measure the resistance to differential attacks of cipher-text images. NPCR and UACI respectively represent the number of changed pixels between two encrypted images and the average change intensity between two encrypted images [25,26]. The corresponding ideal values are respectively NPCR = 99.6094% and UACI = 33.4635%. NPCR value and UACI value of the scheme are obtained according to the following calculation formula.

$$\mathrm{NPCR}=\frac{{\sum }_{ij}D\left(i,j\right)}{M\times N}\times 100\%,$$

(21)

$$\mathrm{ACI}=\frac{1}{M\times N}\times \frac{\sum \left(C_1\left(i,j\right)-C_2\left(i,j\right)\right)}{255}\times 100\%,$$

(22)

$$\mathrm{D}\left(\mathrm{i},\mathrm{j}\right)=\mathrm{f}\left(\mathrm{x}\right)=\{\begin{array}{c}1,C_1\left(i,j\right)\ne C_2\left(i,j\right)\\ 0, otherwise\end{array},$$

(23)

where M and N, respectively, represent the width and height of the two cipher-texts, $C_1\left(i,j\right),C_2\left(i,j\right)$, respectively, represent two images in $\left(i,j\right)$ pixel value of the position.

Table 6 shows the comparison between our scheme and other schemes. The results show that the NPCR and UACI of our scheme reach 99.62% and 33.69%, which is infinitely close to the ideal value. Compared with other algorithms, the NPCR and UACI values of our scheme are closer to the ideal value, and our scheme is more resistant to differential attacks.

Table 6. Performance of NPCR and UACI.

Algorithms	NPCR (%)	UACI (%)
Ours	99.62	33.69
Ref. [55]	99.59	33.41
Ref. [58]	99.61	33.47
Ref. [59]	99.46	33.10
Ref. [60]	99.62	31.83

4.6. Other Attack Analysis

Due to the particularity of pure black or white images, sometimes attackers will crack the encryption algorithm in the presence of ordinary images. We select the special images of all black $\left(256\times 256\right)$ and all white $\left(256\times 256\right)$ as the input images. The encryption results are shown in Figure 8 and Table 7.

Figure 8. Experimental results of special images: (a,d) special image; (b,e) encrypted image; (c,f) cipher-text histogram.

Table 7. Information entropy of special image and correlation of each direction.

	Information Entropy	Relevance
		Level	Vertical	Diagonal
All black cipher-text image	7.9973	−0.0094	0.0098	−0.0016
All white cipher-text image	7.9974	−0.0169	−0.0094	0.0056

According to the results in Figure 8 and Table 7, after analysis, we can find that the attacker cannot execute the encryption scheme according to the special image to obtain useful information, and then attack the encryption scheme, so our scheme is safe and reliable.

5. Discussion

The chaotic image encryption scheme based on the artificial fish swarm algorithm and DNA coding presented in this paper can resist various classical attacks in addition to its excellent security. However, it also has certain limitations. As we need to repeat the artificial fish swarm algorithm on the block image, the encryption speed is not fast enough, but it is still within the acceptable range, which requires us to continue to optimize the algorithm and improve the encryption implementation scheme in the future research, so as to improve the execution speed of the encryption scheme.

6. Conclusions

In this study, the foraging behavior of the artificial fish school algorithm is improved, and a chaotic image encryption scheme based on the artificial fish school and DNA coding is proposed. By hashing the original image, the correlation between the key and the plaintext is closer. Secondly, the foraging behavior of the artificial fish is improved to obtain the optimal solution of the block image, and the image is scrambled to improve the complexity and security of encryption. However, due to the need to carry out this artificial fish swarm algorithm for each word block image, its time cost is high. In the diffusion stage, the DNA method is used to obtain a better diffusion effect. The encryption method in this paper can be applied to different image types, such as gray images and color images. It also applies to images of any size. The experimental results show that the encryption scheme has the advantages of large key space, high sensitivity to key and pure image, security, and reliability. The proposed encryption scheme is easy to operate. All these satisfactory characteristics make the proposed scheme a potential candidate for multimedia data encryption (such as images, audio, and even video).