On the Significance of Parameters in the Choice and Collection Schemata in the 2nd Order Peano Arithmetic

Abstract

We make use of generalized iterations of the Sacks forcing to define cardinal-preserving generic extensions of the constructible universe L in which the axioms of ZF hold and in addition either (1) the parameter-free countable axiom of choice ${\mathbf{AC}}_{\omega }^{*}$ fails, or (2) ${\mathbf{AC}}_{\omega }^{*}$ holds but the full countable axiom of choice ${\mathbf{AC}}_{\omega }$ fails in the domain of reals. In another generic extension of L, we define a set $X\subseteq \mathcal{P}\left(\omega \right)$, which is a model of the parameter-free part ${\mathbf{PA}}_2^{*}$ of the 2nd order Peano arithmetic ${\mathbf{PA}}_2$, in which $\mathbf{CA}\left({\mathsf{\Sigma }}_2^1\right)$ (Comprehension for ${\mathsf{\Sigma }}_2^1$ formulas with parameters) holds, yet an instance of Comprehension $\mathbf{CA}$ for a more complex formula fails. Treating the iterated Sacks forcing as a class forcing over ${\mathbf{L}}_{{\omega }_1}$, we infer the following consistency results as corollaries. If the 2nd order Peano arithmetic ${\mathbf{PA}}_2$ is formally consistent then so are the theories: (1) ${\mathbf{PA}}_2+\neg {\mathbf{AC}}_{\omega }^{*}$, (2) ${\mathbf{PA}}_2+{\mathbf{AC}}_{\omega }^{*}+\neg {\mathbf{AC}}_{\omega }$, (3) ${\mathbf{PA}}_2^{*}+\mathbf{CA}\left({\mathsf{\Sigma }}_2^1\right)+\neg \mathbf{CA}$.

1. Introduction

In this paper, we let ${\mathbf{PA}}_2$ be the second-order Peano arithmetic without the schema of (countable) Choice. Discussing the structure and deductive properties of ${\mathbf{PA}}_2$, one of founders of modern proof theory Georg Kreisel ([1], § III, page 366) wrote that the selection of subsystems “is a central problem”. In particular, Kreisel notes, that

[…] if one is convinced of the significance of something like a given axiom schema, it is natural to study details, such as the effect of parameters.

Recall that parameters in this context are free variables in various axiom schemata in $\mathbf{PA}$, ${\mathbf{PA}}_2$, $\mathbf{ZFC}$, and other similar theories. Thus the most obvious way to study “the effect of parameters” is to compare the strength of a given axiom schema S with its parameter-free subschema $S^{*}$. (The asterisk will refer to the parameter-free subschema in this paper).

Some research in this direction was accomplished in the early years of modern set theory. In particular Levy [2] proved that the generic collapse of cardinals below ${\aleph }_{\omega }$ (called the Levy collapse, see Solovay [3]) results in a generic extension of $\mathbf{L}$ in which ${\mathbf{AC}}_{\omega }^{*}$ fails, where ${\mathbf{AC}}_{\omega }^{*}$ is the parameter-free subschema of the (countable) Choice schema ${\mathbf{AC}}_{\omega }$ in the language of ${\mathbf{PA}}_2$. This result by Levy implies the formal consistency of ${\mathbf{PA}}_2+\neg {\mathbf{AC}}_{\omega }^{*}$.

Later Guzicki [4] established that the Levy-style generic collapse below ${\aleph }_{{\omega }_1}$ results in a generic extension of $\mathbf{L}$ in which ${\mathbf{AC}}_{\omega }$ (in the language of ${\mathbf{PA}}_2$) fails, but the parameter-free subschema ${\mathbf{AC}}_{\omega }^{*}$ holds, so that ${\mathbf{AC}}_{\omega }^{*}$ is strictly weaker than ${\mathbf{AC}}_{\omega }$, or saying it differently, ${\mathbf{PA}}_2+{\mathbf{AC}}_{\omega }^{*}+\neg {\mathbf{AC}}_{\omega }$ is consistent. (This can be compared with an opposite result for the dependent choice schema $\mathbf{DC}$, in the language of ${\mathbf{PA}}_2$, which happens to be equivalent to its parameter-free subschema ${\mathbf{DC}}^{*}$ by a simple argument given for instance in [4]).

We may note that the Levy and Guzicki results above involve uncountable cardinals up to ${\aleph }_{\omega }$ (Levy) and ${\aleph }_{{\omega }_1}$ (Guzicki), so that the consequent consistency results are based on set theoretic tools far beyond the axiomatic system ${\mathbf{PA}}_2$ itself. This discrepancy motivated us to conduct this research, aimed at cardinal-preserving constructions of models with the same properties, with the final goal to obtain the consistency results as above on the basis of the consistency of ${\mathbf{PA}}_2$ alone.

Outside of the domain of ${\mathbf{PA}}_2$, some results related to parameter-free versions of the Separation and Replacement axiom schemata in $\mathbf{ZFC}$ also are known from [5,6,7]. This gives us an additional motivation to include the ${\mathbf{PA}}_2$ Comprehension schema $\mathbf{CA}$ in our study, which is a direct ${\mathbf{PA}}_2$ counterpart of the $\mathbf{ZFC}$ Separation and Replacement schemata.

To conclude, our paper is devoted to further clarification of the role of parameters in the Choice and and Comprehension schemata ${\mathbf{AC}}_{\omega }$ and $\mathbf{CA}$ in ${\mathbf{PA}}_2$. The main integrated result is that the parameter-free versions of both ${\mathbf{AC}}_{\omega }$ and $\mathbf{CA}$ are strictly weaker than the full versions of the schemata (Theorems 1 and 2 below), but still the parameter-free version ${\mathbf{AC}}_{\omega }^{*}$ of ${\mathbf{AC}}_{\omega }$ is not provable in ${\mathbf{PA}}_2$ (Theorem 3). Special attention will be paid to the evaluation of those proof theoretic tools used in the arguments. That is, we show that the formal consistency of ${\mathbf{PA}}_2$ suffices. This is the main contribution of this paper. It has a crucial advantage comparably to the above-mentioned earlier results and approaches by Levy [2] and Guzicki [4], which involve cardinal-collapse forcing notions and thereby definitely cannot be rendered on the basis of the consistency of ${\mathbf{PA}}_2$.

The following Theorems 1–3 are the main results of this paper.

Theorem 1. 

In $\mathbf{ZF}$, let $\mathbf{L}$ be the constructible universe. Then:

(i)

There is a cardinal-preserving generic extension of $\mathbf{L}$ in which ${\mathbf{AC}}_{\omega }\left(\mathrm{OD}\right)$ (that is, ${\mathbf{AC}}_{\omega }$ for ordinal-definable relations) holds, but the full ${\mathbf{AC}}_{\omega }$ fails in the domain of reals.

(ii)

If ${\mathbf{PA}}_2$ is consistent then ${\mathbf{PA}}_2+{\mathbf{AC}}_{\omega }^{*}$ does not prove ${\mathbf{AC}}_{\omega }$.

Theorem 1 is entirely new. Part (i) greatly surpasses the above-mentioned result of Guzicki [4] by the requirement of cardinal-preservation. This is a conditio sine qua non for Claim (ii) to be obtained by a similar technique, because the involvement of uncountable cardinals in the arguments, as in [4], is definitely beyond the formal consistency of ${\mathbf{PA}}_2$.

In the next theorem, ${\mathbf{PA}}_2^{*}$ is the subtheory of ${\mathbf{PA}}_2$ in which the full schema $\mathbf{CA}$ is replaced by its parameter-free version $\mathbf{CA}{}^{*}$, and the Induction principle is formulated as a schema rather than one sentence.

Theorem 2. 

In $\mathbf{ZF}$, let $\mathbf{L}$ be the constructible universe. Then:

(i)

There is a cardinal-preserving generic extension of $\mathbf{L}$, and a set $M\subseteq \mathcal{P}\left(\omega \right)$ in this extension, such that $\mathcal{P}\left(\omega \right)\cap \mathbf{L}\subseteq M$ and M models ${\mathbf{PA}}_2^{*}+\mathbf{CA}\left({\mathsf{\Sigma }}_2^1\right)+\neg \mathbf{CA}$.

(ii)

If ${\mathbf{PA}}_2$ is consistent then ${\mathbf{PA}}_2^{*}+\mathbf{CA}\left({\mathsf{\Sigma }}_2^1\right)$ does not prove $\mathbf{CA}$.

This is a new result as well, appeared in our recent ArXiv preprint [8].

The next theorem, albeit not entirely new in part (i), is added in for good measure, because its proof involves basically the same type of generic extensions.

Theorem 3. 

In $\mathbf{ZF}$, let $\mathbf{L}$ be the constructible universe. Then:

(i)

There is a cardinal-preserving generic extension of $\mathbf{L}$ in which ${\mathbf{AC}}_{\omega }^{*}$ fails.

(ii)

If ${\mathbf{PA}}_2$ is consistent then ${\mathbf{PA}}_2$ does not prove ${\mathbf{AC}}_{\omega }^{*}$.

Part (i) of this theorem essentially follows from a result by Enayat [9], where it is shown that using the finite-support infinite product of Jensen’s minimal-${\Delta }_3^1$-real forcing [10] results in a permutation model of $\mathbf{ZF}$ with an infinite Dedekind-finite ${\Pi }_2^1$ set of reals, and the existence of such a set implies the refutation of ${\mathbf{AC}}_{\omega }^{*}$. Part (ii) is new.

The first claims of all three theorems will be established by means of a complex iteration of the Sacks forcing which resembles the generalized iteration by Groszek and Jech [11], but is carried out in a pure geometric way that avoids any formalism of forcing iterations. We call this technique arboreal Sacks iterations. The associated coding by degrees of constructibility is also involved, more or less along the lines discussed in ([12], p. 143).

To conclude, the main novelty of all three theorems is that the unified forcing technique of arboreal Sacks iterations is used to define generic cardinal-preserving models of set theory and second-order Peano arithmetic with different effects related to parameters in the Choice and Comprehension schemata in ${\mathbf{PA}}_2$, to subsequently prove that the parameter-free versions of the schemata are weaker than the full versions. This leads to further development of the research line outlined by Georg Kreisel [1], see a quote above. The other principal novelty is that we demonstrate, by claims (ii) of all three theorems, that the ensuing consistency results can be obtained on the basis of the consistency of ${\mathbf{PA}}_2$ alone, rather than on the basis of full-scale set theoretic forcing technique. Claims (i) of Theorems 1 and 2 are new as they stand; claim (i) of Theorem 3 is a corollary of a known result.

It remains to note that topics in subsystems of second order arithmetic remain of big interest in modern studies, see e.g., [13,14,15], and our paper contributes to this research line.

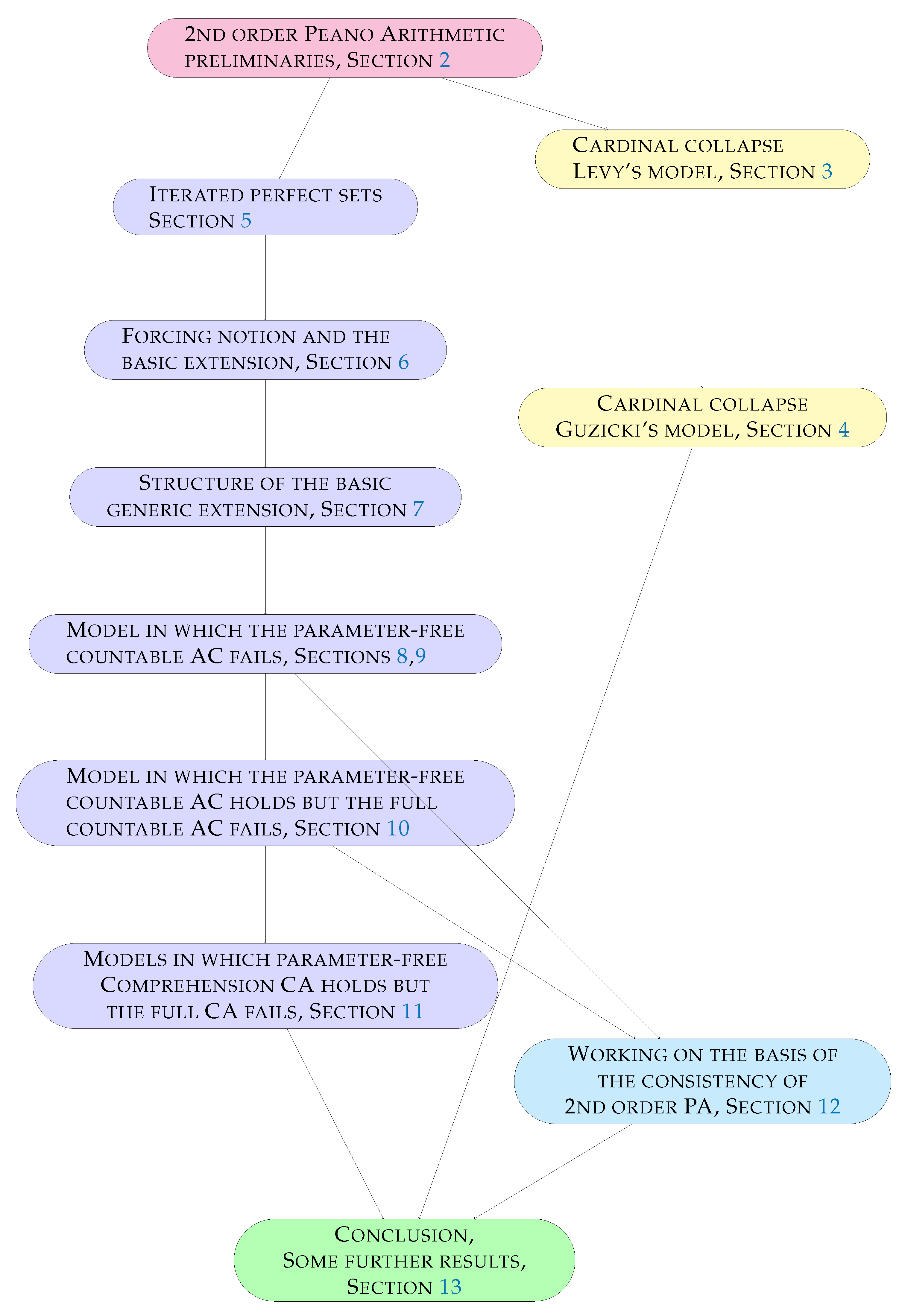
The paper is organized as follows. After a short review of ${\mathbf{PA}}_2$ preliminaries in Section 2, we take some space to briefly describe the aforementioned cardinal-collapse models by Levy [2] and Guzicki [4] in Section 3 and Section 4.

Our basic forcing notion $\mathbb{P}$ is introduced in Section 5; it consists of iterated perfect sets. The structure of $\mathbb{P}$-generic extensions $\mathbf{L}\left[G\right]$ of $\mathbf{L}$ is studied in Section 6 and Section 7. In particular, Theorem 4 provides the cardinal preservation, and Theorem 5 presents several important results on the degrees of constructibility of reals and the relation of true ${⩽}_{\mathbf{L}}$-successor in the generic extensions considered.

The proof of Theorem 3(i) is carried out in Section 8 modulo an important lemma (Lemma 11) established in Section 9. Basically, a generic extension that proves Theorem 3(i) will be obtained as a certain subextension of a $\mathbb{P}$-generic extension $\mathbf{L}\left[G\right]$, which is the content of Theorem 6.

Claims (i) of Theorems 1 and 2 are established in Section 10 and Section 11, via certain other subextensions of a $\mathbb{P}$-generic extension, studied by Theorems 7 and 8 respectively.

Finally Section 12 contains the proof of claims (ii) of all three theorems. To accomplish this proof, we will redo the proofs of claims (i) of all three theorems in some uniform manner. This will involve a rather well-known Theorem 9 on the equiconsistency of ${\mathbf{PA}}_2$ and the set theory $\mathbf{ZFC}$ without the Power Set axiom.

The paper ends with a usual conclusion-style material in Section 13.

A flowchart follows on page 4, Figure 1 for the convenience of the reader.

2. Second Order Peano Arithmetic Preliminaries

Following [1,16,17] we consider the second order Peano arithmetic ${\mathbf{PA}}_2$ as a theory in the language $\mathcal{L}\left({\mathbf{PA}}_2\right)$ with two sorts of variables—for natural numbers and for sets of them. We use $j,k,m,n$ for variables over $\omega$ and $x,y,z$ for variables over $\mathcal{P}\left(\omega \right)$, reserving capital letters for subsets of $\mathcal{P}\left(\omega \right)$ and other sets. The axioms are as follows in (1)–(4):

(1)

Peano’s axioms for numbers.

(2)

The Induction schema: $\mathsf{\Phi }\left(0\right)\wedge \forall k\left(\mathsf{\Phi }\right(k\left)⟹\mathsf{\Phi }\right(k+1\left)\right)⟹\forall k\mathsf{\Phi }\left(k\right)$, for every formula $\mathsf{\Phi }\left(k\right)$ in $\mathcal{L}\left({\mathbf{PA}}_2\right)$, and in $\mathsf{\Phi }\left(k\right)$ we allow parameters, i.e., free variables other than k. (We do not formulate Induction as one sentence here because the Comprehension schema $\mathbf{CA}$ will not be assumed in full generality in Section 11).

(3)

Extensionality for sets of natural numbers.

(4)

The Comprehension schema $\mathbf{CA}$: $\exists x\forall k(k\in x⟺\mathsf{\Phi }(k\left)\right)$, for every formula $\mathsf{\Phi }$ in which x does not occur, and in $\mathsf{\Phi }$ we allow parameters.

${\mathbf{PA}}_2$ is also known as $A_2^{-}$ (see e.g., an early survey [16]), as $Z_2$ (see e.g., Simpson [17] and Friedman [18]), as $Z_2^{-}$ (in [19] or elsewhere). Note that the schema of Choice (see below) is not included in ${\mathbf{PA}}_2$.

The following schemata are not assumed to be parts of ${\mathbf{PA}}_2$, yet they are often considered in the context of and in connection with ${\mathbf{PA}}_2$.

The Schema of Choice ${\mathbf{AC}}_{\omega }$: 

$\forall k\exists x\mathsf{\Phi }(k,x)⟹\exists x\forall k\mathsf{\Phi }(k,{\left(x\right)}_k))$, for every formula $\mathsf{\Phi }$, where we allow parameters in $\mathsf{\Phi }$, and ${\left(x\right)}_k=\{j:2^k(2j+1)-1\in x\}$, as usual.

We use ${\mathbf{AC}}_{\omega }$ instead of AC, more common in ${\mathbf{PA}}_2$ studies, because AC is the general axiom of choice in the $\mathbf{ZFC}$ context.

Dependent Choices DC: 

$\forall x\exists y\mathsf{\Phi }(x,y)⟹\exists x\forall k\mathsf{\Phi }({\left(x\right)}_k,{\left(x\right)}_{k+1}))$, for every formula $\mathsf{\Phi }$, and in $\mathsf{\Phi }$ we allow parameters.

We let $\mathbf{CA}{}^{*}$ be the parameter-free sub-schema of $\mathbf{CA}$ (that is, $\mathsf{\Phi }\left(k\right)$ contains no free variables other than k). We define the parameter-free sub-schema ${\mathbf{AC}}_{\omega }^{*}\subseteq {\mathbf{AC}}_{\omega }$ the same way. The parameter-free sub-schema ${\mathbf{DC}}^{*}\subseteq \mathbf{DC}$ can be defined as well, but this does not make much sense because ${\mathbf{DC}}^{*}$ is known to be equivalent to $\mathbf{DC}$ by a simple argument, see e.g., [4].

In set-theoretic setting, ${\mathbf{AC}}_{\omega }$ and $\mathbf{DC}$ can be considered in the assumption that $\mathsf{\Phi }$ is a set-theoretic binary relation on $\omega \times \mathcal{P}\left(\omega \right)$, whose type can be restricted in this or another way depending on the context. In particular, ${\mathbf{AC}}_{\omega }\left(\mathrm{OD}\right)$ assumes that $\mathsf{\Phi }$ is an $\mathrm{OD}$ (ordinal-definable) relation. (See [20] on ordinal definability). In addition, say ${\mathbf{AC}}_{\omega }^{*}\left({\Pi }_3^1\right)$ or ${\mathbf{AC}}_{\omega }\left({\mathsf{\Pi }}_3^1\right)$ means the restriction to the type of lightface ${\Pi }_3^1$ (parameter-free) or resp. boldface ${\mathsf{\Pi }}_3^1$ (with parameters in $\mathcal{P}\left(\omega \right)$ allowed) formulas.

3. A Cardinal-Collapse Model Where the Parameter-Free ${\mathbf{AC}}_{\omega }^{*}$ Fails

Here we recall an old model by Levy [2] in which the parameter-free ${\mathbf{AC}}_{\omega }^{*}$ fails for a certain (lightface) ${\Pi }_2^1$ relation. This is basically any model of $\mathbf{ZF}+({\aleph }_1={\aleph }_{\omega }^{\mathbf{L}})$. To obtain this model, Levy makes use of the collapse below ${\aleph }_{\omega }$, i.e., a Cohen-style generic sequence $f={\langle f_n\rangle }_{n<\omega }$ of (generic) collapse maps $f_n:\omega \stackrel{\mathrm{onto}}{⟶}{\aleph }_n^{\mathbf{L}}$ is adjoined to the Gödel-constructible universe $\mathbf{L}$. Consider the set $F=\{f_n:n<\omega \}$ and the class $N=\mathrm{HOD}\left(F\right)$ of all sets hereditarily F-ordinal-definable in $\mathbf{L}\left[f\right]$. Then N is a model of $\mathbf{ZF}+({\aleph }_1={\aleph }_{\omega }^{\mathbf{L}})$.

We may note that the set $\mathcal{P}\left(\omega \right)\cap N$ of all reals in N is equal to the set $\mathcal{P}\left(\omega \right)\cap {\bigcup }_{n<\omega }\mathbf{L}[f_0,f_1,\cdots ,f_n]$.

To prove that ${\mathbf{AC}}_{\omega }$ fails under ${\aleph }_1={\aleph }_{\omega }^{\mathbf{L}}$, Levy considers the relation $R(n,f):=$ $n<\omega$, $f\in {\omega }^{\omega },$ and f codes a well-ordering of length $\ge {\aleph }_n^{\mathbf{L}}$.

Then, first, ${\mathbf{AC}}_{\omega }$ fails for R under ${\aleph }_1={\aleph }_{\omega }^{\mathbf{L}}$ by obvious reasons, and second, R can be presented as a lightface ${\Pi }_2^1$ relation.

To prove the second claim, we may note, following Levy, that $R(n,f)$ is equivalent to the following relation:

$R^{\prime }(n,f):=$$n<\omega$, $f\in {\omega }^{\omega },$f codes a well-ordering, whose length we denote by $\alpha$, and, for every countable transitive set X which models $\mathbf{ZF}$ minus the Power Set axiom, if $\alpha \in X$ then it is true in $\langle X;\in \rangle$ that “there are at least $n+1$ infinite cardinals $\le \alpha$”.

To see that $R^{\prime }$ is a ${\Pi }_2^1$ relation, Levy uses well-founded relations on $\omega$ as a substitution for countable transitive sets. Since the well-foundedness is a ${\Pi }_1^1$ property, the definition of $R^{\prime }$ can be converted to a ${\Pi }_2^1$ form.

From a more modern perspective, we may note that $R^{\prime }$ is a ${\Pi }_1^{\mathrm{HC}}$ relation, where $\mathrm{HC}=H_{{\omega }_1}$ is the transitive set of all hereditarily countable sets, and then make use of the conversion theorem (see e.g., Theorem 25.25 in [20]) saying that ${\Pi }_1^{\mathrm{HC}}$ relations on the reals are the same as ${\Pi }_2^1$ relations.

4. A Cardinal-Collapse Model Where the Parameter-Free ${\mathbf{AC}}_{\omega }^{*}$ Holds but the Full ${\mathbf{AC}}_{\omega }$ Fails

The Guzicki model with such an effect appeared in [4]. It is similar to Levy’s model of [2], yet it makes use of the Levy collapse below ${\aleph }_{{\omega }_1}$. To obtain such a model, we adjoin, to the Gödel constructible universe $\mathbf{L}$, a Cohen-style (finite-support) generic sequence $f={\langle f_{\xi }\rangle }_{\xi <{\omega }_1^{\mathbf{L}}}$ of (generic) collapsing maps $f_{\xi }:\omega \stackrel{\mathrm{onto}}{⟶}{\aleph }_{\xi }^{\mathbf{L}}$. Consider the set $F=\{f\upharpoonright \beta :\beta <{\omega }_1^{\mathbf{L}}\}$ and the class N of all sets hereditarily F-real-ordinal definable in $\mathbf{L}\left[f\right]$. Then N is a model of $\mathbf{ZF}+({\aleph }_1={\aleph }_{{\omega }_1}^{\mathbf{L}})$.

The set $\mathcal{P}\left(\omega \right)\cap N$ of all reals in N is equal to $\mathcal{P}\left(\omega \right)\cap {\bigcup }_{\beta <{\omega }_1^{\mathbf{L}}}\mathbf{L}\left[f\upharpoonright \beta \right]$.

To check that ${\mathbf{AC}}_{\omega }$ fails in N for a ${\mathsf{\Pi }}_2^1$ relation, let $p\in N,p\subseteq \omega$ code a strictly increasing map $g=g_p:\omega \to {\omega }_1^{\mathbf{L}}$ whose range is cofinal in ${\omega }_1^{\mathbf{L}}$. Accordingly the sequence of cardinals ${\aleph }_{g\left(n\right)}^{\mathbf{L}}\in N$ is cofinal in ${\aleph }_{{\omega }_1}^{\mathbf{L}})$. This allows to accomodate the arguments in Section 3, with minor changes mutatis mutandis, and prove that ${\mathbf{AC}}_{\omega }$ fails in N for a ${\mathsf{\Pi }}_2^1$ relation similar to R but defined with p as a parameter.

To see that the parameter-free ${\mathbf{AC}}_{\omega }^{*}$, and even ${\mathbf{AC}}_{\omega }\left(\mathrm{OD}\right)$ for all ordinal-definable relations holds in N, let $\phi (k,x,\gamma )$ be an ∈-formula with an ordinal $\gamma$ as the only parameter. Assume that $\forall k\exists x\subseteq \omega \phi (k,x,\gamma )$ holds in N. Then for every k there exist ordinals $\beta <{\omega }_1^{\mathbf{L}}$ such that a set $x\subseteq \omega$ satisfying $\phi (k,x,\gamma )$ in N exists in $\mathbf{L}\left[f\upharpoonright \beta \right]$. Let ${\beta }_k$ be the least such an ordinal. The sequence ${\langle {\beta }_n\rangle }_{n<\omega }$ immediately belongs to $\mathbf{L}\left[f\right]$. Yet using the homogeneous character of the product collapse forcing that yields f, one can prove that in fact the sequence ${\langle {\beta }_n\rangle }_{n<\omega }$ in fact belongs to $\mathbf{L}$. Therefore $\beta ={sup}_n{\beta }_n<{\omega }_1^{\mathbf{L}}$, and accordingly for any k there is a set $x\subseteq \omega ,x\in \mathbf{L}\left[f\upharpoonright \beta \right]$ satisfying $\phi (k,x,\gamma )$ in N. It remains to note that $\mathbf{L}\left[f\upharpoonright \beta \right]\subseteq N$.

5. Iterated Perfect Sets

Here we begin the proof of Theorems 1–3. The proof involves the engine of generalized iterated Sacks forcing developed in [21,22] on the base of earlier papers [11,23,24] and others. We consider the constructible universe $\mathbf{L}$ as the ground model.

Arguing in $\mathbf{L}$ in this section, we define, in $\mathbf{L}$, the set

$$\mathit{I}={\omega }_1^{<\omega }\setminus \left\{\mathsf{\Lambda }\right\};\mathit{I}\in \mathbf{L};$$

of all non-empty tuples $\mathit{i}=\langle {\xi }_0,\dots ,{\xi }_n\rangle$, $n<\omega$, of ordinals ${\xi }_k<{\omega }_1$, partially ordered by the extension ⊂ of tuples. $\mathit{I}$ is a tree without the minimal node $\mathsf{\Lambda }$ (the empty tuple), which we exclude.

Our plan is to define a generic extension $\mathbf{L}\left[\mathbf{a}\right]$ of $\mathbf{L}$ by an array $\mathbf{a}={\langle {\mathbf{a}}_{\mathit{i}}\rangle }_{\mathit{i}\in \mathit{I}}$ of reals ${\mathbf{a}}_{\mathit{i}}\subseteq \omega$, in which the structure of “sacksness” is determined by this set $\mathit{I}$, so that in particular each ${\mathbf{a}}_{\mathit{i}}$ is Sacks-generic over the submodel $\mathbf{L}\left[{\langle {\mathbf{a}}_{\mathit{j}}\rangle }_{\mathit{j}\subset \mathit{i}}\right]$. Then Theorems 1–3 will be obtained via submodels of the basic model $\mathbf{L}\left[\mathbf{a}\right]$.

Let $\Xi$ be the set of all countable and finite initial segments (in the sense of ⊂) $\zeta \subseteq \mathit{I}$. If $\zeta \in \Xi$ then ${\mathrm{IS}}_{\zeta }$ is the set of all initial segments of $\zeta$.

Greek letters $\xi ,\eta ,\zeta ,\vartheta$ will denote sets in $\Xi$.

Characters $\mathit{i},\mathit{j}$ are used to denote elements of $\mathit{I}$.

For any $\mathit{i}\in \zeta \in \Xi ,$ we consider initial segments $\zeta [\subset \mathit{i}]=\{\mathit{j}\in \zeta :\mathit{j}\subset \mathit{i}\}$ and $\zeta \left[⊈\mathit{i}\right]=\{\mathit{j}\in \zeta :\mathit{j}⊈\mathit{i}\},$ and $\zeta [\subseteq \mathit{i}],$$\zeta \left[\not\subset \mathit{i}\right]$ defined analogously.

We consider $\mathcal{P}\left(\omega \right)$ as identical to $2^{\omega },$ so that both $\mathcal{P}\left(\omega \right)$ and $\mathcal{P}{\left(\omega \right)}^{\xi }$ for $\xi \in \Xi$ are homeomorphic Polich compact spaces. Points of $\mathcal{P}\left(\omega \right)$ will be called reals.

Assume that $\eta \subseteq \xi \in \Xi$. If $x\in \mathcal{P}{\left(\omega \right)}^{\xi }$ then let $x\upharpoonright \eta \in \mathcal{P}{\left(\omega \right)}^{\eta }$ denote the usual restriction. If $X\subseteq \mathcal{P}{\left(\omega \right)}^{\xi }$ then let $X\upharpoonright \eta =\{x\upharpoonright \eta :x\in X\}$. To save space, let $X{\upharpoonright }_{\subset \mathit{i}}$ mean $X\upharpoonright \xi [\subset \mathit{i}]$, $X{\upharpoonright }_{⊈\mathit{i}}$ mean $X\upharpoonright \xi \left[⊈\mathit{i}\right]$, etc.

But if $Y\subseteq \mathcal{P}{\left(\omega \right)}^{\eta }$ then we put $Y{\upharpoonright }^{-1}\xi =\{x\in \mathcal{P}{\left(\omega \right)}^{\xi }:x\upharpoonright \eta \in Y\}$.

To describe the idea behind the definition of iterated perfect sets, recall that the Sacks forcing consists of perfect subsets of $\mathcal{P}{\left(\omega \right)}^{}$, that is, sets of the form $H{}^{\prime \prime }\mathcal{P}\left(\omega \right)=\{H\left(a\right):a\in \mathcal{P}\left(\omega \right)\}$, where $H:\mathcal{P}{\left(\omega \right)}^{}\stackrel{\mathrm{onto}}{⟶}X$ is a homeomorphism.

To obtain a product Sacks model, with two factors (the case of a two-element unordered set as the length of iteration), we have to consider sets $X\subseteq \mathcal{P}{\left(\omega \right)}^2$ of the form $X=H{}^{\prime \prime }\mathcal{P}{\left(\omega \right)}^2$ where H is any homeomorphism defined on $\mathcal{P}{\left(\omega \right)}^2$ so that it splits in obvious way into a pair of one-dimensional homeomorphisms.

To obtain an iterated Sacks model, with two stages of iteration (the case of a two-element ordered set as the length of iteration), we have to consider sets $X\subseteq \mathcal{P}{\left(\omega \right)}^2$ of the form $X=H{}^{\prime \prime }\mathcal{P}{\left(\omega \right)}^2$, where H is any homeomorphism defined on $\mathcal{P}{\left(\omega \right)}^2$ such that if $H(a_1,a_2)=\langle x_1,x_2\rangle$ and $H(a_1^{\prime },a_2^{\prime })=\langle x_1^{\prime },x_2^{\prime }\rangle$ then $a_1=a_1^{\prime }⟺x_1=x_1^{\prime }$.

The combined product/iteration case results in the following definition.

Definition 1 

(iterated perfect sets, [21,22]). For any $\zeta \in \Xi ,$ ${\mathbf{Perf}}_{\zeta }$ is the collection of all sets $X\subseteq \mathcal{P}{\left(\omega \right)}^{\zeta }$ such that there is a homeomorphism $H:\mathcal{P}{\left(\omega \right)}^{\zeta }\stackrel{\mathrm{onto}}{⟶}X$ satisfying

$$x_0\upharpoonright \xi =x_1\upharpoonright \xi ⟺H\left(x_0\right)\upharpoonright \xi =H\left(x_1\right)\upharpoonright \xi$$

for all $x_0,x_1\in \mathtt{dom}H$ and $\xi \in \Xi$, $\xi \subseteq \zeta$. Homeomorphisms H satisfying this requirement will be called projection–keeping. In other words, sets in ${\mathbf{Perf}}_{\zeta }$ are images of $\mathcal{P}{\left(\omega \right)}^{\zeta }$ via projection–keeping homeomorphisms.

We put $\mathbf{Perf}={\bigcup }_{\xi \in \Xi }{\mathbf{Perf}}_{\xi }$.

Remark 1. 

Note that ⌀, the empty set, formally belongs to Ξ, and then $\mathcal{P}{\left(\omega \right)}^{⌀}=\{⌀\}$, and we easily see that $1=\{⌀\}$ is the only set in ${\mathbf{Perf}}_{⌀}$.

For the convenience of the reader, we now present five lemmas on sets in ${\mathbf{Perf}}_{\zeta }$ established in [21,22].

Lemma 1 

(Proposition 4 in [22]). Let $\zeta \in \Xi$. Every set $X\in {\mathbf{Perf}}_{\zeta }$ is closed and satisfies the following properties:

1. 

If $\mathit{i}\in \zeta$ and $z\in X{\upharpoonright }_{\subset \mathit{i}}$ then $D_{Xz}\left(\mathit{i}\right)=\{x\left(\mathit{i}\right):x\in X\wedge x{\upharpoonright }_{\subset \mathit{i}}=z\}$ is a perfect set in $\mathcal{P}{\left(\omega \right)}^{}$.

2. 

If $\xi \in {\mathrm{IS}}_{\zeta }$, and a set $X^{\prime }\subseteq X$ is open in X (in the relative topology) then the projection $X^{\prime }\upharpoonright \xi$ is open in $X\upharpoonright \xi$. In other words, the projection from X to $X\upharpoonright \xi$ is an open map.

3. 

If $\xi ,\eta \in {\mathrm{IS}}_{\zeta }$, $x\in X\upharpoonright \xi$, $y\in X\upharpoonright \eta$, and $x\upharpoonright (\xi \cap \eta )=y\upharpoonright (\xi \cap \eta ),$ then $x\cup y\in X\upharpoonright (\xi \cup \eta )$.

Proof (sketch). 

Clearly $\mathcal{P}{\left(\omega \right)}^{\zeta }$ satisfies P-1, P-2, P-3, and one easily shows that projection–keeping homeomorphisms preserve the requirements. □

Lemma 2 

(Lemma 5 in [22]). Suppose that $\xi ,\zeta ,\vartheta \in \Xi$, $\xi \cup \zeta \subseteq \vartheta$, $W\in {\mathbf{Perf}}_{\vartheta }$, $C\subseteq W\upharpoonright \zeta$ is any set, and $U=W\cap \left(C{\upharpoonright }^{-1}\vartheta \right)$. Then $U\upharpoonright \xi =\left(W\upharpoonright \xi \right)\cap \left(C\upharpoonright (\xi \cap \zeta ){\upharpoonright }^{-1}\xi \right)$.

Lemma 3 

(Lemma 6 in [22]). If $\zeta \in \Xi$, $X\in {\mathbf{Perf}}_{\zeta }$, $\xi \in {\mathrm{IS}}_{\zeta }$, then $X\upharpoonright \xi \in {\mathbf{Perf}}_{\xi }$.

Lemma 4 

(Lemma 8 in [22]). If $\zeta \in \Xi$, $X\in {\mathbf{Perf}}_{\zeta }$, a set $U\subseteq X$ is open in X, and $x_0\in U,$ then there is a set $X^{\prime }\in {\mathbf{Perf}}_{\zeta }$, $X^{\prime }\subseteq U,$ clopen in X and containing $x_0$.

Lemma 5 

(Lemma 9 in [22]). Suppose that $\zeta \in \Xi$, $\eta \in {\mathrm{IS}}_{\zeta }$, $X\in {\mathbf{Perf}}_{\zeta }$, $Y\in {\mathbf{Perf}}_{\eta },$ and $Y\subseteq X\upharpoonright \eta$. Then $Z=X\cap \left(Y{\upharpoonright }^{-1}\zeta \right)$ belongs to ${\mathbf{Perf}}_{\zeta }$.

In particular $Y{\upharpoonright }^{-1}\zeta \in {\mathbf{Perf}}_{\zeta }$, since obviously $\mathcal{P}{\left(\omega \right)}^{\zeta }\in {\mathbf{Perf}}_{\zeta }$.

Corollary 1. 

Assume that $\xi ,\eta \in \Xi$, $\vartheta =\xi \cup \eta$, $X\in {\mathbf{Perf}}_{\xi }$, $Y\in {\mathbf{Perf}}_{\eta }$, and $X\upharpoonright (\xi \cap \eta )=Y\upharpoonright (\xi \cap \eta )$. Then $Z=\left(X{\upharpoonright }^{-1}\vartheta \right)\cap \left(Y{\upharpoonright }^{-1}\vartheta \right)\in {\mathbf{Perf}}_{\vartheta }$.

Proof. 

The bigger set $X^{\prime }=X{\upharpoonright }^{-1}\vartheta$ belongs to ${\mathbf{Perf}}_{\vartheta }$ by Lemma 5. In addition, $X^{\prime }\upharpoonright \eta =X\upharpoonright (\xi \cap \eta ){\upharpoonright }^{-1}\eta$ by Lemma 2 (with $C=X$, $W=\mathcal{P}{\left(\omega \right)}^{\vartheta }$). It follows that $Y\subseteq X^{\prime }\upharpoonright \eta$, because $Y\upharpoonright (\xi \cap \eta )=X\upharpoonright (\xi \cap \eta )$. We conclude that $X^{\prime }\cap \left(Y{\upharpoonright }^{-1}\vartheta \right)\in {\mathbf{Perf}}_{\vartheta }$ by Lemma 5. Finally, we have $X^{\prime }\cap \left(Y{\upharpoonright }^{-1}\vartheta \right)=Z$ by construction. □

Corollary 2. 

Assume that ${\xi }_0,{\xi }_1,{\xi }_2,\cdots \in \Xi$ are pairwise disjoint, $\vartheta ={\bigcup }_k{\xi }_k$, and $X_k\in {\mathbf{Perf}}_{{\xi }_k}$ for each k. Then the set $Z={\bigcap }_k\left(X_k{\upharpoonright }^{-1}\vartheta \right)$ belongs to ${\mathbf{Perf}}_{\vartheta }$, $Z\upharpoonright {\xi }_k=X_k$ and $Z⩽X_k$ for all k.

Proof. 

For each k, there exists a projection–keeping homeomorphism $H_k:\mathcal{P}{\left(\omega \right)}^{{\xi }_k}\stackrel{\mathrm{onto}}{⟶}{X}_k$. Define $H:\mathcal{P}{\left(\omega \right)}^{\vartheta }\to \mathcal{P}{\left(\omega \right)}^{\vartheta }$ by $H\left(x\right)\upharpoonright {\xi }_k=H_k\left(x\upharpoonright {\xi }_k\right)$ for all k. Then H is projection–keeping and $H:\mathcal{P}{\left(\omega \right)}^{\vartheta }\stackrel{\mathrm{onto}}{⟶}Z$. □

Still arguing in $\mathbf{L}$, we let $\mathsf{\Pi }$ be the group of all permutations $\pi$ of the index set $\mathit{I}$, i.e. all bijections $\pi :\mathit{I}\stackrel{\mathrm{onto}}{⟶}\mathit{I}$ such that $\mathit{i}\subset \mathit{j}⟺\pi \left(\mathit{i}\right)\subset \pi \left(\mathit{j}\right)$. Any such a permutation $\pi \in \mathsf{\Pi }$ induces a transformation acting on several types of objects as follows.

• If $\xi \in \Xi$, or generally $\xi \subseteq \mathit{I}$, then $\pi \xi =\pi {}^{\prime \prime }\xi =\{\pi \left(\mathit{i}\right):\mathit{i}\in \xi \}$.
• If $\xi \subseteq \mathit{I}$ and $x\in \mathcal{P}{\left(\omega \right)}^{\xi }$ then $\pi x\in \mathcal{P}{\left(\omega \right)}^{\pi \xi }$ is defined by $\pi x\left(\pi \right(\mathit{i}\left)\right)=x\left(\mathit{i}\right)$ for all $\mathit{i}\in \xi$. That is, formally $\pi x=x\circ {\pi }^{-1}$, the superposition.
• If $\xi \subseteq \mathit{I}$ and $X\subseteq \mathcal{P}{\left(\omega \right)}^{\xi }$ then $\pi X=\{\pi x:x\in X\}$.
• If $G\subseteq \mathbf{Perf}$ then $\pi G=\{\pi X:X\in G\}$.

The following lemma is obvious.

Lemma 6. 

If $X\in {\mathbf{Perf}}_{\xi }$ then $\pi X\in {\mathbf{Perf}}_{\pi \xi }$.

Moreover π is an order preserving automorphism of $\mathbf{Perf}$.

6. The Forcing Notion and the Basic Extension

This section introduces the forcing notion we consider and the according generic extension called the basic extension.

We continue to argue in $\mathbf{L}$. Recall that a partially ordered set $\mathit{I}\in \mathbf{L}$ is defined in Section 5, and $\Xi$ is the set of all at most countable initial segments $\xi \subseteq \mathit{I}$ in $\mathbf{L}$. For any $\zeta \in \Xi ,$ let ${\mathbb{P}}_{\zeta }={\left({\mathbf{Perf}}_{\zeta }\right)}^{\mathbf{L}}$.

The set $\mathbb{P}={\mathbb{P}}_{\mathit{I}}={\bigcup }_{\zeta \in \Xi }{\mathbb{P}}_{\zeta }\in \mathbf{L}$ will be the forcing notion.

To define the order, we put $\parallel X\parallel =\zeta$ whenever $X\in {\mathbb{P}}_{\zeta }$. Now we set $X⩽Y$ (i.e. X is stronger than Y) if and only if $\zeta =\parallel Y\parallel \subseteq \parallel X\parallel$ and $X\upharpoonright \zeta \subseteq Y$.

Remark 2. 

We may note that the set $\mathrm{𝟙}=\{⌀\}$ as in Remark 1 belongs to $\mathbb{P}$ and is the $⩽$-largest (i.e., the weakest) element of $\mathbb{P}$.

Now let $G\subseteq \mathbb{P}$ be a $\mathbb{P}$-generic set (filter) over $\mathbf{L}$.

Remark 3. 

If $X\in {\mathbb{P}}_{\zeta }$ in $\mathbf{L}$ then X is not even a closed set in $\mathcal{P}{\left(\omega \right)}^{\zeta }$ in $\mathbf{L}\left[G\right]$. However we can transform it to a perfect set in $\mathbf{L}\left[G\right]$ by the closure operation. Indeed the topological closure $X^{\#}$ of such a set X in $\mathcal{P}{\left(\omega \right)}^{\zeta }$ taken in $\mathbf{L}\left[G\right]$ belongs to ${\mathbf{Perf}}_{\zeta }$ from the point of view of $\mathbf{L}\left[G\right]$.

It easily follows from Lemma 4 that there exists a unique array $\mathbf{a}\left[G\right]={\langle {\mathbf{a}}_{\mathit{i}}\left[G\right]\rangle }_{\mathit{i}\in \mathit{I}}$, all ${\mathbf{a}}_{\mathit{i}}\left[G\right]$ being elements of $\mathcal{P}\left(\omega \right)$, such that $\mathbf{a}\left[G\right]\upharpoonright \xi \in X^{\#}$ whenever $X\in G$ and $\parallel X\parallel =\xi \in \Xi$. Then $\mathbf{L}\left[G\right]=\mathbf{L}\left[{\langle {\mathbf{a}}_{\mathit{i}}\left[G\right]\rangle }_{\mathit{i}\in \mathit{I}}\right]=\mathbf{L}\left[\mathbf{a}\left[G\right]\right]$ is a $\mathbb{P}$-generic extension of $\mathbf{L}$, which we call the basic extension.

For the sake of convenience, let ${\mathbf{a}}_{\mathsf{\Lambda }}\left[G\right]=⌀$.

Theorem 4 

(Thm 24 in both [21,22]). Every cardinal in $\mathbf{L}$ remains a cardinal in $\mathbf{L}\left[G\right]$. Every ${\mathbf{a}}_{\mathit{i}}\left[G\right]$ is Sacks generic over the model $\mathbf{L}\left[\mathbf{a}\right[G\left]{\upharpoonright }_{\subset \mathit{i}}\right]$.

Proof (idea). 

The forcing ${\mathbf{Perf}}_{}$ has the following property in $\mathbf{L}$, common with the ordinary one-step Sacks forcing:

(∗)

if sets $D_n\subseteq {\mathbf{Perf}}_{}$ are open dense in ${\mathbf{Perf}}_{}$, and $X\in {\mathbf{Perf}}_{}$, then there is a stronger condition $Y\in {\mathbf{Perf}}_{}$, $Y⩽X$, and finite sets $D_n^{\prime }\subseteq D_n$ pre-dense in ${\mathbf{Perf}}_{}$ below Y, in the sense that any stronger $Z\in {\mathbf{Perf}}_{}$, $Z⩽Y$, is compatible with some $Z^{\prime }\in D_n$.

This property, established in [21,22] by means of a splitting/fusion technique, easily implies the preservation of all $\mathbf{L}$-cardinals in $\mathbb{P}$-generic extensions of $\mathbf{L}$. □

Here follow several lemmas on reals in $\mathbb{P}$-generic models $\mathbf{L}\left[G\right]$, established in [21]. In the lemmas, we let $G\subseteq \mathbb{P}$ be a set $\mathbb{P}$-generic over $\mathbf{L}$.

Lemma 7 

(Lemma 22 in [21]). Suppose that sets $\eta ,\xi \in \Xi$ satisfy $\forall \mathit{j}\in \eta \exists \mathit{i}\in \xi (\mathit{j}\subseteq \mathit{i})$. Then $\mathbf{a}\left[G\right]\upharpoonright \eta \in \mathbf{L}\left[\mathbf{a}\right[G\left]\upharpoonright \xi \right]$.

Lemma 8 

(Lemma 26 in [21]). Suppose that $K\in \mathbf{L}$ is an initial segment in $\mathit{I}$, and $\mathit{i}\in \mathit{I}\setminus K$. Then ${\mathbf{a}}_{\mathit{i}}\left[G\right]\notin \mathbf{L}\left[\mathbf{a}\left[G\right]\upharpoonright K\right]$.

Lemma 9 

(Corollary 27 in [21]). If $\mathit{i}\ne \mathit{j}$ then ${\mathbf{a}}_{\mathit{i}}\left[G\right]\ne {\mathbf{a}}_{\mathit{j}}\left[G\right]$ and even $\mathbf{L}\left[{\mathbf{a}}_{\mathit{i}}\left[G\right]\right]\ne \mathbf{L}\left[{\mathbf{a}}_{\mathit{j}}\left[G\right]\right]$.

Lemma 10 

(Lemma 29 in [21]). If $K\in \mathbf{L}$ is an initial segment of $\mathit{I}$, and $r\in \mathcal{P}\left(\omega \right)\cap \mathbf{L}\left[G\right]$, then either $r\in \mathbf{L}\left[\mathbf{a}\right[G\left]\upharpoonright K\right]$ or ${\mathbf{a}}_{\mathit{i}}\left[G\right]\in \mathbf{L}\left[r\right]$ for some $\mathit{i}\in \mathit{I}\setminus K$.

7. Structure of the Basic Extension

We apply the lemmas above in the proof of the next theorem. Let ${⩽}_{\mathbf{L}}$ denote the Gödel well-ordering on $\mathcal{P}\left(\omega \right),$ so that $x{⩽}_{\mathbf{L}}y$ if and only if $x\in \mathbf{L}\left[y\right]$. Let $x{<}_{\mathbf{L}}y$ mean that $x{⩽}_{\mathbf{L}}y$ but $y{\nleqq }_{\mathbf{L}}x$, and $x{\equiv }_{\mathbf{L}}y$ mean that $x{⩽}_{\mathbf{L}}y$ and $y{⩽}_{\mathbf{L}}x$.

Say that y is a true${⩽}_{\mathbf{L}}$-successor of x (where $x,y\in \mathcal{P}\left(\omega \right)$) if and only if $x{<}_{\mathbf{L}}y$ and any real $z\in \mathcal{P}\left(\omega \right)$ satisfies $z{<}_{\mathbf{L}}y⟹z{⩽}_{\mathbf{L}}x$.

Theorem 5. 

Let $G\subseteq \mathbb{P}$ be a set $\mathbb{P}$-generic over $\mathbf{L}$, and $\mathit{i}\in \mathit{I}$. Then we have the following:

(i)

if $\mathit{j}\in \mathit{I}$ and $\mathit{j}\subseteq \mathit{i}$ then ${\mathbf{a}}_{\mathit{j}}\left[G\right]{⩽}_{\mathbf{L}}{\mathbf{a}}_{\mathit{i}}\left[G\right];$

(ii)

if $\mathit{j}\in \mathit{I}$ and $\mathit{j}⊈\mathit{i}$ then ${\mathbf{a}}_{\mathit{j}}\left[G\right]{\nleqq }_{\mathbf{L}}{\mathbf{a}}_{\mathit{i}}\left[G\right];$

(iii)

if $r\in \mathbf{L}\left[G\right]\cap \mathcal{P}\left(\omega \right)$ and $r{⩽}_{\mathbf{L}}{\mathbf{a}}_{\mathit{i}}\left[G\right]$ then $r\in \mathbf{L}$ or $r{\equiv }_{\mathbf{L}}{\mathbf{a}}_{\mathit{j}}\left[G\right]$ for some $\mathit{j}\in \mathit{I}$, $\mathit{j}\subseteq \mathit{i};$

(iv)

if $\mathit{i}\in \mathit{I}$, $\gamma <{\omega }_1^{\mathbf{L}}$, then ${\mathbf{a}}_{\mathit{i}⌢\gamma }\left[G\right]$ is a true ${⩽}_{\mathbf{L}}$-successor of ${\mathbf{a}}_{\mathit{i}}\left[G\right];$

(v)

if $\mathit{i}\in \mathit{I}$, and $y\in \mathcal{P}\left(\omega \right)\cap \mathbf{L}\left[G\right]$ is a true ${⩽}_{\mathbf{L}}$-successor of ${\mathbf{a}}_{\mathit{i}}\left[G\right]$, then there is $\gamma <{\omega }_1^{\mathbf{L}}$ such that $y{\equiv }_{\mathbf{L}}{\mathbf{a}}_{\mathit{i}⌢\gamma }\left[G\right];$

(vi)

if $\gamma <{\omega }_1^{\mathbf{L}}$, then ${\mathbf{a}}_{\langle \gamma \rangle }\left[G\right]$ is a true ${⩽}_{\mathbf{L}}$-successor of ${\mathbf{a}}_{\mathsf{\Lambda }}\left[G\right];$

(vii)

if $y\in \mathcal{P}\left(\omega \right)\cap \mathbf{L}\left[G\right]$ is a true ${⩽}_{\mathbf{L}}$-successor of ${\mathbf{a}}_{\mathsf{\Lambda }}\left[G\right]$, then there is $\gamma <{\omega }_1^{\mathbf{L}}$ such that $x{\equiv }_{\mathbf{L}}{\mathbf{a}}_{\langle \gamma \rangle }\left[G\right].$

Proof. 

(i) Apply Lemma 7 with $\eta =\left\{\mathit{j}\right\}$ and $\xi =\left\{\mathit{i}\right\}$.

(ii) Apply Lemma 8 with $K=[\subseteq \mathit{i}]$.

(iii) If there are elements $\mathit{j}\in \mathcal{I}$, $\mathit{j}\subseteq \mathit{i}$, such that ${\mathbf{a}}_{\mathit{j}}\left[G\right]\in \mathbf{L}\left[r\right]$, then let $\mathit{j}$ be the largest such one. Let $\xi =[\subseteq \mathit{j}]$ (a finite initial segment of $\mathit{I}$). By Lemma 10, either $r\in \mathbf{L}\left[\mathbf{a}\right[G\left]\upharpoonright \xi \right]$, or there is ${\mathit{i}}^{\prime }\notin \xi$ such that ${\mathbf{a}}_{{\mathit{i}}^{\prime }}\left[G\right]\in \mathbf{L}\left[r\right]$. In the “either” case, we have $r\in \mathbf{L}\left[{\mathbf{a}}_{\mathit{j}}\left[G\right]\right]$ by (i), so that $\mathbf{L}\left[r\right]=\mathbf{L}\left[{\mathbf{a}}_{\mathit{j}}\left[G\right]\right]$ by the choice of $\mathit{j}$. In the “or” case we have ${\mathbf{a}}_{{\mathit{i}}^{\prime }}\left[G\right]\in \mathbf{L}\left[a_{\mathit{i}}\left[G\right]\right]$, hence ${\mathit{i}}^{\prime }\subseteq \mathit{i}$ by (ii). However, this contradicts the choice of $\mathit{j}$ and ${\mathit{i}}^{\prime }$.

Finally if there is no $\mathit{j}\in \mathcal{I}$, $\mathit{j}\subseteq \mathit{i}$, such that ${\mathbf{a}}_{\mathit{j}}\left[G\right]\in \mathbf{L}\left[r\right]$, then the same argument with $\xi =⌀$ gives $r\in \mathbf{L}$.

(iv) The relation ${\mathbf{a}}_{\mathit{i}}\left[G\right]{<}_{\mathbf{L}}{\mathbf{a}}_{\mathit{i}⌢\gamma }\left[G\right]$ is implied by Lemmas 7 and 8. If now $z{<}_{\mathbf{L}}{\mathbf{a}}_{\mathit{i}⌢\gamma }\left[G\right]$ then $z\in \mathbf{L}$ or $z{\equiv }_{\mathbf{L}}{\mathbf{a}}_{\mathit{j}}\left[G\right]$ for some $\mathit{j}\subseteq \mathit{i}⌢\gamma$ by (iii), and in the latter case in fact $\mathit{j}\subset \mathit{i}⌢\gamma$, hence $\mathit{j}\subseteq \mathit{i}$, and then $z{⩽}_{\mathbf{L}}{\mathbf{a}}_{\mathit{i}}\left[G\right]$.

(v) As $y{\nleqq }_{\mathbf{L}}{\mathbf{a}}_{\mathit{i}}\left[G\right]$, by Lemma 10 there is $\mathit{j}\in \mathit{I}$ such that $\mathit{j}⊈\mathit{i}$ and ${\mathbf{a}}_{\mathit{j}}\left[G\right]{⩽}_{\mathbf{L}}y$. If ${\mathbf{a}}_{\mathit{j}}\left[G\right]{<}_{\mathbf{L}}y$ strictly then ${\mathbf{a}}_{\mathit{j}}\left[G\right]{⩽}_{\mathbf{L}}{\mathbf{a}}_{\mathit{i}}\left[G\right]$ by the true ${⩽}_{\mathbf{L}}$-successor property, hence $\mathit{j}\subseteq \mathit{i}$ by (ii), contrary to the choice of $\mathit{j}$. Therefore in fact ${\mathbf{a}}_{\mathit{j}}\left[G\right]{\equiv }_{\mathbf{L}}y$. Then we have $\mathit{i}\subset \mathit{j}$ still by the true ${⩽}_{\mathbf{L}}$-successor property and (i), (ii). This implies $\mathit{j}=\mathit{i}⌢\gamma$ for some $\gamma <{\omega }_1^{\mathbf{L}}$, because if say $\mathit{j}=\mathit{i}⌢\gamma ⌢\delta$ then $z={\mathbf{a}}_{i⌢\gamma }\left[G\right]$ is strictly between ${\mathbf{a}}_{\mathit{i}}\left[G\right]$ and ${\mathbf{a}}_{\mathit{j}}\left[G\right]$, contrary to the true ${⩽}_{\mathbf{L}}$-successor property.

(vi) Similar to (iv). Recall that ${\mathbf{a}}_{\mathsf{\Lambda }}\left[G\right]=⌀\in \mathbf{L}$. This implies ${\mathbf{a}}_{\mathsf{\Lambda }}\left[G\right]{⩽}_{\mathbf{L}}{\mathbf{a}}_{\langle \gamma \rangle }\left[G\right]$. On the other hand, ${\mathbf{a}}_{\langle \gamma \rangle }\left[G\right]{\nleqq }_{\mathbf{L}}{\mathbf{a}}_{\mathsf{\Lambda }}\left[G\right]$ holds by Lemma 8 with $K=⌀$. If now $z{<}_{\mathbf{L}}{\mathbf{a}}_{\langle \gamma \rangle }\left[G\right]$ then $z\in \mathbf{L}$ or $z{\equiv }_{\mathbf{L}}{\mathbf{a}}_{\mathit{j}}\left[G\right]$ for some $\mathit{j}\subseteq \langle \gamma \rangle$ by (iii), and in the latter case in fact $\mathit{j}=\langle \gamma \rangle$, hence then $z{\equiv }_{\mathbf{L}}{\mathbf{a}}_{\langle \gamma \rangle }\left[G\right]$, contrary to the choice of z.

(vii) As $y{\nleqq }_{\mathbf{L}}{\mathbf{a}}_{\mathsf{\Lambda }}\left[G\right]\in \mathbf{L}$, by Lemma 10 (with $K=⌀$) there is $\mathit{j}\in \mathit{I}$ such that ${\mathbf{a}}_{\mathit{j}}\left[G\right]{⩽}_{\mathbf{L}}y$. If ${\mathbf{a}}_{\mathit{j}}\left[G\right]{<}_{\mathbf{L}}y$ strictly then ${\mathbf{a}}_{\mathit{j}}\left[G\right]{⩽}_{\mathbf{L}}{\mathbf{a}}_{\mathsf{\Lambda }}\left[G\right]$ by the true ${⩽}_{\mathbf{L}}$-successor property, hence ${\mathbf{a}}_{\mathit{j}}\left[G\right]\in \mathbf{L}$, contrary to Lemma 8 with $K=⌀$. Therefore in fact ${\mathbf{a}}_{\mathit{j}}\left[G\right]{\equiv }_{\mathbf{L}}y$. This implies $\mathit{j}=\langle \gamma \rangle$ for some $\gamma <{\omega }_1^{\mathbf{L}}$, because if, say, $\mathit{j}=\langle \gamma ,\delta \rangle$ then $y={\mathbf{a}}_{\langle \gamma \rangle }\left[G\right]$ is strictly between ${\mathbf{a}}_{\mathsf{\Lambda }}\left[G\right]$ and $y{\equiv }_{\mathbf{L}}{\mathbf{a}}_{\mathit{j}}\left[G\right]$, contrary to the true ${⩽}_{\mathbf{L}}$-successor property. □

Now consider the following formula:

$\mathfrak{A}(n,\overrightarrow{x}):=$$\overrightarrow{x}=\langle x_0,x_1,\dots ,x_n\rangle$ is a tuple of reals $x_k\subseteq \omega$ such that $x_0=⌀$ and each $x_k$ ($0<k\le n$) is a true ${⩽}_{\mathbf{L}}$-successor of $x_{k-1}$.

Thus $\mathfrak{A}(n,\overrightarrow{x})$ separates tuples of true successor iterations, of length n.

Remark 4. 

$\mathfrak{A}(n,\overrightarrow{x})$ is a ${\Pi }_3^1$ relation, absolute for any transitive model of $\mathbf{ZF}$ containing the true ${\omega }_1$, and component-wise ${\equiv }_{\mathbf{L}}$-invariant in the argument $\overrightarrow{x}=\langle x_0,x_1,\dots ,x_n\rangle$. Indeed to see that $\mathfrak{A}$ is ${\Pi }_3^1$ note that ‘being a true ${⩽}_{\mathbf{L}}$-successor’ is ${\Pi }_3^1$ by direct estimation. To see the absoluteness note that both ‘being a true ${⩽}_{\mathbf{L}}$-successor’ and $\mathfrak{A}$ are relativized to the lower ${⩽}_{\mathbf{L}}$-cone of the arguments. The invariance is obvious.

Corollary 3 

(of Theorem 5). Let $G\subseteq \mathbb{P}$ be a set $\mathbb{P}$-generic over $\mathbf{L}$.

(i)

If $\mathit{i}=\langle {\gamma }_1,{\gamma }_2,\dots ,{\gamma }_n\rangle \in \mathit{I}$, $\mathtt{dom}\mathit{i}=n\ge 1$, and

$${\mathbf{a}}_{\subseteq \mathit{i}}\left[G\right]=\langle {\mathbf{a}}_{\mathsf{\Lambda }}\left[G\right],{\mathbf{a}}_{\langle {\gamma }_1\rangle }\left[G\right],{\mathbf{a}}_{\langle {\gamma }_1,{\gamma }_2\rangle }\left[G\right],\dots ,{\mathbf{a}}_{\langle {\gamma }_1,{\gamma }_2,\dots ,{\gamma }_n\rangle }\left[G\right]\rangle ,$$

(1)

then $\mathfrak{A}(n,{\mathbf{a}}_{\subseteq \mathit{i}}\left[G\right])$ holds in $\mathbf{L}\left[G\right]$.

(ii)

Conversely if $\overrightarrow{x}=\langle x_0,x_1,\dots ,x_n\rangle \in \mathbf{L}\left[G\right]$ and $\mathfrak{A}(n,\overrightarrow{x})$ holds in $\mathbf{L}\left[G\right]$ then there is $\mathit{i}=\langle {\gamma }_1,{\gamma }_2,\dots ,{\gamma }_n\rangle \in \mathit{I}$ such that $\overrightarrow{x}{\equiv }_{\mathbf{L}}{\mathbf{a}}_{\subseteq \mathit{i}}\left[G\right]$ component-wise, that is, $x_0{\equiv }_{\mathbf{L}}{\mathbf{a}}_{\mathsf{\Lambda }}\left[G\right]$, $x_1{\equiv }_{\mathbf{L}}{\mathbf{a}}_{\langle {\gamma }_1\rangle }\left[G\right]$, $x_2{\equiv }_{\mathbf{L}}{\mathbf{a}}_{\langle {\gamma }_1,{\gamma }_2\rangle }\left[G\right]$, …, $x_n{\equiv }_{\mathbf{L}}{\mathbf{a}}_{\langle {\gamma }_1,{\gamma }_2,\dots ,{\gamma }_n\rangle }\left[G\right]$.

8. A Model in Which the Parameter-Free ${\mathbf{AC}}_{\omega }^{*}$ Fails

Here we prove Theorem 3(i). Let us fix a set $G\subseteq \mathbb{P}$, $\mathbb{P}$-generic over $\mathbf{L}$ and consider the according $\mathbb{P}$-generic array $\mathbf{a}\left[G\right]={\langle {\mathbf{a}}_{\mathit{i}}\left[G\right]\rangle }_{\mathit{i}\in \mathit{I}}$ and the $\mathbb{P}$-generic extension $\mathbf{L}\left[G\right]=\mathbf{L}\left[\mathbf{a}\right[G\left]\right]$. The goal is to define a sub-extension of $\mathbf{L}\left[G\right]$ in which the parameter-free ${\mathbf{AC}}_{\omega }^{*}$ fails.

• Let $\mathsf{\Omega }\in \mathbf{L}$ be the set of all finite or $\mathbf{L}$-countable initial segments $\xi \subseteq \mathit{I}$ such that there is a number $n<\omega$ satisfying $\mathtt{dom}\mathit{i}<n$ for all $\mathit{i}\in \xi$.
• Let $W\left[G\right]\in \mathbf{L}\left[G\right]$ be the set of all restrictions of the form $\mathbf{a}\left[G\right]\upharpoonright \xi$, $\xi \in \mathsf{\Omega }$, of the generic array $\mathbf{a}\left[G\right]$.
• Let $\mathrm{OD}{\left(W\left[G\right]\right)}^{\mathbf{L}\left[G\right]}$ be the class of all sets $W\left[G\right]$-ordinal-definable in $\mathbf{L}\left[G\right]$. Thus $x\in \mathrm{OD}{\left(W\left[G\right]\right)}^{\mathbf{L}\left[G\right]}$ iff x is definable in $\mathbf{L}\left[G\right]$ by a set-theoretic formula with parameters in $W\left[G\right]\cup \mathbf{Ord}$.

Here $\mathbf{Ord}$ is the class of all ordinals, as usual. See [20,25] on ordinal definability.

• Let ${\mathfrak{M}}_G=\mathrm{HOD}{\left(W\left[G\right]\right)}^{\mathbf{L}\left[G\right]}$ be the class of all sets $x\in \mathbf{L}\left[G\right]$, hereditarily $W\left[G\right]$-ordinal-definable in $\mathbf{L}\left[G\right]$, i.e., it is required that x itself, all elements of x, all elements of elements of x, etc., belong to the above defined class $\mathrm{OD}{\left(W\left[G\right]\right)}^{\mathbf{L}\left[G\right]}$ in $\mathbf{L}\left[G\right]$.

The following theorem implies Theorem 3(i). Indeed the model ${\mathfrak{M}}_G$ is a cardinal-preserving extension of $\mathbf{L}$ by Theorem 4.

Theorem 6. 

If a set $G\subseteq \mathbb{P}$ is $\mathbb{P}$-generic over $\mathbf{L}$ then ${\mathfrak{M}}_G$ is a model of $\mathbf{ZF}$ in which the parameter-free/ ${\mathbf{AC}}_{\omega }^{*}\left({\Pi }_3^1\right)$ fails.

It follows that ${\mathfrak{M}}_G\cap \mathcal{P}\left(\omega \right)$ is a model of ${\mathbf{PA}}_2+\neg {\mathbf{AC}}_{\omega }^{*}\left({\Pi }_3^1\right)$.

Proof. 

That classes of the form $\mathrm{HOD}\left(X\right)$ model $\mathbf{ZF}$ see [20], Chapter 13.

Note that if $\mathit{i}\in \mathit{I}$ then ${\mathbf{a}}_{\mathit{i}}\left[G\right]\in {\mathfrak{M}}_G=\mathrm{HOD}{\left(W\left[G\right]\right)}^{\mathbf{L}\left[G\right]}$ via the initial segment $\xi =[\subseteq a]=\{\mathit{j}\in \mathit{I}:\mathit{j}\subseteq \mathit{i}\}\in \mathsf{\Omega }$, and hence ${\mathbf{a}}_{\subseteq \mathit{i}}\left[G\right]\in {\mathfrak{M}}_G$ as well. It follows by Corollary 3(i) that $\exists x\mathfrak{A}(m,x)$ is true in ${\mathfrak{M}}_G$, where $m=\mathtt{dom}\mathit{i}$. Our goal will be to show that the parameter-free formula $\exists x\forall m\mathfrak{A}(m,{\left(x\right)}_m)$, the right-hand side of ${\mathbf{AC}}_{\omega }$, fails in ${\mathfrak{M}}_G$, meaning that ${\mathbf{AC}}_{\omega }^{*}$ fails in ${\mathfrak{M}}_G$ for the formula $\mathfrak{A}$.

Suppose to the contrary that there is $x\in {\mathfrak{M}}_G$ satisfying $\forall m\mathfrak{A}(m,{\left(x\right)}_m)$. This obviously results in a sequence ${\langle {\overrightarrow{y}}_m\rangle }_{m<\omega }\in {\mathfrak{M}}_G$ of tuples ${\overrightarrow{y}}_m=\langle y_0^m,y_1^m,\dots ,y_m^m\rangle \in {\mathfrak{M}}_G$ of reals $y_k^m\subseteq \omega$ satisfying $\mathfrak{A}(k,{\overrightarrow{y}}_k)$, that is, $y_0^m=⌀$ and each $y_k$ ($0<k\le m$) is a true ${⩽}_{\mathbf{L}}$-successor of $y_{k-1}$.

By definition there is an $\in$-formula $\phi (m,k,y,\mathbf{a}[G\left]\upharpoonright \xi \right)$ with free variables $m,k,y$, a parameter of the form $\mathbf{a}\left[G\right]\upharpoonright \xi$, where $\xi \in \mathsf{\Omega }$, and some ordinals as parameters—such that if $k\le m<\omega$ and $y\in {\mathfrak{M}}_G\cap \mathcal{P}\left(\omega \right)$ then $\phi (m,k,y,\mathbf{a}[G\left]\upharpoonright \xi \right)$ is true in $\mathbf{L}\left[G\right]$ iff $y=y_k^m$. (The case of several parameters of the form $\mathbf{a}\left[G\right]\upharpoonright \xi$, $\xi \in \mathsf{\Omega }$, can be easily reduced to the case of one parameter).

As $\xi \in \mathsf{\Omega }$, there is a number $1\le m<\omega$ such that $\mathtt{dom}\mathit{i}<m$ for all $\mathit{i}\in \xi$. Fix this m and consider the tuple ${\overrightarrow{y}}_m=\langle y_0^m,y_1^m,\dots ,y_m^m\rangle \in {\mathfrak{M}}_G=\mathrm{HOD}{\left(W\left[G\right]\right)}^{\mathbf{L}\left[G\right]}$. By Corollary 3(ii), there is a tuple $\mathit{j}=\langle {\gamma }_1,{\gamma }_2,\dots ,{\gamma }_m\rangle \in \mathit{I}$, such that ${\overrightarrow{y}}_m{\equiv }_{\mathbf{L}}{\mathbf{a}}_{\subseteq \mathit{j}}\left[G\right]$ component-wise, that is, $y_k^m{\equiv }_{\mathbf{L}}{\mathbf{a}}_{\mathit{j}}\left[G\right]={\mathbf{a}}_{\langle {\gamma }_1,{\gamma }_2,\dots ,{\gamma }_k\rangle }\left[G\right]$ for all $k\le m$.

Note that $\mathit{j}\notin \xi$ by the choice of m. There is a number $n\le m$ such that still ${\mathit{i}}_0=\langle {\gamma }_1,{\gamma }_2,\dots ,{\gamma }_{n-1},{\gamma }_n\rangle \notin \xi$ but the shorter tuple $\mathit{i}=\langle {\gamma }_1,{\gamma }_2,\dots ,{\gamma }_{n-1}\rangle$ belongs to $\xi$, and hence ${\mathbf{a}}_{\subseteq \mathit{i}}\left[G\right]\in \mathrm{HOD}{\left(W\left[G\right]\right)}^{\mathbf{L}\left[G\right]}$. Then by Corollary 3 the $\mathbf{L}$-degree ${\left[{\mathbf{a}}_{{\mathit{i}}_0}\left[G\right]\right]}_{\mathbf{L}}=\left\{a\subseteq \omega :a{\equiv }_{\mathbf{L}}{\mathbf{a}}_{{\mathit{i}}_0}\left[G\right]\right\}$ is definable in $\mathbf{L}\left[G\right]$ by the next formula, in which $\left(\mathbf{a}\left[G\right]\upharpoonright \xi \right)\left(\mathit{i}\right)={\mathbf{a}}_{\mathit{i}}\left[G\right]$.

$$\psi (a,\mathbf{a}[G\left]\upharpoonright \xi \right):=a\subseteq \omega \mathrm{is}\mathrm{a}\mathrm{true}{⩽}_{\mathbf{L}}-\mathrm{successor}\mathrm{of}\left(\mathbf{a}\right[G\left]\upharpoonright \xi \right)\left(\mathit{i}\right).$$

To conclude, ${\mathit{i}}_0\notin \xi \in \mathsf{\Omega }$ and the $\mathbf{L}$-degree ${\left[{\mathbf{a}}_{{\mathit{i}}_0}\left[G\right]\right]}_{\mathbf{L}}$ is definable in $\mathbf{L}\left[G\right]$ by an $\in$-formula with $\mathbf{a}\left[G\right]\upharpoonright \xi$ and ordinals as parameters. But this contradicts Lemma 11 that follows in the next Section. The contradiction refutes the contrary assumption above.

We finally note that $\mathfrak{A}$ is a ${\Pi }_3^1$ formula by Remark 4. □

9. The Non-Definability Lemma

Here we prove the following lemma.

Lemma 11. 

If a set $G\subseteq \mathbb{P}$ is $\mathbb{P}$-generic over $\mathbf{L}$, $\xi \in \Xi$, and ${\mathit{i}}_0\in \mathit{I}\setminus \xi$ then the $\mathbf{L}$-degree ${\left[{\mathbf{a}}_{{\mathit{i}}_0}\left[G\right]\right]}_{\mathbf{L}}=\left\{a\subseteq \omega :a{\equiv }_{\mathbf{L}}{\mathbf{a}}_{{\mathit{i}}_0}\left[G\right]\right\}$ cannot be defined in $\mathbf{L}\left[G\right]$ by an $\in$-formula with $\mathbf{a}\left[G\right]\upharpoonright \xi$ and ordinals as parameters.

Proof. 

Suppose to the contrary that $\psi (x,\mathbf{a}[G\left]\upharpoonright \xi \right)$ is a formula as indicated, and it holds in $\mathbf{L}\left[G\right]$ that ${\left[{\mathbf{a}}_{{\mathit{i}}_0}\left[G\right]\right]}_{\mathbf{L}}=\left\{x\subseteq \omega :\psi (x,\mathbf{a}\left[G\right]\upharpoonright \xi )\right\}$. Then there is a “condition” $X_0\in G$ such that

$$X_0\parallel -{\left[{\mathbf{a}}_{{\mathit{i}}_0}\left[\underline{G}\right]\right]}_{\mathbf{L}}=\left\{x\subseteq \omega :\psi (x,\mathbf{a}\left[\underline{G}\right]\upharpoonright \xi )\right\},$$

(2)

where $\parallel -$ is the $\mathbb{P}$-forcing relation over $\mathbf{L}$, and $\underline{G}$ is the canonical $\mathbb{P}$-name for the generic filter G. Let $\zeta =\parallel X_0\parallel$, so that $X_0\in {\mathbb{P}}_{\zeta }$.

We argue in $\mathbf{L}$. Thus $X\in {\mathbf{Perf}}_{\zeta }$. See Section 5 on permutations of $\mathit{I}$.

As $\xi ,\zeta$ are countable initial segments of $\mathit{I}$, it does not take much effort to define, in $\mathbf{L}$, a permutation $\pi \in \mathsf{\Pi }$ satisfying the following:

(A)

$\pi \upharpoonright \xi$ is the identity

(B)

$\pi \left({\mathit{i}}_0\right)\ne {\mathit{i}}_0$, and if $\mathit{i}\in (\zeta \setminus \xi )$ then $\pi \left(\mathit{i}\right)\notin \zeta \setminus \xi$.

Coming back to (2) above, we put $Y_0=\pi X_0$, ${\mathit{j}}_0=\pi \left({\mathit{i}}_0\right)$. Note that $Y_0\in {\mathbb{P}}_{{\zeta }^{\prime }}$ by Lemma 6, where ${\zeta }^{\prime }=\pi \zeta =\pi {}^{\prime \prime }\zeta$. We claim that

$$Y_0\parallel -{\left[{\mathbf{a}}_{{\mathit{j}}_0}\left[\underline{G}\right]\right]}_{\mathbf{L}}=\left\{x\subseteq \omega :\psi (x,\mathbf{a}\left[\underline{G}\right]\upharpoonright \xi )\right\}$$

(3)

To prove the claim, let $H^{\prime }\subseteq \mathbb{P}$ be $\mathbb{P}$-generic over $\mathbf{L}$, and $Y_0\in H^{\prime }$. We have to check that, in $\mathbf{L}\left[H^{\prime }\right]$, ${\left[{\mathbf{a}}_{{\mathit{j}}_0}\left[H^{\prime }\right]\right]}_{\mathbf{L}}=\left\{x\subseteq \omega :\psi (x,\mathbf{a}\left[H^{\prime }\right]\upharpoonright \xi )\right\}$.

The set $H={\pi }^{-1}{H}^{\prime }$ is $\mathbb{P}$-generic over $\mathbf{L}$ and obviously $X_0\in H$. It follows from (2) that ${\left[{\mathbf{a}}_{{\mathit{i}}_0}\left[H\right]\right]}_{\mathbf{L}}=\left\{x\subseteq \omega :\psi (x,\mathbf{a}\left[H\right]\upharpoonright \xi )\right\}$ in $\mathbf{L}\left[H\right]$. Yet $\mathbf{L}\left[H\right]=\mathbf{L}\left[H^{\prime }\right]$ (since $\pi \in \mathbf{L}$), $\mathbf{a}\left[H^{\prime }\right]\upharpoonright \xi =\mathbf{a}\left[H\right]\upharpoonright \xi$ by (A), and finally ${\mathbf{a}}_{{\mathit{j}}_0}\left[H^{\prime }\right]={\mathbf{a}}_{{\mathit{i}}_0}\left[H\right]$ by construction. Thus, indeed ${\left[{\mathbf{a}}_{{\mathit{j}}_0}\left[H^{\prime }\right]\right]}_{\mathbf{L}}=\left\{x\subseteq \omega :\psi (x,\mathbf{a}\left[H^{\prime }\right]\upharpoonright \xi )\right\}$ in $\mathbf{L}\left[H^{\prime }\right]$, as required. This completes the proof of (3).

The next step is to establish

(C)

$X_0$ and $Y_0$ are compatible in $\mathbb{P}$.

We check this claim arguing in $\mathbf{L}$, so that $X_0\in {\mathbf{Perf}}_{\zeta }$ and $Y_0\in {\mathbf{Perf}}_{{\zeta }^{\prime }}$, where ${\zeta }^{\prime }=\pi \zeta =\pi {}^{″}\zeta$. It follows from (A), (B) that the set $\eta =\zeta \cap \xi \in \Xi$ satisfies $\eta ={\zeta }^{\prime }\cap \xi ={\zeta }^{\prime }\cap \zeta$, and in addition $X_0\upharpoonright \eta =Y_0\upharpoonright \eta$. Let $\vartheta =\zeta \cup {\zeta }^{\prime }$. Then $Z=\left(X_0{\upharpoonright }^{-1}\vartheta \right)\cup \left(Y_0{\upharpoonright }^{-1}\vartheta \right)$ belongs to ${\mathbf{Perf}}_{\vartheta }$ by Corollary 1. Thus $Z\in \mathbb{P}$, hence (C) holds. This implies (3) since $Z⩽X_0,Y_0$ is obvious.

But it follows from (2) and (3) that $X_0$ and $Y_0$ force contradictory statements (because ${\mathit{i}}_0\ne {\mathit{j}}_0$, and hence ${\left[{\mathbf{a}}_{{\mathit{i}}_0}\left[G\right]\right]}_{\mathbf{L}}\ne {\left[{\mathbf{a}}_{{\mathit{j}}_0}\left[G\right]\right]}_{\mathbf{L}}$). The contradiction obtained completes the proof of the lemma. This accomplishes the proof of Theorem 6 as well. □

10. A Model in Which the Parameter-Free ${\mathbf{AC}}_{\omega }^{*}$ Holds but the Full ${\mathbf{AC}}_{\omega }$ Fails

Here we prove Theorem 1(i). The model will be a modification of the model studied in Section 8. We still fix a set $G\subseteq \mathbb{P}$, $\mathbb{P}$-generic over $\mathbf{L}$ and consider the $\mathbb{P}$-generic array $\mathbf{a}\left[G\right]={\langle {\mathbf{a}}_{\mathit{i}}\left[G\right]\rangle }_{\mathit{i}\in \mathit{I}}$ and the $\mathbb{P}$-generic extension $\mathbf{L}\left[G\right]=\mathbf{L}\left[\mathbf{a}\right[G\left]\right]$. We are going to define a sub-extension of $\mathbf{L}\left[G\right]$ in which the parameter-free ${\mathbf{AC}}_{\omega }^{*}$ holds but the full ${\mathbf{AC}}_{\omega }$ fails.

• Let ${\mathsf{\Omega }}^{\prime }\in \mathbf{L}$ be the set of all finite or $\mathbf{L}$-countable initial segments $\xi \subseteq \mathit{I}$ such that for any $\gamma <{\omega }_1$ there is a number $n=n_{\gamma }<\omega$ satisfying $\mathtt{dom}\mathit{i}<n$ for all $\mathit{i}\in \xi$ satisfying $\mathit{i}\left(0\right)=\gamma$.
• Let $W^{\prime }\left[G\right]\in \mathbf{L}\left[G\right]$ be the set of all restrictions of the form $\mathbf{a}\left[G\right]\upharpoonright \xi$, $\xi \in {\mathsf{\Omega }}^{\prime }$, of the generic array $\mathbf{a}\left[G\right]$.
• Let $\mathrm{OD}{\left(W^{\prime }\left[G\right]\right)}^{\mathbf{L}\left[G\right]}$ be the class of all sets $W^{\prime }\left[G\right]$-ordinal-definable in $\mathbf{L}\left[G\right]$. Thus $x\in \mathrm{OD}{\left(W^{\prime }\left[G\right]\right)}^{\mathbf{L}\left[G\right]}$ if and only if x is definable in $\mathbf{L}\left[G\right]$ by a set-theoretic formula with sets in $W^{\prime }\left[G\right]\cup \mathbf{Ord}$ as parameters.
• Let ${\mathfrak{M}}_G^{\prime }=\mathrm{HOD}{\left(W^{\prime }\left[G\right]\right)}^{\mathbf{L}\left[G\right]}$ be the class of all sets $x\in \mathbf{L}\left[G\right]$, hereditarily $W^{\prime }\left[G\right]$-ordinal-definable in $\mathbf{L}\left[G\right]$.

The following theorem implies Theorem 1(i). Indeed it follows from Theorem 4 that the model ${\mathfrak{M}}_G^{\prime }$ is a cardinal-preserving extension of $\mathbf{L}$.

Theorem 7. 

If a set $G\subseteq \mathbb{P}$ is $\mathbb{P}$-generic over $\mathbf{L}$ then ${\mathfrak{M}}_G^{\prime }$ is a model of $\mathbf{ZF}$ in which the parameter-free/ ${\mathbf{AC}}_{\omega }^{*}$ holds, even ${\mathbf{AC}}_{\omega }\left(\mathrm{OD}\right)$ (with ordinals as parameters) holds, but the full ${\mathbf{AC}}_{\omega }\left({\mathsf{\Pi }}_3^1\right)$ fails. It follows that ${\mathfrak{M}}_G^{\prime }\cap \mathcal{P}\left(\omega \right)$ is a model of ${\mathbf{PA}}_2+{\mathbf{AC}}_{\omega }^{*}+\neg {\mathbf{AC}}_{\omega }\left({\mathsf{\Pi }}_3^1\right)$.

Proof. 

Let ${\mathfrak{A}}^{\prime }(n,\overrightarrow{x})$ be the formula ‘$\mathfrak{A}(n,\overrightarrow{x})\wedge x_0={\mathbf{a}}_{\langle 0\rangle }\left[G\right]$’. (See the definition of $\mathfrak{A}$ in Section 7). Note the parameter ${\mathbf{a}}_{\langle 0\rangle }\left[G\right]$ in this formula. Similarly to the proof of Theorem 6, if $\mathit{i}\in \mathit{I}$ then ${\mathbf{a}}_{\mathit{i}}\left[G\right]\in {\mathfrak{M}}_G^{\prime }$ and ${\mathbf{a}}_{\subseteq \mathit{i}}\left[G\right]\in {\mathfrak{M}}_G^{\prime }$. It still follows by Corollary 3(i) that $\exists x{\mathfrak{A}}^{\prime }(n,x)$ is true in ${\mathfrak{M}}_G$, where $n=\mathtt{dom}\mathit{i}$. Moreover, arguments similar to the proof of Theorem 6, which we leave for the reader, show that the formula $\exists x\forall m\mathfrak{A}(k,{\left(x\right)}_m)$, the right-hand side of ${\mathbf{AC}}_{\omega }$, fails in ${\mathfrak{M}}_G^{\prime }$. Thus ${\mathbf{AC}}_{\omega }\left({\mathsf{\Pi }}_3^1\right)$ (with real parameters) fails in ${\mathfrak{M}}_G^{\prime }$.

It remains to prove that ${\mathbf{AC}}_{\omega }\left(\mathrm{OD}\right)$ (with ordinals as parameters) holds in ${\mathfrak{M}}_G^{\prime }$. Suppose towards the contrary that $\phi (k,x)$ is an $\in$-formula with ordinals as parameters, such that ${\mathbf{AC}}_{\omega }$ fails for $\phi$ in ${\mathfrak{M}}_G^{\prime }$. Thus there exists a condition $X^{*}\in G$ satisfying

(†)

$X^{*}\parallel -$ “it holds in ${\mathfrak{M}}_{\underline{G}}^{\prime }=\mathrm{HOD}{\left(W^{\prime }\left[\underline{G}\right]\right)}^{\mathbf{L}\left[\underline{G}\right]}$ that $\forall k\exists x\phi (k,x)$ but $\neg \exists x\forall k\phi (k,{\left(x\right)}_k)$”.

Here $\parallel -$ is the $\mathbb{P}$-forcing relation over $\mathbf{L}$, and $\underline{G}$ is the canonical $\mathbb{P}$-name for the generic filter G, as above.

As $\forall k\exists x\phi (k,x)$ holds in ${\mathfrak{M}}_G^{\prime }$, there is a sequence ${\langle x_k\rangle }_{k<\omega }\in \mathbf{L}\left[G\right]$ of reals $x_k\in {\mathfrak{M}}_G^{\prime },x_k\subseteq \omega$, satisfying $\phi (k,x_k)$, $\forall k$. By definition, for any k there is a set ${\delta }_k\in {\mathsf{\Omega }}^{\prime }$ such that $x_k\in \mathrm{HOD}{\left[\mathbf{a}\left[G\right]\upharpoonright {\delta }_k\right]}^{\mathbf{L}\left[G\right]}$ (meaning that only $\mathbf{a}\left[G\right]\upharpoonright {\delta }_k$ and ordinals are admitted as parameters), and the sequence ${\langle {\delta }_k\rangle }_{k<\omega }$ belongs to $\mathbf{L}\left[G\right]$ as well. Furthermore, as the forcing relation is definable in $\mathbf{L}$, there exist sequences ${\langle X_k\rangle }_{k<\omega }\in \mathbf{L}$ of conditions $X_k\in \mathbb{P}$ (possibly $X_k\notin G$), and ${\langle {\tau }_k\rangle }_{k<\omega }\in \mathbf{L}$ of sets ${\tau }_k\in {\mathsf{\Omega }}^{\prime }$, such that

$$X_k\parallel -\exists x\in \mathrm{HOD}\left[\mathbf{a}\left[\underline{G}\right]\upharpoonright {\tau }_k\right]\left({\mathfrak{M}}_{\underline{G}}^{\prime }|=(k,x)\right).$$

(4)

Now, arguing in $\mathbf{L}$, we let ${\xi }_k=\parallel X_k\parallel$, ${\eta }_k={\xi }_k\cup {\tau }_k$, and ${\xi }^{*}=\parallel X^{*}\parallel$. Thus ${\xi }^{*}$ and all ${\tau }_k,{\xi }_k,{\eta }_k$ belong to $\Xi$. Clearly there exists a sequence of permutations ${\pi }_k\in \mathsf{\Pi }$ (see Section 5), $k<\omega$, such that the sets ${\eta }_k^{\prime }={\pi }_k{}^{\prime \prime }{\eta }_k=\{{\pi }_k\left(\mathit{i}\right):\mathit{i}\in {\eta }_k\}\in \Xi$ are pairwise disjoint and disjoint with ${\xi }^{*}$.

Let $X_k^{\prime }={\pi }_k{X}_k$, so that $X_k^{\prime }\in {\mathbf{Perf}}_{{\xi }_k^{\prime }}$ in $\mathbf{L}$ by Lemma 6, where ${\xi }_k^{\prime }={\pi }_k{}^{\prime \prime }{\xi }_k=\{{\pi }_k\left(\mathit{i}\right):\mathit{i}\in {\xi }_k\}\subseteq {\eta }_k^{\prime }$. Define $\zeta ={\xi }^{*}\cup {\bigcup }_k{\xi }_k^{\prime }$; $\zeta \in \Xi$. It follows by Corollary 2 that the set $X^{\prime }=\left(X^{*}{\upharpoonright }^{-1}\zeta \right)\cap {\bigcap }_k\left(X_k^{\prime }{\upharpoonright }^{-1}\zeta \right)$ belongs to ${\mathbf{Perf}}_{\zeta }$ and $X^{\prime }⩽X^{*}$, $X^{\prime }⩽X_k^{\prime }$ for all k.

On the other hand, the sets ${\tau }_k^{\prime }={\pi }_k{}^{\prime \prime }{\tau }_k$ belong to ${\mathsf{\Omega }}^{\prime }$ (because so do ${\tau }_k$) and are pairwise disjoint (because so are the sets ${\eta }_k^{\prime }={\xi }_k^{\prime }\cup {\tau }_k^{\prime }$). However ${\mathsf{\Omega }}^{\prime }$ is closed in $\mathbf{L}$ under countable disjoint union, hence ${\tau }^{\prime }={\bigcup }_k{\tau }_k^{\prime }\in {\mathsf{\Omega }}^{\prime }$.

We still work in $\mathbf{L}$. Starting with (4) and arguing as in the proof of Lemma 11 (the proof of 3 on page 13), we deduce that, for all k,

$$X_k^{\prime }\parallel -\exists x\in \mathrm{HOD}\left[\mathbf{a}\left[\underline{G}\right]\upharpoonright {\tau }_k^{\prime }\right]\left({\mathfrak{M}}_{\underline{G}}^{\prime }|=(k,x)\right),$$

and hence

$$X^{\prime }\parallel -\forall k\exists x\in \mathrm{HOD}\left[\mathbf{a}\left[\underline{G}\right]\upharpoonright {\tau }^{\prime }\right]\left({\mathfrak{M}}_{\underline{G}}^{\prime }|=(k,x)\right),$$

(5)

because $X^{\prime }⩽X_k^{\prime }$ and ${\tau }_k^{\prime }\subseteq {\tau }^{\prime }$.

Finally, if H is $\mathbb{P}$-generic then the class $\mathrm{HOD}\left[\mathbf{a}\left[H\right]\upharpoonright {\tau }^{\prime }\right]$ has a well-ordering, say ${\preccurlyeq }_H$, also $\left\{\mathbf{a}\left[H\right]\upharpoonright {\tau }^{\prime }\right\}$-ordinal-definable in $\mathrm{HOD}\left[\mathbf{a}\left[H\right]\upharpoonright {\tau }^{\prime }\right]$. See e.g., [20], Section 13, the class $\mathrm{HOD}\left[\mathbf{a}\left[H\right]\upharpoonright {\tau }^{\prime }\right]$ is identical to $\mathrm{HOD}\left[\mathbf{a}\left[H\right]\upharpoonright {\tau }^{\prime }\right]$ as in [20]. Therefore, if H is any $\mathbb{P}$-generic set over $\mathbf{L}$ containing $X^{\prime }$, then, arguing on the basis of (5), we can define $y\subseteq \omega$ in ${\mathfrak{M}}_H^{\prime }$ such that, for each k, ${\left(y\right)}_k$ is equal to the ${\preccurlyeq }_H$-least set $x\subseteq \omega$ in $\mathrm{HOD}\left[\mathbf{a}\left[H\right]\upharpoonright {\tau }^{\prime }\right]$, satisfying $\phi (k,x)$. This proves that ${\mathfrak{M}}_H^{\prime }|=y\forall k\phi (k,{\left(y\right)}_k)$ for any such H, and hence

$$X^{\prime }\parallel -\left({\mathfrak{M}}_{\underline{G}}^{\prime }|=y\forall k\phi (k,{\left(y\right)}_k)\right).$$

But this contradicts (†) above since $X^{\prime }⩽X^{*}$. □

11. Models in Which the Parameter-Free $\mathbf{CA}{}^{*}$ Holds but the Full $\mathbf{CA}$ Fails

Here we sketch a proof of Theorem 2(i). See a full proof in our recent ArXiv preprint [8]. Thus the goal is to define a set $X\subseteq \mathcal{P}\left(\omega \right)$ in a cardinal-preserving generic extension of $\mathbf{L}$, which is a model of ${\mathbf{PA}}_2^{*}$ (with the parameter-free Comprehension $\mathbf{CA}{}^{*}$) in which the full $\mathbf{CA}$ fails.

Following the arguments above, assume that $G\subseteq \mathbb{P}$ is a set $\mathbb{P}$-generic over $\mathbf{L}$, define ${\mathbf{a}}_{\mathit{i}}\left[G\right]\subseteq \omega$ ($\mathit{i}\in \mathit{I}$) and the array $\mathbf{a}\left[G\right]={\langle {\mathbf{a}}_{\mathit{i}}\left[G\right]\rangle }_{\mathit{i}\in \mathit{I}}$ as above, and consider the set

$$\mathit{J}\left[G\right]=\{\gamma ⌢0^n:\gamma <{\omega }_1\wedge n<\omega \}\cup \{\gamma ⌢0^{n}1:\gamma <{\omega }_1\wedge n\in {\mathbf{a}}_{\gamma ⌢1}\left[G\right]\}.$$

Here $\gamma ⌢0^n=\langle \gamma ,\underset{n0\mathrm{s}}{\underbrace{0,\dots ,0}}\rangle$, $\gamma ⌢0^n⌢1=\langle \gamma ,\underset{n0\mathrm{s}}{\underbrace{0,\dots ,0}},1\rangle$, $\gamma ⌢1=\langle \gamma ,1\rangle$.

Thus $\mathit{J}\left[G\right]\subseteq \mathit{I}$ and $\mathit{J}\left[G\right]\in \mathbf{L}\left[G\right]$. (Not necessarily $\mathit{J}\left[G\right]\in \mathbf{L}$.) We put

$$M_G=\mathcal{P}\left(\omega \right)\cap \bigcup _{{\mathit{i}}_1,\dots ,{\mathit{i}}_n\in \mathit{J}\left[G\right]}\mathbf{L}[{\mathbf{a}}_{{\mathit{i}}_1}\left[G\right],\dots ,{\mathbf{a}}_{{\mathit{i}}_n}\left[G\right]];M_G\subseteq \mathcal{P}\left(\omega \right).$$

The next theorem implies Theorem 2(i) since it follows from Theorem 4 that the set $M_G$ belongs to a cardinal-preserving extension of $\mathbf{L}$.

Theorem 8. 

If a set $G\subseteq \mathbb{P}$ is $\mathbb{P}$-generic over $\mathbf{L}$ then $M_G$ is a model of ${\mathbf{PA}}_2^{*}$ (with the parameter-free Comprehension $\mathbf{CA}{}^{*}$)in which the full $\mathbf{CA}\left({\mathsf{\Sigma }}_2^1\right)$ holds but the full $\mathbf{CA}\left({\mathsf{\Sigma }}_4^1\right)$ fails.

Proof (sketch, see [8] for a full proof). 

That $M_G$ is a model of $\mathbf{CA}\left({\mathsf{\Sigma }}_2^1\right)$ (with parameters) follows by the Shoenfield absoluteness theorem, because $M_G$ is Gödel-closed downwards by construction. That the parameter-free ${\mathbf{AC}}_{\omega }^{*}$ holds in $M_G$ follows by the ordinary permutation technique by a method rather similar to the verification of ${\mathbf{AC}}_{\omega }^{*}$ in the proof of Theorem 7 above.

Finally, $M_G$ fails to satisfy the full $\mathbf{CA}$. Indeed the reals ${\mathbf{a}}_{\gamma 1}\left[G\right]$ ($\gamma <{\omega }_1$) do not belong to $M_G$, since $\gamma ⌢1\notin \mathit{J}\left[G\right]$ by construction. On the other hand, each ${\mathbf{a}}_{\gamma ⌢1}\left[G\right]$ is analytically definable in $M_G$ as the set containing the numbers $n\ge 1$ such that the structure of true ${⩽}_{\mathbf{L}}$-successors above ${\mathbf{a}}_{\langle \gamma \rangle }\left[G\right]$ has a split at $n$-th level, and possibly containing or not containing 0. Note the role of ${\mathbf{a}}_{\langle \gamma \rangle }\left[G\right]\in M_G$ as a parameter in this definition of ${\mathbf{a}}_{\gamma ⌢1}\left[G\right]$ in $M_G$. The ensuing definability formula for ${\mathbf{a}}_{\gamma ⌢1}\left[G\right]$ is ${\mathsf{\Sigma }}_4^1$ by direct estimation, because it is based on the ${\Pi }_3^1$ definability of the relation of ‘being a true ${⩽}_{\mathbf{L}}$-successor’. □

Another model of ${\mathbf{PA}}_2^{*}$, in which $\mathbf{CA}$ fails even in the most elementary form of the nonexistence of complements of some its members, is also presented in [8]. It has the form $M=(\mathcal{P}\left(\omega \right)\cap \mathbf{L})\cup \{y_n:n<\omega \}$, where ${\langle y_n\rangle }_{n<\omega }$ is a Cohen-generic sequence over $\mathbf{L}$. Note that the complements $y_n^{\prime }=\omega \setminus y_n$ are not adjoined to M, so that $\mathbf{CA}$ is violated in M even in the form $\exists x\forall k(k\in x⟺k\notin y_n)$, with $y_n$ as a parameter. On the other hand, the parameter-free $\mathbf{CA}{}^{*}$ holds in M by ordinary permutation arguments.

12. Working on the Basis of the Consistency of ${\mathbf{PA}}_2$

This section is devoted to claims (ii) of our main Theorems 1–3. We recall that the consistency of ${\mathbf{PA}}_2$ is a common assumption in claims (ii). As the proofs of claims (i) of the theorems, given above, contain a heavy dose of the forcing technique, first of all we have to adequately replace ${\mathbf{PA}}_2$ with a more $\mathbf{ZFC}$-like, forcing-friendly theory. This will be ${\mathbf{ZFC}}^{-}$, a subtheory of $\mathbf{ZFC}$ obtained as follows:

(a)

the Power Set axiom PS is excluded;

(b)

the Axiom of Choice AC is replaced with the well-orderability axiom WA saying that every set can be well-ordered;

(c)

the Replacement schema, which is not sufficiently strong in the absence of PS, is replaced with the Collection schema;

See, e.g., [26] for a comprehensive account of main features of ${\mathbf{ZFC}}^{-}$.

Two more principles are considered in the context of ${\mathbf{ZFC}}^{-},$ namely

$\mathbf{HC}$: 

every set is finite or countable,

$\mathbf{V}=\mathbf{L}$: 

every set is Gödel-constructible, i.e., the axiom of constructibility.

Theorem 9. 

Theories ${\mathbf{PA}}_2$ and ${\mathbf{ZFC}}^{-}+\mathbf{HC}+(\mathbf{V}=\mathbf{L})$ are equiconsistent. In fact they are interpretable in each other.

Proof. 

This has been a well-known fact since while ago, see e.g., Theorem 5.25 in [16]. A more natural way of proof is as follows.

Firstly the theory ${\mathbf{Z}}^{-}$ (i.e., ${\mathbf{ZFC}}^{-}$ without WA and Collection) is interpreted in ${\mathbf{PA}}_2$ by the tree interpretation described e.g., in [16], § 5, especially Theorem 5.11, or in [17], Definition VII.3.10 ff. Kreisel [1], VI(a)(ii), attributed this interpretation to the category of “crude” results. Secondly the whole theory ${\mathbf{ZFC}}^{-}+\mathbf{HC}+(\mathbf{V}=\mathbf{L})$ is interpeted in ${\mathbf{Z}}^{-}$ by means of the same tree interpretation, but restricted to only those trees that define sets constructible below the first gap ordinal, see a rather self-contained proof in [27]. This second part belongs to the category of “delicate” results of Kreisel [1], VI(b)(ii). □

Theorem 9 allows us to replace the consistency of ${\mathbf{PA}}_2$ in claims (ii) of our Theorems 1–3 by the equivalent consistency of ${\mathbf{ZFC}}^{-}$, which is a much more forcing-friendly theory.

This makes it possible to argue in the frameworks of ${\mathbf{ZFC}}^{-}$ in the following proof of Theorem 3(ii). The proof is an adaptation of the proof of the statement (i) of the same Theorem 3, on the basis of ${\mathbf{ZFC}}^{-}+\mathbf{HC}+(\mathbf{V}=\mathbf{L})$.

Proof of Claims (ii) of Theorems 1–3. 

We argue on the basis of ${\mathbf{ZFC}}^{-}+\mathrm{HC}+(\mathbf{V}=\mathbf{L})$. In other words, all sets are countable and constructible, so that the ground universe behaves like ${\mathbf{L}}_{{\omega }_1}$ in many ways. Yet, to avoid unnecessary misunderstanding, we accept the following.

Definition 2. 

The ground universe of ${\mathbf{ZFC}}^{-}+\mathrm{HC}+(\mathbf{V}=\mathbf{L})$ is denoted by $\mathbf{L}{}_{\phantom{1}}^{-}$. Accordingly ${\omega }_1^{-}$ will be the collection (a proper $\mathbf{L}{}_{\phantom{1}}^{-}$-class) of all ordinals in $\mathbf{L}{}_{\phantom{1}}^{-}$.

Emulating the construction in Section 5, we define proper classes $\mathit{I}={\left({\omega }_1^{-}\right)}^{<\omega }\setminus \left\{\mathsf{\Lambda }\right\}$ and $\Xi$, and sets ${\mathrm{IS}}_{\zeta }$, $\zeta [\subset \mathit{i}]$, $\zeta \left[⊈\mathit{i}\right]$, etc., similar to Section 5. But coming to Definition 1, we face a problem. Indeed, each space $\mathcal{P}{\left(\omega \right)}^{\xi }$ and any homeomorphism $H:\mathcal{P}{\left(\omega \right)}^{\xi }\to \mathcal{P}{\left(\omega \right)}^{\xi }$ is now a proper class, hence ${\mathbf{Perf}}_{\xi }$ as by Definition 1 is a class of proper classes, which cannot be considered. Therefore we have to parametrize homeomorphisms by sets.

Definition 3. 

(${\mathbf{ZFC}}^{-}$ form of Definition 1).

Arguing in $\mathbf{L}{}_{\phantom{1}}^{-}$, let $\xi \in \Xi$. Define

$$Q_{\xi }=\left\{x\in \mathcal{P}{\left(\omega \right)}^{\xi }:theset\{\langle \mathit{i},k\rangle :x\left(\mathit{i}\right)\left(k\right)=1\}isfinite\right\};$$

this is a countable dense subset of $\mathcal{P}{\left(\omega \right)}^{\xi }$ in ${\mathbf{ZFC}}^{-}$.

Let $h:Q_{\xi }\to \mathcal{P}{\left(\omega \right)}^{\xi }$ be any map (a set in $\mathbf{L}{}_{\phantom{1}}^{-}$). Let $\left[h\right]$ be its extension defined on $\mathcal{P}{\left(\omega \right)}^{\xi }$ by $\left[h\right]\left(x\right)={lim}_{y\to x}h\left(y\right)$ whenever the limit exists, so $\left[h\right]:\mathtt{dom}\left[h\right]\to \mathcal{P}{\left(\omega \right)}^{\xi }$ is a continuous map defined on $\mathtt{dom}\left[h\right]$, a topologically closed “subset” or rather subclass of $\mathcal{P}{\left(\omega \right)}^{\xi }$ (also a proper class).

We define ${\mathcal{H}}_{\xi }$ to be the class of all maps $h:Q_{\xi }\to \mathcal{P}{\left(\omega \right)}^{\xi }$ such that $\mathtt{dom}\left[h\right]=\mathcal{P}{\left(\omega \right)}^{\xi }$, $\left[h\right]$ is $1-1$ and $\left[h\right]$ is a projection–keeping homeomorphism.

Finally if $h\in {\mathcal{H}}_{\xi }$ then let $X_h=\left[h\right]{}^{\prime \prime }\mathcal{P}{\left(\omega \right)}^{\xi }=\{\left[h\right]\left(x\right):x\in \mathcal{P}{\left(\omega \right)}^{\xi }\}$.

Then ${\mathbf{Perf}}_{\xi }^{-}={\mathcal{H}}_{\xi }$ and ${\mathbf{Perf}}_{}^{-}={\bigcup }_{\xi \in \Xi }{\mathbf{Perf}}_{\xi }^{-}$ are proper classes, of course.

It is quite obvious that in the $\mathbf{ZFC}$ setting ${\mathbf{Perf}}_{\xi }$ coincides with the collection of all sets $X_h$, $h\in {\mathcal{H}}_{\xi }$. This allows us to use the map $h\to X_h$ as a parametrization of ${\mathbf{Perf}}_{}$ in $\mathbf{L}{}_{\phantom{1}}^{-}$, so that ${\mathbf{Perf}}_{}^{-}$ is the set of codes for the ${\mathbf{Perf}}_{}$ and each particular ${\mathbf{Perf}}_{\xi }^{-}={\mathcal{H}}_{\xi }$ is the set of codes for ${\mathbf{Perf}}_{\xi }$. We will use ${\mathbf{Perf}}_{}^{-}$ as a forcing notion, that is, put ${\mathbb{P}}^{-}={\mathbf{Perf}}_{}^{-}$, with the order $g⩽h$ if and only if $X_g⩽X_h$ in the sense of Section 5.

Note that both (∗) and the order are definable proper classes in $\mathbf{L}{}_{\phantom{1}}^{-}$.

Conditions $h\in {\mathbb{P}}^{-}$ should be informally identified with corresponding objects (parametrically defined proper classes) $X_g$.

The property (∗) in the proof of Theorem 4 transforms to the following property of the forcing ${\mathbf{Perf}}_{}^{-}$ has a property in $\mathbf{L}{}_{\phantom{1}}^{-}$:

(∗⁻)

if a parametrized sequence of classes $D_n\subseteq {\mathbf{Perf}}_{}^{-}$ is such that each $D_n$ is open dense in ${\mathbf{Perf}}_{}^{-}$, and $X\in {\mathbf{Perf}}_{}$, then there is a stronger condition $Y\in {\mathbf{Perf}}_{}$, $Y⩽X$, and finite sets $D_n^{\prime }\subseteq D_n$ pre-dense in ${\mathbf{Perf}}_{}^{-}$ below Y.

In other words, ${\mathbf{Perf}}_{}^{-}$ is a pretame forcing notion in $\mathbf{L}{}_{\phantom{1}}^{-}$ in the sense of [28] or [29].

It follows (see e.g., [29]) that any ${\mathbf{Perf}}_{}^{-}$-generic extension of $\mathbf{L}{}_{\phantom{1}}^{-}$ is still a model of ${\mathbf{ZFC}}^{-}$, and the forcing and definability theorems hold similar to the case of usual set-size forcing. Furthermore all constructions and arguments involved in the proofs of Theorems 6–8 above (i.e., claims (i) of Theorems 1–3), as well as the results of [21,22] cited in the course of the proofs, can be reproduced mutatis mutandis on the basis of the theory ${\mathbf{ZFC}}^{-}+\mathrm{HC}+(\mathbf{V}=\mathbf{L})$. In particular, Theorem 6 takes the form asserting that the $\mathcal{P}\left(\omega \right)$-part of a certain subextension of any ${\mathbb{P}}^{-}$-generic extension of $\mathbf{L}{}_{\phantom{1}}^{-}$ satisfies ${\mathbf{PA}}_2+\neg {\mathbf{AC}}_{\omega }^{*}\left({\Pi }_3^1\right)$.

Metamathematically, this means that the formal consistency of ${\mathbf{ZFC}}^{-}+\mathrm{HC}+(\mathbf{V}=\mathbf{L})$ implies the consistency of ${\mathbf{PA}}_2+\neg {\mathbf{AC}}_{\omega }^{*}\left({\Pi }_3^1\right)$. However the consistency of ${\mathbf{ZFC}}^{-}+\mathrm{HC}+(\mathbf{V}=\mathbf{L})$ is equivalent to the consistency of ${\mathbf{PA}}_2$ by Theorem 9. This concludes the proof of Claim (ii) of Theorem 3.

Pretty similarly, Theorems 7 and 8 take appropriate forms sufficient to infer the consistency of resp.

$${\mathbf{PA}}_2+{\mathbf{AC}}_{\omega }^{*}+\neg {\mathbf{AC}}_{\omega }\left({\mathsf{\Pi }}_3^1\right)\hspace{1em}\hspace{1em}{\mathbf{PA}}_2^{*}+\mathbf{CA}\left({\mathsf{\Sigma }}_2^1\right)+\neg \mathbf{CA}\left({\mathsf{\Pi }}_4^1\right),$$

from the consistency of ${\mathbf{PA}}_2$, as required. This completes the proof of Claims (ii) of Theorems 1–3. □

13. Conclusions, Remarks, and Problems

In this study, the method of generalized arboreal iterations of the Sacks forcing is employed to the problem of obtaining cardinal-preserving models of $\mathbf{ZFC}$, and models of ${\mathbf{ZFC}}^{-}$ and the second-order Peano arithmetic ${\mathbf{PA}}_2$, in which the parameter-free version of the Comprehension or Choice schema holds but the full schema fails. These results (Theorems 1–3 above) contribute to the ongoing study of both subsistems and extensions of ${\mathbf{PA}}_2$ as in [13,14,15,17,30,31] among many others, as well as to modern studies of forcing extensions in class theories and ${\mathbf{ZFC}}^{-}$-like theories as in [26,32,33,34].

From our study, it is concluded that the technique of generalized arboreal iterations of the Sacks forcing succeeds to solve important problems in descriptive set theory and second-order Peano arithmetic related to parameter-free versions of such crucial axiom schemata as Comprehension and Choice, by our Theorems 1–3.

From the results of this paper, the following remarks and problems arise.

Remark 5. 

Identifying the theories with their deductive closures, we may present the concluding statements of Theorems 1–3 as resp.

$${\mathbf{PA}}_2+{\mathbf{AC}}_{\omega }^{*}⫋{\mathbf{PA}}_2+{\mathbf{AC}}_{\omega },{\mathbf{PA}}_2^{*}+\mathbf{CA}\left({\mathsf{\Sigma }}_2^1\right)⫋{\mathbf{PA}}_2,{\mathbf{PA}}_2⫋{\mathbf{PA}}_2+{\mathbf{AC}}_{\omega }^{*}.$$

(6)

Studies on subsystems of ${\mathbf{PA}}_2$ have discovered many cases in which $S⫋S^{\prime }$ holds for a given pair of subsystems $S,S^{\prime }$, see e.g., [17]. And it is a rather typical case that such a strict extension is established by demonstrating that $S^{\prime }$ proves the consistency of S. One may ask whether this is the case for the results in (6). The answer is in the negative: namely

$$thetheories{\mathbf{PA}}_2^{*},{\mathbf{PA}}_2^{*}+\mathbf{CA}\left({\mathsf{\Sigma }}_2^1\right),\mathit{and}\mathit{the}\mathit{full}{\mathbf{PA}}_2\mathit{are}\mathit{equiconsistent}$$

by a result in [18], also mentioned in [19]. This equiconsistency result also follows from a somewhat sharper theorem in [35], 1.5.

Remark 6. 

There is another meaningful submodel of the basic model $\mathbf{L}\left[G\right]=\mathbf{L}\left[\mathbf{a}\right[G]$. Namely, consider the set $W^{\prime \prime }$ of all finite or countablewell-foundedinitial segments $\xi \in \mathbf{L}$, $\xi \subseteq \mathit{I}$, instead of the sets W (as in Section 8) and $W^{\prime }$ (as in Section 10). Define a corresponding submodel ${\mathfrak{M}}_G^{\prime \prime }$ accordingly. Then ${\mathbf{AC}}_{\omega }$ holds in ${\mathfrak{M}}_G^{\prime \prime }$ but $\mathbf{DC}\left({\Pi }_3^1\right)$ fails. Yet a better model is defined in [31], in which ${\mathbf{AC}}_{\omega }$ holds but even $\mathbf{DC}\left({\Pi }_2^1\right)$ (the best possible in this case) fails.

Remark 7. 

It will be interesting to study problems considered in this paper in the frameworks of non-ZF-oriented set theories like Quine’s New FoundationsNF[36], various non-well-founded and anti-foundational theories (see [37]), or (as suggested by one of the anonymous reviewers) the ideal set theory or the ideal calculus as in [38]—which is essentially a nave set or class theory with a rather vague axiomatic. Yet it seems to us that those theories haven’t so far developed an adequate instrumentarium to study and answer such sort of questions.

We proceed with a list of open problems.

Problem 1. 

Is the parameter-free countable choice schema ${\mathbf{AC}}_{\omega }^{*}$ in the language $\mathcal{L}\left({\mathbf{PA}}_2\right)$ true in the models defined in Section 11?

We expect that ${\mathbf{AC}}_{\omega }^{*}$ fails in the first model in Section 11 via the relation $\mathsf{\Phi }(k,x):=$ $x\subseteq \omega$ codes k${⩽}_{\mathbf{L}}$-incomparable reals minimal over $\mathbf{L}$, and it’s a separate problem how to modify this model to allow ${\mathbf{AC}}_{\omega }^{*}+\neg \mathbf{CA}$.

Problem 2. 

Can we sharpen the result of Theorem 8 by specifying that $\mathbf{CA}\left({\mathsf{\Sigma }}_3^1\right)$, rather than ${\mathsf{\Sigma }}_4^1$, is violated? The combination $\mathbf{CA}\left({\mathsf{\Sigma }}_2^1\right)$ plus $\neg \mathbf{CA}\left({\mathsf{\Sigma }}_3^1\right)$ over ${\mathbf{PA}}_2^{*}$ would be optimal for Theorem 2. Can we similarly sharpen the result of Theorems 6 and 7 by specifying that ${\mathbf{AC}}_{\omega }^{*}\left({\mathsf{\Sigma }}_2^1\right)$, resp., ${\mathbf{AC}}_{\omega }\left({\mathsf{\Sigma }}_2^1\right)$ are violated?

As conjectured by V. Gitman, Jensen’s iterated forcing may lead to the solution of Problem 2 by methods outlined in [31]. Such a construction makes use of the consecutive “jensenness”, known to be a ${\Pi }_2^1$ relation, instead of the consecutive “sacksness”, which can help to define the counterexamples required at minimally possible levels.

Problem 3. 

As a generalization of Problem 2, prove that, for any $n\ge 2$, ${\mathbf{PA}}_2^{*}+\mathbf{CA}\left({\mathsf{\Sigma }}_n^1\right)$ does not imply $\mathbf{CA}\left({\mathsf{\Sigma }}_{n+1}^1\right)$. In this case, it would be possible to conclude that the full schema $\mathbf{CA}$ is not finitely axiomatizable over ${\mathbf{PA}}_2^{*}$. There are similar questions related to Theorems 6 and 7, of course. Compare to Problem 9 in ([16], § 11).

We expect that methods of inductive construction of forcing notions in $\mathbf{L}$ that are similar to the iterated Jensen forcing as in [31] but carry hidden automorphisms, recently developed in our papers [39,40,41,42,43], may lead to the solution of Problem 3.

Problem 4 

(Communicated by Ali Enayat). A natural question is whether the results of this note also hold for second order set theory (the Kelley–Morse theory of classes), with suitable reformulations of the Choice and Comprehension schemata.

This may involve a generalization of the Sacks forcing to uncountable cardinals, as e.g., in Kanamori [44], as well as the new models of set theory recently defined by Fuchs [45], on the basis of further development of the methods of class forcing introduced by S. D. Friedman [28].