Statistical Analysis of Descending Open Cycles of Collatz Function
Abstract
1. Introduction
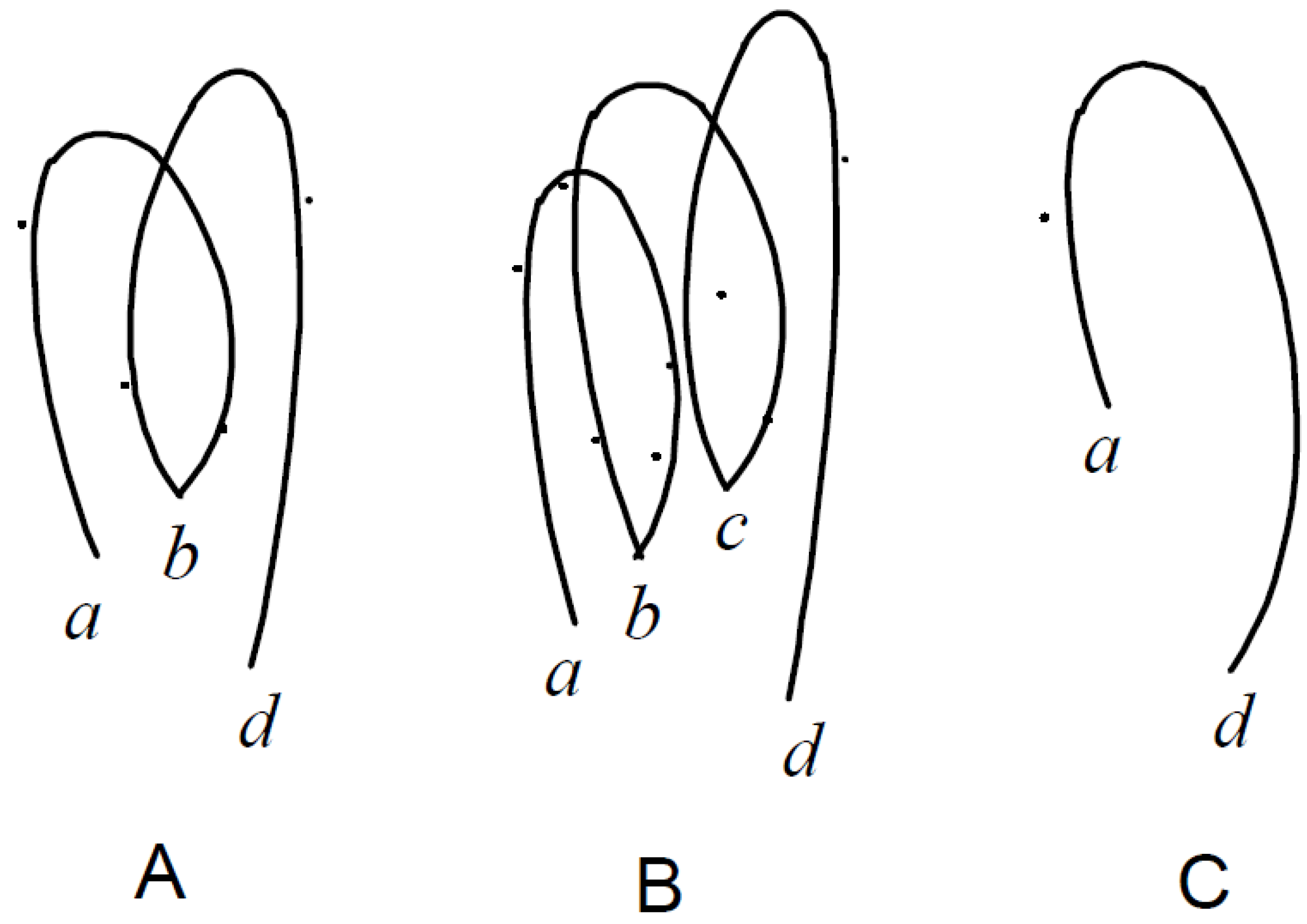
2. Open Cycles of Collatz Function
3. Distribution of Open Cycles over the Natural Numbers
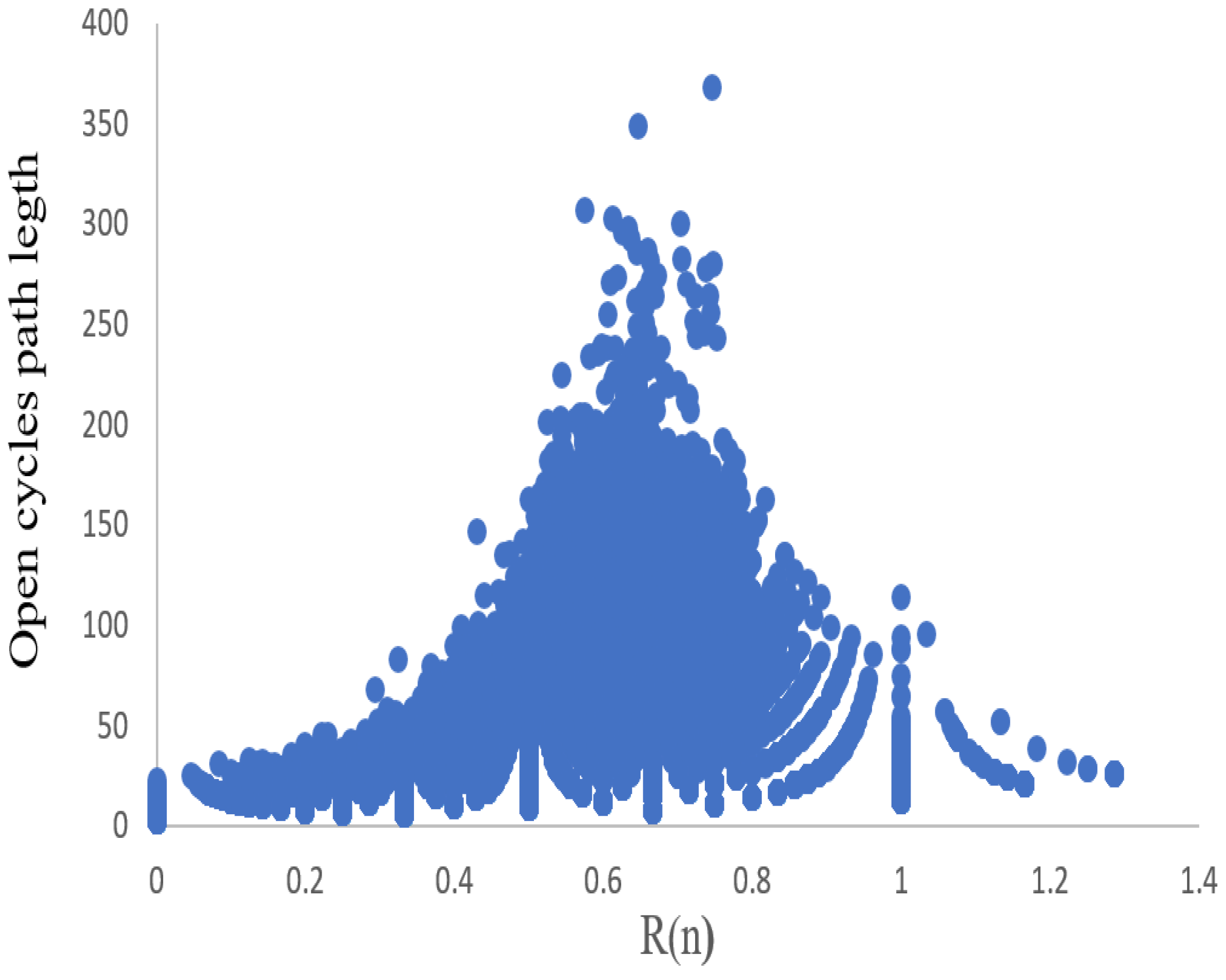
4. Relationship between and the Path Length of Open Cycles
5. Analysis of Collatz Function’s Upper Bound Path-Lengths
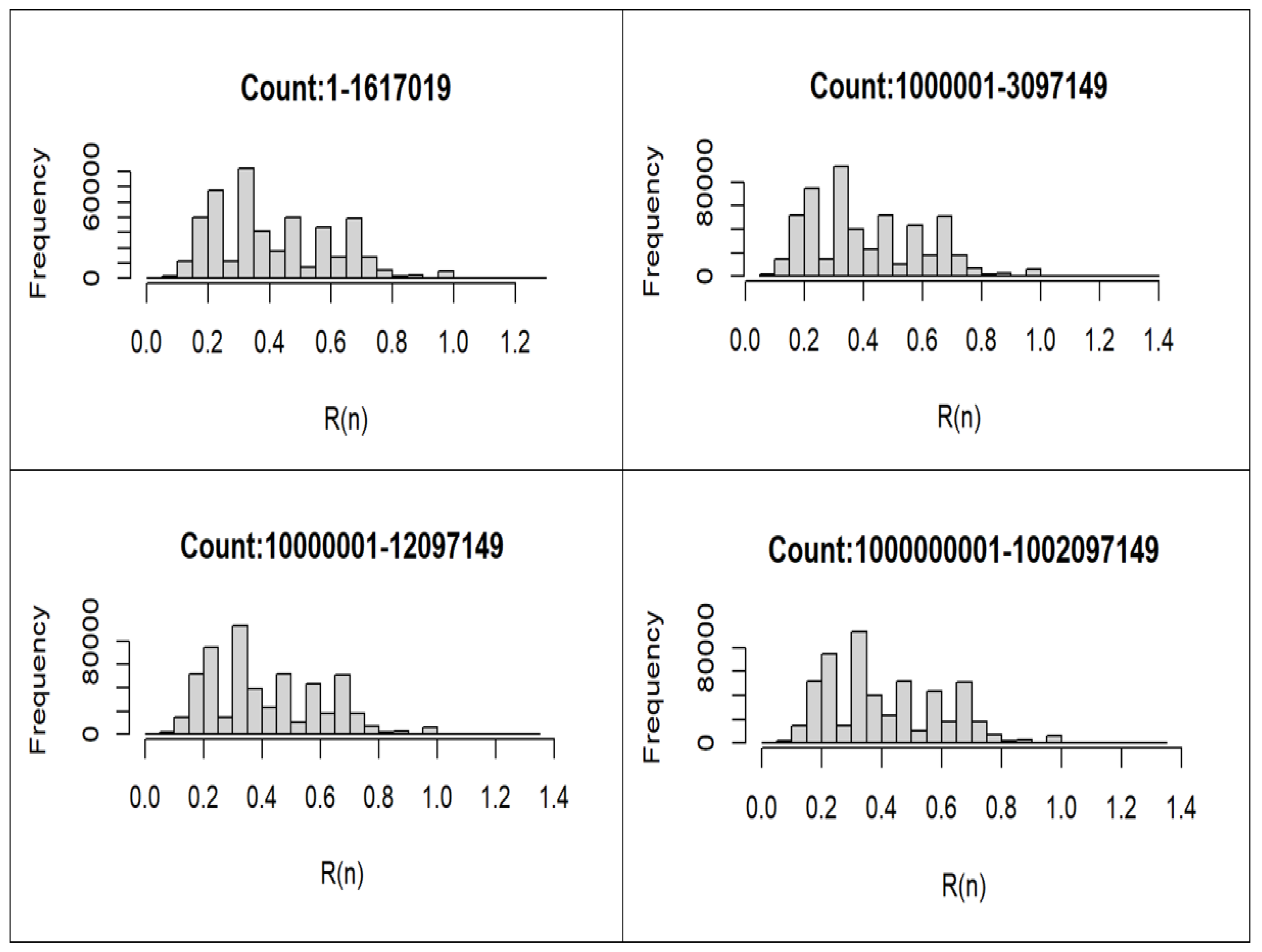
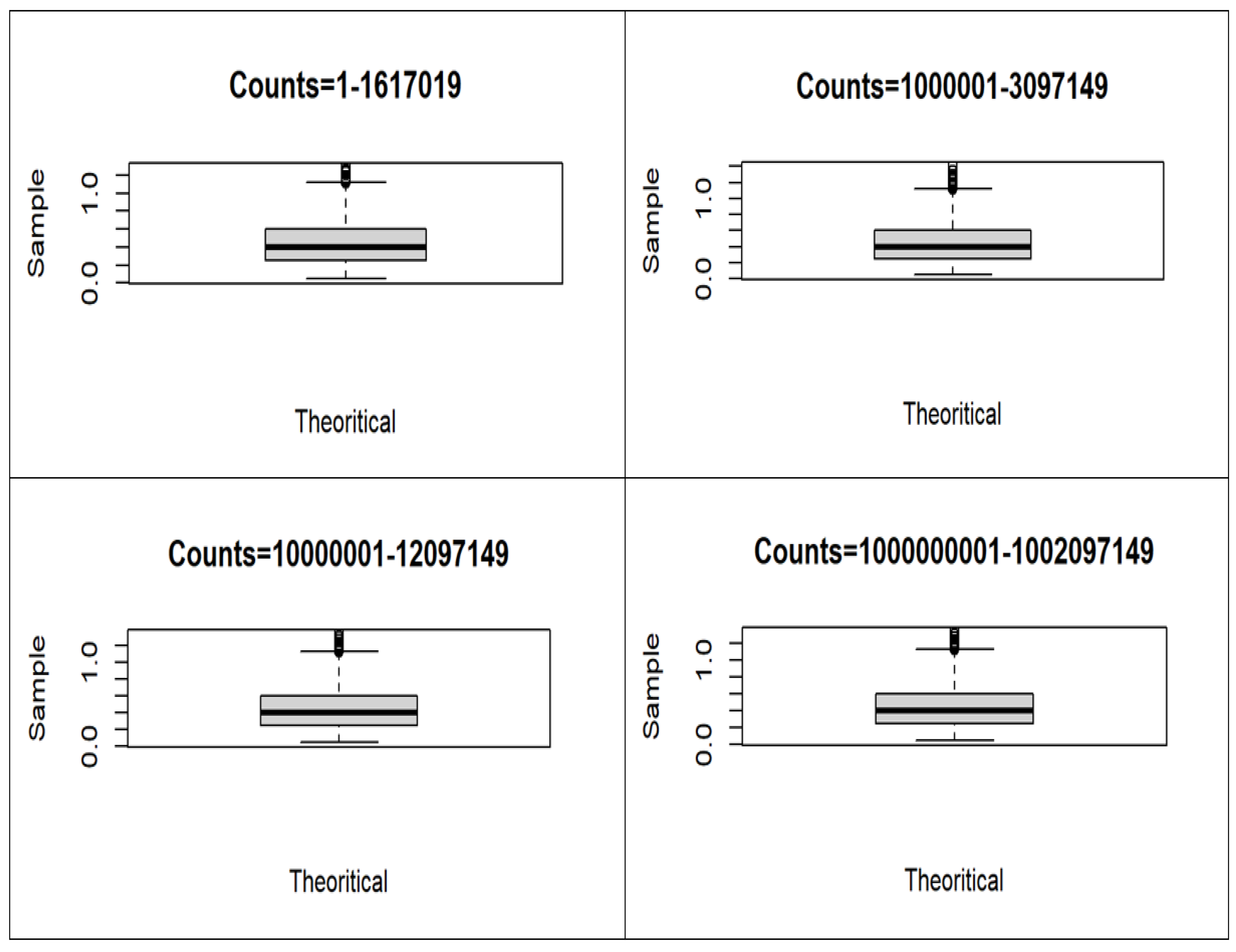
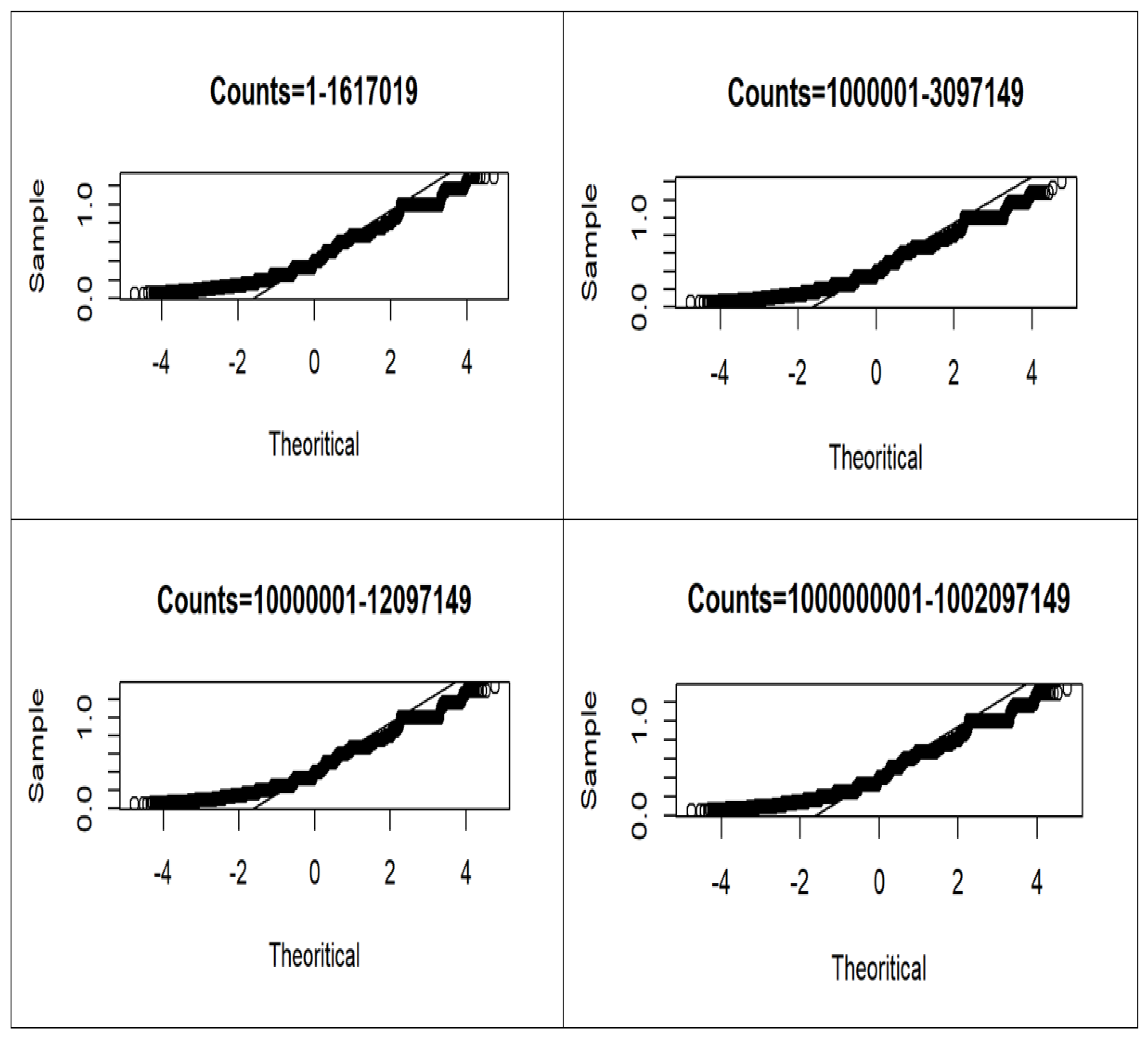
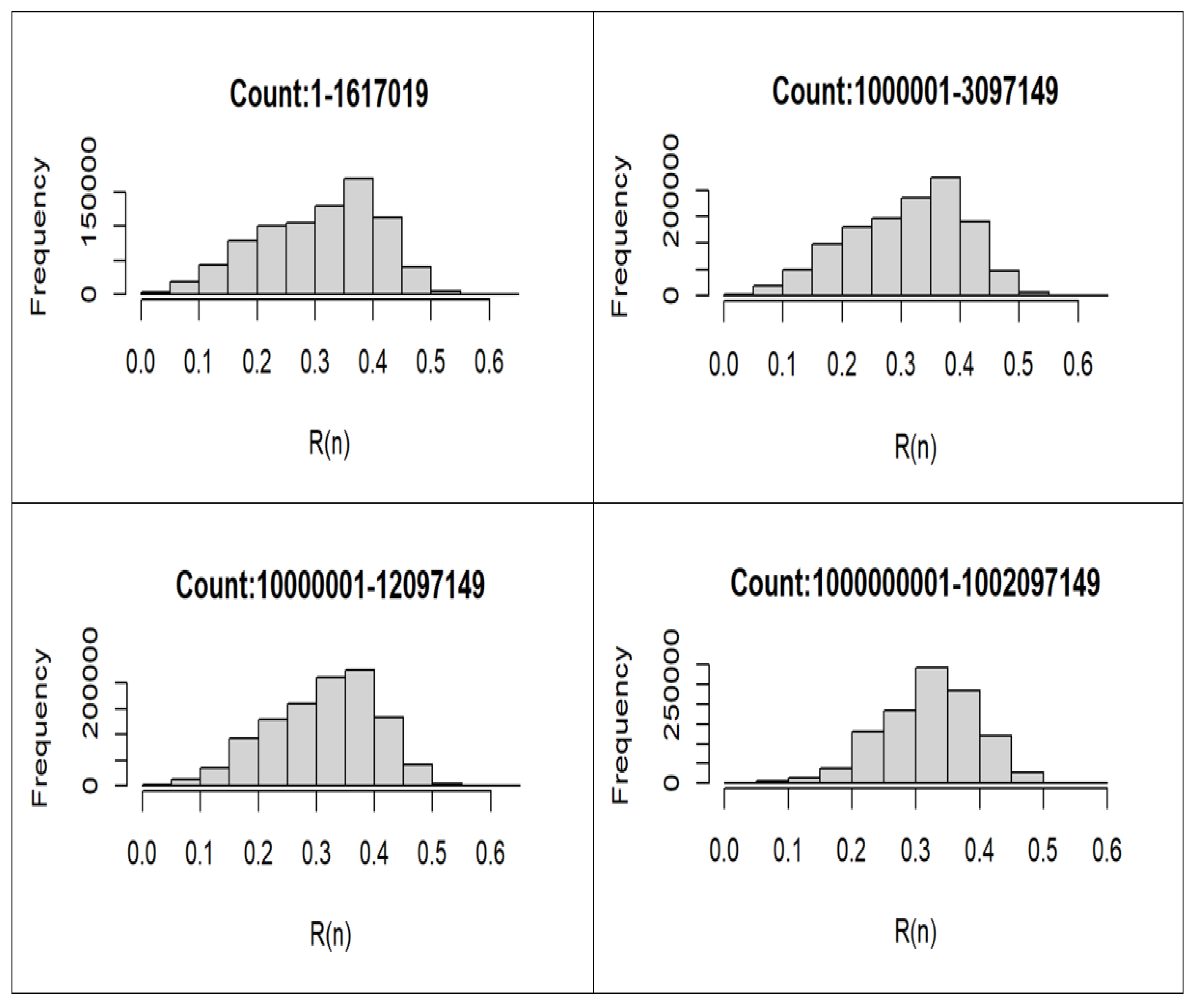
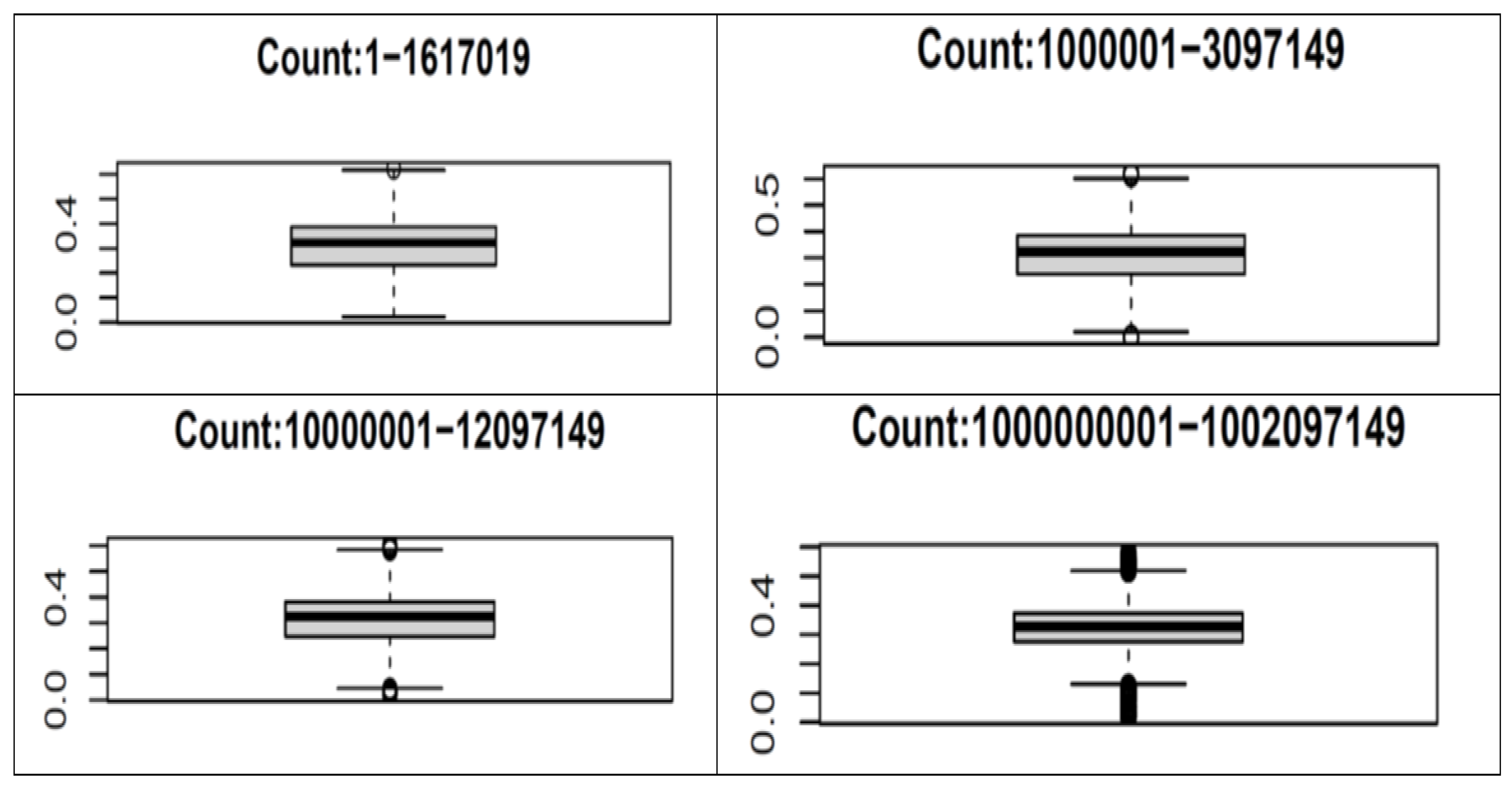
6. Comparative Statistical Analysis of 4 Datasets of Open Cycles
7. Comparative Statistical Analysis of 4 Datasets of Collatz Orbits to 1;
8. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A
| # | F | 3n + 1 | F | 3n + 1 | F | 3n + 1 | F | 3n + 1 | F | 3n + 1 | F | 3n + 1 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 4 | 16 | 6 | 64 | 8 | 256 | 10 | 1024 | 12 | 4096 | 24 | 16,777,216 | |
| 1 | 1 | 22 | 1 | 70 | 1 | 262 | 1 | 1030 | 1 | 4102 | 1 | 16,777,222 |
| 2 | 2 | 28 | 2 | 76 | 2 | 268 | 2 | 1036 | 2 | 4108 | 2 | 16,777,228 |
| 3 | 1 | 34 | 1 | 82 | 1 | 274 | 1 | 1042 | 1 | 4114 | 1 | 16,777,234 |
| 4 | 3 | 40 | 3 | 88 | 3 | 280 | 3 | 1048 | 3 | 4120 | 3 | 16,777,240 |
| 5 | 1 | 46 | 1 | 94 | 1 | 286 | 1 | 1054 | 1 | 4126 | 1 | 16,777,246 |
| 6 | 2 | 52 | 2 | 100 | 2 | 292 | 2 | 1060 | 2 | 4132 | 2 | 16,777,252 |
| 7 | 1 | 58 | 1 | 106 | 1 | 298 | 1 | 1066 | 1 | 4138 | 1 | 16,777,258 |
| 8 | 4 | 112 | 4 | 304 | 4 | 1072 | 4 | 4144 | 4 | 16,777,264 | ||
| 9 | 1 | 118 | 1 | 310 | 1 | 1078 | 1 | 4150 | 1 | 16,777,270 | ||
| 10 | 2 | 124 | 2 | 316 | 2 | 1084 | 2 | 4156 | 2 | 16,777,276 | ||
| 11 | 1 | 130 | 1 | 322 | 1 | 1090 | 1 | 4162 | 1 | 16,777,282 | ||
| 12 | 3 | 136 | 3 | 328 | 3 | 1096 | 3 | 4168 | 3 | 16,777,288 | ||
| 13 | 1 | 142 | 1 | 334 | 1 | 1102 | 1 | 4174 | 1 | 16,777,294 | ||
| 14 | 2 | 148 | 2 | 340 | 2 | 1108 | 2 | 4180 | 2 | 16,777,300 | ||
| 15 | 1 | 154 | 1 | 346 | 1 | 1114 | 1 | 4186 | 1 | 16,777,306 | ||
| 16 | 5 | 160 | 5 | 352 | 5 | 1120 | 5 | 4192 | 5 | 16,777,312 | ||
| 17 | 1 | 166 | 1 | 358 | 1 | 1126 | 1 | 4198 | 1 | 16,777,318 | ||
| 18 | 2 | 172 | 2 | 364 | 2 | 1132 | 2 | 4204 | 2 | 16,777,324 | ||
| 19 | 1 | 178 | 1 | 370 | 1 | 1138 | 1 | 4210 | 1 | 16,777,330 | ||
| 20 | 3 | 184 | 3 | 376 | 3 | 1144 | 3 | 4216 | 3 | 16,777,336 | ||
| 21 | 1 | 190 | 1 | 382 | 1 | 1150 | 1 | 4222 | 1 | 16,777,342 | ||
| 22 | 2 | 196 | 2 | 388 | 2 | 1156 | 2 | 4228 | 2 | 16,777,348 | ||
| 23 | 1 | 202 | 1 | 394 | 1 | 1162 | 1 | 4234 | 1 | 16,777,354 | ||
| 24 | 4 | 208 | 4 | 400 | 4 | 1168 | 4 | 4240 | 4 | 16,777,360 | ||
| 25 | 1 | 214 | 1 | 406 | 1 | 1174 | 1 | 4246 | 1 | 16,777,366 | ||
| 26 | 2 | 220 | 2 | 412 | 2 | 1180 | 2 | 4252 | 2 | 16,777,372 | ||
| 27 | 1 | 226 | 1 | 418 | 1 | 1186 | 1 | 4258 | 1 | 16,777,378 | ||
| 28 | 3 | 232 | 3 | 424 | 3 | 1192 | 3 | 4264 | 3 | 16,777,384 | ||
| 29 | 1 | 238 | 1 | 430 | 1 | 1198 | 1 | 4270 | 1 | 16,777,390 | ||
| 30 | 2 | 244 | 2 | 436 | 2 | 1204 | 2 | 4276 | 2 | 16,777,396 | ||
| 31 | 1 | 250 | 1 | 442 | 1 | 1210 | 1 | 4282 | 1 | 16,777,402 | ||
| 32 | 6 | 448 | 6 | 1216 | 6 | 4288 | 6 | 16,777,408 | ||||
Appendix B
References
- Lagarias, J.C. The 3x + 1 problem: An annotated bibliography (1963–1999) (sorted by author). arXiv 2011, arXiv:math/0309224. [Google Scholar]
- Lagarias, J.C. The 3x + 1 problem: An annotated bibliography, II (2000–2009) (sorted by author). arXiv 2012, arXiv:math/0608208. [Google Scholar]
- Oliveira, T.S. Empirical Verification of the 3x + 1 and Related Conjectures. In The Ultimate Challenge: The 3x+1 Problem (book edited by Jeffrey C. Lagarias). Am. Math. Soc. 2010, 189–207. [Google Scholar]
- Oliveira, T.S. Computational Verification of the 3x+1 Conjecture. Available online: http://sweet.ua.pt/tos/3x_plus_1.html (accessed on 25 May 2022).
- Borovkov, K.; Pfeifer, D. Estimates for the Syracuse problem via a probabilistic model. Theory Probab. Its Appl. 2000, 45, 300–310. [Google Scholar] [CrossRef]
- Rawsthorne, D.W. Imitation of an iteration. Math. Mag. 1985, 58, 172–176. [Google Scholar] [CrossRef]
- Wagon, S. The collatz problem. Math. Lntelligencer T 1985, 72–76. [Google Scholar] [CrossRef]
- Terence, T. Almost all orbits of the Collatz map attain almost bounded values. arXiv 2019, arXiv:1909.03562. [Google Scholar]
- Grauer, J.A. Analogy Between the Collatz Conjecture and Sliding Mode Control; Langley Research Center: Hampton, VA, USA, 2021; NASA/TM–20210019810. [Google Scholar]
- Austin, T. Measure concentration and the weak Pinsker property. arXiv 2018, arXiv:1705.00302. [Google Scholar] [CrossRef]
- Barghout, K. On the Probabilistic Proof of the Convergence of the Collatz Conjecture. J. Probab. Stat. 2019, 2019, 6814378. [Google Scholar] [CrossRef]
- Andrei, Ş.; Kudlek, M.; Niculescu R, Ş. Some results on the Collatz problem. Acta Inform. 2000, 37, 145. [Google Scholar] [CrossRef]
- Leavens, G.T.; Vermeulen, M. 3x + 1 Search Programs. Comput. Math. Appl. 1992, 24, 79–99. [Google Scholar] [CrossRef]
- Cesaro, E. Demonstration elementaire et generalisation de quelques theoremes de M. Berger. Mathesis 1881, 1, 99–102. [Google Scholar]
- Bach, E.; Jeffrey, S. Algorithmic Number Theory: Efficient algorithms, Volume 1. Foundation of Computing Series; The MIT Press: Cambridge, MA, USA, 1996. [Google Scholar]
- Xu, D.; Tamir, D.E. Pseudo-random number generators based on the Collatz conjecture. Int. J. Inf. Technol. 2019, 11, 453–459. [Google Scholar] [CrossRef]
- Shapiro, S.S.; Wilk, M.B. An analysis of variance for normality (complete samples). Biometrika 1965, 52, 591–611. [Google Scholar] [CrossRef]

| Odd Number | Open Cycle | Action | |
|---|---|---|---|
| 3 | 0.25 | ||
| 5 | 0 | ||
| 7 | 0.4 | ||
| 9 | 0 | ||
| ⁞ | ⁞ | ⁞ | ⁞ |
| Number | RatioToOne | StepsToOne | Max | StepsToMax | RatioToMin | StepsToMin |
|---|---|---|---|---|---|---|
| 3 | 0.25 | 7 | 16 | 3 | 0.25 | 7 |
| 5 | 0 | 5 | 16 | 1 | 0 | 5 |
| 7 | 0.222222 | 16 | 52 | 5 | 0.4 | 11 |
| 9 | 0.181818 | 19 | 52 | 8 | 0 | 3 |
| 11 | 0.111111 | 14 | 52 | 3 | 0.2 | 9 |
| 13 | 0 | 9 | 40 | 1 | 0 | 4 |
| ⁞ | ⁞ | ⁞ | ⁞ | ⁞ | ⁞ | ⁞ |
| Range | Counts | Skewness | Kurtosis | Mean | Median | Mode |
|---|---|---|---|---|---|---|
| 1–1,617,019 | 404255 | 0.56901 | −0.29603 | 0.42513 | 0.4 | 0.33333 |
| 1,000,001–3,097,149 | 524287 | 0.57060 | −0.28961 | 0.42515 | 0.4 | 0.33333 |
| 10,000,001–12,097,149 | 524286 | 0.56957 | −0.29350 | 0.42516 | 0.4 | 0.33333 |
| 1,000,000,001–1,002,097,149 | 524287 | 0.56900 | −0.29513 | 0.42515 | 0.42515 | 0.33333 |
| Range | Counts | Skewness | Kurtosis | Mean | Median | Mode |
|---|---|---|---|---|---|---|
| 1–1,617,019 | 807518 | −0.35485 | −0.60907 | 0.30845 | 0.32307 | 0.33333 |
| 10,000,01–3,097,149 | 1048575 | −0.39579 | −0.33109 | 0.35463 | 0.36585 | 0.33333 |
| 10,000,001–12,097,149 | 1048352 | −0.35770 | −0.40866 | 0.31237 | 0.325 | 0.35714 |
| 1,000,000,001–1,002,097,149 | 1048495 | −0.37734 | 0.20894 | 0.32110 | 0.32653 | 0.24719 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Barghout, K.; Hajji, W.; Abu-Libdeh, N.; Al-Jamal, M. Statistical Analysis of Descending Open Cycles of Collatz Function. Mathematics 2023, 11, 675. https://doi.org/10.3390/math11030675
Barghout K, Hajji W, Abu-Libdeh N, Al-Jamal M. Statistical Analysis of Descending Open Cycles of Collatz Function. Mathematics. 2023; 11(3):675. https://doi.org/10.3390/math11030675
Chicago/Turabian StyleBarghout, Kamal, Wadii Hajji, Nidal Abu-Libdeh, and Mohammad Al-Jamal. 2023. "Statistical Analysis of Descending Open Cycles of Collatz Function" Mathematics 11, no. 3: 675. https://doi.org/10.3390/math11030675
APA StyleBarghout, K., Hajji, W., Abu-Libdeh, N., & Al-Jamal, M. (2023). Statistical Analysis of Descending Open Cycles of Collatz Function. Mathematics, 11(3), 675. https://doi.org/10.3390/math11030675






