Delicate Comparison of the Central and Non-Central Lyapunov Ratios with Applications to the Berry–Esseen Inequality for Compound Poisson Distributions
Abstract
1. Introduction
2. Formulations of Main Results
3. Reduction to the Case of Two-Point Distributions
- it is a linear combination , of the functions generating the given moment conditions ; and
- it has exactly two tangent points with .
4. Analysis of Two-Point Distributions
5. Proofs of Main Results
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| i.i.d. | independent and identically distributed |
| r.v. | random variable |
| iff | if and only if |
References
- Cramér, H. Collective Risk Theory; Skandia Jubilee Volume: Stockholm, Sweden, 1955. [Google Scholar]
- Grandell, J. Aspects of risk theory; Springer: New York, NY, USA, 1991. [Google Scholar]
- Gnedenko, B.V.; Korolev, V.Y. Random Summation: Limit Theorems and Applications; CRC Press: Boca Raton, FL, USA, 1996. [Google Scholar]
- Bening, V.E.; Korolev, V.Y. Generalized Poisson Models and Their Applications in Insurance and Finance; VSP: Utrecht, The Netherlands, 2002. [Google Scholar]
- Shevtsova, I.G. On the accuracy of the normal approximation to compound Poisson distributions. Theory Probab. Appl. 2014, 58, 138–158. [Google Scholar] [CrossRef]
- Korolev, V.; Dorofeyeva, A. Bounds of the accuracy of the normal approximation to the distributions of random sums under relaxed moment conditions. Lith. Math. J. 2017, 57, 38–58. [Google Scholar] [CrossRef]
- Kruglov, V.M.; Korolev, V.Y. Limit Theorems for Random Sums; Moscow University Press: Moscow, Russia, 1990. [Google Scholar]
- Englund, G. A remainder term estimate in a random–sum central limit theorem. Theory Probab. Appl. 1984, 28, 149–157. [Google Scholar] [CrossRef]
- Rotar, G.V. Some Problems of Planning of Reserve. Ph.D. Thesis, Central Institute of Economics and Mathematics, Moscow, Russia, 1972. (In Russian). [Google Scholar]
- Rotar, G.V. On a problem of control of reserves. Econ. Math. Methods 1976, 12, 733–739. (In Russian) [Google Scholar]
- Von Chossy, R.; Rappl, G. Some approximation methods for the distribution of random sums. Insur. Math. Econ. 1983, 2, 251–270. [Google Scholar] [CrossRef]
- Berry, A.C. The accuracy of the Gaussian approximation to the sum of independent variates. Trans. Am. Math. Soc. 1941, 49, 122–136. [Google Scholar] [CrossRef]
- Esseen, C.G. On the Liapounoff limit of error in the theory of probability. Ark. Mat. Astron. Fys. 1942, A28, 1–19. [Google Scholar]
- Michel, R. On Berry–Esseen results for the compound Poisson distribution. Insur. Math. Econ. 1993, 13, 35–37. [Google Scholar] [CrossRef]
- Korolev, V.Y.; Shorgin, S.Y. On the absolute constant in the remainder term estimate in the central limit theorem for Poisson random sums. In Proceedings of the Probabilistic Methods in Discrete Mathematics, Proceedings of the Fourth International Petrozavodsk Conference, VSP, Petrozavodsk, Russia, 3–7 June 1997; pp. 305–308. [Google Scholar]
- Korolev, V.Y.; Shevtsova, I.G. Sharpened upper bounds for the absolute constant in the Berry–Esseen inequality for mixed Poisson random sums. Dokl. Math. 2010, 81, 180–182. [Google Scholar] [CrossRef]
- Esseen, C.G. A moment inequality with an application to the central limit theorem. Skand. Aktuarietidskr. 1956, 39, 160–170. [Google Scholar] [CrossRef]
- Korolev, V.; Shevtsova, I. An improvement of the Berry–Esseen inequality with applications to Poisson and mixed Poisson random sums. Scand. Actuar. J. 2012, 2012, 81–105. [Google Scholar] [CrossRef]
- Korolev, V.Y.; Bening, V.E.; Shorgin, S.Y. Mathematical Foundations of Risk Theory, 2nd ed.; Fizmatlit: Moscow, Russia, 2011. (In Russian) [Google Scholar]
- Shevtsova, I.G. On the absolute constants in the Berry–Esseen-type inequalities. Dokl. Math. 2014, 89, 378–381. [Google Scholar] [CrossRef]
- Nefedova, Y.S.; Shevtsova, I.G. On the accuracy of the normal approximation to distributions of Poisson random sums. Inform. Its Appl. 2011, 5, 39–45. (In Russian) [Google Scholar]
- Shevtsova, I.G. On the absolute constants in Nagaev–Bikelis–type inequalities. In Inequalities and Extremal Problems in Probability and Statistics; Pinelis, I., Ed.; Elsevier: Amsterdam, The Netherlands, 2017; Chapter 3; pp. 47–102. [Google Scholar]
- Shevtsova, I.G. On the asymptotically exact constants in the Berry–Esseen–Katz inequality. Theory Probab. Appl. 2011, 55, 225–252, Original Russian text: Teor. Veroyatn. Primen. 2010, 55, 271–304. [Google Scholar] [CrossRef]
- Shorgin, S.Y. On the accuracy of the normal approximation to ditributions of random sums with infinitely divisible indices. Theory Probab. Appl. 1997, 41, 798–805. [Google Scholar] [CrossRef]
- Korolev, V.Y. Generalized hyperbolic laws as limit distributions for random sums. Theory Probab. Appl. 2014, 58, 63–75. [Google Scholar] [CrossRef]
- Zaks, L.M.; Korolev, V.Y. Variance-generalized-gamma-distributions as limit laws for random sums. Inform. Its Appl. 2013, 7, 105–115. (In Russian) [Google Scholar]
- Grigor’eva, M.E.; Korolev, V.Y. On convergence of the distributions of random sums to skew exponential power laws. Inform. Its Appl. 2013, 7, 66–74. (In Russian) [Google Scholar]
- Bening, V.E.; Zaks, L.M.; Korolev, V.Y. Estimates of the rate of convergence of the distributions of random sums to the skew Student distribution. Sistemy i Sredstva Inform. 2012, 22, 132–141. (In Russian) [Google Scholar]
- Bening, V.E.; Zaks, L.M.; Korolev, V.Y. Estimates of the rate of convergence of the distributions of random sums to variance-gamma distributions. Inform. Its Appl. 2012, 6, 69–73. (In Russian) [Google Scholar]
- Shorgin, S.Y. Approximation of generalized Poisson distributions: Comparison of Lyapunov fractions. In Proceedings of the 21st Seminar on Stability Problems for Stochastic Models, Eger, Hungary, 28 January–3 February 2001; Abstracts. House of University of Debrecen: Eger, Hungary, 2001; pp. 166–167. [Google Scholar]
- Korolev, V.Y.; Shevtsova, I.G.; Shorgin, S.Y. On the Berry–Esseen type inequalities for Poisson random sums. Inform. Its Appl. 2011, 5, 64–66. (In Russian) [Google Scholar]
- Hoeffding, W. The extrema of the expected value of a function of independent random variables. Ann. Math. Statist. 1955, 26, 268–275. [Google Scholar] [CrossRef]
- Hoeffding, W.; Shrikhande, S.S. Bounds for the distribution function of a sum of independent, identically distributed random variables. Ann. Math. Statist. 1955, 26, 439–449. [Google Scholar] [CrossRef]
- Mulholland, H.P.; Rogers, C.A. Representation theorems for distribution functions. Proc. Lond. Math. Soc. 1958, 8, 177–223. [Google Scholar] [CrossRef]
- Zolotarev, V.M. Probability metrics. Theory Probab. Appl. 1984, 28, 278–302. [Google Scholar] [CrossRef]
- Nefedova, Y.S.; Shevtsova, I.G. On non-uniform convergence rate estimates in the central limit theorem. Theory Probab. Appl. 2013, 57, 28–59. [Google Scholar] [CrossRef]
- Pinelis, I. Optimal re-centering bounds, with applications to Rosenthal-type concentration of measure inequalities. In High Dimensional Probability VI; Progress in Probability; Houdré, C., Mason, D.M., Rosiński, J., Wellner, J.A., Eds.; Springer: Basel, Switzerland, 2013; Volume 66, pp. 81–93. [Google Scholar]
- Shevtsova, I.G. A moment inequality with application to convergence rate estimates in the global CLT for Poisson–binomial random sums. Theory Probab. Appl. 2018, 62, 278–294, Original Russian text: Teor. Veroyatn. Primen. 2017, 62, 345–364. [Google Scholar] [CrossRef]
- Richter, H. Parameterfreie Abschätzung und Realisierung von Erwartungswerten. Bl. Deutsch. Ges. Versicherungsmath. Bl. Deutsch. Ges. Versicherungsmath. 1957, 3, 147–162. [Google Scholar]
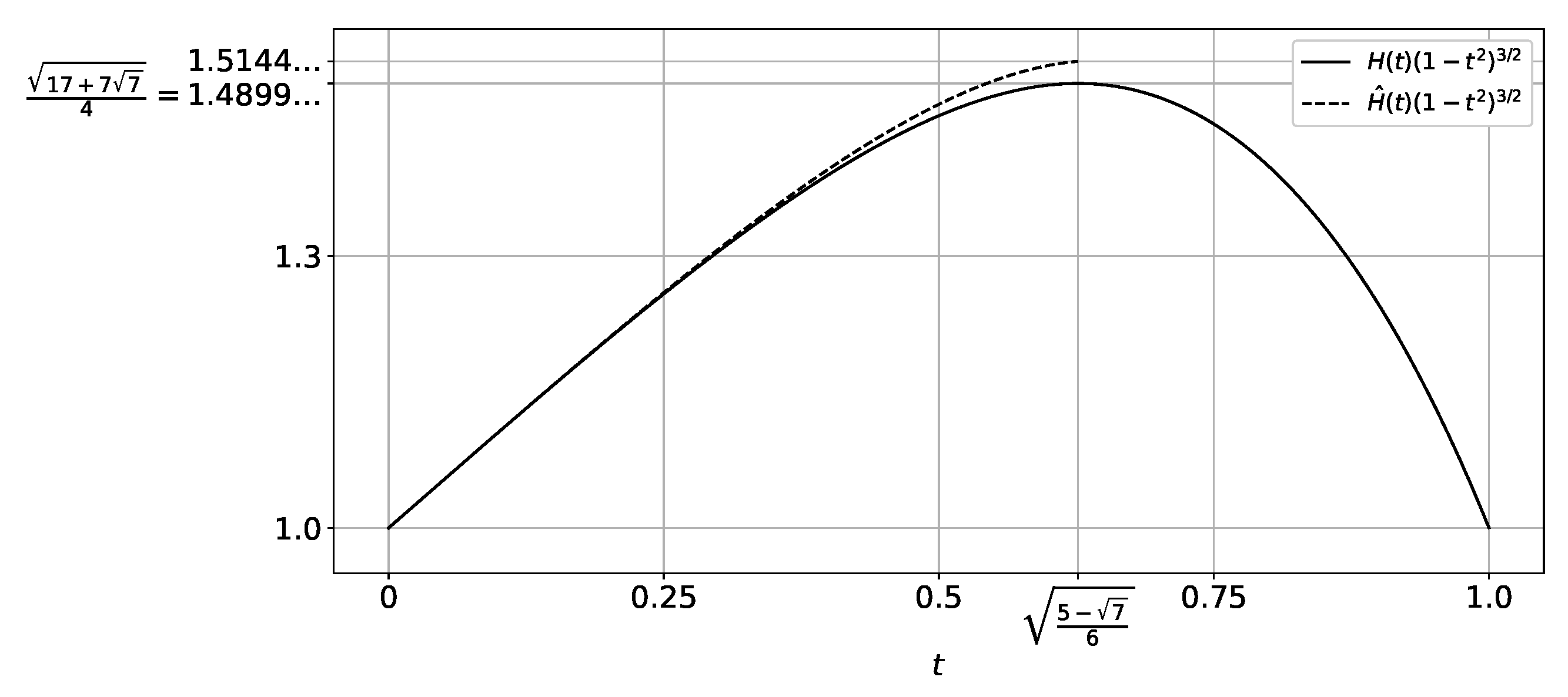
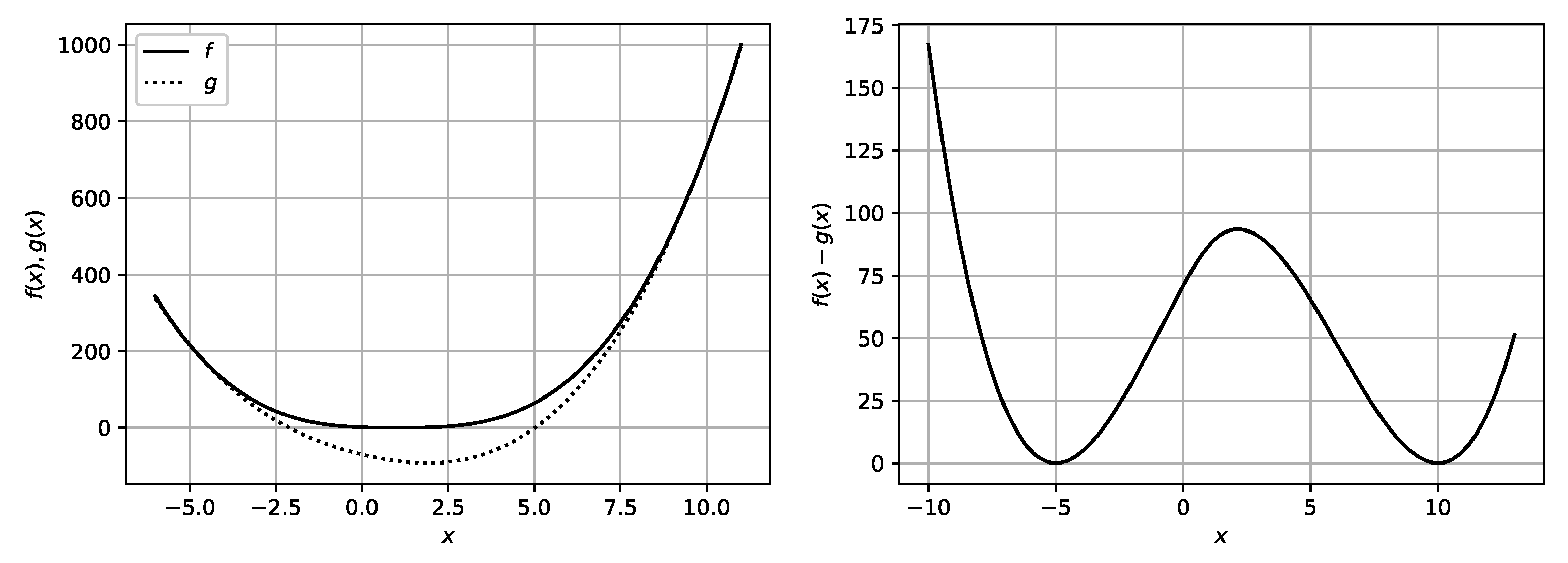
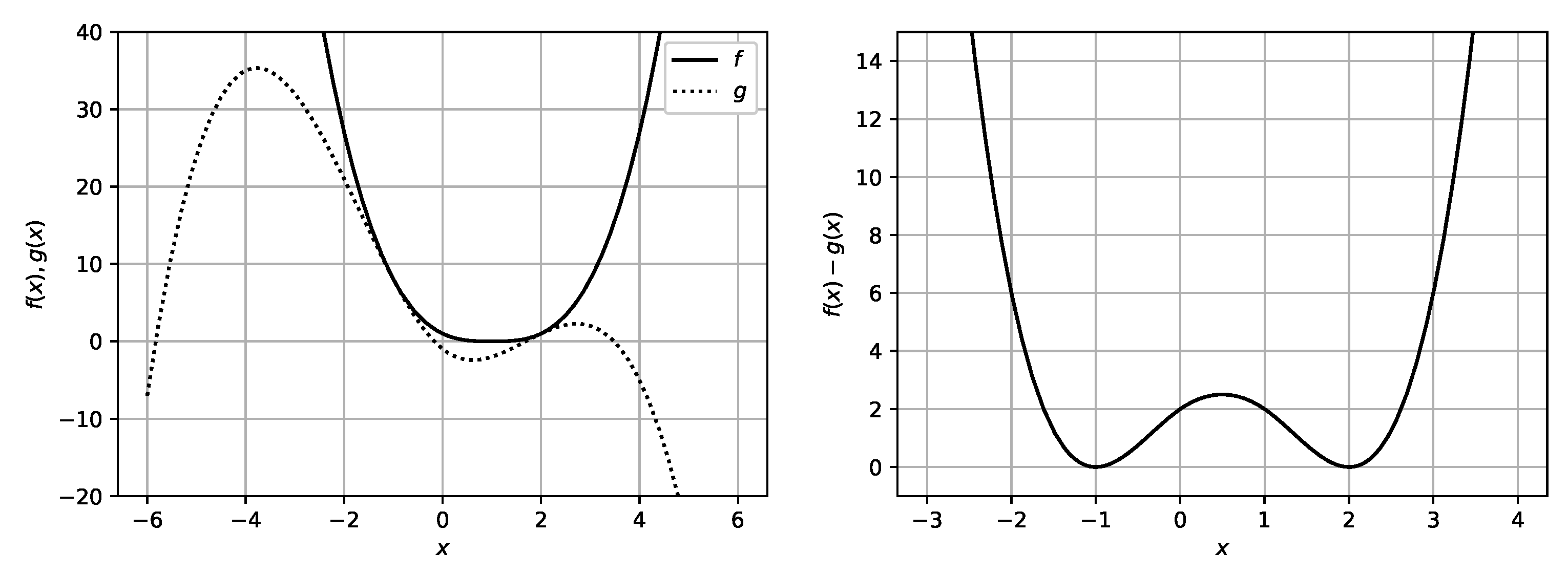

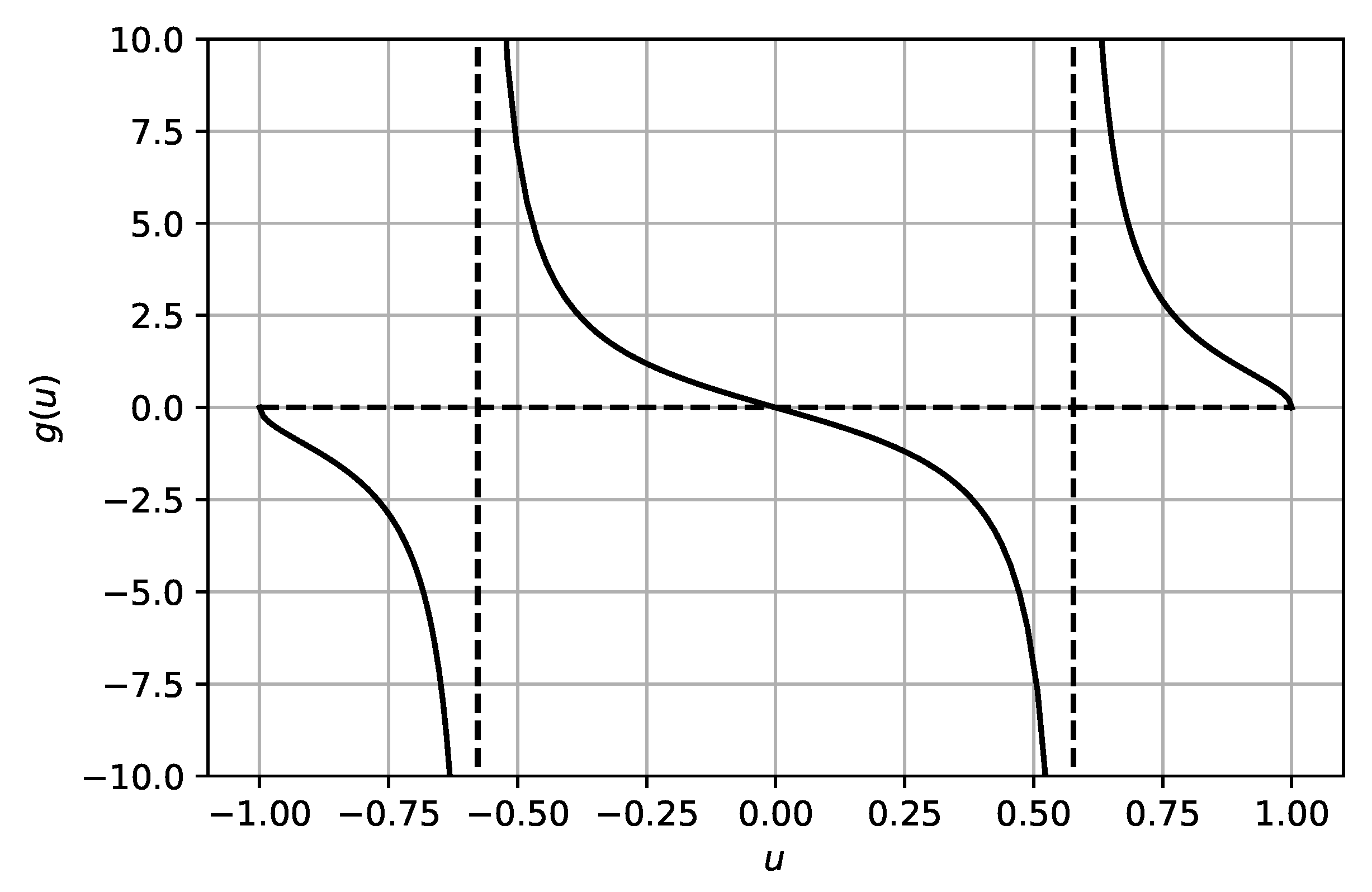
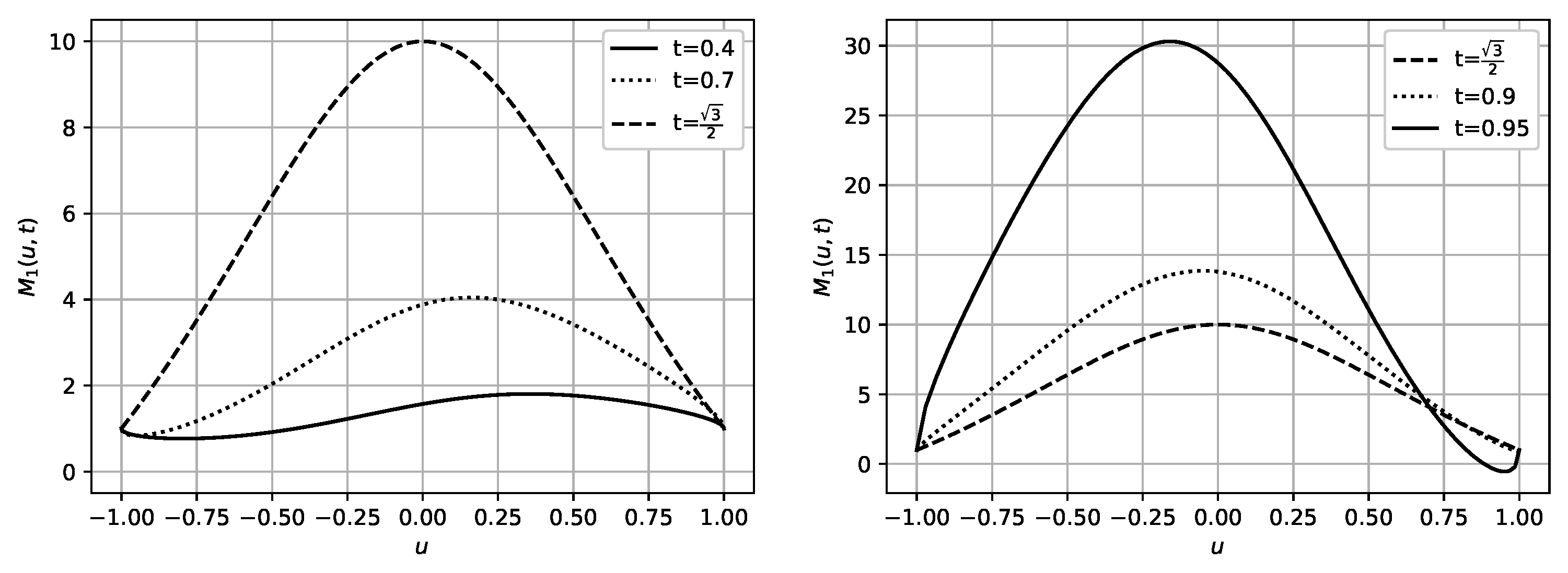

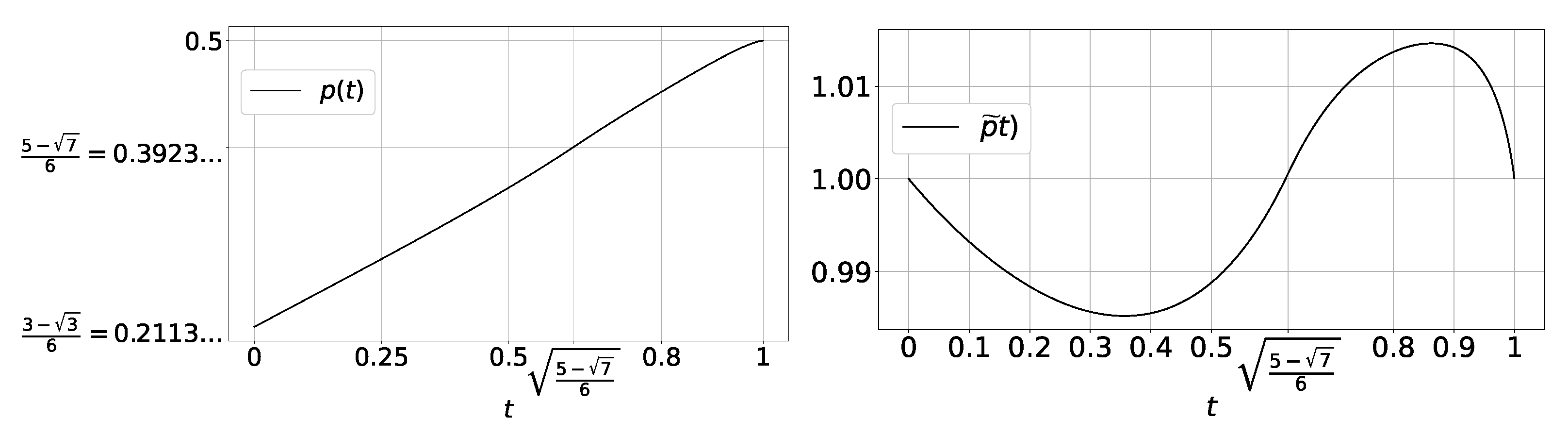
| t | ||||
|---|---|---|---|---|
| 0 | 1 | 1 | ||
| 1 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Makarenko, V.; Shevtsova, I. Delicate Comparison of the Central and Non-Central Lyapunov Ratios with Applications to the Berry–Esseen Inequality for Compound Poisson Distributions. Mathematics 2023, 11, 625. https://doi.org/10.3390/math11030625
Makarenko V, Shevtsova I. Delicate Comparison of the Central and Non-Central Lyapunov Ratios with Applications to the Berry–Esseen Inequality for Compound Poisson Distributions. Mathematics. 2023; 11(3):625. https://doi.org/10.3390/math11030625
Chicago/Turabian StyleMakarenko, Vladimir, and Irina Shevtsova. 2023. "Delicate Comparison of the Central and Non-Central Lyapunov Ratios with Applications to the Berry–Esseen Inequality for Compound Poisson Distributions" Mathematics 11, no. 3: 625. https://doi.org/10.3390/math11030625
APA StyleMakarenko, V., & Shevtsova, I. (2023). Delicate Comparison of the Central and Non-Central Lyapunov Ratios with Applications to the Berry–Esseen Inequality for Compound Poisson Distributions. Mathematics, 11(3), 625. https://doi.org/10.3390/math11030625