Optimization of the 24-Bit Fixed-Point Format for the Laplacian Source

Abstract

The 32-bit floating-point (FP32) binary format, commonly used for data representation in computers, introduces high complexity, requiring powerful and expensive hardware for data processing and high energy consumption, hence being unsuitable for implementation on sensor nodes, edge devices, and other devices with limited hardware resources. Therefore, it is often necessary to use binary formats of lower complexity than FP32. This paper proposes the usage of the 24-bit fixed-point format that will reduce the complexity in two ways, by decreasing the number of bits and by the fact that the fixed-point format has significantly less complexity than the floating-point format. The paper optimizes the 24-bit fixed-point format and examines its performance for data with the Laplacian distribution, exploiting the analogy between fixed-point binary representation and uniform quantization. Firstly, the optimization of the 24-bit uniform quantizer is performed by deriving two new closed-form formulas for a very accurate calculation of its maximal amplitude. Then, the 24-bit fixed-point format is optimized by optimization of its key parameter and by proposing two adaptation procedures, with the aim to obtain the same performance as of the optimal uniform quantizer in a wide range of variance of input data. It is shown that the proposed 24-bit fixed-point format achieves for 18.425 dB higher performance than the floating-point format with the same number of bits while being less complex.

1. Introduction

Due to the dominance of digital systems, almost all data are represented in binary formats. As the number of bits in the binary representation is limited, special attention should be paid to ensure required accuracy for a specific application, taking into account the dynamic range and statistical characteristics of data. In addition, due to the increasing amount of data being generated, it is necessary to find efficient binary representation that will provide sufficient accuracy with as few bits as possible. All of this proves the importance of studying binary formats.

The 32-bit floating-point (FP32) binary format defined by the IEEE 754 standard [1] is commonly used in practice, especially for data representation in computers. Using a large number of bits, FP32 provides high accuracy of binary representation in a very wide range of variance of input data. Nevertheless, the floating-point formats (including the FP32) introduce high complexity, requiring powerful and expensive hardware for data processing, as well as high energy consumption [2]. Furthermore, the FP32 format requires large memory space for data storage. It is especially impractical to implement the FP32 format on widespread sensor nodes, edge devices, and other devices with limited hardware resources (i.e., with limited processing power, memory capacity, and available energy). In fact, many embedded devices do not support the floating-point formats at all [3].

The FP32 format is also standardly used to represent the parameters of deep neural networks (DNNs) [4], which are currently one of the most powerful techniques for solving problems such as object detection [5], autonomous driving [6], natural language processing [7], computer vision [8], and speech recognition [9]. A particularly current research direction that involves great research effort is implementation of DNNs on sensor nodes (obtaining smart sensors) and edge devices, in order to increase their availability and applicability [10]. However, the fact that parameters in DNNs are represented in the FP32 format significantly limits the implementation of DNNs on sensor nodes and edge devices [3,11].

Based on the common practice of using digital words whose length is an integer multiple of 8 bits, the first solution that arises as a replacement for 32-bit formats is the usage of 24-bit formats, enabling a reduction in complexity without significantly degrading performance. However, the reduction in complexity that would be achieved by using the FP24 (24-bit floating-point) format [12] instead of the FP32 is often insufficient since the FP24 also belongs to the class of floating-point formats.

The paper proposes the 24-bit fixed-point format as a better replacement for the FP32 format than the FP24 format. This will reduce the complexity in two ways, by decreasing the number of bits and by using the fixed-point format that has significantly less computational complexity, consumes less power, requires less area on chip, and provides faster calculations than floating-point formats [11,13,14,15,16,17,18,19,20,21,22,23], being much more suitable for implementation on sensor nodes and devices with limited hardware resources (a typical microcontroller has 128 KB RAM and 1 MB of flash, while a mobile phone can have 4 GB of RAM and 64 GB of storage [24]). Therefore, the main goal of the paper is to optimize the 24-bit fixed-point format and to examine its performance. To achieve this goal, the analogy between fixed-point binary representation and uniform quantization established in [25] will be exploited, allowing us to express accuracy of fixed-point formats using objective performance measures (distortion and SQNR (signal-to-quantization noise ratio)) of the uniform quantizer.

To find an optimal binary representation of some dataset, the probability density function (PDF) of data should be taken into account. In this paper, the Laplacian PDF is considered since it can be used for statistical modeling of a number of data types [26,27].

The approach applied in the paper, based on the above mentioned analogy, is to first optimize the 24-bit uniform quantizer and after that to optimize the 24-bit fixed-point format with the aim to achieve the same performance as of the 24-bit optimal uniform quantizer. Therefore, the design and performance calculation of the 24-bit optimal uniform quantizer is firstly considered, deriving two new closed-form approximate formulas for a very accurate calculation of its key parameter (the maximal amplitude) as a significant result of the paper. It is worth noting that the derived approximate formulas are valid for any bit-rate R, having general importance. Then, the 24-bit fixed-point format is optimized by exploring the influence of the parameter n (the number of bits used to represent the integer part of data) on the performance. The optimal value of n = 5 is obtained for the unit variance Laplacian PDF. An important conclusion obtained from the analysis is that a wrong choice for the value of n can drastically reduce the accuracy of the fixed-point representation.

Even with the optimal value n = 5, the 24-bit fixed-point format achieves lower SQNR compared to the optimal uniform quantizer, due to a mismatch in the maximal amplitude. Therefore, the paper proposes an adaptation procedure (called Adaptation 1) which enables the 24-bit fixed-point format to achieve the maximal possible SQNR of 122.194 dB for the unit variance, just like the optimal uniform quantizer.

However, there is a problem related to the 24-bit fixed-point format that SQNR changes with the change of data variance. To solve this problem, the paper proposes an additional adaptation procedure (called Adaptation_2) that converts the variance of the input data to 1. The proposed joint application of Adaptation_1 and Adaptation_2 allows for the 24-bit fixed-point quantizer to achieve the maximal SQNR for any variance of the input data, being a notable result of the paper.

Finally, the comparison with the FP24 format is performed, whereby the performance of the FP24 is calculated using the analogy between the floating-point representation and piecewise uniform quantization established in [28]. It is shown that the proposed 24-bit fixed-point format with double adaptation achieves for 18.425 dB higher SQNR than the FP24 format. An important conclusion that can be made based on the achieved results is that the proposed 24-bit fixed-point format with the double adaptation is a much better solution than the FP24 format, for two reasons: it achieves a significantly higher SQNR having significantly less implementation complexity.

2. Design of the Optimal Uniform Quantizer

An R-bit uniform quantizer with N = 2^R levels and with the support region $[-x_{\max },x_{\max }]$ is defined by its decision thresholds $x_i=-x_{\max }+i\cdot \mathsf{\Delta }$, ($i=0,\dots ,N$) and representation levels $y_i=-x_{\max }+(i-1/2)\cdot \mathsf{\Delta }$, ($i=1,\dots ,N$), where $x_{\max }$ represents the maximal amplitude and $\mathsf{\Delta }=2x_{\max }/N$ represents the quantization step-size. The uniform quantizer maps each quantization interval $[x_{i-1},x_i)$ into the representation level $y_i=(x_{i-1}+x_i)/2$ placed in the middle of that interval [25].

In order to design an optimal quantizer, the probability density function (PDF) of the input data has to be taken into account. This paper considers the Laplacian PDF defined as [27]:

$$p(x)=\frac{1}{\sqrt{2}\sigma }\exp \left(-\frac{\left|x\right|\sqrt{2}}{\sigma }\right),$$

(1)

where ${\sigma }^2$ represents the variance of the input data.

Quantization process is shown in Figure 1. Let the input dataset consists of M elements $r_i$ ($i=1,\dots ,M$). The variance of the input data is calculated as [26]:

$${\sigma }^2=\frac{1}{M}{\displaystyle \sum _{i=1}^M{r}_i^2}.$$

(2)

By quantization, each input element $r_i$ is compared with decision thresholds $\{x_0,x_1,\dots ,x_N\}$ of the quantizer, determining the quantization interval where the input element belongs and generating an R-bit code-word (in our case, R = 24) that corresponds to the determined quantization interval. The code-word is stored in memory. When we want to reconstruct data from the binary form, a decoding has to be performed. Let $r_i^{*}$ denotes the reconstructed value of the input element $r_i$. The decoding is done in a way that the reconstructed element $r_i^{*}$ takes the value of one of N discrete representation values $\{y_1,\dots ,y_N\}$ of the quantizer that is nearest to the value of the input element $r_i$. An irreversible error occurs during quantization, since the reconstructed values $r_i^{*}$ differ from the original values $r_i$ ($i=1,\dots ,M$). Distortion D represents the mean-square quantization error and based on the Figure 1, it can be defined as:

$$D=\frac{1}{M}{\displaystyle \sum _{i=1}^M{(r_i-r_i^{*})}^2}.$$

(3)

The distortion D can be also defined in another way, based on the statistical approach, as [26]:

$$D={\displaystyle \sum _{j=1}^N{\displaystyle \underset{x_{j-1}}{\overset{x_j}{\int }}p(x){(x-y_j)}^{2}dx}},$$

(4)

where $p(x)$ denotes the probability density function (PDF) of the input data.

For the asymptotic analysis which assumes that the number of quantization levels N is large enough, Formulas (3) and (4) for the distortion D are equivalent. For further analysis in this section, we will use the Formula (4) which for the uniform quantizer becomes [25,29]:

$$D=\frac{{\mathsf{\Delta }}^2}{12}+2{\displaystyle \underset{x_{\max }}{\overset{+\infty }{\int }}{(x-x_{\max })}^{2}p(x)dx}.$$

(5)

The first term in (5) represents the granular distortion that occurs during quantization of data from the support region $[-x_{\max },x_{\max }]$, while the second term in (5) represents the overload distortion that occurs during quantization of data outside of the support region. For $p(x)$ defined by (1) and for $\mathsf{\Delta }=2x_{\max }/N$, the expression (5) becomes:

$$D(\sigma )=\frac{x_{\max }^2}{3N^2}+{\sigma }^2\exp \left(-\frac{x_{\max }\sqrt{2}}{\sigma }\right).$$

(6)

The quality of quantization is usually measured by SQNR which is defined as [16]:

$$\mathrm{SQNR}(\sigma ) \left[\mathrm{dB}\right]=10\cdot {\log }_{10}\frac{{\sigma }^2}{D(\sigma )}.$$

(7)

Standard approach for designing quantizers is to minimize distortion D or to maximize SQNR for some referent variance ${\sigma }_0^2.$ Common practice in literature [26], that will also be applied in this paper, is to take the unit variance as the referent variance (${\sigma }_0^2$= 1). Expressions (6) and (7) for the distortion and SQNR of the uniform quantizer for ${\sigma }_0^2$ = 1 becomes, respectively:

$$D(\sigma =1)=\frac{x_{\max }^2}{3N^2}+\exp \left(-x_{\max }\sqrt{2}\right),$$

(8)

$$\mathrm{SQNR}(\sigma =1) \left[\mathrm{dB}\right]=-10\cdot {\log }_{10}D(\sigma =1)=-10\cdot {\log }_{10}\left[\frac{x_{\max }^2}{3N^2}+\exp \left(-x_{\max }\sqrt{2}\right)\right].$$

(9)

The maximal amplitude $x_{\max }$ can be considered as a key parameter of the uniform quantizer, since all other parameters ($\mathsf{\Delta },$$x_i$, $y_i$) can be calculated based on $x_{\max }$. Therefore, the key task in designing the uniform quantizer is to determine the optimal value of $x_{\max }$ by minimizing the distortion $D(\sigma =1)$.

Lemma 1.

Distortion $D(\sigma =1)$ of the uniform quantizer has a unique global minimum.

Proof of Lemma 1.

For $D(\sigma =1)$ defined with (8), we have that:

$$\frac{\partial D(\sigma =1)}{\partial x_{\max }}=\frac{2x_{\max }}{3N^2}-\sqrt{2}\exp \left(-\sqrt{2}{x}_{\max }\right),$$

(10)

$$\frac{{\partial }^{2}D(\sigma =1)}{\partial x_{\max }^2}=\frac{2}{3N^2}+2\exp \left(-\sqrt{2}{x}_{\max }\right).$$

(11)

From the condition $\partial D(\sigma =1)/\partial x_{\max }=0$ we obtain the equation $\sqrt{2}{x}_{\max }/(3N^2)=\exp \left(-\sqrt{2}{x}_{\max }\right)$. As the increasing linear function $\sqrt{2}{x}_{\max }/(3N^2)$ and the decreasing exponential function $\exp \left(-\sqrt{2}{x}_{\max }\right)$ have a unique intersection point for $x_{\max }$ > 0, the distortion $D(\sigma =1)$ must have a unique extremum. It follows from (11) that ${\partial }^{2}D(\sigma =1)/\partial x_{\max }^2>0$, meaning that this unique extremum of $D(\sigma =1)$ is in fact a unique minimum of distortion $D(\sigma =1)$, being a global minimum of $D(\sigma =1)$. This proves Lemma 1. □

Let $x_{\max }^{opt}$ denote the value of $x_{\max }$ where $D(\sigma =1)$ achieves the global minimum. For $x_{\max }=x_{\max }^{opt}$, the uniform quantizer achieves the maximal SQNR that is expressed, using (9), as:

$${\mathrm{SQNR}}_{\max }=-10 {\log }_{10}\left[\frac{{\left(x_{\max }^{opt}\right)}^2}{3N^2}+\exp \left(-\sqrt{2}{x}_{\max }^{opt}\right)\right].$$

(12)

The value of $x_{\max }^{opt}$ can be calculated numerically in the Mathematica software package. For the 24-bit uniform quantizer we obtain the value $x_{\max }^{opt}$= 21.876, achieving ${\mathrm{SQNR}}_{\max }$ of 122.194 dB.

Nevertheless, to facilitate the design of the uniform quantizer, it is desirable to derive an approximate closed-form formula for calculation of the optimal $x_{\max }$. The following approximate formula for $x_{\max }$ was proposed in [29]:

$$x_{\max }=\sqrt{2}\ln N.$$

(13)

However, this formula is not accurate enough: for R = 24 bits it gives $x_{\max }$= 23.526, producing an error of 7.542 % in relation to the optimal value $x_{\max }^{opt}$, that can be too high for a number of applications.

As an important contribution of the paper, we will derive below two closed-form approximate formulas for very accurate calculation of $x_{\max }$. For the optimal value of $x_{\max }$, the distortion $D(\sigma =1)$ should be minimal, meaning that its first derivative defined by (10) should be equal to 0. If we equate the expression (10) with 0, it follows that $\exp (-\sqrt{2}{x}_{\max })=\sqrt{2}{x}_{\max }/(3N^2)$. By logarithmization of this expression, it is obtained that:

$$x_{\max }=\frac{1}{\sqrt{2}}\ln \frac{3N^2}{\sqrt{2}{x}_{\max }}.$$

(14)

Based on the Equation (14), we can define the iterative process

$$x_{\max }^{(i)}=\frac{1}{\sqrt{2}}\ln \frac{3N^2}{\sqrt{2}{x}_{\max }^{(i-1)}},$$

(15)

for calculation of $x_{\max }$. If we take the value defined by (13) as the starting point $x_{\max }^{(0)}$ of the iterative process (15), i.e., $x_{\max }^{(0)}=\sqrt{2}\ln N$, we will obtain a value for $x_{\max }$ that is very close to $x_{\max }^{opt}$ just after the first iteration. Therefore, we can take the expression for the first iteration $x_{\max }^{(1)}$ as a closed-form approximate formula for $x_{\max }$:

$$x_{\max }\cong x_{\max }^{(1)}=\frac{1}{\sqrt{2}}\ln \frac{3N^2}{2\ln N}.$$

(16)

For R = 24 bits, the Formula (16) gives the value of $x_{\max }$ = 21.825, producing an error of only 0.235 % in relation to the optimal value $x_{\max }^{opt}$. Thus, the formula (16) is much more accurate than the Formula (13), providing satisfactory accuracy for a lot of applications. However, if an even more accurate calculation of $x_{\max }$ is required for some applications, the second iteration $x_{\max }^{(2)}$ of the iterative process (15), obtained by putting (16) in (15), can be used as a closed-form approximate formula for a very accurate calculation of $x_{\max }:$

$$x_{\max }\cong x_{\max }^{(2)}=\frac{1}{\sqrt{2}}\ln \frac{3N^2}{\ln \frac{3N^2}{2\ln N}}.$$

(17)

For R = 24 bits, the Formula (17) gives the value $x_{\max }$= 21.878 that differs from $x_{\max }^{opt}$ by only 0.009 %.

3. 24-Bit Fixed-Point Quantizer

A real number x can be represented in the R-bit fixed-point representation as [25]:

$$x={(s{a}_{n-1}{a}_{n-2}\dots a_1{a}_0 . a_{-1}\dots a_{-m})}_2,$$

(18)

where we use one bit ‘s’ to encode the sign of x, n bits ($a_{n-1}{a}_{n-2}\dots a_1{a}_0$) to encode the integer part of x and m bits ($a_{-1}\dots a_{-m}$) to encode the fractional part of x. Hence, we have that R = n + m + 1. Each bit $a_i$ ($i=-m,\dots ,n-1$) in the fixed-point representation has the weight of $2^i,$ allowing for easy calculation of x from the fixed-point binary form as $x=$ ${(-1)}^s{\displaystyle {\sum }_{i=-m}^{n-1}{a}_i{2}^i}.$ The number 0 is represented with all bits equal to 0. The largest positive number that can be represented in the fixed-point format is $x_{\max }={(1\dots 1.1\dots 1)}_2=$ ${\displaystyle {\sum }_{i=-m}^{n-1}{2}^i}=2^{-m}{\displaystyle {\sum }_{i=0}^{n+m-1}{2}^i}=2^{-m}(2^{n+m}-1)=2^n-2^{-m}\approx 2^n.$ Due to the symmetry with respect to 0, the largest negative number that can be represented is $-2^n$.

Let us consider the first few positive numbers represented in the R-bit fixed-point format. The smallest positive number that can be represented is ${(\mathrm{0...0.0...01})}_2=2^{-m}$, the next number is ${(\mathrm{0...0.0...010})}_2=2^{-(m-1)}=2\cdot 2^{-m}$, the next is ${(\mathrm{0...0.0...011})}_2=$$2^{-(m-1)}+2^{-m}=$ $3\cdot 2^{-m}$, and so on. All these numbers are equidistant, placed on mutual distance $2^{-m}$. Hence, we can conclude that the R-bit fixed-point representation can represent uniformly placed numbers from the range $[-2^n, 2^n]$ with the step-size $\mathsf{\Delta }=2^{-m}$, whereby all other real numbers are rounded to the nearest one of these numbers. Therefore, the R-bit fixed-point representation can be considered as a uniform quantizer with parameters $x_{\max }=2^n$ and $\mathsf{\Delta }=2^{-m}$. This uniform quantizer that corresponds to the R-bit fixed-point representation will be called the R-bit fixed-point quantizer. This analogy between the fixed-point binary representation and the uniform quantization is very important, allowing us to use SQNR of the R-bit fixed-point uniform quantizer as an objective measure to assess the quality of the R-bit fixed-point representation [25].

The distortion of the fixed-point quantizer can be calculated using (6) as:

$$D_{\mathrm{fxp}}(\sigma )=\frac{2^{2n}}{3N^2}+{\sigma }^2\exp \left(\frac{-\sqrt{2}\cdot 2^n}{\sigma }\right)=\frac{1}{3}{2}^{2(n-R)}+{\sigma }^2\exp \left(\frac{-2^{n+1/2}}{\sigma }\right).$$

(19)

For the unit variance, the expression (19) becomes:

$$D_{\mathrm{fxp}}(\sigma =1)=\frac{2^{2n}}{3N^2}+\exp \left(-\sqrt{2}\cdot 2^n\right)=\frac{1}{3}{2}^{2(n-R)}+\exp \left(-2^{n+1/2}\right).$$

(20)

Our goal is to examine the influence of the parameter n on the performance of the fixed-point quantizer. The optimal value of n can be found by minimizing the distortion $D_{\mathrm{fxp}}(\sigma =1)$, from the condition

$$\frac{d{D}_{\mathrm{fxp}}(\sigma =1)}{dn}=2^n\ln 2\cdot \left(\frac{1}{3}{2}^{n-2R+1}-\sqrt{2}\exp \left(-2^{n+1/2}\right)\right)=0.$$

(21)

From (21), we obtain the condition $2^{n-2R+1}=3\sqrt{2}\exp \left(-2^{n+1/2}\right)$ that leads to the equation:

$$n=\frac{\ln (3\sqrt{2})}{\ln 2}+2R-1-\frac{\sqrt{2}}{\ln 2}{2}^n.$$

(22)

For R = 24, Equation (22) becomes

$$n=49.085-2.04028\cdot 2^n.$$

(23)

By numerical solution of Equation (23), we obtain that the optimal value of n is 4.45. However, n must be an integer, so the optimal value of n can be 4 or 5. To determine the optimal value of n, but also to better understand how the value of n affects performance, we calculate SQNR for different values of n, using (9) and (20). The results are shown in

Table 1. SQNR (dB) of the 24-bit fixed-point quantizer for different values of the parameter n.

n	SQNR (dB)	n	SQNR (dB)	n	SQNR (dB)
0	6.142	8	101.101	16	52.936
1	12.284	9	95.080	17	46.915
2	24.567	10	89.060	18	40.895
3	49.135	11	83.039	19	34.874
4	98.261	12	77.018	20	28.854
5	119.163	13	70.998	21	22.833
6	113.142	14	64.977	22	16.812
7	107.121	15	58.957	23	10.792

, where we can see that n = 5 gives the highest value of SQNR, being the optimal value of n. To summarize: for the 24-bit fixed-point representation, the optimal values of parameters are n = 5, m = 18,$x_{\max }=2^n$= 32, and $\mathsf{\Delta }=2^{-m}=2^{-18}$, achieving the maximal SQNR of 119.163 dB. Another important conclusion from Table 1 is that the wrong choice of the value of n drastically reduces the SQNR (i.e., the accuracy of the fixed-point representation).

4. Adaptive 24-Bit Fixed-Point Quantizer

Adaptation procedures for further improvement of the performance of the 24-bit fixed-point format is presented below.

4.1. Adaptation for Data with the Unit Variance ${\sigma }^2=1$

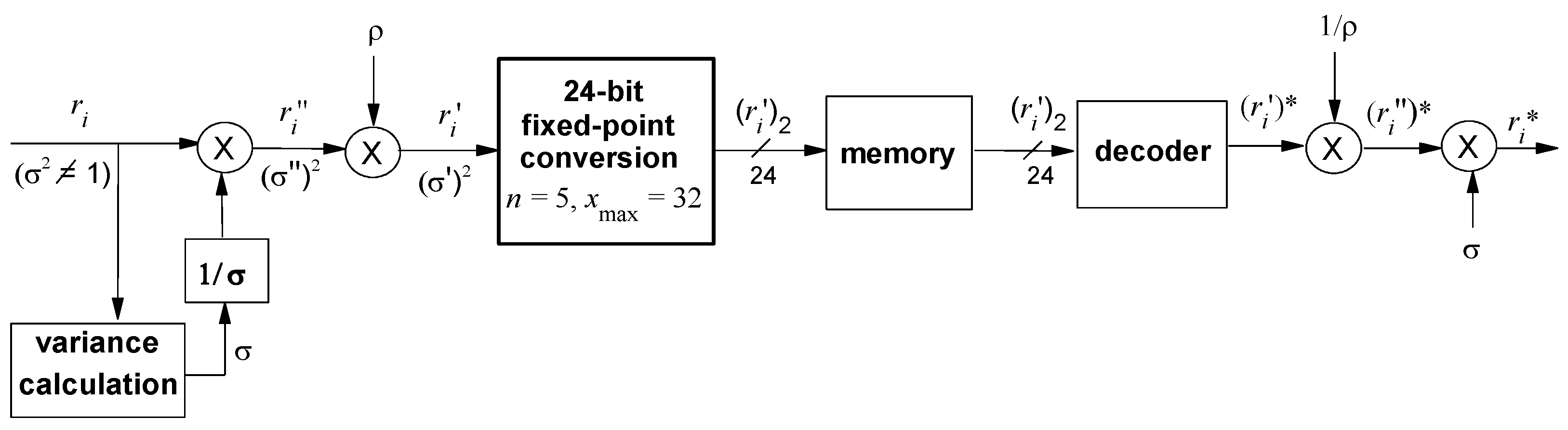
In this subsection, we will consider data with the unit variance. To recall: for data modeled by the unit-variance Laplacian PDF, the 24-bit fixed-point quantizer with parameters n = 5 and $x_{\max }$ = 32 achieves SQNR of 119.163 dB while the 24-bit optimal uniform quantizer with the maximal amplitude $x_{\max }^{opt}$ = 21.876 achieves ${\mathrm{SQNR}}_{\max }$ = 122.194 dB. Thus, the 24-bit fixed-point quantizer achieves for 3.031 dB lower SQNR compared to the 24-bit optimal uniform quantizer, due to the mismatch of $x_{\max }$. To enable the 24-bit fixed-point quantizer to achieve the maximal SQNR of 122.194 dB, we need to adapt the input data as follows.

Adaptation_1. Input data, modeled by the unit-variance Laplacian PDF, should be firstly multiplied by $\rho =2^n/x_{\max }^{opt}=32/21.876 = 1.463$ before the conversion to the 24-bit fixed point format, as it is shown in Figure 2, where $r_i$ ($i=1,\dots ,M$) denotes an element of the input data, $r_i{}^{\prime }=\rho \cdot r_i$ denotes the adapted element, ${(r_i{}^{\prime })}_2$ denotes a 24-bit binary code-word of the adapted element $r_i{}^{\prime }$, ${(r_i{}^{\prime })}^{*}$ denotes a reconstructed value of the adapted element $r_i{}^{\prime }$ and $r_i^{*}={(r_i{}^{\prime })}^{*}/\rho$ denotes a reconstructed value of the input element $r_i$.

Lemma 2.

If the variance of the input data $r_i$ ($i=1,\dots ,M$) is ${\sigma }^2=1$, then the variance of the adapted data $r_i{}^{\prime }=\rho \cdot r_i$ ($i=1,\dots ,M$) is ${(\sigma {}^{\prime })}^2={\rho }^2$.

Proof of Lemma 2.

It is given that the variance of the input data is equal to 1, i.e., ${\sigma }^2=\frac{1}{M}{\displaystyle {\sum }_{i=1}^M{(r_i)}^2=}1$. Then, we have that:

$${(\sigma {}^{\prime })}^2=\frac{1}{M}{\displaystyle {\sum }_{i=1}^M{(r_i{}^{\prime })}^2=\frac{1}{M}{\displaystyle {\sum }_{i=1}^M{(\rho \cdot r_i)}^2=}}{\rho }^2\frac{1}{M}{\displaystyle {\sum }_{i=1}^M{(r_i)}^2=}{\rho }^2\cdot {\sigma }^2={\rho }^2\cdot 1={\rho }^2,$$

(24)

proving the Lemma 2. □

Theorem 1.

For the input data with the unit variance, the SQNR of the adapted 24-bit fixed-point quantizer (according to the Adaptation_1), marked as ${\mathrm{SQNR}}_{\mathrm{adapt}\_1}$, is equal to the maximal SQNR of the optimal uniform quantizer ${\mathrm{SQNR}}_{\max }$ defined with (12), i.e., ${\mathrm{SQNR}}_{\mathrm{adapt}\_1}$ = ${\mathrm{SQNR}}_{\max }$.

Proof of Theorem 1.

According to Figure 2, the distortion of the adapted 24-bit fixed-point quantizer is calculated as:

$$D_{\mathrm{adapt}\_1}=\frac{1}{M}{\displaystyle \sum _{i=1}^M{(r_i-r_i^{*})}^2}=\frac{1}{M}{\displaystyle \sum _{i=1}^M{\left(\frac{r_i{}^{\prime }}{\rho }-\frac{{(r_i{}^{\prime })}^{*}}{\rho }\right)}^2}=\frac{1}{{\rho }^2}\frac{1}{M}{\displaystyle \sum _{i=1}^M{\left(r_i{}^{\prime }-{(r_i{}^{\prime })}^{*}\right)}^2}.$$

(25)

The input of the 24-bit fixed-point quantizer consists of the adapted data elements $r_i{}^{\prime }$, whose reconstructed values are ${(r_i{}^{\prime })}^{*}$, $i=1,\dots ,M$; hence, according to (3), the distortion of the 24-bit fixed-point quantizer is calculated as:

$$D_{\mathrm{fxp}}=\frac{1}{M}{\displaystyle \sum _{i=1}^M{\left(r_i{}^{\prime }-{(r_i{}^{\prime })}^{*}\right)}^2}.$$

(26)

On the other hand, the distortion of the 24-bit fixed-point quantizer can be calculated by (19) where we should use $\sigma {}^{\prime }$ instead of $\sigma$, since the variance of the adapted data $r_i{}^{\prime }$ is denoted as ${(\sigma {}^{\prime })}^2$. Since from Lemma 2 it follows that $\sigma {}^{\prime }=\rho$, the distortion of the 24-bit fixed-point quantizer can be expressed, based on (19), as:

$$D_{\mathrm{fxp}}\equiv D_{\mathrm{fxp}}(\rho )=\frac{2^{2n}}{3N^2}+{\rho }^2\exp \left(\frac{-\sqrt{2}\cdot 2^n}{\rho }\right).$$

(27)

Due to the equivalence of formulas (3) and (4), as well as knowing that expression (26) comes from the formula (3) while expression (27) is derived from formula (4), it follows that expressions (26) and (27) for the distortion of the 24-bit fixed-point quantizer are equivalent. Based on this equivalence we have that:

$$\frac{1}{M}{\displaystyle \sum _{i=1}^M{\left(r_i{}^{\prime }-{(r_i{}^{\prime })}^{*}\right)}^2}=\frac{2^{2n}}{3N^2}+{\rho }^2\exp \left(\frac{-\sqrt{2}\cdot 2^n}{\rho }\right).$$

(28)

Putting (28) into (25), it is obtained that:

$$D_{\mathrm{adapt}\_1}=\frac{1}{{\rho }^2}\left(\frac{2^{2n}}{3N^2}+{\rho }^2\exp \left(\frac{-\sqrt{2}\cdot 2^n}{\rho }\right)\right)=\frac{2^{2n}}{3N^2{\rho }^2}+\exp \left(\frac{-\sqrt{2}\cdot 2^n}{\rho }\right)=\frac{{(2^n/\rho )}^2}{3N^2}+\exp \left(-\sqrt{2}\cdot \frac{2^n}{\rho }\right).$$

(29)

Since $x_{\max }^{opt}=2^n/\rho$, the expression (29) becomes:

$$D_{\mathrm{adapt}\_1}=\frac{{(x_{\max }^{opt})}^2}{3N^2}+\exp \left(-\sqrt{2}\cdot x_{\max }^{opt}\right).$$

(30)

Since the variance of the input data $r_i$ ($i=1,\dots ,M$) is equal to 1, SQNR of the adaptive 24-bit fixed-point quantizer can be calculated based on (9) and (30), as:

$${\mathrm{SQNR}}_{\mathrm{adapt}\_1}=-10\cdot {\log }_{10}{D}_{\mathrm{adapt}\_1}=-10\cdot {\log }_{10}\left[\frac{{(x_{\max }^{opt})}^2}{3N^2}+\exp \left(-\sqrt{2}{x}_{\max }^{opt}\right)\right].$$

(31)

Comparing (30) and (12), it follows that ${\mathrm{SQNR}}_{\mathrm{adapt}\_1}$ = ${\mathrm{SQNR}}_{\max }$, thus completing the proof of Theorem 1. □

Theorem 1 shows that by Adaptation_1 SQNR of the 24-bit fixed-point representation increases for 3.031 dB for the unit-variance Laplacian PDF, achieving the maximal possible value ${\mathrm{SQNR}}_{\max }$ = 122.194 dB.

4.2. Double Adaptation for Data with the Variance ${\sigma }^2\ne 1$

In this subsection, we consider the case that the variance of the input data differs from 1. Let us define the following adaptation procedure.

Adaptation_2. Calculate the variance of the input data ${\sigma }^2$ according to (2) and if it differs from 1, divide all input elements $r_i$ ($i=1,\dots ,M$) by $\sigma$.

Lemma 3.

The variance ${(\sigma {}^{″})}^2$ of data $r_i{}^{″}=r_i/\sigma$($i=1,\dots ,M$), obtained by applying of the Adaptation_2 procedure, is ${(\sigma {}^{″})}^2$ = 1.

Proof of Lemma 3.

The variance of the input data is ${\sigma }^2=\left({\displaystyle {\sum }_{ i=1}^M{r}_i^2}\right)/M$. Then, the variance of data $r_i{}^{″}$ obtained by the Adaptation_2 procedure is:

$${(\sigma {}^{″})}^2=\frac{1}{M}{\displaystyle \sum _{i=1}^M{(r_i{}^{″})}^2}=\frac{1}{M}{\displaystyle \sum _{i=1}^M{(r_i/\sigma )}^2}=\frac{1}{{\sigma }^2}\frac{1}{M}{\displaystyle \sum _{i=1}^M{r}_i{}^2}=\frac{{\sigma }^2}{{\sigma }^2}=1,$$

(32)

proving Lemma 3. □

Lemma 3 shows that by the Adaptation_2, we obtain data with the unit variance.

Our aim is to provide the same quality of the 24-bit fixed-point representation for data whose variance differs from 1 as for data whose variance is equal to 1. To achieve this, we need to perform a double adaptation, as follows.

Double adaptation. If the variance of the input data differs from 1, apply the Adaptation_2 followed by the Adaptation_1 before conversion to the 24-bit fixed-point format. This is shown in Figure 3, where $r_i$ ($i=1,\dots ,M$) denotes an element of the input data, $r_i{}^{″}=r_i/\sigma$ denotes the value of the element after Adaptation_2, $r_i{}^{\prime }=\rho \cdot r_i{}^{″}$ denotes the value of the element after the Adaptation_1, ${(r_i{}^{\prime })}_2$ denotes a 24-bit binary code-word for $r_i{}^{\prime }$ that is stored in memory, ${(r_i{}^{\prime })}^{*}$ denotes a reconstructed value of $r_i{}^{\prime },$ ${(r_i{}^{″})}^{*}=$ ${(r_i{}^{\prime })}^{*}/\rho$ denotes a reconstructed value of $r_i{}^{″}$, and $r_i^{*}=\sigma \cdot {(r_i{}^{″})}^{*}$ denotes a reconstructed value of the input element $r_i$.

Theorem 2.

For an arbitrary variance ${\sigma }^2$ of the input data, the SQNR of the 24-bit fixed-point quantizer with the double adaptation, marked as ${\mathrm{SQNR}}_{\mathrm{double}\_\mathrm{adapt}}$, is equal to the maximal SQNR of the optimal uniform quantizer ${\mathrm{SQNR}}_{\max }$ defined with (8), i.e., ${\mathrm{SQNR}}_{\mathrm{double}\_\mathrm{adapt}}=$ ${\mathrm{SQNR}}_{\max }$.

Proof of Theorem 2.

The distortion of the double adaptation system shown in Figure 3 is calculated as:

$$D_{\mathrm{double}\_\mathrm{adapt}}=\frac{1}{M}{\displaystyle \sum _{i=1}^M{(r_i-r_i^{*})}^2}=\frac{1}{M}{\displaystyle \sum _{i=1}^M{\left(\sigma \cdot r_i{}^{″}-\sigma \cdot {(r_i{}^{″})}^{*}\right)}^2}={\sigma }^2\frac{1}{M}{\displaystyle \sum _{i=1}^M{\left(r_i{}^{″}-{(r_i{}^{″})}^{*}\right)}^2}.$$

(33)

The data $r_i{}^{″}$ ($i=1,\dots ,M$), whose variance is equal to 1 according to Lemma 3, represents the input of the Adaptation_1 procedure, hence the distortion of the Adaptation_1 is defined as $D_{\mathrm{adapt}\_1}=\frac{1}{M}{\displaystyle \sum _{i=1}^M{\left(r_i{}^{″}-{(r_i{}^{″})}^{*}\right)}^2}$. Thus, the expression (33) becomes:

$$D_{\mathrm{double}\_\mathrm{adapt}}={\sigma }^2{D}_{\mathrm{adapt}\_1}.$$

(34)

Since the variance of the input data is ${\sigma }^2$, SQNR of the double adaptation system (marked as ${\mathrm{SQNR}}_{\mathrm{double}\_\mathrm{adapt}}$) can be defined using the expression (7). Starting from (7) and using (34) and (30), the following expression for ${\mathrm{SQNR}}_{\mathrm{double}\_\mathrm{adapt}}$ is obtained:

$$\begin{array}{l}{\mathrm{SQNR}}_{\mathrm{double}\_\mathrm{adapt}}=10\cdot {\log }_{10}\frac{{\sigma }^2}{D_{\mathrm{double}\_\mathrm{adapt}}}=10\cdot {\log }_{10}\frac{{\sigma }^2}{{\sigma }^2\cdot D_{\mathrm{adapt}\_1}}\\ =-10\cdot {\log }_{10}{D}_{\mathrm{adapt}\_1}=-10\cdot {\log }_{10}\left[\frac{{(x_{\max }^{opt})}^2}{3N^2}+\exp \left(-\sqrt{2}{x}_{\max }^{opt}\right)\right]\end{array}.$$

(35)

Comparing (35) and (12), it follows that ${\mathrm{SQNR}}_{\mathrm{double}\_\mathrm{adapt}} = {\mathrm{SQNR}}_{\max }$, completing the proof of Theorem 2. □

Thus, for data with ${\sigma }^2\ne 1$, we have the double adaptation: firstly, the Adaptation 2 is applied, converting the variance of the input data to 1, and after that the Adaptation 1 is performed adjusting data to the maximal amplitude of the fixed-point quantizer. In this way, as an important result of the double-adaptation, we obtain the maximal SQNR value of 122.194 dB of the 24-bit fixed-point quantizer, i.e., the highest possible accuracy of the 24-bit fixed-point representation, for any value of variance ${\sigma }^2$ of the input data.

5. Comparison of 24-Bit Fixed-Point and Floating-Point Quantizer

In this section, we compare performance of the proposed 24-bit fixed-point format with the double adaptation and performance of the FP24 (24-bit floating-point) format. To do that, we will briefly recall some basics about the floating-point representation, defined by the IEEE 754 standard [1]. A real number x, represented in the 24-bit floating-point format as $x={(s{e}_1{e}_2\dots e_8{m}_1{m}_2\dots m_{15})}_2$ is calculated as:

$$x={(-1)}^s{2}^{E-bias}\cdot {( 1. m_1{m}_2\dots m_{15})}_2.$$

(36)

The biased exponent $E^{*}=E-127$ (where $E={\displaystyle {\sum }_{i=1}^8{e}_i\cdot 2^{8-i}}$) takes values from −126 to 127, since values −127 and 128 are reserved for other purposes [1]. The mantissa $M={(m_1{m}_2\dots m_{15})}_2={\displaystyle {\sum }_{i=1}^{15}{m}_i\cdot 2^{15-i}}$ takes values from 0 to $2^{15}-1$.

The FP24 format is symmetrical with respect to zero. The largest positive FP24 number obtained for $E^{*}$= 127 and M = $2^{15}-1$ is $2^{127}\left(1+(2^{15}-1)/2^{15}\right)\approx 2^{128}$. For each of 254 different values of $E^{*}$, there are $2^{15}$ different positive real numbers represented in FP24 format, each of which corresponds to a different value of M. The difference of any two consecutive numbers that have the same value of $E^{*}$ is constant:

$${\mathsf{\Delta }}_{E^{*}}=2^{E^{*}}\cdot \left(1+\frac{M+1}{2^{15}}\right)-2^{E^{*}}\cdot \left(1+\frac{M}{2^{15}}\right)=2^{E^{*}-15},$$

(37)

meaning that the numbers with the same value of $E^{*}$ are equidistant. Thus, if we look at positive numbers displayed in FP24 format, there are 254 groups of $2^{15}$ uniformly distributed (i.e., equidistant) numbers, where each group corresponds to one value of $E^{*}$. Due to the symmetry, the same structure exists for negative numbers. We can see that the structure of the numbers represented in the FP24 format corresponds to the structure of a symmetrical 24-bit piecewise uniform quantizer with the maximal amplitude $x_{\max }=2^{128},$ which has 254 linear segments in the positive part, where the uniform quantization with $2^{15}$ levels and quantization step ${\mathsf{\Delta }}_{E^{*}}=2^{E^{*}-15}$ is performed within each linear segment. This 24-bit piecewise uniform quantizer whose structure is equivalent to the 24-bit floating-point format (FP24), will be called the 24-bit floating-point quantizer. This analogy between the FP24 format and the 24-bit floating-point quantizer will allow us to express performance of the FP24 format using objective performance (distortion and SQNR) of the 24-bit floating-point quantizer [28].

The distortion of the 24-bit floating-point quantizer, for input data modeled with the unit-variance Laplacian PDF can be calculated as [28]:

$$D(\sigma )=2{\displaystyle \sum _{E^{*}=-126}^{127}\frac{{\mathsf{\Delta }}_{E^{*}}^2}{12}}{P}_{E^{*}}(\sigma )+{\sigma }^2\exp \left(-\frac{\sqrt{2}{x}_{\max }}{\sigma }\right),$$

(38)

where $P_{E^{*}}(\sigma )={\displaystyle {\int }_{2^{E^{*}}}^{2^{E^{*}}+1}p(x)dx}$ represents the probability of the linear segment that corresponds to some specific value of $E^{*}$. The first term in (38) represents the granular distortion (where each member of the sum represents the granular distortion in one linear segment), while the second term represents the overload distortion. For the Laplacian PDF $p(x)$ defined with (1), the expression (38) becomes:

$$D(\sigma )={\displaystyle \sum _{E^{*}=-126}^{127}\frac{{\mathsf{\Delta }}_{E^{*}}^2}{12}}\left(\exp \left(-\frac{2^{E^{*}+1/2}}{\sigma }\right)-\exp \left(-\frac{2^{E^{*}+3/2}}{\sigma }\right)\right)+{\sigma }^2\exp \left(-\frac{\sqrt{2}{x}_{\max }}{\sigma }\right).$$

(39)

Using (7) and (39), we can obtain that the 24-bit floating-point quantizer achieves constant SQNR of 103.769 dB for the very wide range of variance of input data.

Based on the achieved results, it follows that the proposed 24-bit fixed-point quantizer with the double adaptation achieves for 18.425 dB higher SQNR (i.e., higher quality of binary representation) in a wide range of data variance compared to the FP24 format, as a result of the optimization of n as well as of the proposed double adaptation procedure. Having much smaller complexity in the same time, the proposed 24-bit fixed-point quantizer with the double adaptation can be considered as a much better solution for binary representation of data, compared to the FP24 format.

6. Simulation Results

Simulations of the considered 24-bit digital formats were performed in the MATLAB software, by generating random numbers from the Laplacian PDF with variance ${\sigma }^2$ in the manner described in [30]. Each simulation was performed using 1,000,000 generated random numbers with the appropriate value of the variance ${\sigma }^2$. The results of the simulations are shown below.

-

By simulating the optimized 24-bit fixed-point format with n = 5 for the unit variance $({\sigma }^2$= 1), described in Section 3, SQNR of 119.160 dB was achieved. Recall that the theoretically obtained value of SQNR was 119.163 dB.

-

By simulating the adaptive 24-bit fixed-point format with n = 5 for the unit variance (${\sigma }^2$= 1) based on Adaptation_1 described in Section 4.1, SQNR of 122.453 dB was achieved. Recall that the theoretically obtained SQNR value was 122.194 dB.

-

By simulating the adaptive 24-bit fixed-point format with n = 5 based on the double adaptation procedure described in Section 4.2 for different values of variance, values of SQNR presented in

Table 2. Values of SQNR (dB) obtained by simulation of the adaptive 24-bit fixed-point format with n = 5 based on the double adaptation described in Section 4.2, for different values of variance σ².

σ2	SQNR (dB)
${10}^{-8}$	122.459
${10}^{-4}$	122.468
${10}^{-2}$	122.460
${10}^2$	122.457
${10}^4$	122.457
${10}^8$	122.451

are obtained. Recall that the theoretically obtained SQNR value was 122.194 dB for all considered variances. We can see that the SQNR values obtained by simulations are almost completely constant in a wide range of variance, which is fully in line with the theoretical results.

-

By simulating the 24-bit floating-point format FP24 for different values of variance, values of SQNR presented in

Table 3. Values of SQNR (dB) obtained by simulation of the 24-bit floating-point format FP24 for different values of variance σ².

σ2	SQNR (dB)
${10}^{-8}$	103.780
${10}^{-4}$	103.788
${10}^{-2}$	103.768
1	103.774
${10}^2$	103.750
${10}^4$	103.776
${10}^8$	103.753

are obtained. Recall that the theoretically obtained SQNR value was 103.769 dB for all considered variances. We can see that the SQNR values obtained by simulations are almost completely constant in a wide range of variance, which is fully in line with the theoretical results.

We can see that all simulation results are very close to the corresponding theoretical results, confirming the correctness of the developed theory.

Based on [28], the FP32 format achieves the constant SQNR value of 151.93 dB in a very wide range of the variance, which is an unnecessarily large value for most applications. By using the proposed adaptive 24-bit fixed-point format, an SQNR value of 122.194 dB is achieved, which is quite sufficient for the vast majority of applications, with a significant reduction in the implementation complexity compared to the FP32 format.

7. Conclusions

The main goal of the paper was to optimize the 24-bit fixed-point format, as well as to examine and improve its performance, for data modeled by the Laplacian PDF. In achieving this goal, the following contributions were achieved. Two new closed-form expressions for highly accurate calculation of the maximal amplitude of the uniform quantizer were derived for the Laplace PDF. Based on the analogy between fixed-point representation and uniform quantization, expressions for the performance of the 24-bit fixed-point binary format were derived. The parameter n (the number of bits used to represent the integer part of data) was optimized, showing that n = 5 is the optimal value for data with the unit variance. It was also shown that the wrong choice of the value of n drastically reduces the performance of the fixed-point representation. It was observed that even with the optimal value of n = 5, the 24-bit fixed-point format achieves weaker performance in relation to the maximum possible (determined for the optimal uniform quantizer) for the unit variance, due to the mismatch of the maximal amplitude. In order to solve this problem, an adaptive procedure (Adaptation_1) was proposed, improving the quality of the 24-bit fixed-point representation by 3.031 dB. An additional adaptation procedure (Adaptation_2) was also proposed, which should be applied together with Adaptation_1 when the variance of the input data differs from 1. This double adaptation allows for the 24-bit fixed-point representation to achieve the maximum quality for any value of the variance of the input data. For the purpose of comparison, the FP24 (24-bit floating-point) format was also analyzed and expressions for its performance were derived, using the analogy between floating-point representation and piecewise uniform quantization. It was shown that the proposed 24-bit fixed-point quantizer with the double adaptation represents a much better solution than the FP24 format, for two reasons: it achieves a significantly higher SQNR (for 18.425 dB) and has significantly less implementation complexity.