Abstract
The study gives a brief overview of publications on exact solutions for functional PDEs with delays of various types and on methods for constructing such solutions. For the first time, second-order wave-type PDEs with a nonlinear source term containing the unknown function with proportional time delay, proportional space delay, or both time and space delays are considered. In addition to nonlinear wave-type PDEs with constant speed, equations with variable speed are also studied. New one-dimensional reductions and exact solutions of such PDEs with proportional delay are obtained using solutions of simpler PDEs without delay and methods of separation of variables for nonlinear PDEs. Self-similar solutions, additive and multiplicative separable solutions, generalized separable solutions, and some other solutions are presented. More complex nonlinear functional PDEs with a variable time or space delay of general form are also investigated. Overall, more than thirty wave-type equations with delays that admit exact solutions are described. The study results can be used to test numerical methods and investigate the properties of the considered and related PDEs with proportional or more complex variable delays.
Keywords:
nonlinear wave-type equations; PDEs with proportional delay; delay Klein–Gordon equations; PDEs with variable delay; partial functional-differential equations; reductions and exact solutions; self-similar solutions; additive and multiplicative separable solutions; generalized separable solutions MSC:
35L05; 35L70; 35R10; 35C05
Contents
- 1. Introduction
- 1.1. Delay ODEs
- 1.2. Delay First-Order PDEs
- 1.3. Delay Reaction-Diffusion PDEs
- 1.4.Delay Wave-Type PDEs
- 2. Exact Solutions: Definition and Construction Methods
- 2.1. Reductions. Term ‘Exact Solution’ for Nonlinear PDEs with Proportional Delay
- 2.2. Construction of Exact Solutions of Nonlinear PDEs with Proportional Delay
- 3. Exact Solutions of Nonlinear Wave-Type PDEs with Proportional Arguments
- 3.1. Equations with Constant Speed
- 3.2. Equations with Variable Speed
- 4. Exact Solutions to Nonlinear Wave-Type PDEs with Variable Delays of General Form
- 4.1. Equations with Constant Speed
- 4.2. Equations with Variable Speed
- 5. Brief Conclusions
- References
1. Introduction
1.1. Delay ODEs
Delay naturally arises in processes and systems that exhibit heredity, where the current state is influenced by the prehistory or, particularly, by a certain moment in the past. The simplest cases are described by delay ODEs of the form
where is the unknown function, is a given function, and is a constant delay.
Equations of the form (1) and more complex ODEs with constant delay are often used to model various processes in population theory, medicine, epidemiology, economics, and many other fields (e.g., see [1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21]).
Let us now consider a broader class of ODEs with a variable delay of general form:
where is a given function that satisfies the conditions
The second inequality for the derivative in (3) is optional and is introduced here temporarily for a clearer interpretation of the models under consideration (note that the second condition is not used further in Section 4).
Inequalities (3) can be non-strict at one or more isolated points, including the initial point . The delay function in (2) is often written in the alternative form , where . For example, a variable delay may occur when the transmission rate of the control signal from one object to another is finite and constant, and these objects are moving away from each other at a constant or variable speed.
Let us expand the function in a Taylor series for small t. Neglecting the terms of the order of and higher, we obtain
where and . From conditions (3) for small t, it follows that the coefficients in Formula (4) must satisfy the inequalities
where two equal signs cannot be taken simultaneously.
Note that in the neighborhood of any point , one can obtain a local linear approximation of the delay function in the form . In this case, the coefficients and q will depend on the point and satisfy the inequalities and , which follow from conditions (3).
We show that the simple Formula (4) describes the two most important cases frequently arising in the mathematical modeling of processes with delay. Indeed, substituting (4) with and () into (2), we arrive at the ODE with constant delay (1). Next, substituting (4) with into (2), we come to the ODE with proportional delay
The function appearing on the right-hand side of ODE (6) differs from the function by dilation of the argument t by a factor of . Equations of the form (6) are sometimes called ‘pantograph-type ODEs.’
Equations of the form (6) and more complex ODEs with proportional delay are used to describe various phenomena in electrodynamics [22], population theory [23], number theory [24], stochastic games [25], graph theory [26], risk and queueing theory [27], and theory of artificial neural networks [28,29,30]. Importantly, related ordinary functional differential equations with the function , where , are used to describe various processes in biology [31,32,33] and astrophysics [34].
Approximate analytical and numerical methods for solving ODEs with proportional delay are relatively well developed (e.g., see [35,36,37,38,39,40,41,42,43,44,45,46,47] for analytical and [48,49,50,51,52,53,54,55,56,57,58,59,60,61,62,63,64,65,66,67,68,69,70,71,72,73] for numerical methods).
Currently, analytical and numerical methods for solving ODEs with constant and variable delays can be regarded as well elaborated.
Notably, the vast majority of analytical methods that allow one to successfully find exact solutions for nonlinear PDEs without delay either are inapplicable to constructing exact solutions for nonlinear PDEs with constant or variable delay or have a minimal area of applicability.
1.2. Delay First-Order PDEs
There are some studies concerned with first-order delay PDEs. A complete group classification of the first-order Hopf-type equation with constant delay
is given in [74]. It obtained three exact solutions, other than traveling waves, with arbitrary functions and free parameters. The article [75] treats the first-order PDE with a variable speed, proportional space delay, and constant time delay
where , as a model of proliferative stem and precursor cell production in the bone marrow. The case of several space variables is investigated in [76]. The existence, uniqueness, invariance, and asymptotic behavior of solutions of such PDEs are studied in [75,76] by using semigroup theory and characteristic theory, respectively. Another first-order PDE with constant time delay and variable space delay,
is used in [77] to describe the biological process of hematological cell development from a pluripotential stem cell population. Here, x is the so-called maturation variable, which could be associated with the intracellular hemoglobin concentration (for detailed biological description, see [77] Section 2.1). The variable space delay is used to model the population behavior’s dependence on the behavior at a previous maturation level.
The study [78] models the growth and division of cells structured by size with a linear first-order PDE with proportional delay. Its solution is shown to have the form of a series whose terms are determined from simpler equations without delay.
Numerical methods of integration of first-order delay PDEs are studied, for example, in [79,80,81,82].
1.3. Delay Reaction–Diffusion PDEs
. Delay reaction–diffusion PDEs with constant delay. More complex equations can take into account spatial heterogeneity, which leads to delay PDEs of the form
which are often referred to as ‘delay reaction–diffusion equations’. Such equations describe various processes in many areas, including population theory [83,84,85,86,87,88,89,90,91,92,93,94,95,96,97,98], medicine [99,100,101,102,103,104,105,106,107], epidemiology [108,109,110,111,112,113,114,115,116,117,118], biology [119,120,121,122,123,124], chemistry [125,126,127,128,129], control theory [130,131,132,133], theory of artificial neural networks [134,135,136,137,138,139] and many others (e.g., see [131,140]). Delay PDEs (7) admit traveling-wave solutions, , where (e.g., see [131,141,142,143]), but do not have self-similar solutions, , which non-delay PDEs often have. Reductions and exact solutions with additive, multiplicative, and generalized separation of variables and more complex solutions for delay PDEs are obtained in [144,145,146,147,148,149,150,151,152,153,154,155,156] (see also [157] for a brief review, which, in addition to exact solutions, describes the main numerical methods for solving such equations).
. Delay reaction–diffusion PDEs with proportional delay. Consider the following reaction–diffusion equations involving a delay with time variability:
For example, PDEs with variable time delay can be used to describe changes in population density when the maturation period (modeled by a variable time delay) depends on the ambient temperature that varies non-linearly. Choosing a more specific form of the delay, , we arrive at PDEs with proportional delay that have the following general form:
where . Referring to the example above, case (8) would correspond to a simpler model in which the ambient temperature would change linearly.
There are also PDEs with a proportional space argument,
and proportional delays in both the time and space arguments,
where p and q are scaling parameters ( and ). In what follows, PDEs containing a nonlinear function with will often be called equations with two proportional arguments.
Publications on the properties and solutions of diffusion-type PDEs with proportional delay are much less common than those for PDEs with constant delay. In [158], an asymptotic solution of a linear reaction–diffusion equation with proportional delay is obtained. The study [159] constructs exact solutions of linear heat and wave equations with proportional delay using the method of separation of variables. Many nonlinear reaction–diffusion PDEs with proportional delay that admit reductions and exact solutions with additive, multiplicative, generalized, and functional separation of variables are described in [160,161,162]. Approximate analytical methods for solving some linear and nonlinear PDEs with proportional delays are considered in [163,164]. Numerical methods for solving PDEs with proportional delay are developed in [165,166], and those for PDEs with more complex varying delay are studied in [167].
1.4. Delay Wave-Type PDEs
Nonlinear wave-type equations with constant delay of the form
are more complex than Equation (7); here, a is a positive constant ( is the speed) and is the source function. These equations are often referred to as ‘delay Klein–Gordon equations’.
The studies [168,169,170,171,172] describe a number of exact solutions and reductions of nonlinear wave equations of the form (11) and related hyperbolic PDEs with constant delay.
The article [173] carries out a complete group analysis of a two-dimensional Klein–Gordon equation with a time-varying delay and describes its exact invariant solutions.
The present paper describes, for the first time, different classes of exact solutions to nonlinear wave-type functional PDEs:
and
where is the unknown function, is the variable speed, is the source function, and p and q are scaling parameters.
2. Exact Solutions: Definition and Construction Methods
2.1. Reductions. Term ‘Exact Solution’ for Nonlinear PDEs with Proportional Delay
Reductions of a mathematical equation are generally understood as ways for constructing its solutions (perhaps, not all but some) using solutions of simpler equations. For nonlinear PDEs, one-dimensional reductions are the most important; these allow one to describe solutions for these PDEs in terms of solutions to ODEs, which are much simpler than PDEs. Moreover, reductions of various differential and functional differential equations are crucial in finding their exact solutions.
Below we will use the term ‘exact solution’ for nonlinear PDEs with constant or variable delay (including proportional delay) in cases where the solution is expressed in terms of:
- (i)
- Elementary functions, functions appearing in the PDE (this is necessary when the PDE contains arbitrary functions), and indefinite or/and definite integrals;
- (ii)
- Solutions of usual non-delay ODEs or systems of non-delay ODEs;
- (iii)
- Solutions of ODEs with constant or variable delay (including proportional delay), or systems of such equations.
Solutions from Items (i)–(iii) can be combined. The above definition generalizes the term ‘exact solution’ used for nonlinear PDEs with constant delay in [146,148].
2.2. Construction of Exact Solutions to Nonlinear PDEs with Proportional Delay
In many cases, reductions and exact solutions of PDEs with proportional delay (12) and (13) are obtained using the principle of analogy of solutions, whose detailed description and application examples can be found in [160] (see also [161,162]). The method relies on the fact that a solution to a nonlinear partial differential equation with proportional delay can often (but not always) be sought in the same form as a solution to a simpler non-delay PDE obtained from (12) and (13) by setting . The use of the principle of analogy of solutions has shown its high efficiency for nonlinear reaction–diffusion equations with proportional delay in [160].
Figure 1 displays a schematic of applying the principle of analogy to wave-type PDEs with proportional delays.
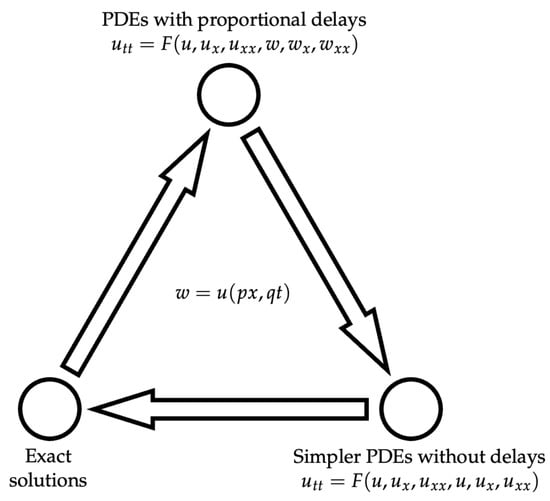
Figure 1.
A schematic of using the principle of analogy to construct exact solutions for nonlinear wave-type PDEs with proportional delays.
Below we illustrate the use of the principle of analogy of solutions with a simple specific example.
Example 1.
Consider the wave-type PDE with proportional delay and power-law nonlinearity
Following the principle of analogy of solutions, we set in Equation (14) to obtain a simpler wave-type PDE without delay:
More complex reductions and exact solutions are constructed for nonlinear PDEs using the methods of separation of variables [174,175,176], modifications of the method of functional constraints [146,151], or by combining these methods with the principle of analogy.
As a result, we have found many nonlinear wave-type PDEs with proportional delay that admit self-similar solutions, solutions with additive, multiplicative, or generalized separation of variables, as well as some other exact solutions. Special attention has been paid to nonlinear wave-type PDEs with proportional delay that involve arbitrary functions. Such equations and their solutions are of utmost interest for testing numerical and approximate analytical methods of solving the corresponding nonlinear initial-boundary value problems.
In what follows, for the generality of the results, we will assume that in wave-type functional PDEs of the form (12) and (13), the scaling parameters p and q can be any positive constants, and , that cannot simultaneously be equal to one. Such functional PDEs will be called ‘PDEs with proportional arguments’ (in the special case of and , these equations are ‘PDEs with proportional delays’). We also consider more complex PDEs with variable delay, which, in addition to the unknown function , contain the function , where is any function that satisfies conditions (3) (one can take, for example, the linear function ).
The following sections arrange equations following the principle ‘from simple to complex.’ We only present the final results without intermediate calculations. The solutions below can be easily verified by directly substituting them into the equations considered.
Remark 1.
In the present paper, we dismiss trivial solutions of the form (which correspond to equilibria) for both the equations considered and the simpler equations obtained by reductions. Moreover, we also neglect degenerate solutions that depend on only one independent variable, t or x.
3. Exact Solutions to Nonlinear Wave-Type PDEs with Proportional Arguments
3.1. Equations with Constant Speed
Equation 1. Consider the equation with proportional delay and quadratic nonlinearity
It has the following exact solutions.
. Multiplicative separable solution:
where is an arbitrary constant, and the function is described by the second-order autonomous ODE .
. For a self-similar solution of this PDE with proportional delay, see Equation (17) below with , , , and .
Equation 2. The equation with proportional time-argument and power-law nonlinearity
admits the following exact solutions.
. Multiplicative separable solution:
where is an arbitrary constant, and the function is described by the second-order autonomous ODE .
. For a self-similar solution of this PDE with proportional argument, see Equation (17) below with , , and .
Equation 3. The equation with two proportional arguments and power-law nonlinearity
admits the following exact solutions.
. Self-similar solution for :
where the function is described by the second-order ODE with proportional argument
. Traveling wave solution for :
where k and are arbitrary constants, and the function is described by the second-order ODE with proportional argument
. Multiplicative separable solution for :
where is an arbitrary constant, and the function is described by the second-order ODE with proportional argument
. Multiplicative separable solution for :
where is an arbitrary constant, and the function is described by the second-order ODE with proportional argument
Equation 4. The equation with two proportional arguments and exponential nonlinearity
has an exact solution of the form:
where the function is described by the second-order ODE with proportional argument
For , this equation simplifies to become a usual ODE.
Equation 5. The equation with two proportional arguments and more complex exponential nonlinearity
for , admits an exact solution of the form
where the function is described by the second-order ODE with proportional argument
For , this equation simplifies to become a usual ODE.
Equation 6. The equation with two proportional arguments and logarithmic nonlinearity
admits a multiplicative separable solution
where the functions and are described by the second-order ODEs with proportional argument
Equation 7. The equation with a proportional time argument and an arbitrary function f dependent on the difference :
has an additive separable solution
where and are arbitrary constants, and the function is described by the second-order ODE with proportional argument
Equation 8. The equation with a proportional space argument and an arbitrary function f dependent on the difference :
admits an additive separable solution
where and are arbitrary constants, and the function is described by the second-order ODE with proportional argument
Equation 9. Consider the following equation with a proportional time argument and an arbitrary function f dependent on the difference :
It has the following exact solutions.
. Additive separable solution for :
where A and B are arbitrary constants, and the function is described by the second-order ODE with proportional argument
. Additive separable solution for :
where A and B are arbitrary constants, and the function is described by the second-order ODE with proportional argument (18).
Equation 10. The equation with two proportional arguments
where f is an arbitrary function dependent on the difference , admits an exact solution of the form
where the function is described by the second-order ODE with proportional argument
For , this equation simplifies to become a usual ODE.
Equation 11. Consider the following equation with a proportional space argument and an arbitrary function f dependent on the ratio :
It admits the following exact solutions.
. Multiplicative separable solution:
where A, B, and are arbitrary constants; the function is described by the second-order ODE with proportional argument
. Multiplicative separable solution:
where A, B, and are arbitrary constants; the function is described by the second-order ODE with proportional argument
Equation 12. The equation with proportional time argument
where is an arbitrary function, admits a multiplicative separable solution:
Here is an arbitrary constant, and the function is described by the second-order autonomous ODE .
3.2. Equations with Variable Speed
Equation 13. Consider the following equation with a proportional time argument and a nonlinear power-law speed:
where f is an arbitrary function dependent on the ratio . This equation admits a multiplicative separable solution:
where the functions and are described by a non-delay ODE and an ODE with proportional argument:
b is an arbitrary constant.
Equation 14. Consider the equation with a proportional space argument and a nonlinear power-law speed
where is an arbitrary function. This equation admits the following solutions.
. Multiplicative separable solution:
where the function is described by the ODE
. This equation also has a solution of the more complex form
where is an arbitrary constant, and the function is described by the ODE with proportional argument
Equation 15. Consider the equation with a proportional time argument and a nonlinear power-law speed
where f is an arbitrary function dependent on the ratio . This equation has the following exact solutions.
. Multiplicative separable solution with :
where and are arbitrary constants, and the function is described by the second-order ODE with proportional argument
. Multiplicative separable solution with :
where and are arbitrary constants, and the function is described by the second-order ODE with proportional argument (19).
. Multiplicative separable solution with :
where and are arbitrary constants, and the function is described by the second-order ODE with proportional argument (19).
Equation 16. Consider the equation with a proportional time argument and a nonlinear power-law speed
where f is an arbitrary function dependent on the ratio . This equation admits an exact solution of the form
where is an arbitrary constant, and the function is described by the second-order ODE with proportional argument
For , the last equation simplifies to become a usual ODE.
Equation 17. Consider the equation with two proportional arguments and a nonlinear power-law speed
where f is an arbitrary function dependent on the ratio . This equation admits the following exact solutions.
. Self-similar solution for :
where the function is described by the second-order ODE with proportional argument
For , this equation simplifies to become a usual ODE.
. Traveling-wave solution for :
where k and are arbitrary constants, and the function is described by the second-order ODE with proportional argument
Equation 18. Consider the equation with a proportional time argument and a nonlinear exponential speed
where f is an arbitrary function dependent on the difference . This equation has an additive separable solution:
where A, B, and C are arbitrary constants, and the function is described by the second-order ODE with proportional argument
Equation 19. Consider the equation with two proportional arguments and a nonlinear exponential speed
where f is an arbitrary function dependent on the difference . This equation admits an exact solution of the form
where the function is described by the second-order ODE with proportional argument
For , this equation simplifies to become a usual ODE.
4. Exact Solutions to Nonlinear Wave-Type PDEs with Variable Delays of General Form
4.1. Equations with Constant Speed
Equation 20. The equation with variable time and space delays and a logarithmic nonlinearity
admits a multiplicative separable solution:
where the functions and are described by the ODEs with variable argument
K is an arbitrary constant.
Equation 21. The equation with a variable time delay and an arbitrary function f dependent on the ratio :
has the following exact solutions.
. Multiplicative separable solution:
where A, B, and are arbitrary constants, and the function is described by the ODE with variable argument
. Multiplicative separable solution:
where A, B, and are arbitrary constants, and the function is described by the ODE with variable argument
. Degenerate solution with multiplicative separation of variables:
where A and B, and the function is described by the ODE with variable argument (20) with .
Equation 22. The equation with a variable space delay and an arbitrary function f dependent on the ratio :
admits the following exact solutions.
. Multiplicative separable solution:
where A, B, and are arbitrary constants, and the function is described by the ODE with variable argument
. Multiplicative separable solution:
where A, B, and are arbitrary constants, and the function is described by the ODE with variable argument
. Degenerate solution with multiplicative separation of variables:
where A and B are arbitrary constants, and the function is described by the ODE with variable argument (21) with .
Equation 23. The equation with a variable time delay and an arbitrary function f dependent on the difference :
admits an additive separable solution:
where and are arbitrary constants, and the function is described by the ODE with variable argument
Equation 24. The equation with a variable time delay and an arbitrary function f dependent on the ratio :
has a multiplicative separable solution:
where the functions and are described by the ODE and the ODE with variable argument
is an arbitrary constant. A particular one-parameter solution of the first ODE can be represented in the explicit form
where is an arbitrary constant.
Equation 25. The equation with a variable time delay and an arbitrary function f dependent on the difference :
admits the following exact solutions.
. Additive separable solution for :
where A and B are arbitrary constants, and the function is described by the ODE with variable argument
. Additive separable solution for :
where A and B are arbitrary constants, and the function is described by the ODE with variable argument
Equation 26. The equation with a variable space delay and an arbitrary function f dependent on the difference :
admits an additive separable solution:
where C is an arbitrary constant, and the function is described by the ODE with variable argument
4.2. Equations with Variable Speed
Equation 27. Consider the equation with a variable time delay and a quadratic nonlinearity
which admits the following exact solutions.
. Generalized separable solution quadratic in x:
where the functions and are described by the ODE system with variable delay
. More complex generalized separable solution:
where the functions and are described by the ODE system with variable delay
Equation 28. Consider the equation with a variable time delay and a nonlinear power-law speed
where f is an arbitrary function dependent on the ratio . This equation has a multiplicative separable solution:
where the functions and are described by the ODE and the ODE with variable argument
b is an arbitrary constant.
Equation 29. Consider the equation with a variable time delay and a nonlinear power-law speed
where f is an arbitrary function dependent on the ratio . This equation admits the following exact solutions.
. Multiplicative separable solution for :
where and are arbitrary constants, and the function is described by the ODE with variable argument
. Multiplicative separable solution for :
where and are arbitrary constants, and the function is described by the ODE with variable argument (22).
. Multiplicative separable solution for :
where and are arbitrary constants, and the function is described by the ODE with variable argument (22).
Equation 30. Consider the equation with a variable space delay and a nonlinear power-law speed
where f is an arbitrary function dependent on the ratio . This equation admits a multiplicative separable solution:
where the function is described by the ODE with variable argument
Equation 31. Consider the equation with a variable time delay and a nonlinear speed of the exponential form
where f is an arbitrary function dependent on the difference . This equation admits an additive separable solution:
where A, B, and C are arbitrary constants, and the function is described by the ODE with variable argument
Equation 32. Consider the equation with a variable time delay and a nonlinear exponential speed
where f is an arbitrary function dependent on the difference . This equation has the following exact solutions.
. Additive separable solution for :
where and are arbitrary constants, and the function is described by the ODE with variable argument
. Additive separable solution for :
where and are arbitrary constants, and the function is described by the ODE with variable argument (23).
Equation 33. Consider the equation with a variable space delay and a nonlinear exponential speed
where f is an arbitrary function dependent on the difference . This equation admits an additive separable solution:
where the function is described by the ODE with variable argument
Equation 34. Consider the equation with a variable time delay and nonlinear logarithmic speed
where f is an arbitrary function dependent on the ratio . This equation has a multiplicative separable solution:
where the function is described by the ODE with variable argument
5. Brief Conclusions
We have considered many nonlinear wave-type PDEs that involve, in addition to the unknown function , also functions of the form , or , or , where p and q are free ’scaling’ parameters (for PDEs with proportional delay, and . A number of more complex nonlinear wave-type PDEs with variable delays of general form and involving functions or have also been investigated. We have described over thirty such equations that admit exact solutions. In addition, many self-similar, additive separable, multiplicative separable, generalized separable, and other solutions have been specified. The study results fit for testing numerical methods and investigating the properties of the considered and related equations with proportional delay.
Author Contributions
Conceptualization, A.D.P. and V.G.S.; methodology, A.D.P. and V.G.S.; validation, V.G.S.; investigation, A.D.P. and V.G.S.; writing—original draft preparation, V.G.S.; writing—review and editing, A.D.P. and V.G.S.; supervision, A.D.P.; project administration, A.D.P.; funding acquisition, A.D.P. All authors have read and agreed to the published version of the manuscript.
Funding
The study was supported by the Ministry of Education and Science of the Russian Federation within the framework of the State Assignment (Reg. No. AAAA-A20-120011690135-5).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Acknowledgments
We express our deep gratitude to Alexei Zhurov for his help with the English editing of the paper.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Kuang, Y. Delay Differential Equations with Applications in Population Dynamics; Academic Press: San Diego, CA, USA, 2012. [Google Scholar]
- Hutchinson, G.E. Circular causal systems in ecology. Ann. N. Y. Acad. Sci. 1948, 50, 221–246. [Google Scholar] [CrossRef] [PubMed]
- Gurney, W.S.C.; Blythe, S.P.; Nisbet, R.M. Nicholson’s blowflies revisited. Nature 1980, 287, 17–21. [Google Scholar] [CrossRef]
- Gourley, S.A.; Chaplain, M.A.J. Travelling fronts in a food-limited population model with time delay. Proc. R. Soc. Edinb. Sect. A 2002, 132, 75–89. [Google Scholar] [CrossRef]
- Berezansky, L.; Braverman, E.; Idels, L. Nicholson’s blowflies differential equations revisited: Main results and open problems. Appl. Math. Model. 2010, 34, 1405–1417. [Google Scholar] [CrossRef]
- Schiesser, W.E. Time Delay ODE/PDE Models: Applications in Biomedical Science and Engineering; CRC Press: Boca Raton, FL, USA, 2019. [Google Scholar]
- Herz, A.V.; Bonhoeffer, S.; Anderson, R.M.; May, R.M.; Nowak, M.A. Viral dynamics in vivo: Limitations on estimates of intracellular delay and virus decay. Proc. Natl. Acad. Sci. USA 1996, 93, 7247–7251. [Google Scholar] [CrossRef]
- Nelson, P.W.; Perelson, A.S. Mathematical analysis of delay differential equation models of HIV-1 infection. Math. Biosci. 2002, 179, 73–94. [Google Scholar] [CrossRef]
- Gourley, S.A.; Kuang, Y.; Nagy, J.D. Dynamics of a delay differential equation model of hepatitis B virus infection. J. Biol. Dynam. 2008, 2, 140–153. [Google Scholar] [CrossRef]
- Mackey, M.C.; Glass, L. Oscillation and chaos in physiological control system. Science 1977, 197, 287–289. [Google Scholar] [CrossRef]
- Liu, B. New results on the positive almost periodic solutions for a model of hematopoiesis. Nonlinear Anal. Real World Appl. 2014, 17, 252–264. [Google Scholar] [CrossRef]
- Cooke, K.L. Stability analysis for a vector disease model. Rocky Mountain J. Math. 1979, 9, 31–42. [Google Scholar] [CrossRef]
- Beretta, E.; Takeuchi, Y. Global stability of an SIR epidemic model with time delays. J. Math. Biol. 1995, 33, 250–260. [Google Scholar] [CrossRef] [PubMed]
- Yang, W. Modeling COVID-19 pandemic with hierarchical quarantine and time delay. Dyn. Games and Appl. 2021, 11, 892–914. [Google Scholar] [CrossRef] [PubMed]
- González-Parra, G.; Sultana, S.; Arenas, A.J. Mathematical modeling of toxoplasmosis considering a time delay in the infectivity of oocysts. Mathematics 2022, 10, 354. [Google Scholar] [CrossRef]
- Cesare, L.D.; Sportelli, M. A dynamic IS-LM model with delayed taxation revenues. Chaos Solitons Fractals 2005, 25, 233–244. [Google Scholar] [CrossRef]
- Zhang, X.; Zhu, H. Hopf bifurcation and chaos of a delayed finance system. Complexity 2019, 2019, 6715036. [Google Scholar] [CrossRef]
- Suarez, M.J.; Schopf, P.S. A delayed action oscillator for ENSO. J. Atmos. Sci. 1988, 45, 3283–3287. [Google Scholar] [CrossRef]
- Kalmár-Nagy, T.; Stépán, G.; Moon, F.C. Subcritical HOPF bifurcation in the delay equation model for machine tool vibrations. Nonlinear Dyn. 2001, 26, 121–142. [Google Scholar] [CrossRef]
- Arik, S. Global asymptotic stability of a larger class of neural networks with constant time delay. Phys. Lett. A 2003, 311, 504–511. [Google Scholar] [CrossRef]
- Wu, J.; Campbell, S.A.; Bélair, J. Time-delayed neural networks: Stability and oscillations. In Encyclopedia of Computational Neuroscience; Springer: New York, NY, USA, 2015; pp. 2966–2972. [Google Scholar]
- Dehghan, M.; Shakeri, F. The use of the decomposition procedure of Adomian for solving a delay differential equation arising in electrodynamics. Phys. Scr. 2008, 78, 065004. [Google Scholar] [CrossRef]
- Ajello, W.G.; Freedman, H.I.; Wu, J. Analysis of a model representing stage-structured population growth with state-dependent time delay. SIAM J. Appl. Math. 1992, 52, 855–869. [Google Scholar] [CrossRef]
- Mahler, K. On a special functional equation. J. Lond. Math. Soc. 1940, 1, 115–123. [Google Scholar] [CrossRef]
- Ferguson, T.S. Lose a dollar or double your fortune. In Proceedings of the 6th Berkeley Symposium on Mathematical Statistics and Probability, Volume 3; Le Cam, L.M., Neyman, J., Scott, E.L., Eds.; University California Press: Berkeley, CA, USA, 1972; pp. 657–666. [Google Scholar]
- Robinson, R.W. Counting labeled acyclic digraphs. In New Directions in the Theory of Graphs; Harari, F., Ed.; Academic Press: New York, NY, USA, 1973; pp. 239–273. [Google Scholar]
- Gaver, D.P. An absorption probablility problem. J. Math. Anal. Appl. 1964, 9, 384–393. [Google Scholar] [CrossRef]
- Zhang, F.; Zhang, Y. State estimation of neural networks with both time-varying delays and norm-bounded parameter uncertainties via a delay decomposition approach. Commun. Nonlinear Sci. Numer. Simul. 2013, 18, 3517–3529. [Google Scholar] [CrossRef]
- Yang, X.; Song, Q.; Cao, J.; Lu, J. Synchronization of coupled Markovian reaction-diffusion neural networks with proportional delays via quantized control. IEEE Trans. Neural Netw. Learn. Syst. 2019, 30, 951–958. [Google Scholar] [CrossRef] [PubMed]
- Wan, P.; Sun, D.; Chen, D.; Zhao, M.; Zheng, L. Exponential synchronization of inertial reaction-diffusion coupled neural networks with proportional delay via periodically intermittent control. Neurocomputing 2019, 356, 195–205. [Google Scholar] [CrossRef]
- Hall, A.J.; Wake, G.C. A functional differential equation arising in the modelling of cell growth. J. Aust. Math. Soc. Ser. B. Appl. Math. 1989, 30, 424–435. [Google Scholar] [CrossRef]
- Hall, A.J.; Wake, G.C.; Gandar, P.W. Steady size distributions for cells in one dimensional plant tissues. J. Math. Biol. 1991, 30, 101–123. [Google Scholar] [CrossRef]
- Derfel, G.; van Brunt, B.; Wake, G.C. A cell growth model revisited. Funct. Differ. Equat. 2012, 19, 71–81. [Google Scholar]
- Ambartsumyan, V.A. On the fluctuation of the brightness of the Milky Way. Dokl. Akad. Nauk SSSR 1944, 44, 223–226. [Google Scholar]
- Ockendon, J.R.; Tayler, A.B. The dynamics of a current collection system for an electric locomotive. Proc. R. Soc. Lond. A 1971, 332, 447–468. [Google Scholar] [CrossRef]
- Fox, L.; Mayers, D.F.; Ockendon, J.R.; Tayler, A.B. On a functional differential equation. IMA J. Appl. Math. 1971, 8, 271–307. [Google Scholar] [CrossRef]
- Iserles, A. On the generalized pantograph functional differential equation. Eur. J. Appl. Math. 1993, 4, 1–38. [Google Scholar] [CrossRef]
- Kate, T.; McLeod, J.B. Functional-differential equation y′ = ay(λt) + by(t). Bull. Am. Math. Soc. 1971, 77, 891–937. [Google Scholar] [CrossRef]
- Liu, M.Z.; Li, D. Properties of analytic solution and numerical solution of multi-pantograph equation. Appl. Math. Comput. 2004, 155, 853–871. [Google Scholar] [CrossRef]
- Van Brunt, B.; Wake, G.C. A Mellin transform solution to a second-order pantograph equation with linear dispersion arising in a cell growth model. Eur. J. Appl. Math. 2011, 22, 151–168. [Google Scholar] [CrossRef]
- Yüzbasi, S.; Sezer, M. An exponential approximation for solutions of generalized pantograph-delay differential equations. Appl. Math. Model. 2013, 37, 9160–9173. [Google Scholar] [CrossRef]
- Reutskiy, S.Y. A new collocation method for approximate solution of the pantograph functional differential equations with proportional delay. Appl. Math. Comput. 2015, 266, 642–655. [Google Scholar] [CrossRef]
- Isik, O.R.; Turkoglu, T. A rational approximate solution for generalized pantograph-delay differential equations. Math. Meth. Appl. Sci. 2016, 39, 2011–2024. [Google Scholar] [CrossRef]
- Patade, J.; Bhalekar, S. Analytical solution of pantograph equation with incommensurate delay. Phys. Sci. Rev. 2017, 2, 20165103. [Google Scholar] [CrossRef]
- Bahgat, M.S.M. Approximate analytical solution of the linear and nonlinear multi-pantograph delay differential equations. Phys. Scr. 2020, 95, 055219. [Google Scholar] [CrossRef]
- Hou, C.-C.; Simos, T.E.; Famelis, I.T. Neural network solution of pantograph type differential equations. Math. Meth. Appl. Sci. 2020, 43, 3369–3374. [Google Scholar] [CrossRef]
- Alrabaiah, H.; Ahmad, I.; Shah, K.; Rahman, G.U. Qualitative analysis of nonlinear coupled pantograph differential equations of fractional order with integral boundary conditions. Bound. Value Probl. 2020, 2020, 138. [Google Scholar] [CrossRef]
- Liu, Y. On the θ-method for delay differential equations with infinite lag. J. Comput. Appl. Math. 1996, 71, 177–190. [Google Scholar] [CrossRef]
- Bellen, A.; Guglielmi, N.; Torelli, L. Asymptotic stability properties of θ-methods for the pantograph equation. Appl. Numer. Math. 1997, 24, 279–293. [Google Scholar] [CrossRef]
- Koto, T. Stability of Runge–Kutta methods for the generalized pantograph equation. Numer. Math. 1999, 84, 233–247. [Google Scholar] [CrossRef]
- Bellen, A. Preservation of superconvergence in the numerical integration of delay differential equations with proportional delay. IMA J. Numer. Anal. 2002, 22, 529–536. [Google Scholar] [CrossRef]
- Guglielmi, N.; Zennaro, M. Stability of one-leg θ-methods for the variable coefficient pantograph equation on the quasi-geometric mesh. IMA J. Numer. Anal. 2003, 23, 421–438. [Google Scholar] [CrossRef]
- Xu, Y.; Liu, M.Z. H-stability of Runge–Kutta methods with general variable stepsize for pantograph equation. Appl. Math. Comput. 2004, 148, 881–892. [Google Scholar] [CrossRef]
- Evans, D.J.; Raslan, K.R. The Adomian decomposition method for solving delay differential equation. Int. J. Comput. Math. 2005, 82, 49–54. [Google Scholar] [CrossRef]
- Li, D.; Liu, M.Z. Runge–Kutta methods for the multi-pantograph delay equation. Appl. Math. Comput. 2005, 163, 383–395. [Google Scholar] [CrossRef]
- Liu, M.Z.; Yang, Z.W.; Xu, Y. The stability of modified Runge–Kutta methods for the pantograph equation. Math. Comput. 2006, 75, 1201–1215. [Google Scholar] [CrossRef]
- Sezer, M.; Akyüz-Dascioglu, A. A Taylor method for numerical solution of generalized pantograph equations with linear functional argument. J. Comput. Appl. Math. 2007, 200, 217–225. [Google Scholar] [CrossRef]
- Sezer, M.; Yalçinbaş, S.; Sahin, N. Approximate solution of multi-pantograph equation with variable coefficients. J. Comput. Appl. Math. 2008, 214, 406–416. [Google Scholar] [CrossRef]
- Saadatmandi, A.; Dehghan, M. Variational iteration method for solving a generalized pantograph equation. Comput. Math. Appl. 2009, 58, 2190–2196. [Google Scholar] [CrossRef]
- Brunner, H.; Huang, Q.; Xie, H. Discontinuous Galerkin methods for delay differential equations of pantograph type. SIAM J. Numer. Anal. 2010, 48, 1944–1967. [Google Scholar] [CrossRef]
- Shakeri, F.; Dehghan, M. Application of the decomposition method of Adomian for solving the pantograph equation of order m. Z. Naturforsch. 2010, 65a, 453–460. [Google Scholar] [CrossRef]
- Yusufoğlu, E. An efficient algorithm for solving generalized pantograph equations with linear functional argument. Appl. Math. Comput. 2010, 217, 3591–3595. [Google Scholar] [CrossRef]
- Gülsu, M.; Sezer, M. A Taylor collocation method for solving high-order linear pantograph equations with linear functional argument. Numer. Meth. Partial Differ. Equat. 2011, 27, 1628–1638. [Google Scholar] [CrossRef]
- Yalçinbaş, S.; Aynigül, M.; Sezer, M. A collocation method using Hermite polynomials for approximate solution of pantograph equations. J. Frankl. Inst. 2011, 348, 1128–1139. [Google Scholar] [CrossRef]
- Yüzbaşi, S.; Şahin, N.; Sezer, M. A Bessel collocation method for numerical solution of generalized pantograph equations. Numer. Methods Partial Differ. Equ. 2011, 28, 1105–1123. [Google Scholar] [CrossRef]
- Sedaghat, S.; Ordokhani, Y.; Dehghan, M. Numerical solution of the delay differential equations of pantograph type via Chebyshev polynomials. Commun. Nonlinear Sci. Numer. Simul. 2012, 17, 4815–4830. [Google Scholar] [CrossRef]
- Tohidi, E.; Bhrawy, A.H.; Erfani, K. A collocation method based on Bernoulli operational matrix for numerical solution of generalized pantograph equation. Appl. Math. Model. 2013, 37, 4283–4294. [Google Scholar] [CrossRef]
- Doha, E.H.; Bhrawy, A.H.; Baleanu, D.; Hafez, M. A new Jacobi rational-Gauss collocation method for numerical solution of generalized pantograph equations. Appl. Numer. Math. 2014, 77, 43–54. [Google Scholar] [CrossRef]
- Li, X.Y.; Wu, B.Y. A continuous method for nonlocal functional differential equations with delayed or advanced arguments. J. Math. Anal. Appl. 2014, 409, 485–493. [Google Scholar] [CrossRef]
- Wang, W. High order stable Runge–Kutta methods for nonlinear generalized pantograph equations on the geometric mesh. Appl. Math. Model. 2015, 39, 270–283. [Google Scholar] [CrossRef]
- Wang, W. Fully-geometric mesh one-leg methods for the generalized pantograph equation: Approximating Lyapunov functional and asymptotic contractivity. Appl. Numer. Math. 2017, 117, 50–68. [Google Scholar] [CrossRef]
- Yang, C. Modified Chebyshev collocation method for pantograph-type differential equations. Appl. Numer. Math. 2018, 134, 132–144. [Google Scholar] [CrossRef]
- Yang, C.; Lv, X. Generalized Jacobi spectral Galerkin method for fractional pantograph differential equation. Math. Methods Appl. Sci. 2021, 44, 153–165. [Google Scholar] [CrossRef]
- Tanthanuch, J. Symmetry analysis of the nonhomogeneous inviscid Burgers equation with delay. Commun. Nonlinear Sci. Numer. Simulat. 2012, 17, 4978–4987. [Google Scholar] [CrossRef]
- Dyson, J.; Villella-Bresson, R.; Webb, G.F. A singular transport equation modelling a proliferating maturity structured cell population. Can. Appl. Math. Quart. 1996, 4, 65–95. [Google Scholar]
- Zhou, L.; Fu, Y.; Webb, G.F.; He, M.; Song, K. Solutions of a class of a first order partial differential equations with delay. In Nonlinear Partial Differential Equations and Applications: Proceedings of the Conference; Guo, B., Yang, D., Eds.; World Scientific Publ.: Singapore, 1998. [Google Scholar]
- Mackey, M.C.; Rudnicki, R. A new criterion for the global stability of simultaneous cell replication and maturation processes. J. Math. Biol. 1999, 38, 195–219. [Google Scholar] [CrossRef]
- Zaidi, A.A.; van Brunt, B.; Wake, G.C. Solutions to an advanced functional partial differential equation of the pantograph type. Proc. R. Soc. A 2015, 471, 20140947. [Google Scholar] [CrossRef] [PubMed]
- Singh, P.; Sharma, K.K. Numerical solution of first-order hyperbolic partial differential-difference equation with shift. Numer. Methods Partial Differ. Equ. 2010, 26, 107–116. [Google Scholar] [CrossRef]
- Pimenov, V.; Sviridov, S. Numerical methods for advection equations with delay. AIP Conf. Proc. 2014, 1631, 114–121. [Google Scholar] [CrossRef]
- Solodushkin, S.I.; Yumanova, I.F.; Staelen, R.D. First-order partial differential equations with time delay and retardation of a state variable. J. Comput. Appl. Math. 2015, 289, 322–330. [Google Scholar] [CrossRef]
- Sampath, K.; Veerasamy, S.; Agarwal, R.P. Stable difference schemes with interpolation for delayed one-dimensional transport equation. Symmetry 2022, 14, 1046. [Google Scholar] [CrossRef]
- Huang, J.; Zou, X. Traveling wavefronts in diffusive and cooperative Lotka—Volterra system with delays. J. Math. Anal. Appl. 2002, 271, 455–466. [Google Scholar] [CrossRef]
- Mei, M.; So, J.; Li, M.; Shen, S. Asymptotic stability of travelling waves for Nicholson’s blowflies equation with diffusion. Proc. Roy. Soc. Edinb. Sect. A 2004, 134, 579–594. [Google Scholar] [CrossRef]
- Kuang, Y.; Gourley, S.A. Wavefronts and global stability in a time-delayed population model with stage structure. Proc. Roy. Soc. Lond. A 2003, 459, 1563–1579. [Google Scholar] [CrossRef]
- Pao, C. Global asymptotic stability of Lotka—Volterra competition systems with diffusion and time delays. Nonlinear Anal. Real World Appl. 2004, 5, 91–104. [Google Scholar] [CrossRef]
- Faria, T.; Trofimchuk, S. Nonmonotone travelling waves in a single species reaction–diffusion equation with delay. J. Differ. Equ. 2006, 228, 357–376. [Google Scholar] [CrossRef]
- Trofimchuk, E.; Tkachenko, V.; Trofimchuk, S. Slowly oscillating wave solutions of a single species reaction–diffusion equation with delay. J. Differ. Equ. 2008, 245, 2307–2332. [Google Scholar] [CrossRef]
- Davidson, F.A.; Gourley, S.A. The effects of temporal delays in a model for a food-limited, diffusing population. J. Math. Anal. Appl. 2001, 261, 633–648. [Google Scholar] [CrossRef]
- Su, Y.; Wei, J.; Shi, J. Hopf bifurcation in a reaction-diffusion population model with delay effect. J. Differ. Equ. 2009, 247, 1156–1184. [Google Scholar] [CrossRef]
- Yang, Y.; So, J.W.-H. Dynamics for the diffusive Nicholson blowflies equation. In Dynamical Systems and Differential Equations; Chen, W., Hu, S., Eds.; Southwest Missouri State University: Springfield, MO, USA, 1998; Volume 2, pp. 333–352. [Google Scholar]
- So, J.W.-H.; Yang, Y. Dirichlet problem for the diffusive Nicholson’s blowflies equation. J. Differ. Equ. 1998, 150, 317–348. [Google Scholar] [CrossRef]
- Saker, S.H. Oscillation of continuous and discrete diffusive delay Nicholson’s blowflies models. Appl. Math. Comput. 2005, 167, 179–197. [Google Scholar] [CrossRef]
- Yi, T.; Zou, X. Global attractivity of the diffusive Nicholson blowflies equation with Neumann boundary condition: A non-monotone case. J. Differ. Equ. 2008, 245, 3376–3388. [Google Scholar] [CrossRef]
- Li, W.-T.; Yan, X.-P.; Zhang, C.-H. Stability and Hopf bifurcation for a delayed cooperation diffusion system with Dirichlet boundary conditions. Chaos Solitons Fractals 2008, 38, 227–237. [Google Scholar] [CrossRef]
- Faria, T. Stability and bifurcation for a delayed predator–prey model and the effect of diffusion. J. Math. Anal. Appl. 2001, 254, 433–463. [Google Scholar] [CrossRef]
- Lv, G.; Wang, M. Traveling wave front in diffusive and competitive Lotka—Volterra system with delays. Nonlinear Anal. Real World Appl. 2010, 11, 1323–1329. [Google Scholar] [CrossRef]
- Al Noufaey, K.S. Stability analysis of a diffusive three-species ecological system with time delays. Symmetry 2021, 13, 2217. [Google Scholar] [CrossRef]
- Hattaf, K.; Yousfi, N. A generalized HBV model with diffusion and two delays. Comput. Math. Appl. 2015, 69, 31–40. [Google Scholar] [CrossRef]
- Hattaf, K.; Yousfi, N. Global dynamics of a delay reaction–diffusion model for viral infection with specific functional response. Comput. Appl. Math. 2015, 34, 807–818. [Google Scholar] [CrossRef]
- Zhang, Y.; Xu, Z. Dynamics of a diffusive HBV model with delayed Beddington—DeAngelis response. Nonlinear Anal. Real World Appl. 2014, 15, 118–139. [Google Scholar] [CrossRef]
- Chí, N.C.; Vales, E. Á; Almeida, G.G. Analysis of a HBV model with diffusion and time delay. J. Appl. Math. 2012, 2012, 578561. [Google Scholar] [CrossRef]
- Xu, R.; Ma, Z.E. An HBV model with diffusion and time delay. J. Theor. Biol. 2009, 257, 499–509. [Google Scholar] [CrossRef]
- Wang, K.; Wang, W. Propagation of HBV with spatial dependence. Math. Biosci. 2007, 210, 78–95. [Google Scholar] [CrossRef]
- Banerjee, S.; Sarkar, R.R. Delay-induced model for tumor–immune interaction and control of malignant tumor growth. Biosystems 2008, 91, 268–288. [Google Scholar] [CrossRef]
- Piotrowska, M.J.; Foryś, U.; Bodnar, M.; Poleszczuk, J. A simple model of carcinogenic mutations with time delay and diffusion. Math. Biosci. Eng. 2013, 10, 861–872. [Google Scholar] [CrossRef]
- Jia, Y. Bifurcation and pattern formation of a tumor–immune model with time-delay and diffusion. Math. Comput. Simul. 2020, 178, 92–108. [Google Scholar] [CrossRef]
- Yang, J.; Liang, S.; Zhang, Y. Travelling waves of a delayed SIR epidemic model with nonlinear incidence rate and spatial diffusion. PLoS ONE 2011, 6, e21128. [Google Scholar] [CrossRef] [PubMed]
- Gan, Q.; Xu, R.; Yang, P. Travelling waves of a delayed SIRS epidemic model with spatial diffusion. Nonlinear Anal. Real World Appl. 2011, 12, 52–68. [Google Scholar] [CrossRef]
- Xu, Z. Traveling waves in a Kermack—Mckendrick epidemic model with diffusion and latent period. Nonlinear Anal. 2014, 111, 66–81. [Google Scholar] [CrossRef]
- Bai, Z.; Wu, S.-L. Traveling waves in a delayed SIR epidemic model with nonlinear incidence. Appl. Meth. Comput. 2015, 263, 221–232. [Google Scholar] [CrossRef]
- Cheng, Y.; Lu, D.; Zhou, J.; Wei, J. Existence of traveling wave solutions with critical speed in a delayed diffusive epidemic model. Adv. Differ. Equ. 2019, 2019, 494. [Google Scholar] [CrossRef]
- Berezovsky, F.; Karev, G.; Song, B.; Castillo-Chavez, C. A simple epidemic model with surprising dynamics. Math. Biosci. Eng. 2005, 2, 133–152. [Google Scholar] [CrossRef]
- Li, J.; Sun, G.-Q.; Jin, Z. Pattern formation of an epidemic model with time delay. Phys. A Stat. Mech. Its Appl. 2014, 403, 100–109. [Google Scholar] [CrossRef]
- Liu, P.-P. Periodic solutions in an epidemic model with diffusion and delay. Appl. Math. Comput. 2015, 265, 275–291. [Google Scholar] [CrossRef]
- Cai, Y.; Yan, S.; Wang, H.; Lian, X.; Wang, W. Spatiotemporal dynamics in a reaction-diffusion epidemic model with a time-delay in transmission. Int. J. Bifurc. Chaos Appl. Sci. Eng. 2015, 25, 1550099. [Google Scholar] [CrossRef]
- Hwang, T.-W.; Kuang, Y. Deterministic extinction effect of parasites on host populations. J. Math. Biol. 2003, 46, 17–30. [Google Scholar] [CrossRef]
- Zhu, C.-C.; Zhu, J. Dynamic analysis of a delayed COVID-19 epidemic with home quarantine in temporal-spatial heterogeneous via global exponential attractor method. Chaos Solitons Fractals 2021, 143, 110546. [Google Scholar] [CrossRef] [PubMed]
- Wang, X.; Li, Z. Dynamics for a type of general reaction-diffusion model. Nonlinear Anal. 2007, 67, 2699–2711. [Google Scholar] [CrossRef]
- Ramirez-Carrasco, C.; Molina-Garay, J. Existence and approximation of traveling wavefronts for the diffusive Mackey—Glass equation. Aust. J. Math. Anal. Appl. 2021, 18, 1–12. [Google Scholar]
- Ling, Z.; Lin, Z. Traveling wavefront in a Hematopoiesis model with time delay. Appl. Math. Lett. 2010, 23, 426–431. [Google Scholar] [CrossRef]
- Wang, X.; Zhang, H.; Li, Z.X. Oscillation for a class of diffusive hematopoiesis model with several arguments. Acta Math. Sin. Eng. Ser. 2012, 28, 2345–2354. [Google Scholar] [CrossRef]
- Ling, Z.; Zhu, L. Traveling wavefronts of a diffusive hematopoiesis model with time delay. Appl. Math. 2014, 5, 2172–2718. [Google Scholar] [CrossRef]
- Pan, X.; Shu, H.; Wang, L.; Wang, X.-S. Dirichlet problem for a delayed diffusive hematopoiesis model. Nonlinear Anal. Real World Appl. 2019, 48, 493–516. [Google Scholar] [CrossRef]
- Wu, J.; Zou, X. Traveling wave fronts of reaction-diffusion systems with delay. J. Dyn. Differ. Equations 2001, 13, 651–687. [Google Scholar] [CrossRef]
- Ma, S. Traveling wavefronts for delayed reaction-diffusion systems via a fixed point theorem. J. Differ. Equ. 2001, 171, 294–314. [Google Scholar] [CrossRef]
- Lin, G.; Li, W.-T. Travelling wavefronts of Belousov—Zhabotinskii system with diffusion and delay. Appl. Math. Lett. 2009, 22, 341–346. [Google Scholar] [CrossRef]
- Trofimchuk, E.; Pinto, M.; Trofimchuk, S. Traveling waves for a model of the Belousov—Zhabotinsky reaction. J. Differ. Equ. 2013, 254, 3690–3714. [Google Scholar] [CrossRef]
- Zhang, G.-B. Asymptotics and uniqueness of traveling wavefronts for a delayed model of the Belousov—Zhabotinsky reaction. Appl. Anal. 2020, 99, 1639–1660. [Google Scholar] [CrossRef]
- Wang, P.K.C. Asymptotic stability of a time-delayed diffusion system. J. Appl. Mech. 1963, 30, 500–504. [Google Scholar] [CrossRef]
- Wu, J. Theory and Applications of Partial Functional Differential Equations; Springer: New York, NY, USA, 1996. [Google Scholar]
- Vandewalle, S.; Gander, M.J. Optimized overlapping Schwarz methods for parabolic PDEs with time-delay. In Domain Decomposition Methods in Science and Engineering; Springer: Berlin, Germany, 2005; pp. 291–298. [Google Scholar]
- Zubik-Kowal, B. Delay partial differential equations. Scholarpedia 2008, 3, 2851. [Google Scholar] [CrossRef]
- Liang, J.; Cao, J. Global exponential stability of reaction-diffusion recurrent neural networks with time-varying delays. Phys. Lett. A 2003, 314, 434–442. [Google Scholar] [CrossRef]
- Lou, X.-Y.; Cui, B.-T. Asymptotic synchronization of a class of neural networks with reaction-diffusion terms and time-varying delays. Comput. Math. Appl. 2006, 52, 897–904. [Google Scholar] [CrossRef]
- Wang, K.; Teng, Z.; Jiang, H. Global exponential synchronization in delayed reaction-diffusion cellular neural networks with the Dirichlet boundary conditions. Math. Comput. Model. 2010, 52, 12–24. [Google Scholar] [CrossRef]
- Yang, Z.; Xu, D. Global dynamics for non-autonomous reaction-diffusion neural networks with time-varying delays. Theor. Comput. Sci. 2008, 403, 3–10. [Google Scholar] [CrossRef]
- Wang, L.; Gao, Y. Global exponential robust stability of reaction–diffusion interval neural networks with time-varying delays. Phys. Lett. A 2006, 350, 342–348. [Google Scholar] [CrossRef]
- Lu, J.G. Global exponential stability and periodicity of reaction–diffusion delayed recurrent neural networks with Dirichlet boundary conditions. Chaos Solitons Fractals 2008, 35, 116–125. [Google Scholar] [CrossRef]
- Polyanin, A.D.; Sorokin, V.G.; Vyazmin, A.V. Reaction-diffusion models with delay: Some properties, equations, problems, and solutions. Theor. Found. Chem. Eng. 2018, 52, 334–348. [Google Scholar] [CrossRef]
- Polyanin, A.D.; Sorokin, V.G. Nonlinear delay reaction-diffusion equations: Traveling-wave solutions in elementary functions. Appl. Math. Lett. 2015, 46, 38–43. [Google Scholar] [CrossRef]
- Mei, M.; Lin, C.-K.; Lin, C.-T.; So, J.W.-H. Traveling wavefronts for time-delayed reaction-diffusion equation: (I) Local nonlinearity. J. Differ. Equ. 2009, 247, 495–510. [Google Scholar] [CrossRef]
- Lv, G.; Wang, Z. Stability of traveling wave solutions to delayed evolution equation. J. Dyn. Control Syst. 2015, 21, 173–187. [Google Scholar] [CrossRef]
- Meleshko, S.V.; Moyo, S. On the complete group classification of the reaction-diffusion equation with a delay. J. Math. Anal. Appl. 2008, 338, 448–466. [Google Scholar] [CrossRef]
- Polyanin, A.D.; Zhurov, A.I. Exact solutions of linear and nonlinear differential-difference heat and diffusion equations with finite relaxation time. Int. J. Non-Linear Mech. 2013, 54, 115–126. [Google Scholar] [CrossRef]
- Polyanin, A.D.; Zhurov, A.I. Functional constraints method for constructing exact solutions to delay reaction-diffusion equations and more complex nonlinear equations. Commun. Nonlinear Sci. Numer. Simul. 2014, 19, 417–430. [Google Scholar] [CrossRef]
- Polyanin, A.D.; Zhurov, A.I. Exact separable solutions of delay reaction-diffusion equations and other nonlinear partial functional-differential equations. Commun. Nonlinear Sci. Numer. Simul. 2014, 19, 409–416. [Google Scholar] [CrossRef]
- Polyanin, A.D.; Zhurov, A.I. New generalized and functional separable solutions to nonlinear delay reaction-diffusion equations. Int. J. Non-Linear Mech. 2014, 59, 16–22. [Google Scholar] [CrossRef]
- Polyanin, A.D.; Zhurov, A.I. Nonlinear delay reaction-diffusion equations with varying transfer coefficients: Exact methods and new solutions. Appl. Math. Lett. 2014, 37, 43–48. [Google Scholar] [CrossRef]
- Polyanin, A.D.; Zhurov, A.I. Non-linear instability and exact solutions to some delay reaction-diffusion systems. Int. J. Non-Linear Mech. 2014, 62, 33–40. [Google Scholar] [CrossRef]
- Polyanin, A.D.; Zhurov, A.I. The functional constraints method: Application to non-linear delay reaction-diffusion equations with varying transfer coefficients. Int. J. Non-Linear Mech. 2014, 67, 267–277. [Google Scholar] [CrossRef]
- Polyanin, A.D.; Zhurov, A.I. The generating equations method: Constructing exact solutions to delay reaction-diffusion systems and other non-linear coupled delay PDEs. Int. J. Non-Linear Mech. 2015, 71, 104–115. [Google Scholar] [CrossRef]
- Polyanin, A.D. Generalized traveling-wave solutions of nonlinear reaction-diffusion equations with delay and variable coefficients. Appl. Math. Lett. 2019, 90, 49–53. [Google Scholar] [CrossRef]
- Aibinu, M.O.; Thakur, S.C.; Moyo, S. Exact solutions of nonlinear delay reaction-diffusion equations with variable coefficients. Partial Differ. Equ. Appl. Math. 2021, 4, 100170. [Google Scholar] [CrossRef]
- Polyanin, A.D.; Zhurov, A.I. Multi-parameter reaction-diffusion systems with quadratic nonlinearity and delays: New exact solutions in elementary functions. Mathematics 2022, 10, 1529. [Google Scholar] [CrossRef]
- Polyanin, A.D.; Sorokin, V.G. Reductions and exact solutions of Lotka—Volterra and more complex reaction-diffusion systems with delays. Appl. Math. Lett. 2022, 125, 107731. [Google Scholar] [CrossRef]
- Sorokin, V.G.; Vyazmin, A.V. Nonlinear reaction-diffusion equations with delay: Partial survey, exact solutions, test problems, and numerical integration. Mathematics 2022, 10, 1886. [Google Scholar] [CrossRef]
- Efendiev, M.; van Brunt, B.; Wake, G.C.; Zaidi, A.A. A functional partial differential equation arising in a cell growth model with dispersion. Math. Meth. Appl. Sci. 2018, 41, 1541–1553. [Google Scholar] [CrossRef]
- Liu, C.-S. Basic theory of a class of linear functional differential equations with multiplication delay. arXiv 2018, arXiv:1605.06734. [Google Scholar]
- Polyanin, A.D.; Sorokin, V.G. Nonlinear pantograph-type diffusion PDEs: Exact solutions and the principle of analogy. Mathematics 2021, 9, 511. [Google Scholar] [CrossRef]
- Aksenov, A.V.; Polyanin, A.D. Methods for constructing complex solutions of nonlinear PDEs using simpler solutions. Mathematics 2021, 9, 345. [Google Scholar] [CrossRef]
- Aksenov, A.V.; Polyanin, A.D. Review of methods for constructing exact solutions of equations of mathematical physics based on simpler solutions. Theor. Math. Phys. 2022, 211, 567–594. [Google Scholar] [CrossRef]
- Abazari, R.; Ganji, M. Extended two-dimensional DTM and its application on nonlinear PDEs with proportional delay. Int. J. Comput. Math. 2011, 88, 1749–1762. [Google Scholar] [CrossRef]
- Grover, D.; Sharma, D.; Singh, P. Accelerated HPSTM: An efficient semi-analytical technique for the solution of nonlinear PDE’s. Nonlinear Eng. 2020, 9, 329–337. [Google Scholar] [CrossRef]
- Sakar, M.G.; Uludag, F.; Erdogan, F. Numerical solution of time-fractional nonlinear PDEs with proportional delays by homotopy perturbation method. Appl. Math. Model. 2016, 40, 6639–6649. [Google Scholar] [CrossRef]
- Bekela, A.S.; Belachew, M.T.; Wole, G.A. A numerical method using Laplace-like transform and variational theory for solving time-fractional nonlinear partial differential equations with proportional delay. Adv. Differ. Equat. 2020, 2020, 586. [Google Scholar] [CrossRef]
- Tang, C.; Zhang, C. A fully discrete θ-method for solving semi-linear reaction–diffusion equations with time-variable delay. Math. Comput. Simul. 2021, 179, 48–56. [Google Scholar] [CrossRef]
- Polyanin, A.D.; Zhurov, A.I. Generalized and functional separable solutions to nonlinear delay Klein–Gordon equations. Commun. Nonlinear Sci. Numer. Simul. 2014, 19, 2676–2689. [Google Scholar] [CrossRef]
- Polyanin, A.D.; Sorokin, V.G.; Vyazmin, A.V. Exact solutions and qualitative features of nonlinear hyperbolic reaction-diffusion equations with delay. Theor. Found. Chem. Eng. 2015, 49, 622–635. [Google Scholar] [CrossRef]
- Long, F.-S.; Meleshko, S.V. On the complete group classification of the one-dimensional nonlinear Klein–Gordon equation with a delay. Math. Methods Appl. Sci. 2016, 39, 3255–3270. [Google Scholar] [CrossRef]
- Polyanin, A.D.; Sorokin, V.G. New exact solutions of nonlinear wave type PDEs with delay. Appl. Math. Lett. 2020, 108, 106512. [Google Scholar] [CrossRef]
- Lobo, J.Z.; Valaulikar, Y.S. Group analysis of the one dimensional wave equation with delay. Appl. Math. Comput. 2020, 378, 125193. [Google Scholar] [CrossRef]
- Long, F.-S.; Meleshko, S.V. Symmetry analysis of the nonlinear two-dimensional Klein–Gordon equation with a time-varying delay. Math. Methods Appl. Sci. 2017, 40, 4658–4673. [Google Scholar] [CrossRef]
- Polyanin, A.D.; Zaitsev, V.F. Handbook of Nonlinear Partial Differential Equations, 2nd ed.; CRC Press: Boca Raton, FL, USA, 2012. [Google Scholar]
- Galaktionov, V.A.; Svirshchevskii, S.R. Exact Solutions and Invariant Subspaces of Nonlinear Partial Differential Equations in Mechanics and Physics; Chapman & Hall/CRC Press: Boca Raton, FL, USA, 2007. [Google Scholar]
- Polyanin, A.D.; Zhurov, A.I. Separation of Variables and Exact Solutions of Nonlinear PDEs; CRC Press: Boca Raton, FL, USA, 2021. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).