Abstract
The propagation of acceleration waves in dilute granular gases was investigated. Acceleration waves propagating in elastic gases, mixtures, and other materials are widely studied in the literature, but not in granular gases. A thirteen-moment theory for granular gas was considered in the framework of Grad’s theory. The spatially homogeneous solutions were determined, and the hyperbolicity of the model is discussed. The propagation of acceleration waves in a non-constant state was investigated; the amplitude of the fastest mode was derived, and the critical time was evaluated. The acceleration wave propagation velocity in inelastic gases was shown to be lower than in elastic gases.
MSC:
82B40; 76P05; 82C40
1. Introduction
Kinetic theory [1,2] is a very prolific field of applied mathematics, which models gases as systems of particles governed by a distribution function. This function depends on macroscopic variables, such as time and space, and microscopic variables, such as particle velocity. The distribution function must satisfy the Boltzmann equation [1,2], which defines the evolution in time and space of the particle distribution. The interaction between particles of different natures is represented by the collision operator, which gives a measure of the change in the distribution function. From the Boltzmann equation, the balance laws of the mass density, velocity, and energy of a gas are derived under appropriate assumptions [1,2,3]. This is useful if one aims to study the behavior of a gas from a macroscopic point of view. In a rarefied gas, that is when the gas molecules are subject to elastic collisions, there is the relaxation of the gas towards a state of equilibrium, characterized by a Maxwellian distribution function [1,2,3]. Instead, in this paper, we dealt with granular gases, which are gases in which the molecules interact by inelastic collisions. In this case, the total energy is not conserved, but part of it turns into heat, and that means a decay of the gas temperature. Many researchers, having noticed the analogy between granular materials and molecular fluids, have developed theoretical methods for the study of granular fluids based on kinetic theory within the framework of the Boltzmann equation. The first works in which granular materials have been studied in the context of kinetic theory were [4,5]; the first dealt with the theory for almost elastic granular flows, while the second took into account granular flows with arbitrary inelasticity. Much work has been performed more generally in granular materials, which are conglomerations of discrete macroscopic particles characterized by collision dissipation. In [6,7,8], hydrodynamic equations were obtained for granular materials. In [9], Brey introduced kinetic equations for low-density granular flows. In [10], Garzo studied shear flow, while in [11,12], a Grad model was introduced for inelastic granular flows. In [13], Brillantov studied in detail the kinetic theory of granular gas. Granular materials are prevalent in various industries, for example in the chemical, agricultural, and food industries, but also in nature, for example in blood flows [14,15], the asteroid belt, sand dunes, debris, lava volcanoes, biofuel [16,17].
Jenkins and Richman [4], two among the first researchers to deal with granular gases, applied the Grad method of moments [18] to dense inelastic gaseous particles. They developed a 13-moment theory for dense gases based on the Boltzmann equation and specifically determined all the fluxes and production terms of the balance laws. In the present paper, we used the field equations derived by Jenkins and Richman [4], limiting our study to the case of dilute granular gases. So, we deal with a thirteen-moment theory, where the unknown fields are mass density, velocity, stress tensor, and heat flux. Kremer and Marques [19] introduced a 14-moment theory for dilute granular gases, adding to the thirteen moments a fourth-order scalar moment. They studied the spatially homogeneous solutions, showing that the time decay of the temperature is very close to that predicted by Haff’s law [20]. Then, they observed that, for the thirteen-moment theory, this homogeneous solution is unstable with respect to longitudinal and transverse waves, and this has been carried out by other authors (see [21]). In order to recover more information about the stability of perturbation, in this paper, we studied the condition of the stability of homogeneous solutions with respect to acceleration waves. More precisely, we analyzed the evolution of acceleration waves [22,23] in dilute granular gases in the framework of the Grad 13-moment theory [4,18].
An acceleration wave or weak discontinuity [22,23] is a disturbance that propagates in an unperturbed state through which all field variables are continuous, while the first derivatives have a jump. The objective is to establish a critical value of the amplitude of the wave below which the acceleration wave does not degenerate into a shock. This analysis has also been recently investigated in different materials, such as fluids [24], bubbles [25,26], fluid mixtures [27], and biological models [28,29].
In this perspective, we show that the equations in [4] restricted to dilute gases form a hyperbolic set of field equations. We determined a non-constant spatially homogeneous solution, and we analyzed the propagation of acceleration waves starting from this spatially homogeneous solution. Normally, studies conducted on acceleration waves consider perturbations propagating in two constant equilibrium solutions. We investigated the stability of the acceleration waves, evaluating the critical time and the formation of shocks.
The rest of the paper is as follows: The field equations are introduced in Section 2, and in Section 3, a spatially homogeneous solution is determined. Section 4 is devoted to the general description of the propagation of acceleration waves, and in Section 5, the spatially homogeneous case is analyzed. Finally, in Section 6, we discuss the conclusions and future research perspectives.
2. Field Equations
It is possible to study the state of a dilute granular gas by describing its density , its velocity , its granular temperature , the traceless part of the stress tensor , and the components of the heat flux at time t and in position . The field equations for this gas were obtained by Jenkins and Richman in 1985 [4] in the context of the Grad 13 theory [18]. The field equations of a dilute granular gas assume the form:
where m and are the mass and the diameter of the spherical particles and e is the normal restitution coefficient with . The case corresponds to inelastic collisions, while refers to elastic collisions.
As can be easily seen, the set (1) consists of a closed system of 13 field equations in the 13 field variables , , , , and . The first two equations of (1) represent the conservation laws of mass and momentum. The third equation is the balance law of energy. It is not a conservation law for the dissipation of energy due to the inelastic collisions. In the elastic case, the production vanishes. The other equations are the balance laws for the stress tensor and the heat flux, which, in the Grad 13-moment theory, are considered as additional field variables.
It is possible to show that the equations (1) can be also obtained in the context of the Rational Extended Thermodynamics theory [3,30,31]. This macroscopic theory considers as the field variables not only the classical ones like mass density velocity and temperature, but also the stress tensors, the heat flux, and others. The constitutive relations are obtained by the use of physical universal principles like the Galilean invariance and the entropy principles. The propagation of acceleration waves in Rational Extended Thermodynamics is well-developed, providing interesting results; see, for example, [3,24,25,26,28,29,30,31] and the references therein.
In this paper, for simplicity, we restricted our analysis to the one-dimensional case. Therefore, assuming that the fields depend only on t and , the set of field Equation (1) becomes
with , , and .
This system can be recast in the following matrix form:
where the vector field is given by
the matrix of the coefficients A is
while the vector with the production terms is
For further purposes, we evaluated the eigenvalues and eigenvectors of the matrix A: first of all, the characteristic polynomial associated with the system (2) has the form:
with .
This polynomial coincides with the corresponding one in the 13-moment theory of elastic gases since the left-hand sides of the equations coincide. In fact, it does not depend on the restitution coefficient e.
The polynomial (7) was studied in detail in [3] (p. 179). In particular, it was proven that the first root is called the contact wave since it propagates with the same velocity of the fluid. The remaining four roots of (7) are real, at least in the hyperbolicity region. Hyperbolicity guarantees finite speeds of propagation, while symmetric hyperbolic systems imply the well-posedness of Cauchy problems (i.e., existence, uniqueness, and continuous dependence on the data).
The eigenvectors associated with the eigenvalues are given by
The coefficient must be determined using the condition In this way, it is possible to obtain the following value for the coefficient :
3. Time-Dependent Solutions
Due to the dissipation of energy, the system (2) does not admit constant solutions. In this section, we describe a homogeneous solution of the field equations already obtained and discussed by different authors [19,21]. Indeed, assuming that the fields depend only on time, the field Equation (2) becomes
We deduced that the density and velocity of the granular gas remain constant in time, while the other equations form a system of coupled ordinary differential equations.
Assuming, as initial conditions, , , , and , the equations are analytically integrated, providing the following expressions for the density, velocity, temperature, stress tensor, and heat flux:
In terms of the dimensionless values:
the solution reads
which are illustrated in Figure 1. In particular, Figure 1a shows the behavior of the granular temperature, heat flux, and stress tensor for the particular case of . We observed that the stress tensor and heat flux decay to the equilibrium value. The stress tensor curve tends to an equilibrium value more rapidly than that of the heat flux. Figure 1b illustrates the temperature field for different values of the restitution coefficient in order to study the solution of the model for different degrees of inelastic microscopic collisions. These cases take into account also different degrees of dissipation of the total energy. By increasing the value of the restitution coefficient, the decay of the granular temperature is less marked. In the elastic case (), the temperature remains constant, while the stress tensor and the heat flux have an exponential temporal decay, due to the non-vanishing initial conditions for and
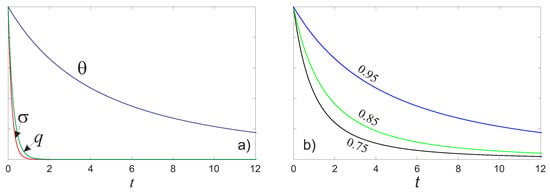
Figure 1.
(a) Temperature, heat flux, and stress tensor for . (b) Temperature field for different values of the restitution coefficient e.
We observed that the time decay of the temperature follows the law of Haff, which describes the dissipation of the total energy in a fluid of inelastic particles through inelastic collisions. Haff [20] discovered that, in a freely cooling granular gas (with a constant coefficient of restitution), the decay rate of the granular temperature is given by
where n is the average number density. The solution of [20] is given by
where is an inverse time scale. This solution is known as Haff’s law for the evolution of the granular temperature of a freely cooling granular gas. The energy’s decay is proportional to and depends on the average number of collisions suffered by a particle within time t, and also on , which expresses the degree of inelasticity.
4. Acceleration Waves
In this paper, we studied particular solutions of the system (1), called weak discontinuity waves or acceleration waves. We assumed that there exists a moving curve , called the wave front, of Cartesian equation , across which the field variables are continuous, whereas their first derivatives may be discontinuous [22,23,24], i.e.,
The square brackets represent the jump across , that is the difference between the values on the two sides of the wave front:
More precisely, the superscript “+” denotes the values in the region ahead of the wave front, where the fields are unperturbed, while “−” in the region behind it.
As is well known [22,23,24], the normal speed of propagation V of the wave front is equal to the characteristic velocity evaluated in the unperturbed field , while the jump is proportional to the right eigenvector (corresponding to the eigenvalue ) evaluated in , that is
The amplitude of the jump satisfies a Bernoulli-like equation:
where d/dt is the derivative along the bi-characteristic lines. In this case, since we are dealing with only one spatial coordinate, we have d/d.
The coefficients and are known functions of the unperturbed fields , and in the one-dimensional case, they are given by
where ∇ is the nabla operator and is the left eigenvector corresponding to satisfying . The suffix “0” means that the quantities must be evaluated in the unperturbed state . The coefficient can be obtained by integrating the Cauchy problem:
Once the coefficients and are determined, they can be inserted into the Bernoulli Equation (19) in order to obtain the amplitude as a known function of time.
In the following section, we evaluate the coefficients and considering as the unperturbed state the homogeneous state (11). Since, in the inelastic gases, the unperturbed state is not constant, the calculations are more complex than the elastic case [3] (p. 182). Examples in the literature of the acceleration wave propagating into non-constant states are the cases of a gravitating atmosphere [24] and, more recently, gas bubbles [25,26].
5. Acceleration Waves Propagating into the Homogeneous State
We considered acceleration waves propagating in the homogeneous state characterized by the solution of (11). In this case, the eigenvalues of the matrix A, obtained as solutions of the characteristic polynomial (7), are evidently functions of time. Therefore, also the velocity of propagation of these acceleration waves, V, must depend on time.
In Figure 2a, the two positive solutions of (7), obtained with , are shown as a function of . The remaining two solutions coincide with those illustrated in Figure 2a, but with a negative sign. This shows explicitly that all roots of the characteristic Equation (7) evaluated in (11) are real, so we can conclude once more that the system is hyperbolic, at least in a neighborhood of the homogeneous state (11).
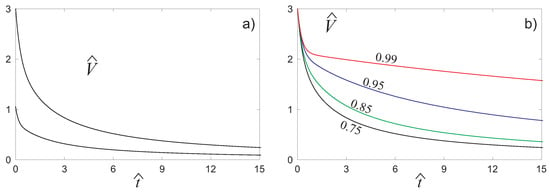
Figure 2.
(a) Velocities of propagation of the acceleration waves for . (b) Velocities for different values of the restitution coefficient e.
The velocity of propagation of the fastest acceleration wave, decreases when the time increases. In Figure 2b, the velocities of the fastest waves are illustrated. They were obtained with different values of the restitution coefficient in order to put in evidence the effect of e. As can be easily seen, when e tends to 1, the velocity tends to the constant value that was obtained for elastic collisions.
In order to derive the amplitude of the jump (18), we need to evaluate the coefficients and from (20) and integrate the Bernoulli Equation (19).
First of all, our unperturbed state depends only on t and not on x, so we have , and the integration of the Cauchy problem (21) yields .
The expressions of from (20) is obtained differentiating (7) with respect the five field variables , v, , , and q in order to obtain the five components of in terms of and the five fields. Then, this vector can be evaluated in the unperturbed state and multiplied by the right eigenvector in (8) evaluated in . This was performed analytically, but for simplicity, we skip here all the analytical results and present in Figure 3 the plot of as a function of time for different values of the restitution coefficient e. It must be observed that, except in the region , where the fields and are more pronounced, the coefficient is proportional to the velocity with a constant of proportionality equal to . This coefficient of proportionality was also obtained in the elastic case (see [3] (p. 185)).
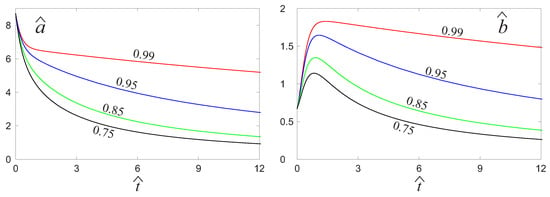
Figure 3.
Coefficients and for different values of the restitution coefficient e, as illustrated in the same figures.
The second coefficient can be evaluated from (20). The calculations were carried out analytically, but, as for , we illustrate here only the numerical values in the figures. It must be said that the derivative of the field variables in the unperturbed state is dd, and the second term in (20) vanishes since depends only on t and not on x. Figure 3 illustrates for different values of e. From this figure, it can be easily seen that grows rapidly in the region , where, again, the non-equilibrium fields and are more pronounced.
In Figure 4a, we illustrate the dimensionless amplitude of the jump solution of the Bernoulli Equation (19) for and different values of the initial value. As can be easily seen, if , the initial discontinuity in the derivatives is too strong and cannot be damped. We observed that it becomes unbounded and the acceleration wave evolves into a shock wave at a critical time . Instead, if , the perturbation is attenuated, and after some time, it disappears.
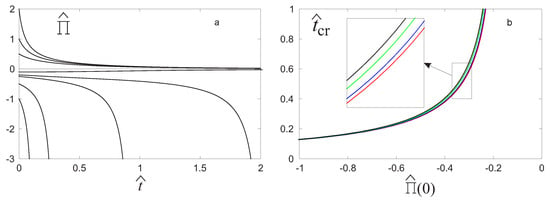
Figure 4.
(a) Amplitude of the jump as a function of for different values of the initial discontinuity. (b) Critical time in terms of the initial discontinuity for different values of the restitution coefficient e.
In Figure 4b, the critical time is shown in terms of the initial discontinuity for different values of the restitution coefficient e. The dependence of the critical time on the restitution coefficient e is not pronounced; indeed, there is only a small difference between the four curves. This implies that, although and depend strongly on their ratio does not depend on it. The condition of the stability of the homogeneous solution with respect acceleration waves can be expressed as
This equation is satisfied if the initial perturbation is not too pronounced. In this way, the disturbance decays in a very short time of the same order of magnitude as the time necessary for and to reach the equilibrium state.
6. Possible Applications in Real Fields
Granular materials are employed in different fields: an important sector is represented by industries, such as the chemical (coal), agricultural (fertilizer), and food industries (rice, coffee, cornflakes). They also can be applied to nature, such as ice floes, the asteroid belt, sand dunes, avalanches, and the variation of coastal erosion. Another application field is human health research, such as blood flow [14,32]. Acceleration waves have been applied to different real phenomena, such as the application of fluids in a gravitational atmosphere [24], fluid bubbles [25], fluid mixtures [27], biological applications in chemo-taxis [28], and in chronic wasting diseases [29].
7. Assumptions and Limitations of the Present Study
In the present paper, a dilute granular gas was considered. Clearly, denser gases need different appropriate models. The Grad theory [4], which we used, is limited to monoatomic gases. When polyatomic gases are investigated, other models must be taken into account. In the derivation of field equations [4], Jenkins and Richman worked in the neighborhood of equilibrium, so it is not possible to investigate the phenomena far from equilibrium. The field equations are valid for all values of e between 0 and but for the sake of simplicity, we limited our attention to the range Finally, we considered perturbations that depend on time and only one-dimensional space. So, it could be interesting to extend the study to the 2D case.
8. Conclusions and Final Remarks
The propagation of acceleration waves in a dilute granular gas was analyzed. To this aim, the field equations obtained by Jenkins and Richman in the context of the 13-moment Grad theory were used under the assumption of dilute gases. Due to the dissipation of energy, this system does not admit a constant solution. We studied, then, acceleration waves propagating into the non-constant and homogeneous state. The coefficients appearing in the Bernoulli differential equation were evaluated analytically, but their numerical values were shown for different values of the restitution coefficient. The Bernoulli equation was integrated, and the time evolution of the amplitude of the jump was shown for different values of the initial disturbance. The critical time, when the weak discontinuity evolves into strong discontinuity, was evaluated in terms of the initial amplitude. Finally, the condition of the stability of the homogeneous solution with respect acceleration waves was analyzed and discussed.
The results herein determined have the same structure as the results for the dilute elastic case [3]. In all figures, the results for practically coincide with the elastic solutions, expect in the narrow region where the fluxes are more pronounced. By comparison of the elastic and inelastic cases, our analysis revealed that, when the gas particles are more inelastic, the velocity of the acceleration waves decreases, due to the energy dissipation (see Figure 2b). We also observed that the coefficients and are smaller when e decreases, but the ratio is essentially constant in e.
In the paper, it must be also said that the values of the restitution coefficient e were considered between and 1. We avoided considering smaller values of e, since probably, in these cases, more-complex models must be adopted. Probably, a theory with more moments must be taken into account.
Furthermore, we started to evaluate the propagation of the acceleration waves in the homogeneous state, where all variables decrease due to the dissipation of energy. It could be interesting to study the behavior for acceleration waves propagating spatially in one-dimensional, or two-dimensional solutions, or solutions that depend both on x and These are projects for further studies.
Finally, an effective method to model discontinuities in solid mechanics was presented in [33]. It seems to be an analog to the present study, and we think it may inspire future research.
Author Contributions
E.B. and A.P. contributed equally to this work. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by Istituto Nazionale di Alta Matematica Francesco Severi: GNFM and Prin Project No. 2017YBKNCE “Multiscale phenomena in Continuum Mechanics: singular limits, off-equilibrium and transitions”.
Data Availability Statement
Data are contained within the article.
Acknowledgments
The authors are grateful to the anonymous referees for their helpful remarks and suggestions.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Chapman, S. Cowling TG the Mathematical Theory of Non-Uniform Gases, 3rd ed.; Cambridge University Press: Cambridge, UK, 1970. [Google Scholar]
- Cercignani, C. The Boltzmann Equation; Springer: New York, NY, USA, 1988. [Google Scholar]
- Müller, I.; Ruggeri, T. Rational Extended Thermodynamics; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2003; Volume 37. [Google Scholar]
- Jenkins, J.T.; Richman, M.W. Grad’s 13-moment system for a dense gas of inelastic spheres. Arch. Rat. Mech. Anal. 1985, 87, 355–377. [Google Scholar] [CrossRef]
- Lun, C.K.; Savage, S.B.; Jeffrey, D.J.; Chepurniy, N. Kinetic theories for granular flow: Inelastic particles in Couette flow and slightly inelastic particles in a general flowfield. J. Fluid Mech. 1984, 140, 223–256. [Google Scholar] [CrossRef]
- Goldshtein, A.; Shapiro, M. Mechanics of collisional motion of granular materials. Part 1. General hydrodynamic equations. J. Fluid Mech. 1995, 282, 75–114. [Google Scholar] [CrossRef]
- Brey, J.J.; Dufty, J.W.; Kim, C.S.; Santos, A. Hydrodynamics for granular flow at low density. Phys. Rev. E 1998, 58, 4638. [Google Scholar] [CrossRef]
- Sela, N.; Goldhirsch, I. Hydrodynamic equations for rapid flows of smooth inelastic spheres, to Burnett order. J. Fluid Mech. 1998, 361, 41–74. [Google Scholar] [CrossRef]
- Brey, J.J.; Moreno, F.; Dufty, J.W. Model kinetic equation for low-density granular flow. Phys. Rev. E 1996, 54, 445. [Google Scholar] [CrossRef]
- Garzó, V.; Santos, A. Kinetic Theory of Gases in Shear Flows: Nonlinear Transport; Springer Science and Business Media: Berlin/Heidelberg, Germany, 2003; Volume 131. [Google Scholar]
- Bisi, M.; Spiga, G.; Toscani, G. Grad’s equations and hydrodynamics for weakly inelastic granular flows. Phys. Fluids 2004, 16, 4235–4247. [Google Scholar] [CrossRef]
- Kremer, G.M.; Santos, A.; Garzó, V. Transport coefficients of a granular gas of inelastic rough hard spheres. Phys. Rev. E 2014, 90, 022205. [Google Scholar] [CrossRef]
- Brilliantov, N.V.; Poschel, T. Kinetic Theory of Granular Gases; Oxford University Press: Oxford, MI, USA, 2004. [Google Scholar]
- Gidaspow, D.; Huang, J. Kinetic theory based model for blood flow and its viscosity. Ann. Biomed. Eng. 2009, 37, 1534–1545. [Google Scholar] [CrossRef]
- Gidaspow, D. Multiphase Flow and Fluidization: Continuum and Kinetic Theory Descriptions; Academic Press: Cambridge, MA, USA, 1994. [Google Scholar]
- Dobran, F.; Neri, A.; Macedonio, G. Numerical simulation of collapsing volcanic columns. J. Geophys. Res. Solid Earth 1993, 98, 4231–4259. [Google Scholar] [CrossRef]
- Friedman, G.D.; Cutter, G.R.; Donahue, R.P.; Hughes, G.H.; Hulley, S.B.; Jacobs, D.R., Jr.; Liu, K.; Savage, P.J. CARDIA: Study design, recruitment, and some characteristics of the examined subjects. J. Clin. Epidemiol. 1988, 41, 1105–1116. [Google Scholar] [CrossRef] [PubMed]
- Grad, H. On the kinetic theory of rarefied gases. Commun. Pure Appl. Math. 1949, 2, 331–407. [Google Scholar] [CrossRef]
- Kremer, G.M.; Marques, W., Jr. Fourteen moment theory for granular gases. Kinet. Relat. Model. 2011, 4, 317–331. [Google Scholar] [CrossRef]
- Haff, P.K. Grain flow as a fluid-mechanical phenomenon. J. Fluid Mech. 1983, 134, 401–430. [Google Scholar] [CrossRef]
- Gupta, V.K.; Shukla, P.; Torrilhon, M. Higher-order moment theories for dilute granular gases of smooth hard spheres. J. Fluid Mech. 2018, 836, 451–501. [Google Scholar] [CrossRef]
- Boillat, G. La Propagation des Ondes; Gauthier Villars: Paris, France, 1975. [Google Scholar]
- Boillat, G.; Ruggeri, T. On the evolution law of weak discontinuities for hyperbolic quasi-linear systems. Wave Motion 1979, 1, 149–152. [Google Scholar] [CrossRef]
- Muracchini, A.; Ruggeri, T. Acceleration waves, shock formation and stability in a gravitating atmosphere. Astrophys. Space Sci. 1989, 153, 127–142. [Google Scholar] [CrossRef]
- Brini, F.; Seccia, L. Acceleration waves and oscillating gas bubbles modelled by rational extended thermodynamics. Proc. R. Soc. A 2022, 478, 20220246. [Google Scholar] [CrossRef]
- Brini, F.; Seccia, L. Acceleration Waves in Cylindrical Shrinking Gas Bubbles. Nucl. Sci. Eng. 2023, 197, 2301–2316. [Google Scholar] [CrossRef]
- Barbera, E.; Brini, F. Mathematical and Physical Properties of an Extended Thermodynamics Multi-temperature Model for the Description of Gas Mixtures. Acta Appl. Math. 2012, 122, 19–35. [Google Scholar] [CrossRef]
- Barbera, E.; Valenti, G. Wave features of a hyperbolic reaction–diffusion model for Chemotaxis. Wave Motion 2018, 78, 116–131. [Google Scholar] [CrossRef]
- Barbera, E.; Pollino, A. A hyperbolic reaction-diffusion model of chronic wasting desease. Ric. Mat. 2023. [Google Scholar] [CrossRef]
- Ruggeri, T.; Sugiyama, M. Rational Extended Thermodynamics beyond the Monatomic Gas; Springer: New York, NY, USA, 2015. [Google Scholar]
- Ruggeri, T.; Sugiyama, M. Classical and Relativistic Rational Extended Thermodynamics of Gases; Springer: Berlin/Heidelberg, Germany, 2021. [Google Scholar]
- Barbera, E.; Pollino, A. An extended thermodynamics model for blood flow. Mathematics 2022, 10, 2977. [Google Scholar] [CrossRef]
- Long, G.; Liu, Y.; Xu, W.; Zhou, P.; Zhou, J.; Xu, G.; Xiao, B. Analysis of crack problems in multilayered elastic medium by a consecutive stiffness method. Mathematics 2022, 10, 4403. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).