Abstract
This paper reviews the recent literature on the “social ranking problem”, that is, the problem of converting group rankings into individual rankings. We introduce and categorize existing social ranking methods and we briefly explain their attributes. Three main categories of social ranking methods are identified: lexicographic social rankings, methods based on voting mechanisms, and those inspired by the theory of coalitional games. An open-source R package called socialranking for computing the majority of the existing social rankings is also presented and discussed.
MSC:
91A12; 91-08
1. Introduction
Various problems that may seem unrelated at first glance—like ranking researchers or athletes in team sports [1], understanding the importance of diseases in interconnected health graphs of co-morbidities [2,3], understanding how a formula contributes to the inconsistency in a belief base [4], measuring someone’s influence on a social network [5,6], explaining the impact of different factors in multi-criteria decision-making [7], and many more—in fact all come down to a common social ranking problem: how to turn rankings that involve sets of elements or coalitions into an informative ranking that applies to individual ones. Therefore, a social ranking solution aims to address the essential question of how to rank the elements within a set N in a way that aligns with an established ranking of its subsets. Additionally, it strives to ensure that this ranking accurately represents the ordinal influence of each individual element on the ranking positions of the subsets.
Inspired by the framework of three-valued simple games [8], a ranking over coalitions of political parties may represent, for instance, a bicameral legislature wherein the two houses are formed by and members, respectively. Each political party i of a set N is represented by precisely and in house 1 and 2, respectively. As it is the case for the States General of the Netherlands [8], assume that the first house can accept (reject) a bill if there is (is not) a majority in favor. In case of acceptance by the first house, the bill is sent to the second house that follows the same rule to give a final ruling on whether to accept or reject the bill. If the bill is accepted by the two houses, it becomes a law. However, only the first house has the right to submit a bill and start the procedure. Precisely, any coalition of S of the set N of political parties can reach one of the following three outcomes denoted as :
- if the parties in coalition S form a majority in both houses (i.e., and );
- if the parties in coalition S form a majority in the first house but not in the second one (i.e., and );
- in all the remaining cases.
Such a situation can be represented as a ranking of the subsets of N such that, for any pair of coalitions S and T, we have that S “is at least as powerful as T” whenever is at least as large as . Notice that, in this situation, the outcomes associated to coalitions are purely ordinal, as the ordering only encodes an increasing preference of political parties over the possible outcomes, and not a specific amount of utility. Nevertheless, it seems rather appealing to try to estimate the relative importance of the different political parties, taking into account their role in determining the most preferred levels of acceptance of a bill through the formation of alternative coalitions. The theory of social rankings is aimed at addressing this kind of problems by proposing a portfolio of alternative solutions. This paper aims to systematically categorize those solutions, clearly outlining their key features and demonstrating how they are computed using numerical examples. Furthermore, we will provide a concise overview of the socialranking R package [9], which facilitates the computation of social rankings for more intricate cases.
Our analysis has delineated three distinct categories of social ranking solutions within the existing literature:
- Lexicographic social rankings. These rankings prioritize elements based on a predetermined hierarchy of importance related to the roles played within coalitions. Additionally, they may factor in the size of the coalitions, offering a nuanced approach to ranking [10,11,12].
- Social rankings based on voting rules: This category assesses the impact of individual elements by examining their unique contributions to various coalitions. These rankings maintain consistency (ceteris paribus) by altering only one element at a time while keeping all other factors constant. The aggregation of individual contributions in this approach is guided by principles akin to classical voting systems [13,14,15].
- Game theory-inspired social rankings: These rankings are grounded in the principles of cooperative game theory. They leverage established solution concepts from this field to formulate rankings, providing a theoretical and strategic framework for understanding social rankings [15,16,17,18].
We start in the next section with some preliminary definitions. The three aforementioned families of social rankings are presented in Section 3, Section 4 and Section 5, respectively. Section 6 is devoted to a short introduction of the socialranking package. We conclude in Section 7 with a mention to related studies and applications of social rankings from the literature.
2. Preliminaries and Notations
Consider a finite set of elements . The set of subsets of N (also called coalitions) is denoted by (for many social rankings, like the lexicographic ones in Section 3, the empty coalition Ø, and the coalition of all elements N, are irrelevant and can be omitted from . For other social rankings, however (e.g., the ordinal Banzhaf index in Section 5), these two special coalitions play an important role). The set of coalitions without i is denoted by , whereas the set of coalitions containing neither i nor j is denoted by , for any , .
A binary relation on N is a set and it is: reflexive, if for each , ; transitive, if for each , and ⇒ ; total, if for each , or ; antisymmetric, if for each , and ⇒ . A total preorder or ranking is a reflexive, transitive, and total binary relation. A total or linear order is an antisymmetric ranking. and denote, respectively, the set of rankings and the one of linear orders on N.
The lexicographic order and the lexicographic* order among vectors and are defined, respectively, as follows:
- if either or there exists t such that and for all .
- if either or there exists t such that and for all .
Hereafter, a total preorder is referred to as a power relation. In the following, for all , or, equivalently, is interpreted as “coalition S is at least as powerful as coalition T according to the power relation ≿”. We denote by ∼ the symmetric part of ≿ (i.e., for all , and ) and by ≻ the asymmetric part of ≿ (i.e., for all , and not ). Therefore, for all , means that “coalition S is strictly more powerful than coalition T”, whereas means that “coalitions S and T are equally powerful”.
Let be a power relation of the form The quotient order of ≿ is denoted as in which the subsets are grouped in the equivalence classes generated by the symmetric part of ≿. This means that all the sets in are equally powerful to and are strictly better than the sets in , and so on. Given a power relation ≿ and its associated quotient order we denote by the number of sets in containing i for and by the l-dimensional vector associated to ≿.
A social ranking (solution) on N is a function associating to each power relation a total preorder (or ) over the elements of N. By this definition, the notion means that “applying the social ranking R to the power relation ≿ gives the result that i is ranked higher than or equal to j”. We denote by the symmetric part of , and by its asymmetric part.
A trivial social ranking, neglecting the position of non-singletons coalitions in the power relation, is the map such that for all and all . Another extremely simple social ranking may only look at the comparisons of coalitions containing all-but-one elements, like the map such that for all .
Example 1.
Let and consider the power relation ≿ as follows (in the remaining of this paper, we will continue to use the concise notation introduced in this example to save space in the expression of a ranking. So, for example, the notation indicates a power relation ≿ such that , and also , due to the transitivity of ≻; similarly, for a relation R on the individual elements with , we have that , , and also ; etc.):
The quotient order of ≿ is such that
So, returns the ranking while yields the ranking .
The remaining of this section is devoted to the presentation of families of social ranking solutions from the literature.
3. Lexicographic Social Rankings
The lexicographic excellence (lex-cel) [12] has received increasing attention in the recent literature on social rankings. The lex-cel is based on the idea that the most influential individuals are those appearing more frequently in the highest positions in the ranking of coalitions. Precisely, to compare two elements i and j in N, lex-cel proceeds in a lexicographic way over the vectors of occurrences of the two elements in the equivalence classes of a power relation. With the objective to award the excellence of the elements in contributing to the best-ranked sets, the lex-cel first compares the occurrences of i and j in the first equivalence class of a power relation (i.e., the equivalence class with the lowest index in the quotient order, on the left side), placing the element occurring the most above the other. In case of a tie, i.e., i and j occur the same number of times in the sets of the first equivalence class, lex-cel demands to compare the occurrences of i and j in the second equivalence class of the power relation, again placing the element occurring the most above the other or, in case of a tie, proceeding with the examination of the third equivalence class, and so on, until one finds a difference between the number of occurrences in a certain equivalence class (declaring a strict preference for the element occurring the most) or the last equivalence class is reached with all ties and, in this case, i and j are declared indifferent by the lex-cel. More formally,
Definition 1
(Lexicographic-excellence (lex-cel) [12]). The lexicographic excellence (lex-cel) is the map such that for all :
for any power relation (following the same convention as before, and stand for the symmetric part and the asymmetric part of , respectively).
Example 2.
Let and let us consider the power relation ≿ of Example 1. We have , and . Notice that . So, the lex-cel returns the following ranking: .
While the lex-cel solution rewards excellence, its dual definition may be used to punish mediocrity. Therefore, to compare two elements i and j in N, the dual lexicographic-excellence (dual-lex) [12] first compares the occurrences of i and j in the last equivalence class of a power relation (i.e., the sets in the equivalence class with the highest index in the quotient order, on the right side), placing the element occurring the least above the other one, for appearing more frequently in the worst equivalent class denotes weakness. In case of a tie, i.e., i and j occur equally in the sets of the last equivalence class, the dual-lex focuses on the occurrences of i and j in the penultimate equivalence class, always punishing the less frequent element and proceeding to the next equivalence class in case of a tie, and so on, from the right to the left side. Once again, if the number of occurrences remains the same over all equivalence classes, the dual-lex declares i and j indifferent.
Definition 2
(Dual lexicographic-excellence (dual-lex) [12]). The dual-lexicographic (dual-lex) solution is the map such that, for all ,
for any power relation ( and stand for the symmetric part and the asymmetric part of , respectively).
Example 3.
Let be the set of agents and let us consider the power relation ≿ of Example 1. Notice that . So, the dual-lex returns the following ranking: .
Other lexicographic social rankings have been introduced in [10]. Like lex-cel, the two social rankings and proposed in [10] are aimed at rewarding the excellence of elements in contributing to the best coalitions in a power relation, but the excellence is mediated by the size of the coalitions, promoting the importance of smaller ones. More precisely, as lex-cel, starts the comparison of two elements i and j looking at the first equivalence class of a power relation (from the left). Different from lex-cel, distinguishes the number of occurrences in coalitions of different sizes giving, as a secondary principle (after the principle of excellence), priority to smaller coalitions. The main argument supporting such a principle is that, in an ordinal framework, where it is not possible to quantify the performance of coalitions, individual contributions to smaller coalitions are likely more relevant and should count more. So, in the first equivalence classes, first focuses on the occurrences of i and j as singletons; then, in case of a tie (i.e., both singletons do or do not belong to the first equivalence class), it considers coalitions of size 2, and so on, until all possible coalition sizes are considered. Possibly, the smallest coalition size such that i and j occur differently determines a strict relation in favor of the most frequent one; otherwise, in case i and j occur equally over coalitions of the same sizes throughout the first equivalence class, looks at the second equivalence class and it compares again elements’ occurrences based on the size of coalitions, like for the first equivalence class, and so on proceeding from left to right over all possible equivalence classes. An indifference may arise according to only in case all the per-size occurrences are equal in all equivalence classes. To formally introduce , we need some further notations.
Given a power relation , with quotient order , we define the matrix for any element such that denotes the number of coalitions of size containing i in the equivalence class , . Notice that , so .
Definition 3
( ranking [10]). The -solution is the map such that, for any power relation and ,
and
( and stand for the symmetric part and the asymmetric part of , respectively).
Example 4.
Let be the set of agents. Consider the power relation ≿ defined as
where all coalitions not explicitly listed belong to the last equivalent class. The quotient order of ≿ can be expressed as
Focusing on elements 2 and 4, their respective vectors are and . Consequently, lex-cel yields .
On the other hand, we have that
It is easy to verify that, according to Definition 3, with and , the solution produces .
Based on a per-size comparison within each equivalence class, may completely reverse a strict relation between two elements yielded by lex-cel (see, for instance, the relation between elements 2 and 4 in Example 4). One can argue that, if the overall excellence is the main criterion to rank elements, then reversing the indication of the total amount of occurrences within a discriminating equivalence class is too extreme.
To rectify this, the authors in [10] introduce another social ranking solution, namely . Like , also begins by examining the equivalence classes from left to right and counts occurrences on a per-size basis. However, the per-size comparison is only allowed to determine a strict relation between two elements when there is an inequality in the total number of occurrences within an equivalence class.
To formalize the social ranking solution as introduced in [10], we extend our notation for the matrix . Let denote the sum of the values of column , calculated as . Then, is defined as follows:
Definition 4
( ranking [10]). The -solution is the map such that, for any power relation and ,
and
( and stand for the symmetric part and the asymmetric part of , respectively).
Example 5.
Let be the set of agents and let us consider again the power relation ≿ of Example 1. We have that
To compute the social ranking between 1 and 2, notice that for all and , but . As such, according to Definition 3, . In a similar way, but . So, returns the ranking .
The social ranking yields the same ranking on N, but for different reasons. In fact, while and , which implies that 3 is ranked higher than both 1 and 2 according to Definition 4. One can verify that returns the ranking .
Example 6.
Let be the set of agents and consider the power relation ≿ from Example 4.
According to Definition 4, with parameters and , one obtains . Therefore, yields the relation , which aligns with the outcome from the lex-cel solution.
However, it is easy to find an example wherein the and lex-cel solutions diverge in their rankings. Consider the slightly different power relation such that
where all not explicitly listed belong to the same last equivalence class. The quotient order of can be represented as
Focusing on elements 2 and 4, their respective vectors under lex-cel are and . Consequently, lex-cel produces .
On the other hand, the matrices for are as follows:
For column , both and add up to 1. However, with , . As such, yields .
Two other lexicographic social ranking solutions have been introduced more recently in the paper [11] with the name of and . These solutions aim to use the information about the performance of coalitions only in the case of a tie between two elements whose singleton coalitions belong to the same equivalence class in the power relation. The procedure to compute the social ranking is as follows (if , we denote by the index of the equivalence class to which and belong, and we have ):
Definition 5
( ranking [11]). The -solution is the map such that, for any power relation and ,
if one of the following conditions hold:
- (1)
- ;
- (2)
- and there exists such that
- (i)
- if , then for all ,
- (ii)
Otherwise, if and for all , we have that .
Example 7.
In the power relation ≿ of Example 2, by condition , we immediately have the ranking .
Now, consider a slightly different power relation such that
The quotient order of ≿ is such that
As before, and . But now, and we have that .
Notice that and . So, there is no such that condition in Definition 5 is satisfied, subsequently yielding (also notice that both and in this example place 1 above 2, as in, and ).
The social ranking solution resolves ties between two elements who exhibit identical individual performances counting the coalitions with a size of two, followed by those of size three, and so forth, that belong to equivalence classes above the one of the two singletons. Consequently, the ranking is not concerned by the actual performance levels exhibited by the considered coalitions, as long as they outperform the singletons’ performance. An alternative social ranking solution, referred to as , is designed to rectify this particular effect.
Definition 6
( ranking [11]). The -solution is the map such that, for any power relation and ,
if one of the following conditions holds:
- (1)
- ;
- (2)
- and there exists and such that
- (i)
- if , then for all and ;
- (ii)
- if , then for all ;
- (iii)
- .
Otherwise, if and for all and , we have that .
Example 8.
Consider the power relation of Example 7. According to Definition 6, the ranking gives us immediately and by condition 6.1. On the other hand, for and , conditions and are automatically satisfied, as well as condition , for . So, we have .
For alternative axiomatic characterizations of lex-cel, dual-lex, , , , and , we refer to the original papers wherein these solutions have been introduced [10,11,12].
4. Social Rankings Inspired by Voting Rules
The family of weighted majority relations was introduced in [15] to rank individuals based on the comparisons of coalitions that are identical except for one element (also called CP-comparisons in [14]). More precisely, for any pair of individuals i and j in N, we consider the set of coalitions and we refer to the CP-comparisons for i and j as the set of comparisons between and , for any . Roughly speaking, a CP-comparison vs. can be interpreted as the expression of a “voter” casting a preference relation over i and j.
To introduce the family of weighted majority relations, we first define the notion of ordinal difference between individuals i and j within a coalition S. For any power relation , and , define the ordinal difference such that
Definition 7 (Weighted majority relation).
Let and let be a weight scheme such that for all and . The weighted majority relation associated to is the binary relation (notice that is not necessarily transitive; therefore, it cannot be denoted using the notation , which is reserved to well-defined social rankings). such that for all ,
Example 9.

Consider the power relation ≿ of Example 1 and a weight system such that . As indicated in Table 1, to compare elements 1 and 2, we compute
and so . In a similar way, we have that
implying that and
which implies , too.

Table 1.
The weight scheme of Example 9 on the power relation of Example 1 concerning the CP-comparisons for individuals 1 and 2.
In a special case, all CP-comparisons are assigned an equal weight of 1. With such a weight system, the corresponding weighted majority ranking is also known as the Ceteris Paribus (CP-)majority relation that has been introduced and axiomatically studied in [14].
Definition 8
(CP-majority [14]). The CP-majority relation is the binary relation such that, for all ,
for any power relation .
In voting theory, the majority rule is not necessarily a ranking when there are more than two individuals, as illustrated by May’s work [19]. This is also true for weighted majority relations. The following example demonstrates an instance of a CP-majority relation that fails to satisfy transitivity.
Example 10.
Consider the power relation ≿ of Example 1. We have that , and both and equal 0. Consequently, the CP-majority relation gives us and , yet also .
Special weight systems can be generated to guarantee that the corresponding weighted majority relation is transitive. For instance, in [15] a special weight system was considered wherein is exactly the number of coalitions S and that are comprised between and in the power relation ≿. Precisely, let be the set of coalitions that are strictly between and in the power relation ≿. The weight for the CP-comparison then corresponds to the number of coalitions in that are also in . More formally,
Clearly, (i.e., if , we obtain ).
Example 11.

Consider the linear power relation such that
The CP-comparisons and the corresponding weights are shown in Table 2.

Table 2.
CP-comparisons and the weight scheme on the power relation of Example 11.
Notice that the CP-majority yields and , but also , breaking transitivity again. In contrast, using the weighted majority relation with weights , we obtain the ranking .
For any linear power relation, the weighted majority relation with weights yields a ranking which holds for any linear power ranking. This is proven in [15] by showing that coincides with the ordinal Banzhaf ranking, a social ranking solution introduced in [15] that is inspired by the celebrated Banzhaf index [20] for coalitional games (see also Theorem 2 in Section 5).
Alternative methods to eliminate cycles in the CP-majority solution have been studied in [13], which proposes social ranking solutions inspired by established voting rules. For instance, a solution akin to the Copeland’s rule [21] has been introduced. This approach ranks individuals by balancing the number of favorable pairwise comparisons against defeats, taking into account the full range of CP-comparisons.
Definition 9
(Copeland-like social ranking [13]). The Copeland-like solution is the map such that for each and
where
Example 12.
Consider the power relation ≿ of Example 1 and the CP-majority relation of Example 10. The corresponding scores are , , and . The Copeland-like solution therefore yields the ranking .
Another approach studied in [13] draws inspiration from the Kramer–Simpson methodology in social choice theory, commonly referred to as Minmax REF. In this approach, individuals are ranked in reverse order according to their worst pairwise defeat, taking into account all possible CP-comparisons.
Definition 10
(Kramer–Simpson (KS)-like social ranking [13]). The KS-like social ranking is the map such that for each and
where (we point out a difference in Definition 4 in [13] concerning the notion of , which seems to count ties as defeats).
Example 13.
Consider the power relation ≿ of Example 1. Individual 1 is defeated once by 2 () and once by 3 (); thus, ; individual 2 is also defeated only once by 3 (), so ; finally, individual 3 is defeated as well once by 1 () and once by 2 (); hence, . It follows that, according to the KS-like social ranking, .
5. Social Ranking Based on Solution Concepts for Coalitional Games
We start this section by introducing some basic definitions from coalitional game theory. A coalitional game on a set N is a map that satisfies . Let be a vector of n non-negative weights such that . A semivalue is defined as the sum
where is the marginal contribution of i to , for each and . Since can be seen as the probability that a coalition of size s forms, for each , represents an expected marginal contribution of player i to all possible subsets of N containing i. Semivalues have been used in the literature to convert the information of a game v into an overall personal attribution of element i (see, for instance, [22,23,24]). Well-studied semivalues in the literature (also interpreted as power indices) are the Shapley value [25], with , and the Banzhaf value [20], with , for each .
The use of semivalues is rather limited in the ordinal framework, for two distinct coalitional games that are “consistent” with the same power relation may lead to contradictory orderings over the elements. Consider for instance a power relation ≿ on with and two elements i and j in N. Take a coalitional game v consistent with ≿, such that
for all . One can verify that a semivalue computed on v yields a relation between i and j corresponding to the sign of the difference
where . It is obvious that, except for some particular situations, the difference in relation (5) can be made negative or positive, with a suitable choice of game v (for instance, if , we necessarily have that and ). So, in general, any attempt to use semivalues to rank individuals seems strongly affected by an arbitrary choice of the game v (among those which are consistent with a given power relation).
The restricted domain of power relations where the ranking provided by a semivalue is invariant to the choice of compatible coalitional games has been studied in the papers [17,26]. For instance, a necessary and sufficient condition for a power relation such that the Banzhaf value of i is larger than the Banzhaf value of element j for all games satisfying condition (4) is given in Definition 11.
Definition 11
([17,26]). Let be a power relation and . Consider the sequence of sets with and and the sequence with and , for all and such that
and
We say that i orderly responds to j if
for all .
Theorem 1
([17,26]). Let be a power relation and . Consider the semivalue with , for each .
Then, for all coalitional games v such that if and only if i orderly responds to j.
Example 14.
Consider the power relation of Example 4. For element 1, we have
and for element 4,
Notice that , , and . Consequently, 1 orderly responds to 4 as well as 4 to 1. By Theorem 14, for any coalitional game that satisfies relation (4) with respect to ≿ of Example 4, we have that the Banzhaf value of element 1 is identical to the Banzhaf value of element 4 (a similar consideration can be made between 1 and 3 and between 3 and 4). One can also verify that 2 orderly responds to 1, but it is not true that 1 orderly responds to 2. So, again by Theorem 14, for any coalitional game that satisfies relation (4) with respect to ≿ of Example 4 we have that the Banzhaf value of 2 is strictly larger than the Banzhaf value of 1 (and the one of 3 and of 4).
Another approach inspired by semivalues and applying to a larger family of power relation has been introduced in [15], starting with the counterpart of the notion of marginal contribution in an ordinal framework.
Definition 12
(Ordinal marginal contribution [15]). Let . For each element and all , we define the ordinal marginal contribution of i to coalition in ≿ as follows:
Clearly, the ordinal marginal contribution of an element i to a coalition only depends on the power relation , and not on the choice of a coalitional game consistent with ≿ according to relation (4). Then, the ordinal Banzhaf relation is simply defined as a map that associates to each power relation a ranking over N induced by the average ordinal marginal contribution of each element of N to all possible coalitions containing it. Precisely,
Definition 13
(Ordinal Banzhaf relation [15]). Let . The ordinal Banzhaf ranking is such that
for all elements .
Example 15.

Consider the power relation from Example 11.
As shown by the sum of ordinal marginal contributions in Table 3, the ordinal Banzhaf ranking on ≿ is such that .

Table 3.
Ordinal marginal contributions derived from the power relation in Example 11.
Since the ordinal Banzhaf relation is represented by a numerical score, it is obvious that it always provides a ranking over the elements of N. It is less obvious that the weighted majority relation with weights yields a ranking in general. Nevertheless, in [15] the authors proved that the weighted majority relation with weights and the ordinal Banzhaf relation coincide on linear power relations.
Theorem 2
([15]). Let . Then, .
As a consequence of Theorem 2, and as already stated in the previous section, the weighted majority relation with weights is a well-defined ranking solution when it is applied to the domain of linear power relations.
A social ranking that is strongly based on models of coalition formation has been introduced in [16]. More precisely, in [16] the authors study a notion of set-valued social ranking that is defined as a set-valued function associating to each power relation a subset of rankings over the individuals . In particular, core stability, a widely studied notion in the field of coalition formation games [27,28], is a central notion for the set-valued social ranking studied in [16]. To introduce this notion, we need some further notations. A partition , for some integer , where N is a collection of m non-empty subsets of N that are disjoint (i.e., for all ) and cover N (i.e., ). Given a partition of N and an individual , we denote as the (unique) coalition in containing i.
Now, given a partition of N and a power relation , we say that is blocked by a non-empty coalition if for all . So, a partition is considered blocked by a coalition S when, for every individual i within S, coalition S attains a higher rank in the power relation, compared to the rank of the coalition within that contains i. The intuition here is that, if individuals prefer to stay in top-ranked coalitions, each individual’s inclination leans toward S over the coalition assigned to them by partition (in other words, is not “stable”). A partition is referred to as a core-partition if it achieves stability, meaning it is not blocked by any coalition S. Formally, a partition of N is core-stable in if for each , , there exists such that . The set of core-stable partitions in ≿ is denoted by .
Example 16.
Consider again the power relation ≿ of Example 1. The set of core-stable partitions in ≿ is as follows:
As remarked in [16], the non-emptiness of the core-partition social ranking can be directly proved as a consequence of some results shown in [29]. A simple procedure has been proposed in [16] to compute an element of a core-partition social rankings. We introduce the procedure as the following pseudo-code (Algorithm 1).
| Algorithm 1: Finding core-partitions on power relations |
 |
Based on the fact that the set of core-stable partitions is always non-empty, in [16] the authors introduce the notion of core-partition social ranking as the set-valued social ranking associating to each power ranking the set of rankings “induced” by partitions , as follows:
Definition 14
(Core-partition social ranking [16]). The core-partition social ranking is the map set-valued social ranking associating to each power ranking the set of rankings
where a ranking R induced by a partitions Π is such that
Example 17.
Continue to consider Example 16. The core-partitions on ≿ is
6. An R Package for Social Ranking Computation
The socialranking package in R, available on CRAN, serves as a practical tool for researchers interested in experimenting with these social ranking methodologies. It encompasses many of the aforementioned solution concepts and offers the ability to introduce new ones. This section serves to highlight the fundamental structure and usage of the package. A more complete guide is available as a vignette on the CRAN page [9].
Vectors of unit types (such as number or character) represent coalitions. For example, c(1,2,3) is the coalition , c(1) (or just 1) a singleton, and c() the empty set.
Orders between coalitions are represented by a list of lists, wherein each nested list can be thought of as an equivalence class containing one or more vectors of coalitions.
Trying to construct the power relation ≿ from Example 1, Listing 1 shows how it can be achieved by passing a list of equivalence classes to PowerRelation(). This function returns a PowerRelation object. As a more convenient alternative, as.PowerRelation() can be passed a character string. Here, every alphanumerical character represents an individual element. Coalitions are ranked intuitively with the ˜ and > symbols.
| Listing 1. Creating power relations. |
 |
Once the PowerRelation object is constructed, it can be passed to a social ranking function to construct a SocialRanking object, which is an ordinal relation between the elements. Additionally, ranking solutions make use of some numerical comparisons to rank its elements, such as the lex-cel comparing vectors of the number of occurrences in each equivalence class, or the ordinal Banzhaf method comparing the number of positive versus negative ordinal marginal contributions an element makes by joining a coalition. These values can also be requested by passing the PowerRelation object to a scores function, as shown in Listing 2.
| Listing 2. Applying social ranking functions. |
 |
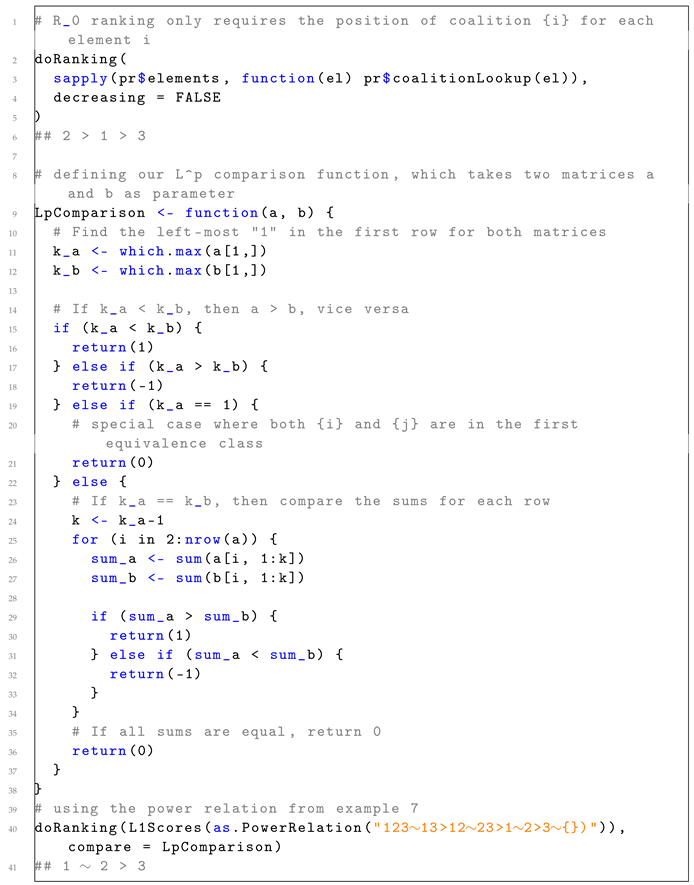
For introducing one’s own ranking function, Listing 3 demonstrates the simple solution from the introduction, as well as the much more sophisticated -solution from Definition 5, both of which are not currently present in the package. The function doRanking() aids us in creating a SocialRanking object.
In the case of , it is easy for each element i to determine k such that . We construct a vector of numbers wherein each index represents the index k for each element in pr$elements by calling pr$coalitionLookup(el). Then, elements with a lower number, implying that its singleton belongs to a higher-ranking equivalence class, will be strictly preferred over elements with a higher number.
As for , L1Scores() already produces the correct matrix for each element . However, the way the matrices are compared and sorted is fairly different, which requires either the introduction of new R classes or a custom comparison function which is passed as a parameter to doRanking(). This comparison function takes two parameters, say a and b, and returns a positive number if a > b, a negative number if a < b, or 0.
To enhance user experience and encourage further exploration, the package includes a set of helper functions. These functions streamline common tasks such as generating power sets with createPowerSet(), augmenting existing PowerRelation objects with appendMissingCoalitions(), modifying it such that it becomes monotonic (), and dynamically generating permutations of power relations via powerRelationGenerator(). Listing 4 briefly demonstrates these functionalities.
| Listing 3. An implementation of the and -solution. |
 |
The socialranking package is designed to be a versatile tool for researchers and practitioners in computational social choice. Its architecture is modular, facilitating the addition of new social ranking algorithms and methodologies, as illustrated in Listing 3. As also explained in the vignette [9], contributions from the academic and broader communities are highly encouraged to enhance the package’s capabilities, improve its reliability, and broaden its applicability. Such contributions can substantially enrich this open-source initiative, further establishing it as an additional resource for research in the framework of social rankings.
| Listing 4. Helper functions in the socialranking package. |
 |
We conclude this section with a numerical example representing an (invented) bicameral legislature on the same lines of the one presented in Section 1 with the objective to show that the use of our package may offer a concrete opportunity to facilitate the social ranking computation in practical problems.
Example 18.

To illustrate a potential application of the socialranking package in practice, following the example of a bicameral legislature introduced in Section 1, we consider a situation with a set of four political parties and where the first house is composed by members while the second house is composed by members. Following the example in Section 1, we imagine a country with a bicameral legislature comprising two houses. The seats in House 1 and seats in House 2 are distributed between the four major ruling parties, the Progressive Party (1), the Conservative Party (2), the Green Party (3), and the Libertarian Party (4), . Suppose that each political party in N is represented in the two respective houses, as shown in Table 4.

Table 4.
Distributions of seats in a bicameral legislature.
So, the three-valued function representing the outcomes of the coalitions is
One can easily verify that for all , , for all , and for all the remaining coalitions . Such a function yields the power relation ≿ such that
where all coalitions not explicitly listed belong to the last equivalent class.
By means of the instructions introduced in this section, we can use our socialranking package to compute the social rankings presented in this paper. As simple games are monotonic, inputting the information in R can be greatly simplified by, one, only specifying the minimal winning coalitions for the first two equivalence classes, and two, utilizing the combination of appendMissingCoalitions and makePowerRelationMonotonic to make the power relation object total and monotonic. Alternatively, if one were to experiment more with three-valued simple games with associated weight vectors, Listing 5 also demonstrates how this could be achieved.
Running the data through all the solutions, it is found that a large majority of social rankings, precisely lex-cel, dual-lex, , , , Copeland-like, and ordinal Banzhaf, all yield the same output, that is, the ranking (note that parties 2 and 4 are equally ranked, despite the fact that the weight of 2 in each house is strictly larger than the one of 4). Only the and -like solutions give the slightly different ranking , where parties 2, 3, and 4 are equally ranked.
| Listing 5. Applying the socialranking package. |
 |
7. Conclusions
In this paper, we have undertaken a comprehensive examination of various social rankings presented in the recent literature. To better understand which social ranking solution is most suitable for a given application context, we suggest that the interested readers look at the original papers wherein such solutions were introduced. In fact, almost all social rankings considered in this paper were originally proposed trough an axiomatic approach, grounded in properties motivated by specific application contexts. Although interesting, a comprehensive analysis of those properties from the literature is beyond the scope of this paper. On the other hand, to guide the interested reader toward the appropriate choice of a social ranking, we recommend to adopt the following general strategy. If the application context requires a prioritization in the evaluation of some particular criteria of performance, such as the positions in a power relation, or other criteria, like the size of coalitions, we suggest to look at solutions in the family of lexicographic social rankings (Section 3). Differently, if the objective is to highlight the differences between individuals in terms of their ability to collaborate with predefined groups, the family of solutions to be considered should be the one of social rankings based on voting rules (Section 4). Finally, if the main objective is to rank individuals considering a fairness principle, or even a notion of stability within coalitions, the family of social rankings inspired by solutions for coalitional games (Section 5) could be the most suitable one.
Our primary aim has been to provide a self-contained and readily applicable reference to existing methodologies aimed at ranking elements within a set based on a ranking over their subsets. It is noteworthy that certain social rankings discussed in this paper have also been employed in diverse contexts in the related literature, and we herein cite a selection of illustrative instances.
Algorithm 1 has also been studied in [18], where it served as a preliminary framework for the integration of coalition formation models with the domain of social rankings. Within the context of [18], the authors explore alternate models of coalition formation, wherein rational agents possess preferences over partitions of the agent set. In this framework, agents take into consideration both the relative ranking of the coalitions they are part of, as determined by a power relation, and their position in the social ranking computed within each element of a partition. More sophisticated algorithms presented in [18] take in as input, in addition to a power relation, the lex-cel to evaluate the position of agents within coalitions.
Other promising directions for the application of social rankings are in the field of the value alignment problem [30] where, given a collection of candidate norms, a decision-maker wants to select the set of norms (called a norm system) that is best “aligned” with some predefined moral values. Given the preferences of the decision-maker, over moral values in a value system, and the relations of promotion and demotion between norms and moral values (also interpreted as norm features) some adaptations of the lex-cel are used in this framework to generate a ranking over single norms from preferences over sets of norm features.
The social ranking problem has also been studied under slightly different perspectives. An axiomatic study on a restricted domain of coalitions has been presented in [31]. Computational aspects via numerical simulations of the CP-majority have been analyzed in [32].
Author Contributions
Conceptualization, F.F., S.M. and J.S.; Methodology, S.M.; Software, F.F. and J.S.; Writing—original draft, F.F. and S.M.; Writing—review & editing, F.F., S.M. and J.S. All authors have read and agreed to the published version of the manuscript.
Funding
Financial support from the ANR project THEMIS (ANR-20-CE23-0018) is gratefully acknowledged.
Data Availability Statement
No new data were created.
Acknowledgments
We are grateful to the reviewers for their suggestions to modify a first version of this manuscript.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Rodolfo, M.; Gnecco, G. Measuring players’ importance in basketball using the generalized Shapley value. Ann. Oper. Res. 2023, 325, 441–465. [Google Scholar]
- Martínez, R.; Sánchez-Soriano, J. Mathematical indices for the influence of risk factors on the lethality of a disease. J. Math. Biol. 2021, 83, 74. [Google Scholar] [CrossRef] [PubMed]
- Rafferty, J.; Watkins, A.; Lyons, J.; Lyons, R.A.; Akbari, A.; Peek, N.; Jalali-najafabadi, F.; Ba Dhafari, T.; Pate, A.; Martin, G.P.; et al. Ranking sets of morbidities using hypergraph centrality. J. Biomed. Inform. 2021, 122, 103916. [Google Scholar] [CrossRef] [PubMed]
- Hunter, A.; Konieczny, S. On the measure of conflicts: Shapley inconsistency values. Artif. Intell. 2010, 174, 1007–1026. [Google Scholar] [CrossRef]
- Gomez, D.; González-Arangüena, E.; Manuel, C.; Owen, G.; del Pozo, M.; Tejada, J. Centrality and power in social networks: A game theoretic approach. Math. Soc. Sci. 2003, 46, 27–54. [Google Scholar] [CrossRef]
- Lindelauf, R.H.A.; Hamers, H.J.M.; Husslage, B.G.M. Cooperative game theoretic centrality analysis of terrorist networks: The cases of jemaah is-lamiyah and al qaeda. Eur. J. Oper. Res. 2013, 229, 230–238. [Google Scholar] [CrossRef]
- Labreuche, C.; Fossier, S. Explaining multi-criteria decision aiding models with an extended shapley value. In Proceedings of the 27th International Joint Conference on Artificial Intelligence, Stockholm, Sweden, 13–19 July 2018; pp. 331–339. [Google Scholar]
- Musegaas, M.; Borm, P.E.M.; Quant, M. Three-valued simple games. Theory Decis. 2018, 85, 201–224. [Google Scholar] [CrossRef]
- Fritz, F.; Staudacher, J.; Stefano, M. Socialranking: Social Ranking Solutions for Power Relations on Coalitions. R Package Version 1.0.1. Available online: https://cran.r-project.org/package=socialranking (accessed on 1 October 2023).
- Algaba, E.; Moretti, S.; Rémila, E.; Solal, P. Lexicographic solutions for coalitional rankings. Soc. Choice Welf. 2021, 57, 817–849. [Google Scholar] [CrossRef] [PubMed]
- Béal, S.; Rémila, E.; Solal, P. Lexicographic solutions for coalitional rankings based on individual and collective performances. J. Math. Econ. 2022, 102, 102738. [Google Scholar] [CrossRef]
- Bernardi, G.; Lucchetti, R.; Moretti, S. Ranking objects from a preference relation over their subsets. Soc. Choice Welf. 2019, 52, 589–606. [Google Scholar] [CrossRef]
- Allouche, T.; Escoffier, B.; Moretti, S.; Oztürk, M. Social Ranking Manipulability for the CP-Majority, Banzhaf and Lexicographic Excellence Solutions. In Proceedings of the 29th International Conference on Artificial Intelligence (IJCAI-PRICAI-20), Yokohama, Japan, 7–15 January 2021; pp. 17–23. [Google Scholar]
- Haret, A.; Khani, H.; Moretti, S.; Oztürk, M. Ceteris Paribus Majority for social ranking. In Proceedings of the 27th International Joint Conference on Artificial Intelligence (IJCAI-ECAI-18), Stockholm, Sweden, 13–19 July 2018; pp. 303–309. [Google Scholar]
- Khani, H.; Moretti, S.; Oztürk, M. An Ordinal Banzhaf Index for Social Ranking. In Proceedings of the 28th International Joint Conference on Artificial Intelligence (IJCAI 2019), Macao, China, 10–16 August 2019; pp. 378–384. [Google Scholar]
- Béal, S.; Ferrières, S.; Solal, P. A core-partition ranking solution to coalitional ranking problems. Group Decis. Negot. 2023, 32, 965–985. [Google Scholar] [CrossRef]
- Doignon, J.-P.; Moretti, S.; Oztürk, M. On the ordinal invariance of power indices on coalitional games. In Proceedings of the 31st International Joint Conference on Artificial Intelligence, Vienna, Autriche, 23–29 July 2022; pp. 258–264. [Google Scholar]
- Lucchetti, R.; Moretti, S.; Rea, T. Coalition formation games and social ranking solutions. In Proceedings of the 21st International Conference on Autonomous Agents and Multiagent Systems (AAMAS 2022), Auckland, New Zealand, 9–13 May 2022. [Google Scholar]
- May, K.O. A set of independent necessary and sufficient conditions for simple majority decision. Econom. J. Econom. Soc. 1952, 20, 680–684. [Google Scholar] [CrossRef]
- Banzhaf, J.F., III. Weighted voting doesn’t work: A mathematical analysis. Rutgers Law Rev. 1964, 19, 317. [Google Scholar]
- Copeland, A.H. A Reasonable Social Welfare Function; Technical report, mimeo; University of Michigan: Ann Arbor, MI, USA, 1951. [Google Scholar]
- Carreras, F.; Freixas, J. On ordinal equivalence of power measures given by regular semivalues. Math. Soc. Sci. 2008, 55, 221–234. [Google Scholar] [CrossRef]
- Lucchetti, R.; Radrizzani, P.; Munarini, E. A new family of regular semivalues and applications. Int. J. Game Theory 2010, 40, 1–21. [Google Scholar] [CrossRef]
- Owen, G. Game Theory; Academic Press: New York, NY, USA, 1995. [Google Scholar]
- Shapley, L.S. A value for n-person games. In Contributions to the Theory of Games II; Kuhn, H., Tucker, A.W., Eds.; Princeton University Press: Princeton, NJ, USA, 1953; pp. 307–317. [Google Scholar]
- Lucchetti, R.; Moretti, S.; Patrone, F. Ranking sets of interacting objects via semivalues. Top 2015, 23, 567–590. [Google Scholar] [CrossRef]
- Dreze, J.H.; Greenberg, J. Hedonic coalitions: Optimality and stability. Econom. J. Econom. Soc. 1980, 48, 987–1003. [Google Scholar] [CrossRef]
- Iehlé, V. The core-partition of a hedonic game. Math. Soc. Sci. 2007, 54, 176–185. [Google Scholar] [CrossRef][Green Version]
- Farrell, J.; Scotchmer, S. Partnerships. Q. J. Econ. 1988, 103, 279–297. [Google Scholar] [CrossRef]
- Serramia, M.; Lopez-Sanchez, M.; Rodriguez-Aguilar, J.A. A qualitative approach to composing value-aligned norm systems. In Proceedings of the 19th International Conference on Autonomous Agents and MultiAgent Systems (AAMAS 2020), Auckland, New Zealand, 9–13 May 2020; pp. 1233–1241. [Google Scholar]
- Suzuki, T.; Horita, M. Social ranking problem based on rankings of restricted coalitions. In Proceedings of the International Conference on Group Decision and Negotiation, Toronto, ON, Canada, 6–10 June 2021; pp. 55–67. [Google Scholar]
- Fayard, N.; Oztürk, M. Ordinal social ranking: Simulation for cp-majority rule. In Proceedings of the DA2PL’2018 (From Multiple Criteria Decision Aid to Preference Learn-ing), Poznan, Pologne, 22–23 November 2018. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).