A Generalized Log Gamma Approach: Theoretical Contributions and an Application to Companies’ Life Expectancy
Abstract
1. Introduction
2. Generalized Log-Gamma Distribution: Theoretical Framework and Complements
2.1. Generalized Log-Gamma Density Function
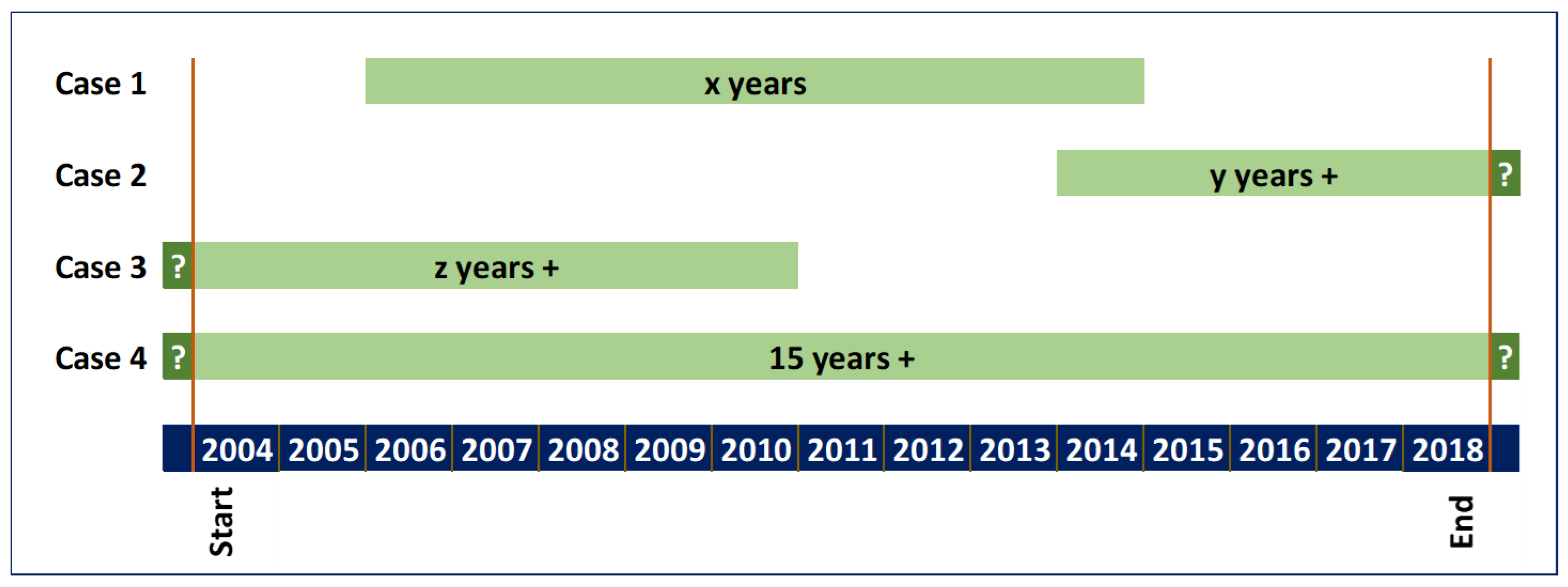
- Case 1: , is increasing with , and assume all values from to
- Case 2: , decreases with , and assume all values from to
2.2. Particular Cases of Generalized Log Gamma Distribution
2.2.1. Generalized Gamma Distribution
2.2.2. Gamma Distribution
2.2.3. Weibull Distribution
2.2.4. Log-Normal Distribution
2.3. Theoretical Contributions to the Study of the Generalized Log Gamma Distribution
2.3.1. Theoretical Contributions
- Case 1:
- Case 2:
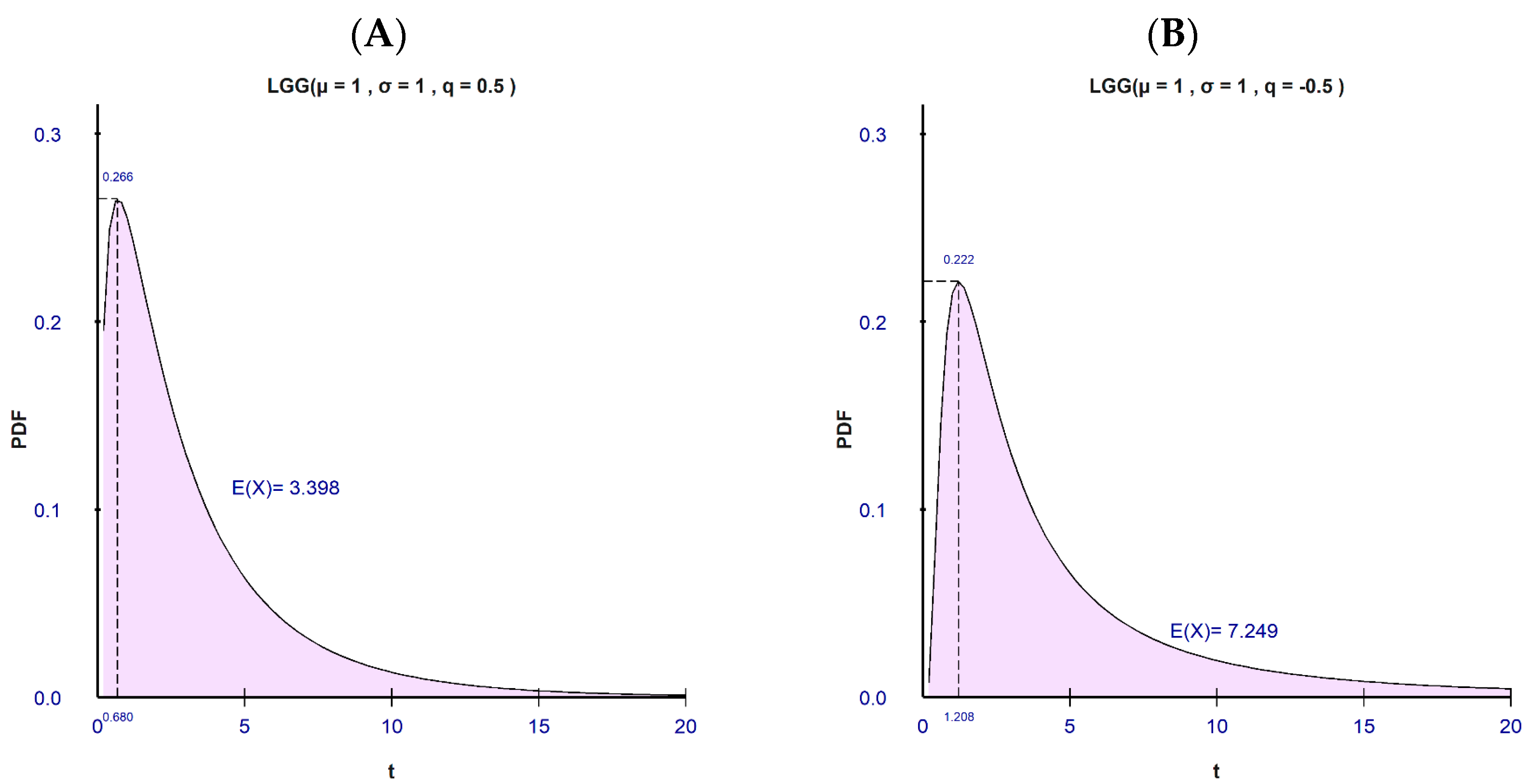
2.3.2. Density function: Graphical Representations
- First situation:
- Second situation:
- Third situation:
2.3.3. Expected Value, Variance, and Mode as Functions of the Shape Parameter
3. Data and Methods
3.1. Data
3.2. Methods: Estimation Methodology with Censored Data
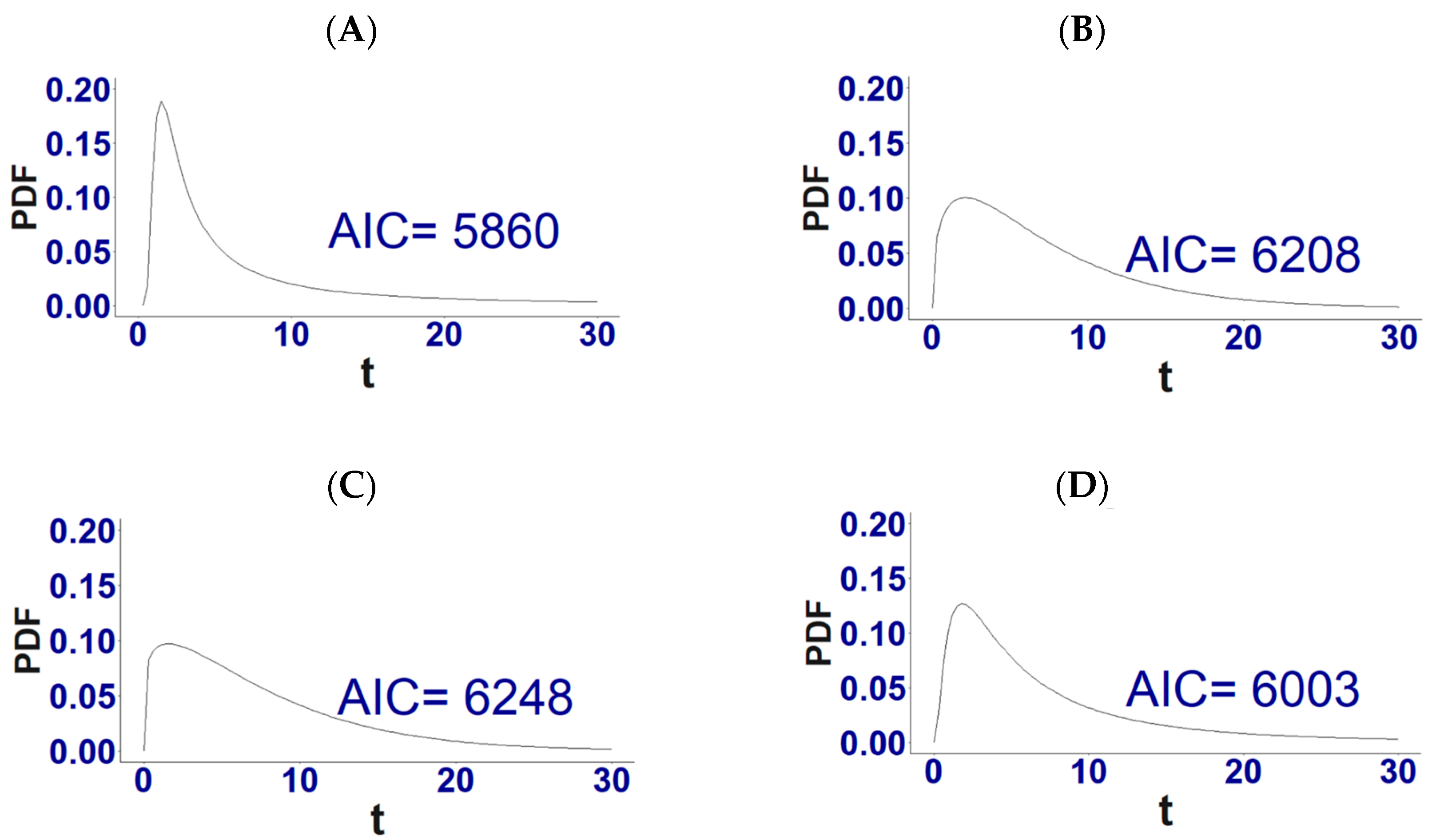
4. Results
5. Discussion and Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Altman, E.I. Why Businesses Fail. J. Bus. Strategy 1983, 3, 15–21. [Google Scholar] [CrossRef]
- Baumard, P.; Starbuck, W.H. Learning from Failures: Why It May Not Happen. Long Range Plann 2005, 38, 281–298. [Google Scholar] [CrossRef]
- Benedettini, O.; Neely, A.; Swink, M. Why Do Servitized Firms Fail? A Risk-Based Explanation. Int. J. Oper. Prod. Manag. 2015, 35, 946–979. [Google Scholar] [CrossRef]
- Mourdoukoutas, P.; Stefanidis, A. Why Companies Succeed or Fail: Corporate Cycles and Firm Function in Tandem. J. Bus. Strategy 2023, 44, 76–86. [Google Scholar] [CrossRef]
- Mata, J.; Portugal, P. Life Duration of New Firms. J. Ind. Econ. 1994, 42, 227–245. [Google Scholar] [CrossRef]
- Mata, J.; Portugal, P.; Guimarães, P. The Survival of New Plants: Start-up Conditions and Post-Entry Evolution. Int. J. Ind. Organ. 1995, 13, 459–481. [Google Scholar] [CrossRef]
- Mata, J.; Portugal, P. Patterns of Entry, Post-Entry Growth and Survival. Small Bus. Econ. 2004, 22, 283–298. [Google Scholar] [CrossRef]
- Geroski, P.A.; Mata, J.; Portugal, P. Founding Conditions and the Survival of New Firms. Strateg. Manag. J. 2010, 31, 510–529. [Google Scholar] [CrossRef]
- Reis, P.N.; Augusto, M.G. What Is a Firm’s Life Expectancy? Empirical Evidence in the Context of Portuguese Companies. J. Bus. Valuat. Econ. Loss Anal. 2015, 10, 45–75. [Google Scholar] [CrossRef]
- Daepp, M.I.G.; Hamilton, M.J.; West, G.B.; Bettencourt, L.M.A. The Mortality of Companies. J. R. Soc. Interface 2015, 12, 20150120. [Google Scholar] [CrossRef]
- Sharma, K.; Dixit, M.R. Live Long and Prosper: The Search for Business Longevity. In Strategic Direction; Emerald Group Publishing Ltd.: Bingley, UK, 2017; pp. 1–3. [Google Scholar] [CrossRef]
- Clark, D. Average Company Lifespan on Standard&Poor’s 500 Index. Available online: https://www.statista.com/statistics/1259275/average-company-lifespan/ (accessed on 10 June 2021).
- Stacy, E.W. A Generalization of the Gamma Distribution. Ann. Math. Stat. 1962, 33, 1187–1192. [Google Scholar] [CrossRef]
- Stacy, E.W.; Mihram, G.A. Parameter Estimation for a Generalized Gamma Distribution. Technometrics 1965, 7, 349–358. [Google Scholar] [CrossRef]
- Prentice, R.L. A Log Gamma Model and Its Maximum Likelihood Estimation. Biometrika 1974, 61, 539–544. [Google Scholar] [CrossRef]
- Bourguignon, M.; Lima, M.d.C.S.; Leão, J.; Nascimento, A.D.C.; Pinho, L.G.B.; Cordeiro, G.M. A New Generalized Gamma Distribution with Applications. Am. J. Math. Manag. Sci. 2015, 34, 309–342. [Google Scholar] [CrossRef]
- Lahcene, B. A New Extended-Gamma Family of Distributions: Properties and Applications. J. Appl. Math. Comput. 2021, 5, 9–17. [Google Scholar] [CrossRef]
- Lawless, J.F. Inference in the Generalized Gamma and Log Gamma Distributions. Technometrics 1980, 22, 409–419. [Google Scholar] [CrossRef]
- DiCiccio, T.J. Approximate Inference for the Generalized Gamma Distribution. Technometrics 1987, 29, 33–40. [Google Scholar] [CrossRef]
- Agostinelli, C.; Marazzi, A.; Yohai, V.J. Robust Estimators of the Generalized Log-Gamma Distribution. Technometrics 2014, 56, 92–101. [Google Scholar] [CrossRef]
- de Pascoa, M.A.R.; Ortega, E.M.M.; Cordeiro, G.M. The Kumaraswamy Generalized Gamma Distribution with Application in Survival Analysis. Stat. Methodol. 2011, 8, 411–433. [Google Scholar] [CrossRef]
- Kaneko, R. Elaboration of the Coale-McNeil Nuptiality Model as The Generalized Log Gamma Distribution: A New Identity and Empirical Enhancements. Demogr. Res. 2003, 9, 223–262. [Google Scholar] [CrossRef]
- Ortega, E.M.; Cancho, V.G.; Lachos, V.H. A Generalized Log-Gamma Mixture Model for Cure Rate: Estimation and Sensitivity Analysis. Indian J. Stat. 2009, 71-B, 1–29. [Google Scholar]
- Cordeiro, G.M.; Ortega, E.M.M.; Silva, G.O. The Exponentiated Generalized Gamma Distribution with Application to Lifetime Data. J. Stat. Comput. Simul. 2011, 81, 827–842. [Google Scholar] [CrossRef]
- Ramos, P.L.; Nascimento, D.C.; Ferreira, P.H.; Weber, K.T.; Santos, T.E.G.; Louzada, F. Modeling Traumatic Brain Injury Lifetime Data: Improved Estimators for the Generalized Gamma Distribution under Small Samples. PLoS ONE 2019, 14, e0221332. [Google Scholar] [CrossRef] [PubMed]
- Ramos, P.L.; Mota, A.L.; Ferreira, P.H.; Ramos, E.; Tomazella, V.L.D.; Louzada, F. Bayesian Analysis of the Inverse Generalized Gamma Distribution Using Objective Priors. J. Stat. Comput. Simul. 2021, 91, 786–816. [Google Scholar] [CrossRef]
- Shang, X.; Ng, H.K.T. On Parameter Estimation for the Generalized Gamma Distribution Based on Left-truncated and Right-censored Data. Comput. Math. Methods 2021, 3, e1091. [Google Scholar] [CrossRef]
- Ahmed, E.A.; El-Morshedy, M.; Al-Essa, L.A.; Eliwa, M.S. Statistical Inference on the Entropy Measures of Gamma Distribution under Progressive Censoring: EM and MCMC Algorithms. Mathematics 2023, 11, 2298. [Google Scholar] [CrossRef]
- Tovar-Falón, R.; Martínez-Flórez, G.; Bolfarine, H. Modelling Asymmetric Data by Using the Log-Gamma-Normal Regression Model. Mathematics 2022, 10, 1199. [Google Scholar] [CrossRef]
- Prataviera, F.; Ortega, E.M.M.; Cordeiro, G.M.; Braga, A.d.S. The Heteroscedastic Odd Log-Logistic Generalized Gamma Regression Model for Censored Data. Commun. Stat. Simul. Comput. 2019, 48, 1815–1839. [Google Scholar] [CrossRef]
- Prataviera, F.; Ortega, E.M.M.; Cordeiro, G.M.; Pescim, R.R.; Verssani, B.A.W. A New Generalized Odd Log-Logistic Flexible Weibull Regression Model with Applications in Repairable Systems. Reliab. Eng. Syst. Saf. 2018, 176, 13–26. [Google Scholar] [CrossRef]
- Alzaatreh, A.; Carl, L.; Famoye, F. Family of Generalized Gamma Distributions: Properties and Applications. Hacet. J. Math. Stat. 2016, 45, 869–886. [Google Scholar] [CrossRef]
- Rashid, A.; Ahmad, Z.; Jan, T.R. A New Lifetime Distribution for Series System: Model, Properties and Application. J. Mod. Appl. Stat. Methods 2018, 17, 43–67. [Google Scholar] [CrossRef]
- Cooray, K.; Ananda, M.M.A. A Generalization of the Half-Normal Distribution with Applications to Lifetime Data. Commun. Stat. Theory Methods 2008, 37, 1323–1337. [Google Scholar] [CrossRef]
- Cordeiro, G.M.; Alizadeh, M.; Pescim, R.R.; Ortega, E.M.M. The Odd Log-Logistic Generalized Half-Normal Lifetime Distribution: Properties and Applications. Commun. Stat. Theory Methods 2017, 46, 4195–4214. [Google Scholar] [CrossRef]
- Okorie, I.E.; Akpanta, A.C.; Ohakwe, J.; Chikezie, D.C.; Onyemachi, C.U.; Obi, E.O. The Adjusted Log-Logistic Generalized Exponential Distribution with Application to Lifetime Data. Int. J. Stat. Probab. 2017, 5, 1. [Google Scholar] [CrossRef][Green Version]
- Lancaster, H.O. Forerunners of the Pearson Χ2. Aust. N. Z. J. Stat. 1966, 8, 117–126. [Google Scholar] [CrossRef]
- Johnson, N.L.; Kotz, S.; Balakrishnan, N. Continuous Univariate Distributions, 2nd ed.; John Wiley & Sons: Hoboken, NJ, USA, 1995; Volume 2. [Google Scholar]
- Abramowitz, M.; Stegun, I.A.; Romer, R.H. Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables; American Association of Physics Teachers: College Park, MD, USA, 1988. [Google Scholar]
- Bartlett, M.S.; Kendall, D.G. The Statistical Analysis of Variance-Heterogeneity and the Logarithmic Transformation. Suppl. J. R. Stat. Soc. 1946, 8, 128–138. [Google Scholar] [CrossRef]
- Hager, H.W.; Bain, L.J. Inferential Procedures for the Generalized Gamma Distribution. J. Am. Stat. Assoc. 1970, 65, 1601–1609. [Google Scholar] [CrossRef]
- Amoroso, L. Ricerche Intorno Alla Curva Dei Redditi. Ann. Mat. Pura Appl. 1925, 2, 123–159. [Google Scholar] [CrossRef]
- Farewell, V.T.; Prentice, R.L. A Study of Distributional Shape in Life Testing. Technometrics 1977, 19, 69–75. [Google Scholar] [CrossRef]
- Lawless, J.F. Statistical Models and Methods for Lifetime Data; John Wiley & Sons: Hoboken, NJ, USA, 2011. [Google Scholar]
- Wickham, H.; Chang, W.; Wickham, M.H. Package ‘Ggplot2′: Create Elegant Data Visualisations Using the Grammar of Graphics; R Foundation for Statistical Computing: Vienna, Austria, 2016; pp. 1–189. [Google Scholar]
- Therneau, T. A Package for Survival Analysis in R; R Foundation for Statistical Computing: Vienna, Austria, 2023. [Google Scholar]
- Jackson, C.; Metcalfe, P.; Amdahl, J.; Jackson, M.C. Package ‘Flexsurv’: Flexible Parametric Survival and Multi-State Models; R Foundation for Statistical Computing: Vienna, Austria, 2023. [Google Scholar]
- Mandel, M. Simulation-Based Confidence Intervals for Functions with Complicated Derivatives. Am. Stat. 2013, 67, 76–81. [Google Scholar] [CrossRef]
- INE. Documento Metodológico—Sistema de Contas Integradas das Empresas. Available online: https://smi.ine.pt/DocumentacaoMetodologica/Detalhes/1211 (accessed on 15 June 2021).
- Prinja, S.; Gupta, N.; Verma, R. Censoring in Clinical Trials: Review of Survival Analysis Techniques. Indian J. Community Med. 2010, 35, 217. [Google Scholar] [CrossRef] [PubMed]
- Patti, S.; Biganzoli, E.; Boracchi, P. Review of the Maximum Likelihood Functions for Right Censored Data. A New Elementary Derivation; COBRA Preprint Series; The Berkeley Electronic Press: Berkeley, CA, USA, 2007. [Google Scholar]
- Akaike, H. A New Look at the Statistical Model Identification. In Selected Papers of Hirotugu Akaike; Parzen, E., Tanabe, K., Kitagawa, G., Eds.; Springer: New York, NY, USA, 1998; pp. 215–222. [Google Scholar] [CrossRef]




| Designation | Number |
|---|---|
| Companies with observed life expectations | 1010 |
| Companies with censored life expectations | 912 |
| Censored life expectations—Case 2 | (714) |
| Censored life expectations—Case 3 | (150) |
| Censored life expectations—Case 4 | (48) |
| Count | Mean | Q1 | Median | Q3 | Max. |
|---|---|---|---|---|---|
| 1010 | 3.3 | 2 | 3 | 4 | 14 |
| Times of Activity (Censored) | Number | ||
|---|---|---|---|
| Case 2 | Case 3 | Case 4 | |
| 1+ | 126 | 26 | 0 |
| 2+ | 107 | 22 | 0 |
| 3+ | 88 | 7 | 0 |
| 4+ | 76 | 24 | 0 |
| 5+ | 56 | 17 | 0 |
| 6+ | 55 | 8 | 0 |
| 7+ | 41 | 3 | 0 |
| 8+ | 49 | 8 | 0 |
| 9+ | 24 | 12 | 0 |
| 10+ | 17 | 7 | 0 |
| 11+ | 33 | 8 | 0 |
| 12+ | 10 | 4 | 0 |
| 13+ | 10 | 3 | 0 |
| 14+ | 14 | 1 | 0 |
| 15+ | 8 | 0 | 48 |
| Generalized Log Gamma | Gamma | Weibull | Log Normal | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| PAR | EST | LCL | UCL | PAR | EST | LCL | UCL | PAR | EST | LCL | UCL | PAR | EST | LCL | UCL |
| 0.92 | 0.78 | 1.05 | β | 5.16 | 4.63 | 5.74 | β | 7.87 | 7.45 | 8.30 | meanlog | 1.65 | 1.59 | 1.70 | |
| 0.93 | 0.86 | 1.00 | γ | 1.41 | 1.31 | 1.52 | n | 1.18 | 1.12 | 1.23 | sdlog | 1.02 | 0.98 | 1.07 | |
| −1.69 | −2.02 | −1.36 | - | - | - | - | - | - | - | - | - | - | - | - | |
| Time | Generalized Log Gamma | Gamma | Weibull | Log Normal | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| LCL | EST | UCL | LCL | EST | UCL | LCL | EST | UCL | LCL | EST | UCL | |
| 1 | 0.96 | 0.97 | 0.97 | 0.92 | 0.93 | 0.94 | 0.91 | 0.92 | 0.92 | 0.94 | 0.95 | 0.95 |
| 2 | 0.77 | 0.79 | 0.81 | 0.82 | 0.83 | 0.85 | 0.80 | 0.82 | 0.83 | 0.81 | 0.82 | 0.84 |
| 3 | 0.63 | 0.65 | 0.67 | 0.72 | 0.73 | 0.75 | 0.71 | 0.72 | 0.74 | 0.69 | 0.70 | 0.72 |
| 4 | 0.53 | 0.55 | 0.58 | 0.62 | 0.64 | 0.66 | 0.62 | 0.64 | 0.66 | 0.58 | 0.60 | 0.62 |
| 5 | 0.47 | 0.49 | 0.51 | 0.53 | 0.55 | 0.57 | 0.54 | 0.56 | 0.58 | 0.49 | 0.52 | 0.54 |
| 6 | 0.41 | 0.44 | 0.46 | 0.45 | 0.47 | 0.50 | 0.46 | 0.48 | 0.50 | 0.42 | 0.44 | 0.47 |
| 7 | 0.37 | 0.40 | 0.42 | 0.38 | 0.41 | 0.43 | 0.40 | 0.42 | 0.44 | 0.36 | 0.39 | 0.41 |
| 8 | 0.34 | 0.37 | 0.39 | 0.32 | 0.35 | 0.37 | 0.34 | 0.36 | 0.38 | 0.31 | 0.34 | 0.36 |
| 9 | 0.31 | 0.34 | 0.36 | 0.27 | 0.29 | 0.32 | 0.29 | 0.31 | 0.33 | 0.27 | 0.30 | 0.32 |
| 10 | 0.29 | 0.32 | 0.34 | 0.23 | 0.25 | 0.27 | 0.24 | 0.27 | 0.29 | 0.24 | 0.26 | 0.28 |
| 11 | 0.27 | 0.30 | 0.33 | 0.19 | 0.21 | 0.24 | 0.20 | 0.23 | 0.25 | 0.21 | 0.23 | 0.25 |
| 12 | 0.26 | 0.28 | 0.31 | 0.16 | 0.18 | 0.20 | 0.17 | 0.19 | 0.22 | 0.19 | 0.21 | 0.23 |
| 13 | 0.24 | 0.27 | 0.30 | 0.13 | 0.15 | 0.17 | 0.14 | 0.16 | 0.19 | 0.17 | 0.19 | 0.21 |
| 14 | 0.23 | 0.26 | 0.28 | 0.11 | 0.13 | 0.15 | 0.12 | 0.14 | 0.16 | 0.15 | 0.17 | 0.19 |
| 15 | 0.22 | 0.25 | 0.27 | 0.09 | 0.11 | 0.13 | 0.10 | 0.12 | 0.14 | 0.13 | 0.15 | 0.17 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dias Gonçalves, J.H.; Ferreira Gomes, J.J.; Rubio, L.; Ramos, F.R. A Generalized Log Gamma Approach: Theoretical Contributions and an Application to Companies’ Life Expectancy. Mathematics 2023, 11, 4792. https://doi.org/10.3390/math11234792
Dias Gonçalves JH, Ferreira Gomes JJ, Rubio L, Ramos FR. A Generalized Log Gamma Approach: Theoretical Contributions and an Application to Companies’ Life Expectancy. Mathematics. 2023; 11(23):4792. https://doi.org/10.3390/math11234792
Chicago/Turabian StyleDias Gonçalves, José H., João J. Ferreira Gomes, Lihki Rubio, and Filipe R. Ramos. 2023. "A Generalized Log Gamma Approach: Theoretical Contributions and an Application to Companies’ Life Expectancy" Mathematics 11, no. 23: 4792. https://doi.org/10.3390/math11234792
APA StyleDias Gonçalves, J. H., Ferreira Gomes, J. J., Rubio, L., & Ramos, F. R. (2023). A Generalized Log Gamma Approach: Theoretical Contributions and an Application to Companies’ Life Expectancy. Mathematics, 11(23), 4792. https://doi.org/10.3390/math11234792








