A Novel Fuzzy Unsupervised Quadratic Surface Support Vector Machine Based on DC Programming: An Application to Credit Risk Management
Abstract
:1. Introduction
- In this study, we propose a fuzzy unsupervised quadratic surface support vector machine for credit risk assessment. This kernel-free unsupervised learning method can solve classification problems on unlabeled credit datasets. The algorithm was tested on several public credit datasets, and its performance was compared with the previously mentioned unsupervised SVM-based methods. The results showed that the proposed method outperformed unsupervised classification methods in terms of accuracy and robustness;
- For weakening outlier points, we propose a fuzzy membership method based on Tomek link method. In unlabeled datasets, this method effectively reduces the impact of outliers and noise points on decision-making. With this fuzzy membership function, we can distinguish noise points that belong to different classes in unlabeled samples based on their connections and relationships;
- After proving its boundness and convergence, a new DC algorithm (DCA) was developed to implement the proposed nonconvex model on numerous artificial and real-world benchmark datasets.
2. Review of DC Programming and the Unsupervised Quadratic Surface Support Vector Machine
2.1. DC Programming and DCA
- , where g and h are convex functions;
- , where and C are convex functions.
2.2. Unsupervised Quadratic Surface Support Vector Machine
3. Proposed Method
3.1. Fuzzy Membership Function
3.2. Fuzzy Unsupervised Quadratic Surface Support Vector Machine
3.3. Decomposition Algorithm
- Step 1: Set an initial estimation and .
- Step 2: Calculate .
- Step 3: Calculate .
- Step 4: If , then set and go to Step 2; otherwise stop and output as an optimal solution.
- 1.
- The optimal value of the problem is finite;
- 2.
- The sequences and in the algorithm are bounded;
- 3.
- Each limit optimal point of sequence is a local optimal solution of the problem in (11).
4. Results
4.1. Experimental Setup
- TP (True Positive) represents the number of positive class samples that were accurately predicted by the classifier;
- FN (False Negative) means the number of positive class samples that the classifier mistakenly predicted to belong to the negative class;
- FP (False Positive) represents instances of the negative class that were incorrectly identified as members of the positive class by the classifier;
- TN (True Negative) corresponds to the number of negative class samples that were correctly identified by the classifier.
4.2. Experiment Results
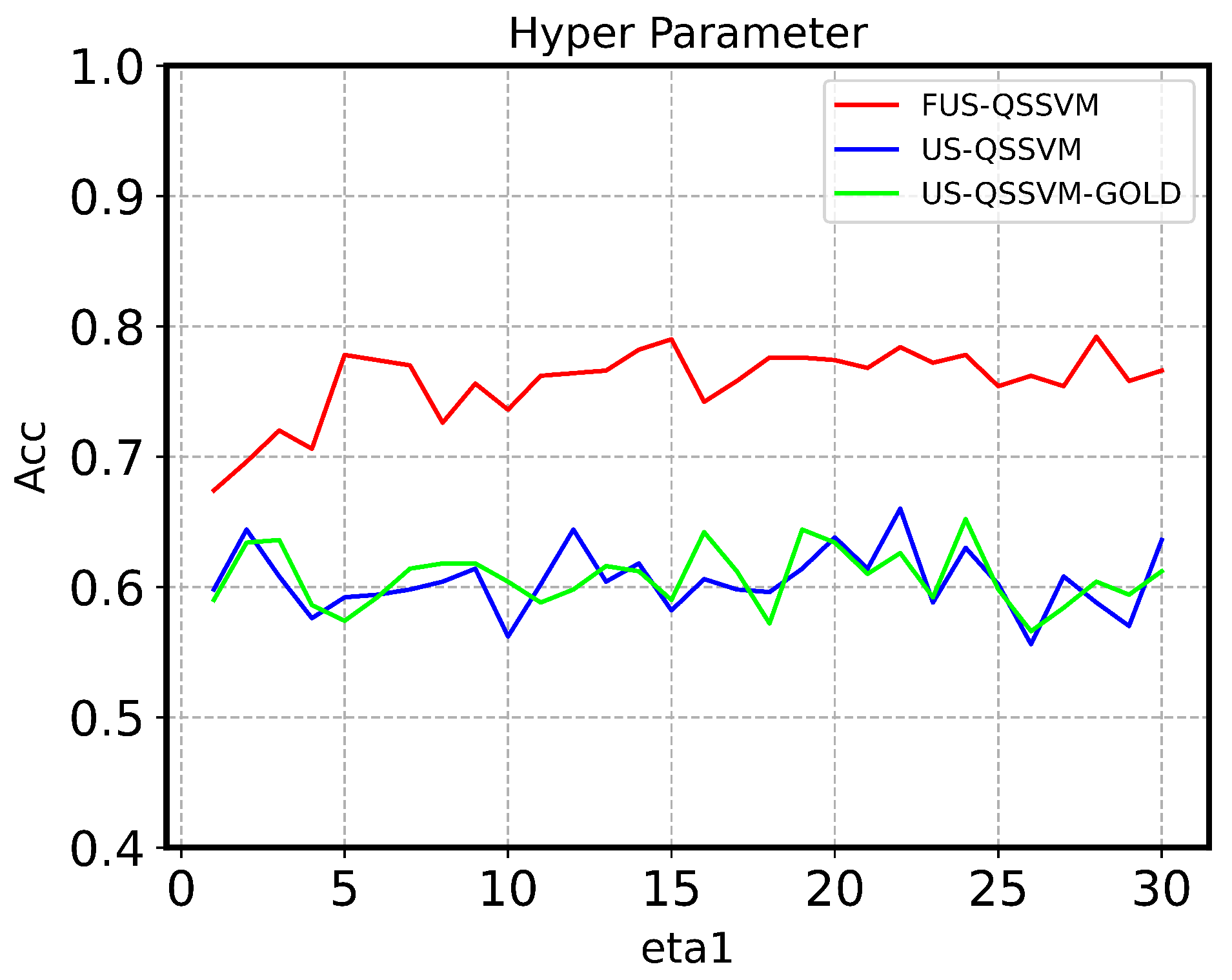
4.3. Fuzzy Membership
5. Conclusions
- Drawing on comprehensive numerical findings, the proposed FUS-QSSVM approach is in strong competition with other well-known classification techniques in credit datasets, including three SVM-based methods and K-means. A key advantage of the proposed method is its ability to benefit from the high classification accuracy of SVM models. In addition, it minimizes the shortcomings associated with classification algorithms based on SVMs. These include factors such as unstable results due to random initialization, reduced effectiveness due to kernel dependencies, and noise points and outliers;
- The fuzzy join function optimizes the hyperplane position and shape by reducing noise points and outliers. Therefore, this enhancement bolsters both the accuracy and robustness of the model. Application of this technique is particularly useful when the dataset contains outliers or uneven distributions between two classes. By minimizing the impact of such data points, the model captures the underlying structure of the data. As a result, more robust predictions of the proposed model can be made about default applicants;
- As a result of the DCA design, the nonconvex FUS-QSSVM model was significantly more efficient in solving. In addition, this reduces reliance on initial values and tuning parameters, thus improving calculation efficiency.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
- By the definition, is non-negative and . Moreover, there exist a constant such that . Therefore, . Hence, the minimum of is finite.
- The sequence is a solution with ; hence, the sequence is bounded by the constraint . Furthermore, the sequence is bounded. Then, we can prove that the sequences and are bounded. It is simple to verify that the objective value of the problem is finite. There exists a constant for all k such that . Since , , and for all , thenMoreover, since and for all , it is obvious that the sequence is bounded. Overall, the sequences and in the algorithm are bounded.
References
- Cortes, C.; Vapnik, V. Support-Vector Networks. Mach. Learn. 1995, 20, 273–297. [Google Scholar] [CrossRef]
- Almotairi, S.; Badr, E.; Abdul, S.M.; Ahmed, H. Breast Cancer Diagnosis Using a Novel Parallel Support Vector Machine with Harris Hawks Optimization. Mathematics 2023, 11, 3251. [Google Scholar] [CrossRef]
- Jovanovic, D.; Antonijevic, M.; Stankovic, M.; Zivkovic, M.; Tanaskovic, M.; Bacanin, N. Tuning Machine Learning Models Using a Group Search Firefly Algorithm for Credit Card Fraud Detection. Mathematics 2022, 10, 2272. [Google Scholar] [CrossRef]
- Shen, F.; Yang, Z.Y.; Zhao, X.Z.; Lan, D. Reject inference in credit scoring using a three-way decision and safe semi-supervised support vector machine. Inf. Sci. 2022, 606, 614–627. [Google Scholar] [CrossRef]
- Endri, E.; Kasmir, K.; Syarif, A. Delisting sharia stock prediction model based on financial information: Support Vector Machine. Decis. Sci. Lett. 2020, 9, 207–214. [Google Scholar] [CrossRef]
- Harris, T. Quantitative credit risk assessment using support vector machines: Broad versus Narrow default definitions. Expert Syst. Appl. 2013, 40, 4404–4413. [Google Scholar] [CrossRef]
- Twala, B. Multiple classifier application to credit risk assessment. Expert Syst. Appl. 2010, 37, 3326–3336. [Google Scholar] [CrossRef]
- Luo, J.; Yan, X.; Tian, Y. Unsupervised quadratic surface support vector machine with application to credit risk assessment. Eur. J. Oper. Res. 2020, 280, 1008–1017. [Google Scholar] [CrossRef]
- Camastra, F.; Verri, A. A novel kernel method for clustering. IEEE Trans. Pattern Anal. Mach. Intell. 2005, 27, 801–805. [Google Scholar] [CrossRef]
- Bicego, M.; Figueiredo, M.A. Soft clustering using weighted one-class support vector machines. Pattern Recognit. 2009, 42, 27–32. [Google Scholar] [CrossRef]
- Luo, J.; Tian, Y.; Yan, X. Clustering via fuzzy one-class quadratic surface support vector machine. Soft Comput. 2017, 21, 5859–5865. [Google Scholar] [CrossRef]
- Fung, G.M.; Mangasarian, O.L. Unsupervised and semisupervised classification via absolute value inequalities. J. Optim. Theory Appl. 2016, 168, 551–558. [Google Scholar] [CrossRef]
- Lin, C.F.; Wang, S.D. Fuzzy support vector machines. IEEE Trans. Neural Netw. 2002, 13, 464–471. [Google Scholar]
- Manh, C.N.; Van, T.N. A method for reducing the number of support vectors in fuzzy support vector machine. In Advanced Computational Methods for Knowledge Engineering: Proceedings of the 4th International Conference on Computer Science, Applied Mathematics and Applications, ICCSAMA 2016, Vienna, Austria, 2–3 May 2016; Springer: Berlin/Heidelberg, Germany, 2016; p. 17. [Google Scholar]
- Lessmann, S.; Baesens, B.; Seow, H.V.; Thomas, L.C. Benchmarking state-of-the-art classification algorithms for credit scoring: An update of research. Eur. J. Oper. Res. 2015, 247, 124–136. [Google Scholar] [CrossRef]
- Hartman, P. On functions representable as a difference of convex functions. Pac. J. Math. 1959, 9, 707–713. [Google Scholar] [CrossRef]
- Tao, P.D. Algorithms for solving a class of nonconvex optimization problems. Methods of subgradients. North-Holl. Math. Stud. 1986, 129, 249–271. [Google Scholar]
- Le Thi, H.A.; Pham Dinh, T. DC programming and DCA: Thirty years of developments. Math. Program. 2018, 169, 5–68. [Google Scholar] [CrossRef]
- Yogendran, D.; Punniyamoorthy, M. Improved bias value and new membership function to enhance the performance of fuzzy support vector Machine. Expert Syst. Appl. 2022, 208, 118003. [Google Scholar]
- Luo, J.; Fang, S.C.; Bai, Y.Q.; Deng, Z.B. Fuzzy quadratic surface support vector machine based on fisher discriminant analysis. J. Ind. Manag. Optim. 2017, 12, 357–373. [Google Scholar] [CrossRef]
- Tomek, I. Two Modifications of CNN. IEEE Trans. Syst. Man Cybern. 1976, 6, 769–772. [Google Scholar]
- Schaible, S.; Shi, J.M. Fractional programming: The sum-of-ratios case. Optim. Methods Softw. 2003, 18, 219–229. [Google Scholar] [CrossRef]
- Pham Dinh, T.; Le Thi, H.A. A DC optimization algorithm for solving the trust-region subproblem. SIAM J. Optim. 1998, 8, 476–505. [Google Scholar]
- Liu, C.; Xie, J.; Zhao, Q.; Xie, Q.W.; Liu, C.Q. Novel evolutionary multi-objective soft subspace clustering algorithm for credit risk assessment. Expert Syst. Appl. 2019, 138, 112827. [Google Scholar] [CrossRef]
- Obermann, L.; Waack, S. Demonstrating non-inferiority of easy interpretable methods for insolvency prediction. Expert Syst. Appl. 2015, 42, 9117–9128. [Google Scholar] [CrossRef]
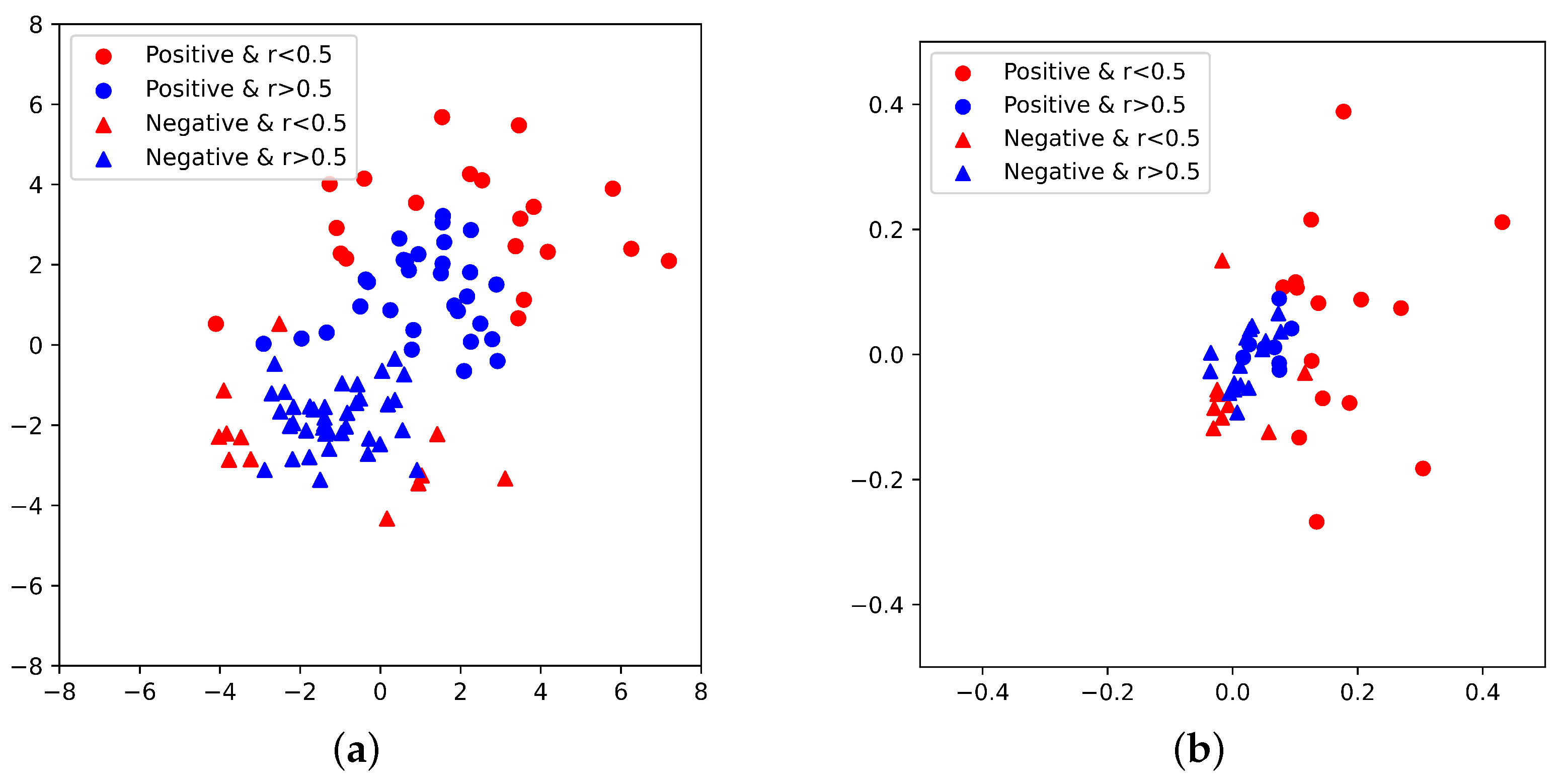
| Dataset | #Instances | #Negative | #Positive | #Attributes |
|---|---|---|---|---|
| Credit approval | 690 | 383 | 307 | 15 |
| Bankruptcy | 100 | 50 | 50 | 5 |
| Japanese 1 | 651 | 357 | 294 | 15 |
| Australian | 690 | 383 | 307 | 14 |
| Prosper 1 | 20,222 | 13,062 | 7160 | 49 |
| Predicted Label | |||
|---|---|---|---|
| Positive | Negative | ||
| Actual label | Positive | TP | FN |
| Negative | FP | TN | |
| Accuracy | Recall | Precision | F1-Measure | ||
|---|---|---|---|---|---|
| Bankruptcy | FUS-QSSVM | 0.7760 | 0.7560 | 0.7876 | 0.7715 |
| US-QSSVM | 0.5860 | 0.5240 | 0.6366 | 0.5748 | |
| US-QSSVM-GOLD | 0.6480 | 0.4600 | 0.7801 | 0.5787 | |
| UAVIC | 0.6000 | 0.5600 | 0.6087 | 0.5833 | |
| K-means | 0.6270 | 0.2540 | 1.000 | 0.4051 | |
| Japanese | FUS-QSSVM | 0.6749 | 0.6418 | 0.6400 | 0.6409 |
| US-QSSVM | 0.5777 | 0.5348 | 0.5308 | 0.5328 | |
| US-QSSVM-GOLD | 0.5841 | 0.5945 | 0.5362 | 0.5638 | |
| UAVIC | 0.6190 | 0.8299 | 0.5520 | 0.6630 | |
| K-means | 0.6410 | 0.7377 | 0.5809 | 0.6500 | |
| Australian | FUS-QSSVM | 0.6891 | 0.8313 | 0.5754 | 0.6801 |
| US-QSSVM | 0.5675 | 0.4442 | 0.4675 | 0.4556 | |
| US-QSSVM-GOLD | 0.5684 | 0.4471 | 0.4486 | 0.4478 | |
| UAVIC | 0.6255 | 0.0640 | 0.9286 | 0.1197 | |
| K-means | 0.6720 | 0.6318 | 0.5846 | 0.6073 | |
| Credit approval | FUS-QSSVM | 0.5531 | 0.5389 | 0.4987 | 0.5180 |
| US-QSSVM | 0.5499 | 0.5009 | 0.4970 | 0.4990 | |
| US-QSSVM-GOLD | 0.5428 | 0.4860 | 0.4885 | 0.4860 | |
| UAVIC | 0.5580 | 0.0052 | 1 | 0.0103 | |
| K-means | 0.6814 | 0.6908 | 0.6275 | 0.6576 | |
| Prosper | FUS-QSSVM | 0.6463 | 0.8322 | 0.5003 | 0.6250 |
| US-QSSVM | 0.5716 | 0.4169 | 0.4282 | 0.4225 | |
| US-QSSVM-GOLD | 0.5975 | 0.3308 | 0.4358 | 0.3761 | |
| UAVIC | 0.5608 | 0.4824 | 0.4399 | 0.4602 | |
| K-means | 0.5406 | 0.3507 | 0.3781 | 0.3638 |
| Accuracy | Recall | Precision | F1-Measure | ||
|---|---|---|---|---|---|
| Japanese | FUS-QSSVM | 0.6749 | 0.6418 | 0.6400 | 0.6409 |
| US-QSSVM | 0.5777 | 0.5348 | 0.5308 | 0.5328 | |
| US-QSSVM-GOLD | 0.5841 | 0.5945 | 0.5362 | 0.5638 | |
| UAVIC | 0.6190 | 0.8299 | 0.5520 | 0.6630 | |
| K-means | 0.6410 | 0.7377 | 0.5809 | 0.6500 | |
| Japanese-5 1 | FUS-QSSVM | 0.6962 | 0.6855 | 0.6578 | 0.6714 |
| US-QSSVM | 0.5560 | 0.4343 | 0.5136 | 0.4706 | |
| US-QSSVM-GOLD | 0.5647 | 0.5727 | 0.5214 | 0.5458 | |
| UAVIC | 0.5837 | 0.3946 | 0.5550 | 0.4613 | |
| K-means | 0.5453 | 0.2112 | 0.2591 | 0.2327 | |
| Japanese-10 2 | FUS-QSSVM | 0.6846 | 0.7034 | 0.6368 | 0.6684 |
| US-QSSVM | 0.5759 | 0.5329 | 0.4583 | 0.4928 | |
| US-QSSVM-GOLD | 0.5536 | 0.4719 | 0.4788 | 0.4753 | |
| UAVIC | 0.6175 | 0.3537 | 0.6380 | 0.4551 | |
| K-means | 0.5716 | 0.1668 | 0.2053 | 0.1840 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yu, T.; Huang, W.; Tang, X. A Novel Fuzzy Unsupervised Quadratic Surface Support Vector Machine Based on DC Programming: An Application to Credit Risk Management. Mathematics 2023, 11, 4661. https://doi.org/10.3390/math11224661
Yu T, Huang W, Tang X. A Novel Fuzzy Unsupervised Quadratic Surface Support Vector Machine Based on DC Programming: An Application to Credit Risk Management. Mathematics. 2023; 11(22):4661. https://doi.org/10.3390/math11224661
Chicago/Turabian StyleYu, Tao, Wei Huang, and Xin Tang. 2023. "A Novel Fuzzy Unsupervised Quadratic Surface Support Vector Machine Based on DC Programming: An Application to Credit Risk Management" Mathematics 11, no. 22: 4661. https://doi.org/10.3390/math11224661
APA StyleYu, T., Huang, W., & Tang, X. (2023). A Novel Fuzzy Unsupervised Quadratic Surface Support Vector Machine Based on DC Programming: An Application to Credit Risk Management. Mathematics, 11(22), 4661. https://doi.org/10.3390/math11224661







