Effects of Search Strategies on Collective Problem-Solving
Abstract
:1. Introduction
2. Model
2.1. Problem Space
2.2. Agent
2.2.1. Agent’s Memory
2.2.2. Agent’s Individual Utility Function
2.2.3. Agent’s Other Properties
2.3. Group Solution
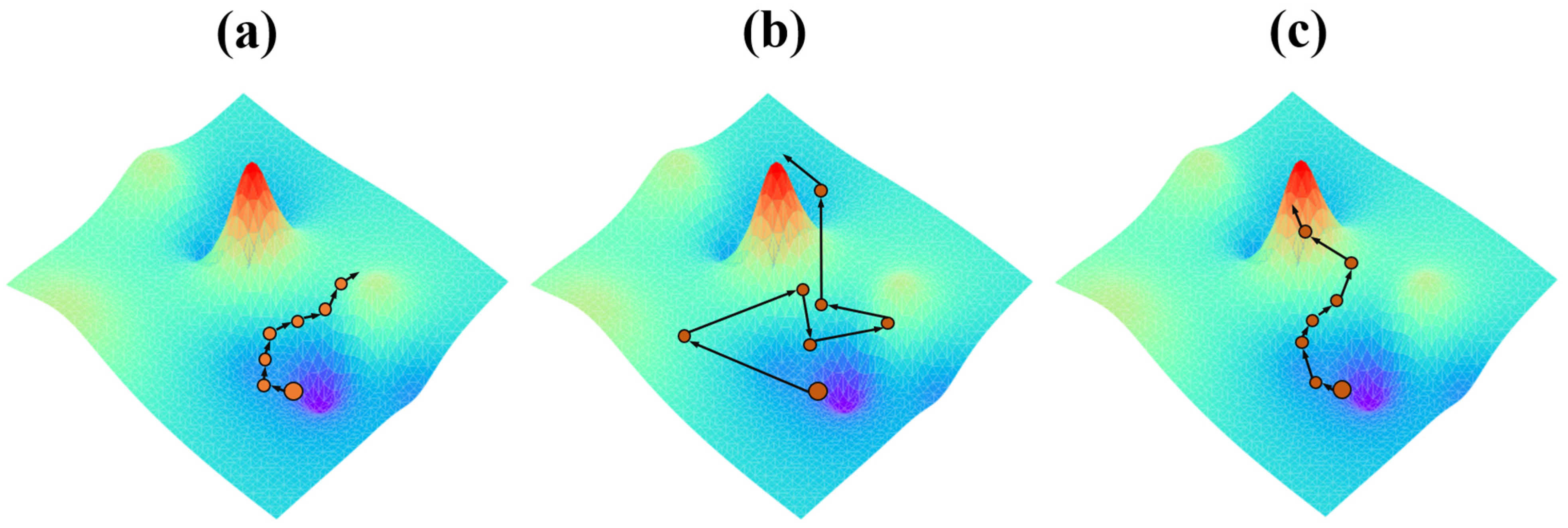
2.4. Search Strategies
2.4.1. Simple Local Search
2.4.2. Random Search
2.4.3. Adaptive Search
2.5. Search Errors
2.6. Social Interactions
2.7. Procedure in Each Iteration of Simulation
- Firstly, every agent conducts an individual search and updates their memory and current solution as necessary.
- Secondly, a speaker is randomly chosen from among the group members. If the speaker’s current solution is deemed superior to the current group solution, as per the speaker’s judgment, it is proposed as a potential candidate for the group solution. Otherwise, the process proceeds to the next iteration.
- Thirdly, other agents assess the proposed candidate group solution based on their individual utility functions, expressing either support or rejection.
- Finally, the evaluation results are summarized, leading to the ultimate group decision. This decision involves either adopting or rejecting the candidate group solution as the new collective solution at the group level.
3. Results
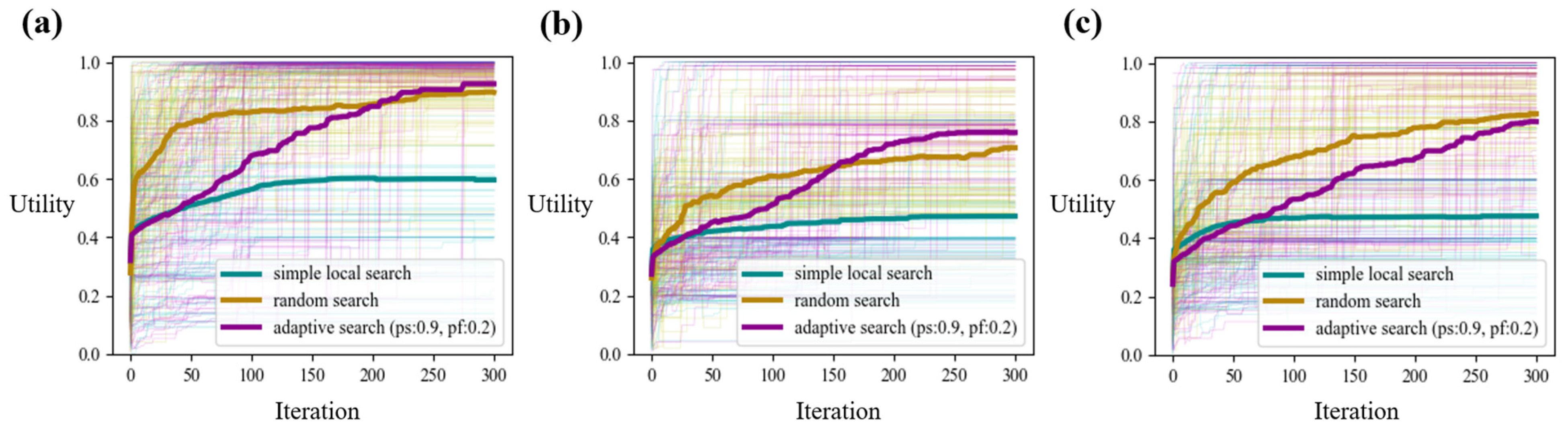
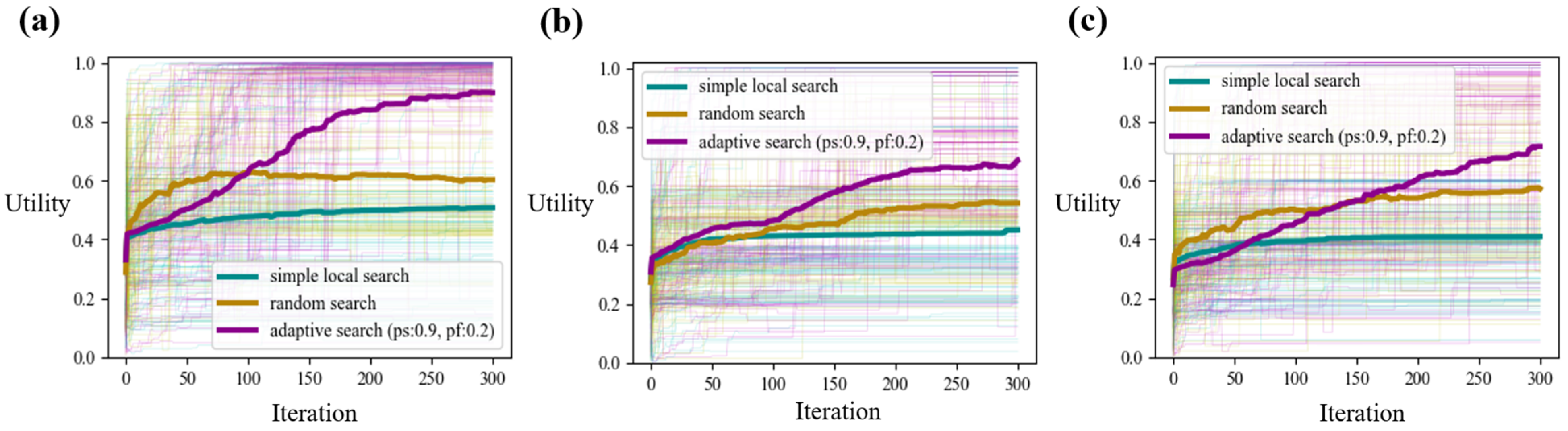
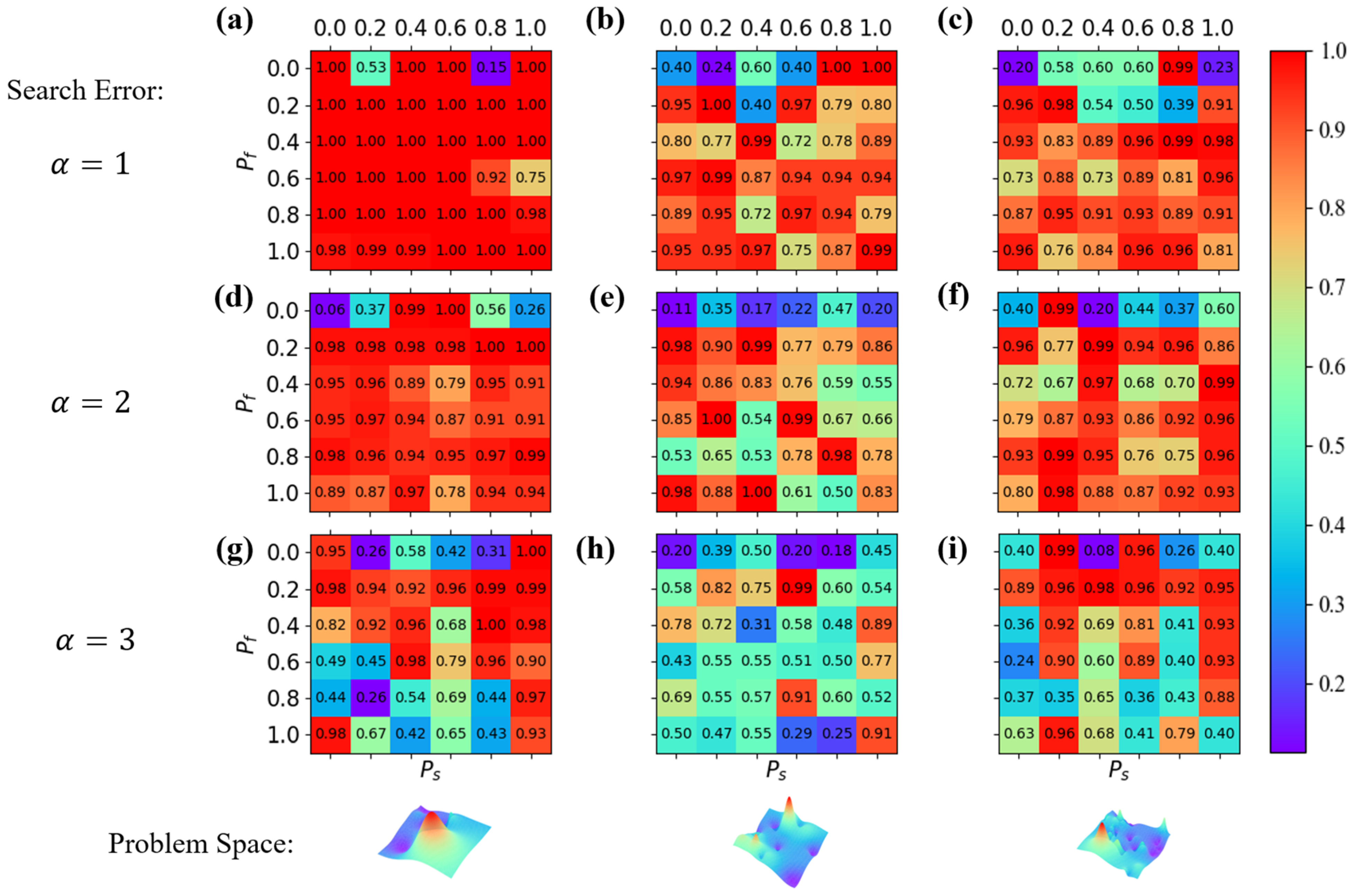
3.1. Group Processes over Various Search Errors and Problem Spaces
3.2. Optimal and Parameters in Adaptive Search
4. Discussion
Funding
Data Availability Statement
Conflicts of Interest
References
- Wu, L.; Wang, D.; Evans, J.A. Large teams develop and small teams disrupt science and technology. Nature 2019, 566, 378–382. [Google Scholar] [CrossRef]
- Comfort, L.K.; Kapucu, N.; Ko, K.; Menoni, S.; Siciliano, M. Crisis decision-making on a global scale: Transition from cognition to collective action under threat of COVID-19. Public Adm. Rev. 2020, 80, 616–622. [Google Scholar] [CrossRef]
- Victor, D.G. Toward effective international cooperation on climate change: Numbers, interests and institutions. Glob. Environ. Politics 2006, 6, 90–103. [Google Scholar] [CrossRef]
- Yammarino, F.J.; Mumford, M.D.; Connelly, M.S.; Dionne, S.D. Leadership and team dynamics for dangerous military contexts. Mil. Psychol. 2010, 22 (Suppl. S1), S15–S41. [Google Scholar] [CrossRef]
- Wuchty, S.; Jones, B.F.; Uzzi, B. The increasing dominance of teams in production of knowledge. Science 2007, 316, 1036–1039. [Google Scholar] [CrossRef]
- Fortus, D.; Krajcik, J.; Dershimer, R.C.; Marx, R.W.; Mamlok-Naaman, R. Design-based science and real-world problem-solving. Int. J. Sci. Educ. 2005, 27, 855–879. [Google Scholar] [CrossRef]
- Milojević, S. Principles of scientific research team formation and evolution. Proc. Natl. Acad. Sci. USA 2014, 111, 3984–3989. [Google Scholar] [CrossRef]
- Aggarwal, I.; Woolley, A.W.; Chabris, C.F.; Malone, T.W. The impact of cognitive style diversity on implicit learning in teams. Front. Psychol. 2019, 10, 112. [Google Scholar] [CrossRef]
- Veissière, S.P.; Constant, A.; Ramstead, M.J.; Friston, K.J.; Kirmayer, L.J. Thinking through other minds: A variational approach to cognition and culture. Behav. Brain Sci. 2020, 43, e90. [Google Scholar] [CrossRef]
- Woolley, A.W.; Aggarwal, I. Collective intelligence and group learning. In The Oxford Handbook of Group and Organizational Learning; Oxford University Press: Oxford, UK, 2017. [Google Scholar]
- Reese, E.; Fivush, R. The development of collective remembering. Memory 2008, 16, 201–212. [Google Scholar] [CrossRef]
- Isurin, L. Collective Remembering; Cambridge University Press: Cambridge, UK, 2017. [Google Scholar]
- Bell, D.E.; Raiffa, H.; Tversky, A. (Eds.) Decision Making: Descriptive, Normative, and Prescriptive Interactions; Cambridge University Press: Cambridge, UK, 1988. [Google Scholar]
- Davis, J.H. Group decision and social interaction: A theory of social decision schemes. Psychol. Rev. 1973, 80, 97–125. [Google Scholar] [CrossRef]
- Gross, J.; De Dreu, C.K. Individual solutions to shared problems create a modern tragedy of the commons. Sci. Adv. 2019, 5, eaau7296. [Google Scholar] [CrossRef] [PubMed]
- Chiu, M.M. Group Problem-Solving Processes: Social Interactions and Individual Actions. J. Theory Soc. Behav. 2000, 30, 26–49. [Google Scholar] [CrossRef]
- Xu, W.; Edalatpanah, S.A.; Sorourkhah, A. Solving the Problem of Reducing the Audiences’ Favor toward an Educational Institution by Using a Combination of Hard and Soft Operations Research Approaches. Mathematics 2023, 11, 3815. [Google Scholar] [CrossRef]
- Malone, T.W. Superminds: The Surprising Power of People and Computers Thinking Together; Little, Brown Spark: Boston, MA, USA, 2018. [Google Scholar]
- Perc, M.; Gómez-Gardenes, J.; Szolnoki, A.; Floría, L.M.; Moreno, Y. Evolutionary dynamics of group interactions on structured populations: A review. J. R. Soc. Interface 2013, 10, 20120997. [Google Scholar] [CrossRef]
- Arguello, J.; Butler, B.S.; Joyce, E.; Kraut, R.; Ling, K.S.; Rosé, C.; Wang, X. Talk to me: Foundations for successful individual-group interactions in online communities. In Proceedings of the SIGCHI Conference on Human Factors in Computing Systems, Montreal, QC, Canada, 22–27 April 2006; pp. 959–968. [Google Scholar]
- Long, M.H. Task, Group, and Task-Group Interactions; ERIC—Institute of Education Sciences: Washington, DC, USA, 1990. [Google Scholar]
- Luria, A.R. The Working Brain: An Introduction to Neuropsychology; Basic Books: New York, NY, USA, 1973. [Google Scholar]
- Mayo, A.T.; Woolley, A.W. Variance in group ability to transform resources into performance, and the role of coordinated attention. Acad. Manag. Discov. 2021, 7, 225–246. [Google Scholar] [CrossRef]
- Hoffman, L.R. Group problem solving. In Advances in Experimental Social Psychology; Academic Press: Cambridge, MA, USA, 1965; Volume 2, pp. 99–132. [Google Scholar]
- Fleming, L. Recombinant uncertainty in technological search. Manag. Sci. 2001, 47, 117–132. [Google Scholar] [CrossRef]
- Levinthal, D.A. Adaptation on rugged landscapes. Manag. Sci. 1997, 43, 934–950. [Google Scholar] [CrossRef]
- Rivkin, J.W. Imitation of complex strategies. Manag. Sci. 2000, 46, 824–844. [Google Scholar] [CrossRef]
- Billinger, S.; Stieglitz, N.; Schumacher, T.R. Search on rugged landscapes: An experimental study. Organ. Sci. 2014, 25, 93–108. [Google Scholar] [CrossRef]
- Ganco, M.; Hoetker, G. NK modeling methodology in the strategy literature: Bounded search on a rugged landscape. In Research Methodology in Strategy and Management; Emerald Group Publishing Limited: Leeds, UK, 2009; pp. 237–268. [Google Scholar]
- Moreland, R.L.; Levine, J.M.; Wingert, M.L. Creating the ideal group: Composition effects at work. In Understanding Group Behavior; Psychology Press: London, UK, 2018; pp. 11–35. [Google Scholar]
- Wilkinson, I.A.; Fung, I.Y. Small-group composition and peer effects. Int. J. Educ. Res. 2002, 37, 425–447. [Google Scholar] [CrossRef]
- Woolley, A.W.; Chabris, C.F.; Pentland, A.; Hashmi, N.; Malone, T.W. Evidence for a collective intelligence factor in the performance of human groups. Science 2010, 330, 686–688. [Google Scholar] [CrossRef] [PubMed]
- Spearman, C. “General Intelligence” Objectively Determined and Measured. Am. J. Psychol. 1961, 15, 201–292. [Google Scholar] [CrossRef]
- Engel, D.; Woolley, A.W.; Jing, L.X.; Chabris, C.F.; Malone, T.W. Reading the mind in the eyes or reading between the lines? Theory of mind predicts collective intelligence equally well online and face-to-face. PLoS ONE 2014, 9, e115212. [Google Scholar] [CrossRef] [PubMed]
- O’Reilly , C.A., III; Williams, K.Y.; Barsade, S. Group demography and innovation: Does diversity help? In Composition; Elsevier Science: Amsterdam, The Netherlands, 1998. [Google Scholar]
- Kozhevnikov, M.; Evans, C.; Kosslyn, S.M. Cognitive style as environmentally sensitive individual differences in cognition: A modern synthesis and applications in education, business, and management. Psychol. Sci. Public Interest 2014, 15, 3–33. [Google Scholar] [CrossRef]
- Gouran, D.S. Communication in groups. In The Handbook of Group Communication Theory and Research; SAGE: Thousand Oaks, CA, USA, 1999; pp. 3–34. [Google Scholar]
- Keyton, J. Relational communication in groups. In The Handbook of Group Communication Theory and Research; SAGE: Thousand Oaks, CA, USA, 1999; pp. 192–222. [Google Scholar]
- Albrecht, T.L.; Johnson, G.M.; Walther, J.B. Understanding communication processes in focus groups. Success. Focus Groups Adv. State Art 1993, 5, 1–64. [Google Scholar]
- Finholt, T.; Sproull, L.; Kiesler, S. Communication and performance in ad hoc task groups. In Intellectual Teamwork; Psychology Press: London, UK, 2014; pp. 305–340. [Google Scholar]
- Morrison, E.W.; Wheeler-Smith, S.L.; Kamdar, D. Speaking up in groups: A cross-level study of group voice climate and voice. J. Appl. Psychol. 2011, 96, 183. [Google Scholar] [CrossRef]
- Parker, K.C. Speaking turns in small group interaction: A context-sensitive event sequence model. J. Personal. Soc. Psychol. 1988, 54, 965. [Google Scholar] [CrossRef]
- Bernstein, E.; Shore, J.; Lazer, D. How intermittent breaks in interaction improve collective intelligence. Proc. Natl. Acad. Sci. USA 2018, 115, 8734–8739. [Google Scholar] [CrossRef]
- Zhang, Z.; Gao, Y.; Li, Z. Consensus reaching for social network group decision making by considering leadership and bounded confidence. Knowl.-Based Syst. 2020, 204, 106240. [Google Scholar] [CrossRef]
- Becker, J.; Brackbill, D.; Centola, D. Network dynamics of social influence in the wisdom of crowds. Proc. Natl. Acad. Sci. USA 2017, 114, E5070–E5076. [Google Scholar] [CrossRef]
- Iyer, A.; Leach, C.W. Emotion in inter-group relations. Eur. Rev. Soc. Psychol. 2008, 19, 86–125. [Google Scholar] [CrossRef]
- Bruner, M.W.; Eys, M.A.; Wilson, K.S.; Côté, J. Group cohesion and positive youth development in team sport athletes. Sport Exerc. Perform. Psychol. 2014, 3, 219. [Google Scholar] [CrossRef]
- Carron, A.V.; Brawley, L.R. Cohesion: Conceptual and measurement issues. Small Group Res. 2012, 43, 726–743. [Google Scholar] [CrossRef]
- Whitton, S.M.; Fletcher, R.B. The Group Environment Questionnaire: A multilevel confirmatory factor analysis. Small Group Res. 2014, 45, 68–88. [Google Scholar] [CrossRef]
- Kinicki, A.J.; Jacobson, K.J.; Peterson, S.J.; Prussia, G.E. Development and validation of the performance management behavior questionnaire. Pers. Psychol. 2013, 66, 1–45. [Google Scholar] [CrossRef]
- Knierim, M.T.; Hariharan, A.; Dorner, V.; Weinhardt, C. Emotion feedback in small group collaboration: A research agenda for group emotion management support systems. In Proceedings of the 17th International Conference on Group Decision and Negotiation (GDN), Stuttgart, Germany, 14–18 August 2017; pp. 1–12. [Google Scholar]
- Moye, N.A.; Langfred, C.W. Information sharing and group conflict: Going beyond decision making to understand the effects of information sharing on group performance. Int. J. Confl. Manag. 2014, 15, 381–410. [Google Scholar] [CrossRef]
- Gigone, D.; Hastie, R. The common knowledge effect: Information sharing and group judgment. J. Personal. Soc. Psychol. 1993, 65, 959. [Google Scholar] [CrossRef]
- Toma, C.; Butera, F. Hidden profiles and concealed information: Strategic information sharing and use in group decision making. Personal. Soc. Psychol. Bull. 2009, 35, 793–806. [Google Scholar] [CrossRef]
- Devine, D.J. Effects of cognitive ability, task knowledge, information sharing, and conflict on group decision-making effectiveness. Small Group Res. 1999, 30, 608–634. [Google Scholar] [CrossRef]
- Phillips, K.W.; Mannix, E.A.; Neale, M.A.; Gruenfeld, D.H. Diverse groups and information sharing: The effects of congruent ties. J. Exp. Soc. Psychol. 2004, 40, 497–510. [Google Scholar] [CrossRef]
- Tang, Q.; Wang, C.; Feng, T. Research on the Group Innovation Information-Sharing Strategy of the Industry–University–Research Innovation Alliance Based on an Evolutionary Game. Mathematics 2023, 11, 4161. [Google Scholar] [CrossRef]
- Berger-Tal, O.; Nathan, J.; Meron, E.; Saltz, D. The exploration-exploitation dilemma: A multidisciplinary framework. PLoS ONE 2014, 9, e95693. [Google Scholar] [CrossRef] [PubMed]
- Uotila, J.; Maula, M.; Keil, T.; Zahra, S.A. Exploration, exploitation, and financial performance: Analysis of S&P 500 corporations. Strateg. Manag. J. 2009, 30, 221–231. [Google Scholar]
- Hoang, H.A.; Rothaermel, F.T. Leveraging internal and external experience: Exploration, exploitation, and R&D project performance. Strateg. Manag. J. 2010, 31, 734–758. [Google Scholar]
- Brunet, A.P.; New, S. Kaizen in Japan: An empirical study. Int. J. Oper. Prod. Manag. 2003, 23, 1426–1446. [Google Scholar] [CrossRef]
- Stasser, G. Computer simulation as a research tool: The DISCUSS model of group decision making. J. Exp. Soc. Psychol. 1988, 24, 393–422. [Google Scholar] [CrossRef]
- Mollona, E. Computer simulation in social sciences. J. Manag. Gov. 2008, 12, 205–211. [Google Scholar] [CrossRef]
- Lapp, S.; Jablokow, K.; McComb, C. KABOOM: An agent-based model for simulating cognitive style in team problem solving. Des. Sci. 2019, 5, e13. [Google Scholar] [CrossRef]
- Bergner, Y.; Andrews, J.J.; Zhu, M.; Gonzales, J.E. Agent-based modeling of collaborative problem solving. ETS Res. Rep. Ser. 2016, 2016, 1–14. [Google Scholar] [CrossRef]
- Hill, L.A. Orientation to the Subarctic Survival Situation; Harvard Business School Background Note 494-073; Harvard Business School: Boston, MA, USA, 1995. [Google Scholar]
- Sun, L.; Hong, L.J.; Hu, Z. Balancing exploitation and exploration in discrete optimization via simulation through a Gaussian process-based search. Oper. Res. 2014, 62, 1416–1438. [Google Scholar] [CrossRef]
- Ajdari, A.; Mahlooji, H. An adaptive exploration-exploitation algorithm for constructing metamodels in random simulation using a novel sequential experimental design. Commun. Stat.-Simul. Comput. 2014, 43, 947–968. [Google Scholar] [CrossRef]
- Gilbert, N. Agent-Based Models; Sage Publications: Newcastle upon Tyne, UK, 2019. [Google Scholar]
- Bankes, S.C. Agent-based modeling: A revolution? Proc. Natl. Acad. Sci. USA 2002, 99 (Suppl. S3), 7199–7200. [Google Scholar] [CrossRef]
- Macal, C.M.; North, M.J. Agent-based modeling and simulation. In Proceedings of the 2009 Winter Simulation Conference (WSC), Austin, TX, USA, 13–16 December 2009; IEEE: Piscataway, NJ, USA, 2009; pp. 86–98. [Google Scholar]
- Cao, S.; MacLaren, N.G.; Cao, Y.; Marshall, J.; Dong, Y.; Yammarino, F.J.; Dionne, S.D.; Mumford, M.D.; Connelly, S.; Martin, R.W.; et al. Group Size and Group Performance in Small Collaborative Team Settings: An Agent-Based Simulation Model of Collaborative Decision-Making Dynamics. Complexity 2022, 2022, 8265296. [Google Scholar] [CrossRef]
- Siggelkow, N. Evolution toward fit. Adm. Sci. Q. 2002, 47, 125–159. [Google Scholar] [CrossRef]
- Tushman, M.L.; Romanelli, E. Organizational evolution: A metamorphosis model of convergence and reorientation. Res. Organ. Behav. 1985, 7, 171–222. [Google Scholar]
- Arthur, W.B. Designing economic agents that act like human agents: A behavioral approach to bounded rationality. Am. Econ. Rev. 1991, 81, 353–359. [Google Scholar]
- Edmonds, B. Towards a descriptive model of agent strategy search. Comput. Econ. 2001, 18, 111–133. [Google Scholar] [CrossRef]
- Kennedy, J. Swarm intelligence. In Handbook of Nature-Inspired and Innovative Computing: Integrating Classical Models with Emerging Technologies; Springer: Boston, MA, USA, 2006; pp. 187–219. [Google Scholar]
- Beni, G. Swarm intelligence. In Complex Social and Behavioral Systems: Game Theory and Agent-Based Models; Springer: New York, NY, USA, 2020; pp. 791–818. [Google Scholar]
- Poria, S.; Cambria, E.; Bajpai, R.; Hussain, A. A review of affective computing: From unimodal analysis to multimodal fusion. Inf. Fusion 2017, 37, 98–125. [Google Scholar] [CrossRef]
- Talbi, E.G. Metaheuristics: From Design to Implementation; John Wiley & Sons: Hoboken, NJ, USA, 2009. [Google Scholar]
- Almufti, S.M. Historical survey on metaheuristics algorithms. Int. J. Sci. World 2019, 7, 1. [Google Scholar] [CrossRef]
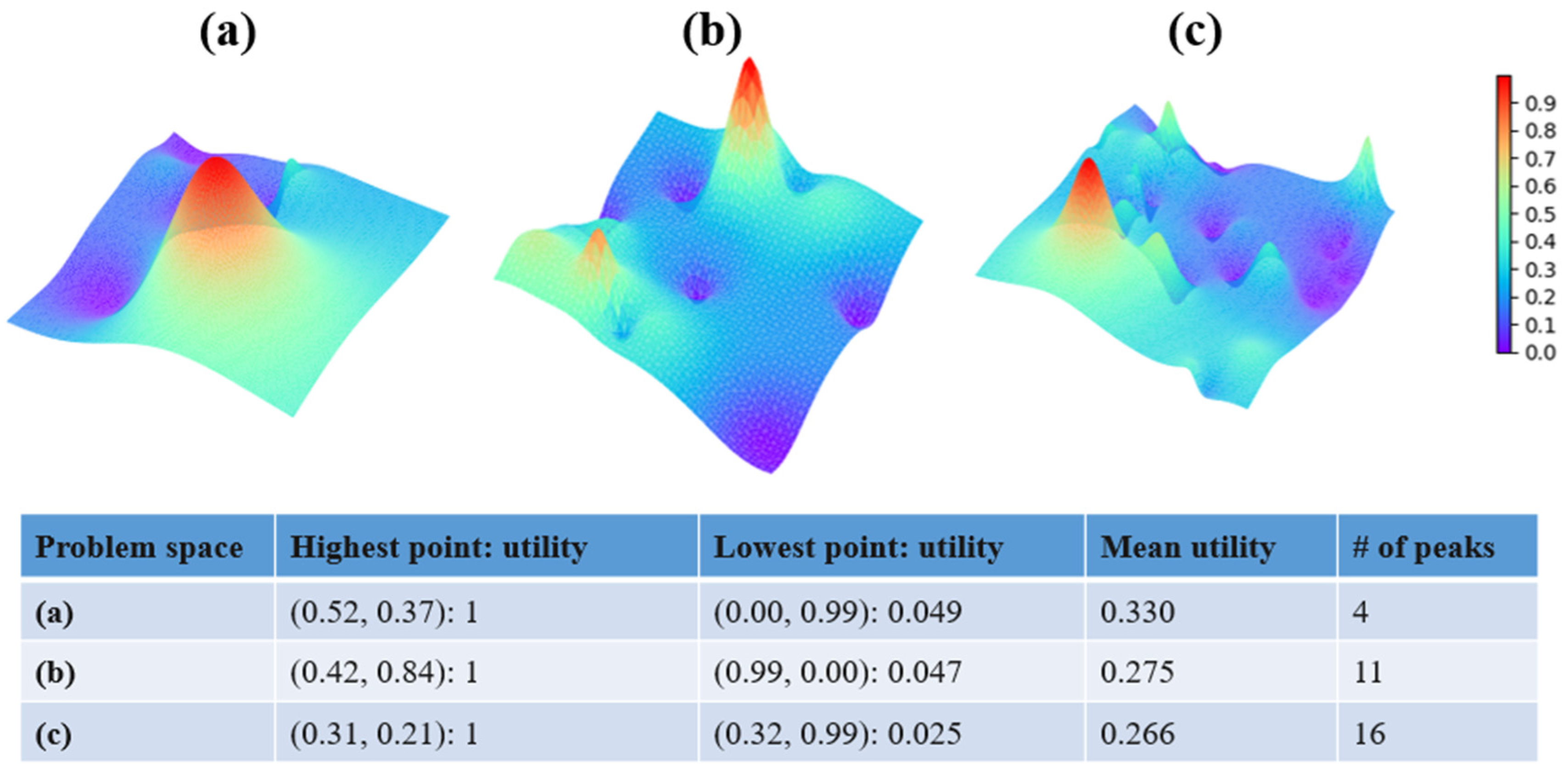

| Parameters | Description | Value |
|---|---|---|
| dimension of a problem space | 2 | |
| number of choices in each dimension | 100 | |
| number of initial solutions for problem space generation | 5, 20, 50 | |
| group size | 4 | |
| capacity of each agent’s memory | 20 | |
| ’s initial solution | random | |
| ’s initial solution | ||
| group’s initial solution | random | |
| probabilities of decreasing search distance (success) | 0.9 | |
| probabilities of increasing search distance (failure) | 0.2 | |
| index for search errors | 1, 2, 3 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cao, S. Effects of Search Strategies on Collective Problem-Solving. Mathematics 2023, 11, 4642. https://doi.org/10.3390/math11224642
Cao S. Effects of Search Strategies on Collective Problem-Solving. Mathematics. 2023; 11(22):4642. https://doi.org/10.3390/math11224642
Chicago/Turabian StyleCao, Shun. 2023. "Effects of Search Strategies on Collective Problem-Solving" Mathematics 11, no. 22: 4642. https://doi.org/10.3390/math11224642
APA StyleCao, S. (2023). Effects of Search Strategies on Collective Problem-Solving. Mathematics, 11(22), 4642. https://doi.org/10.3390/math11224642






