On Topp-Leone-G Power Series: Saturation in the Hausdorff Sense and Applications
Abstract
:1. Introduction
2. Approximation Results
2.1. Hausdorff Approximation
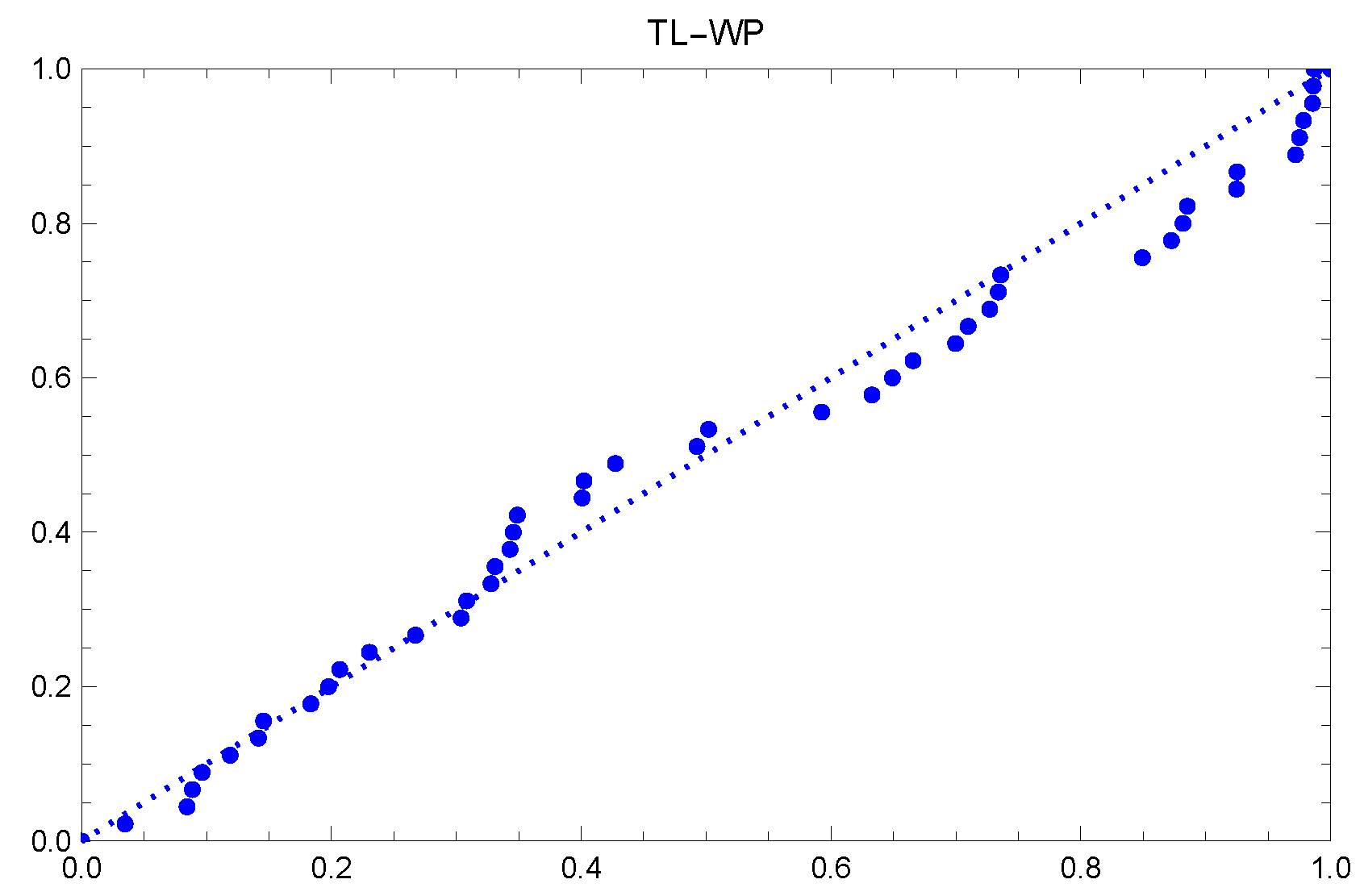
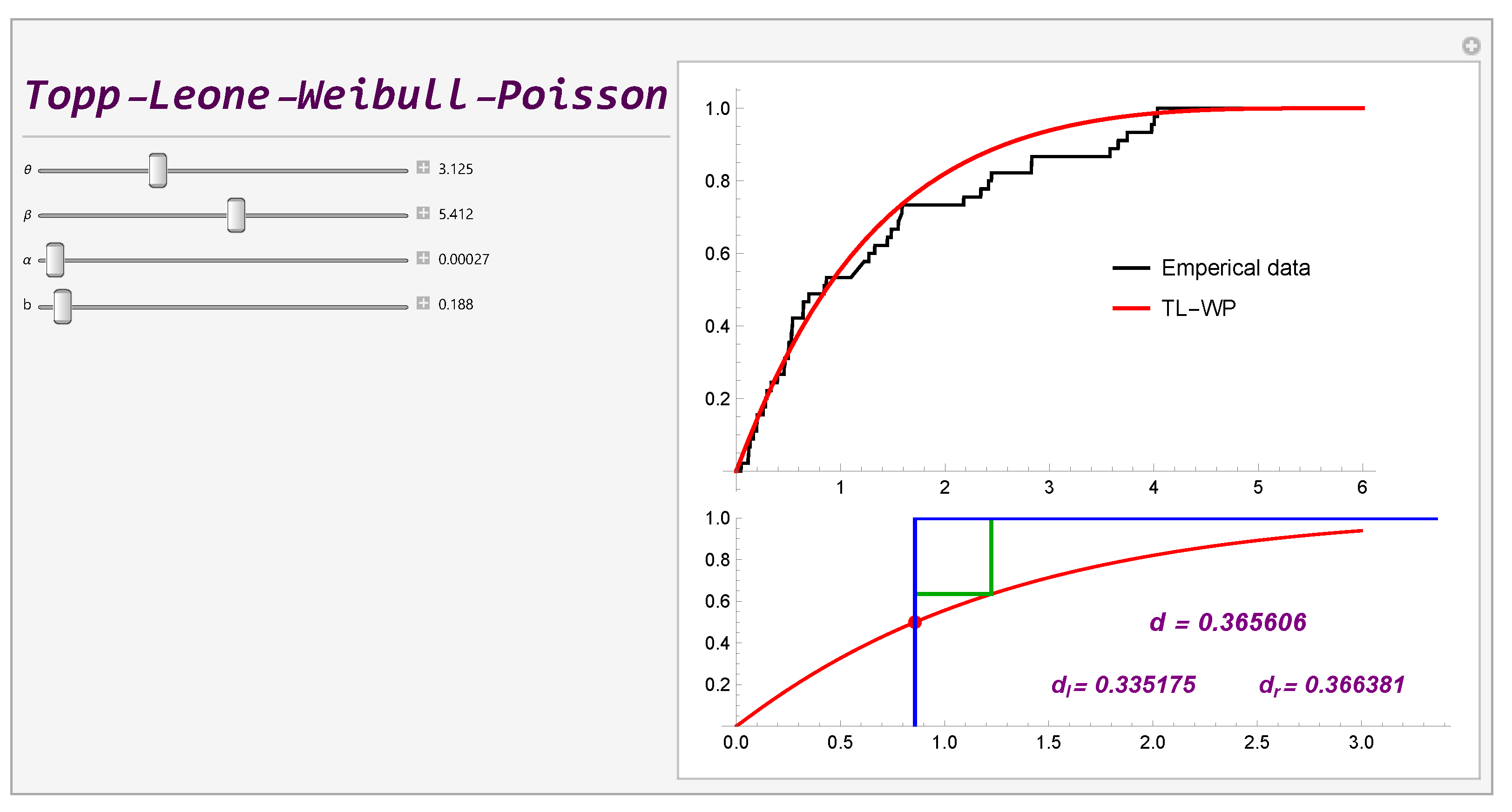
2.2. Some Applications
| data—chemotherapy | |||||||||
| 0.047 | 0.115 | 0.121 | 0.132 | 0.164 | 0.197 | 0.203 | 0.260 | 0.282 | 0.296 |
| 0.334 | 0.395 | 0.458 | 0.466 | 0.501 | 0.507 | 0.529 | 0.534 | 0.540 | 0.641 |
| 0.644 | 0.696 | 0.841 | 0.863 | 1.099 | 1.219 | 1.271 | 1.326 | 1.447 | 1.485 |
| 1.553 | 1.581 | 1.589 | 2.178 | 2.343 | 2.416 | 2.444 | 2.825 | 2.830 | 3.578 |
| 3.658 | 3.743 | 3.978 | 4.003 | 4.033 | |||||
| Statistic | p-Value | |
| Anderson–Darling | 1.20184 | 0.266033 |
| Cramér–von Mises | 0.11562 | 0.513591 |
| Kolmogorov–Smirnov | 0.116999 | 0.530605 |
| Kuiper | 0.168146 | 0.360015 |
| Pearson | 6.33333 | 0.706149 |
| Watson | 0.0836651 | 0.38578 |
| automobile insurance claims | ||||||||||
| 1103 | 1939 | 4339 | 1491 | 3801 | 387 | 1299 | 326 | 1789 | 3310 | 443 |
| 673 | 6524 | 1217 | 1526 | 109 | 1279 | 852 | 1285 | 417 | 1333 | 3231 |
| 493 | 2201 | 464 | 773 | 4746 | 2596 | 1724 | 2132 | 1715 | 879 | 2467 |
| 4631 | 1856 | 911 | 966 | 789 | 1115 | 1716 | 841 | 385 | 1326 | 450 |
| 66 | 46 | 419 | 2315 | 508 | 48 | 34 | 261 | 3314 | 558 | 86 |
| 308 | 255 | 467 | 822 | 514 | 3047 | 298 | 220 | 182 | 61 | 411 |
| 111 | 381 | 198 | 552 | 28 | 278 | 703 | 535 | 407 | 138 | 193 |
| 27 | 88 | 318 | 11 | 8 | 38 | 53 | 88 | 49 | 99 | 12 |
| 123 | 125 | 10 | 77 | 43 | 21 | 382 | 64 | 61 | 42 | 9 |
| 56 | 44 | 26 | 41 | 44 | 91 | 40 | 509 | 47 | 143 | 59 |
| 70 | 19 | 153 | 483 | 107 | 93 | 135 | 122 | 62 | 150 | 370 |
| 48 | 73 | 656 | 172 | 54 | 34 | 143 | 26 | 22 | 116 | 70 |
| 243 | 462 | 49 | 69 | 157 | 215 | 128 | 46 | 45 | 190 | 90 |
| 46 | 37 | 91 | 519 | 111 | 44 | 21 | 102 | 25 | 32 | 95 |
| 64 | 113 | 617 | 511 | 46 | 65 | 0 | 34 | 24 | 71 | 97 |
| 30 | 11 | 17 | 35 | 15 | 24 | 35 | 0 | 912 | 75 | 5 |
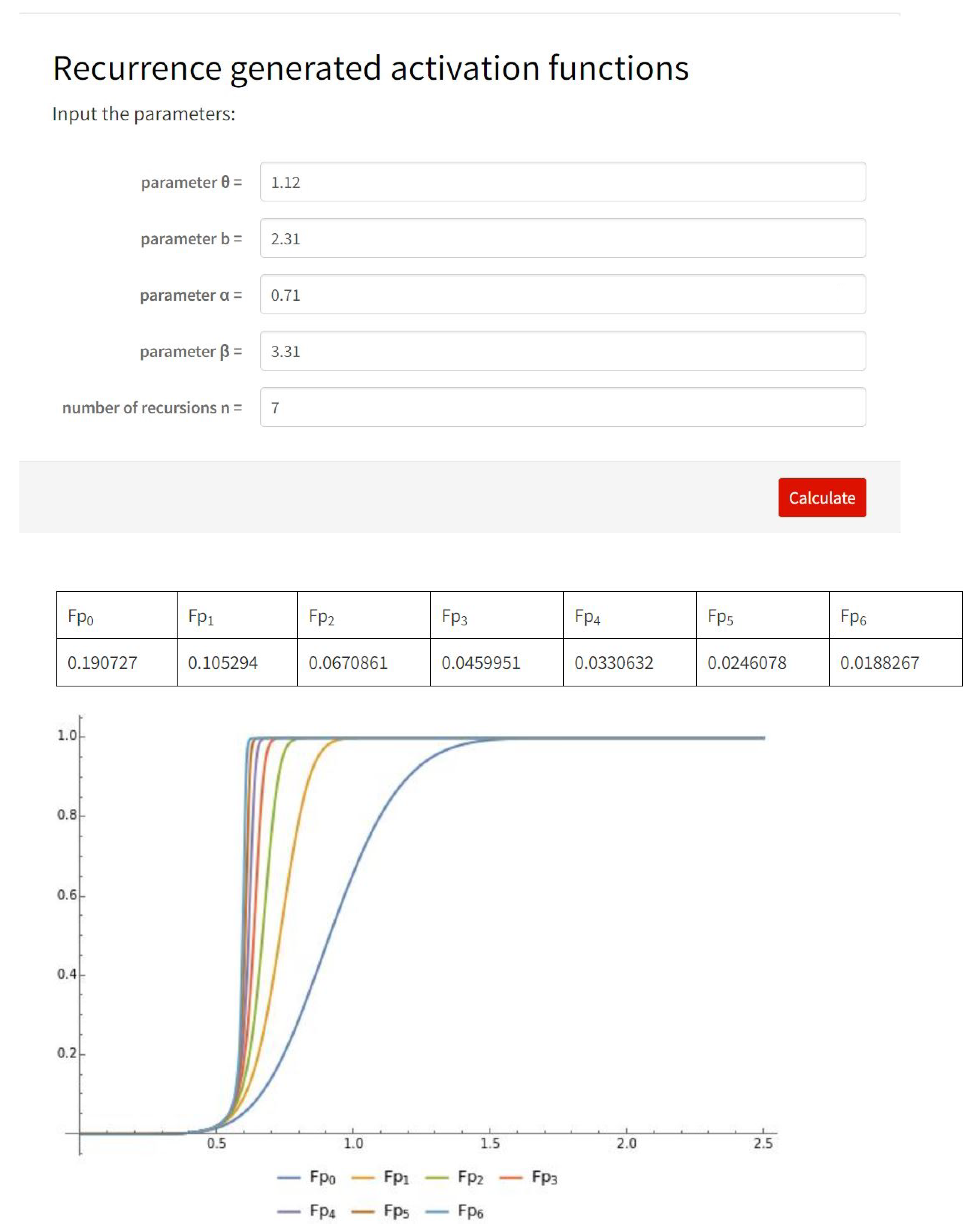
3. Family of Recurrence Generated Activation Functions
4. Conclusions
Funding
Data Availability Statement
Conflicts of Interest
References
- Bagheri, S.; Bahrami Samani, E.; Ganjali, M. The generalized modified Weibull power series distribution: Theory and applications. Comput. Stat. Data Anal. 2016, 94, 136–160. [Google Scholar] [CrossRef]
- Jafari, A.; Tahmasebi, S. Gompertz-power series distributions. Commun. Stat. Theory Methods 2016, 45, 3761–3781. [Google Scholar] [CrossRef]
- Sobhan Shafiei, S.; Darijani, S.; Saboori, H. Inverse Weibull power series distributions: Properties and applications. J. Stat. Comput. Simul. 2016, 86, 1069–1094. [Google Scholar] [CrossRef]
- Nasir, A.; Yousof, H.M.; Jamal, F.; Korkmaz, M.Ç. The Exponentiated Burr XII power series distribution: Properties and applications. Stats 2019, 2, 15–31. [Google Scholar] [CrossRef]
- Nasiru, S.; Mwita, P.N.; Ngesa, O. Exponentiated generalized power series family of distributions. Ann. Data Sci. 2019, 6, 463–489. [Google Scholar] [CrossRef]
- Oluyede, B.; Moakofi, T.; Chipepa, F. The odd power generalized Weibull-G power series class of distributions: Properties and applications. Stat. Transit. New Ser. (SITNS) 2022, 23, 89108. [Google Scholar] [CrossRef]
- Noack, A. A class of random variables with discrete distributions. Ann. Math. Stat. 1950, 21, 127–132. [Google Scholar] [CrossRef]
- Kosambi, D. Characteristic properties of series distributions. Proc. Nat. Inst. Sci. India 1949, 15, 109–113. [Google Scholar]
- Al-Shomrani, A.; Arif, O.; Shawky, A.; Hanif, S.; Shahbaz, M. Topp-Leone family of distributions: Some properties and application. Pak. J. Stat. Oper. Res. 2016, 12, 443–451. [Google Scholar] [CrossRef]
- Rezaei, S.; Sadr, B.B.; Alizadeh, M.; Nadarajah, S. Topp–Leone generated family of distributions: Properties and applications. Commun. Stat. Theor. Methods 2017, 46, 2893–2909. [Google Scholar] [CrossRef]
- Bantan, R.; Jamal, F.; Chesneau, C.; Elgarhy, M. A new power Topp–Leone generated family of distributions with applications. Entropy 2019, 21, 1177. [Google Scholar] [CrossRef]
- Ali, Z.; Ali, A.; Ozel, G. A modification in generalized classes of distributions: A new Topp–Leone class as an example. Commun. Stat. Theory Methods 2020, 50, 1–23. [Google Scholar] [CrossRef]
- Chesneau, C.; Sharma, V.; Bakouch, H. Extended Topp–Leone family of distributions as an alternative to beta and Kumaraswamy type distributions: Application to glycosaminoglycans concentration level in urine. Int. J. Biomath. 2021, 14, 2050088. [Google Scholar] [CrossRef]
- Eghwerido, J.T.; Agu, F.I. The statistical properties and applications of the alpha power Topp-Leone-G distribution. Heliyon 2022, 8, e09775. [Google Scholar] [CrossRef]
- Muhammad, M.; Liu, L.; Abba, B.; Muhammad, I.; Bouchane, M.; Zhang, H.; Musa, S. A new extension of the Topp–Leone-family of models with applications to real data. Ann. Data Sci. 2023, 10, 225–250. [Google Scholar] [CrossRef]
- Makubate, B.; Rannona, K.; Oluyede, B.; Chipepa, F. The Topp Leone-G power series class of distributions with applications. Pak. J. Stat. Oper. Res. 2021, 17, 827–846. [Google Scholar]
- Ali, M.; Ali, I.; Yousof, H.; Ibrahim, M. G Families of Probability Distributions: Theory and Practices; CRC Press: Boca Raton, FL, USA, 2023. [Google Scholar]
- Roozegar, R.; Nadarajah, S. A new class of Topp–Leone power series distributions with reliability application. J. Fail. Anal. Prev. 2017, 17, 955–970. [Google Scholar] [CrossRef]
- Condino, F.; Domma, F. A new distribution function with bounded support: The reflected generalized Topp-Leone power series distribution. METRON 2017, 75, 51–68. [Google Scholar] [CrossRef]
- Kunjiratanachot, N.; Bodhisuwan, W.; Volodin, A. The Topp-Leone generalized exponential Power series distribution with applications. J. Prob. Stat. Sci. (JPSS) 2018, 16, 197–208. [Google Scholar]
- Moakofi, T.B.; Oluyede, B.; Chipepa, F. Type II exponentiated half-logistic-Topp-Leone-G power series class of distributions with applications. Pak. J. Stat. Oper. Res 2021, 17, 885–909. [Google Scholar] [CrossRef]
- Chipepa, F.; Oluyede, B.; Wanduku, D.; Moakofi, T. The Exponentiated half Logistic-Topp-Leone-G power series class of distributions: Model, properties and applications. In Methods of Mathematical Modelling and Computation for Complex Systems. Studies in Systems, Decision and Control; Singh, J., Dutta, H., Kumar, D., Baleanu, D., Hristov, J., Eds.; Springer: Cham, Switzerland, 2022; Volume 373, pp. 341–374. [Google Scholar]
- Makubate, B.; Matsuokwane, M.; Gabaitiri, L.; Oluyede, B.; Chamunorwa, S. The type II Topp-Leone-G power series distribution with applications on bladder cancer. J. Nig. Soc. Phys. Sci. 2022, 4, 848. [Google Scholar] [CrossRef]
- Hausdorff, F. Set Theory, 2nd ed.; Chelsea Publication: New York, NY, USA, 1962. [Google Scholar]
- Sendov, B.L. Hausdorff approximations. In Mathematics and Its Applications; Springer Science & Business Media: Berlin/Heidelberg, Germany, 1990; Volume 50, pp. 1–367. [Google Scholar]
- Zaevski, T.; Kyurkchiev, N. On some composite Kies families: Distributional properties and saturation in Hausdorff sense. Mod. Stoch. Theory Appl. 2023, 10, 1–26. [Google Scholar] [CrossRef]
- Iliev, A.; Rahnev, A.; Kyurkchiev, N.; Markov, S. A study on the Unit–logistic, Unit–Weibull and Topp–Leone cumulative sigmoids. Biomath Commun. 2019, 6, 1–16. [Google Scholar] [CrossRef]
- Kyukchiev, N. Selected Topics in Mathematical Modeling: Some New Trends. Dedicated to Academician Blagovest Sendov (1932–2020); LAP LAMBERT Academic Publishing: Saarbrucken, Germany, 2020. [Google Scholar]
- Kyurkchiev, N. A new class of activation functions. Some related problems andapplications. Biomath 2020, 9, 2005033. [Google Scholar] [CrossRef]
- Kyurkchiev, N.; Iliev, A.; Rahnev, A.; Terzieva, T. Properties of a Power Topp-Leone G-family with baseline Gompertz cumulative distribution function. Int. J. Differ. Equ. Appl. 2020, 19, 1–14. [Google Scholar]
- Malinova, A.; Pavlov, N.; Terzieva, T.; Rahneva, O.; Kumaraswamy, C.D.F. On the “saturation” by the type II Topp–Leone transmuted inverted. Neural Parallel Sci. Comput. 2020, 28, 27–35. [Google Scholar]
- Vasileva, M.; Rahneva, O.; Malinova, A.; Arnaudova, V. The odd Weibull-Topp-Leone-G power series family of distributions. Int. J. Differ. Equ. Appl. 2021, 20, 43–58. [Google Scholar]
- Oluyede, B.; Dingalo, N.; Chipepa, F. The Topp-Leone-Harris-G family of distributions with applications. Int. J. Math. Oper. Res. 2023, 24, 554. [Google Scholar] [CrossRef]
- Ahmad, Z.; Mahmoudi, E.; Hamedani, G. A class of claim distributions: Properties, characterizations and applications to insurance claim data. Commun. Stat. Theory Methods 2022, 51, 2183–2208. [Google Scholar] [CrossRef]
- Kyurkchiev, N. Some intrinsic properties of Tadmor–Tanner functions: Related problems and possible applications. Mathematics 2020, 8, 1963. [Google Scholar] [CrossRef]
- Vasileva, M. Some notes on the Omega distribution and the Pliant probability distribution family. Algorithms 2020, 13, 324. [Google Scholar] [CrossRef]
- Kyurkchiev, N.; Rahneva, O.; Iliev, A.; Malinova, A.; Rahnev, A. Investigations on Some Generalized Trigonometric Distributions. Properties and Applications; Plovdiv University Press: Plovdiv, Bulgaria, 2021; ISBN 978-619-7663-01-3. [Google Scholar]
- Vasileva, M. Some notes for two generalized trigonometric families of distributions. Axioms 2022, 11, 149. [Google Scholar] [CrossRef]
- Vasileva, M. Approximation Problems and Applications; Plovdiv University Press: Plovdiv, Bulgaria, 2023; ISBN 978-619-7663-77-8. [Google Scholar]
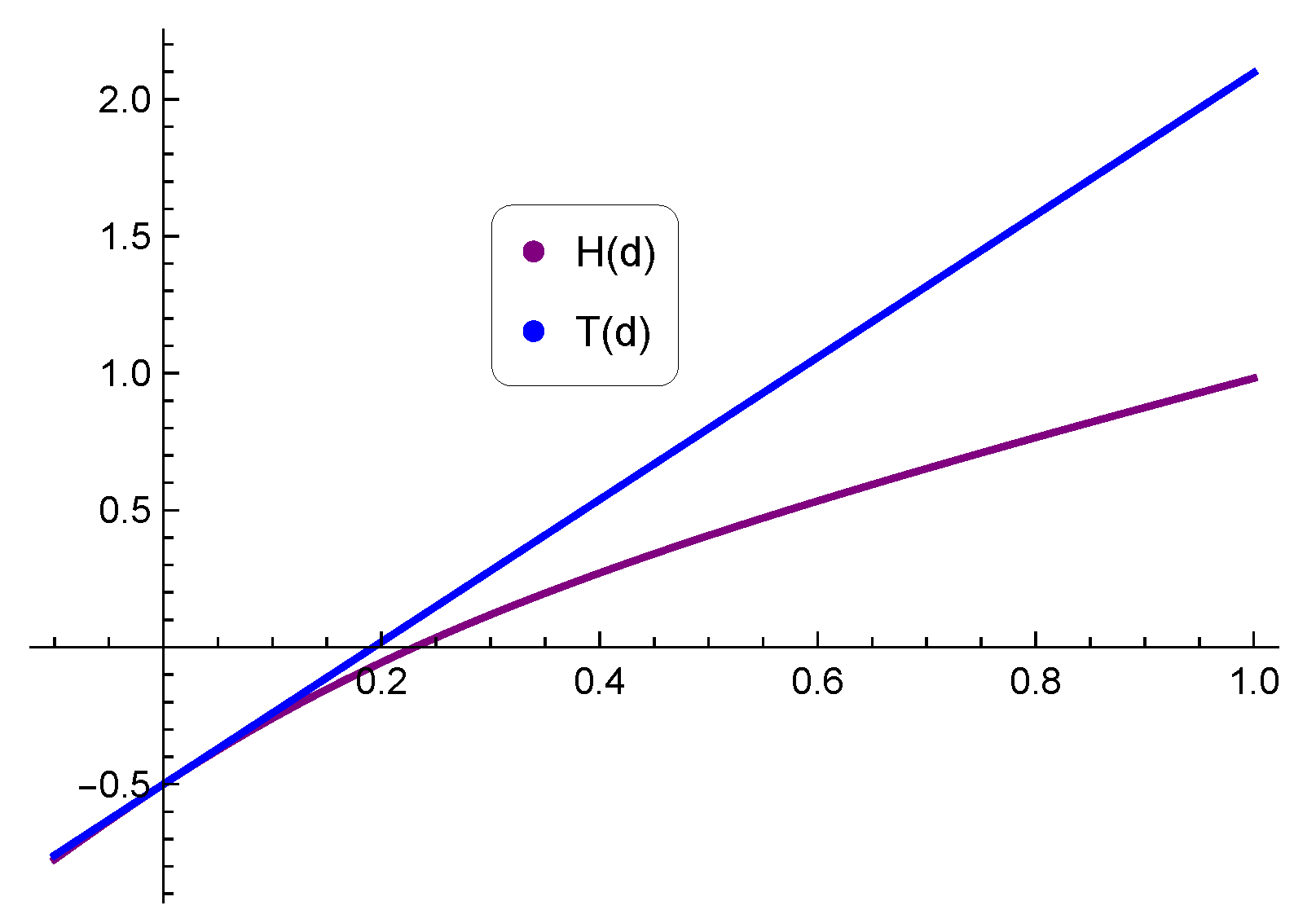



| Distribution | CDF Function | ||
|---|---|---|---|
| Topp-Leone-G Poisson | |||
| Topp-Leone-G Geometric | 1 | ||
| Topp-Leone-G Logarithmic | |||
| Topp-Leone-G Binomial |
| b | d Computed by (4) | |||||
|---|---|---|---|---|---|---|
| 0.12 | 1.31 | 1.71 | 8.31 | 0.096279 | 0.111481 | 0.225342 |
| 6.15 | 3.04 | 1.86 | 2.44 | 0.102241 | 0.130553 | 0.233152 |
| 0.63 | 2.01 | 3.05 | 0.71 | 0.092198 | 0.157327 | 0.219784 |
| 1.75 | 2.33 | 2.95 | 1.93 | 0.127773 | 0.165547 | 0.262893 |
| 0.75 | 0.64 | 1.56 | 2.14 | 0.186514 | 0.222460 | 0.313204 |
| 1.83 | 4.14 | 0.75 | 1.71 | 0.206195 | 0.240883 | 0.325568 |
| 0.15 | 0.98 | 0.89 | 0.68 | 0.235214 | 0.297660 | 0.340416 |
| 1.25 | 0.96 | 0.54 | 0.36 | 0.182461 | 0.307016 | 0.310406 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Vasileva, M.T. On Topp-Leone-G Power Series: Saturation in the Hausdorff Sense and Applications. Mathematics 2023, 11, 4620. https://doi.org/10.3390/math11224620
Vasileva MT. On Topp-Leone-G Power Series: Saturation in the Hausdorff Sense and Applications. Mathematics. 2023; 11(22):4620. https://doi.org/10.3390/math11224620
Chicago/Turabian StyleVasileva, Maria T. 2023. "On Topp-Leone-G Power Series: Saturation in the Hausdorff Sense and Applications" Mathematics 11, no. 22: 4620. https://doi.org/10.3390/math11224620
APA StyleVasileva, M. T. (2023). On Topp-Leone-G Power Series: Saturation in the Hausdorff Sense and Applications. Mathematics, 11(22), 4620. https://doi.org/10.3390/math11224620






