Structure of Analytical and Numerical Wave Solutions for the Nonlinear (1 + 1)-Coupled Drinfel’d–Sokolov–Wilson System Arising in Shallow Water Waves
Abstract
:1. Introduction
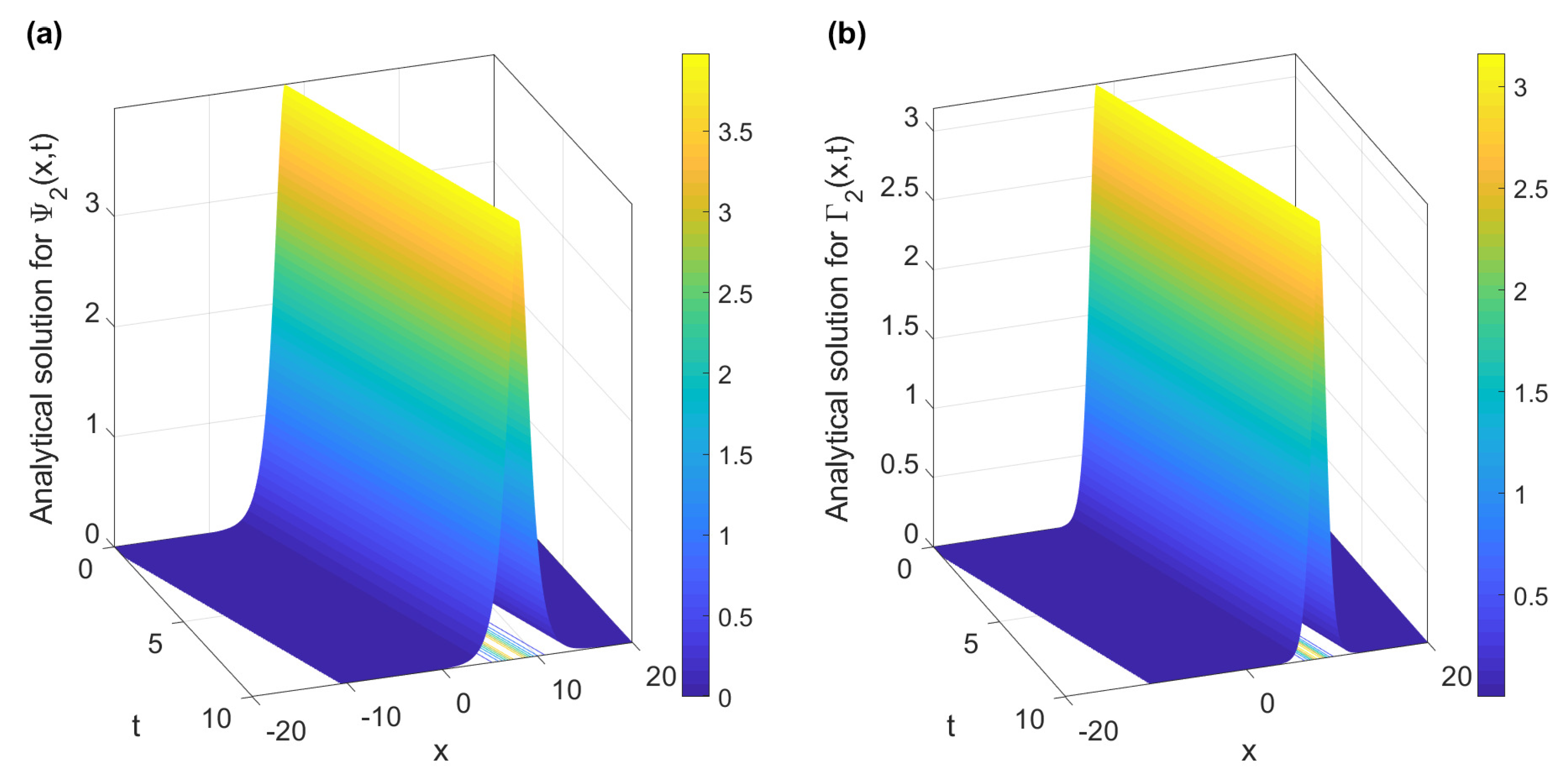
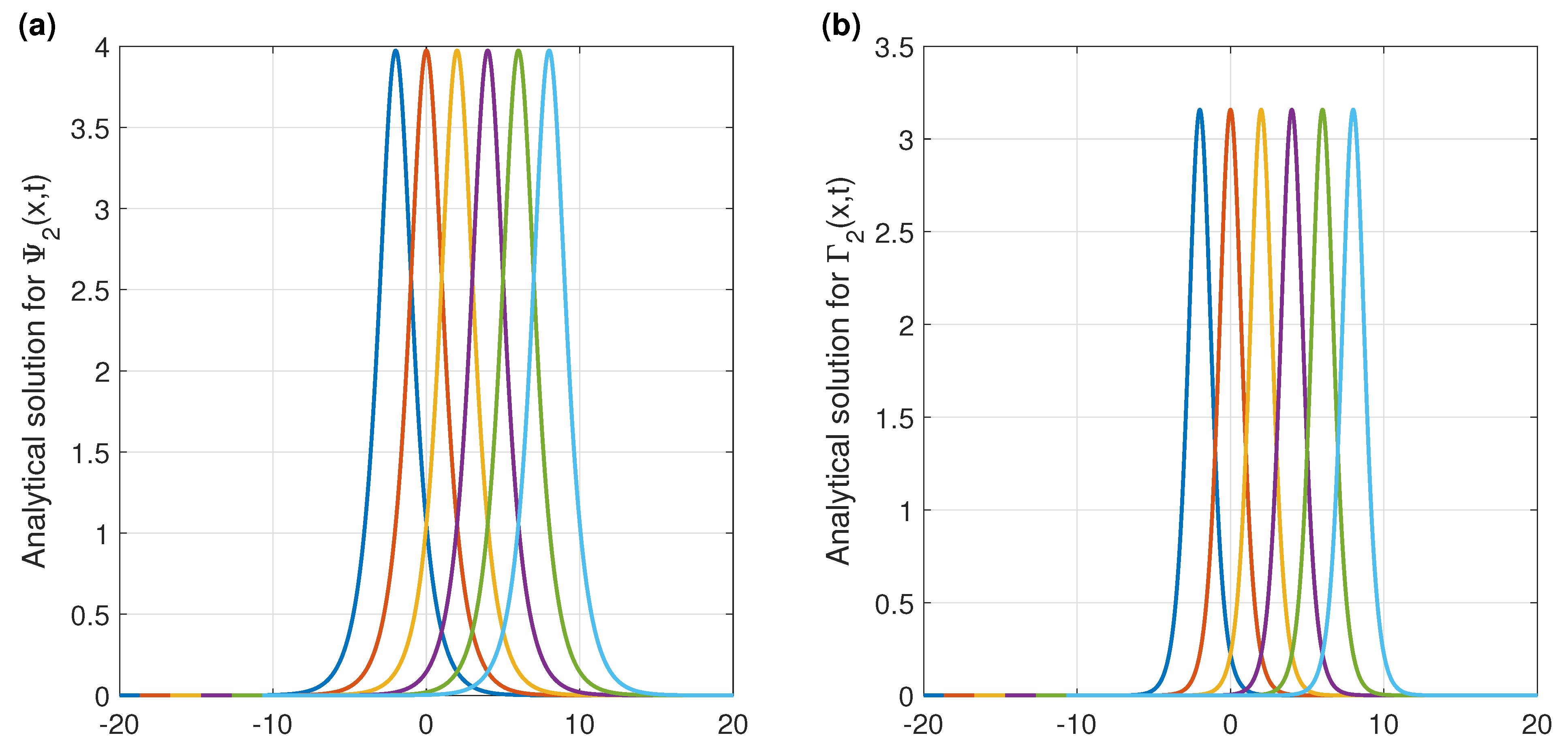
2. Exact Solutions of the Coupled Drinfel’d–Sokolov–Wilson System
2.1. The MVNK Method
2.2. The GERFM Method
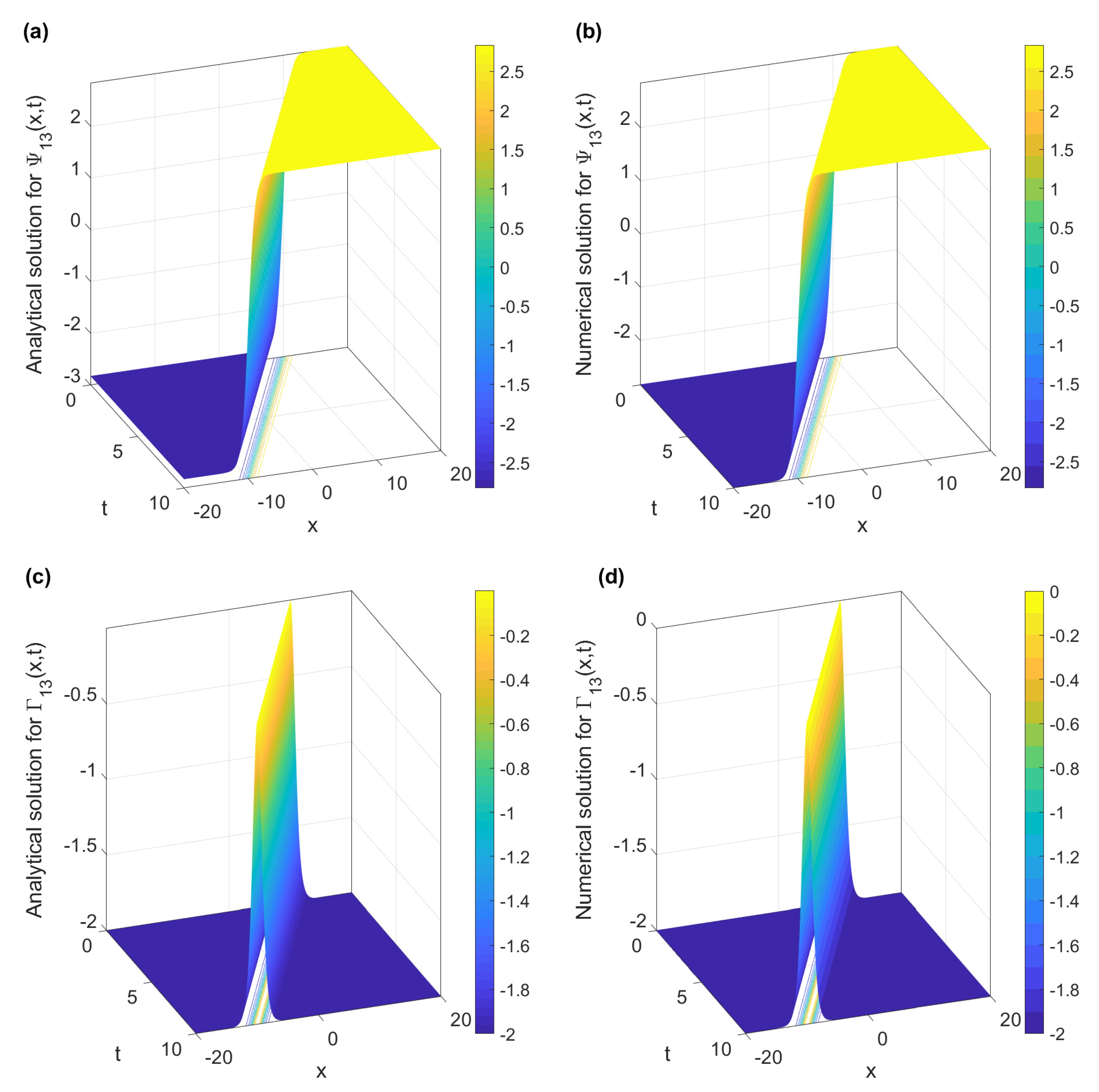
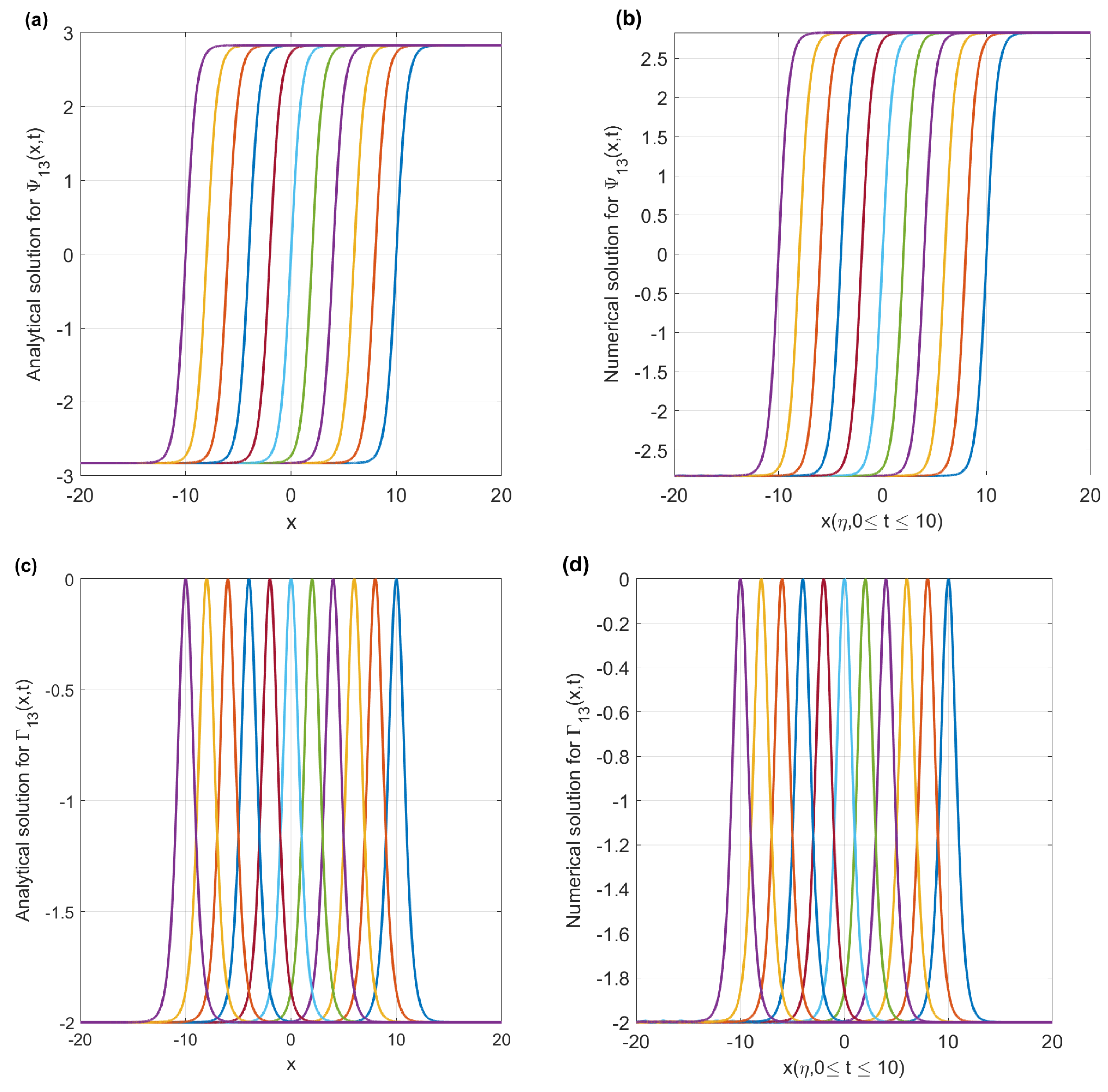
3. Numerical Results
3.1. Numerical Solutions Using a Uniform Mesh
3.1.1. Stability
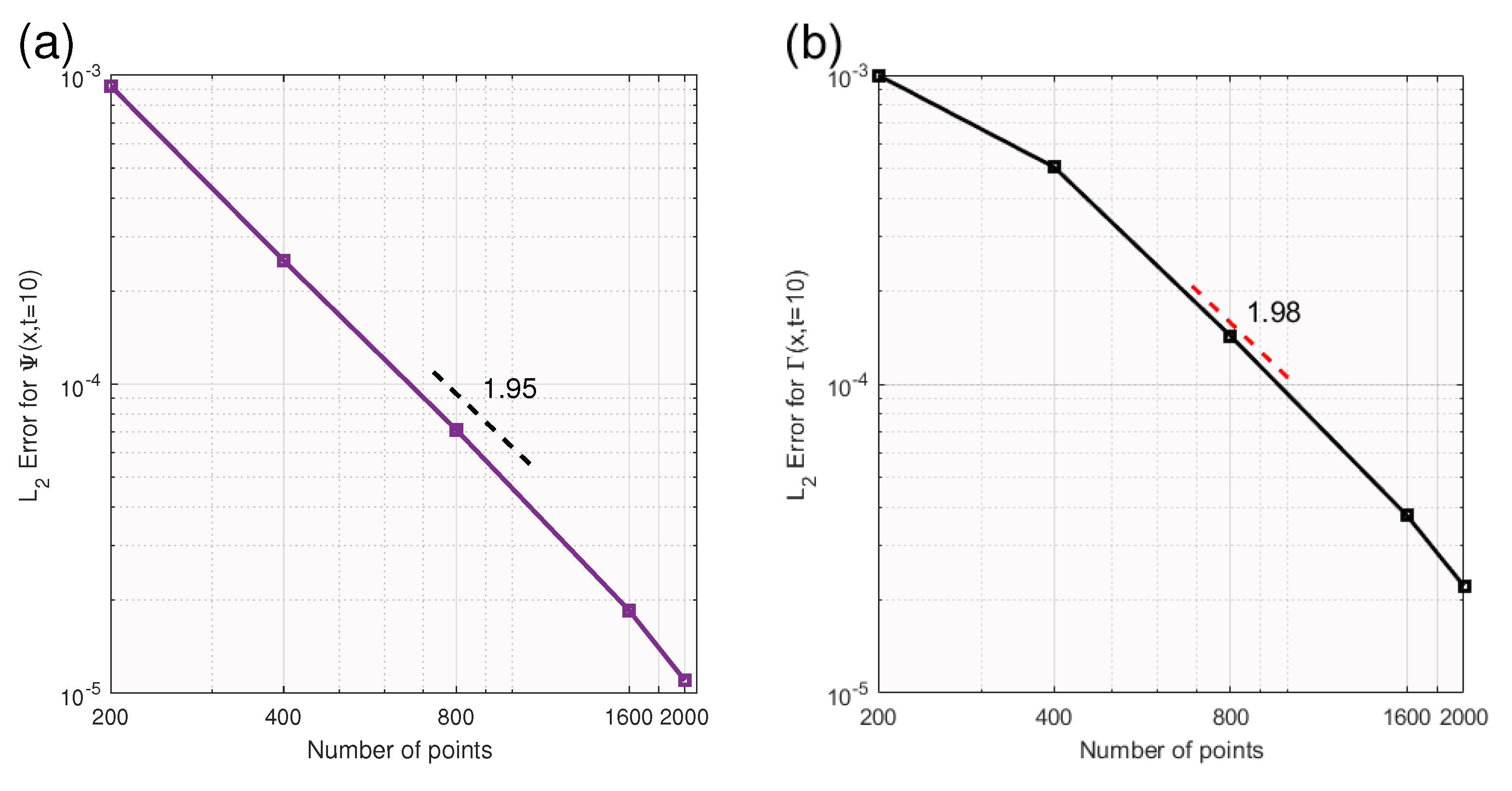
3.1.2. Error Analysis
3.1.3. Convergence
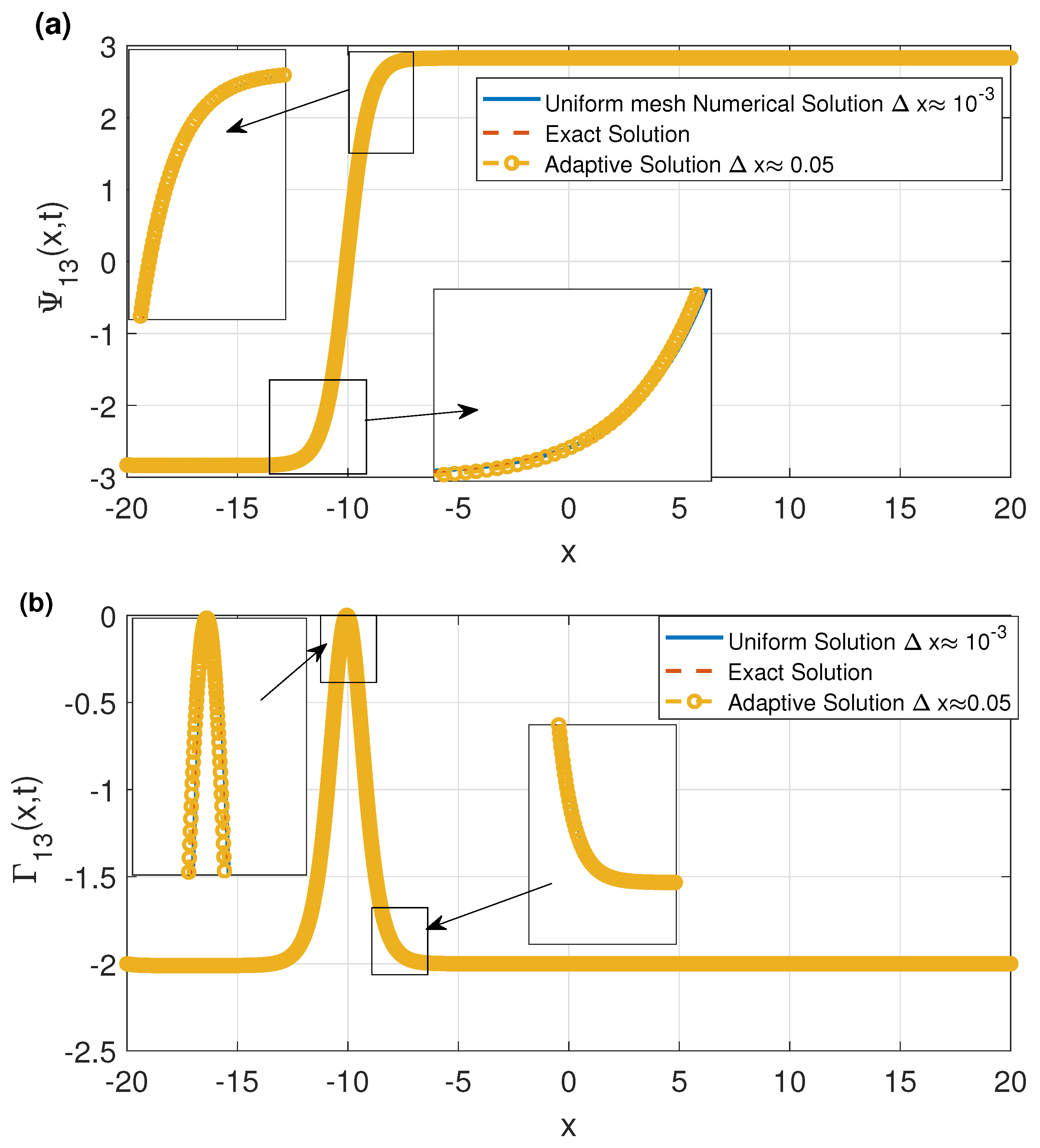
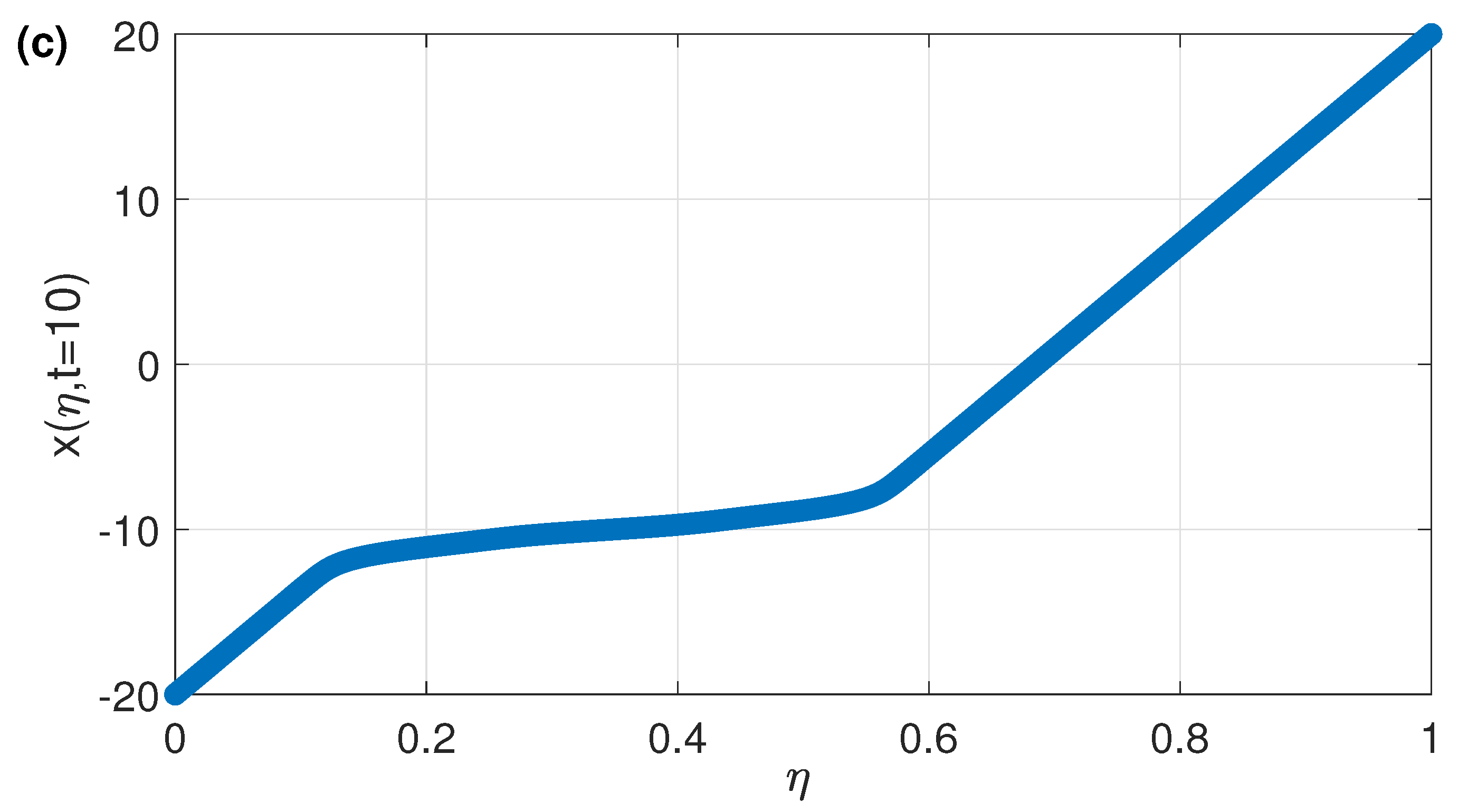
3.2. Numerical Solutions Using an Adaptive Mesh
3.3. Results and Discussion
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Li, T.; Viglialoro, G. Analysis and Explicit Solvability of Degenerate Tensorial Problems. Bound. Value Probl. 2018, 2018, 2. [Google Scholar] [CrossRef]
- Lu, D.; Seadawy, A.R.; Ali, A. Dispersive Analytical Wave Solutions of Three Nonlinear Dynamical Water Waves Models via Modified Mathematical Method. Results Phys. 2019, 13, 102177. [Google Scholar] [CrossRef]
- Shen, S.; Yang, Z.; Li, X. Periodic Propagation of Complex-Valued Hyperbolic-Cosine-Gaussian Solitons and Breathers with Complicated Light Field Structure in Strongly Nonlocal Nonlinear Media. Commun. Nonlinear Sci. Numer. Simul. 2021, 103, 106005. [Google Scholar] [CrossRef]
- Shen, S.; Yang, Z.; Pang, Z.; Ge, Y. The Complex-Valued Astigmatic Cosine-Gaussian Soliton Solution of the Nonlocal Nonlinear Schrödinger Equation and Its Transmission Characteristics. Appl. Math. Lett. 2022, 125, 107755. [Google Scholar] [CrossRef]
- Song, L.; Yang, Z.; Li, X. Coherent Superposition Propagation of Laguerre–Gaussian and Hermite–Gaussian Solitons. Appl. Math. Lett. 2020, 102, 106114. [Google Scholar] [CrossRef]
- Zou, Z.; Guo, R. The Riemann–Hilbert Approach for the Higher-Order Gerdjikov–Ivanov Equation, Soliton Interactions and Position Shift. Commun. Nonlinear Sci. Numer. Simul. 2023, 124, 107316. [Google Scholar] [CrossRef]
- Nasreen, N.; Seadawy, A.R.; Lu, D.; Arshad, M. Construction of Modulation Instability Analysis and Optical Soliton Solutions of Pertubed Nonlinear Schrödinger Dynamical Equation with Power Law Nonlinearity in Non-Kerr Medium. Results Phys. 2019, 13, 102263. [Google Scholar] [CrossRef]
- Shehzad, K.; Seadawy, A.R.; Wang, J.; Arshad, M. Multi Peak Solitons and Btreather Types Wave Solutions of Unstable NLSEs with Stability and Applications in Optics. Opt. Quantum Electron. 2022, 55, 7. [Google Scholar] [CrossRef]
- Wazwaz, A. Completely Integrable Coupled KdV and Coupled KP Systems. Commun. Nonlinear Sci. Numer. Simul. 2010, 15, 2828–2835. [Google Scholar] [CrossRef]
- Hao, W. An Adaptive Homotopy Tracking Algorithm for Solving Nonlinear Parametric Systems with Applications in Nonlinear ODEs. Appl. Math. Lett. 2022, 125, 107767. [Google Scholar] [CrossRef]
- Kumar, D.; Seadawy, A.R.; Joardar, A.K. Modified Kudryashov Method via New Exact Solutions for Some Conformable Fractional Differential Equations Arising in Mathematical Biology. Chin. J. Phys. 2018, 56, 75–85. [Google Scholar] [CrossRef]
- Bekir, A.; Ünsal, Ö. Analytic Treatment of Nonlinear Evolution Equations Using First Integral Method. Pramana 2012, 79, 3–17. [Google Scholar] [CrossRef]
- Chen, B.; Chen, B.; Zhao, H. A New Generalized Algebraic Method and Its Application in Nonlinear Evolution Equations with Variable Coefficients. Z. Naturforschung 2005, 60, 211–220. [Google Scholar] [CrossRef]
- Aasaraai, A. The Application of Modified F-Expansion Method Solving the MacCari’s System. Br. J. Math. Comput. Sci. 2015, 11, 1–14. [Google Scholar] [CrossRef]
- Shi-Kuo, L.; Fu, Z.; Liu, S.; Zhao, Q. Jacobi Elliptic Function Expansion Method and Periodic Wave Solutions of Nonlinear Wave Equations. Phys. Lett. 2001, 289, 69–74. [Google Scholar] [CrossRef]
- Alharbi, A.; Almatrafi, M.B.; Seadawy, A.R. Construction of the Numerical and Analytical Wave Solutions of the Joseph–Egri Dynamical Equation for the Long Waves in Nonlinear Dispersive Systems. Int. J. Mod. Phys. B 2020, 34, 2050289. [Google Scholar] [CrossRef]
- Kupershmidt, B.A. Lie Algebras and Korteweg-de Vries Equations. Phys. D Nonlinear Phenom. 1987, 27, 294–310. [Google Scholar] [CrossRef]
- Liu, C.; Liu, X. Exact Solutions of the Classical Drinfel’d–Sokolov–Wilson Equations and the Relations among the Solutions. Phys. Lett. 2002, 303, 197–203. [Google Scholar] [CrossRef]
- Zhao, X.; Zhi, H. An Improved F-Expansion Method and Its Application to Coupled Drinfel’d–Sokolov–Wilson Equation. Commun. Theor. Phys. 2008, 50, 309–314. [Google Scholar] [CrossRef]
- İnç, M. On Numerical Doubly Periodic Wave Solutions of the Coupled Drinfel’d–Sokolov–Wilson Equation by the Decomposition Method. Appl. Math. Comput. 2006, 172, 421–430. [Google Scholar] [CrossRef]
- Ren, B.; Lou, Z.-M.; Liang, Z.-F.; Tang, X. Nonlocal Symmetry and Explicit Solutions for Drinfel’d-Sokolov-Wilson System. Eur. Phys. J. Plus 2016, 131, 441. [Google Scholar] [CrossRef]
- Mısırlı, E.; Gürefe, Y. Exp-Function Method for Solving Nonlinear Evolution Equations. Math. Comput. Appl. 2011, 16, 258–266. [Google Scholar] [CrossRef]
- Sahoo, S.; Ray, S.S. New Double-Periodic Solutions of Fractional Drinfeld–Sokolov–Wilson Equation in Shallow Water Waves. Nonlinear Dyn. 2017, 88, 1869–1882. [Google Scholar] [CrossRef]
- Bibi, S.; Mohyud-Din, S.T. New Traveling Wave Solutions of Drinefel’d–Sokolov–Wilson Equation Using Tanh and Extended Tanh Methods. J. Egypt. Math. Soc. 2014, 22, 517–523. [Google Scholar] [CrossRef]
- Al-Askar, F.M.; Cesarano, C.; Mohammed, W.W. The Analytical Solutions of Stochastic-Fractional Drinfel’d-Sokolov-Wilson Equations via (Ǵ/G)-Expansion Method. Symmetry 2022, 14, 2105. [Google Scholar] [CrossRef]
- Al-Askar, F.M.; Mohammed, W.W.; Samura, S.K.; El-Morshedy, M. The Exact Solutions for Fractional-Stochastic Drinfel’d–Sokolov–Wilson Equations Using a Conformable Operator. J. Funct. Spaces 2022, 2022, 1–9. [Google Scholar] [CrossRef]
- Meral, G. Numerical Solution of Drinfel’d Sokolov Wilson System Using Differential Quadrature and Finite Difference Methods. Karaelmas Sci. Eng. J. 2019, 9, 232–236. [Google Scholar] [CrossRef]
- Islam, S.; Wang, H. Some Analytical Soliton Solutions of the Nonlinear Evolution Equations. J. Ocean. Eng. Sci. 2022. [Google Scholar] [CrossRef]
- Alharbi, A. A Study of Traveling Wave Structures and Numerical Investigation of Two-Dimensional Riemann Problems with Their Stability and Accuracy. Cmes-Comput. Model. Eng. Sci. 2023, 134, 2193–2209. [Google Scholar] [CrossRef]
- Ghanbari, B.; Yusuf, A.; İnç, M.; Băleanu, D. The New Exact Solitary Wave Solutions and Stability Analysis for the (2 + 1) (2 + 1)-Dimensional Zakharov–Kuznetsov Equation. Adv. Differ. Equ. 2019, 2019, 49. [Google Scholar] [CrossRef]
- Alharbi, A.R. Numerical Solution of Thin-Film Flow Equations Using Adaptive Moving Mesh Methods. Keele University, 2016. Available online: https://eprints.keele.ac.uk/id/eprint/2356 (accessed on 1 March 2016).

| The Relative Error () | The Relative Error () | |
|---|---|---|
| 400 | ||
| 800 | ||
| 1600 | ||
| 2000 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Alhejaili, S.H.; Alharbi, A. Structure of Analytical and Numerical Wave Solutions for the Nonlinear (1 + 1)-Coupled Drinfel’d–Sokolov–Wilson System Arising in Shallow Water Waves. Mathematics 2023, 11, 4598. https://doi.org/10.3390/math11224598
Alhejaili SH, Alharbi A. Structure of Analytical and Numerical Wave Solutions for the Nonlinear (1 + 1)-Coupled Drinfel’d–Sokolov–Wilson System Arising in Shallow Water Waves. Mathematics. 2023; 11(22):4598. https://doi.org/10.3390/math11224598
Chicago/Turabian StyleAlhejaili, Sumayah Hamzah, and Abdulghani Alharbi. 2023. "Structure of Analytical and Numerical Wave Solutions for the Nonlinear (1 + 1)-Coupled Drinfel’d–Sokolov–Wilson System Arising in Shallow Water Waves" Mathematics 11, no. 22: 4598. https://doi.org/10.3390/math11224598
APA StyleAlhejaili, S. H., & Alharbi, A. (2023). Structure of Analytical and Numerical Wave Solutions for the Nonlinear (1 + 1)-Coupled Drinfel’d–Sokolov–Wilson System Arising in Shallow Water Waves. Mathematics, 11(22), 4598. https://doi.org/10.3390/math11224598





