Prediction of the Transient Local Energy by Energy Finite Element Analysis
Abstract
:1. Introduction
2. Energy Flow Model
2.1. Energy Density Governing Equation
2.2. Analytical Solution of the Transient Equation
2.3. Energy Transmission Coefficients for Beams
3. Validation and Discussion
3.1. Numerical Simulations and Verifications
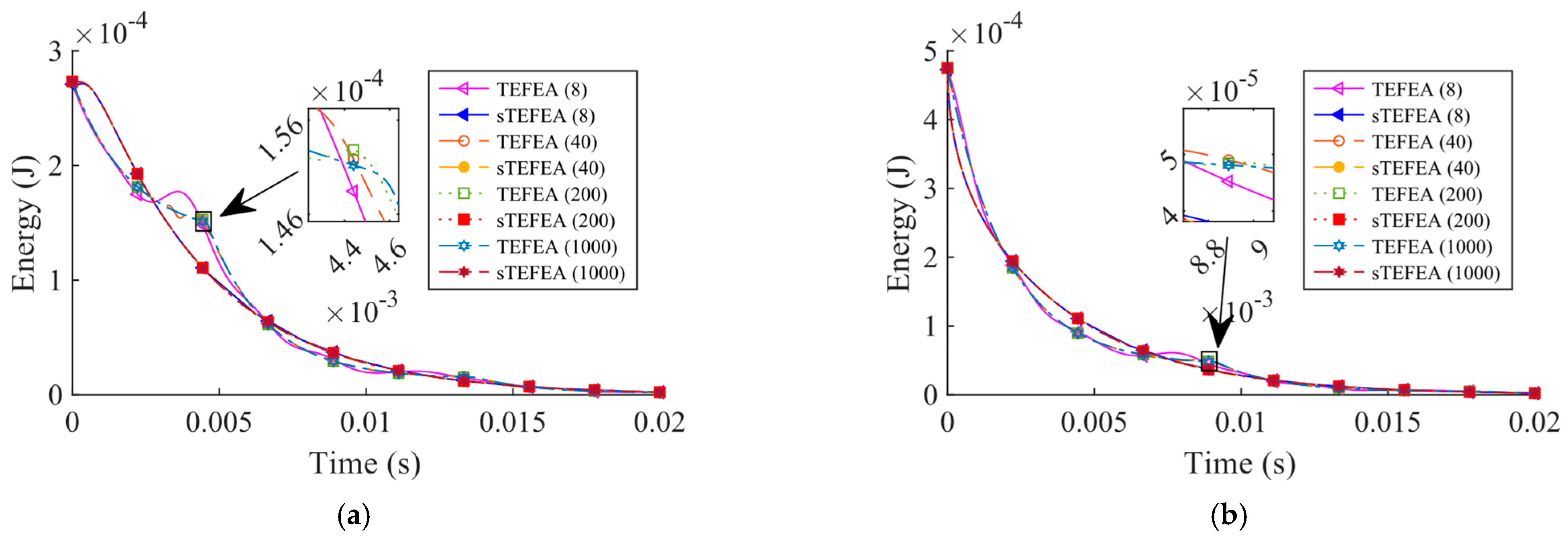
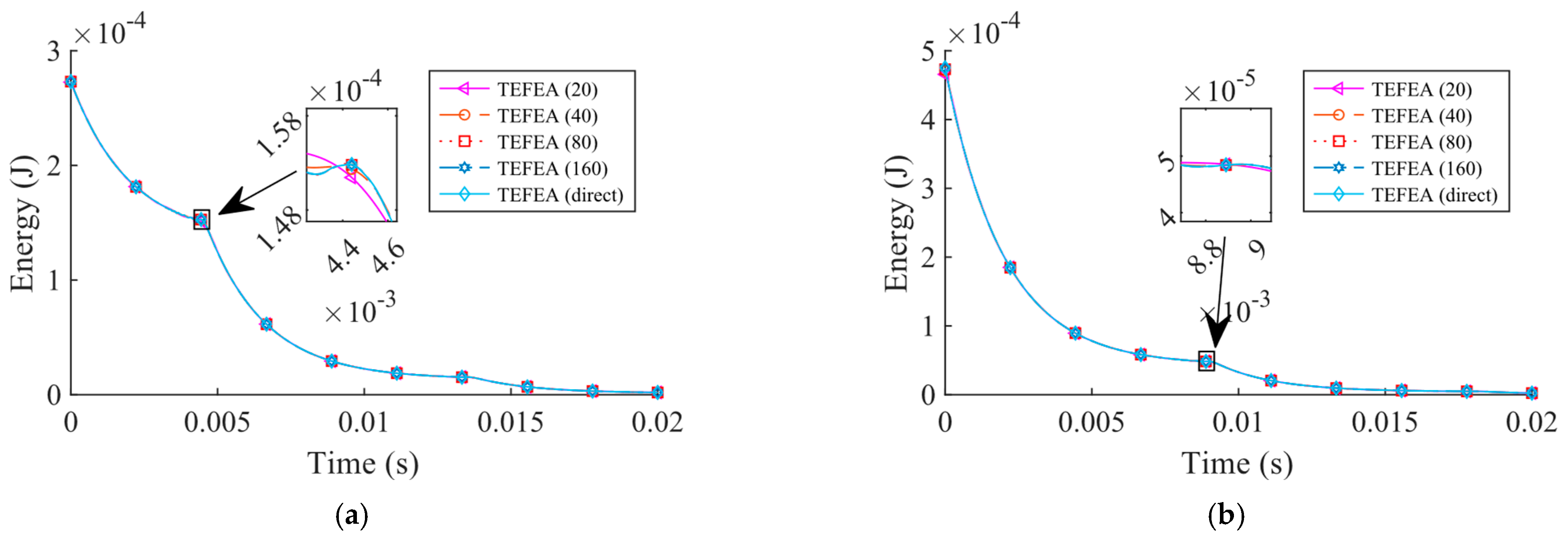
3.2. A Single Beam under the Unloading Condition
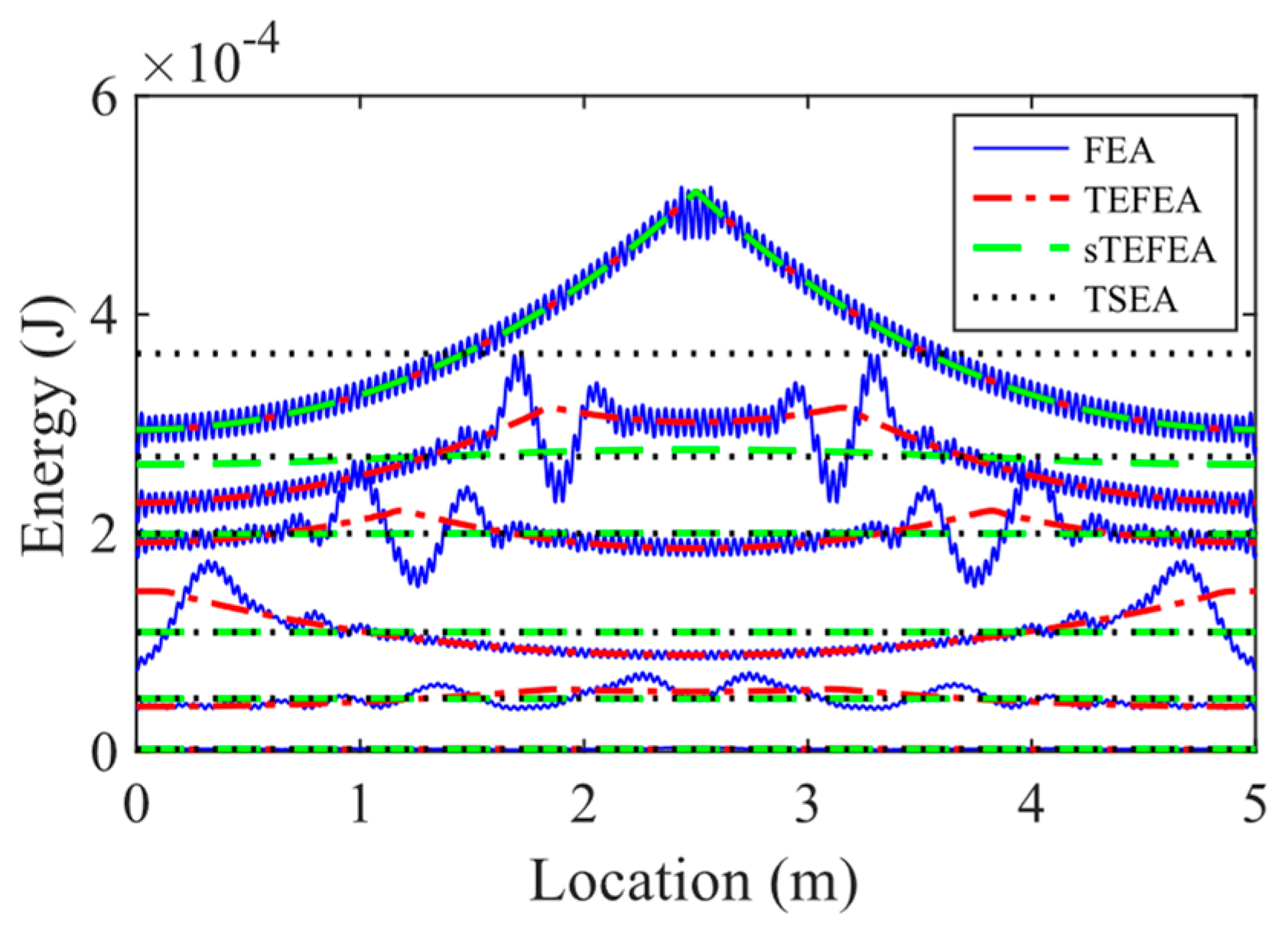
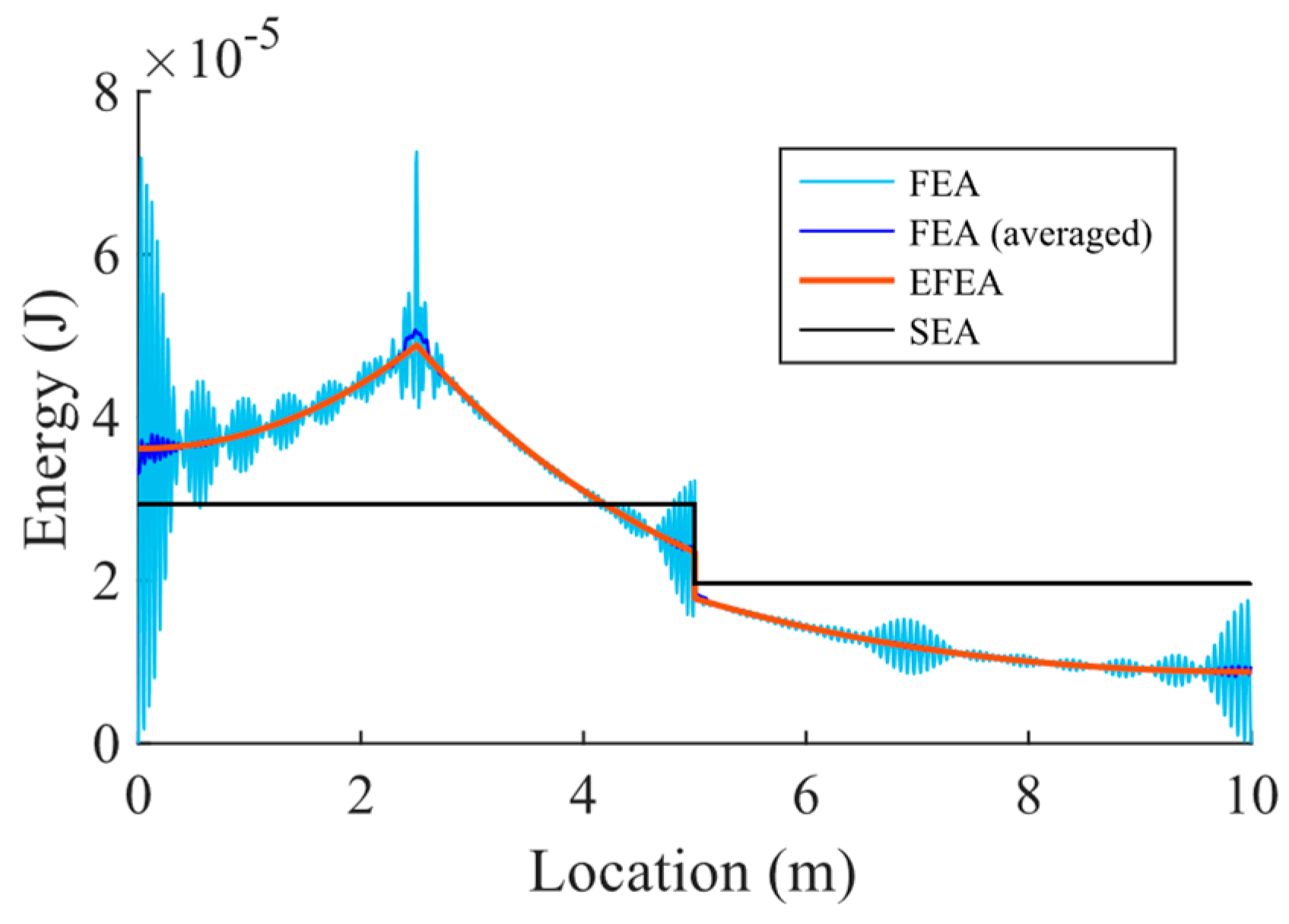
3.3. Coupled Beams under Unloading Condition
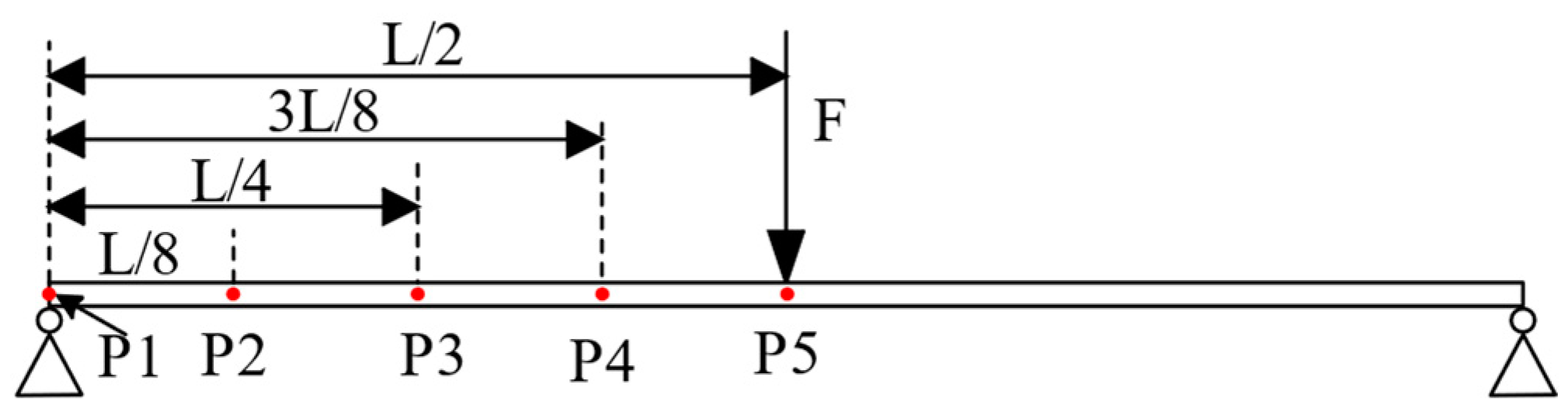
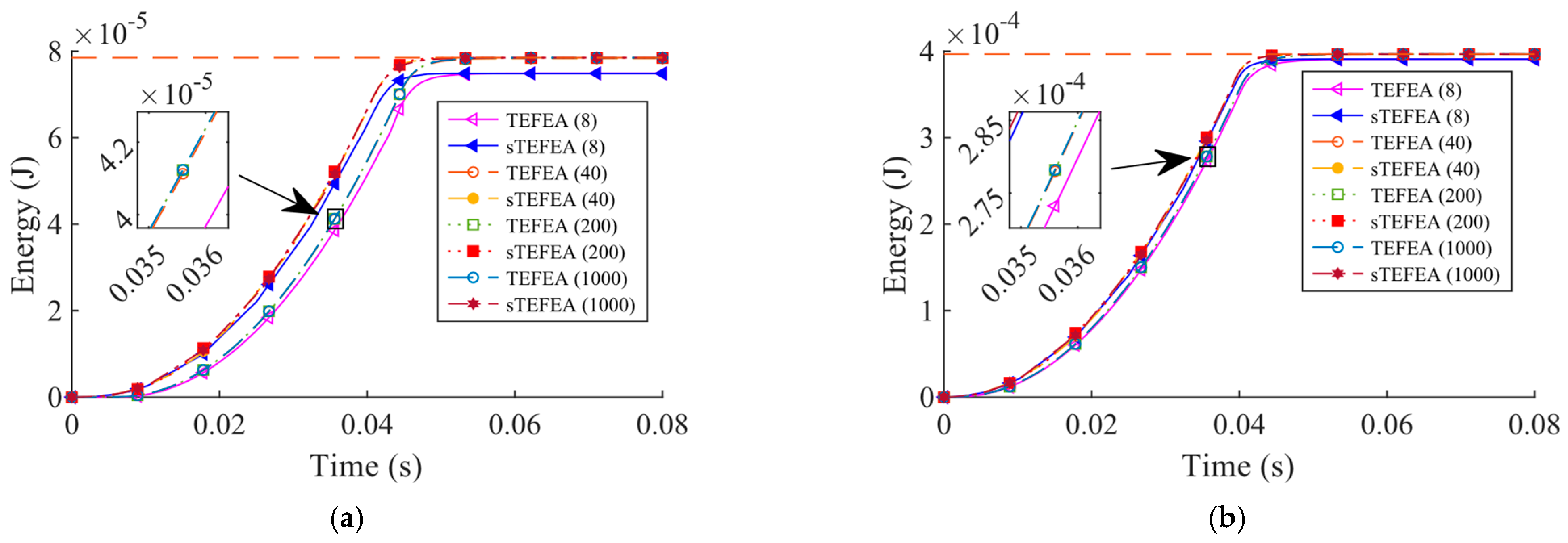
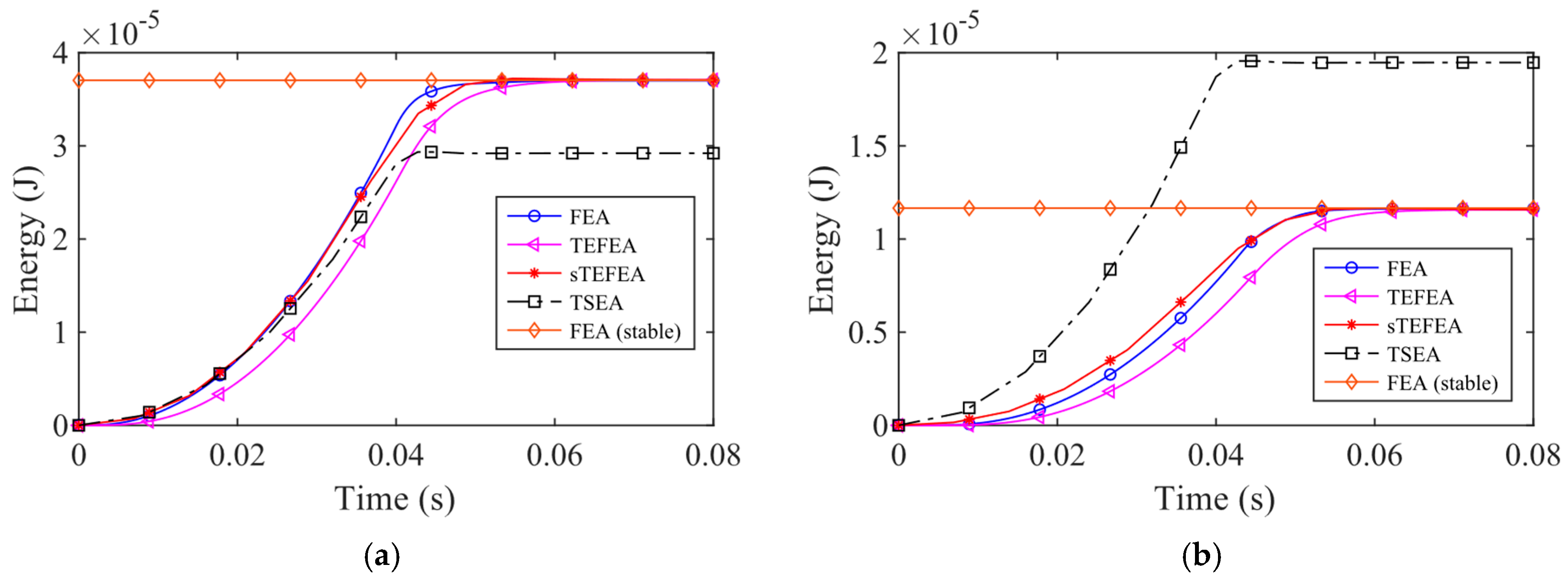
3.4. Coupled Beams under the Loading Conditions
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
Appendix B
References
- Lyon, R.H.; DeJong, R.G. Theory and Application of Statistical Energy Analysis, 2nd ed.; Newnes: Boston, MA, USA, 1995. [Google Scholar] [CrossRef]
- Desmet, W. Mid-frequency vibro-acoustic modelling: Challenges and potential solutions. In Proceedings of the ISMA, Lueven, Belgium, 16–18 September 2002; p. 12. [Google Scholar]
- Roque, C.M.C.; Ferreira, A.J.M.; Reddy, J.N. Analysis of Timoshenko nanobeams with a nonlocal formulation and meshless method. Int. J. Eng. Sci. 2011, 49, 976–984. [Google Scholar] [CrossRef]
- Banerjee, J.R. Free vibration analysis of a twisted beam using the dynamic stiffness method. Int. J. Solids Struct. 2001, 38, 6703–6722. [Google Scholar] [CrossRef]
- Banerjee, J.R.; Ananthapuvirajah, A. An exact dynamic stiffness matrix for a beam incorporating Rayleigh–Love and Timoshenko theories. Int. J. Mech. Sci. 2019, 150, 337–347. [Google Scholar] [CrossRef]
- Wang, T.; Altabey, W.A.; Noori, M.; Ghiasi, R. A Deep Learning Based Approach for Response Prediction of Beam-like Structures. Struct. Durab. Health Monit. 2020, 14, 315. [Google Scholar] [CrossRef]
- Rajasekaran, S.; Khaniki, H.B.; Ghayesh, M.H. On the mechanics of shear deformable micro beams under thermo-mechanical loads using finite element analysis and deep learning neural network. Mech. Based Des. Struct. Mach. 2022, 51, 6612–6656. [Google Scholar] [CrossRef]
- Liu, Z.; Niu, J.; Gao, X. An improved approach for analysis of coupled structures in Energy Finite Element Analysis using the coupling loss factor. Comput. Struct. 2018, 210, 69–86. [Google Scholar] [CrossRef]
- Manning, J.E. Predicting mechanical shock transmission. Shock Vib. Bull. 1968, 37, 65–70. [Google Scholar]
- Pinnington, R.J.; Lednik, D. Transient statistical energy analysis of an impulsively excited two oscillator system. J. Sound Vib. 1996, 189, 249–264. [Google Scholar] [CrossRef]
- Pinnington, R.J.; Lednik, D. Transient energy flow between two coupled beams. J. Sound Vib. 1996, 189, 265–287. [Google Scholar] [CrossRef]
- Langley, R.S.; Hawes, D.H.; Butlin, T.; Ishii, Y. A derivation of the Transient Statistical Energy Analysis (TSEA) equations with benchmark applications to plate systems. J. Sound Vib. 2019, 445, 88–102. [Google Scholar] [CrossRef]
- Hawes, D.H.; Langley, R.S.; Butlin, T.; Ishii, Y. A hybrid Finite Element-Statistical Energy Analysis method for impulsive and transient loading. J. Sound Vib. 2019, 459, 114849. [Google Scholar] [CrossRef]
- Nefske, D.J.; Sung, S.H. Power Flow Finite Element Analysis of Dynamic Systems: Basic Theory and Application to Beams. J. Vib. Acoust. 1989, 111, 94–100. [Google Scholar] [CrossRef]
- Wohlever, J.; Bernhard, R. Energy distributions in rods and beams. In Proceedings of the 12th Aeroacoustic Conference, San Antonio, TX, USA, 10–12 April 1989; p. 1122. [Google Scholar]
- Bouthier, O.; Bernhard, R. Simple models of energy flow in vibrating membranes. J. Sound Vib. 1995, 182, 129–147. [Google Scholar] [CrossRef]
- Bouthier, O.M.; Bernhard, R.J. Models of space-averaged energetics of plates. AIAA J. 1992, 30, 616–623. [Google Scholar] [CrossRef]
- Bouthier, O.; Bernhard, R. Simple models of the energetics of transversely vibrating plates. J. Sound Vib. 1995, 182, 149–164. [Google Scholar] [CrossRef]
- Park, D.-H.; Hong, S.-Y.; Kil, H.-G.; Jeon, J.-J. Power flow models and analysis of in-plane waves in finite coupled thin plates. J. Sound Vib. 2001, 244, 651–668. [Google Scholar] [CrossRef]
- Park, Y.-H.; Hong, S.-Y. Vibrational Energy Flow Analysis of Corrected Flexural Waves in Timoshenko Beam—Part I: Theory of an Energetic Model. Shock Vib. 2006, 13, 137–165. [Google Scholar] [CrossRef]
- Park, Y.-H.; Hong, S.-Y. Vibrational power flow models for transversely vibrating finite Mindlin plate. J. Sound Vib. 2008, 317, 800–840. [Google Scholar] [CrossRef]
- Park, Y.-H. Energy flow finite element analysis of general Mindlin plate structures coupled at arbitrary angles. Int. J. Nav. Archit. Ocean Eng. 2019, 11, 435–447. [Google Scholar] [CrossRef]
- Han, J.-B.; Hong, S.-Y.; Song, J.-H.; Kwon, H.-W. Vibrational energy flow models for the Rayleigh–Love and Rayleigh–Bishop rods. J. Sound Vib. 2014, 333, 520–540. [Google Scholar] [CrossRef]
- Yan, X. Energy Finite Element Analysis Developments for High Frequency Vibration Analysis of Composite Structures. Ph.D. Thesis, The University of Michigan, Ann Arbor, MI, USA, 2008. [Google Scholar]
- Lin, Z.; Chen, X.; Zhang, B. Application of the energy finite element analysis to vibration of beams with stepped thickness and variable cross-section. J. Vibroeng. 2018, 20, 2237–2252. [Google Scholar] [CrossRef]
- Zhang, W.; Vlahopoulos, N.; Wu, K. An energy finite element formulation for high-frequency vibration analysis of externally fluid-loaded cylindrical shells with periodic circumferential stiffeners subjected to axi-symmetric excitation. J. Sound Vib. 2005, 282, 679–700. [Google Scholar] [CrossRef]
- Zhang, W.; Wang, A.; Vlahopoulos, N.; Wu, K. A vibration analysis of stiffened plates under heavy fluid loading by an energy finite element analysis formulation. Finite Elem. Anal. Des. 2005, 41, 1056–1078. [Google Scholar] [CrossRef]
- Xie, M.; Li, L.; Shang, X.; Zhao, J. Initial Investigation of Energy Finite Element Validation on High-Frequency Flexural Vibration of Stiffened Thin Orthotropic Plates. Shock Vib. 2018, 2018, 10. [Google Scholar] [CrossRef]
- Nokhbatolfoghahai, A.; Navazi, H.; Haddadpour, H. High-frequency random vibrations of a stiffened plate with a cutout using energy finite element and experimental methods. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 2020, 234, 3297–3317. [Google Scholar] [CrossRef]
- Teng, X.; Han, Y.; Jiang, X.; Chen, X.; Zhou, M. Energy Flow Analysis Model of High-Frequency Vibration Response for Plates with Free Layer Damping Treatment. Mathematics 2023, 11, 1379. [Google Scholar] [CrossRef]
- Wang, D.; Xie, M.; Li, Y. High-Frequency Dynamic Analysis of Plates in Thermal Environments Based on Energy Finite Element Method. Shock Vib. 2015, 2015, 14. [Google Scholar] [CrossRef]
- Chen, Z.; Yang, Z.; Guo, N.; Zhang, G. An energy finite element method for high frequency vibration analysis of beams with axial force. Appl. Math. Model. 2018, 61, 521–539. [Google Scholar] [CrossRef]
- Xie, M.X.; Chen, H.L.; Wu, J.H.; Sun, F.G. Application of Energy Finite Element Method to High-frequency Structural-acoustic Coupling of an Aircraft Cabin with Truncated Conical Shape. Comput. Model. Eng. Sci. 2010, 61, 1–22. [Google Scholar] [CrossRef]
- Vlahopoulos, N.; Schiller, N.; Lee, S. Energy finite element analysis developments for vibration analysis of composite aircraft structures. SAE Int. J. Aerosp. 2011, 4, 593–601. [Google Scholar] [CrossRef]
- Shen, Y.; Xu, Y.; Sheng, X.; Wan, S.; Yin, X. Vibration Energy Transfer Characteristics of Panels with Multiple Coupling Forms in Satellites. Int. J. Aeronaut. Space Sci. 2023, 24, 1231–1243. [Google Scholar] [CrossRef]
- Zhang, W.; Wang, A.; Vlahopoulos, N. An alternative energy finite element formulation based on incoherent orthogonal waves and its validation for marine structures. Finite Elem. Anal. Des. 2002, 38, 1095–1113. [Google Scholar] [CrossRef]
- Homg, S.B.; Vlahopoulos, N. Application of a hybrid finite-element formulation for structure-borne vibration in an automotive vehicle structure. J. Acoust. Soc. Am. 2006, 119, 3297–3298. [Google Scholar] [CrossRef]
- Vlahopoulos, N.; Wu, K. Energy finite element analysis of naval vehicles. J. Acoust. Soc. Am. 2010, 127, 1850. [Google Scholar] [CrossRef]
- Zheng, X.; Dai, W.; Qiu, Y.; Hao, Z. Prediction and energy contribution analysis of interior noise in a high-speed train based on modified energy finite element analysis. Mech. Syst. Signal Process. 2019, 126, 439–457. [Google Scholar] [CrossRef]
- Ichchou, M.N.; Le Bot, A.; Jezequel, L. A transient local energy approach as an alternative to transient sea: Wave and telegraph equations. J. Sound Vib. 2001, 246, 829–840. [Google Scholar] [CrossRef]
- Sui, F.S.; Ichchou, M.N.; Jezequel, L. Prediction of vibroacoustics energy using a discretized transient local energy approach and comparison with TSEA. J. Sound Vib. 2002, 251, 163–180. [Google Scholar] [CrossRef]
- Sui, F.; Ichchou, M.N. Prediction of Time-Varying Vibroacoustic Energy Using a New Energy Approach. J. Vib. Acoust. 2004, 126, 184–189. [Google Scholar] [CrossRef]
- Chen, Q.; Fei, Q.; Li, Y.; Wu, S.; Yang, X. Prediction of the transient energy response for complex vibro-acoustic systems. J. Mech. Sci. Technol. 2019, 33, 495–504. [Google Scholar] [CrossRef]
- Cremer, L.; Heckl, M.; Petersson, B.A.T. Structure-Borne Sound: Structural Vibrations and Sound Radiation at Audio Frequencies, 3rd ed.; Springer: Berlin/Heidelberg, Germany, 2005. [Google Scholar]
- Cho, P.E.-H. Energy Flow Analysis of Coupled Structures. Ph.D. Thesis, Purdue University, West Lafayette, IN, USA, 1993. [Google Scholar]
- Langley, R.S.; Heron, K.H. Elastic wave transmission through plate/beam junctions. J. Sound Vib. 1990, 143, 241–253. [Google Scholar] [CrossRef]
- Lai, M.; Soom, A. Statistical energy analysis for the time-integrated transient response of vibrating systems. J. Vib. Acoust. 1990, 112, 206–213. [Google Scholar] [CrossRef]
- Kong, X.; Chen, H.; Zhu, D.; Zhang, W. Study on the validity region of Energy Finite Element Analysis. J. Sound Vib. 2014, 333, 2601–2616. [Google Scholar] [CrossRef]
- Chen, Q.; Fei, Q.; Wu, S.; Li, Y.; Yang, X. An efficient transient analysis method for time-varying structures based on statistical energy analysis. Mech. Res. Commun. 2018, 91, 93–99. [Google Scholar] [CrossRef]










Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, H.; Yu, K.; Zhao, R. Prediction of the Transient Local Energy by Energy Finite Element Analysis. Mathematics 2023, 11, 4590. https://doi.org/10.3390/math11224590
Wang H, Yu K, Zhao R. Prediction of the Transient Local Energy by Energy Finite Element Analysis. Mathematics. 2023; 11(22):4590. https://doi.org/10.3390/math11224590
Chicago/Turabian StyleWang, Huaizhi, Kaiping Yu, and Rui Zhao. 2023. "Prediction of the Transient Local Energy by Energy Finite Element Analysis" Mathematics 11, no. 22: 4590. https://doi.org/10.3390/math11224590
APA StyleWang, H., Yu, K., & Zhao, R. (2023). Prediction of the Transient Local Energy by Energy Finite Element Analysis. Mathematics, 11(22), 4590. https://doi.org/10.3390/math11224590





