1. Introduction and Background
Generalized equations are introduced by Robinson [
1] with the following form:
where
is a single-valued mapping and
is a set-valued mapping between arbitrary Banach spaces. Model (
1) as well as its various specifications have been widely recognized as a useful way to study optimization-related mathematical problems, such as linear and nonlinear complementarity problems, variational inequalities, first-order necessary conditions for nonlinear programming, equilibrium problems in both engineering and economics, etc.; see, e.g., [
2,
3,
4,
5,
6] and the references therein. Specifically, it is called a variational system when
F stands for the set of limiting subgradients. When we have
F representing normal cone mapping associated with a closed convex set, it is called a variational inequality. For more details, please refer to [
7,
8] and the bibliographies therein.
To find an approximate solution to the generalized equation, there have been extensive studies of different versions of Newton’s method which are based on the assumption of strong metric regularity (cf. [
9,
10,
11,
12,
13,
14,
15,
16,
17,
18,
19,
20,
21]). Newton’s method for unconstrained generalized Equation (
1) dates back to Josephy [
22], which is stated as follows. For the
kth iterate
, the
th iterate
is computed according to the following inclusion:
where
represents the derivative of
f. It simplifies to the regular version of Newton’s method for solving the nonlinear equation
when
F is the zero mapping. When the single-valued mapping
f is smooth, convergence rate results of Newton’s method (
2) were established under the assumption that the partial linearization of the set-valued mapping
is (strongly) metrically regular around
for 0, where
is the solution of (
1). It is well understood that there exists a sequence generated by (
2) which converges linearly if
is continuous on a neighborhood of
and converges quadratically, provided that
is Lipschitz continuous on a neighborhood of
, respectively. When the function
f in (
2) is nonsmooth, we cannot use the usual method of partially linearizing on
f anymore. In this situation, there are different ways of constructing abstract iterative procedures which are mainly based on the idea of point-based approximation (PBA). The concept of PBA was first developed by Robinson [
23] and has been studied by many researchers. Geoffroy and Piétrus proposed in [
24] a generalized concept of point-based approximation to generate an iterative procedure for generalized equations. The authors obtained convergence results on the nonsmooth Newton-type procedure which includes both local and semilocal versions (see [
12,
13,
16,
24,
25,
26] and the references therein).
Inexact Newton methods for solving smooth equation
in finite dimensions (i.e., (
1) with
and
) were introduced by Dembo, Eisenstat, and Steihaug [
27]. Specifically, for a given sequence
and a starting point
, the
th iterate is selected to satisfy the condition
where
stands for the closed ball of radius
centered at 0. For solving generalized Equation (
1) in the Banach space setting, Dontchev and Rockafellar [
15] proposed the following inexact Newton method:
where
is a sequence of set-valued mappings with closed graphs which represent the inexactness of the general model (
1) and are not actually calculated in a specified manner. Under the metric regularity assumption, Dontchev and Rockafellar [
15] show that the aforementioned method is executable and generate a sequence which converges either linearly, superlinearly, or quadratically.
In this paper, we focus on the study of a general iterative procedure for solving the nonsmooth constrained generalized equation
where
is an open set,
is a closed convex set,
is a single-valued mapping which is not necessarily smooth, and
is a closed set-valued mapping. Due to the presence of the constraint set
C, constrained generalized Equation (
5) can be viewed as an abstract model which covers several constrained optimization problems such as the Constrained Variational Inequality Problem, and, in particular, the Split Variational Inequality Problem. For more details about these problems, please refer to [
28,
29] and the references therein.
For solving the constrained generalized Equation (
5) when
f is smooth, Oliveira et al. [
30] proposed a Newton’s method with feasible inexact projection (the Newton-InexP method). The procedure of incorporating a feasible inexact projection rectifies the shortcoming that, in standard Newton’s method (
2), the next iterate
may be infeasible for the constraint set
C. Under the condition of metric regularity and assuming that the derivative
is Lipschitz continuous, the authors in [
30] established linear and quadratic convergence for the Newton-InexP method.
When the single-valued mapping
f in the constrained generalized Equation (
5) is not smooth, the partial linearization technique in the Newton-InexP approach in [
30] is no longer applicable, and hence a new approach without involving the derivative of
f is in demand. To this end, in this paper, we introduce a weak version of point-based approximation. For a class of single-valued functions which admit weak point-based approximations, we address a general inexact iterative procedure for solving (
5) which incorporates a feasible inexact projection onto the constraint set. We aim to establish higher order convergence results for the proposed method assuming metric regularity on the weak point-based approximation of the mapping which generates the generalized equation. Taking into account the fact that in general metric regularity property cannot guarantee that every sequence generated with this method converges to a solution, we consider a restricted version of the aforementioned generalized procedure and establish convergence results for each iterative sequence accordingly.
The rest of this paper is structured in the following way. In
Section 2, we provide the notations and a few technical results that we will use in the rest of the paper. In
Section 3, we define the general iterative procedure for nonsmooth generalized Equation (
5) and conduct local convergence analysis. Exact conditions are provided to ensure higher order convergence for this method as well as convergence for the arbitrary iterative sequence of a restricted version of the aforementioned procedure. In
Section 5, we provide a numerical example to illustrate the assumptions and the local convergence result of the proposed approach.
2. Notation and Auxiliary Results
In this section, we display a few notations, definitions, and results that are utilized all through the paper. Let
. The symbol
stands for the closed unit ball of the space
, while
indicates the closed ball of radius
centered at
. Given subsets
, define the distance from
to
C and the excess from
C to
D using
respectively, with the convention that
,
if
, and
if
. Let
be a set-valued mapping and its graph be defined as
F is said to have a closed graph if the set
is closed in the product space
. We use
to represent the inverse mapping of
F with
for all
. For a single-valued mapping
, it is said to be Hölder calm at
of order
, if there exist constants
such that
We say that
g is Lipschitzian on
with modulus
L, if
We first recall the concept of
-point-based approximation (also called
-PBA), which was introduced in [
24].
Definition 1. Let Ω be an open subset of a metric space , Y be a normed linear space, and be a single-valued mapping. Fix and . We say that the mapping is an -PBA on Ω for f with modulus , if both of the following assertions hold:
(a) for all , where ;
(b) The mapping is Lipschitzian on Ω with modulus , where is a positive function of κ.
It is easy to see that when both
n and
take the value of one in the above assertions, the
-PBA reduces to the PBA of
f on
according to Robinson [
23]. In the nonsmooth framework, the normal maps are referred to as functions that have a (1,1)-PBA. For the smooth case, the authors showed in [
24] that, if a function
f is twice Fréchet differentiable on
and satisfies that
is
with exponent
and with constant
, then it has a
-PBA represented by
. For more details, please refer to the appendix in [
24].
Next, we define the concept of
-weak-point-based approximation for single-valued mappings at given points, which is essential in the generalized iterative procedure studied in
Section 3.
Definition 2. Let Ω be an open subset of a metric space , Y be a normed linear space, and be a single-valued mapping. Fix and . We say that the mapping is an -weak-point-based approximation (-WPBA) at for f with modulus and constant , if both of the following assertions hold:
(a) for all , where ;
(b) For any , the mapping is Lipschitzian on Ω with modulus , where is a positive function of κ.
It is clear that the notion of
-WPBA is weaker than the notion of
-PBA. In the smooth setting, the authors proved in Lemma 3.1 of [
31] that any continuously differentiable mapping
f around
such that the derivative
is Hölder calm (which is weaker than the Lipschitz continuity) of order
admits a
-PBA given by
. Let us observe that relation
implies in particular that
.
In the following, we present the definition of (strong) metric regularity, which plays an important role in our later analysis.
Definition 3. Let , be a set-valued mapping and . F is said to be metrically regular at for with constants , and b, if F is said to be strongly metrically regular at for with constants , and b, if (7) holds and is singleton for each . It is widely understood that
F is strongly metrically regular at
for
with constants
, and
b if and only if the mapping
is single-valued and Lipschitz continuous on
; for more details, see [
7]. If
is smooth around
, then
f is strongly metrically regular at
for
if and only if
is invertible.
In [
30], the authors introduced the following concept of feasible inexact projection, which is the basic structure of the Newton-InexP method studied therein.
Definition 4. Let be a closed convex set, , and . The feasible inexact projection mapping relative to x with error tolerance θ is denoted by . The definition is as follows:Any element is said to be a feasible inexact projection of u onto C with respect to x and with error tolerance θ. Since
is a closed convex set, Proposition 2.1.3 of [
32] implies that for each
and
, we have
and
, where
denotes the exact projection mapping (see Remark 2 of [
30]). In particular, the point
is an approximate feasible solution for the projection subproblem
, which satisfies
for all
.
The next result, Lemma 1 of [
30], is useful in the remainder of this paper.
Lemma 1. Let , , and . Then, for any , we have We end this section by recalling the well-known contraction mapping principle for set-valued mappings (see Theorem 5E.2 of [
7]).
Lemma 2. Let be a set-valued mapping defined on a complete metric space X, , and let be such that the set is closed in . Given , impose the following assumptions:
- 1.
.
- 2.
.
Then, Φ has a fixed point in , i.e., there exists such that . In addition, if Φ is single-valued, then Φ has a unique fixed point in .
3. Convergence Analysis
In this section, employing the notions of
-WPBA and the feasible inexact projection defined in
Section 2, we propose a general iterative procedure for solving nonsmooth constrained generalized Equation (
5).
Let
be such that
and
be an
-WPBA at
for
f. To formulize the iterative procedure, we choose
,
as the input data and
for
as the inexactness (Algorithm 1).
| Algorithm 1 General inexact projection method |
Step 0. Let and be given, and set .
Step 1. If , then stop; otherwise, compute such that
Step 2. If , set ; otherwise, take any satisfying
Step 3. Set , and go to Step 1. |
Note that in comparison with (
4), the mapping
in Step 1 which represents inexactness now depends on the current iteration
only. In Step 2, we utilize the weak point-based approximation of
f in place of the linearization technique for the smooth case applied in [
30]. In Step 3, the symbol
represents
’s feasible inexact projections onto
C relative to
with error tolerance
.
To conduct convergence analysis for the proposed method, for each fixed
, we need to define the auxiliary mapping
:
For convenience, we define
as the approximation of the set-valued mapping
:
We analyze based on the assumption that an approximation of the set-valued mapping ensures metric regularity/strong metric regularity, and that f has weak point-based approximation which is weaker than the condition of point-based approximation.
To prove our main result, we will first explain some technical results that will be helpful in our later analysis. The following Lemma can be shown with some simple calculations.
Lemma 3. Let , , and be a single-valued mapping. Assume that is an -WPBA at for f with modulus κ and constant a. Then,and Proof. Since
A is an
-WPBA at
for
f with modulus
and constant
a, we have
Note that
for any fixed
and
, one has
which establishes (
12) and (
13). □
Pick
,
and let them be fixed. For convenience, we define the following auxiliary set-valued mapping:
where
denotes the inverse of
defined as in (
11). It is easy to observe that
if and only if
, and
v satisfy
Lemma 4. Assume that the assumptions in Lemma 3 hold. Let be such thatIf is metrically regular at for 0 with constants , and b, then for any and , there exists a fixed point such thatIn particular, . In addition, if the mapping is strongly metrically regular at for 0, then the mapping has exactly one fixed point in such that (16) holds. Proof. Pick any
and
. Let
It is easy to obtain from the choice of the constants that
and
Recall that
is metrically regular at
for 0 with constants
, and
b. We have
which indicates that
for any
. By (
13) and (
15), we have
and
Then,
is well-defined on
. Since
, it follows from (
17)–(
19) that
Furthermore, it follows from (
12) and (
18) that
holds for all
. Note that
and
, and applying Lemma 2 with
, and
ensures the existence of
, i.e., inequality (
16) holds with
. Due to the fact that
, we arrive at
.
Next, we assume that the mapping
is strongly metrically regular at
for 0. Then, the mapping
is single-valued, and thus the mapping
is single-valued (thanks to (
20)). Similar to the proofs of (
21) and (
22), we have
and
It follows from Lemma 2 (2) that
has a unique fixed point in
. Besides, since
,
has a unique fixed point in
. By the first part of the proof, we know that
has a fixed point
satisfying (
16); hence,
is the unique fixed point of
in
, which completes the proof. □
The following Lemma shows that there exists a unique solution in
for generalized Equation (
1) under the strong metric regularity assumption.
Lemma 5. Let the assumptions in Lemmas 3 and 4 hold. If the mapping is strongly metrically regular at for 0 with constants , and b, then is the unique solution of (1) in . Proof. Let
be a solution of (
1) in
. Since
A is an
-WPBA for
f, we have
Recall that
is strongly metrically regular at
for 0 with constants
, and
b. The mapping
is single-valued on
and (
18) holds. Furthermore, we know that
Hence, we conclude that
Note that
. By (
18) and (
23), one has
Since
(thanks to the third inequality in (
15)), then
. Hence,
is the unique solution of (
1) in
. □
The next Lemma plays an important role in the convergence analysis, the proof of which follows from the lines of Lemma 4 of [
30].
Lemma 6. Let the assumptions in Lemma 4 hold and . If and satisfies (16), then, for any , we have Proof. Pick any
. Then, applying Lemma 1 with
, we have
Note that
and
. It follows from (
16) that
which establishes (
24). □
Now, we are ready to present our main result. We derive the exact relationship between the rate of convergence of the proposed method and the constant of the weak point-based approximation.
Theorem 1. Consider the nonsmooth constrained generalized Equation (5). Let , , ; and , , which satisfy (15) andAssume that with , the set-valued mapping is metrically regular at for 0 with constants , and b, and the function is an -WPBA at for f with modulus κ and constant a. Furthermore, suppose that the sequence of set-valued mappings satisfiesThen, for every starting point , there exists a sequence generated by the general inexact projection method associated with and , which is contained in and converges to with the following condition:In particular, if for all , thenand converges to superlinearly of order . Furthermore, if the mapping is strongly metrically regular at for 0, then is the unique solution of (5) in , and every sequence generated by the general inexact projection method starting at which is contained in and associated with satisfies (27) and converges to . Proof. First, we will show by induction on
k that, for any starting point
, there exists a sequence
generated by the proposed method satisfying (
27) and there exist sequences
and
associated with
such that
To this end, take
and
. By (
26), one has
. According to Lemma 4, we obtain
such that
and (
16) holds with
, and
. Then,
If
, then set
, and by using (
16) we conclude that (
27) holds for
. Otherwise, if
, then take
. Moreover, by using Lemma 6 with
, and
, we obtain from (
24) that (
27) holds for
. Note that
and
. By (
25), one has
and then
. Therefore, there exist
, and
satisfying (
27) and (
29) for
. Assume for induction that there exists
,
, and
satisfying (
27) and (
29) for
. Taking
and arguing similar to the case of
, we obtain
, and
satisfying (
27) and (
29) for
, and then the induction step is complete. Therefore, there exists a sequence
generated by the general inexact projection method, associated with
and starting at
, and it satisfies (
27).
Now, we proceed to show that the sequence
converges to
. Indeed, it is easy to observe from (
25) that, for any
,
Then, we conclude from (
27) that
for all
. This implies that
converges to
, at least linearly. On the other hand, if
for all
, then, (
28) follows directly from (
27). Consequently,
converges to
of order
.
Furthermore, if the mapping
is strongly metrically regular at
for 0, then Lemma 5 implies that
is the unique solution of (
5) in
. By the first part of the proof, we know that the general inexact projection method is surely executable. To show the last statement of the theorem, we take arbitary iterative sequence
which is contained in
and associated with
with the starting point
. According to the structure of the proposed method, there exist
and
associated with
satisfying
It follows from the second part of Lemma 4 that
is the unique fixed point of
in
for each
. Then, taking into account the construction of
, we conclude that (
27) holds for each
. Indeed, if
, then
, and then Lemma 4 implies that (
27) holds. If
, then
. And then, we obtain from Lemma 6 that (
27) holds. By using similar arguments as in the first part of the proof, we can show that such a sequence converges to
. For the sake of simplicity, we omit the details here. □
Remark 1. It is worth mentioning that, for positive , conditions (15) and (25) hold true as long as we pick a value for that is sufficiently small. In this case, if , then converges to superlinearly. In fact, passing to the limit in (27) as , we obtainFor , one needs to make , and η sufficiently small to ensure the validity of (15) and (25), and in this case we have linear convergence. Remark 2. For the case of f being smooth, under the condition of metric regularity (strong metric regularity) for an approximation of the set-valued mapping and assuming Lipschitz continuity for the derivative , the authors show in Theorem 2 of [30] that the sequence generated by the Newton-InexP method converges to a solution of (5) with a linear, superlinear, and Q-quadratic convergence rate, respectively. In contrast, the proposed method that we investigated in Theorem 1 incorporates both inexactness and nonsmoothness. In fact, if f is continuously differentiable around , we can set . Then, by Lemma 3.1 of [31], the condition that the derivative is Hölder calm of order indicates that is a -WPBA at for f. Recall that the Hölder calmness property of the derivative is strictly weaker than the Lipschitz continuity used in Theorem 2 of [30] (see Example 3.1 of [31]). Therefore, even in the smooth case, Theorem 1 is an improvement of Theorem 2 of [30]. Additionally, it is worth pointing out that, even for generalized equations without constraint, i.e., , Theorem 1 is also new and is a supplement of Theorem 3.1 of [31]. In general, under the assumption of metric regularity, the sequence generated by the general inexact projection method is not unique.
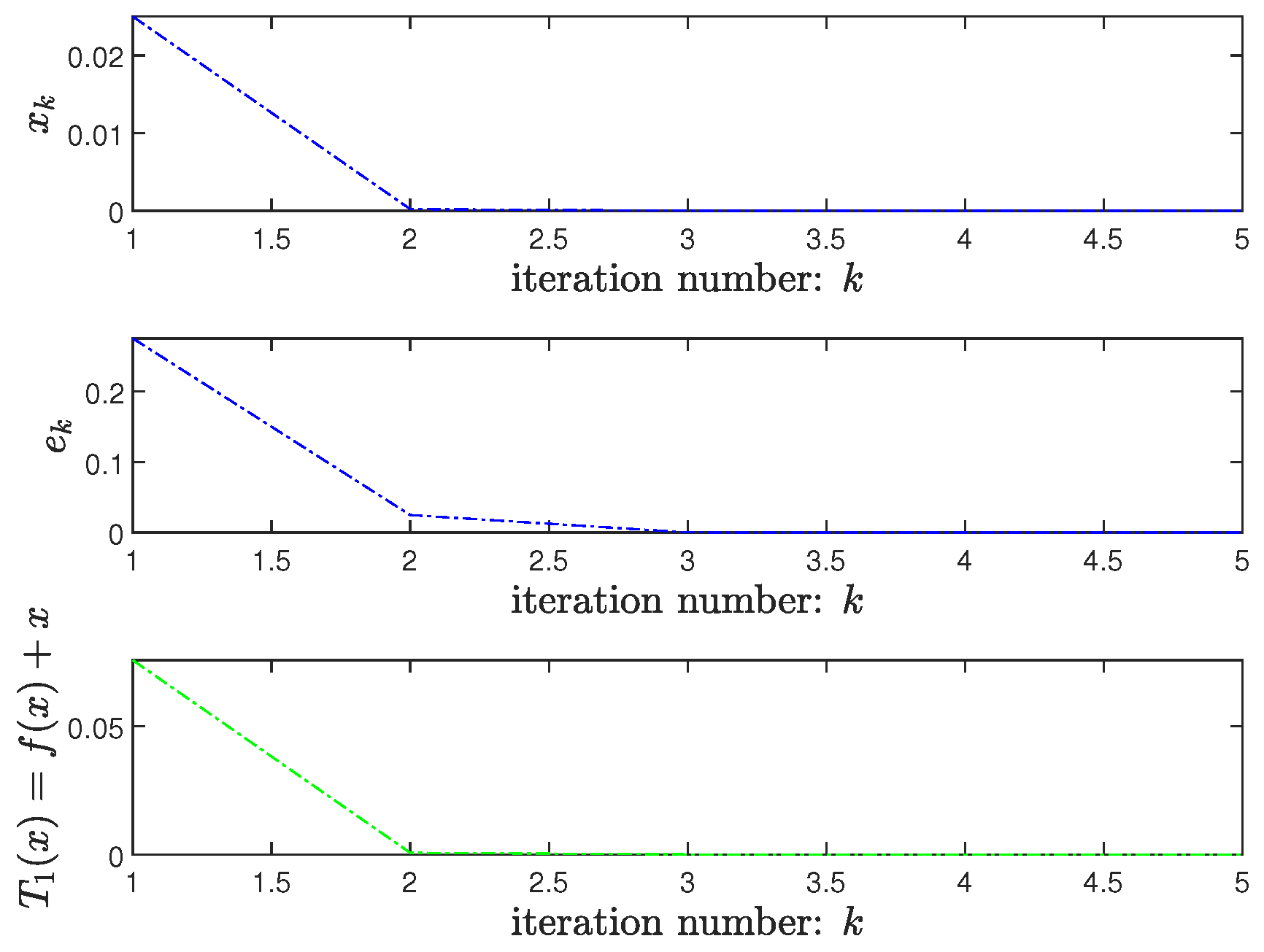
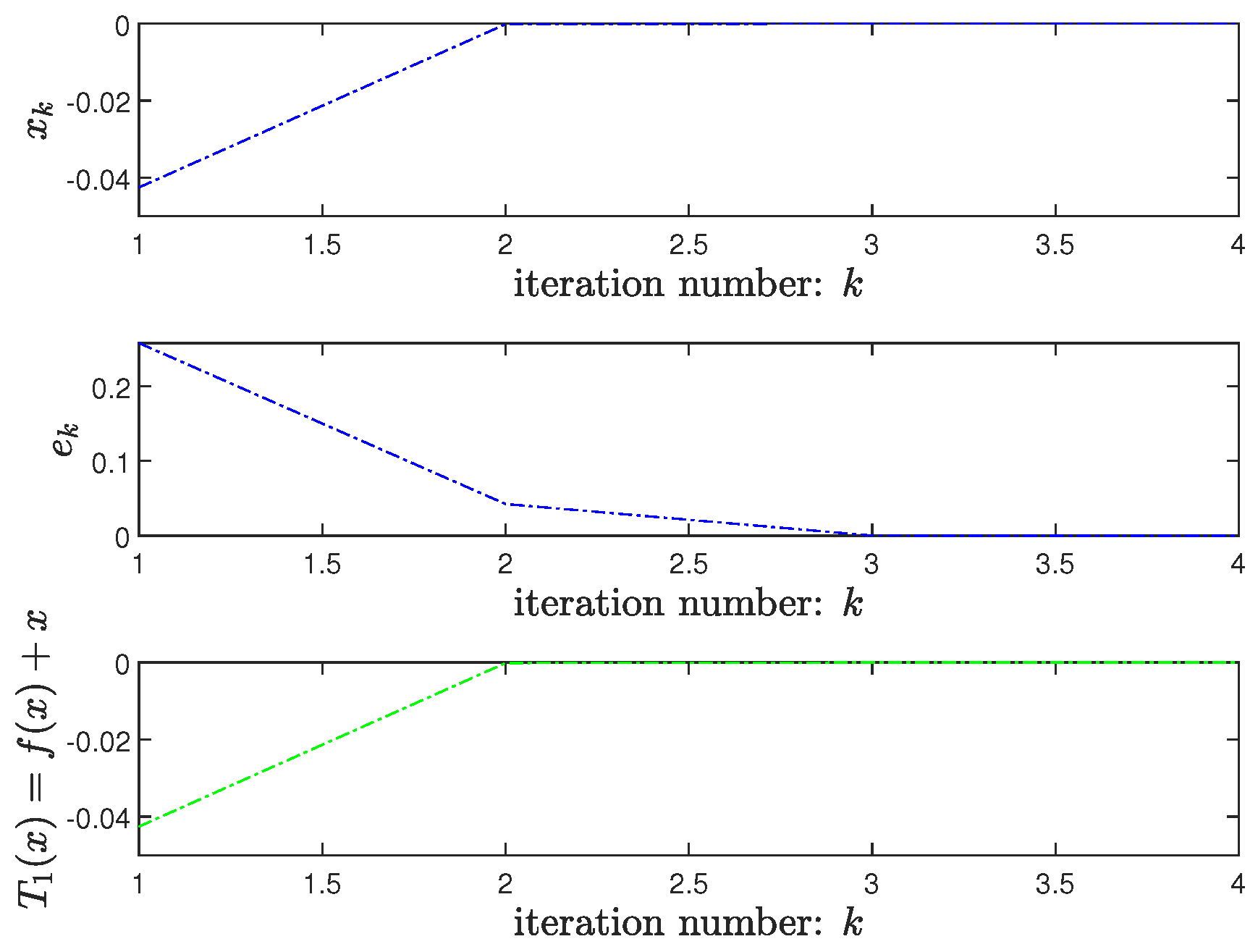
The following example shows that, under the assumption of Theorem 1, one cannot guarantee that every iterative sequence converges to a solution, even for the case of for all .
Example 1. Let be such that for all , and for all . Then, f is not differentiable at 0. Let , and be such that for all and for all . It is clear that A is a -WPBA at 0 for f. Let , (for all ), and be such that for all . It is easy to see that is metrically regular at 0 for 0, and it is not strongly metrically regular at 0 for 0. Then, it follows from Theorem 1 that, for any , there exists a sequence generated by the proposed method and contained in C which converges to 0 superlinearly of order 2. For each , let be the kth generation of the proposed method. In fact, if , we know that any element taken from satisfies (8), so we choose . For the case of , since any element taken from satisfies (8), we pick . Note that , so we set . We also have . This shows that the sequence converges to 0 superlinearly of order 2. On the other hand, for the starting point , we can find a sequence which is generated with the proposed method and does not converge to a solution of the aforementioned constrained generalized equation.
Clearly, the condition of
satisfying (
8) is equivalent to the fact that
. It is easy to observe from Example 1 that
should be chosen around the boundary of
and not be too far away from the given solution point.
To overcome the shortcoming that not every sequence produced by the general inexact projection method reaches a solution, we examine a modified version of the proposed method for solving nonsmooth constrained generalized equations (Algorithm 2).
| Algorithm 2 Restricted generalized inexact projection method |
Step 0. Let , , and be given, and set .
Step 1. If , then stop; otherwise, compute such that
Step 2. If , set ; otherwise, take any satisfying
Step 3. Set , and go to Step 1. |
It is clear that (
30) is equivalent to the relationship
Since
, then the restricted generalized inexact projection method is surely executable when
for any
x near
and
.
For convergence analysis of the restricted method, we need the following lemma.
Lemma 7. Assume that the assumptions of Lemmas 3 and 4 hold. Then, for any and , we have and Proof. Pick any
and
. Note that
. One has
and then, it follows from (
13) that
For any sufficiently small
, take
such that
. Let
It is clear that
, and then
.
According to the assumption that
is metrically regular at
for 0 with constants
, and
b, we conclude that (
18) holds, and then
for any
. By (
20), we have
, and, therefore,
is well defined on
, where
is defined by (
14). Note that
. We have
In combination with (
18), we have
Furthermore, for any
, it follows from (
22) that
Since
, and
, by applying Lemma 2 with
,
, and
, we obtain a fixed point
, which establishes that
and
. Then, we have
Since
is arbitarily chosen, we conclude that (
33) holds. □
The following result shows that under proper conditions, every sequence generated with the aforementioned restricted method converges a solution of the nonsmooth constrained generalized equation.
Theorem 2. Consider the constrained generalized Equation (5) and assume that the assumptions of Theorem 1 hold. Let be such thatThen, for every sequence generated by the restricted generalized inexact projection method, which starts from , associated with , and contained in , we have the following convergence:In particular, if for all , thenand converges to superlinearly of order . Proof. Take any
, and
. By (
26), one has
. Then, it follows from Lemma 7 that
. Since
, then the restricted generalized inexact projection method is surely executable. Now, pick any
and consider any iterative sequence
generated by the aforementioned method associated with
and starting at
. Then, for each
, there exist
and
associated with
satisfying
If
, then
; otherwise,
. By (
37), one has
Next, we show by induction that
and (
35) holds for each
. Since
, we have
If
, it follows from (
26), (
33), and (
38) that
In this case,
. Hence, (
39) implies that (
35) holds for
. If
, then
. Similar to the proof of Lemma 6 when applying (
39) in place of (
16), we obtain that (
35) holds for
. Note that
. By (
34) and (
35), one has
. Hence,
. Assume for induction that
and (
35) holds for
. Note that
. One has
If
, it follows from (
26), (
33), and (
38) that
In this case
, and, hence, (
39) implies that (
35) holds for
. If
, then
. Similar to the proof of Lemma 6 with the application of (
40) instead of (
16), we obtain that (
35) holds for
. Note that
. By (
34) and (
35), one has
, and then
. Thus, the induction step is complete. Therefore, we have that (
35) holds. If
for all
, then (
36) follows directly from (
35). □