Abstract
Dynamic neural networks (DNNs) are a type of artificial neural network (ANN) designed to work with sequential data where context in time is important. Unlike traditional static neural networks that process data in a fixed order, dynamic neural networks use information about past inputs, which is important if the dynamic of a certain process is emphasized. They are commonly used in natural language processing, speech recognition, and time series prediction. In industrial processes, their use is interesting for the prediction of difficult-to-measure process variables. In an industrial isomerization process, it is crucial to measure the quality attributes that affect the octane number of gasoline. Process analyzers commonly used for this purpose are expensive and subject to failure. Therefore, to achieve continuous production in the event of a malfunction, mathematical models for estimating product quality attributes are imposed as a solution. In this paper, mathematical models were developed using dynamic recurrent neural networks (RNNs), i.e., their subtype of a long short-term memory (LSTM) architecture. The results of the developed models were compared with the results of several types of other data-driven models developed for an isomerization process, such as multilayer perceptron (MLP) artificial neural networks, support vector machines (SVM), and dynamic polynomial models. The obtained results are satisfactory, suggesting a good possibility of application.
Keywords:
dynamic neural networks; industrial process; recurrent neural networks; long short-term memory MSC:
93B30
1. Introduction
Dynamic neural networks are an important tool in various fields such as natural language processing, speech recognition, time series prediction, computer vision, and others. Their architecture allows for the training of deeper, more accurate and more efficient models. Unlike static neural networks, whose structure can be sufficient for simpler tasks with fixed input sizes and architectures, dynamic networks are often preferred for tasks where adaptability and flexibility are crucial. In these tasks, the number of layers, units, or connections can be changed depending on the input data or the learning progress of the network. Therefore, they have advantageous properties that static networks do not have. In general, dynamic networks have the following advantages: efficiency, adaptability, compatibility, generality, and interpretability [1].
There are several types of dynamic neural network architectures: recurrent neural networks [2], transformer-based neural networks [3], temporal convolutional networks (TCNs) [4], echo state networks (ESNs) [5], neural turing machines (NTMs) [6], differentiable neural computers (DNCs) [7], neural networks with attention mechanisms [8], neural networks with adaptive components [9], and functional neural networks (FNNs) [10].
The choice of architecture depends on the specific problem and the nature of the data being processed.
Recurrent networks are a widely used type of dynamic neural network. They store information in repeated functional loops. RNNs are a popular option for classification and regression problems due to a number of characteristics. These include their ability to recognize sequential patterns even in the presence of sequential biases, their flexibility in using contextual information (since they can learn what to store and what to ignore), and their acceptance of a wide variety of data types and representations. They, however, have a number of drawbacks that have restricted their use in solving classification or regression issues in the real world. The inability of typical RNNs to hold information over extended periods of time is their most significant flaw. Another problem is that they can only access contextual information in one direction. This is quite useful for time series prediction, but not for classification. Although they were developed for one-dimensional sequences, some of their properties, such as robustness to biases and flexible use of context, are also desirable in multidimensional domains such as image and video processing [11].
To solve the vanishing gradient problem and other problems in traditional RNNs, long short-term memory networks have been introduced to enable effective modeling and learning from data sequences [12]. LSTM neural networks operate according to the gate principle. Thus, this controls the importance of data in different time intervals in such a way that it ignores the irrelevant ones and stores the important information of the input data in the past time intervals, thus preventing the vanishing gradient problem [11].
Due to their exceptional capabilities, LSTM networks are mainly used in language processing and speech recognition. They are used by Google to improve its speech recognition and translation tools and are widely used by Facebook [13]. However, it is interesting to see how they can handle data from real industrial processes, e.g., predicting difficult-to-measure process variables such as product quality or the amount of pollutant emissions. A lot of research has been conducted in this area in recent years, and numerous papers have been published, ranging from basic research to applications.
Fault detection and diagnosis in industrial processes are very important for planning overhauls and reducing plant downtime. Several papers have been published on this subject [14,15,16,17,18,19]. There are many examples where mathematical models based on LSTM prediction of critical quality characteristics of a product are used to replace failure-prone and expensive process analyzers. In references [20,21], the authors developed mathematical models (soft sensors) to predict the concentrations of sulfur dioxide and hydrogen sulfide at a sulfur production plant. Furthermore, such models are presented for the penicillin fermentation process [22], the industrial polyethylene process [23], the grinding–classification process [24], the polypropylene process [25], the roasting process of oxidizing zinc sulfide concentrates [26], plasma enhanced chemical vapor deposition (PECVD)—the most important process in the manufacturing of solar panels [27], and the industrial hydrocracking process [28]. There are several recent works related to emissions [29,30,31]. There are several recent works on the application of LSTM-based models related to the steel industry [32], the paper industry [33], and the latest industrial processes related to the production of green hydrogen and decarbonization [34]. LSTM also finds application in predictive production planning in energy-intensive manufacturing industries in line with Industry 4.0 and the Internet of Things (IoT) [35].
As for the isomerization process, several papers have been published recently on the subject of mathematically modeling this process. The authors have presented the development and optimization of the kinetic model of catalytic reactions [36], the development of the MLP-based model [37], and the development of the SVM-based model [38] for estimating the quality of isomerate gasoline. One of the first papers dealing with the development of data-driven mathematical models for the estimation of product quality in an isomerization process is the work by Lukec et al. in 2007 [39]. No papers applying LSTM models to the isomerization process in refineries were found in the existing relevant literature.
This paper presents the development of mathematical models in an industrial isomerization process using the LSTM network architecture. Here, it is crucial to continuously estimate the critical quality components that influence the octane number of gasoline. These are the components of 2,2- and 2,3-dimethylbutanes (2,2- and 2,3-DMB) and 2- and 3-methylpentanes (2- and 3-MP) in the isomerizate—the product of the process. The isomerization process is a complex industrial nonlinear process with emphasized process dynamics. It is better to develop empirical, data-driven models rather than fundamental (first-principle) ones. Because of its structure, i.e., the idea of a dynamic neural network that allows data to be manipulated in past time intervals, and other advantages, LSTM is a suitable technique for developing models for such a process. The achieved results were compared with the results of various types of other data-driven models developed for an isomerization process, such as MLP artificial neural networks, SVMs, and dynamic polynomial models, presented and published earlier [40,41,42,43].
The traditional steps of data-driven model development include the selection of historical data from a plant database, data preprocessing, model structure and regressor selection, model estimation, and validation [44,45].
2. Materials and Methods
2.1. Theoretical Background
Artificial neural networks were originally developed as mathematical models capable of processing information like a biological brain.
The fundamental structure of ANNs is a system of small junctions linked by weighted connections. According to the biological paradigm, neurons are represented by junctions, and the strength of the synapses between neurons is represented by connection weights. By giving some or all of the junctions an input, one may activate the entire network, and this activation will then spread across it via the weighted connections [11].
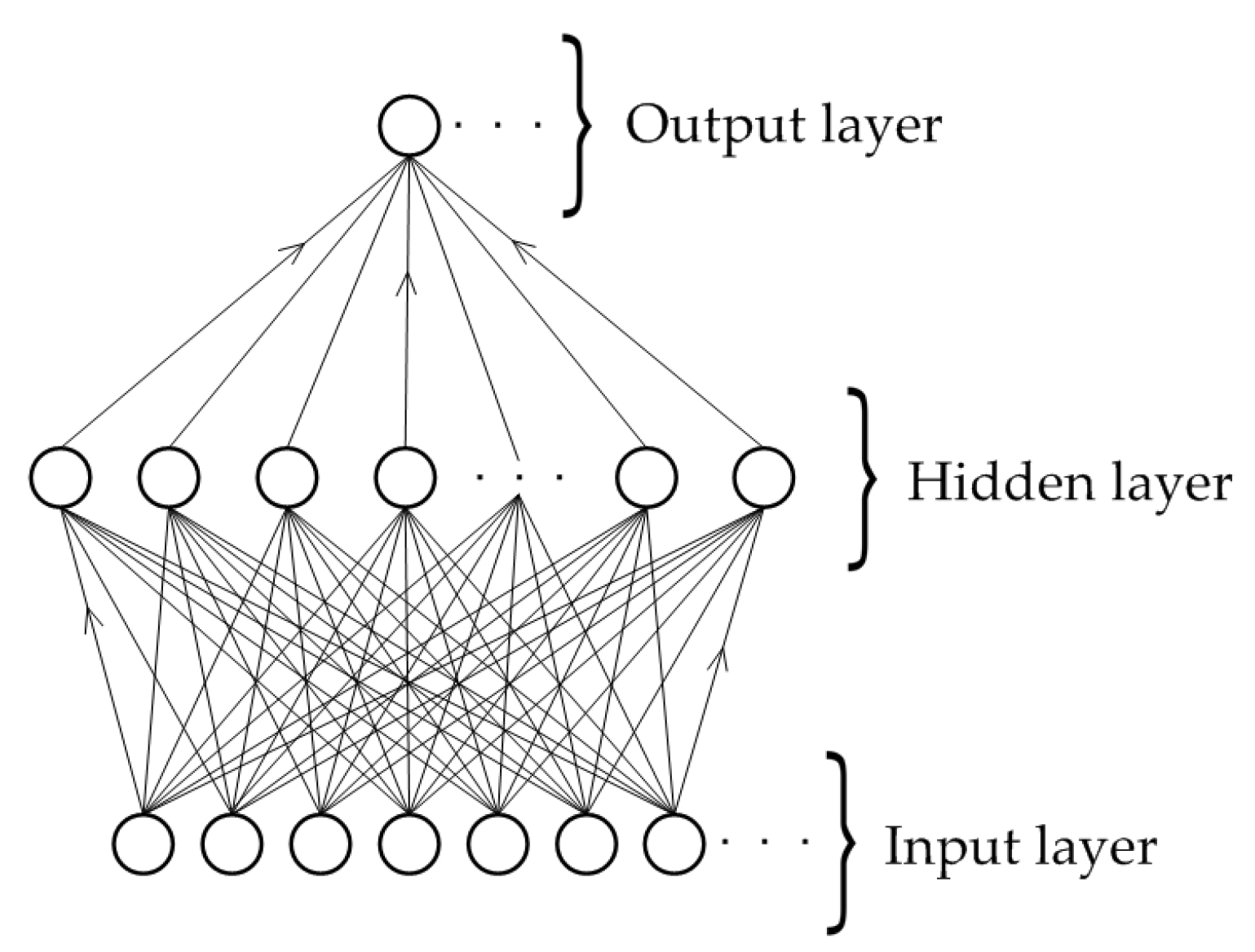
As shown in Figure 1, the units in a multilayer perceptron, a class of ANNs, are arranged in layers, with connections passing from one layer to the next. The input patterns are presented to the input layer and then passed through the hidden layers to the output layer. This process is referred to as feedforward pass of the network. Since the output of an MLP depends only on the current input and not on past or future inputs, an MLP can find it more difficult to deal with dynamic problems like time series regression. An MLP with a particular set of weights defines a function of network output on input data. By changing the weights, a single MLP can express many different functions [11].
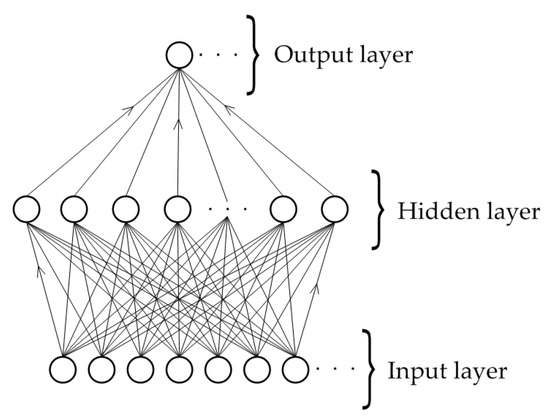
Figure 1.
A multilayer perceptron artificial neural network structure [11].
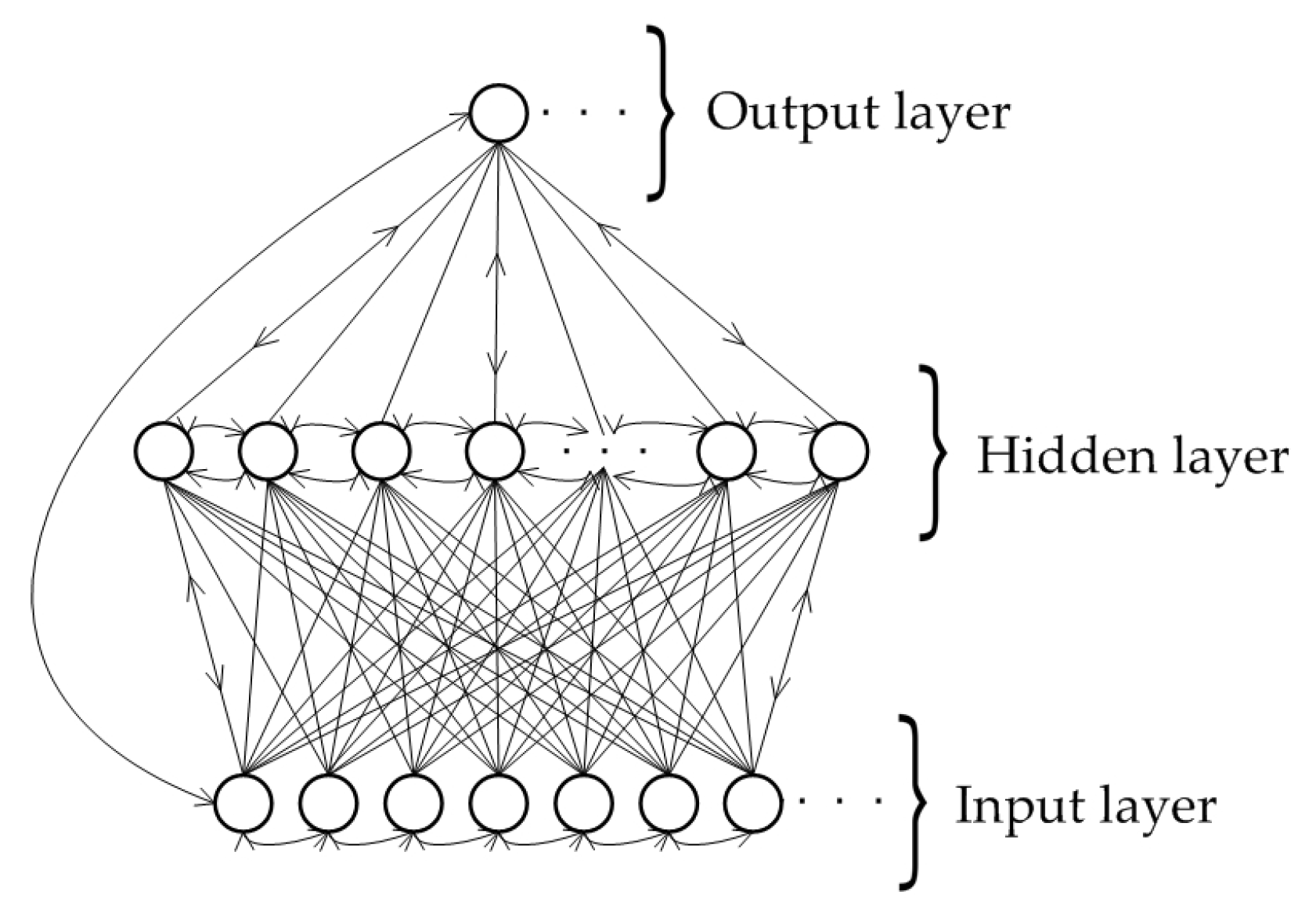
While MLPs only map from input to output vectors, RNNs can, in principle, map the entire history of previous inputs to each output. RNNs with a sufficient number of hidden units can approximate any measurable sequence-to-sequence mapping with certain accuracy. The key point is that the recurrent connections allow a “memory” of previous inputs to persist in the internal state of the network, thereby affecting the network output (Figure 2) [11].
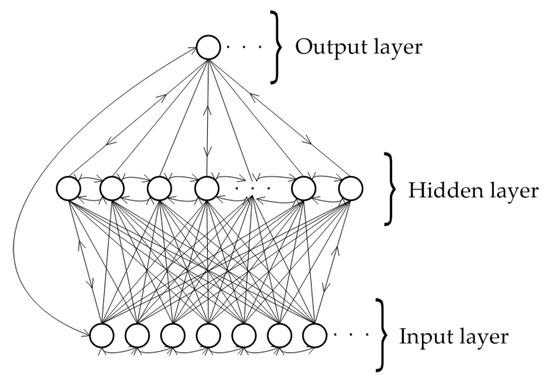
Figure 2.
A recurrent neural network structure [11].
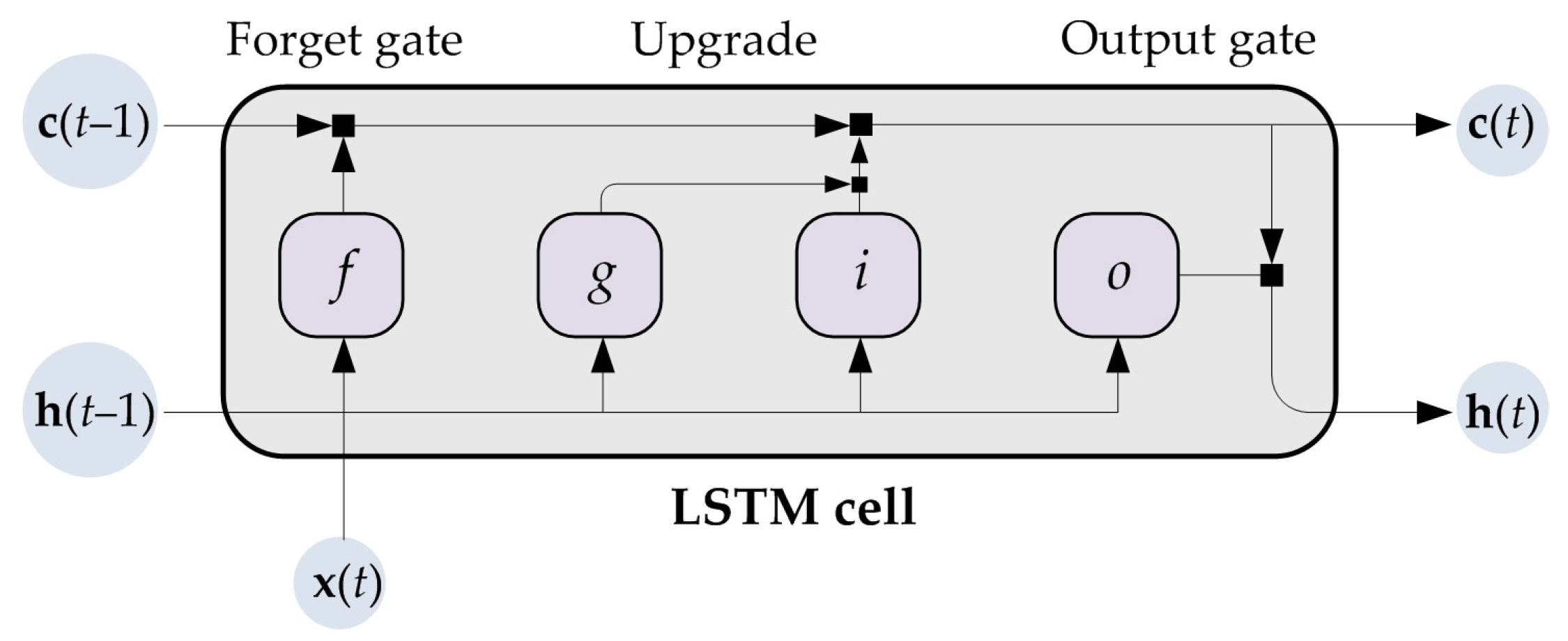
To overcome the vanishing gradient problem, basic RNNs are replaced by LSTM networks when long-term dependencies are learned. The LSTM architecture consists of recurrently connected sub-networks, known as memory units. One unit consists of a memory cell and nonlinear gates that selectively keep current information that is relevant and forget past information that is not [12,13,21,46]. A typical LSTM unit is shown in Figure 3.
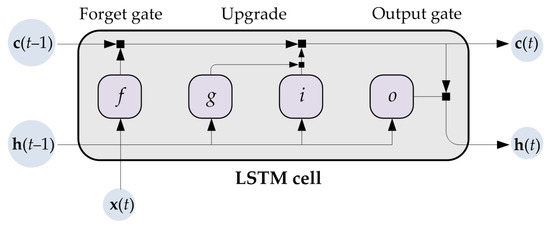
Figure 3.
A typical LSTM unit structure [47].
At a time t, the unit stage incorporates the output stage, h(t), which includes the output at that time, and the cell stage, c(t), which includes the information acquired from earlier time steps ( and ). In every time step, c(t) is upgraded by attaching or discarding information using gates. The latest input is x(t).
The components of which the LSTM unit consists are an input gate, i—which upgrades the inputs by combining the current input and the previous output and cell stages; a forget gate, f—which determines which information should be removed from the previous cell stage; an output gate, o—which calculates output information; and a cell input, g—which upgrades the inputs by combining the current input and the previous output stage.
The learnable weights of the LSTM unit are the input weights, W, the recurrent weights, R, and the bias, b. The matrices with which they are represented follow:
where i, f, g, and o denote the input gate, forget gate, cell input, and output gate, respectively [47].
The states of the components of the LSTM unit at the time t are represented by the following equations:
where and denote the activation functions—the sigmoid and hyperbolic tangent, respectively. The sigmoid is always used as a gate activation function, while the hyperbolic tangent is often used as a cell input.
Finally, the cell state, c(t), and the initial state, h(t), are calculated as follows:
where ⊙ is the Hadamard product—the point-wise multiplication of two vectors.
The parameters (weights and biases) are determined by minimizing the loss function using learning algorithms like stochastic gradient descent (SDG), stochastic gradient descent with momentum (SGDM), adaptive moment estimation (ADAM), Nesterov accelerated adaptive moment estimation (NADAM), and root mean square propagation (RMSProp) [48].
2.2. Process Description
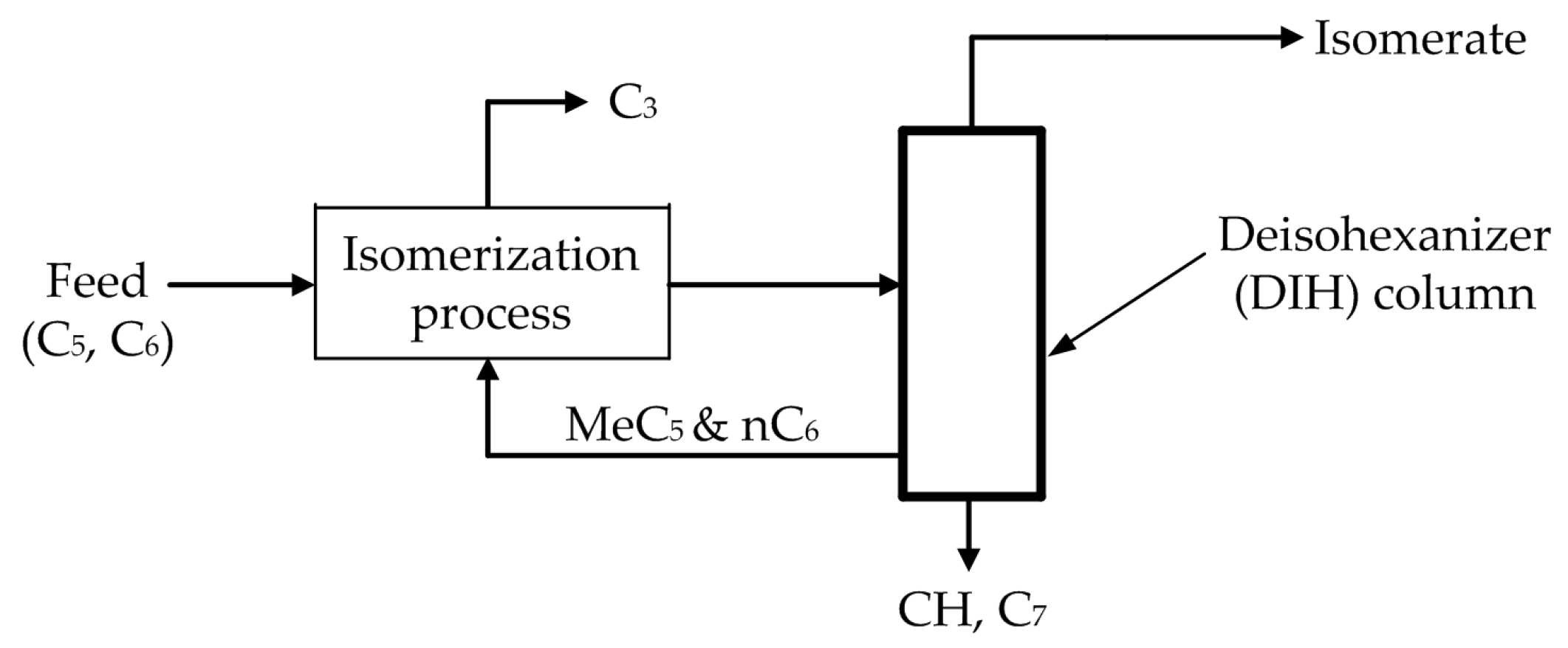
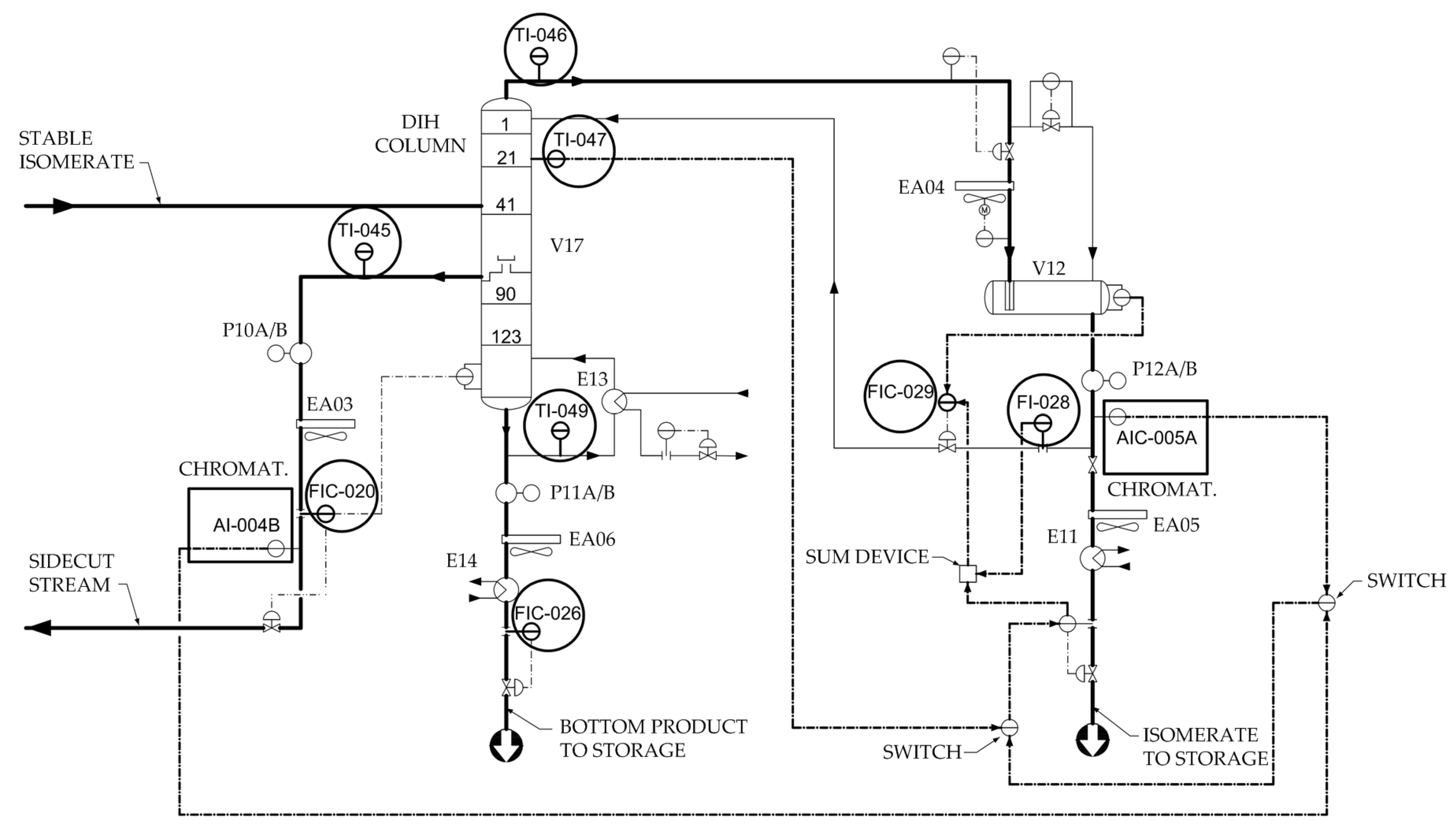
The octane number of light straight-run naphtha is increased via the industrial process of catalytic isomerization of pentane, hexane, and their mixes. The reactions occur over a stationary catalyst bed in the presence of hydrogen, with operating parameters that reduce hydrocracking and maximize isomerization. The primary outcome of the isomerization process is the transformation of n-paraffins into i-paraffins, or structures with a high-octane content. Thermodynamic equilibrium, which is more advantageous at low temperatures, governs the response. A deisohexanizer (DIH) column, which separates the basic isomerization result into normal and isoparaffin components, can be added to enhance the basic isomerization process. The unconverted n-paraffins and the freshly generated low-octane methylpentanes are concentrated in the side stream of the DIH column and recycled to the isomerization reactor section [49,50] (Figure 4).
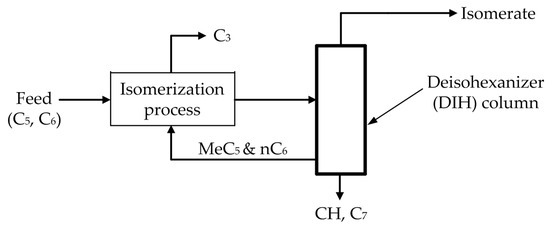
Figure 4.
Methylpentane and n-paraffin recycling process [49].
By controlling the concentration of critical quality product components, the technological process seeks to maintain the low-octane 2- and 3-MP in the side stream of the DIH column and the high-octane 2,2- and 2,3-DMB in the top stream.
2.3. Model Development
When developing a data-driven model, it is important to select easily measured influencing (input) variables that affect output variables that are difficult to measure and often unavailable. In this case, the output variables are critical quality product components—2,3-DMB and 3-MP. Indicators of product quality also include 2,2-DMB and 2-MP, but since 2,2-DMB is a high-octane component and 2-MP is a low-octane component correlated with 2,3-DMB and 3-MP, respectively, it is often sufficient to consider only one pair of components.
To successfully perform the selection of input variables, it is important to gain theoretical insight into the process, but it is even more important to talk to the operators of the observed plant, who will point out possible input variables. After selecting a specific number of input variables, the final number is determined using various correlation analysis techniques. Table 1 shows the potential input variables for 2,3-DMB and 3-MP content model development.

Table 1.
Potential input variables for 2,3-DMB and 3-MP content model development.
Potential input variables as well as output variables, measured using the process analyzers AI-004B (measuring of 2,3-DMB) and AIC-005A (measuring of 3-MP content), are shown in a process scheme of the deisohexanizer section of the process (Figure 5).
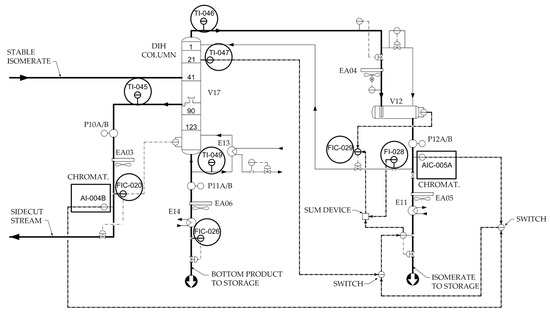
Figure 5.
Deisohexanizer section of isomerization process [43].
The correlation analysis performed for the potentially influential variables omitted some variables as model inputs because they showed little correlation with the outputs [41]. FIC-020 (DIH column side product flow) was excluded for 2,3-DMB content model development, and FIC-020 and FIC-026 (DIH column bottom product flow) were excluded for 3-MP.
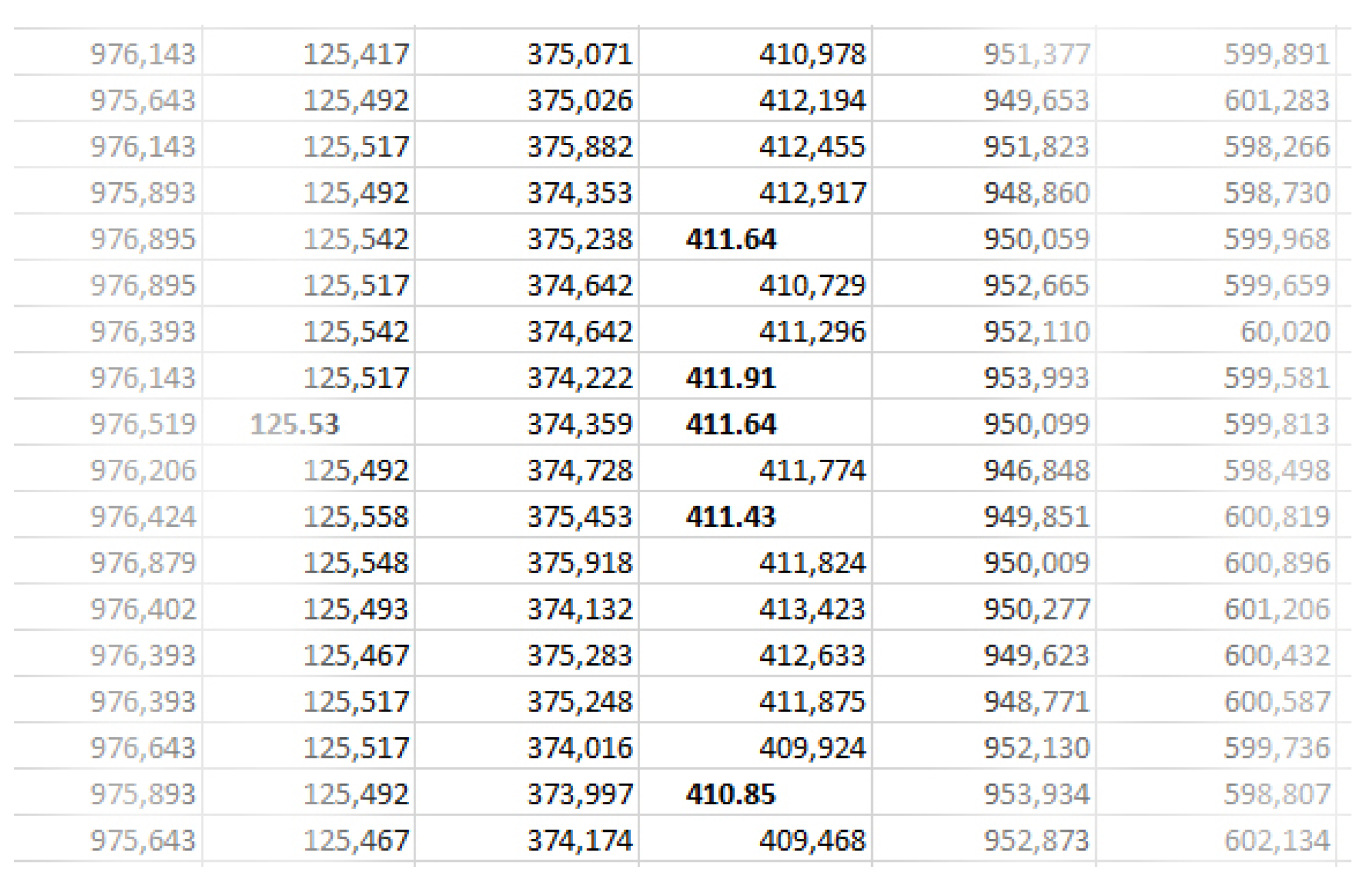
The selection of the influencing variables is followed by data collection and preprocessing. Data collection and the selection of an appropriate data period took a lot of time during the research and were a major challenge. Although the process data were stored in plant history databases, which are an integral part of the distributed control system (DCS), companies often have their own software solutions for representing measurement data, which have certain drawbacks when the data are considered in more detail for scientific research purposes. The data set may be corrupted due to character encoding errors (Figure 6).
Figure 6.
Character encoding errors [51].
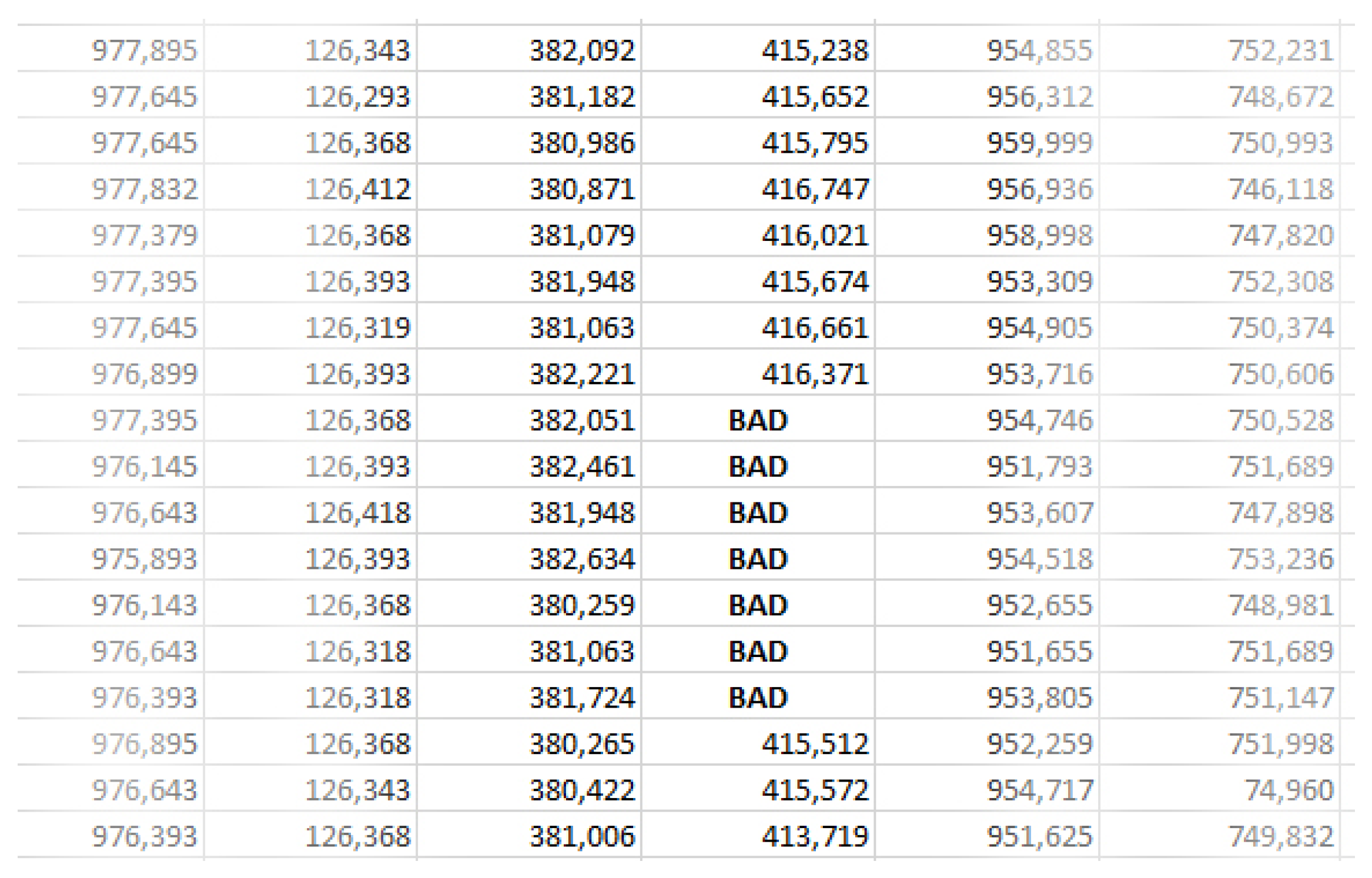
A common problem may also be that parts of data can be missed due to problems with measurement equipment (Figure 7).
Figure 7.
Missing data [51].
Also, the data set can hold poor information, cover insignificant process dynamics, or have disturbance periods that are unfavorable for model development.
A continuous data set for a period of 2 to 3 weeks is needed for the selected input variables and for the outputs. It is also important that the selected data belong to different process dynamics’ regimes, if possible. In the search for a period with emphasized process dynamics, two different data sets were selected, one for the development of a model to estimate the content of 2,3-DMB and the other for 3-MP. Regarding the detection of outliers, one of the common methods for their detection is 3-sigma method, as well as the Jolliffe method, which is based on a principal component analysis (PCA) and partial least squares (PLS) techniques. All of these techniques merely examine the data statistically and have a tendency to exclude peak values that may provide important details about the dynamics of the process. As a result, outlier detection cannot be carried out entirely automatically, and data should always be examined visually [51]. Fortunately, there were not many outliers, missing data, or noise. Although the input data were available every minute, the sampling period was set to 3 min since the process dynamics of such a large industrial plant allow it. The output variables are measured using on-line chromatographs with a sampling time of 30 min. Since it is necessary to coordinate the sampling periods of the input and output variables, the 30 min period of the output data is supplemented by interpolation data using cubic spline interpolation.
LSTM network models for estimating the contents of 2,3-DMB and 3-MP were developed using Python 3.9.6 programming language paired with Keras library 2.13.1 for deep learning in combination with an M1 Apple processor working at 3.2 GHz. Model development data sets consist of 6667 and 10,078 continuous samples for the development of 2,3-DMB and 3-MP content models, respectively. The data are divided into a training and test set in a ratio of 85:15. The structure of the LSTM network consisted of a hidden layer, with the number of hidden units studied ranging from 5 to 50. The activation functions used as cell inputs are the hyperbolic tangent (tanh), sigmoid, and rectified linear unit (ReLU). The learning algorithms ADAM and NADAM were used to determine and optimize the parameters (weights and biases). The loss function, represented by the mean-squared error (MSE) as a function of the number of past time steps of the input variables, was minimized. Attention should be paid to the optimal number of past time steps—too many lead to overfitting, too few lead to poor generalization capabilities. The number of past time steps of the input variables was studied in the range of 5 to 200, with a sampling period of 3 min.
Based on the hyperparameter variations (changes in hidden layers, hidden units, activation functions, learning algorithms), a series of experiments was conducted. Eighteen percent of the training data sets were taken for validation, which is 15% of the entire data sets, as was implemented in previous work. The MSE was simultaneously examined to find the optimum batch size and epoch to avoid overfitting. The hyperparameters with the best performance were then thoroughly analyzed at different past time steps and by adding additional hidden layers. Based on the results, computational effort and time, and the nature of the data sets, the developed LSTM models were presented in the manuscript.
An evaluation of the developed models was performed on the training and test data sets based on four statistical indicators: the Pearson correlation coefficient (R), the coefficient of determination (), the root mean square error (RMSE), and the mean absolute error (MAE):
where is the measured input, is the measured output, is the model output, is the mean of all measured inputs, is the mean of all measured outputs, and n is the number of values in the observed data set.
The results of the LSTM network models were compared with the results of data-driven models, whose development methodology and materials are presented in reference [40] for an MLP, in references [41,42] for SVMs, and in references [42,43] for dynamic polynomial (finite impulse response—FIR, autoregressive with exogenous inputs—ARX, output error—OE, nonlinear ARX—NARX, Hammerstein–Wiener—HW) models.
All the compared models were developed using the same data sets (2,3-DMB content models from 6667 and 3-MP from 10,078 continuous samples) and validated on independent parts of the data sets (test sets) using the same evaluation criteria (R, R2, RMSE and MAE). This methodology allows the validity of the developed models to be compared and interpreted.
3. Results
Table 2 and Table 3 show the optimal evaluation results of the developed 2,3-DMB and 3-MP content models using LSTM networks. The results are based on the evaluation criteria shown in equations [11,12,13,14], applied separately to the training and test sets. In the cases of the 2,3-DMB and 3-MP models, the optimal results were obtained with the ADAM optimization algorithm and the tanh activation function, with 25 hidden units in the hidden layer. The optimal number of past time steps in the case of the 2,3-DMB model was 45, while in the case of the 3-MP model, it was 55.

Table 2.
The 2,3-DMB content LSTM model evaluation results.

Table 3.
The 3-MP content LSTM model evaluation results.
For both models, very high Pearson correlation coefficient (R) and coefficient of determination () values can be observed, along with low root mean square error (RMSE) and mean absolute error (MAE) values.
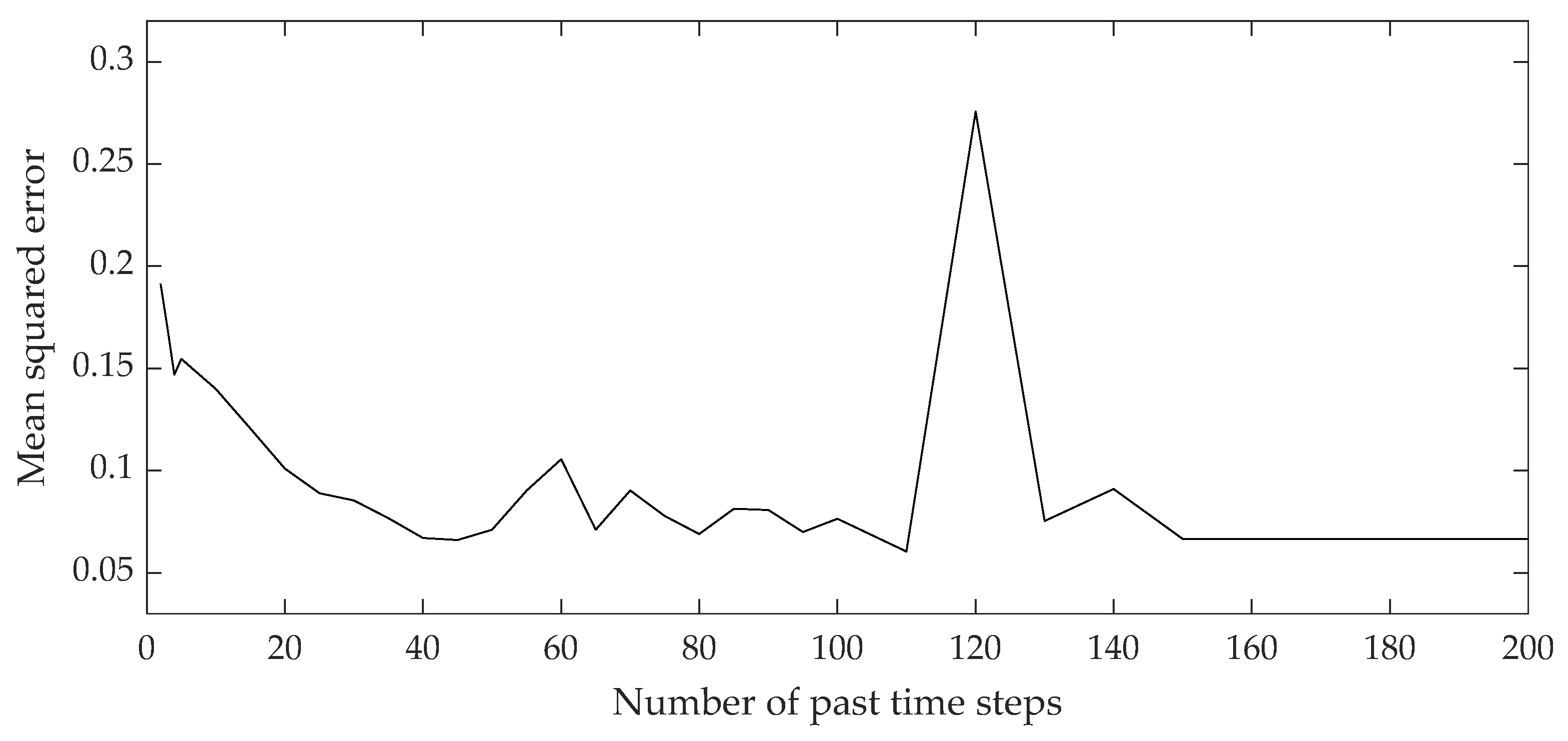
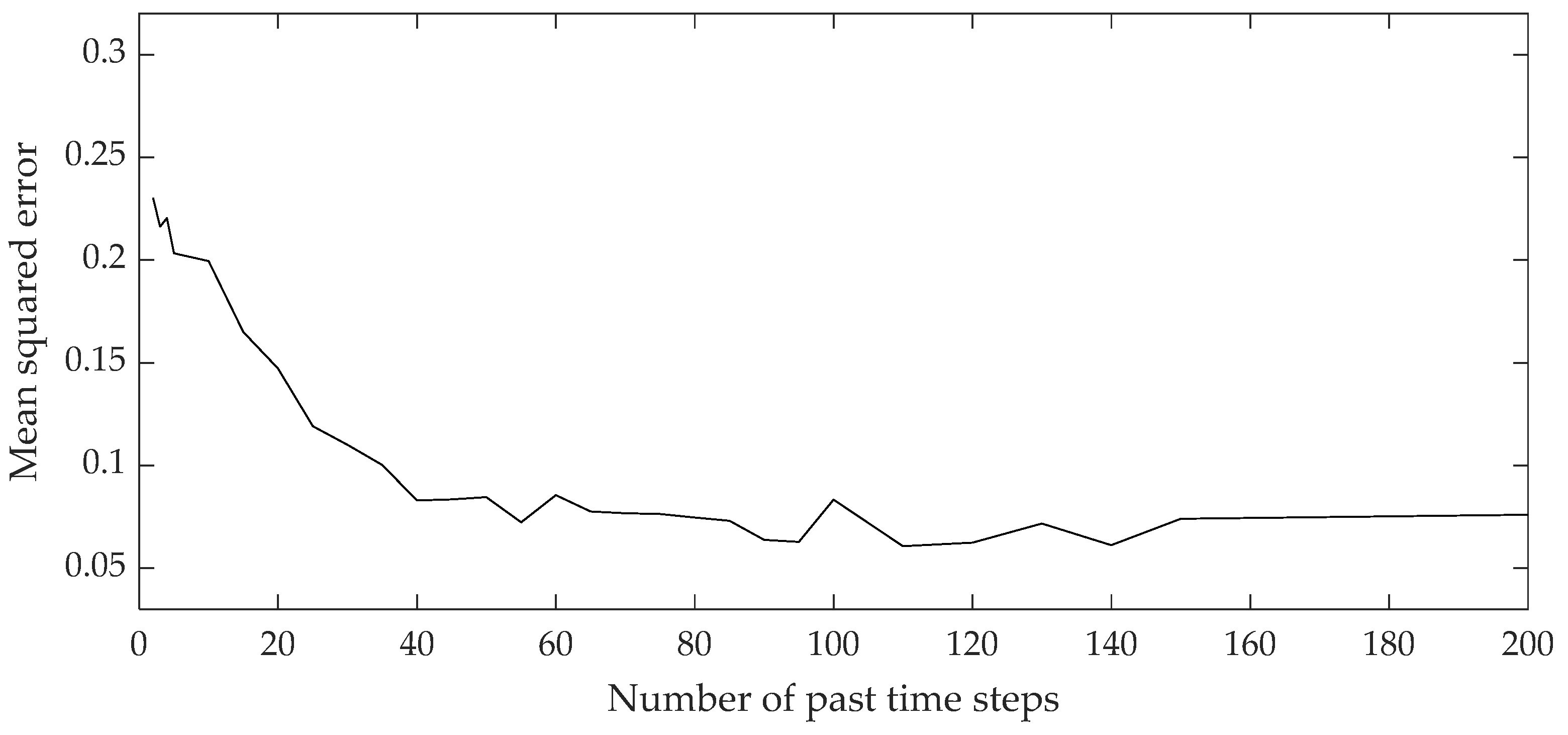
Figure 8 and Figure 9 show the curves of the loss functions during the training process of the 2,3-DMB and 3 MP content models. During the training process, a minimum mean squared error was targeted, which depends on the number of past time steps of the input variables, ranging from 5 to 200.
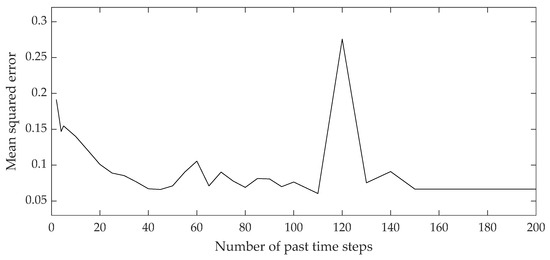
Figure 8.
Curve of loss function during 2,3-DMB content LSTM network training.
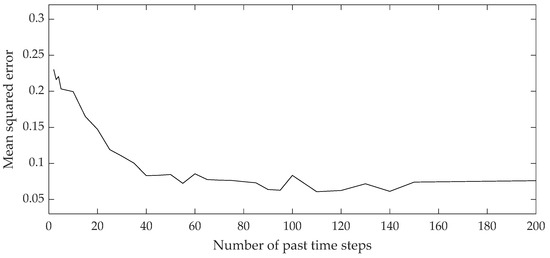
Figure 9.
Curve of loss function during 3-MP content LSTM network training.
The optimal network structure of the developed models was assumed to be the one where the MSE reaches the minimum value for the minimum number of past time steps, since the MSE remains relatively stable by increasing the number of time steps. The values of the Pearson correlation coefficient and the coefficient of determination of the developed and presented models do not deviate significantly in the mutual comparison for a specific data set and model, which is a good sign that the developed models are not overfitted, i.e., they have good generalization capabilities.
Based on a thorough analysis of the LSTM hyperparameters, the LSTM network models did not achieve noticeably better performances with more than one hidden layer, leading to the conclusion that is not necessary to use more computational power and time.
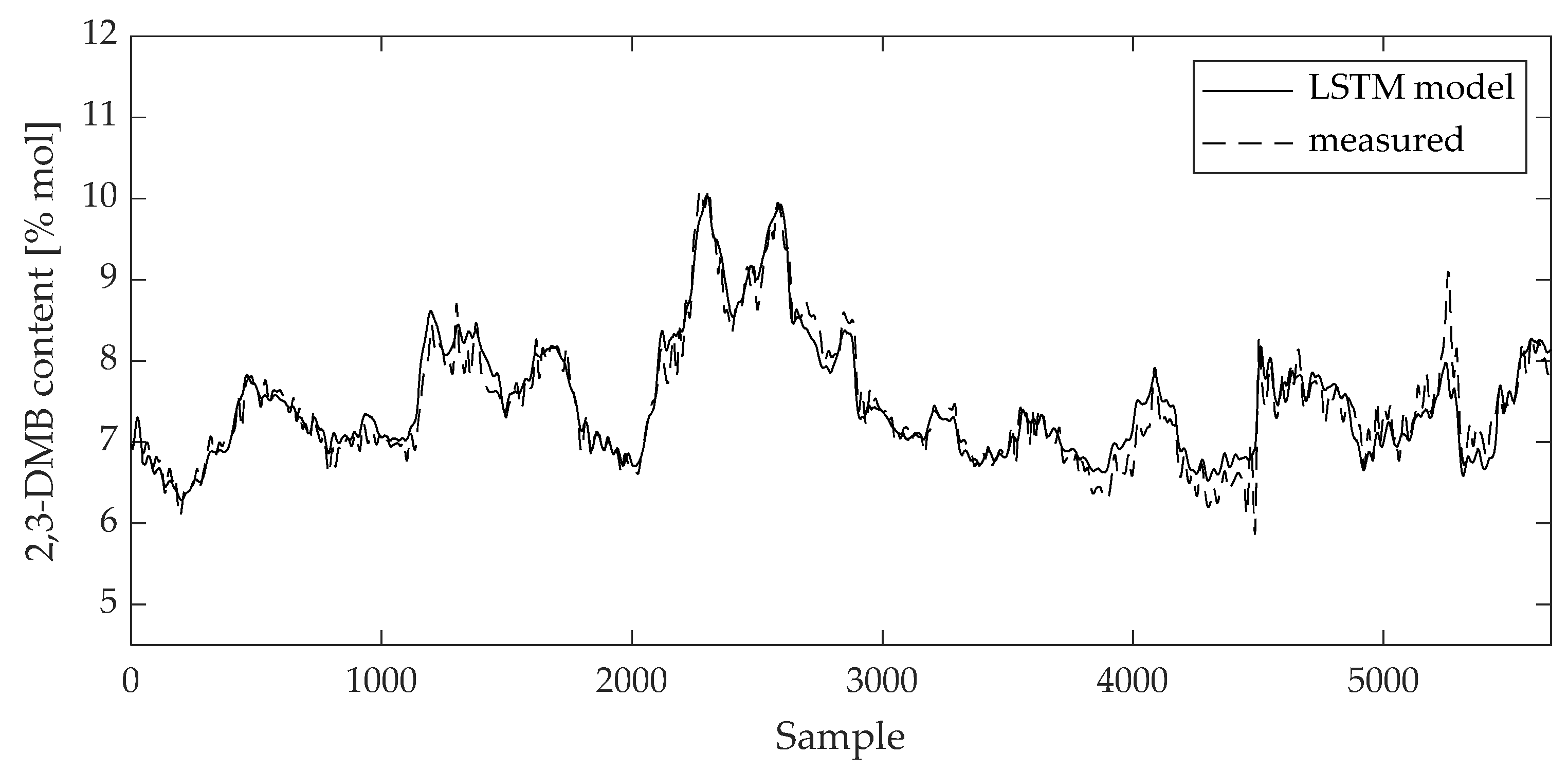
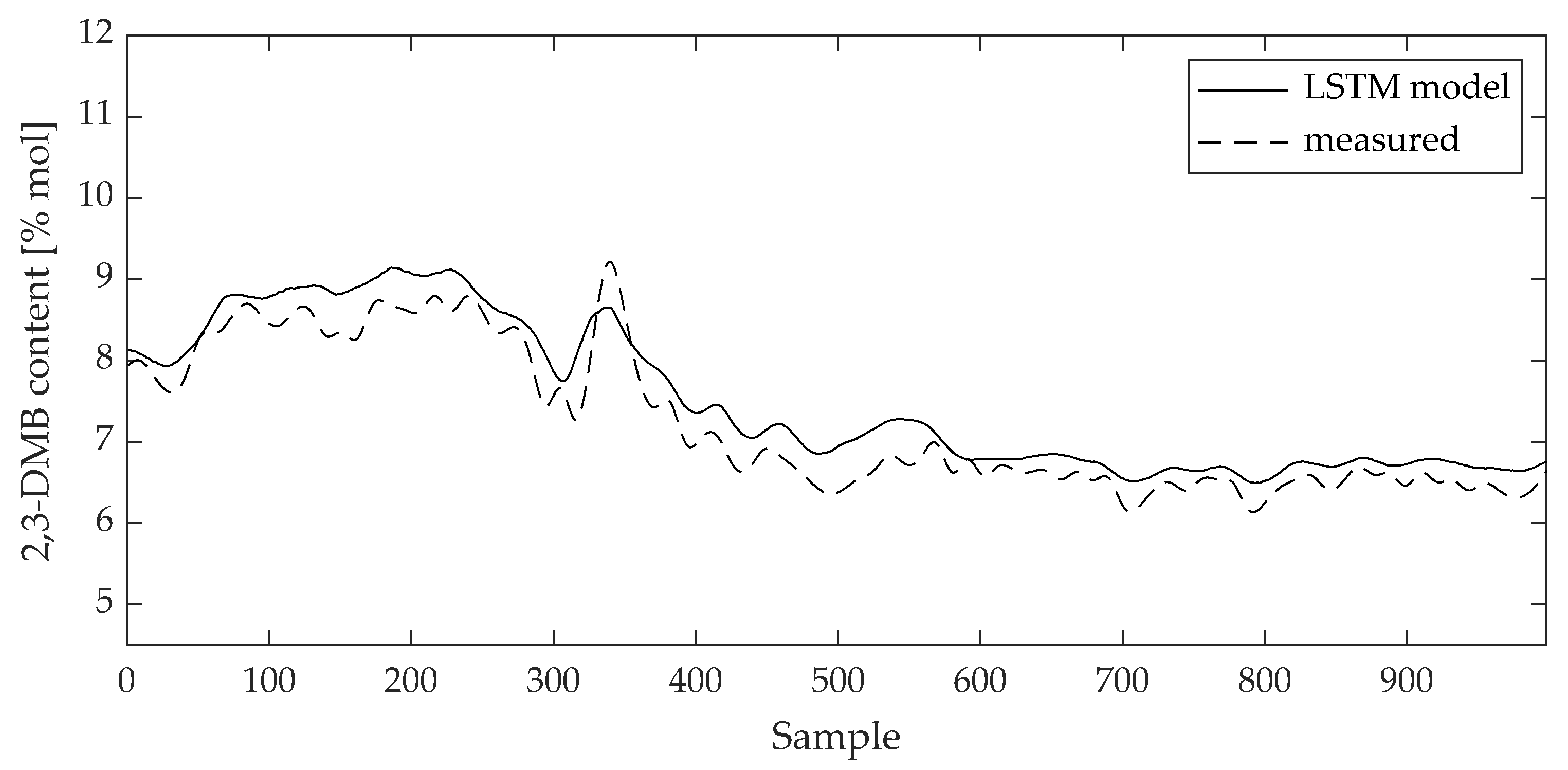
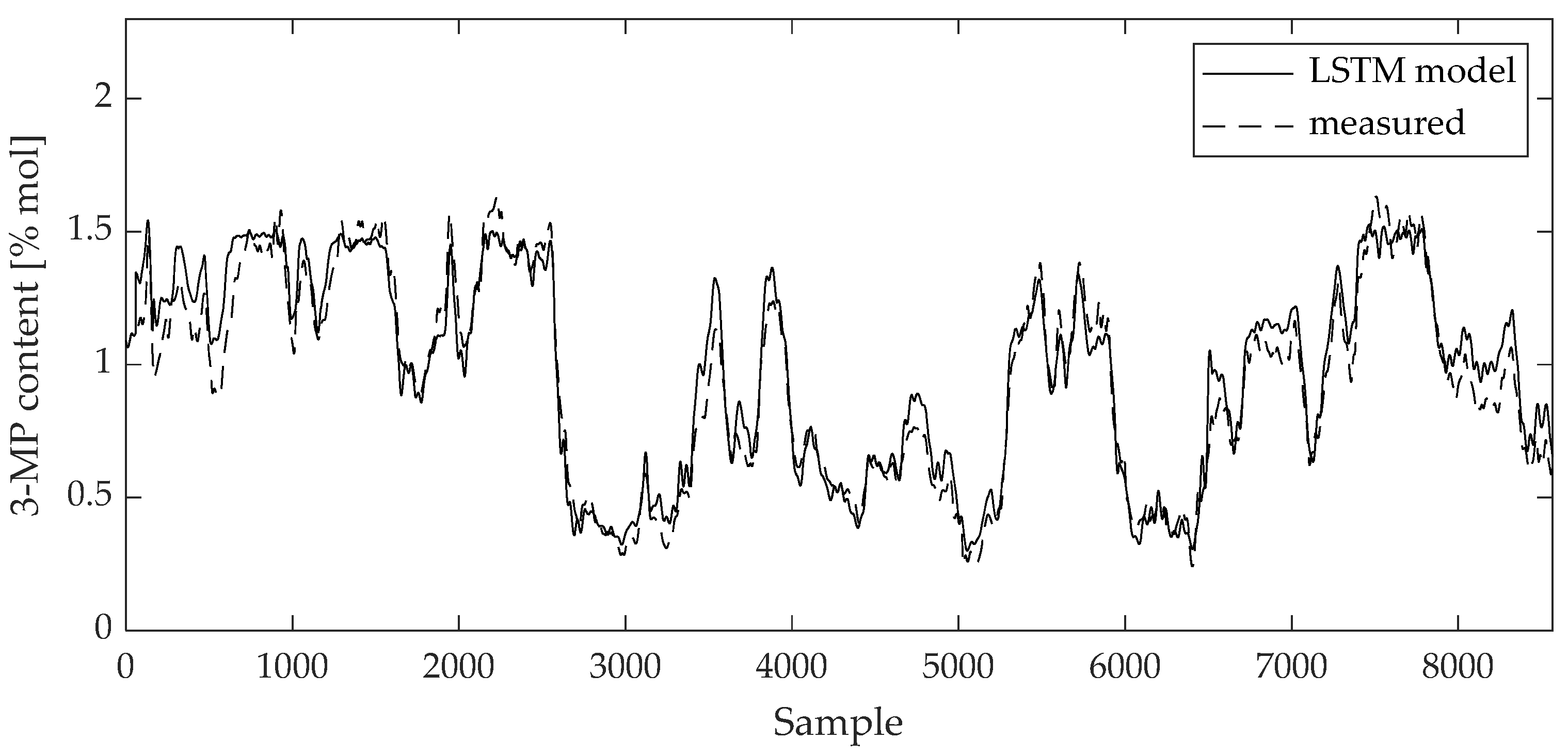
The validity of the model can be visually evaluated by a direct comparison between the measured data and the model values on the training and test data sets (Figure 10, Figure 11, Figure 12 and Figure 13). The curves of the model results correspond with the data from Table 2 and Table 3.
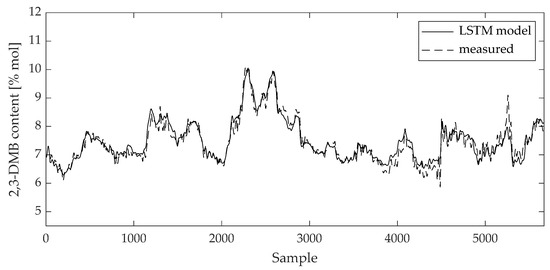
Figure 10.
Comparison between measured data and 2,3-DMB content LSTM model result for training data set.
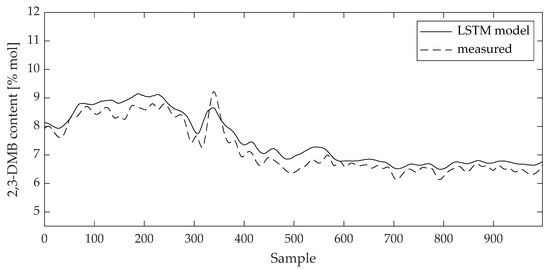
Figure 11.
Comparison between measured data and 2,3-DMB content LSTM model result for test data set.
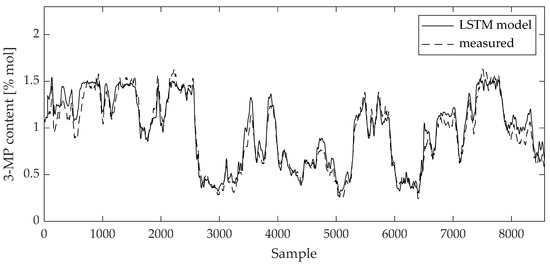
Figure 12.
Comparison between measured data and 3-MP content LSTM model result for training data set.
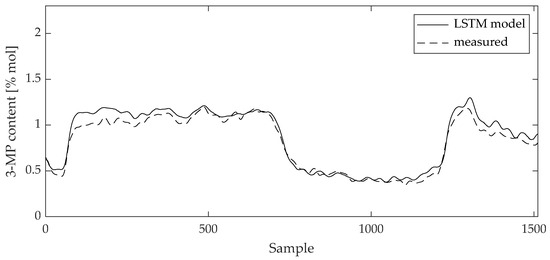
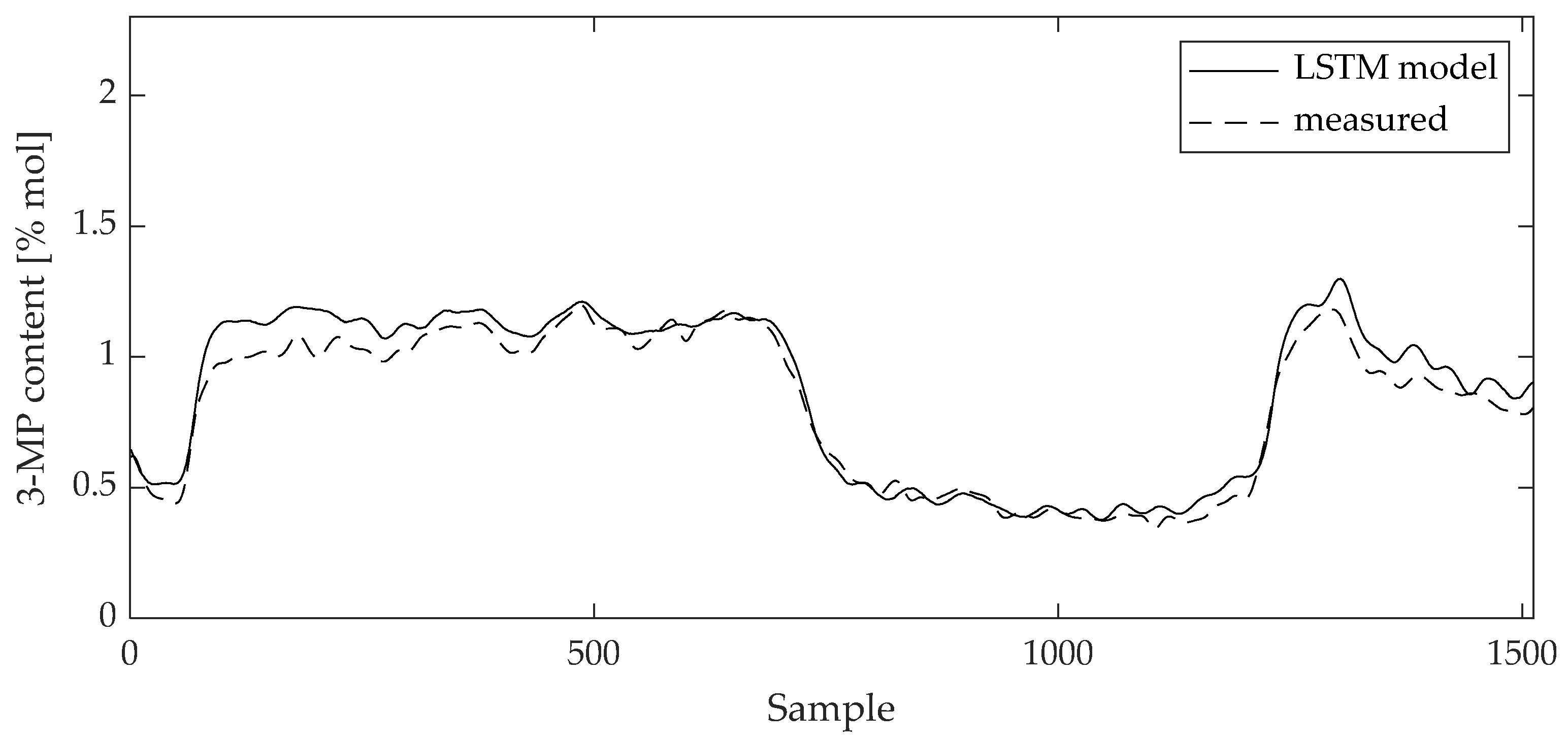
Figure 13.
Comparison between measured data and 3-MP content LSTM model result for test data set.
Table 4 and Table 5 show the comparison of the results of the LSTM network models presented above with MLP, SVM, and dynamic polynomial models (FIR, ARX, OE, NARX, and HW).

Table 4.
Comparison between 2,3-DMB LSTM and various types of model evaluation results.

Table 5.
Comparison between 3-MP LSTM and various types of model evaluation results.
For the 2,3-DMB content, the LSTM-based model evaluated by the Pearson correlation coefficient showed a better result than the MLP-, FIR-, ARX-, OE-, NARX-, and HW-based models. The robust SVM-based model performed slightly better according to this criterion. According to other statistical criteria, the LSTM-based model proved to be inferior. However, in terms of application, the results are within a satisfactory range since the mean square error and the mean absolute error are relatively small.
The curves of comparison show good agreement between the measured data and the 2,3-DMB and 3-MP model output, respectively, both on the training and test data sets.
In the case of the content of 3-MP, the LSTM-based model showed superior results compared to MLP-, SVM-, FIR-, ARX-, and NARX-based models for all statistical indicators. Only the dynamic polynomial models OE and HW with complex model structures are only slightly better in terms of statistical indicators. Based on the results, the models can be applied.
The MAE is one of the most intuitive indicators of model validity because it displays the error in the same units as the measured output variable. The model is considered valid if the MAE value does not exceed 10% of the difference between the minimum and maximum value of the measured output variable for the studied process. In the case of the 2,3-DMB content model, this percentage is 4.2%, while in the case of the 3-MP content model, it is only 1.4% for the worst of the compared models according to this criterion. Therefore, it is concluded that the compared models, including the LSTM-based models, estimate the output variable with satisfactory accuracy.
While developing MLP models, the early stopping method was implemented to prevent the model from overfitting. Early stopping involves monitoring the model’s performance and halting training when the performance starts to degrade, thus preventing overfitting [40]. The fact that none of the models presented in Table 4 and Table 5 were overfitted is evident from the very high and similar values of the coefficients of determination for both the training and test sets, which are very close to one, and the very small and similar values of the mean square error for the training and test data sets, which are very close to zero. For the dynamic polynomial models (FIR, ARX, OE, NARX, and HW), the final prediction criterion was also used as an indicator for evaluating the models [42,43]. This criterion represents the trade-off between model accuracy, expressed by the accuracy of the estimated parameters, and model complexity, expressed by the number of parameters used to parameterize the model. Complex models are more prone to overfitting, so this criterion helps in preventing overfitting by favoring simpler models that still perform well.
4. Discussion
The main hypothesis was to verify whether the recently widely used LSTM networks can satisfactorily estimate critical quality product components in a complex nonlinear industrial process and thus be successfully applied to the control systems of such processes. The research has shown that they can do so. The overall results of the developed models using LSTM networks are satisfactory. LSTM networks have a unique structure that allows them to selectively choose data from the past to correctly estimate future states, which means that there are no long computational times, which is very important in the industry.
In the paper under reference [40], it was found that an MLP generally describes the complex dynamics of a process worse than the dynamic polynomial models commonly used in these cases, in terms of the 2- and 3-MP content model groups, and the question of developing dynamic networks arose. It can now be seen that dynamic LSTM networks in this case give better results than most other models, including the robust SVM. They are only slightly worse than the structurally very complex models of OE and HW.
To directly compare the developed LSTM-based models with other already developed models for an isomerization process, two data sets were used from those previously defined. The set for the development of the 2,2- and 2,3-DMB content model groups has lower process dynamics (6667 continuous samples). The descriptive statistics of the data, which support this, are presented in Table 6 and Table 7. In the development of dynamic models, especially models with a simpler structure such as FIR and ARX, the problem of developing a satisfactory model arose because of this. Static MLP and SVM models showed better results, especially due to the randomization of the entire training data set. Due to the lower process dynamics and the characteristic structure of the LSTM network, the LSTM-based models gave slightly worse results compared to the other models, especially in terms of their higher mean square errors and mean absolute errors.

Table 6.
Descriptive statistics for 2,2- and 2,3-DMB content model group data [42].

Table 7.
Descriptive statistics for 2- and 3-MP content model group data [42].
Considering the characteristic data set, the highlighted advantages of LSTM networks did not come into play in this case.
The developed LSTM models of 2,3-DMB and 3-MP content are of satisfactory accuracy and have low errors overall, so they are recommended for application in the plant measurement and control system.
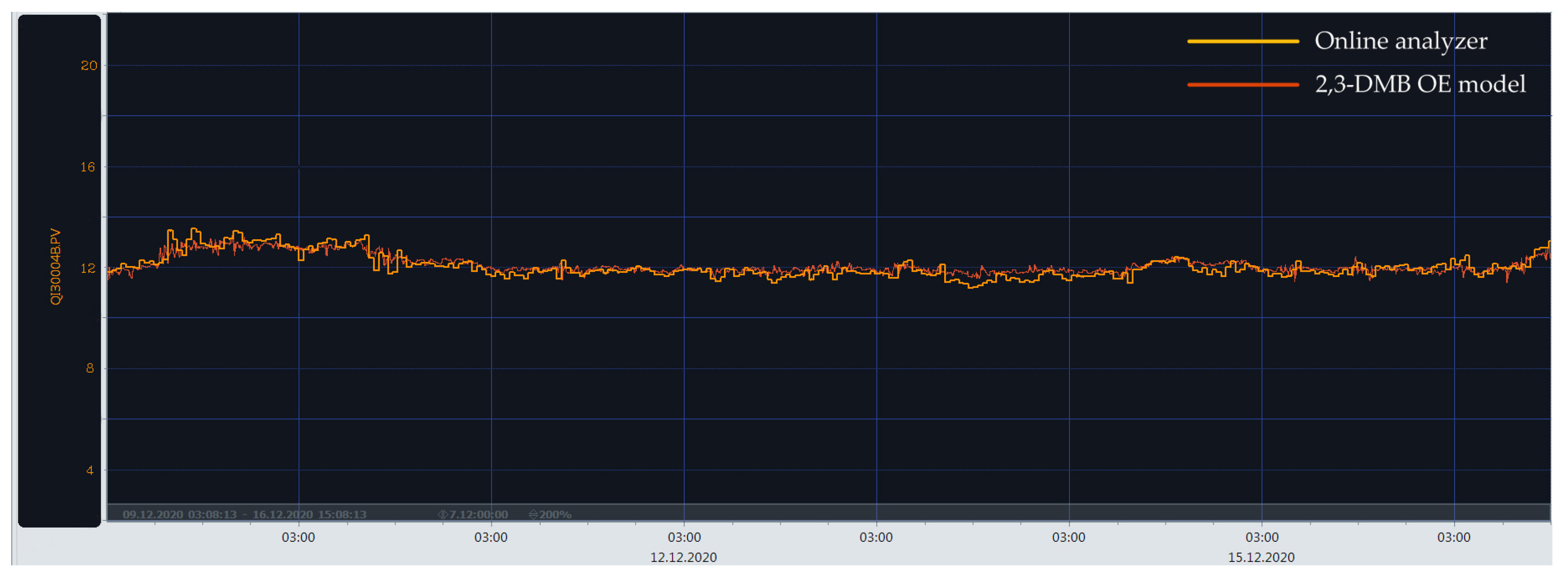
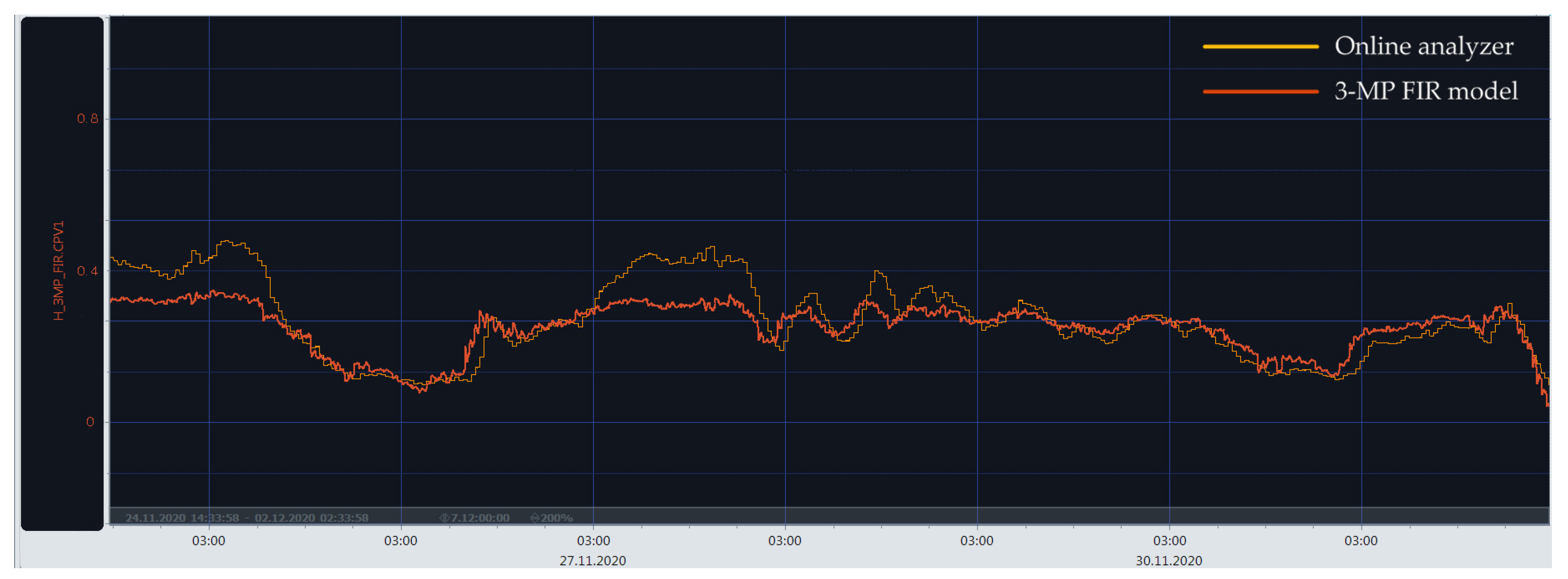
Based on the earlier developed dynamic polynomial model results, some of them were successfully implemented in a real plant. Figure 14 and Figure 15 show portions of the time plots in the parallel operation of process analyzers (yellow curve) and estimations from data-driven polynomial models (red curve) for 2,3-DMB and 3-MP content. A mostly good agreement between the analyzer and model results can be observed. In the case of the 2,3-DMB content OE model (Figure 14), it is clear that the process dynamics are not emphasized, which can often be the case and what is actually aimed for in a real process. Regarding the 3-MP content FIR model (Figure 15), there is some discrepancy between the analyzer and model evaluation results in the parts of the time plot where the process dynamics are more emphasized. This is mainly due to the less accurate and simple FIR model structure. A similar behavior can be assumed for the developed LSTM models. When the operating conditions significantly change, there can undoubtedly be significant changes in the values of certain input variables, and then the model must be retrained, which is a normal and common procedure.
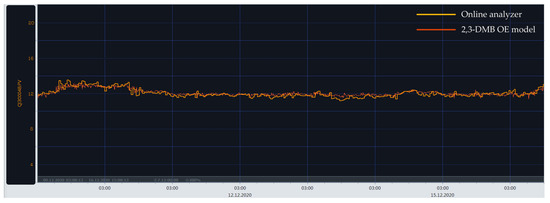
Figure 14.
The 2,3-DMB content OE model implementation results in the real plant [51].
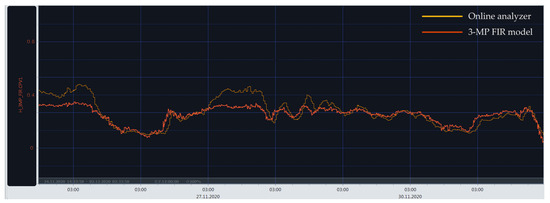
Figure 15.
The 3-MP content FIR model implementation results in the real plant [51].
The LSTM networks have a complex structure, and their estimations involve the study of memory cells and gates (as explained in Section 2.1). In the end, the pre-trained LSTM network model will be applied in a real plant, so the computation in the plant will not be particularly demanding. In this way, estimations and computations can be performed in real time without the need for constant retraining or high computational requirements in the plant.
Based on the available literature, the advantage of LSTM networks is most evident in natural language processing and speech recognition, where the data are inherently sequential. Industrial data, especially in stable plant operation regimes, can have fewer dynamics, so they are not so suitable for the LSTM architecture technique. In that sense, it is a certain drawback of LSTM.
Improvements in the developed LSTM models are possible by introducing an additional hidden layer; however, in this case, there is a risk of excessively complicating the model at the expense of a questionable improvement for practical applications.
Future studies in the field of soft sensor application in isomerization processes could explore the use of hybrid models that combine LSTM networks with other machine learning techniques, such as convolutional neural networks (CNN), to improve estimation accuracy and interpretability. Deep LSTM networks can also be considered, as well as random forest models. Global optimization methods such as genetic algorithms could be explored to estimate the hyperparameters of the LSTM network considering the large search space of possible parameter values, reducing the need for manual trial and error methods.
5. Conclusions
This paper presents the development of data-driven models based on dynamic LSTM networks and their comparison with several types of previously developed models, including MLP, SVM, FIR, ARX, OE, NARX, and HW. The LSTM-based models developed for estimating the contents of 2,3-DMB and 3-MP in an industrial process of isomerization show satisfactory results and are suitable for this application. In comparison with other models, the 3-MP content LSTM model shows generally better results, while the 2,3-DMB content LSTM model shows slightly worse results, mainly due to fewer available process dynamics.
Author Contributions
Conceptualization, S.H. and Ž.U.A.; methodology, S.H.; software, N.R.; validation, S.H., Ž.U.A. and N.R.; formal analysis, N.B.; investigation, N.B.; resources, N.B.; data curation, N.R.; writing—original draft preparation, S.H.; writing—review and editing, Ž.U.A.; visualization, Ž.U.A.; supervision, N.B.; project administration, Ž.U.A.; funding acquisition, N.B. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
Data sharing not applicable.
Conflicts of Interest
The authors declare no conflict of interest. The funders had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript; or in the decision to publish the results.
References
- Han, Y.; Huang, G.; Song, S.; Yang, L.; Wang, H.; Wang, Y. Dynamic Neural Networks: A Survey. IEEE Trans. Pattern Anal. Mach. Intell. 2022, 44, 7436–7456. [Google Scholar] [CrossRef] [PubMed]
- Medsker, L.R.; Jain, L.C. (Eds.) Recurrent Neural Networks Design and Applications; CRC Press: Boca Raton, FL, USA, 2001. [Google Scholar]
- Gillioz, A.; Casas, J.; Mugellini, E.; Khaled, O.A. Overview of the Transformer-based Models for NLP Tasks. In Proceedings of the 2020 15th Conference on Computer Science and Information Systems (FedCSIS), Sofia, Bulgaria, 6–9 September 2020. [Google Scholar] [CrossRef]
- Wan, R.; Mei, S.; Wang, J.; Liu, M.; Yang, F. Multivariate Temporal Convolutional Network: A Deep Neural Networks Approach for Multivariate Time Series Forecasting. Electronics 2019, 8, 876. [Google Scholar] [CrossRef]
- Yao, X.; Shao, Y.; Fan, S.; Cao, S. Echo state network with multiple delayed outputs for multiple delayed time series prediction. J. Frank. Inst. 2022, 359, 11089–11107. [Google Scholar] [CrossRef]
- Faradonbe, S.M.; Safi-Esfahani, F.; Karimian-Kelishadrokhi, M. A Review on Neural Turing Machine (NMT). SN Comput. Sci. 2020, 1, 333. [Google Scholar] [CrossRef]
- Rakhmatullin, A.K.; Gibadullin, R.F. Synthesis and Analysis of Elementary Algorithms for a Differential Neural Computer. Lobachevskii J. Math. 2022, 43, 473–483. [Google Scholar] [CrossRef]
- Soydaner, D. Attention mechanism in neural networks: Where it comes and where it goes. Neural Comput. Appl. 2022, 34, 13371–13385. [Google Scholar] [CrossRef]
- Widrow, B.; Winter, R. Neural nets for adaptive filtering and adaptive pattern recognitions. Computer 1988, 21, 25–39. [Google Scholar] [CrossRef]
- Rao, A.R.; Reimherr, M. Nonlinear Functional Modeling Using Neural Networks. J. Comput. Graph. Stat. 2023, 1–10. [Google Scholar] [CrossRef]
- Graves, A. Supervised Sequence Labelling with Reccurent Neural Networks; Springer: New York, NY, USA, 2012. [Google Scholar]
- Hochreiter, S.; Schmidhuber, J. Long Short-Term Memory. Neural Comput. 1997, 9, 1735–1780. [Google Scholar] [CrossRef]
- Van Houdt, G.; Mosquera, C.; Nápoles, G. A review on the long short-term memory model. Artif. Intell. Rev. 2020, 53, 5929–5955. [Google Scholar] [CrossRef]
- Liu, Y.; Young, R.; Jafarpour, B. Long–short-term memory encoder–decoder with regularized hidden dynamics for fault detection in industrial processes. J. Process Control 2023, 124, 166–178. [Google Scholar] [CrossRef]
- Aghaee, M.; Krau, S.; Tamer, M.; Budman, H. Unsupervised Fault Detection of Pharmaceutical Processes Using Long Short-Term Memory Autoencoders. Ind. Eng. Chem. Res. 2023, 62, 9773–9786. [Google Scholar] [CrossRef]
- Yao, P.; Yang, S.; Li, P. Fault Diagnosis Based on RseNet-LSTM for Industrial Process. In Proceedings of the 2021 IEEE 5th Advanced Information Technology, Electronic and Automation Control Conference (IAEAC), Chongqing, China, 12–14 March 2021. [Google Scholar]
- Zhang, H.; Niu, G.; Zhang, B.; Miao, Q. Cost-Effective Lebesgue Sampling Long Short-Term Memory Networks for Lithium-Ion Batteries Diagnosis and Prognosis. IEEE Trans. Ind. Electron. 2021, 69, 1958–1964. [Google Scholar] [CrossRef]
- He, R.; Chen, G.; Sun, S.; Dong, C.; Jiang, S. Attention-Based Long Short-Term Memory Method for Alarm Root-Cause Diagnosis in Chemical Processes. Ind. Eng. Chem. Res. 2020, 59, 11559–11569. [Google Scholar] [CrossRef]
- Yu, J.; Liu, X.; Ye, L. Convolutional Long Short-Term Memory Autoencoder-Based Feature Learning for Fault Detection in Industrial Processes. IEEE Trans. Instrum. Meas. 2020, 70, 3505615. [Google Scholar] [CrossRef]
- Tan, Q.; Li, B. Soft Sensor Modeling Method for Sulfur Recovery Process Based on Long Short-Term Memory Artificial Neural Network (LSTM). In Proceedings of the 2023 9th International Conference on Energy Materials and Environment Engineering (ICEMEE 2023), Kuala Lumpur, Malaysia, 8–10 June 2023. [Google Scholar]
- Curreri, F.; Patanè, L.; Xibilia, M.G. RNN- and LSTM-Based Soft Sensors Transferability for an Industrial Process. Sensors 2021, 21, 823. [Google Scholar] [CrossRef]
- Yuan, X.; Li, L.; Wang, Y. Nonlinear Dynamic Soft Sensor Modeling With Supervised Long Short-Term Memory Network. IEEE Trans. Ind. Inform. 2020, 16, 3168–3176. [Google Scholar] [CrossRef]
- Liu, Q.; Jia, M.; Gao, Z.; Xu, L.; Liu, Y. Correntropy long short term memory soft sensor for quality prediction in industrial polyethylene process. Chemom. Intell. Lab. Syst. 2022, 231, 104678. [Google Scholar] [CrossRef]
- Zhou, J.; Wang, X.; Yang, C.; Xiong, W. A Novel Soft Sensor Modeling Approach Based on Difference-LSTM for Complex Industrial Process. IEEE Trans. Ind. Inform. 2022, 18, 2955–2964. [Google Scholar] [CrossRef]
- Geng, Z.; Chen, Z.; Meng, Q.; Han, Y. Novel Transformer Based on Gated Convolutional Neural Network for Dynamic Soft Sensor Modeling of Industrial Processes. IEEE Trans. Ind. Inform. 2022, 18, 1521–1529. [Google Scholar] [CrossRef]
- Feng, Z.; Li, Y.; Sun, B. A multimode mechanism-guided product quality estimation approach for multi-rate industrial processes. Inf. Sci. 2022, 596, 489–500. [Google Scholar] [CrossRef]
- Sun, M.; Zhang, Z.; Zhou, Y.; Xia, Z.; Zhou, Z.; Zhang, L. Convolution and Long Short-Term Memory Neural Network for PECVD Process Quality Prediction. In Proceedings of the 2021 Global Reliability and Prognostics and Health Management (PHM-Nanjing), Nanjing, China, 15–17 October 2021. [Google Scholar]
- Tang, Y.; Wang, Y.; Liu, C.; Yuan, X.; Wang, K.; Yang, C. Semi-supervised LSTM with historical feature fusion attention for temporal sequence dynamic modeling in industrial processes. Eng. Appl. Artif. Intell. 2023, 117, 105547. [Google Scholar] [CrossRef]
- Lei, R.; Guo, Y.B.; Guo, W. Physics-guided long short-term memory networks for emission prediction in laser powder bed fusion. J. Manuf. Sci. Eng. 2023, 146, 011006. [Google Scholar] [CrossRef]
- Jin, N.; Zeng, Y.; Yan, K.; Ji, Z. Multivariate Air Quality Forecasting With Nested Long Short Term Memory Neural Network. IEEE Trans. Ind. Inform. 2021, 17, 8514–8522. [Google Scholar] [CrossRef]
- Xu, B.; Pooi, C.K.; Tan, K.M.; Huang, S.; Shi, X.; Ng, H.Y. A novel long short-term memory artificial neural network (LSTM)-based soft-sensor to monitor and forecast wastewater treatment performance. J. Water Process Eng. 2023, 54, 104041. [Google Scholar] [CrossRef]
- Wang, T.; Leung, H.; Zhao, J.; Wang, W. Multiseries Featural LSTM for Partial Periodic Time-Series Prediction: A Case Study for Steel Industry. IEEE Trans. Instrum. Meas. 2020, 69, 5994–6003. [Google Scholar] [CrossRef]
- Mateus, B.C.; Mendes, M.; Farinha, J.T.; Cardoso, A.M. Anticipating Future Behavior of an Industrial Press Using LSTM Networks. Appl. Sci. 2021, 11, 6101. [Google Scholar] [CrossRef]
- Kazi, M.K.; Eljack, F. Practicality of Green H2 Economy for Industry and Maritime Sector Decarbonization through Multiobjective Optimization and RNN-LSTM Model Analysis. Ind. Eng. Chem. Res. 2022, 61, 6173–6189. [Google Scholar] [CrossRef]
- Ma, S.; Zhang, Y.; Lv, J.; Ge, Y.; Yang, H.; Li, L. Big data driven predictive production planning for energy-intensive manufacturing industries. Energy 2020, 211, 118320. [Google Scholar] [CrossRef]
- Hamied, R.S.; Shakor, Z.M.; Sadeiq, A.H.; Abdul Razak, A.A.; Khadim, A.T. Kinetic Modeling of Light Naphtha Hydroisomerization in an Industrial Universal Oil Products Penex™ Unit. Energy Eng. 2023, 120, 1371–1386. [Google Scholar] [CrossRef]
- Khajah, M.; Chehadeh, D. Modeling and active constrained optimization of C5/C6 isomerization via Artificial Neural Networks. Chem. Eng. Res. Des. 2022, 182, 395–409. [Google Scholar] [CrossRef]
- Abdolkarimi, V.; Sari, A.; Shokri, S. Robust prediction and optimization of gasoline quality using data-driven adaptive modeling for a light naphtha isomerization reactor. Fuel 2022, 328, 125304. [Google Scholar] [CrossRef]
- Lukec, I.; Lukec, D.; Sertić Bionda, K.; Adžamić, Z. The possibilities of advancing isomerization process through continuous optimization. Goriva I Maz. 2007, 46, 234–245. [Google Scholar]
- Ujević Andrijić, Ž.; Herceg, S.; Bolf, N. Data-driven estimation of critical quality attributes on industrial processes. In Proceedings of the 19th Ružička Days “Today Science—Tomorrow Industry” international conference, Vukovar, Croatia, 21–23 September 2022. [Google Scholar]
- Herceg, S.; Ujević Andrijić, Ž.; Bolf, N. Support vector machine-based soft sensors in the isomerization process. Chem. Biochem. Eng. Q. 2020, 34, 243–255. [Google Scholar] [CrossRef]
- Herceg, S.; Ujević Andrijić, Ž.; Bolf, N. Development of soft sensors for isomerization process based on support vector machine regression and dynamic polynomial models. Chem. Eng. Res. Des. 2019, 149, 95–103. [Google Scholar] [CrossRef]
- Herceg, S.; Ujević Andrijić, Ž.; Bolf, N. Continuous estimation of the key components content in the isomerization process products. Chem. Eng. Trans. 2018, 69, 79–84. [Google Scholar] [CrossRef]
- Fortuna, L.; Graziani, S.; Rizzo, A.; Xibilia, M.G. Soft Sensors for Monitoring and Control of Industrial Processes (Advances in Industrial Control); Springer: London, UK, 2007. [Google Scholar]
- Kadlec, P.; Gabrys, B.; Strandt, S. Data-driven Soft Sensors in the process industry. Comput. Chem. Eng. 2009, 33, 795–814. [Google Scholar] [CrossRef]
- Greff, K.; Srivastava, R.K.; Koutník, J.; Steunebrink, B.R.; Schmidhuber, J. LSTM: A Search Space Odyssey. IEEE Trans. Neural Netw. Learn. Syst. 2017, 28, 2222–2232. [Google Scholar] [CrossRef]
- Beale, M.H.; Hagan, M.T.; Demuth, H.B. Deep Learning Toolbox™ User’s Guide; The MathWorks, Inc.: Natick, MA, USA, 2020; pp. 53–64. [Google Scholar]
- Goodfellow, I.; Bengio, Y.; Courville, A. Deep Learning; The MIT Press: Cambridge, MA, USA, 2016; pp. 267–320. [Google Scholar]
- Cusher, N.A. UOP Penex Process. In Handbook of Petroleum Refining Processes, 3rd ed.; Meyers, R.A., Ed.; McGraw-Hill: New York, NY, USA, 2003; pp. 9.15–9.27. [Google Scholar]
- Cerić, E. Nafta, Procesi i Proizvodi; IBC d.o.o.: Sarajevo, Bosnia and Herzegovina, 2012. [Google Scholar]
- Herceg, S. Development of Soft Sensors for Advanced Control of Isomerization Process. Doctoral Thesis, University of Zagreb, Zagreb, Croatia, 30 September 2021. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).