Abstract
Federated learning is a distributed learning framework designed to protect user privacy, widely applied across various domains. However, existing federated learning algorithms face challenges, including slow convergence, significant loss fluctuations during aggregation, and imbalanced client sampling. To address these issues, this paper introduces a high-performance federated learning aggregation algorithm. This algorithm combines a cyclic adaptive learning rate adjustment strategy with client-weighted random sampling, addressing the aforementioned problems. Weighted random sampling assigns client weights based on their sampling frequency, balancing client sampling rates and contributions to enhance model aggregation. Additionally, it adapts the learning rate based on client loss variations and communication rounds, accelerating model convergence and reducing communication costs. To evaluate this high-performance algorithm, experiments are conducted using well-known datasets MNIST and CIFAR-10. The results demonstrate significant improvements in convergence speed and loss stability. Compared to traditional federated learning algorithms, our approach achieves faster and more stable convergence while effectively reducing training costs.
Keywords:
distributed learning; federated learning; aggregation algorithm; weighted sampling; learning rate adjustment MSC:
68W15
1. Introduction
With the rapid development of artificial intelligence [1] and IoT (Internet of Things) technology, an increasing number of data are dispersed across various terminal devices and edge servers. Therefore, data silos and data privacy protection are the two primary challenges in artificial intelligence technology [2]. In 2016, Google first introduced the concept of federated learning in a paper published on arXiv [3], which allows users to protect their dataset privacy while jointly training and sharing models. As an emerging distributed machine learning approach, federated learning has emerged as a solution to effectively address privacy preservation and data security issues [4] by conducting model training locally on devices, avoiding centralized data collection and storage.
However, federated learning faces several challenges, including significant resource consumption and low aggregation efficiency when aggregating client model parameters during the training process. In traditional federated learning, all clients typically use the same fixed learning rate for local model training, as shown in Figure 1. Nevertheless, due to variations in client performance and data heterogeneity, using a fixed learning rate may result in slow convergence or performance degradation of the global model. For instance, on mobile devices, certain clients may have limited computational resources and higher energy consumption, leading to slower processing speeds, while other high-performance servers can complete model training more quickly. Consequently, there is a need to introduce a learning rate adjustment strategy into the federated learning framework to dynamically adjust the learning rate, personalized to adapt to the characteristics of different clients, and enhance the algorithm’s performance and convergence speed.
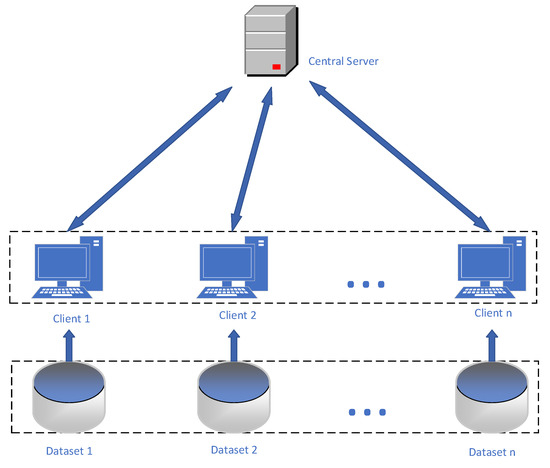
Figure 1.
Federated learning architecture diagram.
Another challenge is to select the participating clients carefully during the aggregation process in federated learning. Traditional federated averaging algorithms often employ random selection or follow certain rules to choose clients. However, such selection methods may overlook the contributions of certain clients or lead to excessive participation, thereby affecting the accuracy and stability of the aggregation results. For example, some clients may have a high accuracy in model aggregation but may not be able to participate in a timely manner, resulting in delayed model updates. To address this issue, a multi-client selection scheme is needed, which takes into account factors such as client accuracy and data scale to make a rational choice of participating clients and better balance their contributions.
To address the above challenges, this paper proposes a federated learning aggregation algorithm with improved efficiency. In this method, we introduce cyclic adaptive learning rate adjustment to adjust the learning rate of local clients dynamically, based on the progress and performance of their local training, to accelerate the convergence speed of the model. Simultaneously, we design a client-weighted sampling algorithm, considering the sampling frequency of clients, to avoid the drawbacks of multiple sampling for some clients and nonsampling for others, and assign different weights to clients to enhance the accuracy and stability of the aggregation process.
The following sections will provide a detailed description of our algorithm design and experimental results to validate the effectiveness and performance advantages of the proposed improvements. Through experimental evaluations comparing different learning rate schemes and real-world application scenarios, we will demonstrate the superiority of cyclic adaptive learning rate and client-weighted sampling algorithms in federated learning aggregation models. We will also explore their potential in improving model convergence speed, accuracy, and stability. This research will provide new insights and solutions for the development of federated learning, promoting its widespread application in practical scenarios and further research.
The main contributions of this paper are as follows:
- Traditional learning rate strategies lack adaptability and cannot adjust the learning rate based on dynamic changes during the training process. The proposed cyclic adaptive learning rate adjustment algorithm replaces the traditional approach of fixed learning rates for clients. Experimental results on various datasets show that it improves the training effectiveness of local models and enhances the performance of the global model;
- Addressing the issue of slow aggregation caused by traditional random sampling of clients, this paper introduces a client sampling strategy to balance the frequency of client sampling and their contributions, effectively enhancing the efficiency of model training in federated learning. The proposed federated learning client-weighted sampling method eliminates the impact of a single randomly selected client on global weights, addressing existing issues in client sampling algorithms;
- This paper conducts experimental evaluations on two representative datasets. The experimental results on these datasets demonstrate that, compared to baseline algorithms, the enhanced algorithm achieves the same test accuracy with an average reduction of 27.65% in training rounds on the MNIST dataset and an average reduction of 27.75% in training rounds on the CIFAR-10 dataset.
2. Related Work
Federated learning is a machine learning framework that protects user data privacy, allowing multiple participants to locally train models without sharing raw data [5]. Many researchers have combined federated learning with technologies such as secret sharing [6], differential privacy [7], secure multi-party computation [8], and homomorphic encryption [9,10] to achieve secure and efficient federated learning solutions. In recent years, the field of federated learning has seen a surge in new algorithms and optimization techniques to address challenges related to communication efficiency, model security, and convergence speed.
One of the most commonly used algorithms in federated learning is the FedAvg [3] algorithm. In the federated learning research, Briggs et al. [11] introduced hierarchical clustering based on FedAvg. They clustered and separated clients according to the similarity between the local updates of clients and the global model, thereby improving aggregation efficiency. Karimireddy et al. [12] corrected the direction of client local updates by estimating the difference between the server and client update directions, successfully overcoming the problem of non-uniform data distribution. This correction strategy enables faster model convergence within fewer communication rounds, accelerating the federated learning training process.
Ye et al. [13] introduced the FedCNM algorithm, which employs global momentum to mitigate “client drift”, leading to a significant improvement in test accuracy, with an enhancement ranging from 1.46% to 11.12%. Additionally, the use of local optimizers, SGD + M and NAG, further improved test accuracy by 10.53% and 10.44%, respectively. Ref. [14] presented the Client-Level Federated Learning (CL-FL) method, primarily addressing client contribution protection in federated learning. This method adds Gaussian noise to each participant’s contributions through a central server to hide their contributions and designs a dynamic differential privacy adjustment method to improve training efficiency. Chen et al. [15] divided the neural network in federated learning into shallow and deep layers and observed that the update frequency of deep layers was lower than that of shallow layers. Based on this observation, they proposed an asynchronous update strategy, effectively reducing the number of parameters transmitted in each round by reducing the transmission of deep-layer parameters during the communication process.
Haddadpour et al. [16] reduced communication overhead in federated learning by employing gradient compression and local computation on top of FedAvg, thereby improving the algorithm’s efficiency. Specifically, the algorithm computes gradients locally, compresses them, and then uploads them to the server, reducing the amount of communication. Zhang et al. [17] designed a federated learning method for mechanical fault diagnosis and proposed a dynamic verification scheme based on the federated learning framework to adaptively adjust the model aggregation process. They also introduced a self-supervised learning scheme to learn structural information from limited training data. Meng et al. [18], in the context of differentially private federated learning, addressed the problem of gradient explosion caused by a learning rate that is too large or too small during the neural network training process. They proposed the CAdabelief algorithm and integrated it into the framework of differentially private federated learning, conducting federated learning differential privacy experiments with the MNIST dataset. The experimental results demonstrated that under the same privacy budget, the CAdabelief algorithm outperformed three comparative algorithms: SGD [19], Adam [20], and Adabelief [21]. In this paper, we improve the federated learning algorithm by changing the learning rate allocation scheme and client sampling scheme, aiming to accelerate model training speed, reduce loss, and minimize communication rounds.
3. Theoretical Knowledge
Regarding the proposed cyclic adaptive learning rate adjustment algorithm and client-weighted sampling strategy, this paper not only provides detailed definitions and computational steps in subsequent sections but also analyzes their abilities in reducing communication overhead and improving model convergence speed through experimental analysis. Therefore, this section will introduce the federated learning knowledge relevant to the experiments conducted in this study, as well as the model structures used in the experiments.
3.1. Federated Learning
Federated learning [3] is a distributed training approach that utilizes decentralized datasets from multiple participants through privacy-preserving techniques to collaboratively build a joint model [22]. During the training process, participants exchange model-related information such as model structure, model parameters, and gradient information while keeping their local data securely stored on their own devices. Information transmission is performed using encryption or noise addition techniques. Compared to traditional machine learning algorithms, federated learning does not require centralization of all participants’ data, effectively preserving the privacy of individual data owners. The trained federated learning model can be shared and deployed among the participants. In summary, the characteristics of federated learning can be summarized as follows:
- There are two or more participants who aim to cooperatively build a consensus model that can be shared;
- During the federated learning training process, each participant’s local dataset is strictly kept on their device;
- Model-related information of federated learning participants is transmitted and exchanged in an encrypted manner, ensuring that no participant can infer the local dataset of other participants based on their model-related information;
- The performance of the joint model obtained through federated learning should closely approximate the performance of traditional centralized training machine learning models.
Figure 2 presents a typical data distribution chart for Horizontal Federated Learning (HFL). Based on different distribution patterns in the sample space and feature space of training data, federated learning can be categorized into Horizontal Federated Learning (HFL), Vertical Federated Learning (VFL), and Federated Transfer Learning (FTL) [23]. The work in this paper is based on the Horizontal Federated Learning architecture, which is suitable for scenarios where participants have significant feature overlap in their data but limited sample overlap. Under the Horizontal Federated Learning (HFL) architecture, participants with the same model structure and data format collaboratively train a joint model under the coordination of the aggregation server. All participant clients’ local models are aggregated through the central server, while their original data are strictly kept locally and do not leave the local clients.
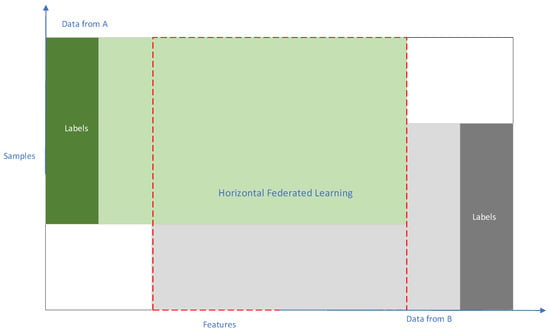
Figure 2.
Horizontal Federated Learning data distribution chart.
Figure 3 illustrates the process of model parameter aggregation in federated learning. The steps are explained below:
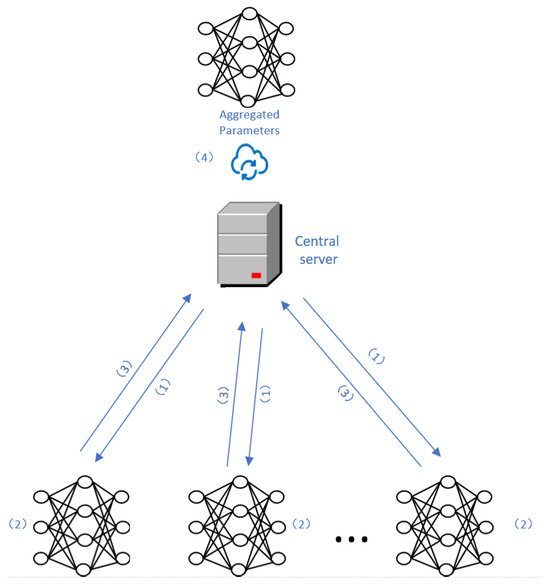
Figure 3.
Federated learning parameter aggregation process.
- At the beginning of the training process, the central server sends initial parameters to the local clients;
- Each local client uses the received model parameters to update its own model and then performs local model training. After local training, each client obtains its local model parameters, which are then encrypted using techniques such as homomorphic encryption or differential privacy;
- All clients send their encrypted data to the central server;
- The server receives the encrypted data without decrypting them. It uses secure federated learning aggregation algorithms to aggregate the parameters uploaded by the participants.
The above steps 1–4 are repeated until the federated learning model reaches the desired testing accuracy or until the maximum allowed number of iterations between the clients and the server is reached, as set by the program.
In the above training process, participants interact with the central server by exchanging encrypted model parameter information. The central server aggregates the received encrypted model parameters and sends back the averaged model to the participants. This method is referred to as model averaging in federated learning [3]. Another approach involves directly sharing the locally computed model gradient information. This method is known as gradient averaging [24]. In this paper, we focus on the model averaging aggregation algorithm, which has advantages such as independence from specific optimization algorithms and better privacy protection compared to gradient averaging. All experiments are conducted based on the model averaging aggregation algorithm.
3.2. MLP and ResNet
A Convolutional Neural Network (CNN) [25] is a type of deep learning model primarily used for image recognition tasks, widely applied in the field of computer vision. A CNN is capable of automatically learning hierarchical feature representations from images. It comprises multiple layers, including convolutional layers, pooling layers, and fully connected layers. The convolutional layers perform convolution operations on the input images to extract local features, while the pooling layers down sample the feature maps to reduce computational complexity. The fully connected layers, also known as dense layers, integrate the extracted features together to make the final predictions.
MLP (Multi-layer Perceptron) is a fundamental feed-forward neural network model and one of the simplest deep learning models. It consists of multiple fully connected layers (also known as hidden layers), with each hidden layer applying a nonlinear transformation using an activation function. The last hidden layer is connected to the output layer, which typically uses the softmax activation function for classification tasks. By introducing more neurons in each hidden layer, the MLP model can learn and represent more complex features.
ResNet (Residual Network) [26] was proposed to address the issues of gradient vanishing and degradation in deep neural networks. It introduced residual connections (skip connections), allowing the network to learn residual mappings, i.e., learning the residuals within each residual block, which enables effective training of deeper networks. ResNet has shown remarkable performance in image classification tasks, capable of handling complex image features and achieving higher classification accuracy. Table 1 below compares several common network parameters and their adaptability range.

Table 1.
Comparison of common CNN network parameters and adaptability range.
In the experiments of this paper on federated learning, two types of neural networks, MLP and ResNet, are used as the client models for local training. The local client models are trained and then sent to the central server. The central server employs a certain strategy to sample clients from all participants and aggregate the local model parameters. Finally, the aggregated model parameters are returned to the clients by the central server for the next round of training.
4. High-Performance Aggregation Mechanism
By introducing the improved approach of cyclic adaptive learning rate adjustment and weighted random client sampling, we can effectively enhance the aggregation performance of the federated learning aggregation algorithm, reducing communication overhead and accelerating the convergence speed of the model. The cyclic adaptive learning rate adjustment strategy enables clients to automatically adjust the learning rate based on their local model’s performance and loss, allowing them to better adapt to their training progress. The weighted random client sampling strategy takes into account the historical sampling frequency of clients, assigning different sampling weights to clients to reduce the sampling weight of clients that are frequently sampled randomly. This balances the contributions of each client and increases the diversity of the aggregated model. Through these improvement measures, we can significantly reduce unnecessary communication overhead, improve the efficiency of federated learning, and accelerate the convergence speed of the global model, thereby providing better performance and scalability for practical applications of federated learning.
4.1. Cyclic Adaptive Learning Rate Strategy
In this work, we address the learning rate issue in the Federated Averaging (FedAvg) aggregation algorithm used in federated learning. We propose a cyclic adaptive learning rate (CALR) adjustment strategy based on the change in loss. This strategy replaces the traditional fixed learning rate used in FedAvg, as a fixed learning rate can result in slow or unstable convergence during model training. The content of Adaptive Learning Rate Adjustment Algorithm 1 is as follows:
| Algorithm 1 Learning Rate Adjustment. |
| function ADJUST_LEARNING_RATE(Passing values: communication round number , current loss , historical loss , and loss ratio threshold threshold) |
| Calculate loss ratio: |
| Calculate rate of change: |
| if then |
| end if |
| Calculate learning rate adjustment factor: |
| if then |
| Set new learning rate: |
| else if and then Calculate : |
| else if and then Calculate : |
| else |
| Set new learning rate: |
| Unchanged |
| end if |
The cyclic adaptive learning rate algorithm takes into account the model aggregation rounds and the loss change rate , and it constrains the range of learning rate variations. The algorithm sets the maximum value and the minimum value for the learning rate, enabling it to cycle within a certain range. The learning rate variation range is determined through practical measurements, and, within each cycle, the learning rate adapts dynamically based on specific factors. The formula for the learning rate in the ith round is as follows:
The adaptive learning rate variation depends on the magnitude of the change in loss between two consecutive training iterations. Therefore, the first step is to calculate the rate of change in loss between these iterations:
The specific learning rate variation coefficient is related to the rate of change in loss and the communication round . The learning rate variation coefficient is calculated as follows:
The relationship between and can be expressed as follows:
: Learning rate. is the learning rate for the ith (i > 0) round, and the initial learning rate is set to 0.001.
: is the number of iterations between the client and the central server.
: is the change rate of the learning rate with respect to the historical learning rates, based on which the decay coefficient is generated.
: The learning rate change coefficient represents how fast the learning rate changes, with a larger leading to faster learning rate variations.
: The client model training initialization parameters represent the initial model parameters for client training. After the learning rate changes, the model parameters are updated, allowing the client to use the new learning rate for training in the next round.
In this paper, the improved algorithm monitors the loss variation of each client in every round and adjusts the learning rate based on the training iterations. If a client’s loss decreases slowly in a particular round, it indicates that its training process may be challenging and requires a smaller learning rate for finer adjustments. Conversely, if a client’s loss decreases rapidly, it suggests that its training process is smooth, and a larger learning rate can be used to accelerate the convergence speed. By dynamically adapting the learning rate based on the loss variation and training rounds, the algorithm aims to achieve faster and more stable convergence during the federated learning process.
When the model’s loss function exhibits oscillations or instability during the training process, the learning rate is reduced:
When the training process reveals slow convergence or a gradual decrease in the loss function, the learning rate is increased:
4.2. Weighted Random Sampling Strategy
In each round of federated learning communication, the server selects a subset of available clients to participate in training. The server’s operations include client sampling and assigning weights to the sampled clients. Common methods for client sampling are random selection and weighted averaging. In random selection, a portion of clients is randomly chosen to participate in training, and each client is assigned the same weight. The server then calculates the weighted average of the model parameters from the sampled clients and sends it back to the clients as the new version of the global model for the next round of training.
However, random selection may lead to some clients having low participation rates, especially when there are differences in computational power, data size, and other factors among clients. The contributions of clients with different data distributions may be underestimated, which can result in some clients’ data not being fully utilized during training, leading to a decrease in the performance of the global model on those data distributions and, subsequently, affecting the overall model’s performance.
To address this issue, this paper introduces the innovative weighted random sampling (WRS) strategy for clients. WRS balances the relationship between the client sampling frequency and the random sampling weights. Initially, all clients have zero sampling frequency and equal sampling weights. However, after each round of communication and aggregation, the client sampling frequency is updated, and the sampling weights are adjusted accordingly. For example, if a client is repeatedly selected in multiple rounds, its sampling weight may be reduced. By dynamically adjusting the sampling weights, WRS ensures a balanced client selection and avoids extreme selection results.
The detailed steps of the client-weighted random sampling strategy are as follows:
- Initialization: For each client, its sampling weight is determined based on the number of times it has been sampled. Therefore, a global list is defined to record the sampling count for each client. The sampling count for all clients in the list is initially set to 0;
- Initial Weight Assignment: represents the weight of random sampling for each client. The initial sampling weights for each client are defined as equal, with the initial unnormalized value for each client being ;
- Sampling Round Update: The sampling count in the list is increased by 1 for the selected clients in each sampling round. represents the weight of the client during the ith interaction between the client and the central server;
- Weight Adjustment: Based on the number of times each client has been sampled, the client’s sampling weight is adjusted. Typically, clients with more sampling will receive lower weights to balance the sampling results. The client weight adjustment formula is as follows:
- Weight Normalization: To ensure that the total sum of sampling weights for all clients is equal to 1, the client’s sampling weights are normalized. The weight normalization formula is as follows:
- Random Sampling: Based on the sampling ratio and the client’s sampling weights , random sampling is performed. The sampling ratio determines the probability of selecting each client;
- Updating Sampling Counts: The sampling count for the selected clients is increased by 1 to reflect their participation;
- Returning Sampling Results: The finally selected clients are assembled into a list and returned to the aggregation algorithm for further parameter aggregation.
Below is the pseudo code for Algorithm 2, which is a weighted random client sampling strategy. This strategy selects clients and passes their parameters to the federated learning aggregation algorithm for parameter aggregation.The server then returns the aggregated parameters to the clients for the next round of training.
| Algorithm 2 Sample Clients. |
| function Sample_Clients(Passing values: sample ratio ) |
| if sampler=None then |
| Sampler <- RandomSampler() |
| end if |
| Define :this list records the number of times each client has been sampled. |
| When a client is selected multiple times, update the sampling count for each client in the : |
| After that, normalize the weights of each client: |
| Perform weighted random sampling with the given total number of clients , individual client weights , and sampling ratio : |
| Sampled <- random.choices(range(), , ) |
| for in Sampled do |
| end for |
| assert |
| return |
| end function |
4.3. Complexity Analysis of CALR-WRS Algorithm
A total of clients is assumed, each with a local dataset size of , model parameter size of , and clients participating in model aggregation in each round, with each client conducting local iterations.
- Analysis of Client-Side Computational Complexity:
The computational complexity of each client’s local updates typically depends on the number of samples updated in each round and the number of communication rounds. Therefore, the time complexity of local updates on each client is .
- Analysis of Server-Side Aggregation Complexity:
Parameter Aggregation: The server’s aggregation complexity is generally related to the number of clients participating in aggregation () and the dimension of the global model parameters (). Hence, the time complexity of aggregating parameters on the server can be represented as .
Weight Update: On the server side, the weights of clients are recalculated based on the sampling counts of all clients, and since there are clients in total, its time complexity can be expressed as .
- Analysis of Communication Cost:
Communication costs include two parts: transmitting local model parameters from clients to the central server and returning the aggregated parameters from the central server to clients. In the first part, only the clients participating in aggregation need to transmit model parameters, resulting in a complexity of . In the second part, the central server needs to return updated model parameters to all clients, resulting in a complexity of . Therefore, the communication cost can be expressed as .
The comparison of complexity between the proposed improved algorithm and FedAvg and FedProx algorithms is shown in Table 2. Our algorithm achieves improved communication efficiency while maintaining lower complexity.

Table 2.
Complexity comparison table.
5. Experiment and Performance Evaluation
The experiments in this paper were conducted using Python programming language version 3.7. The federated learning framework used was FedLab version 1.3.0. The total number of clients in the federated learning experiment was set to 100, and the maximum number of training rounds was set to 10,000. The client sampling ratio was set to 0.2, with each client performing five epochs and a batch size of 600. The hardware and software used for the experiments are summarized in Table 3.

Table 3.
Experimental equipment configuration.
The experiments in this paper were conducted to evaluate the algorithm’s performance on two image recognition tasks using the MNIST [28] and CIFAR-10 [29] datasets. The MNIST dataset consists of 70,000 grayscale images of handwritten digits (0–9), with each image having a size of 28 × 28 pixels. The dataset is divided into 10 classes, each representing a digit from 0 to 9. There are 7000 images in each class, with 60,000 images used for training and 10,000 images used for testing.
The CIFAR-10 dataset consists of 60,000 color images with a size of 32 × 32 pixels. It is also divided into 10 classes representing different objects: airplane, automobile, bird, cat, deer, dog, frog, horse, ship, and truck. Each class contains 6000 images, with 50,000 images used for training and 10,000 images used for testing. Each sample in the dataset is associated with a label that indicates its corresponding class. The experiments were designed to assess the performance of the proposed algorithm on these two datasets, and the results will be used to demonstrate the effectiveness and efficiency of the improvements made to the federated learning process.
In our federated learning aggregation experiments, we trained the MNIST dataset using MLP networks with termination conditions set at either 10,000 communication rounds or an accuracy of 0.97. Key metrics of interest included communication rounds at the experiment’s end, accuracy changes, and loss changes. For the CIFAR-10 dataset, ResNet networks were employed under similar termination criteria: 10,000 communication rounds or an accuracy of 0.75. We also focused on metrics such as communication rounds, accuracy changes, and loss changes. These metrics are standard in the machine learning field.
In addition, we conducted training on various datasets and deep learning network architectures. The Adam algorithm is commonly best practice in optimization, and, in line with best practices, this study initialized parameters using the Adam optimization algorithm in experiments. Additionally, experiments were compared against various traditional baseline methods, including fixed learning rates, cyclic learning rates, and random client sampling. By contrasting these widely used traditional methods and evaluating model performance with standard metrics, we have drawn robust experimental conclusions.
5.1. Cyclic Adaptive Learning Rate Algorithm
In this section, we present the cyclic adaptive learning rate (CALR) algorithm and compare its performance with several other non-CALR algorithms on different datasets. We evaluate the test accuracy and loss variation during the training process. The experimental results demonstrate that the proposed algorithm significantly improves the convergence speed and reduces the loss in the federated learning aggregation process.
Comparison of various algorithm strategies on the MNIST dataset with MLP model is shown in Figure 4, Figure 5, Figure 6 and Figure 7.
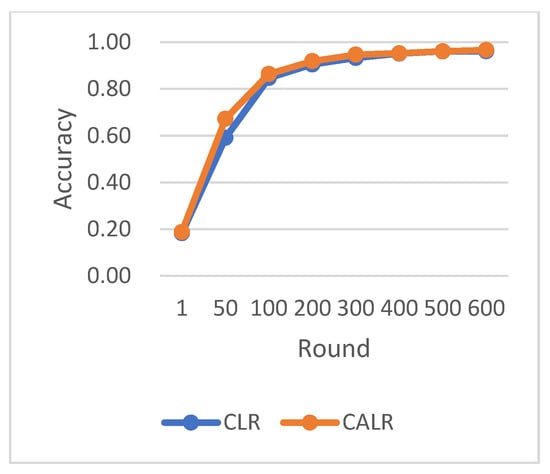
Figure 4.
Comparison chart of accuracy change between CLR and CALR.
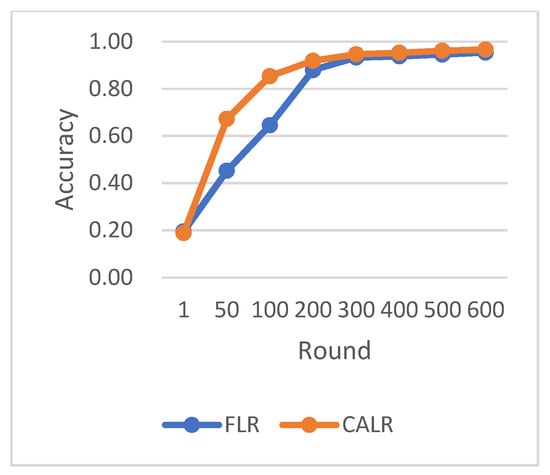
Figure 5.
Comparison chart of accuracy change between FLR and CALR.
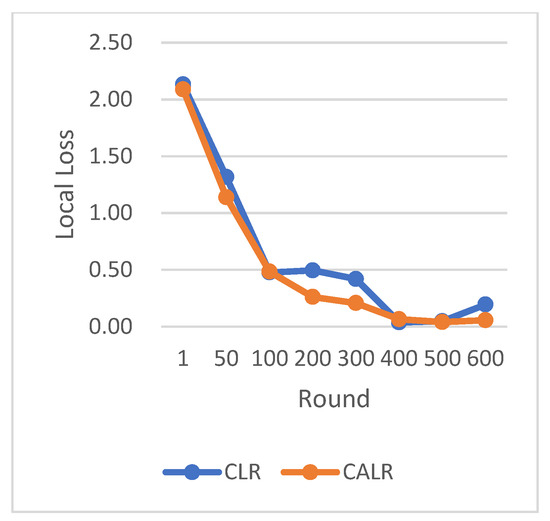
Figure 6.
Comparison chart of loss change between CLR and CALR.
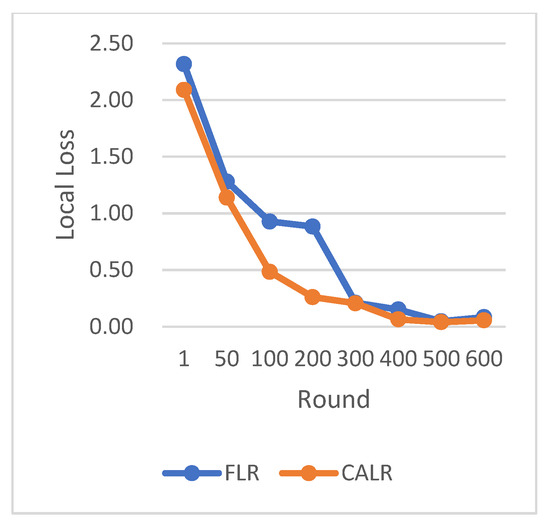
Figure 7.
Comparison chart of loss change between FLR and CALR.
CLR refers to the traditional cyclic learning rate strategy, FLR represents the fixed learning rate strategy, and CALR denotes the cyclic adaptive learning rate adjustment strategy proposed in this paper. From the graphs, it is evident that the CALR strategy proposed in this paper exhibits a more stable and efficient improvement in accuracy compared to both the traditional fixed learning rate strategy and the CLR cyclic learning rate strategy. Since the CALR strategy in this paper adjusts the current learning rate based on the client’s loss and training epochs in federated learning, the changes in loss are more stable and persistent.
CALR represents the cyclic adaptive learning rate adjustment strategy proposed in Figure 8, FLR1 corresponds to a fixed learning rate of 0.0005, FLR2 corresponds to a fixed learning rate of 0.003, and CLR denotes the traditional cyclic learning rate strategy. In this experiment, training is stopped when the test accuracy reaches 97%. By comparing the training epochs under various learning rate strategies for federated learning aggregation algorithms, it is observed that the CALR strategy improves the worst-performing strategy by 56.2% and the best strategy by 13.3%. This indicates that the training epochs in this paper are minimized, leading to faster achievement of the aggregated model accuracy.
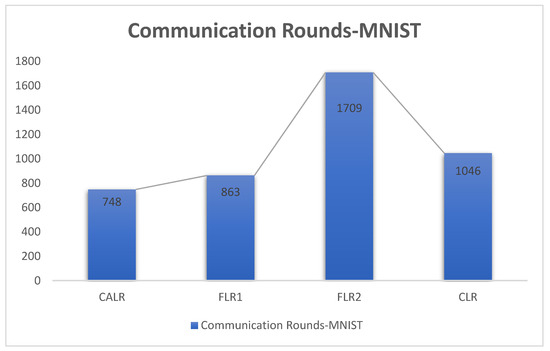
Figure 8.
Communication rounds comparison chart.
Based on the CIFAR-10 dataset and using the ResNet neural network model, the comparison of multiple algorithm strategies is shown below in Figure 9, Figure 10, Figure 11 and Figure 12.
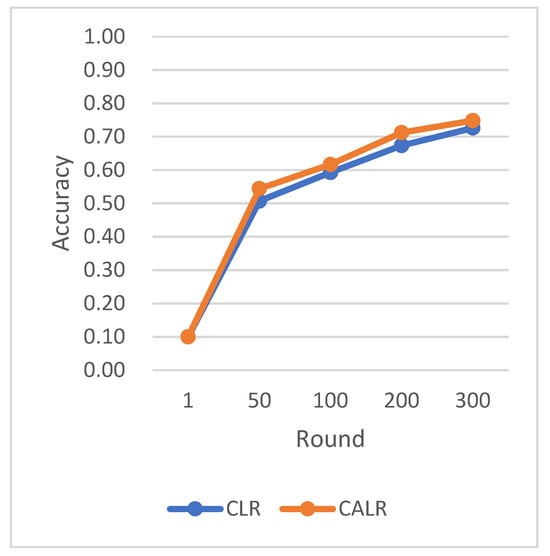
Figure 9.
Comparison chart of accuracy change between CLR and CALR.
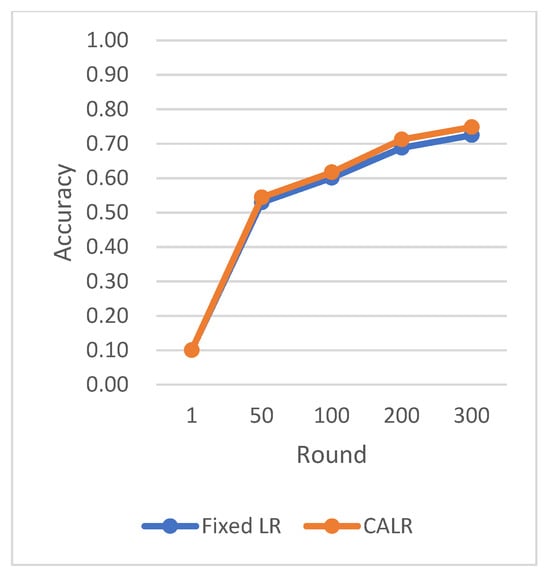
Figure 10.
Comparison chart of accuracy change between FLR and CALR.
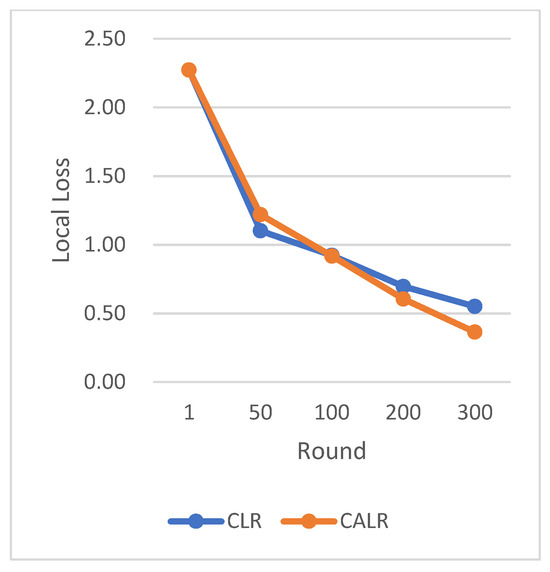
Figure 11.
Comparison chart of loss change between CLR and CALR.
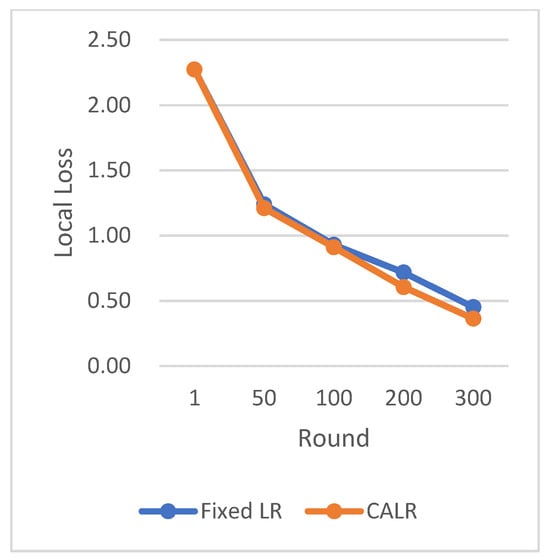
Figure 12.
Comparison chart of loss change between FLR and CALR.
The CLR adopts the traditional cyclic learning rate strategy, Fixed LR represents the fixed learning rate strategy, and CALR denotes the cyclic adaptive learning rate adjustment strategy designed in this paper.
The chart results clearly demonstrate the excellent performance of our proposed cyclic adaptive learning rate adjustment strategy on the CIFAR-10 dataset. Compared to the traditional fixed learning rate strategy and the traditional cyclic learning rate strategy (CLR), our method shows slightly more stable and efficient accuracy improvement. Additionally, our approach exhibits a persistent and stable advantage in reducing losses, demonstrating its effectiveness in optimizing the learning process.
In this experiment, User represents the cyclic adaptive learning rate adjustment strategy proposed in this paper, FLR1 corresponds to a fixed learning rate of 0.001, FLR2 corresponds to a fixed learning rate of 0.0005, and CLR denotes the traditional cyclic learning rate strategy. The training is stopped when the test accuracy reaches 75%. By comparing the training epochs under various learning rate strategies for federated learning aggregation algorithms, it is observed that our proposed strategy requires the fewest training epochs, effectively accelerating the model convergence speed. In Figure 13, it can be seen that our approach has improved by 27.7% compared to the worst-performing strategy and achieved a 13% improvement compared to the best strategy. From the test accuracy comparison experiment, it can be seen that both our proposed algorithm and the comparison algorithms show similar convergence speeds in the early stages of model training. However, in the later stages of model convergence, our algorithm, which adjusts the learning rate based on the loss, significantly accelerates the model convergence speed, effectively improving algorithm performance.
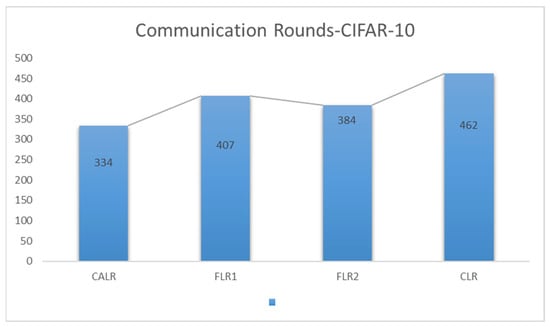
Figure 13.
Communication rounds comparison chart.
5.2. Weighted Random Sampling Based on Sampling Times
In this section, we conducted experiments comparing the weighted random sampling (WRS) algorithm, based on the number of samples, with the traditional random sampling strategy under different datasets and learning rates. During the experimental process, we observed that the proposed improvement algorithm strategy achieved positive effects in both the test accuracy during the federated learning aggregation process and the loss during the training process.
Comparison of various algorithm strategies on the MNIST dataset with MLP model is shown in Figure 14, Figure 15, Figure 16, Figure 17, Figure 18 and Figure 19.
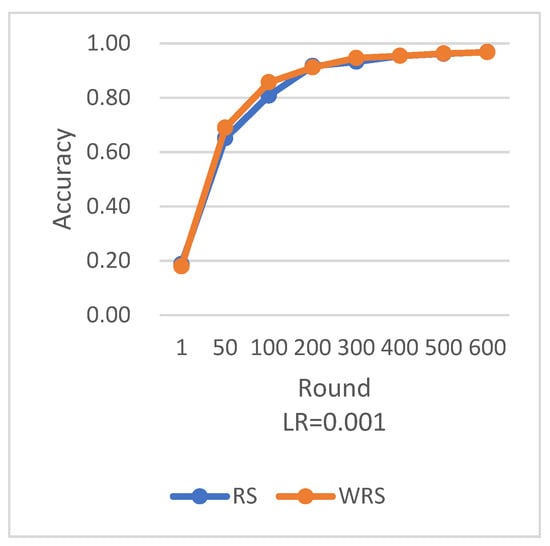
Figure 14.
Comparison chart of accuracy change between RS and WRS.
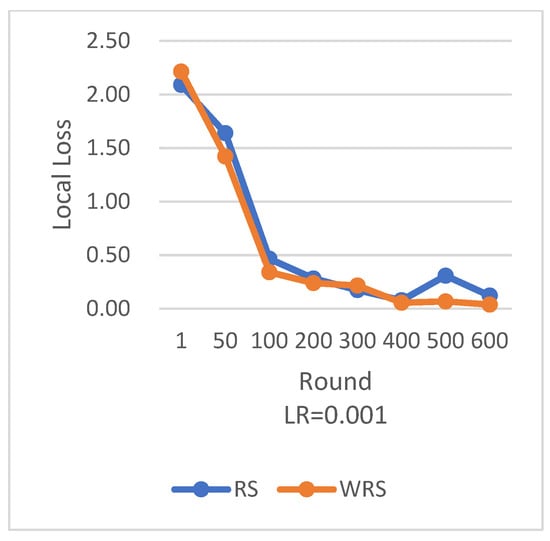
Figure 15.
Comparison chart of loss change between RS and WRS.
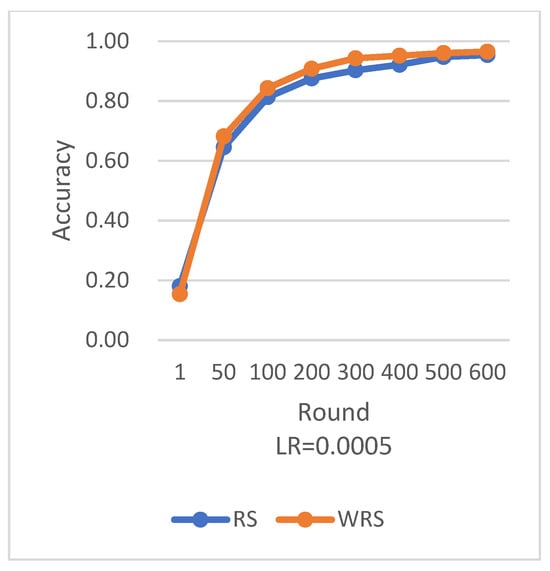
Figure 16.
Comparison chart of accuracy change between RS and WRS.
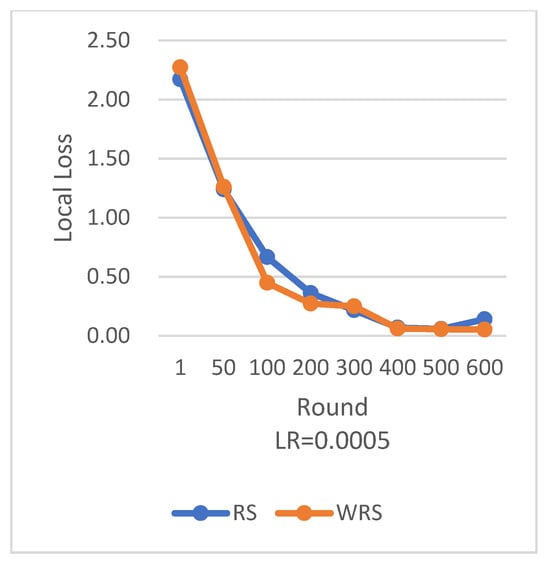
Figure 17.
Comparison chart of loss change between RS and WRS.
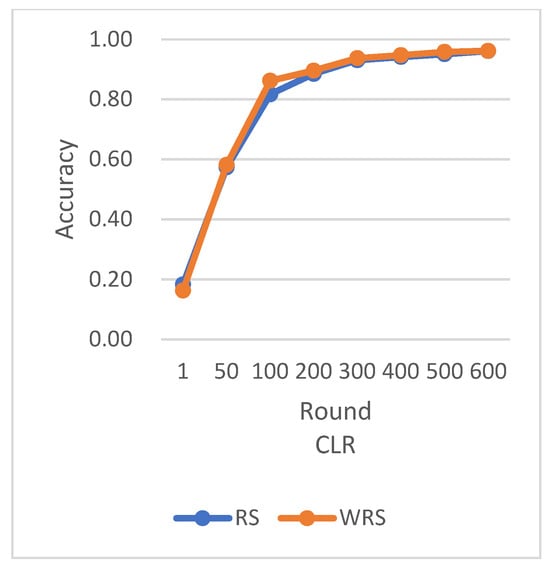
Figure 18.
Comparison chart of accuracy change between RS and WRS.
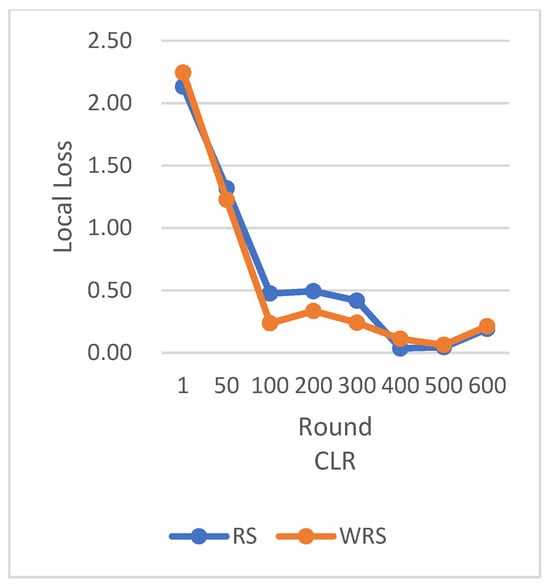
Figure 19.
Comparison chart of loss change between RS and WRS.
RS employs the traditional random sampling strategy, while WRS is the weighted random sampling strategy designed in this paper based on the number of samples.
Under different learning rates, random sampling employs the traditional random sampling strategy, while WRS is the weighted random sampling strategy designed in this paper based on the number of samples. In this experiment conducted on the MNIST dataset, the training process is stopped when the test accuracy reaches 97%. By comparing the training iterations of the federated learning aggregation algorithm with traditional random sampling, it can be observed that, regardless of the learning rate, the training iterations in this paper are fewer than random sampling. In Figure 20, it is evident that when the learning rate is set to 0.0005, the maximum improvement in convergence iterations is 16.8%, while with a learning rate of 0.001, the minimum improvement in convergence iterations is 2.5%.
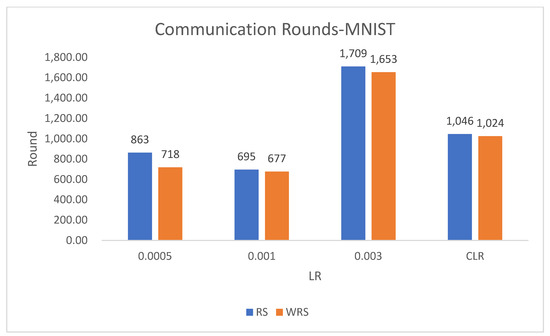
Figure 20.
Communication rounds comparison chart.
Under the scenario of using the CIFAR-10 dataset and the ResNet neural network model, the comparison of various algorithm strategies is as follows in Figure 21, Figure 22, Figure 23 and Figure 24.
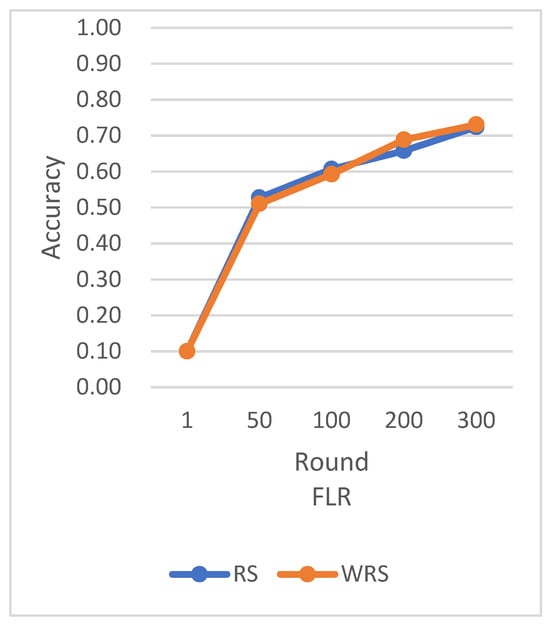
Figure 21.
Comparison chart of accuracy change between RS and WRS.
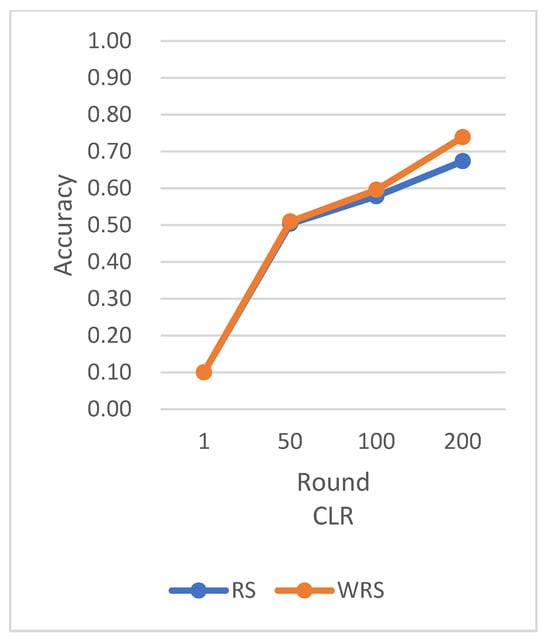
Figure 22.
Comparison chart of accuracy change between RS and WRS.
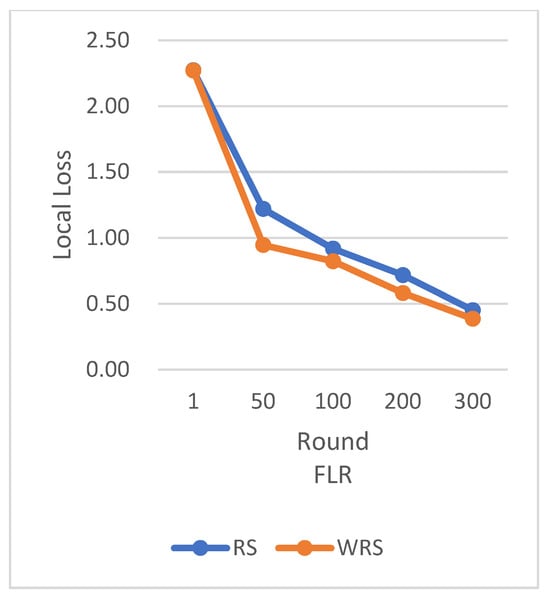
Figure 23.
Comparison chart of loss change between RS and WRS.
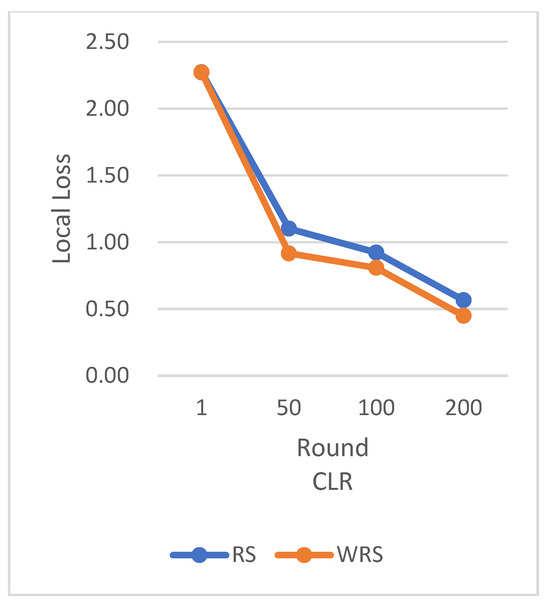
Figure 24.
Comparison chart of loss change between RS and WRS.
RS uses the traditional random sampling strategy and USER based on the number of samples designed in this paper.
In this experiment using the CIFAR-10 dataset, the training is stopped when the test accuracy reaches 75%. By comparing the training rounds of the traditional random sampling strategy (RS) and our weighted random sampling strategy based on the number of samples (USER), it can be observed that our algorithm consistently requires fewer training rounds regardless of the learning rate used. At a learning rate of 0.001, the convergence speed is improved by 15.4%, and with the traditional CLR learning rate, the convergence speed is improved by 37.6%.
The results from Figure 25 clearly demonstrate that our weighted random sampling algorithm based on the number of samples outperforms the traditional random sampling strategy in terms of test accuracy on both the MNIST and CIFAR-10 datasets. This indicates that our algorithm can better utilize the importance weights of each sample, resulting in improved classification accuracy on the test set.
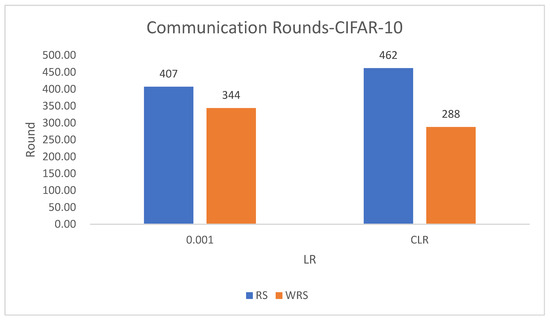
Figure 25.
Communication rounds comparison chart.
In terms of loss function reduction, our algorithm exhibits more stable and persistent behavior. By observing the loss function, it is evident that the weighted random sampling algorithm based on the number of samples can better control the loss reduction during training, avoiding significant fluctuations and oscillations. This indicates that our algorithm can more stably guide the model to learn data features and patterns, leading to improved training effectiveness. The convergence round data of the algorithm under different datasets and learning rates show that our algorithm can effectively accelerate the model convergence speed in federated learning, thereby enhancing model performance.
5.3. High-Performance Federated Learning Aggregation Algorithm
In this section, we achieved significant improvements in federated learning by combining the cyclic adaptive learning rate adjustment algorithm with the weighted random sampling strategy. We compared various strategies based on the convergence speed and loss function changes of the federated learning model.
The comparison of multiple algorithm strategies based on the MNIST dataset and using the MLP neural network model is as follows in Figure 26, Figure 27 and Figure 28:
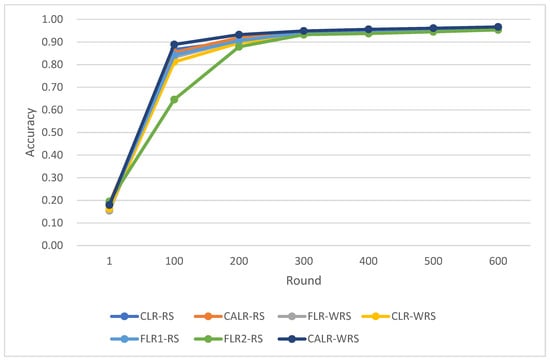
Figure 26.
Comparison chart of test accuracy trends across multiple algorithms.
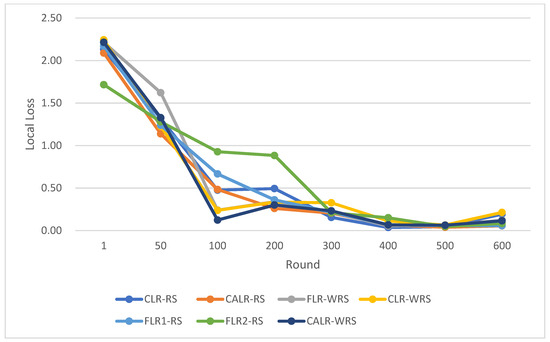
Figure 27.
Comparison chart of loss trends across multiple algorithms.
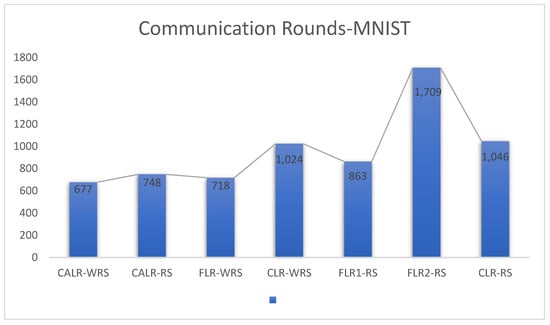
Figure 28.
Comparison chart of communication rounds across multiple algorithms.
CLR-RS: cyclic learning rate—random sampling strategy;
FLR-WRS: fixed learning rate—weighted random sampling strategy;
FLR1-RS: fixed learning rate 0.0005—random sampling strategy;
FLR2-RS: fixed learning rate 0.003—random sampling strategy;
CALR-RS: cyclic adaptive learning rate—random sampling strategy;
CLR-WRS: cyclic learning rate—weighted random sampling strategy;
CALR-WRS: cyclic adaptive learning rate—weighted random sampling strategy.
The above data demonstrate that the CALR-WRS algorithm exhibits superior convergence performance on the MNIST dataset compared to other algorithms, showing significant improvements.
The comparison of various algorithmic strategies based on the CIFAR-10 dataset and using the ResNet neural network model is as follows in Figure 29, Figure 30 and Figure 31:
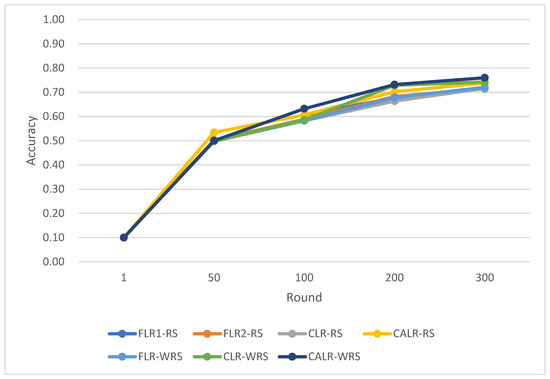
Figure 29.
Comparison chart of test accuracy trends across multiple algorithms.
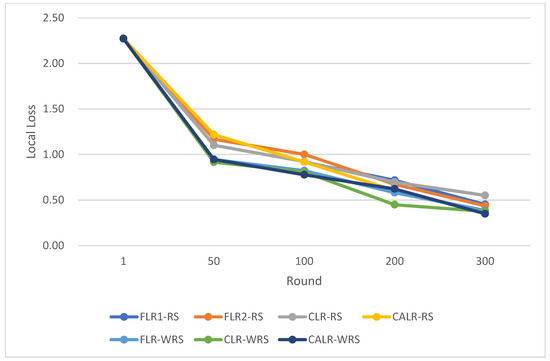
Figure 30.
Comparison chart of loss trends across multiple algorithms.
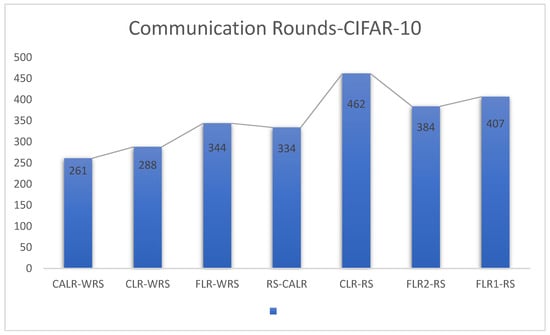
Figure 31.
Comparison chart of communication rounds across multiple algorithms.
CLR-RS: cyclic learning rate—random sampling strategy;
FLR-WRS: fixed learning rate—weighted random sampling strategy;
FLR1-RS: fixed learning rate 0.005—random sampling strategy;
FLR2-RS: fixed learning rate 0.001—random sampling strategy;
CALR-RS: cyclic adaptive learning rate—random sampling strategy;
CLR-WRS: cyclic learning rate—weighted random sampling strategy;
CALR-WRS: cyclic adaptive learning rate—weighted random sampling strategy.
In this study, we also conducted comparisons between the improved algorithm and baseline algorithms to assess their convergence performance under uneven client sample distributions. Specifically, we examined the performance of different algorithmic strategies using the CIFAR-10 dataset and the ResNet neural network model in scenarios where client sample distributions were uneven. Below are the comparative results of our analysis.
Based on the above Figure 32, Figure 33 and Figure 34, it is evident that even in the case of non-uniform distribution of client dataset sizes, our algorithm can achieve convergence more rapidly. Furthermore, our algorrithm exhibits faster accuracy improvement, smoother loss changes, and an increase in training rounds of 4.84%, further saving communication time costs.
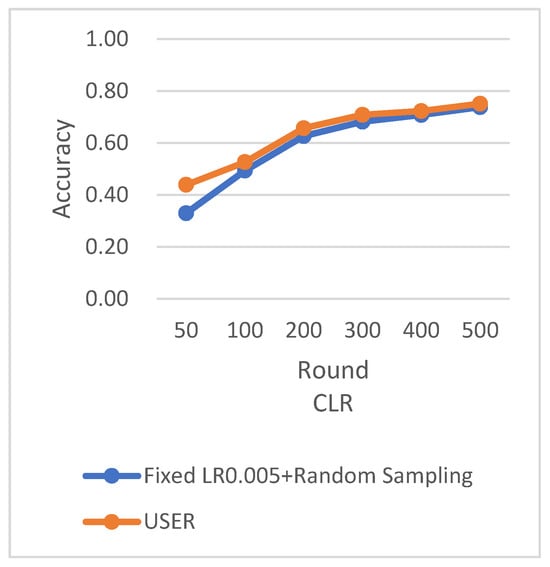
Figure 32.
Comparison chart of accuracy change among different algorithms.
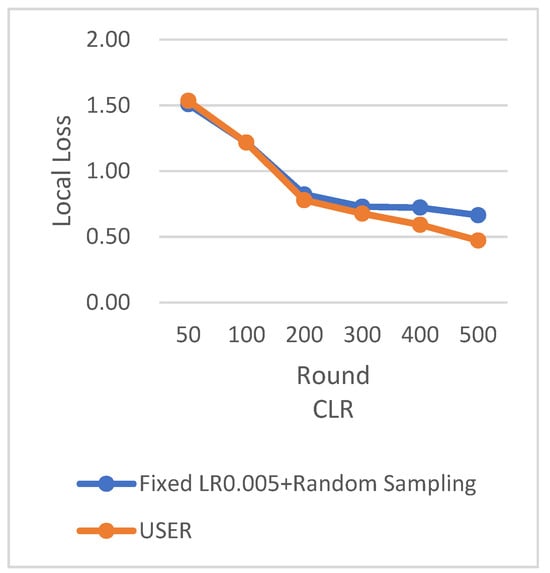
Figure 33.
Comparison chart of loss change among different algorithms.
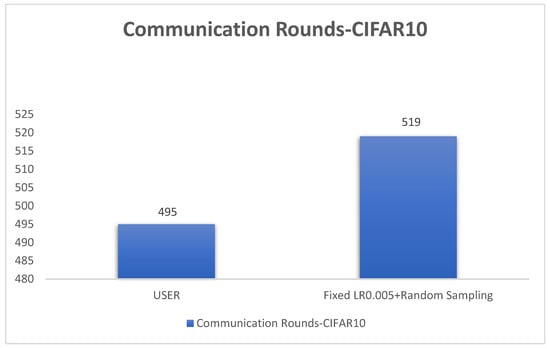
Figure 34.
Comparison chart of communication rounds among different algorithms.
In this study, we compared various learning rate adjustment and client sampling strategies in the federated learning aggregation process. Experimental results demonstrate that the CALR-WRS strategy has achieved significant performance improvements on the MNIST and CIFAR-10 datasets. As shown in Figure 26, Figure 27 and Figure 28, the CALR-WRS algorithm, on average across training rounds, increased performance by 27.65% compared to the baseline algorithm, achieving similar test accuracy on the MNIST dataset. In Figure 29, Figure 30 and Figure 31, it is evident that on the CIFAR-10 dataset, there was an average improvement of 27.75%. In terms of accuracy improvement rate, CALR-WRS demonstrated greater stability and efficiency compared to traditional fixed learning rate and other cyclic learning rate strategies. Moreover, CALR-WRS showed more stable and persistent loss reduction.
The CALR-WRS strategy exhibited clear superiority in the aggregation process of federated learning, and it is of great significance for improving the performance and efficiency of federated learning. The algorithm design presented in this study provides new insights and solutions for the development of federated learning, and it is expected to promote its wide application and further research in practical scenarios.
6. Discussion
In this paper, we propose a novel approach to improve the performance and efficiency of federated learning aggregation. We address two key challenges in the federated learning process: selecting appropriate learning rates for client and designing a weighted random client sampling strategy for client aggregation.
Combining CALR and WRS, we propose the CALR-WRS strategy, a comprehensive improvement for the federated learning aggregation process. By dynamically adjusting the learning rate and using weighted random sampling, CALR-WRS effectively addresses the challenges of client selection and convergence speed. This research provides new insights and solutions for federated learning, promoting its widespread application and further research in practical scenarios. However, although the CALR-WRS strategy demonstrates good performance in the aggregation process, it may still have some limitations in specific scenarios. For example, in cases of highly imbalanced data distribution, the contributions of certain clients may still be neglected. Hence, future research could explore more complex client selection strategies to further enhance the efficiency and accuracy of the aggregation process.
Finally, this study focuses on improving the aggregation process of federated learning, while research on other aspects of federated learning, such as privacy protection and security, is relatively limited. Future exploration can investigate the broader application of federated learning in various scenarios, incorporating more optimization techniques and privacy protection mechanisms to build a more comprehensive and efficient federated learning system.
7. Evaluation
In our study, a comprehensive performance evaluation of the proposed CALR-WRS strategy was conducted. The performance comparison is presented in Table 4. We tested this strategy on multiple datasets to assess its performance under various data distributions. The experimental results reveal that the CALR-WRS strategy exhibits significant improvements across various aspects. Firstly, we observed that our strategy can accelerate the model’s convergence speed, thereby reducing training time and computational costs. Secondly, the global models generated by the CALR-WRS strategy consistently outperform traditional random sampling methods, resulting in higher accuracy and lower loss. These evaluation results underscore the exceptional performance of the CALR-WRS strategy in the context of federated learning, providing an efficient and dependable solution for distributed machine learning.

Table 4.
Comparison of CALR-WRS algorithm with baseline algorithm metrics.
Our strategy introduces the cyclic adaptive learning rate (CALR) algorithm, which dynamically adjusts the learning rate based on the local training progress and performance of clients. This innovative approach expedites the model’s convergence across different clients, thereby enhancing the efficiency of federated learning. Additionally, we designed the weighted random sampling (WRS) strategy to ensure a more balanced contribution from each client, mitigating the bias issues often associated with traditional random sampling. These enhancements emphasize the novelty of the CALR-WRS strategy presented in this paper.
In summary, our research not only demonstrates outstanding performance but also highlights the strategy’s innovation and practicality. It holds the potential to have a profound impact on the field of federated learning.
8. Conclusions
Our research introduces the CALR-WRS strategy, a novel approach to federated learning aggregation. This strategy effectively addresses challenges related to client selection, convergence speed, and model performance. Our comprehensive evaluation highlights its exceptional performance, with accelerated convergence, reduced training time, and improved model accuracy. The CALR-WRS strategy holds promise for practical applications and contributes to the advancement of federated learning in the machine learning field with potential for broader applications and lasting impact.
Author Contributions
Conceptualization, Y.G.; methodology, Y.G.; software, Y.G.; validation, Y.G.; formal analysis, J.G.; investigation, J.G. and J.L.; data curation, Y.G.; writing—original draft preparation, Y.G.; writing—review and editing, G.L.; visualization, Y.G.; supervision, G.L.; project administration, G.L.; funding acquisition, G.L. All authors have read and agreed to the published version of the manuscript.
Funding
This paper is financially supported by the project of Research and Application Demonstration of Key Technologies of Yunnan Autonomous Controllable Blockchain Basic Service Platform (grant No. 202102AD080006).
Data Availability Statement
Not applicable.
Acknowledgments
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Harika, J.; Baleeshwar, P.; Navya, K.; Shanmugasundaram, H. A Review on artificial intelligence with deep human reasoning. In Proceedings of the 2022 International Conference on Applied Artificial Intelligence and Computing (ICAAIC), Salem, India, 9–11 May 2022; IEEE Press: Piscataway, NJ, USA, 2022; pp. 81–84. [Google Scholar]
- Wang, J.Z.; Kong, L.W.; Huang, Z.; Chen, L.; Liu, Y.; He, A.; Xiao, J. Research review of federated learning algorithms. Big Data 2020, 6, 64–82. [Google Scholar]
- McMahan, B.; Moore, E.; Ramage, D.; Hampson, S.; y Arcas, B.A. Communication-efficient learning of deep networks from decentralized data. arXiv 2017, arXiv:1602.05629. [Google Scholar]
- Zhang, X.; Li, X.; Tang, W.; Hao, Y.; Xue, J. A Verifiable Privacy-Preserving Cross-Domain Federated Learning Scheme for Cloud-Edge Fusion. Comput. Eng. 2023, 1–11. [Google Scholar]
- Cao, Z.; Shao, L.; Zhao, W. Federated Optimization Algorithm for Heterogeneous Networks. Ind. Control. Comput. 2023, 36, 10–12. [Google Scholar]
- Bonawitz, K.; Ivanov, V.; Kreuter, B.; Marcedone, A.; McMahan, H.B.; Patel, S.; Ramage, D.; Segal, A.; Seth, K. Practical secure aggregation for privacy preserving machine learning. In Proceedings of the 2017 ACM SIGSAC Conference on Computer and Communications Security, Dallas, TX, USA, 30 October–3 November 2017; pp. 1175–1191. [Google Scholar]
- Xie, Y. Privacy-Preserving Federated Learning Method Based on Local Differential Privacy. Inf. Technol. Inform. 2023, 2023, 160–163. [Google Scholar]
- McMahan, H.B.; Ramage, D.; Talwar, K.; Zhang, L. Learning differentially private recurrent language models. arXiv 2017, arXiv:1710.06963. [Google Scholar]
- Li, Y.; Long, C.; Wei, J.; Li, J.; Yang, F.; Li, J. Privacy-Preserving Face Recognition Method Based on Homomorphic Encryption. Inf. Secur. Res. 2023, 9, 843–850. [Google Scholar]
- Cheng, K.; Fan, T.; Jin, Y.; Liu, Y.; Chen, T.; Papadopoulos, D.; Yang, Q. Secure boost: A lossless federated learning framework. IEEE Intell. Syst. 2021, 36, 87–98. [Google Scholar] [CrossRef]
- Briggs, C.; Fan, Z.; Andras, P. Federated learning with hierarchical clustering of local updates to improve training on non-IID data. In Proceedings of the 2020 International Joint Conference on Neural Networks (IJCNN), Glasgow, UK, 19–24 July 2020; IEEE: Piscataway, NJ, USA; pp. 1–9. [Google Scholar] [CrossRef]
- Karimireddy, S.P.; Kale, S.; Mohri, M.; Reddi, S.; Stich, S.; Suresh, A.T. Scaffold: Stochastic controlled averaging for federated learning. In Proceedings of the 37th International Conference on Machine Learning, Virtual, 13–18 July 2020; pp. 5132–5143. [Google Scholar]
- Ye, J.; Wei, T.; Hu, L.; Luo, S.; Li, X. An Efficient Federated Learning Algorithm for the Internet of Intelligent Things. Comput. Eng. 2023, 1–11. [Google Scholar] [CrossRef]
- Geyer, R.C.; Klein, T.; Nabi, M. Differentially Private Federated Learning: A Client Level Perspective. arXiv 2017, arXiv:1712.07557. [Google Scholar]
- Chen, Y.; Sun, X.; Jin, Y. Communication-efficient federated deep learning with layer wise asynchronous model update and temporally weighted aggregation. IEEE Trans. Neural Netw. Learn. Syst. 2020, 31, 4229–4238. [Google Scholar] [CrossRef] [PubMed]
- Haddadpour, F.; Kamani, M.M.; Mokhtari, A.; Mahdavi, M. Federated learning with compression: Unified analysis and sharp guarantees. In Proceedings of the 24th International Conference on Artificial Intelligence and Statistics, San Diego, CA, USA, 13–15 April 2021; pp. 2350–2358. [Google Scholar]
- Zhang, W.; Li, X.; Ma, H.; Luo, Z.; Li, X. Federated learning for machinery fault diagnosis with dynamic validation and self-supervision. Knowledgeased Syst. 2021, 213, 106679. [Google Scholar] [CrossRef]
- Meng, X.; Liu, T.; Xie, R. A Privacy-preserving Scheme of Learning Rate Clipping Gradient Optimization for Federated Learning. J. Beijing Electron. Sci. Technol. Inst. 2023, 31, 45–53. [Google Scholar]
- Mercier, Q.; Poirion, F.; Desideri, J.A. A stochastic multiple gradient descent algorithm. Eur. J. Oper. Res. 2018, 271, 808–817. [Google Scholar] [CrossRef]
- Zhou, Y.; Zhang, M.; Zhu, J.; Zheng, R.; Wu, Q. Arandomized block-coordinate adam online learning optimization algorithm. Neural Comput. Appl. 2020, 32, 12671–12684. [Google Scholar] [CrossRef]
- Shi, H. Research on Multi-Factor Short-Term Load Forecasting Based on AdaBelief Optimized Deep Learning Models. Ph.D. Thesis, Shaanxi University of Technology, Hanzhong, China, 2023. [Google Scholar] [CrossRef]
- Rodríguez-Barroso, N.; Jiménez-López, D.; Luzón, M.V.; Herrera, F.; Martínez-Cámara, E. Survey on Federated Learning Threats: Concepts, taxonomy on attacks and defences, experimental study and challenges. Inf. Fusion 2023, 90, 148–173. [Google Scholar] [CrossRef]
- Liu, Y.; Kang, Y.; Xing, C.; Chen, T.; Yang, Q. A secure federated transfer leaning framework. IEEE Intell. Syst. 2020, 35, 70–82. [Google Scholar] [CrossRef]
- Lee, S.; Sahu, A.K.; He, C.; Avestimehr, S. Partial model averaging in federated learning: Performance guarantees and benefits. arXiv 2022, arXiv:2201.03789. [Google Scholar] [CrossRef]
- Kim, Y. Convolutional Neural Networks for Sentence Classification. arXiv 2014, arXiv:1408.5882. [Google Scholar]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Deep Residual Learning for Image Recognition. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Las Vegas, NV, USA, 26 June–1 July 2016; pp. 770–778. [Google Scholar]
- Krizhevsky, A.; Sutskever, I.; Hinton, G.E. Image net classification with deep convolutional neural networks. In Proceedings of the Advances in Neural Information Processing Systems 25: 26th Annual Conference on Neural Information Processing Systems 2012, Lake Tahoe, NV, USA, 3–6 December 2012; pp. 1097–1105. [Google Scholar]
- LeCun, Y.; Bottou, L.; Bengio, Y.; Haffner, P. Gradient-based learning applied to document recognition. Proc. IEEE 1998, 86, 2278–2324. [Google Scholar] [CrossRef]
- Krizhevsky, A.; Hinton, G. Learning Multiple Layers of Features from Tiny Images. 2009. Available online: https://www.researchgate.net/publication/306218037_Learning_multiple_layers_of_features_from_tiny_images (accessed on 12 September 2023).
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).