Adaptive Finite-Time Fuzzy Control for Uncertain Nonlinear Systems with Asymmetric Full-State Constraints
Abstract
:1. Introduction
2. Problem Statement and Preliminaries
3. Main Results
3.1. State-Constrained Function
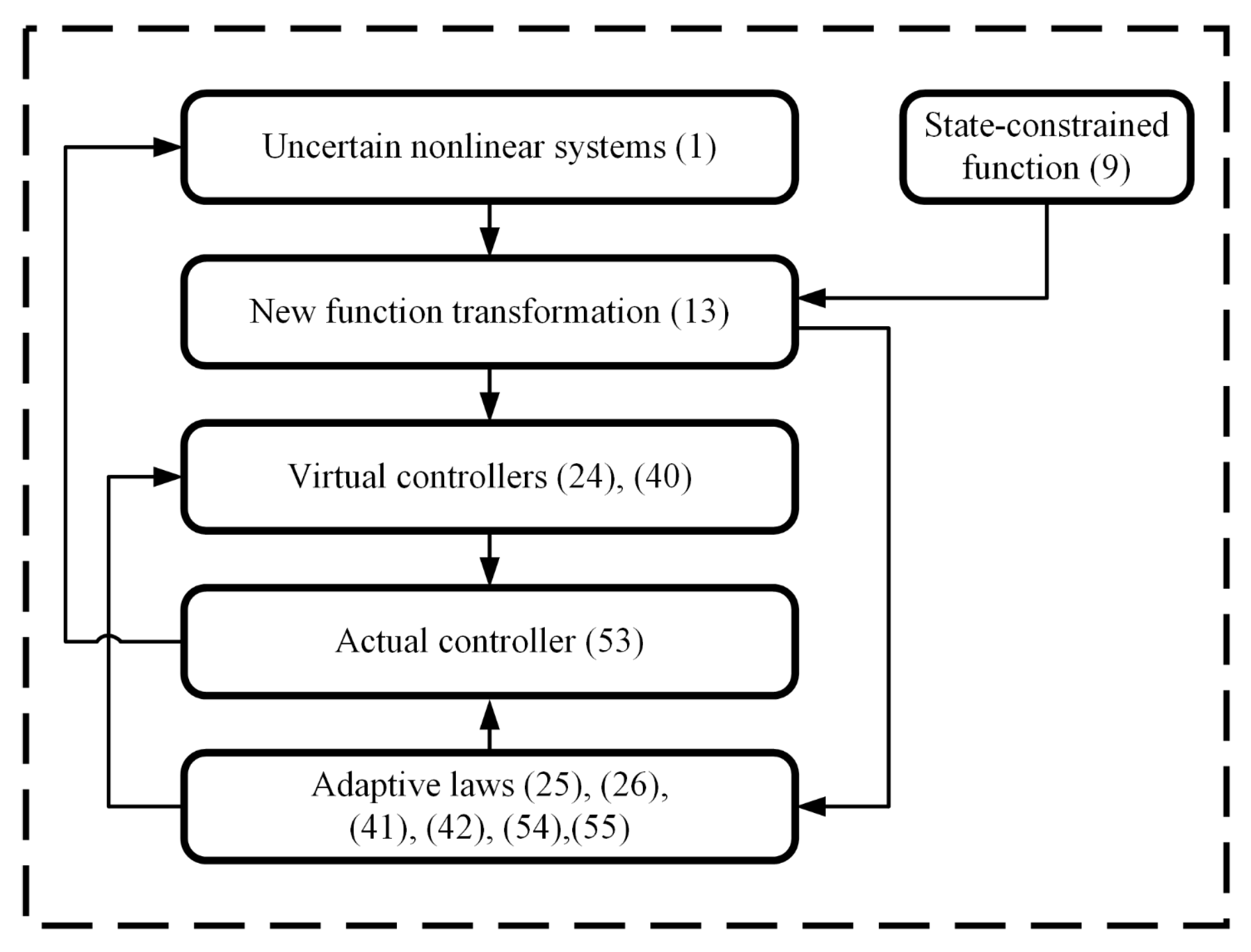
3.2. Adaptive Finite-Time Fuzzy Controller
3.3. Stability Analysis
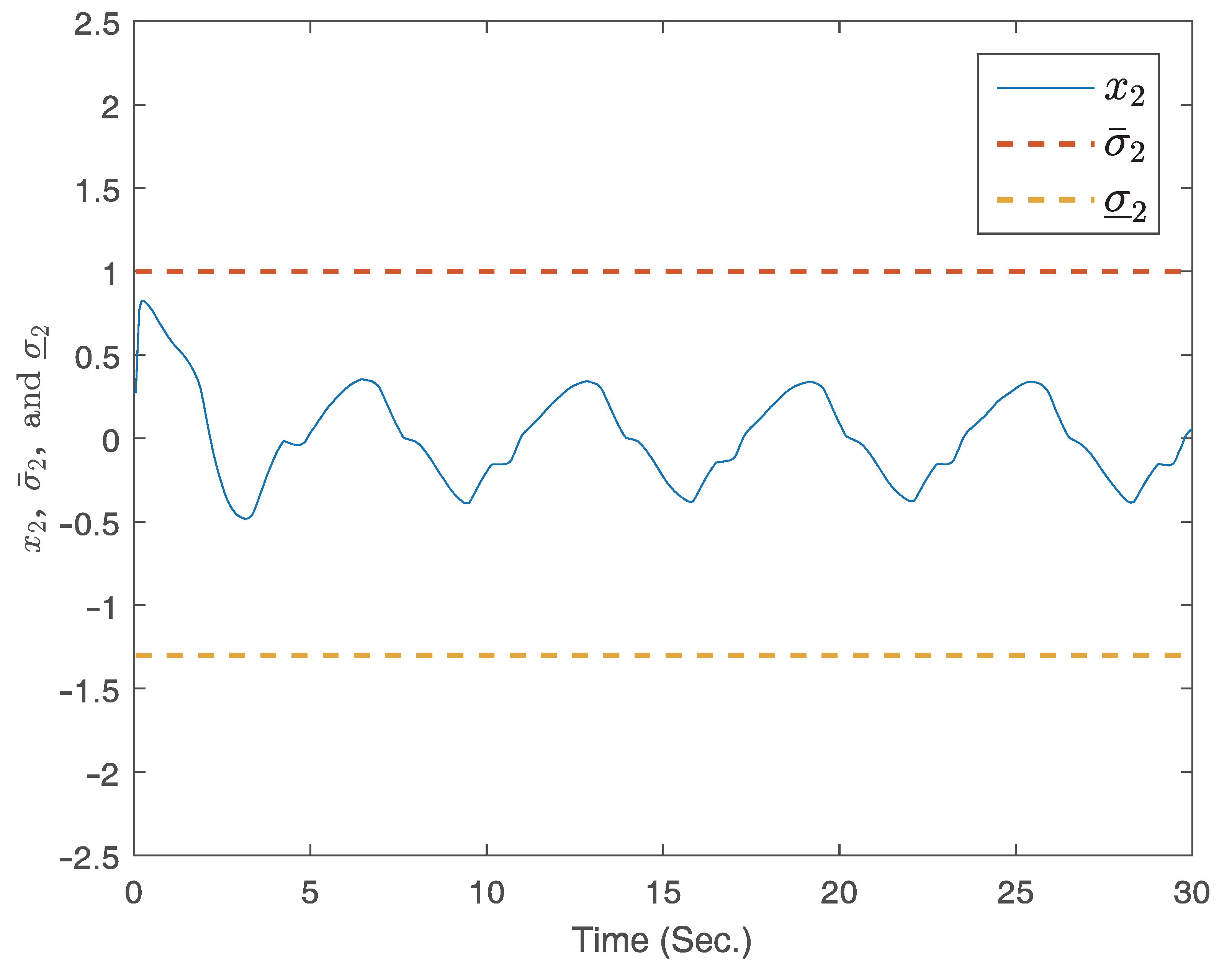
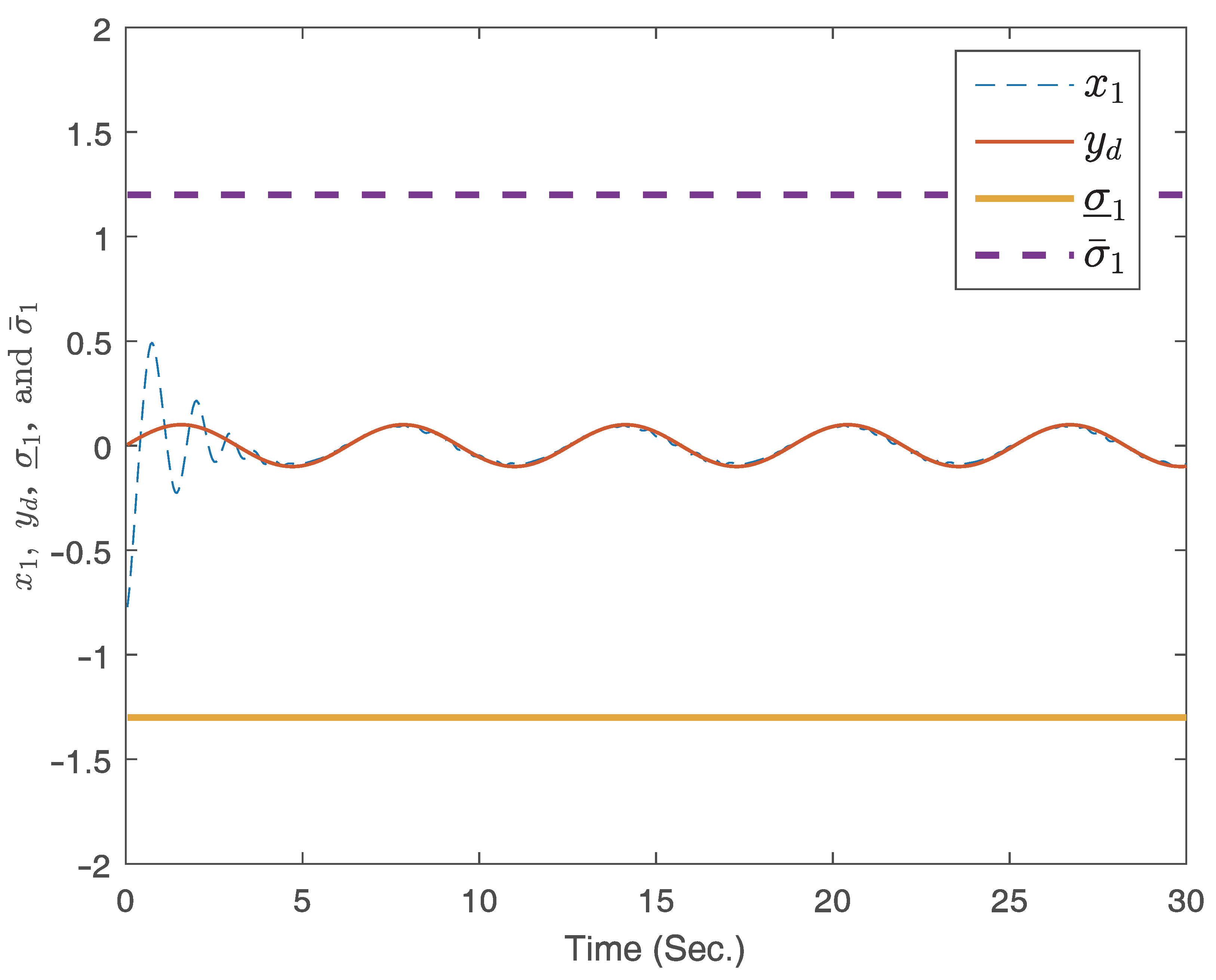
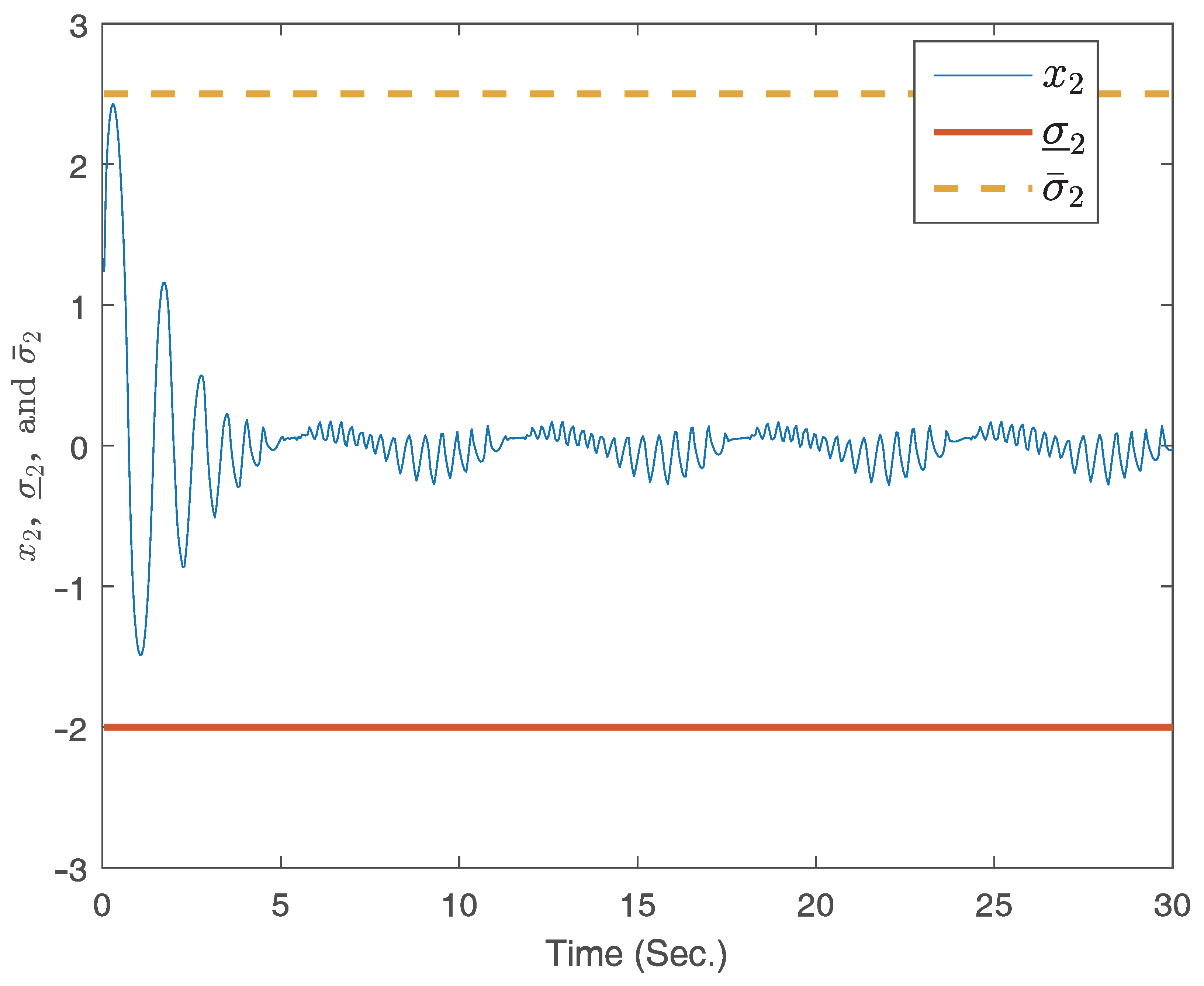
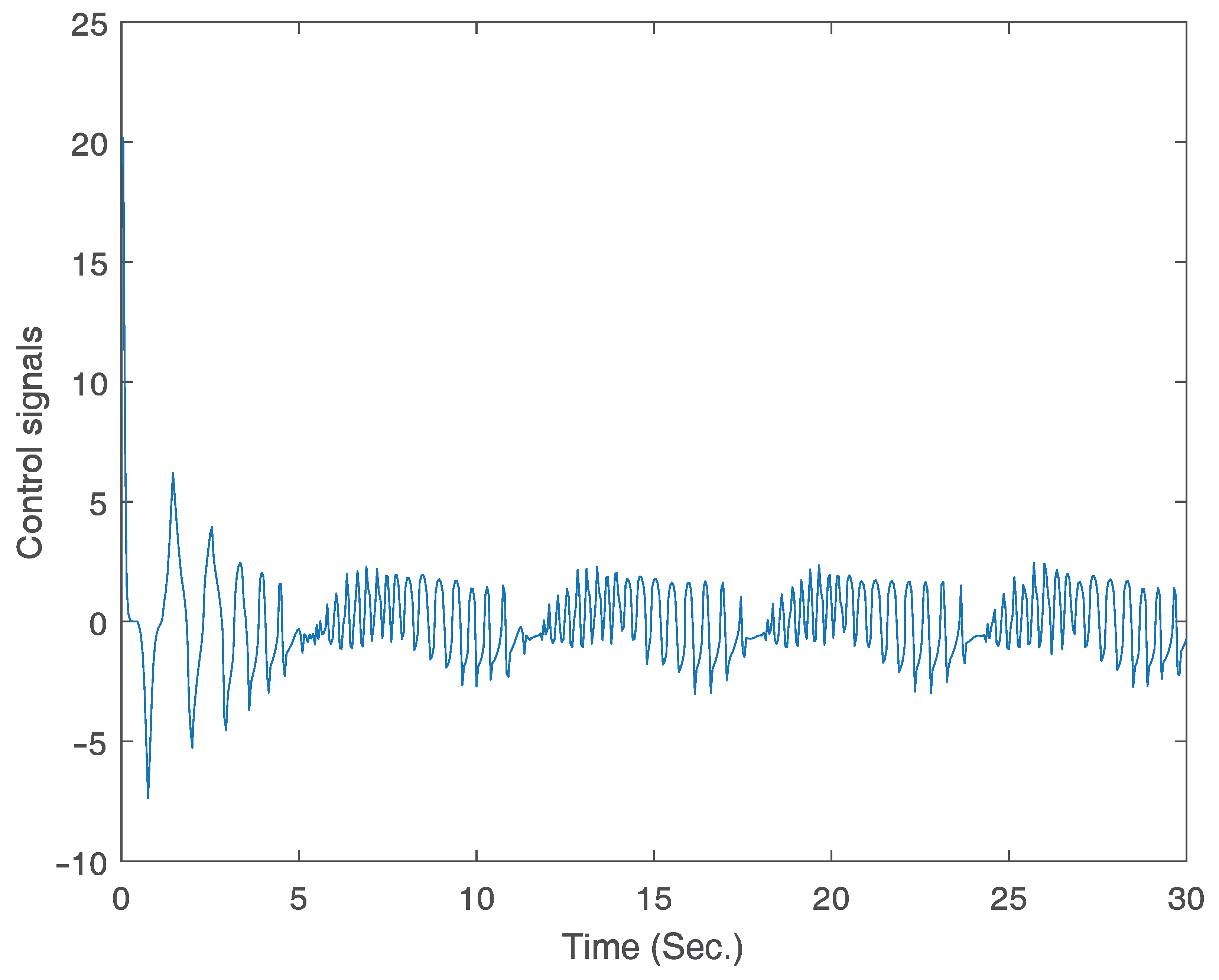
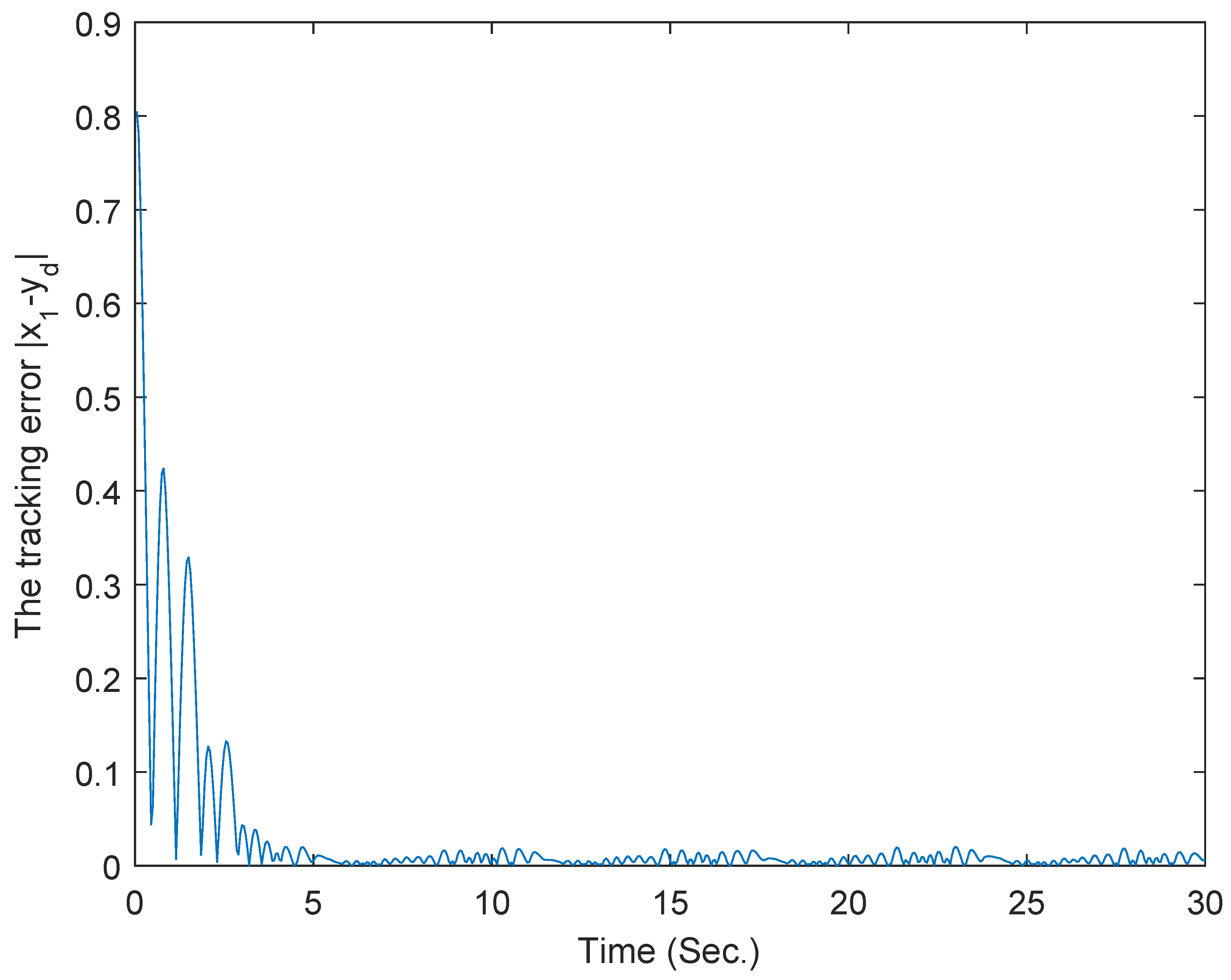
4. Illustrative Examples
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Witkowska, A.; Tomera, M.; Śmierzchalski, R. A backstepping approach to ship course control. Int. J. Appl. Math. Comput. Sci. 2007, 17, 73–85. [Google Scholar] [CrossRef]
- Li, G.; Wang, X.; Li, S. Consensus control of higher-order Lipschitz nonlinear multi-agent systems based on backstepping method. IET Control Theory Appl. 2019, 14, 490–498. [Google Scholar] [CrossRef]
- Kartal, Y.; Subbarao, K.; Gans, N.R.; Dogan, A.; Lewis, F. Distributed backstepping based control of multiple UAV formation flight subject to time delays. IET Control Theory Appl. 2020, 14, 1628–1638. [Google Scholar] [CrossRef]
- Zhuang, H.; Sun, Q.; Chen, Z.; Zeng, X. Robust adaptive sliding mode attitude control for aircraft systems based on back-stepping method. Aerosp. Sci. Technol. 2021, 118, 107069. [Google Scholar] [CrossRef]
- Zhang, L.; Ding, H.; Shi, J.; Huang, Y.; Chen, H.; Guo, K.; Li, Q. An adaptive backstepping sliding mode controller to improve vehicle maneuverability and stability via torque vectoring control. IEEE Trans. Veh. Technol. 2020, 69, 2598–2612. [Google Scholar] [CrossRef]
- Yu, J.; Shi, P.; Zhao, L. Finite-time command filtered backstepping control for a class of nonlinear systems. Automatica 2018, 92, 173–180. [Google Scholar] [CrossRef]
- Capone, A.; Hirche, S. Backstepping for partially unknown nonlinear systems using Gaussian processes. IEEE Control Syst. Lett. 2019, 3, 416–421. [Google Scholar] [CrossRef]
- Xiao, Y.; de Ruiter, A.; Ye, D.; Sun, Z. Attitude coordination control for flexible spacecraft formation flying with guaranteed performance bounds. IEEE Trans. Aerosp. Electron. Syst. 2022, 59, 1534–1550. [Google Scholar] [CrossRef]
- Jiang, S.; Tian, F.; Sun, S.; Liang, W. Integrated guidance and control of guided projectile with multiple constraints based on fuzzy adaptive and dynamic surface. Def. Technol. 2020, 16, 1130–1141. [Google Scholar] [CrossRef]
- Wang, P.; Rui, X.; Yu, H.; Wang, G.; Chen, D. Adaptive control of track tension estimation using radial basis function neural network. Def. Technol. 2021, 17, 1423–1433. [Google Scholar] [CrossRef]
- Zhang, H.; Ye, D.; Xiao, Y.; Sun, Z. Adaptive control on SE(3) for spacecraft pose tracking with harmonic disturbance and input saturation. IEEE Trans. Aerosp. Electron. Syst. 2022, 58, 4578–4594. [Google Scholar] [CrossRef]
- Wu, Y.; Wang, Z. Fuzzy adaptive practical fixed-time consensus for second-order nonlinear multiagent systems under actuator faults. IEEE Trans. Cybern. 2020, 51, 1150–1162. [Google Scholar] [CrossRef] [PubMed]
- Wang, A.; Liu, L.; Qiu, J.; Feng, G. Finite-time adaptive fuzzy control for nonstrict-feedback nonlinear systems via an event-triggered strategy. IEEE Trans. Fuzzy Syst. 2019, 28, 2164–2174. [Google Scholar] [CrossRef]
- Li, Y.; Yang, T.; Tong, S. Adaptive neural networks finite-time optimal control for a class of nonlinear systems. IEEE Trans. Neural Netw. Learn. Syst. 2019, 31, 4451–4460. [Google Scholar] [CrossRef]
- Ye, D.; Sun, J.; Xiao, Y.; Sun, Z. Energy optimal guidance for proximity approach with obstacle avoidance. Aerosp. Sci. Technol. 2022, 130, 107949. [Google Scholar] [CrossRef]
- von Ellenrieder, K.D. Dynamic surface control of trajectory tracking marine vehicles with actuator magnitude and rate limits. Automatica 2019, 105, 433–442. [Google Scholar] [CrossRef]
- Li, Y.; Li, K.; Tong, S. Finite-time adaptive fuzzy output feedback dynamic surface control for MIMO nonstrict feedback systems. IEEE Trans. Fuzzy Syst. 2018, 27, 96–110. [Google Scholar] [CrossRef]
- Ma, H.; Liang, H.; Zhou, Q.; Ahn, C.K. Adaptive dynamic surface control design for uncertain nonlinear strict-feedback systems with unknown control direction and disturbances. IEEE Trans. Syst. Man Cybern. Syst. 2018, 49, 506–515. [Google Scholar] [CrossRef]
- Shi, M.; Ye, D.; Sun, Z.; Zhong, W.; Deng, H. Spacecraft orbital pursuit–evasion games with J2 perturbations and direction-constrained thrust. Acta Astronaut. 2023, 202, 139–150. [Google Scholar] [CrossRef]
- Hua, C.; Chen, J.; Li, Y.; Li, L. Adaptive prescribed performance control of half-car active suspension system with unknown dead-zone input. Mech. Syst. Signal Process. 2018, 111, 135–148. [Google Scholar] [CrossRef]
- Zerari, N.; Chemachema, M.; Essounbouli, N. Neural network based adaptive tracking control for a class of pure feedback nonlinear systems with input saturation. IEEE/CAA J. Autom. Sin. 2018, 6, 278–290. [Google Scholar] [CrossRef]
- Ye, D.; Zou, A.; Sun, Z. Predefined-time predefined-bounded attitude tracking control for rigid spacecraft. IEEE Trans. Aerosp. Electron. Syst. 2021, 58, 464–472. [Google Scholar] [CrossRef]
- Chen, G.; Yao, D.; Zhou, Q.; Li, H.; Lu, R. Distributed event-triggered formation control of USVs with prescribed performance. J. Syst. Sci. Complex. 2022, 35, 820–838. [Google Scholar] [CrossRef]
- Liu, L.; Liu, Y.; Li, D.; Tong, S.; Wang, Z. Barrier Lyapunov function-based adaptive fuzzy FTC for switched systems and its applications to resistance–inductance–capacitance circuit system. IEEE Trans. Cybern. 2019, 50, 3491–3502. [Google Scholar] [CrossRef] [PubMed]
- Fuentes-Aguilar, R.Q.; Chairez, I. Adaptive tracking control of state constraint systems based on differential neural networks: A barrier lyapunov function approach. IEEE Trans. Neural Netw. Learn. Syst. 2020, 31, 5390–5401. [Google Scholar] [CrossRef] [PubMed]
- Wu, Z.; Albalawi, F.; Zhang, Z.; Zhang, J.; Durand, H.; Christofides, P.D. Control lyapunov-barrier function-based model predictive control of nonlinear systems. Automatica 2019, 109, 108508. [Google Scholar] [CrossRef]
- Li, Y. Barrier Lyapunov function-based adaptive asymptotic tracking of nonlinear systems with unknown virtual control coefficients. Automatica 2020, 121, 109181. [Google Scholar] [CrossRef]
- Hwang, Y.; Kang, C.M.; Kim, W. Robust nonlinear control using barrier Lyapunov function under lateral offset error constraint for lateral control of autonomous vehicles. IEEE Trans. Intell. Transp. Syst. 2020, 23, 1565–1571. [Google Scholar] [CrossRef]
- Kong, L.; Yu, X.; Zhang, S. Neuro-learning-based adaptive control for state-constrained strict-feedback systems with unknown control direction. ISA Trans. 2021, 112, 12–22. [Google Scholar] [CrossRef]
- Liu, R.; Du, H.; Li, Y.; Wei, Y. Finite-time control for nonlinear systems with full-state constraints. In Proceedings of the 2023 2nd Conference on Fully Actuated System Theory and Applications (CFASTA), Qingdao, China, 14–16 July 2023; pp. 987–991. [Google Scholar]
- Xia, G.; Liu, C.; Zhao, B.; Chen, X.; Shao, X. Finite time output feedback control for ship dynamic positioning assisted mooring positioning system with disturbances. Int. J. Control Autom. Syst. 2019, 17, 2948–2960. [Google Scholar] [CrossRef]
- Li, K.; Li, Y. Adaptive fuzzy finite-time dynamic surface control for high-order nonlinear system with output constraints. Int. J. Control Autom. Syst. 2021, 19, 112–123. [Google Scholar] [CrossRef]
- Li, S.; Ahn, C.K.; Xiang, Z. Command-filter-based adaptive fuzzy finite-time control for switched nonlinear systems using state-dependent switching method. IEEE Trans. Fuzzy Syst. 2020, 29, 833–845. [Google Scholar] [CrossRef]
- Sun, W.; Wu, Y.; Sun, Z. Command filter-based finite-time adaptive fuzzy control for uncertain nonlinear systems with prescribed performance. IEEE Trans. Fuzzy Syst. 2020, 28, 3161–3170. [Google Scholar] [CrossRef]
- Lv, W. Finite time adaptive fault-tolerant control for nonlinear MIMO systems with actuator faults. Int. J. Control Autom. Syst. 2022, 20, 99–108. [Google Scholar] [CrossRef]
- Liu, Y.; Zhang, H.; Wang, Y.; Sun, S. Adaptive fuzzy control for nonstrict-feedback systems under asymmetric time-varying full state constraints without feasibility condition. IEEE Trans. Fuzzy Syst. 2021, 29, 976–985. [Google Scholar] [CrossRef]
- Hardy, H.; Littlewood, E.; Polya, J. Inequalities; Cambridge University Press: Cambridge, UK, 1995. [Google Scholar]
- Deng, H.; Krstic, M. Output-feedback stochastic nonlinear stabilization. IEEE Trans. Autom. Control 1999, 44, 328–333. [Google Scholar] [CrossRef]
- Wang, F.; Chen, B.; Liu, X.; Lin, C. Finite-time adaptive fuzzy tracking control design for nonlinear systems. IEEE Trans. Fuzzy Syst. 2017, 26, 1207–1216. [Google Scholar] [CrossRef]
- Deng, C.; Yang, G. Distributed adaptive fuzzy control for nonlinear multiagent systems under directed graphs. IEEE Trans. Fuzzy Syst. 2017, 26, 1356–1366. [Google Scholar]
- Liang, Y.; Li, Y.; Che, W.; Hou, Z. Adaptive fuzzy asymptotic tracking for nonlinear systems with nonstrict-feedback structure. IEEE Trans. Cybern. 2021, 51, 853–861. [Google Scholar] [CrossRef]
- Liu, K.; Wang, R. Antisaturation command filtered backstepping control-based disturbance rejection for a quadarotor UAV. IEEE Trans. Circuits Syst. II Express Briefs 2021, 68, 3577–3581. [Google Scholar] [CrossRef]
- Liu, K.; Wang, X.; Wang, R.; Sun, G.; Wang, X. Antisaturation finite-time attitude tracking control based observer for a quadrotor. IEEE Trans. Circuits Syst. II Express Briefs 2020, 68, 2047–2051. [Google Scholar] [CrossRef]
- Liu, K.; Yang, P.; Wang, R.; Jiao, L.; Li, T.; Zhang, J. Observer-based adaptive fuzzy finite-time attitude control for quadrotor UAVs. IEEE Trans. Aerosp. Electron. Syst. 2023. [Google Scholar] [CrossRef]



Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hou, Y.; Xu, X.; Liu, R.; Bai, X.; Liu, H. Adaptive Finite-Time Fuzzy Control for Uncertain Nonlinear Systems with Asymmetric Full-State Constraints. Mathematics 2023, 11, 4313. https://doi.org/10.3390/math11204313
Hou Y, Xu X, Liu R, Bai X, Liu H. Adaptive Finite-Time Fuzzy Control for Uncertain Nonlinear Systems with Asymmetric Full-State Constraints. Mathematics. 2023; 11(20):4313. https://doi.org/10.3390/math11204313
Chicago/Turabian StyleHou, Yinlong, Xiaoling Xu, Ruixia Liu, Xiangyun Bai, and Hui Liu. 2023. "Adaptive Finite-Time Fuzzy Control for Uncertain Nonlinear Systems with Asymmetric Full-State Constraints" Mathematics 11, no. 20: 4313. https://doi.org/10.3390/math11204313
APA StyleHou, Y., Xu, X., Liu, R., Bai, X., & Liu, H. (2023). Adaptive Finite-Time Fuzzy Control for Uncertain Nonlinear Systems with Asymmetric Full-State Constraints. Mathematics, 11(20), 4313. https://doi.org/10.3390/math11204313




