SVD-Based Identification of Parameters of the Discrete-Time Stochastic Systems Models with Multiplicative and Additive Noises Using Metaheuristic Optimization

Abstract

The paper addresses a parameter identification problem for discrete-time stochastic systems models with multiplicative and additive noises. Stochastic systems with additive and multiplicative noises are considered when solving many practical problems related to the processing of measurements information. The purpose of this work is to develop a numerically stable gradient-free instrumental method for solving the parameter identification problems for a class of mathematical models described by discrete-time linear stochastic systems with multiplicative and additive noises on the basis of metaheuristic optimization and singular value decomposition. We construct an identification criterion in the form of the negative log-likelihood function based on the values calculated by the newly proposed SVD-based Kalman-type filtering algorithm, taking into account the multiplicative noises in the equations of the state and measurements. Metaheuristic optimization algorithms such as the GA (genetic algorithm) and SA (simulated annealing) are used to minimize the identification criterion. Numerical experiments confirm the validity of the proposed method and its numerical stability compared with the usage of the conventional Kalman-type filtering algorithm.

1. Introduction

Discrete-time stochastic systems with additive and multiplicative noises are considered when solving many practical problems related to the processing of measurement information (for example, image and signal processing problems, financial mathematics, tracking problems, etc.). The reasons for the appearance of multiplicative noises in the system may have a different nature depending on the problem being solved, or the object or the process being modeled. For example, there are linearization and modeling errors, quantization, physical phenomena such as fading in communication channels, random disturbances in the dynamics of the system or in sensors.

It is well known that, for systems with additive noises, a conventional Kalman filter may suffer from numerical instability caused by machine roundoff errors [1]. This is also true for systems with multiplicative noises [2].

The purpose of this work is to develop a numerically stable instrumental method for solving the parameter identification problem for a class of mathematical models described by discrete-time linear stochastic systems with multiplicative and additive noises based on metaheuristic optimization of the quadratic identification criterion [3] and newly constructed SVD-based Kalman-type filtering algorithm.

Metaheuristics are one of the powerful classes of gradient-free optimization methods used in parameter identification algorithms. They are high-level solution search strategies that can be used to solve a wide range of optimization problems in which the objective function may be nonsmooth, discontinuous, or highly nonlinear. A feature of metaheuristics is that almost all of them are nondeterministic [4].

The singular value decomposition method (or SVD factorization) is known as the most accurate method of matrix factorization, especially for matrices close to singular ones. Moreover, the singular value decomposition exists for any matrix, which cannot be said, for example, about the Cholesky or modified Cholesky decompositions [5]. Therefore, SVD factorization-based modifications of the Kalman filter (KF) have the same improved numerical robustness to machine roundoff errors as all known square-root modifications [1,6]. In addition, as mentioned in [7], SVD filters have additional advantages such as:

(1)

All eigenvalues of the error covariance matrices are automatically computed at each step of the filtering algorithm and can be used for automatic analysis and/or reduction of the original model;

(2)

The information matrices (inverse of the covariance matrices) are easily computed by inverting the diagonal factors in the SVD decomposition, which creates an elegant way to construct information-type algorithms and mixed-type filters with automatic switching from the covariance filtering mode to the information filtering mode.

As far as the authors of this paper know, the idea of constructing a numerically stable modification of the Kalman filter using singular value decomposition was first proposed by Oshman and Bar-Itzhack [8]. The authors named their variant of the SVD filter as the V-$\mathsf{\Lambda }$ filter. To implement the algorithm, both the SVD decomposition and the Cholesky decomposition must be performed, as well as at least three matrix inverse operations. Oshman then proposed an information form of the V-$\mathsf{\Lambda }$ filter [9]. In [10], the V-$\mathsf{\Lambda }$ filter was applied to solve the parameter identification problem of a linear discrete-time stochastic system.

Later, other authors proposed their own variants of the SVD filter corresponding to the standard Kalman [11] and extended Kalman [12] filters. The above modifications are similar to the V-$\mathsf{\Lambda }$ filter in many aspects. The limitation of their application is the requirement of positive definiteness of the noise covariance matrices in the state and the sensor models equations at each iteration of the algorithm, since it is necessary to apply the Cholesky decomposition to compute the square root of the covariance matrix. It is also necessary to perform a minimum of three matrix inversions.

In order to eliminate these drawbacks of the previous versions of the SVD filter, a new, improved version of the SVD Kalman filter was proposed in [13]. Its difference from other known variants is that this modification of the Kalman filter is free from the conditions $Q_k\ge 0$ and $R_k>0$, required both in the standard Kalman filter and in all its square-root modifications [6]. Another significant numerical advantage of the above modification is the presence of only one diagonal matrix inversion in the filter equations. As shown in [13], according to the results of comparative analysis, this variant of the SVD filter showed the best results in terms of numerical stability against machine roundoff errors.

It should also be noted that the SVD filter confirmed its efficiency in solving the problems of parameter identification [14], the problem of estimating the state and the flight parameters of an aircraft [12], the problem of Kalman filtering of inertial measurement unit readings [15], and others.

The main idea of this paper is to develop a new numerically stable parameter identification method that combines the benefits of metaheuristic optimization and SVD factorization. The paper has the following structure. Section 2 provides basic definitions associated with the conventional Kalman-type filtering algorithm for discrete-time stochastic systems with multiplicative and additive noises. Also, the problem of parameter identification is described. Section 3 contains the main result of the paper—the newly constructed SVD-based Kalman-type filtering algorithm for systems with multiplicative and additive noises. Two lemmas that state algebraic equivalence between the SVD-based and conventional Kalman-type filtering algorithms are proved. Section 4 demonstrates how the proposed method can be applied for solving the parameter identification problems of the considered stochastic system models and its numerical superiority in dealing with machine roundoff errors compared with the usage of conventional Kalman-type algorithms. Section 5 concludes the paper.

2. Methodology

2.1. Conventional Kalman-Type Filtering Algorithm for Discrete-Time Stochastic Systems with Multiplicative and Additive Noises

Consider a discrete-time linear stochastic system with multiplicative and additive noises

$$\left\{\begin{array}{cc}\hfill x_k& =(F_{k-1}+{\tilde{F}}_{k-1}{\xi }_{k-1})x_{k-1}+G_{k-1}{w}_{k-1},\hfill \\ \hfill z_k& =(H_k+{\tilde{H}}_k{\zeta }_k)x_k+v_k,\hspace{1em}k=1,2,\cdots ,M\hfill \end{array}\right.$$

(1)

where $x_k\in {\mathbb{R}}^n$ is the system state vector; $z_k\in {\mathbb{R}}^m$ is the measurement vector; matrices $F_k$, ${\tilde{F}}_k\in {\mathbb{R}}^{n\times n}$; $H_k$, ${\tilde{H}}_k\in {\mathbb{R}}^{m\times n}$; $G\in {\mathbb{R}}^{n\times q}$; M is the number of measurements; $x_0\sim \mathcal{N}({\overline{x}}_0,{\Pi }_0)$ is the initial state; ${\xi }_k\in \mathbb{R}\sim \mathcal{N}(0,{\sigma }_{\xi }^2)$ and $w_k\in {\mathbb{R}}^q\sim \mathcal{N}(0,Q_k)$  are multiplicative and additive noises in the system state, respectively; ${\zeta }_k\in \mathbb{R}\sim \mathcal{N}(0,{\sigma }_{\zeta }^2)$ and $v_k\in {\mathbb{R}}^m\sim \mathcal{N}(0,R_k)$ are multiplicative and additive noises in the measurement scheme, respectively; covariance matrices $Q_k$ and $R_k$ of noises $w_k$ and $v_k$, respectively, are positive semidefinite; and all noises and the initial state are mutually independent.

The discrete-time Kalman-type filtering algorithm for the systems under consideration is known (see, for example, [2,16]). It allows for computing linear optimal estimates, ${\widehat{x}}_k$, of the state vector, $x_k$, from the available measurements $z_k$, $k=1,\cdots ,M$.

Let us introduce the following notation:

$$\begin{array}{cc}\hfill {\tilde{w}}_{k-1}& ={\tilde{F}}_{k-1}{\xi }_{k-1}{x}_{k-1}+G_{k-1}{w}_{k-1},\hfill \\ \hfill {\tilde{v}}_k& ={\tilde{H}}_k{\zeta }_k{x}_k+v_k\hfill \end{array}$$

where

$$\begin{array}{cc}\hfill \mathbf{E}\left\{x_k{x}_k^T\right\}& =X_k,X_k=F_{k-1}{X}_{k-1}{F}_{k-1}^T+{\tilde{Q}}_{k-1};\hfill \\ \hfill \mathbf{E}\left\{{\tilde{w}}_k\right\}& =0,\mathbf{E}\left\{{\tilde{w}}_k{\tilde{w}}_k^T\right\}={\tilde{Q}}_k={\sigma }_{\xi }^2{\tilde{F}}_k{X}_k{\tilde{F}}_k^T+G_k{Q}_k{G}_k^T;\hfill \\ \hfill \mathbf{E}\left\{{\tilde{v}}_k\right\}& =0,\mathbf{E}\left\{{\tilde{v}}_k{\tilde{v}}_k^T\right\}={\tilde{R}}_k={\sigma }_{\zeta }^2{\tilde{H}}_k{X}_k{\tilde{H}}_k^T+R_k.\hfill \end{array}$$

Firstly, consider a conventional Kalman-type filtering algorithm for the system (1), Algorithm 1. The derivation of this algorithm can be found, for example, in [16].

Algorithm 1: Conventional Kalman-type filtering algorithm (KF).

Initialization. Calculate $X_0={\mathsf{\Pi }}_0+{\overline{x}}_0{\overline{x}}_0^T$. Set initial values $P_0={\mathsf{\Pi }}_0$, ${\widehat{x}}_0={\overline{x}}_0$. For  $k=1,2,\cdots ,M$  do I. Time Update step. Find a priori covariance estimation error matrix $P_{k|k-1}$ and a priori estimate of the state vector ${\widehat{x}}_{k|k-1}$ as follows: $$\begin{array}{cc}\hfill {\tilde{Q}}_{k-1}& ={\sigma }_{\xi }^2{\tilde{F}}_{k-1}{X}_{k-1}{\tilde{F}}_{k-1}^T+G_{k-1}{Q}_{k-1}{G}_{k-1}^T,\hfill \end{array}$$ (2) $$\begin{array}{cc}\hfill X_k& =F_{k-1}{X}_{k-1}{F}_{k-1}^T+{\tilde{Q}}_{k-1},\hfill \end{array}$$ (3) $$\begin{array}{cc}\hfill P_{k|k-1}& =F_{k-1}{P}_{k-1}{F}_{k-1}^T+{\tilde{Q}}_{k-1},\hfill \end{array}$$ (4) $$\begin{array}{cc}\hfill {\widehat{x}}_{k|k-1}& =F_{k-1}{\widehat{x}}_{k-1}.\hfill \end{array}$$ (5) II. Measurement Update step. Using the a priori estimates $P_{k|k-1}$ and ${\widehat{x}}_{k|k-1}$, find their a posteriori values $P_k$ and ${\widehat{x}}_k$ as follows: $$\begin{array}{cc}\hfill {\tilde{R}}_k& ={\sigma }_{\zeta }^2{\tilde{H}}_k{X}_k{\tilde{H}}_k^T+R_k,\hfill \end{array}$$ (6) $$\begin{array}{cc}\hfill {\mathsf{\Sigma }}_k& =H_k{P}_{k|k-1}{H}_k^T+{\tilde{R}}_k,\hfill \end{array}$$ (7) $$\begin{array}{cc}\hfill K_k& =P_{k|k-1}{H}_k^T{\mathsf{\Sigma }}_k^{-1},\hfill \end{array}$$ (8) $$\begin{array}{cc}\hfill P_k& =(I-K_k{H}_k)P_{k|k-1},\hfill \end{array}$$ (9) $$\begin{array}{cc}\hfill {\widehat{x}}_k& ={\widehat{x}}_{k|k-1}+K_k{e}_k,\hfill \end{array}$$ (10) $$\begin{array}{cc}\hfill {\nu }_k& =z_k-H_k{\widehat{x}}_{k|k-1}.\hfill \end{array}$$ (11) End.

2.2. The Problem of Parameter Identification

Suppose that the matrices defining the equations of the system model (1) depend on the unknown parameters. Let us set the problem of their identification by available measurements $Z_1^M=\{z_1,\dots ,z_k,\dots ,z_M\}$.

Let the vector of the unknown parameters be $\theta \in {\mathbb{R}}^p$. Then the value of the estimation error $e_k=x_k-{\widehat{x}}_k$ will depend on the value of the parameter $\theta$, which is specified in the equations of the discrete-time filtering algorithm. The minimum value of the error $e_k$ can be obtained under the condition of a minimum by $\theta$ of the quadratic functional

$${\mathcal{J}}_k^o\left(\theta \right)=\mathbf{E}\left\{e_k^T\left(\theta \right)e_k\left(\theta \right)\right\}.$$

(12)

The problem is that the functional (12) is not instrumental, i.e., it is not practically feasible because the errors, $e_k$, are not available for direct observation. The most popular approach to solving this problem are MPE (minimum prediction error) methods [17], based on minimizing an identification criterion that depends on the observed measurement residuals. Such criteria include the well-known least squares and maximum likelihood criteria. An alternative approach is the auxiliary performance index method [18]. Thus, the algorithm of numerical minimization of the original functional (12) by the parameter $\theta$ is replaced by the algorithm of numerical minimization of the selected instrumental criterion, which is practically feasible.

To solve the problem of identifying the parameters of the system (1), we construct an instrumental criterion in the form of a negative logarithmic likelihood function:

$${\mathcal{J}}_{\mathrm{KF}}(\theta ;Z_1^M)=\frac{Mm}{2}ln2\pi +\frac{1}{2}\sum _{k=1}^M\left\{ln|{\mathsf{\Sigma }}_k\left(\theta \right)|+||{\nu }_k\left(\theta \right){\left|\right|}_{{\mathsf{\Sigma }}_k^{-1}\left(\theta \right)}^2\right\},$$

(13)

the values of which, for a given $\theta$, we will calculate using Equations (2)–(11) of Algorithm 1.

The identification criterion (13), calculated on the basis of the values obtained by the Kalman filter or its modification, can serve as an objective function for minimization algorithms of various types. If the gradient of the identification criterion is unknown or finding it is computationally expensive, then gradient-free methods such as metaheuristic algorithms can be used for minimization. Also, these methods are extremely useful if the objective function loses its smoothness or continuity properties, for example, due to machine roundoff errors.

Depending on the method of obtaining a solution, most metaheuristic optimization algorithms can be divided into two large groups: trajectory and population algorithms. In trajectory algorithms, the solution search process can be viewed as a movement between individual solutions in the solution space of the problem, while, in population algorithms, the search for an optimal solution involves changing the group of solutions.

One of the most popular trajectory algorithms used in solving global optimization problems is the simulated annealing method (SA). The key feature of the method is the use of a control parameter—temperature, which allows for controlling the nondeterministic process of solution search. As a rule, the temperature decreases during the algorithm operation according to a certain law, starting from some initial value. At each iteration of the algorithm, a randomly generated new solution from the neighborhood of the current solution is accepted, with a probability of 1 if it is better and a probability of less than 1 if it is worse than the current one, and the probability of accepting the worst solution decreases with decreasing temperature. The quality of the solutions is evaluated using a cost function with integer or real values.

A genetic algorithm (GA) is a popular version of evolutionary optimization algorithms based on the modeling of natural selection processes. In evolutionary algorithms, the quality of solutions is evaluated using a fitness function, and the basic idea is that solutions with the best values of this function “survive” during evolution. In a genetic algorithm, at each iteration of the evolutionary process, a new population is obtained from the current population by successive use of one or more genetic operators, the most common of which are crossover, which allows descendant solutions from parental solutions to be obtained, and mutation, which randomly modifies solutions.

3. Main Results

The New SVD-Based Kalman-Type Filtering Algorithm for Discrete-Time Stochastic Systems with Multiplicative and Additive Noises

Now, we are ready to present our new result—the SVD-based Kalman-type filtering Algorithm 2. Consider the SVD factorization [19]. Any matrix, $\mathcal{A}\in {\mathbb{C}}^{m\times n}$, of rank r can be represented as

$$\mathcal{A}=\mathcal{W}\mathsf{\Sigma }{\mathcal{V}}^{*},\mathsf{\Sigma }=\left[\begin{array}{cc}S& 0\\ 0& 0\end{array}\right]\in {\mathbb{C}}^{m\times n},S=\mathrm{diag}\{{\sigma }_1,\dots ,{\sigma }_r\}$$

where $\mathcal{W}\in {\mathbb{C}}^{m\times m}$, $\mathcal{V}\in {\mathbb{C}}^{n\times n}$ are unitary matrices, ${\mathcal{V}}^{*}$ means conjugate and transposed to $\mathcal{V}$, and $S\in {\mathbb{R}}^{r\times r}$ is a real non-negative diagonal matrix. The values ${\sigma }_1\ge {\sigma }_2\ge \dots \ge {\sigma }_r>0$ are singular values of the matrix $\mathcal{A}$. Note that if $r=n$ and/or $r=m$, some of the zero submatrices in $\mathsf{\Sigma }$ are absent.

Algorithm 2: SVD-based Kalman-type filtering algorithm (SVD-KF).

Initialization. Apply SVD factorization for the initial matrices $X_0={\mathsf{\Theta }}_{X_0}{D}_{X_0}{\mathsf{\Theta }}_{X_0}^T$ and ${\mathsf{\Pi }}_0={\mathsf{\Theta }}_{{\mathsf{\Pi }}_0}{D}_{{\mathsf{\Pi }}_0}{\mathsf{\Theta }}_{{\mathsf{\Pi }}_0}^T$. Set the initial values: ${\mathsf{\Theta }}_{P_0}={\mathsf{\Theta }}_{{\mathsf{\Pi }}_0}$, $D_{P_0}=D_{{\mathsf{\Pi }}_0}$ and ${\widehat{x}}_0={\overline{x}}_0$. For  $k=1,2,\cdots ,M$  do I. Time Update step. I.1. Apply SVD factorization for the process noise covariance matrix $Q_{k-1}={\mathsf{\Theta }}_{Q_{k-1}}{D}_{Q_{k-1}}{\mathsf{\Theta }}_{Q_{k-1}}^T$. I.2. Build the pre-arrays and apply the SVD factorization in order to obtain the SVD factors $\{{\mathsf{\Theta }}_{{\tilde{Q}}_{k-1}},D_{{\tilde{Q}}_{k-1}}\}$, $\{{\mathsf{\Theta }}_{X_k},D_{X_k}\}$ and $\{{\mathsf{\Theta }}_{P_{k|k-1}},D_{P_{k|k-1}}\}$ as follows $$\left[\begin{array}{c}{\sigma }_{\xi }{D}_{X_{k-1}}^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.}{\mathsf{\Theta }}_{X_{k-1}}^T{\tilde{F}}_{k-1}^T\\ D_{Q_{k-1}}^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.}{\mathsf{\Theta }}_{Q_{k-1}}^T{G}_{k-1}^T\end{array}\right]={\mathcal{W}}_{\mathrm{TU}}^{\left(1\right)}\left[\begin{array}{c}{D}_{{\tilde{Q}}_{k-1}}^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.}\\ 0\end{array}\right]{\mathsf{\Theta }}_{{\tilde{Q}}_{k-1}}^T;$$ (14) $$\left[\begin{array}{c}{D}_{X_{k-1}}^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.}{\mathsf{\Theta }}_{X_{k-1}}^T{F}_{k-1}^T\\ D_{{\tilde{Q}}_{k-1}}^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.}{\mathsf{\Theta }}_{{\tilde{Q}}_{k-1}}^T\end{array}\right]={\mathcal{W}}_{\mathrm{TU}}^{\left(2\right)}\left[\begin{array}{c}{D}_{X_k}^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.}\\ 0\end{array}\right]{\mathsf{\Theta }}_{X_k}^T;$$ (15) $$\left[\begin{array}{c}{D}_{P_{k-1}}^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.}{\mathsf{\Theta }}_{P_{k-1}}^T{F}_{k-1}^T\\ D_{{\tilde{Q}}_{k-1}}^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.}{\mathsf{\Theta }}_{{\tilde{Q}}_{k-1}}^T\end{array}\right]={\mathcal{W}}_{\mathrm{TU}}^{\left(3\right)}\left[\begin{array}{c}{D}_{P_{k|k-1}}^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.}\\ 0\end{array}\right]{\mathsf{\Theta }}_{P_{k|k-1}}^T.$$ (16) I.3. Given ${\widehat{x}}_{k-1}$, compute a priori estimate ${\widehat{x}}_{k|k-1}$ by (5). II. Measurement Update step. II.1. Apply SVD factorization for the measurements noise covariance matrix $R_k={\mathsf{\Theta }}_{R_k}{D}_{R_k}{\mathsf{\Theta }}_{R_k}^T$. II.2. In order to obtain the SVD factors $\{{\mathsf{\Theta }}_{{\tilde{R}}_k},D_{{\tilde{R}}_k}\}$ and $\{{\mathsf{\Theta }}_{{\mathsf{\Sigma }}_k},D_{{\mathsf{\Sigma }}_k}\}$, apply the SVD factorization to the next left hand side pre-arrays: $$\left[\begin{array}{c}{\sigma }_{\zeta }{D}_{X_k}^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.}{\mathsf{\Theta }}_{X_k}^T{\tilde{H}}_k^T\\ D_{R_k}^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.}{\mathsf{\Theta }}_{R_k}^T\end{array}\right]={\mathcal{W}}_{\mathrm{MU}}^{\left(1\right)}\left[\begin{array}{c}{D}_{{\tilde{R}}_k}^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.}\\ 0\end{array}\right]{\mathsf{\Theta }}_{{\tilde{R}}_k}^T;$$ (17) $$\left[\begin{array}{c}{D}_{P_{k|k-1}}^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.}{\mathsf{\Theta }}_{P_{k|k-1}}^T{H}_k^T\\ D_{{\tilde{R}}_k}^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.}{\mathsf{\Theta }}_{{\tilde{R}}_k}^T\end{array}\right]={\mathcal{W}}_{\mathrm{MU}}^{\left(2\right)}\left[\begin{array}{c}{D}_{{\mathsf{\Sigma }}_k}^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.}\\ 0\end{array}\right]{\mathsf{\Theta }}_{{\mathsf{\Sigma }}_k}^T.$$ (18) II.3. Find the feedback gain $K_k$ as follows: $$K_k={\overline{K}}_k{D}_{{\mathsf{\Sigma }}_k}^{-1}{\mathsf{\Theta }}_{{\mathsf{\Sigma }}_k}^T\mathrm{where}{\overline{K}}_k=P_{k|k-1}{H}_k^T{\mathsf{\Theta }}_{{\mathsf{\Sigma }}_k}.$$ (19) II.4. In order to obtain the SVD factors $\{{\mathsf{\Theta }}_{P_k},D_{P_k}\}$, apply the SVD factorization to the next left hand side pre-array: $$\left[\begin{array}{c}{D}_{P_{k|k-1}}^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.}{\mathsf{\Theta }}_{P_{k|k-1}}^T{(I-K_k{H}_k)}^T\\ D_{{\tilde{R}}_k}^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.}{\mathsf{\Theta }}_{{\tilde{R}}_k}^T{K}_k^T\end{array}\right]={\mathcal{W}}_{\mathrm{MU}}^{\left(2\right)}\left[\begin{array}{c}{D}_{P_k}^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.}\\ 0\end{array}\right]{\mathsf{\Theta }}_{P_k}^T.$$ (20) II.5. Find a posteriori estimate ${\widehat{x}}_k$ as follows: $${\widehat{x}}_k={\widehat{x}}_{k|k-1}+{\overline{K}}_k{D}_{{\mathsf{\Sigma }}_k}^{-1}{\overline{\nu }}_k\mathrm{where}{\overline{\nu }}_k={\mathsf{\Theta }}_{{\mathsf{\Sigma }}_k}^T(z_k-H_k{\widehat{x}}_{k|k-1}).$$ (21) End.

Lemma 1.

Time update steps of the KF and SVD-KF algorithms for system model (1) are algebraically equivalent.

Proof. 

Let us prove that (2) and (14) are equivalent.

From a general form $\mathcal{A}=\mathcal{W}\mathsf{\Sigma }{\mathcal{V}}^T$ we obtain

$${\mathcal{A}}^T\mathcal{A}={\left(\mathcal{W}\mathsf{\Sigma }{\mathcal{V}}^T\right)}^T\left(\mathcal{W}\mathsf{\Sigma }{\mathcal{V}}^T\right)=\mathcal{V}{\mathsf{\Sigma }}^2{\mathcal{V}}^T.$$

(22)

So, from (14) we have

$$\begin{array}{cc}\hfill {\mathcal{A}}^T\mathcal{A}& =\left[\begin{array}{cc}{\sigma }_{\xi }{\tilde{F}}_{k-1}{\mathsf{\Theta }}_{X_{k-1}}{D}_{X_{k-1}}^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.}& G_{k-1}{\mathsf{\Theta }}_{Q_{k-1}}{D}_{Q_{k-1}}^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.}\end{array}\right]\left[\begin{array}{c}{\sigma }_{\xi }{D}_{X_{k-1}}^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.}{\mathsf{\Theta }}_{X_{k-1}}^T{\tilde{F}}_{k-1}^T\\ D_{Q_{k-1}}^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.}{\mathsf{\Theta }}_{Q_{k-1}}^T{G}_{k-1}^T\end{array}\right]\hfill \\ \hfill & ={\sigma }_{\xi }{\tilde{F}}_{k-1}{\mathsf{\Theta }}_{X_{k-1}}{D}_{X_{k-1}}{\mathsf{\Theta }}_{X_{k-1}}^T{\tilde{F}}_{k-1}^T+G_{k-1}{\mathsf{\Theta }}_{Q_{k-1}}{D}_{Q_{k-1}}{\mathsf{\Theta }}_{Q_{k-1}}^T{G}_{k-1}^T\hfill \\ \hfill & ={\sigma }_{\xi }^2{\tilde{F}}_{k-1}{X}_{k-1}{\tilde{F}}_{k-1}^T+G_{k-1}{Q}_{k-1}{G}_{k-1}^T.\hfill \\ \hfill \mathcal{V}{\mathsf{\Sigma }}^2{\mathcal{V}}^T& ={\mathsf{\Theta }}_{{\tilde{Q}}_{k-1}}{D}_{{\tilde{Q}}_{k-1}}{\mathsf{\Theta }}_{{\tilde{Q}}_{k-1}}^T={\tilde{Q}}_{k-1}.\hfill \end{array}$$

Hence, we have (2) from (22). The equivalence of (3) and (15), and (4) and (16) can be proved in the same manner.    □

Lemma 2.

Measurement update steps of the KF and SVD-KF algorithms for system model (1) are algebraically equivalent.

Proof. 

The equivalence of (6) and (17), and (7) and (18) can be proved in the same way as in Lemma 1.

Next, expression (19) for calculating $K_k$ is derived from (8), where the matrix ${\mathsf{\Sigma }}_k$ is the SVD factorized. Indeed,

$$K_k=P_{k|k-1}{H}_k^T{\mathsf{\Sigma }}_k^{-1}=P_{k|k-1}{H}_k^T{\left({\mathsf{\Theta }}_{{\mathsf{\Sigma }}_k}{D}_{{\mathsf{\Sigma }}_k}{\mathsf{\Theta }}_{{\mathsf{\Sigma }}_k}^T\right)}^{-1}={\overline{K}}_k{D}_{{\mathsf{\Sigma }}_k}^{-1}{\mathsf{\Theta }}_{{\mathsf{\Sigma }}_k}^T.$$

Let us prove the equivalence of (9) and (20). Taking into account (20), the left hand side of (22) may be written as follows:

$$\begin{array}{cc}\hfill {\mathcal{A}}^T\mathcal{A}& =\left[\begin{array}{cc}(I-K_k{H}_k){\mathsf{\Theta }}_{P_{k|k-1}}{D}_{P_{k|k-1}}^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.}& K_k{\mathsf{\Theta }}_{{\tilde{R}}_k}{D}_{{\tilde{R}}_k}^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.}\end{array}\right]\left[\begin{array}{c}{D}_{P_{k|k-1}}^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.}{\mathsf{\Theta }}_{P_{k|k-1}}^T{(I-K_k{H}_k)}^T\\ D_{{\tilde{R}}_k}^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.}{\mathsf{\Theta }}_{{\tilde{R}}_k}^T{K}_k^T\end{array}\right]\hfill \\ \hfill & =(I-K_k{H}_k){\mathsf{\Theta }}_{P_{k|k-1}}{D}_{P_{k|k-1}}^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.}{D}_{P_{k|k-1}}^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.}{\mathsf{\Theta }}_{P_{k|k-1}}^T{(I-K_k{H}_k)}^T+K_k{\mathsf{\Theta }}_{{\tilde{R}}_k}{D}_{{\tilde{R}}_k}^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.}{D}_{{\tilde{R}}_k}^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.}{\mathsf{\Theta }}_{{\tilde{R}}_k}^T{K}_k^T\hfill \\ \hfill & =(I-K_k{H}_k)P_{k|k-1}{(I-K_k{H}_k)}^T+K_k{\tilde{R}}_k{K}_k^T.\hfill \end{array}$$

On the other hand,

$$\mathcal{V}{\mathsf{\Sigma }}^2{\mathcal{V}}^T={\mathsf{\Theta }}_{P_k}{D}_{P_k}^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.}{D}_{P_k}^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.}{\mathsf{\Theta }}_{P_k}^T=P_k.$$

Thus,

$$P_k=(I-K_k{H}_k)P_{k|k-1}{(I-K_k{H}_k)}^T+K_k{\tilde{R}}_k{K}_k^T.$$

(23)

Let us rewrite (23) using (7) and (8):

$$\begin{array}{cc}\hfill P_k& =(I-K_k{H}_k)P_{k|k-1}-P_{k|k-1}{H}_k^T{K}_k^T+K_k{H}_k{P}_{k|k-1}{H}_k^T{K}_k^T+K_k{\tilde{R}}_k{K}_k^T\hfill \\ \hfill & =(I-K_k{H}_k)P_{k|k-1}-P_{k|k-1}{H}_k^T{K}_k^T+K_k(H_k{P}_{k|k-1}{H}_k^T+{\tilde{R}}_k)K_k^T\hfill \\ \hfill & =(I-K_k{H}_k)P_{k|k-1}-P_{k|k-1}{H}_k^T{K}_k^T+P_{k|k-1}{H}_k^T{\mathsf{\Sigma }}_k^{-1}{\mathsf{\Sigma }}_k{K}_k^T\hfill \\ \hfill & =(I-K_k{H}_k)P_{k|k-1}-P_{k|k-1}{H}_k^T{K}_k^T+P_{k|k-1}{H}_k^T{K}_k^T\hfill \\ \hfill & =(I-K_k{H}_k)P_{k|k-1}⟹\left(9\right).\hfill \end{array}$$

Finally, expression (21) follows directly from (10), taking into account $K_k=$${\overline{K}}_k{D}_{{\mathsf{\Sigma }}_k}^{-1}{\mathsf{\Theta }}_{{\mathsf{\Sigma }}_k}^T$.    □

Now, to construct the parameter identification procedure, we need to rewrite the expression for computing the negative logarithmic likelihood function (13) in terms of the SVD-KF. Given that

$$det\left({\mathsf{\Sigma }}_k\right)=det\left(D_{{\mathsf{\Sigma }}_k}\right) \mathrm{and} {\nu }_k^T{\mathsf{\Sigma }}_k^{-1}{\nu }_k={\overline{\nu }}_k^T{D}_{{\mathsf{\Sigma }}_k}^{-1}{\overline{\nu }}_k,$$

we can write

$${\mathcal{J}}_{\mathrm{SVD}}(\theta ;Z_1^M)=\frac{Mm}{2}ln\left(2\pi \right)+\frac{1}{2}\sum _{k=1}^M\{ln[det\left(D_{{\mathsf{\Sigma }}_k}\right)]+{\overline{\nu }}_k^T{D}_{{\mathsf{\Sigma }}_k}^{-1}{\overline{\nu }}_k\}$$

(24)

where the diagonal matrix $D_{{\mathsf{\Sigma }}_k}$ and vector ${\overline{\nu }}_k$ are available at each step of Algorithm 2.

To find the optimal value, ${\theta }^{*}$, of unknown parameter $\theta$ with the objective function (24), we use the metaheuristic optimization methods GA and SA.

The identification of unknown parameter $\theta$ and the estimation of state vector $x_k$ of system (1) can be performed simultaneously according to the criterion

$${\theta }^{*}=\underset{\mathcal{D}\left(\theta \right)}{\mathrm{argmin}}{\mathcal{J}}_{\mathrm{SVD}}(\theta ;Z_1^M).$$

(25)

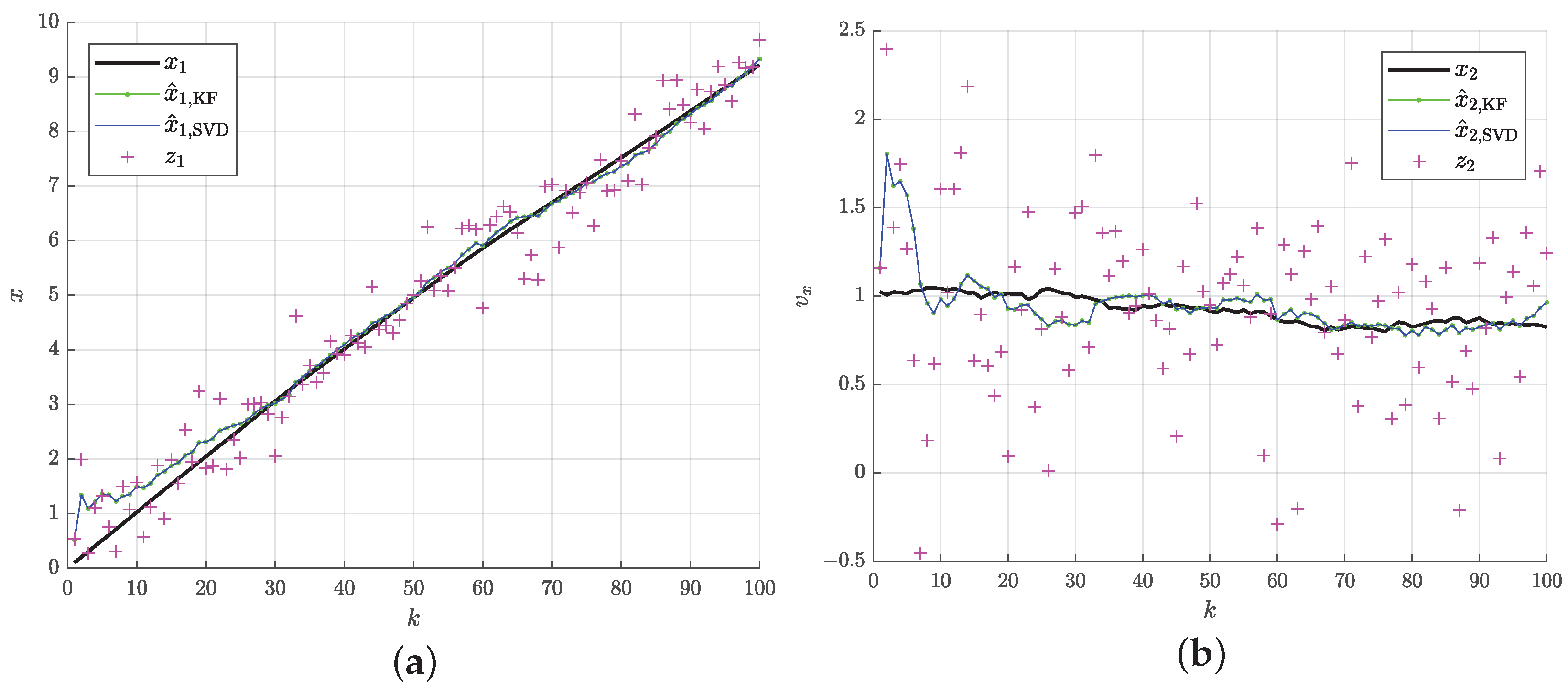
4. Discussion

In this section, we wish to show the validity and numerical superiority of the proposed method in dealing with machine roundoff errors. In order to conduct numerical experiments, we have implemented in MATLAB Algorithms 1 and 2, functions for calculating identification criteria ${\mathcal{J}}_{\mathrm{KF}}(\theta ;Z_1^M)$ and ${\mathcal{J}}_{\mathrm{SVD}}(\theta ;Z_1^M)$ according to (13) and (24), as well as functions for modeling system dynamics and measurements. The functions ga and simulannealbnd from the MATLAB Global Optimization Toolbox were used for numerical minimization of both identification criteria by the GA and SA methods, respectively. All experiments were conducted on the following platform: Windows 11, Intel Core i3-1115G4 CPU @ 3.00 GHz, 8 GB of RAM.

Table 1. Settings of the algorithms.

GA		SA
Parameter	Value	Parameter	Value
TimeLimit	60	TimeLimit	60
Generations	Inf	MaxIter	Inf
StallGenLimit	20	StallIterLimit	100
PopulationSize	10	ReannealInterval	100
PopInitRange	[0; 1]	MaxFunEvals	Inf
MutationFcn	@mutationadaptfeasible

presents the main GA and SA settings used in the numerical experiments. The remaining settings are taken by default.

Example 1. First, let us demonstrate the validity of the proposed method. Consider a nearly constant velocity model for the uniform motion [20] augmented with multiplicative noises ${\xi }_k$ and ${\zeta }_k$:

$$\left\{\begin{array}{cc}\hfill x_k& =\left(\left[\begin{array}{cc}1& \theta \\ 0& 1\end{array}\right]+\left[\begin{array}{cc}0& 0\\ 0& 1\end{array}\right]{\xi }_{k-1}\right)x_{k-1}+\left[\begin{array}{c}\raisebox{1ex}{${\theta }^2$}\!\left/ \!\raisebox{-1ex}{$2$}\right.\\ \theta \end{array}\right]w_{k-1},\hfill \\ \hfill z_k& =\left(\left[\begin{array}{cc}1& 0\\ 0& 1\end{array}\right]+\left[\begin{array}{cc}0& 0\\ 0& 1\end{array}\right]{\zeta }_k\right)x_k+v_k,\hspace{1em}k=1,\dots ,100\hfill \end{array}\right.$$

(26)

where $x_k={[x_1,x_2]}_k^T$, $x_1=x$ is the coordinate of the object, $x_2=v_x$ is its velocity, $x_0\sim \mathcal{N}({[0,1]}^T,10I_2)$, $w_k\sim \mathcal{N}(0,{10}^{-2})$, $v_k\sim \mathcal{N}(0,{\sigma }^2{I}_2)$ ($\sigma =0.1,0.5,1.0$), ${\xi }_k\sim \mathcal{N}(0,{10}^{-4})$, ${\zeta }_k\sim \mathcal{N}(0,{10}^{-4})$, and $\theta$ is the model parameter to be identified. Let us put the “true” value of the parameter equal to ${\theta }^{*}=0.1$.

Figure 1 shows estimation results of the system state vector $x_k$ obtained with Algorithms 1 and 2 for model (26) with $\sigma =0.5$. As one can see, the newly proposed SVD-KF algorithm shows the ability to solve the discrete-time filtering problem successfully and yields the same state estimates as the conventional KF-type algorithm.

Further, we wish to demonstrate how the new Algorithm 2 can be applied to solve the parameter identification problem compared with the conventional Algorithm 1.

A series of 100 numerical experiments was conducted in MATLAB for each value of the noise level, $\sigma$. In each experiment, numerical identification of parameter $\theta$ using both identification criteria was performed based on the results of simulated measurements. The solution, ${\theta }^{*}$, was searched on the segment $[0;1]$.

The average running times of the GA and SA minimizations based on the KF algorithm were 0.886 sec and 0.357 sec, respectively. The average running times of the GA and SA minimizations based on the SVD-KF algorithm were 3.695 sec and 1.376 sec, respectively (see

Table 2. Average time, sec.

	KF		SVD-KF
	GA	SA	GA	SA
$\sigma =1.0$	0.820	0.373	3.442	1.434
$\sigma =0.5$	0.866	0.354	3.526	1.362
$\sigma =0.1$	0.972	0.343	4.118	1.333
Average	0.886	0.357	3.695	1.376

).

We can conclude that for both identification criteria the GA works on average about 2.5–2.7 times slower compared with the SA. This is because the GA works with a group of solutions and performs several genetic operators (selection, crossover, mutation, etc.) at each iteration compared with SA, which works with a single solution and uses much simpler calculations. At the same time, optimization methods based on the SVD-KF algorithm work approximately four times slower than those based on the conventional KF because of the usage of several SVD procedures at each iteration of the algorithm. This may be overcome by using parallel implementations of the SVD procedure.

The results of the numerical identification of parameter $\theta$ are summarized in

Table 3. Identification results (KF).

	GA			SA
	Mean	RMSE	MAPE	Mean	RMSE	MAPE
$\sigma =1.0$	0.099164	0.011193	8.177905	0.098430	0.012116	8.874215
$\sigma =0.5$	0.099261	0.005376	4.403328	0.097789	0.007293	5.773781
$\sigma =0.1$	0.099885	0.001185	0.959292	0.097491	0.005608	3.443892

and

Table 4. Identification results (SVD-KF).

	GA			SA
	Mean	RMSE	MAPE	Mean	RMSE	MAPE
$\sigma =1.0$	0.099131	0.011085	8.164202	0.098504	0.012049	8.949169
$\sigma =0.5$	0.099259	0.005375	4.404718	0.098127	0.006944	5.551390
$\sigma =0.1$	0.099882	0.001186	0.962216	0.096972	0.006581	4.470887

. They show that, with the selected settings, for both identification criteria the GA shows better identification accuracy compared with SA, although it works slower. Also, the accuracy of parameter identification for both identification criteria is practically the same. RMSE and MAPE values decrease with decreasing noise level $\sigma$.

Thus, the results of the numerical experiments confirm the validity of using the proposed SVD-KF algorithm to solve identification problems.

Despite the fact that the SVD-KF algorithm is slower compared with the conventional KF, in the following example we will show that it has an undoubted superiority in terms of numerical robustness to machine roundoff errors.

Example 2. To demonstrate numerical efficiency of the proposed SVD-based identification method, the state-space model with multiplicative and additive noises is explored. The system dynamics considered in [21] is given by equation

$$\begin{array}{cc}\hfill x_k& =\left(\left[\begin{array}{cc}\theta & -0.15\\ 0& 0.15\end{array}\right]+\left[\begin{array}{cc}0.01& 0\\ 0& 0.01\end{array}\right]{\xi }_{k-1}\right)x_{k-1}+\left[\begin{array}{c}\theta \\ 2.5\end{array}\right]w_{k-1},\hspace{1em}k=1,\dots ,100,\hfill \end{array}$$

(27)

$x_0\sim \mathcal{N}({\overline{x}}_0,10I_2)$, ${\overline{x}}_0={[0,1]}^T$, $w_k\sim \mathcal{N}(0,0.1)$, ${\xi }_k\sim \mathcal{N}(0,0.01)$, and $\theta$ is the system parameter that needs to be identified. Let us put the “true” value of the parameter equal to ${\theta }^{*}=0.2$.

Consider the ill-conditioned measurement scheme as in [2]

$$z_k=\left(\left[\begin{array}{cc}1& 1\\ 1& 1+\delta \end{array}\right]+\left[\begin{array}{cc}0& 0\\ 0& 1\end{array}\right]{\zeta }_k\right)x_k+v_k,$$

$v_k\sim \mathcal{N}(0,{\delta }^2{I}_2)$, ${\zeta }_k\sim \mathcal{N}(0,{\delta }^2)$, where ${\delta }^2<{ϵ}_{\mathrm{roundoff}}$ but $\delta >{ϵ}_{\mathrm{roundoff}}$, and ${ϵ}_{\mathrm{roundoff}}$ denotes the unit roundoff error (computer roundoff for floating-point arithmetic is often characterized by a single parameter ${ϵ}_{\mathrm{roundoff}}$, defined as the largest number such that either $1+{ϵ}_{\mathrm{roundoff}}=1$ or $1+{ϵ}_{\mathrm{roundoff}}/2=1$ in machine precision).

A series of 100 numerical experiments was conducted in MATLAB for different values of $\delta$. In each experiment, numerical identification of parameter $\theta$ using both identification criteria was performed based on the results of simulated measurements. The solution, ${\theta }^{*}$, was searched on the segment $[0;1]$.

The average running time of the GA and SA minimizations based on the KF and SVD-KF algorithms is presented in

Table 5. Average time, sec.

	KF		SVD-KF
	GA	SA	GA	SA
$\delta ={10}^{-6}$	0.684	0.421	2.933	1.595
$\delta ={10}^{-7}$	0.765	0.454	2.814	1.653
$\delta ={10}^{-8}$	5.752	–	6.613	3.607
$\delta ={10}^{-9}$	5.560	–	6.928	3.873

. It can be seen that starting from $\delta ={10}^{-8}$ the SA algorithm for identification criterion (13) fails to solve the problem within the required time and the GA starts to slow down dramatically. At the same time, the GA and SA, which use identification criterion (24), perform adequately.

The results of the numerical identification of parameter $\theta$ are summarized in

Table 6. Identification results (KF).

	GA			SA
	Mean	RMSE	MAPE	Mean	RMSE	MAPE
$\delta ={10}^{-6}$	0.201826	0.030241	12.175545	0.202339	0.030573	12.246241
$\delta ={10}^{-7}$	0.196880	0.028717	11.372277	0.197731	0.028353	11.220115
$\delta ={10}^{-8}$	0.126608	0.220648	92.177307	–	–	–
$\delta ={10}^{-9}$	0.319231	0.407681	162.665399	–	–	–

and

Table 7. Identification results (SVD-KF).

	GA			SA
	Mean	RMSE	MAPE	Mean	RMSE	MAPE
$\delta ={10}^{-6}$	0.201787	0.030282	12.221007	0.201656	0.030390	12.089709
$\delta ={10}^{-7}$	0.196823	0.028029	11.152689	0.197950	0.028576	11.303757
$\delta ={10}^{-8}$	0.203242	0.031032	12.662414	0.203419	0.031660	13.103576
$\delta ={10}^{-9}$	0.201195	0.027771	11.557529	0.200827	0.028267	11.554388

. They show that the GA and SA methods based on the SVD-KF Algorithm 2 remain stable for all values of $\delta$ and yield adequate results. At the same time, metaheuristic optimization methods based on Algorithm 1 start to diverge at $\delta ={10}^{-8}$. This happens because the identification criterion (13) loses smoothness and continuity due to machine roundoff errors.

5. Conclusions

The paper proposes an instrumental method for identifying parameters of discrete-time stochastic system models with multiplicative and additive noises. We have constructed a new SVD-based Kalman-type filtering algorithm that allows the calculation of all filter quantities using numerically stable singular value decomposition. It is similar to the existing SVD-based algorithms for systems with additive noises only. In contrast, our newly constructed algorithm takes into account the presence of multiplicative noises in the state and measurement equations of the system model.

Lemmas 1 and 2 contain the main theoretical results of the paper. We have proved the algebraic equivalency of time update and measurement update steps in Algorithms 1 and 2.

With the aim to solve the problem of parameter identification for the considered class of system models, we have constructed an SVD-based identification criterion in the form of a negative logarithmic likelihood function. In order to find the optimal value of the unknown system model parameter, we have used SA and GA methods for its optimization.

Having carried out a series of numerical experiments in MATLAB, we have demonstrated how the new Algorithm 2 can be applied for solving the parameter identification problems. The results of numerical experiments confirm the superiority of the newly developed method in managing machine roundoff errors compared with the one based on conventional Kalman-type filtering. It is worth noting that the GA shows better accuracy in minimizing the identification criteria than SA, although it works slower. Taking into account the speed/accuracy ratio, the usage of the SVD-KF filtering algorithm for computing the identification criterion in conjunction with the SA algorithm for its minimization seems to be the best choice.