The Closed-Form Solution of an Extraction Model and Optimal Stopping Problems with Regime Switching

Abstract

We aim to obtain by viscosity solution method the closed-form solution of a model concerning natural resource extraction in which a firm draws a schedule of when to stop the extraction. In this model, a regime-switching stochastic process is introduced to simulate the price of some natural resource. To solve the model, we first develop a theory, as a part of the results in the paper, that also applies to other optimal stopping problems containing regime-switching ingredients. Then using the theory, we solve the model completely and rigorously. A numerical example is given to display the results of the model.

1. Introduction

Natural resource extraction has received a lot of attention due to its relevance to many issues. Ma et al. [1] and Liu [2] discussed the impact of natural resource extraction on the COP26 target, Alhassan and Kwakwa [3] and Teng [4] examined the effect of natural resource extraction on environmental sustainability, Dadasov et al. [5] studied the relationship of natural resource extraction with corruption and expropriation, and Thorsten [6] researched the role of natural resource extraction in civil conflict.

Therefore, people modeled natural resource extraction from various different perspectives. Bella [7] gave a natural resource extraction model to study the presence of closed orbits that signal economic fluctuations and periodic solutions around the steady state. Engel and Fischer [8] discussed resource extraction contracts in the setting that developing countries need foreign investment in order to develop their natural resources. Under different assumptions on the price of resources, numerous authors [9,10,11] studied when it is optimal to stop the extraction, where the price process and payoff are not regime switching. Ferrari and Yang [12] assumed that the price process follows Bachelier model [13] with regime switching. As Samuelson [14] has pointed out, geometric Brownian motion rather than the Bachelier model is good for describing the price process. In the present paper, we use a regime-switching geometric Brownian motion to simulate the price process.

We state our natural resource extraction model. A firm is extracting a kind of natural resource (oil, gas, etc.). We are interested in determining what time is optimal to stop the extraction.

Let $(\Omega ,\mathcal{F},{\left\{{\mathcal{F}}_t\right\}}_{t\ge 0},\mathbb{P})$ be a filtered probability space. We assume that ${\left\{{\mathcal{F}}_t\right\}}_{t\ge 0}$ satisfies the usual conditions and ${\mathcal{F}}_0$ is the completion of $\{\varnothing ,\Omega \}$.

Let $\left(X\right(t),t\ge 0)$ be a time-homogeneous Markov chain defined on $(\Omega ,\mathcal{F},{\left\{{\mathcal{F}}_t\right\}}_{t\ge 0},\mathbb{P})$ taking values in $\{1,2\}$, with a rate matrix $A:=\left[\begin{array}{cc}-{\lambda }_1& {\lambda }_2\\ {\lambda }_1& -{\lambda }_2\end{array}\right]$ for some positive constants ${\lambda }_1,{\lambda }_2$. As usual, we denote by $X^i$ the Markov chain if it starts from i at time $t=0$.

Let $\left(B\right(t),t\ge 0)$ be a one-dimensional standard Brownian motion, which is independent of X, defined on $(\Omega ,\mathcal{F},{\left\{{\mathcal{F}}_t\right\}}_{t\ge 0},\mathbb{P})$.

We assume that the price process $P^{i,p}$ of the resource is the solution to

$$\mathrm{d}P\left(t\right)=\mu \left(X^i\left(t\right)\right)P\left(t\right)\mathrm{d}t+\sigma \left(X^i\left(t\right)\right)P\left(t\right)\mathrm{d}B\left(t\right),P\left(0\right)=p>0,$$

(1)

where $\mu \left(1\right):={\mu }_1$, $\mu \left(2\right):={\mu }_2$, $\sigma \left(1\right):={\sigma }_1$ and $\sigma \left(2\right):={\sigma }_2$ for some constants ${\mu }_i$ and ${\sigma }_i$, $i=1,2$. Without loss of generality, we will assume that ${\mu }_1\le {\mu }_2$, and ${\sigma }_1,{\sigma }_2>0$. That is to say, the regime for the small drift is named 1, and the volatilities are of course positive.

Applying Itô’s formula [15] (p. 149, Theorem 3.3), we deduce that

$$P^{i,p}\left(t\right)=pexp\left[{\int }_0^t\left(\mu \left(X^i\left(s\right)\right)-\frac{1}{2}\sigma {\left(X^i\left(s\right)\right)}^2\right)\mathrm{d}s+{\int }_0^t\sigma \left(X^i\left(s\right)\right)\mathrm{d}B\left(s\right)\right].$$

(2)

To answer the question of what time is optimal to stop the extraction, we will solve the following optimal problem:

$$J_i\left(p\right):=J(i,p):=\underset{\tau \in \mathcal{T}}{sup}\mathbb{E}\left[{\int }_0^{\tau }exp(-rt)(P^{i,p}\left(t\right)-C)\mathrm{d}t-exp(-r\tau )K\right],$$

(3)

where $\mathcal{T}$ is the collection of all stopping times with respect to ${\left\{{\mathcal{F}}_t\right\}}_{t\ge 0}$, $r>0$ is the discount rate, $C>0$ is the running cost rate, and K is the cost at which the firm stops the extraction. Problems like problem (3) are called optimal problems [16] (p. 96). Problem (3) is solved in Theorems 6, 7, and 8.

Regime-switching processes like (1) are plausible choices of modelling the price processes in many situations such as commodities [17] and financial assets [18,19]. Thus, it is a reasonable choice that we use process (1) to approximate the price of some natural resource.

Assuming the underlying process is governed by a regime-switching geometric Brownian motion, the authors of [20,21,22,23] solved some specific optimal stopping problems which do not involve integral parts by guessing a priori a strategy and then validated it by a verification argument.Under the same assumption, Pemy [24] used the viscosity solution technique to solve American options and selling rules. However, he did not discuss the regularity of the value function, and the forms of optimal stopping intervals are known in advance. Liu claimed in [25] (Theorem 2) that the value function is the unique viscosity solution to some variational inequalities. The research in [25] (Theorem 2) seems not to require any more conditions, but, if checking the proof carefully, we find a crucial condition $\beta >6K$ is needed, and this condition brings great inconvenience and is too restrictive in practice. In particular, the numerical example in [25] invalidates the condition $\beta >6K$. In the application part of [25], the variational inequality (4.3) in [25] is defined on $(0,+\infty )$, not on $\mathbb{R}$; however, the author did not impose boundary conditions. Also, in the application part, the author did not provide any reasons why the exercise time takes the form shown in the paper.

In this paper, we develop a complete general theory and then use it to solve problem (3). We discuss the effect of all the parameters on the optimal decision. It will be seen that an investor may never stop in some regimes; however, the investor should stop within a finite time horizon as an optimal choice if the investor considers all the possible regimes. The numerical Example 2 demonstrates this phenomenon visually.

We outline the structure of this paper. In Section 2, we examine the regularity of the value function (Theorem 3), optimal stopping strategies (Theorem 4), and forms of optimal stopping intervals (Theorem 5) in a general setting. In Section 3, we solve problem (3) using the results obtained in Section 2. Some conclusions are drawn in Section 4.

2. Preliminaries

We leave the specific problem (3) temporarily, but focus on a general case.

We allow the Markov chain $\left(X\right(t),t\ge 0)$ to take values in $I:=\{1,2,\cdots ,m\}$, which may start from any element of I at time $t=0$, whose rate matrix is $A:={\left(a_{ij}\right)}_{m\times m}$ with $a_{ii}<0$, for each $i=1,2,\cdots ,m$, and then generalize (1) to the equation

$$\mathrm{d}Y\left(t\right)=\alpha (X^i\left(t\right),Y\left(t\right))\mathrm{d}t+\beta (X^i\left(t\right),Y\left(t\right))\mathrm{d}B\left(t\right),Y\left(0\right)=y,$$

(4)

where $\alpha :I\times \mathbb{R}\to \mathbb{R}$ and $\beta :I\times \mathbb{R}\to \mathbb{R}$ are two functions such that $\alpha (i,·)$ and $\beta (i,·)$ are Lipschitz continuous for each $i=1,2,\cdots ,m$. We assume that $\beta (·,·)>0$.

Let $Y^{i,y}$ be the solution to Equation (4). In order to solve problem (3), we intend to solve the optimal stopping problem

$$\begin{array}{cc}\hfill V(i,y):=\underset{\tau \in \mathcal{T}}{sup}\mathbb{E}& [{\int }_0^{\tau }exp(-rt)f(X^i\left(t\right),Y^{i,y}\left(t\right))\mathrm{d}t\hfill \\ \hfill & +exp(-r\tau )g(X^i\left(\tau \right),Y^{i,y}\left(\tau \right))],\hfill \end{array}$$

(5)

where $f:I\times \mathbb{R}\to \mathbb{R}$ and $g:I\times \mathbb{R}\to \mathbb{R}$ are two functions such that $f(i,·)$ and $g(i,·)$ are Lipschitz continuous for each $i=1,2,\cdots ,m$. We use the convention $exp(-r\tau )g\left(X\right(\tau ),Y(\tau \left)\right)=0$ on $\{\tau =\infty \}$ since $r>0$ and $g(i,·)$ are Lipschitz continuous.

For each $i=1,2,\cdots ,m$, set ${\alpha }_i(·):=\alpha (i,·)$, ${\beta }_i(·):=\beta (i,·)$, $f_i(·):=f(i,·)$, $g_i(·):=g(i,·)$, and $V_i(·):=V(i,·)$.

We have Theorem 1 showing the viscosity solution property of V, and Theorem 2 telling us the uniqueness of viscosity solutions.

Theorem 1

([26] (Theorem 1)). If

(H1)

the functions $V_i$’s are continuous and grow at most linearly,

then for each fixed $i\in \{1,2,\cdots ,m\}$, $V_i$ is the unique viscosity solution with at most linear growth to the following variational inequality:

$$min\left\{r{V}_i-{\mathcal{L}}_i{V}_i-\sum _{q=1}^m{a}_{qi}{V}_q-f_i,V_i-g_i\right\}=0\mathrm{on}\mathbb{R},$$

(6)

where ${\mathcal{L}}_i$ is defined by ${\mathcal{L}}_i\xi \left(y\right):=\frac{1}{2}{\beta }_i{\left(y\right)}^2\frac{{\partial }^2\xi \left(y\right)}{\partial y^2}+{\alpha }_i\left(y\right)\frac{\partial \xi \left(y\right)}{\partial y}$ for any $\xi \in C^2\left(\mathbb{R}\right)$.

Theorem 2

([26] (Theorem 2)). Assume that

(H2)

there are positive numbers $b_i$’s such that ${\displaystyle \sum _{i=1}^m}{b}_i{h}_{ij}\left(\overline{\lambda }\right)\ge 0$ for some constant $\overline{\lambda }>1$, $j=1,2,\cdots ,m$. Here $h_{ij}\left(\lambda \right):=-a_{ij}$ for $i\ne j$, and $h_{ii}\left(\lambda \right):=r-a_{ii}-{\mu }_i\lambda -\frac{1}{2}{\sigma }_i^2\lambda (\lambda -1)$ with ${\mu }_i:=\underset{x\to \infty }{lim\; sup}\left|\frac{{\alpha }_i\left(x\right)}{x}\right|$ and ${\sigma }_i:=\underset{x\to \infty }{lim\; sup}\left|\frac{{\beta }_i\left(x\right)}{x}\right|$.

Let ${\left\{U_i\right\}}_{i=1}^m$ be a family of functions defined on $\mathbb{R}$ with at most linear growth such that for each fixed i, $U_i$ is a viscosity solution to

$$min\left\{r{U}_i-{\mathcal{L}}_i{U}_i-\sum _{q=1}^m{a}_{qi}{U}_q-f_i,U_i-g_i\right\}=0\mathrm{on}\mathbb{R}.$$

Let ${\left\{W_i\right\}}_{i=1}^m$ be another family of functions defined on $\mathbb{R}$ with the same properties as those of ${\left\{U_i\right\}}_{i=1}^m$. Then $U_i=W_i$ for $i=1,2,\cdots ,m$.

Let us introduce some notations as follows.

$${\mathcal{C}}_i:=\{y:V_i\left(y\right)>g_i\left(y\right)\},{\mathcal{S}}_i:=\{y:V_i\left(y\right)=g_i\left(y\right)\},$$

$${\mathcal{D}}_i:=\{y:r{g}_i\left(y\right)-{\mathcal{L}}_i{g}_i\left(y\right)-\sum _{q=1}^m{a}_{qi}{g}_q\left(y\right)-f_i\left(y\right)\ge 0\},$$

and

$${\widehat{V}}_i\left(y\right):=\mathbb{E}\left[{\int }_0^{\infty }exp(-rt)f(X^i\left(t\right),Y^{i,y}\left(t\right))\mathrm{d}t\right],$$

for each $i=1,2,\cdots ,m$.

We consider the regularity of V in the following theorem.

Theorem 3.

Assume that (H1) holds. Then the function $V_i$ is $C^2$ continuous on ${\mathcal{C}}_i$, $i=1,2,\cdots ,m$. If, furthermore, $g_i$ is $C^1$ continuous, then $V_i$ is $C^1$ continuous on $\partial {\mathcal{C}}_i$.

Proof. 

Fix an $i\in \{1,2,\cdots ,m\}$. By redefining the discount rate, payoff functions, and underlying process, the function $V_i$ is also the value function of a classical optimal stopping problem

$$\begin{array}{cc}\hfill \underset{\tau \in \mathcal{T}}{sup}\mathbb{E}& [{\int }_0^{\tau }exp(-(r-a_{ii})t)\left(f_i\left(Z^z\left(t\right)\right)+\sum _{q\ne i}{a}_{qi}{V}_q\left(Z^z\left(t\right)\right)\right)\mathrm{d}t\hfill \\ & +exp(-r\tau )g_i\left(Z^z\left(\tau \right)\right)],\hfill \end{array}$$

where $Z^z$ is the solution to $\mathrm{d}Z\left(t\right)={\alpha }_i\left(Z\left(t\right)\right)\mathrm{d}t+{\beta }_i\left(Z\left(t\right)\right)\mathrm{d}B\left(t\right)$ along with $Z\left(0\right)=z\in \mathbb{R}$, and (6) is also the variational inequality of this new optimal stopping problem. It follows from $\beta (·,·)>0$ that ${\mathcal{L}}_i$ is uniformly elliptic on any bounded closed domain of ${\mathcal{C}}_i$, $i=1,2,\cdots ,m$. Then, thanks to Theorem 1, we complete the proof by [16] (p. 100, Lemma 5.2.2 and Proposition 5.2.1). □

Theorem 4 provides an optimal stopping strategy for the problem (5).

Theorem 4.

Assume that (H1) holds. Then the stopping time ${\tau }^{*}:=inf\{t>0:(X\left(t\right),Y\left(t\right))\in {\displaystyle \bigcup _{i=1}^m}\left\{i\right\}\times {\mathcal{S}}_i\}$ is an optimal stopping time of the problem (5).

Proof. 

We refer to [16] (pp. 101–102) for the proof. □

Lemma 1 states some properties about ${\mathcal{S}}_i$’s and will be used to study the forms of ${\mathcal{S}}_i$’s in Theorem 5.

Lemma 1.

Assume that (H1) and (H2) hold. Then the following conclusions are true.

(a) 

If ${\displaystyle \bigcup _{i=1}^m}{\mathcal{S}}_i=\varnothing$, then ${\widehat{V}}_i\ge g_i$ for each $i=1,2,\cdots ,m$.

(b) 

If ${\widehat{V}}_i\ge g_i$ for each $i=1,2,\cdots ,m$, then $V_i={\widehat{V}}_i$.

(c) 

If $g_i$ is $C^2$ continuous for some $i\in \{1,2,\cdots ,m\}$, then ${\mathcal{S}}_i$ is included in ${\mathcal{D}}_i$.

Proof. 

By virtue of Theorem 2, (a) and (b) are proved in a similar way to that of [16] (p. 102, Lemma 5.2.3); for the proof of (c), we apply Theorem 2 and refer to [16] (p. 102, Lemma 5.2.4). □

Now we study the forms of ${\mathcal{S}}_i$’s. To do this, we make the following assumption.

(H1′)

The functions $V_i$’s are Lipschitz continuous. Then it is reasonable to set $V_i\left(0\right):=V_i\left(0^{+}\right)$.

(H3)

The process Y takes values in $(0,+\infty )$ and $|{\alpha }_i\left(y\right)|+|{\beta }_i\left(y\right)|\le C|y|$ for some constant C, $i=1,2,\cdots ,m$.

We will use the fact that the matrix $r{I}_{m\times m}-{\left(a_{ij}\right)}_{m\times m}$ is invertible. This follows from the fact that $r{I}_{m\times m}-{\left(a_{ij}\right)}_{m\times m}$ is a strictly diagonally dominant matrix, since $r>0$ and ${\displaystyle \sum _{i=1}^m}{a}_{ij}=0$ for all $j=1,2,\cdots ,m$. Let ${\left(b_{ij}\right)}_{m\times m}$ denote the inverse of $r{I}_{m\times m}-{\left(a_{ij}\right)}_{m\times m}$.

Lemma 2.

Assume that (H1′) and (H3) hold. Then

(a) 

If ${\displaystyle \sum _{q=1}^m}{b}_{qi}{f}_q\left(0\right)\ge g_i\left(0\right)$, $i=1,2,\cdots ,m$, then $V_i\left(0\right)={\displaystyle \sum _{q=1}^m}{b}_{qi}{f}_q\left(0\right)$.

(b) 

If $r{g}_i\left(0\right)-{\displaystyle \sum _{q=1}^m}{a}_{qi}{g}_q\left(0\right)-f_i\left(0\right)\ge 0$, $i=1,2,\cdots ,m$, then $V_i\left(0\right)=g_i\left(0\right)$.

Proof. 

By taking limits as $y\to 0^{+}$, Theorem 1 implies that $V_i\left(0\right)$ is a solution to

$$min\left\{r{V}_i\left(0\right)-\sum _{q=1}^m{a}_{qi}{V}_q\left(0\right)-f_i\left(0\right),V_i\left(0\right)-g_i\left(0\right)\right\}=0.$$

The conclusions follow from the above equations. □

Theorem 5.

Assume that (H1), (H2), and (H3) hold, ${\mathcal{S}}_i$’s are nonempty connected sets, and $g_i$’s are $C^2$ continuous. Then the following are true.

(a) 

If ${\mathcal{D}}_i=[a_i,+\infty )$ for some positive constant $a_i$, $i=1,2,\cdots ,m$, then ${\mathcal{S}}_i=[inf{\mathcal{S}}_i,+\infty )$.

(b) 

If $r{g}_i\left(0\right)-{\displaystyle \sum _{q=1}^m}{a}_{qi}{g}_q\left(0\right)-f_i\left(0\right)\ge 0$ and ${\mathcal{D}}_i=(0,b_i]$ for some positive constant $b_i$, $i=1,2,\cdots ,m$, then ${\mathcal{S}}_i=(0,sup{\mathcal{S}}_i]$.

Proof. 

Set $a_i^{*}:=inf{\mathcal{S}}_i$ in Case (a) and $b_i^{*}:=sup{\mathcal{S}}_i$ in Case (b). Then we define $A_i:=[a_i^{*},+\infty )$ in Case (a) and $A_i:=(0,b_i^{*}]$ in Case (b). We will prove ${\mathcal{S}}_i=A_i$.

Note the following facts:

-

$g_i$’s grow at most linearly;

-

$g_i\left(a_i^{*}\right)=V_i\left(a_i^{*}\right)$ or $g_i\left(b_i^{*}\right)=V_i\left(b_i^{*}\right)$ by the continuity of $g_i$ and $V_i$;

-

in light of Lemma 2, $g_i\left(0\right)=V_i\left(0\right)$ if $r{g}_i\left(0\right)-{\displaystyle \sum _{q=1}^m}{a}_{qi}{g}_q\left(0\right)-f_i\left(0\right)\ge 0$.

Moreover, thanks to $A_i\subset {\mathcal{D}}_i$ by Lemma 1, $g_i$ solves the inequality $r{g}_i-{\mathcal{L}}_i{g}_i-{\displaystyle \sum _{q=1}^m}{a}_{qi}{g}_q-f_i\ge 0$ on $A_i$. Thus, by Theorem 2, it follows that $g_i=V_i$ on $A_i$. The proof is complete. □

3. The Solution to Problem (3)

We apply the results obtained in Section 2 to solve problem (3).

Lemma 3

([22] (Lemma 1)). We have

$$\mathbb{E}\left[exp\left({\int }_0^t\mu \left(X^i\left(s\right)\right)\mathrm{d}s\right)\right]=\frac{x_2-{\mu }_i}{x_2-x_1}exp\left(x_{1}t\right)+\frac{{\mu }_i-x_1}{x_2-x_1}exp\left(x_{2}t\right),$$

where $x_1$ and $x_2$ are the solutions to the quadratic equation $x^2+({\lambda }_1-{\mu }_1+{\lambda }_2-{\mu }_2)x+({\lambda }_1-{\mu }_1)({\lambda }_2-{\mu }_2)-{\lambda }_1{\lambda }_2=0$ with $x_1<x_2$.

Remark 1.

If ${\mu }_1<{\mu }_2$, then $x_1<{\mu }_1<x_2<{\mu }_2$; if ${\mu }_1={\mu }_2$, then $x_1={\mu }_1-{\lambda }_1-{\lambda }_2$ and $x_2={\mu }_1$.

Theorem 6.

Assume $r\le x_2$. Then the optimal stopping time ${\tau }^{*}$ is given by ${\tau }^{*}=+\infty$ a.s., and the function $J_i$ in (3) is given by $J_i\left(p\right)=+\infty$, $i=1,2$.

Proof. 

By (2) and (3), we have, for fixed $T>0$,

$$\begin{array}{cc}\hfill J_i\left(p\right)\ge & p{\int }_0^T\mathbb{E}\left[exp(-rt)exp\left({\int }_0^t\mu \left(X^i\left(s\right)\right)-\frac{1}{2}\sigma {\left(X^i\left(s\right)\right)}^2\mathrm{d}s\right.\right.\hfill \\ & \left.\left.+{\int }_0^t\sigma \left(X^i\left(s\right)\right)\mathrm{d}B\left(s\right)\right)\right]\mathrm{d}t\hfill \\ & -r^{-1}(1-exp(-rT))C-exp(-rT)K.\hfill \end{array}$$

Note that

$$\left(exp\left({\int }_0^t\sigma \left(X^i\left(s\right)\right)\mathrm{d}B\left(s\right)-\frac{1}{2}{\int }_0^t\sigma {\left(X^i\left(s\right)\right)}^2\mathrm{d}s)\right),t\ge 0\right)$$

is a martingale. Then in light of the independence of X and B, we obtain

$$\begin{array}{cc}\hfill J_i\left(p\right)& \ge p{\int }_0^{T}exp(-rt)\mathbb{E}\left[exp\left({\int }_0^t\mu \left(X^i\left(s\right)\right)\right)\mathrm{d}s\right]\mathrm{d}t\hfill \\ & -r^{-1}(1-exp(-rT))C-exp(-rT)K\hfill \\ & =p\left(\frac{x_2-{\mu }_i}{x_2-x_1}{\int }_0^{T}exp\left((x_1-r)t\right)\mathrm{d}t+\frac{{\mu }_i-x_1}{x_2-x_1}{\int }_0^{T}exp\left((x_2-r)t\right)\mathrm{d}t\right)\hfill \\ & -r^{-1}(1-exp(-rT))C-exp(-rT)K,\hfill \end{array}$$

where we have used Lemma 3.

Sending $T\to +\infty$ in the above inequality, we obtain $J_i\left(p\right)=+\infty$ since $r\le x_2$. □

Corollary 1.

If $r\le {\mu }_1$, then the conclusions in Theorem 6 hold.

Proof. 

The proof can be completed by the fact that $r\le {\mu }_1$ implies $r\le x_2$. □

Example 1.

Take ${\mu }_1=0.02$, ${\mu }_2=0.20$, ${\sigma }_1=0.1$, ${\sigma }_2=0.05$, $r=0.05$, ${\lambda }_1=0.2$, ${\lambda }_2=0.5$. Then we have $r=0.05<0.0819=x_2$. Thus, we apply Theorem 6, and find that the firm should never stop the extraction.

In the following discussion, we consider the case $r>x_2$.

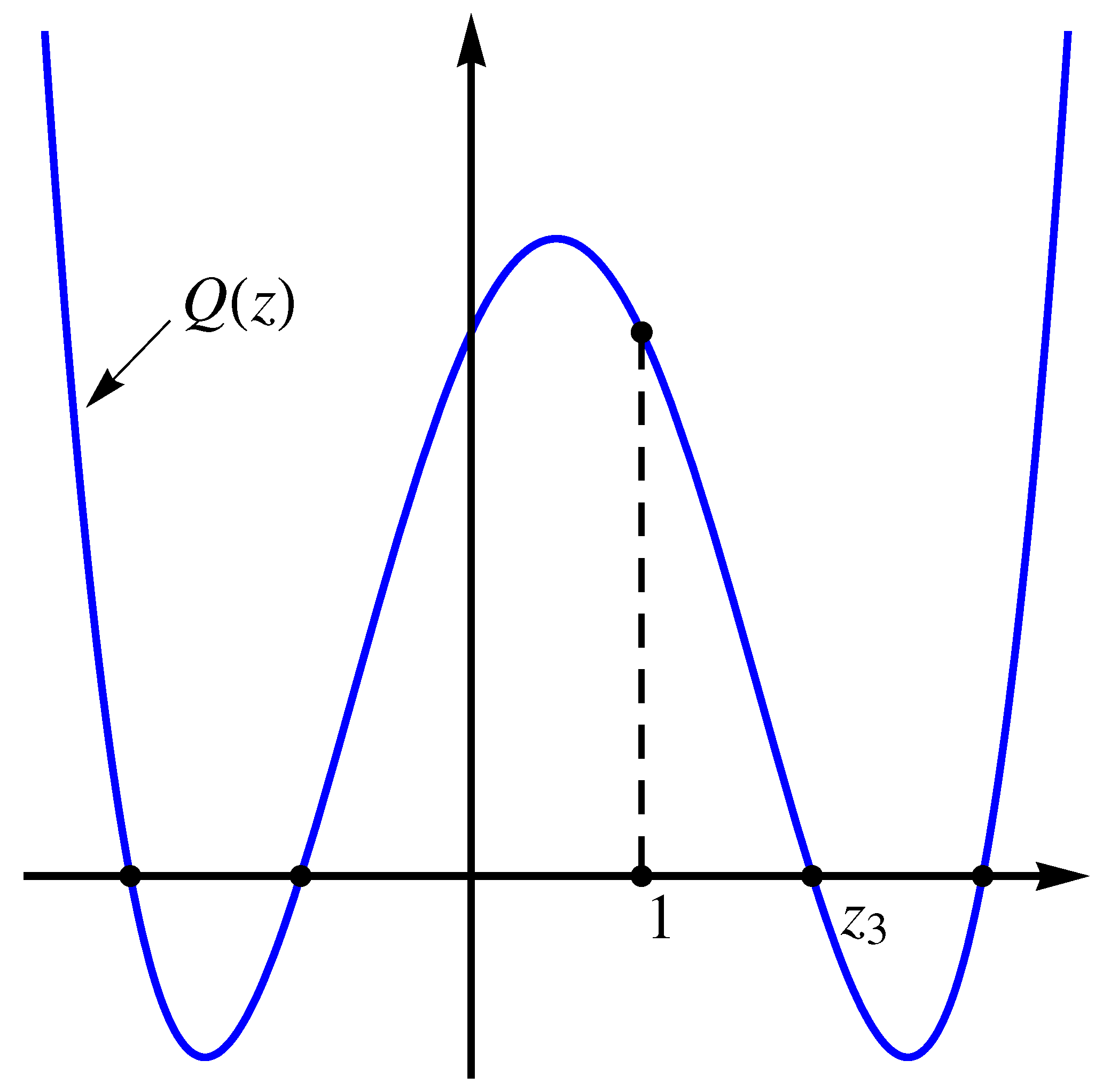
Lemma 4.

(a) Remark 2.1 [20] The following equation $w_1\left(z\right)w_2\left(z\right)-{\lambda }_1{\lambda }_2=0$, where $w_i\left(z\right):=r+{\lambda }_i-{\mu }_{i}z-\frac{{\sigma }_i^2}{2}z(z-1)$, has four distinct solutions $z_i$’s satisfying $z_1<z_2<0<z_3<z_4$ with $w_1\left(z_3\right)>0$.

(b) Assume that $r>x_2$. Then $z_3>1$ and there are positive constants $b_i$’s fulfilling $b_1{w}_1\left(z_3\right)-{\lambda }_1{b}_2=0$ and $b_2{w}_2\left(z_3\right)-{\lambda }_2{b}_1=0$. See Figure 1.

Proof. 

1. Set $Q\left(z\right):=w_1\left(z\right)w_2\left(z\right)-{\lambda }_1{\lambda }_2$. Note that the equation $w_1\left(z\right)=0$ has two solutions, say, $z^1$ and $z^2$ with $z^1<z^2$. Then $Q\left(z^i\right)<0$, where $i=1,2$. In addition, we have $Q\left(0\right)>0$ and $\underset{z\to \infty }{lim}Q\left(z\right)=+\infty$. Therefore, by the intermediate value theorem, it follows that the equation $w_1\left(z\right)w_2\left(z\right)-{\lambda }_1{\lambda }_2=0$ has four distinct solutions $z_i$’s satisfying $z_1<z_2<0<z_3<z_4$. Furthermore, $w_1\left(z_3\right)>0$, since $z^1<z_3<z^2$.

2. Since $r>x_2$, we have

$$r^2+({\lambda }_1-{\mu }_1+{\lambda }_2-{\mu }_2)r+({\lambda }_1-{\mu }_1)({\lambda }_2-{\mu }_2)-{\lambda }_1{\lambda }_2>0$$

(7)

and

$$2r+{\lambda }_1-{\mu }_1+{\lambda }_2-{\mu }_2>0.$$

(8)

Then it follows from (7) that $Q\left(1\right)>0$ and $(r+{\lambda }_1-{\mu }_1)(r+{\lambda }_2-{\mu }_2)>0$. Combining (8) and $(r+{\lambda }_1-{\mu }_1)(r+{\lambda }_2-{\mu }_2)>0$, we have $r+{\lambda }_1-{\mu }_1>0$ and $r+{\lambda }_2-{\mu }_2>0$.

3. In this step, we prove $z_3>1$.

Case 1 ${\mu }_i+{\sigma }_i^2/2>0$, where $i=1,2$. In this case, we have

$$Q^{\prime }\left(1\right)=-(r+{\lambda }_1-{\mu }_1)({\mu }_2+{\sigma }_2^2/2)-(r+{\lambda }_2-{\mu }_2)({\mu }_1+{\sigma }_1^2/2)<0.$$

This and $Q\left(1\right)>0$ imply $z_3>1$.

Case 2 ${\mu }_i+{\sigma }_i^2/2<0$, where $i=1,2$. In this case, we have

$$Q^{‴}\left(1\right)=3{\sigma }_1^2{\sigma }_2^2+3({\sigma }_1^2{\mu }_2+{\sigma }_2^2{\mu }_1)<0.$$

This and $Q\left(1\right)>0$ imply $z_3>1$.

Case 3 $({\mu }_1+{\sigma }_1^2/2)({\mu }_2+{\sigma }_2^2/2)\le 0$. In this case, we have

$$Q^{″}\left(1\right)=-{\sigma }_1^2(r+{\lambda }_2-{\mu }_2)+2({\mu }_1+\frac{{\sigma }_1^2}{2})({\mu }_2+\frac{{\sigma }_2^2}{2})-{\sigma }_1^2(r+{\lambda }_2-{\mu }_2)<0.$$

This and $Q\left(1\right)>0$ imply $z_3>1$.

4. Take $b_1=1$ and $b_2=w_1\left(z_3\right)/{\lambda }_1$. Then we have $b_1{w}_1\left(z_3\right)-{\lambda }_1{b}_2=0$ and $b_2{w}_2\left(z_3\right)-{\lambda }_2{b}_1=0$. □

Lemma 5.

Assume that $r>x_2$. Then $J_i$ is a Lipschitz continuous function, $i=1,2$. In addition, ${\mathcal{S}}_i:=\{p:p\in (0,+\infty )\mathrm{and}{J}_i\left(p\right)=-K\}$ is connected, $i=1,2$.

Proof. 

1. By (2) and (3), we have

$$\begin{array}{cc}& |J_i\left(p_1\right)-J_i\left(p_2\right)|\hfill \\ & \le |p_1-p_2|{\int }_0^{+\infty }\mathbb{E}\left[exp(-rt)exp\left({\int }_0^t\mu \left(X^i\left(s\right)\right)-\frac{1}{2}\sigma {\left(X^i\left(s\right)\right)}^2\mathrm{d}s\right.\right.\hfill \\ & \left.\left.+{\int }_0^t\sigma \left(X^i\left(s\right)\right)\mathrm{d}B\left(s\right)\right)\right]\mathrm{d}t.\hfill \end{array}$$

Note that

$$\left(exp\left({\int }_0^t\sigma \left(X^i\left(s\right)\right)\mathrm{d}B\left(s\right)-\frac{1}{2}{\int }_0^t\sigma {\left(X^i\left(s\right)\right)}^2\mathrm{d}s)\right),t\ge 0\right)$$

is a martingale. Then in light of the independence of X and B, we obtain

$$\begin{array}{cc}& |J_i\left(p_1\right)-J_i\left(p_2\right)|\hfill \\ & \le |p_1-p_2|{\int }_0^{+\infty }exp(-rt)\mathbb{E}\left[exp\left({\int }_0^t\mu \left(X^i\left(s\right)\right)\right)\mathrm{d}s\right]\mathrm{d}t\hfill \\ & =\frac{1}{x_2-x_1}·\left(\frac{x_2-{\mu }_i}{r-x_1}+\frac{{\mu }_i-x_1}{r-x_2}\right)|p_1-p_2|,\hfill \end{array}$$

where we have used Lemma 3 and $r>x_2$ for the equality.

2. We prove that ${\mathcal{S}}_i:=\{p:p\in (0,+\infty )\mathrm{and}{J}_i\left(p\right)=-K\}$ is connected by contradiction. Suppose that $a,b\in {\mathcal{S}}_i$ but there is a point $c\in (a,b)$ with $c\notin {\mathcal{S}}_i$ (i.e., $J_i\left(c\right)>-K$).

Noting that $J_i$ is convex, we have

$$J_i\left(c\right)\le \frac{b-c}{b-a}{J}_i\left(a\right)+\frac{c-a}{b-a}{J}_i\left(b\right)=-K,$$

which contradicts $J_i\left(c\right)>-K$. □

Lemma 6.

Assume $r>x_2$. Then $\{J_1,J_2\}$ is the unique solution with at most linear growth of the following variational inequalities:

$$\left\{\begin{array}{cc}& min\{(r+{\lambda }_1)J_1\left(p\right)-{\mu }_{1}p{J}_1^{\prime }\left(p\right)-\frac{1}{2}{\sigma }_1^2{p}^2{J}_1^{″}\left(p\right)\hfill \\ & -{\lambda }_1{J}_2\left(p\right)-p+C,J_1\left(p\right)+K\}=0\hfill \\ & min\{(r+{\lambda }_2)J_2\left(p\right)-{\mu }_{2}p{J}_2^{\prime }\left(p\right)-\frac{1}{2}{\sigma }_2^2{p}^2{J}_2^{″}\left(p\right)\hfill \\ & -{\lambda }_2{J}_1\left(p\right)-p+C,J_2\left(p\right)+K\}=0\hfill \end{array}\right.$$

with boundary condition $J_i\left(0\right)=-min\{C/r,K\}$, $i=1,2$, on $(0,+\infty )$ in the viscosity sense.

Proof. 

The boundary condition $J_i\left(0\right)=-min\{C/r,K\}$, $i=1,2$, can be obtained by (2) and (3). In fact,

$$\begin{array}{cc}\hfill J_i\left(0\right)& =\underset{\tau \in \mathcal{T}}{sup}\mathbb{E}\left[{\int }_0^{\tau }exp(-rt)(-C)\mathrm{d}t-exp(-r\tau )K\right]\hfill \\ & =-\frac{C}{r}+\underset{\tau \in \mathcal{T}}{sup}\mathbb{E}\left[exp(-r\tau )\left(\frac{C}{r}-K\right)\right]=-min\left\{\frac{C}{r},K\right\}.\hfill \end{array}$$

Then, by Lemmas 4 and 5, the result is a straight corollary of Theorem 2. □

Theorem 7.

Assume that $r>x_2$ and $C\le rK$. Then the optimal stopping time ${\tau }^{*}$ is given by ${\tau }^{*}=+\infty$ a.s.; furthermore, the functions $J_i$’s are given by

$$J_1\left(p\right)=k_{2}p-r^{-1}C,J_2\left(p\right)=k_{1}p-r^{-1}C,$$

where

$$k_i=\frac{r+{\lambda }_1+{\lambda }_2-{\mu }_i}{(r+{\lambda }_1-{\mu }_1)(r+{\lambda }_2-{\mu }_2)-{\lambda }_1{\lambda }_2},i=1,2.$$

Proof. 

Note that, for $i=1,2$, ${\mathcal{S}}_i\subset \{p:0<p\le C-rK\}$ by Lemma 1. Thus, we have ${\mathcal{S}}_i=\varnothing$.

Therefore, it follows from Lemma 6 that

$$J_1\left(p\right)=\frac{(r+{\lambda }_1+{\lambda }_2-{\mu }_2)p}{(r+{\lambda }_1-{\mu }_1)(r+{\lambda }_2-{\mu }_2)-{\lambda }_1{\lambda }_2}-\frac{C}{r}$$

and

$$J_2\left(p\right)=\frac{(r+{\lambda }_1+{\lambda }_2-{\mu }_1)p}{(r+{\lambda }_1-{\mu }_1)(r+{\lambda }_2-{\mu }_2)-{\lambda }_1{\lambda }_2}-\frac{C}{r}.$$

The proof is complete. □

Corollary 2.

If $r>{\mu }_2$ and $C\le rK$, then the conclusions in Theorem 7 hold.

Proof. 

The proof can be completed by the fact that $r>{\mu }_2$ implies $r>x_2$. □

Recall that $z_1$ and $z_2$ are the solutions to $w_1\left(z\right)w_2\left(z\right)-{\lambda }_1{\lambda }_2=0$ with $z_1<z_2<0$ (see Lemma 4).

Theorem 8.

Assume that $r>x_2$ and $C>rK$. Then one and only one of the following holds.

(a) The equation

$$\left[\begin{array}{cc}{p_1}^{-y_1}& 0\\ 0& {p_1}^{-y_2}\end{array}\right]\left[\begin{array}{c}{a}_{11}{p}_1+b_{11}\\ a_{21}{p}_1+b_{21}\end{array}\right]=\left[\begin{array}{cc}{p_2}^{-y_1}& 0\\ 0& {p_2}^{-y_2}\end{array}\right]\left[\begin{array}{c}{a}_{12}{p}_2+b_{12}\\ a_{22}{p}_2+b_{22}\end{array}\right]$$

has a solution $\{p_1^{*},p_2^{*}\}$ with $p_1^{*}<p_2^{*}$, where $y_1$ and $y_2$ are the two solutions to the quadratic equation $r+{\lambda }_1-{\mu }_{1}y-\frac{1}{2}{\sigma }_1^{2}y(y-1)=0$ with $y_1<y_2$,

$$\left[\begin{array}{c}{a}_{11}\\ a_{21}\end{array}\right]={\left[\begin{array}{cc}1& 1\\ y_1& y_2\end{array}\right]}^{-1}\left[\begin{array}{c}\frac{-1}{r+{\lambda }_1-{\mu }_1}\\ \frac{-1}{r+{\lambda }_1-{\mu }_1}\end{array}\right],\left[\begin{array}{c}{b}_{11}\\ b_{12}\end{array}\right]={\left[\begin{array}{cc}1& 1\\ y_1& y_2\end{array}\right]}^{-1}\left[\begin{array}{c}\frac{C-rK}{r+{\lambda }_1}\\ 0\end{array}\right],$$

$$\begin{array}{cc}\hfill \left[\begin{array}{c}{a}_{12}\\ a_{22}\end{array}\right]=& {\left[\begin{array}{cc}1& 1\\ y_1& y_2\end{array}\right]}^{-1}\left(\left[\begin{array}{c}{k}_2-\frac{1}{r+{\lambda }_1-{\mu }_1}\\ k_2-\frac{1}{r+{\lambda }_1-{\mu }_1}\end{array}\right]\right.\hfill \\ & -{\lambda }_1\left.\left[\begin{array}{cc}1& 1\\ z_1& z_2\end{array}\right]{\left[\begin{array}{cc}{w}_1\left(z_1\right)& w_1\left(z_2\right)\\ w_1\left(z_1\right)z_1& w_1\left(z_2\right)z_2\end{array}\right]}^{-1}\left[\begin{array}{c}{k}_1\\ k_1\end{array}\right]\right),\hfill \end{array}$$

and

$$\begin{array}{cc}\hfill \left[\begin{array}{c}{b}_{12}\\ b_{22}\end{array}\right]=& {\left[\begin{array}{cc}1& 1\\ y_1& y_2\end{array}\right]}^{-1}\left(\left[\begin{array}{c}\frac{{\lambda }_{1}K+C}{r+{\lambda }_1}-\frac{C}{r}\\ 0\end{array}\right]\right.\hfill \\ & +{\lambda }_1\left.\left[\begin{array}{cc}1& 1\\ z_1& z_2\end{array}\right]{\left[\begin{array}{cc}{w}_1\left(z_1\right)& w_1\left(z_2\right)\\ w_1\left(z_1\right)z_1& w_1\left(z_2\right)z_2\end{array}\right]}^{-1}\left[\begin{array}{c}\frac{C-rK}{r}\\ 0\end{array}\right]\right).\hfill \end{array}$$

In addition, the optimal stopping time ${\tau }^{*}$ is given by

$${\tau }^{*}=inf\{t:t>0,(X\left(t\right),P\left(t\right))\in \left\{1\right\}\times (0,p_1^{*}]\cup \left\{2\right\}\times (0,p_2^{*}]\},$$

and the $J_i$’s are given by

$$J_1\left(p\right)=\left\{\begin{array}{cc}-K\hfill & \mathrm{on}(0,p_1^{*}]\hfill \\ {\displaystyle \frac{p}{r+{\lambda }_1-{\mu }_1}}-{\displaystyle \frac{{\lambda }_{1}K+C}{r+{\lambda }_1}}+A_1{p}^{y_1}+A_2{p}^{y_2}\hfill & \mathrm{on}(p_1^{*},p_2^{*}]\hfill \\ k_{2}p-r^{-1}C+B_1{p}^{z_1}+B_2{p}^{z_2}\hfill & \mathrm{on}(p_2^{*},+\infty )\hfill \end{array}\right.$$

and

$$J_2\left(p\right)=\left\{\begin{array}{cc}-K\hfill & \mathrm{on}(0,p_2^{*}]\hfill \\ k_{1}p-r^{-1}C+{\lambda }_1^{-1}{w}_1\left(z_1\right)B_1{p}^{z_1}+{\lambda }_1^{-1}{w}_1\left(z_2\right)B_2{p}^{z_2}\hfill & \mathrm{on}(p_2^{*},+\infty ),\hfill \end{array}\right.$$

respectively. Here

$$\left[\begin{array}{c}{A}_1\\ A_2\end{array}\right]=\left[\begin{array}{cc}{p_1^{*}}^{-y_1}& 0\\ 0& {p_1^{*}}^{-y_2}\end{array}\right]\left[\begin{array}{c}{a}_{11}{p}_1^{*}+b_{11}\\ a_{21}{p}_1^{*}+b_{21}\end{array}\right],$$

$$\left[\begin{array}{c}{B}_1\\ B_2\end{array}\right]={\lambda }_1\left[\begin{array}{cc}{p_2^{*}}^{-z_1}& 0\\ 0& {p_2^{*}}^{-z_2}\end{array}\right]{\left[\begin{array}{cc}{w}_1\left(z_1\right)& w_1\left(z_2\right)\\ w_1\left(z_1\right)z_1& w_1\left(z_2\right)z_2\end{array}\right]}^{-1}\left[\begin{array}{c}-k_1{p}_2^{*}+\frac{C-rK}{r}\\ -k_1{p}_2^{*}\end{array}\right].$$

(b) The equation

$$\left[\begin{array}{cc}{p_2}^{-{\overline{y}}_1}& 0\\ 0& {p_2}^{-{\overline{y}}_2}\end{array}\right]\left[\begin{array}{c}{\overline{a}}_{11}{p}_2+{\overline{b}}_{11}\\ {\overline{a}}_{21}{p}_2+{\overline{b}}_{21}\end{array}\right]=\left[\begin{array}{cc}{p_1}^{-{\overline{y}}_1}& 0\\ 0& {p_1}^{-{\overline{y}}_2}\end{array}\right]\left[\begin{array}{c}{\overline{a}}_{12}{p}_1+{\overline{b}}_{12}\\ {\overline{a}}_{22}{p}_1+{\overline{b}}_{22}\end{array}\right]$$

has a solution $\{{\overline{p}}_1^{*},{\overline{p}}_2^{*}\}$ with ${\overline{p}}_1^{*}>{\overline{p}}_2^{*}$, where ${\overline{y}}_1$ and ${\overline{y}}_2$ are the two solutions to the quadratic equation $r+{\lambda }_2-{\mu }_{2}y-\frac{1}{2}{\sigma }_2^{2}y(y-1)=0$ with ${\overline{y}}_1<{\overline{y}}_2$,

$$\left[\begin{array}{c}{\overline{a}}_{11}\\ {\overline{a}}_{21}\end{array}\right]={\left[\begin{array}{cc}1& 1\\ {\overline{y}}_1& {\overline{y}}_2\end{array}\right]}^{-1}\left[\begin{array}{c}\frac{-1}{r+{\lambda }_2-{\mu }_2}\\ \frac{-1}{r+{\lambda }_2-{\mu }_2}\end{array}\right],\left[\begin{array}{c}{\overline{b}}_{11}\\ {\overline{b}}_{12}\end{array}\right]={\left[\begin{array}{cc}1& 1\\ {\overline{y}}_1& {\overline{y}}_2\end{array}\right]}^{-1}\left[\begin{array}{c}\frac{C-rK}{r+{\lambda }_2}\\ 0\end{array}\right],$$

$$\begin{array}{cc}\hfill \left[\begin{array}{c}{\overline{a}}_{12}\\ {\overline{a}}_{22}\end{array}\right]=& {\left[\begin{array}{cc}1& 1\\ {\overline{y}}_1& {\overline{y}}_2\end{array}\right]}^{-1}\left(\left[\begin{array}{c}{k}_1-\frac{1}{r+{\lambda }_2-{\mu }_2}\\ k_1-\frac{1}{r+{\lambda }_2-{\mu }_2}\end{array}\right]\right.\hfill \\ & -{\lambda }_2\left.\left[\begin{array}{cc}1& 1\\ z_1& z_2\end{array}\right]{\left[\begin{array}{cc}{w}_2\left(z_1\right)& w_2\left(z_2\right)\\ w_2\left(z_1\right)z_1& w_2\left(z_2\right)z_2\end{array}\right]}^{-1}\left[\begin{array}{c}{k}_2\\ k_2\end{array}\right]\right),\hfill \end{array}$$

and

$$\begin{array}{cc}\hfill \left[\begin{array}{c}{\overline{b}}_{12}\\ {\overline{b}}_{22}\end{array}\right]=& {\left[\begin{array}{cc}1& 1\\ {\overline{y}}_1& {\overline{y}}_2\end{array}\right]}^{-1}\left(\left[\begin{array}{c}\frac{{\lambda }_{2}K+C}{r+{\lambda }_2}-\frac{C}{r}\\ 0\end{array}\right]\right.\hfill \\ & +{\lambda }_2\left.\left[\begin{array}{cc}1& 1\\ z_1& z_2\end{array}\right]{\left[\begin{array}{cc}{w}_2\left(z_1\right)& w_2\left(z_2\right)\\ w_2\left(z_1\right)z_1& w_2\left(z_2\right)z_2\end{array}\right]}^{-1}\left[\begin{array}{c}\frac{C-rK}{r}\\ 0\end{array}\right]\right).\hfill \end{array}$$

In addition, the optimal stopping time ${\tau }^{*}$ is given by

$${\tau }^{*}=inf\{t:t>0,(X\left(t\right),P\left(t\right))\in \left\{1\right\}\times (0,{\overline{p}}_1^{*}]\cup \left\{2\right\}\times (0,{\overline{p}}_2^{*}]\},$$

and the $J_i$’s are given by

$$J_1\left(p\right)=\left\{\begin{array}{cc}-K\hfill & \mathrm{on}(0,{\overline{p}}_1^{*}]\hfill \\ k_{2}p-r^{-1}C+{\lambda }_2^{-1}{w}_2\left(z_1\right){\overline{B}}_1{p}^{z_1}+{\lambda }_2^{-1}{w}_2\left(z_2\right){\overline{B}}_2{p}^{z_2}\hfill & \mathrm{on}({\overline{p}}_1^{*},+\infty )\hfill \end{array}\right.$$

and

$$J_2\left(p\right)=\left\{\begin{array}{cc}-K\hfill & \mathrm{on}(0,{\overline{p}}_2^{*}]\hfill \\ {\displaystyle \frac{p}{r+{\lambda }_2-{\mu }_2}}-{\displaystyle \frac{{\lambda }_{2}K+C}{r+{\lambda }_2}}+{\overline{A}}_1{p}^{{\overline{y}}_1}+{\overline{A}}_2{p}^{{\overline{y}}_2}\hfill & \mathrm{on}({\overline{p}}_2^{*},{\overline{p}}_1^{*}]\hfill \\ k_{1}p-r^{-1}C+{\overline{B}}_1{p}^{z_1}+{\overline{B}}_2{p}^{z_2}\hfill & \mathrm{on}({\overline{p}}_1^{*},+\infty )\hfill \end{array}\right.,$$

respectively. Here

$$\left[\begin{array}{c}{\overline{A}}_1\\ {\overline{A}}_2\end{array}\right]=\left[\begin{array}{cc}{{\overline{p}}_2^{*}}^{-y_1}& 0\\ 0& {{\overline{p}}_2^{*}}^{-y_2}\end{array}\right]\left[\begin{array}{c}{\overline{a}}_{11}{\overline{p}}_1^{*}+{\overline{b}}_{11}\\ {\overline{a}}_{21}{\overline{p}}_1^{*}+{\overline{b}}_{21}\end{array}\right],$$

$$\left[\begin{array}{c}{\overline{B}}_1\\ {\overline{B}}_2\end{array}\right]={\lambda }_2\left[\begin{array}{cc}{{\overline{p}}_1^{*}}^{-z_1}& 0\\ 0& {{\overline{p}}_1^{*}}^{-z_2}\end{array}\right]{\left[\begin{array}{cc}{w}_2\left(z_1\right)& w_2\left(z_2\right)\\ w_2\left(z_1\right)z_1& w_2\left(z_2\right)z_2\end{array}\right]}^{-1}\left[\begin{array}{c}-k_2{\overline{p}}_1^{*}+\frac{C-rK}{r}\\ -k_2{\overline{p}}_1^{*}\end{array}\right].$$

(c) The equation

$$\left[\begin{array}{c}{\tilde{a}}_{11}p+{\tilde{b}}_{11}\\ {\tilde{a}}_{21}p+{\tilde{b}}_{21}\end{array}\right]=\left[\begin{array}{c}{\tilde{a}}_{12}p+{\tilde{b}}_{12}\\ {\tilde{a}}_{22}p+{\tilde{b}}_{22}\end{array}\right]$$

has a positive solution $p^{*}$, where

$$\left[\begin{array}{c}{\tilde{a}}_{11}\\ {\tilde{a}}_{12}\end{array}\right]={\left[\begin{array}{cc}1& 1\\ z_1& z_2\end{array}\right]}^{-1}\left[\begin{array}{c}-k_2\\ -k_2\end{array}\right],\left[\begin{array}{c}{\tilde{b}}_{11}\\ {\tilde{b}}_{12}\end{array}\right]={\left[\begin{array}{cc}1& 1\\ z_1& z_2\end{array}\right]}^{-1}\left[\begin{array}{c}\frac{C-rK}{r}\\ 0\end{array}\right],$$

$$\left[\begin{array}{c}{\tilde{a}}_{12}\\ {\tilde{a}}_{22}\end{array}\right]={\lambda }_1{\left[\begin{array}{cc}{w}_1\left(z_1\right)& w_1\left(z_2\right)\\ w_1\left(z_1\right)z_1& w_1\left(z_2\right)z_2\end{array}\right]}^{-1}\left[\begin{array}{c}-k_1\\ -k_1\end{array}\right],$$

and

$$\left[\begin{array}{c}{\tilde{b}}_{12}\\ {\tilde{b}}_{22}\end{array}\right]={\lambda }_1{\left[\begin{array}{cc}{w}_1\left(z_1\right)& w_1\left(z_2\right)\\ w_1\left(z_1\right)z_1& w_1\left(z_2\right)z_2\end{array}\right]}^{-1}\left[\begin{array}{c}\frac{C-rK}{r}\\ 0\end{array}\right].$$

In addition, the optimal stopping time ${\tau }^{*}$ is given by

$${\tau }^{*}=inf\{t:t>0,P\left(t\right)\in (0,p^{*}]\},$$

and the $J_i$’s are given by

$$J_1\left(p\right)=\left\{\begin{array}{cc}-K\hfill & \mathrm{on}(0,p^{*}]\hfill \\ k_{2}p-r^{-1}C+{\tilde{B}}_1{p}^{z_1}+{\tilde{B}}_2{p}^{z_2}\hfill & \mathrm{on}(p^{*},+\infty )\hfill \end{array}\right.$$

and

$$J_2\left(p\right)=\left\{\begin{array}{cc}-K\hfill & \mathrm{on}(0,p^{*}]\hfill \\ k_{1}p-r^{-1}C+{\lambda }_1^{-1}{w}_1\left(z_1\right){\tilde{B}}_1{p}^{z_1}+{\lambda }_1^{-1}{w}_1\left(z_2\right){\tilde{B}}_2{p}^{z_2}\hfill & \mathrm{on}(p^{*},+\infty ),\hfill \end{array}\right.$$

respectively. Here

$$\left[\begin{array}{c}{\tilde{B}}_1\\ {\tilde{B}}_2\end{array}\right]=\left[\begin{array}{cc}{p^{*}}^{-z_1}& 0\\ 0& {p^{*}}^{-z_2}\end{array}\right]\left[\begin{array}{c}{\tilde{a}}_{11}{p}^{*}+{\tilde{b}}_{11}\\ {\tilde{a}}_{21}{p}^{*}+{\tilde{b}}_{21}\end{array}\right].$$

Proof. 

1. If ${\mathcal{S}}_i=\varnothing$, we have

$$\begin{array}{cc}\hfill J_i\left(p\right):=\mathbb{E}& \left[{\int }_0^{+\infty }exp(-rt)(P^{i,p}\left(t\right)-C)\mathrm{d}t\right].\hfill \end{array}$$

In particular, $J_i\left(0\right)=-C/r$, but Lemma 6 tells us that $J_i\left(0\right)=-K$ because of $C>rK$. This contradiction leads to ${\mathcal{S}}_i\ne \varnothing$. In addition, the condition $r{g}_i\left(0\right)-{\displaystyle \sum _{q=1}^m}{a}_{qi}{g}_q\left(0\right)-f_i\left(0\right)\ge 0$ in Theorem 5 is equivalent to $C\ge rK$, and we have ${\mathcal{D}}_i=(0,C-rK]$. Therefore, by Theorem 5 and Lemma 5, it follows that ${\mathcal{S}}_i=(0,p_i^{*}]$ for some positive number $p_i^{*}$.

2. Case 1 $p_1^{*}<p_2^{*}$. In this case, by Lemma 6, we have

$$\left\{\begin{array}{c}{J}_1\left(p\right)=-K\hfill \\ J_2\left(p\right)=-K\hfill \end{array}\right.$$

on $(0,p_1^{*}]$,

$$\left\{\begin{array}{c}(r+{\lambda }_1)J_1\left(p\right)-{\mu }_{1}p{J}_1^{\prime }\left(p\right)-\frac{1}{2}{\sigma }_1^2{p}^2{J}_1^{″}\left(p\right)-{\lambda }_1{J}_2\left(p\right)-p+C=0\hfill \\ J_2\left(p\right)=-K\hfill \end{array}\right.$$

(9)

on $(p_1^{*},p_2^{*}]$, and

$$\left\{\begin{array}{c}(r+{\lambda }_1)J_1\left(p\right)-{\mu }_{1}p{J}_1^{\prime }\left(p\right)-\frac{1}{2}{\sigma }_1^2{p}^2{J}_1^{″}\left(p\right)-{\lambda }_1{J}_2\left(p\right)-p+C=0\hfill \\ (r+{\lambda }_2)J_2\left(p\right)-{\mu }_{2}p{J}_2^{\prime }\left(p\right)-\frac{1}{2}{\sigma }_2^2{p}^2{J}_2^{″}\left(p\right)-{\lambda }_2{J}_1\left(p\right)-p+C=0\hfill \end{array}\right.$$

(10)

on $(p_2^{*},+\infty )$.

Note that $r+{\lambda }_1-{\mu }_1>0$ by Step 2 of the proof of Lemma 4. We have by (9)

$$J_1\left(p\right)=\frac{p}{r+{\lambda }_1-{\mu }_1}-\frac{{\lambda }_{1}K+C}{r+{\lambda }_1}+A_1{p}^{y_1}+A_2{p}^{y_2}\mathrm{on}(p_1^{*},p_2^{*}],$$

where $A_1$ and $A_2$ are two constants, and $y_1$ and $y_2$ are the two solutions to the quadratic equation $r+{\lambda }_1-{\mu }_{1}y-\frac{1}{2}{\sigma }_1^{2}y(y-1)=0$ with $y_1<y_2$.

Since $J_1$ and $J_2$ are Lipschitz continuous, we have by (10)

$$\left\{\begin{array}{c}{J}_1\left(p\right)=\frac{(r+{\lambda }_1+{\lambda }_2-{\mu }_2)p}{(r+{\lambda }_1-{\mu }_1)(r+{\lambda }_2-{\mu }_2)-{\lambda }_1{\lambda }_2}-\frac{C}{r}+B_1{p}^{z_1}+B_2{p}^{z_2}\hfill \\ J_2\left(p\right)=\frac{(r+{\lambda }_1+{\lambda }_2-{\mu }_1)p}{(r+{\lambda }_1-{\mu }_1)(r+{\lambda }_2-{\mu }_2)-{\lambda }_1{\lambda }_2}-\frac{C}{r}+{\lambda }_1^{-1}{w}_1\left(z_1\right)B_1{p}^{z_1}\hfill \\ +{\lambda }_1^{-1}{w}_1\left(z_2\right)B_2{p}^{z_2}\hfill \end{array}\right.$$

on $(p_2^{*},+\infty )$, where $B_1$ and $B_2$ are some constants, and $z_1$ and $z_2$ are the solutions introduced in Lemma 4.

Therefore, by $C^1$ continuity of $J_1$ and $J_2$, we have

$$\left\{\begin{array}{c}\frac{p_1^{*}}{r+{\lambda }_1-{\mu }_1}-{\displaystyle \frac{{\lambda }_{1}K+C}{r+{\lambda }_1}}+A_1{p_1^{*}}^{y_1}+A_2{p_1^{*}}^{y_2}=-K\hfill \\ \frac{1}{r+{\lambda }_1-{\mu }_1}+A_1{y}_1{p_1^{*}}^{y_1-1}+A_2{y}_2{p_1^{*}}^{y_2-1}=0,\hfill \end{array}\right.$$

(11)

$$\left\{\begin{array}{c}\frac{p_2^{*}}{r+{\lambda }_1-{\mu }_1}-\frac{{\lambda }_{1}K+C}{r+{\lambda }_1}+A_1{p_2^{*}}^{y_1}+A_2{p_2^{*}}^{y_2}\hfill \\ =\frac{(r+{\lambda }_1+{\lambda }_2-{\mu }_2)p_2^{*}}{(r+{\lambda }_1-{\mu }_1)(r+{\lambda }_2-{\mu }_2)-{\lambda }_1{\lambda }_2}-\frac{C}{r}+B_1{p_2^{*}}^{z_1}+B_2{p_2^{*}}^{z_2}\hfill \\ \frac{1}{r+{\lambda }_1-{\mu }_1}+A_1{y}_1{p_2^{*}}^{y_1-1}+A_2{y}_2{p_2^{*}}^{y_2-1}\hfill \\ =\frac{r+{\lambda }_1+{\lambda }_2-{\mu }_2}{(r+{\lambda }_1-{\mu }_1)(r+{\lambda }_2-{\mu }_2)-{\lambda }_1{\lambda }_2}+B_1{z}_1{p_2^{*}}^{z_1-1}+B_2{z}_2{p_2^{*}}^{z_2-1},\hfill \end{array}\right.$$

(12)

and

$$\left\{\begin{array}{c}\frac{(r+{\lambda }_1+{\lambda }_2-{\mu }_1)p_2^{*}}{(r+{\lambda }_1-{\mu }_1)(r+{\lambda }_2-{\mu }_2)-{\lambda }_1{\lambda }_2}-\frac{C}{r}\hfill \\ +{\lambda }_1^{-1}{w}_1\left(z_1\right)B_1{p_2^{*}}^{z_1}+{\lambda }_1^{-1}{w}_1\left(z_2\right)B_2{p_2^{*}}^{z_2}=-K\hfill \\ \frac{r+{\lambda }_1+{\lambda }_2-{\mu }_1}{(r+{\lambda }_1-{\mu }_1)(r+{\lambda }_2-{\mu }_2)-{\lambda }_1{\lambda }_2}\hfill \\ +{\lambda }_1^{-1}{w}_1\left(z_1\right)B_1{z}_1{p_2^{*}}^{z_1-1}+{\lambda }_1^{-1}{w}_1\left(z_2\right)B_2{z}_2{p_2^{*}}^{z_2-1}=0.\hfill \end{array}\right.$$

(13)

By solving $A_1$ and $A_2$ from (11) and solving $A_1$ and $A_2$ from (12) and (13), we obtain

$$\left[\begin{array}{cc}{p_1^{*}}^{-y_1}& 0\\ 0& {p_1^{*}}^{-y_2}\end{array}\right]\left[\begin{array}{c}{a}_{11}{p}_1^{*}+b_{11}\\ a_{21}{p}_1^{*}+b_{21}\end{array}\right]=\left[\begin{array}{cc}{p_2^{*}}^{-y_1}& 0\\ 0& {p_2^{*}}^{-y_2}\end{array}\right]\left[\begin{array}{c}{a}_{12}{p}_2^{*}+b_{12}\\ a_{22}{p}_2^{*}+b_{22}\end{array}\right].$$

Case 2 $p_1^{*}>p_2^{*}$. This case is similar to Case 1.

Case 3 $p_1^{*}=p_2^{*}=:p^{*}$. By Lemma 6, we have

$$\left\{\begin{array}{c}{J}_1\left(p\right)=-K\hfill \\ J_2\left(p\right)=-K\hfill \end{array}\right.$$

on $(0,p^{*}]$, and

$$\left\{\begin{array}{c}(r+{\lambda }_1)J_1\left(p\right)-{\mu }_{1}p{J}_1^{\prime }\left(p\right)-\frac{1}{2}{\sigma }_1^2{p}^2{J}_1^{″}\left(p\right)-{\lambda }_1{J}_2\left(p\right)-p+C=0\hfill \\ (r+{\lambda }_2)J_2\left(p\right)-{\mu }_{2}p{J}_2^{\prime }\left(p\right)-\frac{1}{2}{\sigma }_2^2{p}^2{J}_2^{″}\left(p\right)-{\lambda }_2{J}_1\left(p\right)-p+C=0\hfill \end{array}\right.$$

(14)

on $(p^{*},+\infty )$.

Since $J_1$ and $J_2$ are Lipschitz continuous, we have by (14)

$$\left\{\begin{array}{c}{J}_1\left(p\right)=\frac{(r+{\lambda }_1+{\lambda }_2-{\mu }_2)p}{(r+{\lambda }_1-{\mu }_1)(r+{\lambda }_2-{\mu }_2)-{\lambda }_1{\lambda }_2}-\frac{C}{r}+{\tilde{B}}_1{p}^{z_1}+{\tilde{B}}_2{p}^{z_2}\hfill \\ J_2\left(p\right)=\frac{(r+{\lambda }_1+{\lambda }_2-{\mu }_1)p}{(r+{\lambda }_1-{\mu }_1)(r+{\lambda }_2-{\mu }_2)-{\lambda }_1{\lambda }_2}-\frac{C}{r}\hfill \\ +{\lambda }_1^{-1}{w}_1\left(z_1\right){\tilde{B}}_1{p}^{z_1}+{\lambda }_1^{-1}{w}_1\left(z_2\right){\tilde{B}}_2{p}^{z_2}\hfill \end{array}\right.$$

on $(p^{*},+\infty )$, where ${\tilde{B}}_1$ and ${\tilde{B}}_2$ are some constants, and $z_1$ and $z_2$ are the solutions introduced in Lemma 4.

Therefore, by $C^1$ continuity of $J_1$ and $J_2$, we have

$$\left\{\begin{array}{c}\frac{(r+{\lambda }_1+{\lambda }_2-{\mu }_2)p^{*}}{(r+{\lambda }_1-{\mu }_1)(r+{\lambda }_2-{\mu }_2)-{\lambda }_1{\lambda }_2}-\frac{C}{r}+{\tilde{B}}_1{p^{*}}^{z_1}+{\tilde{B}}_2{p^{*}}^{z_2}=-K\hfill \\ \frac{r+{\lambda }_1+{\lambda }_2-{\mu }_2}{(r+{\lambda }_1-{\mu }_1)(r+{\lambda }_2-{\mu }_2)-{\lambda }_1{\lambda }_2}+{\tilde{B}}_1{z}_1{p^{*}}^{z_1-1}+{\tilde{B}}_2{z}_2{p^{*}}^{z_2-1}=0,\hfill \end{array}\right.$$

(15)

and

$$\left\{\begin{array}{c}\frac{(r+{\lambda }_1+{\lambda }_2-{\mu }_1)p^{*}}{(r+{\lambda }_1-{\mu }_1)(r+{\lambda }_2-{\mu }_2)-{\lambda }_1{\lambda }_2}-{\displaystyle \frac{C}{r}}\hfill \\ +{\lambda }_1^{-1}{w}_1\left(z_1\right){\tilde{B}}_1{p^{*}}^{z_1}+{\lambda }_1^{-1}{w}_1\left(z_2\right){\tilde{B}}_2{p^{*}}^{z_2}=-K\hfill \\ \frac{r+{\lambda }_1+{\lambda }_2-{\mu }_1}{(r+{\lambda }_1-{\mu }_1)(r+{\lambda }_2-{\mu }_2)-{\lambda }_1{\lambda }_2}+\hfill \\ {\lambda }_1^{-1}{w}_1\left(z_1\right){\tilde{B}}_1{z}_1{p^{*}}^{z_1-1}+{\lambda }_1^{-1}{w}_1\left(z_2\right){\tilde{B}}_2{z}_2{p^{*}}^{z_2-1}=0.\hfill \end{array}\right.$$

(16)

By solving ${\tilde{B}}_1$ and ${\tilde{B}}_2$ from (15) and solving ${\tilde{B}}_1$ and ${\tilde{B}}_2$ from (16), we obtain

$$\left[\begin{array}{c}{\tilde{a}}_{11}{p}^{*}+{\tilde{b}}_{11}\\ {\tilde{a}}_{21}{p}^{*}+{\tilde{b}}_{21}\end{array}\right]=\left[\begin{array}{c}{\tilde{a}}_{12}{p}^{*}+{\tilde{b}}_{12}\\ {\tilde{a}}_{22}{p}^{*}+{\tilde{b}}_{22}\end{array}\right].$$

The proof is complete. □

Corollary 3.

If $r>{\mu }_2$ and $C>rK$, then the conclusions in Theorem 8 hold.

Proof. 

The proof can be completed by the fact that $r>{\mu }_2$ implies $r>x_2$. □

Example 2.

Take ${\mu }_1=0.01$, ${\mu }_2=0.10$, ${\sigma }_1=0.5$, ${\sigma }_2=1$, $r=0.08$, ${\lambda }_1=0.2$, ${\lambda }_2=1$, $C=20$, $K=5$. Then we have $r=0.08>0.0260=x_2$ and $C=20>0.40=rK$. Thus, we apply Theorem 8, and find that (a) of Theorem 8 gives us $(p_1^{*},p_2^{*})=(10.97,245.19)$ and the optimal stopping time ${\tau }^{*}=inf\{t:t>0,(X\left(t\right),P\left(t\right))\in \left\{1\right\}\times (0,10.97]\cup \left\{2\right\}\times (0,245.19]\}$.

It is interesting to compare regime-switching cases with no-regime-switching cases. If there is no regime switching and the price P satisfies $\mathrm{d}P\left(t\right)=0.01P\left(t\right)\mathrm{d}t+0.5P\left(t\right)\mathrm{d}B\left(t\right)$, the optimal stopping time is $inf\{t:t>0,P(t)\in (0,10.35\left]\right\}$ [27] (Theorem 4.5). However, if the price P satisfies $\mathrm{d}P\left(t\right)=0.10P\left(t\right)\mathrm{d}t+P\left(t\right)\mathrm{d}B\left(t\right)$, the firm should never stop the extraction since $r=0.08<0.10={\mu }_2$ [28] (Theorem 5.1).

In summary, the firm may stop the extraction even though it should never stop the extraction in one of the regimes.

Figure 2 shows a realization with initial data $X\left(0\right)=1$ and $P\left(0\right)=200$. In the first interval where $X\left(t\right)=1$, there are several times at which $P\left(t\right)\le p_2^{*}$; however, the firm still should not stop the extraction, because it is now regime 1, and in this regime, the firm stops only when $P\left(t\right)\le p_1^{*}$.

4. Conclusions

Regime-switching processes refer to the prices of financial assets and commodities [17,29,30]. In the present paper, we introduce a regime-switching process to describe the price of some natural resource. We provide a model concerning the extraction of natural resources, and determine the optimal decision on ending the extraction.

We employ the viscosity solution technique to solve the model. To this end, based on [26] (Theorems 1 and 2), we first develop a complete theory consisting of the regularity of the value function, optimal stopping strategies, and forms of optimal stopping intervals, and then use it to determine the optimal decision on ending the extraction.

At the end of the paper, a numerical example is demonstrated. From the example, we come to a conclusion that a firm may stop a project even though it should never stop the project in one of the regimes.

When using our model to solve an actual problem, we should first estimate the parameters involved in the model. We may consult [31,32] about how to estimate the parameters. To obtain closed-form solutions, we assume that there are just two regimes. If abandoning closed-form solutions, we may allow many regimes and obtain numerical solutions by computer. In the present paper, we only consider the optimal exit time; however, this is the first step to solving the so called entry–exit problem. The general theory obtained in our paper can be applied to not only this problem, but also other optimal stopping problems with regime switching.