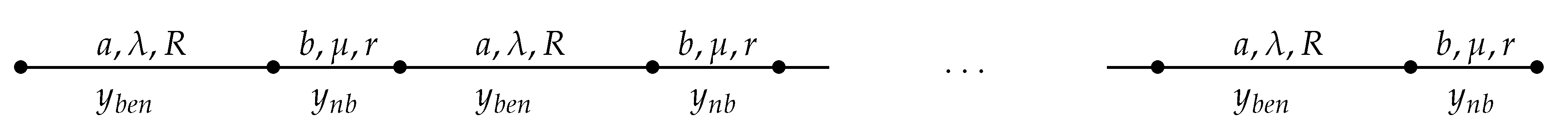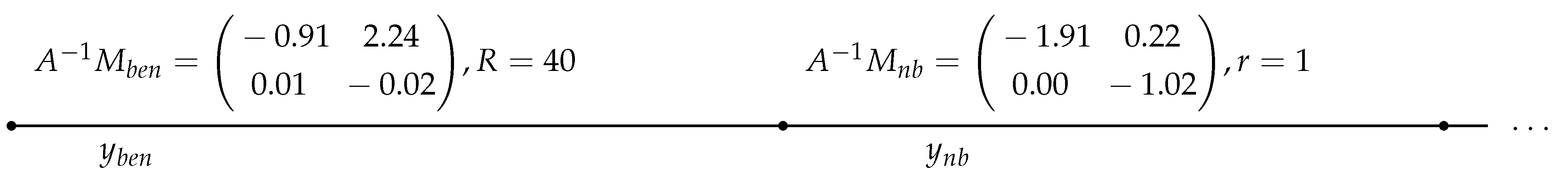2.1. Warm-Up: One-Stage Modeling
In this paper, we address the following question: can one place some barriers, organized by some control zones that are not beneficially for the multiplication of ticks, which would practically stop their propagation beyond these control zones?
Since we are talking about spatial propagation, our model must be necessarily spatially nontrivial. Therefore, we shall apply a diffusion model. As was mentioned above, a diffusion model was developed by Caraco et al. [
14]. Unlike the model of this paper, our model here will be simpler, in the sense that we will stick to linear modeling (unlike the reaction-diffusion setting of [
14]), but, on the other hand, it will include additional complication of being spatially heterogeneous, and precisely the effective control of these heterogeneities will be the main objective.
Remark 1. By not including in the model the quadratic (logistic type) terms of the standard nonlinear model, we are not including the competition between species, thus allowing ticks to multiply and propagate under better conditions than for nonlinear models. Consequently, if we manage to achieve the decay of their propagation in our linear case (what we are doing here), then the same decay will hold as well for the corresponding models with additional nonlinear terms limiting their growth. Moreover, since we are effectively giving stability criteria for the vanishing solution of a linear equation in a strong asymptotic sense (all eigenvalues have negative real part), adding additional quadratic terms can neither spoil this stability, nor improve it. The latter means that if there exists a mode with a positive eigenvalue of the linear part, then the vanishing solution will not be stable even in the presence of quadratic terms. This justifies the use of the linear model for our purposes in general term. Finally, the competition in ticks is performed mostly via available spaces on the bodies of hosts, so that the quadratic term in the equations for the dynamics of ticks is proportional to (see [1]), with the number of ticks V, the number of hosts N, and the maximum number M of ticks per host. Therefore, when hosts are in abundance, as compared to the basic equilibrium concentration of ticks (for instance, this occurs in many areas of Siberian taiga, see [28,37]), quadratic terms can be considered as overall negligible as compared to linear terms. In order to not overcomplicate the story, we will not distinguish between infected and noninfected ticks, aiming at their total eradication (at least locally) and we shall not include explicitly the dynamics of hosts (mice, deer, etc.), their overall influence being reflected just by specifying certain average speed of motion of ticks, which will be effectively modeled as the diffusion coefficient. Moreover, though the natural state space for the dynamics of ticks is two-dimensional, we shall stick here to a one-dimensional modeling having in mind the propagation in a certain direction, with the second coordinate averaged out.
The ticks are known to have several stages in their development (larvae, nymphs, adult). To better explain our ideas, we shall first consider the model, where all generations are averaged out, and next describe the modifications arising when several distinct generations are explicitly included in the model.
Thus, we start with the simplest diffusion model for the dynamic of ticks in some area of their habitat (we denote the derivatives with respect to time and space by a dot and a prime, respectively):
Here
is a diffusion coefficient reflecting the average speed of their random wandering and the coefficient
reflects the speed of their multiplication (usually represented as the difference of average birth rates and average mortality). The density
on some interval
evolves according to (
1) subject to additional boundary conditions, which can be taken as the Dirichlet conditions (
), or as the Neumann conditions (
) (or more general mixing Robin conditions that we shall not touch here), or rather periodic conditions (
,
).
Remark 2. The Dirichlet conditions arise in the situation, when ticks cannot survive at the boundary, which can be given, for instance, as a water reservoir, or as a temperature barrier. The Neumann conditions arise in the situation with reflecting barrier, such as a natural or artificial hedge. In other words, this is the situation, when no flux of matter crosses the border of the system either from outside or from inside. Periodic conditions do not seem to have a natural interpretation, but they are often convenient for the analysis (and therefore are abundantly used in physics), and can be also used as an intermediate step. In particular, the Dirichlet conditions are clearly the most disastrous for ticks, and therefore, if one can prove the dying out of ticks for periodic conditions, then the same will hold for the Dirichlet conditions. It is also intuitively clear (and again widely used in physics) that for large intervals the difference in boundary conditions does not affect the solutions in any essential way.
The main point in our modeling is the possibility to attach to the main region
(the background or the beneficial zone) a control zone of (much smaller length)
r, which is not beneficial for ticks, meaning that their reproduction coefficient becomes negative there. One may also be able to control the diffusion coefficient shifting it to a different value
b. Thus, instead of a homogeneous model (
1) we consider a model with two distinctive regions:
where positive
are our control parameters. Here
stands for the background beneficial region for ticks, which is not under our control, and
stands for the small non-beneficial region, where we are supposed to have control over at least some parameters. To make the problem well posed we should add, as above, some boundary conditions for
and
and moreover, the standard gluing conditions for diffusions with discontinuous coefficients (see, e.g., [
38]):
Let the operator
L be defined on the functions of the interval
by the formula
It is a standard fact from the theory of diffusion operators that, restricted to the functions satisfying the gluing condition (
3) and either Dirichlet, or Neumann or periodic conditions, the operator
L becomes self-adjoint with a discrete spectrum in the Hilbert space of the square integrable functions
on
. Moreover, this operator is bounded from above, so that there exist a decreasing sequence of eigenvalues
and the corresponding orthonormal basis
in
(depending on the chosen boundary conditions) such that
for all
j. This implies that for any initial function
from
the solution to (
2) with this initial condition is given by the convergent series
Consequently, if all are negative, i.e., the operator L is negative, then this solution tends to zero for any initial conditions. Thus, the condition of eventual eradication of ticks in our model is the condition of negativity of L, or equivalently, the condition of the absence of nonnegative eigenvalues. In the rare case of vanishing maximal eigenvalues, the solution converges to a finite limit as .
Theorem 1. Assume the Dirichlet boundary conditions. (i) IfL has a positive eigenvalue (independently of !). (ii) Ifthe operator L is negative if and only if L has no nonnegative eigenvalues (and is negative in the case of the strict inequality).
Statement (i) is the well-known (initial) result of the KISS model yielding the critical patch size
see [
21,
22]. Statement (ii) was proved for the limit
in [
22].
Evidently, for the Neumann and periodic boundary condition the situation is different. There is no critical size, as the population can survive on any small interval. However, as the following results show, by introducing appropriate control zones, one can eradicate the population in a similar way to the above.
Theorem 2. Assume the Neumann boundary conditions. (i) IfL has a positive eigenvalue (independently of !). (ii) Otherwise, L is negative if and only ifso that one can achieve negativity by choosing appropriate μ and r. Theorem 3. Assume the periodic boundary conditions. (i) If (5) holds, then L has a positive eigenvalue. (ii) Otherwise, L is negative if and only if One sees that Theorem 3 provides the same condition as Theorem 2 though with
and
instead of
R and
r. On the other hand, the boundary KISS value of (
5) is the same for the Dirichlet and the periodic conditions. Moreover, one can check explicitly from conditions (
8) and (
6) that, as expected (see Remark 2), if the operator
L is negative under the periodic condition, then it is also negative under the Dirichlet conditions.
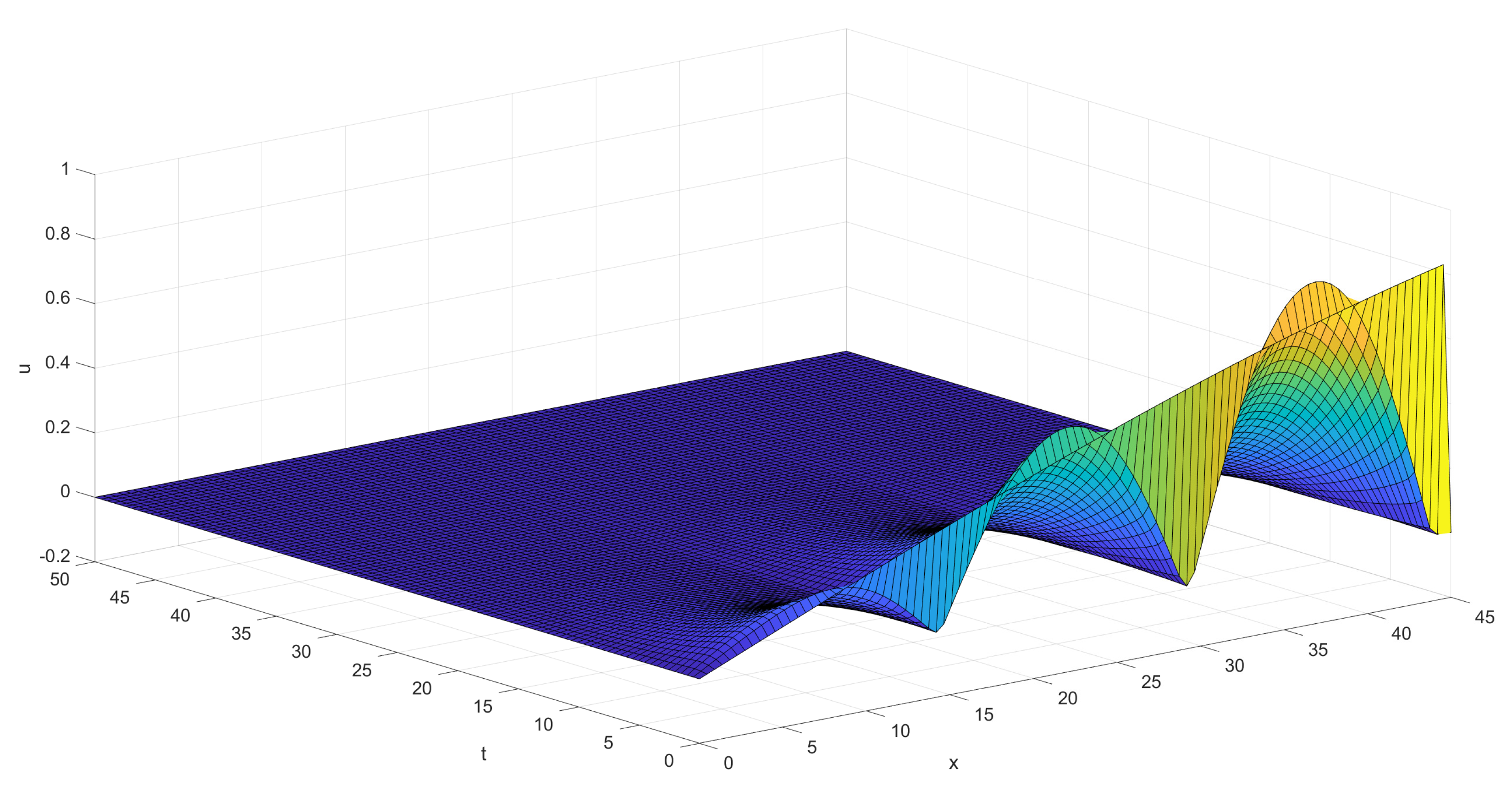
Theorems 1 and 3 provide exact information on how can be tuned in order to achieve negativity of L and hence the eventual eradication of ticks. We see, in particular, that if R does not exceed certain critical level, one can eradicate the ticks by introducing a control zone of arbitrary small length r, if a sufficiently high level of mortality can be imposed on this control zone.
On the other hand, the theorems show that if is large enough, then no control zone can efficiently influence the global growth of the tick population. This observation leads to a natural idea that, in the case of a large territory, one can fight with the growth of ticks by arranging several small control zones placed in a periodic (patched) fashion. As we are going to show, if this is organized in a way that each pair of adjacent zones satisfies the conditions of the previous theorem, the ticks will be eradicated in the whole patched territory.
Thus, assume that our territory of habitat is represented as the interval
, with some natural
K, and that it is decomposed into
subintervals, odd
,
, ⋯,
, so that
for
, and even
, so that
for
. Assume that on the long odd intervals we have some background parameters
, and on the short even intervals we have some (controllable) parameters
, so that the diffusion is given by the first and second equations of (
4) on even and odd intervals, respectively; see
Figure 1.
Evidently, the gluing conditions (
3) are supposed to hold on the interface of all intervals. Theorem 3 (valid for the case
) can now be extended to the case of arbitrary
K as follows.
Theorem 4. Assume the periodic boundary conditions for such diffusion on . Then for any K the conditions of Theorem 3 provide also the conditions for the corresponding diffusion operator L on to be negative or not.
Remark 3. As we already mentioned, if all positive solutions for the periodic conditions tend to zero, as , then the same holds for the Dirichlet conditions. It is intuitively clear, as the Dirichlet conditions are less beneficial for survival. Formally it follows from the representations of solutions in terms of the Feynmann–Kac formula.
2.2. Several-Stage Modeling: Trivial Case
Until now, we have considered the situation with all stages of ticks’ lives averaged out. In more precise modeling, one has to take into account the presence of several stages. For ticks these are eggs, larvae, nymphs, and adults. With some reasonable averaging one can reduce the consideration of the lifespan of ticks to the two basic periods, from eggs to nymphs, and from nymphs to hatching female adults. On the other hand, a more detail analysis, can include not only the stages, but their time developments. Namely, say, nymphs can develop to adults in the same season as their own molting takes place, or after a diapause (wintering), so one can distinguish not only the stage, but also whether it develops in one year or two years.
Let us consider the general case of
n stages (could be also generations for other species). The basic Equation (
1) is generalized to the vector-valued equation
where
and
M is the birth-and-death matrix showing the progression of ticks from their birth through their various stages of development. This matrix
has the standard form (used by many authors, see, e.g., [
12] or [
16]) reflecting the sequential propagation through various stages. They have elements
with all other elements vanishing, where all parameters
and
are positive.
For instance, for dimensions 2 and 3, these matrixes have the form
It is easy to see that a matrix
M of type (
10) always has a real eigenvalue.
Let us assume now that we can set a control zone with the increased death rates for ticks. Namely, let us consider the extension of Equation (
2) of the form
where
is the unit matrix. Notice that
here has a slightly different meaning as in (
2), referring to the relative decrease in the death rates. The corresponding diffusion operator becomes matrix-valued:
It turns out that the results of Theorems 1–4 have a straightforward extension to this case with the role of played by the largest eigenvalue of M.
Theorem 5. Assume that the maximal real eigenvalue of the matrix M in (12) is positive (if all eigenvalues of M have negative real parts, then the population would die out even in the background territory, the case of no interest to us) and all other eigenvalues have negative real part and are different (the latter conditions are technical simplifications that are not essential). Assume also that (otherwise the ticks could survive even in the control zone alone). Assume the Dirichlet boundary conditions for L. (i) IfL has a positive eigenvalue. (ii) Ifthe operator L is negative if and only if (iii) IfL has no nonnegative eigenvalues (and is negative in the case of the strict inequality). Assume now that the territory of habitat is represented by the interval
(with some natural
K), decomposed into
subintervals in the same way as formulated before Theorem 4, and that on the odd and even intervals our diffusion follows the first and the second equation of (
12), respectively, with the usual gluing condition on the interfaces.
Theorem 6. Let the conditions of Theorem 5 for M hold and K be arbitrary. Assume that the periodic boundary conditions are chosen. (i) If (13) holds, then L has a positive eigenvalue. (ii) Otherwise the operator L is negative if and only if 2.3. Several-Stage Modeling: Advanced Case
This section contains our main theoretical results.
Until now, we have looked at the case when diffusion coefficients differ in beneficial and control zones, but are independent of the stage. Evidently, usual averaging allows one to apply this model for ticks. However, for many types of ticks, larvae and nymphs use small rodents as hosts, while adult ticks use large mammals, such as deer, or birds, so that the displacement, and hence the diffusion coefficient differs drastically for the adults and the earlier stages of ticks. Hence it is more natural to use the model with different diffusions on different stages. Moreover, the matrixes
M specifying the birth and death rates, can be of course quite different for the background and control zones, thus differing not only by a multiple of the unit matrix, as in (
12).
Let us start with a simple extension of the KISS model. Namely, let us consider the extension of Equation (
9) with variable diffusion, i.e., the equation
where
A is a diagonal matrix with diagonal elements
,
.
Theorem 7. Let M be a matrix of type (10). Suppose that the maximal eigenvalue of the matrix is strictly positive. Then the critical patch size equals . That is, there exists a nontrivial solution to the equation with the Dirichlet boundary conditions and with some positive E if and only if . The story becomes more complicated when we put together the original and a control zones. It seems difficult to expect here explicit necessary and sufficient conditions for the negativity of the spectrum, such as in the cases analyzed above. However, reasonable sufficient conditions can be obtained, as we are going to show now.
Let us consider the system
with symmetric positive matrixes
,
and arbitrary matrixes
,
, where matrixes
,
are supposed to depend on some control parameters. We assume the periodic boundary conditions and the usual gluing conditions (
,
) on the interface.
Equations for the eigenvalues are
Theorem 8. Assume exactly k out of n eigenvalues of the symmetric matrix are positive, and all eigenvalues of the symmetric matrix are negative (by T we denote the transposition). Ifandthen system (20) has no solutions with non-negative E (and periodic boundary conditions). This result extends automatically to the case of the territory represented by the interval
, with some natural
K, which is decomposed into
subintervals in the same way as formulated before Theorem 4 (see also Theorem 6), so that on the odd and even intervals the diffusion follows the first and the second equation of (
19).
Notice that the l.h.s. of (
22) increases as
as in our previous results, but the r.h.s. is of order
(for
R far away from
), unlike
in Theorem 3.
In Theorem 7, the condition of the existence of a positive eigenvalue is given in terms of the maximal eigenvalue
of the matrix
and in Theorem 8 a sufficient condition for negativity is linked with the maximal eigenvalue of the corresponding symmetrized matrix. Hence from the combination of these two theorems nothing can be said for sizes
R such that
In order to work with these sizes, the effective method of symmetrization used in Theorem 8 cannot be applied, and the analysis in arbitrary dimension seems to be quite involved. Working in dimension , where explicit formulas for eigenvectors allow for a rather detailed analysis, possible results seem to depend strongly on the structure of diffusion coefficients and the matrix M. We present one such result valid for a range of coefficients that can be applied to tick populations.
Let us look at the equations
and the corresponding eigenvalue problem
with the usual gluing condition:
coincides with
and
coincides with
on the interface of two regions.
Let . For a , denote by the eigenvalues of the matrix , and by the eigenvalues of the matrix . Let and be such that . Assume that and for all . Let and be the corresponding bases of eigenvectors of and , and be the matrix that takes the basis to the basis .
Theorem 9. Assume the bases of eigenvectors can be chosen in such a way thatfor . Then, ifthere are no solutions to Equation (25) with periodic boundary conditions and non-negative E. Comparing (
27) with (
8) we see that under (
26) our two-dimensional condition of negativity is the exact extension of the one-dimensional case.
Remark 4. The technically convenient assumptions (26) (and especially the first of these two) are not very natural and should not hold in a general situation. However, as we show below, they can be achieved by an appropriate proportional change of the elements of the birth-and-death matrix. Let us now look at a concrete situation when (
26) holds. Namely, consider the system (
24) where
, the matrix
A is diagonal with the diagonal elements
has the form
from (
11) and
has the same form with
and
instead of
and
. Thus
Assume that we can control the non-beneficial zone by a proportional decrease of the reproduction coefficients, i.e., calibrating
by choosing an appropriate parameter
and choosing
in such a way that
For real ticks, is usually much less than (see numeric examples below). Hence the assumptions of the next theorem are fully relevant.
Theorem 10. Assume that (this enures that ) andAssume that and satisfy (28) and (29). Then the conditions of Theorem 9 (namely, inequalities (26)) hold, so that (27) is sufficient for the absence of nonnegative eigenvalues.