Smart Production System with Random Imperfect Process, Partial Backordering, and Deterioration in an Inflationary Environment
Abstract
1. Introduction
2. Literature Review
2.1. Inventory Models with Carbon Emissions
2.2. Inventory Models with Backlogging
2.3. Inventory Models with Random Imperfect Production Rate
2.4. Inventory Models with Inflation
2.5. Research Gap and Research Contributions
- To make goodwill in the market, screening items is necessary before satisfying the demand of customers. An attempt is made to develop a smart production system by considering that the screening process is performed with the help of an automated machine system.
- Due to the production process, due to storage, and other different operational activities, carbon emission is unavoidable. To make the model environment sustainable, carbon emissions due to different activities associated with manufacturing systems have been considered.
- Further, obtaining the goal of sustainability is achieved with help of reworking and proper waste management.
- The benefits of a flexible manufacturing system are explored by considering the production rate-dependent production cost.
- The fluctuating nature of the market is absorbed into the model by considering inflation.
- The model is analyzed under the effect of partial backlogging.
3. Assumptions, Notation, and Problem Description
3.1. Assumptions
- Nowadays, production systems have gradually shifted from manual to the machine. Thus, in the current study, we consider a smart production system with an automated screening process. Moreover, we have considered a single-type product inventory.
- To avoid overstocking and understocking in the production system, it is very crucial to tune up the production rate with the demand for the product. Thus, the production rate p is variable (due to the smart production system).
- Demand rate d is constant and known.
- Due to the presence of inventory in the stock, deterioration is unavoidable. Thus, it is important to consider its effect on the model as it has some economical value. Thus, in the current study, the rate of deterioration of inventory is considered as the constant parameter θ, where θ .
- Practically, it is observed that the production cost consists of different components such as raw material cost, tool cost, labor cost, energy cost, etc., and depends on the production rate. Thus, the production cost is considered as follows:where are raw material cost, labor/energy charges, and tool/die cost, respectively.
- Shortages are permitted and partially backlogged, i.e., a portion of the demand is backlogged and has been taken as B(t) = , where t is the time of waiting and is the backlogging parameter.
- The rate of imperfect production is random and follows the known probability distribution.
- A portion of the defective items will be reworkable, while the remainder will be scrapped immediately if they cannot be reworked successfully.
- To absorb the market disturbance, the whole of the study is analyzed under the effect of inflation.
- Due to the different operational activities associated with the production system, the emission of carbon is unavoidable. Thus, to control carbon emissions, a regulatory mechanism is considered.
3.2. Notation
| Parameters | Unit | Expression |
| units/unit time | Production rate | |
| years | Time at which production starts | |
| years | Time at which production stop |
| years | Time at which backordered cleared partially | |
| years | Rework process starting time | |
| years | Rework process ending time | |
| years | Whole length of a complete cycle | |
| d | units/unit time | Demand rate |
| θ | units/unit time | Deterioration rate |
| units/unit time | Rework process rate | |
| r | unit | Discount rate |
| i | unit | Rate of inflation |
| >0 | Shape parameter of backorder rate | |
| USD per setup | Setup cost for production | |
| USD per setup | Setup cost for reworking station | |
| USD/unit | Production cost | |
| USD/unit | Deterioration cost | |
| USD/unit | Cost of rework | |
| USD/unit/unit time | Backorder cost | |
| USD/unit | Scrapping cost | |
| USD/unit | Lost sale cost | |
| USD/unit | Raw material cost | |
| USD/unit | Labor/energy charges | |
| USD/unit | Tool/die cost | |
| USD/unit/unit time | Serviceable items holding cost | |
| USD/unit/unit time | Reworkable items holding cost | |
| kg/unit | Carbon emissions by production | |
| kg/setup | Carbon emissions by setup process of production | |
| kg/setup | Carbon emissions by setup process of reworking station | |
| kg/unit | Carbon emissions by holding the items in a warehouse | |
| kg/unit | Carbon emissions due to reworking | |
| kg/unit | Carbon emissions by deterioration | |
| kg/unit | Carbon emissions by scrapping | |
| USD/kg | Carbon tax per kg | |
| Z | USD | Total cost |
| USD/cycle | Total cost per cycle | |
| unit | Serviceable inventory level at time t, i = 1, 2, 3, 4, 5, 6 | |
| unit | Reworkable inventory level at time t, j = 7, 8, 9 | |
| - | Defective proportion in production | |
| - | Defective proportion in rework | |
| - | Expected value of defective proportion in production | |
| - | Expected value of defective proportion in rework |
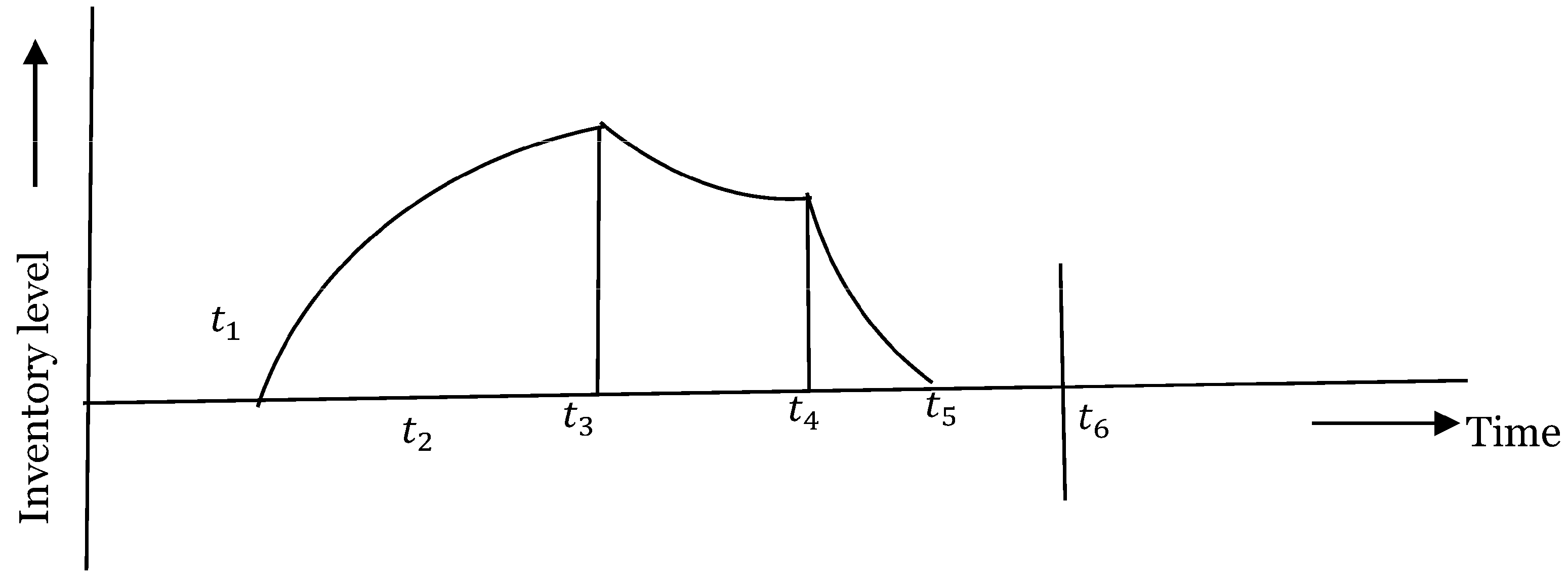
3.3. Problem Descriptions
4. Mathematical Model of Smart Production System
- Carbon emissions cost due to setup of production and reworking station
- Per cycle carbon emissions cost due to production
- Per cycle carbon emissions cost due to rework
- Per cycle carbon emissions cost due to scrapping
- Per cycle carbon emissions cost due to holding inventory
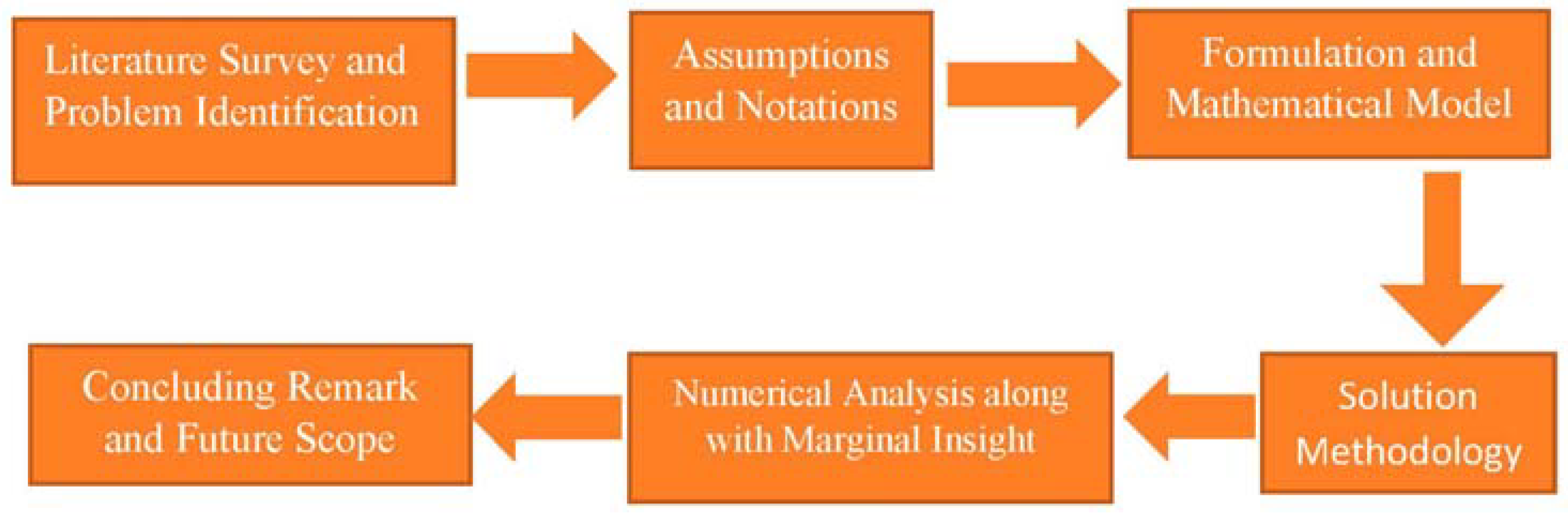
5. Solution Methodology
- Step 1: The values of all parameters are put in the objective functions in Equations (26) and (27).
- Step 2: Different derivatives of objective functions , , and are evaluated, and then each expression is put to zero to obtain the stationary points:On solving the above system of equations, we obtain the values .
- Step 3: The Hessian matrix is obtained as follows to check the convexity of the objective function.
- Step 4: Thus, is an extreme point and is the optimal value of the objective function.
6. Numerical Analysis
7. Sensitivity Analysis
- (i)
- The total cost of the system changes only slightly due to the rise in the holding cost for serviceable products, but there is a significant rise due to a rise in the holding cost for reworkable items.
- (ii)
- A minor change in the total inventory cost in the system is detected due to increases in the scrapping cost, setup cost for the reworking station, and setup cost for serviceable products.
- (iii)
- A high inclination in the total inventory cost of the system is observed due to the increase in the customer base.
- (iv)
- A high change in the total cost of the system is observed due to the change in emission by production, while a slight change is observed due to the change in emission by rework.
- (v)
- It is observed that holding cost, reworkable cost, scrapping cost, backorder cost, lost-sale cost, and carbon emissions costs are all positively correlated with total cost.
8. Managerial Insights
- To lessen the influence of human mistakes in the screening process, the current study advises that automated screening procedures be established.
- According to the study, the cost of carbon emissions related to production has a significant impact on the system’s total cost. As a result, managers must consider measures to reduce carbon emissions from manufacturing from both an environmental and economic standpoint.
- Managers will have an understanding of how rework benefits the environment and how it can be used to meet customer requests as a result of this research.
- Inflation is extremely sensitive in developing economies such as India, Bangladesh, and others. As a result, managers must consider this element when designing the optimal strategies for the system.
9. Concluding Remarks and Future Extension
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A
References
- Hua, G.; Cheng, T.; Wang, S. Managing carbon footprints in inventory management. Int. J. Prod. Econ. 2011, 132, 178–185. [Google Scholar] [CrossRef]
- Benjaffar, S.; Li, Y.; Daskin, M. Carbon footprint and the management of supply chain: Insights from simple model. IEEE Trans. Autom. Sci. Eng. 2012, 10, 99–116. [Google Scholar] [CrossRef]
- Lou, G.X.; Yang, H.; Zhang, J.Q.; Fan, T.J. Investment strategy of emission reduction technology in a supply chain. Sustainability 2015, 7, 10684–10708. [Google Scholar] [CrossRef]
- Datta, T.K. Effect of green technology investment on a production-inventory system with carbon tax. Adv. Oper. Res. 2017, 2017, 4834839. [Google Scholar] [CrossRef]
- Daryanto, Y.; Wee, H.M.; Astanti, R.D. Three-echelon supply chain model considering carbon emission and item deterioration. Transp. Res. Part E Logist. Transp. Rev. 2019, 122, 368–383. [Google Scholar] [CrossRef]
- Jauhari, W.A.; Adam, N.A.F.P.; Rosyidi, C.N.; Pujawan, I.N.; Shah, N.H. A closed-loop supply chain model with rework waste disposal, and carbon emission. Oper. Res. Perspect. 2020, 7, 100155. [Google Scholar] [CrossRef]
- Mishra, M.; Ghosh, S.K.; Sarkar, B. Maintaining energy efficiencies and reducing carbon emissions under a sustainable supply chain management. AIMS Environ. Sci. 2022, 9, 603–635. [Google Scholar] [CrossRef]
- Yadav, D.; Singh, R.; Kumar, A.; Sarkar, B. Reduction of pollution through sustainable and flexible production by controlling by-products. J. Environ. Inform. 2022, 40, 106–124. [Google Scholar] [CrossRef]
- Sarkar, B.; Kar, S.; Basu, K.; Guchhait, R. A sustainable managerial decision-making problem for a substitutable product in a dual-channel under carbon tax policy. Comput. Ind. Eng. 2022, 172, 108635. [Google Scholar] [CrossRef]
- Sarkar, M.; Sarkar, B.; Dolgui, A. An automated smart production with system reliability under a leader-follower strategy of supply chain management. In Advances in Production Management Systems. Smart Manufacturing and Logistics Systems: Turning Ideas into Action. APMS 2022. IFIP Advances in Information and Communication Technology; Kim, D.Y., von Cieminski, G., Romero, D., Eds.; Springer: Cham, Switzerland, 2022; Volume 663, pp. 459–467. [Google Scholar] [CrossRef]
- Wee, H.M.; Huang, Y.D.; Wang, W.T.; Cheng, Y.L. An EPQ model with partial backorders considering two backordering costs. Appl. Math. Comput. 2014, 232, 898–907. [Google Scholar] [CrossRef]
- Mishra, U.; Cárdenas Barrón, L.E.; Tiwari, S.; Shaikh, A.A.; Trevino-Gazra, G. An inventory model under price and stock dependent demand for controllable deterioration rate with shortages and preservation technology investment. Ann. Oper. Res. 2017, 254, 165–190. [Google Scholar] [CrossRef]
- Singh, S.R.; Rani, M. An inventory model for exponential time—Sensitive demand and parabolic time linked holding cost under inflation and shortages with salvage value. PalArchs J. Archaeol. Egypt Egyptol. 2020, 17, 10941–10949. [Google Scholar]
- Palanivel, M.; Suganya, M. Partial backlogging inventory model with price and stock level dependent demand, time varying holding cost and quantity discounts. J. Manag. Anal. 2021, 9, 32–59. [Google Scholar] [CrossRef]
- Kumar, N.; Dahiya, S.; Kumar, S. Two warehouse inventory model for deteriorating items with fixed shelf-life stock-dependent demand and partial backlogging. J. Math. Comput. Sci. 2022, 12, 85. [Google Scholar] [CrossRef]
- Sarkar, B.; Takeyeva, D.; Guchhait, R.; Sarkar, M. Optimized radio-frequency identification system for different warehouse shapes. Knowl. Based Syst. 2022, 258, 109811. [Google Scholar] [CrossRef]
- Jawla, P.; Singh, S. Multi-item economic production quantity model for imperfect items with multiple production setups and rework under the effect of preservation technology and learning environment. Int. J. Ind. Eng. Comput. 2016, 7, 703–716. [Google Scholar] [CrossRef]
- Khara, B.; Dey, J.K.; Mondal, S.K. An inventory model under development cost-dependent imperfect production and reliability dependent demand. J. Manag. Anal. 2017, 4, 258–275. [Google Scholar] [CrossRef]
- Al-Salamah, M. Economic production quantity in an imperfect manufacturing process with synchronous and Asynchronous flexible rework rates. Oper. Res. Perspect. 2019, 6, 100103. [Google Scholar] [CrossRef]
- Sarkar, B.; Ganguly, B.; Pareek, S.; Cárdenas-Barrón, L.E. A three-echelon green supply chain management for biodegradable products with three transportation modes. Comp. Indust. Eng. 2022, 174, 108727. [Google Scholar] [CrossRef]
- Gupta, S.; Vijaygargy, L.; Sarkar, B. A bi-objective integrated transportation and inventory management under a supply chain network considering multiple distribution networks. RAIRO-Operat. Res. 2022, 56, 3991–4022. [Google Scholar] [CrossRef]
- Lin, H.J. An economic production quantity model with backlogging and imperfect rework process for uncertain demand. Int. J. Prod. Res. 2021, 59, 467–482. [Google Scholar] [CrossRef]
- Chandra, M.J.; Michael, L.B. The effect of inflation and the time value of money on some inventory system. Int. J. Prod. Res. 2007, 23, 723–730. [Google Scholar] [CrossRef]
- Yang, H.L.; Teng, J.T.; Chern, M.S. An inventory model under inflation for deteriorating items with stock-dependent consumption rate and partial backlogging shortages. Int. J. Prod. Econ. 2010, 123, 8–23. [Google Scholar] [CrossRef]
- Palanivel, M.; Uthayakumar, R. An EPQ model with variable production, Probabilistic deterioration and partial backlogging under inflation. J. Manag. Anal. 2014, 1, 200–223. [Google Scholar] [CrossRef]
- Rani, S.; Ali, R.; Agarwal, A. Green supply chain inventory model for deteriorating items with variable demand under inflation. Int. J. Bus. Forecast. Mark. Intell. 2017, 3, 50–77. [Google Scholar] [CrossRef]
- Huang, X.; Yang, S.; Wang, Z. Optimal pricing and replenishment policy for perishable food supply chain under inflation. Comput. Ind. Eng. 2021, 158, 107433. [Google Scholar] [CrossRef]
- Alamri, O.A.; Jayaswal, M.K.; Khan, F.A.; Mittal, M. An EOQ Model with Carbon Emissions and Inflation for Deteriorating Imperfect Quality Items under Learning Effect. Sustainability 2022, 14, 1365. [Google Scholar] [CrossRef]
- Padiyar, S.V.S.; Vandana, V.; Bhagat, N.; Singh, S.R.; Sarkar, B. Joint replenishment strategy for deteriorating multi-item through multi-echelon supply chain model with imperfect production under imprecise and inflationary environment. RAIRO-Oper. Res. 2022, 56, 3071–3096. [Google Scholar] [CrossRef]
- Singh, S.R.; Sharma, S. A partially backlogged supply chain model for deteriorating items under reverse logistics, imperfect production/ remanufacturing and inflation. Int. J. Logist. Syst. Manag. 2019, 33, 221–255. [Google Scholar] [CrossRef]
- Rout, C.; Chakraborty, D.; Goswami, A. An EPQ model for deteriorating items with imperfect production, two type of inspections errors and rework under complete backordering. Int. Game Theory Rev. 2020, 22, 2040011. [Google Scholar] [CrossRef]
- Bachar, R.K.; Bhuniya, S.; Ghosh, S.K.; Sarkar, B. Sustainable green production model considering variable demand, partial outsourcing, and rework. AIMS Environ. Sci. 2022, 9, 325–353. [Google Scholar] [CrossRef]
- Oryani, B.; Moridian, A.; Sarkar, B.; Rezania, S.; Kamyab, H.; Khan, M.K. Assessing the financial resourse curse hypothesis in Iran: The novel dynamic ARDL approach. Resour. Pol. 2022, 78, 102899. [Google Scholar] [CrossRef]
- Hota, S.K.; Ghosh, S.K.; Sarkar, B. Involvement of smart technologies in an advanced supply chain management to solve unreliability under distribution robust approach. AIMS Environ. Sci. 2022, 9, 461–492. [Google Scholar] [CrossRef]

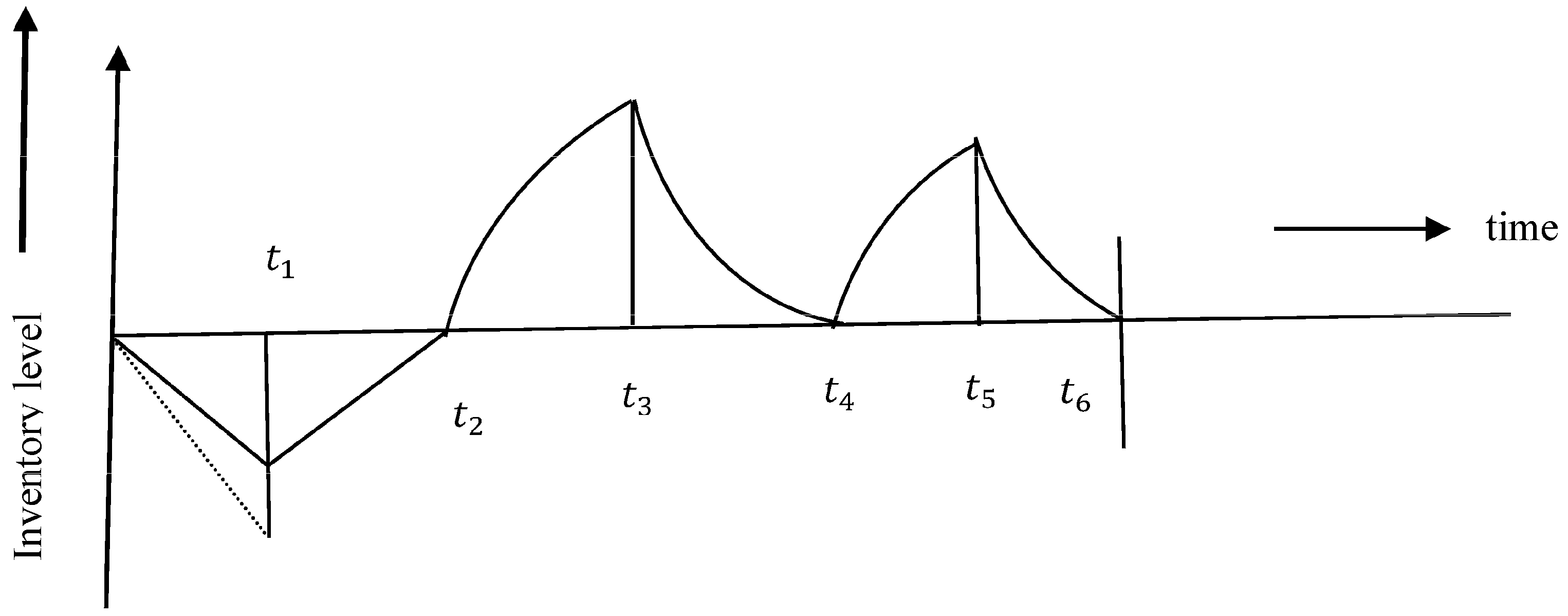
| Author(s) | Model Type | Carbon Emission | Volume Flexibility | Inflation | Backorder | Imperfect Process |
|---|---|---|---|---|---|---|
| Hua et al. [1] | EOQ | √ | - | - | - | - |
| Benjaafar et al. [2] | SCM | √ | - | - | Full | - |
| Lou et al. [3] | EOQ | √ | ||||
| Datta [4] | EPQ | √ | - | - | - | Other |
| Daryanto et al. [5] | SCM | √ | - | - | - | Constant |
| Jauhari et al. [6] | SCM | √ | - | - | - | Constant |
| Mishra at el. [7] | SCM | √ | - | - | - | - |
| Yadav et al. [8] | SCM | √ | √ | - | Partial | Constant |
| Sarkar et al. [9] | SCM | √ | - | - | - | - |
| Sarkar et al. [10] | SCM | - | - | - | - | Random |
| Wee et al. [11] | EPQ | - | - | - | Partial | - |
| Mishra et al. [12] | EOQ | - | - | - | Both | - |
| Singh and Rani [13] | EOQ | - | - | √ | Partial | - |
| Kumar [15] | EOQ | - | - | - | Partial | - |
| Sarkar et al. [16] | SCM | - | - | - | - | - |
| Jawla and Singh [17] | EPQ | - | - | √ | - | Constant |
| Khara [18] | EPQ | - | - | - | - | Constant |
| Al-Salamah [19] | EPQ | - | - | - | Full | Constant |
| Sarkar et al. [20] | SCM | √ | - | - | - | - |
| Sarkar et al. [21] | EOQ | - | - | - | - | - |
| Lin [22] | EPQ | - | - | - | Full | Constant |
| Chandra and Michael [23] | EOQ | - | - | √ | Full | - |
| Yang et al. [24] | EOQ | - | - | √ | Partial | - |
| Palanivel and Uthayakumar [25] | EPQ | - | - | √ | Partial | - |
| Rani and Ali [26] | SCM | - | - | √ | - | - |
| Huang et al. [27] | EOQ | - | - | √ | - | - |
| Alamri et al. [28] | EOQ | √ | - | √ | - | Random |
| Padiyar et al. [29] | SCM | - | - | √ | - | Constant |
| Singh and Sharma [30] | SCM | - | - | √ | Partially | Constant |
| This paper | EPQ | √ | √ | √ | √ | √ |
| Parameters | % Change | TC | % Change in TC |
|---|---|---|---|
| Serviceable items holding cost () | +20 | 85,114.9 | +0.014 |
| +10 | 85,109 | +0.007 | |
| −10 | 85,097.3 | −0.007 | |
| −20 | 85,091.5 | −0.014 | |
| Reworkable items holding cost () | +20 | 90,048.8 | +5.81 |
| +10 | 87,576 | +2.91 | |
| −10 | 82,630.4 | −2.91 | |
| −20 | 80,157.6 | −5.81 | |
| Scrapping cost () | +20 | 85,108.4 | +0.006 |
| +10 | 85,105.8 | +0.003 | |
| −10 | 85,100.6 | −0.003 | |
| −20 | 85,098 | −0.006 | |
| Setup cost for production (sp) | +20 | 85,132 | +0.034 |
| +10 | 85,117.6 | +0.017 | |
| −10 | 85,088.8 | −0.017 | |
| −20 | 85,074.4 | −0.034 | |
| Setup cost for reworking station (sr) | +20 | 85,114.7 | +0.014 |
| +10 | 85,108.9 | +0.007 | |
| −10 | 85,097.4 | −0.007 | |
| −20 | 85,091.7 | −0.014 | |
| Demand rate () | +20 | 103,356 | +21.45 |
| +10 | 93,765.1 | +10.18 | |
| −10 | 76,909.6 | −9.63 | |
| −20 | 68,973.7 | −18.95 | |
| Backorder cost () | +20 | 85,536.5 | +0.51 |
| +10 | 85,319.9 | +0.26 | |
| −10 | 84,886 | −0.26 | |
| −20 | 84,669.9 | −0.51 | |
| Carbon tax per cycle () | +20 | 91,084.2 | +7.03 |
| +10 | 88,093.7 | +3.51 | |
| −10 | 82,112.7 | −3.51 | |
| −20 | 79,122.2 | −7.03 | |
| Carbon emission by production () | +20 | 90,612.4 | +6.47 |
| +10 | 87,857.8 | +3.24 | |
| −10 | 82,348.6 | −3.24 | |
| −20 | 79,594 | −6.47 | |
| Carbon emission due to re-working () | +20 | 85,305.8 | +0.24 |
| +10 | 85,204.5 | +0.12 | |
| −10 | 85,001.9 | −0.12 | |
| −20 | 84,900.6 | −0.24 | |
| Carbon emission by holding the items in warehouse () | +20 | 85,185.1 | +0.096 |
| +10 | 85,144.1 | +0.048 | |
| −10 | 85,062.3 | −0.048 | |
| −20 | 85,021.3 | −0.096 | |
| Carbon emission by deterioration () | +20 | 85,117.7 | +0.017 |
| +10 | 85,110.4 | +0.008 | |
| −10 | 85,095.9 | −0.009 | |
| −20 | 85,088.7 | −0.012 | |
| Carbon emission by scrapping () | +20 | 85,189.8 | +0.10 |
| +10 | 85,146.5 | +0.05 | |
| −10 | 85,059.9 | −0.05 | |
| −20 | 85,016.6 | −0.10 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yadav, D.; Chand, U.; Goel, R.; Sarkar, B. Smart Production System with Random Imperfect Process, Partial Backordering, and Deterioration in an Inflationary Environment. Mathematics 2023, 11, 440. https://doi.org/10.3390/math11020440
Yadav D, Chand U, Goel R, Sarkar B. Smart Production System with Random Imperfect Process, Partial Backordering, and Deterioration in an Inflationary Environment. Mathematics. 2023; 11(2):440. https://doi.org/10.3390/math11020440
Chicago/Turabian StyleYadav, Dharmendra, Umesh Chand, Ruchi Goel, and Biswajit Sarkar. 2023. "Smart Production System with Random Imperfect Process, Partial Backordering, and Deterioration in an Inflationary Environment" Mathematics 11, no. 2: 440. https://doi.org/10.3390/math11020440
APA StyleYadav, D., Chand, U., Goel, R., & Sarkar, B. (2023). Smart Production System with Random Imperfect Process, Partial Backordering, and Deterioration in an Inflationary Environment. Mathematics, 11(2), 440. https://doi.org/10.3390/math11020440








