Abstract
The present article mainly focuses on the transient thermal dispersal within a moving plate using the non-Fourier heat flux model. Furthermore, the innovative, sophisticated artificial neural network strategy with the Levenberg-Marquardt backpropagated scheme (ANNS-LMBS) is proposed for determining the transient temperature in the convective-radiative plate. Using dimensionless terms, the energy model for transient heat exchange is simplified into a non-dimensional form. The arising partial differential equation (PDE) is then numerically tackled using the finite difference method (FDM). A data set for the various scenarios of the thermal parameters influencing the thermal variation through the plate has been generated using the FDM. In addition, the effect of the dimensionless physical variables on the thermal profile of a moving plate has been examined and discussed in detail. Increments in the convection-conduction and radiation-conduction parameters are figured to yield a reduction in the transient thermal dispersion. An upsurge in the Peclet number caused the improvement of thermal dispersal in the plate.
MSC:
65M06; 74S20; 68T07; 74F05
1. Introduction
Heat transfer improvement is an approach for enhancing heat exchange systems’ thermal and hydrodynamic performance. It is also recognized as heat augmentation or intensification, and this augmentation is essential in various applications such as automotive cooling, refrigeration, heat exchangers, and chemical processes. Thus, investigators are interested in studying innovative techniques that could enhance heat transfer rates. Heat transmission could be passively boosted by modifying flow geometry, boundary conditions, or increasing fluid thermal conductivity. A variety of methods have been suggested to improve fluids’ ability to transfer heat. Suspending small solid particles, such as metallic and non-metallic particles, in conventional fluids may be an impactful method of strengthening heat transfer performance. Nanofluids are heat transfer fluids that incorporate designed suspended nanomaterials that are distributed throughout the base liquid. Water, organic fluids, motor oil, polymeric formulations, biofluids, and other conventional fluids are generally utilized as the base fluids. The usage of nanofluids has revealed a wide range of potential applications. Over the past several years, researchers and investigators have operated on various aspects of nanoliquids [1,2,3,4,5,6,7]. The ever-increasing problem of the extreme heat disposal requirements from advanced electronic apparatus prompted extensive research into improving the effectiveness of thermal management. The addition of the extended surface to the heat-transferring object is considered one of the most viable solutions to this issue because of its greater heat-transfer performance. Extended surfaces/fins are used when the available surface area is inadequate to transport the required heat energy with the available temperature difference. Fins are widely used in various industrial applications, including electrical chips and machinery for chemical processing. Because of this, numerous researchers have conducted comprehensive analyses on heat transfer through fins [8,9,10,11,12].
Fourier’s and Fick’s laws explain and interpret many heat conduction and mass diffusion issues. These classical diffusion theories are well recognized to fail when handling unsteady problems in an exceptionally short period, with remarkably increased flux, or at very relatively low temperatures. Following that, a modified flux model with a wave possessing finite speed is proposed for the energy transfer. A relaxation process is incorporated into the Cattaneo model-based hyperbolic heat conduction equation to modify an alteration in the temperature gradient steadily. This model delivers the hyperbolic diffusion formula within the continuum presumption and is a productive continuation of the classical diffusion concept. In several application fields, including solidifying mechanisms, surface thermal processing with lasers, monitoring the temperature of superconductors, laser surgery, and freezing, non-Fourier heat conduction takes a significant position. Thus, numerous investigators working on the heat transmission have emphasized the potentially practicable attributes of non-Fourier heat conduction. The non-Fourier heat conduction problem (NFHCP) was studied by Das et al. [13], who also discussed the impact of the corresponding physical parameter by deriving the numerical solution for the considered NFHCP. Kundu and Lee [14] explained the aspects of temperature and heat transmission in the fin by modeling the NFHCP. The unsteady nature of functionally graded convective extended surfaces was examined by Zhang and Li [15] with the aid of non-Fourier law (NFL). Kumar et al. [16] debriefed the variation of temperature in the semi-circular wetted extended surface with the consideration of the NFL. Ghasemi et al. [17] delineated the time-variant thermal variation in the functionally graded cylinder by modeling the NFHCP. The heat transmission in the semi-spherical fin was discussed by Jagadeesha et al. [18], and the corresponding balanced equation was presented with the help of the NFL. The notion of radiation is deduced from waves propagating in all directions. When energy moves from one place to another, it appears as a waveform, and this movement is known as radiation. Due to its numerous technological and industrial characteristics, such as its use in geothermal energy systems, nuclear safety, and thermal storage, thermal radiation significantly necessitates further investigations. It was explored that various physiological mechanisms, technological systems, and scientific field facilities are significantly impacted by energy transfer and thermal radiation at high temperatures. Sowmya et al. [19] considered the thermal radiation impact to discuss the heat transference in a moving rectangular rod and provided the analytical expression for the governing equation. The dissipative flow of a nanoliquid past a stretchy sheet was examined by Kausar et al. [20] with the effect of thermal radiation. Biswas et al. [21] scrutinized the radiative magnetic stream of the nanoliquid over a stretchable surface with a chemical reaction impact. By considering the thermal radiative effect, Mansoor et al. [22] probed the chemically reactive flow nature of a non-Newtonian liquid over an exponentially stretchable surface. The radiative impact was considered by Correa et al. [23] to examine the heat transmission in a permeable fin. The numerical solution for the heat transfer equation of the fin was procured by Sowmya et al. [24] using the collocation method, and the thermal radiative impact on heat transfer was also studied.
Investigators are aware of the importance of heat transport analysis past a continuously moving sheet or plate because of its manufacturing and technological applications, such as the cooling of stripes, drawing of rubber sheets, polymer extrusion process, continuous casting, paper production, and marking of plastics. Ferdows et al. [25] investigated the steady convective stream of a viscous nanoliquid past a moving plate with radiation and dissipation impacts. The unsteady radiative heat transmission through a moveable plate was scrutinized by Kumar et al. [26] with convective heat dissipation at the tip. With the thermophoresis consequence, Mabood et al. [27] probed the aspects of a chemically reactive stream of a liquid over a moving plate. Arulmozhi et al. [28] considered the radiation and magnetic impacts to investigate the flow of a nanoliquid past a vertically moving plate. The application of soft computing is a potential approach that could be used to analyze heat transfer characteristics. An artificial intelligence technique that mimics neuronal information transmission is widely known as the artificial neural network (ANN), which investigators have used to tackle complex problems in recent years. An ANN is parallel computing with a non-linear structure composed of numerous basic neurons. Although each neuron’s computational operation is very restricted, the network’s rich features and fast response are due to the parallel tasks of a group of neurons. While the ANN model does not require specific model variables, it manages complicated systems with non-linearities, manages experimental data, and articulates variable efficiencies. Artificial intelligence technologies are receiving greater recognition as sophisticated emerging technologies that solve non-linear issues and, after being adequately trained, accurately predict and generalize quickly [29,30,31,32,33,34]. Its benefits include fast computation, reliable performance and error tolerance, strong self-learning, adaptive abilities, and the approximation of any non-linear relationship. As a result, Ullah et al. [35] used the ANN technique to predict the fluid flow velocity past a stretchy sheet with the consequence of magnetic strength. The execution of the ANN algorithm was conducted by Raza et al. [36] to analyze the flow and thermal variations of a dusty liquid past a permeable sheet. Alhadri et al. [37] estimated the radiative flow and thermal behavior of a hybrid nanoliquid past a stretchable surface using the ANN approach.
Several research works on problems of heat transfer in a moving plate or rod have been addressed over the last few decades. Aziz and Lopez [38] discussed the steady-state nature of the radiative-convective heat transmission in a moving rod with the aid of Fourier law. In their study, the non-linear dimensionless equation, along with boundary conditions, were numerically solved using the fourth-fifth order Runge-Kutta-Fehlberg (RKF 45) strategy. By employing the numerical approximation technique, i.e., the spectral collocation method (SCM), Sun et al. [39] explicated the heat dispersion in the moveable plate with the combined radiative-conductive-convective impact, and the corresponding mathematical model was developed using Fourier law. The impact of time on the radiative unsteady heat transmission in a moving plate was studied by Ma et al. [40], and SCM was implemented to achieve the numerical solution to the thermal problem. Although these investigations on classical Fourier heat conduction problems are significant, examining non-Fourier heat transport problems is prominent due to their applications in laser heating, nuclear engineering, and other fields. Encouraged by this fact, the current work focuses on the non-Fourier impact on the moving plate. Also, it is observed from the aforementioned publications that the stochasticated artificial neural network strategy based on the appropriate optimization algorithm is still not utilized for the non-Fourier heat transfer problem of the moving plate. Accordingly, in this investigation, non-Fourier unsteady thermal dispersion in the moving plate was probed by implementing an artificial neural network strategy with the Levenberg-Marquardt backpropagated scheme (ANNS-LMBS). The heat transfer mechanism in the plate was noticed by taking the radiative phenomenon and the internal heat generation into account. The thermal model for unsteady energy transfer was simplified into a non-dimensional form using dimensionless terms, and the resulting PDE was then numerically solved using FDM. A set of data for the diverse scenarios of the thermal variables influencing the temperature difference in the plate was generated through the use of the FDM. Using these datasets for specific scenarios, the training, validation, and testing stages for the ANNS-LMBS were provided. Comparisons with the numerical solutions were then performed to authenticate the applicability and robustness of the proposed ANNS-LMBS.
2. Mathematical Formulation
This investigation emphasizes the aspects of unsteady energy transfer through a moveable plate. Figure 1 shows an illustration of a plate with the dimensions, thickness , length , and width that radiates heat to the fluid around it through convection and radiation. The plate is moving horizontally in the direction at a constant speed . The plate is initially in thermal equilibrium with the ambient temperature , and is the temperature at the left end of the plate. The other end is insulated or maintained at adiabatic conditions. The internal heat produced per unit volume and heat lost from a plate’s surface by radiation are considered temperature-dependent.
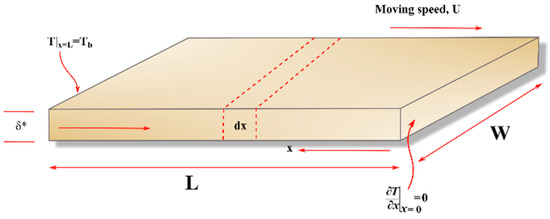
Figure 1.
Physical configuration of a moving plate.
In most cases, Fourier behavior is implied when investigating heat transfer phenomena. The classic theory of thermal conduction, known as Fourier law, predicts an instant change to a temperature gradient and results in a parabolic differential equation for the progression of temperature. The speed at which heat moves through a body is believed to be infinite according to the classical Fourier law of heat conduction. In other words, any position of the body would experience a modification in temperature at any spot concurrently. When it comes to extremely instantaneous heat conduction over very quick time scales, the theory is not valid. To address this issue, many researchers modified Fourier’s law. Cattaneo and Vernotte proposed the following hyperbolic heat modeling approach for energy transfer with a finite propagation speed:
Here, is the temperature, is the relaxation time, is the thermal conductivity, and is the heat flux. With all these inferences stated above, the mathematical equation for unsteady-state energy transfer through a moveable plate is provided by (Kumar et al. [26] and Ma et al. [40]):
Equation (2) could also be written as
where,
Eliminating using Equations (1) and (3) yields:
The thermal conductivity present in Equation (5) is presumed as the linear function of temperature, whereas the is presumed to be the power-law function of temperature and is mathematically expressed as (Sowmya et al. [41]):
where denotes the thermal conductivity at ambient temperature . represents the exponent constant of the heat transfer coefficient, which describes the mode of heat transfer.
and present in Equation (5), which depend on temperature change are symbolized as (Ma et al. [42]):
By using Equations (6) and (7), Equation (5) would become:
where signifies the measure of surface emissivity difference with temperature.
The appropriate conditions used at the ends of the plate are:
The following non-dimensional variables are employed to simplify Equation (8)
The dimensionless form of governing Equation (8) is:
Equation (9) is reduced as:
3. Finite Difference Scheme
For tackling the equation of the moving plate, the implicit Crank-Nicolson finite difference method is employed in the spatial and temporal domains , respectively. These domains are indicated by a finite number of mesh points, i.e., and .
Equation (11) is discretized using the Crank-Nicolson approach to yield the finite difference expression that pertains to the internal nodes with time and space steps and , respectively.
The method employed is accurate in both the time and space domains with the following discretized BC,
The Crank-Nicolson scheme is an accurate second-order strategy in . After solving Equation (13) with Equation (14) using FDM, the numerical results are subjected to ANN training in the form of datasets. Figure 2 depicts the overall procedure involved in examining the thermal distribution within the plate.
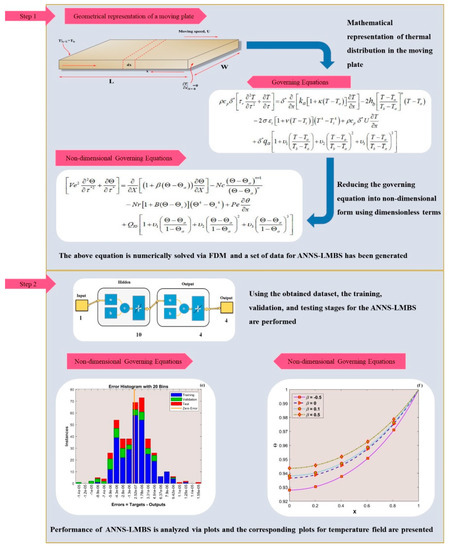
Figure 2.
Model development of the ANNS-LMBS for the thermal distribution in a moving plate.
4. Artificial Neural Network (ANN)
The most basic ANN, the backpropagation neural network, is a multilayer feedforward neural network. Error backpropagation and forward signal transmission are this network’s two key features. The forward transfer involves processing the input transmission layer by layer, starting at the input layer and moving through the hidden units to the output units. Only the subsequent layer’s neurons are impacted by the condition of those in the layer below. When an output unit is unable to produce the desired result, it would switch to backpropagation and would reconfigure the network weight and large value following the prediction error, which would help the backpropagation neural network (BPNN) prediction output consistently be closer to the desired result. The weights and biases are considered learnable parameters from the perspective of a BPNN. An optimization algorithm must be used to reduce the overall ANN error for the dataset. The stochastic Levenberg-Marquardt algorithm (LMA) was implemented to train the artificial neural network. The Gauss-Newton technique’s better convergence near the minima and the lowered error results achieved from the gradient descent are combined in the LM algorithm, which is employed for curve fitting. This process, which comprises the training, is anticipated to produce a set of ideal parameters. Every tracking data is read in training, and an epoch is defined, resulting in a change in the parameters. The entire dataset should be divided into three subgroups: training, validation, and testing. The first enables training, while the third evaluates the trained model’s generalization performance. The validation subset is not utilized to update the parameters of the ANN during training; instead, it is used to evaluate the selected accuracy metric. Its goal is to prevent overfitting, which occurs when the model becomes too sophisticated in the training sample and cannot extract accurate responses for situations outside it.
In order to properly train ANN models, data optimization is vital. An insufficient quantity of training data prevents the system model from learning the correlations between the data adequately, while an abundance of it could result in issues such as over-fitting the model and memorization. Thus, to train the network, a total of 100 data points was taken. Three subgroups of the data were generated, with 70%, 15%, and 15% of the total data points being used for training, validation, and testing, respectively. The activation function performs as a mathematical gate between the current layered neuron’s input and the output of the next layer. Following a comparison of the ANN’s model performance levels, the activation function opted. The function is preferred in the output layer, and the transfer function is used in the hidden layer, which is formulated as:
For each segment of data, the mean squared error (MSE) and coefficient of determination (R2) of the network are calculated to assess the strongest ANN architecture. The performance metrics, such as the MSE (loss function) and R2 with error metrics, are employed in the network and are denoted as:
The working flow chart of the proposed ANNS-LMBS for performing the network training is portrayed in Figure 3.
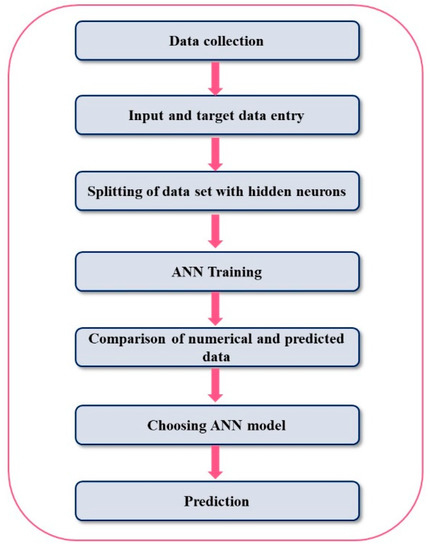
Figure 3.
Working flow chart of the ANNS-LMBS.
5. Result and Discussion
In the present analysis, the non-linear governing energy Equation (11) along with Equation (12) represents the non-dimensional hyperbolic heat conduction (HHC) thermal equation of a moving plate, and this equation is tackled using the ANNS-LMBS. The significance of non-dimensional thermo-physical properties, such as , , , and on the thermal field , is appraised in this section with the aid of the graphical description. The NF effect in the transient thermal dispersal of a moving plate is inspected by varying the dimensionless length of the plate along the positive x-axis with the enhancement in the magnitude of the aforementioned physical parameters. The set of thermal profile values collected by solving Equation (11) along with Equation (12) using FDM is subjected to the ANNS-LMBS training purposes. There are input, hidden, and output layers in the ANN algorithm. FDM thermal data, by varying the parameters, were adapted as the target vectors, and independent variable’s data were utilized as the input vectors. Table 1 provides the details on the data utilized in the network training for various scenarios and cases. Each scenario is developed by varying the corresponding values of thermal parameters (, , , and ). In each case, 100 data points are utilized for training the network. Finally, 70%, 15%, and 15% of the total number of data points were divided into three subgroups, with the corresponding percentages being used for training, validation, and testing.

Table 1.
Parameter variations for the ANNS-LMBS.
The numerical outcomes of using the ANNS-LMBS are compared with the outcome of FDM in Table 2 and Table 3. The network is trained for the 100 data points of , and the corresponding absolute error (AE) is also mentioned in this table.

Table 2.
Comparison of the ANNS-LMBS results with the FDM results by varying .

Table 3.
Comparison of the ANNS-LMBS results with the FDM results by varying .
In particular, for the various cases of , the numerical results of the ANNS-LMBS at specified values of are tabulated in Table 2. The temperature profile values of the plate exhibit a decreasing nature, indicating the temperature distribution from the plate’s left end to its right side. In addition, the thermal profile shows a lower value for improvement in from two to four, implying heat transfer enhancement. In a similar manner, Table 3 includes the outcomes of the ANNS-LMBS for by varying the Vernotte number . The non-dimensional coordinate with a value of 1 denotes the left edge of the plate. It is clear from the numerical data in Table 3 that for both the considered Vernotte numbers, the thermal profile has the highest values at and the distribution of temperature tends to decrease from the left to right end of the plate. Moreover, as the Vernotte number increase, the thermal values decrease. It is clear from both tables that the FDM and ANNS-LMBS results are in close agreement.
The performed ANNS-LMBS procedure has a relatively quick convergence speed and a considerably large calculation accuracy. The trained network performance and parameter results on the provided data set of all the scenarios and cases are summarized in Table 4 by means of time, Mu, epoch, MSE processes, performance, and gradient.

Table 4.
ANNS-LMBS training results for the thermal problem of the moving plate.
The variation in transient thermal distribution with the influence of the dimensionless convection–conduction parameter is displayed in Figure 4a–g with the implementation of the ANN. Also, Figure 5a–g portrays the impact of on the thermal distribution along the length of the plate. The relation between the advective heat transport rate and the diffuse heat transport rate is indicated by the Peclet number and the behavior of the transient thermal distribution , with the consequence of is presented in Figure 6a–g by training the network. The variation in for a higher magnitude of is observed in Figure 7a–g using the results obtained by training the thermal profile data. By training the neural network, the aspects of with the effect on the heat generation parameter is explicated in Figure 8a–g. The training, validation, and testing results in terms of the mean square error (MSE) for the variation in , , , , and are exposed in Figure 4a, Figure 5a, Figure 6a, Figure 7a and Figure 8a, respectively, as a model of how well the network performed. In all these figures, the MSE diminishes with network training, and the lowest error of 4.17 × 10−11, 5.93 × 10−11, 1.78 × 10−10, 2.56 × 10−11, and 7.14 × 10−11 is reached at 64, 51, 56, 40, and 58 epoch for , , , , and respectively. This implied that the results of data training were comparable to the tolerance value, and the estimated outcomes with the ANN were close to the FDM numerical data. The ANN training findings in the form of the state transitions for the cases of , , , , and is represented in Figure 4b, Figure 5b, Figure 6b, Figure 7b and Figure 8b, respectively. For 64, 51, 56, 40, and 58 epoch, the Mu would be 1 × 10−10, 1 × 10−10, 1 × 10−10, 1 × 10−11, and 1 × 10−10 with gradients of 9.55 × 10−8, 9.77 × 10−8, 8.77 × 10−8, 9.92 × 10−8, and 9.38 × 10−8, respectively. Furthermore, the error histogram in Figure 4c, Figure 5c, Figure 6c, Figure 7c and Figure 8c determines the error features for the cases of , , , , and , respectively. The error size distribution for the training, test, and validation data is provided here and the number of dataset values that fall into a certain bin is represented by each bar in these plots. The network’s accuracy is evidenced by the determined error, which is usually close to zero and has a distribution that is not far from zero. Figure 4d, Figure 5d, Figure 6d, Figure 7d and Figure 8d depict the regression curve of training, validation, testing, and all values of an ANNS-LMBS-trained mechanism for the , , , , and cases. The group of sampled data demonstrates the size of the dataset used to train the neural network. Additionally, each of the four subplots contains a fit line that indicates that values nearer to that line would be superior and, as a result, the regression value obtained would be much nearer to one. The value of regression in the training, validation phase, and testing phase is one for the , , , , and cases. Thus, a close correlation between the estimated and desired values indicated by could be seen in all these figures. In Figure 4e, Figure 5e, Figure 6e, Figure 7e and Figure 8e, the function fitness curve of the neural trained network is presented for the , , , , and cases. The trained, validated, and tested ANNS-LMBS outputs are compared against the desired target datasets in these figures which exhibit a closer agreement. For the thermal parameters , , , , and , the thermal distribution nature is provided in Figure 4f, Figure 5f, Figure 6f, Figure 7f and Figure 8f and the absolute error (AE) is provided in Figure 4g, Figure 5g, Figure 6g, Figure 7g and Figure 8g. In Figure 4f, the transient thermal distribution reduces gradually for an increasing magnitude of . The non-dimensional variable signifies the ratio of convection to conduction in terms of how much heat is removed from the plate’s surface. The surface convection endorses the heat dissipation from the plate, so increasing the magnitude of this variable encourages the heat transfer rate by lowering the temperature profile. In this analysis, the temperature variation through the plate is performed with the influence of thermal radiation, and the dimensionless variables and represent the radiative phenomenon. Unlike conductive and convective heat flux, which are more or less linearly dependent on temperature fluctuations, radiant heat fluxes are generally proportional to the variations in the fourth power of temperature. In addition, is considered to be temperature dependent in this scrutiny. An increase in the values cause the decrease in , as shown in Figure 5f. As radiation becomes sturdier, the plate provides heat to the surroundings efficiently and thereby the temperature drops in the plate. From a physical point of view, the transfer of thermal energy by radiation improves the heat transference rate from the plate. It is perceived from Figure 6f that, an upgrade in the provokes the enhancement of the transient thermal distribution . At the specific initial time , enhances with the escalating magnitude of near the hot boundary region. Physically, as upsurges the plate travels quicker and the exposure time to the ambient fluid reduces, thus, upsurges. The thermal profile improves for the diverse magnitude of along the plate length, as exhibited in Figure 7f. In other words, as the value of declines, so does the temperature in the plate, indicating an elevated heat loss to the surrounding fluid. The temperature inside the moving plate rises as a result of the improved heat conduction caused by an increase in the thermal conductivity gradient. There are numerous instances where heat is internally produced in a system. This may happen as a result of an electric current flow, such as in an electrical filament, or as a result of an atomic or chemical reaction taking place inside a reactor. It is important to investigate the effect of internal heat generation during the heat transfer mechanism, and this process is indicated by the internal heat generation parameter, which is usually taken as thermally dependent. With an increment in , the thermal profile enhances, as depicted in Figure 8f. The temperature gradient is elevated to a greater value by enhancing the heat generation parameter. Thus, the increased heat generation raises the temperature of the plate because the plate must diffuse more heat into the environment.
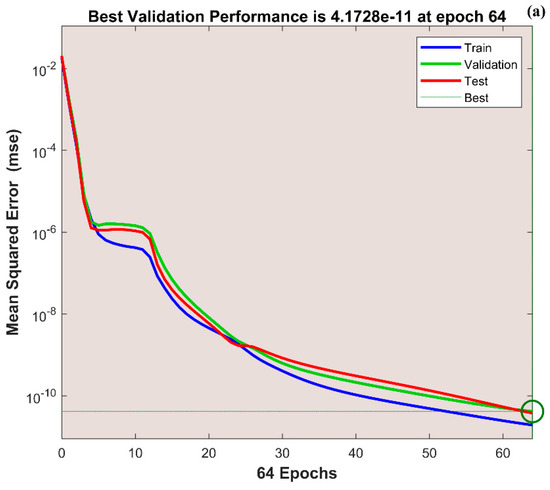
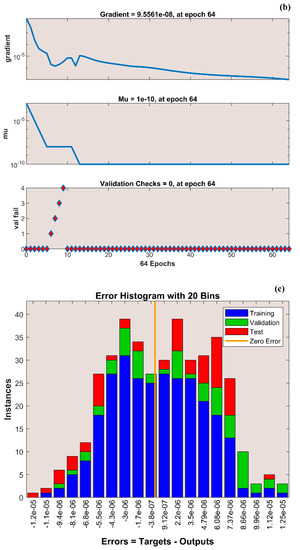
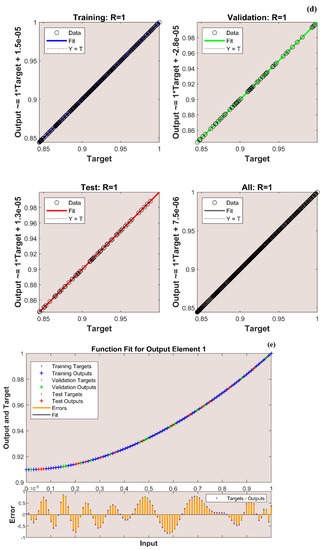
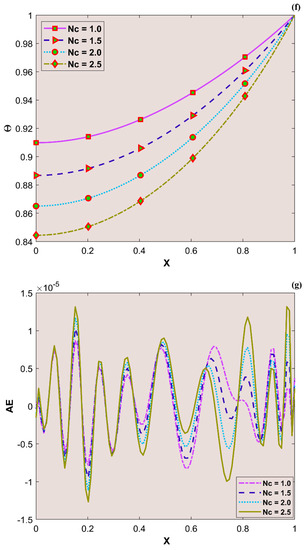
Figure 4.
(a) Training performance. (b) Training status. (c) Error histogram. (d) Regression. (e) Fit curve. (f) Thermal variation. (g) Error analysis of the ANNS-LMBS for various values.
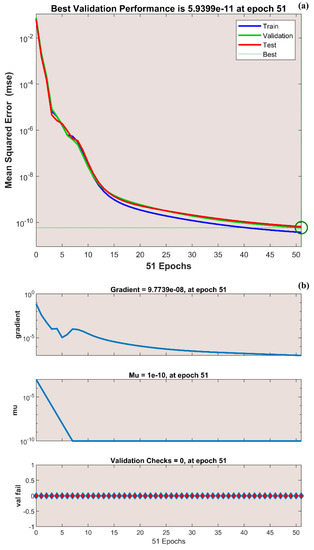
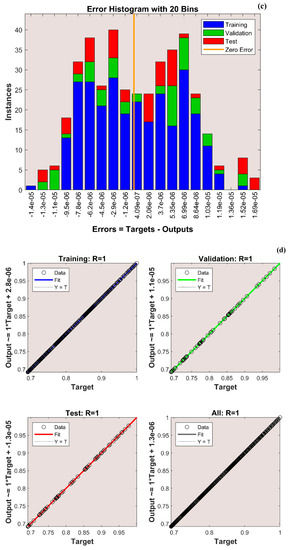
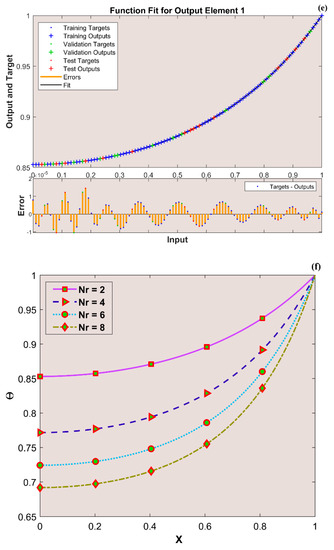
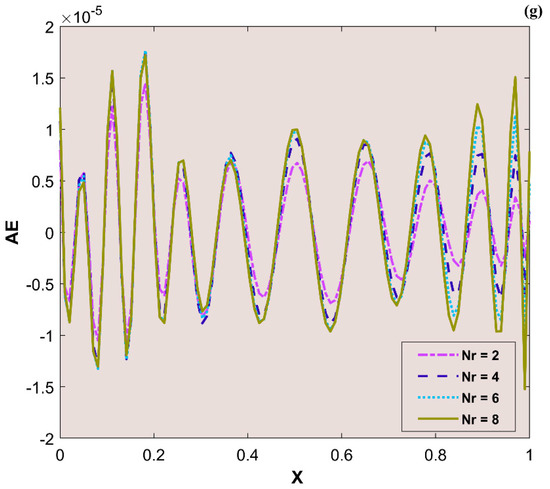
Figure 5.
(a) Training performance. (b) Training status. (c) Error histogram. (d) Regression. (e) Fit curve. (f) Thermal variation. (g) Error analysis of the ANNS-LMBS for various values.
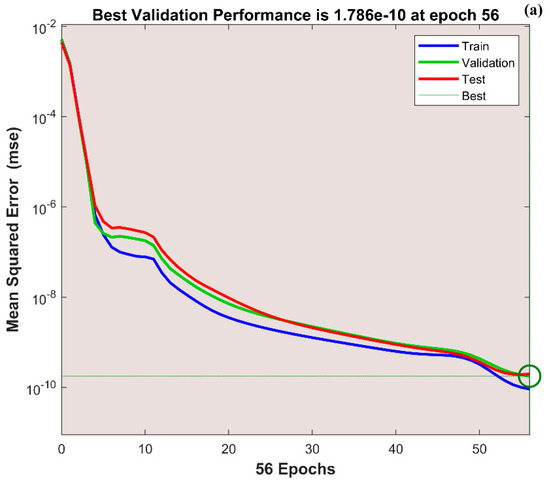
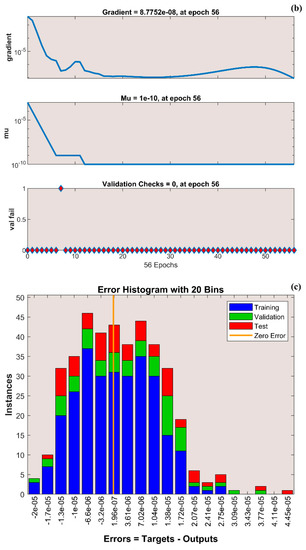
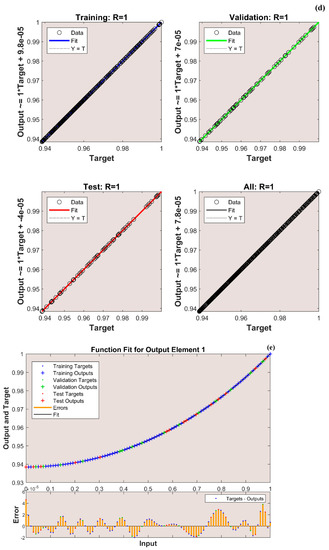
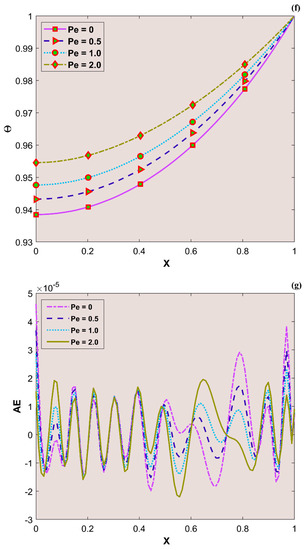
Figure 6.
(a) Training performance. (b) Training status. (c) Error histogram. (d) Regression. (e) Fit curve. (f) Thermal variation. (g) Error analysis of the ANNS-LMBS for various values.
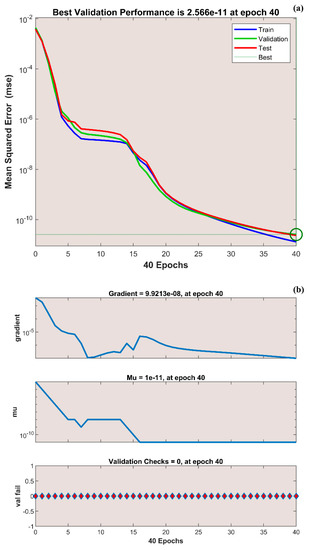
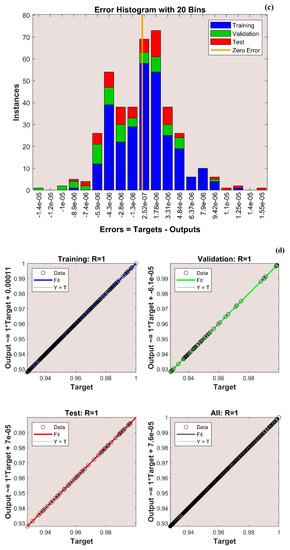
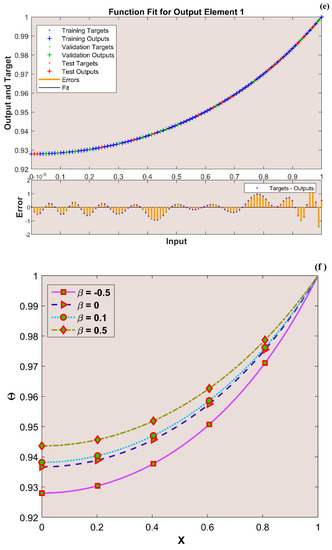
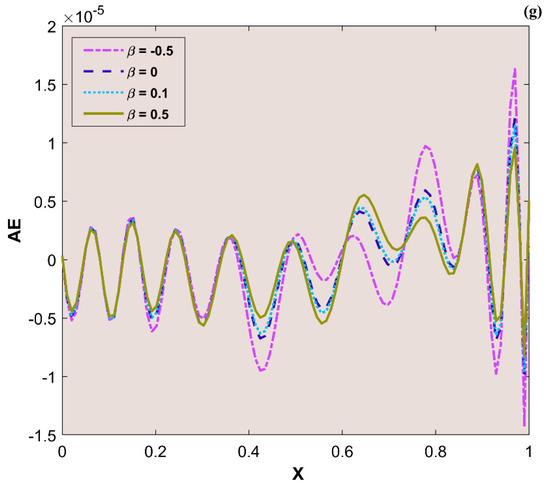
Figure 7.
(a) Training performance. (b) Training status. (c) Error histogram. (d) Regression. (e) Fit curve. (f) Thermal variation. (g) Error analysis of the ANNS-LMBS for various values.
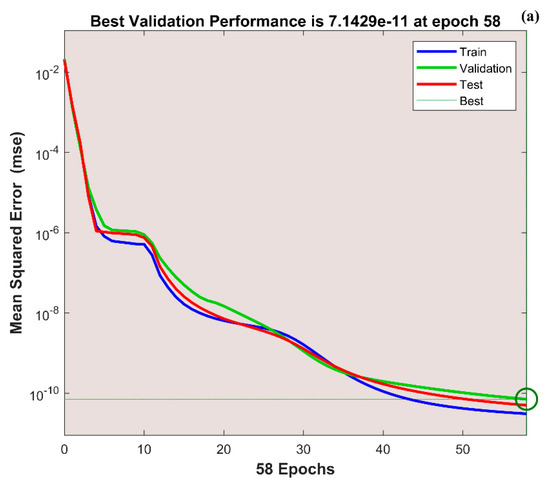
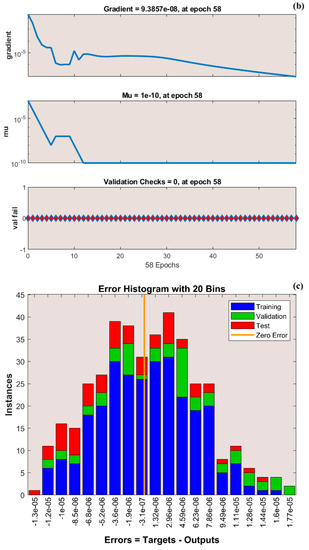
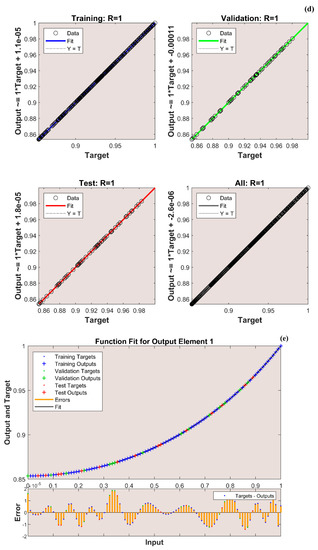
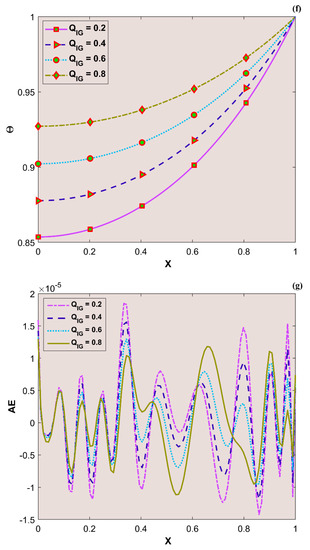
Figure 8.
(a) Training performance. (b) Training status. (c) Error histogram. (d) Regression. (e) Fit curve. (f) Thermal variation. (g) Error analysis of the ANNS-LMBS for various values.
6. Final Remarks
In the present investigation, the unsteady NF temperature dispersal within a moving plate in the presence of radiation and convection phenomena with linear temperature-dependent thermal conductivity and non-linear heat transfer coefficient is scrutinized using ANNS-LMBS modeling. Additionally, various dimensionless thermo-physical parameters’ impacts on non-dimensional temperature profiles are systematically inspected. The major outcomes may be abridged as follows:
- The transient thermal dispersion diminishes with an upsurge in the convection-conduction parameter’s magnitude. A hike in the scale of the radiation-conduction variable encourages a decrement in the thermal distribution.
- As the Peclet number heightens, the thermal dispersal improves in the moving plate.
- As the heat generation variable scale upsurges, the moving plate’s thermal distribution increases gradually.
- The transient temperature dispersion is improved when the thermal conductivity parameter’s magnitude improves.
- The variance in the thermal response of the non-Fourier model is influenced by the Vernotte number. A higher scale of this number indicates that the thermal wave is nearer to the plate’s initial side.
- The main reason for using the ANNS-LMBS to solve the HHC equation is that it has advantages such as continuous and differentiable approximate solutions, excellent interpolation features, and less memory.
- The unsteady thermal profile values of the moving plate were predicted using the data set using an artificial neural network model. The ANNS-LMBS model could accurately predict thermal values according to the analysis of the obtained MSE, coefficient of determination (R), and error rate values. The current interpretation revealed that the ANNS-LMBS methodology is a precise, useful, and practical technique for simulating the temperature distribution in the plate. The results indicated that the ANNS-LMBS is the best tool for predicting temperature values.
Author Contributions
Conceptualization, B.C.P. and I.E.S.; methodology, B.C.P. and I.E.S.; software, M.D.A. and R.S.V.K.; validation, B.C.P. and I.E.S.; formal analysis, S.R. and R.S.V.K.; investigation, S.R.; resources, I.E.S.; data curation, B.C.P.; writing—original draft preparation, S.R. and M.D.A.; writing—review and editing, I.E.S. and B.C.P.; visualization, M.D.A. and R.S.V.K.; supervision, B.C.P. and I.E.S.; project administration, I.E.S.; funding acquisition, N/A. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
Nomenclature
| Length | Time | ||
| Base temperature | Coordinate in x-direction | ||
| Density | Temperature | ||
| Specific heat capacity | Dimensionless thermal conductivity parameter | ||
| Thermal conductivity | Surface emissivity | ||
| Heat transfer coefficient | Dimensionless radiative sink parameter | ||
| Thickness | Thermal conductivity at ambient temperature | ||
| Dimensionless radiation–conduction parameter | Dimensionless time | ||
| Speed of the plate | Dimensionless convective -sink temperature | ||
| Ambient temperature | Width | ||
| Internal heat generation | Dimensionless temperature | ||
| Heat transfer coefficient | Peclet number | ||
| Stefan-Boltzmann constant | Exponent constant | ||
| Dimensionless convection–conduction parameter | Dimensionless heat generation parameter | ||
| Dimensionless axial coordinate |
References
- Shams, M.; Asghar, S.; Asif Farooq, M. The Effect of Radiation and Porosity on MHD Nanofluid Flow and Heat Transfer across a Stretching Cylinder. Waves Random Complex Media 2022, 1–19. [Google Scholar] [CrossRef]
- Batool, S.; Rasool, G.; Alshammari, N.; Khan, I.; Kaneez, H.; Hamadneh, N. Numerical Analysis of Heat and Mass Transfer in Micropolar Nanofluids Flow through Lid Driven Cavity: Finite Volume Approach. Case Stud. Therm. Eng. 2022, 37, 102233. [Google Scholar] [CrossRef]
- M Metwally, A.S.; Khalid, A.; Khan, A.A.; Iskakova, K.; Gorji, M.R.; Ehab, M. Radiation Consequences on Sutterby Fluid over a Curved Surface. J. Eng. Thermophys. 2022, 31, 315–327. [Google Scholar] [CrossRef]
- Adnan. Heat Transfer Inspection in [(ZnO-MWCNTs)/Water-EG(50:50)]Hnf with Thermal Radiation Ray and Convective Condition over a Riga Surface. Waves Random Complex Media 2022, 1–15. [Google Scholar] [CrossRef]
- Varun Kumar, R.S.; Sowmya, G. A Novel Analysis for Heat Transfer Enhancement in a Trapezoidal Fin Wetted by MoS2 + Fe3O4 + NiZnFe2O4- Methanol Based Ternary Hybrid Nanofluid. Waves Random Complex Media 2022, 1–19. [Google Scholar] [CrossRef]
- Khan, S.U.; Usman; Raza, A.; Kanwal, A.; Javid, K. Mixed Convection Radiated Flow of Jeffery-Type Hybrid Nanofluid Due to Inclined Oscillating Surface with Slip Effects: A Comparative Fractional Model. Waves Random Complex Media 2022, 1–22. [Google Scholar] [CrossRef]
- Algehyne, E.A.; Abdelmohsen, S.A.M.; Gowda, R.J.P.; Kumar, R.N.; Abdelbacki, A.M.M.; Gorji, M.R.; Prasannakumara, B.C. Mathematical Modeling of Magnetic Dipole Effect on Convective Heat Transfer in Maxwell Nanofluid Flow: Single and Multi-Walled Carbon Nanotubes. Waves Random Complex Media 2022, 1–16. [Google Scholar] [CrossRef]
- Varun Kumar, R.; Sowmya, G.; Jagadeesha, K.C.; Prasannakumara, B.C.; Shehzad, S.A. Inspection of Thermal Distribution through a Porous Fin of Triangular Profile with Internal Heat Generation and Electromagnetic Field. Waves Random Complex Media 2022, 1–21. [Google Scholar] [CrossRef]
- Roy, P.K.; Mondal, H.; Raj, B. Analytical and Numerical Solution of the Longitudinal Porous Fin with Multiple Power-Law-Dependent Thermal Properties and Magnetic Effects. Heat Transf. 2022, 51, 2702–2722. [Google Scholar] [CrossRef]
- Kumar, R.S.V.; Kumar, R.N.; Sowmya, G.; Prasannakumara, B.C.; Sarris, I.E. Exploration of Temperature Distribution through a Longitudinal Rectangular Fin with Linear and Exponential Temperature-Dependent Thermal Conductivity Using DTM-Pade Approximant. Symmetry 2022, 14, 690. [Google Scholar] [CrossRef]
- Gouran, S.; Ghasemi, S.E.; Mohsenian, S. Effect of Internal Heat Source and Non-Independent Thermal Properties on a Convective–Radiative Longitudinal Fin. Alex. Eng. J. 2022, 61, 8545–8554. [Google Scholar] [CrossRef]
- Sowmya, G.; Varun Kumar, R.S.; Alsulami, M.D.; Prasannakumara, B.C. Thermal Stress and Temperature Distribution of an Annular Fin with Variable Temperature-Dependent Thermal Properties and Magnetic Field Using DTM-Pade Approximant. Waves Random Complex Media 2022, 1–29. [Google Scholar] [CrossRef]
- Das, R.; Mishra, S.C.; Kumar, T.B.P.; Uppaluri, R. An Inverse Analysis for Parameter Estimation Applied to a Non-Fourier Conduction–Radiation Problem. Heat Transf. Eng. 2011, 32, 455–466. [Google Scholar] [CrossRef]
- Kundu, B.; Lee, K.-S. A Non-Fourier Analysis for Transmitting Heat in Fins with Internal Heat Generation. Int. J. Heat Mass Transf. 2013, 64, 1153–1162. [Google Scholar] [CrossRef]
- Zhang, X.-Y.; Li, X.-F. Thermal Performance of a Convective Functionally Graded Fin Using Fractional Non-Fourier Heat Conduction. J. Thermophys. Heat Transf. 2022, 36, 3–12. [Google Scholar] [CrossRef]
- Varun Kumar, R.S.; Sowmya, G.; Prasannakumara, B.C. Significance of Non-Fourier Heat Conduction in the Thermal Analysis of a Wet Semi-Spherical Fin with Internal Heat Generation. Waves Random Complex Media 2022, 1–17. [Google Scholar] [CrossRef]
- Ghasemi, M.H.; Hoseinzadeh, S.; Memon, S. A Dual-Phase-Lag (DPL) Transient Non-Fourier Heat Transfer Analysis of Functional Graded Cylindrical Material under Axial Heat Flux. Int. Commun. Heat Mass Transf. 2022, 131, 105858. [Google Scholar] [CrossRef]
- Jagadeesha, K.C.; Kumar, R.S.V.; Elattar, S.; Kumar, R.; Prasannakumara, B.C.; Khan, M.I.; Malik, M.Y. A Physical Depiction of a Semi-Spherical Fin Unsteady Heat Transfer and Thermal Analysis of a Fully Wetted Convective-Radiative Semi-Spherical Fin. J. Indian Chem. Soc. 2022, 99, 100457. [Google Scholar] [CrossRef]
- Sowmya, G.; Sarris, I.E.; Vishalakshi, C.S.; Kumar, R.S.V.; Prasannakumara, B.C. Analysis of Transient Thermal Distribution in a Convective–Radiative Moving Rod Using Two-Dimensional Differential Transform Method with Multivariate Pade Approximant. Symmetry 2021, 13, 1793. [Google Scholar] [CrossRef]
- Kausar, M.S.; Hussanan, A.; Waqas, M.; Mamat, M. Boundary Layer Flow of Micropolar Nanofluid towards a Permeable Stretching Sheet in the Presence of Porous Medium with Thermal Radiation and Viscous Dissipation. Chin. J. Phys. 2022, 78, 435–452. [Google Scholar] [CrossRef]
- Biswas, R.; Hossain, M.S.; Islam, R.; Ahmmed, S.F.; Mishra, S.R.; Afikuzzaman, M. Computational Treatment of MHD Maxwell Nanofluid Flow across a Stretching Sheet Considering Higher-Order Chemical Reaction and Thermal Radiation. J. Comput. Math. Data Sci. 2022, 4, 100048. [Google Scholar] [CrossRef]
- Mansoor, M.; Nawaz, Y.; Ul-Hassan, Q.M. Nonsimilar Numerical Analysis for the Mixed Convective Flow of Casson Fluid with Thermal Radiations and Chemical Reactions. Waves Random Complex Media 2022, 1–18. [Google Scholar] [CrossRef]
- Correa, E.D.; Quirino, J.M.; Sobral, R.L.; Corrêa, J.F.; Gama, R.M.S. An Analytical and a Numerical Method for Nonlinear Convection-Radiation Problems in Porous Fins. Adv. Math. Phys. 2022, 2022, e9033324. [Google Scholar] [CrossRef]
- Sowmya, G.; Lashin, M.M.A.; Khan, M.I.; Kumar, R.S.V.; Jagadeesha, K.C.; Prasannakumara, B.C.; Guedri, K.; Bafakeeh, O.T.; Mohamed Tag-ElDin, E.S.; Galal, A.M. Significance of Convection and Internal Heat Generation on the Thermal Distribution of a Porous Dovetail Fin with Radiative Heat Transfer by Spectral Collocation Method. Micromachines 2022, 13, 1336. [Google Scholar] [CrossRef]
- Ferdows, M.; Shamshuddin, M.D.; Salawu, S.O.; Zaimi, K. Numerical Simulation for the Steady Nanofluid Boundary Layer Flow over a Moving Plate with Suction and Heat Generation. SN Appl. Sci. 2021, 3, 264. [Google Scholar] [CrossRef]
- Varun Kumar, R.S.; Saleh, B.; Sowmya, G.; Afzal, A.; Prasannakumara, B.C.; Punith Gowda, R.J. Exploration of Transient Heat Transfer through a Moving Plate with Exponentially Temperature-Dependent Thermal Properties. Waves Random Complex Media 2022, 1–19. [Google Scholar] [CrossRef]
- Mabood, F.; Shamshuddin, M.D.; Mishra, S.R. Characteristics of Thermophoresis and Brownian Motion on Radiative Reactive Micropolar Fluid Flow towards Continuously Moving Flat Plate: HAM Solution. Math. Comput. Simul. 2022, 191, 187–202. [Google Scholar] [CrossRef]
- Arulmozhi, S.; Sukkiramathi, K.; Santra, S.S.; Edwan, R.; Fernandez-Gamiz, U.; Noeiaghdam, S. Heat and Mass Transfer Analysis of Radiative and Chemical Reactive Effects on MHD Nanofluid over an Infinite Moving Vertical Plate. Results Eng. 2022, 14, 100394. [Google Scholar] [CrossRef]
- Abellán García, J.; Fernández Gómez, J.; Torres Castellanos, N. Properties Prediction of Environmentally Friendly Ultra-High-Performance Concrete Using Artificial Neural Networks. Eur. J. Environ. Civ. Eng. 2022, 26, 2319–2343. [Google Scholar] [CrossRef]
- Bas, E.; Egrioglu, E.; Kolemen, E. Training Simple Recurrent Deep Artificial Neural Network for Forecasting Using Particle Swarm Optimization. Granul. Comput. 2022, 7, 411–420. [Google Scholar] [CrossRef]
- Gupta, P.; Kumar, P.; Rao, S.M.V. Artificial Neural Network Model for Single-Phase Real Gas Ejectors. Appl. Therm. Eng. 2022, 201, 117615. [Google Scholar] [CrossRef]
- Zhu, Y.; Newbrook, D.W.; Dai, P.; de Groot, C.H.K.; Huang, R. Artificial Neural Network Enabled Accurate Geometrical Design and Optimisation of Thermoelectric Generator. Appl. Energy 2022, 305, 117800. [Google Scholar] [CrossRef]
- Churyumov, A.; Kazakova, A.; Churyumova, T. Modelling of the Steel High-Temperature Deformation Behaviour Using Artificial Neural Network. Metals 2022, 12, 447. [Google Scholar] [CrossRef]
- Elahi, E.; Zhang, Z.; Khalid, Z.; Xu, H. Application of an Artificial Neural Network to Optimise Energy Inputs: An Energy- and Cost-Saving Strategy for Commercial Poultry Farms. Energy 2022, 244, 123169. [Google Scholar] [CrossRef]
- Ullah, H.; Khan, I.; Fiza, M.; Hamadneh, N.N.; Fayz-Al-Asad, M.; Islam, S.; Khan, I.; Raja, M.A.Z.; Shoaib, M. MHD Boundary Layer Flow over a Stretching Sheet: A New Stochastic Method. Math. Probl. Eng. 2021, 2021, e9924593. [Google Scholar] [CrossRef]
- Raja, M.A.Z.; Shoaib, M.; Hussain, S.; Nisar, K.S.; Islam, S. Computational Intelligence of Levenberg-Marquardt Backpropagation Neural Networks to Study Thermal Radiation and Hall Effects on Boundary Layer Flow Past a Stretching Sheet. Int. Commun. Heat Mass Transf. 2022, 130, 105799. [Google Scholar] [CrossRef]
- Alhadri, M.; Raza, J.; Yashkun, U.; Lund, L.A.; Maatki, C.; Khan, S.U.; Kolsi, L. Response Surface Methodology (RSM) and Artificial Neural Network (ANN) Simulations for Thermal Flow Hybrid Nanofluid Flow with Darcy-Forchheimer Effects. J. Indian Chem. Soc. 2022, 99, 100607. [Google Scholar] [CrossRef]
- Aziz, A.; Lopez, R.J. Convection-Radiation from a Continuously Moving, Variable Thermal Conductivity Sheet or Rod Undergoing Thermal Processing. Int. J. Therm. Sci. 2011, 50, 1523–1531. [Google Scholar] [CrossRef]
- Sun, Y.-S.; Ma, J.; Li, B.-W. Spectral Collocation Method for Convective–Radiative Transfer of a Moving Rod with Variable Thermal Conductivity. Int. J. Therm. Sci. 2015, 90, 187–196. [Google Scholar] [CrossRef]
- Ma, J.; Sun, Y.; Li, B. Spectral Collocation Method for Transient Thermal Analysis of Coupled Conductive, Convective and Radiative Heat Transfer in the Moving Plate with Temperature Dependent Properties and Heat Generation. Int. J. Heat Mass Transf. 2017, 114, 469–482. [Google Scholar] [CrossRef]
- Sowmya, G.; Gamaoun, F.; Abdulrahman, A.; Varun Kumar, R.S.; Prasannakumara, B.C. Significance of Thermal Stress in a Convective-Radiative Annular Fin with Magnetic Field and Heat Generation: Application of DTM and MRPSM. Propuls. Power Res. 2022, in press. [Google Scholar] [CrossRef]
- Ma, J.; Sun, Y.; Li, B. Simulation of Combined Conductive, Convective and Radiative Heat Transfer in Moving Irregular Porous Fins by Spectral Element Method. Int. J. Therm. Sci. 2017, 118, 475–487. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).