Abstract
Long-term fiber tissue remodeling and the progressive thickening of the aortic valve leaflets called calcific aortic stenosis lead to cardiac blood outflow obstruction. This disease is the most prevalent heart valve pathology in developed countries. Surgeons can perform aortic valve replacement through traditional open-heart surgery involving a cut (incision) in the chest or use minimally invasive methods such as transcatheter aortic valve implantation (TAVI). These types of surgery have numerous advantages and limitations. Recently, the Ozaki operation for aortic valve replacement using tissue from the autologous pericardium has been proposed. Despite being a promising technique for aortic valve pathology treatment, there is a lack of long-term results and optimal selection of leaflet sizing. Numerical fluid simulations can help surgeons predict operation outcomes for each patient. Nevertheless, the description of the material model for leaflet mechanics leaves an open question. Furthermore, selecting the most suitable model to describe the different conditions of the aortic valve is difficult. We performed a numerical analysis of aortic valve leaflet material models to describe the hemodynamics in normal, pathological, and Ozaki cases. We also reveal wall shear stress, von Mises stress, and displacement distributions. Based on the parameters mentioned above, we found that the Ozaki case model behaved similarly to the mathematical model describing the normal case. Numerical simulations also provide information on the mechanisms of aortic valve work in different states of the heart cycle.
Keywords:
numerical simulations; aortic valve; leaflet; blood flow; FSI; mathematical model; hyperelasticity MSC:
76Z05
1. Introduction
Aortic stenosis is a common valvular disorder, especially in the elderly (over 15% of adults aged 70 suffer from this pathology), leading to obstruction of the left ventricular outflow tract [1]. Aortic stenosis results in blood flow decrease to the vertebral, basilar, and carotid arteries. Moreover, an aortic valve pathological constriction narrows the valve aperture, and leaflet deformation disturbs blood flow between the left ventricle and the aorta. Aortic valve leaflet calcification appears to be the reason for such disorders. Calcinosis spreads from the base of the cusps to the free edge, reducing their mechanical function and effective orifice area [2]. It also imposes an additional load on the heart, causing it to work more intensively. Therefore, it may lead to disorders in heart muscle work.
Furthermore, severe aortic valve stenosis is one of the major causes of premature mortality among older adults. As life expectancy increases, the number of people living with aortic valve disorders is expected to triple from 290,000 in 2003 to over 850,000 by 2050 [3,4,5].
There are more than 275,000 aortic valve reconstructive operations in the world annually [6]. In the past, management options were either open-heart surgery or transcatheter aortic valve implantation (TAVI). However, a rapid evolution in the approach to TAVI and selection and stability guidelines has emerged in the last 5–10 years, as approved by numerous papers [7,8,9,10,11,12].
Artificial valves can generally be divided into two categories: mechanical and bioprosthetic valves. The major disadvantages of mechanical valves are thromboembolic complications and the need for lifelong anticoagulation therapy. On the contrary, bioprosthetic valves are completely devoid of the drawbacks of mechanical valves. Nevertheless, these implants are prone to structural valve degeneration, consequently causing repeated surgery [13]. The bioprosthetic valve leaflets are fabricated from specific porcine valves or bovine heart tissues. Despite advancements in artificial bioprosthetic valve technology, the hemodynamic characteristics are still not comparable to native human valves [14].
A solution was proposed by S. Ozaki et al. [15,16,17,18,19]. The technique of aortic valve reconstruction using glutaraldehyde-treated autologous pericardium has been actively adopted in clinical practice [20,21,22]. Daily Ozaki surgeries performed worldwide help gather meaningful statistics. The conventional Ozaki procedure requires a large amount of pericardium tissue; therefore, the technique still requires conventional sternotomy. Thus, aortic valve neo-cuspidation procedure (AVNeo) improvement methodologies have been suggested. For example, the authors of [23,24] introduced a mini-invasive method of the Ozaki operation and its potential for young people and pediatric patients with congenital heart disease.
The Ozaki procedure is a relatively new technique for treating aortic valve pathology. Although it shows good mid-term results, data on long-term circumstances are few. Therefore, it is too early to discuss the Ozaki procedure’s absolute superiority over other methods of aortic valve replacement. The best option depends on the specific aortic valve problem, as well as the expertise and experience of the health care team.
Computational modeling and in silico simulations may be crucial in predicting long-term adverse outcomes. Computational models of aortic valve performance can be used to develop decision-making support software based on robust machine learning algorithms [25,26,27,28,29].
There are various methods utilized for aortic valve hemodynamic simulation. A substantial review of contemporary aortic valve models has previously been presented [30]. Papers [31,32,33,34] are devoted to different aspects of aortic leaflet geometric design and modeling. Experimental methods, primarily PIV (particle image velocimetry), have been adopted to visualize streamlines and vortical flow fields through artificial aortic valves, as presented in [35,36,37]. Most papers discuss FSI (fluid–structure interaction) models falling into two general categories: (a) immersed boundary methods (a solid body is immersed in a fixed fluid mesh); and (b) an arbitrary Lagrangian–Eulerian approach (a fluid mesh is moving simultaneously with a solid-body grid).
Peskin developed the first categorical approach (called the immersed boundary method) in 1972 [38] to simulate fluid–structure interaction. A fixed grid discretizes the fluid domain; Navier–Stokes equations are written in a Eulerian coordinate system, while the structure is represented in Lagrangian coordinates. The development of this method is presented in papers [39,40]. The advantages of the immersed boundary method include low computational costs and a simplified grid generation, which avoids mesh movement/regeneration. On the other hand, this method exhibits less accurate blood pressure on the leaflet and wall shear stress, which is an important hemodynamic factor in assessing cardiovascular pathology development due to boundary smearing [41,42].
Another category of methods is based on the ALE (arbitrary Lagrangian–Eulerian) approach considering mesh deformation in the fluid domain with respect to the solid domain motion. The ALE–FSI approach provides more accurate results at the fluid–structure interface. Although, the method demands significantly higher computational resources.
Two-dimensional (2D) models of aortic valve blood flow are proposed in [43,44]. Additionally, biotransport aspects due to aortic valve pathology are discussed in [45]. Three-dimensional (3D) models are presented in papers [46,47,48]. Patient-specific models are presented in papers [49,50,51]. Furthermore, there are alternative methods of FSI problem solution for aortic valve hemodynamic simulation such as the smoothed particle hydrodynamics method (SPH) [52,53] and the lattice Boltzmann method (LBM) [54]. Recently, studies on the performance of the aortic valve cusp’s mechanical properties during blood flow are of major interest to researchers [55]. However, the correct choice of the leaflet material model and the appropriate parameters are still an open question. Table 1 compares the models used with parameters from various sources. Thus, choosing the most appropriate model to describe aortic valve biomechanics under various conditions is still challenging. In the present work, we describe a numerical analysis of aortic valve leaflet material models to simulate blood flow for the following three cases: blood flow in the healthy state, pathology, and post-Ozaki procedure. We assume similar results for the normal state and Ozaki case but different results for the pathological case, suggesting the use of appropriate material models.

Table 1.
Comparison of material models to describe aortic valve biomechanics.
2. Materials and Methods
We solved the problem with the FSI approach using COMSOL Multiphysics (Comsol Inc., Stockholm, Sweden) software. An idealized two-dimensional aortic valve geometry was designed on the basis of ultrasound images and the literature review. We performed a numerical analysis of the hemodynamic characteristics depending on the aortic valve leaflet material model used in different situations. Velocity, pressure, WSS, and OSI were computed for three cases: normal, pathological, and Ozaki procedure.
2.1. Geometry and Meshing
Using data from [42,44], we designed an idealized 2D geometry including the aortic valve cusp, aorta root, Valsalva sinus, and ascending aorta (Figure 1). The geometric dimensions are also shown in Figure 1b.
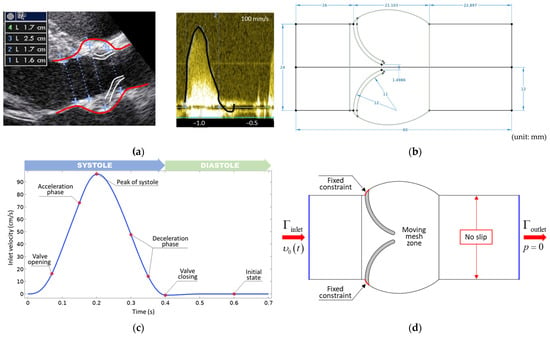
Figure 1.
(a) B-mode views are used to determine aortic valve dimensions and the time-dependent inlet velocity profile measured via pulsed Doppler mode [44]. (b) Idealized 2D geometry with dimensions. (c) Velocity profile applied at the inlet boundary. (d) Boundary conditions.
A mesh convergence study was performed at steady-state peak velocity to determine the optimum mesh density. We observed that the accuracy of the solution does not change for models with more than 10,000 elements. We used five boundary layers to calculate accurately near the walls. Additionally, the mesh was denser in the valve leaflets’ closure as shown in Figure 2a.
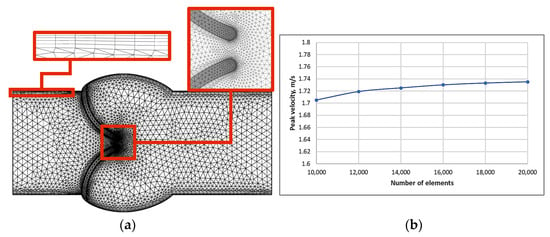
Figure 2.
(a) Mesh view and (b) the peak velocity’s dependence on the number of mesh elements.
We conducted a sensitivity analysis of the velocity components to satisfy the mesh independency requirement. The dependence of the peak velocity on several mesh elements is shown in Figure 2b. Increasing the number of mesh elements does not result in a large change in peak velocity values.
2.2. Fluid Properties
Blood flow is considered an incompressible Newtonian fluid flow with a constant density of 1060 kg/m3 and dynamic viscosity of 0.004 Pa∙s. The average Reynolds number is equal to 3685, approving the turbulent nature of the fluid flow through the valve. Furthermore, the modeled flow is pulsatile, so turbulent zones are expected to occur in the downstream regions. Blood, a multiphase fluid comprising plasma, blood cells, and platelets, exhibits a shear-thinning behavior at low shear rates and near-Newtonian behavior at higher shear rates. Recently, blood flow was shown to be Newtonian in turbulent downstream flows [63].
Many turbulent models are used for hemodynamic modeling in the aortic valve. Some authors have used a RANS-based model, such as Spalart–Allmaras [64], [44], [49], or other models. Another approach is to use a large eddy simulation (LES) model; unlike RANS models, Navier–Stokes equations are filtered from eddies that are too small to be calculated using computational discretization. A LES model was used for aortic valve simulation in [65,66]. We should note that LES models do not apply to 2D geometry. Furthermore, there is a direct numerical simulation (DNS) where full Navier–Stokes equations are solved without averaging, filtering, or assumptions about the production and dissipation of turbulence. This kind of simulation requires very fine temporal and spatial discretization and, consequently, considerable computational resources for its solution.
We used a RANS model to simulate turbulent flow. The model introduced two additional transport equations and two dependent variables: the turbulent kinetic energy (k) and the turbulent dissipation rate (ε).
2.3. Mechanical Properties of Aortic Valve Leaflets
To model three cases of aortic valve cusps (healthy state, pathology, and Ozaki procedure), it is necessary to describe the mechanical properties of the aortic valve leaflet corresponding to these cases.
2.3.1. Mechanical Properties of Aortic Valve Leaflets in the Healthy State
The three-parameter isotropic hyperelastic Mooney–Rivlin model was adopted to model aortic cusps in the healthy state:
where . We described healthy state aortic valve leaflets using an isotropic hyperelastic model following the study of May-Newman et al. [67]. They showed that invariant-based law prediction requires fewer computations than fiber-based descriptions for computational efficiency. They showed a strain energy function of two strain invariants, which used only three coefficients, and accurately predicted the stress–strain behavior over a wide range of deformations.
We must acknowledge that mechanical models, either isotropic or anisotropic, consider structural composition effects but do not show mechanical compliance by themselves. We did not obtain the anisotropic hyperelastic model for compliant tissue or the isotropic hyperelastic model for strengthened tissue. Experimental tests for aortic valve leaflets provided us with a J-shape curve that either isotropic or anisotropic models could successfully approximate. The prevalent structural component of aortic valve (AV) tissue is collagen [68]. If we assume that healthy leaflets’ mechanical properties strongly depend on the mechanical behavior of collagen fibers, a transversally isotropic model can be applied to such a case.
The thickness of the AV is less than the other two in-plane dimensions (by two orders of magnitude), and the AV is considered a planar tissue [69,70]; therefore, the 2D case described here is also valid. Weinberg et al. [71] confirmed that transversally isotropic models can be used with several limitations, such as 2D cases.
The tensile strength of collagen is approximately 120 MPa, which is only one order of magnitude lower than that of high tensile steel (about 1110 MPa), and an elastic modulus of about 1.2 GPa, which confers substantial stiffness [71]. However, it stretches only minimally (about 13%) [72]. On the other hand, elastic fibers are the most extensible biosolids with a low modulus of approximately 0.3–1.1 MPa and can reach failure strains of >150%. However, elastic fibers demonstrate a low tensile strength of approximately 2 MPa, which limits their load-bearing capacity [68].
Therefore, we assumed that the fibrous architecture of the aortic valve tissue was a homogeneous distribution of collagen fibers oriented in a single direction, circumferential to the longitudinal axis.
2.3.2. Mechanical Properties of Calcified Aortic Valve Leaflets
Following Qin et al. [73], the calcification was assumed to be homogeneous, isotropic, and linear elastic. We assumed that the leaflets were completely calcified. The calcified cusps become stiffer, and a non-linear response due to soft tissue can be neglected. Authors of various papers on calcified valve hemodynamic simulation also share this assumption [44,49]. The linear elastic material can be described using Young’s modulus () and Poisson’s ratio () (Table 1).
2.3.3. Mechanical Properties of AVNeo Aortic Valve Leaflets (Ozaki Operation)
When performing the Ozaki procedure, aortic valve leaflets are cut from the pericardium with a heterogeneous distribution of collagen fibers. Anisotropic hyperelastic models such as the Holzapfel–Gasser–Ogden model [74] can be exploited in this case:
where , , , , and are the material parameters; is the first deviatoric strain invariant; and is the pseudo-invariant of and . Parameter κ (0 ≤ κ ≤ 1/3) describes the level of dispersion in the fiber directions. When κ = 0, the fibers are completely aligned (no dispersion). When κ = 1/3, the fibers are randomly distributed, and the material becomes isotropic.
2.4. Mathematical Problem Statement
We used Navier–Stokes equations and an incompressibility equation to describe fluid flow:
where is the fluid velocity, is the stress tensor, is the fluid density, is the pressure, and is the extra stress tensor. We used the model to describe turbulent flow:
where is the turbulent kinetic energy; is the turbulent viscosity; is the turbulent kinetic energy dissipation rate; and , , , , and are the model parameters. Considering rigid body dynamics, the equation of motion is written as:
where is the density, is the displacement field, is the Cauchy stress tensor, and is the volumetric force/force per deformed volume in the actual configuration.
For hyperelastic materials, the relationship between stress and strain is defined as follows:
where is the strain energy density.
2.5. Boundary Conditions
Equations (4)–(9) must be supplemented by initial and boundary conditions to provide the system closure.
No-slip boundary condition:
Velocity profile set at the inlet:
Pressure is set at the outlet.
The FSI interface states that the fluid displacements and solid domain must be compatible. Tractions at this boundary must be at equilibrium, and the fluid must obey the no-slip condition. The following equations create these conditions:
2.6. FSI Problem
The FSI problem was solved using the ALE–FSI approach in the COMSOL Multiphysics software (Comsol Inc., Stockholm, Sweden) package. In the ALE method, the movement of a solid body is described using a reference coordinate system that can be arbitrarily moved without any relation to the structure’s transformation or fluid movement. As a result, both parts effectively combine, and the description located in the transformation flow becomes possible. We used the Navier–Stokes equation to describe the fluid motion. Then, we determined the total force acting on the solid:
where is pressure, is dynamic viscosity, and is normal to the solid body boundary.
The Navier–Stokes equations are solved in the spatial (deformed) frame, whereas the equations of solid mechanics are defined in the material (undeformed) frame, a transformation of the force is necessary:
where and are the mesh element scale factors for the spatial frame and the material frame, respectively.
3. Results
In this section, we present the results obtained for velocity, pressure, von Mises stress, wall shear stress (WSS), and oscillatory shear index (OSI) for three aortic valve cases: normal, aortic stenosis (calcification of cusps), and aortic valve neo-cuspidation (Ozaki operation).
3.1. Velocity Field and Pressure
The inlet velocity profile is shown in Figure 1c, with a maximum velocity of 98 cm/s at 0.21 s. Figure 3a–c shows the flow velocity profiles through the aortic valve. The maximum flow rate for a healthy valve was 1.7 m/s at 0.19 s; for calcified leaflets, the maximum rate reached 2.8 m/s at 0.2 s; for the Ozaki procedure model of the aortic valve, the maximum rate was 1.53 m/s at 0.18 s. The maximum values throughout the cardiac cycle are shown in Figure 1d.
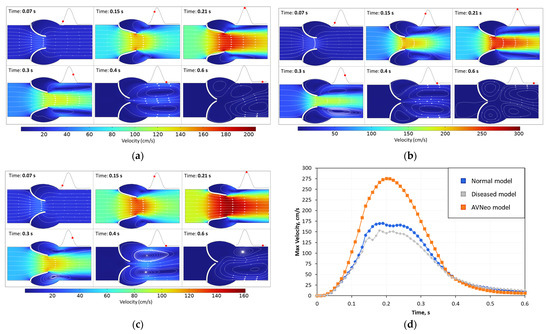
Figure 3.
Velocity field and streamlines for (a) healthy state, (b) diseased model, (c) AVNeo model, and (d) maximum velocity. Time points are shown with red dots on the cardiac cycle. Flow direction is demonstrated with streamlines.
Comparing the results, we can say that the first case with a maximal velocity of 1.7 m/s describes normal conditions, the second with a maximal velocity of 2.8 m/s simulates mild aortic stenosis, and the third with a maximal velocity of 1.53 m/s indicates the absence of stenosis and normal blood flow. Similar results can also be observed in papers [75,76,77]. Many papers have not considered the turbulent nature of fluid flow despite the average Reynolds number values being about 3000 for similar geometries and flow velocities, which suggests a transient regime.
Furthermore, vortex phenomena can be observed in Figure 3a–c. In the first case, vortices begin forming at t = 0.15 because the leaflets move. However, they disappear quickly, and two new circulating streams are created only in the middle of the diastolic phase (t = 0.4 s). The vortices are directed clockwise and counterclockwise. After full closure, the vortices practically dissolve because the velocity is close to zero.
Figure 4 compares the calculated results of the peak velocities for the normal and Ozaki cases with in vivo experimental data [78]. The results provide a fairly accurate description of the experimental data.
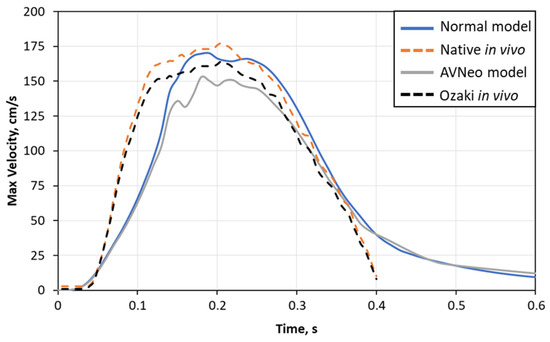
Figure 4.
Comparison between peak velocity from model and in vivo experimental data [78].
The values of the transvalvular pressure gradient are shown in Figure 5. In the calcified aortic valve cusps, there is an elevated pressure relative to other cases, reaching a maximum of 17.8 mmHg. The peak pressures for the healthy state and Ozaki procedure are 7 and 6 mmHg, respectively.
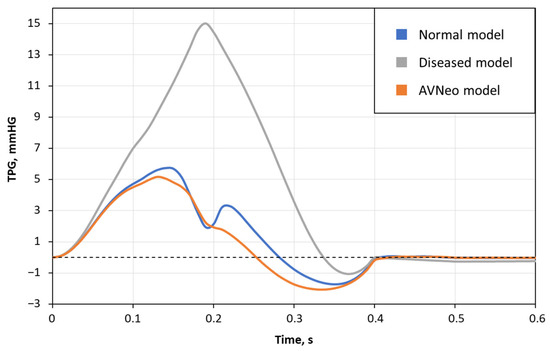
Figure 5.
Transvalvular pressure gradient (TPG) for healthy, calcified, and neo-cuspidated aortic valves.
Vortices form earlier and are maintained longer with the calcified leaflets. Unlike the first case, two circulation streams begin to form at t = 0.3. They point in opposite directions too. However, they do not disappear completely during the full cardiac cycle. Moreover, two other vortices form in the sinus, suggesting that the next blood flow portion will face alongside them and vortices can accumulate. We can observe asymmetric vortices in the third case because different leaflets move. One vortex becomes larger than the other as a result of symmetry.
3.2. Von Mises Stress
The distribution of von Mises stress in the aortic valve leaflets is shown in Figure 6a–c. The maximum stress values are concentrated at the base of the valve cusps. At peak systole, the maximum values were 555.4 kPa in the calcified valves, 210.4 kPa in the healthy valve leaflets, and 133.5 kPa in the case of the behavior after the Ozaki procedure.
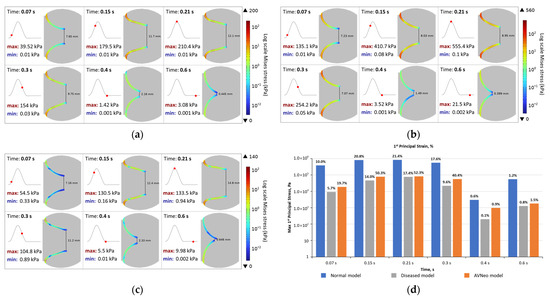
Figure 6.
Von Mises stress and minimal distance between leaflets for (a) healthy state, (b) diseased model, (c) AVNeo model, and (d) maximum first principal stress and strain. Time points are shown with red dots on the cardiac cycle. Von Mises stress is shown on a logarithmic scale with maximum and minimum values.
We also obtained the values of the first principal stresses and strains, as shown in Figure 6d. We found the highest stresses in the healthy valve model and the highest de-formations in the AVNeo model (up to 60%). Conversely, the calcified leaflet model showed minimal deformations (up to 20%).
3.3. Wall Shear Stress and Hemodynamic Indicators
Two of the key characteristics in analyzing hemodynamic models of the aortic valve are wall shear stress (WSS) and the oscillatory shear index (OSI).
The shear stress tensor can be expressed via the stress tensor and the vector of the normal to the boundary:
The oscillatory shear index shows the deviation of the wall shear stress vector direction from the prevailing direction of the blood flow during the cardiac cycle:
The WSS obtained in this study corresponds well with previous results [79,80]. The averaged WSS ranges from 0.1 up to 10 Pa. As seen in Figure 7, the WSS values are low and do not exceed 15 Pa, whereas peak magnitudes are observed at the edges of the aortic valve leaflets. The maximal values of WSS quantitively correlate with the results presented in paper [80], ranging from 23 to 32 Pa in different cases. In our case, the maximum value is 51.6 Pa for the calcified cusps model and 20.4 Pa and 23.8 Pa for the models describing normal conditions and AV neo-cuspidation of the aortic valve, respectively.
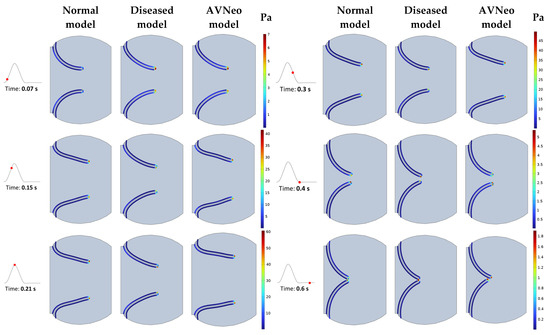
Figure 7.
Wall shear stress (WSS) distribution along the aortic valve leaflets for the healthy state, diseased, and AVNeo model during the cardiac cycle represented with red dots at key time moments.
The large WSS values for the second case are explained by the increased flow velocity, which increased relative to the normal case as a result of the decreased elasticity of the aortic valve cusps, which did not allow them to open wide enough. An OSI of 0 indicates a unidirectional net forward flow, whereas 0.5 reflects a 180-degree change in the direction of the shear vector during the cardiac cycle. The OSI values for the considered models are presented in Table 2. The wall shear stress is shown in Figure 7. The maximum values are concentrated at the ends of the leaflets and range from 5 to 55 Pa. The maximum WSS values are shown in Figure 8a.

Table 2.
The hemodynamic key indicators for normal, calcified, and AVNeo computational models.
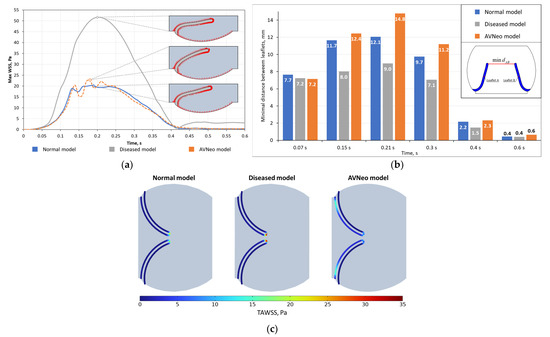
Figure 8.
(a) Maximum wall shear stress with shear vectors along the boundary; (b) minimal distance between leaflets; (c) time-averaged wall shear stress (TAWSS).
A key variable in analyzing 3D models is the effective orifice area (EOA), and the analog for 2D models is the minimum distance between the aortic valve leaflets (Figure 6b). Figure 6b shows that in this model, the distance between the leaflets was minimal and, at peak systole (t = 0.21 s), was 26% less than the normal valve condition. By contrast, the third case had the largest opening of the cusps, and at the peak systole, the distance between the leaflets was 22% greater than the normal valve condition.
Wall shear stress is one of the main characteristics of studying the biomechanics of the aortic valve. Low and high WSS affect arterial surfaces at the cellular level [81].
4. Discussion
4.1. Wall Shear Stress
Prognostic data that modern visualization methods cannot provide can be evaluated with the help of CFD and FSI modeling and biomechanical methods [86,87,88]. Nowadays, advanced computational algorithms make it possible to produce realistic and accurate 2D and 3D models, considering blood pressure, detailed anatomy, feedback mechanisms in the circulatory system, and deformation of the vessel wall [89,90,91,92]. A clinician can determine temporally and spatially varying hemodynamic parameters in a non-invasive way, including wall shear stress, oscillatory shear index, relative residence time, and pressure that cannot be studied through visualization or clinical measurements [93,94,95,96].
Hemodynamic alterations significantly affect WSS distribution on the aortic valve leaflets and are a key factor in calcification progression [49]. When leaflets become stiffer, the efficiency of blood flow transport through the restricted aortic valve decreases. The model that can capture this effect has also been approved by clinical observations [97].
In the case of blood flow, WSS may play a role in the pathogenesis of aneurysmal disease and atherosclerosis development. Lower WSS promotes atherosclerotic plaque development in blood vessels [98].
Altered wall shear stress in aortic valve leaflets may cause pathological developments such as calcification progress or structural and morphological changes. According to our results, the diseased aortic valve cusps were exposed to dramatically high WSS compared to the healthy leaflets as previously suggested by Salman et al. [80].
We should also note that the developed model demonstrates a correlation between the WSS values and small gap vicinity (the central gap between the leaflets), which was recently approved by Nowak et al. [99]. When the leaflets open, the WSS average values rapidly decrease.
4.2. Deformations
As mentioned earlier, the minimum distance between the cusps is similar to the effective opening area (EOA) in the 3D case. The obtained regularities qualitatively correlate with the results presented by Amindari et al. [55]. They also investigated aortic valve leaflet deformations in various cases. The maximum first principal deformations ranged from 15% for a normal valve condition to 35% for a calcified valve. In our model, we obtained slightly different results: For the model with calcified valves, the maximum deformations were 17.4% in peak systole, 21.4% for the normal state, and 52.3% for the AVNeo model. The experimental data for porcine valve leaflets [100] indicate deformations in the range of 30% at peak systole.
4.3. Hemodynamic Indicators
Hemodynamic indices play a crucial role in the evaluation of aortic valve performance. According to medical data [13], aortic stenosis is classified into three categories: mild, moderate, and severe. The corresponding blood flow velocities are <3.0 m/s, 3.0–4.0 m/s, and >4.0 m/s, respectively.
In this regard, it is worth noticing the vortices’ formation in Figure 2. When simulating the normal valve state, two circulating flows (t > 0.3 s) form and persist throughout the cardiac cycle, indicating a unidirectional flow. A similar pattern can be observed when simulating flow through calcified valve leaflets; however, vortices begin to form earlier and persist until the end of the diastole. Earlier vortex formation is associated with a higher flow velocity. In the simulation of the third case, we can observe a slight asymmetry in the movement of the valve cusps and, consequently, the displacement of the vortices relative to the middle.
The unidirectional flow is also indicated by the oscillatory shear index (OSI), which is equal to 0.024 for the normal model, 0.03 for calcified cusps, and 0.04 for the AVNeo model (Ozaki procedure), respectively.
In mild aortic stenosis, the average transvalvular pressure gradient is <25 mmHg; in moderate, it is 25–40 mmHg; and in severe, it is >40 mmHg [82]. The maximal values of transvalvular pressure obtained in this model are shown in Figure 3.
4.4. Vortices
It is well-established that vortices formation is related to the presence of the Valsalva sinuses [101]. Nevertheless, there are different views on blood flow dynamics within the sinuses [85,102].
Some authors consider that these chambers hold and expand the vortex ring during the systole stage, and the vortex also promotes leaflet closure [103,104,105].
Another point of view states that the vortex ring generated during valve opening is convected away toward the aorta, and a secondary vortex with an opposite rotation forms and remains within the sinus until the valve begins to close [106,107]. Our study also suggests that secondary vortices occur before the aortic leaflet closing stage. Moreover, multiple vortices occur in various cases.
4.5. Limitations
4.5.1. Geometry
Our proposed approach has some limitations. We considered an idealized 2D geometry of the aortic valve, which significantly reduces computational resources and does not accurately describe the structure of a real aortic valve. In the future, we plan to implement a 3D model considering the personalized geometry of the aortic valve.
4.5.2. Boundary Conditions
Furthermore, one of the simplifications was our description of aortic walls as absolutely rigid. In the future, a model of linearly elastic material can represent them, as implemented in the works of [45,47].On the other hand, Kivi et al. [108] compared the influence of rigid and flexible walls. They demonstrated a 0.1% difference for pressure and velocity, but computational time increased by about 20% for flexible walls.
There are ways to set outlet boundary conditions, zero outlet pressure, pressure with lag, and the Windkessel model. We used zero outlet pressure to accelerate calculations, representing one more limitation of the present model.
Despite the consistency of the model results with other studies, it would not be superfluous to specify the model parameter values on the basis of experimental data.
5. Conclusions
Our study complements existing works in the field of applicability analysis for different material models describing various medical cases. We propose a mathematical model of aortic valve biomechanics to describe the hemodynamics in the healthy state, pathology (calcification), and post-Ozaki operation (AV neo-cuspidation).
We implemented three models to describe the biomechanics of the aortic valve cusps: the three-parameter Mooney–Rivlin model, the linear elastic model, and the HGO model. We obtained the distributions of WSS and flow velocity fields. The strain values and hemodynamic indices were evaluated. The results are in qualitative and quantitative agreement with previously published works.
The linear elastic model accurately described the calcified state of the aortic valve. The HGO model described the valve leaflets after neo-cuspidation in the various ranges of key indices close to the normal aortic valve leaflets.
Author Contributions
Conceptualization, A.G.K. and N.P.; methodology, A.G.K. and N.P.; investigation, N.P. and A.G.K.; writing—original draft preparation, N.P., B.K., V.A. and A.G.K.; writing—review and editing, A.G.K.; funding acquisition, A.G.K. All authors have read and agreed to the published version of the manuscript.
Funding
This work is financially supported by the Perm Scientific and Educational Center “Rational Subsoil Use”, 2022.
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Iung, B.; Delgado, V.; Rosenhek, R.; Price, S.; Prendergast, B.; Wendler, O.; De Bonis, M.; Tribouilloy, C.; Evangelista, A.; Bogachev-Prokophiev, A.; et al. Contemporary presentation and management of valvular heart disease: The EUrobservational research programme valvular heart disease II survey. Circulation 2019, 140, 1156–1169. [Google Scholar] [CrossRef] [PubMed]
- Sucosky, P.; Shar, J.A.; Barrientos, J. Cardiovascular mechanics and disease. In Mechanobiology: From Molecular Sensing to Disease; Elsevier: Amsterdam, The Netherlands, 2019; pp. 23–45. ISBN 9780128179314. [Google Scholar]
- De Santo, L.S.; Romano, G.; Della Corte, A.; D’Oria, V.; Nappi, G.; Giordano, S.; Cotrufo, M.; De Feo, M. Mechanical aortic valve replacement in young women planning on pregnancy: Maternal and fetal outcomes under low oral anticoagulation, a pilot observational study on a comprehensive pre-operative counseling protocol. J. Am. Coll. Cardiol. 2012, 59, 1110–1115. [Google Scholar] [CrossRef] [PubMed]
- Sitges, M.; Borregaard, B.; De Paulis, R.; Nolan, P.; Woan, W.; Pearce, K.; Näumann, J.; Johnson, N.; Wait, S. Creating a better journey of care for patients with heart valve disease. Eur. Heart J. Open 2021, 1, oeab034. [Google Scholar] [CrossRef]
- Yacoub, M.H.; Takkenberg, J.J.M. Will heart valve tissue engineering change the world? Nat. Clin. Pract. Cardiovasc. Med. 2005, 2, 60–61. [Google Scholar] [CrossRef] [PubMed]
- Clark, M.A.; Duhay, F.G.; Thompson, A.K.; Keyes, M.J.; Svensson, L.G.; Bonow, R.O.; Stockwell, B.T.; Cohen, D.J. Clinical and economic outcomes after surgical aortic valve replacement in Medicare patients. Risk Manag. Healthc. Policy 2012, 5, 117–126. [Google Scholar] [CrossRef]
- Vogl, B.J.; El Shaer, A.; Crestanello, J.A.; Alkhouli, M.; Hatoum, H. Flow dynamics in the sinus and downstream of third and fourth generation balloon expandable transcatheter aortic valves. J. Mech. Behav. Biomed. Mater. 2022, 127, 105092. [Google Scholar] [CrossRef]
- Hatoum, H.; Askegaard, G.; Iyer, R.; Dasi, L.P. Atrial and ventricular flows across a transcatheter mitral valve. Interact. Cardiovasc. Thorac. Surg. 2021, 33, 1–9. [Google Scholar] [CrossRef]
- Hatoum, H.; Lilly, S.; Maureira, P.; Crestanello, J.; Dasi, L.P. The hemodynamics of transcatheter aortic valves in transcatheter aortic valves. J. Thorac. Cardiovasc. Surg. 2021, 161, 565–576.e2. [Google Scholar] [CrossRef]
- Hatoum, H.; Yousefi, A.; Lilly, S.; Maureira, P.; Crestanello, J.; Dasi, L.P. An in vitro evaluation of turbulence after transcatheter aortic valve implantation. J. Thorac. Cardiovasc. Surg. 2018, 156, 1837–1848. [Google Scholar] [CrossRef]
- Qiu, D.; Barakat, M.; Hopkins, B.; Ravaghi, S.; Azadani, A.N. Transcatheter aortic valve replacement in bicuspid valves: The synergistic effects of eccentric and incomplete stent deployment. J. Mech. Behav. Biomed. Mater. 2021, 121, 104621. [Google Scholar] [CrossRef]
- Khodaee, F.; Barakat, M.; Abbasi, M.; Dvir, D.; Azadani, A.N. Incomplete expansion of transcatheter aortic valves is associated with propensity for valve thrombosis. Interact. Cardiovasc. Thorac. Surg. 2020, 30, 39–46. [Google Scholar] [CrossRef]
- Otto, C.M.; Nishimura, R.A.; Bonow, R.O.; Carabello, B.A.; Erwin, J.P., 3rd; Gentile, F.; Jneid, H.; Krieger, E.V.; Mack, M.; McLeod, C.; et al. 2020 ACC/AHA Guideline for the Management of Patients With Valvular Heart Disease: Executive Summary: A Report of the American College of Cardiology/American Heart Association Joint Committee on Clinical Practice Guidelines. Circulation 2021, 143, E35–E71. [Google Scholar] [CrossRef]
- Ozaki, S.; Kawase, I.; Yamashita, H.; Uchida, S.; Nozawa, Y.; Takatoh, M.; Hagiwara, S. A total of 404 cases of aortic valve reconstruction with glutaraldehyde-treated autologous pericardium. J. Thorac. Cardiovasc. Surg. 2014, 147, 301–306. [Google Scholar] [CrossRef]
- Ozaki, S.; Kawase, I.; Yamashita, H.; Uchida, S.; Takatoh, M.; Kiyohara, N. Midterm outcomes after aortic valve neocuspidization with glutaraldehyde-treated autologous pericardium. J. Thorac. Cardiovasc. Surg. 2018, 155, 2379–2387. [Google Scholar] [CrossRef]
- Ozaki, S.; Kawase, I.; Yamashita, H.; Uchida, S.; Takatoh, M.; Hagiwara, S.; Kiyohara, N. Aortic valve reconstruction using autologous pericardium for aortic stenosis. Circ. J. 2015, 79, 1504–1510. [Google Scholar] [CrossRef]
- Tochii, M.; Muramatsu, T.; Amano, K.; Ishikawa, M.; Hoshino, N.; Miyagi, M.; Yamada, A.; Takami, Y.; Ozaki, Y.; Takagi, Y. “Twin Icicle” Calcifications Cause Aortic Annular Rupture. Ann. Thorac. Surg. 2018, 106, e53–e55. [Google Scholar] [CrossRef] [PubMed]
- Terazawa, T.; Kawashima, T.; Umeno, T.; Wada, T.; Ozaki, S.; Miyamoto, S.; Nakayama, Y. Mechanical characterization of an in-body tissue-engineered autologous collagenous sheet for application as an aortic valve reconstruction material. J. Biomech. 2020, 99, 109528. [Google Scholar] [CrossRef] [PubMed]
- Takami, Y.; Hoshino, N.; Kato, Y.; Sakurai, Y.; Amano, K.; Higuchi, Y.; Tochii, M.; Ishida, M.; Ishikawa, H.; Takagi, Y.; et al. Recovery from anthracycline-induced cardiomyopathy with biventricular assist and valve repairs: A case report and literature review. Int. J. Artif. Organs 2018, 41, 413–417. [Google Scholar] [CrossRef] [PubMed]
- Sá, M.P.B.O.; Perazzo, Á.M.; Zhigalov, K.; Komarov, R.; Kadyraliev, B.; Enginoev, S.; Ennker, J.; Popov, A.F.; Quarto, C.; Weymann, A.; et al. Aortic valve neocuspidization with glutaraldehyde-treated autologous pericardium (Ozaki procedure)—A promising surgical technique. Braz. J. Cardiovasc. Surg. 2019, 34, 610–614. [Google Scholar] [CrossRef]
- Okada, K.; Inoue, Y.; Haida, H.; Suzuki, S. Aortic valve reconstruction using autologous pericardium (Ozaki procedure) for active infective endocarditis: A case report. Gen. Thorac. Cardiovasc. Surg. 2018, 66, 546–548. [Google Scholar] [CrossRef]
- Komarov, R.; Chernov, I.; Enginoev, S.; Sá, M.P.B.O.; Tarasov, D. The russian conduit—Combining bentall and ozaki procedures for concomitant ascending aorta replacement and aortic valve neocuspidization. Braz. J. Cardiovasc. Surg. 2019, 34, 618–623. [Google Scholar] [CrossRef] [PubMed]
- Nguyen, D.H.; Vo, A.T.; Le, K.M.; Vu, T.T.; Nguyen, T.T.; Vu, T.T.; Pham, C.V.T.; Truong, B.Q. Minimally Invasive Ozaki Procedure in Aortic Valve Disease The Preliminary Results. Innovations 2018, 13, 332–337. [Google Scholar] [CrossRef]
- Chivers, S.C.; Pavy, C.; Vaja, R.; Quarto, C.; Ghez, O.; Daubeney, P.E.F. The Ozaki Procedure With CardioCel Patch for Children and Young Adults With Aortic Valve Disease: Preliminary Experience—A Word of Caution. World J. Pediatr. Congenit. Heart Surg. 2019, 10, 724–730. [Google Scholar] [CrossRef] [PubMed]
- Balu, A.; Nallagonda, S.; Xu, F.; Krishnamurthy, A.; Hsu, M.C.; Sarkar, S. A Deep Learning Framework for Design and Analysis of Surgical Bioprosthetic Heart Valves. Sci. Rep. 2019, 9, 18560. [Google Scholar] [CrossRef] [PubMed]
- Ferdian, E.; Dubowitz, D.J.; Mauger, C.A.; Wang, A.; Young, A.A. WSSNet: Aortic Wall Shear Stress Estimation Using Deep Learning on 4D Flow MRI. Front. Cardiovasc. Med. 2022, 8, 769927. [Google Scholar] [CrossRef]
- Du, P.; Zhu, X.; Wang, J.-X. Deep learning-based surrogate model for 3-D patient-specific computational fluid dynamics. Phys. Fluids 2022, 34, 081906. [Google Scholar] [CrossRef]
- Morales Ferez, X.; Mill, J.; Juhl, K.A.; Acebes, C.; Iriart, X.; Legghe, B.; Cochet, H.; De Backer, O.; Paulsen, R.R.; Camara, O. Deep Learning Framework for Real-Time Estimation of in-silico Thrombotic Risk Indices in the Left Atrial Appendage. Front. Physiol. 2021, 12, 694945. [Google Scholar] [CrossRef]
- Sodhani, D.; Reese, S.; Aksenov, A.; Soğanci, S.; Jockenhövel, S.; Mela, P.; Stapleton, S.E. Fluid-structure interaction simulation of artificial textile reinforced aortic heart valve: Validation with an in-vitro test. J. Biomech. 2018, 78, 52–69. [Google Scholar] [CrossRef]
- Marom, G. Numerical Methods for Fluid–Structure Interaction Models of Aortic Valves. Arch. Comput. Methods Eng. 2015, 22, 595–620. [Google Scholar] [CrossRef]
- Hsu, M.C.; Kamensky, D.; Xu, F.; Kiendl, J.; Wang, C.; Wu, M.C.H.; Mineroff, J.; Reali, A.; Bazilevs, Y.; Sacks, M.S. Dynamic and fluid–structure interaction simulations of bioprosthetic heart valves using parametric design with T-splines and Fung-type material models. Comput. Mech. 2015, 55, 1211–1225. [Google Scholar] [CrossRef]
- Hoeijmakers, M.J.M.M.; Waechter-Stehle, I.; Weese, J.; Van de Vosse, F.N. Combining statistical shape modeling, CFD, and meta-modeling to approximate the patient-specific pressure-drop across the aortic valve in real-time. Int. J. Numer. Methods Biomed. Eng. 2020, 36, e3387. [Google Scholar] [CrossRef]
- Wu, M.C.H.; Muchowski, H.M.; Johnson, E.L.; Rajanna, M.R.; Hsu, M.C. Immersogeometric fluid-structure interaction modeling and simulation of transcatheter aortic valve replacement. Comput. Methods Appl. Mech. Eng. 2019, 357, 112556. [Google Scholar] [CrossRef]
- Travaglino, S.; Murdock, K.; Tran, A.; Martin, C.; Liang, L.; Wang, Y.; Sun, W. Computational optimization study of transcatheter aortic valve leaflet design using porcine and bovine leaflets. J. Biomech. Eng. 2020, 142, 011007. [Google Scholar] [CrossRef]
- Ismail, M.; Kabinejadian, F.; Nguyen, Y.N.; Wui, E.T.L.; Kim, S.; Leo, H.L. Hemodynamic assessment of extra-cardiac tricuspid valves using particle image velocimetry. Med. Eng. Phys. 2017, 50, 1–11. [Google Scholar] [CrossRef] [PubMed]
- Hatoum, H.; Maureira, P.; Dasi, L.P. A turbulence in vitro assessment of On-X and St Jude Medical prostheses. J. Thorac. Cardiovasc. Surg. 2020, 159, 88–97. [Google Scholar] [CrossRef]
- Barakat, M.; Dvir, D.; Azadani, A.N. Fluid Dynamic Characterization of Transcatheter Aortic Valves Using Particle Image Velocimetry. Artif. Organs 2018, 42, E357–E368. [Google Scholar] [CrossRef]
- Piskin, C.S. Flow Patterns Around Heart Valves: A Numerical Method. J. Comput. Phys. 1972, 10, 252–271. [Google Scholar] [CrossRef]
- dos Santos, N.D.; Gerbeau, J.F.; Bourgat, J.F. A partitioned fluid-structure algorithm for elastic thin valves with contact. Comput. Methods Appl. Mech. Eng. 2008, 197, 1750–1761. [Google Scholar] [CrossRef]
- Ge, L.; Sotiropoulos, F. A numerical method for solving the 3D unsteady incompressible Navier-Stokes equations in curvilinear domains with complex immersed boundaries. J. Comput. Phys. 2007, 225, 1782–1809. [Google Scholar] [CrossRef] [PubMed]
- Sturla, F.; Votta, E.; Stevanella, M.; Conti, C.A.; Redaelli, A. Impact of modeling fluid-structure interaction in the computational analysis of aortic root biomechanics. Med. Eng. Phys. 2013, 35, 1721–1730. [Google Scholar] [CrossRef]
- Chandra, S.; Rajamannan, N.M.; Sucosky, P. Computational assessment of bicuspid aortic valve wall-shear stress: Implications for calcific aortic valve disease. Biomech. Model. Mechanobiol. 2012, 11, 1085–1096. [Google Scholar] [CrossRef]
- Torrado, A. Analysis of Hemodynamic Indicators in Bicuspid Aortic Valves Using a Computational Mathematical Model. Ph.D. Thesis, Instituto Superior Técnico, Lisboa, Portugal, 2015. [Google Scholar]
- Amindari, A.; Saltik, L.; Kirkkopru, K.; Yacoub, M.; Yalcin, H.C. Assessment of calcified aortic valve leaflet deformations and blood flow dynamics using fluid-structure interaction modeling. Inform. Med. Unlocked 2017, 9, 191–199. [Google Scholar] [CrossRef]
- Sadrabadi, M.S.; Hedayat, M.; Borazjani, I.; Arzani, A. Fluid-structure coupled biotransport processes in aortic valve disease. J. Biomech. 2021, 117, 110239. [Google Scholar] [CrossRef] [PubMed]
- Xu, F.; Johnson, E.L.; Wang, C.; Jafari, A.; Yang, C.H.; Sacks, M.S.; Krishnamurthy, A.; Hsu, M.C. Computational investigation of left ventricular hemodynamics following bioprosthetic aortic and mitral valve replacement. Mech. Res. Commun. 2021, 112, 103604. [Google Scholar] [CrossRef] [PubMed]
- Yan, W.; Li, J.; Wang, W.; Wei, L.; Wang, S. A Fluid-Structure Interaction Study of Different Bicuspid Aortic Valve Phenotypes Throughout the Cardiac Cycle. Front. Physiol. 2021, 12, 716015. [Google Scholar] [CrossRef]
- Tango, A.M.; Salmonsmith, J.; Ducci, A.; Burriesci, G. Validation and Extension of a Fluid–Structure Interaction Model of the Healthy Aortic Valve. Cardiovasc. Eng. Technol. 2018, 9, 739–751. [Google Scholar] [CrossRef] [PubMed]
- Kivi, A.R.; Sedaghatizadeh, N.; Cazzolato, B.S.; Zander, A.C.; Roberts-Thomson, R.; Nelson, A.J.; Arjomandi, M. Fluid structure interaction modelling of aortic valve stenosis: Effects of valve calcification on coronary artery flow and aortic root hemodynamics. Comput. Methods Programs Biomed. 2020, 196, 105647. [Google Scholar] [CrossRef]
- Luraghi, G.; Migliavacca, F.; Chiastra, C.; Rossi, A.; Reimers, B.; Stefanini, G.G.; Rodriguez Matas, J.F. Does clinical data quality affect fluid-structure interaction simulations of patient-specific stenotic aortic valve models? J. Biomech. 2019, 94, 202–210. [Google Scholar] [CrossRef]
- Kong, F.; Caballero, A.; McKay, R.; Sun, W. Finite element analysis of MitraClip procedure on a patient-specific model with functional mitral regurgitation. J. Biomech. 2020, 104, 109730. [Google Scholar] [CrossRef]
- Mao, W.; Li, K.; Sun, W. Fluid-Structure Interaction Study of Transcatheter Aortic Valve Dynamics Using Smoothed Particle Hydrodynamics. Cardiovasc. Eng. Technol. 2016, 7, 374–388. [Google Scholar] [CrossRef] [PubMed]
- McLoone, M.; Quinlan, N.J. Coupling of the meshless finite volume particle method and the finite element method for fluid–structure interaction with thin elastic structures. Eur. J. Mech. B Fluids 2022, 92, 117–131. [Google Scholar] [CrossRef]
- Yun, B.M.; Dasi, L.P.; Aidun, C.K.; Yoganathan, A.P. Computational modelling of flow through prosthetic heart valves using the entropic lattice-Boltzmann method. J. Fluid Mech. 2014, 743, 170–201. [Google Scholar] [CrossRef]
- Amindari, A.; Kırkköprü, K.; Saltık, İ.L.; Sünbüloğlu, E. Effect of non-linear leaflet material properties on aortic valve dynamics-a coupled fluid-structure approach. Eng. Solid Mech. 2021, 9, 123–136. [Google Scholar] [CrossRef]
- Feng, Y.; Cao, Y.; Wang, W.; Zhang, H.; Wei, L.; Jia, B.; Wang, S. Computational modeling for surgical reconstruction of aortic valve by using autologous pericardium. IEEE Access 2020, 8, 97343–97352. [Google Scholar] [CrossRef]
- Luraghi, G.; Matas, J.F.R.; Beretta, M.; Chiozzi, N.; Iannetti, L.; Migliavacca, F. The impact of calcification patterns in transcatheter aortic valve performance: A fluid-structure interaction analysis. Comput. Methods Biomech. Biomed. Eng. 2020, 24, 375–383. [Google Scholar] [CrossRef]
- Gilmanov, A.; Stolarski, H.; Sotiropoulos, F. Non-linear rotation-free shell finite-element models for aortic heart valves. J. Biomech. 2017, 50, 56–62. [Google Scholar] [CrossRef]
- Gilmanov, A.; Stolarski, H.; Sotiropoulos, F. Flow-Structure Interaction Simulations of the Aortic Heart Valve at Physiologic Conditions: The Role of Tissue Constitutive Model. J. Biomech. Eng. 2018, 140, 041003. [Google Scholar] [CrossRef] [PubMed]
- Gilmanov, A.; Barker, A.; Stolarski, H.; Sotiropoulos, F. Image-guided fluid-structure interaction simulation of transvalvular hemodynamics: Quantifying the effects of varying aortic valve leaflet thickness. Fluids 2019, 4, 119. [Google Scholar] [CrossRef]
- Pham, T.; Kong, F.; Martin, C.; Wang, Q.; Primiano, C.; McKay, R.; Elefteriades, J.; Sun, W. Finite Element Analysis of Patient-Specific Mitral Valve with Mitral Regurgitation. Cardiovasc. Eng. Technol. 2017, 8, 3–16. [Google Scholar] [CrossRef]
- Laville, C.; Pradille, C.; Tillier, Y. Mechanical characterization and identification of material parameters of porcine aortic valve leaflets. J. Mech. Behav. Biomed. Mater. 2020, 112, 104036. [Google Scholar] [CrossRef]
- Costa, R.P.; Nwotchouang, B.S.T.; Yao, J.; Biswas, D.; Casey, D.; McKenzie, R.; Steinman, D.A.; Loth, F. Transition to Turbulence Downstream of a Stenosis for Whole Blood and a Newtonian Analog Under Steady Flow Conditions. J. Biomech. Eng. 2022, 144, 031008. [Google Scholar] [CrossRef] [PubMed]
- Ge, L.; Leo, H.L.; Sotiropoulos, F.; Yoganathan, A.P. Flow in a mechanical bileaflet heart valve at laminar and near-peak systole flow rates: CFD simulations and experiments. J. Biomech. Eng. 2005, 127, 782–797. [Google Scholar] [CrossRef] [PubMed]
- Manchester, E.L.; Pirola, S.; Salmasi, M.Y.; O’Regan, D.P.; Athanasiou, T.; Xu, X.Y. Evaluation of Computational Methodologies for Accurate Prediction of Wall Shear Stress and Turbulence Parameters in a Patient-Specific Aorta. Front. Bioeng. Biotechnol. 2022, 10, 836611. [Google Scholar] [CrossRef]
- Manchester, E.L.; Pirola, S.; Salmasi, M.Y.; O’Regan, D.P.; Athanasiou, T.; Xu, X.Y. Analysis of Turbulence Effects in a Patient-Specific Aorta with Aortic Valve Stenosis. Cardiovasc. Eng. Technol. 2021, 12, 438–453. [Google Scholar] [CrossRef] [PubMed]
- May-Newman, K.; Lam, C.; Yin, F.C.P. A hyperelastic constitutive law for aortic valve tissue. J. Biomech. Eng. 2009, 131, 081009. [Google Scholar] [CrossRef] [PubMed]
- Korossis, S. Structure-Function Relationship of Heart Valves in Health and Disease. In Structural Insufficiency Anomalies in Cardiac Valves; IntechOpen: London, UK, 2018. [Google Scholar]
- Sacks, M.S.; Yoganathan, A.P. Heart valve function: A biomechanical perspective. Philos. Trans. R. Soc. B Biol. Sci. 2007, 362, 1369–1391. [Google Scholar] [CrossRef] [PubMed]
- Sacks, M.S.; Merryman, W.D.; Schmidt, D.E. On the biomechanics of heart valve function. J. Biomech. 2009, 42, 1804–1824. [Google Scholar] [CrossRef]
- Weinberg, E.J.; Kaazempur-Mofrad, M.R. On the constitutive models for heart valve leaflet mechanics. Cardiovasc. Eng. 2005, 5, 37–43. [Google Scholar] [CrossRef]
- Gosline, J.; Lillie, M.; Carrington, E.; Guerette, P.; Ortlepp, C.; Savage, K. Elastic proteins: Biological roles and mechanical properties. Philos. Trans. R. Soc. B Biol. Sci. 2002, 357, 121–132. [Google Scholar] [CrossRef]
- Qin, T.; Caballero, A.; Mao, W.; Barrett, B.; Kamioka, N.; Lerakis, S.; Sun, W. The role of stress concentration in calcified bicuspid aortic valve. J. R. Soc. Interface 2020, 17, 20190893. [Google Scholar] [CrossRef]
- Holzapfel, G.A.; Ogden, R.W. Constitutive modelling of arteries. Proc. R. Soc. A Math. Phys. Eng. Sci. 2010, 466, 1551–1597. [Google Scholar] [CrossRef]
- Loureiro-Ga, M.; Veiga, C.; Fdez-Manin, G.; Jimenez, V.A.; Calvo-Iglesias, F.; Iñiguez, A. A biomechanical model of the pathological aortic valve: Simulation of aortic stenosis. Comput. Methods Biomech. Biomed. Eng. 2020, 23, 303–311. [Google Scholar] [CrossRef] [PubMed]
- Vahidkhah, K.; Azadani, A.N. Supra-annular Valve-in-Valve implantation reduces blood stasis on the transcatheter aortic valve leaflets. J. Biomech. 2017, 58, 114–122. [Google Scholar] [CrossRef]
- Luraghi, G.; Matas, J.F.R.; Migliavacca, F. In silico approaches for transcatheter aortic valve replacement inspection. Expert Rev. Cardiovasc. Ther. 2021, 19, 61–70. [Google Scholar] [CrossRef]
- Saisho, H.; Scharfschwerdt, M.; Schaller, T.; Sadat, N.; Aboud, A.; Ensminger, S.; Fujita, B. Ex vivo evaluation of the Ozaki procedure in comparison with the native aortic valve and prosthetic valves. Interact. Cardiovasc. Thorac. Surg. 2022, 35, ivac199. [Google Scholar] [CrossRef]
- Liu, J.; Shar, J.A.; Sucosky, P. Wall Shear Stress Directional Abnormalities in BAV Aortas: Toward a New Hemodynamic Predictor of Aortopathy? Front. Physiol. 2018, 9, 993. [Google Scholar] [CrossRef]
- Salman, H.E.; Saltik, L.; Yalcin, H.C. Computational analysis of wall shear stress patterns on calcified and bicuspid aortic valves: Focus on radial and coaptation patterns. Fluids 2021, 6, 287. [Google Scholar] [CrossRef]
- Ben-Saadon, S.; Gavriel, M.; Zaretsky, U.; Jaffa, A.J.; Grisaru, D.; Elad, D. Tissue-engineered arterial intima model exposed to steady wall shear stresses. J. Biomech. 2021, 117, 110236. [Google Scholar] [CrossRef] [PubMed]
- Hälvä, R.; Vaara, S.M.; Peltonen, J.I.; Kaasalainen, T.T.; Holmström, M.; Lommi, J.; Suihko, S.; Rajala, H.; Kylmälä, M.; Kivistö, S.; et al. Peak flow measurements in patients with severe aortic stenosis: A prospective comparative study between cardiovascular magnetic resonance 2D and 4D flow and transthoracic echocardiography. J. Cardiovasc. Magn. Reson. 2021, 23, 132. [Google Scholar] [CrossRef]
- Chaothawee, L. Diagnostic approach to assessment of valvular heart disease using magnetic resonance imaging, part II: A practical approach for native and prosthetic heart valve stenosis. Heart Asia 2014, 4, 171–175. [Google Scholar] [CrossRef]
- Castel, A.L.; Maréchaux, S.; Laaouaj, J.; Rusinaru, D.; Levy, F.; Tribouilloy, C. Relationship between cutoff values of peak aortic valve velocity and those of other Doppler echocardiographic parameters of severity in patients with aortic stenosis and normal flow. Echocardiography 2012, 29, 1150–1156. [Google Scholar] [CrossRef]
- Yap, C.H.; Saikrishnan, N.; Tamilselvan, G.; Yoganathan, A.P. Experimental measurement of dynamic fluid shear stress on the aortic surface of the aortic valve leaflet. Biomech. Model. Mechanobiol. 2012, 11, 171–182. [Google Scholar] [CrossRef]
- Romarowski, R.; Lefieux, A.; Veneziani, A.; Morganti, S.; Auricchio, F. Patient-specific CFD modelling in the thoracic aorta with PC-MRI–based boundary conditions: A least-square three-element Windkessel approach. Int. J. Numer. Methods Biomed. Eng. 2018, 34, e3134. [Google Scholar] [CrossRef]
- Lin, S.; Han, X.; Bi, Y.; Ju, S.; Gu, L. Fluid-structure interaction in abdominal aortic aneurysm: Effect of modeling techniques. BioMed Res. Int. 2017, 2017, 7023078. [Google Scholar] [CrossRef] [PubMed]
- Kuchumov, A.G.; Vedeneev, V.; Samartsev, V.; Khairulin, A.; Ivanov, O. Patient-specific fluid–structure interaction model of bile flow: Comparison between 1-way and 2-way algorithms. Comput. Methods Biomech. Biomed. Eng. 2021, 24, 1693–1717. [Google Scholar] [CrossRef] [PubMed]
- Quarteroni, A.; Lassila, T.; Rossi, S.; Ruiz-Baier, R. Integrated heart—Coupling multiscale and multiphysics models for the simulation of the cardiac function. Comput. Methods Appl. Mech. Eng. 2017, 314, 345–407. [Google Scholar] [CrossRef]
- Balzani, D.; Deparis, S.; Fausten, S.; Forti, D.; Heinlein, A.; Klawonn, A.; Quarteroni, A.; Rheinbach, O.; Schröder, J. Numerical modeling of fluid-structure interaction in arteries with anisotropic polyconvex hyperelastic and anisotropic viscoelastic material models at finite strains. Int. J. Numer. Methods Biomed. Eng. 2016, 32, e02756. [Google Scholar] [CrossRef]
- Reymond, P.; Crosetto, P.; Deparis, S.; Quarteroni, A.; Stergiopulos, N. Physiological simulation of blood flow in the aorta: Comparison of hemodynamic indices as predicted by 3-D FSI, 3-D rigid wall and 1-D models. Med. Eng. Phys. 2012, 35, 784–791. [Google Scholar] [CrossRef]
- Kuchumov, A.G.; Selyaninov, A. Application of computational fluid dynamics in biofluids simulation to solve actual surgery tasks. Adv. Intell. Syst. Comput. 2020, 1018, 576–580. [Google Scholar] [CrossRef]
- Kuchumov, A.G.; Khairulin, A.R.; Biyanov, A.N.; Porodikov, A.A.; Arutyunyan, V.B.; Sinelnikov, Y.S. Effectiveness of blalock-taussig shunt performance in the congenital heart disease children. Russ. J. Biomech. 2020, 24, 65–83. [Google Scholar] [CrossRef]
- Sinelnikov, Y.S.; Arutunyan, V.B.; Porodikov, A.A.; Biyanov, A.N.; Tuktamyshev, V.S.; Shmurak, M.I.; Khairulin, A.R.; Kuchumov, A.G. Application of mathematical modelling for the evaluation of the results of systemic-pulmonary shunts formation. Patol. Krovoobrashcheniya Kardiokhirurgiya 2020, 24, 45–61. [Google Scholar] [CrossRef]
- Kamaltdinov, M.R.; Kuchumov, A.G. Application of a mathematical model of systemic circulation for determination of blood flow parameters after modified blalock-taussig shunt operation in newborns. Russ. J. Biomech. 2021, 25, 268–284. [Google Scholar]
- Kuchumov, A.G.; Khairulin, A.; Shmurak, M.; Porodikov, A.; Merzlyakov, A. The Effects of the Mechanical Properties of Vascular Grafts and an Anisotropic Hyperelastic Aortic Model on Local Hemodynamics during Modified Blalock–Taussig Shunt Operation, Assessed Using FSI Simulation. Materials 2022, 15, 2719. [Google Scholar] [CrossRef]
- Lindman, B.R.; Clavel, M.A.; Mathieu, P.; Iung, B.; Lancellotti, P.; Otto, C.M.; Pibarot, P. Calcific aortic stenosis. Nat. Rev. Dis. Primers 2016, 2, 16006. [Google Scholar] [CrossRef]
- Samady, H.; Eshtehardi, P.; McDaniel, M.C.; Suo, J.; Dhawan, S.S.; Maynard, C.; Timmins, L.H.; Quyyumi, A.A.; Giddens, D.P. Coronary artery wall shear stress is associated with progression and transformation of atherosclerotic plaque and arterial remodeling in patients with coronary artery disease. Circulation 2011, 124, 779–788. [Google Scholar] [CrossRef]
- Nowak, M.; Divo, E.; Adamczyk, W.P. Fluid-Structure Interaction methods for the progressive anatomical and artificial aortic valve stenosis. Int. J. Mech. Sci. 2022, 227, 107410. [Google Scholar] [CrossRef]
- Yap, C.H.; Kim, H.-S.; Balachandran, K.; Weiler, M.; Haj-Ali, R.; Yoganathan, A.P. Dynamic deformation characteristics of porcine aortic valve leaflet under normal and hypertensive conditions. Am. J. Physiol. Circ. Physiol. 2010, 298, H395–H405. [Google Scholar] [CrossRef] [PubMed]
- Peskin, C.S. Fluid dynamics of heart valves: Experimental, theoretical, and computational methods. Annu. Rev. Fluid Mech. 1982, 14, 235–259. [Google Scholar] [CrossRef]
- Moore, B.; Dasi, L.P. Spatiotemporal complexity of the aortic sinus vortex. Exp. Fluids 2014, 55, 1770. [Google Scholar] [CrossRef]
- Korakianitis, T.; Shi, Y. Numerical simulation of cardiovascular dynamics with healthy and diseased heart valves. J. Biomech. 2006, 39, 1964–1982. [Google Scholar] [CrossRef]
- Katayama, S.; Umetani, N.; Sugiura, S.; Hisada, T. The sinus of Valsalva relieves abnormal stress on aortic valve leaflets by facilitating smooth closure. J. Thorac. Cardiovasc. Surg. 2008, 136, 1528–1535.e1. [Google Scholar] [CrossRef] [PubMed]
- Markl, M.; Kilner, P.J.; Ebbers, T. Comprehensive 4D velocity mapping of the heart and great vessels by cardiovascular magnetic resonance. J. Cardiovasc. Magn. Reson. 2011, 13, 7. [Google Scholar] [CrossRef] [PubMed]
- Saikrishnan, N.; Yap, C.H.; Milligan, N.C.; Vasilyev, N.V.; Yoganathan, A.P. In vitro characterization of bicuspid aortic valve hemodynamics using particle image velocimetry. Ann. Biomed. Eng. 2012, 40, 1760–1775. [Google Scholar] [CrossRef] [PubMed]
- Fukui, T.; Morinishi, K. Influence of Vortices in the Sinus of Valsalva on Local Wall Shear Stress Distribution. Int. J. Life Sci. Med. Res. 2013, 3, 94–102. [Google Scholar] [CrossRef]
- Kivi, A.R.; Sedaghatizadeh, N.; Cazzolato, B.S.; Zander, A.C.; Nelson, A.J.; Roberts-Thomson, R.; Yoganathan, A.; Arjomandi, M. Hemodynamics of a stenosed aortic valve: Effects of the geometry of the sinuses and the positions of the coronary ostia. Int. J. Mech. Sci. 2020, 188, 106015. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).