Multi-Strategy Enhanced Harris Hawks Optimization for Global Optimization and Deep Learning-Based Channel Estimation Problems
Abstract
1. Introduction
2. Harris Hawks Optimization
2.1. Exploration Phase
2.2. Exploitation Phase
2.2.1. Soft Besiege
2.2.2. Hard Besiege
2.2.3. Soft Besiege with Progressive Rapid Dives
2.2.4. Hard Besiege with Progressive Rapid Dives
3. Multi-Strategy Enhanced Harris Hawks Optimization
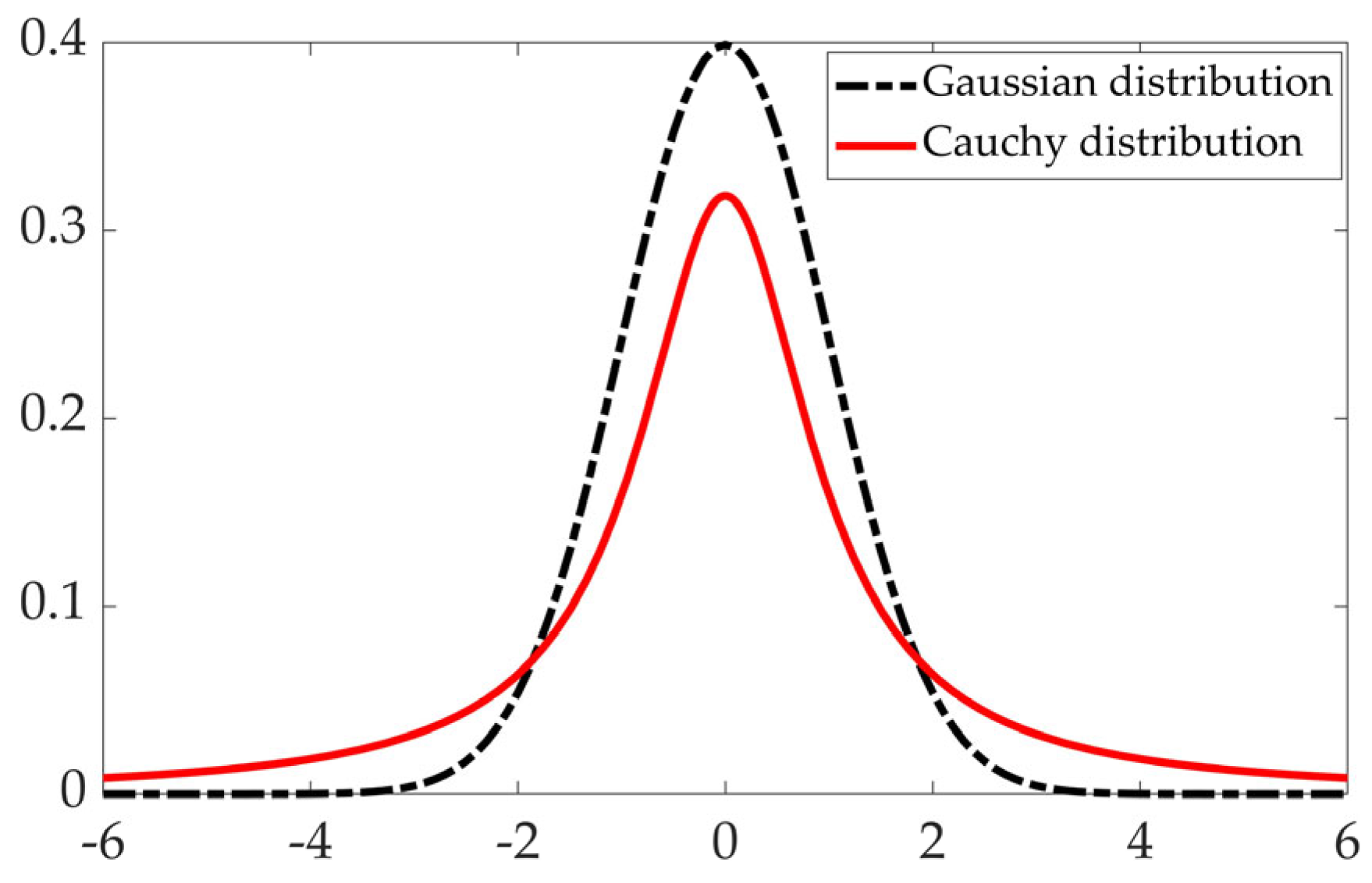
3.1. Improved Strategy Based on Map-Compass Operator and Cauchy Mutation
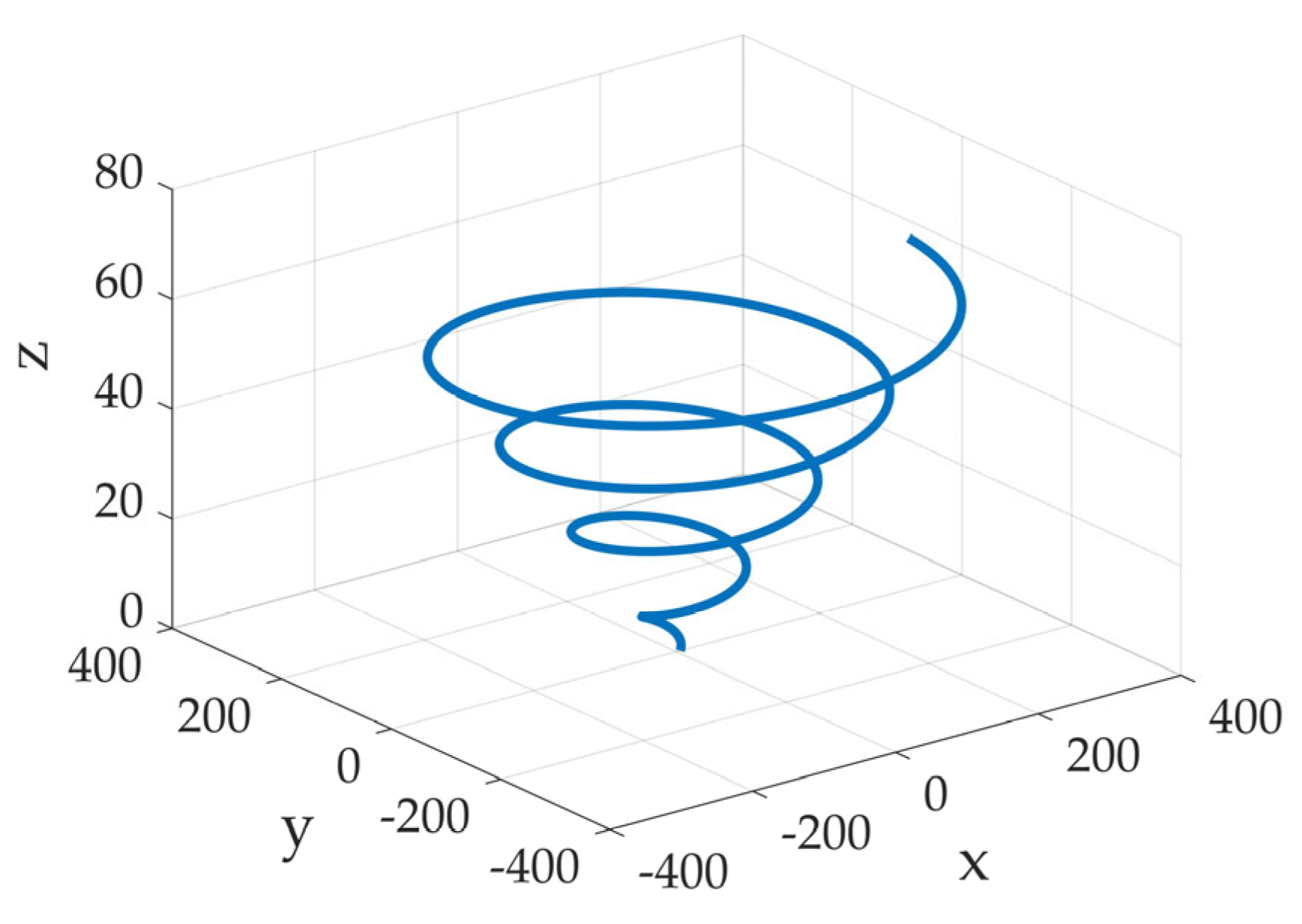
3.2. Position Update Mechanism Based on Spiral Motion and Greedy Strategy
| Algorithm 1. Pseudo-code of Proposed MEHHO |
| Inputs: The population size and the maximum iterations . |
| Outputs: The location of prey. |
| 1: Initialize the random population in a provided search space. |
| 2: While do |
| 3: Calculate the fitness values of each hawk. |
| 4: Select the best individual position as the prey position. |
| 5: Update the location using Equation (20) that incorporates the map-compass operator and the Cauchy mutation, calculate the individual fitness again and update . |
| 6: for (each hawk) do |
| 7: Update the initial energy and jump strength . |
| 8: Update the using Equation (1). 9: if then |
| 10: Update the location of members using Equation (22). |
| 11: if then |
| 12: if , then |
| 13: Update the location of members using Equation (4). |
| 14: else if , then |
| 15: Update the location of members using Equation (7). |
| 16: else if , then |
| 17: Update the location of members using Equation (8). |
| 18: else if , then |
| 19: Update the location of members using Equation (14). |
| 20: Return . |
4. Experiment and Discussion: Global Optimization
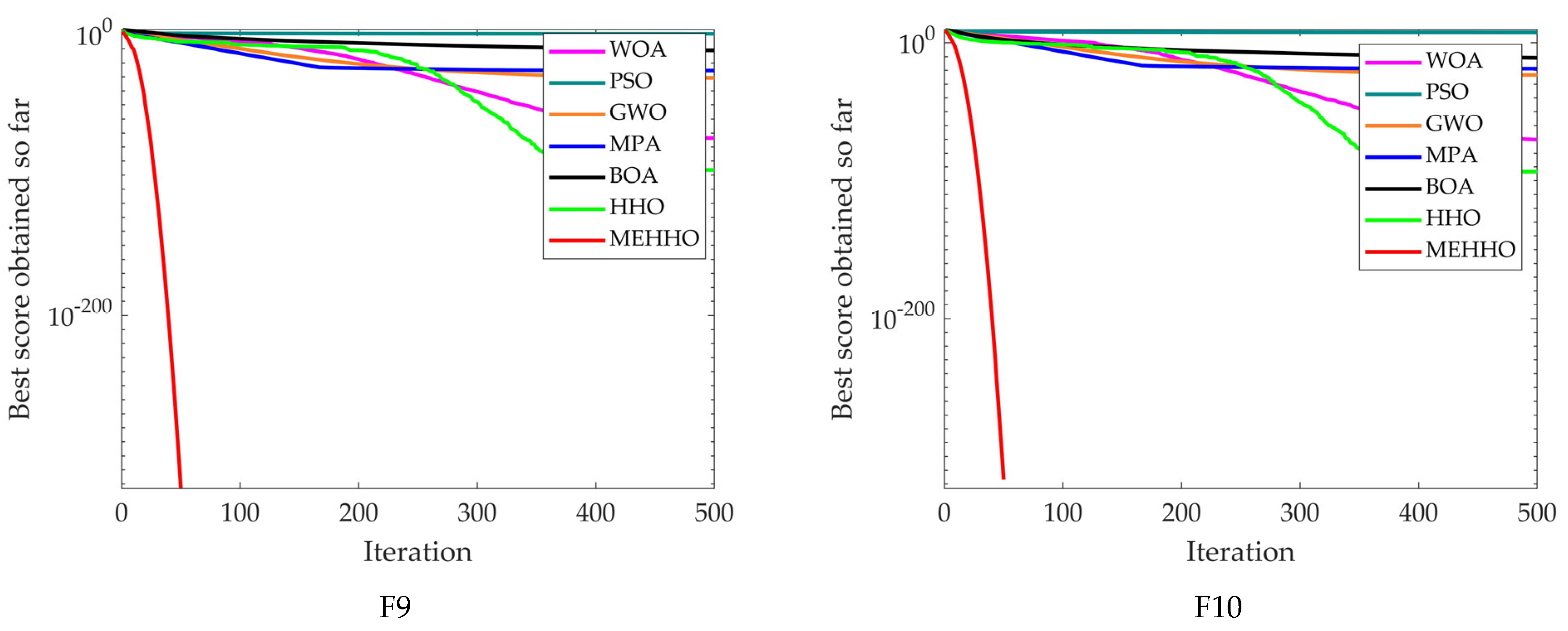
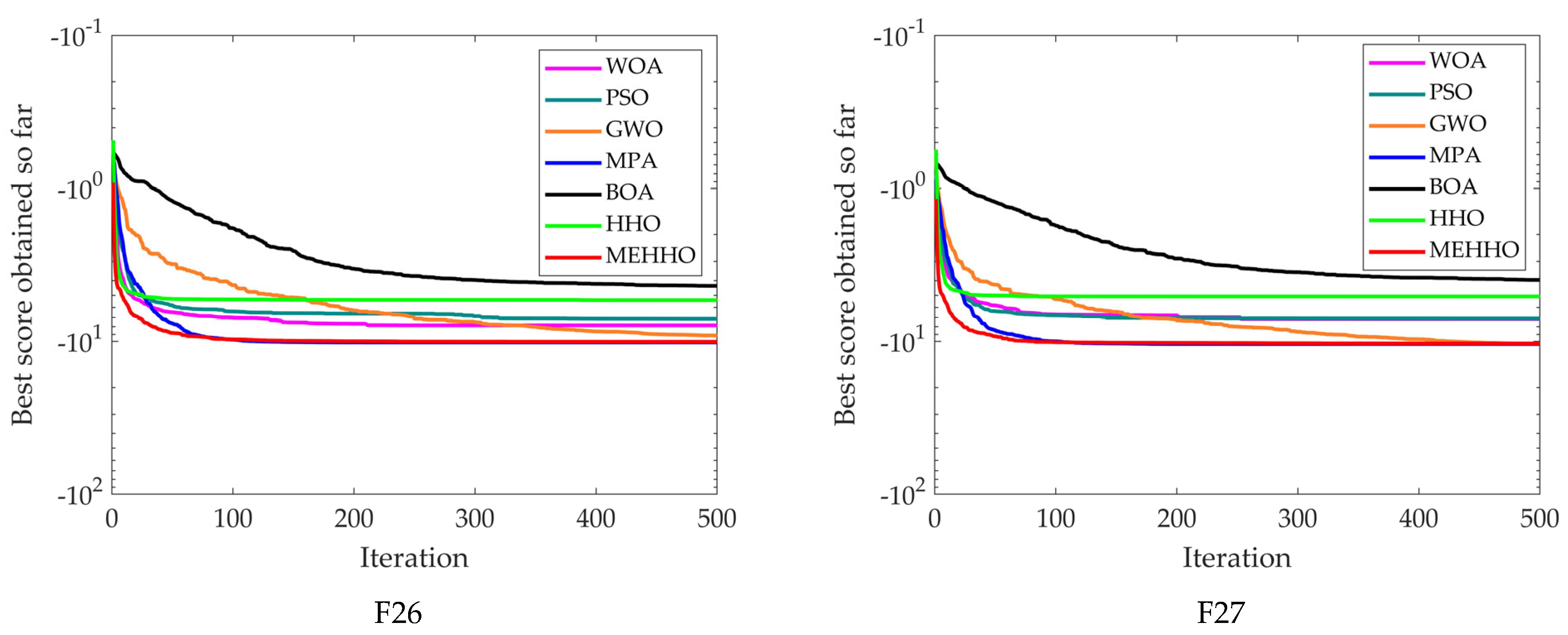
4.1. Comparison with Other Meta-Heuristic Algorithms
4.2. Comparison and Significance Verification with Original Harris Hawks Optimization in Different Dimensions
4.3. Comparison with Other Improved Harris Hawks Optimization
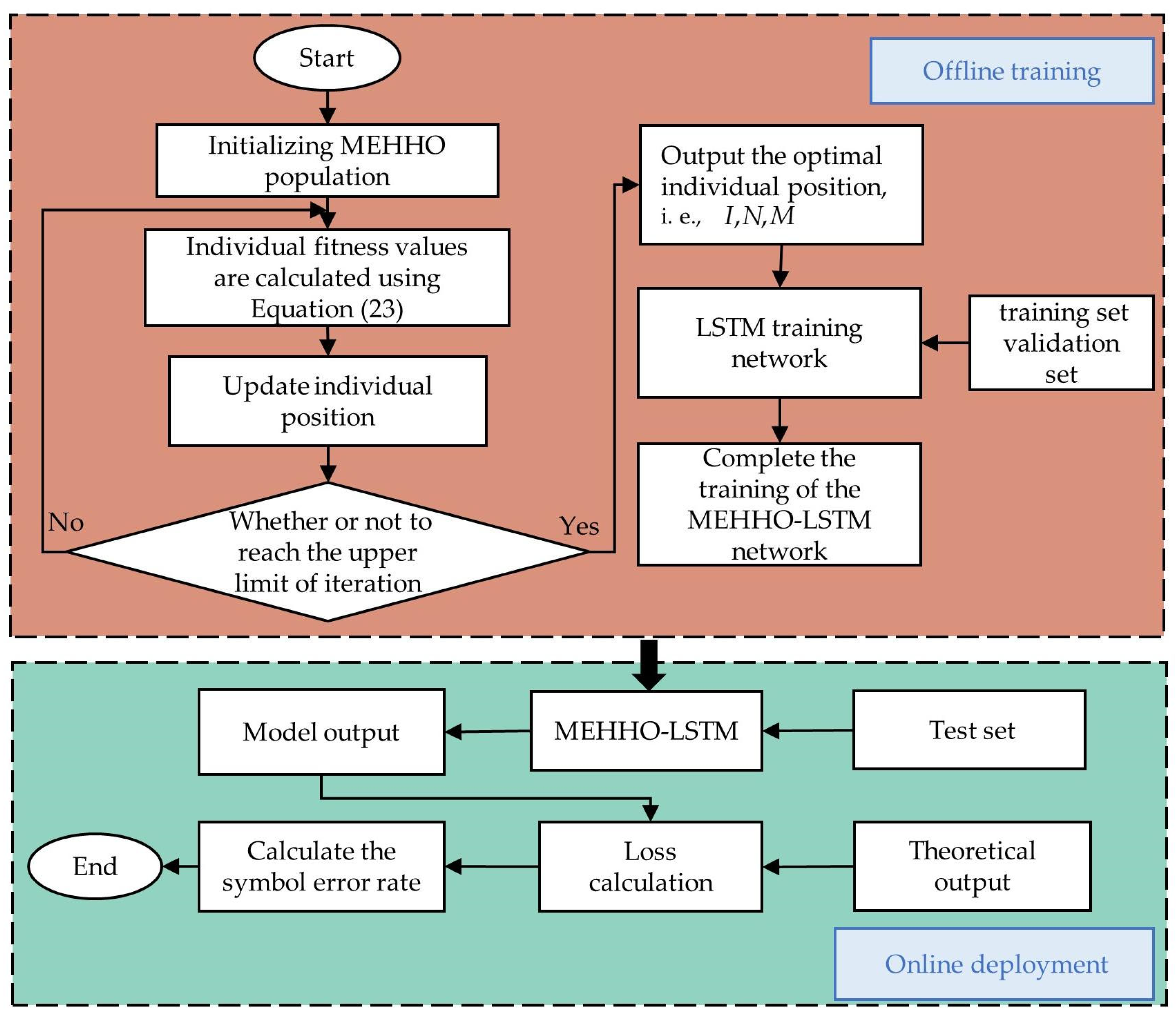
5. Application in Channel Estimation
5.1. Channel Estimation and Signal Detection Model
- Step1: Establish the mathematical model of the OFDM system, and generate the training set, verification set, and test set required by LSTM model under the 3GPP TR38.901 channel model;
- Step2: Establish the LSTM channel estimation and signal detection model;
- Step3: Initialize the MEHHO, take the initial learning rate , training times , and batch size in the LSTM model as optimization objectives, and establish the MEHHO-LSTM model corresponding to each dimension in the HHO;
- Step4: Calculate the fitness value of each individual according to Formula (23), and update the individual position according to the fitness value;
- Step5: Determine whether the maximum number of iterations is reached. If so, output the optimal solution position, namely the best parameter of LSTM; Otherwise, return to Step4.
- Step6: Substitute the optimal parameters into the LSTM network model for OFDM channel estimation and signal detection.
5.2. Experimental Parameter Setting
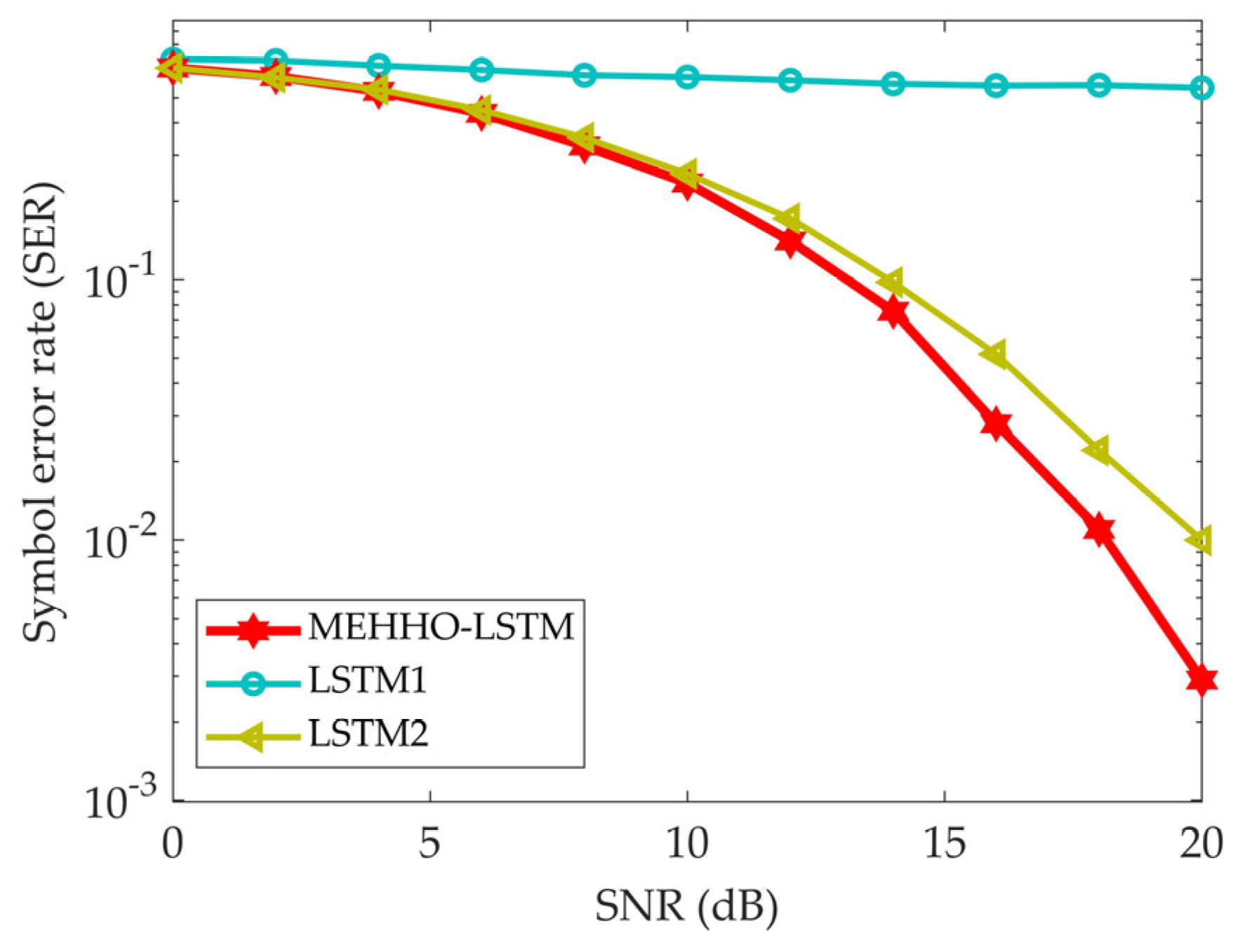
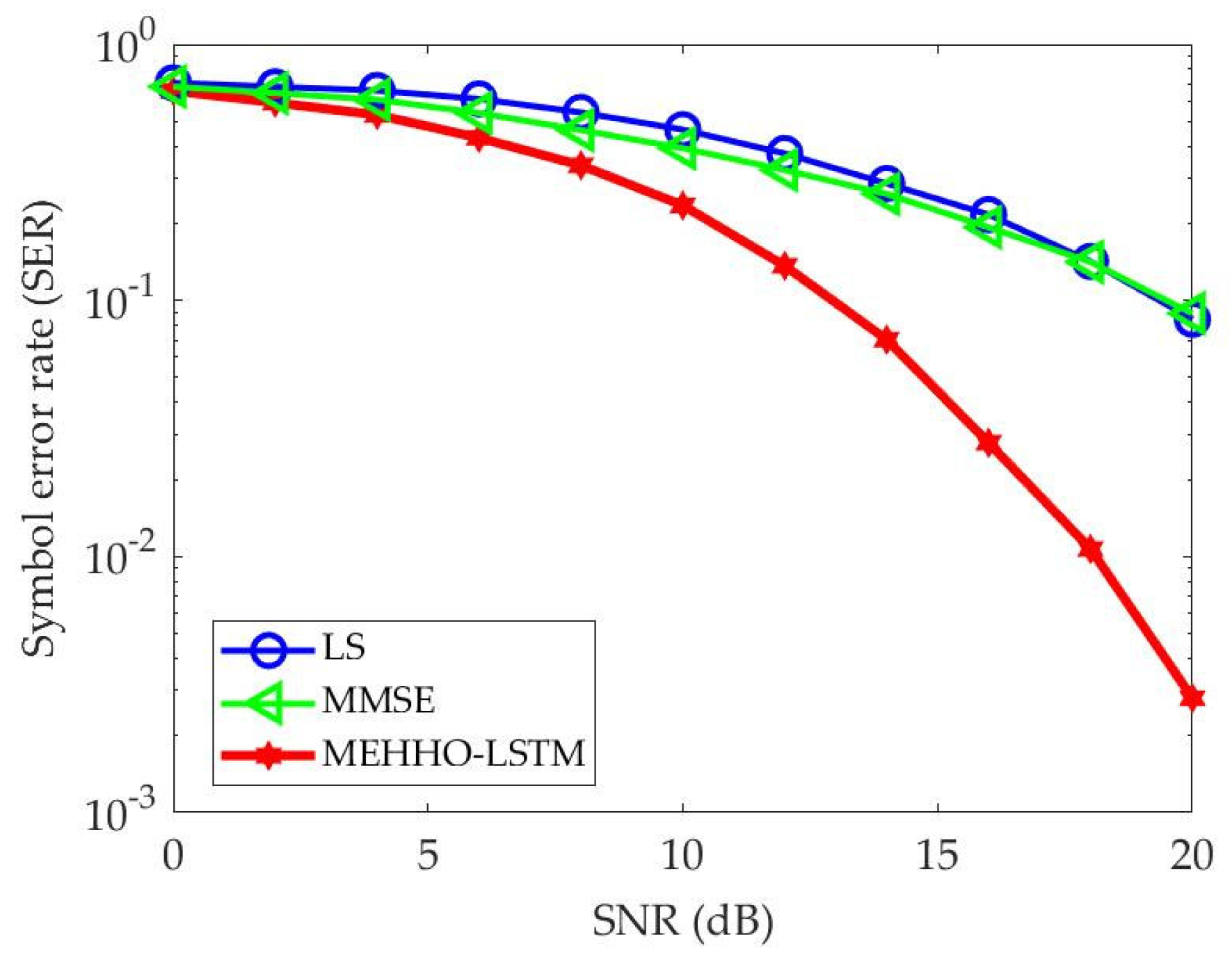
5.3. Results and Discussion
6. Conclusions and Prospect
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Arufe, L.; González, M.A.; Oddi, A.; Rasconi, R.; Varela, R. Quantum circuit compilation by genetic algorithm for quantum approximate optimization algorithm applied to maxcut problem. Swarm Evol. Comput. 2022, 69, 101030. [Google Scholar] [CrossRef]
- Wang, M.; Ma, Y.; Wang, P. Parameter and strategy adaptive differential evolution algorithm based on accompanying evolution. Inf. Sci. 2022, 607, 1136–1157. [Google Scholar] [CrossRef]
- Alnowibet, K.A.; Mahdi, S.; El-Alem, M.; Abdelawwad, M.; Mohamed, A.W. Guided Hybrid Modified Simulated Annealing Algorithm for Solving Constrained Global Optimization Problems. Mathematics 2022, 10, 1312. [Google Scholar] [CrossRef]
- Hashim, F.A.; Houssein, E.H.; Mabrouk, M.S.; Al-Atabany, W.; Mirjalili, S. Henry gas solubility optimization: A novel physics-based algorithm. Futur. Gener. Comp. Syst. 2019, 101, 646–667. [Google Scholar] [CrossRef]
- Zhao, W.; Wang, L.; Zhang, Z. A novel atom search optimization for dispersion coefficient estimation in groundwater. Futur. Gener. Comp. Syst. 2019, 91, 601–610. [Google Scholar] [CrossRef]
- Kassoul, K.; Zufferey, N.; Cheikhrouhou, N.; Belhaouari, S.B. Exponential particle swarm optimization for global optimization. IEEE Access 2022, 10, 78320–78344. [Google Scholar] [CrossRef]
- Li, S.; Wei, Y.; Liu, X.; Zhu, H.; Yu, Z. A New Fast Ant Colony Optimization Algorithm: The Saltatory Evolution Ant Colony Optimization Algorithm. Mathematics 2022, 10, 925. [Google Scholar] [CrossRef]
- Kaya, E. A New Neural Network Training Algorithm Based on Artificial Bee Colony Algorithm for Nonlinear System Identification. Mathematics 2022, 10, 3487. [Google Scholar] [CrossRef]
- Mirjalili, S.; Lewis, A. The whale optimization algorithm. Adv. Eng. Softw. 2016, 95, 51–67. [Google Scholar] [CrossRef]
- Mirjalili, S.; Gandomi, A.H.; Mirjalili, S.Z.; Saremi, S.; Faris, H.; Mirjalili, S.M. Salp Swarm Algorithm: A bio-inspired optimizer for engineering design problems. Adv. Eng. Softw. 2017, 114, 163–191. [Google Scholar] [CrossRef]
- Arora, S.; Singh, S. Butterfly optimization algorithm: A novel approach for global optimization. Soft Comput. 2019, 23, 715–734. [Google Scholar] [CrossRef]
- Faramarzi, A.; Heidarinejad, M.; Mirjalili, S.; Gandomi, A.H. Marine Predators Algorithm: A nature-inspired metaheuristic. Expert Syst. Appl. 2020, 152, 113377. [Google Scholar] [CrossRef]
- Zervoudakis, K.; Tsafarakis, S. A mayfly optimization algorithm. Comput. Ind. Eng. 2020, 145, 106559. [Google Scholar] [CrossRef]
- Abualigah, L.; Yousri, D.; Abd Elaziz, M.; Ewees, A.A.; Al-Qaness, M.A.; Gandomi, A.H. Aquila optimizer: A novel meta-heuristic optimization algorithm. Comput. Ind. Eng. 2021, 157, 107250. [Google Scholar] [CrossRef]
- Abualigah, L.; Diabat, A.; Mirjalili, S.; Abd Elaziz, M.; Gandomi, A.H. The arithmetic optimization algorithm. Comput. Meth. Appl. Mech. Eng. 2021, 376, 113609. [Google Scholar] [CrossRef]
- Seyyedabbasi, A.; Kiani, F. Sand Cat swarm optimization: A nature-inspired algorithm to solve global optimization problems. Eng. Comput. 2022, 38, 1–25. [Google Scholar] [CrossRef]
- Ahmadianfar, I.; Heidari, A.A.; Noshadian, S.; Chen, H.; Gandomi, A.H. INFO: An efficient optimization algorithm based on weighted mean of vectors. Expert Syst. Appl. 2022, 195, 116516. [Google Scholar] [CrossRef]
- Abd El-Sattar, H.; Kamel, S.; Hassan, M.H.; Jurado, F. Optimal sizing of an off-grid hybrid photovoltaic/biomass gasifier/battery system using a quantum model of Runge Kutta algorithm. Energy Conv. Manag. 2022, 258, 115539. [Google Scholar] [CrossRef]
- Shao, K.; Fu, W.; Tan, J.; Wang, K. Coordinated approach fusing time-shift multiscale dispersion entropy and vibrational Harris hawks optimization-based SVM for fault diagnosis of rolling bearing. Measurement 2021, 173, 108580. [Google Scholar] [CrossRef]
- Zhang, A.; Yu, D.; Zhang, Z. TLSCA-SVM Fault Diagnosis Optimization Method Based on Transfer Learning. Processes 2022, 10, 362. [Google Scholar] [CrossRef]
- Dokeroglu, T.; Deniz, A.; Kiziloz, H.E. A Comprehensive Survey on Recent Metaheuristics for Feature Selection. Neurocomputing 2022, 494, 269. [Google Scholar] [CrossRef]
- Ewees, A.A.; Ismail, F.H.; Ghoniem, R.M.; Gaheen, M.A. Enhanced Marine Predators Algorithm for Solving Global Optimization and Feature Selection Problems. Mathematics 2022, 10, 4154. [Google Scholar] [CrossRef]
- Abbasi, A.; Firouzi, B.; Sendur, P. On the application of Harris hawks optimization (HHO) algorithm to the design of microchannel heat sinks. Eng. Comput. 2021, 37, 1409–1428. [Google Scholar] [CrossRef]
- Chacko, A.; Chacko, S. Deep learning-based robust medical image watermarking exploiting DCT and Harris hawks optimization. Int. J. Intell. Syst. 2022, 37, 4810–4844. [Google Scholar] [CrossRef]
- Badashah, S.J.; Basha, S.S.; Ahamed, S.R.; Subba Rao, S.P.V. Fractional-Harris hawks optimization-based generative adversarial network for osteosarcoma detection using Renyi entropy-hybrid fusion. Int. J. Intell. Syst. 2021, 36, 6007–6031. [Google Scholar] [CrossRef]
- Bandyopadhyay, R.; Kundu, R.; Oliva, D.; Sarkar, R. Segmentation of brain MRI using an altruistic Harris Hawks’ Optimization algorithm. Knowl. -Based Syst. 2021, 232, 107468. [Google Scholar] [CrossRef]
- Kaur, N.; Kaur, L.; Cheema, S.S. An enhanced version of Harris Hawks optimization by dimension learning-based hunting for breast cancer detection. Sci. Rep. 2021, 11, 21933. [Google Scholar] [CrossRef]
- Alweshah, M.; Almiani, M.; Almansour, N.; Al Khalaileh, S.; Aldabbas, H.; Alomoush, W.; Alshareef, A. Vehicle routing problems based on Harris Hawks optimization. J. Big Data 2022, 9, 42. [Google Scholar] [CrossRef]
- Zhang, R.; Li, S.; Ding, Y.; Qin, X.; Xia, Q. UAV Path Planning Algorithm Based on Improved Harris Hawks Optimization. Sensors 2022, 22, 5232. [Google Scholar] [CrossRef]
- Golilarz, N.A.; Addeh, A.; Gao, H.; Ali, L.; Roshandeh, A.M.; Munir, H.M.; Khan, R.U. A new automatic method for control chart patterns recognition based on ConvNet and harris hawks meta heuristic optimization algorithm. IEEE Access 2019, 7, 149398–149405. [Google Scholar] [CrossRef]
- Abd Elaziz, M.; Abualigah, L.; Ibrahim, R.A.; Attiya, I. IoT workflow scheduling using intelligent arithmetic optimization algorithm in fog computing. Comput. Intell. Neurosci. 2021, 2021, 9114113. [Google Scholar] [CrossRef] [PubMed]
- Seyfollahi, A.; Ghaffari, A. Reliable data dissemination for the Internet of Things using Harris hawks optimization. Peer Peer Netw. Appl. 2020, 13, 1886–1902. [Google Scholar] [CrossRef]
- Saravanan, G.; Ibrahim, A.M.; Kumar, D.S.; Vanitha, U.; Chandrika, V.S. Iot based speed control of bldc motor with Harris hawks optimization controller. Int. J. Grid Distrib. Comput. 2020, 13, 1902–1915. [Google Scholar]
- Heidari, A.A.; Mirjalili, S.; Faris, H.; Aljarah, I.; Mafarja, M.; Chen, H. Harris hawks optimization: Algorithm and applications. Futur. Gener. Comp. Syst. 2019, 97, 849–872. [Google Scholar] [CrossRef]
- Ramadan, A.; Kamel, S.; Korashy, A.; Almalaq, A.; Domínguez-García, J.L. An enhanced Harris Hawk optimization algorithm for parameter estimation of single, double and triple diode photovoltaic models. Soft Comput. 2022, 26, 7233–7257. [Google Scholar] [CrossRef]
- Naeijian, M.; Rahimnejad, A.; Ebrahimi, S.M.; Pourmousa, N.; Gadsden, S.A. Parameter estimation of PV solar cells and modules using Whippy Harris Hawks Optimization Algorithm. Energy Rep. 2021, 7, 4047–4063. [Google Scholar] [CrossRef]
- Chen, H.; Jiao, S.; Wang, M.; Heidari, A.A.; Zhao, X. Parameters identification of photovoltaic cells and modules using diversification-enriched Harris hawks optimization with chaotic drifts. J. Clean Prod. 2020, 244, 118778. [Google Scholar] [CrossRef]
- Jia, H.; Lang, C.; Oliva, D.; Song, W.; Peng, X. Dynamic harris hawks optimization with mutation mechanism for satellite image segmentation. Remote Sens. 2019, 11, 1421. [Google Scholar] [CrossRef]
- Wunnava, A.; Naik, M.K.; Panda, R.; Jena, B.; Abraham, A. A differential evolutionary adaptive Harris hawks optimization for two dimensional practical Masi entropy-based multilevel image thresholding. J. King Saud Univ.-Comput. Inf. Sci. 2020, 34, 3011–3024. [Google Scholar] [CrossRef]
- Rodríguez-Esparza, E.; Zanella-Calzada, L.A.; Oliva, D.; Heidari, A.A.; Zaldivar, D.; Pérez-Cisneros, M.; Foong, L.K. An efficient Harris hawks-inspired image segmentation method. Expert Syst. Appl. 2020, 155, 113428. [Google Scholar] [CrossRef]
- Srinivas, M.; Amgoth, T. EE-hHHSS: Energy-efficient wireless sensor network with mobile sink strategy using hybrid Harris hawk-salp swarm optimization algorithm. Int. J. Commun. Syst. 2020, 33, 4569. [Google Scholar] [CrossRef]
- Bhat, S.J.; Venkata, S.K. An optimization based localization with area minimization for heterogeneous wireless sensor networks in anisotropic fields. Comput. Netw. 2020, 179, 107371. [Google Scholar] [CrossRef]
- Kaveh, A.; Rahmani, P.; Eslamlou, A.D. An efficient hybrid approach based on Harris Hawks optimization and imperialist competitive algorithm for structural optimization. Eng. Comput. 2022, 38, 1555–1583. [Google Scholar] [CrossRef]
- Dehkordi, A.A.; Sadiq, A.S.; Mirjalili, S.; Ghafoor, K.Z. Nonlinear-based chaotic harris hawks optimizer: Algorithm and internet of vehicles application. Appl. Soft. Comput. 2021, 109, 107574. [Google Scholar] [CrossRef]
- Gupta, S.; Deep, K.; Heidari, A.A.; Moayedi, H.; Wang, M. Opposition-based learning Harris hawks optimization with advanced transition rules: Principles and analysis. Expert Syst. Appl. 2020, 158, 113510. [Google Scholar] [CrossRef]
- Fan, Q.; Chen, Z.; Xia, Z. A novel quasi-reflected Harris hawks optimization algorithm for global optimization problems. Soft Comput. 2020, 24, 14825–14843. [Google Scholar] [CrossRef]
- Liu, C. An improved Harris hawks optimizer for job-shop scheduling problem. J. Supercomput. 2021, 77, 14090–14129. [Google Scholar] [CrossRef]
- Abualigah, L.; Diabat, A.; Altalhi, M.; Elaziz, M.A. Improved gradual change-based Harris Hawks optimization for real-world engineering design problems. Eng. Comput. 2022, 38, 1–41. [Google Scholar] [CrossRef]
- Duan, H.; Qiao, P. Pigeon-inspired optimization: A new swarm intelligence optimizer for air robot path planning. Int. J. Intell. Comput. Cybern. 2014, 7, 24–37. [Google Scholar] [CrossRef]
- Luo, J.; Chen, H.; Heidari, A.A.; Xu, Y.; Zhang, Q.; Li, C. Multi-strategy boosted mutative whale-inspired optimization approaches. Appl. Math. Model. 2019, 73, 109–123. [Google Scholar] [CrossRef]
- Ou, X.; Wu, M.; Pu, Y.; Tu, B.; Zhang, G.; Xu, Z. Cuckoo search algorithm with fuzzy logic and Gauss–Cauchy for minimizing localization error of WSN. Appl. Soft Comput. 2022, 125, 109211. [Google Scholar] [CrossRef]
- Jia, H.; Peng, X.; Lang, C. Remora optimization algorithm. Expert Syst. Appl. 2021, 185, 115665. [Google Scholar] [CrossRef]
- Hayyolalam, V.; Kazem, A.A.P. Black widow optimization algorithm: A novel meta-heuristic approach for solving engineering optimization problems. Eng. Appl. Artif. Intell. 2020, 87, 103249. [Google Scholar] [CrossRef]
- Mohammadi-Balani, A.; Nayeri, M.D.; Azar, A.; Taghizadeh-Yazdi, M. Golden eagle optimizer: A nature-inspired metaheuristic algorithm. Comput. Ind. Eng. 2021, 152, 107050. [Google Scholar] [CrossRef]
- Zhao, W.; Zhang, Z.; Wang, L. Manta ray foraging optimization: An effective bio-inspired optimizer for engineering applications. Eng. Appl. Artif. Intell. 2020, 87, 103300. [Google Scholar] [CrossRef]
- Mirjalili, S.; Mirjalili, S.M.; Lewis, A. Grey wolf optimizer. Adv. Eng. Softw. 2014, 69, 46–61. [Google Scholar] [CrossRef]
- Sarma, R.; Bhargava, C.; Jain, S.; Kamboj, V.K. Application of ameliorated Harris Hawks optimizer for designing of low-power signed floating-point MAC architecture. Neural Comput. Appl. 2021, 33, 8893–8922. [Google Scholar] [CrossRef]
- Nandi, A.; Kamboj, V.K. A Canis lupus inspired upgraded Harris hawks optimizer for nonlinear, constrained, continuous, and discrete engineering design problem. Int. J. Numer. Methods Eng. 2021, 122, 1051–1088. [Google Scholar] [CrossRef]
- Kamboj, V.K.; Nandi, A.; Bhadoria, A.; Sehgal, S. An intensify Harris Hawks optimizer for numerical and engineering optimization problems. Appl. Soft. Comput. 2020, 89, 106018. [Google Scholar] [CrossRef]
- Ye, H.; Li, G.Y.; Juang, B.H. Power of deep learning for channel estimation and signal detection in OFDM systems. IEEE Wirel. Commun. Lett. 2017, 7, 114–117. [Google Scholar] [CrossRef]
- Essai Ali, M.H. Deep learning-based pilot-assisted channel state estimator for OFDM systems. IET Commun. 2021, 15, 257–264. [Google Scholar] [CrossRef]
- Ali, M.H.E.; Taha, I.B. Channel state information estimation for 5G wireless communication systems: Recurrent neural networks approach. PeerJ Comput. Sci. 2021, 7, e682. [Google Scholar]
- Mai, Z.; Chen, Y.; Zhao, H.; Du, L.; Hao, C. A UAV Air-to-Ground Channel Estimation Algorithm Based on Deep Learning. Wirel. Pers. Commun. 2022, 124, 2247–2260. [Google Scholar] [CrossRef]
- Mirjalili, S. SCA: A sine cosine algorithm for solving optimization problems. Knowl. -Based Syst. 2016, 96, 120–133. [Google Scholar] [CrossRef]





| Function | Dim | Range | |
|---|---|---|---|
| 30, 50, 100, 500 | 0 | ||
| 30, 50, 100, 500 | 0 | ||
| 30, 50, 100, 500 | 0 | ||
| 30, 50, 100, 500 | 0 | ||
| 30, 50, 100, 500 | 0 | ||
| 30, 50, 100, 500 | 0 | ||
| 30, 50, 100, 500 | 0 | ||
| 30, 50, 100, 500 | 0 | ||
| 30, 50, 100, 500 | 0 | ||
| 30, 50, 100, 500 | 0 |
| Function | Dim | Range | |
|---|---|---|---|
| 30, 50, 100, 500 | 0 | ||
| 30, 50, 100, 500 | 0 | ||
| 30, 50, 100, 500 | 0 | ||
| 30, 50, 100, 500 | 0 | ||
| 30, 50, 100, 500 | 0 | ||
| 30, 50, 100, 500 | 0 | ||
| 30, 50, 100, 500 | 0 | ||
| 30, 50, 100, 500 | 0 | ||
| 30, 50, 100, 500 | 0 | ||
| 30, 50, 100, 500 | 0 |
| Function | Dim | Range | |
|---|---|---|---|
| 2 | −1.0316 | ||
| 2 | 0.398 | ||
| 3 | 3 | ||
| 3 | −3.86 | ||
| 6 | −3.32 | ||
| 4 | −10.1532 | ||
| 4 | −10.4028 | ||
| 4 | −10.5363 |
| Function | Metric | MEHHO | HHO | WOA | MPA | GWO | PSO | BOA |
|---|---|---|---|---|---|---|---|---|
| F1 | Mean | 0 | 1.36 × 10−96 | 8.44 × 10−72 | 5.98 × 10−23 | 2.94 × 10−27 | 2.69 × 103 | 1.27 × 10−11 |
| Std | 0 | 4.95 × 10−96 | 4.60 × 10−71 | 7.77 × 10−23 | 1.21 × 10−26 | 1.47 × 103 | 9.19 × 10−13 | |
| Time | 0.038 | 0.080 | 0.041 | 0.102 | 0.069 | 0.007 | 0.054 | |
| F2 | Mean | 0 | 2.67 × 10−51 | 1.68 × 10−50 | 2.85 × 10−13 | 1.12 × 10−16 | 3.20 × 101 | 3.96 × 10−9 |
| Std | 0 | 9.90 × 10−51 | 9.05 × 10−50 | 2.75 × 10−13 | 7.44 × 10−17 | 1.33 × 101 | 1.84 × 10−9 | |
| Time | 0.041 | 0.088 | 0.062 | 0.084 | 0.072 | 0.011 | 0.070 | |
| F3 | Mean | 0 | 1.88 × 10−72 | 4.22 × 104 | 2.41 × 10−4 | 7.18 × 10−6 | 8.15 × 103 | 1.25 × 10−11 |
| Std | 0 | 1.03 × 10−71 | 1.28 × 104 | 5.09 × 10−4 | 1.43 × 10−5 | 3.74 × 103 | 9.15 × 10−13 | |
| Time | 0.121 | 0.394 | 0.012 | 0.240 | 0.221 | 0.014 | 0.330 | |
| F4 | Mean | 0 | 4.21 × 10−49 | 5.14 × 101 | 3.79 × 10−9 | 8.78 × 10−7 | 2.51 × 101 | 6.14 × 10−9 |
| Std | 0 | 2.23 × 10−48 | 2.50 × 101 | 2.56 × 10−9 | 6.16 × 10−7 | 4.83 | 3.95 × 10−10 | |
| Time | 0.037 | 0.100 | 0.006 | 0.082 | 0.064 | 0.007 | 0.093 | |
| F5 | Mean | 6.90 × 10−3 | 1.34 × 10−2 | 2.80 × 101 | 2.52 × 101 | 2.71 × 101 | 4.29 × 105 | 2.90 × 101 |
| Std | 7.80 × 10−3 | 1.86 × 10−2 | 4.66 × 10−1 | 3.35 × 10−1 | 7.35 × 10−1 | 4.72 × 105 | 2.49 × 10−2 | |
| Time | 0.014 | 0.029 | 0.009 | 0.021 | 0.017 | 0.004 | 0.016 | |
| F6 | Mean | 5.28 × 10−5 | 1.19 × 10−4 | 3.87 × 10−1 | 8.93 × 10−8 | 7.79 × 10−1 | 2.13 × 103 | 6.17 |
| Std | 1.42 × 10−4 | 1.20 × 10−4 | 2.57 × 10−1 | 2.65 × 10−7 | 4.09 × 10−1 | 9.04 × 102 | 5.76 × 10−1 | |
| Time | 0.053 | 0.063 | 0.015 | 0.361 | 0.029 | 0.012 | 0.026 | |
| F7 | Mean | 5.45 × 10−5 | 1.40 × 10−4 | 3.90 × 10−3 | 1.50 × 10−3 | 2.10 × 10−3 | 1.33 | 1.00 × 10−3 |
| Std | 5.54 × 10−5 | 1.49 × 10−4 | 5.50 × 10−3 | 5.97 × 10−4 | 9.10 × 10−4 | 5.76 × 10−1 | 4.54 × 10−4 | |
| Time | 0.033 | 0.035 | 0.053 | 0.086 | 0.024 | 0.011 | 0.060 | |
| F8 | Mean | 0 | 2.60 × 10−89 | 4.00 × 10−65 | 3.74 × 10−17 | 5.91 × 10−22 | 1.96 × 109 | 1.55 × 10−11 |
| Std | 0 | 1.40 × 10−88 | 2.19 × 10−64 | 4.11 × 10−17 | 5.52 × 10−22 | 8.19 × 108 | 1.15 × 10−12 | |
| Time | 0.069 | 0.134 | 0.083 | 0.251 | 0.137 | 0.016 | 0.094 | |
| F9 | Mean | 0 | 4.21 × 10−97 | 2.29 × 10−74 | 3.67 × 10−26 | 1.82 × 10−31 | 3.99 | 7.87 × 10−12 |
| Std | 0 | 1.61 × 10−96 | 1.17 × 10−73 | 4.46 × 10−26 | 2.75 × 10−31 | 1.21 | 1.09 × 10−12 | |
| Time | 0.057 | 0.157 | 0.072 | 0.259 | 0.140 | 0.022 | 0.104 | |
| F10 | Mean | 0 | 3.68 × 10−94 | 7.58 × 10−71 | 1.98 × 10−19 | 5.62 × 10−24 | 3.27 × 107 | 1.40 × 10−11 |
| Std | 0 | 1.06 × 10−93 | 2.87 × 10−70 | 2.37 × 10−19 | 1.34 × 10−23 | 1.84 × 107 | 1.20 × 10−12 | |
| Time | 0.100 | 0.260 | 0.162 | 0.263 | 0.190 | 0.017 | 0.203 |
| Function | Metric | MEHHO | HHO | WOA | MPA | GWO | PSO | BOA |
|---|---|---|---|---|---|---|---|---|
| F11 | Mean | 0 | 0 | 1.89 × 10−15 | 0 | 2.01 | 1.44 × 102 | 2.79 × 10−13 |
| Std | 0 | 0 | 1.04 × 10−14 | 0 | 3.58 | 3.01 × 101 | 6.73 × 10−13 | |
| Time | 0.048 | 0.103 | 0.066 | 0.146 | 0.057 | 0.019 | 0.115 | |
| F12 | Mean | 8.88 × 10−16 | 8.88 × 10−16 | 5.15 × 10−15 | 1.25 × 10−12 | 9.68 × 10−14 | 1.10 × 101 | 6.04 × 10−9 |
| Std | 0 | 0 | 1.59 × 10−15 | 5.26 × 10−13 | 1.53 × 10−14 | 1.40 | 2.28 × 10−10 | |
| Time | 0.033 | 0.084 | 0.064 | 0.128 | 0.115 | 0.007 | 0.140 | |
| F13 | Mean | 0 | 0 | 0 | 0 | 4.20 × 10−3 | 2.08 × 101 | 8.08 × 10−12 |
| Std | 0 | 0 | 0 | 0 | 8.90 × 10−3 | 9.54 | 3.42 × 10−12 | |
| Time | 0.020 | 0.076 | 0.052 | 0.104 | 0.035 | 0.008 | 0.134 | |
| F14 | Mean | 2.99 × 10−6 | 8.14 × 10−6 | 2.75 × 10−2 | 6.53 × 10−6 | 5.12 × 10−2 | 7.74 × 102 | 7.27 × 10−1 |
| Std | 5.33 × 10−6 | 9.83 × 10−6 | 4.88 × 10−2 | 2.7 × 10−5 | 3.03 × 10−2 | 1.69 × 103 | 1.75 × 10−1 | |
| Time | 0.044 | 0.135 | 0.017 | 0.417 | 0.021 | 0.237 | 0.024 | |
| F15 | Mean | 4.6 × 10−5 | 9.1 × 10−5 | 6.03 × 10−1 | 5.60 × 10−3 | 6.05 × 10−1 | 1.45 × 105 | 2.98 |
| Std | 6.89 × 10−5 | 1.16 × 10−4 | 2.85 × 10−1 | 1.40 × 10−2 | 2.53 × 10−1 | 2.26 × 105 | 3.83 × 10−2 | |
| Time | 0.075 | 0.093 | 0.042 | 0.725 | 0.055 | 0.090 | 0.038 | |
| F16 | Mean | 0 | 3.47 × 10−51 | 1.04 × 10−31 | 1.09 × 10−13 | 4.27 × 10−4 | 1.62 × 101 | 4.07 × 10−9 |
| Std | 0 | 1.7 × 10−50 | 5.72 × 10−31 | 1.33 × 10−13 | 4.23 × 10−4 | 4.25 | 1.13 × 10−9 | |
| Time | 0.039 | 0.096 | 0.041 | 0.102 | 0.031 | 0.005 | 0.124 | |
| F17 | Mean | 0 | 0 | 3.90 × 10−3 | 4.90 × 10−3 | 5.80 × 10−3 | 5.00 × 10−1 | 5.00 × 10−3 |
| Std | 0 | 0 | 2.00 × 10−3 | 2.52 × 10−16 | 3.60 × 10−3 | 1.46 × 10−5 | 2.46 × 10−4 | |
| Time | 0.046 | 0.089 | 0.030 | 0.118 | 0.086 | 0.013 | 0.077 | |
| F18 | Mean | 0 | 3.43 × 10−48 | 1.57 × 10−1 | 1.40 × 10−1 | 1.90 × 10−1 | 6.55 | 1.86 × 10−1 |
| Std | 0 | 1.87 × 10−47 | 8.97 × 10−2 | 4.98 × 10−2 | 4.81 × 10−2 | 1.37 | 3.29 × 10−2 | |
| Time | 0.067 | 0.133 | 0.014 | 0.066 | 0.014 | 0.012 | 0.025 | |
| F19 | Mean | 0 | 1.1 × 10−280 | 5.8 × 10−115 | 7.49 × 10−64 | 9.18 × 10−66 | 5.30 × 10−4 | 5.32 × 10−12 |
| Std | 0 | 0 | 3.2 × 10−114 | 1.91 × 10−63 | 2.91 × 10−65 | 4.70 × 10−4 | 2.81 × 10−12 | |
| Time | 0.040 | 0.232 | 0.133 | 0.163 | 0.184 | 0.038 | 0.111 | |
| F20 | Mean | 0 | 3.51 × 10−12 | 4.41 × 10−12 | 6.47 × 10−12 | 3.65 × 10−8 | 2.88 × 10−7 | 2.36 × 10−7 |
| Std | 0 | 5.98 × 10−15 | 1.47 × 10−12 | 3.16 × 10−12 | 9.40 × 10−8 | 4.27 × 10−7 | 2.43 × 10−7 | |
| Time | 0.116 | 0.043 | 0.013 | 0.070 | 0.021 | 0.029 | 0.071 |
| Function | Metric | MEHHO | HHO | WOA | MPA | GWO | PSO | BOA |
|---|---|---|---|---|---|---|---|---|
| F21 | Mean | −1.03 | −1.03 | −1.03 | −1.03 | −1.03 | −1.03 | −3.56 |
| Std | 4.60 × 10−7 | 2.47 × 10−9 | 2.87 × 10−9 | 4.34 × 10−16 | 8.77 × 10−9 | 7.14 × 10−5 | 8.35 × 10−2 | |
| Time | 0.041 | 0.048 | 0.014 | 0.042 | 0.011 | 0.015 | 0.037 | |
| F22 | Mean | 3.98 × 10−1 | 3.98 × 10−1 | 3.98 × 10−1 | 3.98 × 10−1 | 3.98 × 10−1 | 3.98 × 10−1 | 7.97 × 10−1 |
| Std | 2.99 × 10−5 | 4.95 × 10−6 | 6.86 × 10−6 | 0 | 2.30 × 10−7 | 8.10 × 10−6 | 1.01 | |
| Time | 0.015 | 0.019 | 0.008 | 0.020 | 0.006 | 0.008 | 0.006 | |
| F23 | Mean | 3.00 | 3.00 | 3.00 | 3.00 | 3.00 | 3.00 | 5.82 |
| Std | 3.29 × 10−5 | 4.91 × 10−7 | 1.40 × 10−4 | 1.66 × 10−15 | 4.25 × 10−5 | 1.08 × 10−4 | 5.33 | |
| Time | 0.017 | 0.027 | 0.009 | 0.033 | 0.009 | 0.011 | 0.008 | |
| F24 | Mean | −3.00 × 10−1 | −3.00 × 10−1 | −3.00 × 10−1 | −3.00 × 10−1 | −3.00 × 10−1 | −3.86 | 6.14 × 10−9 |
| Std | 2.26 × 10−16 | 2.26 × 10−16 | 2.26 × 10−16 | 2.26 × 10−16 | 2.26 × 10−16 | 6.34 × 10−5 | 3.24 × 10−4 | |
| Time | 0.013 | 0.016 | 0.007 | 0.018 | 0.005 | 0.008 | 0.011 | |
| F25 | Mean | −3.07 | −3.08 | −3.21 | −3.32 | −3.27 | −3.31 | 2.90 × 101 |
| Std | 1.55 × 10−1 | 1.36 × 10−1 | 1.03 × 10−1 | 5.20 × 10−12 | 7.22 × 10−2 | 3.16 × 10−2 | 4.50 × 10−1 | |
| Time | 0.024 | 0.043 | 0.009 | 0.032 | 0.010 | 0.010 | 0.009 | |
| F26 | Mean | −1.00 × 101 | −5.05 | −7.89 | −1.02 × 101 | −9.65 | −6.85 | −4.26 |
| Std | 1.73 × 10−1 | 5.64 × 10−3 | 2.53 | 2.43 × 10−11 | 1.54 | 2.82 | 3.26 × 10−1 | |
| Time | 0.026 | 0.028 | 0.009 | 0.040 | 0.034 | 0.011 | 0.110 | |
| F27 | Mean | −1.03 × 101 | −5.57 | −7.90 | −1.04 × 101 | −1.02 × 101 | −7.56 | −3.85 |
| Std | 1.70 × 10−1 | 1.49 | 3.16 | 2.43 × 10−11 | 9.70 × 10−1 | 3.16 | 4.23 × 10−1 | |
| Time | 0.025 | 0.028 | 0.011 | 0.046 | 0.036 | 0.012 | 0.088 | |
| F28 | Mean | −1.05 × 101 | −5.61 | −7.63 | −1.05 × 101 | −1.05 × 101 | −7.57 | −3.78 |
| Std | 1.12 × 10−1 | 1.49 | 3.25 | 2.93 × 10−11 | 4.51 × 10−4 | 3.56 | 6.20 × 10−1 | |
| Time | 0.029 | 0.031 | 0.009 | 0.038 | 0.030 | 0.020 | 0.082 |
| Function | Optimizer | Mean | Std | Best | Worst |
|---|---|---|---|---|---|
| F1 | HHO | 5.38 × 10−95 | 2.28 × 10−94 | 2.8 × 10−112 | 1.24 × 10−93 |
| MEHHO | 0 | 0 | 0 | 0 | |
| F2 | HHO | 9.2 × 10−49 | 4.87 × 10−48 | 3.32 × 10−61 | 2.67 × 10−47 |
| MEHHO | 0 | 0 | 0 | 0 | |
| F3 | HHO | 5.07 × 10−63 | 2.21 × 10−62 | 2.35 × 10−92 | 1.17 × 10−61 |
| MEHHO | 0 | 0 | 0 | 0 | |
| F4 | HHO | 1.43 × 10−48 | 5.9 × 10−48 | 9.29 × 10−59 | 3.2 × 10−47 |
| MEHHO | 0 | 0 | 0 | 0 | |
| F5 | HHO | 1.89 × 10−2 | 2.95 × 10−2 | 5.48 × 10−5 | 1.22 × 10−1 |
| MEHHO | 1.80 × 10−2 | 2.10 × 10−2 | 2.89 × 10−6 | 9.28 × 10−2 | |
| F6 | HHO | 2.85 × 10−4 | 4.02 × 10−4 | 6.20 × 10−8 | 1.70 × 10−3 |
| MEHHO | 1.32 × 10−4 | 2.12 × 10−4 | 1.69 × 10−8 | 8.55 × 10−4 | |
| F7 | HHO | 1.62 × 10−4 | 1.99 × 10−4 | 1.10 × 10−5 | 1.10 × 10−3 |
| MEHHO | 5.54 × 10−5 | 5.47 × 10−5 | 2.32 × 10−6 | 2.61 × 10−4 | |
| F8 | HHO | 2.61 × 10−4 | 1.51 × 10−86 | 1.54 × 10−105 | 8.27 × 10−86 |
| MEHHO | 0 | 0 | 0 | 0 | |
| F9 | HHO | 7.00 × 10−98 | 3.41 × 10−97 | 3.36 × 10−114 | 1.87 × 10−96 |
| MEHHO | 0 | 0 | 0 | 0 | |
| F10 | HHO | 9.4 × 10−88 | 5.15 × 10−87 | 1.9 × 10−110 | 2.82 × 10−86 |
| MEHHO | 0 | 0 | 0 | 0 | |
| F11 | HHO | 0 | 0 | 0 | 0 |
| MEHHO | 0 | 0 | 0 | 0 | |
| F12 | HHO | 8.88 × 10−16 | 0 | 8.88 × 10−16 | 8.88 × 10−16 |
| MEHHO | 8.88 × 10−16 | 0 | 8.88 × 10−16 | 8.88 × 10−16 | |
| F13 | HHO | 0 | 0 | 0 | 0 |
| MEHHO | 0 | 0 | 0 | 0 | |
| F14 | HHO | 5.75 × 10−6 | 8.57 × 10−6 | 5.02 × 10−8 | 3.42 × 10−5 |
| MEHHO | 1.80 × 10−6 | 2.31 × 10−6 | 8.82 × 10−11 | 8.65 × 10−6 | |
| F15 | HHO | 1.06 × 10−4 | 1.32 × 10−4 | 2.71 × 10−7 | 4.74 × 10−4 |
| MEHHO | 6.03 × 10−5 | 7.24 × 10−5 | 1.51 × 10−9 | 2.39 × 10−4 | |
| F16 | HHO | 6.23 × 10−50 | 3.24 × 10−49 | 3 × 10−62 | 1.78 × 10−48 |
| MEHHO | 0 | 0 | 0 | 0 | |
| F17 | HHO | 0 | 0 | 0 | 0 |
| MEHHO | 0 | 0 | 0 | 0 | |
| F18 | HHO | 3.28 × 10−48 | 1.67 × 10−47 | 5.39 × 10−55 | 9.14 × 10−47 |
| MEHHO | 0 | 0 | 0 | 0 | |
| F19 | HHO | 1 × 10−293 | 0 | 0 | 3 × 10−292 |
| MEHHO | 0 | 0 | 0 | 0 | |
| F20 | HHO | 1.21 × 10−20 | 9.22 × 10−24 | 1.21 × 10−20 | 1.21 × 10−20 |
| MEHHO | 0 | 0 | 0 | 0 |
| Function | Optimizer | Mean | Std | Best | Worst |
|---|---|---|---|---|---|
| F1 | HHO | 5.65 × 10−95 | 3.07 × 10−94 | 2.1 × 10−110 | 1.68 × 10−93 |
| MEHHO | 0 | 0 | 0 | 0 | |
| F2 | HHO | 2.45 × 10−50 | 1.11 × 10−49 | 7.88 × 10−60 | 6.09 × 10−49 |
| MEHHO | 0 | 0 | 0 | 0 | |
| F3 | HHO | 2.62 × 10−59 | 9.96 × 10−59 | 2.79 × 10−92 | 4.11 × 10−58 |
| MEHHO | 0 | 0 | 0 | 0 | |
| F4 | HHO | 7.75 × 10−48 | 4.16 × 10−47 | 2.27 × 10−55 | 2.28 × 10−46 |
| MEHHO | 0 | 0 | 0 | 0 | |
| F5 | HHO | 4.21 × 10−2 | 7.05 × 10−2 | 1.65 × 10−4 | 3.50 × 10−1 |
| MEHHO | 2.37 × 10−2 | 2.94 × 10−2 | 6.65 × 10−5 | 1.00 × 10−1 | |
| F6 | HHO | 8.52 × 10−4 | 1.30 × 10−3 | 1.66 × 10−8 | 4.70 × 10−3 |
| MEHHO | 1.82 × 10−4 | 2.52 × 10−4 | 5.89 × 10−7 | 1.20 × 10−3 | |
| F7 | HHO | 2.04 × 10−4 | 2.16 × 10−4 | 5.36 × 10−7 | 8.43 × 10−4 |
| MEHHO | 5.88 × 10−5 | 6.43 × 10−5 | 3.56 × 10−7 | 2.22 × 10−4 | |
| F8 | HHO | 3.63 × 10−87 | 1.98 × 10−86 | 2.96 × 10−106 | 1.08 × 10−85 |
| MEHHO | 0 | 0 | 0 | 0 | |
| F9 | HHO | 8.06 × 10−96 | 4.17 × 10−95 | 4.03 × 10−113 | 2.29 × 10−94 |
| MEHHO | 0 | 0 | 0 | 0 | |
| F10 | HHO | 3.12 × 10−90 | 1.71 × 10−89 | 1.9 × 10−109 | 9.35 × 10−89 |
| MEHHO | 0 | 0 | 0 | 0 | |
| F11 | HHO | 0 | 0 | 0 | 0 |
| MEHHO | 0 | 0 | 0 | 0 | |
| F12 | HHO | 8.88 × 10−16 | 0 | 8.88 × 10−16 | 8.88 × 10−16 |
| MEHHO | 8.88 × 10−16 | 0 | 8.88 × 10−16 | 8.88 × 10−16 | |
| F13 | HHO | 0 | 0 | 0 | 0 |
| MEHHO | 0 | 0 | 0 | 0 | |
| F14 | HHO | 3.13 × 10−6 | 4.40 × 10−6 | 7.29 × 10−9 | 1.59 × 10−5 |
| MEHHO | 1.57 × 10−6 | 2.31 × 10−6 | 2.58 × 10−11 | 1.11 × 10−5 | |
| F15 | HHO | 2.79 × 10−4 | 5.00 × 10−4 | 6.34 × 10−7 | 2.10 × 10−3 |
| MEHHO | 5.83 × 10−5 | 7.05 × 10−5 | 1.14 × 10−9 | 2.87 × 10−4 | |
| F16 | HHO | 2.55 × 10−6 | 1.4 × 10−5 | 9.63 × 10−60 | 7.65 × 10−5 |
| MEHHO | 0 | 0 | 0 | 0 | |
| F17 | HHO | 0 | 0 | 0 | 0 |
| MEHHO | 0 | 0 | 0 | 0 | |
| F18 | HHO | 1.5 × 10−49 | 6.76 × 10−49 | 1.32 × 10−55 | 3.68 × 10−48 |
| MEHHO | 0 | 0 | 0 | 0 | |
| F19 | HHO | 2.8 × 10−298 | 0 | 0 | 8.4 × 10−297 |
| MEHHO | 0 | 0 | 0 | 0 | |
| F20 | HHO | 4.68 × 10−42 | 6.21 × 10−44 | 4.66 × 10−42 | 5.00 × 10−42 |
| MEHHO | 4.66 × 10−43 | 1.42 × 10−42 | 0 | 4.66 × 10−42 |
| Function | Optimizer | Mean | Std | Best | Worst |
|---|---|---|---|---|---|
| F1 | HHO | 1.97 × 10−96 | 6.88 × 10−96 | 5.9 × 10−114 | 3.63 × 10−95 |
| MEHHO | 0 | 0 | 0 | 0 | |
| F2 | HHO | 1.59 × 10−49 | 3.83 × 10−49 | 8.98 × 10−59 | 1.69 × 10−48 |
| MEHHO | 0 | 0 | 0 | 0 | |
| F3 | HHO | 1.09 × 10−37 | 5.96 × 10−37 | 1.26 × 10−74 | 3.27 × 10−36 |
| MEHHO | 0 | 0 | 0 | 0 | |
| F4 | HHO | 2.56 × 10−47 | 8.68 × 10−47 | 4.67 × 10−56 | 4.04 × 10−46 |
| MEHHO | 0 | 0 | 0 | 0 | |
| F5 | HHO | 2.31 × 10−1 | 3.76 × 10−1 | 2.00 × 10−3 | 1.80 |
| MEHHO | 1.53 × 10−1 | 1.73 × 10−1 | 1.35 × 10−4 | 6.49 × 10−1 | |
| F6 | HHO | 3.60 × 10−3 | 6.00 × 10−3 | 1.22 × 10−5 | 2.29 × 10−2 |
| MEHHO | 1.40 × 10−3 | 2.10 × 10−3 | 3.00 × 10−7 | 7.60 × 10−3 | |
| F7 | HHO | 2.08 × 10−4 | 2.96 × 10−4 | 1.59 × 10−5 | 1.30 × 10−3 |
| MEHHO | 5.58 × 10−5 | 5.40 × 10−5 | 6.12 × 10−7 | 2.33 × 10−4 | |
| F8 | HHO | 1.04 × 10−89 | 2.66 × 10−89 | 1.05 × 10−104 | 1.03 × 10−88 |
| MEHHO | 0 | 0 | 0 | 0 | |
| F9 | HHO | 5.01 × 10−99 | 2.06 × 10−98 | 3.54 × 10−110 | 1.13 × 10−97 |
| MEHHO | 0 | 0 | 0 | 0 | |
| F10 | HHO | 1.62 × 10−88 | 8.84 × 10−88 | 4.1 × 10−116 | 4.84 × 10−87 |
| MEHHO | 0 | 0 | 0 | 0 | |
| F11 | HHO | 0 | 0 | 0 | 0 |
| MEHHO | 0 | 0 | 0 | 0 | |
| F12 | HHO | 8.88 × 10−16 | 0 | 8.88 × 10−16 | 8.88 × 10−16 |
| MEHHO | 8.88 × 10−16 | 0 | 8.88 × 10−16 | 8.88 × 10−16 | |
| F13 | HHO | 0 | 0 | 0 | 0 |
| MEHHO | 0 | 0 | 0 | 0 | |
| F14 | HHO | 2.13 × 10−6 | 3.37 × 10−6 | 4.33 × 10−8 | 1.24 × 10−5 |
| MEHHO | 7.06 × 10−7 | 1.71 × 10−6 | 6.05 × 10−10 | 9.20 × 10−6 | |
| F15 | HHO | 6.12 × 10−4 | 7.75 × 10−4 | 3.00 × 10−6 | 2.90 × 10−3 |
| MEHHO | 2.64 × 10−4 | 3.69 × 10−4 | 7.17 × 10−7 | 1.40 × 10−3 | |
| F16 | HHO | 3.51 × 10−5 | 1.92 × 10−4 | 3.64 × 10−57 | 1.10 × 10−3 |
| MEHHO | 0 | 0 | 0 | 0 | |
| F17 | HHO | 0 | 0 | 0 | 0 |
| MEHHO | 0 | 0 | 0 | 0 | |
| F18 | HHO | 9.02 × 10−48 | 4.45 × 10−47 | 7.89 × 10−57 | 2.44 × 10−46 |
| MEHHO | 0 | 0 | 0 | 0 | |
| F19 | HHO | 1.3 × 10−288 | 0 | 0 | 3.8 × 10−287 |
| MEHHO | 0 | 0 | 0 | 0 | |
| F20 | HHO | 4.51 × 10−215 | 0 | 4.46 × 10−215 | 4.72 × 10−215 |
| MEHHO | 4.47 × 10−215 | 0 | 4.46 × 10−215 | 4.50 × 10−215 |
| Function | Value | Dim=30 | Dim=50 | Dim=100 | Dim=500 |
|---|---|---|---|---|---|
| F1 | p-value | 2.00 × 10−6 | 2.00 × 10−6 | 2.00 × 10−6 | 2.00 × 10−6 |
| conclusion | + | + | + | + | |
| F2 | p-value | 2.00 × 10−6 | 2.00 × 10−6 | 2.00 × 10−6 | 2.00 × 10−6 |
| conclusion | + | + | + | + | |
| F3 | p-value | 2.00 × 10−6 | 2.00 × 10−6 | 2.00 × 10−6 | 2.00 × 10−6 |
| conclusion | + | + | + | + | |
| F4 | p-value | 2.00 × 10−6 | 2.00 × 10−6 | 2.00 × 10−6 | 2.00 × 10−6 |
| conclusion | + | + | + | + | |
| F5 | p-value | 0.405 | 0.453 | 0.066 | 0.781 |
| conclusion | - | - | - | - | |
| F6 | p-value | 0.004 | 0.01 | 0.014 | 0.465 |
| conclusion | + | + | + | - | |
| F7 | p-value | 0.005 | 0.004 | 0.004 | 1.60 × 10−4 |
| conclusion | + | + | + | + | |
| F8 | p-value | 2.00 × 10−6 | 2.00 × 10−6 | 2.00 × 10−6 | 2.00 × 10−6 |
| conclusion | + | + | + | + | |
| F9 | p-value | 2.00 × 10−6 | 2.00 × 10−6 | 2.00 × 10−6 | 2.00 × 10−6 |
| conclusion | + | + | + | + | |
| F10 | p-value | 2.00 × 10−6 | 2.00 × 10−6 | 2.00 × 10−6 | 2.00 × 10−6 |
| conclusion | + | + | + | + |
| Function | Value | Dim=30 | Dim=50 | Dim=100 | Dim=500 |
|---|---|---|---|---|---|
| F11 | p-value | NA | NA | NA | NA |
| conclusion | = | = | = | = | |
| F12 | p-value | NA | NA | NA | NA |
| conclusion | = | = | = | = | |
| F13 | p-value | NA | NA | NA | NA |
| conclusion | = | = | = | = | |
| F14 | p-value | 0.002 | 5.30 × 10−5 | 0.329 | 0.141 |
| conclusion | + | + | - | - | |
| F15 | p-value | 0.766 | 1.20 × 10−5 | 0.237 | 0.006 |
| conclusion | - | + | - | + | |
| F16 | p-value | 2.00 × 10−6 | 2.00 × 10−6 | 2.00 × 10−6 | 2.00 × 10−6 |
| conclusion | + | + | + | + | |
| F17 | p-value | NA | NA | NA | NA |
| conclusion | = | = | = | = | |
| F18 | p-value | 2.00 × 10−6 | 2.00 × 10−6 | 2.00 × 10−6 | 2.00 × 10−6 |
| conclusion | + | + | + | + | |
| F19 | p-value | 8.70 × 10−5 | 1.32 × 10−4 | 1.32 × 10−4 | 2.92 × 10−4 |
| conclusion | + | + | + | + | |
| F20 | p-value | 2.00 × 10−6 | 2.00 × 10−6 | 2.00 × 10−6 | 4.90 × 10−5 |
| conclusion | + | + | + | + |
| Function | F21 | F22 | F23 | F24 | F25 | F26 | F27 | F28 |
|---|---|---|---|---|---|---|---|---|
| p-value | 2.00 × 10−6 | 0.001 | 5.00 × 10−6 | NA | 0.079 | 2.00 × 10−6 | 2.00 × 10−6 | 2.00 × 10−6 |
| conclusion | + | + | + | = | - | + | + | + |
| Function | Metric | MEHHO | hHHO-PSO | hHHO-GWO | hHHO-SCA |
|---|---|---|---|---|---|
| F1 | Mean | 0 | 7.62 × 10−98 | 4.61 × 10−96 | 1.86 × 10−91 |
| Std | 0 | 3.11 × 10−97 | 2.50 × 10−95 | 9.49 × 10−91 | |
| F2 | Mean | 0 | 2.49 × 10−51 | 1.55 × 10−48 | 2.46 × 10−51 |
| Std | 0 | 1.20 × 10−50 | 8.42 × 10−48 | 1.11 × 10−50 | |
| F3 | Mean | 0 | 7.38 × 10−75 | 1.53 × 10−68 | 8.88 × 10−72 |
| Std | 0 | 4.02 × 10−74 | 8.36 × 10−68 | 4.86 × 10−71 | |
| F4 | Mean | 0 | 1.23 × 10−47 | 3.30 × 10−49 | 8.02 × 10−49 |
| Std | 0 | 6.73 × 10−47 | 1.21 × 10−48 | 2.83 × 10−48 | |
| F5 | Mean | 6.90 × 10−3 | 7.32 × 10−3 | 1.70 × 10−2 | 1.43 × 10−2 |
| Std | 7.80 × 10−3 | 8.53 × 10−3 | 2.16 × 10−2 | 2.02 × 10−2 | |
| F6 | Mean | 5.28 × 10−5 | 1.44 × 10−4 | 1.64 × 10−4 | 2.24 × 10−4 |
| Std | 1.42 × 10−4 | 2.5 × 10−4 | 3.08 × 10−4 | 3.38 × 10−4 | |
| F7 | Mean | 5.45 × 10−5 | 1.77 × 10−4 | 1.49 × 10−4 | 1.22 × 10−4 |
| Std | 5.54 × 10−5 | 1.74 × 10−4 | 1.15 × 10−4 | 1.10 × 10−4 | |
| F11 | Mean | 0 | 0 | 0 | 0 |
| Std | 0 | 0 | 0 | 0 | |
| F12 | Mean | 8.88 × 10−16 | 8.88 × 10−16 | 8.88 × 10−16 | 8.88 × 10−16 |
| Std | 0 | 0 | 0 | 0 | |
| F13 | Mean | 0 | 0 | 0 | 0 |
| Std | 0 | 0 | 0 | 0 | |
| F14 | Mean | 2.99 × 10−6 | 1.13 × 10−5 | 1.13 × 10−5 | 1.13 × 10−5 |
| Std | 5.33 × 10−6 | 1.50 × 10−5 | 1.5 × 10−5 | 1.5 × 10−5 | |
| F15 | Mean | 4.6 × 10−5 | 1.13 × 10−4 | 1.13 × 10−4 | 1.13 × 10−4 |
| Std | 6.89 × 10−5 | 1.66 × 10−4 | 1.66 × 10−4 | 1.66 × 10−4 | |
| F21 | Mean | −1.03 | −1.03 | −1.03 | −1.03 |
| Std | 4.60 × 10−7 | 4.80 × 10−9 | 3.97 × 10−10 | 1.80 × 10−9 | |
| F22 | Mean | 3.98 × 10−1 | 3.98 × 10−1 | 3.98 × 10−1 | 3.98 × 10−1 |
| Std | 2.99 × 10−5 | 3.49 × 10−5 | 1.86 × 10−5 | 2.15 × 10−5 | |
| F23 | Mean | 3.00 | 3.00 | 3.00 | 3.00 |
| Std | 3.29 × 10−5 | 5.28 × 10−7 | 2.65 × 10−7 | 9.98 × 10−7 | |
| F24 | Mean | −3.00 × 10−1 | −3.86 | −3.86 | −3.86 |
| Std | 2.26 × 10−16 | 3.41 × 10−3 | 4.30 × 10−3 | 3.00 × 10−3 | |
| F25 | Mean | −3.07 | −3.10 | −3.11 | −3.09 |
| Std | 1.55 × 10−1 | 1.03 × 10−1 | 1.21 × 10−1 | 1.09 × 10−1 | |
| F26 | Mean | −1.00 × 101 | −5.05 | −5.22 | −5.21 |
| Std | 1.73 × 10−1 | 6.60 × 10−3 | 8.97 × 10−1 | 8.95 × 10−1 | |
| F27 | Mean | −1.03 × 101 | −5.08 | −5.14 | −5.25 |
| Std | 1.70 × 10−1 | 4.12 × 10−3 | 1.10 | 9.26 × 10−1 | |
| F28 | Mean | −1.05 × 101 | −5.12 | −5.30 | −5.28 |
| Std | 1.12 × 10−1 | 5.77 × 10−3 | 9.55 × 10−1 | 8.65 × 10−1 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sun, Y.; Huang, Q.; Liu, T.; Cheng, Y.; Li, Y. Multi-Strategy Enhanced Harris Hawks Optimization for Global Optimization and Deep Learning-Based Channel Estimation Problems. Mathematics 2023, 11, 390. https://doi.org/10.3390/math11020390
Sun Y, Huang Q, Liu T, Cheng Y, Li Y. Multi-Strategy Enhanced Harris Hawks Optimization for Global Optimization and Deep Learning-Based Channel Estimation Problems. Mathematics. 2023; 11(2):390. https://doi.org/10.3390/math11020390
Chicago/Turabian StyleSun, Yunshan, Qian Huang, Ting Liu, Yuetong Cheng, and Yanqin Li. 2023. "Multi-Strategy Enhanced Harris Hawks Optimization for Global Optimization and Deep Learning-Based Channel Estimation Problems" Mathematics 11, no. 2: 390. https://doi.org/10.3390/math11020390
APA StyleSun, Y., Huang, Q., Liu, T., Cheng, Y., & Li, Y. (2023). Multi-Strategy Enhanced Harris Hawks Optimization for Global Optimization and Deep Learning-Based Channel Estimation Problems. Mathematics, 11(2), 390. https://doi.org/10.3390/math11020390






