On Control Polygons of Planar Sextic Pythagorean Hodograph Curves
Abstract
1. Introduction
2. Bézier Representation for Sextic PH Curves
3. Properties of Sextic PH Curves
- Class I
- Polynomials and are quadratic and linear, respectively. Regardless of the symmetry of control points, we rewrite the factors of in Bernstein form aswhere . Remark: if or , the curve is indeed a Class II sextic PH curve, which will be discussed later. If , then is a linear polynomial with real coefficients, which has exactly one real root. Denoting by the root of , we haveThat is to say, a sextic PH curve with the hodograph of the form (4) has a cusp occurring at . Otherwise, if (i.e., ), the corresponding sextic curve degenerates to a Class I quintic PH curve [10]. On the contrary, a quintic Class I PH curve can also be considered as a sextic PH curve of this class using one step of degree elevation.
- Class II
- Polynomials and are linear and cubic, respectively. We rewrite the factors of in Bernstein form asfor some , , and , . Let , , be roots of the cubic polynomial in Equation (6). According to the fundamental theorem of algebra, there is at least one real root. We assume , then and are either real numbers or a pair of conjugate complex numbers. Hence, a Class II sextic PH curve presents one or three cusps, depending on the real root number of . Note that, when the cubic real polynomial degenerates to a quadratic, linear, or constant polynomial, the sextic PH curve degenerates to a Class II quintic, quartic, or cubic PH curve, respectively. Equally, cubic, quartic, and Class II quintic PH curves can be converted to Class II sextic PH curves using three steps to one step of degree elevation. A Class II sextic PH curve degenerates to a line segment when or , which is not discussed in this paper.
4. Geometric Characteristics of Sextic PH Curves
4.1. Class I Sextic PH Curve
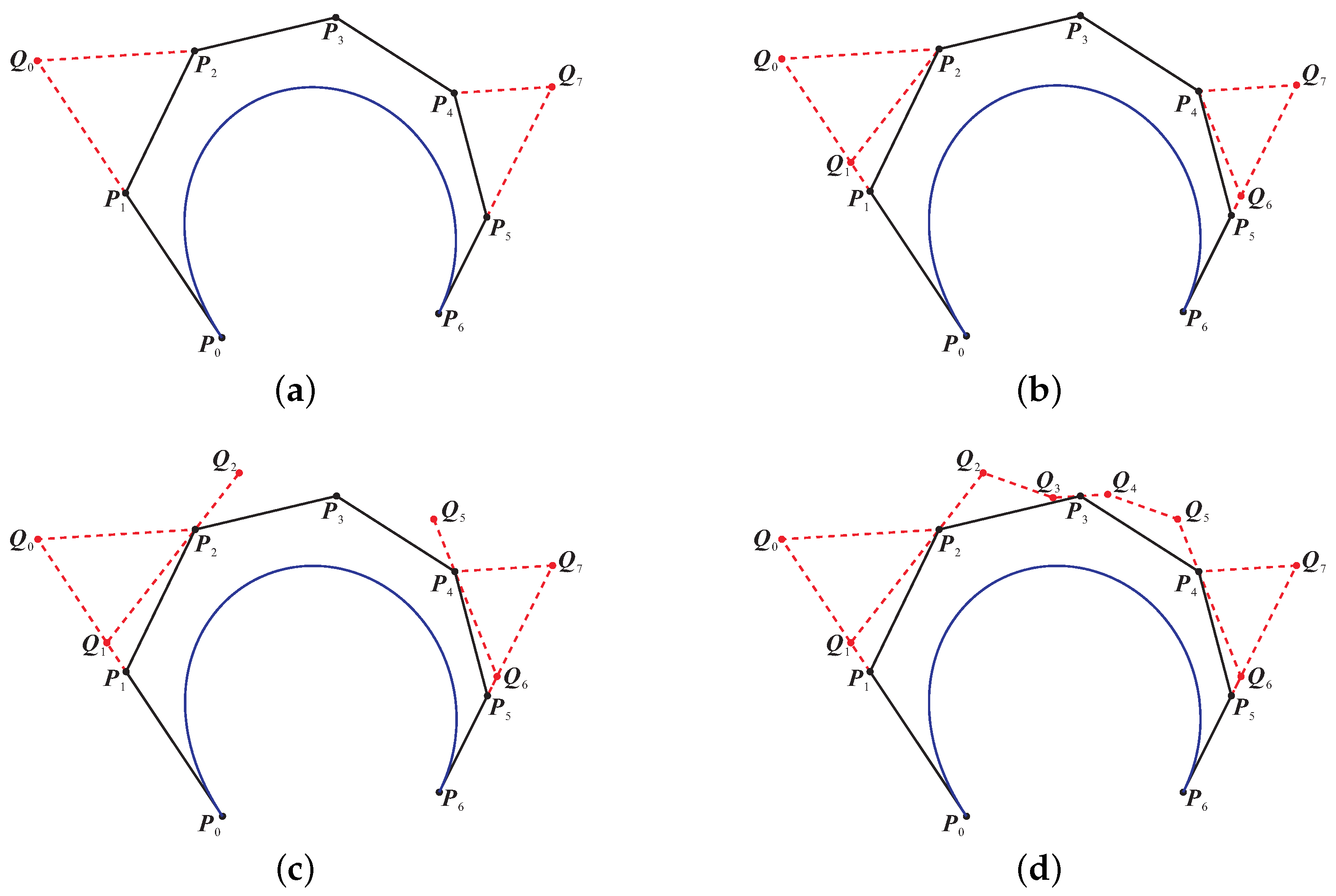
- Let , andwhere
- Letthus, we obtainwhere x is a solution of the system of cubic equations as follows:We defer deriving this system until the proof of Theorem 1. Note that the roots of the third equation of System (13) come in pairs:Hence, we solve the system (13) by verifying if the roots of the third equation of Equation (13) satisfy the first two equations. Although there are four candidate solutions due to different signs, the number of roots is no more than three for the cubic system. For each real solution, Steps 3–4 are further performed, respectively. If there are no real roots for the above system, the curve is not a PH curve, and the procedure is terminated immediately.
- Let and be points on lines and , respectively, such that
- Finally, let , and
An Example of a Class I Sextic PH Curve with a Concave Control Polygon
4.2. Class II Sextic PH Curve
- Let ; we obtainwhere
- Compute
- Let , , be points such thatthus, we have , , , as shown in Figure 3.
An Example of a Class II Sextic PH Curve with a Concave Control Polygon
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Farouki, R.T.; Sakkalis, T. Pythagorean hodographs. IBM J. Res. Dev. 1990, 34, 736–752. [Google Scholar] [CrossRef]
- Farouki, R.T.; Manjunathaiah, J.; Nichlas, D.; Yuan, G.F.; Jee, S. Variable-feedrate CNC interpolators for constant material removal rates along Pythagorean hodograph curves. Comput.-Aided Des. 1998, 30, 631–640. [Google Scholar] [CrossRef]
- Elber, G.; Lee, I.-K.; Kim, M.-S. Comparing offset curve approximation methods. IEEE Comput. Graph. Appl. 1997, 17, 62–71. [Google Scholar] [CrossRef]
- Farouki, R.T. Pythagorean-Hodograph Curves: Algebra and Geometry Inseparable; Springer: Berlin/Heidelberg, Germany, 2008. [Google Scholar]
- Farouki, R.T.; Giannelli, C.; Manni, C.; Sestini, A. Identification of spatial PH quintic Hermite interpolants with near-optimal shape measures. Comput. Aided Geom. Des. 2008, 25, 274–297. [Google Scholar] [CrossRef]
- Farouki, R.T.; Šír, Z. Rational Pythagorean hodograph space curves. Comput. Aided Geom. Des. 2011, 28, 75–88. [Google Scholar] [CrossRef]
- Kosinka, J.; Lávička, M. Pythagorean hodograph curves: A survey of recent advances. J. Geom. Graph. 2014, 18, 23–43. [Google Scholar]
- Sakkalis, T.; Farouki, R.T. Pythagorean hodograph curves in Euclidean spaces of dimension greater than 3. J. Comput. Appl. Math. 2012, 236, 4375–4382. [Google Scholar] [CrossRef]
- Farouki, R.T.; Giannelli, C.; Sestini, A. Identification and “reverse engineering” of Pythagorean-hodograph curves. Comput. Aided Geom. Des. 2015, 34, 21–36. [Google Scholar] [CrossRef]
- Fang, L.; Wang, G. Geometric characteristics of planar quintic Pythagorean hodograph curves. J. Comput. Appl. Math. 2018, 330, 117–127. [Google Scholar] [CrossRef]
- Farouki, R.T. The conformal map z↦z2 of the hodograph plane. Comput. Aided Geom. Des. 1994, 11, 363–390. [Google Scholar] [CrossRef]
- Wang, G.; Fang, L. On control polygons of quartic Pythagorean hodograph curves. Comput. Aided Geom. Des. 2009, 26, 1006–1015. [Google Scholar] [CrossRef]
- Wang, H.; Zhu, C.; Li, C. Identification of planar sextic Pythagorean-Hodograph curves. J. Math. Res. Appl. 2017, 37, 59–72. [Google Scholar]
- Šír, Z.; Kosinka, J. Low degree Euclidean and Minkowski Pythagorean hodograph curves. In Proceedings of the International Conference on Mathematical Methods for Curves and Surfaces, Tønsberg, Norway, 26 June–1 July 2008; Dæhlen, M., Floater, M., Lyche, T., Jean-Louis, M., Mørken, K., Schumaker, L.L., Eds.; Springer: Berlin/Heidelberg, Germany, 2010; pp. 394–418. [Google Scholar]
- Kosinka, J.; Lávička, M. On rational Minkowski Pythagorean hodograph curves. Comput. Aided Geom. Des. 2010, 27, 514–524. [Google Scholar] [CrossRef]
- Šír, Z. Classification of planar Pythagorean hodograph curves. Comput. Aided Geom Des. 2020, 80, 101866. [Google Scholar] [CrossRef]
- Fang, L.; Peng, Y.; Li, Y.; Cao, J. Classification of polynomial minimal surfaces. Comput. Aided Geom. Des. 2022, 96, 102106. [Google Scholar] [CrossRef]
- Li, Y.; Fang, L.; Cao, J.; Wang, G. Identification of two classes of planar septic Pythagorean hodograph curves. J. Comput. Appl. Math. 2019, 348, 383–400. [Google Scholar] [CrossRef]
- Lu, X.-J.; Zheng, J.; Cai, Y.; Zhao, G. Geometric characteristics of a class of cubic curves with rational offsets. Comput.-Aided Des. 2016, 70, 36–45. [Google Scholar] [CrossRef]



Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, Y.; Fang, L.; Zheng, Z.; Cao, J. On Control Polygons of Planar Sextic Pythagorean Hodograph Curves. Mathematics 2023, 11, 383. https://doi.org/10.3390/math11020383
Li Y, Fang L, Zheng Z, Cao J. On Control Polygons of Planar Sextic Pythagorean Hodograph Curves. Mathematics. 2023; 11(2):383. https://doi.org/10.3390/math11020383
Chicago/Turabian StyleLi, Yujun, Lincong Fang, Zhihao Zheng, and Juan Cao. 2023. "On Control Polygons of Planar Sextic Pythagorean Hodograph Curves" Mathematics 11, no. 2: 383. https://doi.org/10.3390/math11020383
APA StyleLi, Y., Fang, L., Zheng, Z., & Cao, J. (2023). On Control Polygons of Planar Sextic Pythagorean Hodograph Curves. Mathematics, 11(2), 383. https://doi.org/10.3390/math11020383





