The Optimization of Working Time for a Consecutively Connected Production Line
Abstract
1. Introduction
2. Theoretical Basis
2.1. Learning Curve Theory
2.2. Human Factors Fatigue Curve Theory
3. Problem Description and Model Building
3.1. UGF of the Workstation
- A 10 min rest for every hour of work: skilled workers have an 80% probability of being well rested and new hands have a 60% probability of being well rested;
- A 15 min rest for every 2 h of work: skilled workers have an 80% probability of being well rested and new hands have a 60% probability of being well rested;
- A 20 min rest for every 3 h of work: skilled workers have an 80% probability of being well rested and new hands have a 60% probability of being well rested.
3.2. UGF for Consecutively Connected Production System
3.3. Production Cost
3.3.1. Labor Cost
3.3.2. Material Cost
3.4. Revenue from Product Sales
3.5. Profitability
4. Reliability Analysis
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| MCCS | Multistate consecutively connected system |
| UGF | Universal generating function |
| UM | UGF information matrix |
| Workstation at position | |
| The random variable representing the productivity of the workstation | |
| The when occupies state | |
| The probability of being in work state , where | |
| The producer of type | |
| occupying work state | |
| being in work state | |
| UGF representing the performance distribution of a discrete random variable | |
| The minimum requirement for system reliability | |
| Reliability of the considered MCCS | |
| VE | The total labor cost when completing the work task |
| , where the cost of the machine is the rental cost | |
| The material cost | |
| Total cost of the MCCS | |
| The product sales revenue | |
| The number of products in the specified working time | |
| The selling price of each product | |
| The productivity of the production line system | |
| The total time of production | |
| The number of producers | |
| The time that work is suspended | |
| The time required to complete a product | |
| The total profit |
References
- Bakkari, M.; Khatory, A. Industry 4.0: Strategy for more sustainable industrial development in SMEs. In Proceedings of the IEOM 7th International Conference on Industrial Engineering and Operations Management, Rabat, Morocco, 11–13 April 2017. [Google Scholar]
- Liu, Z.; Xie, K.; Li, L.; Chen, Y. A paradigm of safety management in industry 4.0. Syst. Res. Behav. Sci. 2020, 37, 632–645. [Google Scholar] [CrossRef]
- Wadgaonkar, J.; Mane, N.; Bhole, K.; Shinde, D. Novel, low cost, efficient manual cum automation based alcohol & ethanol production plant. In Proceedings of the 2015 International Conference on Energy Systems and Applications, Pune, India, 30 October–1 November 2015. [Google Scholar]
- Levitin, G.; Yeh, W.C.; Dai, Y. Minimizing bypass transportation expenses in linear multistate consecutively-connected systems. IEEE Trans. Reliab. 2014, 63, 230–238. [Google Scholar] [CrossRef]
- Levitin, G.; Xing, L.; Dai, Y. Optimal arrangement of connecting elements in linear consecutively connected systems with heterogeneous warm standby groups. Reliab. Eng. Syst. Saf. 2017, 165, 395–401. [Google Scholar] [CrossRef]
- Xing, L.; Levitin, G. Connectivity modeling and optimization of linear consecutively connected systems with repairable connecting elements. Eur. J. Oper. Res. 2018, 264, 732–741. [Google Scholar] [CrossRef]
- Zhao, X.; Chai, X.; Sun, J.; Qiu, Q. Joint optimization of mission abort and protective device selection policies for multistate systems. Risk Anal 2022. [Google Scholar] [CrossRef] [PubMed]
- Peng, R.; Wu, D.; Gao, K. Reliability of a Dual Linear Consecutive System with Three Failure Modes. In Proceedings of the International Conference of Celebrating Professor Jinhua Cao’s 80th Birthday, Singapore, 16 October 2019. [Google Scholar]
- Peng, R.; Xie, M.; Ng, S.H.; Levitin, G. Element maintenance and allocation for linear consecutively connected systems. IIE Trans. 2012, 44, 964–973. [Google Scholar] [CrossRef]
- Levitin, G.; Xing, L.; Dai, Y. Optimal Allocation of Connecting Elements in Phase Mission Linear Consecutively-Connected Systems. IEEE Trans. Reliab. 2013, 62, 618–627. [Google Scholar] [CrossRef]
- Gao, K.; Yan, X.; Peng, R.; Xing, L. Economic design of a linear consecutively connected system considering cost and signal loss. IEEE Trans. Syst. Man Cybern. Syst. 2021, 51, 5116–5128. [Google Scholar] [CrossRef]
- Glock, C.H.; Grosse, E.H.; Kim, T.; Neumann, W.P.; Sobhani, A. An integrated cost and worker fatigue evaluation model of a packaging process. Int. J. Prod. Econ. 2019, 207, 107–124. [Google Scholar] [CrossRef]
- Zhang, Z.; Wang, K.; Zhu, L.; Cheng, W. Pareto Hybrid Ant Colony and Genetic Algorithm for Multi-Objective U-Shaped Disassembly Line Balancing Problem. J. Southwest Jiaotong Univ. 2018, 53, 628–637. [Google Scholar]
- Karuppiah, K.; Sankaranarayanan, B.; Ali, S.M.; Kabir, G. Role of Ergonomic Factors Affecting Production of Leather Garment-Based SMEs of India: Implications for Social Sustainability. Symmetry 2020, 12, 1414. [Google Scholar] [CrossRef]
- Zhang, J.; Kong, Q. Fatigue analysis of assembly line work posture. Mod. Manuf. Eng. 2009, 10, 58–61. [Google Scholar]
- Lai, C.; Yao, J. Design of Man–Machine Cooperative Assembly Line Based on Mathematical Model and Simulation. In Proceedings of the International Conference on Man-Machine-Environment System Engineering, Singapore, 22 September 2021. [Google Scholar]
- Shan, H.; Yuan, Y.; Zhang, Y.; Wang, C. Lean, simulation and optimization: The case of steering knuckle arm production line. In Proceedings of the 2018 IEEE International Conference on Industrial Engineering and Engineering Management (IEEM), Bangkok, Thailand, 16–19 December 2018. [Google Scholar]
- Han, D.; Tang, Q.; Zhang, Z.; Li, Z. An Improved Migrating Birds Optimization Algorithm for a Hybrid Flow Shop Scheduling within Steel Plants. Mathematics 2020, 8, 1661. [Google Scholar] [CrossRef]
- Gao, K.; Peng, R.; Qu, L.; Wu, S. Jointly optimizing lot sizing and maintenance policy for a production system with two failure modes. Reliab. Eng. Syst. Saf. 2020, 202, 106996. [Google Scholar] [CrossRef]
- Qu, L.; Liao, J.; Gao, K.; Yang, L. Joint Optimization of Production Lot Sizing and Preventive Maintenance Threshold Based on Nonlinear Degradation. Appl. Sci. 2022, 12, 8638. [Google Scholar] [CrossRef]
- Llopis, J.; Lacasa, A.; Garcia, E.; Montés, N.; Hilario, L.; Vizcaíno, J. Manufacturing Maps, a Novel Tool for Smart Factory Management Based on Petri Nets and Big Data Mini-Terms. Mathematics 2022, 10, 2398. [Google Scholar] [CrossRef]
- Lin, Y.; Guo, J. Research on the method of improving the production efficiency of the assembly line based on JIT. Ind. Eng. Manag. 2012, 17, 124–128. [Google Scholar]
- Corbett, M. From law to folklore: Work stress and the Yerkes-Dodson Law. J. Manag. Psychol. 2015, 30, 741–752. [Google Scholar] [CrossRef]
- Gwyer, P.G. Applying the Yerkes-Dodson Law to Understanding Positive or Negative Emotions. Glob. J. Intell. Dev. Dis. 2017, 3, 37–39. [Google Scholar]
- Shin, W.S.; Son, C.B. A Plans for Attraction-Training-Maintenance of Domestic Construction Skilled Workers. J. Archit. Inst. Korea 2021, 37, 191–200. [Google Scholar]
- Martinez, I.; Revilla, J. Investigating the effect on the learning curve of performing similar work during the break between work stints. Procedia Manuf. 2015, 3, 3456–3462. [Google Scholar] [CrossRef][Green Version]
- Yang, L.; Chen, Y.; Qiu, Q.; Wang, J. Risk Control of Mission-Critical Systems: Abort Decision-Makings Integrating Health and Age Conditions. IEEE Trans. Ind. Inform. 2022, 18, 6887–6894. [Google Scholar] [CrossRef]
- Qiu, Q.; Maillart, L.M.; Prokopyev, O.A.; Cui, L. Optimal Condition-Based Mission Abort Decisions. IEEE. Trans. Reliab. 2022, 5, 1–18. [Google Scholar] [CrossRef]
- Huang, S.; Lei, B.; Gao, K.; Wu, Z.; Wang, Z. Multi-State System Reliability Evaluation and Component Allocation Optimization Under Multi-Level Performance Sharing. IEEE Access 2021, 9, 88820–88834. [Google Scholar] [CrossRef]
- Gao, K.; Peng, R.; Qu, L.; Xing, L.; Wang, S.; Wu, D. Linear system design with application in wireless sensor networks. J. Ind. Inf. Integr. 2022, 27, 100279. [Google Scholar] [CrossRef]
- Gao, K.; Yan, X.; Xiao, H.; Peng, R. Reliability Modelling of Multi-Phased Linear Consecutively Connected Systems. In Stochastic Models in Reliability Engineering, 3rd ed.; Cui, L., Frenkel, L., Eds.; CRC Press: Boca Raton, FL, USA, 2020; pp. 41–48. [Google Scholar]
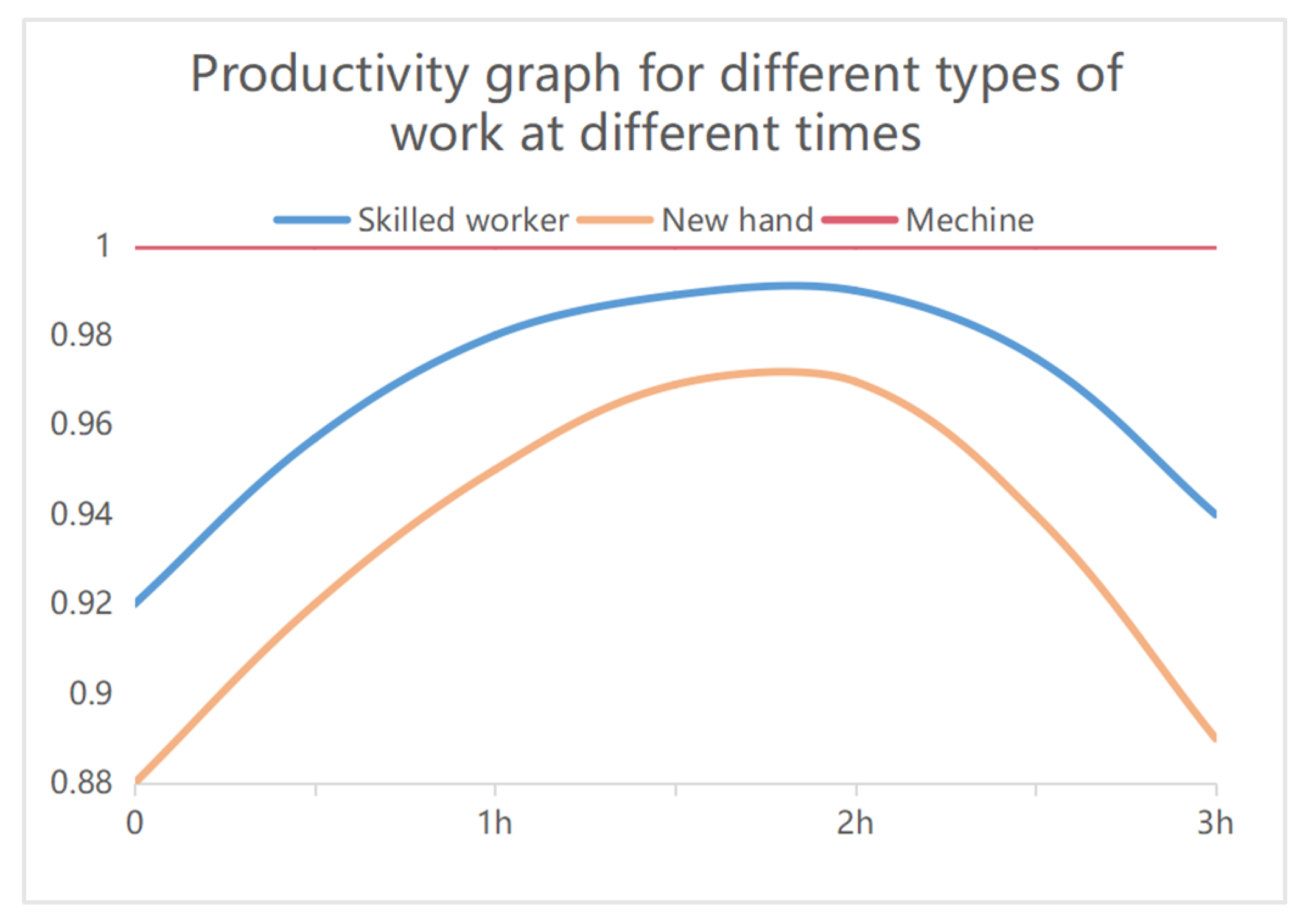


| Skilled Worker | New Hand | Machine | |||
|---|---|---|---|---|---|
| Status | Energetic | Fatigue | Energetic | Fatigue | Status of Use |
| Average productivity during 1 h of work | 0.95 | 0.9 | 0.9 | 0.85 | 1 |
| Average productivity during 2 h of work | 0.99 | 0.95 | 0.95 | 0.9 | |
| Average productivity during 3 h of work | 0.98 | 0.93 | 0.93 | 0.88 | |
| Plan 1 | Plan 2 | Plan 3 | Plan 4 | |
|---|---|---|---|---|
| 1 h work | 7 | 5 | 4 | 3 |
| 2 h work | 0 | 1 | 0 | 2 |
| 3 h work | 0 | 0 | 1 | 0 |
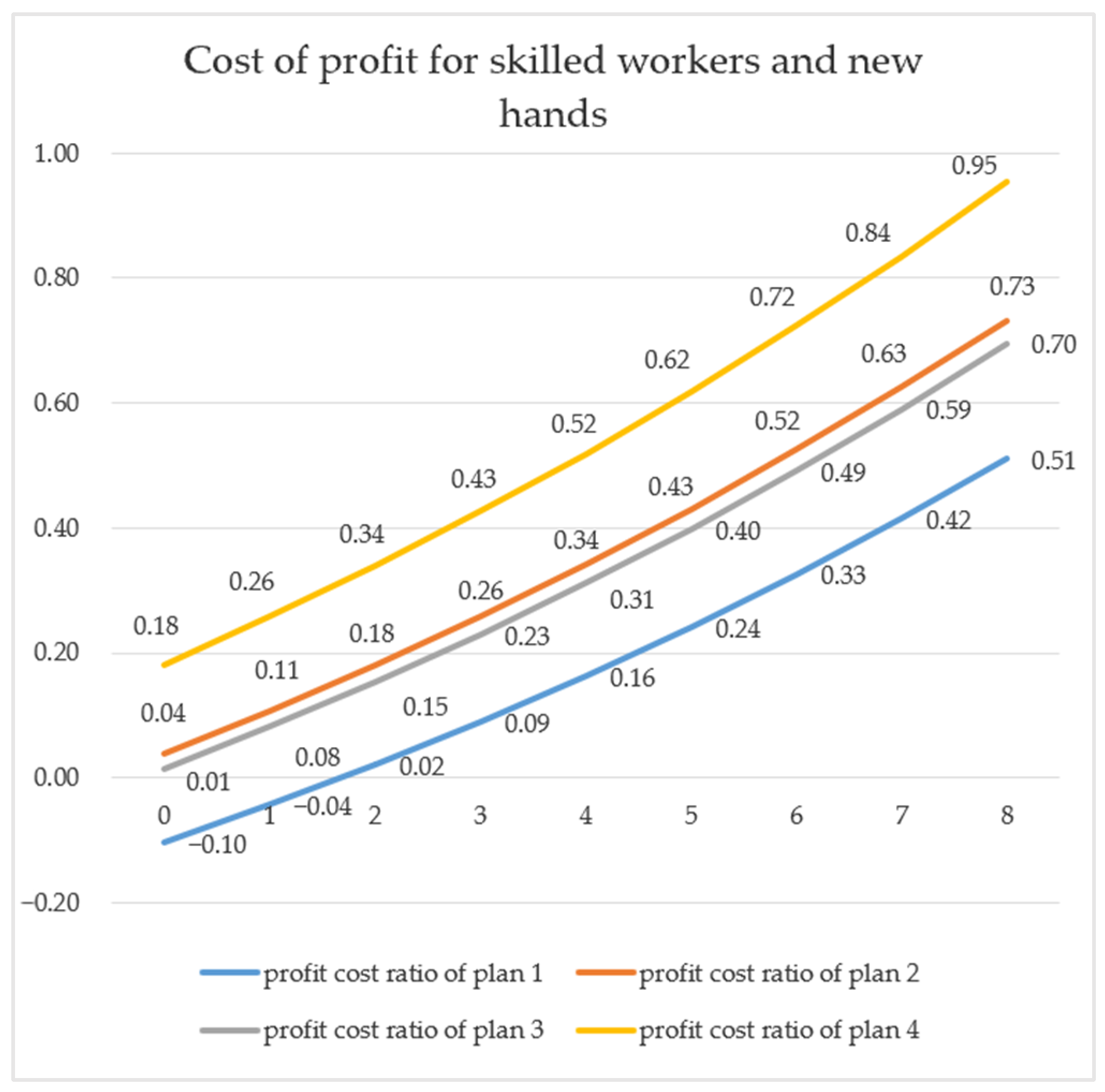
| Number of Skilled Workers | Number of New Hands | Number of Machines | Total Cost | Plan 1 Profit | Plan 2 Profit | Plan 3 Profit | Plan 4 Profit |
|---|---|---|---|---|---|---|---|
| 0 | 0 | 8 | 432,000 | 268,000 | 268,000 | 268,000 | 268,000 |
| 0 | 1 | 7 | 413,100 | 202,900 | 212,900 | 211,900 | 222,900 |
| 0 | 2 | 6 | 394,200 | 147,880 | 165,980 | 163,990 | 184,080 |
| 0 | 3 | 5 | 375,300 | 101,730 | 126,307 | 123,360 | 150,884 |
| 0 | 4 | 4 | 356,400 | 63,387 | 93,058 | 89,203 | 122,729 |
| 0 | 5 | 3 | 337,500 | 31,912 | 65,504 | 60,802 | 99,095 |
| 1 | 0 | 7 | 413,300 | 244,700 | 254,700 | 253,700 | 264,700 |
| 1 | 1 | 6 | 394,400 | 184,640 | 203,340 | 201,290 | 222,040 |
| 1 | 2 | 5 | 375,500 | 134,055 | 159,718 | 156,652 | 185,381 |
| 1 | 3 | 4 | 356,600 | 91,809 | 122,955 | 118,923 | 154,100 |
| 1 | 4 | 3 | 337,700 | 56,900 | 92,271 | 87,339 | 127,643 |
| 2 | 0 | 6 | 394,600 | 223,920 | 243,220 | 241,110 | 262,520 |
| 2 | 1 | 5 | 375,700 | 168,598 | 195,383 | 192,193 | 222,168 |
| 2 | 2 | 4 | 356,800 | 122,182 | 154,868 | 150,652 | 187,553 |
| 2 | 3 | 3 | 337,900 | 83,604 | 120,844 | 115,670 | 158,085 |
| 2 | 4 | 2 | 319,000 | 51,924 | 92,579 | 86,523 | 133,234 |
| 2 | 5 | 1 | 300,100 | 26,313 | 69,421 | 62,567 | 112,529 |
| 3 | 0 | 5 | 375,900 | 205,509 | 233,452 | 230,136 | 261,395 |
| 3 | 1 | 4 | 357,000 | 154,640 | 188,933 | 184,525 | 223,225 |
| 3 | 2 | 3 | 338,100 | 112,143 | 151,344 | 145,917 | 190,546 |
| 3 | 3 | 2 | 319,200 | 77,014 | 119,903 | 113,537 | 162,793 |
| 3 | 4 | 1 | 300,300 | 48,368 | 93,916 | 86,698 | 139,463 |
| 3 | 5 | 0 | 281,400 | 25,428 | 72,768 | 64,791 | 120,108 |
| 4 | 0 | 4 | 357,200 | 189,324 | 225,294 | 220,687 | 261,263 |
| 4 | 1 | 3 | 338,300 | 142,641 | 183,900 | 178,209 | 225,159 |
| 4 | 2 | 2 | 319,400 | 103,828 | 149,070 | 142,378 | 194,311 |
| 4 | 3 | 1 | 300,500 | 71,941 | 120,062 | 112,463 | 168,182 |
| 4 | 4 | 0 | 281,600 | 46,148 | 96,221 | 87,811 | 146,294 |
| 5 | 0 | 3 | 338,500 | 175,233 | 218,650 | 212,682 | 262,067 |
| 5 | 1 | 2 | 319,600 | 132,485 | 180,202 | 173,169 | 227,919 |
| 5 | 2 | 1 | 300,700 | 97,135 | 147,970 | 139,969 | 198,805 |
| 5 | 3 | 0 | 281,800 | 68,295 | 121,255 | 112,389 | 174,215 |
| 6 | 0 | 2 | 319,800 | 163,109 | 213,431 | 206,040 | 263,753 |
| 6 | 1 | 1 | 300,900 | 124,060 | 177,758 | 169,336 | 231,456 |
| 6 | 2 | 0 | 282,000 | 91,965 | 147,975 | 138,629 | 203,985 |
| 7 | 0 | 1 | 301,100 | 152,834 | 209,552 | 200,686 | 266,269 |
| 7 | 1 | 0 | 282,200 | 117,262 | 176,494 | 166,643 | 235,726 |
| 8 | 0 | 0 | 282,400 | 144,298 | 206,933 | 196,551 | 269,569 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lei, B.; Ren, Y.; Wang, Z.; Ge, X.; Li, X.; Gao, K. The Optimization of Working Time for a Consecutively Connected Production Line. Mathematics 2023, 11, 309. https://doi.org/10.3390/math11020309
Lei B, Ren Y, Wang Z, Ge X, Li X, Gao K. The Optimization of Working Time for a Consecutively Connected Production Line. Mathematics. 2023; 11(2):309. https://doi.org/10.3390/math11020309
Chicago/Turabian StyleLei, Bingyin, Yue Ren, Ziyang Wang, Xinquan Ge, Xiaolin Li, and Kaiye Gao. 2023. "The Optimization of Working Time for a Consecutively Connected Production Line" Mathematics 11, no. 2: 309. https://doi.org/10.3390/math11020309
APA StyleLei, B., Ren, Y., Wang, Z., Ge, X., Li, X., & Gao, K. (2023). The Optimization of Working Time for a Consecutively Connected Production Line. Mathematics, 11(2), 309. https://doi.org/10.3390/math11020309







