Effect of Future Price Increase for Products with Expiry Dates and Price-Sensitive Demand under Different Payment Policies

Abstract

The current study works with an inventory management strategy under the discount cash flow approach for perishable commodities with expiry dates, price-sensitive demand, and investment in preservation technology. In addition, this study examines the probable influence of price-increase on the replenishment strategy of the retailer where specific delivery units can be purchased. Furthermore, in this model, two circumstances are deliberated: (I) when the time of the specific delivery matches with the reordering time of the retailer or (II) when the time of the specific delivery emerges within the duration of the sale. Before the price increase, the supplier provides two payment policies to the retailer from which they can choose one. The policies are either: (1) a permissible delay in payment on regular orders or (2) a discount in payment for the specific delivery. The key goal is to optimize the overall profit for the retailer with respect to the sales price, investment in preservation technology, and cycle time during the depletion time of the specific delivery. In addition, an algorithm is created to optimize the results and seven numerical illustrations are discussed to explain the results along with the special case. Finally, to display the pertinence of this model, a sensitivity analysis of the main parameters is performed with important managerial implications. The key findings of this research are (1) before the price increase, the retailer gets the maximum profit if the retailer chooses a discount in payment policy on the specific delivery; (2) how much to order from the supplier and when to place a specific delivery to generate a maximum profit; and (3) the price-sensitive demand and assumption of future price increase negatively affect the retailer’s overall profit, and the retailer gets maximum benefits if the retailer initially orders the maximum number of units from the supplier before the price increase.

1. Introduction

In an economy, demand usually decreases as costs for goods increase, which impacts overall profit. In addition, since the pandemic outbreak, the prices of fruits, vegetables, grains, medicines, and other goods have been rising. Thus, this study considers the principle of price increase, where the supplier proclaims a price increase for a product, which has an impact at a certain point in the future (Ouyang et al. [1], Shah et al. [2]). Moreover, product price directly affects customer demand because as the price of a product increases, the demand decreases and vice versa. Therefore, price-sensitive demand plays an important role in selling any product (Sarkar et al. [3]) and is addressed in this model. The supplier has recently introduced the option of delay-in-payment to boost demand, which allows the retailer to order more items because the retailer can pay the payment after a certain period (Aggarwal and Jaggi [4], Cárdenas-Barrón et al. [5]). In addition, consumers are very aware of the price of the goods, and discounts in payment encourage more customers to purchase a more significant number of products; thus, the supplier provides a discount payment policy to sell a more substantial number of products (Li et al. [6], Moon et al. [7]). Therefore, the current study comprises two payment policies that attract more customers: the trade credit policy and the discount in payment policy. Furthermore, consumers are very interested in purchasing those products which have a maximum fixed lifespan such as food packets, cold beverages, cosmetics, medicines, and milk products. Thus, the maximum fixed lifespan for a deteriorating product is considered in this study. In addition, these products often deteriorate with time, which affects the product’s consistency and consumers are not likely to purchase products that are not fresh (Hwang et al. [8], Moon [9], Hsu et al. [10]). Therefore, to preserve the item and keep the product fresh, the buyer/manufacturer invests some funds in preservation techniques. While managing the inventory, the cost of transportation plays a very important role in finding the overall profit of a retailer (March et al. [11], Michail et al. [12]).

1.1. Contribution

Motivated by the importance of the announcement of future price rises, some researchers keep in mind that before a price rise, sellers are more likely to take specific deliveries to get more value. In contrast, suppliers are ready to provide the retailer with an increasing number of items. Therefore, in this study, the supplier provides the retailer with two choices, where only one selection can be selected by the retailer. Either way, the retailer may opt for a trade credit option on a regular order before the price increase, or they may use the option of a specific delivery discount in payment on specific delivery. Furthermore, if the retailer wishes to make a specific delivery before the price increase, the period for placing an order may or may not coincide with the retailer’s regular replenishment strategy. Therefore, this paper addresses two scenarios: (I) when the time of the specific delivery matches with the reordering time of the retailer and (II) when the time of the specific delivery emerges within the duration of the sale. In both scenarios, the number of specific deliveries is assumed to be more than the regular order quantities. Furthermore, this research considered the following four important events:

• The retailer plans a price rise proclaimed by the supplier at a certain point and determines whether to place a specific delivery.
• The products have a maximum fixed lifespan.
• The demand depends on the sales price, beyond which the demand will decrease as the price of the goods increases.
• The retailer spends the sum to reduce the deterioration of the goods.

Before the price rise, this study optimizes the retailer’s ordering policy to maximize the profit in both scenarios: (i) trade credit policy on regular orders and (ii) discount in payment policy on specific deliveries. Furthermore, the computational process to find the optimal profit function for the retailer, which is the sum of its regular order and the specific delivery, is given, and the numerical examples for all possible cases are provided to demonstrate the theocratical outcomes. In addition, a special case for a retailer is being considered, where the retailer is unwilling to take any specific delivery or trade credit policy. Finally, with respect to key parameters, the analysis of sensitivity is implemented on the optimal result for the trade credit policy and discount in payment policy.

1.2. Flow of This Research

The remainder of the paper is presented in the following pattern: Section 2 examines the existing literature. Section 3 reflects the key notation with assumptions for this study. The formulation of a mathematical model for the suggested problem is described in Section 4. Section 5 offers an approach for optimizing the retailer’s total profit function. Section 6 explores mathematical examples for different cases, sensitivity analysis of critical factors, and managerial implications. Section 7 presents the study’s conclusion and forthcoming opportunities.

2. Literature Review

The existing literature is reviewed in this section under future price-increase, various demand nature, trade credit policy, discount in payment policy, deteriorating inventories, and preservation technology investment.

2.1. Literature Review on Economic Order Quantity (EOQ) Models under Future Price Increase

Global prices of crude oil, gas, diesel, and raw materials have increased over time owing to rising commodity prices globally. This has become a serious problem for enterprises. Therefore, considerations are being made to increase the prices of the company’s goods, particularly once the administrators decide on their inventory strategy. Thus, if the supplier proclaims a potential increase in the cost of the commodity, which starts at a given point in time, each retailer must determine whether to order sufficient stock for a higher profit at the current lower price before the price rise. To achieve additional conclusions in the results associated with inventory insurance, researchers have declared price increases to account for and have prepared several models. Naddor [13] was the first researcher to announce a price increase and developed an infinite horizon inventory model. In Aggarwal [14], an alternate technique was offered to stipulate the best approach. In Lev and Weiss [15], a formulation of ideal policies was recognized to calculate the optimal strategy. Under one-time incentives, a written report of inventory policies was advised by Goyal et al. [16]. A sustainable approach was addressed by Yadav et al. [17], where controlling by-products from a production system with partial back ordering were considered. In Ouyang et al. [1], the inventory model was explored under the proclaimed price rise with limited special-order amounts. Subsequently, with the influence of future price rises, Shah et al. [2] expanded the model of Ouyang et al. [1] and cultivated a mathematical model in which the nature of demand is quadratic.

2.2. Literature Review on EOQ Models under Various Types of Demand

In economics, demand is the need for customers to purchase products and services. It is a key factor in global growth and expansion. Moreover, no firm would bother to be concerned about production if there is no demand. Thus, researchers have taken the definition of demand into account, and the first researcher to establish a simple economic order quantity (EOQ) model was Harris [18], in which demand was regarded as a constant. Mahapatra et al. [19] designed a mathematical model with price-dependent fuzzy demand. In Khanra et al. [20], a model was analyzed under the cross-price elasticity nature of demand for a dual-channel supply chain. In addition, a general reduction in the retail price of certain goods would automatically raise consumer demand, resulting in further sales. Therefore, written reports of specific mathematical models were considered over price-sensitive demand. A novel approach to optimal ordering strategies for an uncertain inflation rate in a constant demand scenario was addressed by Padiyar et al. [21]; in Sarkar et al. [3], an autonomation policy for dual-channel supply was acknowledged under price-sensitive demand. Many researchers noted that some positive correlation exists between the inventory level and the proportion of demand. Therefore, stock-dependent demand inventory models were often considered in mathematical models, and in Habib et al. [22], a mathematical model of biofuel was analyzed with multiple demand zones. In Hota et al. [23], a transportation hazard model with unreliable retailers was cultivated with price- and quality-based demand rates. Sarkar et al. [24] analyzed an analytical application of random demand for warehouse management within a supply chain.

2.3. Literature Review on EOQ Models under Trade Credit Policy

Business loans are a primary method for funding the growth of many companies and sustaining profits; they typically use three types of payment strategies: (1) deferred payment or credit payment, (2) cash on arrival, and (3) pre-payment. As part of their pricing strategy, enterprises mainly introduce deferred payment or credit payment arrangements to resolve ambiguity regarding permanent market rivalry and to encourage customers to purchase and promote their goods. In a recent scenario, offering a credit period is an arrangement where, without paying cash, the retailer may acquire a product and pay the supplier on a scheduled date; this policy is known as the upstream trade credit policy. The first inventory model was elaborated by Goyal [25] and the EOQ model was obtained under the condition of a delay in payment. In Aggarwal and Jaggi [4], a mathematical model was industrialized under the assumption of allowable payment delays. In Wu et al. [26], under the condition of two-stage trade credit financing, an ideal credit duration was recognized, and in Jiang et al. [27], the joint retailer-managed inventory supply chain, cooperative advertising, and profit-sharing decision-making were addressed. Recently, in Cárdenas-Barrón et al. [5], a model of the non-linear cost of holding was cultivated with a single trade credit policy. In Sindhuja et al. [28], a mathematical model had been discussed for perishable goods with shortage conditions under trade credit.

2.4. Literature Review on EOQ Models under Discount in Payment Policy

In the current scenario, payment scheme discounts have gained more consumers, resulting in good business benefits. Because the supplier needs to deliver the products as much as possible, the discount is beneficial in the payment policy to provide the consumer with many goods. The demand for goods rises owing to discounts in the payment policy; thus, researchers have considered discounts in the payment policy. In Shah et al. [29], for an inventory scheme for the expiry dates of perishable products, a mathematical form was recognized with a temporary discount in price. A mathematical model is industrialized in Ebrahim et al. [30], where various forms of discounts for single-item buying problems were addressed. The inventory model is calculated by Taleizadeh et al. [31], where a gradual discount with shortages was considered. The impact of the foundations of dual relegation on pricing policies, in which price discount structures were projected to promote network organization in Li et al. [6]. Subsequently, in Shaikh et al. [32], a model was established for perishable rates with a discount facility, stock-dependent demand, and shortages. Recently, an integrated stochastic supply chain retailer–buyer model was developed by Tiwari et al. [33], where setup cost reduction and backorder price discounts were considered.

2.5. Literature Review on EOQ Models under Deteriorating Inventories

The efficiency of goods is an essential feature of inventory policy, with several factors influencing inventory policy. After some period, the goods may start to deteriorate or lose their value. Therefore, a reduction in inventory practices should be noted. In Moon et al. [7], under time-varying demand, a model was industrialized for deteriorating objects, and in Sana [34], a multi-item EOQ model was established in which the deterioration rate is constant. In Sarkar and Sarkar [35], a model was designed for bio-degradable products and transported in different delivery modes. Subsequently, in Tiwari et al. [36], a model was designed for perishable items that start to deteriorate after some period in the case of additional warehouses, and the model in Bishi et al. [37] used an exponential demand rate. In Shah et al. [38], a model was deliberate with demand dependent on the time–credit cycle with a constant deterioration rate. Economically, the drop in imports negatively affected trade. Recently, with trade credit, Jani et al. [39], allowed discounts for perishable items under time-dependent sale prices. In Udayakumar et al. [40], under permissible delay in payment and conditions of inflation, a mathematical model was industrialized for deteriorating items that start to decline after some time. In Rout et al. [41], a manufacturing model was examined for perishable products under backlog-reliant demand. A manufacturing model was cultivated by Das et al. [42] for deteriorating commodities with the consistent consequence of production and price-reliant demand.

2.6. Literature Review on EOQ Models under Preservation Technology Investment

Companies often rely on deteriorated goods because consumers are less likely to purchase items that deteriorate over time; hence, researchers concentrate on investing in preservation technologies to protect the items and reduce product degradation. A multi-product capacitated economic production quantity (EPQ) model was proposed by Hwang et al. [8], where the initial investment was considered a one-time payment for quality enhancement and setup reduction. A complete formulation was again checked in the model by Hwang et al. [8] and further expanded by Moon [9], where the general investment function was evaluated using the Lagrangian method. A deteriorating order strategy was introduced by Hsu et al. [10], where the retailer invested in preservation technologies to minimize the amount of item deterioration. In Shah et al. [43], an optimal policy was built for maximum fixed lifetime declining objects, in which investment was considered to preserve the deteriorating goods. During the COVID-19 pandemic, the global reduction of marine traffic was tracked by March et al. [11]. In Michail et al. [12], the relationship between shipping freight rates and inflation was established in the European Union.

2.7. Gap Identification and Uniqueness of This Research

Based on these studies and

Table 1. Summary of previously established work and this study.

Reference	Price Increase	Demand	Trade Credit	Discount	Deterioration	Preservation Technology Investment
Ouyang et al. [1]	Yes	Constant	No	No	Constant	No
Shah et al. [2]	Yes	Quadratic	No	No	Constant	No
Aggarwal and Jaggi [4]	No	Constant	Up-stream	No	Constant	No
Cárdenas-Barrón et al. [5]	No	Non-linear stock dependent	Up-stream	No	No	No
Bishi et al. [37]	No	Exponential	No	No	Non-instantaneous	No
Shah et al. [43]	No	Price-trade credit, and quadratic	Two-layered	No	Maximum fixed lifetime	Yes
Sarkar [44]	No	Selling price	No	No	No	No
Moon et al. [45]	No	Constant	No	No	No	No
In this study	Yes	Price-sensitive	Up-stream	Yes	Maximum fixed lifetime	Yes

, many experiments have been conducted on the EOQ model. Still, all combinations, including price rise, deterioration, preservation of technology investment, trade credit, and discount policies, have not been studied yet. Therefore, this study consideres all these combinations. Existing studies did not consider both trade credit and discount policies for expiry date deteriorating items with the assumption of future price rise of a product. To fill this gap, we create a model for certain products, considering both policies under price-sensitive demand, which is the novelty of this study.

Moreover, this study optimizes the retailer’s pricing strategy to maximize the overall profit function, considering the investment for preservation, cycle time, and sales price. In addition, an algorithm is generated for maximization and explored numerical examples to illustrate the theoretical outcomes under different scenarios. Finally, we conduct a sensitivity analysis on the optimal solutions for the key parameters.

2.8. Aim of the Study

Any business organization can utilize the recommended inventory model if the supplier proclaims a future price rise for a product at a specified time in the future, and the retailer can acquire the specific delivery together with its regular order or during the sales period. Considering the aims mentioned above, the following aspects are examined in this study, which will benefit any business.

This model gives the best strategy to the retailer concerning how much to order and when to place an order for specific delivery from the supplier before the price increases. Two policies are considered in this model (1) trade credit policy and (2) discount in payment for a specific delivery, from which the retailer can choose any one; this study provides the best strategy to the retailer regarding both policies and calculates the overall profit for both scenarios. This research provides the optimal sales price, cycle time, and investment for preservation technology for all cases. To use this model in a real case study, this paper gives essential suggestions or managerial implications for the retailer. One special case is discussed where the retailer did not wish to pick any specific delivery option or policy offered by the supplier.

3. Notation and Assumptions

3.1. Notation

To generate a mathematical model for the proposed problem, this article uses the following notation and assumptions.

Parameters
$a$	Scaling parameter of demand; $a>0$
$b$	Parameter of price-elasticity; $0\le b<1$
$P$	Purchasing cost (in $ per unit)
$\omega$	The product’s expiry date (in years)
$h$	Holding cost (in $ per unit per year)
$\mu$	Preservation rate; $\mu >0$
$O$	Cost of ordering (in $ per order)
$M$	Upstream trade credit (years)
$I_g$	Earned interest of the retailer (in % /unit time/year)
$I_l$	The charged interest of the retailer (in % /unit time/year)
$D$	Discount in payment on the specific delivery provided by the supplier ($/unit)
$\tau$	Price rise (in $/unit)

Prior to the price rise

$U$	Preservation technology investment ($ per unit)
$T$	Replenishment time (years)
$S$	Product’s sales price ($ per unit)
$I\left(t\right)$	Inventory level; $0\le t\le T$ (units)
$Q$	Order quantity (units)
$\pi \left(T,S,U\right)$	Retailer’s net profit ($)
${\pi }_i\left(T,S,U\right)$	Net profit of the retailer for both situations; $i=1,2$ ($)
$Q_i$	The retailer’s order quantity for both situations; $i=1,2$ (units)

After the price rise

$S_{\tau }$	Product’s sales price (in $ per unit)
$T_{\tau }$	Replenishment time (in years)
$U_{\tau }$	Preservation technology investment ($ per unit)
$I_{\tau }\left(t\right)$	Inventory level; $0\le t\le T_{\tau }$ (in units)
$Q_{\tau }$	Order quantity (in units)
${\pi }_{\tau }\left(T_{\tau },S_{\tau },U_{\tau }\right)$	Net profit of the retailer ($)

For specific delivery

$Q_{sp}$	Order quantity for specific delivery (in units) (decision variable)
$T_{sp}$	Diminution time for quantity $Q_{sp}$ (in years) (decision variable)
$S_{sp}$	The sales price for quantity $Q_{sp}$ ($/unit) (decision variable)
$U_{sp}$	Capital for preservation technology for quantity $Q_{sp}$ (in $/unit) (decision variable)
$r$	Level of remaining inventory before hiring the specific delivery (in units)
$Q_{sp}+r$	When the specific delivery arrives, the maximum level of inventory (in units)
$t_r$	Diminution time for outstanding quantity $r$ (years)
$T_r$	Diminution time for maximum quantity (years)

For specific delivery matches with reordering time case

$I_{sp}\left(t\right)$	Inventory level; $0\le t\le T_{sp}$ (in units)
${\pi }_{s{p}_1}\left(T_{sp},S_{sp},U_{sp}\right)$	Net profit of the retailer without discount (in $)
${\pi }_{Ds{p}_1}\left(T_{sp},S_{sp},U_{sp}\right)$	Net profit of the retailer with a discount (in $)
${\pi }_{r_1}\left(T_{sp},S_{sp},U_{sp}\right)$	Net profit of regular order for the retailer without trade credit option (in $)
${\pi }_{t{r}_1}\left(T_{sp},S_{sp},U_{sp}\right)$	Net profit of regular order for the retailer with situation 1 (in $)
${\pi }_{t{r}_2}\left(T_{sp},S_{sp},U_{sp}\right)$	Net profit of regular order for the retailer with situation 2 (in $)

For specific delivery emerges within the sales duration case

$I_r\left(t\right)$	Inventory level; $0\le t\le T_{sp}$ (units)
${\pi }_{s{p}_2}\left(T_{sp},S_{sp},U_{sp}\right)$	Net profit of the retailer without discount (in $)
${\pi }_{Ds{p}_2}\left(T_{sp},S_{sp},U_{sp}\right)$	Net profit of the retailer with a discount (in $)
${\pi }_{r_2}\left(T_{sp},S_{sp},U_{sp}\right)$	Net profit of regular order for the retailer without trade credit option (in $)
${\pi }_{t{r}_3}\left(T_{sp},S_{sp},U_{sp}\right)$	Net profit of regular order for the retailer with situation 1 (in $)
${\pi }_{t{r}_4}\left(T_{sp},S_{sp},U_{sp}\right)$	Net profit of regular order for the retailer with situation 2 (in $)

Retailer’s overall profit function

$T{P}_i\left(T_{sp},S_{sp},U_{sp}\right)$	The overall profit of the retailer is the sum of its regular order and specific delivery (in $) for $i=1,2,3,4,5,6$
$TP\left(T,T_{\tau },S,S_{\tau },U,U_{\tau }\right)$	The overall profit of the retailer’s regular order without specific delivery (in $)

3.2. Assumptions

This section lists the significant assumptions of the current model.

• This research model works with a single product only.
• The product demand is sensitive to price and it is defined as $R\left(S\right)=a\exp (-bS)$; which is a function of $S$, where scaling demand is signified as $a$ and the parameter of price elasticity is signified as $b$.
• The maximum fixed lifespan of the deteriorating items is defined as $\theta \left(t\right)=\frac{1}{1+\omega -T}$ where $\omega \ge T$ and the expiry date of the product. Moreover, as $\omega$ it approaches infinity, $\theta \left(t\right)$ approaches zero, which indicates the product is non-declining.
• The credit duration of $M$ years delivered by the supplier to the retailer where from 0 to when the retailer will gain interest $I_g$ on retailed items and will lose interest $I_l$ during the time from $M$ to $T$ on unsold stocks.
• The amount of the abbreviated proportion of perishable is $f_n\left(U\right)=1-\frac{1}{1+\mu U}$, which is a concave function of investment $U$ and is continuously increasing, that is, ${f_n}^{\prime }\left(U\right)>0$, ${f_n}^{″}\left(U\right)>0$ and $f_n\left(0\right)=0$.
• The supplier allows the retailer only one chance to opt for the specific delivery before the price rise.
• If the retailer opts for specific delivery with its regular order, then the supplier provides a discount $D$ in the payment option for the specific delivery.
• At that time, the supplier can provide either trade credit or a discount in payment to the retailer.
• The supplier declares the price rise of the commodity by a certain amount $\tau$ that will impact the future at a certain time.
• For deteriorated units, a replacement is not permitted and repair is not considered during this era.
• The refilling amount is infinite, with no lead time.
• The inventory scheduling limit is endless.
• Shortages are not permitted.

4. Mathematical Model

The mathematical model is discussed in this portion as per the above notation and essential assumptions. The diminution in inventory level depends on the combined effect of non-linear price-sensitive demand and expiry dates of the product with the assumption of future price rises. In addition, to abbreviate the deterioration and sustain the item’s value, the capital in the preservation technology is considered. Thus, the inventory level can be determined by

$$\frac{dI}{dt}=-R\left(S\right)-\theta \left(t\right)\left(1-f_n\left(U\right)\right)I\left(t\right)$$

(1)

with $I\left(T\right)=0$ and by solving (1), the inventory level is

$$I\left(t\right)=\frac{-a\left(1+\mu U\right)\left({\left(1+\omega -T\right)}^{\frac{1+\mu U}{\mu U}}{\left(1+\omega -t\right)}^{\frac{1}{1+\mu U}}-\omega +t-1\right)\exp \left(-bS\right)}{\mu U}.$$

(2)

In addition, the initial order quantity can be obtained as

$$Q=I\left(0\right)=\frac{-a\left(1+\mu U\right)\left({\left(1+\omega -T\right)}^{\frac{1+\mu U}{\mu U}}{\left(1+\omega \right)}^{\frac{1}{1+\mu U}}-\omega -1\right)\exp \left(-bS\right)}{\mu U}.$$

(3)

4.1. Before the Price Rise: Retailer’s Objective Function

When the forthcoming price increase has not yet been proclaimed by the supplier, the sales revenue generated by the retailer throughout $T$ before the price rise is obtained by

$$SR=S{\displaystyle \underset{0}{\overset{T}{\int }}R\left(S\right)dt}.$$

(4)

Next, the subsequent costs related to inventory management are

• Cost of ordering; $OC=O$
• Cost of purchasing; $PC=PQ$
• Cost of holding; $HC=hP{\displaystyle \underset{0}{\overset{T}{\int }}I\left(t\right)dt}$
• Preservation technology capital; $PTI=UT$.

Before the price increase, $Q$ units were ordered by the retailer at the original purchasing cost $P$, and the net benefit is measured by

$$\begin{array}{cc}\hfill \pi \left(T,S,U\right)& =\frac{1}{T}\left(SR-(OC+PC+HC+PTI)\right)\hfill \\ & =\frac{1}{T}\left(S{\displaystyle \underset{0}{\overset{T}{\int }}R\left(S\right)dt}-\left(O+PQ+hP{\displaystyle \underset{0}{\overset{T}{\int }}I\left(t\right)dt}+UT\right)\right)\hfill \end{array}$$

(5)

Thus, by applying the necessary conditions for the optimality

$$\frac{\partial \pi \left(T,S,U\right)}{\partial T}=0,\frac{\partial \pi \left(T,S,U\right)}{\partial S}=0,\mathrm{and}\frac{\partial \pi \left(T,S,U\right)}{\partial U}=0$$

in (5), one can check that $\pi \left(T,S,U\right)$ it is a concave function and obtains unique values $T\left(\mathrm{say}{T}^{*}\right),S\left(\mathrm{say}{S}^{*}\right),U\left(\mathrm{say}{U}^{*}\right)$ that maximize $\pi \left(T,S,U\right)$.

Moreover, the optimal $Q^{*}$ can be obtained as

$$Q^{*}=\frac{-a\left(1+\mu U^{*}\right)\left({\left(1+\omega -T^{*}\right)}^{\frac{1+\mu U^{*}}{\mu U^{*}}}{\left(1+\omega \right)}^{\frac{1}{1+\mu U^{*}}}-\omega -1\right)\exp \left(-b{S}^{*}\right)}{\mu U^{*}}.$$

(6)

4.2. If a Retailer Chooses an Option of Trade Credit Policy on Regular Orders before the Price Rise

Because the supplier provides two options to the retailer before the price rise, the retailer can either choose the option of trade credit on a regular order or adopt a discount in payment policy on the specific delivery. This section discusses the probable effects on net profit if the retailer wants to choose the option of a trade credit before the price rise.

Now, $M$ is the supplier’s fixed credit span, and the retailer has two probable situations (1) $M<T$ and (2) $M\ge T$.

4.2.1. Retailer’s Net Profit Function for Situation 1: $M<T$

Here, the retailer will earn the interest from 0 to $M$ on retailed items, and after the credit duration $M$, for unsold items, the retailer will lose interest through the duration $M$ to $T$. Therefore, the added and lost interest for situation 1 is obtained as

$$I{G}_1=S{I}_g{\displaystyle \underset{0}{\overset{M}{\int }}tR\left(S\right)dt}\mathrm{and}I{L}_1=P{I}_l{\displaystyle \underset{M}{\overset{T}{\int }}I\left(t\right)dt}$$

(7)

Thus, the net profit before the price rise for situation 1 through the cycle time $T$ is measured as

$$\begin{array}{l}{\pi }_1\left(T,S,U\right)=\frac{1}{T}\left(SR-OC-PC-HC-PTI+I{G}_1-I{L}_1\right)\\ =\frac{1}{T}\left(S{\displaystyle \underset{0}{\overset{T}{\int }}R\left(S\right)}dt-O-PQ-hP{\displaystyle \underset{0}{\overset{T}{\int }}I\left(t\right)dt-UT+S{I}_g{\displaystyle \underset{0}{\overset{M}{\int }}tR\left(S\right)dt}-P{I}_l{\displaystyle \underset{M}{\overset{T}{\int }}I\left(t\right)dt}}\right)\end{array}$$

(8)

4.2.2. Retailer’s Net Profit Function for Situation 2: $M\ge T$

When $M\ge T$ the retailer will not lose anything during the entire period, as the retailer has sold all bought units. Thus, the retailer gains interest only from 0 to $M$ and gains extra interest through $M$ to $T$. Hence, the interest added and lost for situation 2 is obtained as follows:

$$I{G}_2=S{I}_g\left({\displaystyle \underset{0}{\overset{M}{\int }}tR\left(S\right)dt}+R\left(S\right)\left(M-T\right)T\right)\mathrm{and}I{L}_2=0$$

(9)

Hence, the retailer’s net profit, prior to the price rise for situation 2, $T$ is measured as

$$\begin{array}{l}{\pi }_2\left(T,S,U\right)=\frac{1}{T}\left((SR+I{G}_2)-(OC+PC+HC+PTI+I{L}_2\right)\\ =\frac{1}{T}\left(S{\displaystyle \underset{0}{\overset{T}{\int }}R\left(S\right)}dt-O-PQ-hP{\displaystyle \underset{0}{\overset{T}{\int }}I\left(t\right)dt-UT+S{I}_g\left({\displaystyle \underset{0}{\overset{M}{\int }}tR\left(S\right)dt}+R\left(S\right)\left(M-T\right)T\right)}\right)\end{array}$$

(10)

Therefore, the retailer’s overall profit function is described for both situations as:

$${\pi }_i\left(T,S,U\right)=\left\{\begin{array}{l}{\pi }_1\left(T,S,U\right);M<T\\ {\pi }_2\left(T,S,U\right);M\ge T\end{array}\right.;i=1,2$$

(11)

Now, by applying the necessary conditions for the optimality

$$\frac{\partial {\pi }_i\left(T,S,U\right)}{\partial T}=0,\frac{\partial {\pi }_i\left(T,S,U\right)}{\partial S}=0,\mathrm{and}\frac{\partial {\pi }_i\left(T,S,U\right)}{\partial U}=0;i=1,2,$$

it can easily check that ${\pi }_i\left(T,S,U\right);i=1,2$, is a concave function and that there exist unique values $T\left(\mathrm{say}{T}^{*}\right),S\left(\mathrm{say}{S}^{*}\right),U\left(\mathrm{say}{U}^{*}\right)$ that maximize ${\pi }_i\left(T,S,U\right);i=1,2$.

The optimal order quantity $Q_i{}^{*}$ for both situations can be evaluated as

$$Q_i{}^{*}=\frac{-a\left(1+\mu U^{*}\right)\left({\left(1+\omega -T^{*}\right)}^{\frac{1+\mu U^{*}}{\mu U^{*}}}{\left(1+\omega \right)}^{\frac{1}{1+\mu U^{*}}}-\omega -1\right)\exp \left(-b{S}^{*}\right)}{\mu U^{*}}$$

(12)

4.3. Retailer’s Net Profit Function after the Price Rise

The forthcoming price rise in the product is proclaimed by the supplier. Therefore, if an increase in the price per unit of the product occurs, from the original cost $P$, the purchasing cost becomes $P+\tau$.

Therefore, the inventory level after the price rise becomes

$$I_{\tau }\left(t\right)=\frac{-a\left(1+\mu U_{\tau }\right)\left({\left(1+\omega -T_{\tau }\right)}^{\frac{1+\mu U_{\tau }}{\mu U_{\tau }}}{\left(1+\omega -t\right)}^{\frac{1}{1+\mu U_{\tau }}}-\omega +t-1\right)\exp \left(-b{S}_{\tau }\right)}{\mu U_{\tau }}$$

(13)

and the order quantity can be found by taking $t=0$ in Equation (13), i.e.,

$$Q_{\tau }=\frac{-a\left(\mu U_{\tau }+1\right)\left[{\left(1+\xi -T_{\tau }\right)}^{\frac{\mu U_{\tau }+1}{\mu U_{\tau }}}{\left(1+\xi \right)}^{\frac{1}{\mu U_{\tau }+1}}-\xi -1\right]\exp \left(-b{S}_{\tau }\right)}{\mu U_{\tau }}$$

(14)

Thus, the sales revenue generated by the retailer after the price rise is given by:

$$S{R}_{\tau }=S_{\tau }{\displaystyle \underset{0}{\overset{T_{\tau }}{\int }}R\left(S_{\tau }\right)dt}$$

(15)

Therefore, cost components after the price rise under $T_{\tau }$ are comprised of

• Cost of purchasing; $P{C}_{\tau }=\left(P+\tau \right)Q_{\tau }$
• Cost of holding; $H{C}_{\tau }=h\left(P+\tau \right){\displaystyle \underset{0}{\overset{T_{\tau }}{\int }}{I}_{\tau }\left(t\right)dt}$
• Preservation technology capital; $PT{I}_{\tau }=U_{\tau }{T}_{\tau }$.

Hence, the net profit after the price rise is measured by

$$\begin{array}{l}{\pi }_{\tau }\left(T_{\tau },S_{\tau },U_{\tau }\right)=\frac{1}{T_{\tau }}\left(S{R}_{\tau }-\left(OC+P{C}_{\tau }+H{C}_{\tau }+PT{I}_{\tau }\right)\right)\\ =\frac{1}{T_{\tau }}\left(S_{\tau }{\displaystyle \underset{0}{\overset{T_{\tau }}{\int }}R\left(S_{\tau }\right)dt}-O-\left(P+\tau \right)Q_{\tau }-h\left(P+\tau \right){\displaystyle \underset{0}{\overset{T_{\tau }}{\int }}{I}_{\tau }\left(t\right)}dt-U_{\tau }{T}_{\tau }\right)\end{array}$$

(16)

Now, by applying the necessary conditions for the optimality

$$\frac{\partial {\pi }_{\tau }\left(T_{\tau },S_{\tau },U_{\tau }\right)}{\partial T_{\tau }}=0,\frac{\partial {\pi }_{\tau }\left(T_{\tau },S_{\tau },U_{\tau }\right)}{\partial S_{\tau }}=0,\mathrm{and}\frac{\partial {\pi }_{\tau }\left(T_{\tau },S_{\tau },U_{\tau }\right)}{\partial U_{\tau }}=0$$

in Equation (16), it can easily check that ${\pi }_{\tau }\left(T_{\tau },S_{\tau },U_{\tau }\right)$, is a concave function, and there exist unique values $T_{\tau }\left(\mathrm{say}{T}_{\tau }{}^{*}\right),S_{\tau }\left(\mathrm{say}{S}_{\tau }{}^{*}\right),U_{\tau }\left(\mathrm{say}{U}_{\tau }{}^{*}\right)$ that maximize ${\pi }_{\tau }\left(T_{\tau },S_{\tau },U_{\tau }\right)$.

In addition, the optimal order quantity $Q_{\tau }{}^{*}$ is evaluated as

$$Q_{\tau }{}^{*}=\frac{-a\left(1+\mu U_{\tau }{}^{*}\right)\left({\left(1+\omega -T_{\tau }{}^{*}\right)}^{\frac{1+\mu U_{\tau }{}^{*}}{\mu U_{\tau }{}^{*}}}{\left(1+\omega \right)}^{\frac{1}{1+\mu U_{\tau }{}^{*}}}-\omega -1\right)\exp \left(-b{S}_{\tau }{}^{*}\right)}{\mu U_{\tau }{}^{*}}.$$

(17)

Subsequently, before the price rise, the supplier gives only one chance to the retailer to place a specific delivery. In the case of a specific delivery, two scenarios may arise for the time of the specific delivery: (I) when the time of the specific delivery matches the reordering time for the retailer, and (II) when the time of the specific delivery emerges within the duration of the sale. In addition, the supplier is eager to provide more goods before the price rise. Thus, the supplier makes as many goods available to the retailer as possible. Hence, before the price rise, the supplier offers another option for a discount in payment on the specific delivery to the retailer. Therefore, this paper studies the above two scenarios individually and studies the probable effects on net profit if the retailer opts for the option of a discount in payment on the specific delivery, before the price rise.

Note: In such cases, the retailer does not wish to order any specific delivery. Therefore, the retailer pursues the regular EOQ model and places its regular order.

4.4. Retailer’s Net Profit Function When the Time of the Specific Delivery Matches with the Retailer’s Reordering Time

We will now discuss the first scenario (Figure 1), where the time for a specific delivery matches the reordering time of the retailer. Therefore, if a retailer chooses the option of specific delivery and orders some extra units, say $Q_{sp}$, along with its regular order units, then the inventory level for the specific delivery can be evaluated as

$$I_{sp}\left(t\right)=\frac{-a\left(1+\mu U_{sp}\right)\left({\left(1+\omega -T_{sp}\right)}^{\frac{1+\mu U_{sp}}{\mu U_{sp}}}{\left(1+\omega -t\right)}^{\frac{1}{1+\mu U_{sp}}}-\omega +t-1\right)\exp \left(-b{S}_{sp}\right)}{\mu U_{sp}}$$

(18)

and specific delivery units at the unit purchasing cost $P$ can be found when $t=0$ in (18), that is

$$Q_{sp}\left(t\right)=\frac{-a\left(1+\mu U_{sp}\right)\left({\left(1+\omega -T_{sp}\right)}^{\frac{1+\mu U_{sp}}{\mu U_{sp}}}{\left(1+\omega \right)}^{\frac{1}{1+\mu U_{sp}}}-\omega -1\right)\exp \left(-b{S}_{sp}\right)}{\mu U_{sp}}.$$

(19)

The generated sales revenue of the specific delivery is given by

$$S{R}_{sp}=S_{sp}{\displaystyle \underset{0}{\overset{T_{sp}}{\int }}R\left(S_{sp}\right)dt}.$$

(20)

Next, the subsequent costs related to inventory management are calculated as

• Purchasing cost; $P{C}_{sp}=P{Q}_{sp}$
• Average holding cost; $H{C}_{sp}=hP{\displaystyle \underset{0}{\overset{T_{sp}}{\int }}{I}_{sp}\left(t\right)dt}$
• Preservation technology capital; $PT{I}_{sp}=U_{sp}{T}_{sp}$.

Hence, the net profit of the specific delivery throughout the period from 0 to $T_{sp}$, can be evaluated as

$$\begin{array}{l}{\pi }_{s{p}_1}\left(T_{sp},S_{sp},U_{sp}\right)=\left(S{R}_{sp}-OC-P{C}_{sp}-H{C}_{sp}-PT{I}_{sp}\right)\\ =\left(S_{sp}{\displaystyle \underset{0}{\overset{T_{sp}}{\int }}R\left(S_{sp}\right)dt}-O-P{Q}_{sp}-hP{\displaystyle \underset{0}{\overset{T_{sp}}{\int }}{I}_{sp}\left(t\right)}dt-U_{sp}{T}_{sp}\right)\end{array}$$

(21)

In contrast, if the retailer pursues the strategy of regular order and places its regular order, two steps and possible conditions may occur. In the first step, before the price rise, the retailer places an order with $Q^{*}$ units during the cycle time $T^{*}$, two possible conditions may arise: (1) the retailer does not opt for the option of trade credit, or (2) the retailer wants to adopt the option of trade credit, and in the second step, $Q_{\tau }{}^{*}$ units that the retailer orders after the price rises during the cycle time $T_{\tau }{}^{*}$ (see Figure 2).

Next, we study the retailer’s net profit of regular orders based on the two steps mentioned above. In the first step, before the price rise, the retailer places an order of $Q^{*}$ units at the purchasing cost $P$, and if the retailer does not want the trade credit option, then before the price rise, the net profit of the retailer is similar to (5), that is,

$$\frac{1}{T^{*}}\left(S^{*}{\displaystyle \underset{0}{\overset{T}{\int }}R\left(S^{*}\right)dt}-\left(O+P{Q}^{*}+U^{*}{T}^{*}+hP{\displaystyle \underset{0}{\overset{T}{\int }}I\left(t\right)dt}\right)\right)$$

(22)

However, if the retailer wants to adopt the option of trade credit, then as mentioned above, the two situations (i.e., (1) $M<T$ or (2) $M\ge T$) occur. Thus, the net profit for situation 1 is similar to Equation (6).

However, if the retailer wants to adopt the option of trade credit, then, as mentioned above, the two situations (i.e., (1) $M<T$ or (2) $M\ge T$) occur. Thus, the net profit for the first situation is similar to (8) and is given by

$$\frac{1}{T^{*}}\left(\begin{array}{l}{S}^{*}{\displaystyle \underset{0}{\overset{T^{*}}{\int }}R\left(S^{*}\right)}dt-O-P{Q}^{*}-U^{*}{T}^{*}-hP{\displaystyle \underset{0}{\overset{T^{*}}{\int }}I\left(t\right)dt+}\\ S^{*}{I}_g{\displaystyle \underset{0}{\overset{M}{\int }}tR\left(S^{*}\right)dt}-P{I}_l{\displaystyle \underset{M}{\overset{T^{*}}{\int }}I\left(t\right)dt}\end{array}\right)$$

(23)

and the second situation is similar to (10), i.e.,

$$\frac{1}{T^{*}}\left(\begin{array}{l}{S}^{*}{\displaystyle \underset{0}{\overset{T^{*}}{\int }}R\left(S^{*}\right)}dt-O-P{Q}^{*}-hP{\displaystyle \underset{0}{\overset{T^{*}}{\int }}I\left(t\right)dt-U^{*}{T}^{*}+}\\ S^{*}{I}_g\left({\displaystyle \underset{0}{\overset{M}{\int }}tR\left(S^{*}\right)dt}+R\left(S^{*}\right)\left(M-T^{*}\right)T^{*}\right)\end{array}\right).$$

(24)

Next, in the second step, the $Q_{\tau }{}^{*}$ units are ordered by the retailer after the price rise at the purchasing cost $P+\tau$. Therefore, the net profit after the price rise can be evaluated using the average profit method, that is,

$$\frac{T_{sp}-T^{*}}{T_{\tau }{}^{*}}\left(S_{\tau }{}^{*}{\displaystyle \underset{0}{\overset{T_{\tau }{}^{*}}{\int }}R\left(S_{\tau }{}^{*}\right)dt}-O-\left(P+\tau \right)Q_{\tau }{}^{*}-U_{\tau }{}^{*}{T}_{\tau }{}^{*}+h\left(P+\tau \right){\displaystyle \underset{0}{\overset{T_{\tau }{}^{*}}{\int }}{I}_{\tau }\left(t\right)}dt\right).$$

(25)

Hence, if the retailer does not opt for a trade credit option, then the net profit of the regular order can be evaluated using (22) and (25), which are given by

$$\begin{array}{l}{\pi }_{r_1}\left(T_{sp},S_{sp},U_{sp}\right)=\frac{1}{T^{*}}\left(S^{*}{\displaystyle \underset{0}{\overset{T^{*}}{\int }}R\left(S^{*}\right)dt}-O-P{Q}^{*}-U^{*}{T}^{*}-hP{\displaystyle \underset{0}{\overset{T^{*}}{\int }}I\left(t\right)dt}\right)+\\ \frac{T_{sp}-T^{*}}{T_{\tau }{}^{*}}\left(S_{\tau }{}^{*}{\displaystyle \underset{0}{\overset{T_{\tau }{}^{*}}{\int }}R\left(S_{\tau }{}^{*}\right)dt}-O-\left(P+\tau \right)Q_{\tau }{}^{*}-U_{\tau }{}^{*}{T}_{\tau }{}^{*}-h\left(P+\tau \right){\displaystyle \underset{0}{\overset{T_{\tau }{}^{*}}{\int }}{I}_{\tau }\left(t\right)}dt\right)\end{array}$$

(26)

In addition, if the retailer wants to adopt a trade credit option, the net profit of the regular order for situation 1 (i.e., $M<T$) can be evaluated using (23) and (25) and is given by

$$\begin{array}{l}{\pi }_{t{r}_1}\left(T_{sp},S_{sp},U_{sp}\right)=\\ \frac{1}{T^{*}}\left(\begin{array}{l}{S}^{*}{\displaystyle \underset{0}{\overset{T^{*}}{\int }}R\left(S^{*}\right)}dt-O-P{Q}^{*}-hP{\displaystyle \underset{0}{\overset{T^{*}}{\int }}I\left(t\right)dt-U^{*}{T}^{*}+}\\ S^{*}{I}_g{\displaystyle \underset{0}{\overset{M}{\int }}tR\left(S^{*}\right)dt}-P{I}_l{\displaystyle \underset{M}{\overset{T^{*}}{\int }}I\left(t\right)dt}\end{array}\right)+\\ \frac{T_{sp}-T^{*}}{T_{\tau }{}^{*}}\left(S_{\tau }{}^{*}{\displaystyle \underset{0}{\overset{T_{\tau }{}^{*}}{\int }}R\left(S_{\tau }{}^{*}\right)dt}-O-\left(P+\tau \right)Q_{\tau }{}^{*}-U_{\tau }{}^{*}{T}_{\tau }{}^{*}-h\left(P+\tau \right){\displaystyle \underset{0}{\overset{T_{\tau }{}^{*}}{\int }}{I}_{\tau }\left(t\right)}dt\right)\end{array}$$

(27)

Situation 2 (i.e., $M\ge T$) can be evaluated using (24) and (25) and is given by

$$\begin{array}{l}{\pi }_{t{r}_2}\left(T_{sp},S_{sp},U_{sp}\right)=\\ \frac{1}{T^{*}}\left(\begin{array}{l}{S}^{*}{\displaystyle \underset{0}{\overset{T^{*}}{\int }}R\left(S^{*}\right)}dt-O-P{Q}^{*}-hP{\displaystyle \underset{0}{\overset{T^{*}}{\int }}I\left(t\right)dt-U^{*}{T}^{*}+}\\ S^{*}{I}_g\left({\displaystyle \underset{0}{\overset{M}{\int }}tR\left(S^{*}\right)dt}+R\left(S^{*}\right)\left(M-T^{*}\right)T^{*}\right)\end{array}\right)\\ +\frac{T_{sp}-T^{*}}{T_{\tau }{}^{*}}\left(S_{\tau }{}^{*}{\displaystyle \underset{0}{\overset{T_{\tau }{}^{*}}{\int }}R\left(S_{\tau }{}^{*}\right)dt}-O-\left(P+\tau \right)Q_{\tau }{}^{*}-h\left(P+\tau \right){\displaystyle \underset{0}{\overset{T_{\tau }{}^{*}}{\int }}{I}_{\tau }\left(t\right)}dt-U_{\tau }{}^{*}{T}_{\tau }{}^{*}\right)\end{array}$$

(28)

4.5. Retailer’s Net Profit Function When the Time of the Specific Delivery Emerges within the Duration of the Sale

In this section, we discuss the second scenario, in which the time of the specific delivery emerges within the duration of the sale. This condition suggests the retailer has decided to place a specific delivery when only a few units (say $r$) are left in its account. Therefore, if the retailer orders $Q_{sp}$ units as a specific delivery, then the maximum stock level in the retailer’s account will become $Q_{sp}+r$ (see Figure 3).

After the retailer receives the specific delivery, the maximum stock level $Q_{sp}+r$ can be assessed as

$$\begin{array}{l}{Q}_{sp}+r=\frac{-a\left(\mu U_{sp}+1\right)\left[{\left(1+\omega -T_{sp}\right)}^{\frac{\mu U_{sp}}{\mu U_{sp}+1}}{\left(1+\omega \right)}^{\frac{1}{\mu U_{sp}+1}}-\omega -1\right]\exp \left(-b{S}_{sp}\right)}{\mu U_{sp}}+\\ \frac{-a\left(\mu U^{*}+1\right)\left[{\left(1+\omega -\left(T^{*}-t_r\right)\right)}^{\frac{\mu U^{*}}{\mu U^{*}+1}}{\left(1+\omega \right)}^{\frac{1}{\mu U^{*}+1}}-\omega -1\right]\exp \left(-b{S}^{*}\right)}{\mu U^{*}}\end{array}$$

(29)

Additionally, the inventory level can be obtained at any moment during time $\left[0,T_r\right]$ as follows:

$$I_r\left(t\right)=\frac{-a\left(\mu U_{sp}+1\right)\left[{\left(1+\omega -T_r\right)}^{\frac{\mu U_{sp}}{\mu U_{sp}+1}}{\left(1+\omega -t\right)}^{\frac{1}{\mu U_{sp}+1}}-\omega +t-1\right]\exp \left(-b{S}_{sp}\right)}{\mu U_{sp}}$$

(30)

Since, $I_r\left(0\right)=Q_{sp}+r$, equating Equations (29) and (30) gives

$$\begin{array}{l}\frac{-a\left(\mu U_{sp}+1\right)\left[{\left(1+\omega -T_r\right)}^{\frac{\mu U_{sp}}{\mu U_{sp}+1}}{\left(1+\omega \right)}^{\frac{1}{\mu U_{sp}+1}}-\omega -1\right]\exp \left(-b{S}_{sp}\right)}{\mu U_{sp}}=\\ \frac{-a\left(\mu U_{sp}+1\right)\left[{\left(1+\omega -T_{sp}\right)}^{\frac{\mu U_{sp}}{\mu U_{sp}+1}}{\left(1+\omega \right)}^{\frac{1}{\mu U_{sp}+1}}-\omega -1\right]\exp \left(-b{S}_{sp}\right)}{\mu U_{sp}}+\\ \frac{-a\left(\mu U^{*}+1\right)\left[{\left(1+\omega -\left(T^{*}-t_r\right)\right)}^{\frac{\mu U^{*}}{\mu U^{*}+1}}{\left(1+\omega \right)}^{\frac{1}{\mu U^{*}+1}}-\omega -1\right]\exp \left(-b{S}^{*}\right)}{\mu U^{*}}\end{array}$$

(31)

Thus, from (31), $T_r$ can be expressed in terms of $T_{sp}$ as

$$\begin{array}{c}{T}_r=\hfill \\ -\exp \left(\frac{1}{\mu U}\right)\left(\left(\ln \left(-\frac{1}{U_{sp}\left(\mu U+1\right)}\left(\begin{array}{l}2F\exp \left(-b{S}_{sp}\right)\omega \mu U{U}_{sp}-F\exp \left(-bS\right)\omega \mu U{U}_{sp}-\\ G{\left(1+\omega -T+t_r\right)}^{\frac{\mu U_{sp}}{\mu U_{sp}+1}}\exp \left(-b{S}_{sp}\right)\mu U{U}_{sp}-\\ G{\left(1+\omega -T_{sp}\right)}^{\frac{\mu U_{sp}}{\mu U_{sp}+1}}\exp \left(-b{S}_{sp}\right)\mu U{U}_{sp}+\\ 2F\exp \left(-b{S}_{sp}\right)\mu U{U}_{sp}-F\exp (-bS)\mu U{U}_{sp}+\\ 2F\exp \left(-b{S}_{sp}\right)\omega U-F\exp \left(-bS\right)\omega U_{sp}-\\ G{\left(1+\omega -T+t_r\right)}^{\frac{\mu U_{sp}}{\mu U_{sp}+1}}\exp \left(-b{S}_{sp}\right)U-\\ G{\left(1+\omega -T_{sp}\right)}^{\frac{\mu U_{sp}}{\mu U_{sp}+1}}\exp \left(-b{S}_{sp}\right)U+\\ 2F\exp \left(-b{S}_{sp}\right)U-F\exp \left(-bS\right)U_{sp}\end{array}\right)\right)+bS\right)\left(\mu U+1\right)\right)+1+\omega \hfill \end{array}$$

(32)

where $F={\left(1+\xi \right)}^{\frac{-1}{\mu U+1}},G={\left(1+\xi \right)}^{\frac{\mu \left(U-U_{sp}\right)}{\left(\mu U+1\right)\left(\mu U_{sp}+1\right)}}$.

Here, the average cost of holding per unit period $T_r$ of the retailer is represented by

$$H{C}_r=hP{\displaystyle \underset{0}{\overset{T_r}{\int }}{I}_r\left(t\right)dt}$$

(33)

Thus, the net benefit of the specific delivery for the retailer generated during the time $\left[0,T_r\right]$ is given by

$$\begin{array}{l}{\pi }_{s{p}_2}\left(T_{sp},S_{sp},U_{sp}\right)=\left(S{R}_{sp}-OC-P{C}_{sp}-H{C}_r-PT{I}_{sp}\right)\\ =\left(S_{sp}{\displaystyle \underset{0}{\overset{T_{sp}}{\int }}R\left(S_{sp}\right)dt}-O-P{Q}_{sp}-hP{\displaystyle \underset{0}{\overset{T_r}{\int }}{I}_r\left(t\right)dt}-U_{sp}{T}_{sp}\right)\end{array}$$

(34)

Conversely, as discussed in Section 4.4, the retailer pursues a regular order strategy and places the regular order, and the net profit is the sum of the specific delivery and the regular order in the time $\left[0,T_r\right]$ (See Figure 3). In addition, in the regular order, two steps and possible conditions can occur for the retailer as per the previous discussion (see Figure 2).

In the first step, if the retailer does not choose a trade credit option, the retailer gains profit only during the residual depletion period $T^{*}-t_r$, and the average profit can be determined as

$$\frac{T^{*}-t_r}{T^{*}}\left(S^{*}{\displaystyle \underset{0}{\overset{T^{*}}{\int }}R\left(S^{*}\right)dt}-O-P{Q}^{*}-U^{*}{T}^{*}-hP{\displaystyle \underset{0}{\overset{T^{*}}{\int }}I\left(t\right)dt}\right).$$

(35)

However, if the retailer wishes to opt for a trade credit option, the retailer gains profit during the residual depletion period $T^{*}-t_r$ and gains interest during the 0 to $M$ period. Therefore, the average profit can be defined for situation 1 as

$$\frac{T^{*}-t_r}{T^{*}}\left(\begin{array}{l}{S}^{*}{\displaystyle \underset{0}{\overset{T^{*}}{\int }}R\left(S^{*}\right)dt}-O-P{Q}^{*}-U^{*}{T}^{*}-\\ hP{\displaystyle \underset{0}{\overset{T^{*}}{\int }}I\left(t\right)dt+S^{*}{I}_g{\displaystyle \underset{0}{\overset{M}{\int }}tR\left(S^{*}\right)dt}-P{I}_l{\displaystyle \underset{M}{\overset{T^{*}}{\int }}I\left(t\right)dt}}\end{array}\right)$$

(36)

and for situation 2 (i.e., $M\ge T$)

$$\frac{T^{*}-t_r}{T^{*}}\left(\begin{array}{l}{S}^{*}{\displaystyle \underset{0}{\overset{T^{*}}{\int }}R\left(S^{*}\right)dt}-O-P{Q}^{*}-U^{*}{T}^{*}-\\ hP{\displaystyle \underset{0}{\overset{T^{*}}{\int }}I\left(t\right)dt+S^{*}{I}_g\left({\displaystyle \underset{0}{\overset{M}{\int }}tR\left(S^{*}\right)dt}+R\left(S^{*}\right)\left(M-T^{*}\right)T^{*}\right)}\end{array}\right)$$

(37)

The retailer pursues a regular EOQ strategy at the unit purchase cost $P$ in the next step, following the unit price rise, $\tau$, per unit. Therefore, the net benefit of this step is provided by using the average profit analysis method, that is,

$$\frac{T_r-\left(T^{*}-t_r\right)}{T_{\tau }{}^{*}}\left(S_{\tau }{}^{*}{\displaystyle \underset{0}{\overset{T_{\tau }{}^{*}}{\int }}R\left(S_{\tau }{}^{*}\right)dt}-O-\left(P+\tau \right)Q_{\tau }{}^{*}-h\left(P+\tau \right){\displaystyle \underset{0}{\overset{T_{\tau }{}^{*}}{\int }}{I}_{\tau }\left(t\right)dt-U_{\tau }{}^{*}{T}_{\tau }{}^{*}}\right)$$

(38)

Accordingly, if the retailer does not opt for a trade credit option, the net profit of the regular order, in this case, can be assessed using (35) and (38) and is determined by:

$$\begin{array}{l}{\pi }_{r_2}\left(T_{sp},S_{sp},U_{sp}\right)=\frac{T^{*}-t_r}{T^{*}}\left(S^{*}{\displaystyle \underset{0}{\overset{T^{*}}{\int }}R\left(S^{*}\right)dt}-O-P{Q}^{*}-hP{\displaystyle \underset{0}{\overset{T^{*}}{\int }}I\left(t\right)dt-U^{*}{T}^{*}}\right)+\\ \frac{T_r-\left(T^{*}-t_r\right)}{T_{\tau }{}^{*}}\left(S_{\tau }{}^{*}{\displaystyle \underset{0}{\overset{T_{\tau }{}^{*}}{\int }}R\left(S_{\tau }{}^{*}\right)dt}-O-\left(P+\tau \right)Q_{\tau }{}^{*}-h\left(P+\tau \right){\displaystyle \underset{0}{\overset{T_{\tau }{}^{*}}{\int }}{I}_{\tau }\left(t\right)dt-U_{\tau }{}^{*}{T}_{\tau }{}^{*}}\right)\end{array}$$

(39)

In addition, if the retailer wishes to follow a trade credit option, the net profit of the regular order for situation 1 (i.e., $M<T$) can be assessed using (36) and (38) and is determined by

$$\begin{array}{l}{\pi }_{t{r}_3}\left(T_{sp},S_{sp},U_{sp}\right)=\\ \frac{T^{*}-t_r}{T^{*}}\left(\begin{array}{l}{S}^{*}{\displaystyle \underset{0}{\overset{T^{*}}{\int }}R\left(S^{*}\right)dt}-O-P{Q}^{*}-hP{\displaystyle \underset{0}{\overset{T^{*}}{\int }}I\left(t\right)dt-U^{*}{T}^{*}}+\\ S^{*}{I}_g{\displaystyle \underset{0}{\overset{M}{\int }}tR\left(S^{*}\right)dt}-P{I}_l{\displaystyle \underset{M}{\overset{T^{*}}{\int }}I\left(t\right)dt}\end{array}\right)\\ +\frac{T_r-\left(T^{*}-t_r\right)}{T_{\tau }{}^{*}}\left(S_{\tau }{}^{*}{\displaystyle \underset{0}{\overset{T_{\tau }{}^{*}}{\int }}R\left(S_{\tau }{}^{*}\right)dt}-O-\left(P+\tau \right)Q_{\tau }{}^{*}-h\left(P+\tau \right){\displaystyle \underset{0}{\overset{T_{\tau }{}^{*}}{\int }}{I}_{\tau }\left(t\right)dt}-U_{\tau }{}^{*}{T}_{\tau }{}^{*}\right)\end{array}$$

(40)

and for situation 2 (i.e., $M\ge T$) can be evaluated using (37) and (38), and is given by:

$$\begin{array}{l}{\pi }_{t{r}_4}\left(T_{sp},S_{sp},U_{sp}\right)=\\ \frac{T^{*}-t_r}{T^{*}}\left(\begin{array}{l}{S}^{*}{\displaystyle \underset{0}{\overset{T^{*}}{\int }}R\left(S^{*}\right)dt}-O-P{Q}^{*}-\\ hP{\displaystyle \underset{0}{\overset{T^{*}}{\int }}I\left(t\right)dt-U^{*}{T}^{*}+S^{*}{I}_g\left({\displaystyle \underset{0}{\overset{M}{\int }}tR\left(S^{*}\right)dt}+R\left(S^{*}\right)\left(M-T^{*}\right)T^{*}\right)}\end{array}\right)+\\ \frac{T_r-\left(T^{*}-t_r\right)}{T_{\tau }{}^{*}}\left(\begin{array}{l}{S}_{\tau }{}^{*}{\displaystyle \underset{0}{\overset{T_{\tau }{}^{*}}{\int }}R\left(S_{\tau }{}^{*}\right)dt}-O-\left(P+\tau \right)Q_{\tau }{}^{*}-\\ h\left(P+\tau \right){\displaystyle \underset{0}{\overset{T_{\tau }{}^{*}}{\int }}{I}_{\tau }\left(t\right)dt-U_{\tau }{}^{*}{T}_{\tau }{}^{*}}\end{array}\right)\end{array}$$

(41)

4.6. If the Retailer Chooses the Option of Discount in Payment on the Specific Delivery Given by the Supplier

This section studies the probable effects on net profit if the retailer chooses the discount option on the specific delivery. In this case, on the specific delivery, the supplier offers a discount, say $D$. Then, if the retailer adopts a specific delivery before the price rise, the original sales cost $P$ will be reduced and becomes $P-D$.

Next, total cost components per cycle time $T_{sp}$ with discount $D$ are comprised of

• Purchasing cost; $P{C}_{DS}=\left(P-D\right)Q_{sp}$
• Average holding cost; $H{C}_{DS}=h\left(P-D\right){\displaystyle \underset{0}{\overset{T_{sp}}{\int }}{I}_{sp}\left(t\right)dt}$.

As per Section 4.4 and Section 4.5, two situations may occur for the specific delivery. This paper studies both situations individually.

In the first situation, if the time for specific delivery matches with reordering time, the net profit for the retailer at the purchasing cost $C-D$ during cycle time $T_{sp}$ is:

$$\begin{array}{l}{\pi }_{Ds{p}_1}\left(T_{sp},S_{sp},U_{sp}\right)=\left(S{R}_{sp}-OC-P{C}_{DS}-H{C}_{DS}-PT{I}_{sp}\right)\\ =\left(S_{sp}{\displaystyle \underset{0}{\overset{T_{sp}}{\int }}R\left(S_{sp}\right)dt}-O-\left(P-D\right)Q_{sp}-h\left(P-D\right){\displaystyle \underset{0}{\overset{T_{sp}}{\int }}{I}_{sp}\left(t\right)dt-U_{sp}{T}_{sp}}\right)\end{array}$$

(42)

Similarly, in the second situation, if the time of the specific delivery emerges within the duration of the sale, then the average holding cost $T_{sp}$ with discount $D$ per unit time is represented by

$$H{C}_{Dq}=h\left(P-D\right){\displaystyle \underset{0}{\overset{T_r}{\int }}{I}_r\left(t\right)dt}$$

(43)

and the total profit is evaluated as

$$\begin{array}{l}{\pi }_{Ds{p}_2}\left(T_{sp},S_{sp},U_{sp}\right)=\left(S{R}_{sp}-OC-P{C}_{DS}-H{C}_{Dq}-PT{I}_{sp}\right)\\ =\left(S_{sp}{\displaystyle \underset{0}{\overset{T_{sp}}{\int }}R\left(S_{sp}\right)dt}-O-\left(P-D\right)Q_{sp}-h\left(P-D\right){\displaystyle \underset{0}{\overset{T_r}{\int }}{I}_r\left(t\right)dt}-U_{sp}{T}_{sp}\right)\end{array}$$

(44)

4.7. Retailer’s Net Profit Function Which Is the Sum of Its Regular Order and Specific Delivery

As discussed earlier, the supplier can give either the option of trade credit on the regular order or the option of a discount in payment for the specific delivery. Therefore, in this section, we study all possible cases and derive the net profit function for the retailer, which is the sum of its regular order and the specific delivery.

Case (i) Retailer’s net profit if the retailer chooses the option of trade credit

Here, the retailer will not get a discount on the specific delivery and, as discussed earlier, for the trade credit option, two possible situations are possible (i.e., (1) $M<T$ or (2) $M\ge T$).

Thus, if the time for specific delivery matches with the retailer’s reordering time, then the overall profit function of the retailer for situations 1 and 2 can be described as

$$\begin{array}{l}T{P}_1\left(T_{sp},S_{sp},U_{sp}\right)={\pi }_{t{r}_1}\left(T_{sp},S_{sp},U_{sp}\right)+{\pi }_{s{p}_1}\left(T_{sp},S_{sp},U_{sp}\right)\\ =\frac{1}{T^{*}}\left(\begin{array}{l}{S}^{*}{\displaystyle \underset{0}{\overset{T^{*}}{\int }}R\left(S^{*}\right)}dt-O-P{Q}^{*}-\\ hP{\displaystyle \underset{0}{\overset{T^{*}}{\int }}I\left(t\right)dt-U^{*}{T}^{*}+S^{*}{I}_g{\displaystyle \underset{0}{\overset{M}{\int }}tR\left(S^{*}\right)dt}-P{I}_l{\displaystyle \underset{M}{\overset{T^{*}}{\int }}I\left(t\right)dt}}\end{array}\right)+\\ \frac{T_{sp}-T^{*}}{T_{\tau }{}^{*}}\left(S_{\tau }{}^{*}{\displaystyle \underset{0}{\overset{T_{\tau }{}^{*}}{\int }}R\left(S_{\tau }{}^{*}\right)dt}-O-\left(P+\tau \right)Q_{\tau }{}^{*}-h\left(P+\tau \right){\displaystyle \underset{0}{\overset{T_{\tau }{}^{*}}{\int }}{I}_{\tau }\left(t\right)}dt-U_{\tau }{}^{*}{T}_{\tau }{}^{*}\right)+\\ \left(S_{sp}{\displaystyle \underset{0}{\overset{T_{sp}}{\int }}R\left(S_{sp}\right)dt}-O-P{Q}_{sp}-hP{\displaystyle \underset{0}{\overset{T_{sp}}{\int }}{I}_{sp}\left(t\right)}dt-U_{sp}{T}_{sp}\right)\end{array}$$

(45)

$$\begin{array}{l}T{P}_2\left(T_{sp},S_{sp},U_{sp}\right)={\pi }_{t{r}_2}\left(T_{sp},S_{sp},U_{sp}\right)+{\pi }_{s{p}_1}\left(T_{sp},S_{sp},U_{sp}\right)\\ =\frac{1}{T^{*}}\left(\begin{array}{l}{S}^{*}{\displaystyle \underset{0}{\overset{T^{*}}{\int }}R\left(S^{*}\right)}dt-O-P{Q}^{*}-\\ hP{\displaystyle \underset{0}{\overset{T^{*}}{\int }}I\left(t\right)dt-U^{*}{T}^{*}+S^{*}{I}_g\left({\displaystyle \underset{0}{\overset{M}{\int }}tR\left(S^{*}\right)dt}+R\left(S^{*}\right)\left(M-T^{*}\right)T^{*}\right)}\end{array}\right)+\\ \frac{T_{sp}-T^{*}}{T_{\tau }{}^{*}}\left(S_{\tau }{}^{*}{\displaystyle \underset{0}{\overset{T_{\tau }{}^{*}}{\int }}R\left(S_{\tau }{}^{*}\right)dt}-O-\left(P+\tau \right)Q_{\tau }{}^{*}-h\left(P+\tau \right){\displaystyle \underset{0}{\overset{T_{\tau }{}^{*}}{\int }}{I}_{\tau }\left(t\right)}dt-U_{\tau }{}^{*}{T}_{\tau }{}^{*}\right)+\\ \left(S_{sp}{\displaystyle \underset{0}{\overset{T_{sp}}{\int }}R\left(S_{sp}\right)dt}-O-P{Q}_{sp}-hP{\displaystyle \underset{0}{\overset{T_{sp}}{\int }}{I}_{sp}\left(t\right)}dt-U_{sp}{T}_{sp}\right).\end{array}$$

(46)

If a specific delivery time emerges within the duration of the sale, then the retailer’s overall profit function for situations 1 and 2 can be described as

$$\begin{array}{l}T{P}_3\left(T_{sp},S_{sp},U_{sp}\right)={\pi }_{t{r}_3}\left(T_{sp},S_{sp},U_{sp}\right)+{\pi }_{s{p}_2}\left(T_{sp},S_{sp},U_{sp}\right)\\ =\frac{T^{*}-t_r}{T^{*}}\left(\begin{array}{l}{S}^{*}{\displaystyle \underset{0}{\overset{T^{*}}{\int }}R\left(S^{*}\right)dt}-O-P{Q}^{*}-U^{*}{T}^{*}-\\ hP{\displaystyle \underset{0}{\overset{T^{*}}{\int }}I\left(t\right)dt+S^{*}{I}_g{\displaystyle \underset{0}{\overset{M}{\int }}tR\left(S^{*}\right)dt}-P{I}_l{\displaystyle \underset{M}{\overset{T^{*}}{\int }}I\left(t\right)dt}}\end{array}\right)+\\ \frac{T_r-\left(T^{*}-t_r\right)}{T_{\tau }{}^{*}}\left(S_{\tau }{}^{*}{\displaystyle \underset{0}{\overset{T_{\tau }{}^{*}}{\int }}R\left(S_{\tau }{}^{*}\right)dt}-O-\left(P+\tau \right)Q_{\tau }{}^{*}-h\left(P+\tau \right){\displaystyle \underset{0}{\overset{T_{\tau }{}^{*}}{\int }}{I}_{\tau }\left(t\right)dt-U_{\tau }{}^{*}{T}_{\tau }{}^{*}}\right)+\\ \left(S_{sp}{\displaystyle \underset{0}{\overset{T_{sp}}{\int }}R\left(S_{sp}\right)dt}-O-P{Q}_{sp}-hP{\displaystyle \underset{0}{\overset{T_r}{\int }}{I}_r\left(t\right)dt}-U_{sp}{T}_{sp}\right)\end{array}$$

(47)

$$\begin{array}{l}T{P}_4\left(T_{sp},S_{sp},U_{sp}\right)={\pi }_{t{r}_4}\left(T_{sp},S_{sp},U_{sp}\right)+{\pi }_{s{p}_2}\left(T_{sp},S_{sp},U_{sp}\right)\\ =\frac{T^{*}-t_r}{T^{*}}\left(\begin{array}{l}{S}^{*}{\displaystyle \underset{0}{\overset{T^{*}}{\int }}R\left(S^{*}\right)dt}-O-P{Q}^{*}-\\ hP{\displaystyle \underset{0}{\overset{T^{*}}{\int }}I\left(t\right)dt-U^{*}{T}^{*}+S^{*}{I}_g\left({\displaystyle \underset{0}{\overset{M}{\int }}tR\left(S^{*}\right)dt}+R\left(S^{*}\right)\left(M-T^{*}\right)T^{*}\right)}\end{array}\right)+\\ \frac{T_r-\left(T^{*}-t_r\right)}{T_{\tau }{}^{*}}\left(S_{\tau }{}^{*}{\displaystyle \underset{0}{\overset{T_{\tau }{}^{*}}{\int }}R\left(S_{\tau }{}^{*}\right)dt}-O-\left(P+\tau \right)Q_{\tau }{}^{*}-h\left(P+\tau \right){\displaystyle \underset{0}{\overset{T_{\tau }{}^{*}}{\int }}{I}_{\tau }\left(t\right)dt-U_{\tau }{}^{*}{T}_{\tau }{}^{*}}\right)+\\ \left(S_{sp}{\displaystyle \underset{0}{\overset{T_{sp}}{\int }}R\left(S_{sp}\right)dt}-O-P{Q}_{sp}-hP{\displaystyle \underset{0}{\overset{T_r}{\int }}{I}_r\left(t\right)dt}-U_{sp}{T}_{sp}\right)\end{array}$$

(48)

Case (ii) Retailer’s overall profit if the retailer chooses the option of a discount in payment on the specific delivery

In this case, the retailer gets a discount, $D$, on the specific delivery; thus, the retailer does not receive the trade credit policy on the regular order. Therefore, if the time for the specific delivery matches the reordering time of the retailer, then the net profit function of the retailer is described as

$$\begin{array}{l}T{P}_5\left(T_{sp},S_{sp},U_{sp}\right)={\pi }_{r_1}\left(T_{sp},S_{sp},U_{sp}\right)+{\pi }_{Ds{p}_1}\left(T_{sp},S_{sp},U_{sp}\right)\\ =\frac{1}{T^{*}}\left(S^{*}{\displaystyle \underset{0}{\overset{T^{*}}{\int }}R\left(S^{*}\right)dt}-O-P{Q}^{*}-hP{\displaystyle \underset{0}{\overset{T^{*}}{\int }}I\left(t\right)dt-U^{*}{T}^{*}}\right)+\\ \frac{T_{sp}-T^{*}}{T_{\tau }{}^{*}}\left(S_{\tau }{}^{*}{\displaystyle \underset{0}{\overset{T_{\tau }{}^{*}}{\int }}R\left(S_{\tau }{}^{*}\right)dt}-O-\left(P+\tau \right)Q_{\tau }{}^{*}-U_{\tau }{}^{*}{T}_{\tau }{}^{*}-h\left(P+\tau \right){\displaystyle \underset{0}{\overset{T_{\tau }{}^{*}}{\int }}{I}_{\tau }\left(t\right)}dt\right)+\\ \left(S_{sp}{\displaystyle \underset{0}{\overset{T_{sp}}{\int }}R\left(S_{sp}\right)dt}-O-\left(P-D\right)Q_{sp}-h\left(P-D\right){\displaystyle \underset{0}{\overset{T_{sp}}{\int }}{I}_{sp}\left(t\right)dt-U_{sp}{T}_{sp}}\right)\end{array}$$

(49)

and if a time of the specific delivery emerges within the duration of the sale, then the retailer’s overall profit function can be described as

$$\begin{array}{l}T{P}_6\left(T_{sp},S_{sp},U_{sp}\right)={\pi }_{r_2}\left(T_{sp},S_{sp},U_{sp}\right)+{\pi }_{Ds{p}_2}\left(T_{sp},S_{sp},U_{sp}\right)\\ =\frac{T^{*}-t_r}{T^{*}}\left(S^{*}{\displaystyle \underset{0}{\overset{T^{*}}{\int }}R\left(S^{*}\right)dt}-O-P{Q}^{*}-hP{\displaystyle \underset{0}{\overset{T^{*}}{\int }}I\left(t\right)dt-U^{*}{T}^{*}}\right)+\\ \frac{T_r-\left(T^{*}-t_r\right)}{T_{\tau }{}^{*}}\left(S_{\tau }{}^{*}{\displaystyle \underset{0}{\overset{T_{\tau }{}^{*}}{\int }}R\left(S_{\tau }{}^{*}\right)dt}-O-\left(P+\tau \right)Q_{\tau }{}^{*}-U_{\tau }{}^{*}{T}_{\tau }{}^{*}-h\left(P+\tau \right){\displaystyle \underset{0}{\overset{T_{\tau }{}^{*}}{\int }}{I}_{\tau }\left(t\right)dt}\right)+\\ \left(S_{sp}{\displaystyle \underset{0}{\overset{T_{sp}}{\int }}R\left(S_{sp}\right)dt}-O-\left(P-D\right)Q_{sp}-h\left(P-D\right){\displaystyle \underset{0}{\overset{T_r}{\int }}{I}_r\left(t\right)dt}-U_{sp}{T}_{sp}\right)\end{array}$$

(50)

Special Case: Retailer’s overall profit if the retailer doesn’t want to adopt any specific deliveries.

Here, if the retailer does not want to place any specific deliveries, then the supplier does not provide any trade credit policy on the regular order. Therefore, the retailer does not get any extra profit based on the specific delivery and will only collect the profit on its regular replenishment order (i.e., profit before the price increase and after the price increase). Hence, the overall profit for the retailer is expressed as

$$\begin{array}{l}TP\left(T^{*},T_{\tau }{}^{*},S^{*},S_{\tau }{}^{*},U^{*},U_{\tau }{}^{*}\right)=\pi \left(T^{*},S^{*},U^{*}\right)+{\pi }_{\tau }\left(T_{\tau }{}^{*},S_{\tau }{}^{*},U_{\tau }{}^{*}\right)\\ =\frac{1}{T^{*}}\left(S^{*}{\displaystyle \underset{0}{\overset{T^{*}}{\int }}R\left(S^{*}\right)dt}-O-P{Q}^{*}-U^{*}{T}^{*}-hP{\displaystyle \underset{0}{\overset{T^{*}}{\int }}I\left(t\right)dt}\right)+\\ \frac{1}{T_{\tau }{}^{*}}\left(S_{\tau }{}^{*}{\displaystyle \underset{0}{\overset{T_{\tau }{}^{*}}{\int }}R\left(S_{\tau }{}^{*}\right)dt}-O-\left(P+\tau \right)Q_{\tau }{}^{*}-U_{\tau }{}^{*}{T}_{\tau }{}^{*}-h\left(P+\tau \right){\displaystyle \underset{0}{\overset{T_{\tau }{}^{*}}{\int }}{I}_{\tau }\left(t\right)dt}\right)\end{array}$$

(51)

In addition, the optimal order quantity $Q_{s{p}_i}{}^{*};i=1,2,3,4,5,6.$ for all the above-mentioned cases can be defined as

$$Q_{s{p}_i}{}^{*}=\frac{-a\left(\mu U_{sp}{}^{*}+1\right)\left[{\left(1+\omega -T_{sp}{}^{*}\right)}^{\frac{\mu U_{sp}{}^{*}}{\mu U_{sp}{}^{*}+1}}{\left(1+\omega \right)}^{\frac{1}{\mu U_{sp}{}^{*}+1}}-\omega -1\right]\exp \left(-b{S}_{sp}{}^{*}\right)}{\mu U_{sp}{}^{*}}.$$

(52)

Remark: Note that if the specific delivery is located only when the overall profit in all such cases is positive then it is beneficial to the retailer. Otherwise, the retailer can ignore the ability to order a specific delivery.

5. Algorithm Rule for Optimality

In this section, the algorithm rule is derived, which determines the optimal solution for the retailer’s overall profit function $T{P}_i\left(T_{sp},S_{sp},U_{sp}\right);i=1,2,3,4,5,6$. This algorithm implements the subsequent steps in Maple $XVIII$ software to check the optimal measures of the main parameters.

Step 1: First, use the essential conditions

$$\frac{\partial T{P}_i\left(T_{sp},S_{sp},U_{sp}\right)}{\partial T_{sp}}=0,\frac{\partial T{P}_i\left(T_{sp},S_{sp},U_{sp}\right)}{\partial S_{sp}}=0,\frac{\partial T{P}_i\left(T_{sp},S_{sp},U_{sp}\right)}{\partial U_{sp}}=0;i=1,2,3,4,5,6$$

to find the optimal decision parameters $T_{sp}{}^{*},S_{sp}{}^{*}\mathrm{and}{U}_{sp}{}^{*}$ to minimize or maximize the overall profit function.

Step 2: In regards to decision variables, find all possible partial derivatives of the second order, that is,

$$\begin{array}{c}\frac{{\partial }^{2}T{P}_i\left(T_{sp}{}^{*},S_{sp}{}^{*},U_{sp}{}^{*}\right)}{\partial T_{sp}{}^2},\frac{{\partial }^{2}T{P}_i\left(T_{sp}{}^{*},S_{sp}{}^{*},U_{sp}{}^{*}\right)}{\partial T_{sp}\partial S_{sp}},\frac{{\partial }^{2}T{P}_i\left(T_{sp}{}^{*},S_{sp}{}^{*},U_{sp}{}^{*}\right)}{\partial T_{sp}\partial U_{sp}},\\ \frac{{\partial }^{2}T{P}_i\left(T_{sp}{}^{*},S_{sp}{}^{*},U_{sp}{}^{*}\right)}{\partial S_{sp}\partial T_{sp}},\frac{{\partial }^{2}T{P}_i\left(T_{sp}{}^{*},S_{sp}{}^{*},U_{sp}{}^{*}\right)}{\partial S_{sp}{}^2},\frac{{\partial }^{2}T{P}_i\left(T_{sp}{}^{*},S_{sp}{}^{*},U_{sp}{}^{*}\right)}{\partial S_{sp}\partial U_{sp}},\\ \frac{{\partial }^{2}T{P}_i\left(T_{sp}{}^{*},S_{sp}{}^{*},U_{sp}{}^{*}\right)}{\partial U_{sp}\partial T_{sp}},\frac{{\partial }^{2}T{P}_i\left(T_{sp}{}^{*},S_{sp}{}^{*},U_{sp}{}^{*}\right)}{\partial U_{sp}\partial S_{sp}},\frac{{\partial }^{2}T{P}_i\left(T_{sp}{}^{*},S_{sp}{}^{*},U_{sp}{}^{*}\right)}{\partial U_{sp}{}^2}\end{array}$$

Step 3: Generate the Hessian Matrix

$$\begin{array}{c}{H}_i\left(T_{sp}{}^{*},S_{sp}{}^{*},U_{sp}{}^{*}\right)=\hfill \\ \left[\begin{array}{c}\frac{{\partial }^{2}T{P}_i\left(T_{sp}{}^{*},S_{sp}{}^{*},U_{sp}{}^{*}\right)}{\partial T_{sp}{}^2}\frac{{\partial }^{2}T{P}_i\left(T_{sp}{}^{*},S_{sp}{}^{*},U_{sp}{}^{*}\right)}{\partial T_{sp}\partial S_{sp}}\frac{{\partial }^{2}T{P}_i\left(T_{sp}{}^{*},S_{sp}{}^{*},U_{sp}{}^{*}\right)}{\partial T_{sp}\partial U_{sp}}\\ \frac{{\partial }^{2}T{P}_i\left(T_{sp}{}^{*},S_{sp}{}^{*},U_{sp}{}^{*}\right)}{\partial S_{sp}\partial T_{sp}}\frac{{\partial }^{2}T{P}_i\left(T_{sp}{}^{*},S_{sp}{}^{*},U_{sp}{}^{*}\right)}{\partial S_{sp}{}^2}\frac{{\partial }^{2}T{P}_i\left(T_{sp}{}^{*},S_{sp}{}^{*},U_{sp}{}^{*}\right)}{\partial S_{sp}\partial U_{sp}}\\ \frac{{\partial }^{2}T{P}_i\left(T_{sp}{}^{*},S_{sp}{}^{*},U_{sp}{}^{*}\right)}{\partial U_{sp}\partial T_{sp}}\frac{{\partial }^{2}T{P}_i\left(T_{sp}{}^{*},S_{sp}{}^{*},U_{sp}{}^{*}\right)}{\partial U_{sp}\partial S_{sp}}\frac{{\partial }^{2}T{P}_i\left(T_{sp}{}^{*},S_{sp}{}^{*},U_{sp}{}^{*}\right)}{\partial U_{sp}{}^2}\end{array}\right];i=1,2,3,4,5,6\end{array}$$

to attain the concavity of profit function.

Step 4: Describe the subsequent minor determinants and compute to prove the Hessian Matrix $H_i\left(T_{sp}{}^{*},S_{sp}{}^{*},U_{sp}{}^{*}\right)$ is negative definite as

$$D_1=\left|\frac{{\partial }^{2}T{P}_i\left(T_{sp}{}^{*},S_{sp}{}^{*},U_{sp}{}^{*}\right)}{\partial T_{sp}{}^2}\right|,D_2=\left|\begin{array}{cc}\frac{{\partial }^{2}T{P}_i\left(T_{sp}{}^{*},S_{sp}{}^{*},U_{sp}{}^{*}\right)}{\partial T_{sp}{}^2}& \frac{{\partial }^{2}T{P}_i\left(T_{sp}{}^{*},S_{sp}{}^{*},U_{sp}{}^{*}\right)}{\partial T_{sp}\partial S_{sp}}\\ \frac{{\partial }^{2}T{P}_i\left(T_{sp}{}^{*},S_{sp}{}^{*},U_{sp}{}^{*}\right)}{\partial S_{sp}\partial T_{sp}}& \frac{{\partial }^{2}T{P}_i\left(T_{sp}{}^{*},S_{sp}{}^{*},U_{sp}{}^{*}\right)}{\partial S_{sp}{}^2}\end{array}\right|,$$

$$D_3=\left|\begin{array}{c}\frac{{\partial }^{2}T{P}_i\left(T_{sp}{}^{*},S_{sp}{}^{*},U_{sp}{}^{*}\right)}{\partial T_{sp}{}^2}\frac{{\partial }^{2}T{P}_i\left(T_{sp}{}^{*},S_{sp}{}^{*},U_{sp}{}^{*}\right)}{\partial T_{sp}\partial S_{sp}}\frac{{\partial }^{2}T{P}_i\left(T_{sp}{}^{*},S_{sp}{}^{*},U_{sp}{}^{*}\right)}{\partial T_{sp}\partial U_{sp}}\\ \frac{{\partial }^{2}T{P}_i\left(T_{sp}{}^{*},S_{sp}{}^{*},U_{sp}{}^{*}\right)}{\partial S_{sp}\partial T_{sp}}\frac{{\partial }^{2}T{P}_i\left(T_{sp}{}^{*},S_{sp}{}^{*},U_{sp}{}^{*}\right)}{\partial S_{sp}{}^2}\frac{{\partial }^{2}T{P}_i\left(T_{sp}{}^{*},S_{sp}{}^{*},U_{sp}{}^{*}\right)}{\partial S_{sp}\partial U_{sp}}\\ \frac{{\partial }^{2}T{P}_i\left(T_{sp}{}^{*},S_{sp}{}^{*},U_{sp}{}^{*}\right)}{\partial U_{sp}\partial T_{sp}}\frac{{\partial }^{2}T{P}_i\left(T_{sp}{}^{*},S_{sp}{}^{*},U_{sp}{}^{*}\right)}{\partial U_{sp}\partial S_{sp}}\frac{{\partial }^{2}T{P}_i\left(T_{sp}{}^{*},S_{sp}{}^{*},U_{sp}{}^{*}\right)}{\partial U_{sp}{}^2}\end{array}\right|$$

Proposition 1.

The Hessian Matrix $H_i\left(T_{sp}{}^{*},S_{sp}{}^{*},U_{sp}{}^{*}\right);i=1,2,3,4,5,6$is said to be a negative definite if $\left|D_1\right|<0$, $\left|D_2\right|>0$, and$\left|D_3\right|<0$(Jani et al. [37]).

Proposition 2.

The total profit function$T{P}_i\left(T_{sp},S_{sp},U_{sp}\right);i=1,2,3,4,5,6$is strictly concave if the Hessian Matrix$H_i\left(T_{sp}{}^{*},S_{sp}{}^{*},U_{sp}{}^{*}\right);i=1,2,3,4,5,6$is negative definite and the optimum point$\left(T_{sp}{}^{*},S_{sp}{}^{*},U_{sp}{}^{*}\right)$is the maximum (Jani et al. [37]).

6. Numerical Examples, Sensitivity Analysis, and Managerial Implications

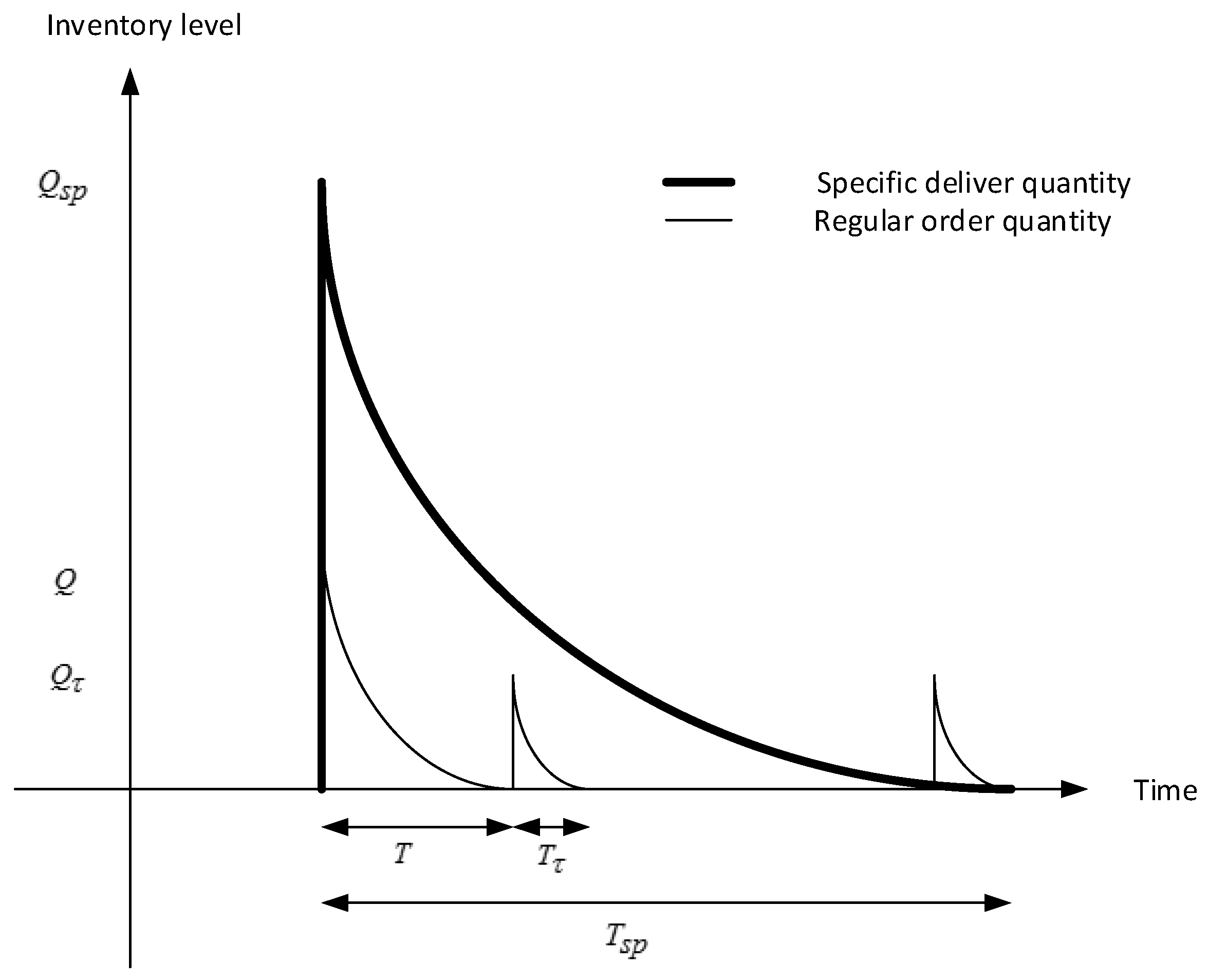
6.1. Numerical Examples

To reveal the resulting model, seven numerical illustrations are studied, which provide the idea of the best optimal solution for the overall profit function $T{P}_i\left(T_{sp},S_{sp},U_{sp}\right);i=1,2,3,4,5,6$.

• Example 1. (For$M<T$and specific delivery matches with reordering time).

The following parameters are used for the given inventory system.

$a=4000$units per year,$b=0.04$units per year,$\omega =2$years,$O=\$100$per order,$h=\$0.3$per unit per year,$P=\$100$per unit,$\tau =\$20$per unit,$\mu =1$,$M=0.3$years,$I_g=0.1$per dollar per year,$I_l=0.15$per dollar per year.

By using the mathematical software Maple$XVIII$and the above-mentioned algorithm, the optimal decision variables are$T_{sp}{}^{*}=1.526$years,$S_{sp}{}^{*}=\$149.80,$$U_{sp}{}^{*}=\$18.36$and hence$Q_{s{p}_1}{}^{*}=15.50$units,${\pi }_{t{r}_1}\left(T_{sp}{}^{*},S_{sp}{}^{*},U_{sp}{}^{*}\right)=\$313.17$, and${\pi }_{s{p}_1}\left(T_{sp}{}^{*},S_{sp}{}^{*},U_{sp}{}^{*}\right)=\$253.18$.

Therefore, the retailer’s overall profit is

$$\begin{array}{c}T{P}_1\left(T_{sp}{}^{*},S_{sp}{}^{*},U_{sp}{}^{*}\right)={\pi }_{t{r}_1}\left(T_{sp}{}^{*},S_{sp}{}^{*},U_{sp}{}^{*}\right)+{\pi }_{s{p}_1}\left(T_{sp}{}^{*},S_{sp}{}^{*},U_{sp}{}^{*}\right)\\ =\$313.17+\$253.18=\$566.35\end{array}$$

and by the above procedure, the Hessian Matrix for this case is$H_1\left(T_{sp}{}^{*},S_{sp}{}^{*},U_{sp}{}^{*}\right)=\left[\begin{array}{ccc}-352.46& 10.26& 1.46\\ 10.26& -0.61& -0.06\\ 1.46& -0.06& -0.16\end{array}\right]$and the determinants are$\left|D_1\right|=-352.46<0$,$\left|D_2\right|=\left|\begin{array}{cc}-352.46& 10.26\\ 10.26& -0.61\end{array}\right|=109.77>0$, and$\left|D_3\right|=\left|\begin{array}{ccc}-352.46& 10.26& 1.46\\ 10.26& -0.61& -0.06\\ 1.46& -0.06& -0.16\end{array}\right|=-16.71<0$. Therefore, the Hessian Matrix$H_1\left(T_{sp}{}^{*},S_{sp}{}^{*},U_{sp}{}^{*}\right)$is negative definite from Proposition 1, and from Proposition 2, the$T{P}_1\left(T_{sp},S_{sp},U_{sp}\right)$is strictly concave and the point$\left(T_{sp}{}^{*},S_{sp}{}^{*},U_{sp}{}^{*}\right)$is the maximum.

• Example 2. (For$M\ge T$and specific delivery matches with reordering time).

Using a similar data set as in Example 1, except for$M=0.45$years, the optimal decision variables are$T_{sp}{}^{*}=1.526$years,$S_{sp}{}^{*}=\$149.80,$$U_{sp}{}^{*}=\$18.36$and hence,$Q_{s{p}_2}{}^{*}=15.50$units,${\pi }_{t{r}_2}\left(T_{sp}{}^{*},S_{sp}{}^{*},U_{sp}{}^{*}\right)=\$356.40$and${\pi }_{s{p}_1}\left(T_{sp}{}^{*},S_{sp}{}^{*},U_{sp}{}^{*}\right)=\$253.18$.

Therefore, the retailer’s overall profit is

$$\begin{array}{c}T{P}_2\left(T_{sp}{}^{*},S_{sp}{}^{*},U_{sp}{}^{*}\right)={\pi }_{t{r}_2}\left(T_{sp}{}^{*},S_{sp}{}^{*},U_{sp}{}^{*}\right)+{\pi }_{s{p}_1}\left(T_{sp}{}^{*},S_{sp}{}^{*},U_{sp}{}^{*}\right)\\ =\$356.40+\$253.18=\$609.58\end{array}$$

and the Hessian Matrix for this case is$H_2\left(T_{sp}{}^{*},S_{sp}{}^{*},U_{sp}{}^{*}\right)=\left[\begin{array}{ccc}-352.46& 10.26& 1.46\\ 10.26& -0.61& -0.06\\ 1.46& -0.06& -0.16\end{array}\right]$and the determinants are$\left|D_1\right|=-352.46<0$,$\left|D_2\right|=\left|\begin{array}{cc}-352.46& 10.26\\ 10.26& -0.61\end{array}\right|=109.77>0$, and$\left|D_3\right|=\left|\begin{array}{ccc}-352.46& 10.26& 1.46\\ 10.26& -0.61& -0.06\\ 1.46& -0.06& -0.16\end{array}\right|=-16.71<0$. Therefore, from Proposition 1, the$H_2\left(T_{sp}{}^{*},S_{sp}{}^{*},U_{sp}{}^{*}\right)$is negative definite, and hence from Proposition 2, the$T{P}_2\left(T_{sp},S_{sp},U_{sp}\right)$is strictly concave and the point$\left(T_{sp}{}^{*},S_{sp}{}^{*},U_{sp}{}^{*}\right)$is the maximum.

• Example 3. (For$M<T$and the specific delivery emerges within the duration of the sale).

Using the same dataset as in Example 1 except$r=5$for units, the optimal decision variables are$T_{sp}{}^{*}=0.916$years,$S_{sp}{}^{*}=\$138.86,$$U_{sp}{}^{*}=\$14.86$and hence,$Q_{s{p}_3}{}^{*}=14.33$units,${\pi }_{t{r}_3}\left(T_{sp}{}^{*},S_{sp}{}^{*},U_{sp}{}^{*}\right)=\$92.68$, and${\pi }_{s{p}_2}\left(T_{sp}{}^{*},S_{sp}{}^{*},U_{sp}{}^{*}\right)=\$66.81$.

Therefore, the retailer’s overall profit is

$$\begin{array}{c}T{P}_3\left(T_{sp}{}^{*},S_{sp}{}^{*},U_{sp}{}^{*}\right)={\pi }_{t{r}_3}\left(T_{sp}{}^{*},S_{sp}{}^{*},U_{sp}{}^{*}\right)+{\pi }_{s{p}_2}\left(T_{sp}{}^{*},S_{sp}{}^{*},U_{sp}{}^{*}\right)\\ =\$92.68+\$66.81=\$159.49\end{array}$$

and the Hessian Matrix for this case is$H_3\left(T_{sp}{}^{*},S_{sp}{}^{*},U_{sp}{}^{*}\right)=\left[\begin{array}{ccc}-520.28& 10.12& 1.33\\ 10.12& -0.61& -0.04\\ 1.33& -0.04& -0.12\end{array}\right]$and the determinants are$\left|D_1\right|=-520.28<0$,$\left|D_2\right|=\left|\begin{array}{cc}-520.28& 10.12\\ 10.12& -0.61\end{array}\right|=217.41>0$, and$\left|D_3\right|=\left|\begin{array}{ccc}-520.28& 10.12& 1.33\\ 10.12& -0.61& -0.04\\ 1.33& -0.04& -0.12\end{array}\right|=-24.40<0$. Therefore, the Hessian Matrix$H_3\left(T_{sp}{}^{*},S_{sp}{}^{*},U_{sp}{}^{*}\right)$is negative definite from Proposition 1 and from Proposition 2, the$T{P}_3\left(T_{sp},S_{sp},U_{sp}\right)$is strictly concave and the point$\left(T_{sp}{}^{*},S_{sp}{}^{*},U_{sp}{}^{*}\right)$is the maximum.

• Example 4. (For$M\ge T$and the specific delivery emerges within the duration of the sale).

Using the same data set as in Example 1 except$r=5$units, the optimal decision parameters are$T_{sp}{}^{*}=0.916$years,$S_{sp}{}^{*}=\$138.86,$$U_{sp}{}^{*}=\$14.86$and hence,$Q_{s{p}_3}{}^{*}=14.33$units,${\pi }_{t{r}_4}\left(T_{sp}{}^{*},S_{sp}{}^{*},U_{sp}{}^{*}\right)=\$99.05$, and${\pi }_{s{p}_2}\left(T_{sp}{}^{*},S_{sp}{}^{*},U_{sp}{}^{*}\right)=\$66.81$.

Therefore, the retailer’s overall profit is

$$\begin{array}{c}T{P}_4\left(T_{sp}{}^{*},S_{sp}{}^{*},U_{sp}{}^{*}\right)={\pi }_{t{r}_4}\left(T_{sp}{}^{*},S_{sp}{}^{*},U_{sp}{}^{*}\right)+{\pi }_{s{p}_2}\left(T_{sp}{}^{*},S_{sp}{}^{*},U_{sp}{}^{*}\right)\\ =\$99.05+\$66.81=\$165.86\end{array}$$

and the Hessian Matrix for this case is$H_4\left(T_{sp}{}^{*},S_{sp}{}^{*},U_{sp}{}^{*}\right)=\left[\begin{array}{ccc}-520.28& 10.12& 1.33\\ 10.12& -0.61& -0.04\\ 1.33& -0.04& -0.12\end{array}\right]$and the determinants are$\left|D_1\right|=-520.28<0$,$\left|D_2\right|=\left|\begin{array}{cc}-520.28& 10.12\\ 10.12& -0.61\end{array}\right|=217.41>0$, and$\left|D_3\right|=\left|\begin{array}{ccc}-520.28& 10.12& 1.33\\ 10.12& -0.61& -0.04\\ 1.33& -0.04& -0.12\end{array}\right|=-24.40<0$. Therefore, the Hessian Matrix$H_4\left(T_{sp}{}^{*},S_{sp}{}^{*},U_{sp}{}^{*}\right)$is negative definite from Proposition 1, and from Proposition 2,$T{P}_4\left(T_{sp},S_{sp},U_{sp}\right)$is strictly concave and the point$\left(T_{sp}{}^{*},S_{sp}{}^{*},U_{sp}{}^{*}\right)$is the maximum.

• Example 5.(For regular orders and the specific delivery matches with the reordering time with discount).

The following values are considered for parameters.

$a=4000$units per year,$b=0.04$units per year,$\omega =2$years,$O=\$100$per order,$h=\$0.3$per unit per year,$P=\$100$per unit,$\tau =\$20$per unit,$\mu =1$, and$D=\$10$per unit, then the optimal decision variables are$T_{sp}{}^{*}=1.682$years,$S_{sp}{}^{*}=\$139.29,$$U_{sp}{}^{*}=\$23.32$and hence,$Q_{s{p}_5}{}^{*}=25.98$units,${\pi }_{r_1}\left(T_{sp}{}^{*},S_{sp}{}^{*},U_{sp}{}^{*}\right)=\$303.37$, and${\pi }_{Ds{p}_1}\left(T_{sp}{}^{*},S_{sp}{}^{*},U_{sp}{}^{*}\right)=\$500.69$.

Therefore, the retailer’s overall profit is

$$\begin{array}{c}T{P}_5\left(T_{sp}{}^{*},S_{sp}{}^{*},U_{sp}{}^{*}\right)={\pi }_{r_1}\left(T_{sp}{}^{*},S_{sp}{}^{*},U_{sp}{}^{*}\right)+{\pi }_{Ds{p}_1}\left(T_{sp}{}^{*},S_{sp}{}^{*},U_{sp}{}^{*}\right)\\ =\$303.37+\$500.69=\$804.06\end{array}$$

and the Hessian Matrix for this case is$H_5\left(T_{sp}{}^{*},S_{sp}{}^{*},U_{sp}{}^{*}\right)=\left[\begin{array}{ccc}-477.00& 15.28& 1.53\\ 15.28& -1.02& -0.07\\ 1.53& -0.07& -0.14\end{array}\right]$and the determinants are$\left|D_1\right|=-477.00<0$,$\left|D_2\right|=\left|\begin{array}{cc}-477.00& 15.28\\ 15.28& -1.02\end{array}\right|=254.87>0$, and$\left|D_3\right|=\left|\begin{array}{ccc}-477.00& 15.28& 1.53\\ 15.28& -1.02& -0.07\\ 1.53& -0.07& -0.14\end{array}\right|=-34.21<0$. Therefore, the Hessian Matrix$H_5\left(T_{sp}{}^{*},S_{sp}{}^{*},U_{sp}{}^{*}\right)$is negative definite from Proposition 1, and from Proposition 2,$T{P}_5\left(T_{sp},S_{sp},U_{sp}\right)$is strictly concave and the point$\left(T_{sp}{}^{*},S_{sp}{}^{*},U_{sp}{}^{*}\right)$is the maximum.

• Example 6. (For regular orders and the specific delivery emerges within the duration of the sale with discount).

Considering the same dataset as in Example 5, the optimal decision variables are$T_{sp}{}^{*}=1.24$years,$S_{sp}{}^{*}=\$132.48,$$U_{sp}{}^{*}=\$20.41$, and hence,$Q_{s{p}_6}{}^{*}=25.02$units,${\pi }_{r_2}\left(T_{sp}{}^{*},S_{sp}{}^{*},U_{sp}{}^{*}\right)=\$104.32$, and${\pi }_{Ds{p}_2}\left(T_{sp}{}^{*},S_{sp}{}^{*},U_{sp}{}^{*}\right)=\$302.06$.

Therefore, the retailer’s overall profit is

$$\begin{array}{c}T{P}_6\left(T_{sp}{}^{*},S_{sp}{}^{*},U_{sp}{}^{*}\right)={\pi }_{r_2}\left(T_{sp}{}^{*},S_{sp}{}^{*},U_{sp}{}^{*}\right)+{\pi }_{Ds{p}_2}\left(T_{sp}{}^{*},S_{sp}{}^{*},U_{sp}{}^{*}\right)\\ =\$104.32+\$302.06=\$406.38\end{array}$$

and the Hessian Matrix for this case is$H_6\left(T_{sp}{}^{*},S_{sp}{}^{*},U_{sp}{}^{*}\right)=\left[\begin{array}{ccc}-602.37& 14.95& 1.39\\ 14.95& -1.02& -0.06\\ 1.39& -0.06& -0.12\end{array}\right]$and the determinants are$\left|D_1\right|=-602.37<0$,$\left|D_2\right|=\left|\begin{array}{cc}-602.37& 14.95\\ 14.95& -1.02\end{array}\right|=391.49>0$, and$\left|D_3\right|=\left|\begin{array}{ccc}-602.37& 14.95& 1.39\\ 14.95& -1.02& -0.06\\ 1.39& -0.06& -0.12\end{array}\right|=-44.21<0$. Therefore, from Proposition 1,$H_6\left(T_{sp}{}^{*},S_{sp}{}^{*},U_{sp}{}^{*}\right)$is negative definite, and hence, from Proposition 2,$T{P}_6\left(T_{sp},S_{sp},U_{sp}\right)$is strictly concave and the point$\left(T_{sp}{}^{*},S_{sp}{}^{*},U_{sp}{}^{*}\right)$is the maximum.

• Example 7. (For the special case of regular order only, and the retailer doesn’t need to order any specific delivery).

By considering the following parameters, for a given inventory system:

$a=4000$units per year,$b=0.04$units per year,$\omega =2$years,$O=\$100$per order,$h=\$0.3$per unit per year,$P=\$100$per unit,$\tau =\$20$per unit, and$\mu =1$, then prior to the price rise, the optimal decision variables are:

$T^{*}=0.571$years,$S^{*}=\$134.33,$ $U^{*}=\$13.22,$optimal order quantity$Q^{*}=10.68$units, and net profit is$\pi \left(T^{*},S^{*},U^{*}\right)=\$275.63$and the Hessian Matrix for this case is$H_{sp1}\left(T^{*},S^{*},U^{*}\right)=\left[\begin{array}{ccc}-1086.33& 12.26& 1.99\\ 12.26& -0.74& -0.04\\ 1.99& -0.04& -0.14\end{array}\right]$and the determinants are$\left|D_1\right|=-1086.33<0$,$\left|D_2\right|=\left|\begin{array}{cc}-1086.33& 12.26\\ 12.26& -0.74\end{array}\right|=656.04>0$, and$\left|D_3\right|=\left|\begin{array}{ccc}-1086.33& 12.26& 1.99\\ 12.26& -0.74& -0.04\\ 1.99& -0.04& -0.14\end{array}\right|=-89.98<0$. Therefore, from Proposition 1,$H_{sp1}\left(T^{*},S^{*},U^{*}\right)$is negative definite and hence, from Proposition 2,$\pi \left(T,S,U\right)$is concave function and the point$\left(T^{*},S^{*},U^{*}\right)$is the maximum, and after the price increase is:$T_{\tau }{}^{*}=0.914\mathrm{years},S_{\tau }{}^{*}=\$163.42,U_{\tau }{}^{*}=\$10.56,Q_{\tau }{}^{*}=5.38\mathrm{units},{\pi }_{\tau }\left(T_{\tau }{}^{*},p_{\tau }{}^{*},u_{\tau }{}^{*}\right)=\$24.97$and the Hessian Matrix is$H_{sp2}\left(T^{*},S^{*},U^{*}\right)=\left[\begin{array}{ccc}-269.91& 4.79& 1.396\\ 4.79& -0.23& -0.04\\ 1.36& -0.04& -0.18\end{array}\right]$and the determinants are$\left|D_1\right|=-269.91<0$,$\left|D_2\right|=\left|\begin{array}{cc}-269.91& 4.79\\ 4.79& -0.23\end{array}\right|=39.64>0$, and$\left|D_3\right|=\left|\begin{array}{ccc}-269.91& 4.79& 1.396\\ 4.79& -0.23& -0.04\\ 1.36& -0.04& -0.18\end{array}\right|=-6.61<0$. Therefore, from Proposition 1,$H_{sp2}\left(T^{*},S^{*},U^{*}\right)$is negative definite, and hence, from Proposition 2,${\pi }_{\tau }\left(T_{\tau },p_{\tau },u_{\tau }\right)$is a concave function and the point$\left(T_{\tau }{}^{*},p_{\tau }{}^{*},u_{\tau }{}^{*}\right)$is the maximum. Therefore, the retailer’s overall profit is

$$TP\left(T^{*},T_{\tau }{}^{*},S^{*},S_{\tau }{}^{*},U^{*},U_{\tau }{}^{*}\right)=\pi \left(T^{*},S^{*},U^{*}\right)+{\pi }_{\tau }\left(T_{\tau }{}^{*},S_{\tau }{}^{*},U_{\tau }{}^{*}\right)=\$275.63+\$24.97=\$300.6$$

A summary of all the cases is shown in Figure 4.

As per the above examples and summary chart (Figure 4), it is observed that if the retailer chooses the option of trade credit, then the maximum profit is USD 609.58, which occurs in Example 2 (comprising the trade credit option for situation 2 and regular order with a specific delivery that matches with the reordering time), whereas if the retailer chooses the option of a discount on a specific delivery, then the maximum profit of USD 804.06 occurs in Example 5 (comprising a discount option and regular order with a specific delivery that matches with the reordering time).

Therefore, for maximum profit, the retailer should choose the option of a discount on a specific delivery provided by the supplier and place a specific delivery when it matches its regular reordering time.

6.2. Comparison of Findings of This Research with Previous Research

Under constant demand, the model of Ouyang et al. [7] discussed the same two circumstances for specific delivery: (I) when the time of the specific delivery matches with the reordering time of the retailer and (II) when the time of the specific delivery emerges within the duration of the sale. The findings of the Ouyang et al. [1] model gave the best strategy for total cost saving between the regular order and specific delivery. The total cost saving for circumstance 1 was $1222.12 and for circumstance 2 was $2134.85. Then, Shah et al. [2] expanded the Ouyang et al. [1] model by considering the quadratic demand for deteriorating products and the results of total cost saving for circumstance 1 was $1763.38 and for circumstance 2 was $846.67. Here, this study considers the retailer’s pricing policy with price-sensitive demand for products with expiry dates and preservation technology investment under different payment policies. The findings of this research suggest that the maximum profit for the retailer is the sum of regular orders and the specific delivery. The total profit under the discount payment policy is $804.06 and under the trade credit policy is $609.58.

6.3. Sensitivity Analysis

In Example 2 and Example 5, the sensitivity analysis is analyzed by altering one parameter as −20 percent, −10 percent, 10 percent, and 20 percent, and the consequences of the sensitivity analysis are shown in

Table 2. Sensitivity analysis (Example 2).

Parameters	Values	${\mathit{T}}_{\mathit{s}\mathit{p}}\left(\mathbf{years}\right)$	${\mathit{S}}_{\mathit{s}\mathit{p}}(\$)$	${\mathit{U}}_{\mathit{s}\mathit{p}}(\$)$	${\mathit{Q}}_{\mathit{s}\mathit{p}}\left(\mathbf{units}\right)$	${\mathit{\pi }}_{\mathit{t}{\mathit{r}}_2}(\$)$	${\mathit{\pi }}_{\mathit{s}{\mathit{p}}_1}(\$)$	$\mathit{T}{\mathit{P}}_2(\$)$
$a$	3200	1.359	147.26	15.80	12.22	217.12	179.20	396.32
	3600	1.444	148.56	17.11	13.88	283.93	216.60	500.53
	4400	1.604	151.01	19.56	17.08	434.08	288.82	722.89
	4800	1.680	152.18	20.71	18.63	516.65	323.39	840.04
$b$	0.032	2.993	179.48	42.68	39.24	2865.16	970.87	3836.03
	0.036	2.538	169.04	28.15	24.44	1175.86	496.01	1617.87
	0.044	1.027	139.72	12.73	8.91	96.73	86.56	183.28
$\omega$	1.6	1.481	149.25	20.06	15.39	351.13	248.54	599.67
	1.8	1.505	149.55	19.16	15.45	353.90	251.01	604.91
	2.2	1.545	150.03	17.65	15.54	358.66	255.11	613.77
	2.4	1.561	150.24	17.01	15.57	360.73	256.84	617.57
	80	1.670	152.20	18.74	15.55	440.15	267.81	707.96
$O$	90	1.592	150.90	18.54	15.52	395.46	261.15	656.61
	110	1.469	148.86	18.19	15.48	321.83	244.31	566.14
	120	1.419	148.04	18.04	15.45	290.94	234.79	525.73
	0.24	1.974	151.04	21.64	19.15	429.27	326.75	756.01
$h$	0.27	1.729	150.45	19.81	17.14	389.04	286.64	675.68
	0.33	1.358	149.17	17.18	14.13	329.37	224.76	554.13
	0.36	1.219	148.56	16.18	12.98	306.51	200.31	506.82
	80	2.846	141.75	35.58	40.16	1809.46	779.93	2589.38
$P$	90	2.146	146.19	24.91	25.27	840.97	466.19	1307.16
	110	1.102	154.98	13.69	9.09	128.62	108.81	237.43
	0.8	1.483	149.33	20.19	15.38	349.87	247.72	597.60
$\mu$	0.9	1.506	149.58	19.21	15.44	353.36	250.67	604.03
	0.11	1.543	150.00	17.62	15.54	359.07	255.37	614.43
	0.12	1.559	150.18	16.97	15.58	361.44	257.29	618.73
	0.08	1.526	149.80	18.36	15.50	343.16	253.18	596.35
$I_g$	0.09	1.526	149.80	18.36	15.50	349.67	253.18	602.85
	0.11	1.526	149.80	18.36	15.50	363.35	253.18	616.53
	0.12	1.526	149.80	18.36	15.50	370.54	253.18	623.72
	0.36	1.526	149.80	18.36	15.50	330.68	253.18	583.86
$M$	0.405	1.526	149.80	18.36	15.50	343.42	253.18	596.61
	0.495	1.526	149.80	18.36	15.50	369.60	253.18	622.78
	0.54	1.526	149.80	18.36	15.50	383.04	253.18	636.22

and

Table 3. Sensitivity analysis (Example 5).

Parameters	Values	${\mathit{T}}_{\mathit{s}\mathit{p}}\left(\mathbf{years}\right)$	${\mathit{S}}_{\mathit{s}\mathit{p}}(\$)$	${\mathit{U}}_{\mathit{s}\mathit{p}}(\$)$	${\mathit{Q}}_{\mathit{s}\mathit{p}}\left(\mathbf{units}\right)$	${\mathit{\pi }}_{{\mathit{r}}_1}(\$)$	${\mathit{\pi }}_{\mathit{D}\mathit{s}{\mathit{p}}_1}(\$)$	$\mathit{T}{\mathit{P}}_5(\$)$
$a$	3200	1.552	137.56	20.23	20.55	183.41	374.75	558.17
	3600	1.619	138.46	21.81	23.27	240.86	437.96	678.82
	4400	1.741	140.07	24.77	28.65	370.26	562.74	933.00
	4800	1.796	140.81	26.17	31.31	441.62	624.52	1066.13
$b$	0.032	2.978	163.88	51.18	64.05	2605.04	1713.23	4317.27
	0.036	2.385	151.94	33.26	40.27	964.90	917.03	1881.93
	0.044	1.250	131.02	16.91	15.90	76.49	235.27	311.76
$\omega$	1.6	1.639	138.82	25.58	25.81	297.94	493.39	791.33
	1.8	1.662	139.07	24.38	25.90	300.81	497.29	798.10
	2.2	1.700	139.48	22.39	26.04	305.69	503.70	809.39
	2.4	1.716	139.65	21.55	26.09	307.80	506.38	814.17
	80	1.783	140.78	23.70	26.05	375.65	516.95	892.60
$O$	90	1.730	139.99	23.50	26.02	337.11	509.24	846.36
	110	1.641	138.68	23.16	25.95	273.56	491.52	765.08
	120	1.603	138.13	23.00	25.91	247.05	481.88	728.93
	0.24	2.124	139.83	27.52	32.18	378.52	632.31	1010.84
$h$	0.27	1.884	139.61	25.17	28.75	337.23	560.11	897.34
	0.33	1.513	138.94	21.81	23.68	275.16	450.89	726.05
	0.36	1.371	138.58	20.56	21.74	251.22	408.53	659.75
	80	2.771	125.80	44.07	73.62	1609.03	1586.25	3195.28
$P$	90	2.197	132.99	31.40	43.69	738.41	905.98	1644.40
	110	1.292	145.96	17.60	15.27	103.44	253.67	357.11
	0.8	1.645	138.93	25.71	25.80	296.74	492.49	789.24
$\mu$	0.9	1.665	139.12	24.42	25.90	300.30	496.91	797.21
	0.11	1.698	139.44	22.36	26.04	306.07	503.98	810.05
	0.12	1.711	139.58	21.51	26.10	308.46	506.87	815.34

for each parameter.

From Table 2 and Table 3, we find the following observations:

• The scaling of demand $\left(a\right)$ rapidly increases cycle time $\left(T_{sp}\right)$ while the price elasticity constraints $\left(b\right)$, holding cost $\left(h\right)$, purchasing cost $\left(P\right)$, and ordering cost $\left(O\right)$ rapidly decrease cycle time $\left(T_{sp}\right)$. However, $\left(\xi \right)$ and $\left(\mu \right)$ are gradually increasing $\left(T_{sp}\right)$.
• The scaling of demand $\left(a\right)$, $\left(P\right)$, $\left(\xi \right)$, and $\left(\mu \right)$ gradually increase the sales price $\left(S_{sp}\right)$ while the holding cost $\left(h\right)$ and ordering cost $\left(O\right)$ decrease the sales price $\left(S_{sp}\right)$. However, the price elasticity constraint $\left(b\right)$ rapidly decreases the sales price $\left(S_{sp}\right)$.
• The scaling of demand $\left(a\right)$ gradually increases preservation technology capital $\left(U_{sp}\right)$ while the holding cost $\left(h\right)$, ordering cost $\left(O\right)$, $\left(\xi \right)$, and $\left(\mu \right)$ gradually decrease preservation technology capital $\left(U_{sp}\right)$. However, price elasticity constraint $\left(b\right)$ and purchasing cost $\left(P\right)$ rapidly decrease preservation technology capital $\left(U_{sp}\right)$.
• The scaling of demand $\left(a\right)$, $\left(\xi \right)$, and $\left(\mu \right)$ gradually increase the specific delivery units $\left(Q_{sp}\right)$ while the holding cost $\left(h\right)$ and ordering cost $\left(O\right)$ gradually decrease the specific delivery units $\left(Q_{sp}\right)$. However, price elasticity constraints $\left(b\right)$ and purchasing costs $\left(P\right)$ rapidly decrease the specific delivery units $\left(Q_{sp}\right)$.
• The scaling of demand $\left(a\right)$ rapidly increases the profit of regular orders with situation 2 $\left({\pi }_{t{r}_2}\right)$ while the price elasticity constraints $\left(b\right)$, purchasing cost $\left(P\right)$, holding cost $\left(h\right)$, and ordering cost $\left(O\right)$ rapidly decrease the profit of regular orders with situation 2 $\left({\pi }_{t{r}_2}\right)$. However, interest gain $\left(I_g\right)$, credit period $\left(M\right)$, $\left(\xi \right)$, and $\left(\mu \right)$ gradually increase the profit of regular orders with situation 2 $\left({\pi }_{t{r}_2}\right)$.
• The scaling of demand $\left(a\right)$ rapidly increases the profit of a special order without discount $\left({\pi }_{s{p}_1}\right)$ while the price elasticity constant $\left(b\right)$, holding cost $\left(h\right)$, and purchasing cost $\left(P\right)$ rapidly decrease the profit of a specific delivery without a discount $\left({\pi }_{s{p}_1}\right)$. However, $\left(\xi \right)$ and $\left(\mu \right)$ gradually increase the profit of a specific delivery without a discount $\left({\pi }_{s{p}_1}\right)$ whereas the ordering cost $\left(O\right)$ gradually decreases the profit of a specific delivery without a discount $\left({\pi }_{s{p}_1}\right)$.
• The scaling of demand $\left(a\right)$ rapidly increases the profit of regular orders $\left({\pi }_{r_1}\right)$ while the price elasticity constraints $\left(b\right)$, purchasing cost $\left(P\right)$, holding cost $\left(h\right)$, and ordering cost $\left(O\right)$ rapidly decrease the profit of regular orders $\left({\pi }_{r_1}\right)$. However, $\left(\xi \right)$ and $\left(\mu \right)$ gradually increase the profit of regular orders $\left({\pi }_{r_1}\right)$.
• The scaling of demand $\left(a\right)$ rapidly increases the profit of a special order with discounts $\left({\pi }_{Ds{p}_1}\right)$ while the price elasticity constant $\left(b\right)$, holding cost $\left(h\right)$, and purchasing cost $\left(P\right)$ rapidly decrease the profit of specific delivery with discounts $\left({\pi }_{Ds{p}_1}\right)$. However, $\left(\xi \right)$ and $\left(\mu \right)$ gradually increase the profit of a specific delivery with a discount $\left({\pi }_{Ds{p}_1}\right)$ whereas the ordering cost $\left(O\right)$ gradually decreases the profit of a specific delivery with a discount $\left({\pi }_{Ds{p}_1}\right)$.
• The scaling of demand $\left(a\right)$ rapidly increases the overall profit with trade credit $\left(T{P}_2\right)$ and overall profit with a discount $\left(T{P}_5\right)$ while the price elasticity constant $\left(b\right)$, purchasing cost $\left(P\right)$, holding cost $\left(h\right)$, and ordering cost $\left(O\right)$ decrease the overall profit with trade credit $\left(T{P}_2\right)$ and overall profit with a discount $\left(T{P}_5\right)$. However, $\left(\xi \right)$ and $\left(\mu \right)$ gradually increase the overall profit with trade credit $\left(T{P}_2\right)$ and overall profit with a discount $\left(T{P}_5\right)$. Moreover, interest gain $\left(I_g\right)$ and credit period $\left(M\right)$ gradually increase the overall profit with trade credit $\left(T{P}_2\right)$.

In summary of the above observations, there is a positive effect of a parameter $\left(a\right)$ and a negative effect of a parameter $\left(b\right)$ on cycle time, sales price, preservation technology capital, order quantity, profit from regular orders and special orders, and hence, on the overall profit function.

In

Table 4. Effect of the parameter $D$ in Example 5.

$\mathit{D}$	${\mathit{T}}_{\mathit{s}\mathit{p}}\left(\mathbf{years}\right)$	${\mathit{S}}_{\mathit{s}\mathit{p}}(\$)$	${\mathit{U}}_{\mathit{s}\mathit{p}}(\$)$	${\mathit{Q}}_{\mathit{s}\mathit{p}}\left(\mathbf{units}\right)$	${\mathit{\pi }}_{{\mathit{r}}_1}(\$)$	${\mathit{\pi }}_{\mathit{D}\mathit{s}{\mathit{p}}_1}(\$)$	$\mathit{T}{\mathit{P}}_5(\$)$
8	1.647	141.38	22.22	23.41	302.50	439.95	742.45
9	1.665	140.33	22.77	24.66	302.93	469.49	772.42
10	1.682	139.29	23.32	25.98	303.37	500.69	804.07
11	1.700	138.25	23.89	27.37	303.82	533.65	837.47
12	1.719	137.22	24.48	28.83	304.29	568.45	872.74

, the effect of the parameter $D$ in Example 5 is shown. As the discount, $D$ increases, the specific delivery units $Q_{sp}$, cycle time $T_{sp}$, and preservation technology capital $U_{sp}$ gradually increase while the sales price $S_{sp}$ of the product gradually decreases. Moreover, as the discount $D$ increases, the profit of regular orders ${\pi }_{r_1}$ gradually increases while the profit of the specific delivery with discounts ${\pi }_{Ds{p}_1}$ rapidly increases. Hence, overall profit $T{P}_5$ rapidly increased.

A simple economic explanation is that the retailer will place a specific delivery with a greater amount if the discount is higher, resulting in a higher profit on the regular order as well as on the specific delivery, which implies a higher net profit for the retailer.

In Table 4, the effect of the parameter $D$ in Example 5 is shown. As the discount $D$ increases, the $\left(Q_{sp}\right)$, $\left(T_{sp}\right)$, and $\left(U_{sp}\right)$ gradually increase while the sales price $\left(S_{sp}\right)$ of the product gradually decreases. Moreover, as the discount $D$ increases, the profit of regular orders $\left({\pi }_{r_1}\right)$ gradually increases while the profit of the specific delivery with discounts $\left({\pi }_{Ds{p}_1}\right)$ rapidly increases. Hence, overall profit $\left(T{P}_5\right)$ rapidly increases.

Economically, this can be simply explained that the retailer places a greater amount for the specific delivery if the discount is higher, resulting in a higher profit on the regular order as well as on the specific delivery, which implies a higher net profit for the retailer.

In

Table 5. Effect of the parameter $\tau$ in Example 2 and Example 5.

$\tau$	${\mathit{T}}_{\mathit{s}\mathit{p}}$(years)	${\mathit{S}}_{\mathit{s}\mathit{p}}$($)	${\mathit{U}}_{\mathit{s}\mathit{p}}$($)	${\mathit{Q}}_{\mathit{s}\mathit{p}}$(units)	${\mathit{\pi }}_{\mathit{t}{\mathit{r}}_2}$($)	${\mathit{\pi }}_{\mathit{s}{\mathit{p}}_1}$($)	$\mathit{T}{\mathit{P}}_2$($)
18	1.610	151.19	18.59	15.52	375.13	250.48	625.62
19	1.565	150.46	18.47	15.51	365.14	252.06	617.20
20	1.526	149.80	18.36	15.50	356.40	253.18	609.58
21	1.490	149.22	18.26	15.49	348.72	253.95	602.68
22	1.458	148.69	18.16	15.48	341.98	254.45	596.43
$\tau$	${\mathit{T}}_{\mathit{s}\mathit{p}}$(years)	${\mathit{S}}_{\mathit{s}\mathit{p}}$($)	${\mathit{U}}_{\mathit{s}\mathit{p}}$($)	${\mathit{Q}}_{\mathit{s}\mathit{p}}$(units)	${\mathit{\pi }}_{{\mathit{r}}_1}$($)	${\mathit{\pi }}_{\mathit{D}\mathit{s}{\mathit{p}}_1}$($)	$\mathit{T}{\mathit{P}}_5$($)
18	1.742	140.17	23.55	26.02	321.55	498.78	820.33
19	1.711	139.71	23.43	26.00	311.95	499.89	811.84
20	1.682	139.29	23.32	25.98	303.37	500.69	804.07
21	1.656	138.91	23.22	25.96	295.70	501.26	796.96
22	1.633	138.57	23.13	25.94	288.83	501.62	790.45

, the effect of the parameter $\tau$ is shown, in which one can observe that there was a negative impact of price increase on the net profit of regular orders ${\pi }_{t{r}_2}$ and an optimistic outcome on the profit of the specific delivery with and without discount ${\pi }_{s{p}_1}\mathrm{and}{\pi }_{Ds{p}_1}$. In addition, as the parameter $\tau$ increases, $T_{sp}$, $S_{sp}$, $Q_{sp}$, and $U_{sp}$ decrease.

Economically, this can be simply explained that the retailer can order smaller specific delivery units as the price rises; thus, the cycle time, expenditure on preservation technology, and product sales price decrease. In addition, a large influence of a price rise on the regular order exists; thus, if the retailer wants to get more benefits, then with either a trade credit option or with a discount option, the retailer can choose a specific delivery.

6.4. Managerial Implications

From the above insights, the following observations can be noted.

• When the ordering and holding cost of a product increase, the sales price, cycle time, specific delivery quantity, and total profit decrease. It is advised that the retailer should order a maximum of units at the beginning of each cycle with specific delivery to reduce the cost of ordering.
• When the initial demand rate is high, the retailer should purchase the maximum number of units from the supplier as the higher initial demand rate allows the retailer to raise the product’s price and hence, generate more profit.
• When the product’s price elasticity rose, the cycle time and specific delivery quantity decrease significantly, indicating less overall revenue for the retailer. Furthermore, it raises the product price, implying that consumers are less likely to be interested in acquiring the product.
• When the maximum lifetime of a product and preservation parameter surges, the overall profit rises; implying that if the expiration date is longer, then the retailer should place more units to increase the investment in preserving the quality of items as customers are more likely to purchase the good quality products which have a long lifespan.
• When the product purchasing cost rose, the overall profit dropped significantly, implying that if the cost of purchasing is high, then the retailer should cancel the order since buyers are unable to afford items with higher purchasing costs.
• As both the credit period and the payment discount enhance the total profit, the retailer should choose at least one of the supplier policies to boost revenue before raising the price.
• Since an increase in the product’s price decreases the total profit, it is recommended that the retailer should purchase more units before the hike in price and choose a specific delivery quantity as per the payment policy discount to generate a higher profit.

7. Conclusions

This study dealt with the announcement of the future price increase by the supplier on the retailer’s reordering approach. The price-sensitive demand was debated in this research. In addition, the product deteriorated over time and was dependent on the expiry dates. Furthermore, to sustain the deteriorating inventory, retailers capitalized some money on preservation technology. In addition, the supplier provided two options to the retailer before the price rise: (1) the retailer could opt for the option of trade credit policy on regular orders with the specific delivery, or (2) it could choose the discount in payment policy on the specific delivery with its regular order. Furthermore, two possible scenarios for selecting the specific delivery time were discussed: (I) the specific delivery time matched with the reordering time of the retailer, or (II) the specific delivery time emerged within the duration of the sale. In this paper, the following important results were obtained: (i) the future price rise played an important role and had a negative impact on regular orders, and therefore, the retailer should order as many units as possible to obtain the maximum profit before the price rise; (ii) because demand was dependent on the sales price, which decreased demand when the price of the product increased, the retailer should adopt a specific delivery that matched with the reordering time to get the maximum profit before the price increased; (iii) trade credit period policy was a recent, faithful method in the business world, and it had a substantial impact on the retailer’s regular ordering policies before the price rise, and (iv) discounts on specific deliveries had a huge impact on the retailer’s profit; hence, if the discount was higher, the retailer should order many units to obtain the maximum profit. Our model provided a practical approach for electronic products, vegetables, fruits, grains, medicines, and other products that deteriorated with time. The key aim of this model was to optimize the objective function, which was the sum of its regular order and the specific delivery. Several cases were deliberated, and the results were authorized using numerical examples. In addition, a special case was discussed with a numerical illustration in which the retailer did not want to opt for any specific delivery. Furthermore, the algorithm was established to obtain the optimality of the objective function. Finally, an analysis of sensitivity was analyzed to study the execution of significant parameters. Hence, from the tables of sensitivity, we found that before the price rise, the retailer should opt for the discount option of payment on the specific delivery and choose the specific delivery time that matches with its regular reordering time to achieve the maximum profit because the price increase of a product has a negative influence on the overall profit for a retailer.

Existing studies can be further extended by including advance payments and other trade credit options. The price-sensitive demand can be changed by fuzzy or stochastic demand. In addition, the present study can further be generalized by allowing shortages [46], inflation, technology sharing [47], economic analysis [48], and diverse demand types, such as advertisement dependence demand and quadratic demand.