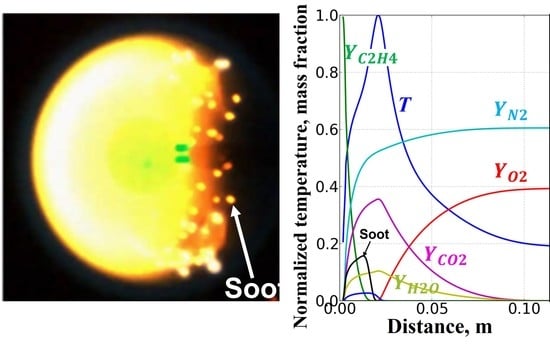
Soot Formation in Spherical Diffusion Flames
Abstract
1. Introduction
2. Materials and Methods
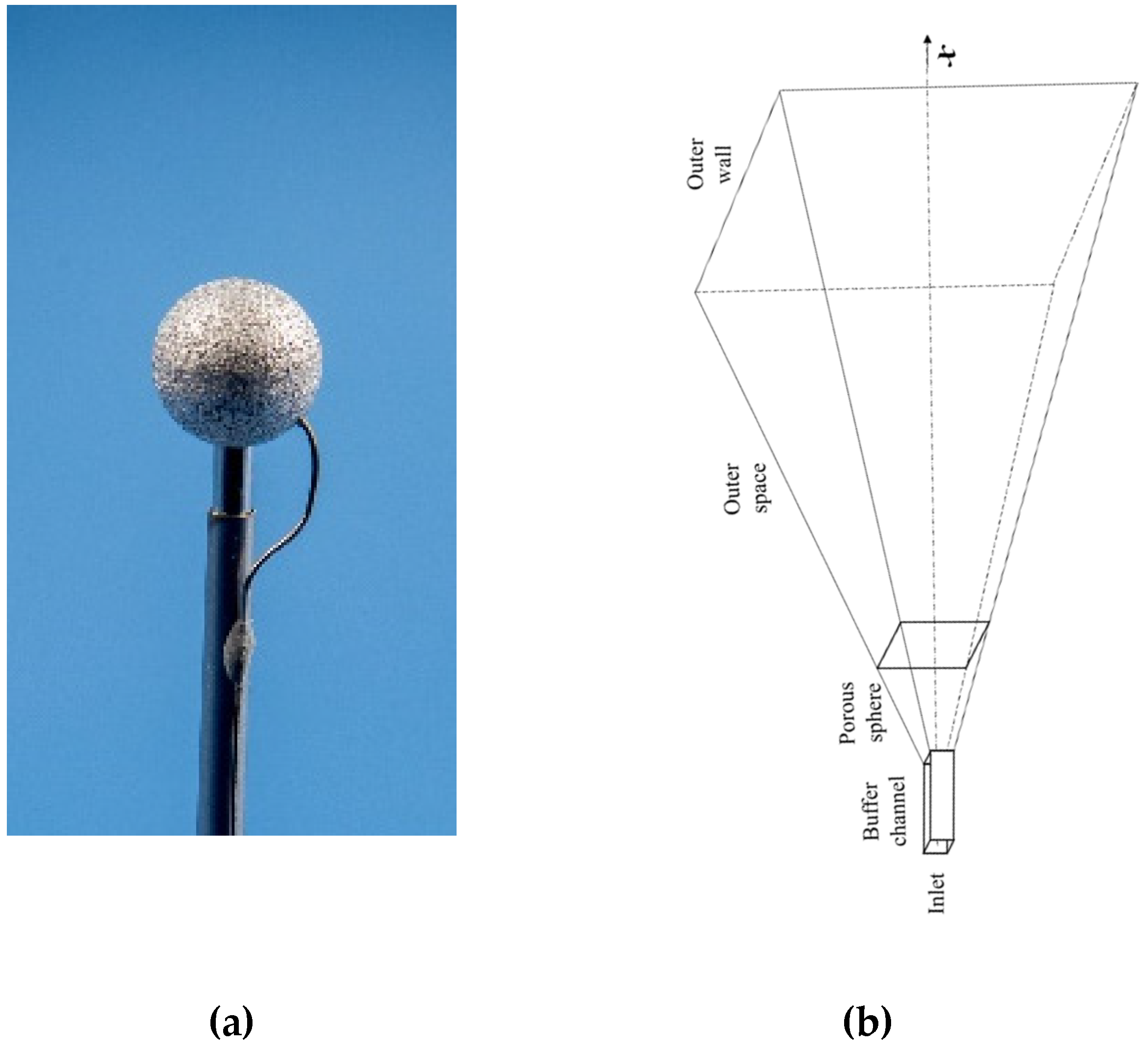
2.1. Statement of the Problem
- 1.
- The gas supply tube does not affect the evolution of the SDF.
- 2.
- All processes are spherically symmetric.
- 3.
- The porous medium in the flow region can be modeled by flow resistance according to the Darcy law and heat exchange with the fluid according to the Newton law, i.e., the porous medium can be represented by added momentum and heat sources, and , respectively, in the governing equations. In addition, since the porous medium reduces the volume accessible for fluid, the local flow velocity, , and superficial velocity inside the porous medium, , are coupled by the undirected porosity value : .
- 4.
- The structural and thermophysical parameters of the PS material are constant.
- 5.
- PS absorbs thermal radiation of soot, H2O, CO2, N2 and O2; thermal radiation of PS is negligible.
- 6.
- Catalytic and gas-phase reactions in the PS are absent.
- 7.
- The gas flow is laminar.
- 8.
- The gas mixture obeys the ideal-gas thermal and caloric equations of state; gas thermophysical properties are variable.
- 9.
- The effect of thermodiffusion is negligible.
- 10.
- Soot is an equivalent gas with the molecular mass of atomic carbon, when simulating soot reactions.
- 11.
- Soot particles are the clusters of 20–25 carbon atoms, have the corresponding constant size, and do not coagulate.
- 12.
- The radiation heat flux is caused solely by soot, H2O, CO2, N2 and O2 emittance.
- 13.
- The outer wall of the chamber is impermeable, isothermal, and non-catalytic.
2.2. Numerical Solution
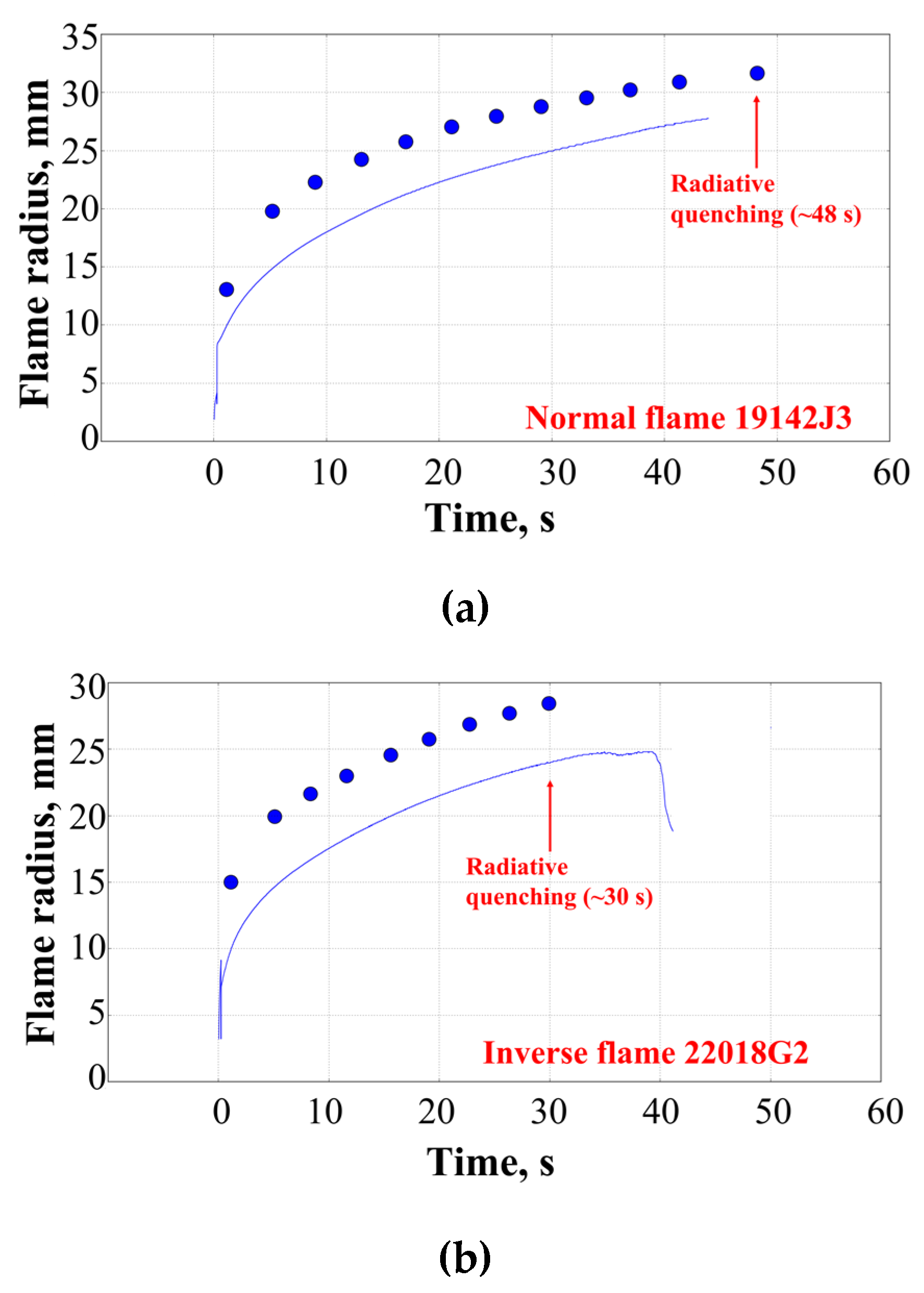
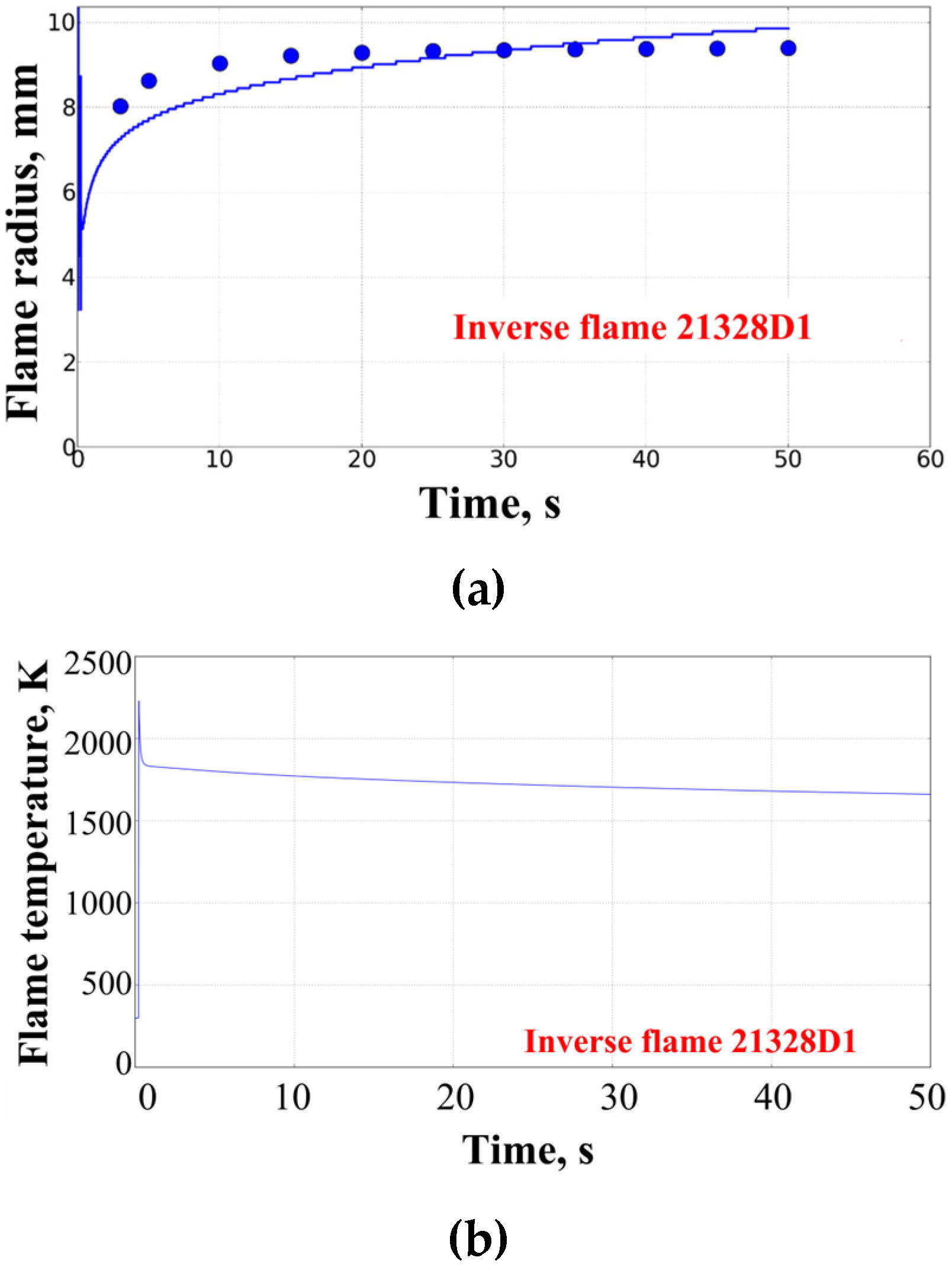
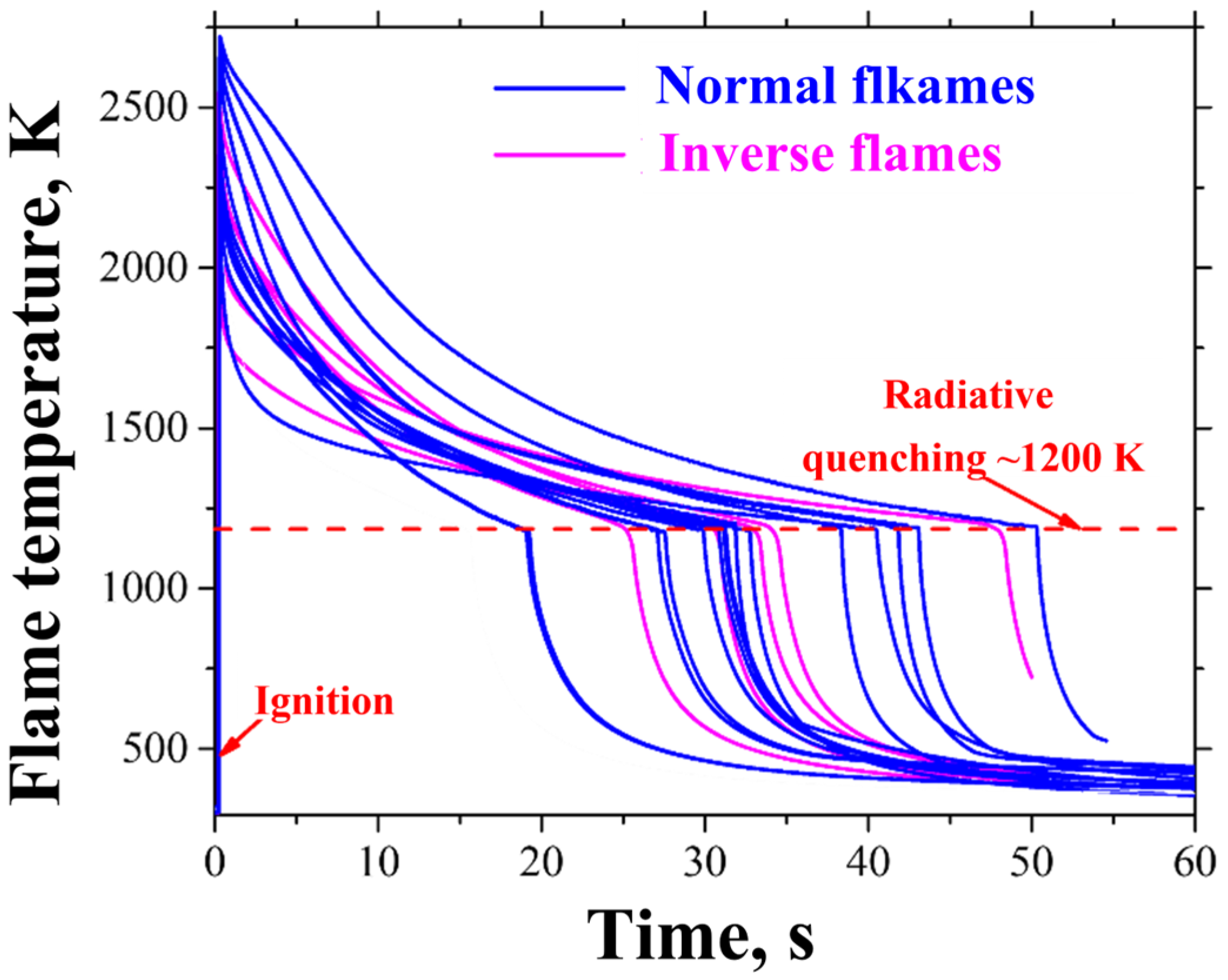
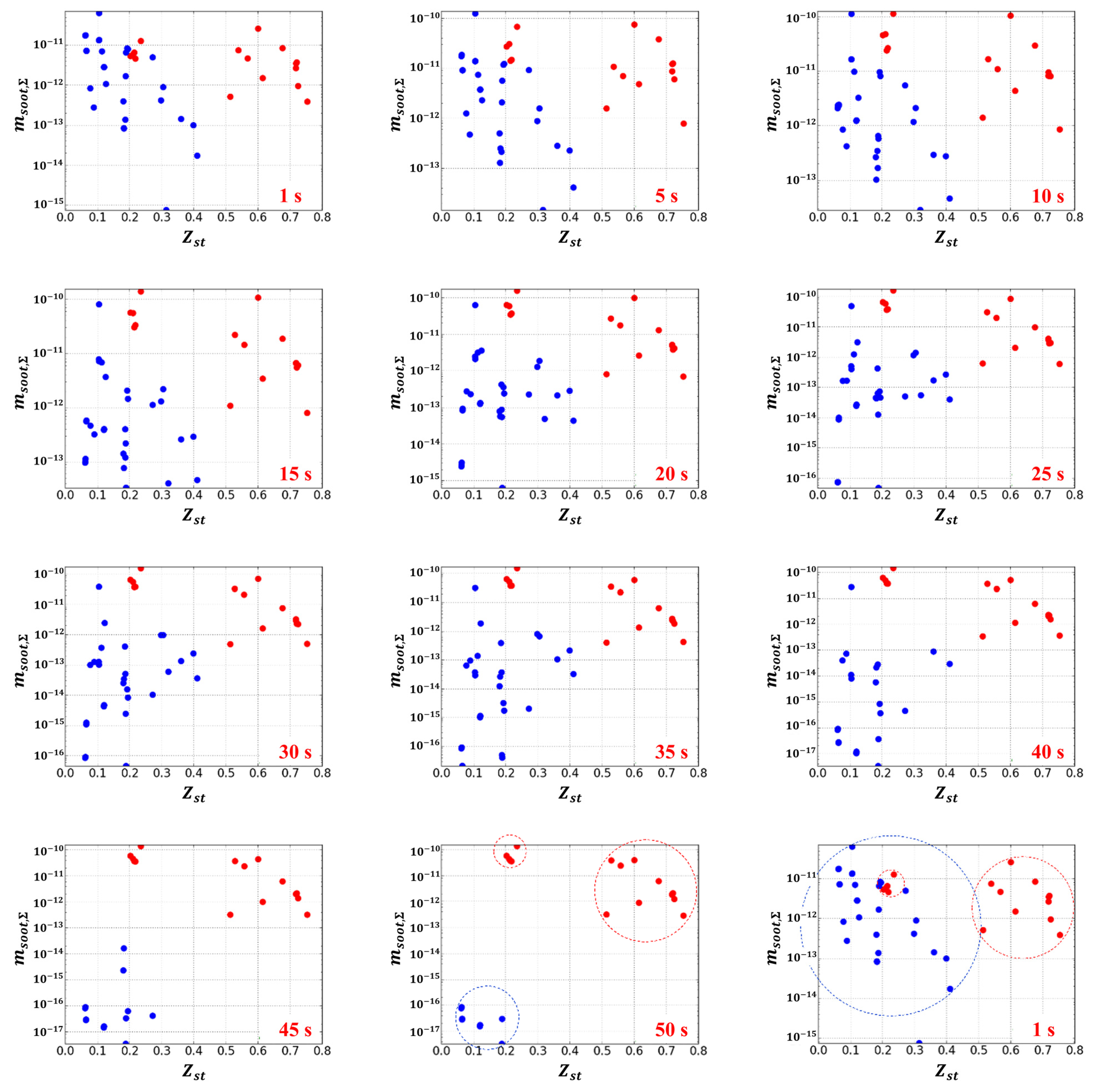
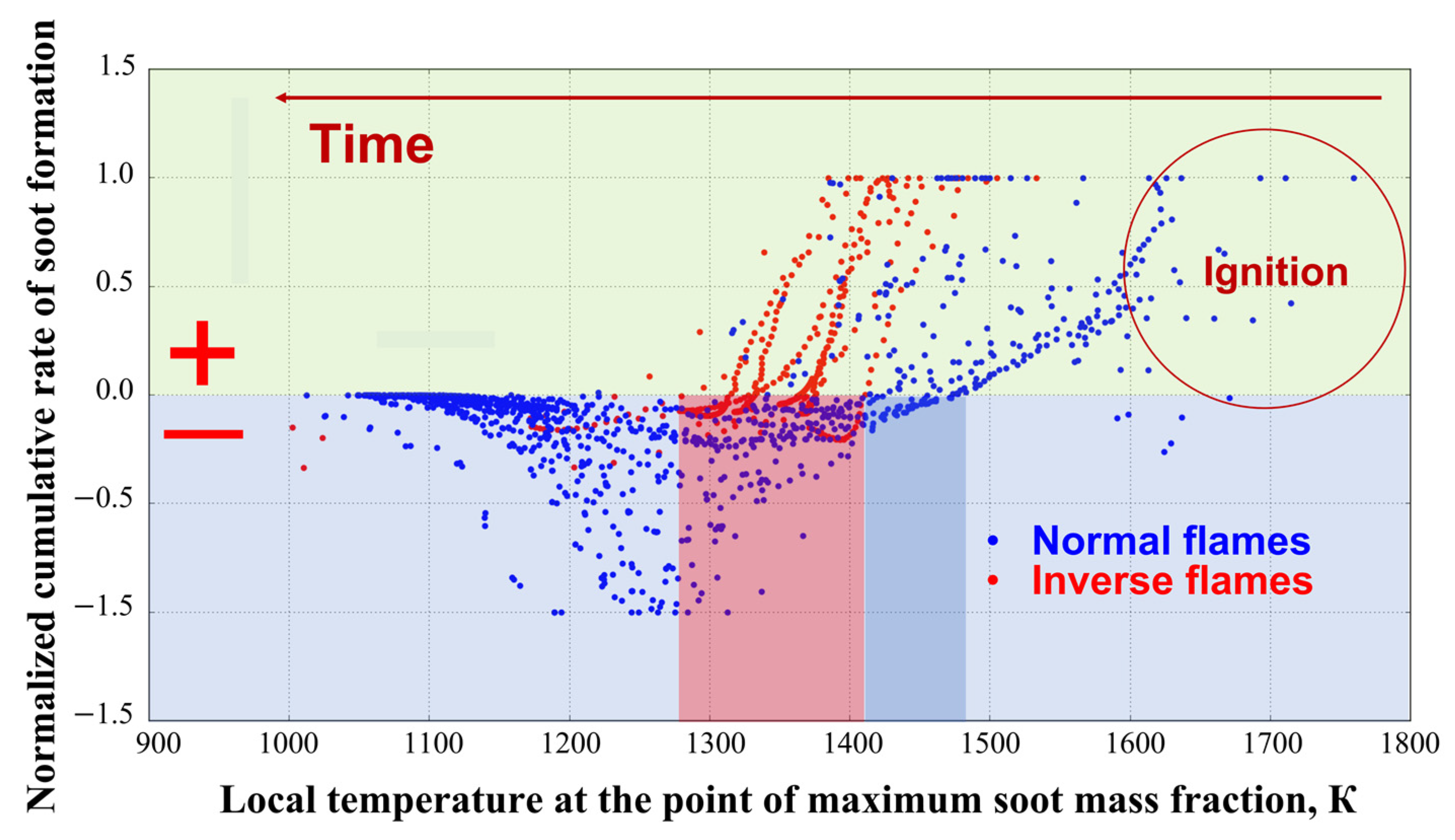
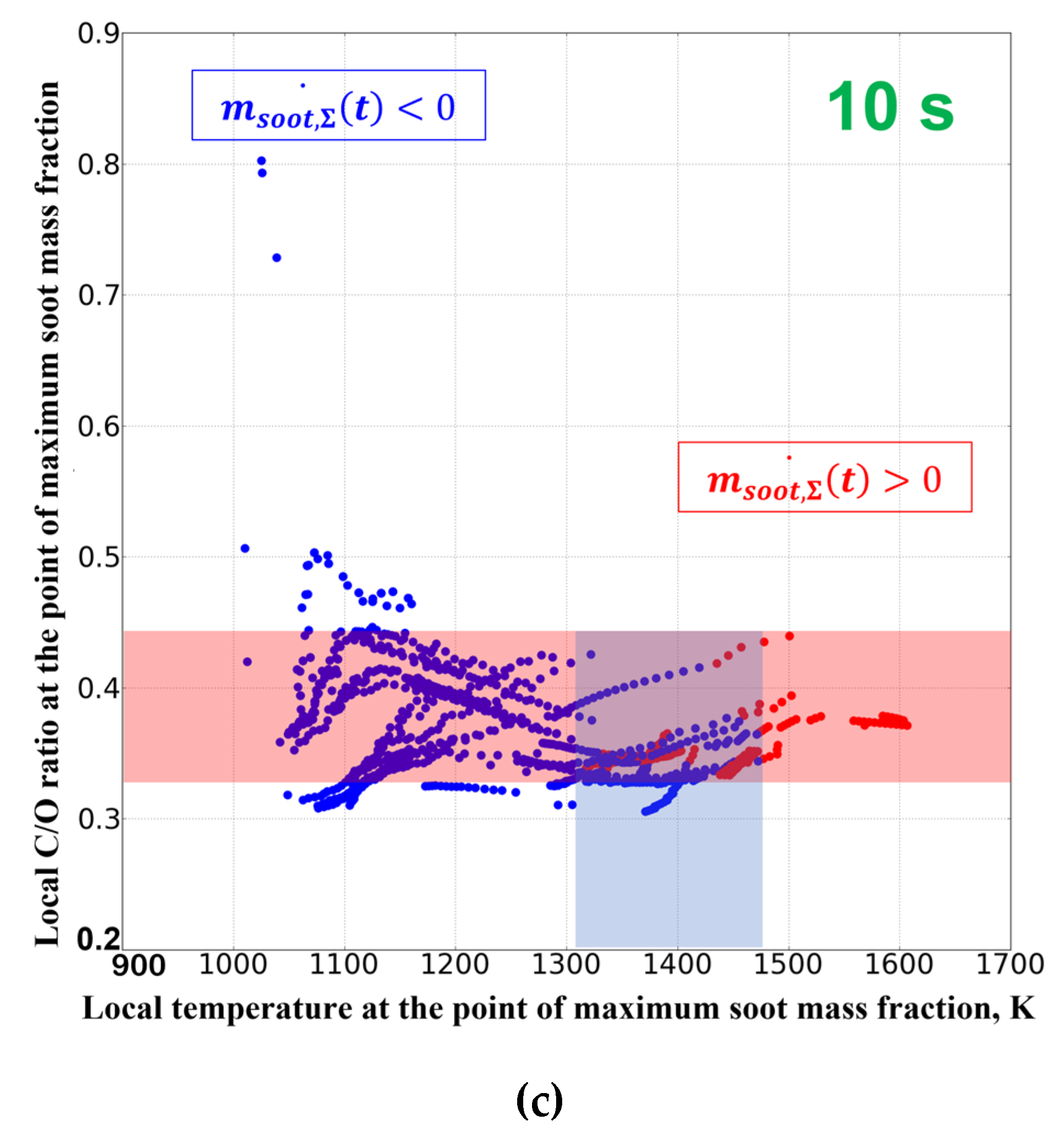
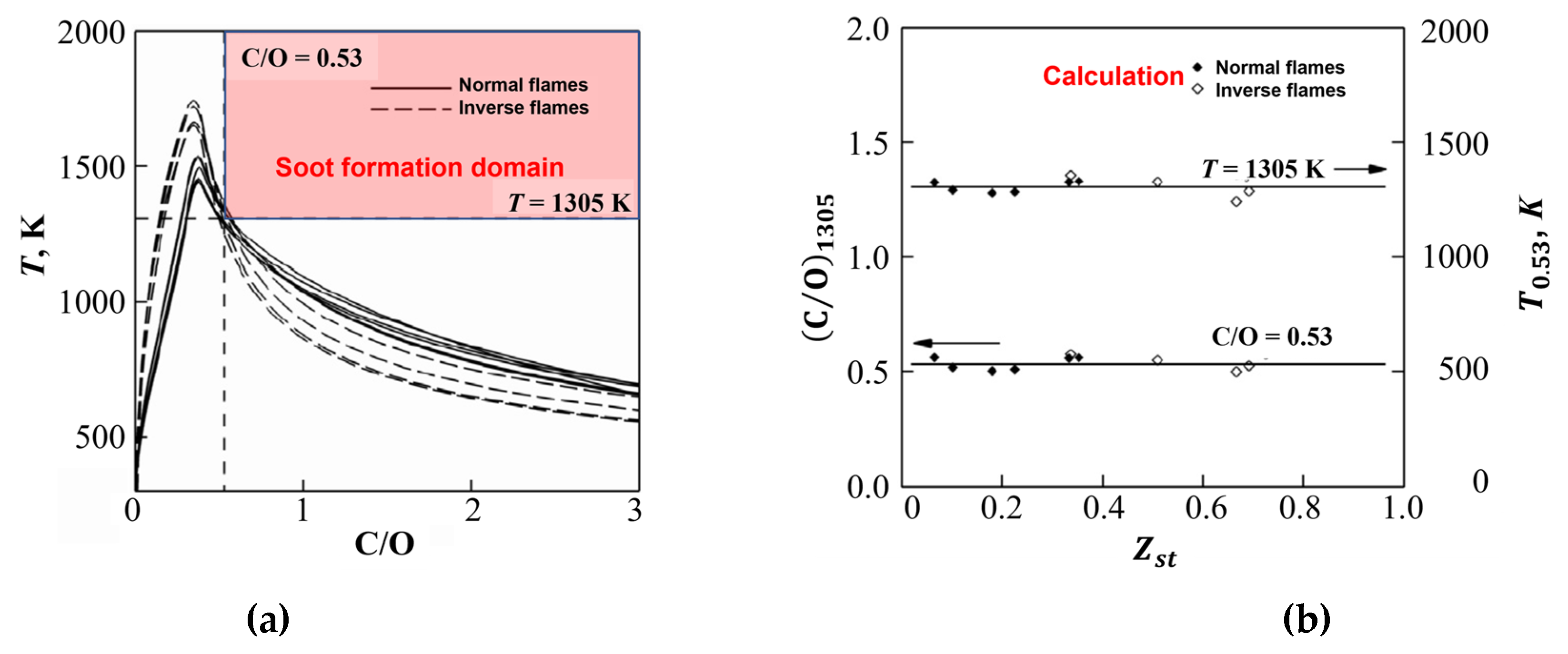
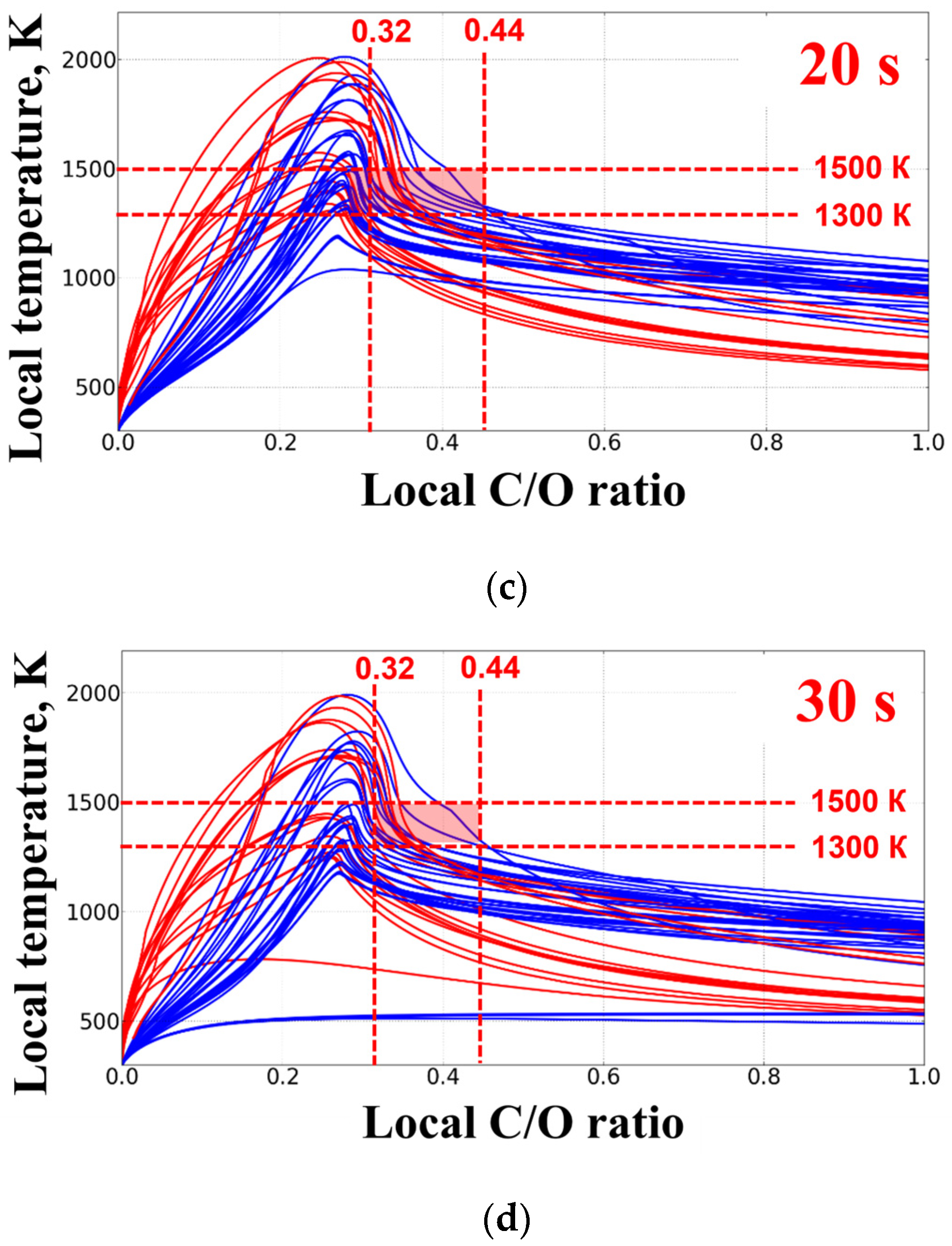
3. Results of Experiments and Calculations
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Nomenclature
| Emissivity of the th emitting gas | |
| Pre-exponential factor | |
| Specific heat at constant pressure | |
| Solid skeleton heat capacity | |
| Threshold local C/O atomic ratio | |
| Characteristic size of solid skeleton | |
| Conditional soot particle size | |
| Effective diffusion coefficient of the th species | |
| Activation energy | |
| Added momentum source in porous medium | |
| Inlet mass flow rate | |
| Mean gas static enthalpy | |
| Standard enthalpy of formation of the th species | |
| Mean gas total enthalpy | |
| Molecular mass flux of the th species | |
| Turbulent mass flux of the th species | |
| Total number of chemical reactions in the gas | |
| Total soot mass | |
| Cumulative rate of soot formation | |
| Temperature exponent | |
| Number of gas species | |
| Mean gas pressure | |
| Initial pressure | |
| Molecular heat flux | |
| Turbulent heat flux | |
| Mean source of energy due to chemical transformations | |
| Length of the buffer channel | |
| Flame radius | |
| Radius of porous sphere | |
| Radius of the outer wall of the chamber | |
| Universal gas constant | |
| Passage area of gas supply tube | |
| Specific surface area of the porous sphere | |
| Specific emitting surface area | |
| Time | |
| Time of ignition | |
| Temperature | |
| Initial temperature | |
| Standard temperature | |
| Threshold local temperature of soot formation | |
| Ignition temperature | |
| Temperature of porous sphere | |
| Superficial velocity inside the porous medium | |
| The th component of the mean gas velocity vector | |
| Chamber volume | |
| Mean source of mass due to chemical transformations | |
| Molecular mass | |
| Molecular mass of oxidizer | |
| Molecular mass of fuel | |
| Cartesian coordinate | |
| Volume fraction of the th emitting gas | |
| Initial species mass fractions | |
| Inlet species mass fractions | |
| Mean mass fraction of the th species | |
| Soot mass fraction | |
| Integral soot mass fraction | |
| Stoichiometric mixture fraction | |
| Heat transfer coefficient between gas and porous sphere | |
| Delta function | |
| Coefficient of radiation absorption by the porous sphere material | |
| Permeability | |
| Thermal conductivity of the th species | |
| Solid skeleton thermal conductivity | |
| Dynamic viscosity of gas | |
| Stoichiometric coefficient of oxidizer in the overall reaction equation | |
| Stoichiometric coefficient of fuel in the overall reaction equation | |
| Stoichiometric coefficients of the th species in the reactants of the th reaction | |
| Stoichiometric coefficients of the th species in the products of the th reaction | |
| Mean gas density | |
| Solid skeleton density | |
| Soot density | |
| Stefan–Boltzmann constant | |
| Tensor of viscous stresses | |
| Tensor of turbulent stresses | |
| Porosity | |
| Added heat source in porous medium | |
| Heat source/sink other than that of chemical nature | |
| Heat source/sink for porous sphere | |
| Radiation absorption |
References
- Haynes, B.S.; Wagner, H.G. Soot formation. Prog. Energy Combust. Sci. 1981, 7, 229–273. [Google Scholar] [CrossRef]
- Kennedy, I.M. Models of soot formation and oxidation. Prog. Energy Combust. Sci. 1997, 23, 95–132. [Google Scholar] [CrossRef]
- Richter, H.; Howard, J.B. Formation of polycyclic aromatic hydrocarbons and their growth to soot—A review of chemical reaction pathways. Prog. Energy Combust. Sci. 2000, 26, 565–608. [Google Scholar] [CrossRef]
- Karatas, A.E.; Gülder, Ö.L. Soot formation in high pressure laminar diffusion flames. Prog. Energy Combust. Sci. 2012, 38, 818–845. [Google Scholar] [CrossRef]
- Wang, Y.; Chung, S.H. Soot formation in laminar counterflow flames. Prog. Energy Combust. Sci. 2019, 74, 152–238. [Google Scholar] [CrossRef]
- Lapuerta, M.; Rodríguez–Fernández, J.; Sánchez-Valdepeñas, J. Soot reactivity analysis and implications on diesel filter regeneration. Prog. Energy Combust. Sci. 2020, 78, 100833. [Google Scholar] [CrossRef]
- Michelsen, H.A.; Colket, M.B.; Bengtsson, P.-E.; D’Anna, A.; Desgroux, P.; Haynes, B.S.; Miller, J.H.; Nathan, G.J.; Pitsch, H.; Wang, H. A review of terminology used to describe soot formation and evolution under combustion and pyrolytic conditions. ACS Nano 2020, 14, 12470–12490. [Google Scholar] [CrossRef]
- Xi, J.; Yang, G.; Cai, J.; Gu, Z. A review of recent research results on soot: The formation of a kind of carbon-based material in flames. Front. Mater. 2021, 8, 695485. [Google Scholar] [CrossRef]
- Gleason, K.; Carbone, F.; Sumner, A.J.; Drollette, B.D.; Plata, D.L.; Gomez, A. Small aromatic hydrocarbons control the onset of soot nucleation. Combust. Flame 2021, 223, 398–406. [Google Scholar] [CrossRef]
- Martin, J.W.; Salamanca, M.; Kraft, M. Soot inception: Carbonaceous nanoparticle formation in flames. Prog. Energy Combust. Sci. 2022, 88, 100956. [Google Scholar] [CrossRef]
- He, J.; Ying, Y.; Chen, M.; Liu, D. Soot formation characteristics in hybrid pyrolysis of zero-carbon fuel ammonia and ethylene mixtures. Front. Energy Res. 2022, 10, 996813. [Google Scholar] [CrossRef]
- Santoro, R.J.; Yeh, T.T.; Horvath, J.J.; Semerjian, H.G. The Transport and Growth of Soot Particles in Laminar Diffusion Flames. Combust. Sci. Technol. 1987, 53, 89–115. [Google Scholar] [CrossRef]
- Glassman, I. Soot formation in combustion processes. Proc. Combust. Inst. 1989, 22, 295–311. [Google Scholar] [CrossRef]
- Glassman, I.; Nishida, O.; Sidebotham, G. Critical temperatures of soot formation. In Soot Formation in Combustion; Springer: Berlin/Heidelberg, Germany, 1994; pp. 316–324. [Google Scholar] [CrossRef]
- Sunderland, P.B.; Faeth, G.M. Soot formation in hydrocarbon/air laminar jet diffusion flames. Combust. Flame 1996, 105, 132–146. [Google Scholar] [CrossRef]
- Glassman, I. Sooting laminar diffusion flames: Effect of dilution, additives, pressure, and microgravity. Proc. Symp. Combust. 1998, 27, 1589–1596. [Google Scholar] [CrossRef]
- Atreya, A.; Agrawal, S.; Sacksteder, K.; Baum, H. Observations of methane and ethylene diffusion flames stabilized around a blowing porous sphere under microgravity conditions. In Proceedings of the 32nd Aerospace Sciences Meeting and Exhibit, Reno, NV, USA, 10–13 January 1994. [Google Scholar]
- Tse, S.D.; Zhu, D.; Sung, C.-J.; Ju, Y.; Law, C.K. Microgravity burner-generated spherical diffusion flames: Experiment and computation, Combust. Flame 2001, 125, 1265–1278. [Google Scholar] [CrossRef]
- Sunderland, P.B.; Axelbaum, R.L.; Urban, D.L.; Chao, B.H.; Liu, S. Effects of structure and hydrodynamics on the sooting behavior of spherical microgravity diffusion flames. Combust. Flame 2003, 132, 25–33. [Google Scholar] [CrossRef]
- Santa, K.J.; Chao, B.H.; Sunderland, P.B.; Urban, D.L.; Stocker, D.P.; Axelbaum, R.L. Radiative extinction of gaseous spherical diffusion flames in microgravity, Combust. Flame 2007, 151, 665–675. [Google Scholar] [CrossRef]
- Chernovsky, M.K.; Atreya, A.; Im, H.G. Effect of CO2 diluent on fuel versus oxidizer side of spherical diffusion flames in microgravity. Proc. Combust. Inst. 2007, 31, 1005–1013. [Google Scholar] [CrossRef]
- Christiansen, E.W.; Tse, S.D.; Law, C.K. A computational study of oscillatory extinction of spherical diffusion flames. Combust. Flame 2003, 134, 327–337. [Google Scholar] [CrossRef]
- Liu, S.; Chao, B.H.; Axelbaum, R.L. A theoretical study on soot inception in spherical burner-stabilized diffusion flames. Combust. Flame 2005, 140, 1–23. [Google Scholar] [CrossRef]
- Lecoustre, V.R.; Sunderland, P.B.; Chao, B.H.; Axelbaum, R.L. Numerical investigation of spherical diffusion flames at their sooting limits. Combust. Flame 2012, 159, 194–199. [Google Scholar] [CrossRef]
- Frenklach, M.; Mebel, A.M. On the mechanism of soot nucleation. Phys. Chem. Chem. Phys. 2020, 22, 5314–5331. [Google Scholar] [CrossRef] [PubMed]
- Frenklach, M.; Clary, D.W.; Gardiner, W.C., Jr.; Stein, S.E. Detailed kinetic modeling of soot formation in shock-tube pyrolysis of acetylene. Proc. Combust. Inst. 1985, 20, 887–901. [Google Scholar] [CrossRef]
- Commodo, M.; Kaiser, K.; De Falco, G.; Minutolo, P.; Schulz, F.; D’Anna, A.; Gross, L. On the early stages of soot formation: Molecular structure elucidation by high-resolution atomic force microscopy. Combust. Flame 2019, 205, 154–164. [Google Scholar] [CrossRef]
- Irimiea, C.; Faccinetto, A.; Mercier, X.; Ortega, I.-K.; Nuns, N.; Therssen, E.; Desgroux, P.; Focsa, C. Unveiling trends in soot nucleation and growth: When secondary ion mass spectrometry meets statistical analysis. Carbon 2019, 144, 815–830. [Google Scholar] [CrossRef]
- Mitra, T.; Zhang, T.; Sediako, A.D.; Thomson, M.J. Understanding the formation and growth of polycyclic aromatic hydrocarbons (PAHs) and young soot from n-dodecane in a sooting laminar coflow diffusion flame. Combust. Flame 2019, 202, 33–42. [Google Scholar] [CrossRef]
- Agafonov, G.L.; Bilera, I.V.; Vlasov, P.A.; Kolbanovskii, Y.A.; Smirnov, V.N.; Teresa, A.M. Soot formation at pyrolysis and oxidation of acetylene and ethylene in shock tubes. Kinet. Catal. 2015, 56, 15. [Google Scholar] [CrossRef]
- Irace, P.H.; Lee, H.J.; Waddell, K.; Tan, L.; Stocker, D.P.; Sunderland, P.B.; Axelbaum, R.L. Observations of long duration microgravity spherical diffusion flames aboard the International Space Station. Combust. Flame 2021, 229, 111373. [Google Scholar] [CrossRef]
- Frolov, S.M.; Medvedev, S.N.; Frolov, F.S. Spherical diffusion flame of ethylene in the spaceflight experiment “Adamant”. Combust. Explos. 2021, 14, 9–21. [Google Scholar] [CrossRef]
- Williams, F.A. Combustion Theory; The Benjamin/Cummings Publishing Company, Inc.: Menlo Park, CA, USA, 1985; pp. 636–637. [Google Scholar]
- Hou, D.; Lindberg, C.S.; Manuputty, M.Y.; You, X.; Kraft, M. Modeling soot formation in a benchmark ethylene stagnation flame with a new detailed population balance model, Combust. Flame 2019, 203, 56–71. [Google Scholar] [CrossRef]
- Basevich, V.Y.; Medvedev, S.N.; Frolov, S.M.; Frolov, F.S.; Basara, B.; Prieching, P. Macrokinetic model for calculating soot emission in Diesel engine. Combust. Explos. 2016, 9, 36–46. [Google Scholar]
- Basevich, V.Y.; Belyaev, A.A.; Posvyanskii, V.S.; Frolov, S.M. Mechanisms of the oxidation and combustion of normal paraffin hydrocarbons: Transition from C1–C10 to C11–C16. Rus. J. Phys. Chem. B 2013, 7, 161–169. [Google Scholar] [CrossRef]
- Forchheimer, P. Wasserbewegung durch boden, Zeitschrift des Vereines deutscher Ingenieure. Sci. Res. 1901, 45, 1781–1788. [Google Scholar]
- Available online: https://tnfworkshop.org/radiation/ (accessed on 20 November 2022).
- Reid, R.C.; Prausnitz, J.M.; Sherwood, T.K. The Properties of Gases and Liquids; McGrawHill: New York, NY, USA, 1977. [Google Scholar]
- Skeen, S.A.; Yablonsky, G.; Axelbaum, R.L. Characteristics of non-premixed oxygen-enhanced combustion: II. Flame structure effects on soot precursor kinetics resulting in soot-free flames. Combust. Flame 2010, 157, 1745–1752. [Google Scholar] [CrossRef]
- Kumfer, B.; Skeen, S.A.; Axelbaum, R.L. Soot inception limits in laminar diffusion flames with application to oxy-fuel combustion. Combust. Flame 2008, 154, 546–556. [Google Scholar] [CrossRef]
- Available online: https://www.flickr.com/photos/space-flames (accessed on 20 November 2022).
- Available online: https://www.facebook.com/space.flames (accessed on 20 November 2022).
- Irace, P.H.; Waddell, K.; Constales, D.; Yablonsky, G.; Kim, M.; Sunderland, P.B.; Axelbaum, R.L. On the existence of steady state gaseous microgravity spherical diffusion flames in the presence of radiation heat loss. To appear. Proc. Combust. Inst. 2023. [Google Scholar] [CrossRef]
- Xia, F.; Axelbaum, R.L. Simplifying the complexity of diffusion flames through interpretation in C/O ratio space. Comput. Math. Appl. 2013, 10, 1625–1632. [Google Scholar] [CrossRef]
- Kumfer, B.; Skeen, S.A.; Chen, R.; Axelbaum, R.L. Measurement and analysis of soot inception limits of oxygen-enriched coflow flames. Combust. Flame 2006, 147, 233–242. [Google Scholar] [CrossRef]
- Minutolo, P.; Gambi, G.; D’Alessio, A. Properties of carbonaceous nanoparticles in flat premixed C2H4/air flames with C/O ranging from 0.4 to soot appearance limit. Proc. Symp. Combust. 1998, 27, 1461–1469. [Google Scholar] [CrossRef]
- Hura, H.S.; Glassman, I. Soot formation in diffusion flames of fuel/oxygen mixtures. Proc. Symp. Combust. 1989, 22, 371–378. [Google Scholar] [CrossRef]
- Valencia-López, A.M.; Bustamante, F.; Loukou, A.; Stelzner, B.; Trimis, D.; Frenklach, M.; Slavinskaya, N.A. Effect of benzene doping on soot precursors formation in non-premixed flames of producer gas (PG). Combust. Flame 2019, 207, 265–280. [Google Scholar] [CrossRef]
- Gleason, K.; Gomez, A. Detailed study of the formation of soot precursors and soot in highly controlled ethylene(/toluene) counterflow diffusion flames. J. Phys. Chem. A 2022. [Google Scholar] [CrossRef] [PubMed]
- Frolov, S.M.; Avdeev, K.A.; Ivanov, V.S.; Vlasov, P.A.; Frolov, F.S.; Semenov, I.V.; Belotserkovskaya, M.S. Evolution of the soot-particle size distribution function in the cylinder and exhaust system of piston engines: Simulation. Atmosphere 2023, 14, 13. [Google Scholar] [CrossRef]





| Reaction | |||
|---|---|---|---|
| I | 1016 | 40,000 | 0 |
| II | 1015 | 40,000 | 0 |
| III | 1015 | 40,000 | 0 |
| IV | 1012 | 0 | 0 |
| Flame | Combustion Chamber | Porous Sphere | p, atm | |||
|---|---|---|---|---|---|---|
| 19115B1 | 0.203 | 0.797 | 1.000 | 0.000 | 0.660 | 1.020 |
| 19206L6 | 0.194 | 0.806 | 0.288 | 0.712 | 0.660 | 1.010 |
| 19171D4 | 0.363 | 0.637 | 1.000 | 0.000 | 1.372 | 1.010 |
| 19189K1 | 0.363 | 0.637 | 0.476 | 0.524 | 1.372 | 1.310 |
| F10 | 0.380 | 0.620 | 1.000 | 0.000 | 1.224 | 1.239 |
| F02 | 0.391 | 0.609 | 0.288 | 0.712 | 1.800 | 1.190 |
| F08 | 0.386 | 0.614 | 0.288 | 0.712 | 3.603 | 1.263 |
| F05 | 0.400 | 0.600 | 0.288 | 0.712 | 4.514 | 1.250 |
| 19156C2 | 0.366 | 0.634 | 1.000 | 0.000 | 2.529 | 1.040 |
| 19142J3 | 0.356 | 0.644 | 1.000 | 0.000 | 2.529 | 0.990 |
| 19150N1 | 0.296 | 0.704 | 0.168 | 0.832 | 4.885 | 1.010 |
| 19150G3 | 0.338 | 0.662 | 0.288 | 0.712 | 8.779 | 1.050 |
| 19175A3 | 0.391 | 0.609 | 1.000 | 0.000 | 1.960 | 1.270 |
| 19206A5 | 0.207 | 0.793 | 0.288 | 0.712 | 8.779 | 1.010 |
| 19206G1 | 0.205 | 0.795 | 1.000 | 0.000 | 2.529 | 1.010 |
| 19206G4 | 0.201 | 0.799 | 1.000 | 0.000 | 0.822 | 1.010 |
| 19206L4 | 0.195 | 0.805 | 0.288 | 0.712 | 2.835 | 1.010 |
| 19115M4 | 0.193 | 0.807 | 0.476 | 0.524 | 1.380 | 1.020 |
| 19123F1 | 0.206 | 0.794 | 0.490 | 0.510 | 2.640 | 1.010 |
| 19123F2 | 0.206 | 0.794 | 0.489 | 0.511 | 2.640 | 1.010 |
| 19123F3 | 0.205 | 0.795 | 0.490 | 0.510 | 2.640 | 1.010 |
| 19123L1 | 0.202 | 0.798 | 1.000 | 0.000 | 2.510 | 1.010 |
| 19123L2 | 0.201 | 0.799 | 1.000 | 0.000 | 2.510 | 1.010 |
| 19150N1 | 0.351 | 0.649 | 0.168 | 0.832 | 4.820 | 1.040 |
| 19189J3 | 0.378 | 0.622 | 0.502 | 0.498 | 5.010 | 1.300 |
| 19200H3 | 0.285 | 0.715 | 0.131 | 0.869 | 4.430 | 1.020 |
| 19115F1 | 0.204 | 0.796 | 0.292 | 0.708 | 2.180 | 1.040 |
| 19123A2 | 0.209 | 0.791 | 1.000 | 0.000 | 1.620 | 1.000 |
| 19123A3 | 0.208 | 0.792 | 1.000 | 0.000 | 1.620 | 1.000 |
| 19123A4 | 0.208 | 0.792 | 1.000 | 0.000 | 1.620 | 1.000 |
| 19123C1 | 0.207 | 0.793 | 0.290 | 0.710 | 4.460 | 1.000 |
| Flame | Combustion Chamber | Porous Sphere | , atm | |||
|---|---|---|---|---|---|---|
| 21328D1 | 0.257 | 0.743 | 0.212 | 0.788 | 10.05 | 1.03 |
| 21349M3 | 0.270 | 0.730 | 0.212 | 0.788 | 9.11 | 1 |
| 22018H2 | 0.097 | 0.903 | 0.497 | 0.503 | 6.37 | 1.01 |
| 22018J1 | 0.096 | 0.904 | 0.318 | 0.682 | 9.73 | 1.01 |
| 22018G3 | 0.098 | 0.902 | 0.850 | 0.150 | 7.89 | 1.01 |
| 22018G2 | 0.099 | 0.901 | 0.850 | 0.150 | 5.90 | 1.01 |
| 22018G1 | 0.099 | 0.901 | 0.850 | 0.150 | 3.90 | 1 |
| 21328N5 | 0.080 | 0.920 | 0.850 | 0.150 | 2.27 | 0.96 |
| 22035J2 | 0.096 | 0.904 | 0.850 | 0.150 | 5.90 | 0.51 |
| 21340M1 | 0.121 | 0.879 | 0.850 | 0.150 | 9.22 | 1.01 |
| 21340M2 | 0.274 | 0.726 | 0.262 | 0.738 | 8.8 | 1.01 |
| 21349N3 | 0.251 | 0.749 | 0.212 | 0.788 | 9.10 | 0.52 |
| 21349N4 | 0.246 | 0.754 | 0.212 | 0.788 | 10.03 | 0.52 |
| 22018B1 | 0.168 | 0.832 | 0.850 | 0.150 | 4.7 | 1 |
| 22024F1 | 0.187 | 0.813 | 0.412 | 0.588 | 9.16 | 1.01 |
| 22024B1 | 0.189 | 0.811 | 0.850 | 0.150 | 5.9 | 1.01 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Frolov, S.M.; Ivanov, V.S.; Frolov, F.S.; Vlasov, P.A.; Axelbaum, R.; Irace, P.H.; Yablonsky, G.; Waddell, K. Soot Formation in Spherical Diffusion Flames. Mathematics 2023, 11, 261. https://doi.org/10.3390/math11020261
Frolov SM, Ivanov VS, Frolov FS, Vlasov PA, Axelbaum R, Irace PH, Yablonsky G, Waddell K. Soot Formation in Spherical Diffusion Flames. Mathematics. 2023; 11(2):261. https://doi.org/10.3390/math11020261
Chicago/Turabian StyleFrolov, Sergey M., Vladislav S. Ivanov, Fedor S. Frolov, Pavel A. Vlasov, Richard Axelbaum, Phillip H. Irace, Grigoriy Yablonsky, and Kendyl Waddell. 2023. "Soot Formation in Spherical Diffusion Flames" Mathematics 11, no. 2: 261. https://doi.org/10.3390/math11020261
APA StyleFrolov, S. M., Ivanov, V. S., Frolov, F. S., Vlasov, P. A., Axelbaum, R., Irace, P. H., Yablonsky, G., & Waddell, K. (2023). Soot Formation in Spherical Diffusion Flames. Mathematics, 11(2), 261. https://doi.org/10.3390/math11020261