Novel Kinds of Fractional λ–Kinetic Equations Involving the Generalized Degenerate Hypergeometric Functions and Their Solutions Using the Pathway-Type Integral
Abstract
:1. Introduction
2. Some Definitions Related to the Concept of DEGENERATE
3. Pathway-Type Transform
- (i)
- is integrable over a finite limit ;
- (ii)
- for arbitrary positive the integral resort to a finite limit as ;
- (iii)
- as where is the standard big notation which means is of order not exceeding
4. Main Results
Special Cases
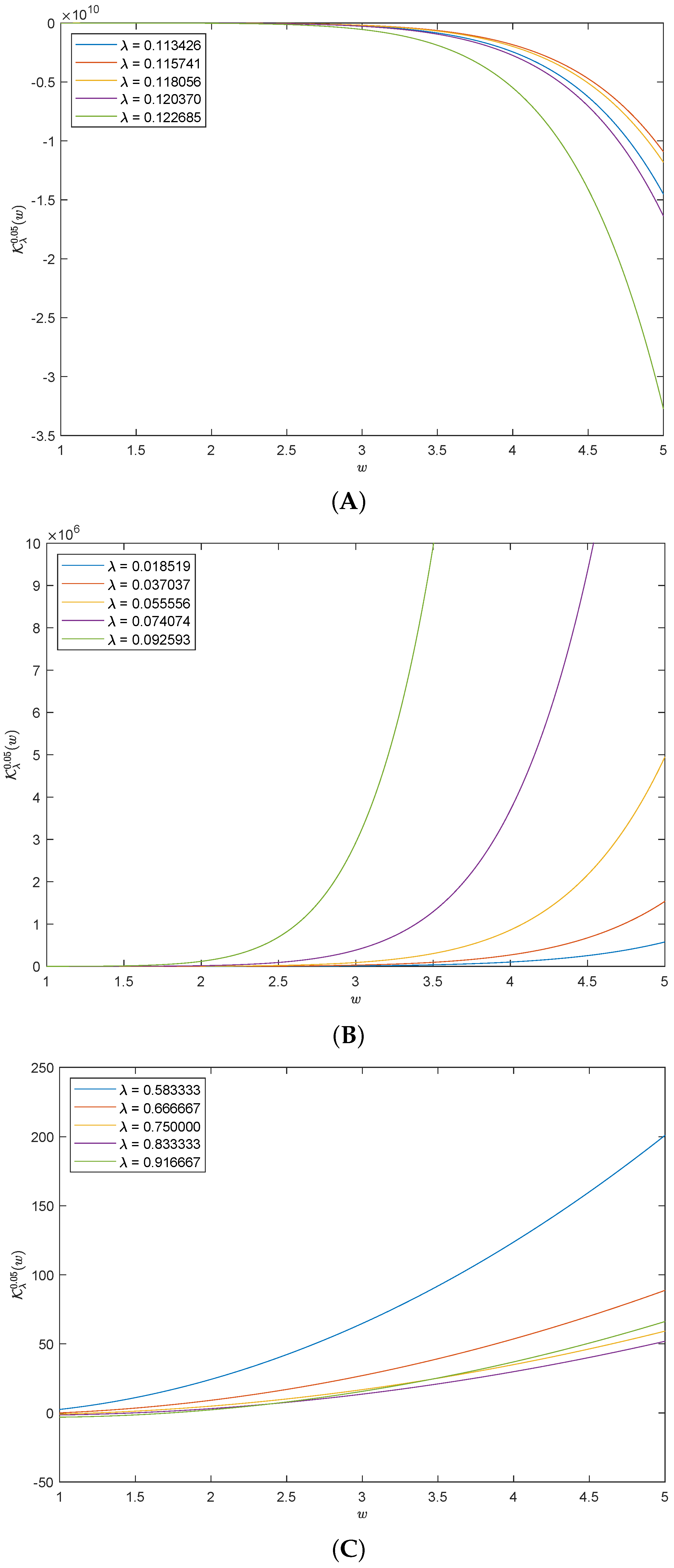
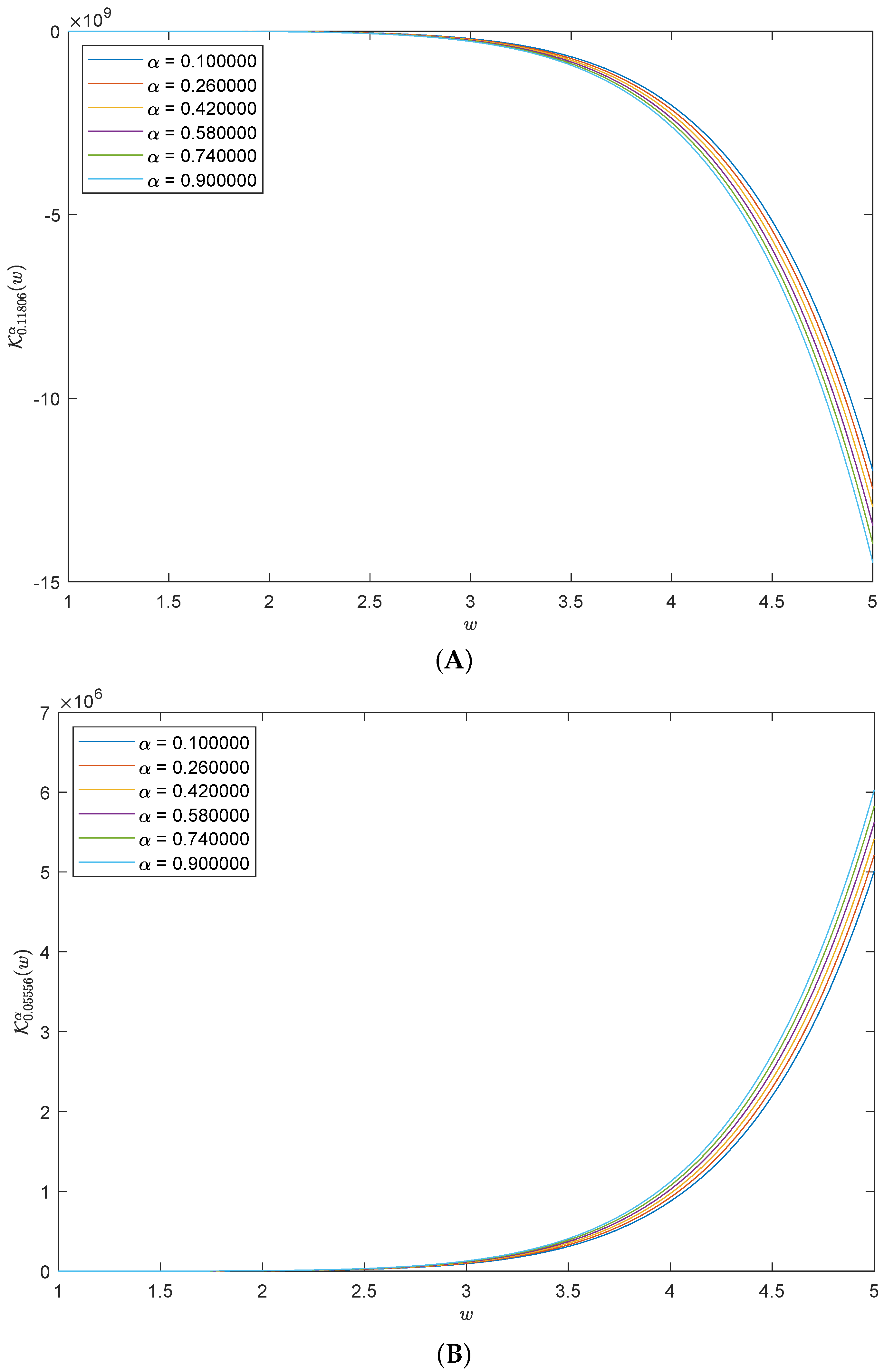
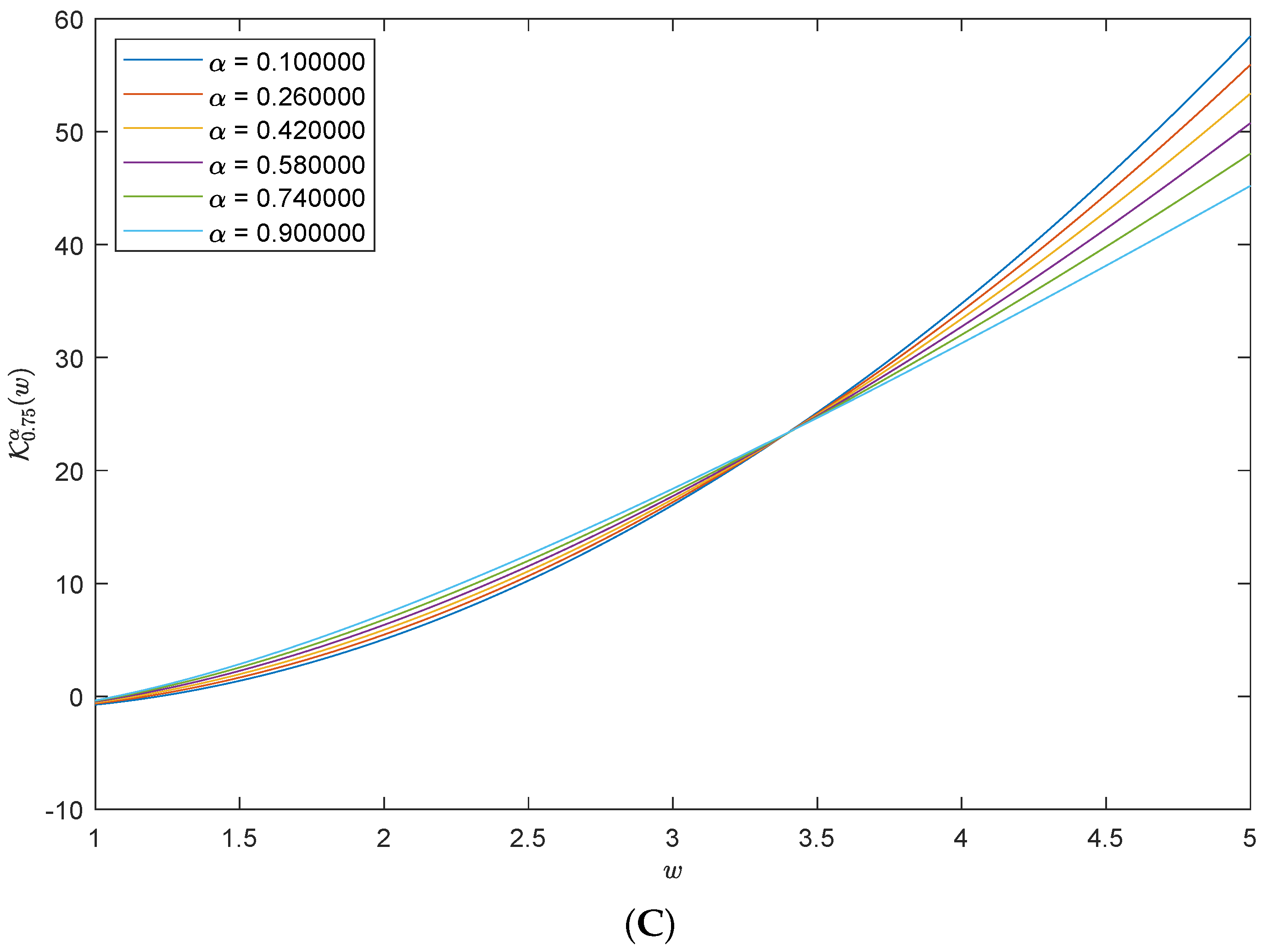
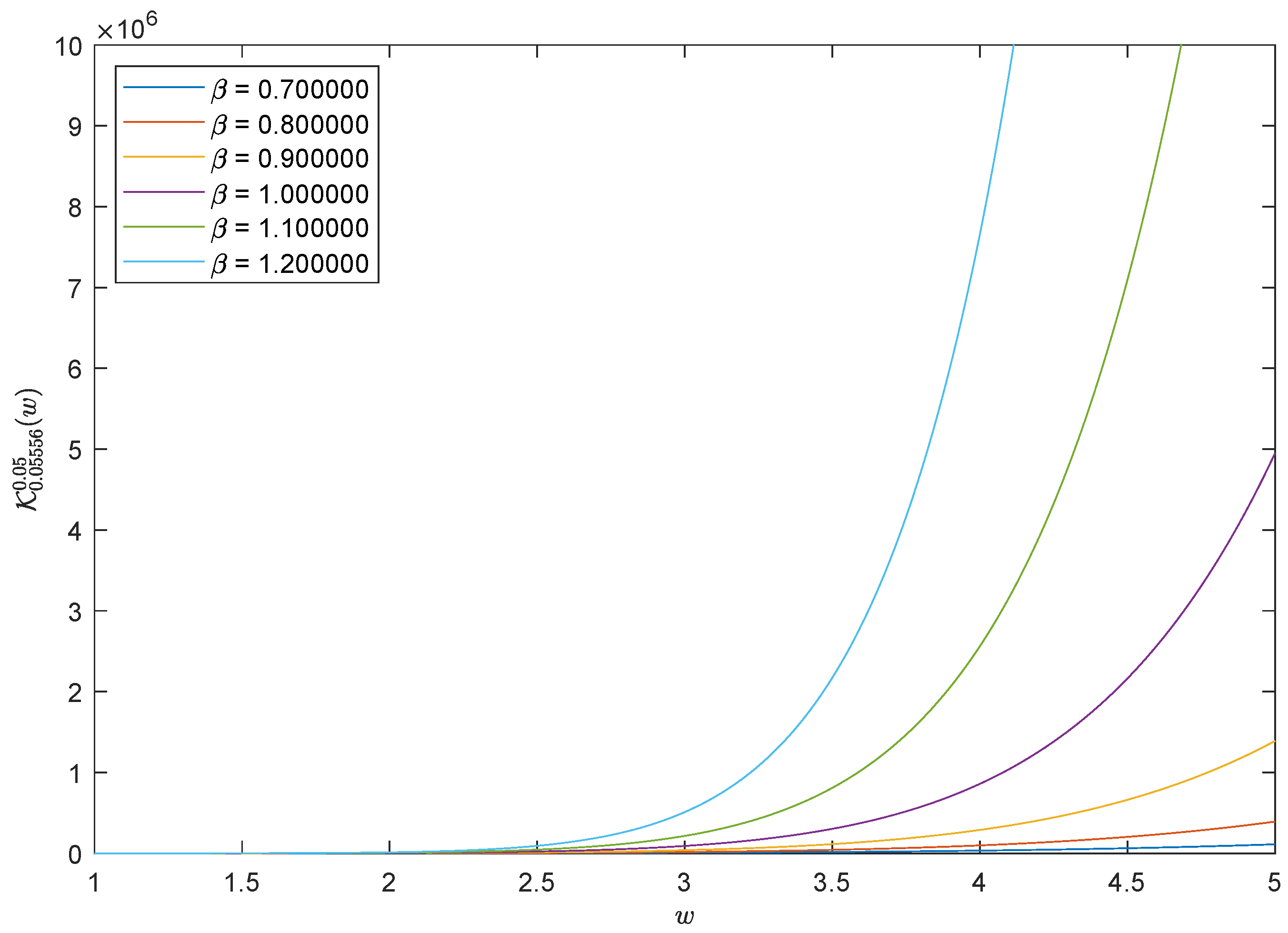
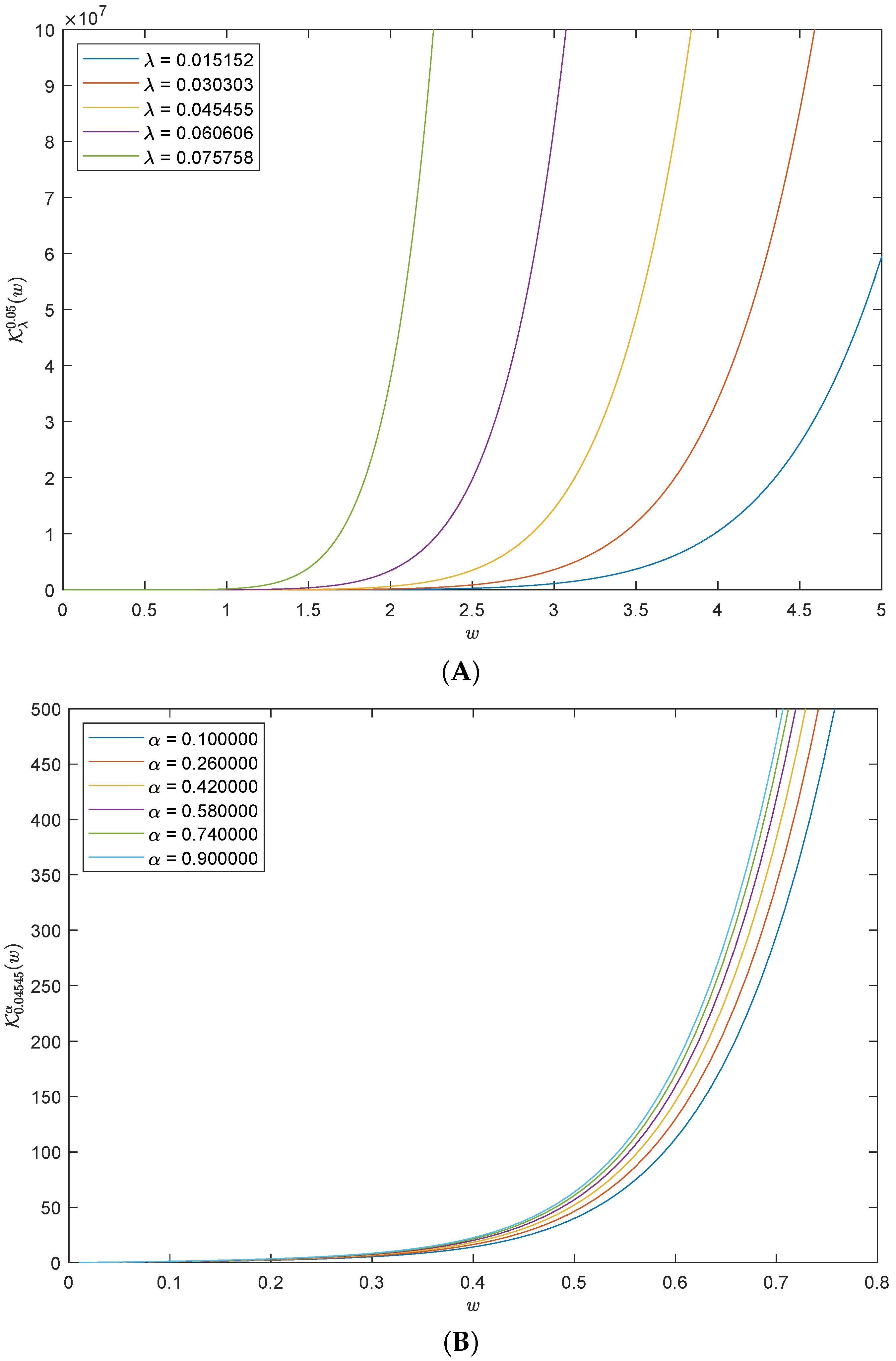
5. Numerical Representations of the Solutions
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Agarwal, P.; Baleanu, D.; Chen, Y.; Momani, S.; Machado, J. Fractional Calculus. In ICFDA: Proceedings of the International Workshop on Advanced Theory and Applications of Fractional Calculus 2018, Amman, Jordan, 16–18 July 2018; Springer Proceedings in Mathematics Statistics Book Series; Springer: Berlin/Heidelberg, Germany, 2020; Volume 303. [Google Scholar]
- Hilfer, R. Applications of Fractional Calculus in Physics; World Scientific: Singapore, 2000. [Google Scholar]
- Fallahgoul, H.A.; Focardi, S.M.; Fabozzi, F.J. Fractional Calculus and Fractional Processes with Applications to Financial Economics, Theory and Application; Elsevier/Academic Press: London, UK, 2017. [Google Scholar]
- Chakraverty, S.; Jena, R.M.; Jena, S.K. Computational Fractional Dynamical Systems: Fractional Differential Equations and Applications; John Wiley and Sons, Inc.: Hoboken, NJ, USA, 2023. [Google Scholar]
- Boulaaras, S.; Rehman, Z.U.; Abdullah, F.; Jan, R.; Jan, M.A.A. Coronavirus dynamics, infections and preventive interventions using fractional-calculus analysis. Aims Math. 2023, 8, 8680–8701. [Google Scholar] [CrossRef]
- Saxena, R.K.; Mathai, A.M.; Haubold, H.J. On fractional kinetic equations. Astrophys. Space Sci. 2002, 282, 281–287. [Google Scholar] [CrossRef]
- Saxena, R.K.; Mathai, A.M.; Haubold, H.J. On generalized fractional kinetic equations. Phys. Stat. Mech. Its Appl. 2004, 344, 657–664. [Google Scholar] [CrossRef]
- Saichev, A.I.; Zaslavsky, G.M. Fractional kinetic equations: Solutions and applications. Chaos Interdiscip. J. Nonlinear Sci. 1997, 7, 753–764. [Google Scholar] [CrossRef] [PubMed]
- Singh, Y.; Gill, V.; Singh, J.; Kumar, D.; Khan, I. Computable generalization of fractional kinetics equation with special functions. J. King Saud Univ. Sci. 2021, 33, 101221. [Google Scholar] [CrossRef]
- Kolokoltsov, V.N.; Troeva, M. A new approach to fractional Kinetic evolutions. Fractal Fract. 2022, 6, 49. [Google Scholar] [CrossRef]
- Almalkia, Y.; Abdalla, M. Analytic solutions to the fractional kinetic equation involving the generalized Mittag-Leffler function using the degenerate Laplace type integral approach. Eur. Phys. J. Spec. Top. 2023. [Google Scholar] [CrossRef]
- Douglas, J.F. Some applications of fractional calculus to polymer science. Adv. Chem. Phys. 2007, 102, 121–191. [Google Scholar]
- Mathai, A.M.; Haubold, H.J. An Introduction to Fractional Calculus; Nova Science Publishers: New York, NY, USA, 2017. [Google Scholar]
- Yang, X.J. Local Fractional Functional Analysis and Its Applications; Asian Academic Publisher Limited: Singapore, 2011. [Google Scholar]
- Alqarni, M.Z.; Bakhet, A.; Abdalla, M. Application of the pathway-type transform to a new form of a fractional kinetic equation involving the generalized incomplete Wright hypergeometric functions. Fractal Fract. 2023, 7, 348. [Google Scholar] [CrossRef]
- Khan, O.; Khan, N.; Choi, J.; Nisar, K.S. A type of fractional Kinetic equations associated with the (p,q)-extented τ-hypergeomtric and confluent hypergeomtric functions. Nonlinear Funct. Anal. Appl. 2021, 26, 381–392. [Google Scholar]
- Abubakar, U.M. Solutions of fractional kinetic equations using the (p,q;l)-extended τ -Gauss hypergeometric function. J. New Theory. 2022, 38, 25–33. [Google Scholar] [CrossRef]
- He, F.; Bakhet, A.; Hidan, M.; Abd-Elmageed, H. On the construction of (p, k)-hypergeometric function and applications. Fractals 2022, 30, 2240261. [Google Scholar] [CrossRef]
- Hidan, M.; Akell, M.; Abd-Elmageed, H.; Abdalla, M. Solution of fractional kinetic equations involving extended (k,t)-Gauss hypergeometric matrix functions. AIMS Math. 2022, 7, 14474–14491. [Google Scholar] [CrossRef]
- Geng, L.L.; Yang, X.J.; Alsolami, A.A. New fractional integral formulas and kinetic model associated with the hypergeometric superhyperbolic sine function. Math. Methods Appl. Sci. 2023, 46, 1809–1820. [Google Scholar] [CrossRef]
- Carlitz, L. Degenerate Stirling, Bernoulli and Eulerian numbers. Utilitas Math. 1979, 15, 51–88. [Google Scholar]
- Carlitz, L. A degenerate Staudt Clausen theorem. Arch. Math. 1956, 7, 28–33. [Google Scholar] [CrossRef]
- Dolgy, D.; Kim, T. Some explicit formulas of degenerate Stirling numbers associated with the degenerate special numbers and polynomials. Proc. Jangjeon Math. Soc. 2018, 21, 309–317. [Google Scholar]
- Kim, D.S.; Kim, T. Stirling numbers associated with sequences of polynomials. Appl. Comput. Math. 2023, 22, 80–115. [Google Scholar]
- Kim, D.S.; Kim, T. A note on new type degenerate Bernoulli numbers. Russ. J. Math. Phys. 2020, 27, 227–235. [Google Scholar] [CrossRef]
- Kim, T.; Kim, D.S. Some identities on truncated polynomials associated with degenerate Bell polynomials. Russ. J. Math. Phys. 2021, 28, 342–355. [Google Scholar] [CrossRef]
- Kim, T.; Dolgy, D.V.; Kim, D.S.; Kim, H.K.; Park, S.H. A note on degenerate generalized Laguerre polynomials and Lah numbers. Adv. Differ. Equ. 2021, 12, 421. [Google Scholar] [CrossRef]
- Duran, U.; Acikgoz, M. Generalized Gould-Hopper based fully degenerate central Bell polynomials. Turk. J. Anal. Number Theory 2019, 7, 124–134. [Google Scholar] [CrossRef]
- Kim, T.; Kim, D.S.; Jang, L.; Lee, H.; Kim, H. Representations of degenerate Hermite polynomials. Adv. Appl. Math. 2022, 139, 102359. [Google Scholar] [CrossRef]
- Alatawi, M.S.; Khan, W.A. New type of degenerate Changhee-Genocchi polynomials. Axioms 2022, 11, 355. [Google Scholar] [CrossRef]
- Kim, T.; Kim, D.S.; Kim, H.K. On generalized degenerate Euler?Genocchi polynomials. Appl. Math. In Science Eng. 2023, 31, 2159958. [Google Scholar] [CrossRef]
- Kim, D.S. A note on the degenerate type of complex Appell polynomials. Symmetry 2019, 11, 1339. [Google Scholar] [CrossRef]
- Kim, T. Degenerate Euler zeta function. Russ. J. Math. Phys. 2015, 22, 469–472. [Google Scholar] [CrossRef]
- Kim, T.; Kim, D.S. Note on the degenerate Gamma function. Russ. J. Math. Phys. 2020, 27, 352–358. [Google Scholar] [CrossRef]
- He, F.L.; Bakhet, A.; Akel, M.; Abdalla, M. Degenerate analogues of Euler zeta, digamma, and polygamma functions. Math. Probl. Eng. 2020, 2020, 8614841. [Google Scholar] [CrossRef]
- Kim, T.; Kim, D.S.; Lee, H.; Kwon, J. Degenerate binomial coefficients and degenerate hypergeometric functions. Adv. Differ. Equ. 2020, 2020, 115. [Google Scholar] [CrossRef]
- Yağci, O.; Şahin, R. Degenerate Pochhammer symbol, degenerate Sumudu transform, and degenerate hypergeometric function with applications. Hacet. J. Math. Stat. 2021, 50, 1448–1465. [Google Scholar] [CrossRef]
- Srivastava, H.M.; Choi, J. Zeta and q-Zeta Functions and Associated Series and Integrals; Elsevier Science Publishers: Amsterdam, The Netherlands, 2012. [Google Scholar]
- Mathur, G.A.R. Solution of fractional kinetic equations by using integral transform. In AIP Conference Proceedings; AIP Publishing: New York, NY, USA, 2020; Volume 2253, p. 020004. [Google Scholar]
- Kumar, D. Solution of fractional kinetic equation by a class of integral transform of pathway type. J. Math. Phys. 2023, 54, 043509. [Google Scholar] [CrossRef]
- Mathai, A.M. A pathway to matrix-variate gamma and normal densities. Linear Algebra Its Appl. 2005, 396, 317–328. [Google Scholar] [CrossRef]
- Mathai, A.M.; Haubold, H.J. Pathway model, superstatistics, Tsallis statistics and a generalize measure of entropy. Phys. A Stat. Mech. Its Appl. 2007, 375, 110–122. [Google Scholar] [CrossRef]
- Mathai, A.M.; Haubold, H.J. On generalized distributions and path-ways. Phys. Lett. A 2019, 372, 2109–2113. [Google Scholar] [CrossRef]
- Baleanu, D.; Agarwal, A. A composition formula of the pathway integral transform operator. Note Mat. 2014, 34, 145–155. [Google Scholar]
- Amsalu, H.; Shimelis, B.; Suthar, D.L. Pathway fractional integral formulas Involving S-Function in the Kerne. Math. Probl. Eng. 2020, 2020, 4236823. [Google Scholar] [CrossRef]
- Nair, S.S. Pathway fractional integration operator. Fract. Calc. Appl. Anal. 2009, 12, 237–252. [Google Scholar]
- Agarwal, P.; Purohit, S.D. The Unified Pathway Fractional Integral Formulae. J. Fract. Calc. Appl. 2013, 4, 1–8. [Google Scholar]
- Kaur, D.; Chand, M.; Rakshit, M. On pathway fractional integral formulae involving new extended hypergeometric functions. Int. J. Manag. Technol. Eng. 2019, IX, 1461–1469. [Google Scholar]
- Abdalla, M.; Akel, M. Contribution of using Hadamard fractional integral operator via Mellin integral transform for solving certain fractional kinetic matrix equations. Fractal Fract. 2022, 6, 305. [Google Scholar] [CrossRef]
- Aydiner, E. The time-fractional kinetic equation for the non-equilibrium processes. Sci. Rep. 2021, 11, 20625. [Google Scholar] [CrossRef] [PubMed]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Alqarni, M.Z.; Abdalla, M. Novel Kinds of Fractional λ–Kinetic Equations Involving the Generalized Degenerate Hypergeometric Functions and Their Solutions Using the Pathway-Type Integral. Mathematics 2023, 11, 4217. https://doi.org/10.3390/math11194217
Alqarni MZ, Abdalla M. Novel Kinds of Fractional λ–Kinetic Equations Involving the Generalized Degenerate Hypergeometric Functions and Their Solutions Using the Pathway-Type Integral. Mathematics. 2023; 11(19):4217. https://doi.org/10.3390/math11194217
Chicago/Turabian StyleAlqarni, Mohammed Z., and Mohamed Abdalla. 2023. "Novel Kinds of Fractional λ–Kinetic Equations Involving the Generalized Degenerate Hypergeometric Functions and Their Solutions Using the Pathway-Type Integral" Mathematics 11, no. 19: 4217. https://doi.org/10.3390/math11194217
APA StyleAlqarni, M. Z., & Abdalla, M. (2023). Novel Kinds of Fractional λ–Kinetic Equations Involving the Generalized Degenerate Hypergeometric Functions and Their Solutions Using the Pathway-Type Integral. Mathematics, 11(19), 4217. https://doi.org/10.3390/math11194217





