Analysis of the Influence of Calculation Parameters on the Design of the Gearbox of a High-Power Wind Turbine

Abstract

As wind turbine power requirements have evolved from the order of kilowatts (kWs) to the order of several megawatts (MWs), wind turbine components have been subjected to more demanding and critical operating conditions. The wind turbine must cope with higher wind loads due to larger blade sizes, which are also time-varying, and, ultimately, higher power levels. One of the challenges in the manufacture of high-power wind turbines lies in the gearbox and consists of achieving ever-greater power density without compromising efficiency, i.e., greater load capacity with lower weight (and production cost) and reduced power losses. Epicyclic geartrains are used to build the gearbox due to various advantages in relation to conventional gear systems, such as higher feasible gear ratios, higher efficiency, compactnesss, and lower weight. In this paper, several epicyclic geartrains with different structures will be analysed to reveal the influence that certain design parameters have on the size and weight of the gearbox components in the selected model and, therefore, of the gearbox itself. For this purpose, the theoretical model of the gearbox will be planned and the influence of the calculation parameters on the gearbox design will be analyzed following ISO 6336. Special emphasis is placed on the influence of the material used; the modulus and tooth width on the size and weight of the gearbox will be observed. Critical stresses are also calculated. The goal is to prepare the theoretical basis for an optimization process subject to geometric, kinematic, and dynamic constraints that will result in a gearbox as compact, energy-dense, and light as possible without compromising the service life of the components.

1. Introduction

As the power requirements of wind turbines have evolved from the order of kilowatts (kWs) to the order of several megawatts (MWs), the wind turbine components have been subjected to more demanding and critical operating conditions.

The wind turbine must cope with higher wind loads due to the larger blade size, which are also time-varying, and, ultimately, to higher power levels [1].

For that reason, is important to consider the dynamic behaviour of a wind turbine as a whole in order to analyse its response to operating conditions (usually strong wind), as in [2].

Moreover, the drive train and gearbox play a key role in a wind turbine. Despite continuous advances in this area, the one challenge that the wind turbine bearing and gearbox industry has yet to overcome is that of longevity. Gearboxes are usually designed for a service life of 20 years, but few exceed 10 years [3].

The environmental and load conditions to which the gearbox is subjected are harsh and the need to ensure a high service life has an impact on the high costs involved. It is a challenge to design and manufacture this element at low cost for wind turbines of several megawatts (MWs) in size and to meet service life expectations.

Despite the use of design standards and procedures for individual components and strict quality controls, failures still occur in these components.

Fundamental design problems have also been observed in gearboxes [4], such as interference fits resulting in unintended movement and wear, inefficient internal lubrication pathways, and sealing problems.

To reduce the cost of the energy produced by wind turbines, the strength of future gearbox, bearing, and lubrication/cooling system designs must be improved [5].

Many gearbox failures are due to an underestimation of the rigorous operating conditions of wind turbines. To manufacture more reliable gearboxes, a precise definition of the wind turbine’s working environment is necessary.

Finally, a specific study of the gearbox components is necessary [6,7].

In this paper, we focus on a geartrain model which is analysed to reveal the influence that certain design parameters have on the size and weight of the gearbox components in the selected model and, therefore, of the gearbox itself. For this purpose, the theoretical model of the gearbox will be planned and the influence of the calculation parameters on the gearbox design will be analyzed following ISO 6336 [8]. Special emphasis is placed on the influence that parameters such as the module, tooth width, and material have on the gearbox, and, especially, on the weight and volume of the gearbox, since the goal is to achieve the most compact and light gearboxes possible without any loss of efficiency [9]. Critical stresses are also calculated.

2. History of Gearbox Problems

In the early days, failures during wind turbine operation were common.

Historically, the gearbox next to the bearings has been the weakest link in the drive chain of a modern commercial-scale wind turbine. With the increasing use of higher-power wind turbines with larger rotor diameters and heavier blades, gearboxes are subjected to more severe operating conditions [10].

Part of the problem is due to an underestimation of the working loads and inherent deficiencies in gearbox design. Failure to fully account for critical design loads, the nonlinearity or unpredictability of the load transfer between the drive train and its attachment, and the mismatched reliability of individual gearbox components were identified as contributing factors to a reduced gearbox life [11].

To overcome these and other problems, a set of internationally recognized standards for wind turbine gearbox design was created.

The evolution towards higher powers led to larger turbines with larger towers, higher torque, and higher gear ratios. Gearboxes became the subject of optimization efforts. The planetary gearbox offered slightly higher power density and lower weight and, above all, a lower production cost [12].

The typical service life of a wind turbine is 20 years. It has been observed that gearboxes operating in the speed range of between 5 rpm and 1600 rpm typically fail within 5 years of operation [13].

The wind industry has always debated the reliability of gearboxes. Discussions are currently shifting from individual component reliability to multi-component system reliability [14].

Failures lead to a significant increase in capital and operating costs and downtime of a turbine, greatly reducing its profitability and reliability.

One of the maintenance requirements introduced is the replacement of the gearbox every 5 years during the 20-year lifetime of the wind turbine. This is a costly task, as the replacement of a gearbox accounts for about 10% of the construction and installation cost of the wind turbine, and will negatively affect the estimated revenue of a wind turbine [15].

Most gearboxes in the 1.5 MW rated power range of wind turbines use a single or two-stage planetary gear system, sometimes referred to as an epicyclic gear system. The ring gear would be connected to the rotor hub, while the sun gear would be connected to the generator. In practice, however, modern gearboxes are much more complicated.

The disadvantages of planetary gear systems are the need for very complex designs, the general inaccessibility of vital components, and the high loads on the shaft bearings [16]. It is the latter that has proven most problematic in wind turbine applications.

Small improvements in gearbox lubrication and the oil filtration system have increased the reliability of wind turbines, but, to significantly improve gearbox reliability, the current planetary gear design must be changed [17]. This reliability improvement is especially important for offshore applications, as wind turbines are typically much larger, and the maintenance cost is much higher.

They require large diameters, necessitating the use of large quantities of rare earth element permanent magnets, and, consequently, are expensive and require a larger and heavier powertrain. In addition, the manufacturing tolerances required are very precise and the detailed design to handle the complex loads add another set of challenges that set an upper limit on the size of such generators [18].

Most wind turbine designs with power ratings around 1.5–3.0 MW still use a planetary gear system.

They can become competitive with their geared counterparts near the upper end of turbine sizes (in the 4–6 MW range) [13].

A different attempt to solve the problems associated with gearbox use in wind turbines greater than 2 MW in size is to employ torque splitting.

Another alternative to the use of gearboxes are continuously variable transmissions, (CVTs). But CVTs can be limited by the amount of torque that can be transmitted by chain, belt, or hydrostatic means. For this reason, magnetic bearings appear to offer a potential solution for a slightly wider range of turbine power ratings than CVTs [19].

Another factor to consider in achieving high gearbox life is maintenance. Proper maintenance increases the service life of the gearbox. Basically, there are three adjustment possibilities: the properties of oil viscosity, oil treatment, and load. It should be noted that the design, optimization, and simulation of mechanical elements is a current topic of maximum interest in the scientific community and research and higher institutions [20,21,22], as well as the contribution of mechanical component applications to the Sustainable Development Goals (SDGs), such as the use of wind turbines to provide renewable energy solutions [23].

As previously mentioned, this paper will analyze the influence of the design parameters of the gearbox to make it as compact and light as possible.

3. Types of Epicyclic Geartrains for Use in High-Power Wind Turbines

The aim is to determine which type of epicyclic geartrain is the most compact [24,25]. For this purpose, the following four geartrains shown in

Table 1. Types of epicyclic geartrains *.

Model 1	Model 2	Model 3	Model 4
P(P)N	P(PP)N	P(PP)P	N(PP)N

* According to Levai’s notation, P stands for external gears (both sun and planet gears) and the letter N for internal gears.

will be analyzed, using Levai’s notation [26]:

Since we are looking for the most compact and smallest volume solution, we will analyze Model 1 and determine how the operating parameters affect the gearbox design.

4. Kinematic Analysis of the Epicyclic Geartrain Model 1

The same geartrain can operate in six different ways depending on its fixed element according to the following

Table 2. Epicyclic geartrain variants.

Fixed Element	Input	Output	Variant
Planet carrier	Sun	Ring	1
	Ring	Sun	2
Sun gear	Ring	Planet carrier	3
	Planet carrier	Ring	4
Ring gear	Sun	Planet carrier	5
	Planet carrier	Sun	6

, from which variants are featured:

In

Table 3. Relationship between input and output shaft speeds.

		Model 1
Willis	$\frac{{\omega }_S-{\omega }_C}{{\omega }_R-{\omega }_C}=-\frac{Z_R}{Z_S}$
Variant		Fixed Ring
6	Input: Planet carrier Output: Sun	$i_{ap}=\frac{{\omega }_S-{\omega }_C}{-{\omega }_C}=-\frac{Z_R}{Z_S}$ $i_{i/o}=\frac{{\omega }_S}{{\omega }_C}=1+\frac{Z_R}{Z_S}=1-i_{ap}$

P stands for Planet, C for Carrier, S for Sun, and R for Ring.

, the relationship between the input and output shaft speeds for Model 1 are shown, where $i_{ap}$ is the velocity ratio according to the Willis formula, $i_{i/o}$ is the ratio between the input and output velocity, ${\omega }_S$ = angular velocity of the sun, ${\omega }_B$ = angular velocity of the planet carrier, $Z_R$ = number of teeth of the ring, $Z_S$ = number of teeth of the sun, and $Z_P$ = number of teeth of the planet. For Model Geartrain 1, the highest gear ratios occur when the ring is fixed; the input is through the planet carrier arm, and the output is through the sun, and their values are shown in Table 4. A diagram for Model 1 is shown in Figure 1.

Depending on the size of the planets and the sun, the gear ratios are as follows:

Table 4. Gear ratios for Epicyclic Geartrain Model 1.

	${\mathit{Z}}_{\mathit{P}}<{\mathit{Z}}_{\mathit{S}}$					${\mathit{Z}}_{\mathit{P}}>{\mathit{Z}}_{\mathit{S}}$
$Z_P/Z_S$	1/6	1/5	1/4	1/3	1/2	1	2	3	4	5	6
$i_{i/o}$	2.33	2.4	2.5	2.67	3	4	6	8	10	12	14
$i_{ap}$	−1.33	−1.4	−1.5	−1.67	−2	−3	−5	−7	−9	−11	−13

Table 4. Gear ratios for Epicyclic Geartrain Model 1.

	${\mathit{Z}}_{\mathit{P}}<{\mathit{Z}}_{\mathit{S}}$					${\mathit{Z}}_{\mathit{P}}>{\mathit{Z}}_{\mathit{S}}$
$Z_P/Z_S$	1/6	1/5	1/4	1/3	1/2	1	2	3	4	5	6
$i_{i/o}$	2.33	2.4	2.5	2.67	3	4	6	8	10	12	14
$i_{ap}$	−1.33	−1.4	−1.5	−1.67	−2	−3	−5	−7	−9	−11	−13

Considering a maximum tooth ratio of up to 6 for spur gears, a gear ratio $i_{i/o}$ = 14 can be achieved.

5. Analysis of the Multiplier Gearbox Multiplier

First, we will analyze the gearbox of a wind turbine for which we have the following design-engineering data given in

Table 5. Design-engineering data.

Rated power (P):	7 MW
$\mathrm{Transmission} \mathrm{ratio} i_{i/o}$	107 ± 2%
Optimal rotor speed	14 rpm
$\mathrm{Gear} \mathrm{safety} \mathrm{coefficient}, X_H=S_{HP}/{\sigma }_H$	1.5
Driving machine	Major shocks
Driven machine	Uniform operation
Φ (rotor diameter)	180 m

where $S_{HP}$ is the maximum allowable contact stress and $X_H$ is the safety coefficient at maximum pressure.

:

We assume a start-up wind speed of 4 m/s, a rated wind speed of 12 m/s, and a wind turbine shutdown wind speed of 25 m/s.

It is considered that the wind delivers the rated maximum power at a wind speed of $v=12 \mathrm{m}/\mathrm{s}$, which corresponds, depending on the rotor blade, to a rotor rotational speed of $14 \mathrm{r}\mathrm{p}\mathrm{m}$, and that the rotational speed of the generator at that time is $\omega =1500 \mathrm{r}\mathrm{p}\mathrm{m}$. Therefore, the transmission ratio will be considered to be $i_{i/o}=107\pm 2\%$. The diameter of the rotor blades is $D_{rotor}=180 \mathrm{m}$.

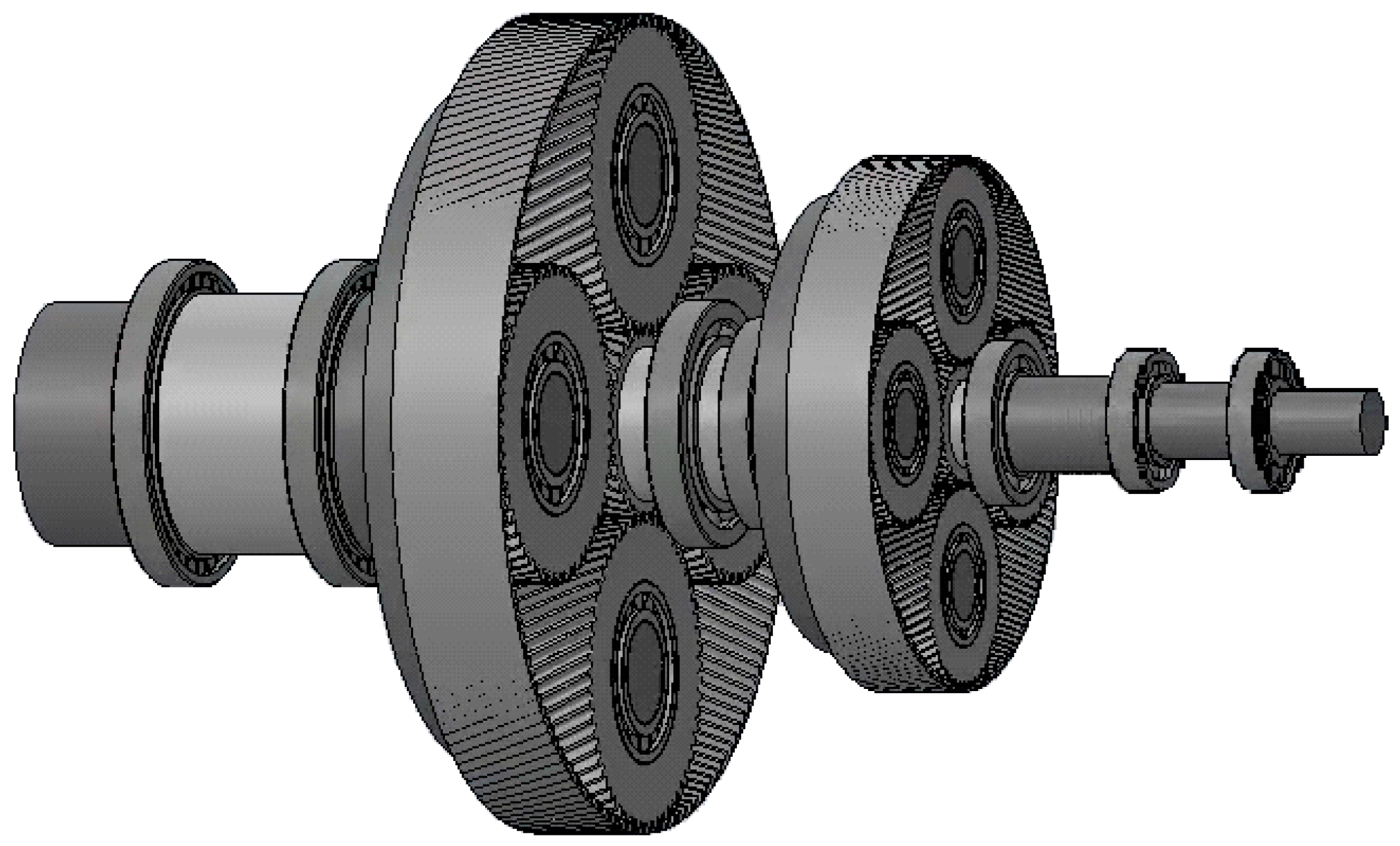
The gearbox will have two stages. In each stage, there is an epicyclic geartrain type Model 1 Variant 6 (this implies that the ring gear is fixed).

See Figure 2 and Figure 3 below:

The influence of the design parameters on the epicyclic geartrain of Stage 1 will be analyzed because it is the most critical, the one that bears the highest loads, and, therefore, where the highest stresses occur.

Considering that the gear ratio is the same in each stage, it is considered that

$$i_T=i_{i/o}=i_1·i_2,\mathrm{w}\mathrm{i}\mathrm{t}\mathrm{h} i_1=i_2=10.35$$

The sun is smaller than the planets, i.e., $Z_s<Z_p$.

From the result of the analysis to be carried out, we intended to design a gearbox of minimum weight and minimum area and volume, capable of transmitting the rated power of the wind turbine P at a transmission ratio of $i_{i/o}=107\pm 2\%$ and a safety coefficient of $X_H$.

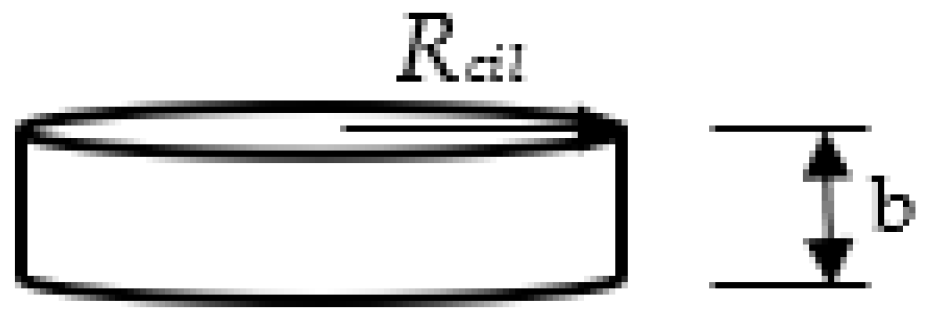
The volume of a gear is considered to be proportional to the volume of the cylinder containing the gear and having the same design parameters as the gear. It is indicated because the gear may have a hub and ribs that lighten the volume of the cylinder containing the gear.

Therefore:

$$V_{engran}\approx V_{cil}=\pi ·R_{cil}^2·b$$

(1)

where $R_{cil}$ is the radius of the cylinder and $b$ its height. See the following figure, Figure 4:

The diameters of the gears D_engra depend on the diameter of the corresponding shaft d.

The shafts must be able to transmit a torque of magnitude T so it must have sufficient torsional stiffness according to the following expression:

$$d=\sqrt[4]{\frac{32·T}{\pi ·G·{\left(\theta /L\right)}_{max}}}\mathrm{w}\mathrm{i}\mathrm{t}\mathrm{h} {\left(\theta /L\right)}_{max}=1.5°/\mathrm{m}.$$

(2)

where $d$ is the shaft diameter, $T$ is the transmitted torque, $G$ is the transverse modulus of elasticity of the shaft material, and $\theta /L$ is the torsional angle per unit length that is allowed to avoid failure due to a high torsional angle.

From the maximum rated power that the wind turbine can generate (which, in turn, depends on the size of the wind turbine blades), the diameter of the input shaft to the gearbox, the diameter of the intermediate shafts, and the output shaft for the Model 1 epicyclic geartrain will be calculated.

The pitch diameters of the gears must respect not only the value of the shaft diameter but also the desired transmission ratio between the input and output shafts $i_{i/o}$, and also the apparent transmission ratio defined by the Willis formula $i_{ap}$.

The mass of each gear may be calculated from the volume of each gear and the density of the material from which it is manufactured. Thus, for gear or constituent element i, the mass will be calculated as

$$m_i={\rho }_i·V_i$$

(3)

In a simplified form, for the calculation of the mass of the epicyclic geartrain, the gears involved and the planet carrier will be considered. The real mass of the train will be proportional to that obtained in the simplified form. The intervention of auxiliary constituent elements, such as bearings, will not be taken into account at this stage of the analysis. Hence, the mass obtained from the present analysis is considered to be proportional to the actual mass of the epicyclic geartrain, which can be calculated with sufficient accuracy later.

Once the wind turbine is in operation, the torque transmitted from the blades to the gearbox is calculated. The knowledge of the torque value $T$ allows us to dimension the whole drive train and, in particular, the gearbox. In this work, the most important elements of the gearbox will be dimensioned, such as the shafts and the constituent gears.

Therefore, for the study and design of the gearbox, it is essential to know the transmitted torques.

The maximum torque on the gearbox input shaft is calculated from the maximum design rated power of the wind turbine. The wind turbine is considered to produce a rated power of P = 7 MW. From the rotor speed ${\omega }_e$ that produces that maximum rated power, the transmitted torque is obtained:

$$T_{i1}=\frac{P_{max}}{{\omega }_{i1}}=\frac{7·{10}^{6 }\mathrm{MW} }{14·\frac{2\pi }{60}\frac{\mathrm{rad}}{\mathrm{s}} }=4774.65 \mathrm{k}\mathrm{N}·\mathrm{m}$$

(4)

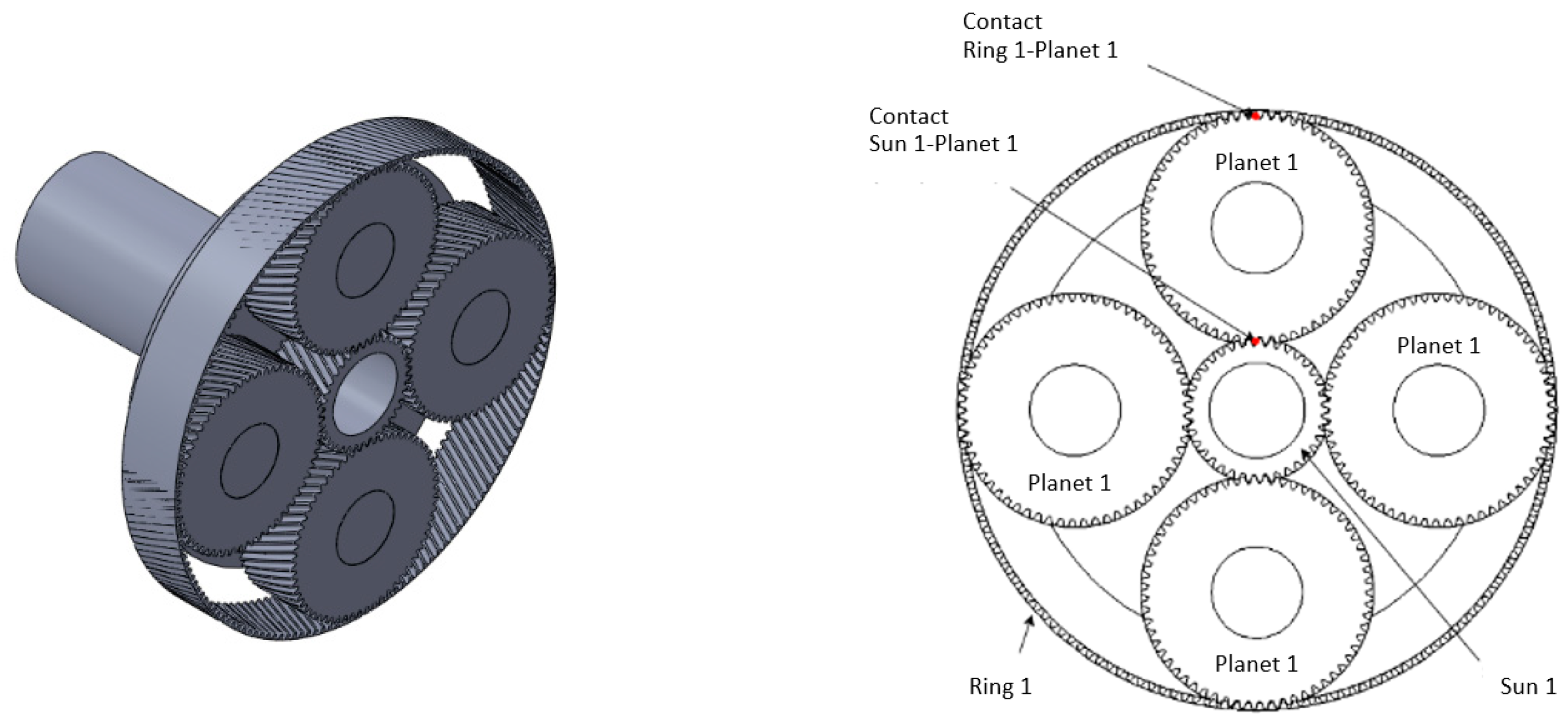
This torque arrives at the gearbox. It is transmitted to the first stage by the first stage epicyclic geartrain planet carrier. See the figure below:

$${T_{C1}=T}_{i1}$$

(5)

It will be assumed that there are no frictional energy losses, which will allow us to calculate the torque transmitted on the shafts of this first stage using the following expressions:

$$1. P_{S1}+P_{R1}+P_{C1}=0$$

(6)

$P_{S1}$ is the power reaching Sun 1, $P_{C1}$ is the power reaching Ring 1, and $P_{B1}$ is the power reaching Planet Carrier 1 [27].

$$2. T_{S1}·w_{S1}+T_{R1}·w_{R1}+T_{C1}·w_{C1}=0$$

(7)

$T_{S1}$ is the torque acting on Sun 1, $T_{R1}$ is the torque supported by Ring 1, and $T_{C1}$ is the torque acting on Planet Carrier 1.

$$3. T_{S1}+T_{R1}+T_{C1}=0$$

(It is considered that the geartrain is running at constant speed, or it changes speed slowly in a way that does not significantly affect its internal kinetic energy, so static equilibrium can be assumed).

Considering that $w_{R1}=0$, since the ring of the first stage is fixed, from Equation (7), the torque on the intermediate shaft and, consequently, on the output shaft of the Epicyclic Geartrain 1 can be obtained:

$$T_{S1}·w_{S1}+T_{C1}·w_{C1}=0\to T_{S1}=-\frac{T_{C1}·w_{C1}}{w_{S1}}$$

Next, the torque on the rest of the axes of each stage is calculated:

Stage E1: Input by Planet Carrier B1 and output by Sun S1. Considering Equation (5), the torque in Sun 1 is:

$$T_{S1}=-\frac{w_{i1}}{w_{S1}}·T_{C1}=-\frac{1}{10.35}·4774.65=-461.2748 \mathrm{k}\mathrm{N}·\mathrm{m}$$

Stage E2: Input by Planet Carrier C2≡S1 and output by Sun S2. Then, the torque in Sun 2 is:

$$T_{S2}=-\frac{w_{S1}}{w_{S2}}·T_{S1}=-\frac{1}{10.34}·(-461.765)=44.5676 \mathrm{k}\mathrm{N}·\mathrm{m}$$

Assuming that the material of the shafts is steel with a transverse stiffness modulus G = 81 GPa and imposing a maximum value to the torsional deflection (1.5°/m), the value of the diameters of each shaft is calculated. For the input shaft:

$${d_{carrier1}=d}_{i1}={\left(\frac{32·T_{i1}}{\pi ·G·\frac{\theta }{L}}\right)}^{\frac{1}{4}}={\left(\frac{32·4774.65·{10}^3}{\pi ·81·{10}^9·1.5·\frac{\pi }{180}}\right)}^{\frac{1}{4}}=0.3891 \mathrm{m}=38.91 \mathrm{c}\mathrm{m}$$

This value is coincident with that of the planet carrier of Stage 1:

For the intermediate shaft:

$$d_{int1}={\left(\frac{32·T_{S1}}{\pi ·G·\frac{\theta }{L}}\right)}^{\frac{1}{4}}={\left(\frac{32·(-461.2748·{10}^3)}{\pi ·81·{10}^9·1.5·\frac{\pi }{180}}\right)}^{\frac{1}{4}}=0.2169 \mathrm{m}=0.2169 \mathrm{c}\mathrm{m}$$

For the output shaft:

$$d_{i2}={\left(\frac{32·T_{S2}}{\pi ·G·\frac{\theta }{L}}\right)}^{\frac{1}{4}}={\left(\frac{32·44.5676·{10}^3}{\pi ·81·{10}^9·1.5·\frac{\pi }{180}}\right)}^{\frac{1}{4}}=0.1209 \mathrm{m}=12.09 \mathrm{c}\mathrm{m}$$

The results for the torques and shaft diameters are shown in

Table 6. Diameters of epicyclic geartrain shafts.

	Shaft Diameters (mm)
di1	389.15
dint1	216.95
di2	120.957

and Figure 5.

Next, the pitch diameters of the gears will be calculated. These diameters depend on the diameter of the shafts and parameters such as the tooth modulus.

Usually, as a first approximation, the pitch diameter of each gear will be obtained from the following formula:

$$D_{engr}=d_{shaft}+2·h_1+2.5·m_t+4·m_t$$

(8)

As it can be seen, the diameter of each gear $D_{engr}$ will depend on the theoretical normal modulus and $h_1$, which is the depth of the keyway, which will be obtained from the shaft diameter according to the standard DIN 3990 [28].

However, in this work and from Equation (8), the pitch diameter of each gear will be obtained from the following formula:

$$D_{engr}=d_{shaft}+K_{engr}$$

(9)

In Figure 6, where $D_{engr}$ is the pitch diameter of the gear being analyzed, and it can be the sun, planet, or ring gear. $d_{shaft}$ is the diameter of the shaft supporting the gear. It must be sufficient to provide the required torsional stiffness. And $K_{engr}$ is a constant parameter that will determine the size of the pitch diameter $D_{engr}$ of the gears from the corresponding shaft diameter.

This parameter $K_{engr}$ considers the apparent gear modulus $m_t$, the tooth height, and the value of $h_1$ (the depth of the keyway in the hub). In this work, the influence of this parameter on the value of the pitch diameter will be analyzed.

With the data of shaft diameters and $K_{engr}$, the values of the pitch diameters of the gears can be obtained.

On the other hand, the minimum number of teeth must also be considered to avoid interferences. As the starting data, the normal pressure angle ${\alpha }_n=20°$, and the helix angle $\beta =20°$ are known for the calculation of the minimum number of teeth, the following expressions are used:

$$\mathit{tan}\left({\alpha }_n\right)=\mathit{tan}\left({\alpha }_t\right)·\cos \left(\beta \right)\to {\alpha }_t=\arctan \left(\frac{\mathit{tan}\left({\alpha }_n\right)}{\cos \left(\beta \right)}\right)=\arctan \left(\frac{\mathit{tan}\left(20°\right)}{\cos \left(25°\right)}\right)=21.88°$$

(10)

$$Z_{min}=\frac{2·\mathrm{c}\mathrm{o}\mathrm{s}\left(\beta \right)}{{sen\left({\alpha }_t\right)}^2}=\frac{2·\mathrm{c}\mathrm{o}\mathrm{s}(25°)}{{sen(21.88°)}^2}=13.05 teeth$$

(11)

In addition, the apparent modulus for spur gears is:

$$m_t=\frac{m_n}{\mathrm{c}\mathrm{o}\mathrm{s}\left(\beta \right)}$$

(12)

The pitch diameters of the gears must also comply with the required gear ratios.

A value in the maximum and minimum deviation of the epicyclic gear ratio of 1% will be assumed; therefore:

$$i_{max}=i_T·1.02=107·1.02=109.14\to i_{imax}=\sqrt[3]{109.14}=10.44$$

$$i_{min}=i_T·0.98=107·0.98=104.86\to i_{imin}=\sqrt[3]{104.86}=10.24$$

A table with possible solutions from various normalized modulus values will be elaborated. It must be considered that the geometrical values of gears obtained must fulfill a set of conditions.

The gearbox consists of two stages, each consisting of an epicyclic planetary gear train. The gear ratio will be equal in each stage and will have to be contained between the maximum and minimum values previously calculated.

$$i_{i1}=i_{i2}=\left(1+\frac{Z_{c1}}{Z_{s1}}\right)=\left(1+\frac{Z_{c2}}{Z_{s2}}\right)=10.34$$

The transmission ratio for the first stage, applying the Willis formula, is:

$$i_{ap1}=\frac{{\omega }_{sun1}-{\omega }_{carrier1}}{-{\omega }_{carrier1}}=-\frac{z_{ring1}}{z_{sun1}}$$

(13)

$$i_{i/o 1}=\frac{{\omega }_{sun1}}{{\omega }_{carrier1}}=1-i_{ap1}$$

(14)

The epicyclic gear Model 1 has some geometrical characteristics that must be taken into account. One of them is the following:

$$D_{ring}=D_{sun}+{2·D}_{planet}$$

(15)

That is, the pitch diameter of the ring is equal to the sum of the pitch diameter of the sun plus twice the pitch diameter of the planet.

It is also advisable to introduce as many satellites as possible so that the loads transmitted in the epicyclic train are better distributed and the risk of gear tooth failure is minimized.

The following geometrical conditions must be met for each stage:

(a)

Coaxiality condition, derived from Equation (15):

$$z_{ring}={2·z}_{pla}+z_{sun}$$

(16)

(b)

Mounting condition—the number of teeth of the sun plus the ring divided by the number of satellites must be a whole number:

$$Integer number=\frac{Z_{ring}+Z_{sun}}{n_{planets}}\mathrm{w}\mathrm{i}\mathrm{t}\mathrm{h} N\in {\mathbb{N}}^{+}$$

(17)

(c)

Contiguity condition—this translates into $\pi ·D_m>n_{planets}·D_{planet}$, that is to say,

$$\frac{\pi }{2}·\frac{Z_{ring}+Z_{Sun}}{Z_{Planet}+2\cos \beta }>n_{planets}$$

(18)

(d)

Maximum number of planets: $n_{planets}=\frac{360°}{2·(90°-arcos\frac{z_{planet}+2}{z_{ring}+z_{sun}})}$

(e)

To avoid interference:

$$z_{min}=\frac{2·cos\beta }{\mathrm{s}\mathrm{i}\mathrm{n}{\left({\alpha }_t\right)}^2}$$

(19)

For Stage 1, see Figure 7:

Calculation of the Weight of the Epicyclic Gear Model 1

In a simplified form, the weight of the epicyclic gear, related to the mass of the train, depends on the volume of each of its elements. It is proportional to the volume of the ring gear assembly, the planets, the sun, the planet carrier, and the auxiliary elements such as bearings and bolts. Therefore:

$$W_{model1}=m_{model}·g$$

(20)

$$m_{model1}=V_{model1}·\rho$$

(21)

With $\rho$ being the density of the material or materials used in the manufacture of the gears and other constituent elements of the epicyclic train.

On the other hand:

$$V_{Train1}=V_{ring1}+V_{planet1}+V_{sun1}+V_{carrier1}$$

(22)

where:

$$V_{ring1}=\frac{\pi ·\left[{\left(D_{sun1}+2·D_{planet1}+8·m_n\right)}^2-{\left(D_{sun1}+2·D_{planet1}\right)}^2\right]·b}{4·{1000}^3}({\mathrm{m}}^3)$$

$$V_{sun1}=\frac{\pi ·{\left(D_{sun1}\right)}^2·b}{4·{1000}^3}({\mathrm{m}}^3)$$

$$V_{planet1}=\frac{\pi ·{\left(D_{planet1}\right)}^2·b}{4·{1000}^3}·n_{planet} ({\mathrm{m}}^3)$$

$$V_{carrier1}=\frac{2·\pi ·{\left(D_{sun1 }+D_{planet1}\right)}^2·0.1·b}{4·{1000}^3}({\mathrm{m}}^3)$$

In the above expressions, $b$ is the width of the tooth, $D_{sun1}$ the pitch diameter of the sun at Stage 1, $D_{planet1}$ the pitch diameter of a planet at Stage 1, $m_n$ the normal modulus, and $n_{planet}$ the number of planets at Stage 1. Carrier for epicyclic geartrain Model 1 is shown in Figure 8:

The determinant value to fulfil the geometrical conditions (a), (b), (c), and (d) is the pitch diameter of each gear, from which the number of teeth of the gears will be calculated. This, in turn, is calculated from the diameter of the corresponding shaft; see Equation (9):

$$D_{engr}=d_{shaft}+K_{engr}$$

For small values of $K_{engr}$, the value of $D_{engr}$ is also small. This circumstance means that the thickness of tooth “$b$”, in order to meet the sizing criteria for a material with known strength characteristics, is very high. These criteria are:

(a)

Tension at the base of the tooth: ${\sigma }_F\le \frac{S_{FP}}{X_F}$

(b)

Surface pressure on the tooth: ${\sigma }_H\le \frac{S_{HP}}{X_H^2}$

This means that, to obtain reasonable values of “$b$”, it is necessary to increase the value of $K_{engr}$.

Next, a series of results for the gear diameters and for the mass of the epicyclic geartrain of Stage 1 will be obtained from the following values of normal moduli:

$m_n\left(\mathrm{mm}\right)$

10

15

20

25

30

35

40

45

50

60

70

80

90

100

The relationship between $m_t$ and $m_n$ is determined by Equation (3). For the calculation of ${\sigma }_H$, the stress supported by the teeth due to surface pressure, we use the following expression:

$${\sigma }_H=Z_H·Z_E·Z_{\epsilon }·Z_{\beta }·\sqrt{\frac{F_t}{d_1·b_H}·\frac{i+1}{i}}·\sqrt{K_A·K_V·K_{H\alpha }·K_{H\beta }} (\frac{\mathrm{N}}{{\mathrm{mm}}^2})$$

(23)

Considering that the following condition must be fulfilled:

$${\sigma }_H\le \frac{S_{HP}}{X_H^2}$$

(24)

where $S_{HP}$ is the maximum allowable contact stress and $X_H$ is the safety coefficient at maximum pressure. It will be assumed that $X_H=1.5$.

From Equation (14), $b_H$ (the tooth width to avoid surface pressure failure) will be obtained. The calculation of the tooth width $b_H$ follows an iterative process. To start the iterative process, a starting material with known allowable stresses $S_{HP}$, an estimate of the type of lubricant required, and an initial modulus will be assumed. The stresses appearing at the tooth-to-tooth contact ${\sigma }_H$ due to pressure and at the tooth base ${\sigma }_F$ due to bending will be calculated. These stresses are compared with the allowable stresses of the material.

In Equation (13):

$F_t$ is the transmitted tangential force. It is calculated as $F_t=\frac{P}{{n·\omega }_1·r_1}$, with ${\omega }_1$ as the angular velocity of the pinion (sun), $n$ the number of planets, $r_1$ the radius of the pinion (sun), and $d_1=z_1·m_t$ the pitch diameter of the pinion. $b_H$ is the width of the pinion tooth to resist the surface pressure. Gear ratio $i$. $Z_H=\sqrt{\frac{2·cos{\beta }_b}{sin{\alpha }_t·cos{\alpha }_t}}$ is the geometrical coefficient (${\alpha }_t$ is the apparent pressure angle and ${\beta }_b$ is the helix angle at the base of the tooth). $Z_E=\sqrt{\frac{1}{\pi ·\left(\frac{1-{\nu }_1^2}{E_1}+\frac{1-{\nu }_2^2}{E_2}\right)}}$ is the elastic coefficient with $\nu$ and $\mathrm{E}$ being the Poisson’s coefficient and the elastic coefficient of the wheel and pinion. $Z_{\epsilon }\left(b\right)$ is the driving coefficient. It depends on the tooth width. $Z_{\beta }=\frac{1}{\sqrt{cos\beta }}$ is the helix angle factor. $K_A$ is the application coefficient. It is consulted in tables. $K_V\left(b\right)=1+\left(\frac{K_1}{K_A·\frac{F_t}{b}}+K_2\right)·\frac{v·z_1}{100}·K_3·\sqrt{\frac{i^2}{1+i^2}}$ is the dynamic coefficient. The constants $K_1$, $K_2$, and $K_3$ depend on the tooth type, finish quality, rotational speed, number of teeth, and gear ratio. $K_{H\alpha }$ is the transverse load distribution coefficient. $K_{H\beta }$ is the longitudinal load distribution coefficient. The tooth width is obtained by isolating from (23):

$$b_H={\left(\frac{Z_H·Z_E·Z_{\epsilon }\left(b\right)·Z_{\beta }}{{\sigma }_H}\right)}^2·\frac{F_t}{d_1·}·\frac{i+1}{i}·K_A·K_V(b)·K_{H\alpha }·K_{H\beta }(b)$$

(25)

To check for failure by breakage at the base of the tooth, the bending stress supported by the teeth is calculated:

$${\sigma }_F=\frac{F_t}{m_n·b_F}·Y_{Fa}·{Y_{\epsilon }·Y}_{Sa}·Y_{\beta }·Y_B·K_A·K_V·K_{F\alpha }·K_{F\beta } (\frac{\mathrm{N}}{{\mathrm{mm}}^2})$$

(26)

where $Y_{Fa}=38.88·z_{1v}^{-1.29}+2.11$ is the shape coefficient, and $z_{1v}=\frac{z_1}{cos{\beta }^3}$ is the virtual number of teeth. $Y_{\epsilon }=0.25+\frac{0.75}{{\epsilon }_{\alpha }}$ is the driving coefficient. ${\epsilon }_{\alpha }$ is the driving ratio. $Y_{Sa}=0.96+0.54·\mathrm{l}\mathrm{o}\mathrm{g}\left(z_{1v}\right)$ is the stress concentrator coefficient. $Y_{\beta }=1-{\epsilon }_{\beta }·\frac{\beta }{120 °}$ is the slope coefficient. $Y_B=1$ is the hoop thickness coefficient. $K_{F\beta }={K_{H\beta }}^{N_F}$ is the longitudinal load distribution coefficient. $K_{F\alpha }$ is the transverse load distribution coefficient. It depends on the finish quality ($Q_{iso}=5-6$). Defining the tooth fracture safety coefficient as:

$$X_F=\frac{S_{FP}}{{\sigma }_F}$$

(27)

The process of calculating the tooth width “$b$” ends when $X_F\ge X_H$.

6. Results and Discussion

For simplicity, only the first stage epicyclic gear train will be analyzed. The following design data in

Table 7. Design data for epicyclic gear trains stage 1.

P	$7 \mathrm{M}\mathrm{W}$
${\omega }_{carrier1}$	$14 \mathrm{r}\mathrm{p}\mathrm{m}$
${\omega }_{sun1}$	$144.9 \mathrm{r}\mathrm{p}\mathrm{m}$
$i_{ap1}$	$-9.35$
$i_{E1}$	$10.35$
$i_T$	$107.1429$

are assumed:

From the solution of Equations (1)–(27), the values represented in the following tables are obtained, which provide data on the characteristics of the gears forming the epicyclic train of Stage 1.

Table 8. For K_engr1 = 6·m_t, and hardening steel.

	dcarr1	ds1	Ds1	zs1	zp1	zcor1	iap1	b	W
mn = 10	389.15	216.95	280.80	26	109	244	9.38	>2500	No
mn = 15	389.15	216.95	312.73	20	84	188	9.4	>2500	No
mn = 20	389.15	216.95	344.65	16	67	150	9.37	>2500	No
mn = 25	389.15	216.95	376.58	14	59	132	9.42	>2500	No
mn = 30	389.15	216.95	408.51	14	55	123	9.46	>2500	No

shows, for different values of the normal values of the normal modulus m_n, the values of the diameter of the input shaft to the epicyclic gear train of Stage 1, which correspond to the planet carrier (d_carr1), diameter of the sun axis in Stage 1 (d_s1), the pitch diameter of the sun in Stage 1 (D_s1), the number of teeth of the sun (z_s1), of the planets (z_p1) and ring at Stage 1 (z_cor1), the apparent gear ratio in Stage 1 (i_ap1), the tooth width for all Stage 1 gears (b) and a proportional estimate of the weight of the epicyclic gear train (W). It can be noticed that, for any value of m_n, the value of the tooth width is excessive. Moreover, the pitch diameter D_s1 is small due to the low value of $K_{engr}$—see Equation (9)— which means that the tooth width is too large to comply with the safety coefficients (Equations (24) and (27)) and the weight of the planetary train of the first stage is excessive. In addition, from the normal modulus 25, interference in the sun of Stage 1 is reached—see Equation (19)—so that it is not possible to use larger moduli.

It is concluded that $K_{engr}=6·m_t$ is useless. The data obtained correspond to a case hardening steel which has very high permissible stress limits. Any other material with lower levels of stress limits would worsen the results. The next step is to increase the value of $K_{engr}$ and the results are shown in

Table 9. For $K_{engr2}=15·m_t$. These data are obtained *.

	dcarrier1	ds1	Ds1	zs1	zp1	zring1	iap1	b2	W2
mn = 10	389.15	216.95	376.58	35	146	327		>2500	No
mn = 15	389.15	216.95	456.39	29	121	271		>2500	No
mn = 20	389.15	216.95	536.21	25	105	234		>2500	No
mn = 25	389.15	216.95	616.02	23	96	215		742	138.44
mn = 30	389.15	216.95	695.83	22	92	206		467	115.60
mn = 35	389.15	216.95	775.65	21	88	196		353	109.16
mn = 40	389.15	216.95	855.46	20	84	187		305	112.61
mn = 45	389.15	216.95	935.27	20	84	187		248	115.87
mn = 50	389.15	216.95	1015.	19	880	178		227	116.64
mn = 60	389.15	216.95	1174.7	18	75	168		178	119.39
mn = 70	389.15	216.95	1334.3	18	75	168		130	118.64
mn = 80	389.15	216.95	1494	18	75	168		99	117.04
mn = 90	389.15	216.95	1652.6	17	71	159		87	117.75
mn = 100	389.15	216.95	1813.2	17	71	159		69	115.84

* Same material as in Table 11. The weight obtained (represented by the letter “W”) is too large and “no”.

,

Table 10. For $K_{engr3}=20·m_t$. These data are obtained *.

	dcarrier1	ds1	Ds1	zs1	zp1	zring	iap1	b3	W3
mn = 10	389.15	216.95	429.79	40	167	374	9.35	>2500	No
mn = 15	389.15	216.95	536.21	34	142	318	9.35	>2500	No
mn = 20	389.15	216.95	642.62	30	126	282	9.4	611	121.41
mn = 25	389.15	216.95	749.04	28	117	262	9.35	391	106.66
mn = 30	389.15	216.95	855.46	27	113	253	9.37	274	100.65
mn = 35	389.15	216.95	961.88	26	109	244	9.38	230	107.01
mn = 40	389.15	216.95	1068.3	25	105	235	9.4	196	110.91
mn = 45	389.15	216.95	1174.7	25	105	235	9.4	157	112.37
mn = 50	389.15	216.95	1281.1	24	100	224	9.33	139	112.15
mn = 60	389.15	216.95	1494.0	23	96	215	9.34	105	112.68
mn = 70	389.15	216.95	1706.8	23	96	215	9.34	76	110.62
mn = 80	389.15	216.95	1919.6	23	96	215	9.34	57	108.85
mn = 90	389.15	216.95	2132.5	22	92	206	9.36	49	108.69
mn = 100	389.15	216.95	2345.3	22	92	206	9.36	39	107.21

* Same material as in Table 11.

and

Table 11. For $K_{engr4}=30·m_t$. These data are obtained *.

	dcarrier1	ds1	Ds1	zs1	zp1	zring	iap1	b4	W4
mn = 10	389.15	216.95	536.21	50	209	468	9.36	>2500	No
mn = 15	389.15	216.95	695.83	44	184	412	9.36	443	105.26
mn = 20	389.15	216.95	855.46	40	167	374	9.35	274	95.69
mn = 25	389.15	216.95	1015.1	38	159	356	9.36	194	96.22
mn = 30	389.15	216.95	1174.7	37	155	347	9.37	151	102.17
mn = 35	389.15	216.95	1334.3	36	151	338	9.38	120	104.09
mn = 40	389.15	216.95	1494	35	146	327	9.34	99	105.55
mn = 45	389.15	216.95	1653.6	35	146	327	9.34	78	105.74
mn = 50	389.15	216.95	1813.2	34	142	318	9.35	64	105.99
mn = 60	389.15	216.95	2132.5	33	138	309	9.36	49	105.46
mn = 70	389.15	216.95	2451.7	33	138	309	9.36	36	104.2
mn = 80	389.15	216.95	2771.0	33	138	309	9.36	27	103.05
mn = 90	389.15	216.95	3090.2	32	134	300	9.37	23	102.53
mn = 100	389.15	216.95	3409.5	32	134	300	9.37	18	101.69

* alloy steel, hardened and tempered.

. The pitch diameters (volume), teeth width, and mass of the epicyclic geartrain have been obtained.

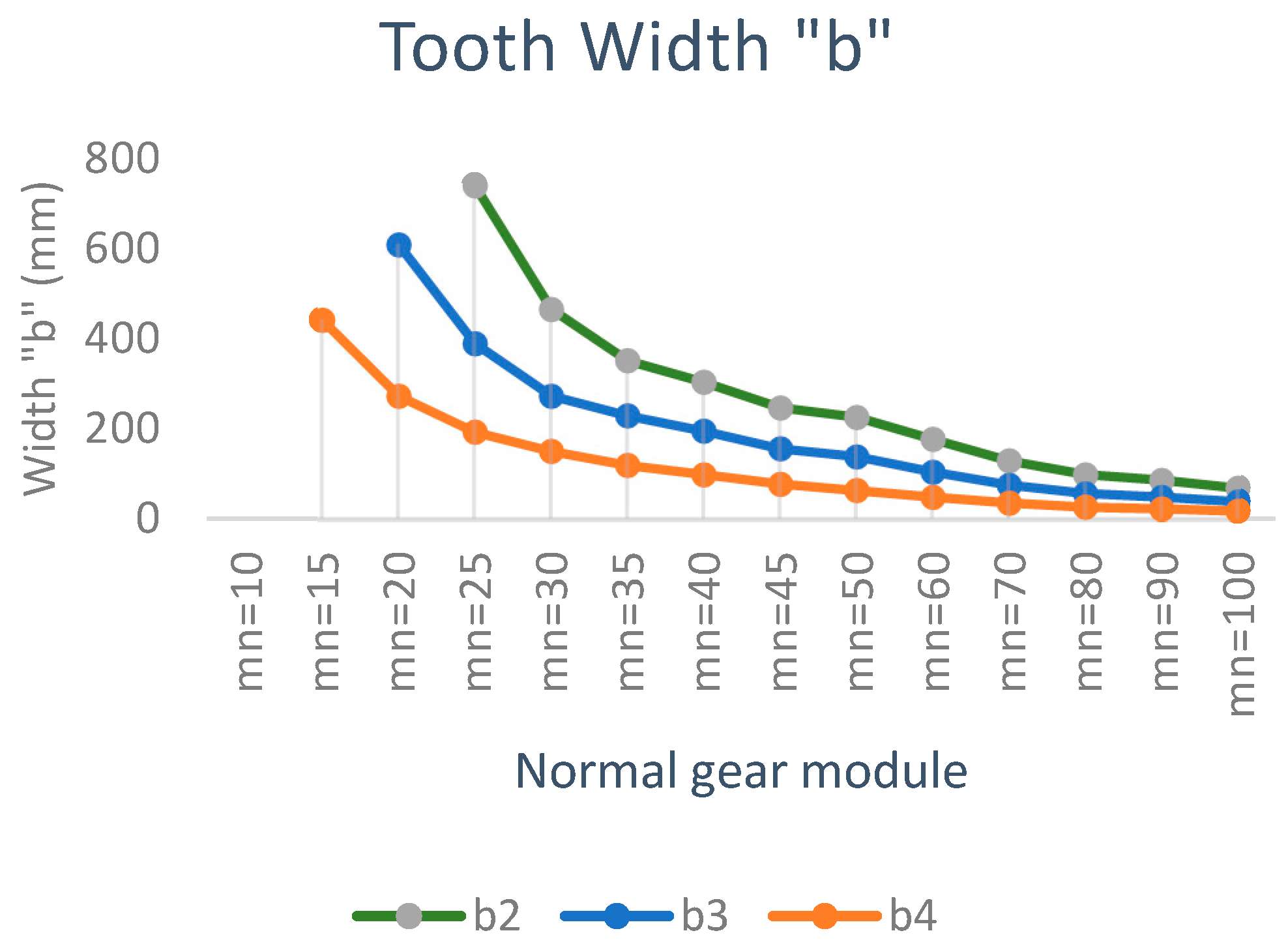
Figure 9 and Figure 10 relate the modulus to the width of the tooth and to the weight of the epicyclic gear train of Stage 1, respectively.

From Figure 9, it can be seen that the tooth width decreases when increasing the module and the pitch diameter through the parameter $K_{engr}$. The larger the $K_{engr}$ ($K_{engr4}$ > $K_{engr3}$ > $K_{engr2}$) is, the smaller the tooth width is. This result has a major influence on the epicyclic geartrain (which is one of the objectives pursued).

From Figure 9 and Figure 10, it can be notice that not all modules are usable, either because they give rise to interferences in the teeth or because the width “b” of the teeth exceeds the value of 2D, which is the recommended value.

In Figure 10, there is an aspect that is not intuitive and very important: when the size of the pitch diameter increases ($K_{engr4}$ > $K_{engr3}$ > $K_{engr2}$), the weight decreases.

Moreover, the weight first decreases, and then it increases as the modulus increases.

This means that there is a value for $K_{engr}$ that minimizes the weight of the epicyclic gear train by acting on the value of the diameters and the tooth width.

It is also observed that the weight increases above a certain value of the normal modulus for each $K_{engr}$.

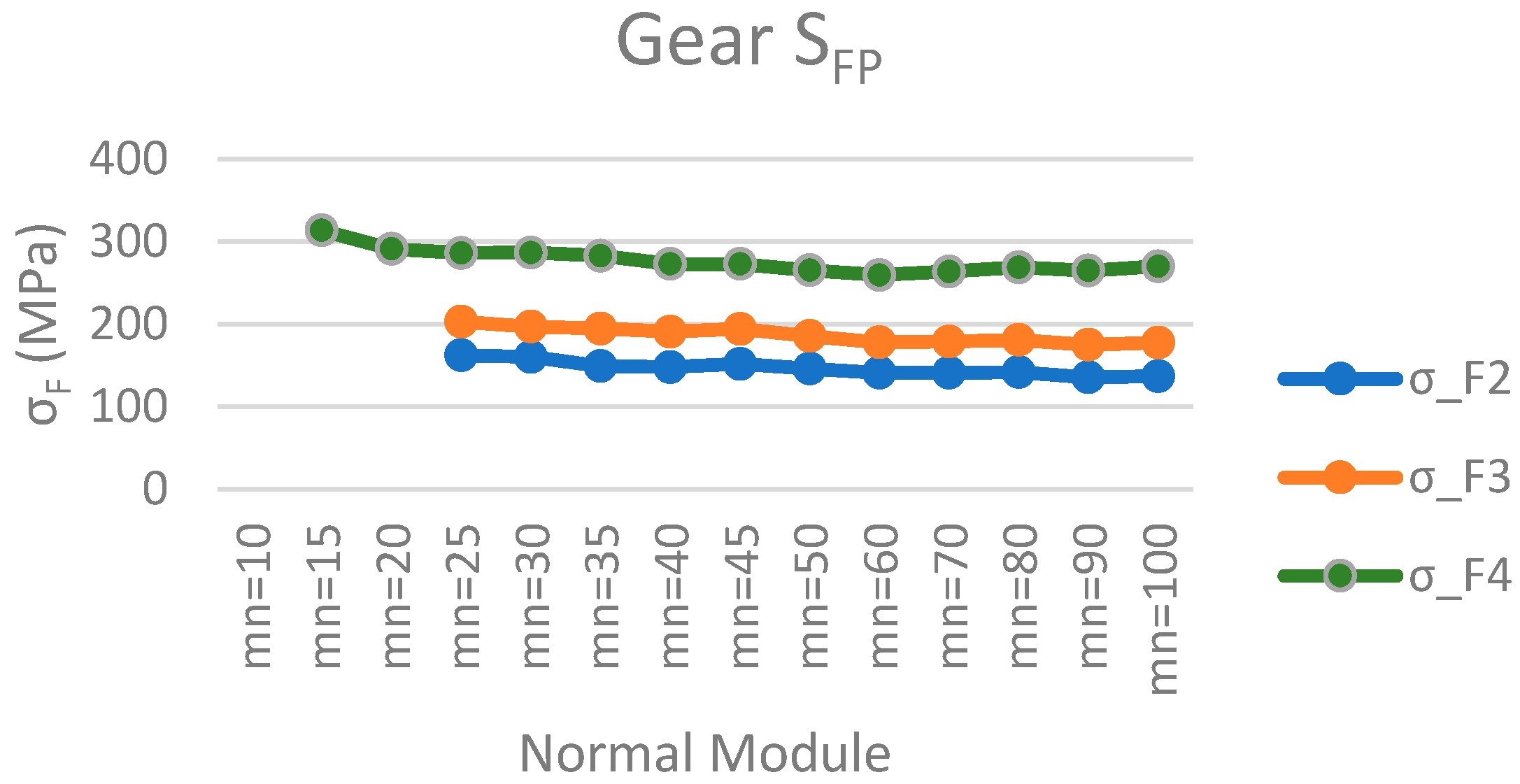
In Figure 11, it is shown that the larger the pitch diameter is, the higher the bending strength at the base of the tooth is.

On the other hand, the bending strength at the base of the tooth decreases slightly as the normal tooth modulus increases.

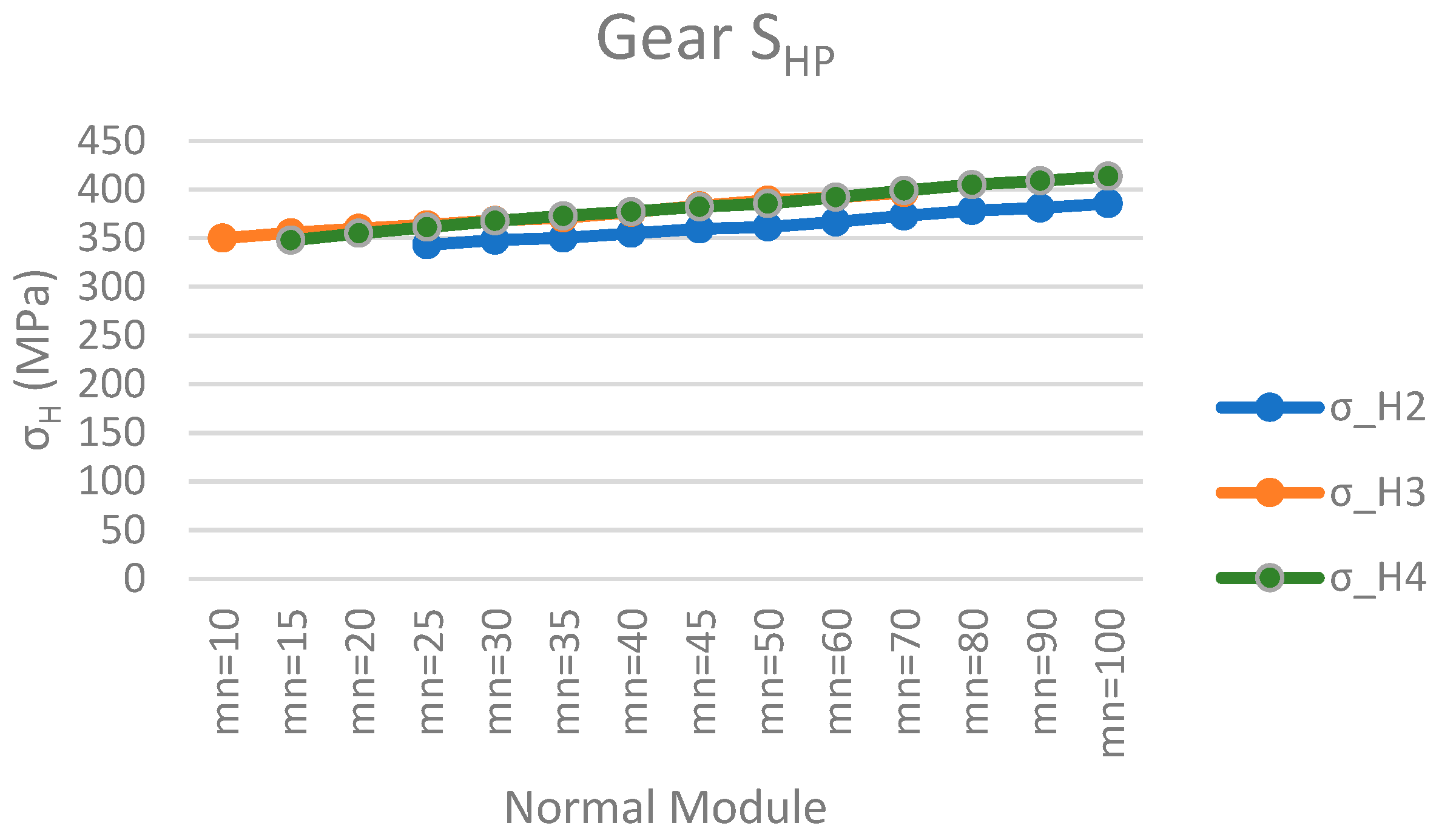
In Figure 12, it is shown that the greater the pitch diameter, the higher the surface pressure resistant limit. On the other hand, the bending strength at the base of the tooth increases slightly as the normal tooth modulus increases.

7. Conclusions

For very small values of $K_{engr}$ (with $K_{engr1}=6·m_t$), the resulting gearing is also too small and results in the width of tooth “b” being too large to support the stresses generated in the teeth.

When $K_{engr}$ is small (such as $K_{engr1}$), the strength properties of the material must be higher; otherwise, the geartrain will have interference or an excessive tooth width, and, thus, an unacceptable mass of the epicyclic gear train, and, therefore, the compactness target of the epicyclic gear train is unattainable.

This means that the pitch diameter is also very small. This determines the number of gear teeth and the width of the gears. For a small pitch diameter, if large modules are used, the number of teeth is too small and causes interference.

If the module is reduced by taking low values, the number of teeth increases, overcoming the problem of interference, but the width of the teeth is too wide to withstand the stresses generated. This means that the volume and weight of the gear train is, therefore, not operational, or useful.

This means that the volume and weight of the gear train is excessive, and, therefore, these modulus values do not serve to meet our objective of determining a minimum-weight planetary gear train.

According to this finding, the value of the pitch diameter must be increased.

It has also been observed that the width of tooth “b” decreases when the pitch diameter of the gears is increased (this means that $K_{engr} \mathrm{i}\mathrm{n}\mathrm{c}\mathrm{r}\mathrm{e}\mathrm{a}\mathrm{s}\mathrm{e}\mathrm{s}$). The larger the $K_{engr}$ ($K_{engr4}$ > $K_{engr3}$ > $K_{engr2}$) is, the smaller the tooth width is. This has an impact on the mass value of the epicyclic train and, therefore, helps to achieve the desired compactness of the epicyclic train.

Therefore, this last result leads to a lower weight of the epicyclic train, as shown in Figure 8, which met the paper’s objectives. However, there is a trade-off between the value of the tooth width and the volume of the epicyclic train, because, as $K_{engr}$ increases, the diameter of the gears also increases, which can lead into an increase in gear train volume, which is an issue to be considered if compact gear trains are to be obtained.

Another item observed is that the tooth width decreases as the value of the normal modulus increases.

On the other hand, not all moduli are usable, either because they give rise to interferences in the toothing or because the width “b” is too large or too small (b > 2D, or b << D, far from the recommended values).

It can also be seen that, when the size of the pitch diameter increases ($K_{engr4}$ > $K_{engr3}$ > $K_{engr2}$), the weight decreases.

This means that there is a value for $K_{engr}$ that minimizes the weight of the gears by acting on the value of the diameters and the value of the tooth width.

Moreover, there is a value for $K_{engr}$ that minimizes the volume of the gears, which, altogether, leads to a change in the weight and the volume of the Epicyclic Geartrain Model 1.

Finally, the Epicyclic Geartrain Model 1 allows us to obtain the lowest volumes, the lowest weight, and, therefore, the maximum compactness and energy density compared to other epicyclic geartrain models.