Damage Metrics for Void Detection in Adhesive Single-Lap Joints
Abstract
:1. Introduction
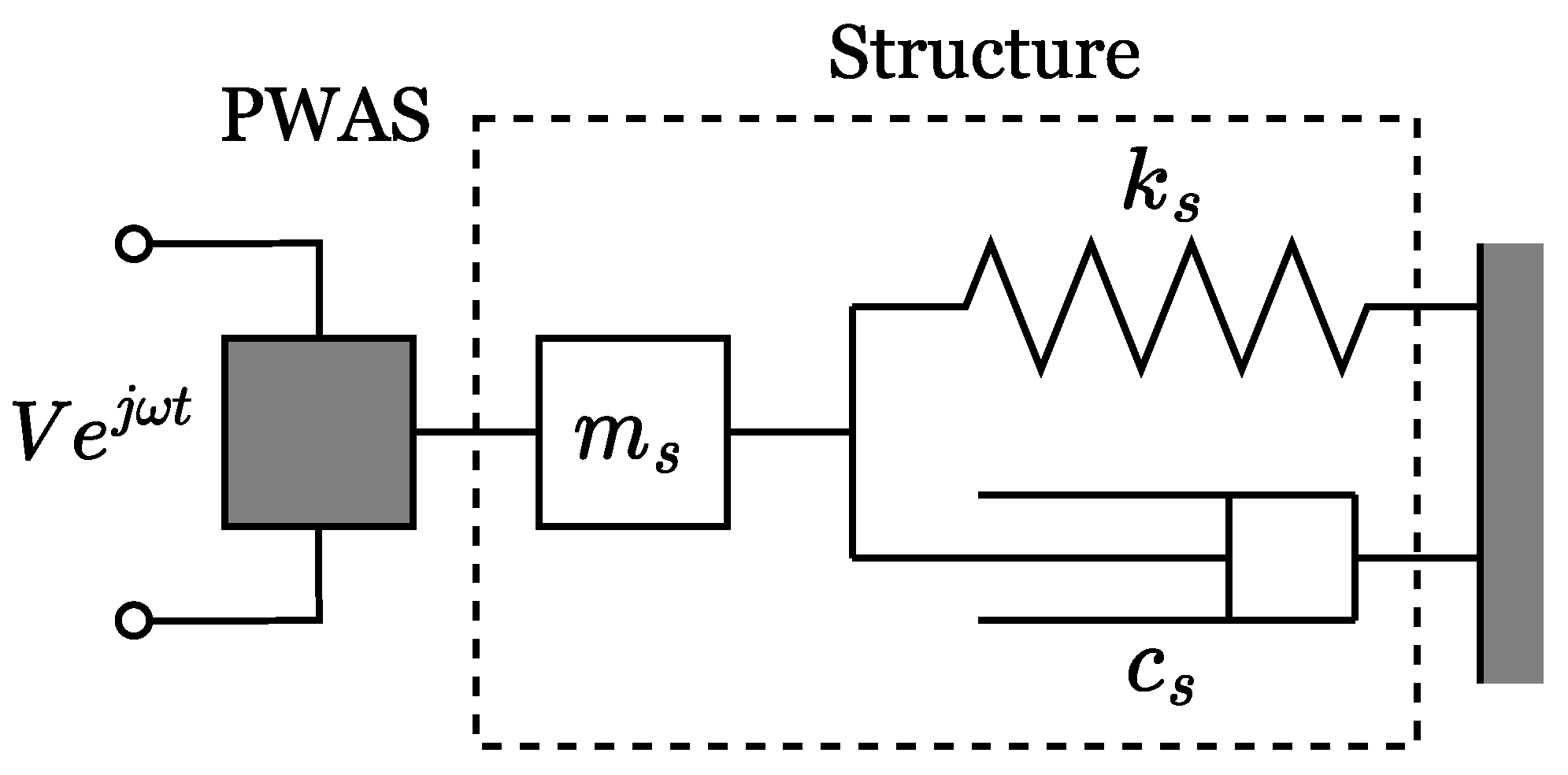
2. Damage Metrics
2.1. Conventional Damage Metrics
2.2. Proposed Damage Metrics
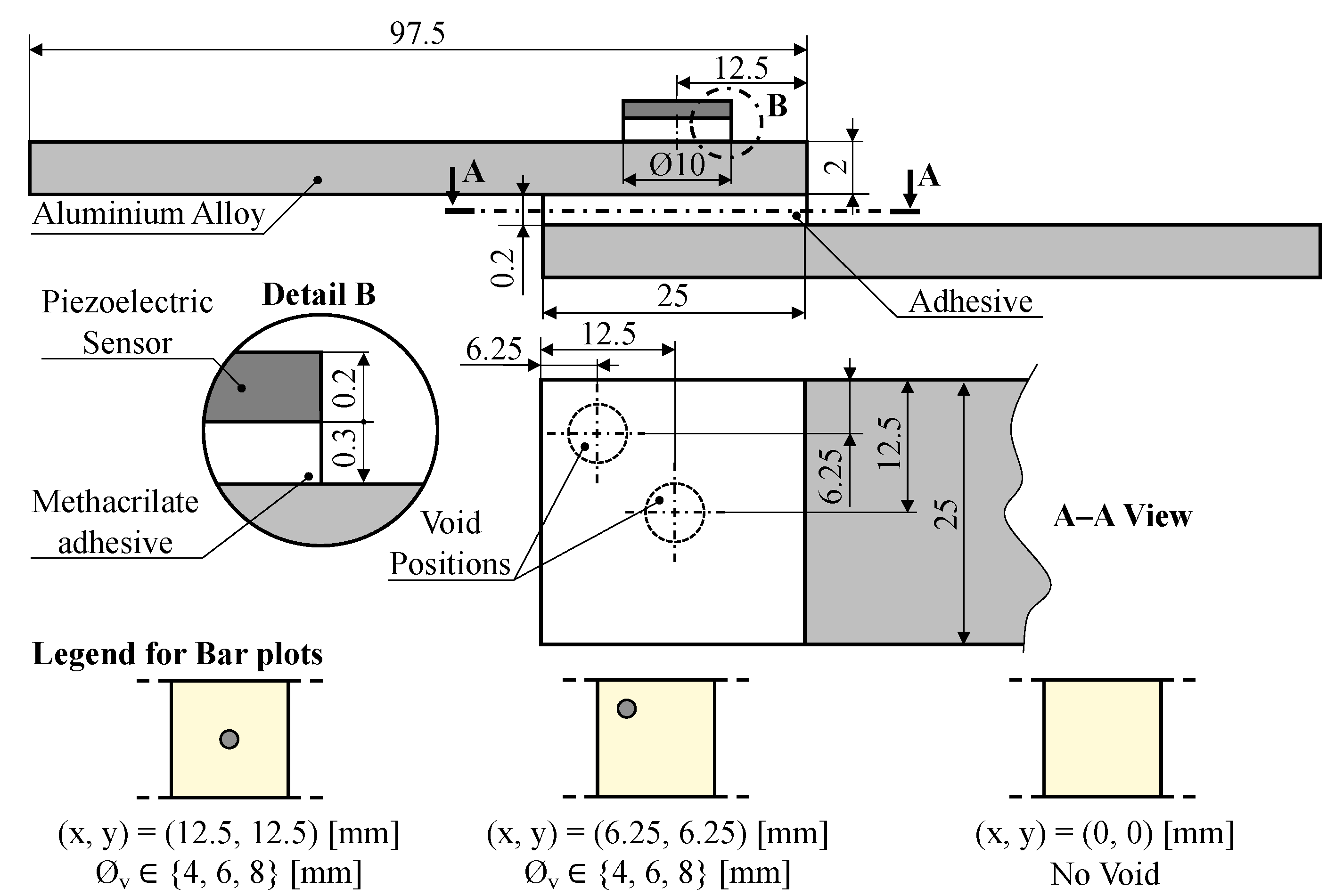
3. Experimental Details
3.1. Materials and Manufacture
3.2. Specimen Instrumentation and Measurements
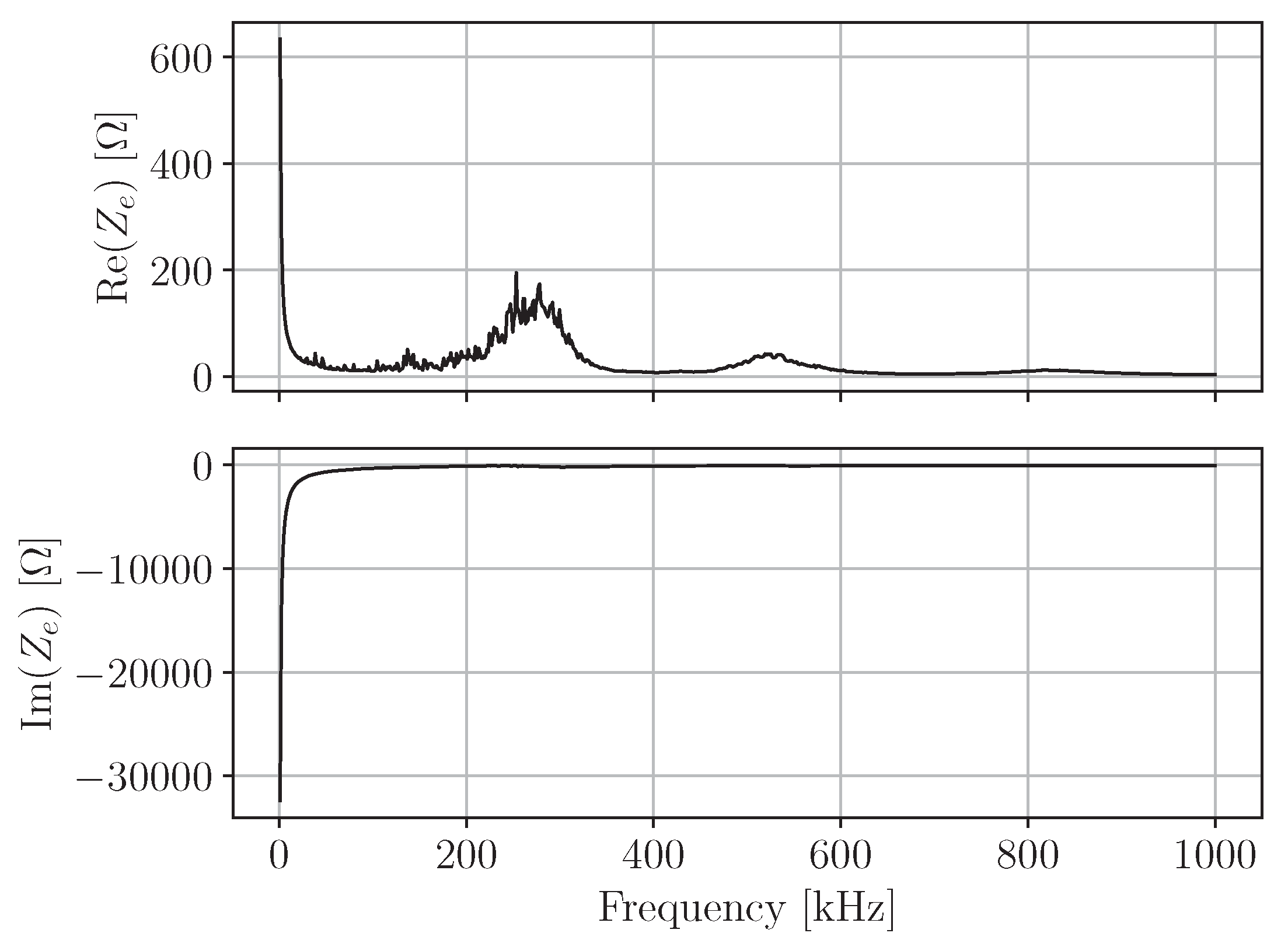
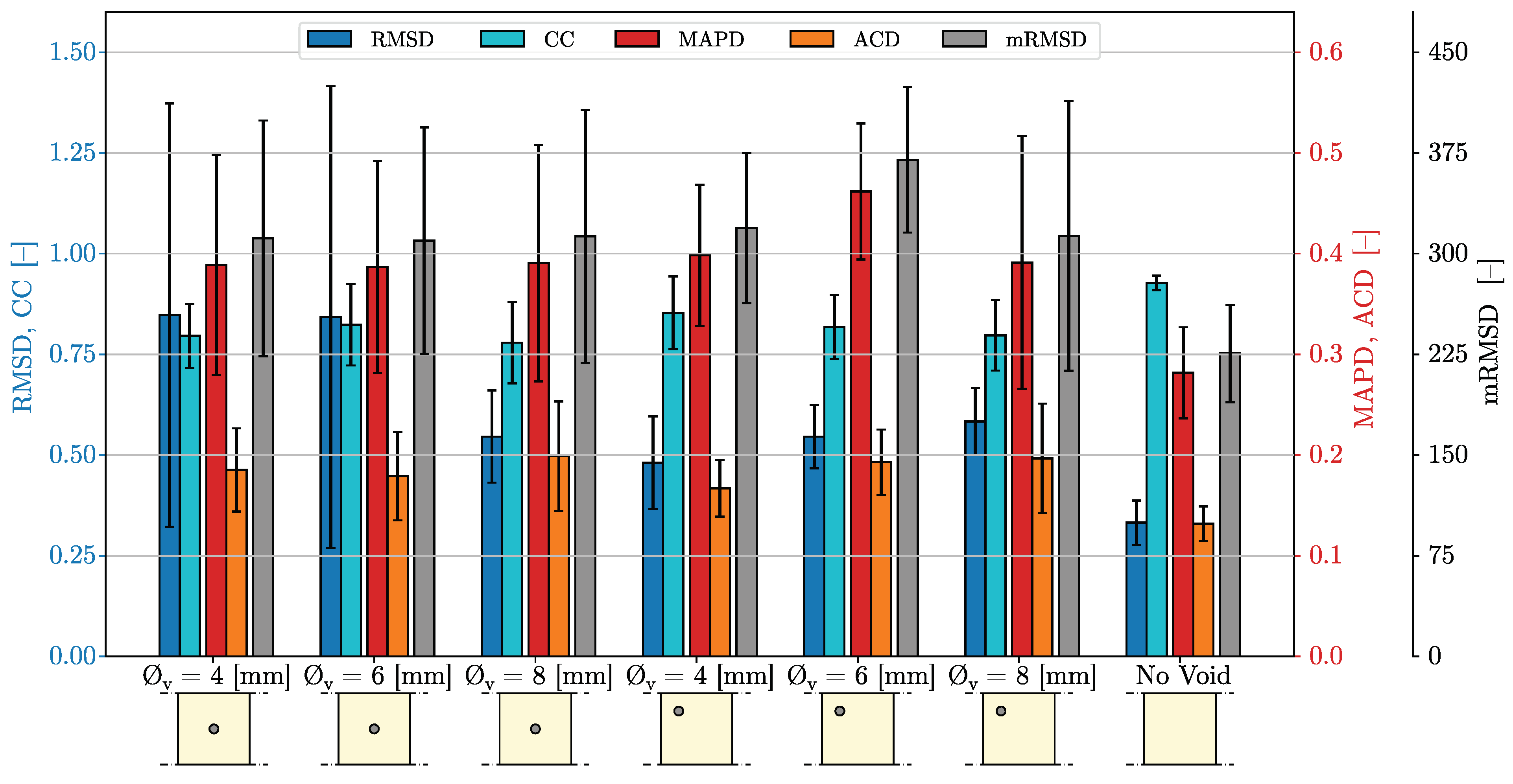
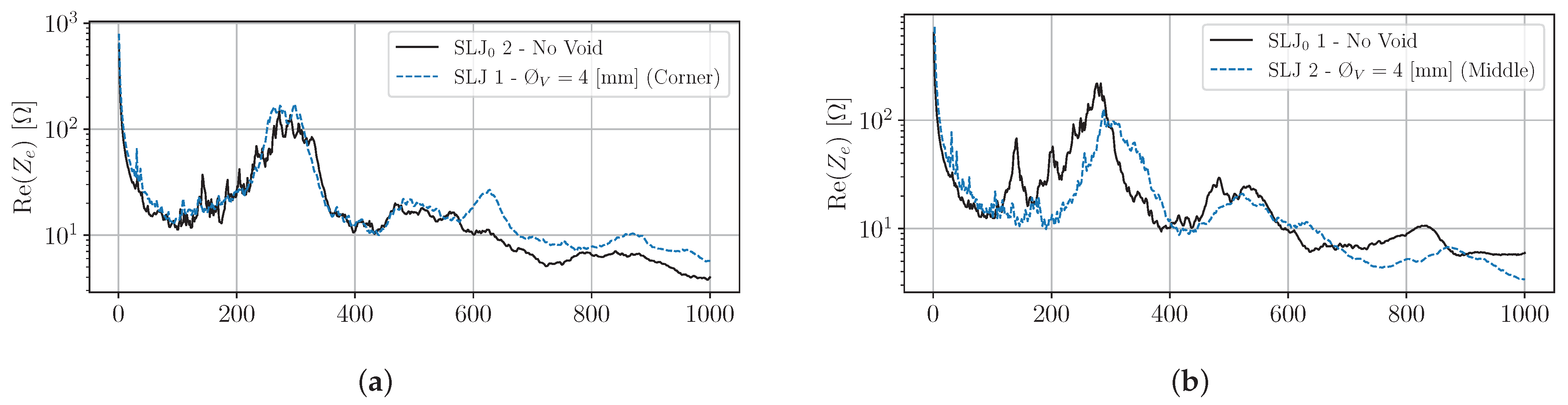
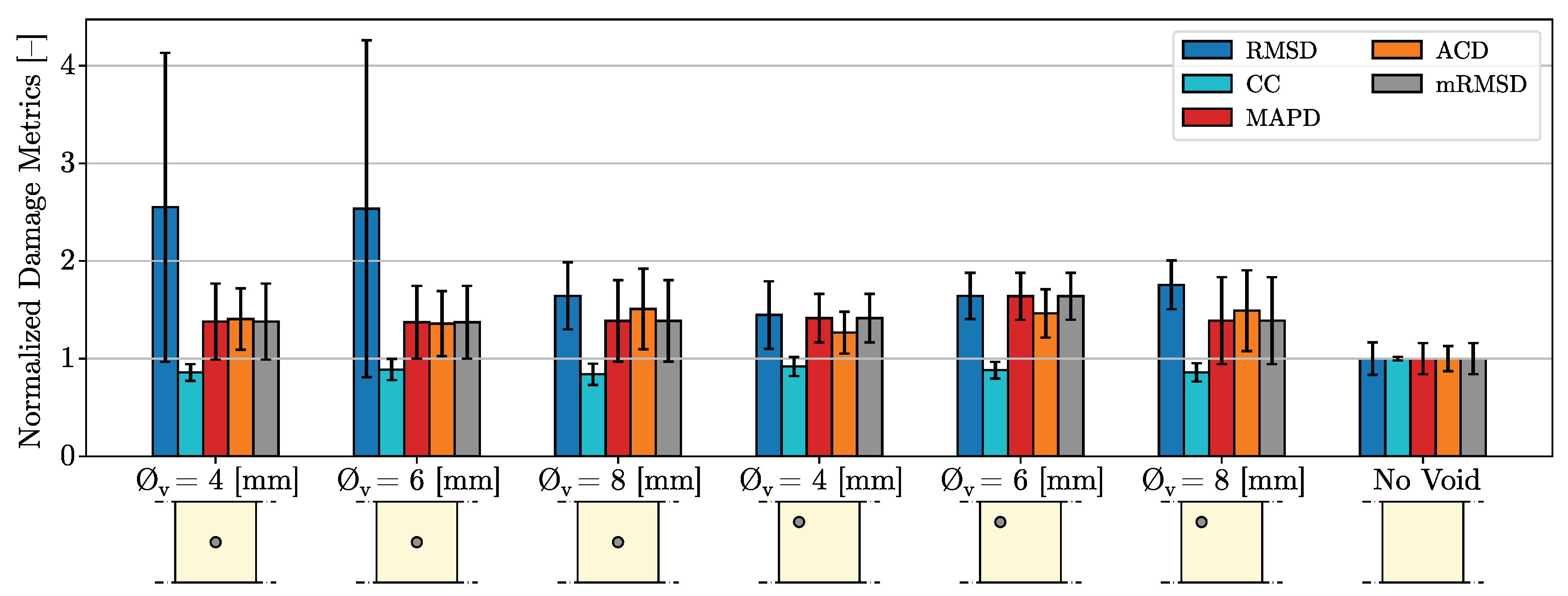
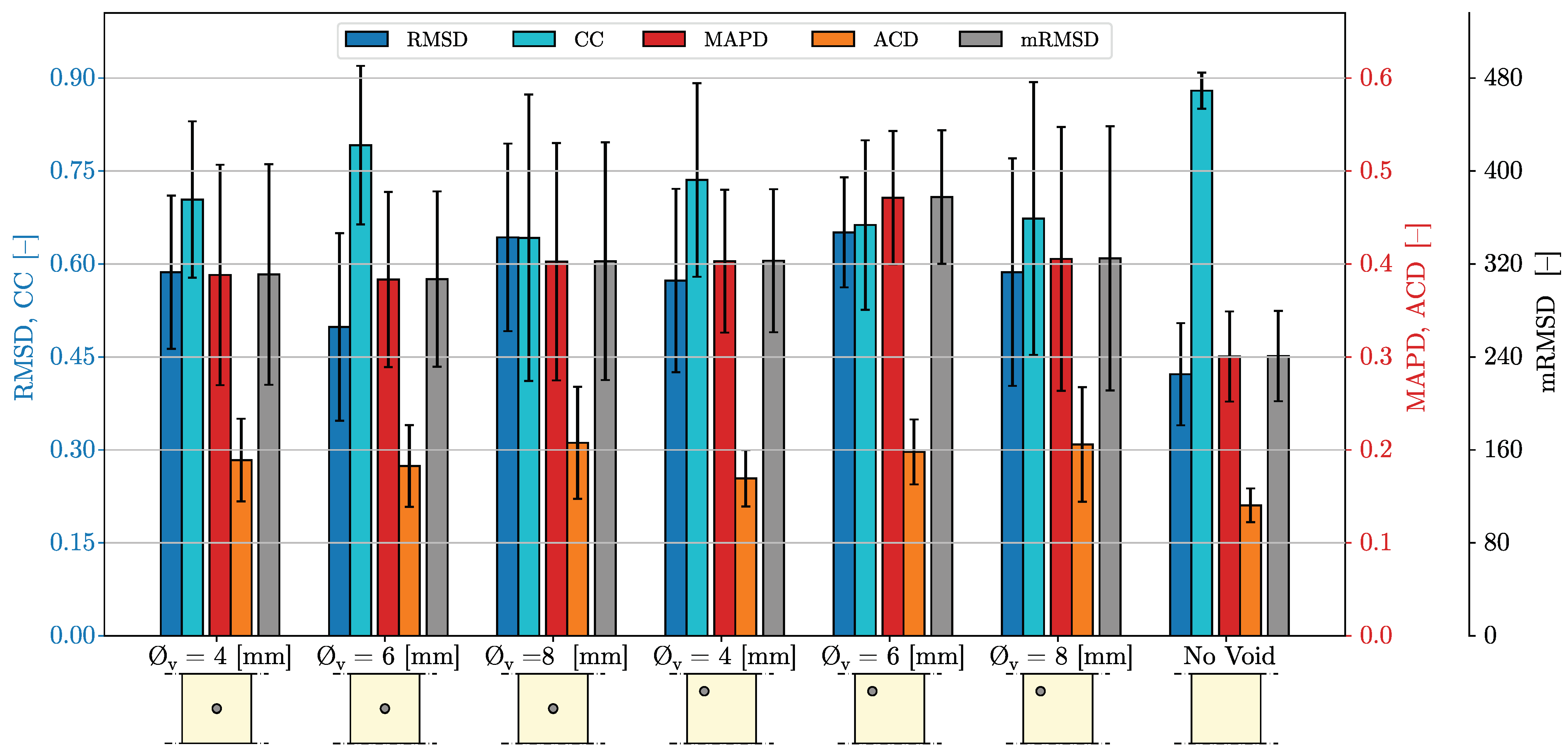
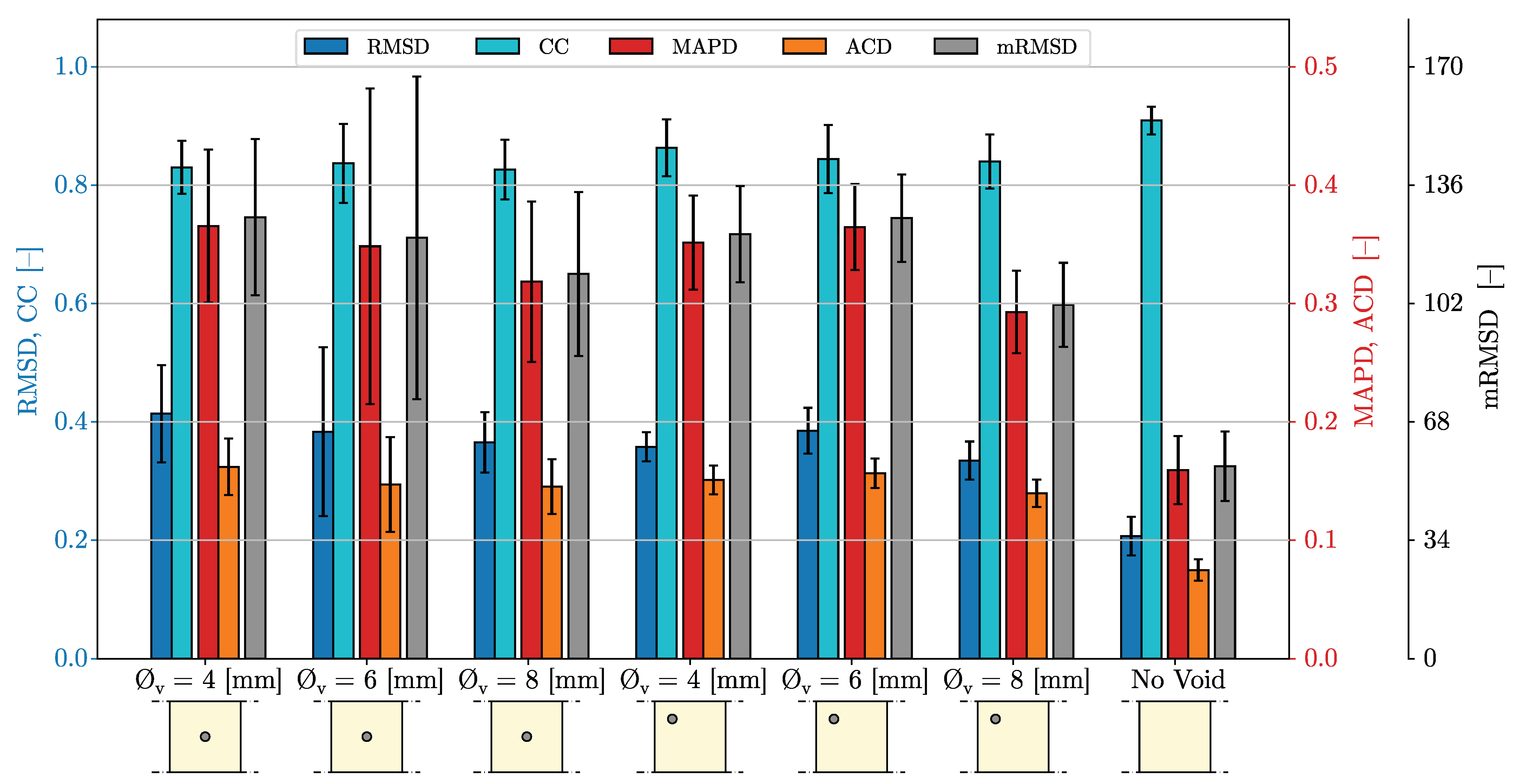
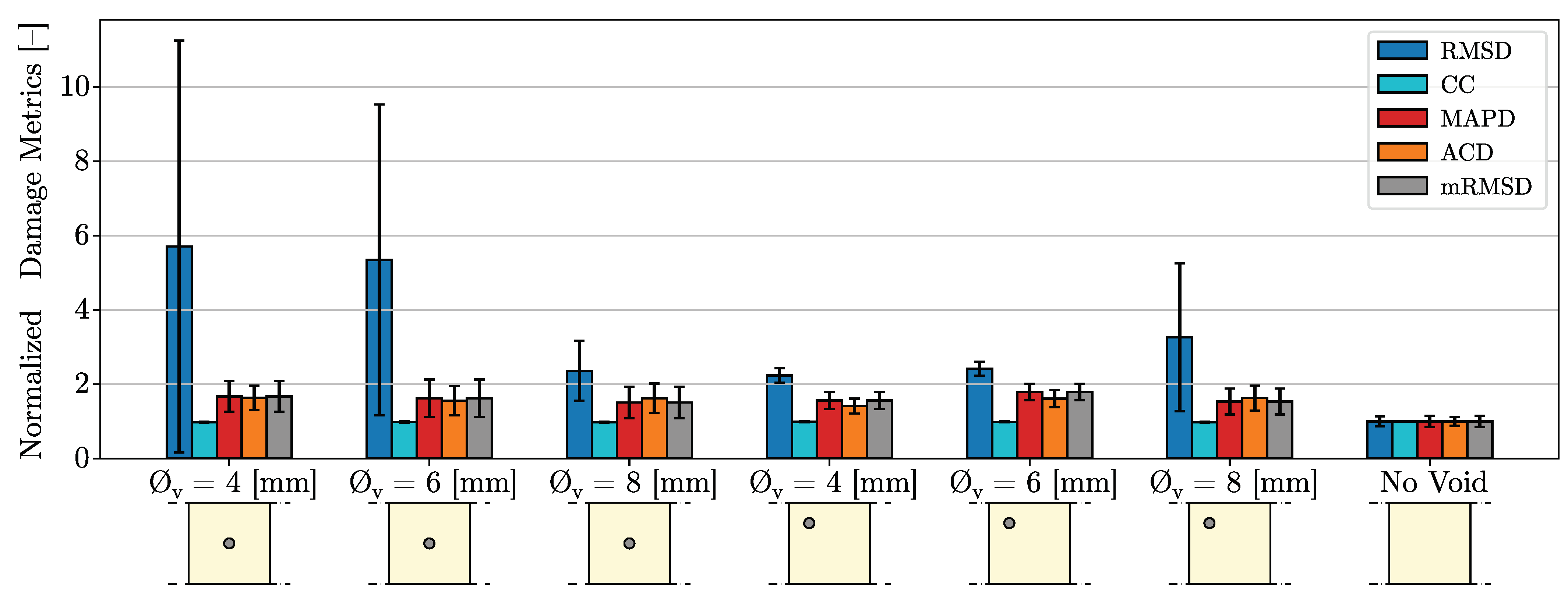
4. Damage Metric Results and Discussion
4.1. Metrics Using the Real Component of the Impedance
4.1.1. Linearly Spaced Spectrum from kHz to MHz
4.1.2. Logarithmically Spaced Spectrum from kHz to MHz
4.1.3. Linearly Spaced Spectrum from kHz to MHz
4.1.4. Logarithmically Spaced Spectrum from kHz to kHz
4.1.5. Combination of the Three Measured Spectra from kHz to MHz
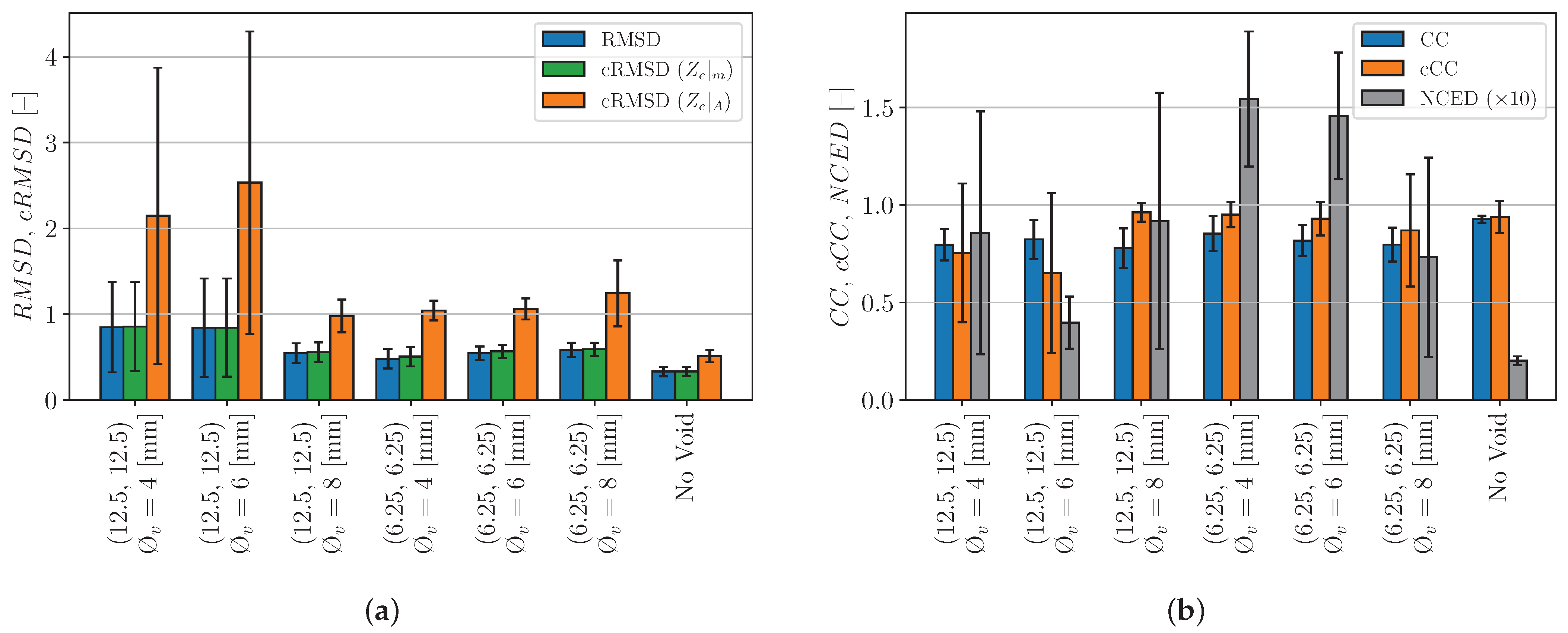
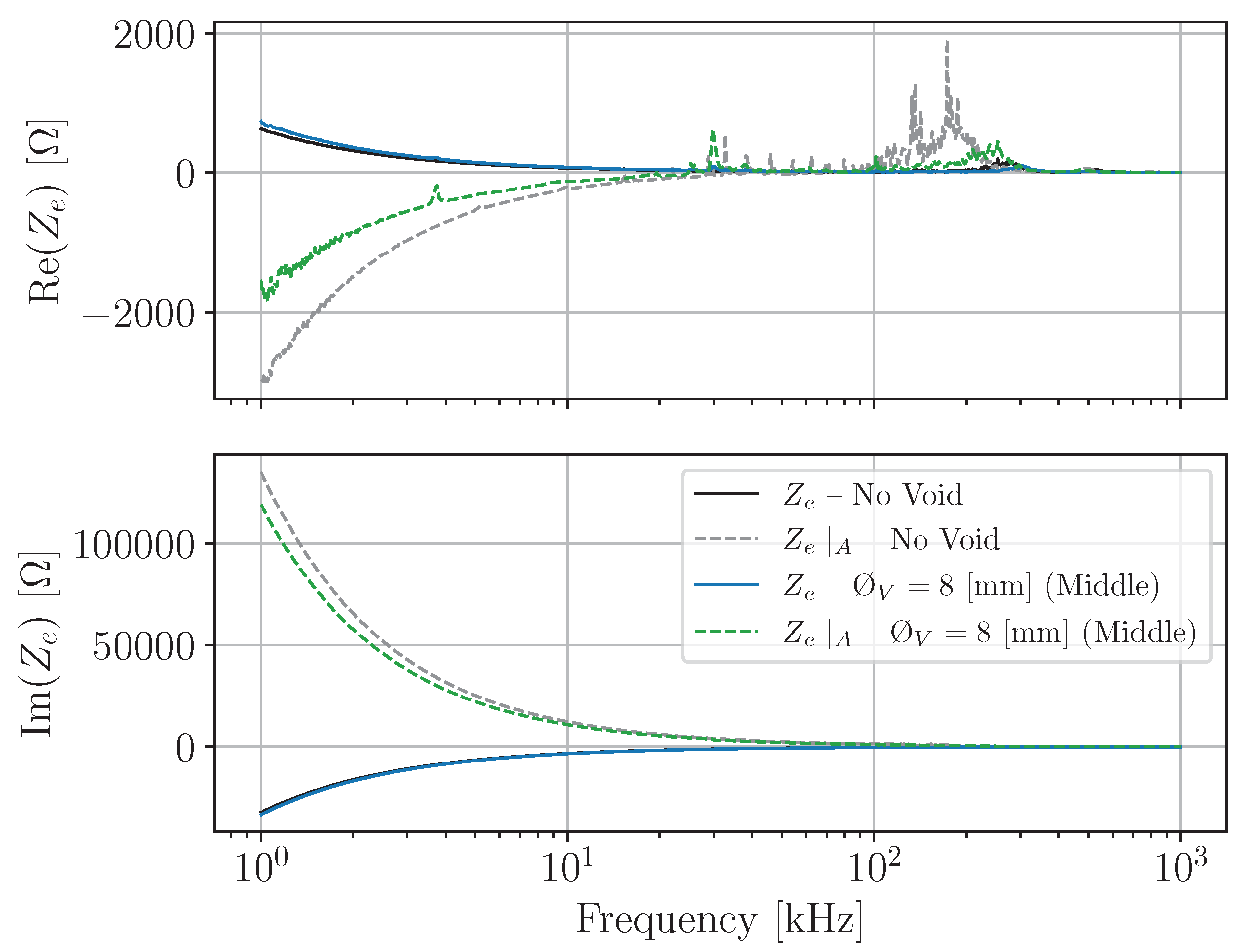
4.2. Metrics Using the Complex Active Impedance
4.2.1. Linearly Spaced Spectrum from kHz to MHz
4.2.2. Linearly Spaced Spectrum from kHz to MHz
4.2.3. Logarithmically Spaced Spectrum from kHz to kHz
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A. Metrics
Appendix A.1. Metrics Using the Real Component of the Impedance
Appendix A.1.1. Linearly Spaced Spectrum from fi = 1 kHz to ff = 1 MHz
| Case | (12.5, 12.5) | (12.5, 12.5) | (12.5, 12.5) | (6.25, 6.25) | (6.25, 6.25) | (6.25, 6.25) | No Void |
|---|---|---|---|---|---|---|---|
| Reference SLJ for Damage Metric Calculation: SLJ 1 | |||||||
| Mean | 0.881747 | 0.847592 | 0.620563 | 0.541951 | 0.615546 | 0.631591 | 0.314935 |
| 0.531134 | 0.612240 | 0.094997 | 0.144474 | 0.049026 | 0.049174 | 0.065269 | |
| SLJ 1 | 0.508978 | 1.554390 | 0.600701 | 0.377542 | 0.559442 | 0.583762 | nan |
| SLJ 2 | 1.489896 | 0.481300 | 0.723921 | 0.648654 | 0.650143 | 0.682007 | 0.361087 |
| SLJ 3 | 0.646365 | 0.507087 | 0.537067 | 0.599656 | 0.637053 | 0.629004 | 0.268783 |
| Reference SLJ for Damage Metric Calculation: SLJ 2 | |||||||
| Mean | 0.802185 | 0.847246 | 0.440877 | 0.408856 | 0.454990 | 0.516274 | 0.383830 |
| 0.707944 | 0.732888 | 0.091309 | 0.045811 | 0.017794 | 0.110137 | 0.040763 | |
| SLJ 1 | 0.336837 | 1.687976 | 0.470309 | 0.376610 | 0.463022 | 0.438675 | 0.412654 |
| SLJ 2 | 1.616902 | 0.510577 | 0.513840 | 0.461294 | 0.467351 | 0.467816 | nan |
| SLJ 3 | 0.452817 | 0.343185 | 0.338481 | 0.388664 | 0.434596 | 0.642331 | 0.355007 |
| Reference SLJ for Damage Metric Calculation: SLJ 3 | |||||||
| Mean | 0.858162 | 0.832527 | 0.576104 | 0.491676 | 0.566757 | 0.601925 | 0.297836 |
| 0.562824 | 0.633286 | 0.093154 | 0.127461 | 0.040423 | 0.046103 | 0.030430 | |
| SLJ 1 | 0.468224 | 1.563525 | 0.563547 | 0.347402 | 0.524166 | 0.548896 | 0.276318 |
| SLJ 2 | 1.503389 | 0.450235 | 0.674900 | 0.589012 | 0.604591 | 0.632492 | 0.319353 |
| SLJ 3 | 0.602873 | 0.483820 | 0.489866 | 0.538615 | 0.571515 | 0.624387 | nan |
| Overall Damage Metric Data | |||||||
| Mean | 0.847365 | 0.842455 | 0.545848 | 0.480828 | 0.545764 | 0.583263 | 0.332200 |
| 0.525611 | 0.572983 | 0.114362 | 0.114857 | 0.078549 | 0.082811 | 0.055022 | |
| Case | (12.5, 12.5) | (12.5, 12.5) | (12.5, 12.5) | (6.25, 6.25) | (6.25, 6.25) | (6.25, 6.25) | No Void |
|---|---|---|---|---|---|---|---|
| Reference SLJ for Damage Metric Calculation: SLJ 1 | |||||||
| Mean | 331.06 | 294.04 | 338.63 | 333.68 | 368.98 | 326.92 | 199.01 |
| 72.06 | 84.17 | 64.91 | 19.17 | 15.50 | 82.78 | 19.71 | |
| SLJ 1 | 259.67 | 377.44 | 376.68 | 325.68 | 361.15 | 378.91 | nan |
| SLJ 2 | 329.75 | 209.13 | 375.53 | 319.82 | 386.84 | 370.40 | 212.94 |
| SLJ 3 | 403.76 | 295.55 | 263.68 | 355.56 | 358.96 | 231.46 | 185.07 |
| Reference SLJ for Damage Metric Calculation: SLJ 2 | |||||||
| Mean | 229.78 | 264.24 | 227.36 | 256.24 | 315.38 | 242.75 | 260.31 |
| 46.75 | 60.57 | 83.93 | 38.30 | 32.69 | 73.54 | 32.15 | |
| SLJ 1 | 216.96 | 327.65 | 312.52 | 297.75 | 285.44 | 322.51 | 237.57 |
| SLJ 2 | 190.78 | 206.98 | 224.85 | 248.71 | 350.26 | 228.13 | nan |
| SLJ 3 | 281.61 | 258.10 | 144.71 | 222.27 | 310.44 | 177.62 | 283.05 |
| Reference SLJ for Damage Metric Calculation: SLJ 3 | |||||||
| Mean | 373.34 | 370.78 | 372.65 | 367.46 | 425.29 | 370.32 | 217.46 |
| 84.22 | 93.09 | 82.76 | 31.05 | 37.04 | 124.60 | 34.30 | |
| SLJ 1 | 306.20 | 461.75 | 438.30 | 384.21 | 396.95 | 473.29 | 193.20 |
| SLJ 2 | 345.97 | 275.71 | 399.97 | 331.63 | 467.20 | 405.84 | 241.72 |
| SLJ 3 | 467.84 | 374.88 | 279.69 | 386.55 | 411.72 | 231.82 | nan |
| Overall Damage Metric Data | |||||||
| Mean | 311.39 | 309.69 | 312.88 | 319.13 | 369.88 | 313.33 | 225.59 |
| 87.75 | 84.38 | 94.12 | 56.02 | 54.18 | 100.51 | 36.21 | |
| Case | (12.5, 12.5) | (12.5, 12.5) | (12.5, 12.5) | (6.25, 6.25) | (6.25, 6.25) | (6.25, 6.25) | No Void |
|---|---|---|---|---|---|---|---|
| Reference SLJ for Damage Metric Calculation: SLJ 1 | |||||||
| Mean | 0.413307 | 0.367095 | 0.422759 | 0.416585 | 0.460652 | 0.408145 | 0.248447 |
| 0.089958 | 0.105075 | 0.081034 | 0.023931 | 0.019352 | 0.103350 | 0.024605 | |
| SLJ 1 | 0.324176 | 0.471213 | 0.470262 | 0.406586 | 0.450877 | 0.473046 | nan |
| SLJ 2 | 0.411675 | 0.261088 | 0.468822 | 0.399275 | 0.482942 | 0.462423 | 0.265845 |
| SLJ 3 | 0.504069 | 0.368982 | 0.329192 | 0.443894 | 0.448138 | 0.288964 | 0.231049 |
| Reference SLJ for Damage Metric Calculation: SLJ 2 | |||||||
| Mean | 0.286868 | 0.329890 | 0.283845 | 0.319902 | 0.393731 | 0.303061 | 0.324982 |
| 0.058370 | 0.075621 | 0.104784 | 0.047818 | 0.040814 | 0.091812 | 0.040142 | |
| SLJ 1 | 0.270860 | 0.409055 | 0.390161 | 0.371724 | 0.356351 | 0.402630 | 0.296597 |
| SLJ 2 | 0.238173 | 0.258398 | 0.280711 | 0.310496 | 0.437277 | 0.284804 | nan |
| SLJ 3 | 0.351572 | 0.322219 | 0.180664 | 0.277486 | 0.387564 | 0.221749 | 0.353366 |
| Reference SLJ for Damage Metric Calculation: SLJ 3 | |||||||
| Mean | 0.466087 | 0.462891 | 0.465237 | 0.458756 | 0.530950 | 0.462320 | 0.271486 |
| 0.105149 | 0.116214 | 0.103318 | 0.038766 | 0.046239 | 0.155551 | 0.042828 | |
| SLJ 1 | 0.382272 | 0.576461 | 0.547197 | 0.479664 | 0.495571 | 0.590879 | 0.241202 |
| SLJ 2 | 0.431917 | 0.344202 | 0.499334 | 0.414025 | 0.583270 | 0.506670 | 0.301769 |
| SLJ 3 | 0.584071 | 0.468010 | 0.349180 | 0.482579 | 0.514010 | 0.289410 | nan |
| Overall Damage Metric Data | |||||||
| Mean | 0.388754 | 0.386625 | 0.390614 | 0.398414 | 0.461778 | 0.391175 | 0.281638 |
| 0.109546 | 0.105345 | 0.117498 | 0.069938 | 0.067644 | 0.125476 | 0.045206 | |
| Case | (12.5, 12.5) | (12.5, 12.5) | (12.5, 12.5) | (6.25, 6.25) | (6.25, 6.25) | (6.25, 6.25) | No Void |
|---|---|---|---|---|---|---|---|
| Reference SLJ for Damage Metric Calculation: SLJ 1 | |||||||
| Mean | 0.739077 | 0.784894 | 0.712721 | 0.796544 | 0.752017 | 0.742571 | 0.927577 |
| 0.063712 | 0.120879 | 0.102763 | 0.106013 | 0.060672 | 0.097335 | 0.028361 | |
| SLJ 1 | 0.811437 | 0.652629 | 0.752830 | 0.918415 | 0.821075 | 0.737922 | nan |
| SLJ 2 | 0.691395 | 0.889643 | 0.595952 | 0.725643 | 0.707276 | 0.647644 | 0.907522 |
| SLJ 3 | 0.714400 | 0.812409 | 0.789381 | 0.745573 | 0.727700 | 0.842146 | 0.947631 |
| Reference SLJ for Damage Metric Calculation: SLJ 2 | |||||||
| Mean | 0.873875 | 0.872934 | 0.868886 | 0.924405 | 0.903613 | 0.871404 | 0.917079 |
| 0.057451 | 0.087767 | 0.053948 | 0.032939 | 0.028585 | 0.033853 | 0.013515 | |
| SLJ 1 | 0.923146 | 0.772023 | 0.872726 | 0.961476 | 0.931589 | 0.856564 | 0.907522 |
| SLJ 2 | 0.810770 | 0.931495 | 0.813121 | 0.898500 | 0.874456 | 0.847505 | nan |
| SLJ 3 | 0.887708 | 0.915284 | 0.920811 | 0.913240 | 0.904795 | 0.910143 | 0.926635 |
| Reference SLJ for Damage Metric Calculation: SLJ 3 | |||||||
| Mean | 0.775366 | 0.813026 | 0.755923 | 0.838629 | 0.796687 | 0.777016 | 0.937133 |
| 0.059034 | 0.112013 | 0.090588 | 0.086733 | 0.051527 | 0.080468 | 0.014847 | |
| SLJ 1 | 0.841546 | 0.694385 | 0.787170 | 0.938277 | 0.852763 | 0.768172 | 0.947631 |
| SLJ 2 | 0.728127 | 0.916958 | 0.653848 | 0.780127 | 0.751425 | 0.701336 | 0.926635 |
| SLJ 3 | 0.756424 | 0.827736 | 0.826751 | 0.797484 | 0.785874 | 0.861541 | nan |
| Overall Damage Metric Data | |||||||
| Mean | 0.796106 | 0.823618 | 0.779177 | 0.853193 | 0.817439 | 0.796997 | 0.927263 |
| 0.079750 | 0.101153 | 0.101469 | 0.090257 | 0.079621 | 0.087238 | 0.017944 | |
| Case | (12.5, 12.5) | (12.5, 12.5) | (12.5, 12.5) | (6.25, 6.25) | (6.25, 6.25) | (6.25, 6.25) | No Void |
|---|---|---|---|---|---|---|---|
| Reference SLJ for Damage Metric Calculation: SLJ 1 | |||||||
| Mean | 0.199087 | 0.176478 | 0.216578 | 0.172232 | 0.193134 | 0.207812 | 0.121839 |
| 0.024083 | 0.043029 | 0.037334 | 0.017802 | 0.024094 | 0.047329 | 0.011662 | |
| SLJ 1 | 0.171598 | 0.213994 | 0.218008 | 0.158128 | 0.176144 | 0.217648 | nan |
| SLJ 2 | 0.209190 | 0.129508 | 0.253176 | 0.166333 | 0.220708 | 0.249450 | 0.130085 |
| SLJ 3 | 0.216473 | 0.185931 | 0.178549 | 0.192234 | 0.182549 | 0.156338 | 0.113593 |
| Reference SLJ for Damage Metric Calculation: SLJ 2 | |||||||
| Mean | 0.138748 | 0.149336 | 0.144150 | 0.135678 | 0.167471 | 0.153320 | 0.140878 |
| 0.019474 | 0.030223 | 0.040807 | 0.012950 | 0.024146 | 0.035980 | 0.015264 | |
| SLJ 1 | 0.134801 | 0.175769 | 0.170352 | 0.148633 | 0.146410 | 0.183983 | 0.130085 |
| SLJ 2 | 0.121550 | 0.116387 | 0.164966 | 0.135666 | 0.193824 | 0.162266 | nan |
| SLJ 3 | 0.159894 | 0.155854 | 0.097133 | 0.122734 | 0.162178 | 0.113711 | 0.151672 |
| Reference SLJ for Damage Metric Calculation: SLJ 3 | |||||||
| Mean | 0.217853 | 0.211173 | 0.235850 | 0.192907 | 0.217909 | 0.228564 | 0.132632 |
| 0.027058 | 0.045375 | 0.041883 | 0.012986 | 0.034048 | 0.061819 | 0.026926 | |
| SLJ 1 | 0.192805 | 0.249831 | 0.247225 | 0.193571 | 0.189610 | 0.257388 | 0.113593 |
| SLJ 2 | 0.214203 | 0.161217 | 0.270870 | 0.179602 | 0.255694 | 0.270707 | 0.151672 |
| SLJ 3 | 0.246550 | 0.222470 | 0.189454 | 0.205548 | 0.208424 | 0.157596 | nan |
| Overall Damage Metric Data | |||||||
| Mean | 0.185229 | 0.178996 | 0.198859 | 0.166939 | 0.192838 | 0.196565 | 0.131783 |
| 0.041281 | 0.043891 | 0.054374 | 0.028163 | 0.032523 | 0.054514 | 0.017080 | |
Appendix A.1.2. Logarithmically Spaced Spectrum from fi = 1 kHz to ff = 1 MHz
| Case | (12.5, 12.5) | (12.5, 12.5) | (12.5, 12.5) | (6.25, 6.25) | (6.25, 6.25) | (6.25, 6.25) | No Void |
|---|---|---|---|---|---|---|---|
| Reference SLJ for Damage Metric Calculation: SLJ 1 | |||||||
| Mean | 0.754661 | 0.716674 | 0.257899 | 0.258360 | 0.276146 | 0.394470 | 0.067530 |
| 0.930806 | 0.701788 | 0.157617 | 0.037594 | 0.033325 | 0.368588 | 0.012561 | |
| SLJ 1 | 0.202885 | 1.495496 | 0.438806 | 0.298382 | 0.305568 | 0.215461 | nan |
| SLJ 2 | 1.829335 | 0.521131 | 0.150194 | 0.252911 | 0.239956 | 0.149573 | 0.076413 |
| SLJ 3 | 0.231763 | 0.133395 | 0.184695 | 0.223788 | 0.282913 | 0.818376 | 0.058648 |
| Reference SLJ for Damage Metric Calculation: SLJ 2 | |||||||
| Mean | 0.773826 | 0.737301 | 0.247847 | 0.266245 | 0.282722 | 0.394143 | 0.072821 |
| 0.963189 | 0.730361 | 0.185275 | 0.049889 | 0.040746 | 0.399604 | 0.007618 | |
| SLJ 1 | 0.205004 | 1.543603 | 0.457289 | 0.320886 | 0.320673 | 0.216495 | 0.078208 |
| SLJ 2 | 1.885924 | 0.548240 | 0.105344 | 0.254724 | 0.239663 | 0.114166 | nan |
| SLJ 3 | 0.230551 | 0.120058 | 0.180909 | 0.223125 | 0.287831 | 0.851768 | 0.067434 |
| Reference SLJ for Damage Metric Calculation: SLJ 3 | |||||||
| Mean | 0.755157 | 0.717311 | 0.253401 | 0.256808 | 0.274928 | 0.391449 | 0.062505 |
| 0.935426 | 0.705344 | 0.162628 | 0.040437 | 0.034716 | 0.373832 | 0.005138 | |
| SLJ 1 | 0.200788 | 1.499863 | 0.439603 | 0.300294 | 0.306591 | 0.213582 | 0.058872 |
| SLJ 2 | 1.835167 | 0.521535 | 0.139217 | 0.249793 | 0.237806 | 0.139761 | 0.066138 |
| SLJ 3 | 0.229516 | 0.130536 | 0.181383 | 0.220338 | 0.280389 | 0.821004 | nan |
| Overall Damage Metric Data | |||||||
| Mean | 0.761215 | 0.723762 | 0.253049 | 0.260471 | 0.277932 | 0.393354 | 0.067619 |
| 0.816933 | 0.617223 | 0.146368 | 0.037464 | 0.031736 | 0.329886 | 0.008351 | |
| Case | (12.5, 12.5) | (12.5, 12.5) | (12.5, 12.5) | (6.25, 6.25) | (6.25, 6.25) | (6.25, 6.25) | No Void |
|---|---|---|---|---|---|---|---|
| Reference SLJ for Damage Metric Calculation: SLJ 1 | |||||||
| Mean | 356.74 | 323.07 | 250.73 | 272.21 | 295.22 | 257.15 | 110.72 |
| 179.92 | 191.42 | 71.76 | 15.92 | 8.76 | 51.92 | 14.63 | |
| SLJ 1 | 209.76 | 543.52 | 333.59 | 258.01 | 287.16 | 248.74 | nan |
| SLJ 2 | 557.38 | 226.87 | 210.32 | 269.20 | 293.95 | 209.95 | 121.06 |
| SLJ 3 | 303.07 | 198.83 | 208.28 | 289.42 | 304.55 | 312.77 | 100.37 |
| Reference SLJ for Damage Metric Calculation: SLJ 2 | |||||||
| Mean | 333.86 | 325.49 | 225.35 | 254.34 | 279.72 | 244.65 | 136.25 |
| 176.06 | 187.82 | 87.49 | 8.27 | 9.82 | 73.08 | 0.63 | |
| SLJ 1 | 201.23 | 539.08 | 325.88 | 259.78 | 270.55 | 247.22 | 136.70 |
| SLJ 2 | 533.61 | 251.27 | 166.47 | 244.82 | 278.52 | 170.31 | nan |
| SLJ 3 | 266.73 | 186.12 | 183.70 | 258.41 | 290.08 | 316.41 | 135.81 |
| Reference SLJ for Damage Metric Calculation: SLJ 3 | |||||||
| Mean | 381.32 | 357.19 | 271.33 | 294.04 | 323.58 | 281.32 | 112.61 |
| 177.90 | 196.11 | 83.49 | 16.46 | 12.91 | 50.65 | 8.67 | |
| SLJ 1 | 233.52 | 582.96 | 367.71 | 284.75 | 309.38 | 290.12 | 106.48 |
| SLJ 2 | 578.77 | 259.55 | 221.24 | 284.34 | 326.76 | 226.85 | 118.74 |
| SLJ 3 | 331.68 | 229.07 | 225.04 | 313.05 | 334.61 | 327.00 | nan |
| Overall Damage Metric Data | |||||||
| Mean | 357.31 | 335.25 | 249.13 | 273.53 | 299.51 | 261.04 | 119.86 |
| 155.49 | 166.93 | 73.09 | 21.09 | 21.36 | 53.96 | 14.83 | |
| Case | (12.5, 12.5) | (12.5, 12.5) | (12.5, 12.5) | (6.25, 6.25) | (6.25, 6.25) | (6.25, 6.25) | No Void |
|---|---|---|---|---|---|---|---|
| Reference SLJ for Damage Metric Calculation: SLJ 1 | |||||||
| Mean | 0.445365 | 0.403336 | 0.313020 | 0.339841 | 0.368563 | 0.321040 | 0.138221 |
| 0.224614 | 0.238981 | 0.089593 | 0.019874 | 0.010937 | 0.064820 | 0.018269 | |
| SLJ 1 | 0.261874 | 0.678546 | 0.416463 | 0.322116 | 0.358505 | 0.310532 | nan |
| SLJ 2 | 0.695855 | 0.283236 | 0.262572 | 0.336081 | 0.366977 | 0.262116 | 0.151140 |
| SLJ 3 | 0.378366 | 0.248226 | 0.260025 | 0.361326 | 0.380207 | 0.390472 | 0.125303 |
| Reference SLJ for Damage Metric Calculation: SLJ 2 | |||||||
| Mean | 0.416799 | 0.406353 | 0.281331 | 0.317527 | 0.349210 | 0.305425 | 0.170106 |
| 0.219804 | 0.234480 | 0.109221 | 0.010325 | 0.012262 | 0.091240 | 0.000783 | |
| SLJ 1 | 0.251219 | 0.673004 | 0.406836 | 0.324324 | 0.337765 | 0.308636 | 0.170660 |
| SLJ 2 | 0.666176 | 0.313694 | 0.207824 | 0.305646 | 0.347712 | 0.212622 | nan |
| SLJ 3 | 0.333001 | 0.232360 | 0.229333 | 0.322610 | 0.362152 | 0.395017 | 0.169552 |
| Reference SLJ for Damage Metric Calculation: SLJ 3 | |||||||
| Mean | 0.476059 | 0.445932 | 0.338736 | 0.367097 | 0.403972 | 0.351214 | 0.140584 |
| 0.222097 | 0.244835 | 0.104232 | 0.020550 | 0.016115 | 0.063235 | 0.010821 | |
| SLJ 1 | 0.291533 | 0.727788 | 0.459062 | 0.355491 | 0.386245 | 0.362203 | 0.132932 |
| SLJ 2 | 0.722560 | 0.324029 | 0.276203 | 0.354975 | 0.407935 | 0.283205 | 0.148235 |
| SLJ 3 | 0.414084 | 0.285978 | 0.280944 | 0.390824 | 0.417737 | 0.408235 | nan |
| Overall Damage Metric Data | |||||||
| Mean | 0.446074 | 0.418540 | 0.311029 | 0.341488 | 0.373915 | 0.325893 | 0.149637 |
| 0.194118 | 0.208406 | 0.091243 | 0.026329 | 0.026662 | 0.067362 | 0.018515 | |
| Case | (12.5, 12.5) | (12.5, 12.5) | (12.5, 12.5) | (6.25, 6.25) | (6.25, 6.25) | (6.25, 6.25) | No Void |
|---|---|---|---|---|---|---|---|
| Reference SLJ for Damage Metric Calculation: SLJ 1 | |||||||
| Mean | 0.984010 | 0.986183 | 0.986347 | 0.989893 | 0.988144 | 0.986067 | 0.995341 |
| 0.007379 | 0.007496 | 0.003706 | 0.004261 | 0.002607 | 0.001758 | 0.001051 | |
| SLJ 1 | 0.989829 | 0.977565 | 0.988048 | 0.994808 | 0.991090 | 0.987016 | nan |
| SLJ 2 | 0.975711 | 0.991197 | 0.982095 | 0.987244 | 0.986133 | 0.984038 | 0.994598 |
| SLJ 3 | 0.986490 | 0.989786 | 0.988897 | 0.987628 | 0.987210 | 0.987146 | 0.996085 |
| Reference SLJ for Damage Metric Calculation: SLJ 2 | |||||||
| Mean | 0.990416 | 0.991065 | 0.993544 | 0.995702 | 0.994904 | 0.992346 | 0.995102 |
| 0.007442 | 0.006154 | 0.001783 | 0.001326 | 0.001210 | 0.000885 | 0.000713 | |
| SLJ 1 | 0.995308 | 0.983975 | 0.993995 | 0.997231 | 0.996117 | 0.993009 | 0.994598 |
| SLJ 2 | 0.981852 | 0.994190 | 0.991579 | 0.994873 | 0.993697 | 0.992688 | nan |
| SLJ 3 | 0.994087 | 0.995028 | 0.995058 | 0.995001 | 0.994897 | 0.991342 | 0.995606 |
| Reference SLJ for Damage Metric Calculation: SLJ 3 | |||||||
| Mean | 0.986226 | 0.988390 | 0.988262 | 0.991647 | 0.989918 | 0.987990 | 0.995845 |
| 0.006226 | 0.006484 | 0.003241 | 0.003538 | 0.002241 | 0.001534 | 0.000338 | |
| SLJ 1 | 0.991190 | 0.981078 | 0.989832 | 0.995730 | 0.992333 | 0.988408 | 0.996085 |
| SLJ 2 | 0.979241 | 0.993436 | 0.984536 | 0.989478 | 0.987904 | 0.986291 | 0.995606 |
| SLJ 3 | 0.988248 | 0.990658 | 0.990420 | 0.989734 | 0.989516 | 0.989271 | nan |
| Overall Damage Metric Data | |||||||
| Mean | 0.986884 | 0.988546 | 0.989384 | 0.992414 | 0.990988 | 0.988801 | 0.995430 |
| 0.006714 | 0.006205 | 0.004156 | 0.003842 | 0.003540 | 0.003053 | 0.000679 | |
| Case | (12.5, 12.5) | (12.5, 12.5) | (12.5, 12.5) | (6.25, 6.25) | (6.25, 6.25) | (6.25, 6.25) | No Void |
|---|---|---|---|---|---|---|---|
| Reference SLJ for Damage Metric Calculation: SLJ 1 | |||||||
| Mean | 0.186704 | 0.169451 | 0.152429 | 0.146724 | 0.159973 | 0.155045 | 0.068149 |
| 0.066003 | 0.072190 | 0.030705 | 0.008539 | 0.008094 | 0.016774 | 0.008864 | |
| SLJ 1 | 0.132395 | 0.252802 | 0.187494 | 0.138734 | 0.151772 | 0.152015 | nan |
| SLJ 2 | 0.260164 | 0.128666 | 0.139439 | 0.145716 | 0.167955 | 0.139993 | 0.074417 |
| SLJ 3 | 0.167552 | 0.126885 | 0.130353 | 0.155722 | 0.160191 | 0.173128 | 0.061881 |
| Reference SLJ for Damage Metric Calculation: SLJ 2 | |||||||
| Mean | 0.167593 | 0.162040 | 0.131412 | 0.135880 | 0.149909 | 0.141345 | 0.074243 |
| 0.060471 | 0.068122 | 0.036702 | 0.002270 | 0.006109 | 0.026538 | 0.000246 | |
| SLJ 1 | 0.119533 | 0.239733 | 0.173720 | 0.136852 | 0.142975 | 0.145140 | 0.074417 |
| SLJ 2 | 0.235491 | 0.133842 | 0.112385 | 0.133286 | 0.154501 | 0.113114 | nan |
| SLJ 3 | 0.147754 | 0.112544 | 0.108130 | 0.137503 | 0.152250 | 0.165781 | 0.074069 |
| Reference SLJ for Damage Metric Calculation: SLJ 3 | |||||||
| Mean | 0.196937 | 0.183557 | 0.162383 | 0.158290 | 0.172696 | 0.165807 | 0.067975 |
| 0.063263 | 0.073801 | 0.034301 | 0.007051 | 0.010871 | 0.015294 | 0.008618 | |
| SLJ 1 | 0.143473 | 0.268769 | 0.201731 | 0.152874 | 0.160919 | 0.169303 | 0.061881 |
| SLJ 2 | 0.266779 | 0.141860 | 0.146619 | 0.155733 | 0.182345 | 0.149069 | 0.074069 |
| SLJ 3 | 0.180560 | 0.140043 | 0.138797 | 0.166263 | 0.174825 | 0.179051 | nan |
| Overall Damage Metric Data | |||||||
| Mean | 0.183745 | 0.171683 | 0.148741 | 0.146965 | 0.160859 | 0.154066 | 0.070122 |
| 0.056305 | 0.062564 | 0.032467 | 0.011231 | 0.012372 | 0.020436 | 0.006386 | |
Appendix A.1.3. Linearly Spaced Spectrum from fi = 100 kHz to ff = 1 MHz
| Case | (12.5, 12.5) | (12.5, 12.5) | (12.5, 12.5) | (6.25, 6.25) | (6.25, 6.25) | (6.25, 6.25) | No Void |
|---|---|---|---|---|---|---|---|
| Reference SLJ for Damage Metric Calculation: SLJ 1 | |||||||
| Mean | 0.669123 | 0.552689 | 0.725040 | 0.635695 | 0.724630 | 0.647266 | 0.384474 |
| 0.090364 | 0.185429 | 0.136827 | 0.192643 | 0.064645 | 0.215598 | 0.078856 | |
| SLJ 1 | 0.598398 | 0.701757 | 0.651203 | 0.415521 | 0.650918 | 0.702932 | nan |
| SLJ 2 | 0.638047 | 0.345046 | 0.882925 | 0.773237 | 0.771678 | 0.829573 | 0.440233 |
| SLJ 3 | 0.770924 | 0.611264 | 0.640993 | 0.718327 | 0.751294 | 0.409294 | 0.328714 |
| Reference SLJ for Damage Metric Calculation: SLJ 2 | |||||||
| Mean | 0.460313 | 0.434451 | 0.521912 | 0.501687 | 0.553089 | 0.494587 | 0.510496 |
| 0.089950 | 0.080553 | 0.140258 | 0.070704 | 0.029375 | 0.168660 | 0.051677 | |
| SLJ 1 | 0.402936 | 0.510434 | 0.469443 | 0.440081 | 0.561432 | 0.566185 | 0.547037 |
| SLJ 2 | 0.414022 | 0.349997 | 0.680841 | 0.578886 | 0.577389 | 0.615637 | nan |
| SLJ 3 | 0.563981 | 0.442922 | 0.415453 | 0.486095 | 0.520445 | 0.301939 | 0.473955 |
| Reference SLJ for Damage Metric Calculation: SLJ 3 | |||||||
| Mean | 0.631016 | 0.508455 | 0.682001 | 0.582717 | 0.675490 | 0.618528 | 0.371504 |
| 0.088761 | 0.200071 | 0.137168 | 0.177919 | 0.055680 | 0.200313 | 0.038993 | |
| SLJ 1 | 0.560072 | 0.650485 | 0.611527 | 0.380110 | 0.617324 | 0.673732 | 0.343932 |
| SLJ 2 | 0.602426 | 0.279646 | 0.840080 | 0.713482 | 0.728297 | 0.785451 | 0.399077 |
| SLJ 3 | 0.730548 | 0.595235 | 0.594397 | 0.654559 | 0.680848 | 0.396402 | nan |
| Overall Damage Metric Data | |||||||
| Mean | 0.586817 | 0.498532 | 0.642985 | 0.573366 | 0.651069 | 0.586794 | 0.422158 |
| 0.123725 | 0.151334 | 0.151311 | 0.147843 | 0.088817 | 0.183578 | 0.082448 | |
| Case | (12.5, 12.5) | (12.5, 12.5) | (12.5, 12.5) | (6.25, 6.25) | (6.25, 6.25) | (6.25, 6.25) | No Void |
|---|---|---|---|---|---|---|---|
| Reference SLJ for Damage Metric Calculation: SLJ 1 | |||||||
| Mean | 334.26 | 292.63 | 352.75 | 340.07 | 378.49 | 341.05 | 212.38 |
| 74.98 | 68.79 | 71.09 | 19.50 | 16.35 | 96.55 | 19.87 | |
| SLJ 1 | 264.95 | 352.68 | 386.19 | 337.24 | 374.70 | 397.90 | nan |
| SLJ 2 | 323.99 | 217.57 | 400.97 | 322.13 | 396.41 | 395.68 | 226.43 |
| SLJ 3 | 413.85 | 307.63 | 271.11 | 360.82 | 364.38 | 229.57 | 198.33 |
| Reference SLJ for Damage Metric Calculation: SLJ 2 | |||||||
| Mean | 221.21 | 256.16 | 227.23 | 254.91 | 318.39 | 246.20 | 277.82 |
| 54.24 | 38.96 | 87.29 | 47.48 | 33.07 | 82.65 | 36.10 | |
| SLJ 1 | 217.72 | 289.99 | 312.54 | 306.27 | 290.97 | 333.88 | 252.29 |
| SLJ 2 | 168.79 | 213.57 | 231.06 | 245.85 | 355.12 | 235.01 | nan |
| SLJ 3 | 277.11 | 264.92 | 138.10 | 212.63 | 309.09 | 169.72 | 303.34 |
| Reference SLJ for Damage Metric Calculation: SLJ 3 | |||||||
| Mean | 377.48 | 372.19 | 387.13 | 373.45 | 435.80 | 387.00 | 231.90 |
| 89.28 | 77.42 | 89.08 | 36.44 | 38.89 | 141.72 | 36.43 | |
| SLJ 1 | 315.05 | 437.97 | 450.63 | 398.06 | 409.01 | 500.31 | 206.14 |
| SLJ 2 | 337.64 | 286.87 | 425.47 | 331.59 | 480.40 | 432.61 | 257.66 |
| SLJ 3 | 479.74 | 391.73 | 285.30 | 390.70 | 417.97 | 228.09 | nan |
| Overall Damage Metric Data | |||||||
| Mean | 310.98 | 306.99 | 322.37 | 322.81 | 377.56 | 324.75 | 240.70 |
| 94.96 | 75.51 | 102.30 | 61.58 | 57.47 | 113.69 | 38.83 | |
| Case | (12.5, 12.5) | (12.5, 12.5) | (12.5, 12.5) | (6.25, 6.25) | (6.25, 6.25) | (6.25, 6.25) | No Void |
|---|---|---|---|---|---|---|---|
| Reference SLJ for Damage Metric Calculation: SLJ 1 | |||||||
| Mean | 0.417305 | 0.365326 | 0.440393 | 0.424552 | 0.472527 | 0.425780 | 0.265148 |
| 0.093605 | 0.085884 | 0.088752 | 0.024344 | 0.020410 | 0.120542 | 0.024807 | |
| SLJ 1 | 0.330775 | 0.440301 | 0.482129 | 0.421028 | 0.467786 | 0.496755 | nan |
| SLJ 2 | 0.404477 | 0.271624 | 0.500583 | 0.402162 | 0.494890 | 0.493987 | 0.282690 |
| SLJ 3 | 0.516663 | 0.384054 | 0.338466 | 0.450466 | 0.454905 | 0.286599 | 0.247607 |
| Reference SLJ for Damage Metric Calculation: SLJ 2 | |||||||
| Mean | 0.276163 | 0.319799 | 0.283689 | 0.318245 | 0.397496 | 0.307371 | 0.346838 |
| 0.067721 | 0.048634 | 0.108971 | 0.059272 | 0.041290 | 0.103183 | 0.045066 | |
| SLJ 1 | 0.271807 | 0.362032 | 0.390192 | 0.382361 | 0.363257 | 0.416832 | 0.314972 |
| SLJ 2 | 0.210725 | 0.266627 | 0.288466 | 0.306926 | 0.443349 | 0.293391 | nan |
| SLJ 3 | 0.345957 | 0.330736 | 0.172408 | 0.265450 | 0.385882 | 0.211891 | 0.378704 |
| Reference SLJ for Damage Metric Calculation: SLJ 3 | |||||||
| Mean | 0.471257 | 0.464656 | 0.483313 | 0.466229 | 0.544064 | 0.483150 | 0.289518 |
| 0.111459 | 0.096658 | 0.111215 | 0.045493 | 0.048550 | 0.176934 | 0.045483 | |
| SLJ 1 | 0.393323 | 0.546783 | 0.562590 | 0.496955 | 0.510629 | 0.624602 | 0.257357 |
| SLJ 2 | 0.421523 | 0.358139 | 0.531168 | 0.413966 | 0.599751 | 0.540093 | 0.321679 |
| SLJ 3 | 0.598924 | 0.489046 | 0.356181 | 0.487765 | 0.521811 | 0.284756 | nan |
| Overall Damage Metric Data | |||||||
| Mean | 0.388242 | 0.383260 | 0.402465 | 0.403009 | 0.471362 | 0.405434 | 0.300501 |
| 0.118552 | 0.094268 | 0.127715 | 0.076883 | 0.071752 | 0.141940 | 0.048477 | |
| Case | (12.5, 12.5) | (12.5, 12.5) | (12.5, 12.5) | (6.25, 6.25) | (6.25, 6.25) | (6.25, 6.25) | No Void |
|---|---|---|---|---|---|---|---|
| Reference SLJ for Damage Metric Calculation: SLJ 1 | |||||||
| Mean | 0.622266 | 0.742590 | 0.542318 | 0.651393 | 0.563916 | 0.607346 | 0.883698 |
| 0.113564 | 0.170569 | 0.265791 | 0.191181 | 0.117978 | 0.292615 | 0.044959 | |
| SLJ 1 | 0.714153 | 0.579105 | 0.709128 | 0.871533 | 0.697941 | 0.591624 | nan |
| SLJ 2 | 0.657344 | 0.919454 | 0.235808 | 0.527045 | 0.475768 | 0.322909 | 0.851907 |
| SLJ 3 | 0.495302 | 0.729211 | 0.682017 | 0.555601 | 0.518039 | 0.907506 | 0.915489 |
| Reference SLJ for Damage Metric Calculation: SLJ 2 | |||||||
| Mean | 0.831398 | 0.861182 | 0.789575 | 0.846404 | 0.800863 | 0.778199 | 0.861729 |
| 0.056031 | 0.038335 | 0.177828 | 0.067021 | 0.065122 | 0.136262 | 0.013890 | |
| SLJ 1 | 0.867427 | 0.824443 | 0.892223 | 0.922288 | 0.864737 | 0.749211 | 0.851907 |
| SLJ 2 | 0.859923 | 0.900935 | 0.584237 | 0.795308 | 0.734562 | 0.658764 | nan |
| SLJ 3 | 0.766844 | 0.858167 | 0.892267 | 0.821615 | 0.803290 | 0.926622 | 0.871551 |
| Reference SLJ for Damage Metric Calculation: SLJ 3 | |||||||
| Mean | 0.658409 | 0.771616 | 0.594816 | 0.708907 | 0.623920 | 0.634469 | 0.893520 |
| 0.100674 | 0.153188 | 0.246282 | 0.162876 | 0.104856 | 0.253035 | 0.031069 | |
| SLJ 1 | 0.741878 | 0.651234 | 0.744664 | 0.896303 | 0.737627 | 0.610501 | 0.915489 |
| SLJ 2 | 0.686746 | 0.944047 | 0.310574 | 0.601410 | 0.531043 | 0.394271 | 0.871551 |
| SLJ 3 | 0.546603 | 0.719566 | 0.729210 | 0.629007 | 0.603089 | 0.898635 | nan |
| Overall Damage Metric Data | |||||||
| Mean | 0.704024 | 0.791796 | 0.642236 | 0.735568 | 0.662900 | 0.673338 | 0.879649 |
| 0.126150 | 0.127959 | 0.231211 | 0.156278 | 0.136639 | 0.219949 | 0.029118 | |
| Case | (12.5, 12.5) | (12.5, 12.5) | (12.5, 12.5) | (6.25, 6.25) | (6.25, 6.25) | (6.25, 6.25) | No Void |
|---|---|---|---|---|---|---|---|
| Reference SLJ for Damage Metric Calculation: SLJ 1 | |||||||
| Mean | 0.204761 | 0.181074 | 0.227880 | 0.175610 | 0.198835 | 0.218562 | 0.129717 |
| 0.023605 | 0.040918 | 0.042809 | 0.018139 | 0.026114 | 0.055057 | 0.011748 | |
| SLJ 1 | 0.178200 | 0.213107 | 0.225318 | 0.162587 | 0.181495 | 0.228937 | nan |
| SLJ 2 | 0.212743 | 0.134980 | 0.271912 | 0.167915 | 0.228870 | 0.267694 | 0.138025 |
| SLJ 3 | 0.223340 | 0.195137 | 0.186409 | 0.196328 | 0.186140 | 0.159056 | 0.121410 |
| Reference SLJ for Damage Metric Calculation: SLJ 2 | |||||||
| Mean | 0.138104 | 0.149447 | 0.147124 | 0.135832 | 0.170606 | 0.158065 | 0.149907 |
| 0.022389 | 0.025627 | 0.044083 | 0.016497 | 0.025853 | 0.041014 | 0.016804 | |
| SLJ 1 | 0.138145 | 0.166545 | 0.172213 | 0.152566 | 0.149088 | 0.191689 | 0.138025 |
| SLJ 2 | 0.115694 | 0.119982 | 0.172937 | 0.135346 | 0.199284 | 0.170136 | nan |
| SLJ 3 | 0.160472 | 0.161814 | 0.096223 | 0.119583 | 0.163445 | 0.112371 | 0.161790 |
| Reference SLJ for Damage Metric Calculation: SLJ 3 | |||||||
| Mean | 0.224262 | 0.217380 | 0.247941 | 0.196777 | 0.224021 | 0.240922 | 0.141600 |
| 0.027340 | 0.043669 | 0.047148 | 0.014294 | 0.037156 | 0.070561 | 0.028553 | |
| SLJ 1 | 0.201433 | 0.250115 | 0.256180 | 0.199977 | 0.193812 | 0.272391 | 0.121410 |
| SLJ 2 | 0.216794 | 0.167797 | 0.290427 | 0.181154 | 0.265510 | 0.290275 | 0.161790 |
| SLJ 3 | 0.254560 | 0.234228 | 0.197217 | 0.209199 | 0.212741 | 0.160102 | nan |
| Overall Damage Metric Data | |||||||
| Mean | 0.189042 | 0.182634 | 0.207648 | 0.169406 | 0.197821 | 0.205850 | 0.140408 |
| 0.044523 | 0.043888 | 0.060297 | 0.030322 | 0.034904 | 0.061654 | 0.018152 | |
Appendix A.1.4. Logarithmically Spaced Spectrum from fi = 10 kHz to ff = 200 kHz
| Case | (12.5, 12.5) | (12.5, 12.5) | (12.5, 12.5) | (6.25, 6.25) | (6.25, 6.25) | (6.25, 6.25) | No Void |
|---|---|---|---|---|---|---|---|
| Reference SLJ for Damage Metric Calculation: SLJ 1 | |||||||
| Mean | 0.415146 | 0.385332 | 0.375259 | 0.355423 | 0.380993 | 0.348802 | 0.207618 |
| 0.079543 | 0.145637 | 0.039697 | 0.027965 | 0.042388 | 0.015298 | 0.041910 | |
| SLJ 1 | 0.357120 | 0.548640 | 0.420312 | 0.332916 | 0.332564 | 0.350533 | nan |
| SLJ 2 | 0.505818 | 0.268920 | 0.360047 | 0.346624 | 0.399067 | 0.332713 | 0.237253 |
| SLJ 3 | 0.382501 | 0.338436 | 0.345417 | 0.386730 | 0.411347 | 0.363160 | 0.177983 |
| Reference SLJ for Damage Metric Calculation: SLJ 2 | |||||||
| Mean | 0.410031 | 0.379741 | 0.353050 | 0.358586 | 0.386809 | 0.317204 | 0.225708 |
| 0.105721 | 0.176132 | 0.072339 | 0.029854 | 0.043957 | 0.045060 | 0.045935 | |
| SLJ 1 | 0.322527 | 0.582962 | 0.435277 | 0.344429 | 0.339190 | 0.328040 | 0.258189 |
| SLJ 2 | 0.527501 | 0.271160 | 0.299215 | 0.338444 | 0.395402 | 0.267715 | nan |
| SLJ 3 | 0.380066 | 0.285102 | 0.324657 | 0.392884 | 0.425835 | 0.355858 | 0.193228 |
| Reference SLJ for Damage Metric Calculation: SLJ 3 | |||||||
| Mean | 0.416436 | 0.385075 | 0.367908 | 0.360042 | 0.388020 | 0.338190 | 0.187373 |
| 0.097533 | 0.170430 | 0.056628 | 0.027311 | 0.046871 | 0.033308 | 0.000316 | |
| SLJ 1 | 0.340822 | 0.579836 | 0.433198 | 0.340980 | 0.335025 | 0.347559 | 0.187597 |
| SLJ 2 | 0.526524 | 0.263250 | 0.332166 | 0.347816 | 0.405000 | 0.301201 | 0.187150 |
| SLJ 3 | 0.381963 | 0.312140 | 0.338361 | 0.391331 | 0.424033 | 0.365810 | nan |
| Overall Damage Metric Data | |||||||
| Mean | 0.413871 | 0.383383 | 0.365406 | 0.358017 | 0.385274 | 0.334732 | 0.206900 |
| 0.082236 | 0.142574 | 0.050989 | 0.024678 | 0.038627 | 0.032208 | 0.032673 | |
| Case | (12.5, 12.5) | (12.5, 12.5) | (12.5, 12.5) | (6.25, 6.25) | (6.25, 6.25) | (6.25, 6.25) | No Void |
|---|---|---|---|---|---|---|---|
| Reference SLJ for Damage Metric Calculation: SLJ 1 | |||||||
| Mean | 123.475 | 115.641 | 107.670 | 117.004 | 121.076 | 98.788 | 50.091 |
| 24.661 | 56.030 | 24.050 | 14.709 | 12.830 | 11.587 | 7.635 | |
| SLJ 1 | 97.296 | 179.208 | 135.005 | 102.608 | 106.262 | 101.706 | nan |
| SLJ 2 | 146.269 | 73.427 | 89.763 | 116.394 | 128.684 | 86.020 | 55.489 |
| SLJ 3 | 126.861 | 94.287 | 98.241 | 132.008 | 128.281 | 108.637 | 44.692 |
| Reference SLJ for Damage Metric Calculation: SLJ 2 | |||||||
| Mean | 125.916 | 123.305 | 110.541 | 123.026 | 127.896 | 101.027 | 65.379 |
| 26.701 | 49.498 | 29.764 | 15.621 | 12.410 | 15.264 | 11.248 | |
| SLJ 1 | 97.657 | 180.394 | 144.161 | 109.910 | 114.100 | 106.486 | 73.332 |
| SLJ 2 | 150.723 | 97.137 | 87.554 | 118.861 | 131.442 | 83.784 | nan |
| SLJ 3 | 129.367 | 92.384 | 99.908 | 140.308 | 138.148 | 112.811 | 57.425 |
| Reference SLJ for Damage Metric Calculation: SLJ 3 | |||||||
| Mean | 131.017 | 123.727 | 113.315 | 125.803 | 130.621 | 105.090 | 50.311 |
| 25.423 | 54.102 | 27.038 | 15.475 | 15.543 | 13.625 | 2.943 | |
| SLJ 1 | 103.820 | 185.774 | 143.794 | 110.741 | 112.826 | 110.807 | 52.392 |
| SLJ 2 | 154.186 | 86.406 | 92.218 | 125.007 | 137.498 | 89.538 | 48.229 |
| SLJ 3 | 135.043 | 99.001 | 103.932 | 141.660 | 141.540 | 114.924 | nan |
| Overall Damage Metric Data | |||||||
| Mean | 126.802 | 120.891 | 110.508 | 121.944 | 126.531 | 101.635 | 55.260 |
| 22.427 | 46.310 | 23.554 | 13.789 | 12.577 | 12.078 | 10.007 | |
| Case | (12.5, 12.5) | (12.5, 12.5) | (12.5, 12.5) | (6.25, 6.25) | (6.25, 6.25) | (6.25, 6.25) | No Void |
|---|---|---|---|---|---|---|---|
| Reference SLJ for Damage Metric Calculation: SLJ 1 | |||||||
| Mean | 0.355836 | 0.333259 | 0.310287 | 0.337186 | 0.348922 | 0.284691 | 0.144353 |
| 0.071070 | 0.161471 | 0.069307 | 0.042389 | 0.036975 | 0.033393 | 0.022003 | |
| SLJ 1 | 0.280392 | 0.516450 | 0.389063 | 0.295702 | 0.306232 | 0.293100 | nan |
| SLJ 2 | 0.421524 | 0.211605 | 0.258683 | 0.335430 | 0.370846 | 0.247897 | 0.159912 |
| SLJ 3 | 0.365593 | 0.271721 | 0.283114 | 0.380426 | 0.369687 | 0.313074 | 0.128794 |
| Reference SLJ for Damage Metric Calculation: SLJ 2 | |||||||
| Mean | 0.362869 | 0.355345 | 0.318563 | 0.354543 | 0.368578 | 0.291144 | 0.188411 |
| 0.076947 | 0.142644 | 0.085774 | 0.045018 | 0.035763 | 0.043989 | 0.032414 | |
| SLJ 1 | 0.281432 | 0.519867 | 0.415449 | 0.316743 | 0.328818 | 0.306876 | 0.211332 |
| SLJ 2 | 0.434359 | 0.279932 | 0.252318 | 0.342540 | 0.378794 | 0.241452 | nan |
| SLJ 3 | 0.372816 | 0.266236 | 0.287921 | 0.404346 | 0.398120 | 0.325104 | 0.165491 |
| Reference SLJ for Damage Metric Calculation: SLJ 3 | |||||||
| Mean | 0.377570 | 0.356562 | 0.326555 | 0.362544 | 0.376430 | 0.302852 | 0.144987 |
| 0.073266 | 0.155913 | 0.077920 | 0.044597 | 0.044792 | 0.039265 | 0.008482 | |
| SLJ 1 | 0.299194 | 0.535372 | 0.414393 | 0.319137 | 0.325148 | 0.319330 | 0.150985 |
| SLJ 2 | 0.444341 | 0.249009 | 0.265757 | 0.360252 | 0.396248 | 0.258033 | 0.138989 |
| SLJ 3 | 0.389173 | 0.285306 | 0.299516 | 0.408243 | 0.407895 | 0.331194 | nan |
| Overall Damage Metric Data | |||||||
| Mean | 0.365425 | 0.348389 | 0.318468 | 0.351424 | 0.364643 | 0.292896 | 0.159251 |
| 0.064631 | 0.133459 | 0.067880 | 0.039738 | 0.036245 | 0.034807 | 0.028838 | |
| Case | (12.5, 12.5) | (12.5, 12.5) | (12.5, 12.5) | (6.25, 6.25) | (6.25, 6.25) | (6.25, 6.25) | No Void |
|---|---|---|---|---|---|---|---|
| Reference SLJ for Damage Metric Calculation: SLJ 1 | |||||||
| Mean | 0.779139 | 0.791750 | 0.776139 | 0.816884 | 0.798089 | 0.791415 | 0.903565 |
| 0.013037 | 0.070195 | 0.033619 | 0.036364 | 0.049424 | 0.022141 | 0.033967 | |
| SLJ 1 | 0.765372 | 0.733458 | 0.805168 | 0.851781 | 0.855123 | 0.791693 | nan |
| SLJ 2 | 0.791298 | 0.869669 | 0.739304 | 0.819658 | 0.767826 | 0.769135 | 0.879547 |
| SLJ 3 | 0.780745 | 0.772122 | 0.783946 | 0.779211 | 0.771318 | 0.813415 | 0.927583 |
| Reference SLJ for Damage Metric Calculation: SLJ 2 | |||||||
| Mean | 0.879327 | 0.881751 | 0.876999 | 0.908565 | 0.889885 | 0.890197 | 0.899993 |
| 0.012560 | 0.047695 | 0.023078 | 0.024953 | 0.042768 | 0.014207 | 0.028914 | |
| SLJ 1 | 0.867038 | 0.833013 | 0.900264 | 0.926850 | 0.938931 | 0.886173 | 0.879547 |
| SLJ 2 | 0.892142 | 0.928331 | 0.854112 | 0.918708 | 0.870362 | 0.878437 | nan |
| SLJ 3 | 0.878800 | 0.883909 | 0.876622 | 0.880138 | 0.860361 | 0.905982 | 0.920438 |
| Reference SLJ for Damage Metric Calculation: SLJ 3 | |||||||
| Mean | 0.831819 | 0.837640 | 0.826890 | 0.864610 | 0.844764 | 0.839143 | 0.924011 |
| 0.012242 | 0.067342 | 0.029658 | 0.030707 | 0.052193 | 0.017783 | 0.005053 | |
| SLJ 1 | 0.818479 | 0.774049 | 0.855358 | 0.893333 | 0.905031 | 0.833393 | 0.927583 |
| SLJ 2 | 0.842537 | 0.908192 | 0.796171 | 0.868253 | 0.814577 | 0.824946 | 0.920438 |
| SLJ 3 | 0.834442 | 0.830678 | 0.829141 | 0.832244 | 0.814685 | 0.859089 | nan |
| Overall Damage Metric Data | |||||||
| Mean | 0.830095 | 0.837047 | 0.826676 | 0.863353 | 0.844246 | 0.840252 | 0.909189 |
| 0.044756 | 0.066733 | 0.050428 | 0.047947 | 0.057698 | 0.045633 | 0.023182 | |
| Case | (12.5, 12.5) | (12.5, 12.5) | (12.5, 12.5) | (6.25, 6.25) | (6.25, 6.25) | (6.25, 6.25) | No Void |
|---|---|---|---|---|---|---|---|
| Reference SLJ for Damage Metric Calculation: SLJ 1 | |||||||
| Mean | 0.165298 | 0.147486 | 0.148882 | 0.151185 | 0.156804 | 0.142783 | 0.076247 |
| 0.026043 | 0.050035 | 0.023230 | 0.013098 | 0.013286 | 0.008259 | 0.013780 | |
| SLJ 1 | 0.139077 | 0.201318 | 0.175683 | 0.137056 | 0.141972 | 0.145293 | nan |
| SLJ 2 | 0.191159 | 0.102400 | 0.136435 | 0.153579 | 0.167614 | 0.133560 | 0.085991 |
| SLJ 3 | 0.165658 | 0.138741 | 0.134528 | 0.162921 | 0.160826 | 0.149495 | 0.066502 |
| Reference SLJ for Damage Metric Calculation: SLJ 2 | |||||||
| Mean | 0.152394 | 0.142662 | 0.137395 | 0.146083 | 0.151235 | 0.131255 | 0.079065 |
| 0.027173 | 0.040053 | 0.028497 | 0.013037 | 0.010581 | 0.013858 | 0.009795 | |
| SLJ 1 | 0.124935 | 0.188883 | 0.170245 | 0.134045 | 0.139168 | 0.137758 | 0.085991 |
| SLJ 2 | 0.179272 | 0.118139 | 0.119311 | 0.144275 | 0.155613 | 0.115341 | nan |
| SLJ 3 | 0.152975 | 0.120965 | 0.122631 | 0.159931 | 0.158925 | 0.140665 | 0.072139 |
| Reference SLJ for Damage Metric Calculation: SLJ 3 | |||||||
| Mean | 0.168557 | 0.151494 | 0.149991 | 0.155612 | 0.162190 | 0.145316 | 0.069321 |
| 0.025733 | 0.047312 | 0.025642 | 0.013120 | 0.015554 | 0.010626 | 0.003986 | |
| SLJ 1 | 0.142140 | 0.203847 | 0.179596 | 0.141319 | 0.144241 | 0.151640 | 0.066502 |
| SLJ 2 | 0.193547 | 0.111798 | 0.134786 | 0.158409 | 0.171706 | 0.133047 | 0.072139 |
| SLJ 3 | 0.169984 | 0.138837 | 0.135591 | 0.167108 | 0.170623 | 0.151260 | nan |
| Overall Damage Metric Data | |||||||
| Mean | 0.162083 | 0.147214 | 0.145423 | 0.150960 | 0.156743 | 0.139784 | 0.074878 |
| 0.023969 | 0.040015 | 0.023212 | 0.012061 | 0.012454 | 0.011637 | 0.008970 | |
Appendix A.1.5. Combination of the Three Measured Spectra from fi = 1 kHz to ff = 1 MHz
| Case | (12.5, 12.5) | (12.5, 12.5) | (12.5, 12.5) | (6.25, 6.25) | (6.25, 6.25) | (6.25, 6.25) | No Void |
|---|---|---|---|---|---|---|---|
| Reference SLJ for Damage Metric Calculation: SLJ 1 | |||||||
| Mean | 0.779328 | 0.723491 | 0.344277 | 0.318448 | 0.345664 | 0.458659 | 0.134231 |
| 0.838973 | 0.634069 | 0.104747 | 0.017085 | 0.014077 | 0.284345 | 0.027017 | |
| SLJ 1 | 0.266822 | 1.437669 | 0.462720 | 0.310932 | 0.352819 | 0.297412 | nan |
| SLJ 2 | 1.747535 | 0.506064 | 0.306279 | 0.338002 | 0.329447 | 0.291591 | 0.153335 |
| SLJ 3 | 0.323627 | 0.226740 | 0.263833 | 0.306410 | 0.354726 | 0.786975 | 0.115127 |
| Reference SLJ for Damage Metric Calculation: SLJ 2 | |||||||
| Mean | 0.770306 | 0.731426 | 0.288385 | 0.288580 | 0.308771 | 0.423924 | 0.148274 |
| 0.910178 | 0.687603 | 0.146699 | 0.040176 | 0.033044 | 0.348401 | 0.015688 | |
| SLJ 1 | 0.223730 | 1.495576 | 0.457771 | 0.329370 | 0.341714 | 0.254377 | 0.159368 |
| SLJ 2 | 1.821003 | 0.536045 | 0.202328 | 0.287324 | 0.275628 | 0.192749 | nan |
| SLJ 3 | 0.266186 | 0.162659 | 0.205057 | 0.249047 | 0.308972 | 0.824647 | 0.137181 |
| Reference SLJ for Damage Metric Calculation: SLJ 3 | |||||||
| Mean | 0.773061 | 0.721221 | 0.328129 | 0.303958 | 0.331189 | 0.447645 | 0.124533 |
| 0.853529 | 0.642525 | 0.112847 | 0.016662 | 0.016291 | 0.297678 | 0.012017 | |
| SLJ 1 | 0.253332 | 1.444184 | 0.456897 | 0.307986 | 0.345060 | 0.284549 | 0.116036 |
| SLJ 2 | 1.758131 | 0.504073 | 0.281018 | 0.318236 | 0.313249 | 0.267158 | 0.133030 |
| SLJ 3 | 0.307720 | 0.215405 | 0.246471 | 0.285651 | 0.335260 | 0.791227 | nan |
| Overall Damage Metric Data | |||||||
| Mean | 0.774232 | 0.725379 | 0.320264 | 0.303662 | 0.328541 | 0.443410 | 0.135680 |
| 0.751810 | 0.567399 | 0.109212 | 0.026706 | 0.025456 | 0.270089 | 0.018387 | |
| Case | (12.5, 12.5) | (12.5, 12.5) | (12.5, 12.5) | (6.25, 6.25) | (6.25, 6.25) | (6.25, 6.25) | No Void |
|---|---|---|---|---|---|---|---|
| Reference SLJ for Damage Metric Calculation: SLJ 1 | |||||||
| Mean | 1014.45 | 903.45 | 935.06 | 939.10 | 1035.95 | 918.50 | 517.74 |
| 251.13 | 320.68 | 179.60 | 51.97 | 29.70 | 132.45 | 52.86 | |
| SLJ 1 | 729.13 | 1263.93 | 1088.32 | 913.97 | 1016.48 | 1018.78 | nan |
| SLJ 2 | 1201.97 | 649.90 | 979.41 | 904.47 | 1070.14 | 968.35 | 555.12 |
| SLJ 3 | 1112.25 | 796.51 | 737.43 | 998.86 | 1021.23 | 768.36 | 480.37 |
| Reference SLJ for Damage Metric Calculation: SLJ 2 | |||||||
| Mean | 780.34 | 839.54 | 676.23 | 760.55 | 908.10 | 729.21 | 670.13 |
| 133.41 | 267.28 | 245.63 | 86.30 | 66.74 | 147.47 | 67.85 | |
| SLJ 1 | 631.24 | 1147.39 | 945.44 | 856.78 | 843.37 | 898.57 | 622.15 |
| SLJ 2 | 888.45 | 666.61 | 618.95 | 734.90 | 976.67 | 629.22 | nan |
| SLJ 3 | 821.33 | 704.63 | 464.30 | 689.99 | 904.26 | 659.82 | 718.11 |
| Reference SLJ for Damage Metric Calculation: SLJ 3 | |||||||
| Mean | 1124.95 | 1093.01 | 1024.34 | 1028.13 | 1176.52 | 1032.58 | 558.08 |
| 238.44 | 340.36 | 231.48 | 76.26 | 80.21 | 237.96 | 79.01 | |
| SLJ 1 | 849.78 | 1473.35 | 1247.81 | 1058.74 | 1108.42 | 1257.00 | 502.21 |
| SLJ 2 | 1254.36 | 817.11 | 1039.60 | 941.32 | 1264.94 | 1057.67 | 613.95 |
| SLJ 3 | 1270.70 | 988.56 | 785.61 | 1084.33 | 1156.20 | 783.06 | nan |
| Overall Damage Metric Data | |||||||
| Mean | 973.25 | 945.33 | 878.54 | 909.26 | 1040.19 | 893.43 | 581.99 |
| 240.11 | 292.51 | 247.11 | 133.85 | 128.30 | 203.93 | 87.84 | |
| Case | (12.5, 12.5) | (12.5, 12.5) | (12.5, 12.5) | (6.25, 6.25) | (6.25, 6.25) | (6.25, 6.25) | No Void |
|---|---|---|---|---|---|---|---|
| Reference SLJ for Damage Metric Calculation: SLJ 1 | |||||||
| Mean | 0.424634 | 0.378171 | 0.391401 | 0.393094 | 0.433632 | 0.384469 | 0.216720 |
| 0.105120 | 0.134230 | 0.075178 | 0.021756 | 0.012434 | 0.055441 | 0.022125 | |
| SLJ 1 | 0.305205 | 0.529062 | 0.455555 | 0.382574 | 0.425483 | 0.426447 | nan |
| SLJ 2 | 0.503129 | 0.272040 | 0.409968 | 0.378597 | 0.447943 | 0.405339 | 0.232364 |
| SLJ 3 | 0.465570 | 0.333409 | 0.308678 | 0.418110 | 0.427470 | 0.321623 | 0.201075 |
| Reference SLJ for Damage Metric Calculation: SLJ 2 | |||||||
| Mean | 0.326639 | 0.351421 | 0.283059 | 0.318357 | 0.380117 | 0.305234 | 0.280508 |
| 0.055844 | 0.111881 | 0.102816 | 0.036124 | 0.027934 | 0.061730 | 0.028402 | |
| SLJ 1 | 0.264230 | 0.480282 | 0.395745 | 0.358633 | 0.353022 | 0.376130 | 0.260424 |
| SLJ 2 | 0.371891 | 0.279033 | 0.259083 | 0.307617 | 0.408821 | 0.263384 | nan |
| SLJ 3 | 0.343796 | 0.294947 | 0.194350 | 0.288821 | 0.378508 | 0.276190 | 0.300591 |
| Reference SLJ for Damage Metric Calculation: SLJ 3 | |||||||
| Mean | 0.470886 | 0.457516 | 0.428774 | 0.430361 | 0.492474 | 0.432222 | 0.233604 |
| 0.099809 | 0.142469 | 0.096893 | 0.031922 | 0.033576 | 0.099608 | 0.033072 | |
| SLJ 1 | 0.355704 | 0.616722 | 0.522316 | 0.443173 | 0.463968 | 0.526160 | 0.210218 |
| SLJ 2 | 0.525056 | 0.342029 | 0.435162 | 0.394023 | 0.529484 | 0.442727 | 0.256989 |
| SLJ 3 | 0.531896 | 0.413798 | 0.328845 | 0.453886 | 0.483970 | 0.327778 | nan |
| Overall Damage Metric Data | |||||||
| Mean | 0.407386 | 0.395703 | 0.367745 | 0.380604 | 0.435408 | 0.373975 | 0.243610 |
| 0.100505 | 0.122440 | 0.103435 | 0.056029 | 0.053706 | 0.085364 | 0.036767 | |
| Case | (12.5, 12.5) | (12.5, 12.5) | (12.5, 12.5) | (6.25, 6.25) | (6.25, 6.25) | (6.25, 6.25) | No Void |
|---|---|---|---|---|---|---|---|
| Reference SLJ for Damage Metric Calculation: SLJ 1 | |||||||
| Mean | 0.958053 | 0.965331 | 0.956908 | 0.968576 | 0.962361 | 0.959597 | 0.987918 |
| 0.011511 | 0.017337 | 0.013531 | 0.015296 | 0.008471 | 0.010950 | 0.004279 | |
| SLJ 1 | 0.970148 | 0.946147 | 0.962304 | 0.986153 | 0.971986 | 0.959809 | nan |
| SLJ 2 | 0.947232 | 0.979881 | 0.941511 | 0.958285 | 0.956041 | 0.948543 | 0.984893 |
| SLJ 3 | 0.956778 | 0.969964 | 0.966907 | 0.961292 | 0.959056 | 0.970440 | 0.990944 |
| Reference SLJ for Damage Metric Calculation: SLJ 2 | |||||||
| Mean | 0.980700 | 0.981733 | 0.982354 | 0.989616 | 0.986975 | 0.981522 | 0.986722 |
| 0.010958 | 0.011867 | 0.006286 | 0.004370 | 0.003593 | 0.002297 | 0.002587 | |
| SLJ 1 | 0.989072 | 0.968051 | 0.982815 | 0.994555 | 0.990454 | 0.980434 | 0.984893 |
| SLJ 2 | 0.968298 | 0.989232 | 0.975850 | 0.986251 | 0.983278 | 0.979970 | nan |
| SLJ 3 | 0.984731 | 0.987915 | 0.988397 | 0.988043 | 0.987192 | 0.984161 | 0.988552 |
| Reference SLJ for Damage Metric Calculation: SLJ 3 | |||||||
| Mean | 0.965152 | 0.971413 | 0.964486 | 0.975806 | 0.970016 | 0.966282 | 0.989748 |
| 0.010123 | 0.015400 | 0.011581 | 0.012288 | 0.007050 | 0.008975 | 0.001691 | |
| SLJ 1 | 0.975682 | 0.954994 | 0.968739 | 0.989922 | 0.977657 | 0.965651 | 0.990944 |
| SLJ 2 | 0.955492 | 0.985536 | 0.951380 | 0.967511 | 0.963763 | 0.957640 | 0.988552 |
| SLJ 3 | 0.964281 | 0.973711 | 0.973340 | 0.969983 | 0.968628 | 0.975557 | nan |
| Overall Damage Metric Data | |||||||
| Mean | 0.967968 | 0.972826 | 0.967916 | 0.977999 | 0.973117 | 0.969134 | 0.988129 |
| 0.013762 | 0.014873 | 0.014738 | 0.013665 | 0.012353 | 0.012089 | 0.002726 | |
| Case | (12.5, 12.5) | (12.5, 12.5) | (12.5, 12.5) | (6.25, 6.25) | (6.25, 6.25) | (6.25, 6.25) | No Void |
|---|---|---|---|---|---|---|---|
| Reference SLJ for Damage Metric Calculation: SLJ 1 | |||||||
| Mean | 0.196741 | 0.175650 | 0.198843 | 0.164764 | 0.183971 | 0.193700 | 0.106372 |
| 0.033674 | 0.047980 | 0.029906 | 0.014741 | 0.019212 | 0.028529 | 0.010673 | |
| SLJ 1 | 0.160608 | 0.226486 | 0.210218 | 0.153135 | 0.169736 | 0.199537 | nan |
| SLJ 2 | 0.227247 | 0.131156 | 0.221391 | 0.159814 | 0.205824 | 0.218859 | 0.113919 |
| SLJ 3 | 0.202369 | 0.169309 | 0.164919 | 0.181343 | 0.176353 | 0.162703 | 0.098825 |
| Reference SLJ for Damage Metric Calculation: SLJ 2 | |||||||
| Mean | 0.148238 | 0.153445 | 0.140971 | 0.135758 | 0.162683 | 0.150901 | 0.121529 |
| 0.015217 | 0.036375 | 0.036671 | 0.009538 | 0.018255 | 0.021641 | 0.010762 | |
| SLJ 1 | 0.130692 | 0.193801 | 0.172181 | 0.145748 | 0.146366 | 0.173664 | 0.113919 |
| SLJ 2 | 0.157828 | 0.123181 | 0.150150 | 0.134778 | 0.182399 | 0.148450 | nan |
| SLJ 3 | 0.156193 | 0.143354 | 0.100582 | 0.126747 | 0.159285 | 0.130590 | 0.129139 |
| Reference SLJ for Damage Metric Calculation: SLJ 3 | |||||||
| Mean | 0.213045 | 0.204030 | 0.215357 | 0.182605 | 0.204711 | 0.211854 | 0.113982 |
| 0.029337 | 0.049915 | 0.034763 | 0.010869 | 0.027041 | 0.039930 | 0.021435 | |
| SLJ 1 | 0.179318 | 0.256376 | 0.234936 | 0.181953 | 0.181302 | 0.233200 | 0.098825 |
| SLJ 2 | 0.232657 | 0.156965 | 0.235914 | 0.172076 | 0.234311 | 0.236575 | 0.129139 |
| SLJ 3 | 0.227159 | 0.198750 | 0.175220 | 0.193784 | 0.198519 | 0.165788 | nan |
| Overall Damage Metric Data | |||||||
| Mean | 0.186008 | 0.177709 | 0.185057 | 0.161042 | 0.183788 | 0.185485 | 0.113961 |
| 0.037534 | 0.044848 | 0.044791 | 0.022932 | 0.026260 | 0.038128 | 0.013557 | |
Appendix A.2. Metrics Using the Complex Active Impedance
Appendix A.2.1. Linearly Spaced Spectrum from fi = 1 kHz to ff = 1 MHz
| Case | (12.5, 12.5) | (12.5, 12.5) | (12.5, 12.5) | (6.25, 6.25) | (6.25, 6.25) | (6.25, 6.25) | No Void |
|---|---|---|---|---|---|---|---|
| Reference SLJ for Damage Metric Calculation: SLJ 1 | |||||||
| Mean | 0.888306 | 0.848320 | 0.628944 | 0.561299 | 0.630622 | 0.636770 | 0.315463 |
| 0.526871 | 0.611719 | 0.094587 | 0.146750 | 0.054990 | 0.043063 | 0.064873 | |
| SLJ 1 | 0.509676 | 1.554531 | 0.622987 | 0.393100 | 0.567391 | 0.597981 | nan |
| SLJ 2 | 1.490020 | 0.482967 | 0.726369 | 0.663213 | 0.667270 | 0.683109 | 0.361335 |
| SLJ 3 | 0.665221 | 0.507463 | 0.537477 | 0.627585 | 0.657205 | 0.629222 | 0.269591 |
| Reference SLJ for Damage Metric Calculation: SLJ 2 | |||||||
| Mean | 0.812173 | 0.847828 | 0.452502 | 0.436961 | 0.477515 | 0.523814 | 0.384130 |
| 0.700657 | 0.732478 | 0.098571 | 0.044701 | 0.013855 | 0.103032 | 0.040650 | |
| SLJ 1 | 0.338086 | 1.688044 | 0.500707 | 0.394135 | 0.473814 | 0.459235 | 0.412874 |
| SLJ 2 | 1.616976 | 0.511703 | 0.517694 | 0.483326 | 0.492844 | 0.469571 | nan |
| SLJ 3 | 0.481456 | 0.343738 | 0.339106 | 0.433421 | 0.465886 | 0.642635 | 0.355386 |
| Reference SLJ for Damage Metric Calculation: SLJ 3 | |||||||
| Mean | 0.867605 | 0.833170 | 0.588123 | 0.519537 | 0.588478 | 0.609823 | 0.298460 |
| 0.556526 | 0.632924 | 0.094270 | 0.129571 | 0.047056 | 0.035447 | 0.030158 | |
| SLJ 1 | 0.470233 | 1.563741 | 0.593844 | 0.371140 | 0.536663 | 0.569274 | 0.277135 |
| SLJ 2 | 1.503662 | 0.450773 | 0.679402 | 0.610239 | 0.628554 | 0.634927 | 0.319785 |
| SLJ 3 | 0.628920 | 0.484996 | 0.491122 | 0.577231 | 0.600216 | 0.625267 | nan |
| Overall Damage Metric Data | |||||||
| Mean | 0.856028 | 0.843106 | 0.556523 | 0.505932 | 0.565538 | 0.590136 | 0.332684 |
| 0.520308 | 0.572613 | 0.115266 | 0.114383 | 0.077775 | 0.077730 | 0.054771 | |
| Case | (12.5, 12.5) | (12.5, 12.5) | (12.5, 12.5) | (6.25, 6.25) | (6.25, 6.25) | (6.25, 6.25) | No Void |
|---|---|---|---|---|---|---|---|
| Reference SLJ for Damage Metric Calculation: SLJ 1 | |||||||
| Mean | 2.150494 | 2.572109 | 0.954573 | 1.020838 | 1.036755 | 1.225825 | 0.482553 |
| 2.033942 | 2.061741 | 0.210635 | 0.104482 | 0.119432 | 0.457442 | 0.077328 | |
| SLJ 1 | 0.833835 | 4.812211 | 1.174676 | 0.910822 | 0.899625 | 1.066591 | nan |
| SLJ 2 | 4.493081 | 2.150077 | 0.934150 | 1.032964 | 1.117989 | 0.869281 | 0.427874 |
| SLJ 3 | 1.124564 | 0.754038 | 0.754894 | 1.118728 | 1.092652 | 1.741604 | 0.537232 |
| Reference SLJ for Damage Metric Calculation: SLJ 2 | |||||||
| Mean | 2.191113 | 2.633881 | 0.926825 | 0.974558 | 1.002551 | 1.224560 | 0.535051 |
| 2.157269 | 2.186830 | 0.226465 | 0.122683 | 0.137629 | 0.494005 | 0.127505 | |
| SLJ 1 | 0.797651 | 5.010481 | 1.160811 | 0.845859 | 0.844738 | 1.054552 | 0.444892 |
| SLJ 2 | 4.676002 | 2.184535 | 0.910948 | 0.987641 | 1.097669 | 0.838010 | nan |
| SLJ 3 | 1.099687 | 0.706625 | 0.708716 | 1.090175 | 1.065248 | 1.781119 | 0.625211 |
| Reference SLJ for Damage Metric Calculation: SLJ 3 | |||||||
| Mean | 2.101113 | 2.392290 | 1.054661 | 1.131452 | 1.142372 | 1.277951 | 0.516859 |
| 1.765284 | 1.823692 | 0.192192 | 0.089802 | 0.107212 | 0.367658 | 0.041283 | |
| SLJ 1 | 0.951229 | 4.417474 | 1.254071 | 1.037822 | 1.019102 | 1.167650 | 0.487668 |
| SLJ 2 | 4.133640 | 1.879520 | 1.039304 | 1.139674 | 1.213890 | 0.978070 | 0.546050 |
| SLJ 3 | 1.218470 | 0.879876 | 0.870608 | 1.216860 | 1.194124 | 1.688134 | nan |
| Overall Damage Metric Data | |||||||
| Mean | 2.147573 | 2.532760 | 0.978686 | 1.042283 | 1.060560 | 1.242779 | 0.511488 |
| 1.725764 | 1.761115 | 0.191152 | 0.115681 | 0.123123 | 0.384464 | 0.073190 | |
| Case | (12.5, 12.5) | (12.5, 12.5) | (12.5, 12.5) | (6.25, 6.25) | (6.25, 6.25) | (6.25, 6.25) | No Void |
|---|---|---|---|---|---|---|---|
| Reference SLJ for Damage Metric Calculation: SLJ 1 | |||||||
| Mean | 0.731113 | 0.691183 | 0.989086 | 0.980003 | 0.973896 | 0.963964 | 0.985472 |
| 0.431745 | 0.442396 | 0.005323 | 0.010848 | 0.012074 | 0.042513 | 0.018707 | |
| SLJ 1 | 0.983409 | 0.182498 | 0.994039 | 0.968247 | 0.976695 | 0.993276 | nan |
| SLJ 2 | 0.232589 | 0.904987 | 0.983458 | 0.982136 | 0.960668 | 0.983410 | 0.972244 |
| SLJ 3 | 0.977341 | 0.986066 | 0.989761 | 0.989626 | 0.984324 | 0.915206 | 0.998700 |
| Reference SLJ for Damage Metric Calculation: SLJ 2 | |||||||
| Mean | 0.927047 | 0.912900 | 0.995970 | 0.992485 | 0.991875 | 0.991281 | 0.998705 |
| 0.114515 | 0.127400 | 0.002144 | 0.004130 | 0.002062 | 0.007508 | 0.000012 | |
| SLJ 1 | 0.995011 | 0.766152 | 0.997603 | 0.988071 | 0.991761 | 0.997122 | 0.998714 |
| SLJ 2 | 0.794834 | 0.977365 | 0.993542 | 0.993128 | 0.989873 | 0.993909 | nan |
| SLJ 3 | 0.991297 | 0.995184 | 0.996766 | 0.996255 | 0.993991 | 0.982812 | 0.998696 |
| Reference SLJ for Damage Metric Calculation: SLJ 3 | |||||||
| Mean | 0.605243 | 0.347038 | 0.900431 | 0.879389 | 0.825213 | 0.654478 | 0.833412 |
| 0.478175 | 0.467435 | 0.021357 | 0.072320 | 0.064932 | 0.473700 | 0.008178 | |
| SLJ 1 | 0.884426 | 0.044831 | 0.898863 | 0.802021 | 0.815447 | 0.960850 | 0.827630 |
| SLJ 2 | 0.053106 | 0.110845 | 0.922529 | 0.890855 | 0.765717 | 0.893712 | 0.839195 |
| SLJ 3 | 0.878196 | 0.885438 | 0.879901 | 0.945292 | 0.894475 | 0.108871 | nan |
| Overall Damage Metric Data | |||||||
| Mean | 0.754468 | 0.650374 | 0.961829 | 0.950626 | 0.930328 | 0.869908 | 0.939196 |
| 0.356042 | 0.410590 | 0.047451 | 0.064999 | 0.085833 | 0.287766 | 0.082659 | |
| Case | (12.5, 12.5) | (12.5, 12.5) | (12.5, 12.5) | (6.25, 6.25) | (6.25, 6.25) | (6.25, 6.25) | No Void |
|---|---|---|---|---|---|---|---|
| Reference SLJ for Damage Metric Calculation: SLJ 1 | |||||||
| Mean | 0.081119 | 0.041578 | 0.086009 | 0.145352 | 0.136958 | 0.067527 | 0.020333 |
| 0.067994 | 0.015058 | 0.071872 | 0.038278 | 0.035559 | 0.055721 | 0.003323 | |
| SLJ 1 | 0.031578 | 0.055789 | 0.166252 | 0.110154 | 0.096403 | 0.131000 | nan |
| SLJ 2 | 0.053140 | 0.043149 | 0.064229 | 0.139799 | 0.151676 | 0.044912 | 0.017983 |
| SLJ 3 | 0.158639 | 0.025795 | 0.027548 | 0.186104 | 0.162795 | 0.026670 | 0.022683 |
| Reference SLJ for Damage Metric Calculation: SLJ 2 | |||||||
| Mean | 0.081506 | 0.036902 | 0.086639 | 0.151201 | 0.142224 | 0.068831 | 0.018765 |
| 0.072117 | 0.014895 | 0.077081 | 0.038090 | 0.035786 | 0.059046 | 0.000941 | |
| SLJ 1 | 0.030654 | 0.051711 | 0.172283 | 0.116695 | 0.101419 | 0.136420 | 0.018099 |
| SLJ 2 | 0.049823 | 0.037072 | 0.064800 | 0.144834 | 0.156985 | 0.042795 | nan |
| SLJ 3 | 0.164041 | 0.021922 | 0.022833 | 0.192073 | 0.168268 | 0.027278 | 0.019431 |
| Reference SLJ for Damage Metric Calculation: SLJ 3 | |||||||
| Mean | 0.094481 | 0.040535 | 0.102619 | 0.166634 | 0.157860 | 0.083431 | 0.021398 |
| 0.074380 | 0.015844 | 0.077001 | 0.038944 | 0.036371 | 0.060200 | 0.002434 | |
| SLJ 1 | 0.046068 | 0.057740 | 0.188075 | 0.131032 | 0.116372 | 0.151951 | 0.023119 |
| SLJ 2 | 0.057249 | 0.026543 | 0.081152 | 0.160645 | 0.172958 | 0.059314 | 0.019677 |
| SLJ 3 | 0.180125 | 0.037322 | 0.038630 | 0.208226 | 0.184251 | 0.039029 | nan |
| Overall Damage Metric Data | |||||||
| Mean | 0.085702 | 0.039671 | 0.091756 | 0.154396 | 0.145681 | 0.073263 | 0.020165 |
| 0.062310 | 0.013395 | 0.065769 | 0.034624 | 0.032490 | 0.051110 | 0.002230 | |
Appendix A.2.2. Linearly Spaced Spectrum from fi = 100 kHz to ff = 1 MHz
| Case | (12.5, 12.5) | (12.5, 12.5) | (12.5, 12.5) | (6.25, 6.25) | (6.25, 6.25) | (6.25, 6.25) | No Void |
|---|---|---|---|---|---|---|---|
| Reference SLJ for Damage Metric Calculation: SLJ 1 | |||||||
| Mean | 1.352921 | 1.132051 | 1.351402 | 1.252441 | 1.286597 | 1.305977 | 0.829478 |
| 0.079012 | 0.273625 | 0.133630 | 0.162613 | 0.181572 | 0.197616 | 0.069397 | |
| SLJ 1 | 1.286721 | 1.256988 | 1.385234 | 1.071973 | 1.082785 | 1.415119 | nan |
| SLJ 2 | 1.331652 | 0.818258 | 1.464865 | 1.297771 | 1.431092 | 1.424952 | 0.780407 |
| SLJ 3 | 1.440391 | 1.320906 | 1.204108 | 1.387580 | 1.345913 | 1.077861 | 0.878549 |
| Reference SLJ for Damage Metric Calculation: SLJ 2 | |||||||
| Mean | 1.227120 | 0.986807 | 1.241473 | 1.124923 | 1.178139 | 1.173564 | 0.939293 |
| 0.119271 | 0.255472 | 0.182134 | 0.214342 | 0.235502 | 0.277852 | 0.191089 | |
| SLJ 1 | 1.137591 | 1.107732 | 1.322740 | 0.890196 | 0.912197 | 1.361026 | 0.804173 |
| SLJ 2 | 1.181255 | 0.693323 | 1.368827 | 1.174314 | 1.360276 | 1.305322 | nan |
| SLJ 3 | 1.362515 | 1.159365 | 1.032852 | 1.310258 | 1.261944 | 0.854344 | 1.074414 |
| Reference SLJ for Damage Metric Calculation: SLJ 3 | |||||||
| Mean | 1.440811 | 1.201361 | 1.427066 | 1.371119 | 1.397872 | 1.402469 | 0.841000 |
| 0.064966 | 0.306678 | 0.108534 | 0.119576 | 0.144531 | 0.138134 | 0.101430 | |
| SLJ 1 | 1.394348 | 1.355709 | 1.471450 | 1.239507 | 1.235214 | 1.490105 | 0.769278 |
| SLJ 2 | 1.413038 | 0.848173 | 1.506374 | 1.400768 | 1.511544 | 1.474067 | 0.912722 |
| SLJ 3 | 1.515047 | 1.400200 | 1.303375 | 1.473081 | 1.446858 | 1.243235 | nan |
| Overall Damage Metric Data | |||||||
| Mean | 1.340284 | 1.106739 | 1.339981 | 1.249494 | 1.287536 | 1.294003 | 0.869924 |
| 0.121754 | 0.259882 | 0.149111 | 0.181771 | 0.190744 | 0.209138 | 0.115055 | |
| Case | (12.5, 12.5) | (12.5, 12.5) | (12.5, 12.5) | (6.25, 6.25) | (6.25, 6.25) | (6.25, 6.25) | No Void |
|---|---|---|---|---|---|---|---|
| Reference SLJ for Damage Metric Calculation: SLJ 1 | |||||||
| Mean | 0.722710 | 0.731421 | 0.680192 | 0.829257 | 0.791979 | 0.719665 | 0.968920 |
| 0.031882 | 0.027068 | 0.110570 | 0.092818 | 0.096103 | 0.187356 | 0.000089 | |
| SLJ 1 | 0.737295 | 0.700589 | 0.789763 | 0.936282 | 0.888211 | 0.677677 | nan |
| SLJ 2 | 0.744691 | 0.742397 | 0.568650 | 0.780696 | 0.696005 | 0.556866 | 0.968983 |
| SLJ 3 | 0.686144 | 0.751277 | 0.682163 | 0.770793 | 0.791722 | 0.924452 | 0.968857 |
| Reference SLJ for Damage Metric Calculation: SLJ 2 | |||||||
| Mean | 0.709602 | 0.520881 | 0.625924 | 0.821473 | 0.898904 | 0.737817 | 0.161579 |
| 0.090016 | 0.256267 | 0.094427 | 0.051212 | 0.024148 | 0.121098 | 0.012631 | |
| SLJ 1 | 0.628221 | 0.574617 | 0.719152 | 0.777628 | 0.909149 | 0.830162 | 0.170511 |
| SLJ 2 | 0.694295 | 0.242007 | 0.628279 | 0.809033 | 0.871323 | 0.600711 | nan |
| SLJ 3 | 0.806290 | 0.746019 | 0.530342 | 0.877759 | 0.916240 | 0.782577 | 0.152648 |
| Reference SLJ for Damage Metric Calculation: SLJ 3 | |||||||
| Mean | 0.703371 | 0.711123 | 0.653377 | 0.829389 | 0.789369 | 0.715122 | 0.785326 |
| 0.024669 | 0.044926 | 0.095550 | 0.093919 | 0.088076 | 0.171675 | 0.242382 | |
| SLJ 1 | 0.704281 | 0.659716 | 0.749927 | 0.937473 | 0.871854 | 0.664645 | 0.613936 |
| SLJ 2 | 0.727572 | 0.742850 | 0.558860 | 0.783038 | 0.696603 | 0.574344 | 0.956715 |
| SLJ 3 | 0.678259 | 0.730805 | 0.651344 | 0.767657 | 0.799651 | 0.906377 | nan |
| Overall Damage Metric Data | |||||||
| Mean | 0.711894 | 0.654475 | 0.653164 | 0.826707 | 0.826751 | 0.724201 | 0.638608 |
| 0.050051 | 0.164992 | 0.090112 | 0.070923 | 0.085579 | 0.141131 | 0.393773 | |
| Case | (12.5, 12.5) | (12.5, 12.5) | (12.5, 12.5) | (6.25, 6.25) | (6.25, 6.25) | (6.25, 6.25) | No Void |
|---|---|---|---|---|---|---|---|
| Reference SLJ for Damage Metric Calculation: SLJ 1 | |||||||
| Mean | 0.313210 | 0.252926 | 0.341746 | 0.317485 | 0.351828 | 0.299703 | 0.176887 |
| 0.055542 | 0.083690 | 0.056381 | 0.090318 | 0.036653 | 0.100506 | 0.035029 | |
| SLJ 1 | 0.272498 | 0.321031 | 0.330758 | 0.213262 | 0.309546 | 0.336047 | nan |
| SLJ 2 | 0.290650 | 0.159500 | 0.402811 | 0.372840 | 0.374586 | 0.376981 | 0.201657 |
| SLJ 3 | 0.376483 | 0.278246 | 0.291668 | 0.366352 | 0.371353 | 0.186081 | 0.152118 |
| Reference SLJ for Damage Metric Calculation: SLJ 2 | |||||||
| Mean | 0.194296 | 0.168821 | 0.224089 | 0.240606 | 0.252418 | 0.201958 | 0.196560 |
| 0.060355 | 0.032630 | 0.055009 | 0.034021 | 0.014498 | 0.071372 | 0.020750 | |
| SLJ 1 | 0.157311 | 0.200062 | 0.244871 | 0.201323 | 0.236698 | 0.248510 | 0.211233 |
| SLJ 2 | 0.161634 | 0.134960 | 0.265679 | 0.260066 | 0.265263 | 0.237578 | nan |
| SLJ 3 | 0.263943 | 0.171441 | 0.161716 | 0.260431 | 0.255292 | 0.119787 | 0.181888 |
| Reference SLJ for Damage Metric Calculation: SLJ 3 | |||||||
| Mean | 0.295184 | 0.228644 | 0.322227 | 0.301584 | 0.334264 | 0.285578 | 0.167184 |
| 0.059195 | 0.090719 | 0.055728 | 0.081505 | 0.033011 | 0.092609 | 0.015622 | |
| SLJ 1 | 0.251990 | 0.294050 | 0.321222 | 0.207479 | 0.296829 | 0.325402 | 0.156138 |
| SLJ 2 | 0.270904 | 0.125079 | 0.378451 | 0.349686 | 0.359205 | 0.351614 | 0.178230 |
| SLJ 3 | 0.362659 | 0.266803 | 0.267008 | 0.347588 | 0.346757 | 0.179719 | nan |
| Overall Damage Metric Data | |||||||
| Mean | 0.267564 | 0.216797 | 0.296020 | 0.286559 | 0.312837 | 0.262413 | 0.180211 |
| 0.075089 | 0.074026 | 0.072866 | 0.072282 | 0.052651 | 0.089645 | 0.023655 | |
Appendix A.2.3. Logarithmically Spaced Spectrum from fi = 10 kHz to ff = 200 kHz
| Case | (12.5, 12.5) | (12.5, 12.5) | (12.5, 12.5) | (6.25, 6.25) | (6.25, 6.25) | (6.25, 6.25) | No Void |
|---|---|---|---|---|---|---|---|
| Reference SLJ for Damage Metric Calculation: SLJ 1 | |||||||
| Mean | 1.066446 | 0.923113 | 1.062975 | 1.131531 | 1.132624 | 1.013796 | 0.635077 |
| 0.138231 | 0.173680 | 0.167036 | 0.101225 | 0.124459 | 0.156911 | 0.064526 | |
| SLJ 1 | 0.929624 | 1.108537 | 1.234420 | 1.024744 | 0.988999 | 1.184887 | nan |
| SLJ 2 | 1.063668 | 0.764234 | 1.053776 | 1.143770 | 1.208801 | 0.979891 | 0.589450 |
| SLJ 3 | 1.206045 | 0.896569 | 0.900728 | 1.226080 | 1.200073 | 0.876608 | 0.680703 |
| Reference SLJ for Damage Metric Calculation: SLJ 2 | |||||||
| Mean | 1.065565 | 0.962622 | 1.028297 | 1.071120 | 1.084544 | 0.981617 | 0.804972 |
| 0.142647 | 0.190595 | 0.169613 | 0.114080 | 0.149372 | 0.156754 | 0.154135 | |
| SLJ 1 | 0.902280 | 1.182589 | 1.207728 | 0.952952 | 0.912100 | 1.157804 | 0.695982 |
| SLJ 2 | 1.128456 | 0.858756 | 1.006567 | 1.079792 | 1.173814 | 0.929445 | nan |
| SLJ 3 | 1.165960 | 0.846522 | 0.870596 | 1.180616 | 1.167717 | 0.857600 | 0.913962 |
| Reference SLJ for Damage Metric Calculation: SLJ 3 | |||||||
| Mean | 1.124266 | 0.933012 | 1.128306 | 1.202823 | 1.203786 | 1.087888 | 0.612888 |
| 0.133223 | 0.213990 | 0.161258 | 0.088382 | 0.111603 | 0.148069 | 0.055788 | |
| SLJ 1 | 1.004546 | 1.130444 | 1.296110 | 1.110359 | 1.074988 | 1.251285 | 0.573440 |
| SLJ 2 | 1.100468 | 0.705622 | 1.114300 | 1.211649 | 1.271854 | 1.049784 | 0.652336 |
| SLJ 3 | 1.267784 | 0.962970 | 0.974507 | 1.286461 | 1.264516 | 0.962594 | nan |
| Overall Damage Metric Data | |||||||
| Mean | 1.085426 | 0.939582 | 1.073193 | 1.135158 | 1.140318 | 1.027767 | 0.684312 |
| 0.123085 | 0.168486 | 0.150341 | 0.105013 | 0.123546 | 0.141445 | 0.122639 | |
| Case | (12.5, 12.5) | (12.5, 12.5) | (12.5, 12.5) | (6.25, 6.25) | (6.25, 6.25) | (6.25, 6.25) | No Void |
|---|---|---|---|---|---|---|---|
| Reference SLJ for Damage Metric Calculation: SLJ 1 | |||||||
| Mean | 0.985319 | 0.974518 | 0.986788 | 0.992460 | 0.990152 | 0.987684 | 0.983142 |
| 0.004655 | 0.013577 | 0.003081 | 0.000595 | 0.001351 | 0.005771 | 0.019618 | |
| SLJ 1 | 0.985945 | 0.960153 | 0.990303 | 0.992446 | 0.991479 | 0.992096 | nan |
| SLJ 2 | 0.980383 | 0.976260 | 0.985507 | 0.993061 | 0.990201 | 0.989803 | 0.997014 |
| SLJ 3 | 0.989629 | 0.987140 | 0.984555 | 0.991871 | 0.988778 | 0.981153 | 0.969270 |
| Reference SLJ for Damage Metric Calculation: SLJ 2 | |||||||
| Mean | 0.749143 | 0.774388 | 0.890915 | 0.929909 | 0.909734 | 0.895834 | 0.822756 |
| 0.261286 | 0.200810 | 0.047342 | 0.024166 | 0.026993 | 0.059042 | 0.005897 | |
| SLJ 1 | 0.856708 | 0.543410 | 0.937685 | 0.903224 | 0.878601 | 0.941616 | 0.826926 |
| SLJ 2 | 0.451244 | 0.907526 | 0.892039 | 0.936185 | 0.926598 | 0.916692 | nan |
| SLJ 3 | 0.939477 | 0.872228 | 0.843021 | 0.950317 | 0.924003 | 0.829195 | 0.818586 |
| Reference SLJ for Damage Metric Calculation: SLJ 3 | |||||||
| Mean | 0.993498 | 0.990492 | 0.993517 | 0.995475 | 0.994814 | 0.993777 | 0.997061 |
| 0.000738 | 0.004122 | 0.000781 | 0.000234 | 0.000916 | 0.002066 | 0.000007 | |
| SLJ 1 | 0.993516 | 0.985922 | 0.994418 | 0.995402 | 0.995781 | 0.995314 | 0.997066 |
| SLJ 2 | 0.992752 | 0.991628 | 0.993040 | 0.995736 | 0.994702 | 0.994587 | 0.997056 |
| SLJ 3 | 0.994227 | 0.993928 | 0.993093 | 0.995285 | 0.993958 | 0.991429 | nan |
| Overall Damage Metric Data | |||||||
| Mean | 0.909320 | 0.913133 | 0.957073 | 0.972614 | 0.964900 | 0.959098 | 0.934320 |
| 0.177532 | 0.144940 | 0.055076 | 0.034259 | 0.043575 | 0.056028 | 0.087124 | |
| Case | (12.5, 12.5) | (12.5, 12.5) | (12.5, 12.5) | (6.25, 6.25) | (6.25, 6.25) | (6.25, 6.25) | No Void |
|---|---|---|---|---|---|---|---|
| Reference SLJ for Damage Metric Calculation: SLJ 1 | |||||||
| Mean | 0.070861 | 0.024927 | 0.084062 | 0.146669 | 0.138525 | 0.064544 | 0.014976 |
| 0.075120 | 0.006817 | 0.078396 | 0.035918 | 0.034188 | 0.059096 | 0.007633 | |
| SLJ 1 | 0.028121 | 0.024461 | 0.172495 | 0.115090 | 0.099542 | 0.132405 | nan |
| SLJ 2 | 0.026864 | 0.031965 | 0.056596 | 0.139173 | 0.152624 | 0.036821 | 0.009579 |
| SLJ 3 | 0.157599 | 0.018354 | 0.023094 | 0.185744 | 0.163408 | 0.024406 | 0.020373 |
| Reference SLJ for Damage Metric Calculation: SLJ 2 | |||||||
| Mean | 0.074994 | 0.024756 | 0.088489 | 0.152232 | 0.144017 | 0.068832 | 0.012744 |
| 0.076379 | 0.003736 | 0.079586 | 0.036095 | 0.034370 | 0.060058 | 0.004408 | |
| SLJ 1 | 0.031688 | 0.026930 | 0.178170 | 0.120519 | 0.104832 | 0.137788 | 0.009627 |
| SLJ 2 | 0.030110 | 0.026897 | 0.061022 | 0.144666 | 0.158158 | 0.040736 | nan |
| SLJ 3 | 0.163184 | 0.020442 | 0.026274 | 0.191510 | 0.169060 | 0.027973 | 0.015861 |
| Reference SLJ for Damage Metric Calculation: SLJ 3 | |||||||
| Mean | 0.090496 | 0.029917 | 0.104444 | 0.169163 | 0.160835 | 0.084510 | 0.018434 |
| 0.077780 | 0.013877 | 0.080856 | 0.036646 | 0.034902 | 0.061055 | 0.003311 | |
| SLJ 1 | 0.046698 | 0.040506 | 0.195507 | 0.136946 | 0.121039 | 0.154589 | 0.020775 |
| SLJ 2 | 0.044491 | 0.014208 | 0.076754 | 0.161514 | 0.175224 | 0.056138 | 0.016093 |
| SLJ 3 | 0.180299 | 0.035038 | 0.041070 | 0.209030 | 0.186243 | 0.042803 | nan |
| Overall Damage Metric Data | |||||||
| Mean | 0.078784 | 0.026533 | 0.092331 | 0.156021 | 0.147792 | 0.072629 | 0.015385 |
| 0.066798 | 0.008348 | 0.069574 | 0.032969 | 0.031518 | 0.052817 | 0.004930 | |
References
- Giurgiutiu, V. Structural Health Monitoring with Piezoelectric Wafer Active Sensors, 2nd ed.; Academic Press: Oxford, UK, 2014. [Google Scholar] [CrossRef]
- Güemes, A.; Fernandez-Lopez, A.; Pozo, A.R.; Sierra-Pérez, J. Structural Health Monitoring for Advanced Composite Structures: A Review. J. Compos. Sci. 2020, 4, 13. [Google Scholar] [CrossRef]
- Cawley, P. Structural health monitoring: Closing the gap between research and industrial deployment. Struct. Health Monit. 2018, 17, 1225–1244. [Google Scholar] [CrossRef]
- Ju, M.; Dou, Z.; Li, J.W.; Qiu, X.; Shen, B.; Zhang, D.; Yao, F.Z.; Gong, W.; Wang, K. Piezoelectric Materials and Sensors for Structural Health Monitoring: Fundamental Aspects, Current Status, and Future Perspectives. Sensors 2023, 23, 543. [Google Scholar] [CrossRef] [PubMed]
- Mitra, M.; Gopalakrishnan, S. Guided wave based structural health monitoring: A review. Smart Mater. Struct. 2016, 25, 053001. [Google Scholar] [CrossRef]
- Tenreiro, A.F.G.; Lopes, A.M.; da Silva, L.F.M. A review of structural health monitoring of bonded structures using electromechanical impedance spectroscopy. Struct. Health Monit. 2022, 21, 228–249. [Google Scholar] [CrossRef]
- Liang, C.; Sun, F.P.; Rogers, C.A. Coupled Electro-Mechanical Analysis of Adaptive Material Systems-Determination of the Actuator Power Consumption and System Energy Transfer. J. Intell. Mater. Syst. Struct. 1997, 8, 335–343. [Google Scholar] [CrossRef]
- Xu, Y.G.; Liu, G.R. A Modified Electro-Mechanical Impedance Model of Piezoelectric Actuator-Sensors for Debonding Detection of Composite Patches. J. Intell. Mater. Syst. Struct. 2002, 13, 389–396. [Google Scholar] [CrossRef]
- Zagrai, A.N.; Giurgiutiu, V. Electro-Mechanical Impedance Method for Crack Detection in Thin Plates. J. Intell. Mater. Syst. Struct. 2001, 12, 709–718. [Google Scholar] [CrossRef]
- Bhalla, S.; Kumar, P.; Gupta, A.; Datta, T.K. Simplified Impedance Model for Adhesively Bonded Piezo-Impedance Transducers. J. Aerosp. Eng. 2009, 22, 373–382. [Google Scholar] [CrossRef]
- Wang, D.; Song, H.; Zhu, H. Embedded 3D electromechanical impedance model for strength monitoring of concrete using a PZT transducer. Smart Mater. Struct. 2014, 23, 115019. [Google Scholar] [CrossRef]
- Tenreiro, A.F.G.; Lopes, A.M.; da Silva, L.F.M.; Amorim, J.D.P. Effect of mechanical properties and geometric dimensions on electromechanical impedance signatures for adhesive joint integrity monitoring. Mech. Adv. Mater. Struct. 2023, 30, 1437–1452. [Google Scholar] [CrossRef]
- Alonso, M.; Finn, E.J. Fundamental University Physics—Volume II Fields and Waves; World Student Series; Addison-Wesley Publishing Company: Reading, MA, USA, 1974; Volume 2. [Google Scholar]
- Bhalla, S.; Surendra, A.; Soh, C.K. Influence of structure-actuator interactions and temperature on piezoelectric mechatronic signatures for NDE. In Proceedings of the Volume 5062, Smart Materials, Structures, and Systems, Bangalore, India, 12–14 December 2002; Volume 5062. [Google Scholar] [CrossRef]
- da Silva, L.F.M.; Öchsner, A.; Adams, R.D. Handbook of Adhesion Technology, 2nd ed.; Springer International Publishing AG: New York, NY, USA, 2018. [Google Scholar]
- Adams, R.D.; Drinkwater, B.W. Nondestructive testing of adhesively-bonded joints. NDT E Int. 1997, 30, 93–98. [Google Scholar] [CrossRef]
- Eslamlou, A.D.; Ghaderiaram, A.; Erik, S.; Fotouhi, M. A review on non-destructive evaluation of construction materials and structures using magnetic sensors. Constr. Build. Mater. 2023, 397, 132460. [Google Scholar] [CrossRef]
- Tenreiro, A.F.G.; Ramalho, G.M.F.; Lopes, A.M.; da Silva, L.F.M. Structural monitoring of adhesive joints using machine learning. In Advances in Structural Adhesive Bonding, 2nd ed.; Dillard, D.A., Ed.; Woodhead Publishing: Sawston, UK, 2023; Chapter 28; pp. 909–949. [Google Scholar] [CrossRef]
- Borges, C.S.P.; Akhavan-Safar, A.; Tsokanas, P.; Carbas, R.J.C.; Marques, E.A.S.; da Silva, L.F.M. From fundamental concepts to recent developments in the adhesive bonding technology: A general view. Discov. Mech. Eng. 2023, 2, 8. [Google Scholar] [CrossRef]
- Çam, S.; Sofuoğlu, H. An investigation on crashworthiness performance of adhesive bonding in automobile hybrid front bumper system subjected to high-speed impact. Int. J. Impact Eng. 2023, 173, 104478. [Google Scholar] [CrossRef]
- Wei, T.; Jingxin, N.; Wenlong, M.; Guangbin, W.; Yao, F. Effects of hygrothermal aging on the mechanical properties of aluminum alloy adhesive joints for high-speed train applications. J. Adhes. 2022, 98, 227–256. [Google Scholar] [CrossRef]
- Jeon, S.W.; Cho, Y.H.; Han, M.G.; Chang, S.H. Design of carbon/epoxy–aluminum hybrid upper arm of the pantograph of high-speed trains using adhesive bonding technique. Compos. Struct. 2016, 152, 538–545. [Google Scholar] [CrossRef]
- Martins, C.; Dias, A.M.; Cruz, H. Bonding performance of Portuguese Maritime pine glued laminated timber. Constr. Build. Mater. 2019, 223, 520–529. [Google Scholar] [CrossRef]
- Brotherhood, C.; Drinkwater, B.; Dixon, S. The detectability of kissing bonds in adhesive joints using ultrasonic techniques. Ultrasonics 2003, 41, 521–529. [Google Scholar] [CrossRef]
- Tighe, R.C.; Dulieu-Barton, J.M.; Quinn, S. Identification of kissing defects in adhesive bonds using infrared thermography. Int. J. Adhes. Adhes. 2016, 64, 168–178. [Google Scholar] [CrossRef]
- Ye, Y.; Ma, K.; Zhou, H.; Arola, D.; Zhang, D. An automated shearography system for cylindrical surface inspection. Measurement 2019, 135, 400–405. [Google Scholar] [CrossRef]
- Yilmaz, B.; Asokkumar, A.; Jasiūnienė, E.; Kažys, R.J. Air-Coupled, Contact, and Immersion Ultrasonic Non-Destructive Testing: Comparison for Bonding Quality Evaluation. Appl. Sci. 2020, 10, 6757. [Google Scholar] [CrossRef]
- Momm, G.G.; Fleming, D. Estimate residual strength of degraded bonded joints by combining analytical models with non-destructive evaluations. J. Adhes. 2023, 99, 783–802. [Google Scholar] [CrossRef]
- Na, S.; Tawie, R.; Lee, H.K. Electromechanical impedance method of fiber-reinforced plastic adhesive joints in corrosive environment using a reusable piezoelectric device. J. Intell. Mater. Syst. Struct. 2012, 23, 737–747. [Google Scholar] [CrossRef]
- Malinowski, P.; Wandowski, T.; Ostachowicz, W. The use of electromechanical impedance conductance signatures for detection of weak adhesive bonds of carbon fibre–reinforced polymer. Struct. Health Monit. 2015, 14, 332–344. [Google Scholar] [CrossRef]
- Roth, W.; Giurgiutiu, V. Structural health monitoring of an adhesive disbond through electromechanical impedance spectroscopy. Int. J. Adhes. Adhes. 2017, 73, 109–117. [Google Scholar] [CrossRef]
- Zhuang, Y.; Kopsaftopoulos, F.; Dugnani, R.; Chang, F.K. Integrity monitoring of adhesively bonded joints via an electromechanical impedance-based approach. Struct. Health Monit. 2018, 17, 1031–1045. [Google Scholar] [CrossRef]
- Malinowski, P.; Tserpes, K.; Ecault, R.; Ostachowicz, W. Mechanical and Non-Destructive Study of CFRP Adhesive Bonds Subjected to Pre-Bond Thermal Treatment and De-Icing Fluid Contamination. Aerospace 2018, 5, 36. [Google Scholar] [CrossRef]
- Tenreiro, A.F.G.; Lopes, A.M.; Da Silva, L.F.; Carbas, R.J. Influence of void damage on the electromechanical impedance spectra of Single Lap Joints. NDT E Int. 2023, 138, 102865. [Google Scholar] [CrossRef]
- Tseng, K.K.H.; Naidu, A.S.K. Non-parametric damage detection and characterization using smart piezoceramic material. Smart Mater. Struct. 2002, 11, 317–329. [Google Scholar] [CrossRef]
- Giurgiutiu, V.; Rogers, C.A. Recent Advancements in the Electro-Mechanical (ElM) Impedance Method for Structural Health Monitoring and NDE. In Proceedings of the SPIE 3329, Smart Structures and Materials 1998: Smart Structures and Integrated Systems, San Diego, CA, USA, 27 July 1998; Volume 3329, p. 12. [Google Scholar] [CrossRef]
- Meyer, P.L. Introductory Probability and Statistical Applications, 1st ed.; Addison-Wesley series in statistics; Addison-Wesley: Reading, MA, USA, 1965. [Google Scholar]
- Park, G.; Sohn, H.; Farrar, C.R.; Inman, D.J. Overview of Piezoelectric Impedance-Based Health Monitoring and Path Forward. Shock Vib. Dig. 2003, 35, 451–463. [Google Scholar] [CrossRef]
- Baptista, F.; Budoya, D.; Almeida, V.; Ulson, J. An Experimental Study on the Effect of Temperature on Piezoelectric Sensors for Impedance-Based Structural Health Monitoring. Sensors 2014, 14, 1208–1227. [Google Scholar] [CrossRef] [PubMed]
- Cha, S.H. Taxonomy of Nominal Type Histogram Distance Measures. In Proceedings of the Recent Advances on Applied Mathematics: Proceedings of the American Conference on Applied Mathematics (MATH ’08), Harvard, MA, USA, 24–26 March 2008; pp. 325–330. [Google Scholar]
- Soares, C.; Tenreiro Machado, J.A.; Lopes, A.M.; Vieira, E.; Delerue-Matos, C. Electrochemical impedance spectroscopy characterization of beverages. Food Chem. 2020, 302, 125345. [Google Scholar] [CrossRef] [PubMed]
- ASTM D3933-98; Standard Guide for Preparation of Aluminum Surfaces for Structural Adhesives Bonding (Phosphoric Acid Anodizing). American Society for Testing and Materials: West Conshohocken, PA, USA, 2004.
- Gottlieb, I.M. Practical Oscillator Handbook; Newes: London, UK, 1997; Volume 1. [Google Scholar] [CrossRef]
- Kumari, N.; Monga, S.; Arif, M.; Sharma, N.; Singh, A.; Gupta, V.; Vilarinho, P.M.; Sreenivas, K.; Katiyar, R. Higher permittivity of Ni-doped lead zirconate titanate, Pb[(Zr0.52Ti0.48)(1-x) Nix]O3, ceramics. Ceram. Int. 2019, 45, 4398–4407. [Google Scholar] [CrossRef]










| E (GPa) | (-) | (kg m) | (-) | |
|---|---|---|---|---|
| Aluminum Al 6082 | 70.0 | 0.33 | 2710 | |
| Nagase T-836/R-810 | 2.55 | 0.41 | 1200 | 0.10 |
| (g cm) | Elastic Compliance Coefficient | Coupling Factor | (-) | ||
|---|---|---|---|---|---|
| (mN) | (mN) | ||||
| 7.80 | 0.62 | 0.47 | 1750 | ||
| E (GPa) | (-) | (kg m) | (-) | |
|---|---|---|---|---|
| Plexus MA 422 | 0.994 | 0.31 | 960 | 0.45 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tenreiro, A.F.G.; Lopes, A.M.; da Silva, L.F.M. Damage Metrics for Void Detection in Adhesive Single-Lap Joints. Mathematics 2023, 11, 4127. https://doi.org/10.3390/math11194127
Tenreiro AFG, Lopes AM, da Silva LFM. Damage Metrics for Void Detection in Adhesive Single-Lap Joints. Mathematics. 2023; 11(19):4127. https://doi.org/10.3390/math11194127
Chicago/Turabian StyleTenreiro, António Francisco G., António M. Lopes, and Lucas F. M. da Silva. 2023. "Damage Metrics for Void Detection in Adhesive Single-Lap Joints" Mathematics 11, no. 19: 4127. https://doi.org/10.3390/math11194127
APA StyleTenreiro, A. F. G., Lopes, A. M., & da Silva, L. F. M. (2023). Damage Metrics for Void Detection in Adhesive Single-Lap Joints. Mathematics, 11(19), 4127. https://doi.org/10.3390/math11194127








