Modeling of Project Portfolio Risk Evolution and Response under the Influence of Interactions
Abstract
:1. Introduction
- RQ1: How can the evolution process of PPRs under the influence of interactions be explored?
- RQ2: How can dynamic responses to PPRs be achieved?
2. Literature Review
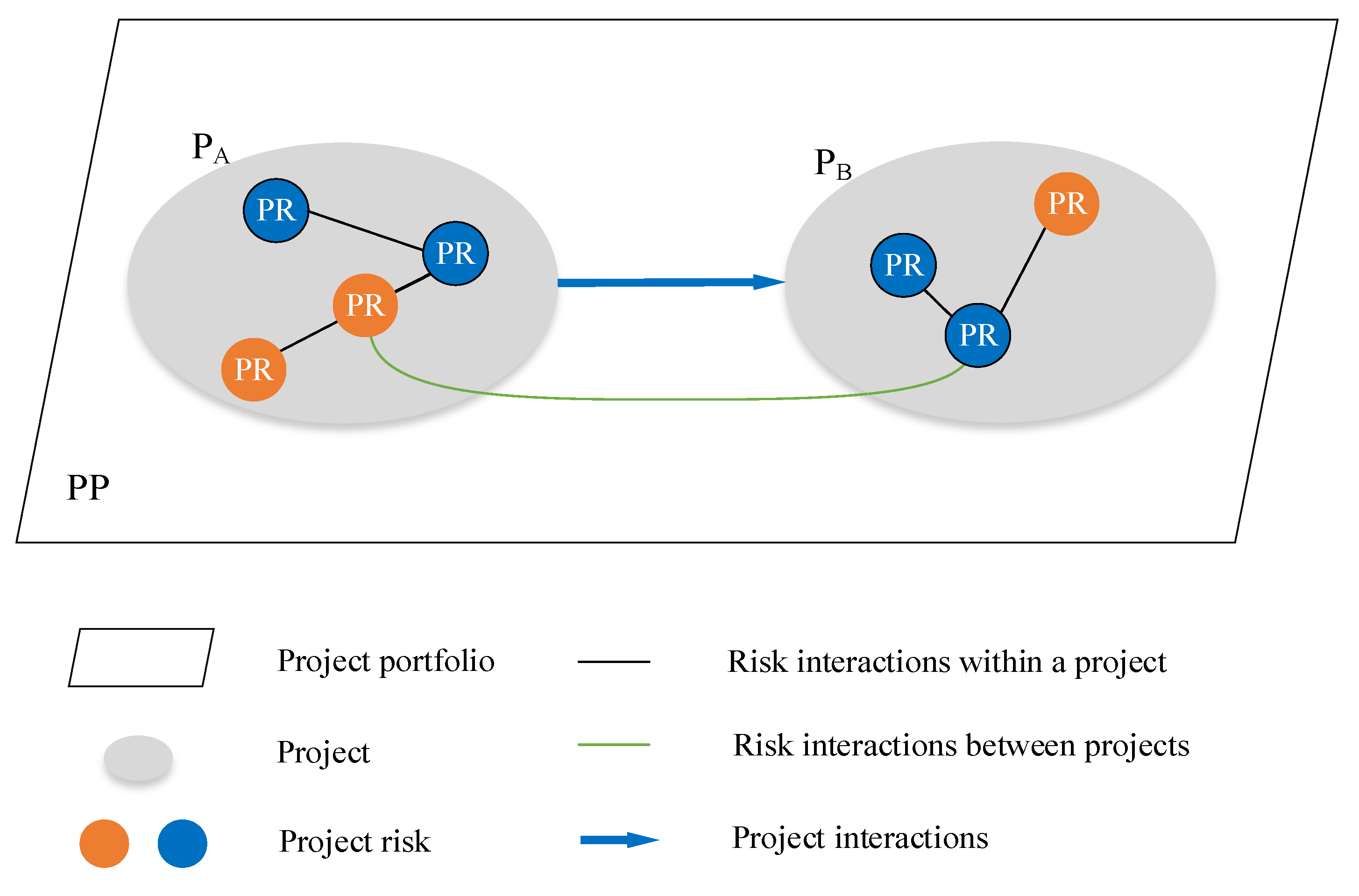
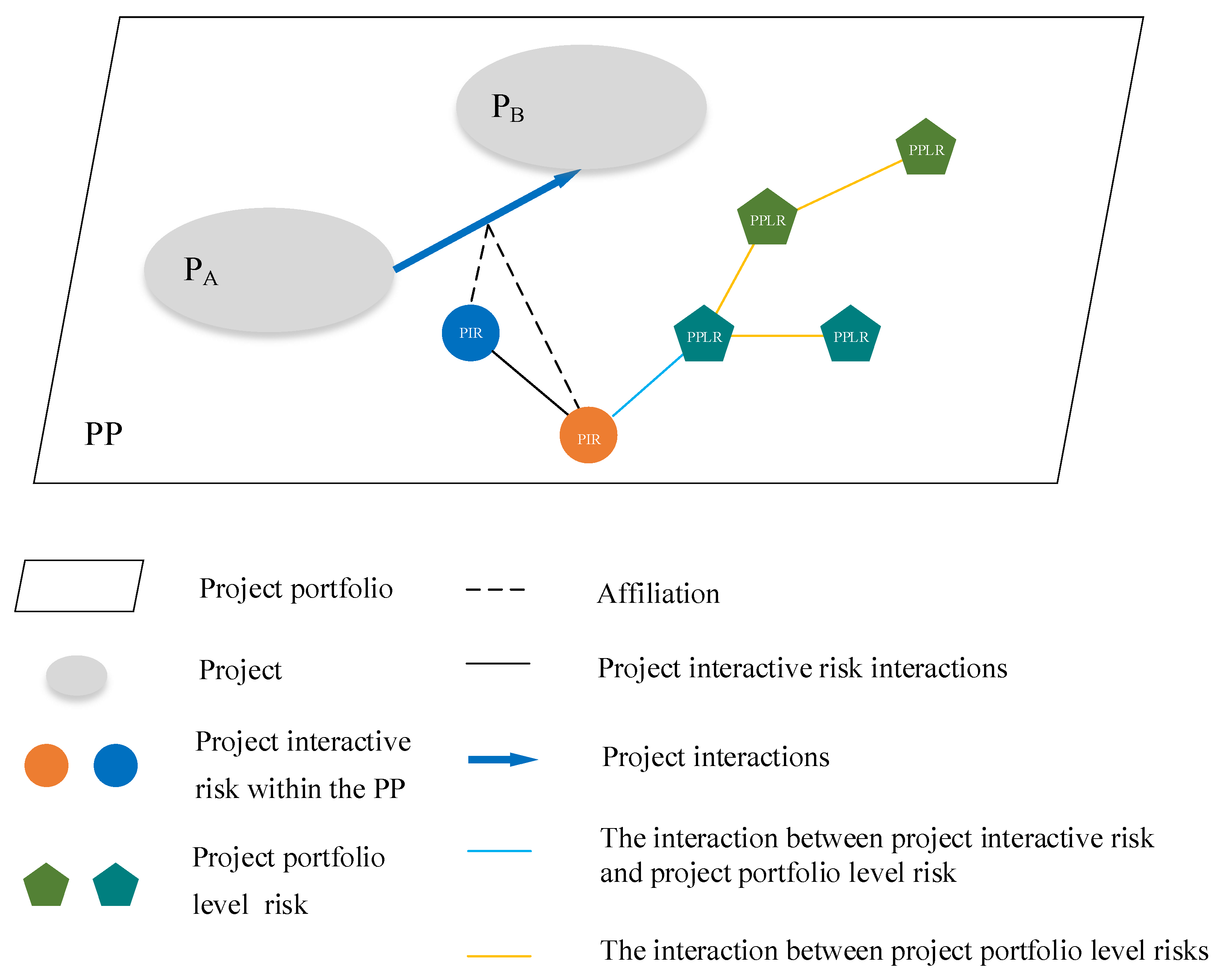
3. Project Portfolio Risk Evolution and Response Model
3.1. Construction of PPRs Evolution Function
- Step 1: Initialization
- Step 2: Definition of attachment principles
- (1)
- Definition of the attachment principles of PRs
- P1: If the newly added risks are PRs, they will first be attached to those in the same cluster and then to the different clusters with a certain probability.
- (2)
- Definition of attachment principles of PIRs
- P2: If the newly added risks are PIRs, they will first be attached to those of the same source, and then to the different sources with a certain probability.
- (3)
- Definition of attachment principles of PPLRs
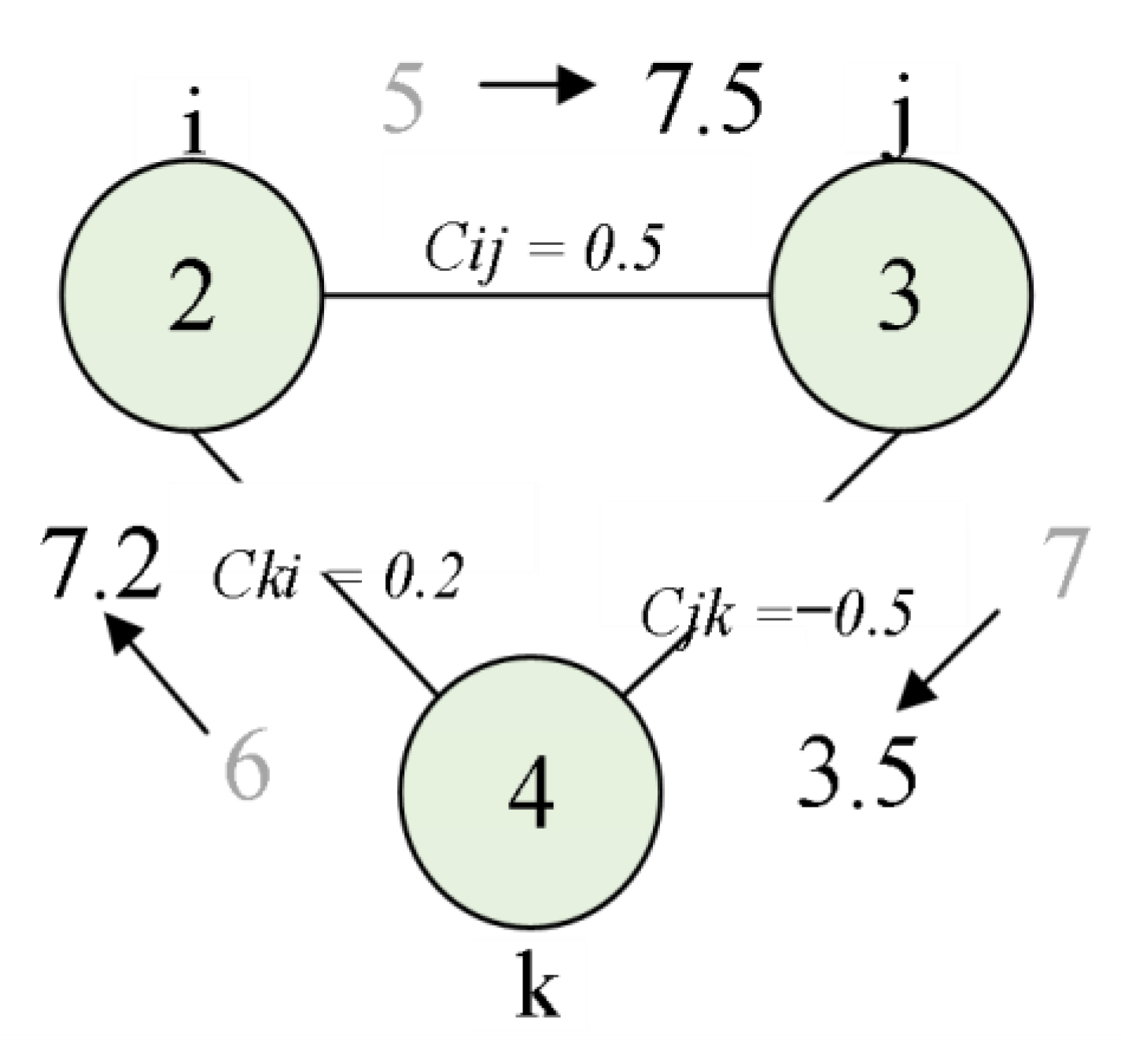
- Step 3: Weight evolution
- (1)
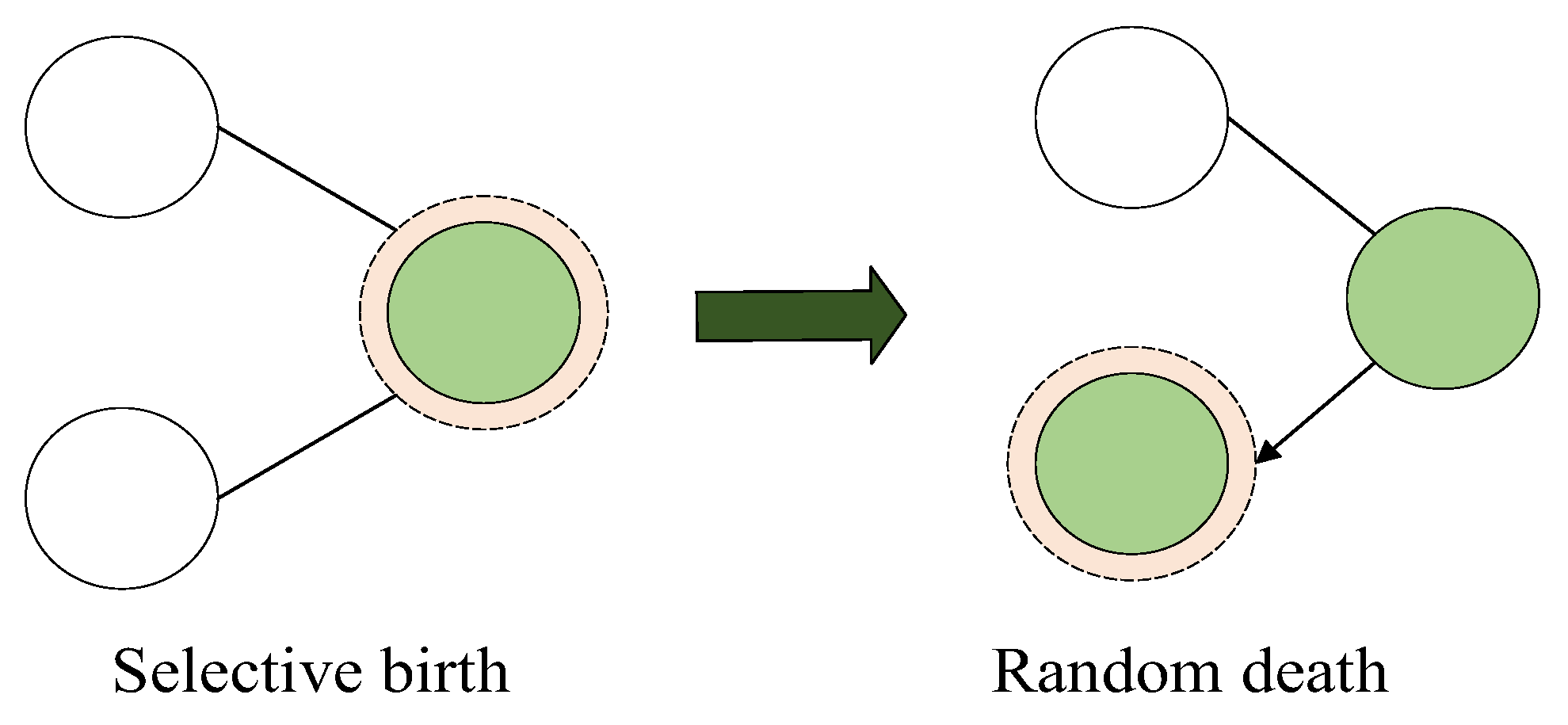
- The risk will exit from the PP when the stage of the life cycle of projects or PP changes. Managers should set the alternative nodes of each stage based on the schedule of PP.
- (2)
- When a project is finished or is eliminated from the portfolio, the PIRs arose by it, and its interactive projects will therewith exit from the PP.
- Step 4: Definition of stability principles
3.2. Construction of PPRs Response Function
4. Application of the PPRER Model
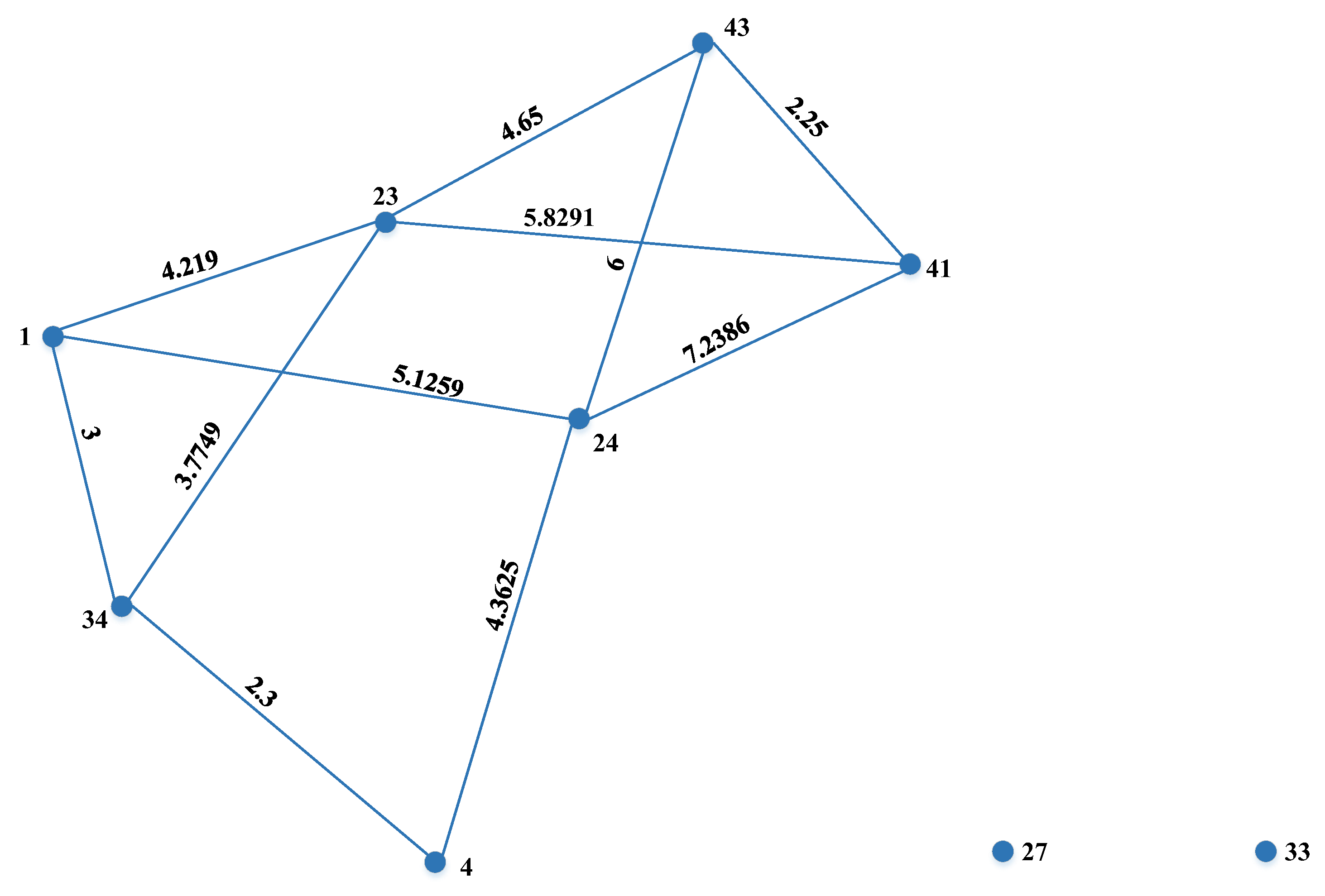
4.1. Problem Statement
4.2. Computational Results
5. Discussion
5.1. Implications for Research
5.2. Implications for Practice
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
| Abbreviation | Full Name |
|---|---|
| PP | Project Portfolio |
| PPR | Project Portfolio Risk |
| PPRER | Project Portfolio Risk Evolution and Response |
| PPREN | Project Portfolio Risk Evolution Network |
| PR | Project Risk |
| PIR | Project Interactive Risk |
| PPLR | Project Portfolio-Level Risk |
References
- Dixit, V.; Tiwari, M.K. Project portfolio selection and scheduling optimization based on risk measure: A conditional value at risk approach. Ann. Oper. Res. 2020, 285, 9–33. [Google Scholar] [CrossRef]
- PMI. A Guide to the Project Management Body of Knowledge; Project Management Institute: Newtown Square, PA, USA, 2021. [Google Scholar]
- Bai, L.; Han, X.; Zhang, Y.; Xie, X. Optimal Project Portfolio Selection Considering Cascading Failure among Projects. IEEE Trans. Eng. Manag. 2023. [Google Scholar] [CrossRef]
- Bai, L.; An, Y.; Sun, Y. Measurement of Project Portfolio Benefits with a GA-BP Neural Network Group. IEEE Trans. Eng. Manag. 2023, 1–13. [Google Scholar] [CrossRef]
- Guan, D.; Guo, P.; Hipel, K.W.; Fang, L. Risk reduction in a project portfolio. J. Syst. Sci. Syst. Eng. 2017, 26, 3–22. [Google Scholar] [CrossRef]
- Guan, L.; Abbasi, A.; Ryan, M.J. Analyzing green building project risk interdependencies using interpretive structural modeling. J. Clean. Prod. 2020, 256, 120372. [Google Scholar] [CrossRef]
- Wang, L.; Sun, T.; Qian, C.; Goh, M.; Mishra, V.K. Applying social network analysis to genetic algorithm in optimizing project risk response decisions. Inf. Sci. 2020, 512, 1024–1042. [Google Scholar] [CrossRef]
- Hatefi, S.M.; Tamosaitiene, J. An Integrated Fuzzy DEMATEL-Fuzzy ANP Model for Evaluating Construction Projects by Considering Interrelation-ships among Risk Factors. J. Civ. Eng. Manag. 2019, 25, 114–131. [Google Scholar] [CrossRef]
- Bai, L.; Song, C.; Zhou, X.; Tian, Y.; Wei, L. Assessing project portfolio risk via an enhanced GA-BPNN combined with PCA. EAAI. 2023, 126, 106779. [Google Scholar] [CrossRef]
- Bai, L.; Zhang, K.; Shi, H.; An, M.; Han, X. Project portfolio resource risk assessment considering project interdependency by the fuzzy Bayesian network. Complexity 2020, 2020, 5410978. [Google Scholar] [CrossRef]
- Sharifighazvini, M.R.; Ghezavati, V.R.; Raissi, S.; Makui, A. Integration of a new MCDM approach based on the DEA, FANP with MONLP for efficiency-risk assessment to optimize project portfolio by branch and bound: A real case-study. Econ. Comput. Econ. Cybern. Stud. Res. 2018, 52, 261–278. [Google Scholar] [CrossRef]
- Jiang, X.; Wu, Y.; Xu, P.; Zhang, W. SD model study on risk evolution in construction of project group. China Saf. Sci. J. 2015, 25, 155–161. [Google Scholar]
- Biffl, S.; Berardinelli, L.; Maetzler, E.; Wimmer, M.; Lueder, A.; Schmidt, N. Model-based risk assessment in multi-disciplinary systems engineering. In Proceedings of the 41st Euromicro Conference on Software Engineering and Advanced Applications, Funchal, Portugal, 26–28 August 2015. [Google Scholar]
- Wang, F.; Zhou, N.; He, Y.; Li, H. Dynamic simulation research on operation safety of main canal of South-to-North water transfer based on risk input. IOP Conf. Ser. Earth Environ. Sci. 2021, 643, 012142. [Google Scholar] [CrossRef]
- Sundararajan, S.K.; Tseng, C.L. Managing project performance risks under uncertainty: Using a dynamic capital structure approach in infrastructure project financing. J. Constr. Eng. Manag. 2017, 143, 04017046. [Google Scholar] [CrossRef]
- Wang, B.; Huang, D.; Li, H.; Zhang, C.; Zheng, Q. Research on social risk evolution and control of the large hydraulic project construction based on society burning theory. In Proceedings of the Computer and Computing Technologies in Agriculture VIII: 8th IFIP WG 5.14 International Conference, Beijing, China, 16–19 September 2014. [Google Scholar]
- Guo, N.; Guo, P. Evolution Mechanism of project portfolio risk based on Lotka-Voherra model. In Proceedings of the IEEE International Conference on Systems, Man, and Cybernetics, Budapest, Hungary, 9–12 October 2016. [Google Scholar]
- Zhao, J.; Guo, P.; Wang, J. Research of network clustering and co-evolution of project portfolio interactive risk. Comput. Eng. Appl. 2018, 54, 198–205. [Google Scholar]
- Zhang, Y. Selecting risk response strategies considering project risk interdependence. Int. J. Proj. Manag. 2016, 34, 819–830. [Google Scholar] [CrossRef]
- Fan, Z.; Li, Y.; Zhang, Y. Generating project risk response strategies based on CBR: A case study. Expert Syst. Appl. 2015, 42, 2870–2883. [Google Scholar] [CrossRef]
- Camilo, M.; Gabriela, F.; Madalena, A. A method for project portfolio risk assessment considering risk interdependencies-a network perspective. Procedia Comput. Sci. 2022, 196, 948–955. [Google Scholar]
- Ghasem, M.; Fatemeh, A. Project Portfolio Risk Response Selection Using Bayesian Belief Networks. Iran. J. Manag. Stud. 2020, 13, 197–219. [Google Scholar]
- Li, Q.; Wei, J.; Liu, F. Construction and application of engineering project group risk contagion network based on complex system. J. Railw. Eng. Soc. 2022, 19, 2757–2765. [Google Scholar]
- Patanakul, P. How to Achieve Effectiveness in Project Portfolio Management. IEEE Trans. Eng. Manag. 2022, 69, 987–999. [Google Scholar] [CrossRef]
- Yang, Q.; Zou, X.; Li, Z. Analyzing the project portfolio risk based on the complex network and random walk method. Syst. Eng. Theory Pract. 2020, 40, 1832–1843. [Google Scholar]
- Cheng, Y.; Yuan, J.; Zhu, L.; Li, W. Risk propagation model and simulation of schedule change in construction projects: A complex network approach. Complexity 2020, 2020, 8854609. [Google Scholar] [CrossRef]
- Zhu, J.; Cheng, Y.; Zhang, Y. Risk propagation mechanism research based on SITR model of complex supply networks. Int. J. Inf. Syst. Supply Chain Manag. (IJISSCM) 2021, 14, 18–38. [Google Scholar] [CrossRef]
- Li, T.; Chen, H.; Yuan, J.; Qian, J.; Siyal, A.W. Quality risk propagation of complex product collaborative manufacturing supply chain network based on CN and SoV. Discrete Dyn. Nat. Soc. 2020, 2020, 8889903. [Google Scholar] [CrossRef]
- Meng, X.; Chen, G.; Zhu, H. Complex network analysis on risk evolution of submarine pipeline leakage. J. Saf. Sci. Technol. 2017, 13, 26–31. [Google Scholar]
- Zhou, C.; Kong, T.; Jiang, S.; Chen, S.; Zhou, Y.; Ding, L. Quantifying the evolution of settlement risk for surrounding environments in underground construction via complex network analysis. Tunn. Undergr. Space Technol. 2020, 103, 103490. [Google Scholar] [CrossRef]
- Guan, L.; Abbasi, A.; Ryan, M.J. A simulation-based risk interdependency network model for project risk assessment. Decis. Support Syst. 2021, 148, 113602. [Google Scholar] [CrossRef]
- Sun, Y.; Tian, Y. Research on key risks of prefabricated building supply chain based on complex network theory. Constr. Econ. 2020, 41, 79–83. [Google Scholar]
- Barrat, A.; Barthelemy, M.; Vespignani, A. Weighted evolving networks: Coupling topology and weight dynamics. Phys. Rev. Lett. 2004, 92, 228701. [Google Scholar] [CrossRef]
- Tavakolan, M.; Etemadinia, H. Fuzzy Weighted Interpretive Structural Modeling: Improved Method for Identification of Risk Interactions in Construction Projects. J. Constr. Eng. Manag. 2017, 143, 0001395. [Google Scholar] [CrossRef]
- Shen, L. Project risk management in Hong Kong. Int. J. Proj. Manag. 1997, 15, 101–105. [Google Scholar] [CrossRef]
- Yang, R.J.; Zou, P.X.W. Stakeholder-associated risks and their interactions in complex green building projects: A social network model. Build. Environ. 2014, 73, 208–222. [Google Scholar] [CrossRef]
- Marle, F.; Vidal, L.; Bocquet, J. Interactions-based risk clustering methodologies and algorithms for complex project management. Int. J. Prod. Econ. 2013, 142, 225–234. [Google Scholar] [CrossRef]
- Vidal, L.A.; Marie, F.; Bocquet, J.C. Interactions-based clustering to assist project risk management. In Proceedings of the 17th International Conference on Engineering Design, Palo Alto, CA, USA, 24–27 August 2009. [Google Scholar]
- PMI. A Guide to the Project Management Body of Knowledge; Project Management Institute: Newtown Square, PA, USA, 2008. [Google Scholar]
- Killen, C.P.; Kjaer, C. Understanding project interdependencies: The role of visual representation, culture and process. Int. J. Proj. Manag. 2012, 30, 554–566. [Google Scholar] [CrossRef]
- Bhattacharyya, R.; Kumar, P.; Kar, S. Fuzzy R&D portfolio selection of interdependent projects. Comput. Math. Appl. 2011, 62, 3857–3870. [Google Scholar]
- Verma, D.; Sinha, K.K. Toward a theory of project interdependencies in high tech R&D environments. J. Oper. Manag. 2020, 20, 451–468. [Google Scholar]
- Schmidt, R.L. A model for R&D project selection with combined benefit, outcome and resource interactions. IEEE Trans. Eng. Manag. 1993, 40, 403–410. [Google Scholar]
- Wagner, S.M.; Eggert, A.; Lindemann, E. Creating and appropriating value in collaborative relationships. J. Bus. Res. 2010, 63, 840–848. [Google Scholar] [CrossRef]
- Wei, H.; Niu, C.; Xia, B.; Dou, Y.; Hu, X. A refined selection method for project portfolio optimization considering project interactions. Expert Syst. Appl. 2020, 142, 112952. [Google Scholar] [CrossRef]
- Foroogh, G.; Mohammad, S.; Vahidreza, Y.; Reza, F.; Jolanta, T. Project portfolio risk identification and analysis, considering project risk interactions and using Bayesian networks. Sustainability 2018, 10, 1609. [Google Scholar] [CrossRef]
- Lazov, I. A methodology for information and capacity analysis of broadband wireless access systems. Telecommun. Syst. 2016, 63, 127–139. [Google Scholar] [CrossRef]
- Lazov, I. Information analysis of queueing systems. Int. J. Gen. Syst. 2017, 46, 616–639. [Google Scholar] [CrossRef]
- Nicolis, S.C. Information flow and information production in a population system. Phys. Rev. E 2011, 84, 011110. [Google Scholar] [CrossRef] [PubMed]
- Franz, M.; Schuelke, O.; Ostner, J. Rapid evolution of cooperation in group-living animals. BMC Evol. Biol. 2013, 13, 235. [Google Scholar] [CrossRef]
- Mitrophanov, A.Y.; Borodovsky, M. Convergence rate estimation for the TKF91 model of biological sequence length evolution. Math. Biosci. 2007, 209, 470–485. [Google Scholar] [CrossRef]
- Bai, L.; Fralix, B.; Liu, L.; Shang, W. Inter-departure times in base-stock inventory-queues. Queueing Syst. 2004, 47, 345–361. [Google Scholar] [CrossRef]
- Xin, M. Analysis on quality control in food supply chain based on dynamics evolutionary game model. In Proceedings of the 2010 International Conference on Optoelectronics and Image Processing, Haikou, China, 11–12 November 2010. [Google Scholar]




| Reference | Project Portfolio Context | Interaction Consideration | Risk Evolution Consideration | Risk Response Consideration | Risk Contagion Consideration |
|---|---|---|---|---|---|
| [3] | √ | ||||
| [4] | √ | √ | √ | ||
| [5] | √ | √ | √ | ||
| [6] | √ | ||||
| [7] | √ | √ | |||
| [8] | √ | √ | |||
| [11] | √ | √ | √ | ||
| [12] | √ | ||||
| [13] | √ | √ | |||
| [14] | √ | ||||
| [15] | √ | ||||
| [16] | √ | ||||
| [17] | √ | √ | |||
| [18] | √ | ||||
| [19] | √ | ||||
| [20] | √ | √ | |||
| [22] | √ | ||||
| This study | √ | √ | √ | √ | √ |
| Risk-ID | Project Portfolio-Level Risks |
|---|---|
| PPLR1 | Choosing projects that are not aligned with strategic objectives of the organization. |
| PPLR2 | Lack of sharing or transparency in information. |
| PPLR3 | Insufficient portfolio risk management. |
| PPLR4 | Portfolio manager’s incompetency. |
| PPLR5 | Portfolio’s imbalance in terms of high-risk projects versus low-risk ones. |
| PPLR6 | Political, social or legislative changes that lead to changing the organizational strategy, and project’s objectives lack of alignment with the new strategy. |
| PPLR7 | Top manager’s interference in governance review board’s decisions. |
| PPLR8 | Choosing too many projects for the available resources. |
| PPLR9 | Inaccuracy and lack of quality in information. |
| PPLR10 | Portfolio’s imbalance between long-term projects and short-term ones. |
| PPLR11 | Governance review board’s incompetency. |
| PPLR12 | Frequent changes in roles, responsibilities and organizational structure. |
| PPLR13 | Lack of clarity in stakeholders’ roles and the intensity of their engagement. |
| PPLR14 | Governance review board’s reluctance to kill poor projects during their implementation, when they are no longer aligned with business strategy. |
| PPLR15 | Governance review board’s reluctance to kill or suspend projects when their required resources are no longer available. |
| PPLR16 | Portfolio’s imbalance across various markets. |
| PPLR17 | Portfolio’s imbalance in terms of project types. |
| Arising from | Risk-ID | Project Portfolio Interactive Risks |
|---|---|---|
| Resource interaction [46] | PIR1 | Lack of or delay in shared resources supply. |
| PIR2 | Error in resource allocation. | |
| PIR3 | Conflicts between project managers. | |
| Technical interaction | PIR4 | Lack of shared technology. |
| PIR5 | Information vulnerability. | |
| PIR6 | Conflicts between project technicians. | |
| Value interaction [46] interaction | PIR7 | Losing the potential value. |
| Risk-ID | PPLR1 | PPLR2 | PPLR3 | PPLR4 | PPLR5 | PPLR6 | PPLR7 | PPLR8 | PPLR9 | PPLR10 | PPLR11 | PPLR12 | PPLR13 | PPLR14 | PPLR15 | PPLR16 | PPLR17 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| PPLR1 | 0 | 1 | 0 | 0 | 0 | 1 | 1 | 0 | 1 | 1 | 0 | 0 | 0 | 1 | 0 | 0 | 0 |
| PPLR2 | 1 | 0 | 0 | 0 | 1 | 0 | 0 | 1 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 1 | 0 |
| PPLR3 | 0 | 0 | 0 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| PPLR4 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 |
| PPLR5 | 0 | 1 | 1 | 0 | 0 | 0 | 1 | 0 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| PPLR6 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| PPLR7 | 1 | 0 | 0 | 0 | 1 | 0 | 0 | 1 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 1 |
| PPLR8 | 0 | 1 | 0 | 0 | 0 | 0 | 1 | 0 | 1 | 1 | 0 | 0 | 0 | 0 | 1 | 0 | 0 |
| PPLR9 | 1 | 0 | 0 | 0 | 1 | 0 | 0 | 1 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 1 | 0 |
| PPLR10 | 1 | 0 | 0 | 0 | 1 | 0 | 0 | 1 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 1 | 1 |
| PPLR11 | 0 | 1 | 0 | 0 | 0 | 0 | 1 | 0 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| PPLR12 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| PPLR13 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| PPLR14 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| PPLR15 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| PPLR16 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 1 |
| PPLR17 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 1 | 0 |
| Risk-ID | PPLR1 | PPLR2 | PPLR3 | PPLR4 | PPLR5 | PPLR6 | PPLR7 | PPLR8 | PPLR9 | PPLR10 | PPLR11 | PPLR12 | PPLR13 | PPLR14 | PPLR15 | PPLR16 | PPLR17 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| PIR1 | 0 | 0 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| PIR2 | 0 | 1 | 1 | 1 | 0 | 0 | 0 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 |
| PIR3 | 0 | 1 | 1 | 1 | 0 | 0 | 0 | 0 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 1 |
| PIR4 | 0 | 1 | 0 | 1 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| PIR5 | 0 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| PIR6 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 1 | 0 | 0 | 0 | 0 |
| PIR7 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 1 |
| Risk ID | Project Risks | Risk Value |
|---|---|---|
| 1 | Variations by the client | 1.7 |
| 2 | Project funding problems | 2.2 |
| 3 | Incomplete or inaccurate cost estimate | 0.8 |
| 4 | Design variations | 1 |
| 5 | Inadequate program scheduling | 2.5 |
| 6 | Bureaucracy of government | 1.9 |
| 7 | Excessive procedures of government approvals | 0.8 |
| 8 | Suppliers’ incompetency to delivery materials on time | 1.8 |
| 9 | Delayed project schedule | 1.9 |
| 10 | Contractors’ poor management ability | 1.8 |
| 11 | Inadequate site information | 1.5 |
| 12 | Price inflation of construction materials | 1 |
| 13 | Unavailability of sufficient professionals and managers | 2.5 |
| 14 | Poor competency of labor | 1.2 |
| 15 | Low management competency of subcontractors | 2.1 |
| 16 | Prosecution due to unlawful disposal of construction waste | 1.3 |
| 17 | No safety insurance for employees | 1.5 |
| 18 | Inadequate safety measures or unsafe operations | 2.5 |
| 19 | No insurance for major equipment | 1.5 |
| 20 | Lack of readily available utilities on site | 0.9 |
| 21 | Contractor’s difficulty in reimbursement | 0.6 |
| Risk-ID | Project Portfolio-Level Risks | Risk Value |
|---|---|---|
| 22 | Choosing projects that are not aligned with strategic objectives of the organization | 1 |
| 23 | Lack of sharing or transparency in information | 2.1 |
| 24 | Insufficient portfolio risk management | 3 |
| 25 | Portfolio manager’s incompetency | 1.8 |
| 26 | Portfolio’s imbalance in terms of high-risk projects versus low-risk ones | 1.8 |
| 27 | Political, social or legislative changes that leads to changes in organizational strategy, and project’s objectives lack of alignment with the new strategy | 1.3 |
| 28 | Top manager’s interference in governance review board’s decisions | 0.9 |
| 29 | Choosing too many projects to share the available resources | 0.3 |
| 30 | Inaccuracy and lack of quality in information | 2.2 |
| 31 | Portfolio’s imbalance between long-term projects and short-term ones | 1.8 |
| 32 | Governance review board’s incompetency | 1.5 |
| 33 | Frequent changes in roles, responsibilities and organizational structure | 1.3 |
| 34 | Lack of clarity in stakeholders’ roles and the intensity of their engagement | 1.3 |
| 35 | Governance review board’s reluctance to kill poor projects during their implementation, when they are no longer aligned with business strategy | 1.7 |
| 36 | Governance review board’s reluctance to kill or suspend projects when their required resources are no longer available | 1.7 |
| 37 | Portfolio’s imbalance across various markets | 2.1 |
| 38 | Portfolio’s imbalance in terms of project types | 1.2 |
| Risk-ID | Project Interactive Risks | Risk Value |
|---|---|---|
| 39 | Lack of or delay in the supply of shared resources. | 1 |
| 40 | Error in resource allocation. | 3.5 |
| 41 | Conflicts between project managers. | 1.5 |
| 42 | Lack of shared technology | 1.5 |
| 43 | Information vulnerability | 1 |
| 44 | Conflicts between project technicians | 1.5 |
| 45 | Potential value loss. | 1 |
| MBD= | ||||||||
|---|---|---|---|---|---|---|---|---|
| 0.9128 | 0 | 0.0254 | 0.0251 | 0.0367 | 0 | 0 | 0 | 0 |
| 0 | 0.9505 | 0 | 0.0213 | 0.0282 | 0 | 0 | 0 | 0 |
| 0.0380 | 0 | 0.8335 | 0 | 0.0462 | 0 | 0.0423 | 0 | 0.0401 |
| 0.0461 | 0.0728 | 0 | 0.7769 | 0 | 0 | 0.0525 | 0 | 0.0517 |
| 0.0270 | 0.0384 | 0.0227 | 0 | 0.9119 | 0 | 0 | 0 | 0 |
| 0 | 0 | 0 | 0 | 0 | 1.0000 | 0 | 0 | 0 |
| 0 | 0 | 0.0351 | 0.0354 | 0 | 0 | 0.9102 | 0 | 0.0194 |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1.0000 | 0 |
| 0 | 0 | 0.0280 | 0.0293 | 0 | 0 | 0.0163 | 0 | 0.9264 |
| MDB= | ||||||||
|---|---|---|---|---|---|---|---|---|
| 0.8889 | 0 | 0.0380 | 0.0461 | 0.0270 | 0 | 0 | 0 | 0 |
| 0 | 0.8889 | 0 | 0.0728 | 0.0384 | 0 | 0 | 0 | 0 |
| 0.0254 | 0 | 0.8889 | 0 | 0.0227 | 0 | 0.0351 | 0 | 0.0280 |
| 0.0251 | 0.0213 | 0 | 0.8889 | 0 | 0 | 0.0354 | 0 | 0.0293 |
| 0.0367 | 0.0282 | 0.0462 | 0 | 0.8889 | 0 | 0 | 0 | 0 |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 0.0423 | 0.0525 | 0 | 0 | 0.8889 | 0 | 0.0163 |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 0.0401 | 0.0517 | 0 | 0 | 0.0194 | 0 | 0.8889 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, Y.; Liu, J.; Xie, X.; Wang, C.; Bai, L. Modeling of Project Portfolio Risk Evolution and Response under the Influence of Interactions. Mathematics 2023, 11, 4091. https://doi.org/10.3390/math11194091
Zhang Y, Liu J, Xie X, Wang C, Bai L. Modeling of Project Portfolio Risk Evolution and Response under the Influence of Interactions. Mathematics. 2023; 11(19):4091. https://doi.org/10.3390/math11194091
Chicago/Turabian StyleZhang, Yipei, Jiale Liu, Xiaoyan Xie, Chenshuo Wang, and Libiao Bai. 2023. "Modeling of Project Portfolio Risk Evolution and Response under the Influence of Interactions" Mathematics 11, no. 19: 4091. https://doi.org/10.3390/math11194091
APA StyleZhang, Y., Liu, J., Xie, X., Wang, C., & Bai, L. (2023). Modeling of Project Portfolio Risk Evolution and Response under the Influence of Interactions. Mathematics, 11(19), 4091. https://doi.org/10.3390/math11194091





