Abstract
This paper considers the verification of decentralized fault pattern diagnosability for discrete event systems, where the pattern is modeled as a finite automaton whose accepted language is the objective to be diagnosed. We introduce a notion of codiagnosability to formalize the decentralized fault pattern diagnosability, which requires the pattern to be detected by one of the external local observers within a bounded delay. To this end, a structure, namely a verifier, is proposed to verify the codiagnosability of the system and the fault pattern. By studying an indeterminate cycle of the verifier, sufficient and necessary conditions are provided to test the codiagnosability. It is shown that the proposed method requires polynomial time at most. In addition, we present an approach to extend the proposed verifier structure so that it can be applied to centralized cases.
Keywords:
discrete event system; decentralized diagnosis; fault pattern; codiagnosability; computational complexity MSC:
93C65
1. Introduction
A discrete-event system (DES) [1,2,3] is an event-driven system whose state space is a discrete set and transitions from one state to another are triggered by the occurrence of events. The state of such a system may have logical or symbolic values that change in response to the event. In the context of DESs [2], fault diagnosis involves determining whether or not a fault has occurred with certainty [4,5]. The problem of diagnosis has been extensively studied [6,7,8,9,10]. Its formal description is located in [7]. The purpose of diagnosability is to determine whether any predetermined failure can be diagnosed within a finite delay (steps) after its occurrence. Experience with monitoring dynamic systems shows that there is a large spectrum of faulty situations in practical systems [11], such as multiple faults, intermittent faults [12], and temporary faults [13] that are not consistent with single-event faults. In order to consider these complex situations, such as temporary and/or intermittent faults, fault pattern diagnosis simultaneously emerges as a promising research area, which provides a general way to solve the diagnosis problems by capturing the occurrences of particular strings in a system and gains extensive attention from both researchers and practitioners, leading to a bulk of documented results [14,15,16,17,18,19,20].
As known, Petri nets (PNs) and finite state automata are two major tools to treat various problems in DESs. Specifically, finite state automata have been investigated for that purpose. In [14], the authors provide the ground foundations for the fault pattern diagnosis that relies on the synchronous product of a system with the pattern and the computation of the determinization of the resulting structure. Then, in [15], the same authors improve the complexity of the approach proposed in [14] by successively using the unobservable closure and a pair verifier to replace the determinization. This also introduces fault patterns in the problem of prediction. The authors of [16] address the fault pattern diagnosis by means of state isolation. In contrast to the approach in [14], which builds a diagnoser with potentially exponential complexity, the method proposed in [16] performs state estimation in a recursive manner. This approach offers the advantage of lower complexity for fault pattern detection. In [17], the authors introduce different notions of diagnosability, namely S-type and T-type pattern diagnosability, depending on whether interweaving events are accepted in the pattern. Note that this work also focuses on S-type patterns (but the T-type patterns are viewed as a particular subclass of S-type patterns, as mentioned in [17]). Moreover, in comparison to existing works, the main contribution of this paper is not only on the centralized systems but also on the decentralized frameworks, which expands the use of fault patterns.
Some contributions also consider the fault pattern diagnosis issues in PNs. On the one hand, the authors in [21] work on the diagnosability analysis of PNs by transforming the diagnosis problem into model checking. Using a particular class of PNs, the diagnosis of fault patterns has been studied according to the matching operator in [22]. With a similar approach, the same authors extended their results to the diagnosability analysis in [23]. On the other hand, stochastic PNs, endowed with Markovian semantics, have been studied to extract weak diagnosability properties for fault patterns [24]. A few researchers also consider fault patterns from the time aspects [25,26].
For the purpose of diagnosability verification, a systematic structure, namely a diagnoser, is proposed in [7], which provides the necessary and sufficient conditions for diagnosability offline. It also can be used for online fault detection based on the observations of system behaviors. The state space of a diagnoser is in the worst case exponential with respect to the size of a system model. To overcome the potential state explosion problem, a so-called “twin machine” technique [9,10], is introduced to provide a worst-case polynomial test with respect to the number of states of a system for diagnosability, without constructing a diagnoser. A state-based method for DES diagnosability is proposed in [6], which provides an algorithm for computing a sequence of test commands to detect faults.
All aforementioned works are centralized fault diagnosis, in which a centralized diagnoser is responsible for the diagnosis in a system. However, many large-sized and complex systems are physically decentralized, where diagnosis information collected by decentralized local sites will be sent to a centralized site for analysis. In this case, a variable communication delay needs to be introduced, which makes the diagnosis technique more complicated. Although all diagnosis information can be collected centrally, due to the data delay, a centralized fault diagnosis method may not always be suitable for decentralized systems.
This work focuses on the decentralized diagnosis of the DESs with multiple local observers, each of which possesses its own sensor without involving any communication among diagnosers, so as to make up for the defects of the centralized diagnosis. The authors in [27] propose a coordinated decentralized architecture with a coordinator, which extends the notion of diagnosability from centralized systems [7] to decentralized cases. In [28], a failure is characterized as a violation of a specification represented by a language, and codiagnosability is studied in a specification language framework, which is later specialized to the failure event framework. In [29], a hierarchical paradigm is developed by incorporating the protocol in [28], which leads to a hierarchy of architectures and encompasses many existing structures for decentralized diagnosis. Considering global consistency conditions, the authors in [30] discuss the diagnosis problem of the distributed setting with fault pattern and define local pattern recognizers for that purpose.
This paper deals with the decentralized fault pattern diagnosability verification of DESs, where the fault patterns are modeled by finite automata. We develop a codiagnosability notion to formalize the decentralized pattern diagnosability of the system and provide an algorithm for its verification. We first compute a synchronous product structure, which encodes a system and a pattern. A failure diagnoser structure is constructed based on the synchronous product by considering the faulty behaviors of the system, and a non-failure diagnoser is calculated based on the normal behaviors. Then, we present a local non-failure diagnoser based on the local projection. In order to verify the codiagnosability of the system and the pattern, a verifier structure is derived by taking the product of failure diagnoser and local non-failure diagnoser. By studying the indeterminate cycles of the verifier, we establish necessary and sufficient verification conditions of codiagnosability. The successive steps of the proposed approach are visualized in Figure 1.
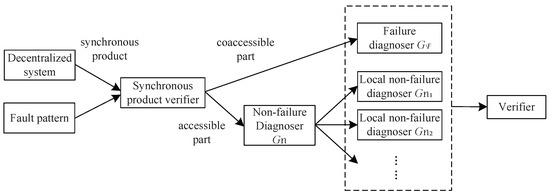
Figure 1.
Methodology.
The first contribution of the paper focuses on the construction of failure and non-failure diagnosers, which track the normal and faulty behaviors of the system, separately. The second contribution is the computation of the local diagnoser with respect to the local projection. The third contribution is to extend the necessary and sufficient conditions stated for pattern diagnosability [14] to a decentralized setting. This is achieved by constructing a verifier structure, which is the product of the failure and local non-failure diagnosers. The proposed method is shown to be of polynomial complexity. We also present a method to extend the proposed verifier so that it can be applied to centralized cases.
The rest of the paper is organized as follows. Section 2 reviews finite state automata. Section 3 begins with the notions of fault patterns and then touches upon decentralized fault pattern diagnosis in DESs. Section 4 provides an algorithm for fault pattern codiagnosability with the local diagnosers. Section 5 analyses the complexity of the proposed method. Section 6 concludes this research.
2. Preliminaries
In this paper, we use to denote the set of strictly positive integers. In what follows, we consider the model of finite automaton and its related notions.
Definition 1.
A deterministic finite automaton (DFA) is a four-tuple , where L is the set of states, Σ is the set of events, is the initial state, and is the partial transition function: means that there is a transition labeled with event from state l to state . Let be the set of all finite strings defined over Σ, including the empty string λ. Transition function δ can be extended to in an usual way: given , , and , and .
For a DFA G with partial observation, the events set can be partitioned into two disjoint subsets , where and represent the set of observable events and the set of unobservable events, respectively. Given two strings , the concatenation of the two strings is a string , where the string is followed by .
For a state , the set of active events at l is defined as . Given a string , its length is defined as the number of items in , denoted by . A string is said to be a prefix of if there exists , such that . The language generated by the DFA G is defined as , where means that “ is defined”. Given a string , denotes the post-language of after , defined as . A run that begins with the initial state has the form:
where , and for . In this case, we say that the run is associated with the string . A run is a cycle if .
For a decentralized system G, we use to denote the set of events observed by the local observer, simply called the local observable event set, and use to denote the set of local unobservable event set, where , , , m is the number of the local sites. For a set of observable events of G, = , . Without loss of generality, we assume that there is no cycle composed only of silent events in the system G. Note that in the decentralized architecture, different sites may have events in common, i.e., for all and , the set of is not necessarily an empty set. Given a site i, , the local projection is defined as follows: for and ,
and = . In other words, a local projection function tracks only its corresponding local observable events. For , a site i has its own set of observable events and does not communicate with each other. For a string ∈, the inverse of the local projection is defined by = ∈ . Let and . The parallel composition is defined as , where , .
Example 1.

Consider a DFA shown in Figure 2 with respect to the local projection , , where is the set of states, 0 is the initial state, is the set of events, and = is the set of observable events with = and = . The transition function is defined as = 1, = 2, = 7, = 7, = 7, = 7, = 3, = 4, = 5, = 6, and = 6. The local projection of system is defined as = a, = b, = = = = λ, and is defined as = a, = c, and = = = = λ. A possible run generated by system from the initial state is
where the associated string of ρ is . The local projection of with respect to is , and with respect to is .

Figure 2.
Deterministic finite automaton .
3. Decentralized Fault Pattern Diagnosis of Automata
A fault pattern, simply called a pattern, is defined as a finite-state automaton whose accepted language is the objective to be diagnosed, which represents the occurrence of complex or composite faults.
Definition 2.
A (fault) pattern of a DFA is , where S is the set of states, Σ is the set of events, is the initial state, is the single final state, and is the transition function. The pattern Ω satisfies a complete condition, i.e., for all , and the final state is stable, i.e., for all , .
We use to denote the set of target events that lead to the occurrence of the pattern, where . The language of pattern , denoted by , satisfies due to its complete condition. We use to denote the accepted language of , defined as , and define the target language of DFA G as .
Example 2.
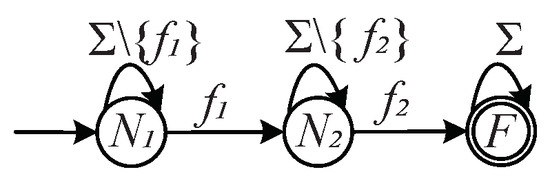
An example of pattern Ω is shown in Figure 3 with the set of states , the set of target events , the final state , and the initial state . The accepted language of the pattern Ω is .
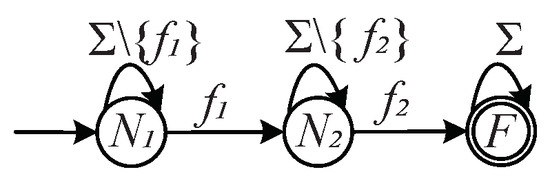
Figure 3.
Pattern .
In the following, we provide a formal definition, namely codiagnosability, with respect to the decentralized system and the pattern, detailed in Definition 3.
Definition 3.
Given a DFA G, a pattern Ω, and the local projection , , G is codiagnosable with regard to Ω and if
According to Definition 3, the system G is codiagnosable with respect to the local projection and the pattern if and only if for any string accepted by the pattern , there does not exist a string , which is not accepted by , such that = . An algorithm of fault pattern codiagnosability test is proposed based on searching for the strings and , such that, for , the two strings and violate the codiagnosability condition of Definition 3.
4. Verification Algorithm
For the purpose of codiagnosability verification, we propose an algorithm and a theorem in this section. Definition 4 introduces a structure that will be used later, namely synchronous product, which encodes the system G and the pattern .
Definition 4.
Given a DFA , and a pattern , a synchronous product of G with respect to Ω is a DFA = , where is the set of states, Σ is the set of events, is the initial state, is the set of final states, and is the transition function, defined as follows: for , , , if and .
Hereafter, we propose a structure, called a verifier, which is used to test the codiagnosability of the decentralized system and the fault pattern. The successive steps of the construction are provided in Algorithm 1. Without loss of generality, we assume that , i.e., there are two local sites with their corresponding local projections and local observable event sets.
| Algorithm 1: Construction of the verifier. |
|
Note that for a state of , it includes three components: , , and , where is a state of , is a state of , and is a state of . The verifier is constructed by tracking the strings of the local non-failure diagnosers and the failure diagnoser that have the same observation with respect to the local projection , . In other words, the transition relation of tracks three sequences: one in the local non-failure diagnoser , one in the local non-failure diagnoser , and another in the failure diagnoser , which generate the same sequence of observed labels.
In Step 1 of Algorithm 1, we construct a synchronous product of a system G and a pattern , which encodes the system and the pattern. Then, a failure diagnoser is computed to track the faulty behavior of the system, which is the co-accessible part of the synchronous product with respect to the faulty strings. By Step 3, we build a non-failure diagnoser structure that is the accessible part of the synchronous product by considering the normal behavior of the system. In Step 4, we establish a local non-failure diagnoser based on the local projection. In this way, the event set can be renamed with respect to the local projection and the set of faulty events. Finally, by taking the product of the local non-failure diagnosers and the failure diagnoser, a verifier of the system G and pattern can be set up, which is used to test the codiagnosability of the decentralized system.
Definition 5.
Given the verifier of a DFA G and a pattern Ω, for , m, , a cycle of is said to be an indeterminate cycle if for state , , , and there exists , , such that .
Theorem 1.
Let G be a DFA with the local projection , , and a pattern Ω. G is not codiagnosable with respect to and Ω if and only if there exists an indeterminate cycle in .
Proof.
(if) Suppose that there exists an indeterminate cycle . Then, there exists a string generating a run in , such that for , . Define
By = , it concludes that ∩∩, where , , and are the generated languages of , , , and , respectively. Consequently, there exists a string in , such that , , and (see Step 2 of Algorithm 1).
Let . There exists a string in , such that and . With a slight abuse of notation, we have . Similar to , there exists a string in and in , such that . For the same reason, we have , where , and (see Step 3 of Algorithm 1). For the string with arbitrary length, the strings and can also be extended long enough. This implies that G is not codiagnosable with respect to pattern and local projection .
(only if) Suppose that G is not codiagnosable with respect to and . Then, there exists a string , , and strings , such that , .
According to Steps 3 and 4 of Algorithm 1, there exists a string in and a string in , such that = and = , where R can be extended from to as the usual way. Consider two prefixes of and of , such that and . Since , holds. As a result, there exist two runs in and , beginning from and generated by , , respectively, with the forms
In addition, since according to Step 2 of Algorithm 1, there exists a run in beginning from generated by s with the form of .
Similarly, three runs in , , can be generated by , , , respectively, with the form of
such that and . Then, there exists a run in of the form
such that and .
The strings and are extended from the string to be as large as possible. Then, there eventually exist two states , in , , such that . For , the set of states of form an indeterminate cycle. This contradicts the assumption and ends the proof. □
Theorem 1 provides an approach to verify codiagnosability by searching for the existence of indeterminate cycles. In the case of at least one indeterminate cycle, there are at least three strings , , and with arbitrary length in non-failure diagnosers , , and the failure diagnoser , respectively, where and have the same observation with respect to the projection , and and have the same observation with respect to the projection , violating the codiagnosability.
Example 3.

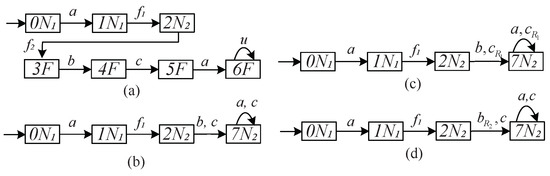
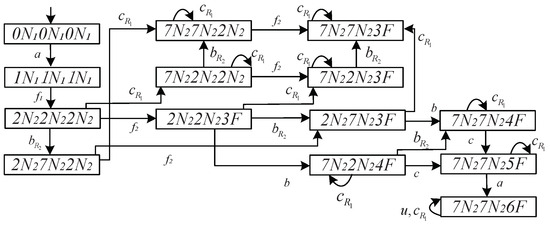
Consider a DFA shown in Figure 2 with the local observable event set , , and a pattern Ω shown in Figure 3. According to the first step of Algorithm 1, we construct the synchronous product , as shown in Figure 4, which encodes the information of the system and the fault pattern Ω. The second step is to obtain the failure diagnoser , which is the co-accessible part of with respect to the set of the faulty states , as shown in Figure 5a. It should be noted that all accepted behaviors of the failure diagnoser are faulty behaviors. Continuing Algorithm 1, we compute a non-failure diagnoser by taking the accessible part of regarding the set of normal states , as shown in Figure 5b. Note that all generated behaviors of the non-failure diagnoser are normal behaviors. Based on Step 4, we can calculate the local non-failure diagnosers and , respectively, by renaming the unobservable event sets and based on function , as shown in Figure 5c,d. It shows that the sets of the events of the local non-failure diagnosers and are and , respectively. The final step of Algorithm 1 is the computation of the verifier of and Ω, which is obtained by , as shown in Figure 6.

Figure 4.
Synchronous product of and .

Figure 5.
(a) Failure diagnoser , (b) non-failure diagnoser , (c) local non-failure diagnoser , and (d) local non-failure diagnoser .

Figure 6.
Verifier of and .
According to Theorem 1, one can know that the verification of the fault pattern codiagnosability is to search for the indeterminate cycles in . The verifier of Figure 6 has several cycles (for example, the cycles , , and ). Notice that only the cycle is an indeterminate cycle (Definition 5). The existence of the indeterminate cycle implies that the system is not codiagnosable with respect to the local projection , , and the pattern Ω (Theorem 1).
Example 4.


Consider a DFA shown in Figure 7a with the local projection , and a pattern Ω in Figure 3, where is the set of events, = , and = . According to the first step of Algorithm 1, we can construct the synchronous product , as shown in Figure 7b. Continuing Algorithm 1, the failure diagnoser can be computed accordingly, as shown in Figure 8a. By Steps 3 and 4 of Algorithm 1, we can obtain the non-failure diagnosers and the local non-failure diagnosers successively. For the sake of simplicity, we keep the local non-failure diagnosers and , which will be used later, as shown in Figure 8b,c. Continuing Step 5 of Algorithm 1, we can calculate the verifier with respect to the local projections, as shown in Figure 8d.

Figure 7.
(a) Deterministic finite automaton and (b) synchronous product .

Figure 8.
(a) Failure diagnoser , (b) local non-failure diagnoser , (c) local non-failure diagnoser , and (d) verifier .
Observe that there exist three cycles in the verifier , i.e., , , and , and the cycle is indeterminate (Definition 5). As a consequence, the system is not codiagnosable with respect to the local projection , , and the pattern Ω (Theorem 1).
Example 5.
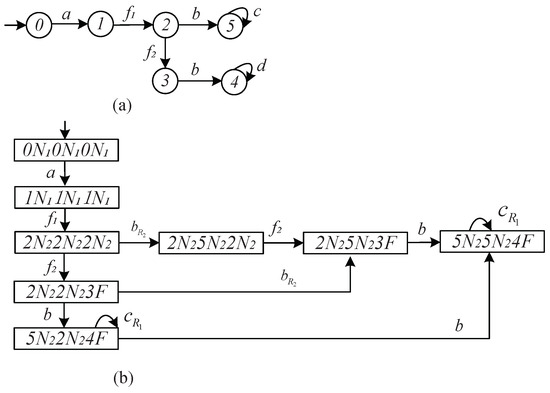
In order to compare the codiagnosability with the system , we consider a DFA , as shown in Figure 9a, and the pattern Ω in Figure 3. The local projection of is , , where is the set of events, = , and = . Following Algorithm 1, the resulting structure can be obtained step by step. For simplicity, we detail the verifier , as shown in Figure 9b. Note that there is no indeterminate cycle (Definition 5). This implies that the system is codiagnosable with respect to the local projection and the pattern Ω (Theorem 1).

Figure 9.
(a) Deterministic finite automaton and (b) verifier .
Note that the pattern diagnosability verification in the centralized case can be easily obtained by marking of Algorithm 1, i.e., the number of the local site is 1. Therefore, the verifier automaton for the centralized case is given as , and the necessary and sufficient condition for the non-diagnosability of G is the existence of an indeterminate cycle in , such that at least one event in the cycle is an event of .
5. Complexity Analysis
From Definitions 1 and 2, we know that the number of states of the system G is , and the number of states of the pattern is . Assume that the number of the local sites is m.
The complexity of performing Step 1 of Algorithm 1, which constructs the synchronous product , is , and that of Step 2 of Algorithm 1, which constructs the failure diagnoser , is . The complexity of performing Step 3 of Algorithm 1, which computes the non-failure diagnoser by deleting all the final states of , is . The complexity of obtaining the local non-failure diagnoser in Step 4 of Algorithm 1, , is . By Step 5, the complexity of verifier construction is .
Thus, the complexity of Algorithm 1 is , which is polynomial with respect to the number of the states of G and , i.e., .
6. Conclusions
The objective of this work is the verification of pattern diagnosability for decentralized DESs. In particular, the fault patterns are modeled by finite automata, providing a general way to formalize different types of failures. This improves the method in [29,31], which only targets single fault scenarios. To this end, we introduce a codiagnosability notion to encapsulate decentralized fault pattern diagnosability, and present an algorithm to test this property. In detail, we first compute a synchronous product structure to encode the system and the pattern. A failure diagnoser and a non-failure diagnoser are calculated based on the synchronous product, where the two structures are obtained by considering the normal and faulty behaviors, respectively. Then, we present a local non-failure diagnoser based on the local projection of the system. A verifier for codiagnosability verification is derived by taking the product of the failure diagnoser with the local non-failure diagnoser. Consequently, the verifier structure can track the strings of the failure and local non-failure diagnosers that have the same observations. The proposed method boasts polynomial complexity, marking an improvement over methods in [17,21]. Moreover, the approach proposed in this paper can be used for decentralized systems as well as centralized systems, enhancing the method presented in [14,15] for centralized systems.
Our future work will consider decentralized diagnosis issues of timed fault patterns, which are characterized by a sequence of events that occur in a given order at specific values of time or within specific time intervals. In certain cases, the time value of the system is compulsory. For example, in some flexible manufacturing systems, the operation of the robot must be finished in a specified time. At this point, a time value needs to be assigned to each event of the system, and the diagnoser should be calculated based on not only the event but also the time value. Another limitation of the algorithm is that an external attack is not considered in the system. With this in mind, we will consider different types of attack forms in future work, including insertion, deletion, and replacement of observations. These observations refer to sequences of observable events observed by external observers as well as intruders (aliases of attackers). Such tampering with system-generated observations may mislead system operators to make inexact, conservative, or even incorrect state estimations that are critical for many problems in the context of DESs, such as supervisory control, opacity verification, enforcement, detectability analysis, and fault diagnosis. Certainly, these problems can be addressed under the framework of centralized and/or decentralized system architectures.
Author Contributions
Methodology, formal analysis, writing—original draft preparation, Y.L.; supervision, writing—review and editing, G.L.; funding acquisition and programming, A.M.E.-S. All authors have read and agreed to the published version of the manuscript.
Funding
This research is supported by the National Key R&D Project of China under grant 2018YFB1700104. The authors extend their appreciation to King Saud University, Saudi Arabia, for funding this work through Researchers Supporting Project number (RSP2023R133), King Saud University, Riyadh, Saudi Arabia.
Data Availability Statement
Enquiries about data availability should be directed to the authors.
Conflicts of Interest
The authors declare that they have no conflict of interest.
References
- Cassandras, C.G. The event-driven paradigm for control, communication and optimization. J. Control Decis. 2014, 1, 3–17. [Google Scholar] [CrossRef]
- Cassandras, C.G.; Lafortune, S. Introduction to Discrete Event Systems; Springer: New York, NY, USA, 2008. [Google Scholar]
- Schuppen, J.; Silva, M.; Seatzu, C. Control of discrete-event systems-Automata and Petri net perspectives. Lect. Notes Control Inf. Sci. 2012, 433, 319–340. [Google Scholar]
- Zaytoon, J.; Lafortune, S. Overview of fault diagnosis methods for discrete event systems. Annu. Rev. Control 2013, 37, 308–320. [Google Scholar] [CrossRef]
- Lafortune, S.; Lin, F.; Hadjicostis, C.N. On the history of diagnosability and opacity in discrete event systems. Annu. Rev. Control 2018, 45, 257–266. [Google Scholar] [CrossRef]
- Lin, F.; Markee, J.; Rado, B. Design and test of mixed signal circuits: A discrete-event approach. In Proceedings of the 32nd IEEE Conference on Decision and Control, San Antonio, TX, USA, 15–17 December 1993; pp. 217–222. [Google Scholar]
- Sampath, M.; Sengupta, R.; Lafortune, S.; Sinnamohideen, K.; Teneketzis, D. Diagnosability of discrete-event systems. IEEE Trans. Autom. Control 1995, 40, 1555–1575. [Google Scholar] [CrossRef]
- Liang, Y.; Lai, A.; El-Meligy, M.A.; Sharaf, M. Intermittent fault manifestability of discrete event systems. Soft Comput. 2023, 27, 6999–7009. [Google Scholar] [CrossRef]
- Jiang, S.; Huang, Z.; Chandra, V.; Kumar, R. A polynomial algorithm for testing diagnosability of discrete-event systems. IEEE Trans. Autom. Control 2001, 46, 1318–1321. [Google Scholar] [CrossRef]
- Yoo, T.S.; Lafortune, S. Polynomial-time verification of diagnosability of partially observed discrete-event systems. IEEE Trans. Autom. Control 2002, 47, 1491–1495. [Google Scholar]
- Zhou, D.; Zhao, Y.; Wang, Z.; He, X.; Gao, M. Review on diagnosis techniques for intermittent faults in dynamic systems. IEEE Trans. Ind. Electron. 2019, 67, 2337–2347. [Google Scholar] [CrossRef]
- Contant, O.; Lafortune, S.; Teneketzis, D. Diagnosis of intermittent faults. Discret. Event Dyn. Syst. 2004, 14, 171–202. [Google Scholar] [CrossRef]
- Biswas, S. Diagnosability of discrete event systems for temporary failures. Comput. Electr. Eng. 2012, 38, 1534–1549. [Google Scholar] [CrossRef]
- Jéron, T.; Marchand, H.; Pinchinat, S.; Cordier, M.O. Supervision patterns in discrete event systems diagnosis. In Proceedings of the 8th International Workshop on Discrete Event Systems, Ann Arbor, MI, USA, 10–12 July 2006; pp. 262–268. [Google Scholar]
- Jéron, T.; Marchand, H.; Genc, S.; Lafortune, S. Predictability of sequence patterns in discrete event systems. IFAC Proc. Vol. 2008, 41, 537–543. [Google Scholar] [CrossRef]
- Liang, Y.; Lefebvre, D.; Li, Z. Fault pattern diagnosis of discrete-event systems by means of logical verifiers. IFAC-PapersOnLine 2022, 55, 551–556. [Google Scholar] [CrossRef]
- Genc, S.; Lafortune, S. Diagnosis of patterns in partially-observed discrete-event systems. In Proceedings of the 45th IEEE Conference on Decision and Control, San Diego, CA, USA, 13–15 December 2006; pp. 422–427. [Google Scholar]
- Wang, Z.; Wang, J.; Wang, Y. An intelligent diagnosis scheme based on generative adversarial learning deep neural networks and its application to planetary gearbox fault pattern recognition. Neurocomputing 2018, 310, 213–222. [Google Scholar] [CrossRef]
- Watanabe, A.T.; Sebem, R.; Leal, A.B.; Hounsell, M.d.S. Fault prognosis of discrete event systems: An overview. Annu. Rev. Control 2021, 51, 100–110. [Google Scholar] [CrossRef]
- Boussif, A.; Ghazel, M.; Basilio, J.C. Intermittent fault diagnosability of discrete event systems: An overview of automaton-based approaches. Discret. Event Dyn. Syst. 2021, 31, 59–102. [Google Scholar] [CrossRef]
- Gougam, H.E.; Pencolé, Y.; Subias, A. Diagnosability analysis of patterns on bounded labeled prioritized Petri nets. Discret. Event Dyn. Syst. 2017, 27, 143–180. [Google Scholar] [CrossRef]
- Pencolé, Y.; Subias, A. Timed pattern diagnosis in timed workflows: A model checking approach. IFAC-PapersOnLine 2018, 51, 94–99. [Google Scholar] [CrossRef]
- Pencolé, Y.; Subias, A. Diagnosability of event patterns in safe labeled time Petri nets: A model-checking approach. IEEE Trans. Autom. Sci. Eng. 2021, 19, 1151–1162. [Google Scholar] [CrossRef]
- Lefebvre, D.; Hadjicostis, C.N. Diagnosability of fault patterns with labeled stochastic Petri nets. Inf. Sci. 2022, 593, 341–363. [Google Scholar] [CrossRef]
- Lefebvre, D.; Li, Z.; Liang, Y. Verifiers for the detection of timed patterns in discrete event systems. IFAC-PapersOnLine 2022, 55, 264–269. [Google Scholar] [CrossRef]
- Lefebvre, D.; Li, Z.; Liang, Y. Diagnosis of timed patterns for discrete event systems by means of state isolation. Automatica 2023, 153, 111045. [Google Scholar] [CrossRef]
- Debouk, R.; Lafortune, S.; Teneketzis, D. Coordinated decentralized protocols for failure diagnosis of discrete event systems. Discret. Event Dyn. Syst. 2000, 10, 33–86. [Google Scholar] [CrossRef]
- Qiu, W.; Kumar, R. Decentralized failure diagnosis of discrete event systems. IEEE Trans. Syst. Man Cybern.-Part A Syst. Hum. 2006, 36, 384–395. [Google Scholar]
- Wang, Y.; Yoo, T.S.; Lafortune, S. Diagnosis of discrete event systems using decentralized architectures. Discret. Event Dyn. Syst. 2007, 17, 233–263. [Google Scholar] [CrossRef]
- Ye, L.; Daguet, P. A general algorithm for pattern diagnosability of distributed discrete event systems. In Proceedings of the 24th IEEE International Conference on Tools with Artificial Intelligence, Athens, Greece, 7–9 November 2012; pp. 130–137. [Google Scholar]
- Moreira, M.V.; Jesus, T.C.; Basilio, J.C. Polynomial time verification of decentralized diagnosability of discrete event systems. IEEE Trans. Autom. Control 2011, 56, 1679–1684. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).