A Novel Vieta–Fibonacci Projection Method for Solving a System of Fractional Integrodifferential Equations
Abstract
1. Introduction
- Examining a system of fractional integrodifferential equations for the first time;
- The utilization of Vieta–Fibonacci polynomials was initially employed to numerically obtain the solution a system of fractional integrodifferential equations;
- Developing a projection method for addressing a system of fractional integrodifferential equations using Vieta–Fibonacci polynomials;
- Establishing a new error analysis in a Vieta–Fibonacci weighted space.
2. Preliminaries
3. System of Fractional Integrodifferential Equations
4. Vieta–Fibonacci Polynomials
5. Development of the Method
6. Convergence Analysis
7. Numerical Example
8. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Araour, M.; Mennouni, A. A New Procedures for Solving Two Classes of Fuzzy Singular Integro-Differential Equations: Airfoil Collocation Methods. Int. J. Appl. Comput. Math. 2022, 8, 35. [Google Scholar] [CrossRef]
- Nieto, J.J. Fractional Euler numbers and generalized proportional fractional logistic differential equation. Fract. Calc. Appl. Anal. 2022, 25, 876–886. [Google Scholar] [CrossRef] [PubMed]
- Kilbas, A.A.; Srivastava, H.M.; Trujillo, J.J. Theory and Applications of Fractional Differential Equations. In North–Holland Mathematics Studies; Elsevier Science B.V.: Amsterdam, The Netherlands, 2006; Volume 204. [Google Scholar]
- Mennouni, A. The iterated projection method for integro-differential equations with Cauchy kernel. J. Appl. Math. Inform. 2013, 31, 661–667. [Google Scholar] [CrossRef][Green Version]
- Kirane, M.; Abdeljabbar, A. Nonexistence of global solutions of systems of time fractional differential equations posed on the Heisenberg group. Math. Methods Appl. Sci. 2022, 45, 7336–7345. [Google Scholar] [CrossRef]
- Zhou, Y. Basic Theory of Fractional Differential Equations; World Scientific: Singapore, 2014; pp. 3–11. [Google Scholar]
- Bentrcia, T.; Mennouni, A. On the asymptotic stability of a Bresse system with two fractional damping terms: Theoretical and numerical analysis. Discrete Contin. Dyn. Syst. Ser. B 2022, 28, 580–622. [Google Scholar] [CrossRef]
- Wang, J.N.; Zhou, Y.; Alsaedi, A.; Ahmad, B. Well-posedness and regularity of fractional Rayleigh–Stokes problems. Z. Angew. Math. Phys. 2022, 73, 161. [Google Scholar] [CrossRef]
- Li, Y. Regularity of mild solutions for fractional abstract Cauchy problem with order μ∈(1,2). Z. Angew. Math. Phys. 2015, 66, 3283–3298. [Google Scholar] [CrossRef]
- Mennouni, A. Improvement by projection for integro-differential equations. Math. Methods Appl. Sci. 2020, 1–7. [Google Scholar] [CrossRef]
- Samko, S.G.; Kilbas, A.A.; Marichev, O.I. Fractional Integrals and Derivatives, Theory and Applications; Gordon and Breach: Amsterdam, The Netherlands, 1993. [Google Scholar]
- Xu, C.; ur Rahman, M.; Baleanu, D. On fractional-order symmetric oscillator with offset-boosting control. Nonlinear Anal. Model. Control 2022, 27, 994–1008. [Google Scholar] [CrossRef]
- Ahmad, B.; Ntouyas, S.K. Existence results for a coupled system of Caputo-type sequential fractional differential equations with nonlocal integral boundary conditions. Appl. Math. Comput. 2015, 266, 615–622. [Google Scholar] [CrossRef]
- Ahmad, B.; Ntouyas, S.K. Nonlocal Nonlinear Fractional-Order Boundary Value Problems; World Scientific: Singapore, 2021. [Google Scholar]
- Luca, R.; Tudorache, A. On a System of Hadamard Fractional Differential Equations with Nonlocal Boundary Conditions on an Infinite Interval. Fractal Fract. 2023, 7, 458. [Google Scholar] [CrossRef]
- Tudorache, A.; Luca, R. On a System of Sequential Caputo Fractional Differential Equations with Nonlocal Boundary Conditions. Fractal Fract. 2023, 7, 181. [Google Scholar] [CrossRef]
- Tao, X.; Xie, Z. The Uniform Convergence of a DG Method for a Singularly Perturbed Volterra Integro-Differential Equation. Acta Math. Sci. 2023, 43, 2159–2178. [Google Scholar] [CrossRef]
- Kumar, A.; Patel, R.; Vijayakumar, V.; Shukla, A. Investigation on the Approximate Controllability of Fractional Differential Systems with State Delay. Circuits Syst. Signal Process. 2023, 42, 4585–4602. [Google Scholar] [CrossRef]
- Ahmad, B.; Agarwal, R.P.; Broom, A.; Alsaedi, A. On a Coupled Integro-Differential System Involving Mixed Fractional Derivatives and Integrals of Different Orders. Acta Math. Sci. 2021, 41, 1366–1384. [Google Scholar] [CrossRef]
- Atta, A.G.; Youssri, Y.H. Advanced shifted first-kind Chebyshev collocation approach for solving the nonlinear time-fractional partial integro-differential equation with a weakly singular kernel. Comput. Appl. Math. 2022, 41, 381. [Google Scholar] [CrossRef]
- Jia, Y.; Xu, M.; Lin, Y.; Jiang, D. An efficient technique based on least-squares method for fractional integro-differential equations. Alex. Eng. J. 2023, 64, 97–105. [Google Scholar] [CrossRef]
- Youssri, Y.H.; Atta, A.G. Spectral Collocation Approach via Normalized Shifted Jacobi Polynomials for the Nonlinear Lane-Emden Equation with Fractal-Fractional Derivative. Fractal Fract. 2023, 7, 133. [Google Scholar] [CrossRef]
- Singh, M.; Das, S.; Rajeev; Ong, S.H. Novel operational matrix method for the numerical solution of nonlinear reaction–advection–diffusion equation of fractional order. Comput. Appl. Math. 2022, 41, 306. [Google Scholar] [CrossRef]
- Hoseini, T.; Ordokhani, Y.; Rahimkhani, P. A Numerical Method Based on the Fractional Vieta–Fibonacci Functions for a Class of Fractional Optimal Control Problems. Iran J. Sci. Technol. Trans. Electr. Eng. 2023, 47, 1117–1128. [Google Scholar] [CrossRef]
- Gupta, R.; Saha Ray, S. A new effective coherent numerical technique based on shifted Vieta–Fibonacci polynomials for solving stochastic fractional integro-differential equation. Comput. Appl. Math. 2023, 42, 256. [Google Scholar] [CrossRef]
- Sadri, K.; Hosseini, K.; Baleanu, D.; Salahshour, S.; Park, C. Designing a Matrix Collocation Method for Fractional Delay Integro-Differential Equations with Weakly Singular Kernels Based on Vieta–Fibonacci Polynomials. Fractal Fract. 2022, 6, 2. [Google Scholar] [CrossRef]
- Althubiti, S.; Mennouni, A. An Effective Projection Method for Solving a Coupled System of Fractional-Order Bagley–Torvik Equations via Fractional Shifted Legendre Polynomials. Symmetry 2022, 14, 1514. [Google Scholar] [CrossRef]
- Althubiti, S.; Mennouni, A. A Novel Projection Method for Cauchy-Type Systems of Singular Integro-Differential Equations. Mathematics 2022, 10, 2694. [Google Scholar] [CrossRef]
- Mennouni, A. A new efficient strategy for solving the system of Cauchy integral equations via two projection methods. Transylv. J. Math. Mech. 2022, 14, 63–71. [Google Scholar]
- Mennouni, A. Airfoil Collocation Method Employing a New Efficient Procedure for Solving System of Two Logarithmic Integro–Differential Equations. Int. J. Appl. Comput. Math. 2022, 8, 208. [Google Scholar] [CrossRef]
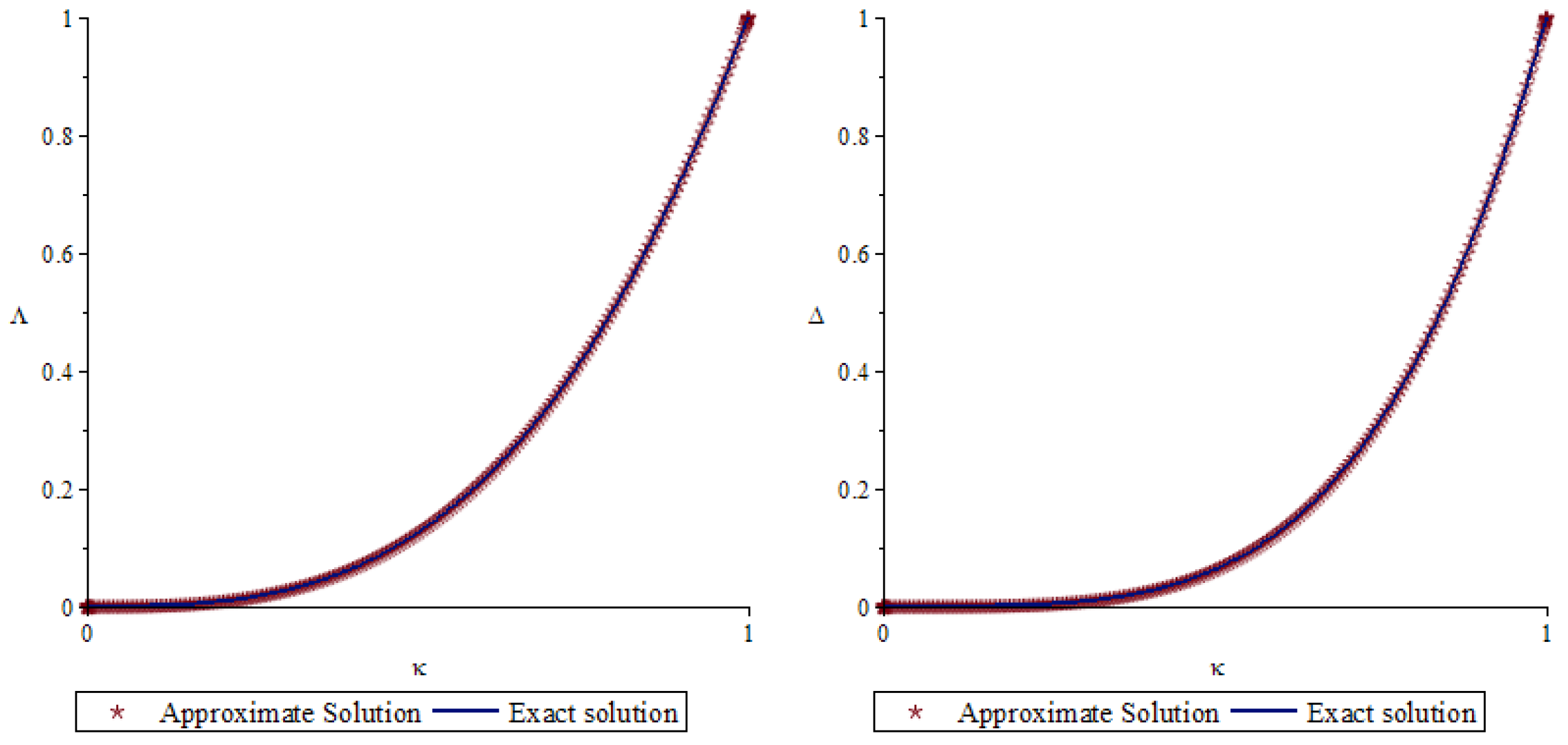
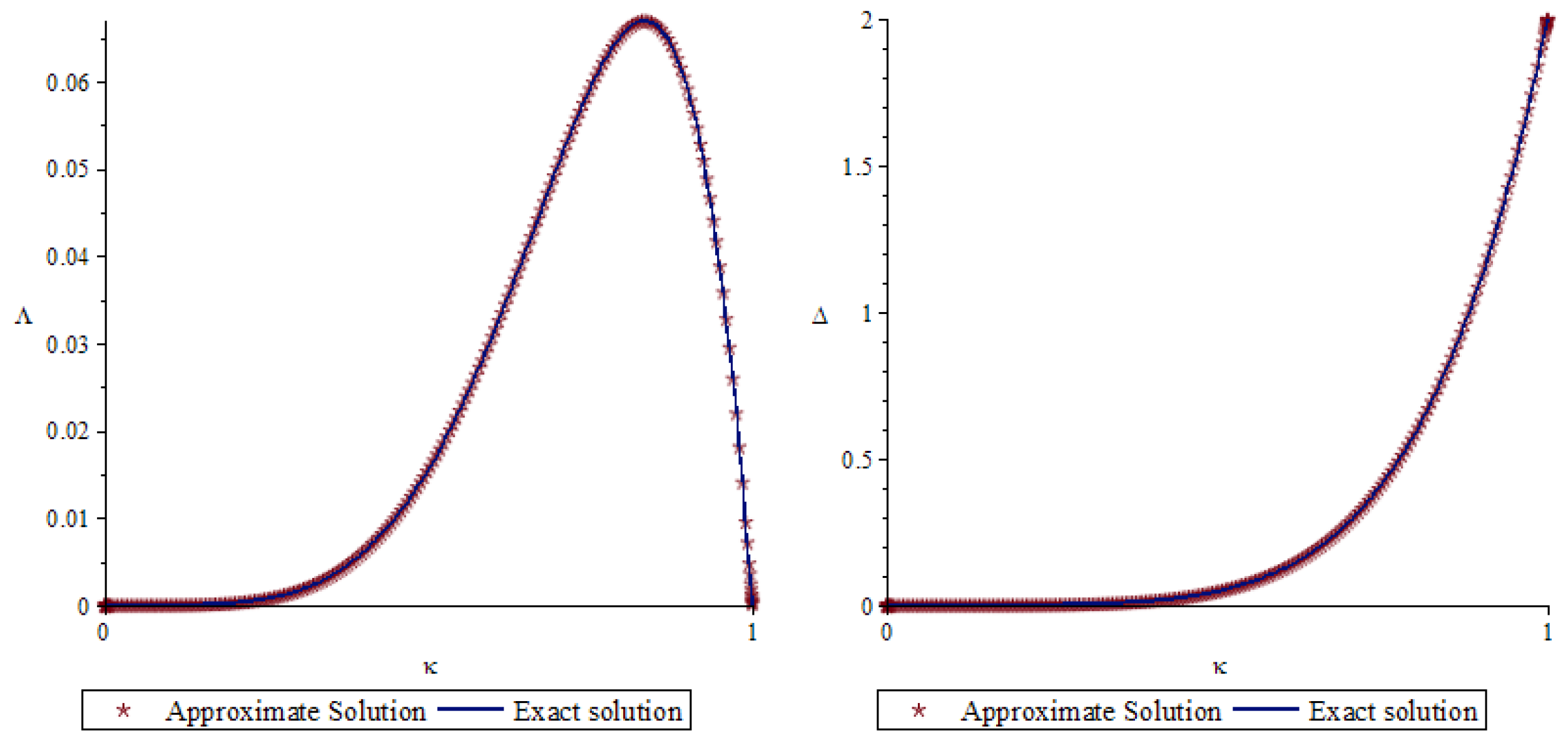
| n | ||
|---|---|---|
| 4 | 3.6466 × 10 | 7.0747 × 10 |
| 6 | 5.5219 × 10 | 2.2673 × 10 |
| 8 | 5.0263 × 10 | 8.2457 × 10 |
| 18 | 6.2351 × 10 | 8.2354 × 10 |
| 23 | 9.2548 × 10 | 8.1254 × 10 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Moumen, A.; Mennouni, A.; Bouye, M. A Novel Vieta–Fibonacci Projection Method for Solving a System of Fractional Integrodifferential Equations. Mathematics 2023, 11, 3985. https://doi.org/10.3390/math11183985
Moumen A, Mennouni A, Bouye M. A Novel Vieta–Fibonacci Projection Method for Solving a System of Fractional Integrodifferential Equations. Mathematics. 2023; 11(18):3985. https://doi.org/10.3390/math11183985
Chicago/Turabian StyleMoumen, Abdelkader, Abdelaziz Mennouni, and Mohamed Bouye. 2023. "A Novel Vieta–Fibonacci Projection Method for Solving a System of Fractional Integrodifferential Equations" Mathematics 11, no. 18: 3985. https://doi.org/10.3390/math11183985
APA StyleMoumen, A., Mennouni, A., & Bouye, M. (2023). A Novel Vieta–Fibonacci Projection Method for Solving a System of Fractional Integrodifferential Equations. Mathematics, 11(18), 3985. https://doi.org/10.3390/math11183985






