Securing an Authenticated Privacy Preserving Protocol in a Group Signature Scheme Based on a Group Ring

Abstract

Group signatures are a leading competing signature technique with a substantial amount of research. With group settings, group signatures provide user anonymity. Any group member with access to the group can generate a signature while remaining anonymous. The group manager, however, has the authority to expose and identify the signer if required. Since the privacy of the sender should be preserved, this is a conflict between privacy and accountability. Concerning high performance on security, we propose a novel, well-balanced security and privacy group signature scheme based on a general linear group over group ring. To the best of our knowledge, our work represents the first comprehensive framework for a group signature scheme that utilizes generic linear groups over group rings. We demonstrate that the competing security goals of message trustworthiness, privacy, and accountability are effectively resolved by our protocol. The results of the performance evaluation and simulation demonstrate that our protocol achieves strong security, system robustness, and high-performance efficiency, making it suitable for practical applications.

1. Introduction

User privacy preservation has become the most important requirement that needs to be met in the digital environment since practically all goods and services are accessible online [1]. Due to the growing concern for user privacy, the development of secure communications between two parties has gained significant interest [2,3]. This drives the evolution of secure communication technology known as digital signatures. A digital signature utilizes a secret key that can only be known by the signer and a cryptographic value that is computed from the data. However, a drawback of a digital signature is that the source of a message cannot be determined. Therefore, the most significant anonymous signature, from a digital signature to a group signature, was developed. Additionally, group signature is one of the cryptographic primitives that addresses the conflicting security goals of message trustworthiness, privacy, and accountability simultaneously. The adoption of group signatures is widespread in applications that preserve user privacy, such as e-commerce systems, vehicle safety communication (VSC) [4,5], key-card access systems, and anonymous attestation [6].

The concept of a group signature scheme was proposed by David Chaum and Eugene van Heyst in 1991 [7]. Group signatures allow each participant to sign on the group’s behalf. A verifier can ascertain that the signer is a member of a group even when they are unable to link the signature to a particular signer. However, a trusted party (TP) can revoke the user’s anonymity. The traceability feature is satisfied when a group signature allows a TP to identify a malicious user’s signature. On the other hand, if a trusted party colludes, all the users in the network are vulnerable to an attack, which may render the network unusable. The conflict between accountability and privacy in this scenario arises from the necessity to preserve a user’s anonymity. Even though group signatures fulfil all the security goals, these signatures suffer from contradictory security goals of message trustworthiness, privacy, and accountability. In view of the shortcoming of conflicting security goals, we propose well-balanced security and privacy in group signatures while attaining better performance efficiency where the underlying work is based on group rings.

Following the application of group signatures in privacy-preserving applications, there has been some interest in constructing a secure cryptosystem via combinatorial group theory. The Diffie–Hellman (DH) key agreement protocol, which was initially published in 1976, allows two parties who have never met to exchange a secret key via an open channel. It uses the cyclic group $F_q^{*}=F_q\backslash \left\{0\right\}$, where $F_q$ is the finite field with $q$elements. Due to the complexity of computing the discrete logarithm problem (DLP), this protocol’s security relies on this DLP in the group $F_q^{\mathrm{*}}$. Since then, a lot of key exchange protocols have been constructed on number theoretic problems, such as the discrete logarithm problem (DLP) and the integer factorization problem (IFP). These protocols frequently have abelian groups as their underlying group structures [8]. This is because the platform for all these hard problems is the intractability of number theory problems [9,10,11,12]. However, the IFP and DLP over these abelian groups may be solved in polynomial time by Shor’s algorithm and other quantum techniques [13,14,15,16,17]. Apart from that, these number theory-based techniques are not appropriate for application in compact computing devices, including economical smart cards with limited processing capabilities. Hence, it motivates us to develop alternative combinatorial group theory cryptosystems that are efficient and secure while not sacrificing the security goal.

2. Literature Review

The swift development of technology has made secure and efficient communication necessary. Numerous academic studies on combinatorial group theory cryptosystems have been presented in [16,18,19,20,21,22,23,24,25,26,27,28,29,30,31,32,33,34,35,36,37,38,39,40,41,42,43,44]. Magyarik and Wagner [33] presented public-key cryptography employing semigroup elements with undecidable word problems in 1985. However, Birget et al. [34] argued that the public key cryptosystem (PKC) built in [33] essentially did not depend on word problems, and consequently, they devised a new scheme that was based on finitely formed groups with hard problems. In 1999, Anshel et al. [35] developed a key exchange protocol using braid group-based cryptography [35,36,37,38,39,40,41], and the hardest problem of this protocol was the difficulty of solving equations over algebraic structures. The authors of [36] suggested PKC braid groups as a safe foundation for number-theory-based cryptosystems. By using braid groups, Ko et al. [37] created a novel key exchange protocol where the conjugacy search problem (CSP) is the underlying hard problem. An innovative approach built on finite noncommutative groups was proposed by Paeng et al. [42]. This technique utilizes the inner automorphism group’s discrete log problem (DLP). Cao et al. [43] introduced a non-polynomial over noncommutative semigroups or rings. The technique was known as the Z modular approach. A noncommutative dihedral group of six orders served as the foundation for Kubo’s [37] implementation of this approach. By utilizing the Z modular technique, Reddy et al. [44] created a signature scheme for division rings and noncommutative groups.

Zhang et al. [29] introduced a key exchange protocol based on infinite non-abelian groups in 2022. They created a shared secret key that contained two difficult problems: the equivalent decomposition problem (EDP) and the discrete logarithm issue (DLP). Using semidirect products of finite groups, Lanel et al. [30] suggested a unique method for non-abelian group-based public-key cryptography protocols. The fundamental mathematical problem for the proposed protocols is given as an intractable problem of finding automorphisms and producing elements of a group. Then they demonstrated how this insoluble task might be reduced to the challenging challenge of identifying the pathways and cycles of Cayley graphs, including Hamiltonian paths and cycles. In [31,32], Gupta et al. developed a novel undeniable signature technique in a non-abelian group over a group ring, whose security depends on the complexity of solving DLP and CSP. However, this approach needs a regular connection with the signer in order to validate the message and credentials, and the signer may not always be available. Therefore, the scheme in [31,32] is impractical for business and confidential transactions. They claimed an undeniable signature is effective; a signer who has access to a private key may publish a publicly available message signature, which may compromise the confidentiality of the signer’s identity. As a result, this scheme is unable to attain privacy-related properties. Non-commutative groups and rings have been used to propose a number of public-key cryptosystems and key exchange protocols [18,19,20]. According to [21,22,23], certain matrices properties, such as their determinant, eigenvalues, and Cayley–Hamilton theorem, can be exploited to create attacks against protocols that employ groups of invertible matrices over finite fields as their platform group. Such attacks reduce the DLP on ${GL}_n\left(F_q\right)$ to the DLP over finite fields or a simple problem of factoring [23]. The semigroup of matrices over group ring: $M_{k\times k}\left(F_q\right[S_r\left]\right)$ under ordinary matrix multiplication operation [24] and the group of invertible matrices over group ring: ${GL}_n\left(F_q\right[S_r\left]\right)$ [21] have been proposed as the platforms to prevent this reduction of DLP to the one over finite field.

Group ring applications in cryptography have received a significant amount of attention over the years. Rososhek [25,26] presented a cryptosystem based on a group ring structure. A key exchange system based on matrices over a group ring was created in 2011 by Kahrobaei et al. [25]. Following that, a number of group ring-based systems were presented [26,27,28]. In [26], the author presented a number of key exchange protocols and public key encryption techniques based on group ring matrices, with the related intractable assumptions being DLP and factorization problems (FP) in group ring matrices, respectively. In 2016, S. Inam and R. Ali [27] developed a new El Gamal public key cryptosystem for which the underlying hard problem is the conjugacy search problem. In their study, they substituted the conjugacy search problem (CSP) over group rings for the exponentiation of elements. The fundamental concept behind the use of group rings in cryptography is predicated on the assumptions that the cardinality of the finite ring $R$ is fixed and that the cardinality of a grouping for a finite group is an exponent of the cardinality of a group $G$. Then, a reliable user can employ polynomial algorithms to conduct cryptographic transformations independently in group $G$ and in ring $R$. However, an unauthorized user is going to encounter difficult complexity in the group ring. In [16], a new El Gamal public key cryptosystem based on matrices over a grouping was proposed. Although the platform of the group ring proposed is commutative, the scheme may be inefficient because there is no explicit performance efficiency stated in [16]. In [45], Mittal et al. developed a robust ID-based encryption system whose security relies on the recently discovered significant problems in the algebraic structure of group rings. However, because the TP also has access to the user’s private keys, identity-based authentication suffers from a key escrow problem. In [46,47], a secure public key cryptography (PKC) based on group rings was constructed. However, managing keys in group-ring-based PKCs can be complex. Hence, this can pose challenges in terms of key distribution and storage burdens.

The schemes discussed in [16,18,19,20,21,22,23,24,25,26,27,28,29,30,31,32,33,34,35,36,37,38,39,40,41,42,43,44,45,46,47] provide a limitation in offering a robust solution for secure authentication and privacy preservation in combinatorial group theory cryptosystems. These studies also lack explicit discussions on addressing the conflicting security requirements. Motivated by the gap in the literature, we construct a group signature scheme over a secure and reliable group ring that fulfils the following two objectives: (1) incorporate the two hard problems in group theory and define a new problem; and (2) address the conflicting requirements of trustworthiness, privacy, and accountability simultaneously. In addition, we conduct a comparative analysis and simulation to compare our protocol to existing schemes.

2.1. Our Contribution

In this work, we construct a group signature scheme over a secure and reliable group ring. As far as we are aware, our work is the first comprehensive framework for a group signature scheme over a group ring that satisfies the contradictory security goals of message trustworthiness, privacy, and accountability. The following is our contribution:

• We incorporate the two hard problems in group theory, which are the DLP and IFP. We modify and extend the existing DLP and IFP to define a new problem, DLP with factorization (DLPF), where the underlying structure is based on group rings. We will also analyze the parameters that are suitable to design an efficient and secure DLPF over a group ring;
• We implement the new problem in DLPF to construct a secure and efficient group signature scheme that simultaneously has the appealing qualities of message trustworthiness, privacy, and accountability. The fundamental advantage of group signatures over digital signatures is that only one key pair must be stored by the user, eliminating the need to maintain many anonymous credentials beforehand;
• We present an analysis that demonstrates how our protocol delivers an effective security level, system robustness, and performance efficiency. Our protocol is then executed using MATLAB R2021b. This computational analysis shows the applicability and usability of our work in practical applications.

2.2. Organization

The remainder of the paper is organized as follows. Section 2 outlines relevant research pertaining to secure group signatures and group ring schemes that present security and privacy issues. In Section 3, we outline the groundwork of our scheme. In Section 4, the new problem (DLPF) is presented. In Section 5, a secure and efficient group signature scheme based on general linearity over a group ring was proposed. Our protocol’s performance analysis and simulation are computed in Section 6. Finally, we conclude the work and provide suggestions for future work in Section 7.

3. Preliminaries

Here, we present some fundamental notions of group rings and general linear groups.

Definition 1 

(General Linear Group) (see [28]). The general linear group is composed of $n\times n$ invertible matrices of degree $n$. The operation is identical to standard matrix multiplication. Since the product of two invertible matrices is also invertible and the inverse of an invertible matrix is equally invertible, this produces a group. For instance, given a ring $R$ with identity, the general linear group ${GL}_n(R$) is the group of $n\times n$ invertible matrices with elements in $R$.

Definition 2 

(Group Ring) (see [26]). Assume $F$ is a field and $G$is a finite or infinite multiplicative group. All finite sums of type [48] form the group ring.

$$x={\sum }_{g\in G}{\alpha }_{g}g,$$

where ${\alpha }_g \in F$ and group ring is designated as $F\left[G\right]$.

Let $y={\sum }_{g\in G}{\beta }_{g}g$ and $z={\sum }_{h\in G}{\gamma }_{h}h$ be elements of $F\left[G\right]$. Then addition and multiplication are defined as follows:

$$x+y={\sum }_{g\in G}{\alpha }_{g}g+{\sum }_{g\in G}{\beta }_{g}g={\sum }_{g\in G}\left({\alpha }_g+{\beta }_g\right)g,$$

$$xz=\left({\sum }_{g\in G}{\alpha }_{g}g\right)\left({\sum }_{h\in G}{\gamma }_{h}h\right)={\sum }_{g,h\in G}\left({\alpha }_g{\gamma }_h\right)gh.$$

Definition 3 

(Decisional Diffie–Hellman problem in group rings (DDHPGR) (see [26]). Let $\mathfrak{a}\in F\left[G\right]$be a randomly chosen element of the group ring. Then DDHPGR states that ${\mathfrak{a}}^{\mathcal{r}\mathcal{s}}\in F\left[G\right]$ should appear like a random element whenever one knows the values of ${\mathfrak{a}}^{\mathcal{r}}$ and ${\mathfrak{a}}^{\mathcal{s}}$ for arbitrary and independently chosen $\mathcal{r}$ and $\mathcal{s}.$

Definition 4 

(Bilinear Pairing) (see [26]). Let ${\mathbb{G}}_1$ and ${\mathbb{G}}_2$ be a non-abelian finite group with identity $e$ of sufficiently large prime order $q$ and generator $p$ over an elliptic curve that is defined on a finite field. Assume ${\mathbb{G}}_1$ = $〈g_1〉$ and ${\mathbb{G}}_2$ = $〈g_2〉$ and $e:{\mathbb{G}}_1\times {\mathbb{G}}_1\to {\mathbb{G}}_2$  is an efficient non-degenerate bilinear map.

3.1. Discrete Logarithm Problem with Factorization (DLPF)

In this section, we introduce the new hard problem, the discrete logarithm problem with factorization, and discuss its security and complexity.

Definition 5 

(Discrete Logarithm Problem) (see [22]). Let $p$ be a prime, and given an element $\beta \in F_p^{*}$ where $F_p^{*}$ is a cyclic group of order $p-1$ generated by $\alpha$, find an integer $t, 0 \le t \le p-1$ such that ${\alpha }^t\equiv \beta mod p.$

Definition 6 

(Factorization Search Problem) (see [22]). Given an element $x \in G$ and subgroups $A and B$of $G$, find two elements $a\in A$ and $b \in B$ such that $a.b=x.$

We combine the above two problems to introduce a new problem, DLP with factorization (DLPF), where the underlying structure is based on a general linear group-over-group ring.

Definition 7 

(Discrete Logarithm Problem with Factorization (DLPF)). Let $(G, •)$ be a finite non-abelian semigroup with $\eta$ elements. Let$x and y$ be arbitrary elements of $F\left[G\right]$. Then, for given $x, y \in F\left[G\right],$ find $z \in F\left[G\right]$ and $w \in Z$ such that $x={ y}^{w}z$.

Remark 1. 

If $z$ is known for a group, the equation $x={ y}^{w}z$ simplifies to $x^{\prime }={xz}^{-1}=y^w$. Now the challenge is to determine $w$ such that, given $x^{\prime }$, $y$ for $x^{\prime }={ y}^w$, which is the DLP.

Additionally, DLPF may be seen as a factorization search problem in which the two unknown factors of $x$ are $a={ y}^w$ (because $w$ is unknown) and $b=z.$

3.2. Security and Complexity of DLPF

3.2.1. Hardness of DDHPGR

Let $\mathfrak{a}\in F\left[G\right]$ be a randomly chosen element of the group ring. Then, as mentioned in Definition 3, DDHP in group rings states that ${\mathfrak{a}}^{\mathcal{r}\mathcal{s}}\in F\left[G\right]$ should appear like a random element whenever we know the values of ${\mathfrak{a}}^{\mathcal{r}}$ and ${\mathfrak{a}}^{\mathcal{s}}$ for arbitrary and independently chosen $\mathcal{r}$ and $\mathcal{s}$.

Informally, it implies that it should not be possible to calculate the value of ${\mathfrak{a}}^{\mathcal{r}\mathcal{s}}$ if one knows the values of ${\mathfrak{a}}^{\mathcal{r}}$ and ${\mathfrak{a}}^{\mathcal{s}}$. However, we are aware that DDHP is solvable if DLPGR (see Definition 5) is solvable. This is because the algorithm used to solve the DLPF can be used to derive $\mathcal{r}$ and $\mathcal{s}$ from ${\mathfrak{a}}^{\mathcal{r}}$ and ${\mathfrak{a}}^{\mathcal{s}}$. After knowing $\mathcal{r}$ and $\mathcal{s}$, it is straightforward to calculate ${\mathfrak{a}}^{\mathcal{r}\mathcal{s}}$. Consequently, in the following subsection, we study the hardness of DLPF in order to study the hardness of DDHP.

3.2.2. Hardness of DLPF in Group Ring

Let $\mathcal{G}=\left\{y_1,y_2,...,y_{\mathcal{n}}\right\}$ be a non-commutative semigroup of $\mathcal{n}$ elements and ${\mathbb{Z}}_{\mathcal{m}}=\left\{\mathrm{0,1},\mathrm{2,3},...,\mathcal{m}-1\right\}$, where $\mathcal{m}$ is a large positive integer. Let $\mathcal{z}\in \mathcal{G}$ and $w\in {\mathbb{Z}}_{\mathcal{m}}\backslash \{0, 1\}$ such that for given $x,y\in \mathcal{G}$, $x={ y}^{w}z$. Since $x, y, z\in \mathcal{G}$, they can be expressed as $x=y_i$, $y=y_j$, $z=y_k$ for some $i,j,k \in \left\{\mathrm{1,2},3,...,\mathcal{n}\right\}$.

The elements $z$ and $w$are chosen from $\mathcal{G}$ and ${\mathbb{Z}}_{\mathcal{m}}\backslash \{0, 1\}$. There are $\mathcal{n}$ and $\mathcal{m}$ options for $z$ and $w$, respectively. The total number of steps required to solve the DLPF using a brute force approach is therefore $\mathbb{O}\left(\mathcal{n}\mathcal{m}\right)$, which is exponential in the size of $\mathcal{n}\mathcal{m}$ in bits, and $d={log}_{e}2$ where:

$$=e^{{{log}_e}^{\mathcal{n}\mathcal{m}}},$$

(1)

$$=e^{{log}_e 2.{ log}_2\mathcal{n}\mathcal{m}},$$

(2)

$$= e^{d.size \left(\mathcal{n}\mathcal{m}\right)}.$$

(3)

In the simplest case, when $F_{\mathcal{q}}$ (a finite field of order $\mathcal{q}$) and $S_{\mathcal{m}}$ (a symmetric group of order $\mathcal{m}$) are given, where $\mathcal{m}$ is a ‘-bit number, we see that DLPF can be solved in $\mathbb{O}=\mathcal{O}({\mathcal{m}}^2\mathcal{n}{\mathcal{l}}^2$) bit operations for some positive integer $\mathcal{l}$. If$\mathcal{n}$ has size $r$bits, i.e., $\mathcal{n}\approx 2^r$, then $\mathbb{O}=\mathcal{O}({\mathcal{m}}^2{2}^r{\mathcal{l}}^2$). This is an exponential time since the input size is in$r$ bits (the order of the unit is input). However, due to standard collision algorithms, such as Shanks babystep giantstep algorithm [49], one can reduce the number of bit operations needed to solve DLPF to $\mathbb{O}=\mathcal{O}({\mathcal{m}}^2{2}^{\frac{r}{2}}{\mathcal{l}}^2$) bit operations, which is again an exponential time. This is because a general collision algorithm tends to reduce the operations by the square root of their times.

Additionally, there are no index calculus-type algorithms for solving DLPF. This is mostly because the settings of group rings cannot be directly transferred to the most well-known sub-exponential algorithm, i.e., the index calculus algorithm [49], due to the latter’s more complex structure than the former. Therefore, we can conclude that there is currently no known polynomial or sub-exponential time solution to solve DLPF.

Example 1. 

We recall from Definition 7 that DLPF in GR is the problem of deducing $z$ from the known values $x$ and $y$ for some positive integer $w$ and $x, y \in F\left[G\right]$. Let the number of elements in $G$ be $m$, which satisfies this equation:

$$x={\sum }_{j=1}^m{z}_j{g}_j with Ord\left(x\right)=n,$$

where $Ord\left(x\right)$ defines the order of $x$. Then $z$ can be deduced from at most $n$ multiplications of $x$ with itself.

Example 2. 

Our proposed platform for the group is${GL}_2\left(F_{\mathcal{q}}\left[S_{\mathcal{n}}\right]\right),$ where $F_{\mathcal{q}}$ is the finite field of order $\mathcal{q}$ and $S_{\mathcal{n}}$ is the symmetric group on a set of $\mathcal{n}$ elements.

Assuming $\mathcal{q}=7$ and $\mathcal{n}=3.$ Using the linear representations of the symmetric group $S_3$ and of the group algebra $\left(F_7\left[S_3\right]\right),\mathrm{t}\mathrm{h}\mathrm{e} \mathrm{g}\mathrm{r}\mathrm{o}\mathrm{u}\mathrm{p} \mathrm{p}\mathrm{r}\mathrm{e}\mathrm{s}\mathrm{e}\mathrm{n}\mathrm{t}\mathrm{a}\mathrm{t}\mathrm{i}\mathrm{o}\mathrm{n} \mathrm{o}\mathrm{f} S_3$ has three irreducible representations, two of dimension one and the third of dimension two. We employ the Wedderburn theorem and compute the following result in [50]:

$${\mathrm{G}\mathrm{L}}_2\left({\mathrm{F}}_7\right[{\mathrm{S}}_3\left]\right)\simeq {\mathrm{G}\mathrm{L}}_2\left({\mathrm{F}}_7\right)\oplus {\mathrm{G}\mathrm{L}}_2\left({\mathrm{F}}_7\right)\oplus {\mathrm{G}\mathrm{L}}_4\left({\mathrm{F}}_7\right),$$

hence

$$\left|{\mathrm{G}\mathrm{L}}_2\left({\mathrm{F}}_7\left[{\mathrm{S}}_3\right]\right)\right|=\left[\right(7^2-1\left)\right(7^2-7\left)\right]\left[\right(7^2-1\left)\right(7^2-7\left)\right]\left[\right(7^2-7^0)\dots (7^4-7^3\left)\right]>7^{16}.$$

As a result, $\left|G\right|\cong 2^{128}$ results from a prime $\mathcal{q}$ of size relatively similar to $2^7$. Additionally, the complexity of DLPF is $e^{{log}_{e\mathcal{n}\mathcal{m}}}=2^{128}$, if we use the 48 bit integer $\mathcal{m}$ in Section 3.2.2, which is the effective security parameter for brute force attacks. Therefore, regardless of the minimal values of $\mathcal{q}$ and $\mathcal{n}$, we demonstrate that our scheme satisfies efficient and superior security requirements.

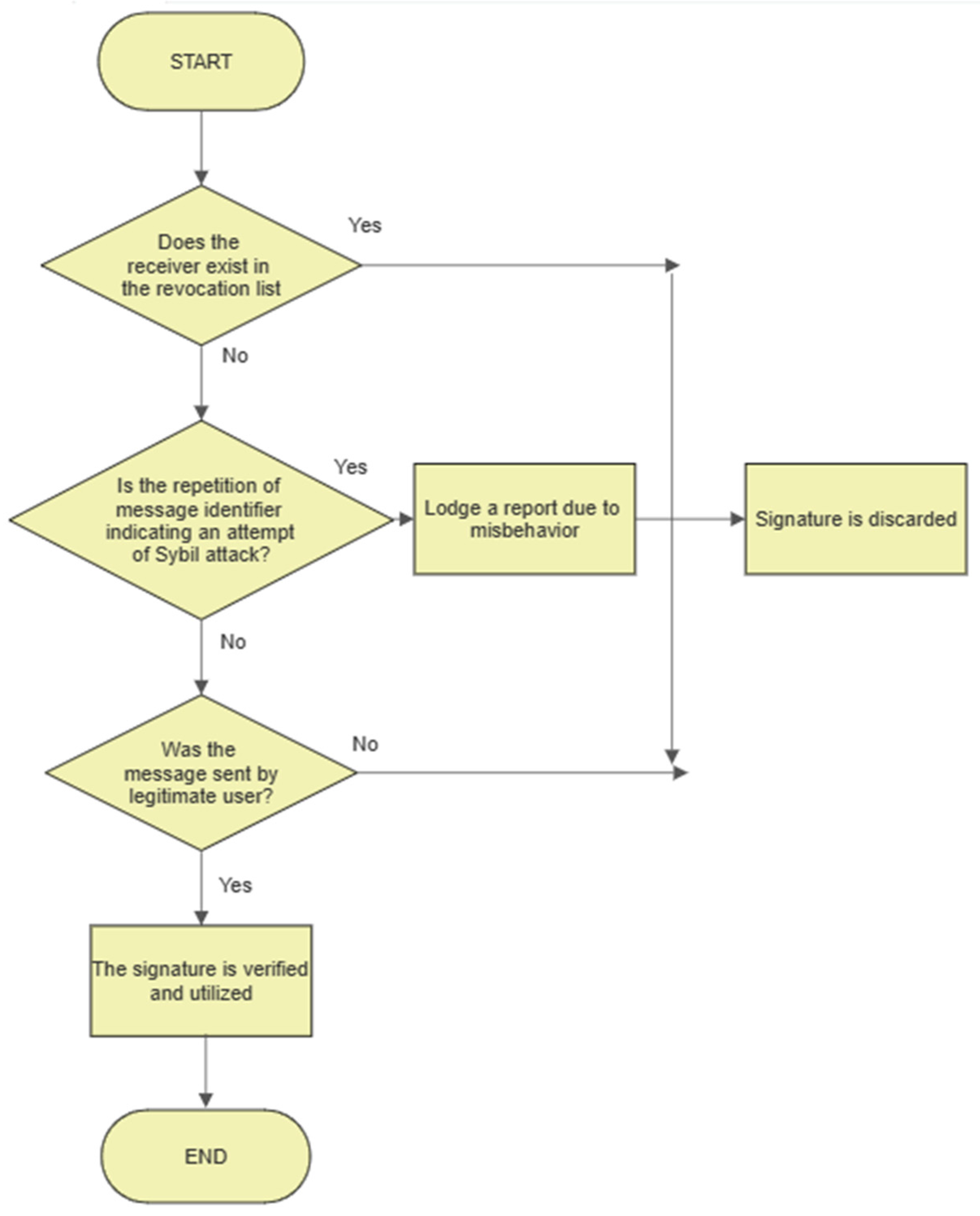
4. System and Network Model

4.1. Entities

The scheme consists of a Trusted Party ($TP$), users, which are composed of a sender ($S$) and a receiver ($R$), and adversaries. We describe each entity’s role in the following manner:

• Trusted Party. We depend on a trusted party ($TP$) to manage user admittance into the system and revoke the malicious user. It is responsible for the issuing and administration of credentials. A $TP$ will only disclose a misbehaving user’s identification if they are discovered to be malicious. Furthermore, the $TP$ verifies and assesses the reliability of the signature;
• Users. Users in our scheme consist of a sender ($S$) to generate and forward the signature and a receiver $\left(R\right)$ that utilizes the verified signature;
• Adversaries. The two types of adversaries are insiders and outsiders. An outside adversary is a malicious entity that does not possess all the valid credentials and authorization to access the network. An inside adversary, on the other hand, is a malicious participant who is genuine and in possession of all necessary credentials.

4.2. Comprehensive Framework

We formulate a comprehensive framework for a secure group signature based on a general linear over group ring, as depicted in Figure 1.

• Registration Phase

• Step 1: $S$ submits a request to the $TP$ in order to obtain a credential in order to access the network;
• Step 2: $TP$ creates, distributes, and keeps credentials in its database to verify $S$’s authenticity within the network;
• Step 3: Following successful authentication, $TP$ returns the credential to $S$;

• Broadcast Phase

• Step 4: $S$ produces a signature and transmits it to the $TP$;

• Verification Phase

• Step 5: $TP$measures the signature’s validity;
• Step 6: $TP$ sends to $R$ the validated signature after a successful verification;
• Step 7: $R$ validates the signature.

• Revocation Phase

• Step 8: If $R$ encounters any wrongdoing during its interaction with $S$, they may lodge a report with the $TP$;
• Step 9: The $TP$ evaluates the validity and trustworthiness of the information after receiving reports before considering eliminating $S$ from the network.

5. Group Signature Scheme over Group Ring

In this section, we highlight our effective and secure group signature scheme based on group rings. The security of this scheme depends on the complexity of the DLPF, which includes the system initialization, entity registration, signature generation, signature verification, and signature revocation phases (illustrated in Figure 1). The extent of trust held by the TP varies across numerous literature works. Some schemes included a fully trusted party in their architecture [51], but other schemes included partial trust towards the trusted party, which is classified as semi-trusted [52,53] and honest-but-curious [4]. A weaker trust assumption in the authority, such as the possibility that the authority may perform fraudulent activity by impersonating an honest user to execute the protocol, motivates us to construct a more secure and robust system. This is due to the fact that a scheme to prevent protocol violations, such as limiting the authority’s accessibility to a user’s access and certificate, since the trusted party in our work does not have access to the user’s secret value and credentials, is depicted as honest but curious. Figure 2 depicts a simplified flowchart of the proposed scheme.

5.1. System Initialization

Our protocol setup algorithm is based on DLPF with bilinear pairing. A $TP$ takes as input a security parameter $\nexists$, and outputs ${\rm Y}=\left({\mathbb{G}}_1,{\mathbb{G}}_2,{g,g}_1,e\right).$Let ${\mathbb{G}}_1$ and ${\mathbb{G}}_2$ be non-abelian finite groups, respectively, and pairing $e:{\mathbb{G}}_1\times {\mathbb{G}}_1\to {\mathbb{G}}_2$ is an efficient non-degenerate bilinear map. This bilinear map satisfies the following properties:

• $e\left(g,\left.g_1\right) \ne 1\right.$ for all $g\in {\mathbb{G}}_1$ and$g_1\in {\mathbb{G}}_1$;
• For all $h_1\in {\mathbb{G}}_1$, $h_2 \in {\mathbb{G}}_1$ and $\mathcal{p},\mathcal{q}\in \mathbb{Z}$, it holds that $e({h_1}^{\mathcal{p}}, {h_2}^{\mathcal{q}})=e{(h_1,h_2)}^{\mathcal{p}\mathcal{q}}$.

Consider $H={GL}_m\left(F_q\right[S_r\left]\right)$ to be a non-abelian group of order $\delta$, $N \mathrm{t}\mathrm{o}$be an abelian subgroup of $H$. Let $H_1$ be a cryptographic hash function from ${\left\{\mathrm{0,1}\right\}}^{*}$ to $H,$ defined as $H_1 :{\left(\mathrm{0,1}\right)}^{*}\mapsto H/N$. We also rely on the Decisional Diffie–Hellman (DDH) assumption. We adopt the DDH assumption in [8,9,54] and refer the readers to [8,9,54] for in-depth understanding. The DDH holds in ${\mathbb{G}}_1$ where $gh,g^a{h}^b,g^c{h}^d\in {\mathbb{G}}_1$ such that $a,b,c,d\in {\mathbb{Z}}_p^{*}$ for any probabilistic polynomial time (PPT) adversary $\mathcal{A}$, the probability decides if $d=abc$ is neglibly away from $\frac{1}{2}$. The system parameters are $\mu =({\mathbb{G}}_1,{\mathbb{G}}_2,{g,g}_1,e, h_1,h_2, V,H,H_1,N,A, X, a)$.

5.2. Entity Registration

• Step 1: $S$ self-generates a key pair $(y_s, x_s$) in order to join the network. $S$ requests validation of its self-generated public key ($y_s)$ at time $t$ from the $TP$ while preserving its secret key ($x_s)$ undisclosed. Assume $A\in H/N$, and the public key is $\left(y_s=X{A}^a{X}^{-1}\right.)$for $X\in N$. Then, using the private key$(x_s=X,a)$ for $a\in {\mathbb{Z}}_p^{*}\backslash \left\{1\right\},$ where $p$ is the set of integers modulo $p$ that are relatively large primes, a user computes its tracing information $T_s=g^{x_s}$. The sender sends$(y_s, T_s$) to$TP$;
• Step 2: $TP$ performs an authentication check by checking$e\left(y_s, g^{x_s}\right)=e(X{A}^a{X}^{-1},T_s)$. Upon successful verification, $TP$ generates a signature on $y_s$. $TP$ sends $y_s$ to $S$. $TP$ then stores$(y_s,T_s$) into its local database;
• Step 3: $TP$ initially authenticates the sender’s validity by verifying the signature on $y_s$. The $TP$ has a key pair denoted by ($y_t,x_t)=\left(e(\left(g^{x_t}\right),g),x_t\right),$ where the $TP$ selects a randomly chosen group element from $x_t$ ∈ ${\mathbb{G}}_1$. $TP$ performs the computation $K_1=g_1^k$ and $K_2=x_t(h_1{y_s)}^{-k},$ where $k$ is a random matrix and element of $N$. Upon successful computation, $TP$ distributes $K_u=\left(K_{1, }{K}_2\right)$ to the legitimate sender. A sender verifies that $e\left(K_{2,}{T}_s\right)e\left(K_{1,}{h}_2\right)e(K_1^{x_s},V)=e(\left(g^{x_t}\right),g)$ to validate the signature. If the check is successful, the sender has successfully registered with $TP$ and can employ $K_u$ as a group certificate over the network. The sender may generate a signature for any message using their $x_s$.

5.3. Signature Generation

During this stage, $S$ generates a message and announces it to the intended users through $TP$. This is described as follows:

• Step 4: $S$ generates the message ($\mathcal{m}$), where $\mathcal{m}=\left(M_{id},t_p,{\mathcal{U}}_{cur},{GID}_u\right).$ Message ID is denoted as $M_{id,}$ which defines the type of message; $t_p$ is the validity period of signature generation; and user position is indicated by ${\mathcal{U}}_{cur}$. Let ${GID}_u$ be the user’s group identity, allowing one to determine which group the user belongs to.

Using the group signature technique, a group member can sign a message on behalf of the entire group. Although signatures may be verified in relation to a certain public key group, this does not reveal the signer’s identity. The user must execute the following computation in order to generate a message-linkable signature:

• Distribute the $K_u$ at random to verify that the signer is a legitimate member of the group while maintaining network anonymity. $S$ computes ${\omega }_1=K_1{g}_1^d, { \omega }_2=K_2(h_1{y_s)}^{-d}$ for a randomly chosen matrix$d\in N$;
• Generate a random $y_s$ for a group member where ${\omega }_3={\omega }_1^{x_s}$ and produce a message link-identifier ${\omega }_4=H_1{\left(\mathcal{m}\right)}^{x_s}$;
• Set up the group signature on $\mathcal{m}$ using the private key $x_s$ in ${\omega }_3={\omega }_1^{x_s}$ and ${\omega }_4=H_1{\left(\mathcal{m}\right)}^{x_s}$.

$S$ performs the following computation in order to establish the group signature:

• Set up at random for an integer where $r\in {\mathbb{Z}}_p^{*}\backslash \left\{1\right\}$ where $p$ is a substantial prime number within the set of integers modulo $p$;
• Compute $R_1=H_1{\left(\mathcal{m}\right)}^r$ and $R_2={\omega }_1^r$;
• Obtain a challenge of $R_1$and $R_2$ where ${\omega }_5=H\left(\mathcal{m}\left|\left|{\omega }_1\right|\right|{\omega }_2\left|\left|{\omega }_3\right|\right|{\omega }_4\left|\left|R_1\right|\right|R_2\right)$;
• Response to the challenge with ${\omega }_6=r-{\omega }_5^{x_s} mod p$and output the group signature as $\omega =({\omega }_1,{\omega }_2,\dots ,{\omega }_{6)}$ of $\mathcal{m}$.

$S$ outputs the group signature as $\omega =({\omega }_1,{\omega }_2,\dots ,{\omega }_{6)}$ of $\mathcal{m}$. $S$ announces a message tuple, $\mathcal{M}=(\mathcal{m},\omega )$. The message link-identifier, ${\omega }_4,$ can only be produced once by $S$ for the same message. $S$ then broadcasts the messages to $TP$.

5.4. Signature Verification

• Step 5: The validity of the safety messages is assessed by $TP$. Since a replay of the same ${\omega }_4$ shows that the same messages were generated by the same user several times, $TP$ rejects signatures that contain the same component of ${\omega }_4$.
• Step 6: For message verification:

$TP$ checks $e\left({\omega }_{2,}{g}^{x_s}\right)e\left({\omega }_{1,}{h}_1\right)e({\omega }_3,V)=e\left(\left(g^{x_t}\right),g\right)$ in order to validate the group certificate.

It then performs a check on:

$${\omega \prime }_5=H\left(\mathcal{m}\left|\left|{\omega }_1\right|\right|{\omega }_2\left|\left|{\omega }_3\right|\right|{\omega }_4\left|\left|H_1{\left(m\right)}^{{\omega }^6}{{\omega }_4}^{{\omega }^5}\right|\right|{{\omega }_1}^{{\omega }^6}{{\omega }_3}^{{\omega }^5}\right).$$

When the message’s freshness is maintained, $TP$ determines that a message is trustworthy if and only if ${\omega \prime }_5={\omega }_5$. Upon successful verification, $TP$ forwards the verified signature, $\mathcal{M},$ to R.

• Step 7: $R$ validates the message’s content by examining the $t_p$. The signature is regarded as trustworthy if both message verification checks succeed and $t_p$ is valid at that time.

5.5. Signature Revocation

• Step 8: Upon detecting malicious behavior in the network, $R$ submits a revocation report to the $TP$.
• Step 9: To revoke misbehaving $S$, the $TP$ verifies the validity of $\mathcal{M}$. We observe that $TP$ possesses some trapdoor knowledge of $\left(y_s\right)$. The $TP$ searches its local database to connect $\left(y_s\right)$ with $S$’s identification for revocation and law enforcement purposes.

The sequential flow of our proposed scheme

Setup: •${\rm Y}=\left({\mathbb{G}}_1,{\mathbb{G}}_2,{g, g}_1,e\right).$ • System parameters: $\mu =({\mathbb{G}}_1,{\mathbb{G}}_2,{g,g}_1,e{,h}_1,h_2,V,H,H_1,N,A, X, a)$. Registration phase: Key Generation: • S’s public key is$\left(y_s=X{A}^a{X}^{-1}\right.)$for $X\in N$; • S’s private key is $\left(x_s=X,a\right)$ for $a\in {\mathbb{Z}}_p^{*}\backslash \left\{1\right\}$; • TP’s keypair is $(y_t,x_t)=\left((e\left(g^{x_t}\right),g), x_t\right)$. User computes $T_s=g^{x_s}$ $\mathrm{S}\stackrel{\hspace{1em}\hspace{1em}\hspace{1em}{y}_S,T_s\hspace{1em}\hspace{1em}\hspace{1em}}{\to }\mathrm{T}\mathrm{P}$ TP verifies: $e\left(y_s, g^{x_s}\right)=e(X{A}^a{X}^{-1},T_s)$. TP computes: $K_1=g_1^k$, $K_2=x_t(h_1{y_s)}^{-k}$ where $k$is a random matrix and element of $N$. $\mathrm{T}\mathrm{P}\stackrel{\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}Ku=\left(K_1,K_2\right)\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}}{\to }\mathrm{S}$ S verifies: $e\left(K_{2,}{T}_s\right)e\left(K_{1,}{h}_2\right)e(K_1^{x_s},V)=e(\left(g^{x_t}\right),g)$. Signing Phase: • The message format is: $\mathcal{m}=\left(M_{id},t_p,{\mathcal{U}}_{cur},{GID}_u\right)$. • The user executes the following computation in order to generate a message-linkable signature: • Randomize $K_u$ where $S$ computes:     ▪ ${\omega }_1=K_1{g}_1^d$;     ▪ ${\omega }_2=K_2(h_1{y_s)}^{-d}$ for a randomly chosen matrix$d\in N$. • Randomize $y_s$ where $S$ computes:   ▪ ${\omega }_3={\omega }_1^{x_s}$;   ▪ Produce a message link-identifier ${\omega }_4=H_1{\left(\mathcal{m}\right)}^{x_s}$. • Generate the group signature using $x_s$ in ${\omega }_3$ and ${\omega }_4$. • To establish a group signature, $S$ computes: • Randomly choses $r\in {\mathbb{Z}}_p^{*}\backslash \left\{1\right\}$; • Compute commitments $R_1=H_1{\left(\mathcal{m}\right)}^r$ and $R_2={\omega }_1^r$; • Acquire a challenge according to the computed commitments ${\omega }_5=H\left(\mathcal{m}\left|\left|{\omega }_1\right|\right|{\omega }_2\left|\left|{\omega }_3\right|\right|{\omega }_4\left|\left|R_1\right|\right|R_2\right)$; • Response to the challenge with ${\omega }_6=r-{\omega }_5^{x_s} mod p$; • Output the group signature as $\omega =({\omega }_1,{\omega }_2,\dots ,{\omega }_{6)}$ of $\mathcal{m}$. Broadcast: $\mathcal{M}=(\mathcal{m},\omega )$. Verification Phase: • For checking purposes: TP verifies:   ▪ $e\left({\omega }_{2,}{g}^{x_s}\right)e\left({\omega }_{1,}{h}_1\right)e({\omega }_3,V)=e(\left(g^{x_t}\right),g)$;   ▪ ${\omega \prime }_5=H\left(\mathcal{m}\left|\left|{\omega }_1\right|\right|{\omega }_2\left|\left|{\omega }_3\right|\right|{\omega }_4\left|\left|H_1{\left(m\right)}^{{\omega }^6}{{\omega }_4}^{{\omega }^5}\right|\right|{{\omega }_1}^{{\omega }^6}{{\omega }_3}^{{\omega }^5}\right)$; $\stackrel{\hspace{1em}\hspace{1em}\hspace{1em}ℳ\hspace{1em}\hspace{1em}\hspace{1em}}{\to }\mathrm{T}\mathrm{P} \mathrm{R}$ • $R$ validates $\mathcal{M}$ by examining the $t_p$. Revocation Phase: • If $R$ encounters misbehavior; $\mathrm{T}\mathrm{P}\stackrel{\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\mathrm{Revocation} \mathrm{report}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}}{\to }\mathrm{R}$ • $TP$ searches its local database to connect $\left(y_s\right)$ with $S$’s identification for revocation.

6. Security and Performance Evaluation

6.1. Security Evaluation

This section examines the security concerns with our proposed protocol and assesses its functionality. There are three fundamental security goals we consider essential issues to address towards a secure group signature scheme over a general linear group-over-group ring: trustworthiness, privacy, and accountability.

• Trustworthiness: A message must be transmitted by a reliable user in its unaltered state for it to be considered reliable (sender authenticity and message integrity). Furthermore, the message conveyed must accurately depict the incident. Additionally, there is a significant probability that the event has already occurred (message truthfulness). Additionally, a minimal percentage of inside adversaries should be tolerable for the system (system robustness).

Claim 1.

The proposed protocol satisfies the third condition of message trustworthiness and is resistant to Sybil attacks.

We discuss the potential of an inside adversary launching a Sybil adversary. An outside adversary is not considered because they do not register as a network participant, which means they pose less of a threat to other users. The Sybil attack happens when an inside adversary generates several signatures and masquerades as various senders to deceive the receiver into believing the message is legitimate on the network.

Proof. 

Let an internal adversary, $\mathsf{\Psi }$ exist. We consider a case in which $\mathsf{\Psi }$ creates two signatures for an identical message and publishes these messages. When TP receives these messages, it examines the message-link identifier, ${\omega }_4$, to ensure that only one authorized network user produced each message. However, it may be recognized when two signatures have the same element of:

$${\omega }_4=H_1{\left(\mathcal{m}\right)}^{x_s}.$$

(4)

By analyzing the component of ${\omega }_4$ on two messages describing the same occurrence, $\Psi$may thus be computationally linked. In order to fulfil the goal of message trustworthiness, our protocol offers the distinguishability of origin that facilitates threshold authentication.

Remember that a one-time public key is used as part of the signature. This shows that ${\omega }_3={\omega }_1^{x_s}$ and ${\omega }_4=H_1{\left(\mathcal{m}\right)}^{x_s}$, where the value of $x_s$ is undisclosed in $({\omega }_3,{\omega }_4)$. The $\mathrm{T}\mathrm{P}$ uses the tracing information $T_s=g^{x_s}$ to identify the group member by checking:

$$e\left(y_s, g^{x_s}\right)=e(X{A}^a{X}^{-1},T_s).$$

(5)

This allows $\mathsf{\Psi }$ to be traceable when the repetition of ${\omega }_4$ is recognized upon validating the same message multiple times. As a result, the message will be discarded, rendering our protocol robust to Sybil attacks.□

• Privacy: If the sending user behaves properly, its identification should be kept private (anonymity). Furthermore, if the same sender produces two distinct messages, they cannot be connected to one another (unlinkability).

Claim 2.

Our protocol protects the privacy of the originators against an inside adversary.

Proof. 

Consider the following anonymity game by an inside adversary, $\mathsf{\chi }$. We generate key pairs as depicted in our work, obtaining $\mathcal{n}$ key pairs: ${{(y}_s}_1,{x_s}_1$), …,${{(y}_s}_n,{x_s}_n$). The system parameters $\mu$ are forwarded to the adversary $\chi$ upon request, where:

$$\mu =({\mathbb{G}}_1,{\mathbb{G}}_2,{g,g}_1,e{,h}_1,h_2, V,H,H_1,N,A, X, a).$$

(6)

We assume that the adversary $\chi$ queries the user’s secret key at index $\mathcal{i}$, $1\le \mathcal{i}\le \mathcal{n}$. We respond with the key pair ${{(y}_s}_i,{x_s}_i)$. We produce a valid signature ${\omega }_{\mathcal{i}}$ on $\mathcal{M}$ using ${x_s}_i$ and forward ${\omega }_{\mathcal{i}}$ to $\chi$. The adversary $\chi$ then generates a message ${\mathcal{M}}^{*}$. We randomly choose a bit $\mathcal{b}{\in }_{\mathcal{R}}\{$0,1} where $\mathcal{b}$ is unknown to us. We then compute a signature ${\omega }^{*}$ on ${\mathcal{M}}^{*}$ using ${{x_s}_i}_{\mathcal{b}}$. We send ${\omega }^{*}$ to $\chi$. When $\chi$ obtains the signature, $\chi$ analyzes the signature and outputs the guess of $\mathcal{b}$’ of $\mathcal{b}$ where $\mathcal{b}\mathrm{’}{\in }_{\mathcal{R}}\{$0,1}. We declare failure, and $\chi$ wins the game, provided that $\chi$can guess the value of $\mathcal{b}$’ = $\mathcal{b}$. This anonymity game defines the advantage of the adversary $\chi$ winning the game as Equation (7), where Pr [$\mathcal{b}$’ = $\mathcal{b}$] represents the probability of $\mathcal{b}$’ = $\mathcal{b}$:

$$\mathrm{Pr} [\mathcal{b}\text{’}=\mathcal{b}]=\frac{1}{2}.$$

(7)

The probability is taken from the coin tosses of the adversary $\mathsf{\chi }$. As a result, the adversary is unable to take advantage of the randomized key generation and signature process to successfully play the anonymity game in polynomial time with a non-zero probability. Therefore, our protocol complies with the privacy goal. □

• Accountability: Users that exhibit improper behavior can be traced. In addition, they must prove non-repudiation, or the assertion that they are the message’s sender (non-repudiation). The violating user’s access to the network can then be revoked (revocation).

Claim 3.

Our protocol achieves all the accountability goals.

Proof. 

The traceability, non-repudiation, and revocation accountability goals are met by our scheme. When the group signature enables the TP to reveal the signature of a malicious user, the traceability property is satisfied. When the same component of ${\mathit{\omega }}_4$ is identified after validating the same message more than once, the identity of an adversary is traceable, and the proof functions similarly to the proof in Claim 1. Since the user is the only one in possession of the signature key, as demonstrated by our scheme, non-repudiation is ensured because TP does not have access to the user’s secret key. The TP, who keeps some trapdoor information to revoke dishonest users, supports the revocation goal. □

We demonstrate that the security goals are satisfied by our security analysis.

Table 1. Comparison of Security Goals.

Security Objective	Security Component	Gupta et al. [31]	Mittal et al. [45]	Our Work
Trustworthiness	Authenticity of sender	/	/	/
	Message integrity	/	/	/
	Message origin authentication	X	X	/
Privacy	Anonymous	/	/	/
	Unlikability	X	/	/
Accountability	Traceability	/	/	/
	Non repudiate	/	X	/
	Revocability	X	X	/

/ = achieve the security component. X = does not achieve the security component.

presents a summary of the security needs analysis. In our work, we effectively balance the functionalities of message trustworthiness, privacy, and accountability. As a conclusion, our scheme seems to be better and more robust than the schemes proposed in [31,45].

6.2. Robustness Analysis

We evaluate the robustness of our protocol in the presence of adversaries. Adversaries who are not authorized to access the network are considered outside adversaries. Inside adversaries, meanwhile, are registered users who possess all the legitimate credentials.

In this study, we consider both attacks initiated by outsiders and inside adversaries. We then define the most probable network attacks, including impersonation attacks and man-in-the-middle attacks, below. In the next sections, we demonstrate how robust our work is against these attacks.

• Impersonation attacks. By adopting their identities, an adversary can manipulate trustworthy communications by disguising themselves as other genuine users;
• Man-in-the-middle attacks. The messages transmitted by the user to the trusted party, who believes they are directly communicating with one another, are eavesdropped on, intercepted, and possibly modified by an adversary.

• Robustness against Impersonation Attacks

Claim 4. 

An inside user is incapable of producing misleading messages by using the identity of another legal user. A user’s certificate must be impersonated by an inside adversary, who must then generate a fraudulent message using the user’s identity. However, because the protocol can recognize a counterfeit, an inside adversary cannot steal a user’s identity or make false accusations against other users in an attempt to mislead them. We consider the following attacks:

• Impersonation attack against outside adversaries.

A message $\mathcal{M}=(\mathcal{m},\mathsf{\omega })$ is announced. In order to forge a message tuple, $\mathcal{M}\mathcal{\prime }=(\mathcal{m}\mathrm{\prime },\mathsf{\omega }\mathrm{\prime })$, an outside adversary has to acquire a $x_s$ to generate a signature on the safety message. However, an outside adversary is not able to disguise itself as another user in the network unless it possesses lawful access to a valid private key, $x_s$. Hence, even if an outside adversary successfully generates a message, the message will not be verified correctly under the verifying procedure.

• Impersonation attack against inside adversaries.

Suppose an adversary impersonates an honest user:

• An adversary randomly chooses an integer ${x\mathrm{\prime }}_s$ for a random value and let $\left({\mathrm{y}\mathrm{\prime }}_{\mathrm{s}}=\left(X{\prime A}^a{X}^{-1}\right.\right.\left)\right)$;
• The signing protocol for the message$,\mathcal{m}$ is executed;
• A fake message, ${\mathcal{M}}^{\mathrm{\prime }}=\left({\mathcal{m}}^{\mathrm{\prime }},{\mathsf{\omega }}^{\mathrm{\prime }}\right),$ is announced.

Let the adversary be $\mathcal{A}$ and the challenger be $\mathcal{C}$. Assume adversary $\mathcal{A}$ is able to forge a valid signature to manipulate other entities in the network without fear of being arrested. If the impersonation attack succeeds, $\mathcal{C}$ executes the following steps. Consider that $\mathcal{A}$ has access to the network.

Suppose $\mathcal{A}$ queries a group certificate and the signature of ${\mathrm{y}}_{\mathrm{s}}$ from $TP$, $\mathrm{a}\mathrm{n}\mathrm{d} \mathcal{C}$ generates the group certificate given that $\mathcal{C}$ knows the valid key pair of $\mathcal{A}$, $({\mathrm{y}\mathrm{\prime }}_{\mathrm{s}},{\mathrm{x}\mathrm{\prime }}_{\mathrm{s}})$. In order to get the value of $x_s$, $\mathcal{C}$ runs a zero-knowledge proof $\mathcal{Z}\mathcal{K}\left\{{\mathrm{x}}_{\mathrm{s}}|{\mathrm{y}}_{\mathrm{s}}=X{A}^a{X}^{-1}\}\right.$ with $\mathcal{A}$ by invoking $\mathcal{A}$ twice according to the Forking Lemma in [52].

Assume, $\mathcal{A}$ is able to impersonate a legitimate user’s identity, which has a group signature $\mathsf{\omega }=({\mathsf{\omega }}_1,{\mathsf{\omega }}_2,\dots ,{\mathsf{\omega }}_{6)}$. Then, the tracing information equation in the name of the false user’s certificate does not hold $e\left(y_s, g^{x_s}\right)=e\left(X{A}^a{X}^{-1},T_s\right).$The challenger $\mathcal{C}$ first sends ${\mathrm{x}}_{\mathrm{s}}$ to the $TP$. The $TP$ randomly chooses a secret integer, ${T\mathrm{\prime }}_v\in$ ${\mathbb{Z}}_p^{\mathrm{*}}$, and sends ${T\mathrm{\prime }}_v$ to $\mathcal{C}$. Then $\mathcal{C}$ computes ${T\mathrm{\prime }}_{\mathrm{s}}={\mathrm{g}}^{{\mathrm{x}\mathrm{\prime }}_{\mathrm{s}}}$. If the equation ${T\mathrm{\prime }}_{\mathrm{s}}={\mathrm{g}}^{{\mathrm{x}\mathrm{\prime }}_{\mathrm{s}}}$ is equal to $T_s=g^{x_s}$ for the same period$,t_p.$ Then, $\mathcal{C}$ verifies the verification equation to determine whether it holds:

$${\mathsf{\omega }\mathrm{\prime }}_5=H\left(\mathcal{m}\left|\left|{\omega }_1\right|\right|{\omega }_2\left|\left|{\omega }_3\right|\right|{\omega }_4\left|\left|H_1{\left(m\right)}^{{\omega }^6}{{\omega }_4}^{{\omega }^5}\right|\right|{{\omega }_1}^{{\omega }^6}{{\omega }_3}^{{\omega }^5}\right).$$

(8)

If the equation holds, the signature is valid, and vice versa. Then $\mathcal{A}$ executes the signing protocol. Note that the equation implies $\mathsf{\omega }=({\mathsf{\omega }}_1,{\mathsf{\omega }}_2,\dots ,{\mathsf{\omega }}_6)$ is a signature on message $\mathcal{m}$ under the one-time public key ${\mathsf{\omega }}_3={\mathsf{\omega }}_1^{x_s}$, ${\omega }_4=H_1{\left(\mathcal{m}\right)}^{x_s}$. When $\mathcal{A}$ requests a group signature on $\mathcal{m}$, it can always be detected by $TP$. Hence, $\mathcal{A}$ fails to impersonate an identity and is incapable of broadcasting a bogus message, $\mathcal{M}\mathcal{\prime }=(\mathcal{m}\mathrm{\prime },\mathsf{\omega }\mathrm{\prime })$.

Apart from that, the probability that $\mathcal{A}$ is able to convince the $TP$ to accept an invalid group signature is not greater than the maximum of $\left(\frac{1}{\psi P}-\frac{1}{\psi -\sigma }\right),$ where $\psi$ is the order of $N$ and $\sigma$ is the order of $H$. Assuming that $\mathcal{A}$ challenges the private key at index $\mathcal{i}$, where $\mathcal{i}$ is $1\le \mathcal{i}\le \mathcal{n}$, we provide the corresponding key pair $({x_s}_{\mathcal{i}}$, ${y_s}_{\mathcal{i}})$ as a response. Using ${x_s}_{\mathcal{i}}$, we generate a legitimate signature ${\omega }_{\mathcal{i}}$ on $\mathcal{M}$ and send it to $\mathcal{A}$. The $\mathcal{A}$ then produces the modified message ${\mathcal{M}}^{\mathsf{\sigma }\mathrm{*}}$. To maintain security, we randomly select bit $\mathcal{c}$ from the set {0, 1}, which is unknown to us. Utilizing ${{x_s}_{\mathcal{i}}}_{\mathcal{c}}$, we construct a signature ${\omega }^{\mathrm{*}}$ on ${\mathcal{M}}^{\mathsf{\sigma }\mathrm{*}}$. We transmit ${\omega }^{\mathrm{*}}$ to $\mathcal{A}$. Upon receiving the signature, $\mathcal{A}$ analyzes it and guesses the value $\mathcal{c}$’ for $\mathcal{c}$, where $\mathcal{c}\mathcal{’}{\in }_{\mathcal{R}}\{0,1\}$. If $\mathcal{A}$ correctly determines that $\mathcal{c}$’ = $\mathcal{c}$, we consider it a failure. The probability of this undesirable scenario occurring is calculated as $\left(\frac{1}{\psi P}-\frac{1}{\psi -\sigma }\right)$. Therefore, $\mathcal{A}$ cannot exploit the randomized key generation and signing process to their advantage within a polynomial time frame and with a significant probability. Therefore, we can conclude that our protocol is robust against impersonation attacks.

2

Robustness against man-in-the-middle attacks

Claim 5.

An inside adversary is unable to launch a man-in-the-middle attack on the message delivered by another user to the trusted party. An inside adversary creates a legitimate message to launch this attack in place of the original message created by another user. Since the protocol demands a verification process between the two parties that are conversing, a man-in-the-middle cannot avoid the verification and continue to intercept the conversation.

Proof. 

We consider an inside adversary $\mathcal{H},$ who launches a man-in-the-middle attack. $\mathcal{H}$ records the message that was produced by another user. Assuming $\mathcal{H}$ is able to alter the message, the trusted party will verify the message after receiving it using a process identical to message authentication. Since Claim 1 states that it is impossible to fabricate a message, the amended message cannot satisfy the two verification equations:

$$e\left({\omega }_{2,}{g}^{x_s}\right)e\left({\omega }_{1,}{h}_1\right)e({\omega }_3,V)=e(\left(g^{x_t}\right),g),$$

(9)

$${\omega \prime }_5=H\left(\mathcal{m}\left|\left|{\omega }_1\right|\right|{\omega }_2\left|\left|{\omega }_3\right|\right|{\omega }_4\left|\left|H_1{\left(m\right)}^{{\omega }^6}{{\omega }_4}^{{\omega }^5}\right|\right|{{\omega }_1}^{{\omega }^6}{{\omega }_3}^{{\omega }^5}\right),$$

(10)

when the communication was delivered to the reliable party. By rejecting the altered message, the protocol will be secured from man-in-the-middle attacks. We may infer that our scheme is resistant to inside adversaries by combining Claims 4 and 5. □

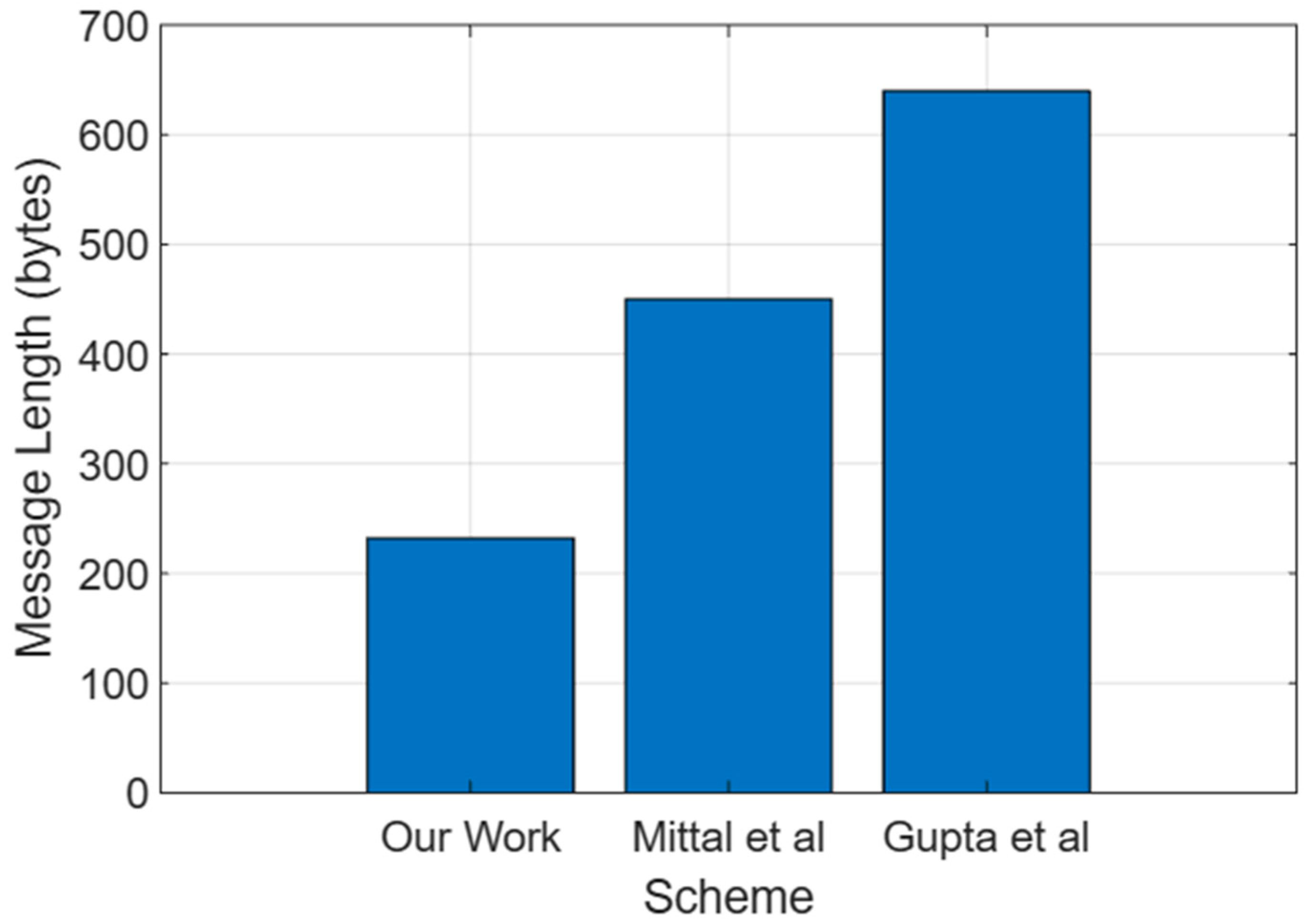
6.3. Performance Analysis

With reference to the existing schemes in [31,45], we compare the performance effectiveness of our proposed protocol in this section. Specifically, we conduct our comparison in three categories: message and signature sizes, computational expense, and computation time.

Message and signature sizes. We configured the element in ${\mathbb{G}}_1$ to be 160 bits long by selecting a suitable curve, such as the National Institute of Standards and Technology (NIST) curve, in order to give a typical 80 bit security level on a hardware platform consisting of an Intel I7-6700 and Windows 7 with 8G processor memory [55]. In our work, a broadcasted message consists of a payload, a time stamp, and a group ID. The length of user-generated messages with an 80 bit security level may be calculated as 100 + 2 + 128 + 2 = 232 bytes if the payload, a time stamp, and a group ID are each represented by 100 bytes, 2 bytes, and 2 bytes, respectively. In Gupta et al. [31], the length of the message is 640 bytes, while in Mittal et al. [45], the message size is 450 bytes. Therefore, compared to [31,45], our protocol successfully achieves lower communication costs. Figure 3 illustrates this.

Computational expense. By repeatedly running the bilinear pairing simulation trials and averaging the results [54],

Table 2. Average amount of time for implementation and operation.

Symbol	Description	Execution Time (ms)
${\mathcal{T}}_{\mathcal{P}\mathcal{B}}$	Bilinear pairing operation	5.5852
${\mathcal{T}}_{\mathcal{P}\mathcal{B}\_\mathcal{S}\mathcal{M}}$	Scalar multiplications in $\mathbb{G}$	0.817
${\mathcal{T}}_{\mathcal{H}}$	General hash function operation	0.0012
${\mathcal{T}}_{\mathcal{M}\mathcal{U}\mathcal{L}}$	Modular multiplication in $\mathbb{G}$	0.0119

provides information on the typical implementation time and operation execution schedule. We compare the current scheme in [31,45] and assess the computational expense of signature generation and verification in message broadcasts for $t=5$. We consider the two most expensive operations, which are scalar multiplication in $\mathbb{G}$ and pairing operations. We will concentrate on measuring the processing time required for signature generation and signature verification. The lengthy bilinear operation in the existing schemes [31,45] produces a comparable time overhead during the signature operation phase, which is one pairing and two scalar multiplications, while the signature verification procedure of our scheme only needs six scalar multiplications. Meanwhile, in the verification operation phase, our schemes perform one pairing and two scalar multiplication operations to verify the legitimacy of the message. These comparisons of signature and verification operations are summarized in Table 2. We note that the computational expense of our scheme is comparable with [31,45].

From the analysis above, our work achieves the lowest communication cost compared to [31,45] and outperforms [31] in terms of computing cost and time. Comparatively to [31,45], we also meet all security goals necessary for the secure group signature scheme, where the underlying work is based on general linear group over group rings. Overall performance is shown in Table 1 and

Table 3. Comparison of performance analyses.

Scheme	Signature Operation		Verification Operation
	Computational Cost	Computation Time (ms)	Computational Cost	Computation Time (ms)
Gupta et al. [31]	$1{\mathcal{T}}_{\mathcal{P}\mathcal{B}}+2.{\mathcal{T}}_{\mathcal{P}\mathcal{B}\_\mathcal{S}\mathcal{M}}+4{\mathcal{T}}_{\mathcal{H}}$	7.24	$1{\mathcal{T}}_{\mathcal{P}\mathcal{B}}+6.{\mathcal{T}}_{\mathcal{P}\mathcal{B}\_\mathcal{S}\mathcal{M}}$	10.49
Mittal et al. [45]	$1{\mathcal{T}}_{\mathcal{P}\mathcal{B}}+2.{\mathcal{T}}_{\mathcal{P}\mathcal{B}\_\mathcal{S}\mathcal{M}}+1{\mathcal{T}}_{\mathcal{H}}$	7.22	$1{\mathcal{T}}_{\mathcal{P}\mathcal{B}}+4{\mathcal{T}}_{\mathcal{P}\mathcal{B}\_\mathcal{S}\mathcal{M}}$	8.85
Our work	$6{\mathcal{T}}_{\mathcal{P}\mathcal{B}\_\mathcal{S}\mathcal{M}}+1{\mathcal{T}}_{\mathcal{M}\mathcal{U}\mathcal{L}}$	4.91	$1{\mathcal{T}}_{\mathcal{P}\mathcal{B}}+2{\mathcal{T}}_{\mathcal{P}\mathcal{B}\_\mathcal{S}\mathcal{M}}$	7.22

.

6.4. Simulation

In this part, we examine a simulation based on user interaction. Using the MATLAB R2021b platform, we assessed two key metrics for user communication, referred to as average message latency ${(MC}_u)$ and average message loss ratio ${(ML}_u)$. We consider the distribution of users and trusted parties to be random. We constructed our performance metric in such a way:

$${MC}_u=\frac{1}{N_u}{\sum }_{N=1}\left(\frac{1}{M_{sent}}{\sum }_{m=1}^{M_{sent}}\left(T_{sign}+\frac{1}{M_{received}}\right)\right),$$

$${ML}_u=1-\frac{1}{N_u}{\sum }_{N=1}^{N_u}\left(\frac{N_u-M_{received})\times T_{verify}}{N_{\mathrm{T}}\times N_u}\right),$$

where $N_u$ and $N_{\mathrm{T}}$, respectively, stand for the numbers of users and trusted parties. As for $M_{sent}$ and $M_{received}$, the former refers to the quantity of messages sent and received, respectively. The total time for signing is shown by $T_{sign}$, while the total time for verifying is indicated by $T_{verify}$. The simulations run 15 min each for seven attempts. We simulate our protocol in the following aspects:

• Message latency with respect to user count: the time needed to carry out cryptographic procedures to authenticate broadcasted messages;
• Message loss ratio with respect to number of users: since there are more revoked users on the $TP$’s database, message delivery times are becoming slower.

Figure 4 and Figure 5 depict the simulation results. We set our threshold in this simulation at $\left(t\right)=20,$ where $\left(t\right)$ represents the message’s degree of reliability and integrity. The reliability of the message may be demonstrated by a user who experiences a similar incident nearby and believes in the broadcasted safety message.

Figure 4 shows the simulation’s average message latency in proportion to the number of users. With a much longer message delay, fewer users will be able to benefit from the authenticated message, which will have an impact on the efficiency of the protocol. We consider that each user will only broadcast one message. We note that Mittal et al. [45] and Gupta et al. [31] approaches are followed by our work in producing the lowest message delay. We believe this is reasonable given that nearby users may get additional validated copies of the same message up to the stated level. This demonstrates that our suggested protocol has a competitive edge over other protocols.

Figure 5 displays the average message loss ratio simulation result with regard to user count. The average message loss proves the reliability and integrity of messages and the validity of the protocol. We discover that, up to a certain level, the average message loss also rises as the number of users expands. We find that this ability is increased when a significant number of messages are lost, since a huge number of the messages are regularly transmitted. In terms of message loss, our method seems to be equivalent to and superior to Mittal et al. [45] and Gupta et al. [31].

7. Conclusions

In this study, we have designed a novel, secure, and efficient group signature scheme that considers the imperative objective of satisfying the conflicting security goals of message trustworthiness, privacy, and accountability. As far as we are aware, this is the first comprehensive framework employing general linear group-over-group ring that exists in the literature and serves as a guideline to design a future group signature scheme based on general linear group-over-group ring. The feasibility and applicability of our protocol in practical implementation are shown through simulations of our work.

Extending the existing protocol to integrate with privacy-preserving applications, for instance, e-commerce systems, vehicle safety communication (VSC), key-card access systems, and infotainment, would be interesting for future development. A future study will focus on how to accomplish this without jeopardizing security. Moreover, it would be interesting to explore the formal definitions of the rich and diverse security properties such as IND-CPA or IND-CCA desired in group signature schemes over group rings and give rigorous proofs of the security of the proposed protocol.