Modal Reconstruction Based on Arbitrary High-Order Zernike Polynomials for Deflectometry
Abstract
:1. Introduction
2. Principle and Method
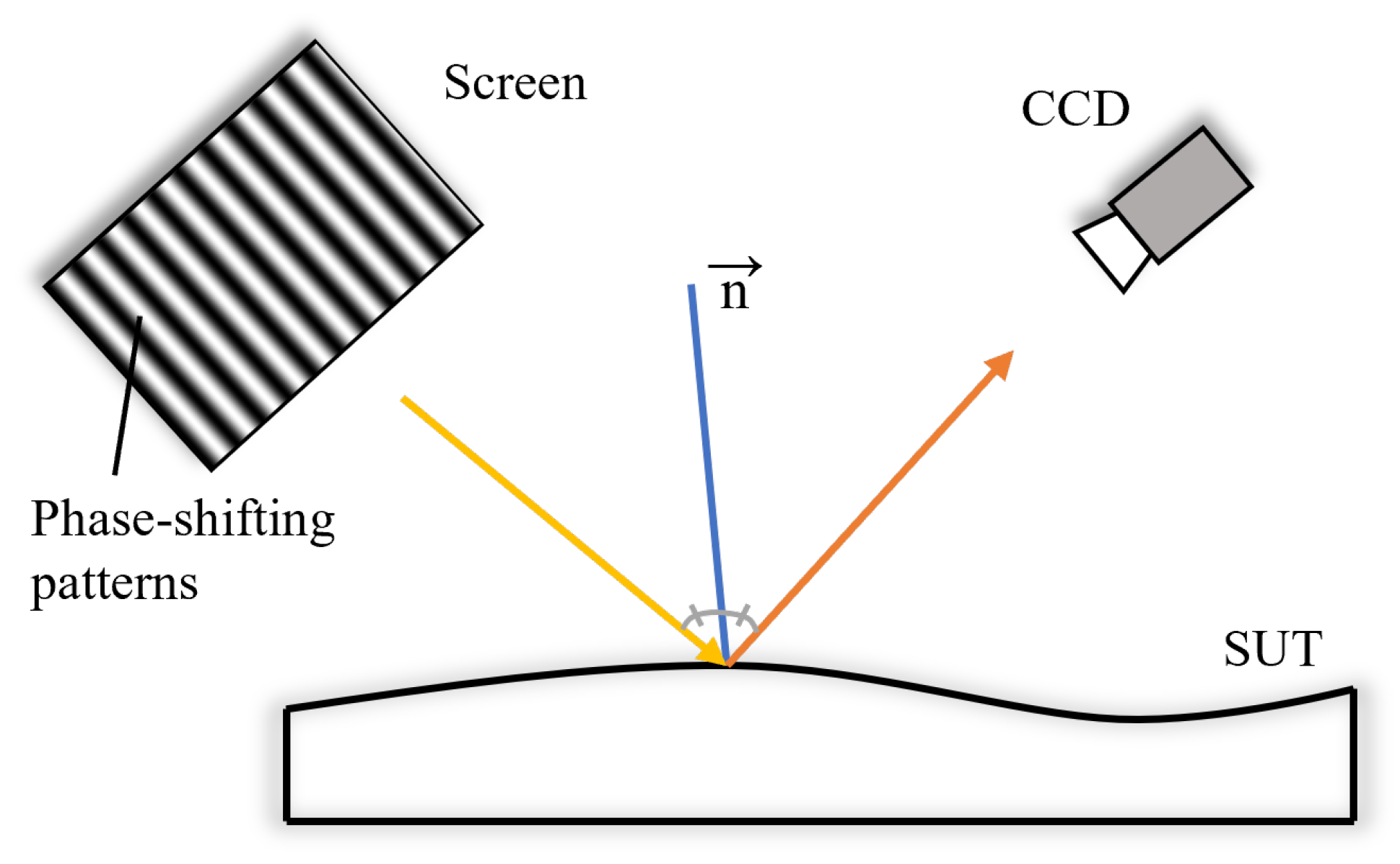
2.1. Deflectometry Principle
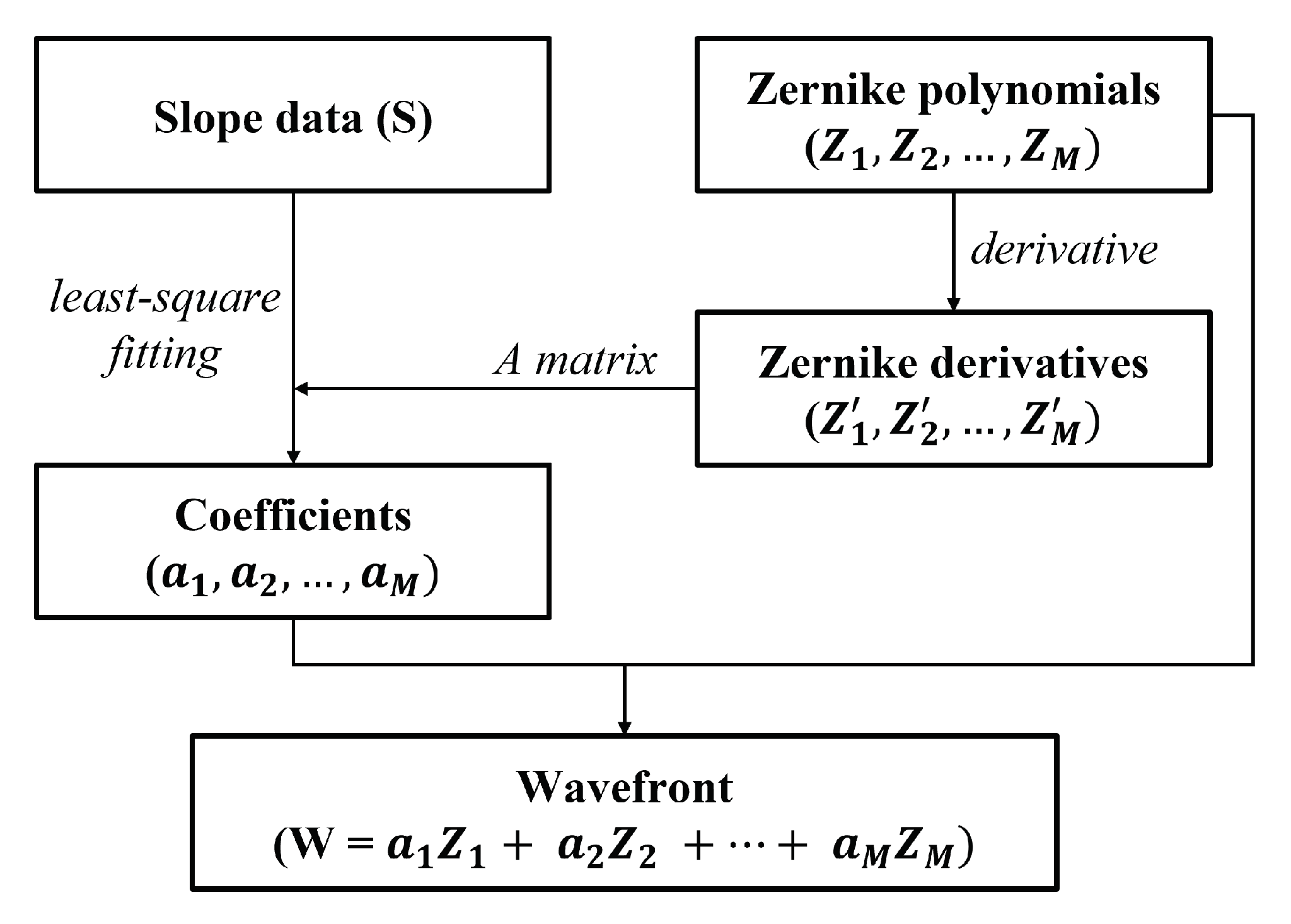
2.2. Reconstruction Using Zernike Polynomials
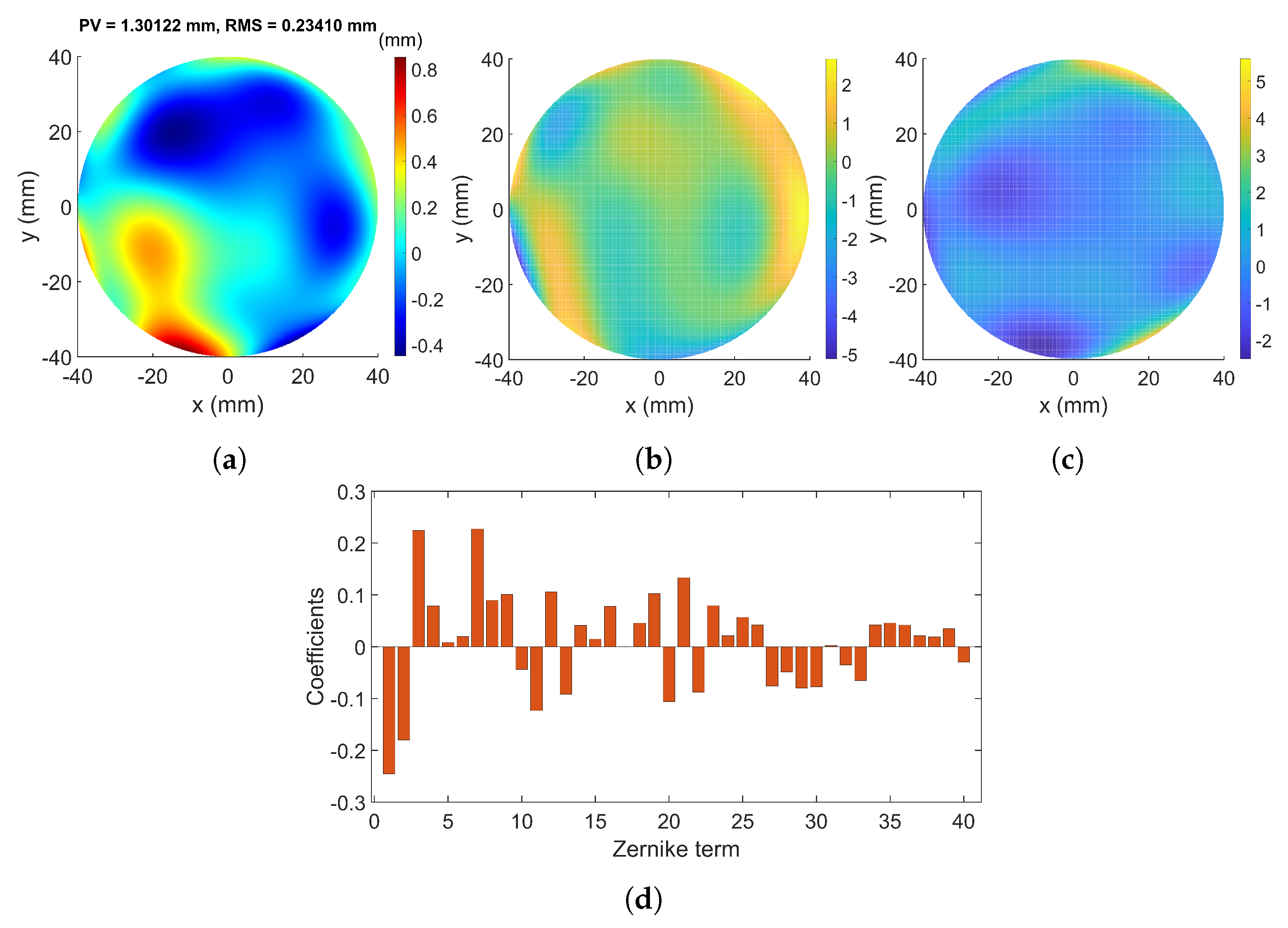
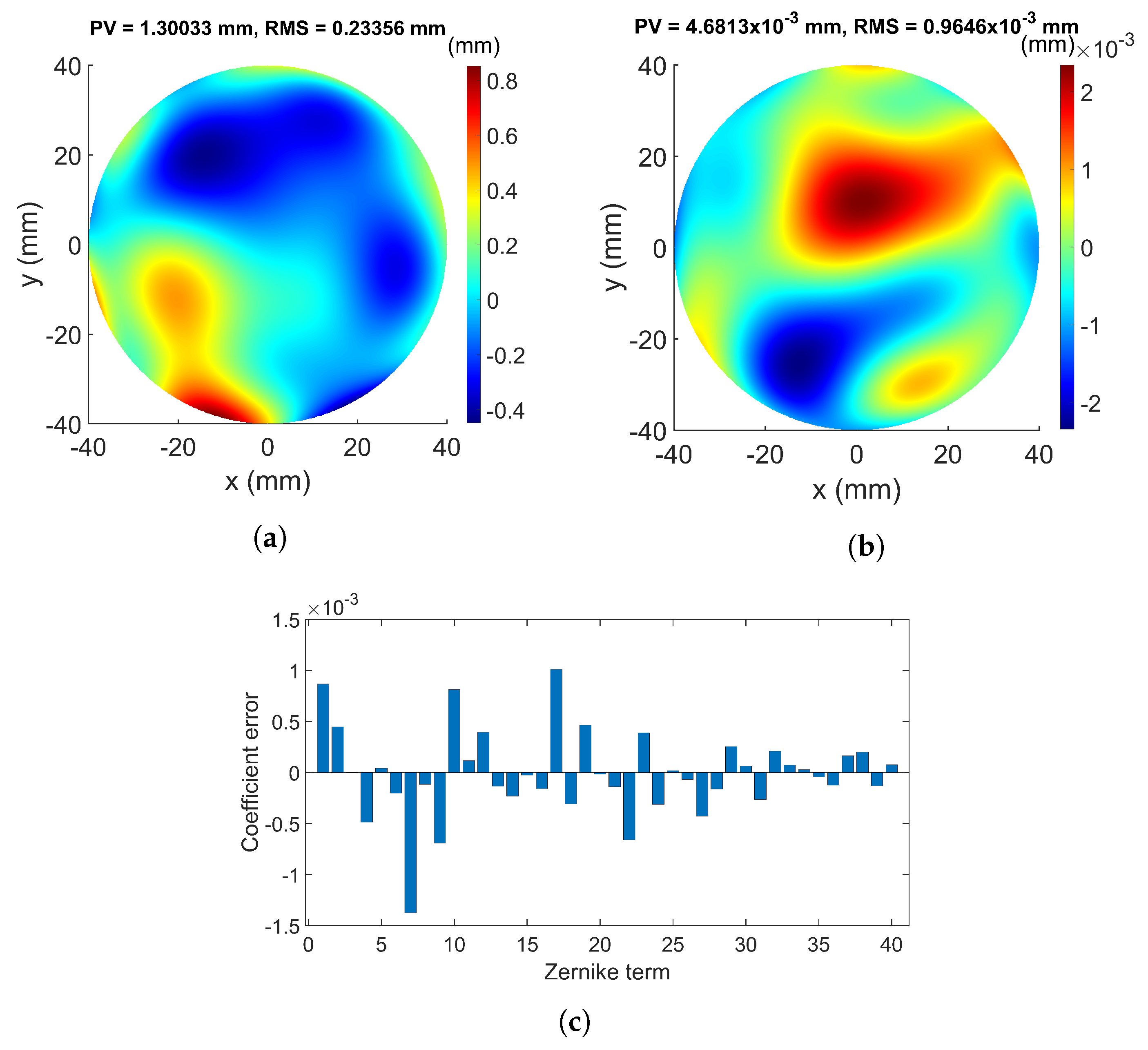
3. Simulation
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| PMD | Phase Measuring Deflectometry |
| SUT | Surface Under Test |
| CCD | Charge-Coupled Device |
| LCD | Liquid Crystal Display |
| SNR | Signal-to-Noise Ratio |
| RMS | Root Mean Square |
| PV | Peak to Valley |
References
- Huang, L.; Idir, M.; Zuo, C.; Asundi, A. Review of phase measuring deflectometry. Opt. Lasers Eng. 2018, 107, 247–257. [Google Scholar] [CrossRef]
- Leopold, J.; Günther, H.; Leopold, R. New developments in fast 3D-surface quality control. Measurement 2003, 33, 179–187. [Google Scholar] [CrossRef]
- Wolf, K.; Roller, D.; Schäfer, D. An approach to computer-aided quality control based on 3D coordinate metrology. J. Mater. Process. Technol. 2000, 107, 96–110. [Google Scholar] [CrossRef]
- Knauer, M.C.; Kaminski, J.; Hausler, G. Phase measuring deflectometry: A new approach to measure specular free-form surfaces. In Proceedings of the Optical Metrology in Production Engineering, Strasbourg, France, 27–30 April 2004; SPIE: Bellingham, WA, USA, 2004; Volume 5457, pp. 366–376. [Google Scholar]
- Sironi, G.; Canestrari, R.; Pareschi, G.; Pelliciari, C. Deflectometry for optics evaluation: Free form segments of polynomial mirror. In Proceedings of the Advances in Optical and Mechanical Technologies for Telescopes and Instrumentation, Montreal, QB, Canada, 28 July 2014; SPIE: Bellingham, WA, USA, 2014; Volume 9151, pp. 258–270. [Google Scholar]
- Wang, D.; Xu, P.; Wu, Z.; Fu, X.; Wu, R.; Kong, M.; Liang, J.; Zhang, B.; Liang, R. Simultaneous multisurface measurement of freeform refractive optics based on computer-aided deflectometry. Optica 2020, 7, 1056–1064. [Google Scholar] [CrossRef]
- Carbone, V.; Carocci, M.; Savio, E.; Sansoni, G.; De Chiffre, L. Combination of a vision system and a coordinate measuring machine for the reverse engineering of freeform surfaces. Int. J. Adv. Manuf. Technol. 2001, 17, 263–271. [Google Scholar] [CrossRef]
- Zhang, Z.; Chang, C.; Liu, X.; Li, Z.; Shi, Y.; Gao, N.; Meng, Z. Phase measuring deflectometry for obtaining 3D shape of specular surface: A review of the state-of-the-art. Opt. Eng. 2021, 60, 020903. [Google Scholar] [CrossRef]
- Southwell, W.H. Wave-front estimation from wave-front slope measurements. JOsA 1980, 70, 998–1006. [Google Scholar] [CrossRef]
- Li, G.; Li, Y.; Liu, K.; Ma, X.; Wang, H. Improving wavefront reconstruction accuracy by using integration equations with higher-order truncation errors in the Southwell geometry. JOsA A 2013, 30, 1448–1459. [Google Scholar] [CrossRef]
- Ren, H.; Gao, F.; Jiang, X. Improvement of high-order least-squares integration method for stereo deflectometry. Appl. Opt. 2015, 54, 10249–10255. [Google Scholar] [CrossRef]
- Ren, H.; Gao, F.; Jiang, X. Least-squares method for data reconstruction from gradient data in deflectometry. Appl. Opt. 2016, 55, 6052–6059. [Google Scholar] [CrossRef]
- Mochi, I.; Goldberg, K.A. Modal wavefront reconstruction from its gradient. Appl. Opt. 2015, 54, 3780–3785. [Google Scholar] [CrossRef]
- Dai, G.M. Modal wave-front reconstruction with Zernike polynomials and Karhunen–Loève functions. JOsA A 1996, 13, 1218–1225. [Google Scholar] [CrossRef]
- Dai, F.; Tang, F.; Wang, X.; Sasaki, O.; Feng, P. Modal wavefront reconstruction based on Zernike polynomials for lateral shearing interferometry: Comparisons of existing algorithms. Appl. Opt. 2012, 51, 5028–5037. [Google Scholar] [CrossRef]
- Kewei, E.; Zhang, C.; Li, M.; Xiong, Z.; Li, D. Wavefront reconstruction algorithm based on Legendre polynomials for radial shearing interferometry over a square area and error analysis. Opt. Express 2015, 23, 20267–20279. [Google Scholar] [CrossRef]
- Cuc, N.T.K.; Tien, V.D.; Binh, C.X.; Dung, V.T. Research and Design of Compact Equipment Using Phase_Shifting Deflectometry Apply in Optical Surface Measurement. In Proceedings of the Regional Conference in Mechanical Manufacturing Engineering, Hanoi, Vietnam, 10–12 December 2021; Springer: Berlin/Heidelberg, Germany, 2021; pp. 905–912. [Google Scholar]
- Zuo, C.; Feng, S.; Huang, L.; Tao, T.; Yin, W.; Chen, Q. Phase shifting algorithms for fringe projection profilometry: A review. Opt. Lasers Eng. 2018, 109, 23–59. [Google Scholar] [CrossRef]
- Ghiglia, D.C.; Pritt, M.D. Two-Dimensional Phase Unwrapping: Theory, Algorithms, and Software, 1st ed.; Wiely-Interscience: Hoboken, NJ, USA, 1998. [Google Scholar]
- Liu, K.; Wang, Y.; Lau, D.L.; Hao, Q.; Hassebrook, L.G. Dual-frequency pattern scheme for high-speed 3-D shape measurement. Opt. Express 2010, 18, 5229–5244. [Google Scholar] [CrossRef]
- Zuo, C.; Chen, Q.; Gu, G.; Feng, S.; Feng, F. High-speed three-dimensional profilometry for multiple objects with complex shapes. Opt. Express 2012, 20, 19493–19510. [Google Scholar] [CrossRef]
- Zuo, C.; Chen, Q.; Gu, G.; Feng, S.; Feng, F.; Li, R.; Shen, G. High-speed three-dimensional shape measurement for dynamic scenes using bi-frequency tripolar pulse-width-modulation fringe projection. Opt. Lasers Eng. 2013, 51, 953–960. [Google Scholar] [CrossRef]
- Nguyen, M.T.; Ghim, Y.S.; Rhee, H.G. Single-shot deflectometry for dynamic 3D surface profile measurement by modified spatial-carrier frequency phase-shifting method. Sci. Rep. 2019, 9, 3157. [Google Scholar] [CrossRef]
- Li, J.; Su, X.; Guo, L. Improved Fourier transform profilometry for the automatic measurement of 3D object shapes. Opt. Eng. 1990, 29, 1439–1444. [Google Scholar]
- Huang, P.S.; Hu, Q.J.; Chiang, F.P. Double three-step phase-shifting algorithm. Appl. Opt. 2002, 41, 4503–4509. [Google Scholar] [CrossRef] [PubMed]
- Zhang, S.; Yau, S.T. High-speed three-dimensional shape measurement system using a modified two-plus-one phase-shifting algorithm. Opt. Eng. 2007, 46, 113603. [Google Scholar] [CrossRef]
- Petz, M.; Tutsch, R. Reflection grating photogrammetry: A technique for absolute shape measurement of specular free-form surfaces. In Proceedings of the Optical Manufacturing and Testing VI, San Diego, CA, USA, 18 August 2005; SPIE: Bellingham, WA, USA, 2005; Volume 5869, pp. 355–366. [Google Scholar]
- Olesch, E.; Faber, C.; Häusler, G. Deflectometric Self-Calibration for arbitrary specular surfaces. In Proceedings of the Deutsche Gesellschaft fur angewandte Optik, Ilmenau, Germany; 2011; p. 27. [Google Scholar]
- Wang, C.; Chen, N.; Heidrich, W. Towards self-calibrated lens metrology by differentiable refractive deflectometry. Opt. Express 2021, 29, 30284–30295. [Google Scholar] [CrossRef] [PubMed]
- Dai, G.M. Wavefront Optics for Vision Correction; SPIE press: Bellingham, WA, USA, 2008; Volume 179. [Google Scholar]
- Niu, K.; Tian, C. Zernike polynomials and their applications. J. Opt. 2022, 24, 123001. [Google Scholar] [CrossRef]
- Dai, F.; Zheng, Y.; Bu, Y.; Wang, X. Zernike polynomials as a basis for modal fitting in lateral shearing interferometry: A discrete domain matrix transformation method. Appl. Opt. 2016, 55, 5884–5891. [Google Scholar] [CrossRef]
- Ye, J.; Wang, W.; Gao, Z.; Liu, Z.; Wang, S.; Benítez, P.; Miñano, J.C.; Yuan, Q. Modal wavefront estimation from its slopes by numerical orthogonal transformation method over general shaped aperture. Opt. Express 2015, 23, 26208–26220. [Google Scholar] [CrossRef]
- Lane, R.; Tallon, M. Wave-front reconstruction using a Shack–Hartmann sensor. Appl. Opt. 1992, 31, 6902–6908. [Google Scholar] [CrossRef]
- Tarabocchia, M.; Holly, S. Dynamic Hartmann wavefront sensor in applications. In Proceedings of the Laser Diagnostics, Boston, MA, USA, 19 November 1982; SPIE: Bellingham, WA, USA, 1982; Volume 343, pp. 93–100. [Google Scholar]
- Strojnik, M.; Paez, G.; Mantravadi, M. Lateral shear interferometers. Opt. Shop Test. 2007, 5, 122–184. [Google Scholar]
- Chanteloup, J.C. Multiple-wave lateral shearing interferometry for wave-front sensing. Appl. Opt. 2005, 44, 1559–1571. [Google Scholar] [CrossRef]
- Shen, W.; Chang, M.w.; Wan, D.S. Zernike polynomial fitting of lateral shearing interferometry. Opt. Eng. 1997, 36, 905–913. [Google Scholar] [CrossRef]
- Ragazzoni, R. Pupil plane wavefront sensing with an oscillating prism. J. Mod. Opt. 1996, 43, 289–293. [Google Scholar] [CrossRef]


| j | m | n | |||
|---|---|---|---|---|---|
| 1 | 0 | 0 | 1 | 0 | 0 |
| 2 | 1 | −1 | 0 | 2 | |
| 3 | 1 | 1 | 2 | 0 | |
| 4 | 2 | −2 | |||
| 5 | 2 | 0 | |||
| 6 | 2 | 2 | |||
| 7 | 3 | −3 | |||
| 8 | 3 | −1 | |||
| 9 | 3 | 1 | |||
| 10 | 3 | 3 | |||
| 11 | 4 | −4 | |||
| 12 | 4 | −2 | |||
| 13 | 4 | 0 | |||
| 14 | 4 | 2 | |||
| 15 | 4 | 4 |
| PV Error (mm) | RMS Error (mm) | |
|---|---|---|
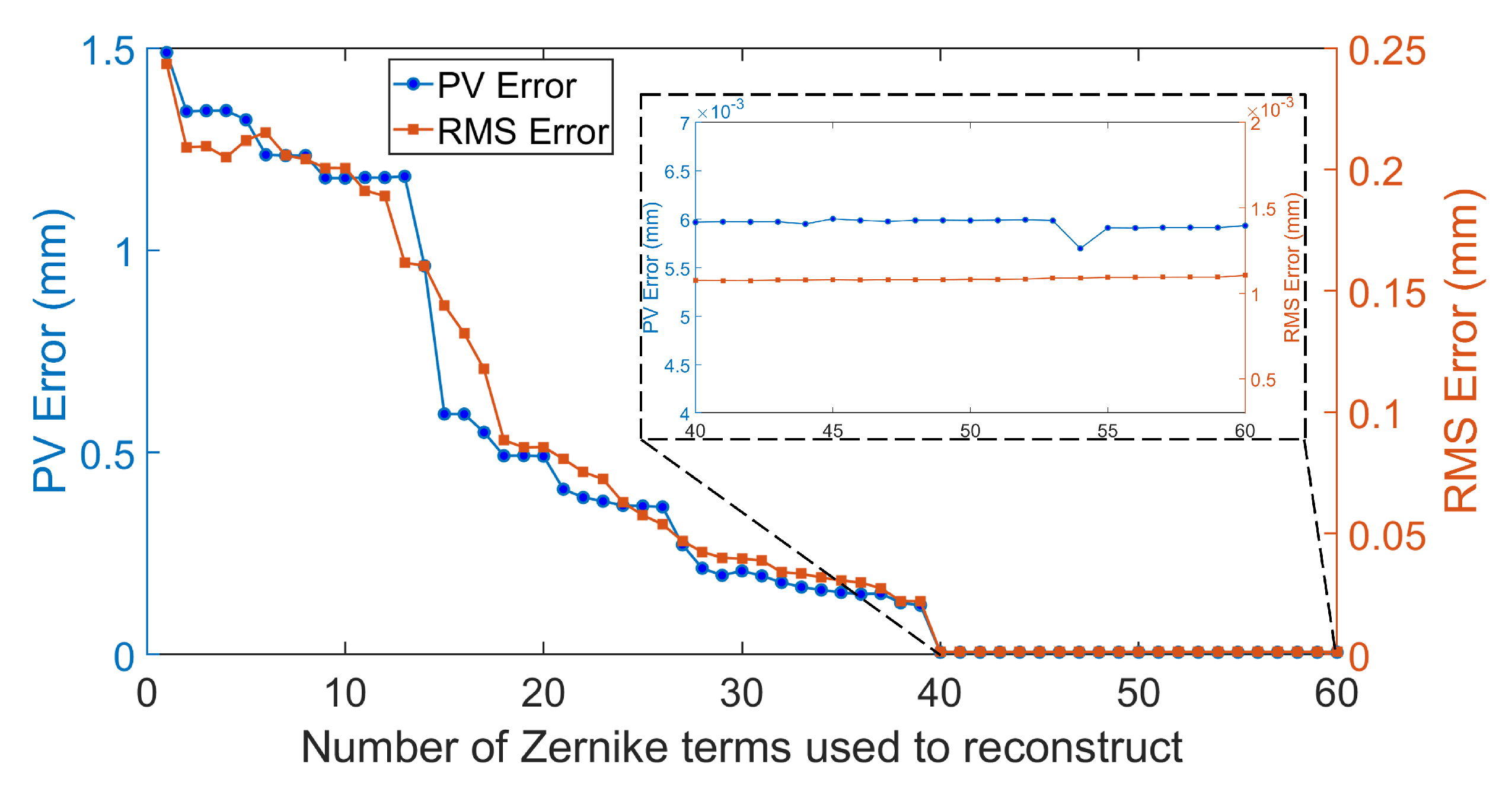
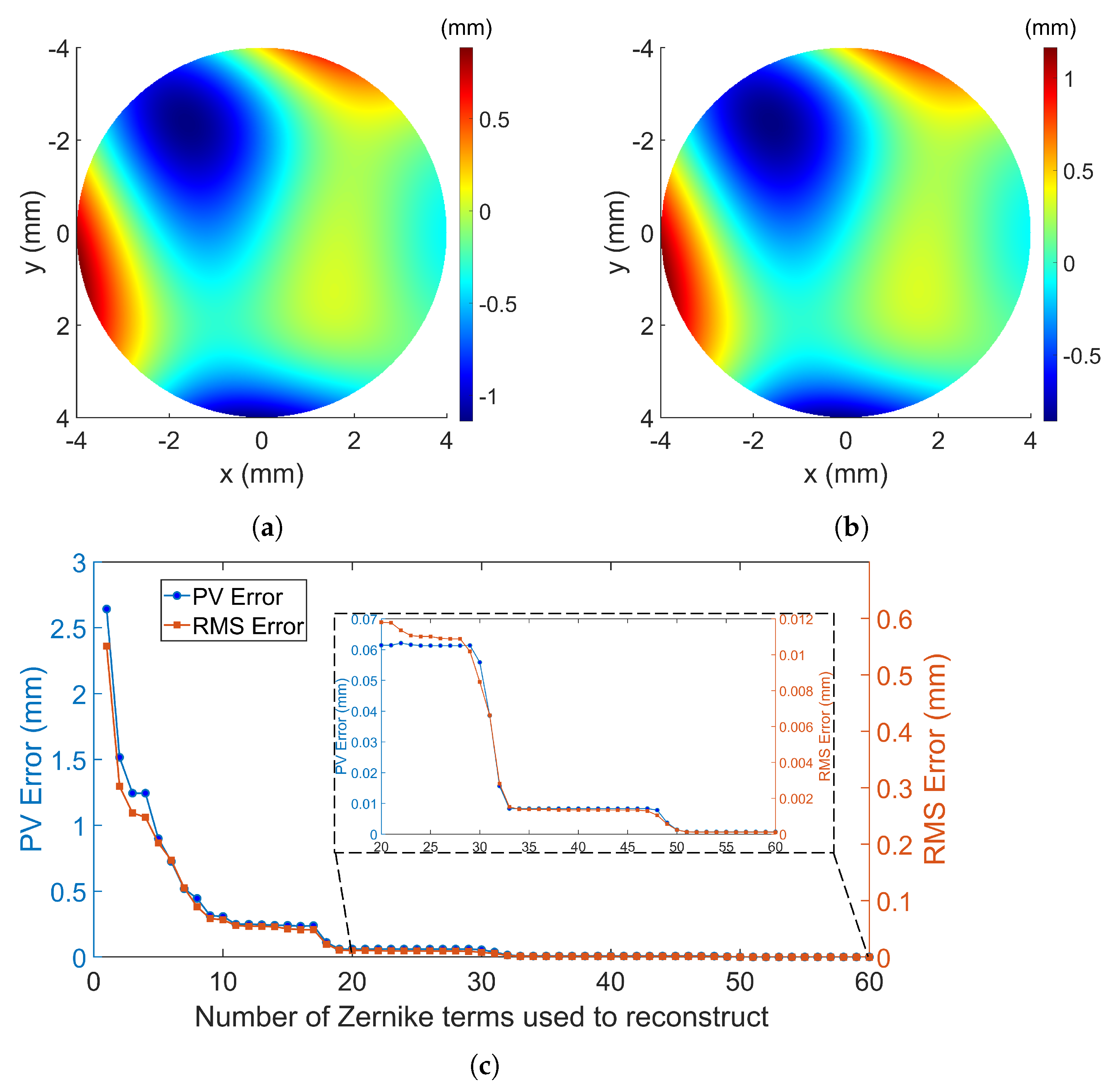
| 22 terms used | 0.0659 | 0.0122 |
| 37 terms used | 0.0085 | 0.0014 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Nguyen, D.-T.; Nguyen, K.C.T.; Cao, B.X.; Tran, V.-T.; Vu, T.; Bui, N.-T. Modal Reconstruction Based on Arbitrary High-Order Zernike Polynomials for Deflectometry. Mathematics 2023, 11, 3915. https://doi.org/10.3390/math11183915
Nguyen D-T, Nguyen KCT, Cao BX, Tran V-T, Vu T, Bui N-T. Modal Reconstruction Based on Arbitrary High-Order Zernike Polynomials for Deflectometry. Mathematics. 2023; 11(18):3915. https://doi.org/10.3390/math11183915
Chicago/Turabian StyleNguyen, Duy-Thai, Kim Cuc Thi Nguyen, Binh X. Cao, Van-Thuc Tran, Tiendung Vu, and Ngoc-Tam Bui. 2023. "Modal Reconstruction Based on Arbitrary High-Order Zernike Polynomials for Deflectometry" Mathematics 11, no. 18: 3915. https://doi.org/10.3390/math11183915
APA StyleNguyen, D.-T., Nguyen, K. C. T., Cao, B. X., Tran, V.-T., Vu, T., & Bui, N.-T. (2023). Modal Reconstruction Based on Arbitrary High-Order Zernike Polynomials for Deflectometry. Mathematics, 11(18), 3915. https://doi.org/10.3390/math11183915








