Asymptotic Behavior of Certain Non-Autonomous Planar Competitive Systems of Difference Equations

Abstract

This paper investigates the dynamics of non-autonomous competitive systems of difference equations with asymptotically constant coefficients. We are mainly interested in global attractivity results for such systems and the application of such results to the evolutionary population of competition models of two species.

1. Introduction

In this paper, we give some global attractivity results for a non-autonomous competitive systems of difference equations,

$$\begin{array}{ccc}\hfill x_{n+1}& =& {\displaystyle a_{n}f(x_n,y_n)}\hfill \\ \hfill y_{n+1}& =& {\displaystyle b_{n}g(x_n,y_n),n=0,1,\dots ,}\hfill \end{array}$$

(1)

where f is non-decreasing in the first variable and is non-increasing in the second variable, and g is non-increasing in the first variable and is non-decreasing in the second variable. Here, $a_n$ and $b_n$ are sequences which are assumed to be asymptotically constant. Our results are motivated by the results for global attractivity of non-autonomous systems of difference equations via linearization in [1], which have significant applications in the mathematical biology of single species [2]. Our techniques are based on difference inequalities, which was a major method used in [2]. The obtained results hold when the limiting system of difference equations is in a hyperbolic case and cannot be extended to the non-hyperbolic case as in [3]. Now we extend the applications from single species models in [2] to the case of two species competition models. Then we apply our results to evolutionary population competition models, which have been considered lately by Cushing, Elaydi, and others, see [4,5,6,7,8,9,10]. A typical result in [2], which will be extended to the competitive planar systems is Theorem 1 [2]:

Theorem 1. 

Consider the difference equation

$$x_{n+1}=a_{n}f\left(x_n\right),n=0,1,\dots ,$$

(2)

where f is a continuous, nondecreasing function, ${\lim }_{n\to \infty }{a}_n=a$, and the limiting difference equation is

$$y_{n+1}=af\left(y_n\right),n=0,1,\dots .$$

(3)

Assume that there exists ${ϵ}_0>0$ such that every solution of difference equation

$$y_{n+1}=Af\left(y_n\right),n=0,1,\dots$$

converges to a constant solution ${\overline{y}}_A$ for every $A\in (a-{ϵ}_0,a+{ϵ}_0)$. If

$$\underset{A\to a}{\lim }{\overline{y}}_A=\overline{y},$$

then every solution of the difference Equation (2) satisfies

$$\underset{n\to \infty }{\lim }{x}_n=\overline{y}.$$

The global attractivity results for the first order autonomous difference equation that will be used in simulations in this paper were proved by Elaydi and Sacker [11] and Singer [12].

Theorem 2 

([11]). Let $f:[a,b]\to [a,b]$ be a continuous function in equation

$$x_{n+1}=f\left(x_n\right),n=0,1,\dots .$$

(4)

Then, the following statements are equivalent:

(a)  

Equation (4) has no minimal period-two solutions in $(a,b)$.

(b)  

Every solution of Equation (4) that starts in $(a,b)$ converges.

As an immediate consequence of the Theorem 2, we have the following important result on global asymptotic stability.

Corollary 1 

([11]). Let $\overline{x}$ be a fixed point of a continuous map f on the closed and bounded interval $I=[a,b]$. Then, $\overline{x}$ is globally asymptotically stable relative to $(a,b)$ if and only if

$$f^2\left(x\right)=f\left(f\left(x\right)\right)>x,x<\overline{x}andf\left(f\left(x\right)\right)<x,x>\overline{x},$$

(5)

for all $x\in (a,b)\setminus \left\{\overline{x}\right\}$, and $a,b$ are not periodic points.

The next result, known as the Singer theorem, see [12], is a very useful and efficient tool for establishing the global dynamics of first order difference equations.

Theorem 3. 

Assume that f is $C^3$ with an equilibrium point $\overline{x}\in [\alpha ,\beta ]$ such that f satisfies the negative feedback condition, that is, $f\left(x\right)>x$ if $x<\overline{x}$ and $f\left(x\right)<x$ if $x>\overline{x}$. Assuming that the Schwarzian derivative

$$Sf\left(x\right)=\frac{f^{‴}\left(x\right)}{f^{\prime }\left(x\right)}-\frac{3}{2}{\left(\frac{f^{″}\left(x\right)}{f^{\prime }\left(x\right)}\right)}^2<0$$

for all $x\in [\alpha ,\beta ]$, then if $|f^{\prime }\left(\overline{x}\right)|\le 1$, then $\overline{x}$ is globally asymptotically stable. Now, condition $|f^{\prime }\left(\overline{x}\right)|\le 1$ is equivalent to local stability or non-hyperbolicity of the equilibrium $\overline{x}$.

Another result we use is the following result from [13], Theorem 1.18:

Theorem 4. 

Let $f:[a,b]\to [a,b]$ be a continuous, non-decreasing function in Equation (4). Then every solution is monotonic and so it converges to an equilibrium.

In this paper, we will use the so-called “north-east” partial ordering of the space ${\mathbb{R}}_{+}^2$ and defined it in the following way:

$$X_n=\left[\begin{array}{c}{x}_n^{\left(1\right)}\\ x_n^{\left(2\right)}\end{array}\right]{\preccurlyeq }_{ne}{Y}_n=\left[\begin{array}{c}{y}_n^{\left(1\right)}\\ y_n^{\left(2\right)}\end{array}\right]⟺\left(x_n^{\left(1\right)}\le y_n^{\left(1\right)}\mathrm{and}{x}_n^{\left(2\right)}\le y_n^{\left(2\right)}\right),$$

and the so-called ”south-east” partial ordering of the space ${\mathbb{R}}_{+}^2$ defined by

$$X_n=\left[\begin{array}{c}{x}_n^{\left(1\right)}\\ x_n^{\left(2\right)}\end{array}\right]{\preccurlyeq }_{se}{Y}_n=\left[\begin{array}{c}{y}_n^{\left(1\right)}\\ y_n^{\left(2\right)}\end{array}\right]⟺\left(x_n^{\left(1\right)}\le y_n^{\left(1\right)}\mathrm{and}{x}_n^{\left(2\right)}\ge y_n^{\left(2\right)}\right).$$

This paper is organized as follows. The next section contains the main results on asymptotic dynamics of non-autonomous systems of difference equations of competitive type in state variables in the plane. The final section presents the application of the main results to the evolutionary (Darwinian) systems of difference equations when, in addition to state variables, we introduce equations or systems of equations that describe dynamics of the traits, which affect the coefficients of state variables.

2. Main Results

This section contains our main results.

Lemma 1. 

Assume that

(a) $F:{\mathbb{R}}_{+}^2\to {\mathbb{R}}_{+}^2$, $F=\left[\begin{array}{c}f\\ g\end{array}\right]$ is a competitive map, i.e., $f,g:{\mathbb{R}}_{+}^2\to \mathbb{R}$ are the functions with the following properties:

(i) f is non-decreasing in the first variable and is non-increasing in the second variable,

(ii) g is non-increasing in the first variable and and is non-decreasing in the second variable;

(b) $\left\{X_n\right\}$, $\left\{Y_n\right\}$, $\left\{Z_n\right\}$ are sequences of the real components in ${\mathbb{R}}_{+}^2$ such that $X_0{\preccurlyeq }_{se}{Y}_0{\preccurlyeq }_{se}{Z}_0$ and

$$\left.\begin{array}{c}{X}_{n+1}{\preccurlyeq }_{se}F\left(X_n\right)\\ Y_{n+1}=F\left(Y_n\right)\\ Z_{n+1}{\succcurlyeq }_{se}F\left(Z_n\right)\end{array}\right\},n=0,1,2,\cdots .$$

Then,

$$X_n{\preccurlyeq }_{se}{Y}_n{\preccurlyeq }_{se}{Z}_n,n=0,1,2,\cdots .$$

(6)

Proof. 

The proof follows by induction. Since

$$X_0{\preccurlyeq }_{se}{Y}_0{\preccurlyeq }_{se}{Z}_0⟺\left\{x_0^{\left(1\right)}\le y_0^{\left(1\right)}\le z_0^{\left(1\right)}\mathrm{and}{x}_0^{\left(2\right)}\ge y_0^{\left(2\right)}\ge z_0^{\left(2\right)}\right\},$$

by using properties of monotonicity of the functions f and g, we obtain

$$\begin{array}{ccc}\hfill x_1^{\left(1\right)}& \le & f\left(x_0^{\left(1\right)},x_0^{\left(2\right)}\right)\le f\left(y_0^{\left(1\right)},y_0^{\left(2\right)}\right)=y_1^{\left(1\right)}\le f\left(z_0^{\left(1\right)},z_0^{\left(2\right)}\right)=z_1^{\left(1\right)}\hfill \\ \hfill x_1^{\left(2\right)}& \ge & g\left(x_0^{\left(1\right)},x_0^{\left(2\right)}\right)\ge g\left(y_0^{\left(1\right)},y_0^{\left(2\right)}\right)=y_1^{\left(1\right)}\ge g\left(z_0^{\left(1\right)},z_0^{\left(2\right)}\right)=z_1^{\left(1\right)},\hfill \end{array}$$

i.e.,

$$X_1{\preccurlyeq }_{se}{Y}_1{\preccurlyeq }_{se}{Z}_1.$$

Analogously, the proof that $X_2{\preccurlyeq }_{se}{Y}_2{\preccurlyeq }_{se}{Z}_2$ follows in the same fashion, and so does the proof of (6). □

Theorem 5. 

Consider the following non-autonomous system of difference equations:

$$X_{n+1}=\left[\begin{array}{c}{a}_{n}f\left(x_n,y_n\right)\\ b_{n}g\left(x_n,y_n\right)\end{array}\right],n=0,1,\cdots ,$$

(7)

where $A_n=\left[\begin{array}{c}{a}_n\\ b_n\end{array}\right]$ and $F=\left[\begin{array}{c}f\\ g\end{array}\right]:{\mathbb{R}}_{+}^2\to {\mathbb{R}}_{+}^2$ is a competitive map. Assume that

$$\underset{n\to \infty }{\lim }{A}_n=\underset{n\to \infty }{\lim }\left[\begin{array}{c}{a}_n\\ b_n\end{array}\right]=\left[\begin{array}{c}\underset{n\to \infty }{\lim }{a}_n\\ \underset{n\to \infty }{\lim }{b}_n\end{array}\right]=\left[\begin{array}{c}a\\ b\end{array}\right]=A,$$

and let

$$Y_{n+1}=\left[\begin{array}{c}af\left(u_n,v_n\right)\\ bg\left(u_n,v_n\right)\end{array}\right],n=0,1,\cdots ,$$

be the limiting system of difference equations of (7). Also, assume that there exists ${\epsilon }_{\mathbf{0}}=\left[\begin{array}{c}{\epsilon }_0^{\left(1\right)}\\ {\epsilon }_0^{\left(2\right)}\end{array}\right]$${\succ }_{ne}\left[\begin{array}{c}0\\ 0\end{array}\right]$ such that every solution of the system

$$Y_{n+1}=\left[\begin{array}{c}\alpha f\left(u_n,v_n\right)\\ \beta g\left(u_n,v_n\right)\end{array}\right],n=0,1,\cdots$$

converges to a constant ${\overline{Y}}_{{\mathit{A}}_{\epsilon }}=\left[\begin{array}{c}{\overline{x}}_{{\mathit{A}}_{\epsilon }}\\ {\overline{y}}_{{\mathit{A}}_{\epsilon }}\end{array}\right]$ for every ${\mathit{A}}_{\epsilon }=\left[\begin{array}{c}\alpha \\ \beta \end{array}\right]$, $\alpha \in \left(a-{\epsilon }_0^{\left(1\right)},a+{\epsilon }_0^{\left(1\right)}\right)$, $\beta \in \left(b-{\epsilon }_0^{\left(2\right)},b+{\epsilon }_0^{\left(2\right)}\right)$.

If

$$\underset{{\mathit{A}}_{\epsilon }\to A}{\lim }{\overline{Y}}_{{\mathit{A}}_{\epsilon }}=\overline{Y},$$

(8)

then every solution of the system (7) satisfies

$$\underset{n\to \infty }{\lim }{X}_n=\overline{Y}.$$

Proof. 

For arbitrary ${\epsilon }_1>0$ and ${\epsilon }_2>0$ there exists $N=N\left({\epsilon }_1,{\epsilon }_2\right)$ such that for $n\ge N$ the following

$$\begin{array}{ccc}\hfill a-{\epsilon }_1& <& a_n<a+{\epsilon }_1,\hfill \\ \hfill b-{\epsilon }_2& <& b_n<b+{\epsilon }_2,\hfill \end{array}$$

holds. So we have

$$\left[\begin{array}{c}\left(a-{\epsilon }_1\right)f\left(x_n,y_n\right)\\ \left(b+{\epsilon }_2\right)g\left(x_n,y_n\right)\end{array}\right]{\preccurlyeq }_{se}{X}_{n+1}=\left[\begin{array}{c}{a}_{n}f\left(x_n,y_n\right)\\ b_{n}g\left(x_n,y_n\right)\end{array}\right]{\preccurlyeq }_{se}\left[\begin{array}{c}\left(a+{\epsilon }_1\right)f\left(x_n,y_n\right)\\ \left(b-{\epsilon }_2\right)g\left(x_n,y_n\right)\end{array}\right],n\ge N.$$

By Lemma 1, we obtain

$$L_n{\preccurlyeq }_{se}{X}_n{\preccurlyeq }_{se}{U}_n,n\ge N,$$

(9)

where $\left\{L_n\right\}=\left\{\left[\begin{array}{c}{l}_n^{\left(1\right)}\\ l_n^{\left(2\right)}\end{array}\right]\right\}$ satisfies

$$L_{n+1}=\left[\begin{array}{c}\left(a-{\epsilon }_1\right)f\left(l_n^{\left(1\right)},l_n^{\left(2\right)}\right)\\ \left(b+{\epsilon }_2\right)g\left(l_n^{\left(1\right)},l_n^{\left(2\right)}\right)\end{array}\right],$$

and $\left\{U_n\right\}=\left\{\left[\begin{array}{c}{u}_n^{\left(1\right)}\\ u_n^{\left(2\right)}\end{array}\right]\right\}$ satisfies

$$U_{n+1}=\left[\begin{array}{c}\left(a+{\epsilon }_1\right)f\left(u_n^{\left(1\right)},u_n^{\left(2\right)}\right)\\ \left(b-{\epsilon }_2\right)g\left(u_n^{\left(1\right)},u_n^{\left(2\right)}\right)\end{array}\right].$$

Inequalities (9) imply

$$\underset{n\to \infty }{\lim }{L}_n{\preccurlyeq }_{se}\underset{n\to \infty }{lim\; inf}{X}_n{\preccurlyeq }_{se}lim\; sup{X}_n{\preccurlyeq }_{se}\underset{n\to \infty }{\lim }{U}_n,$$

i.e.,

$${\overline{Y}}_{{\mathit{\alpha }}_{\mathit{\epsilon }}}{\preccurlyeq }_{se}\underset{n\to \infty }{lim\; inf}{X}_n{\preccurlyeq }_{se}lim\; sup{X}_n{\preccurlyeq }_{se}{\overline{Y}}_{{}_{\mathit{\beta }\mathit{\epsilon }}},$$

(10)

where ${\mathit{\alpha }}_{\mathit{\epsilon }}=\left[\begin{array}{c}a-{\epsilon }_1\\ b+{\epsilon }_2\end{array}\right]$, ${\mathit{\beta }}_{\mathit{\epsilon }}=\left[\begin{array}{c}a+{\epsilon }_1\\ b-{\epsilon }_2\end{array}\right]$, and $\mathit{\epsilon }=\left[\begin{array}{c}{\epsilon }_1\\ {\epsilon }_2\end{array}\right]$.

Since $\underset{\mathit{\epsilon }\to \mathbf{0}}{\lim }{\overline{Y}}_{{\mathit{\alpha }}_{\mathit{\epsilon }}}=\underset{\mathit{\epsilon }\to \mathbf{0}}{\lim }{\overline{Y}}_{{\mathit{\beta }}_{\mathit{\epsilon }}}=\overline{Y}$, where $\mathbf{0}=\left[\begin{array}{c}0\\ 0\end{array}\right]$, (10) implies that

$$\underset{n\to \infty }{lim\; inf}{X}_n=\underset{n\to \infty }{lim\; sup}{X}_n=\underset{n\to \infty }{\lim }{X}_n=\overline{Y}.$$

□

Remark 1. 

The condition (8) is actually a condition of the structural stability of system (7).

Example 1. 

Consider the following system of difference equations modelling competition, [14,15]

$$\left.\begin{array}{c}{x}_{n+1}=a{\displaystyle \frac{1}{1+y_n}}{x}_n\\ y_{n+1}=b{\displaystyle \frac{1}{1+x_n}}{y}_n\end{array}\right\},n=0,1,\cdots ,$$

(11)

where $a>0$, $b>0$, $x_0\ge 0$ and $y_0\ge 0$. This system has the following equilibrium points:

(a) $E_0=\left[\begin{array}{c}0\\ 0\end{array}\right]$, which is locally asymptotically stable if $0<a<1$ and $0<b<1$;

(b) $E_1=\left[\begin{array}{c}b-1\\ a-1\end{array}\right]$ for $a>1$ and $b>1$, which is a saddle point;

(c) every point $E_x=\left[\begin{array}{c}x\\ 0\end{array}\right]$, $x\in {\mathbb{R}}_{+}$ if $a=1$, which is a non-hyperbolic point;

(d) every point $E_y=\left[\begin{array}{c}0\\ y\end{array}\right]$, $y\in {\mathbb{R}}_{+}$ if $b=1$, which is a non-hyperbolic point, and

(e) every point on the x-axis and every point on the y-axis if $a=b=1$, which is a non-hyperbolic point.

It implies from the Jacobi matrix of the map $F=\left[\begin{array}{c}ax\frac{1}{1+y}\\ by\frac{1}{1+x}\end{array}\right]$, which has the form

$$J_F\left(\left[\begin{array}{c}x\\ y\end{array}\right]\right)=\left[\begin{array}{cc}{\displaystyle \frac{a}{1+y}}& -{\displaystyle \frac{ax}{{\left(1+y\right)}^2}}\\ -{\displaystyle \frac{by}{{\left(1+x\right)}^2}}& {\displaystyle \frac{b}{1+x}}\end{array}\right],$$

so that, for example,

$$J_F\left(E_0\right)=\left[\begin{array}{cc}a& 0\\ 0& b\end{array}\right]$$

has eigenvalues ${\lambda }_1=a$ and ${\lambda }_2=b$, while

$$J_F\left(E_1\right)=\left[\begin{array}{cc}1& {\displaystyle \frac{1-b}{a}}\\ {\displaystyle \frac{1-a}{b}}& 1\end{array}\right]$$

has eigenvalues ${\lambda }_{\pm }=1\pm \sqrt{\frac{\left(a-1\right)\left(b-1\right)}{ab}}$.

The fact that $E_0=\left(0,0\right)$ is globally asymptotically stable if $0<a<1$ and $0<b<1$ follows by using the Lyapunov function $V:{\mathbb{R}}_{+}^2\to \mathbb{R}$ of the form $V\left(\left[\begin{array}{c}x\\ y\end{array}\right]\right)=x^2+y^2$ of the map F. Namely, if $x\ge 0$, $y\ge 0$, $\left(x,y\right)\ne \left(0,0\right)$, $0<a<1$, and $0<b<1$, we have that

$$\begin{array}{ccc}\hfill \Delta V& =& V\left(F\left(\left[\begin{array}{c}x\\ y\end{array}\right]\right)\right)-V\left(\left[\begin{array}{c}x\\ y\end{array}\right]\right)={\left(ax{\displaystyle \frac{1}{1+y}}\right)}^2+{\left(by{\displaystyle \frac{1}{1+x}}\right)}^2-x^2-y^2\hfill \\ & =& x^2\left({\left(\frac{a}{1+y}\right)}^2-1\right)+y^2\left({\left(\frac{b}{1+x}\right)}^2-1\right)\hfill \\ & \le & x^2\left(a^2-1\right)+y^2\left(b^2-1\right)<0.\hfill \end{array}$$

Since $V\left(\left[\begin{array}{c}x\\ y\end{array}\right]\right)=x^2+y^2\to \infty$, as $∥\left[\begin{array}{c}x\\ y\end{array}\right]∥\to \infty$ then equilibrium point $E_0=\left(0,0\right)$ is globally asymptotically stable when $0<a<1$ and $0<b<1$.

If we consider the following non-autonomous system

$$\left.\begin{array}{c}{x}_{n+1}=a_n{\displaystyle \frac{1}{1+y_n}}{x}_n\\ y_{n+1}=b_n{\displaystyle \frac{1}{1+x_n}}{y}_n\end{array}\right\},n=0,1,2,\cdots ,$$

(12)

where $\underset{n\to \infty }{\lim }{a}_n=a$ and $\underset{n\to \infty }{\lim }{b}_n=b$ then, by using Theorem 5 taking $f\left(x_n,y_n\right)=\frac{1}{1+y_n}{x}_n$ and $g\left(x_n,y_n\right)=\frac{1}{1+x_n}{y}_n$, all solutions of System (12) globally asymptotically converge to $E_0=\left(0,0\right)$ for $0<a<1$ and $0<b<1$, and for all $x_0\ge 0$ and $y_0\ge 0$.

Theorem 6. 

Consider the following non-autonomous competitive system:

$$X_{n+1}=\left[\begin{array}{c}{\displaystyle \frac{x_n}{a_n+y_n}}\\ {\displaystyle \frac{y_n}{b_n+x_n}}\end{array}\right],n=0,1,\cdots$$

(13)

Assume that $A_n=\left[\begin{array}{c}{a}_n\\ b_n\end{array}\right]$ and

$$\underset{n\to \infty }{\lim }{A}_n=\underset{n\to \infty }{\lim }\left[\begin{array}{c}{a}_n\\ b_n\end{array}\right]=\left[\begin{array}{c}\underset{n\to \infty }{\lim }{a}_n\\ \underset{n\to \infty }{\lim }{b}_n\end{array}\right]=\left[\begin{array}{c}a\\ b\end{array}\right]=A,$$

and let

$$Y_{n+1}=\left[\begin{array}{c}{\displaystyle \frac{x_n}{a+y_n}}\\ {\displaystyle \frac{y_n}{b+x_n}}\end{array}\right],n=0,1,\cdots ,$$

(14)

be the limiting system of System (13). Also, assume that there exists ${\epsilon }_{\mathbf{0}}=\left[\begin{array}{c}{\epsilon }_0^{\left(1\right)}\\ {\epsilon }_0^{\left(2\right)}\end{array}\right]$${\succ }_{ne}\left[\begin{array}{c}0\\ 0\end{array}\right]$ such that every solution of the system

$$Y_{n+1}=\left[\begin{array}{c}{\displaystyle \frac{x_n}{\alpha +y_n}}\\ {\displaystyle \frac{y_n}{\beta +x_n}}\end{array}\right],n=0,1,\cdots$$

converges to a constant ${\overline{Y}}_{{\mathit{A}}_{\epsilon }}=\left[\begin{array}{c}{\overline{x}}_{{\mathit{A}}_{\epsilon }}\\ {\overline{y}}_{{\mathit{A}}_{\epsilon }}\end{array}\right]$ for every ${\mathit{A}}_{\epsilon }=\left[\begin{array}{c}\alpha \\ \beta \end{array}\right]$, $\alpha \in \left(a-{\epsilon }_0^{\left(1\right)},a+{\epsilon }_0^{\left(1\right)}\right)$, $\beta \in \left(b-{\epsilon }_0^{\left(2\right)},b+{\epsilon }_0^{\left(2\right)}\right)$.

If

$$\underset{{\mathit{A}}_{\epsilon }\to A}{\lim }{\overline{Y}}_{{\mathit{A}}_{\epsilon }}=\overline{Y},$$

then every solution of the system (13) satisfies

$$\underset{n\to \infty }{\lim }{X}_n=\overline{Y}.$$

Proof. 

For arbitrary ${\epsilon }_1>0$ and ${\epsilon }_2>0$, there exists $N=N\left({\epsilon }_1,{\epsilon }_2\right)$ such that for $n\ge N$, the following holds:

$$\begin{array}{ccc}\hfill a-{\epsilon }_1& <& a_n<a+{\epsilon }_1,\hfill \\ \hfill b-{\epsilon }_2& <& b_n<b+{\epsilon }_2.\hfill \end{array}$$

This implies that

$$\left[\begin{array}{c}{\displaystyle \frac{x_n}{a+{\epsilon }_1+y_n}}\\ {\displaystyle \frac{y_n}{b-{\epsilon }_2+x_n}}\end{array}\right]{\preccurlyeq }_{se}{X}_{n+1}=\left[\begin{array}{c}{\displaystyle \frac{x_n}{a_n+y_n}}\\ {\displaystyle \frac{y_n}{b_n+x_n}}\end{array}\right]{\preccurlyeq }_{se}\left[\begin{array}{c}{\displaystyle \frac{x_n}{a-{\epsilon }_1+y_n}}\\ {\displaystyle \frac{y_n}{b+{\epsilon }_2+x_n}}\end{array}\right],n\ge N.$$

By Lemma 1, we obtain

$$L_n{\preccurlyeq }_{se}{X}_n{\preccurlyeq }_{se}{U}_n,n\ge N,$$

(15)

where $\left\{L_n\right\}=\left\{\left[\begin{array}{c}{l}_n^{\left(1\right)}\\ l_n^{\left(2\right)}\end{array}\right]\right\}$ satisfies

$$L_{n+1}=\left[\begin{array}{c}{\displaystyle \frac{l_n^{\left(1\right)}}{a+{\epsilon }_1+l_n^{\left(2\right)}}}\\ {\displaystyle \frac{l_n^{\left(2\right)}}{b-{\epsilon }_2+l_n^{\left(1\right)}}}\end{array}\right],$$

and $\left\{U_n\right\}=\left\{\left[\begin{array}{c}{u}_n^{\left(1\right)}\\ u_n^{\left(2\right)}\end{array}\right]\right\}$ satisfies

$$U_{n+1}=\left[\begin{array}{c}{\displaystyle \frac{u_n^{\left(1\right)}}{a-{\epsilon }_1+u_n^{\left(2\right)}}}\\ {\displaystyle \frac{u_n^{\left(2\right)}}{b+{\epsilon }_2+u_n^{\left(1\right)}}}\end{array}\right].$$

Inequalities (15) imply

$$\underset{n\to \infty }{\lim }{L}_n{\preccurlyeq }_{se}\underset{n\to \infty }{lim\; inf}{X}_n{\preccurlyeq }_{se}\underset{n\to \infty }{lim\; sup}{X}_n{\preccurlyeq }_{se}\underset{n\to \infty }{\lim }{U}_n,$$

i.e.,

$${\overline{Y}}_{{\mathit{\alpha }}_{\mathit{\epsilon }}}{\preccurlyeq }_{se}\underset{n\to \infty }{lim\; inf}{X}_n{\preccurlyeq }_{se}\underset{n\to \infty }{lim\; sup}{X}_n{\preccurlyeq }_{se}{\overline{Y}}_{{}_{\mathit{\beta }\mathit{\epsilon }}},$$

(16)

where ${\mathit{\alpha }}_{\mathit{\epsilon }}=\left[\begin{array}{c}a+{\epsilon }_1\\ b-{\epsilon }_2\end{array}\right]$, ${\mathit{\beta }}_{\mathit{\epsilon }}=\left[\begin{array}{c}a-{\epsilon }_1\\ b+{\epsilon }_2\end{array}\right]$, and $\epsilon =\left[\begin{array}{c}{\epsilon }_1\\ {\epsilon }_2\end{array}\right]$.

Since $\underset{\mathit{\epsilon }\to \mathbf{0}}{\lim }{\overline{Y}}_{{\mathit{\alpha }}_{\mathit{\epsilon }}}=\underset{\mathit{\epsilon }\to \mathbf{0}}{\lim }{\overline{Y}}_{{\mathit{\beta }}_{\mathit{\epsilon }}}=\overline{Y}$, where $\mathbf{0}=\left[\begin{array}{c}0\\ 0\end{array}\right]$, (16) implies that

$$\underset{n\to \infty }{lim\; inf}{X}_n=\underset{n\to \infty }{lim\; sup}{X}_n=\underset{n\to \infty }{\lim }{X}_n=\overline{Y}.$$

□

Theorem 7. 

Consider the following non-autonomous competitive system

$$X_{n+1}=\left[\begin{array}{c}{\displaystyle \frac{{\alpha }_n{x}_n}{a_n+y_n}}\\ {\displaystyle \frac{{\beta }_n{y}_n}{b_n+x_n}}\end{array}\right],n=0,1,\cdots .$$

(17)

Assume that $A_n=\left[\begin{array}{c}{\alpha }_n\\ a_n\\ {\beta }_n\\ b_n\end{array}\right]$ and

$$\underset{n\to \infty }{\lim }{A}_n=\underset{n\to \infty }{\lim }\left[\begin{array}{c}{\alpha }_n\\ a_n\\ {\beta }_n\\ b_n\end{array}\right]=\left[\begin{array}{c}\underset{n\to \infty }{\lim }{\alpha }_n\\ \underset{n\to \infty }{\lim }{a}_n\\ \underset{n\to \infty }{\lim }{\beta }_n\\ \underset{n\to \infty }{\lim }{b}_n\end{array}\right]=\left[\begin{array}{c}\alpha \\ a\\ \beta \\ b\end{array}\right]=A,$$

and let

$$Y_{n+1}=\left[\begin{array}{c}{\displaystyle \frac{\alpha x_n}{a+y_n}}\\ {\displaystyle \frac{\beta y_n}{b+x_n}}\end{array}\right],n=0,1,2,\cdots ,$$

(18)

be the limiting system of System (17). Also, assume that there exists ${\epsilon }_{\mathbf{0}}=\left[\begin{array}{c}{\epsilon }_0^{\left(1\right)}\\ {\epsilon }_0^{\left(2\right)}\\ {\epsilon }_0^{\left(3\right)}\\ {\epsilon }_0^{\left(4\right)}\end{array}\right]{\succ }_{ne}\left[\begin{array}{c}0\\ 0\\ 0\\ 0\end{array}\right]$ such that every solution of the system

$$Y_{n+1}=\left[\begin{array}{c}{\displaystyle \frac{\lambda x_n}{\mu +y_n}}\\ {\displaystyle \frac{\nu y_n}{\xi +x_n}}\end{array}\right],n=0,1,2,\cdots$$

converges to a constant ${\overline{Y}}_{{\mathit{A}}_{\epsilon }}=\left[\begin{array}{c}{\overline{x}}_{{\mathit{A}}_{\epsilon }}\\ {\overline{y}}_{{\mathit{A}}_{\epsilon }}\end{array}\right]$ for every ${\mathit{A}}_{\epsilon }=\left[\begin{array}{c}\lambda \\ \mu \\ \nu \\ \xi \end{array}\right]$, $\lambda \in \left(\alpha -{\epsilon }_0^{\left(1\right)},\alpha +{\epsilon }_0^{\left(1\right)}\right)$, $\mu \in \left(a-{\epsilon }_0^{\left(2\right)},a+{\epsilon }_0^{\left(2\right)}\right)$, $\nu \in \left(\beta -{\epsilon }_0^{\left(2\right)},\beta +{\epsilon }_0^{\left(2\right)}\right)$, and $\xi \in \left(b-{\epsilon }_0^{\left(2\right)},b+{\epsilon }_0^{\left(2\right)}\right)$.

If

$$\underset{{\mathit{A}}_{\epsilon }\to A}{\lim }{\overline{Y}}_{{\mathit{A}}_{\epsilon }}=\overline{Y},$$

then every solution of the system (17) satisfies

$$\underset{n\to \infty }{\lim }{X}_n=\overline{Y}.$$

Proof. 

For arbitrary $\epsilon =\left[\begin{array}{c}{\epsilon }_1\\ {\epsilon }_2\\ {\epsilon }_3\\ {\epsilon }_4\end{array}\right]{\succ }_{ne}\left[\begin{array}{c}0\\ 0\\ 0\\ 0\end{array}\right]$, there exists $N=N\left(\epsilon \right)$ such that for $n\ge N$, the following

$$\begin{array}{ccc}\hfill \alpha -{\epsilon }_1& <& {\alpha }_n<\alpha +{\epsilon }_1,\hfill \\ \hfill a-{\epsilon }_2& <& a_n<a+{\epsilon }_2,\hfill \\ \hfill \beta -{\epsilon }_3& <& {\beta }_n<\beta +{\epsilon }_3,\hfill \\ \hfill b-{\epsilon }_4& <& b_n<b+{\epsilon }_4,\hfill \end{array}$$

holds. This implies that

$$\left[\begin{array}{c}{\displaystyle \frac{\left(\alpha -{\epsilon }_1\right)x_n}{a+{\epsilon }_2+y_n}}\\ {\displaystyle \frac{\left(\beta +{\epsilon }_3\right)y_n}{b-{\epsilon }_4+x_n}}\end{array}\right]{\preccurlyeq }_{se}{X}_{n+1}=\left[\begin{array}{c}{\displaystyle \frac{{\alpha }_n{x}_n}{a_n+y_n}}\\ {\displaystyle \frac{{\beta }_n{y}_n}{b_n+x_n}}\end{array}\right]{\preccurlyeq }_{se}\left[\begin{array}{c}{\displaystyle \frac{\left(\alpha +{\epsilon }_1\right)x_n}{a-{\epsilon }_2+y_n}}\\ {\displaystyle \frac{\left(\beta -{\epsilon }_3\right)y_n}{b+{\epsilon }_4+x_n}}\end{array}\right],n\ge N\left(\epsilon \right).$$

Since F is a competitive map, Lemma 1 implies

$$L_n{\preccurlyeq }_{se}{X}_n{\preccurlyeq }_{se}{U}_n,n\ge N\left(\epsilon \right),$$

(19)

where $\left\{L_n\right\}=\left\{\left[\begin{array}{c}{l}_n^{\left(1\right)}\\ l_n^{\left(2\right)}\end{array}\right]\right\}$ satisfies

$$L_{n+1}=\left[\begin{array}{c}{\displaystyle \frac{\left(\alpha -{\epsilon }_1\right)l_n^{\left(1\right)}}{a+{\epsilon }_2+l_n^{\left(2\right)}}}\\ {\displaystyle \frac{\left(\beta +{\epsilon }_3\right)l_n^{\left(2\right)}}{b-{\epsilon }_4+l_n^{\left(1\right)}}}\end{array}\right],$$

and $\left\{U_n\right\}=\left\{\left[\begin{array}{c}{u}_n^{\left(1\right)}\\ u_n^{\left(2\right)}\end{array}\right]\right\}$ satisfies

$$U_{n+1}=\left[\begin{array}{c}{\displaystyle \frac{\left(\alpha +{\epsilon }_1\right)u_n^{\left(1\right)}}{a-{\epsilon }_1+u_n^{\left(2\right)}}}\\ {\displaystyle \frac{\left(\beta -{\epsilon }_3\right)u_n^{\left(2\right)}}{b+{\epsilon }_4+u_n^{\left(1\right)}}}\end{array}\right].$$

Inequalities (19) imply

$$\underset{n\to \infty }{\lim }{L}_n{\preccurlyeq }_{se}\underset{n\to \infty }{lim\; inf}{X}_n{\preccurlyeq }_{se}\underset{n\to \infty }{lim\; sup}{X}_n{\preccurlyeq }_{se}\underset{n\to \infty }{\lim }{U}_n,$$

i.e., (16), where ${\mathit{\alpha }}_{\mathit{\epsilon }}=\left[\begin{array}{c}\alpha -{\epsilon }_1\\ a+{\epsilon }_2\\ \beta +{\epsilon }_3\\ b-{\epsilon }_4\end{array}\right]$, ${\mathit{\beta }}_{\mathit{\epsilon }}=\left[\begin{array}{c}\mathit{\alpha }+{\epsilon }_1\\ a-{\epsilon }_2\\ \beta -{\epsilon }_3\\ b+{\epsilon }_4\end{array}\right]$, and $\mathit{\epsilon }=\left[\begin{array}{c}{\epsilon }_1\\ {\epsilon }_2\\ {\epsilon }_3\\ {\epsilon }_4\end{array}\right]$. Since $\underset{\mathit{\epsilon }\to \mathbf{0}}{\lim }{\overline{Y}}_{{\mathit{\alpha }}_{\mathit{\epsilon }}}=\underset{\mathit{\epsilon }\to \mathbf{0}}{\lim }{\overline{Y}}_{{\mathit{\beta }}_{\mathit{\epsilon }}}=\overline{Y}$, where $\mathbf{0}=\left[\begin{array}{c}0\\ 0\\ 0\\ 0\end{array}\right]$, (16) implies that

$$\underset{n\to \infty }{lim\; inf}{X}_n=\underset{n\to \infty }{lim\; sup}{X}_n=\underset{n\to \infty }{\lim }{X}_n=\overline{Y}.$$

□

Theorem 8. 

Consider the following non-autonomous Leslie–Gower model:

$$X_{n+1}=\left[\begin{array}{c}{\displaystyle \frac{a_n{x}_n}{1+c_n^{\left(11\right)}{x}_n+c^{\left(12\right)}{y}_n}}\\ {\displaystyle \frac{b_n{y}_n}{1+c^{\left(21\right)}{x}_n+c_n^{\left(22\right)}{y}_n}}\end{array}\right],n=0,1,2,\cdots .$$

(20)

Assume that $A_n=\left[\begin{array}{c}{a}_n\\ c_n^{\left(11\right)}\\ b_n\\ c_n^{\left(22\right)}\end{array}\right]$ and

$$\underset{n\to \infty }{\lim }{A}_n=\underset{n\to \infty }{\lim }\left[\begin{array}{c}{a}_n\\ c_n^{\left(11\right)}\\ b_n\\ c_n^{\left(22\right)}\end{array}\right]=\left[\begin{array}{c}\underset{n\to \infty }{\lim }{a}_n\\ \underset{n\to \infty }{\lim }{c}_n^{\left(11\right)}\\ \underset{n\to \infty }{\lim }{b}_n\\ \underset{n\to \infty }{\lim }{c}_n^{\left(22\right)}\end{array}\right]=\left[\begin{array}{c}a\\ c^{\left(11\right)}\\ b\\ c^{\left(22\right)}\end{array}\right]=A,$$

and let

$$Y_{n+1}=\left[\begin{array}{c}{\displaystyle \frac{a{x}_n}{1+c^{\left(11\right)}{x}_n+c^{\left(12\right)}{y}_n}}\\ {\displaystyle \frac{b{y}_n}{1+c^{\left(21\right)}{x}_n+c^{\left(22\right)}{y}_n}}\end{array}\right],n=0,1,2,\cdots .$$

(21)

be the limiting system of System (21). Also, assume that there exists ${\mathit{\epsilon }}_0=\left[\begin{array}{c}{\epsilon }_0^{\left(1\right)}\\ {\epsilon }_0^{\left(2\right)}\\ {\epsilon }_0^{\left(3\right)}\\ {\epsilon }_0^{\left(4\right)}\end{array}\right]{\succ }_{ne}\left[\begin{array}{c}0\\ 0\\ 0\\ 0\end{array}\right]$ such that every solution of the system

$$Y_{n+1}=\left[\begin{array}{c}{\displaystyle \frac{\lambda x_n}{1+\mu x_n+c^{\left(12\right)}{y}_n}}\\ {\displaystyle \frac{\nu y_n}{1+c^{\left(21\right)}{x}_n+\xi y_n}}\end{array}\right],n=0,1,2,\cdots$$

converges to a constant ${\overline{Y}}_{{\mathit{A}}_{\epsilon }}=\left[\begin{array}{c}{\overline{x}}_{{\mathit{A}}_{\epsilon }}\\ {\overline{y}}_{{\mathit{A}}_{\epsilon }}\end{array}\right]$ for every ${\mathit{A}}_{\epsilon }=\left[\begin{array}{c}\lambda \\ \mu \\ \nu \\ \xi \end{array}\right]$, $\lambda \in \left(a-{\epsilon }_0^{\left(1\right)},a+{\epsilon }_0^{\left(1\right)}\right)$, $\mu \in \left(c^{\left(11\right)}-{\epsilon }_0^{\left(2\right)},c^{\left(11\right)}+{\epsilon }_0^{\left(2\right)}\right)$, $\nu \in \left(b-{\epsilon }_0^{\left(2\right)},b+{\epsilon }_0^{\left(2\right)}\right)$, and $\xi \in \left(c^{\left(22\right)}-{\epsilon }_0^{\left(2\right)},c^{\left(22\right)}+{\epsilon }_0^{\left(2\right)}\right)$.If

$$\underset{{\mathit{A}}_{\epsilon }\to A}{\lim }{\overline{Y}}_{{\mathit{A}}_{\epsilon }}=\overline{Y},$$

then every solution of the system (21) satisfies

$$\underset{n\to \infty }{\lim }{X}_n=\overline{Y}.$$

Proof. 

For arbitrary $\epsilon =\left[\begin{array}{c}{\epsilon }_1\\ {\epsilon }_2\\ {\epsilon }_3\\ {\epsilon }_4\end{array}\right]{\succ }_{ne}\left[\begin{array}{c}0\\ 0\\ 0\\ 0\end{array}\right]$, there exists $N=N\left(\epsilon \right)$ such that for $n\ge N$, the following

$$\begin{array}{ccc}\hfill a-{\epsilon }_1& <& a_n<a+{\epsilon }_1,\hfill \\ \hfill c^{\left(11\right)}-{\epsilon }_2& <& c_n^{\left(11\right)}<c^{\left(11\right)}+{\epsilon }_2,\hfill \\ \hfill b-{\epsilon }_3& <& b_n<b+{\epsilon }_3,\hfill \\ \hfill c^{\left(22\right)}-{\epsilon }_4& <& c_n^{\left(22\right)}<c^{\left(22\right)}+{\epsilon }_4,\hfill \end{array}$$

holds. This implies that the following inequalities are satisfied for $n\ge N\left(\epsilon \right)$

$$\left[\begin{array}{c}{\displaystyle \frac{\left(a-{\epsilon }_1\right)x_n}{1+\left(c^{\left(11\right)}+{\epsilon }_2\right)x_n+c^{\left(12\right)}{y}_n}}\\ {\displaystyle \frac{\left(b+{\epsilon }_3\right)y_n}{1+c^{\left(21\right)}{x}_n+\left(c^{\left(22\right)}-{\epsilon }_4\right)y_n}}\end{array}\right]{\preccurlyeq }_{se}{X}_{n+1}{\preccurlyeq }_{se}\left[\begin{array}{c}{\displaystyle \frac{\left(a+{\epsilon }_1\right)x_n}{1+\left(c^{\left(11\right)}-{\epsilon }_2\right)x_n+c^{\left(12\right)}{y}_n}}\\ {\displaystyle \frac{\left(b-{\epsilon }_3\right)y_n}{1+c^{\left(21\right)}{x}_n+\left(c^{\left(22\right)}+{\epsilon }_4\right)y_n}}\end{array}\right].$$

Since $F=\left[\begin{array}{c}{\displaystyle \frac{a_{n}x}{1+c_n^{\left(11\right)}x+c^{\left(12\right)}y}}\\ {\displaystyle \frac{b_{n}y}{1+c^{\left(21\right)}x+c_n^{\left(22\right)}y}}\end{array}\right]$ is a competitive map, Lemma 1 implies

$$L_n{\preccurlyeq }_{se}{X}_n{\preccurlyeq }_{se}{U}_n,n\ge N\left(\epsilon \right),$$

(22)

where $\left\{L_n\right\}=\left\{\left[\begin{array}{c}{l}_n^{\left(1\right)}\\ l_n^{\left(2\right)}\end{array}\right]\right\}$ satisfies

$$L_{n+1}=\left[\begin{array}{c}{\displaystyle \frac{\left(a-{\epsilon }_1\right)l_n^{\left(1\right)}}{1+\left(c^{\left(11\right)}+{\epsilon }_2\right)l_n^{\left(1\right)}+c^{\left(12\right)}{l}_n^{\left(2\right)}}}\\ {\displaystyle \frac{\left(b+{\epsilon }_3\right)l_n^{\left(2\right)}}{1+c^{\left(21\right)}{l}_n^{\left(1\right)}+\left(c^{\left(22\right)}-{\epsilon }_4\right)l_n^{\left(2\right)}}}\end{array}\right],$$

and $\left\{U_n\right\}=\left\{\left[\begin{array}{c}{u}_n^{\left(1\right)}\\ u_n^{\left(2\right)}\end{array}\right]\right\}$ satisfies

$$U_{n+1}=\left[\begin{array}{c}{\displaystyle \frac{\left(a+{\epsilon }_1\right)u_n^{\left(1\right)}}{1+\left(c^{\left(11\right)}-{\epsilon }_2\right)u_n^{\left(1\right)}+c^{\left(12\right)}{u}_n^{\left(2\right)}}}\\ {\displaystyle \frac{\left(b-{\epsilon }_3\right)u_n^{\left(2\right)}}{1+c^{\left(21\right)}{u}_n^{\left(1\right)}+\left(c^{\left(22\right)}+{\epsilon }_4\right)u_n^{\left(2\right)}}}\end{array}\right].$$

Inequalities (22) imply

$$\underset{n\to \infty }{\lim }{L}_n{\preccurlyeq }_{se}\underset{n\to \infty }{lim\; inf}{X}_n{\preccurlyeq }_{se}\underset{n\to \infty }{lim\; sup}{X}_n{\preccurlyeq }_{se}\underset{n\to \infty }{\lim }{U}_n,$$

i.e.,

$${\overline{Y}}_{{\mathit{\alpha }}_{\mathit{\epsilon }}}{\preccurlyeq }_{se}\underset{n\to \infty }{lim\; inf}{X}_n{\preccurlyeq }_{se}\underset{n\to \infty }{lim\; sup}{X}_n{\preccurlyeq }_{se}{\overline{Y}}_{{}_{\mathit{\beta }\mathit{\epsilon }}},$$

(23)

where ${\mathit{\alpha }}_{\mathit{\epsilon }}=\left[\begin{array}{c}a-{\epsilon }_1\\ c^{\left(11\right)}+{\epsilon }_2\\ b+{\epsilon }_3\\ c^{\left(22\right)}-{\epsilon }_4\end{array}\right]$, ${\mathit{\beta }}_{\mathit{\epsilon }}=\left[\begin{array}{c}a+{\epsilon }_1\\ c^{\left(11\right)}-{\epsilon }_2\\ b-{\epsilon }_3\\ c^{\left(22\right)}+{\epsilon }_4\end{array}\right]$, and $\mathit{\epsilon }=\left[\begin{array}{c}{\epsilon }_1\\ {\epsilon }_2\\ {\epsilon }_3\\ {\epsilon }_4\end{array}\right]$.

Since $\underset{\mathit{\epsilon }\to \mathbf{0}}{\lim }{\overline{Y}}_{{\mathit{\alpha }}_{\mathit{\epsilon }}}=\underset{\mathit{\epsilon }\to \mathbf{0}}{\lim }{\overline{Y}}_{{\mathit{\beta }}_{\mathit{\epsilon }}}=\overline{Y}$, where $\mathbf{0}=\left[\begin{array}{c}0\\ 0\\ 0\\ 0\end{array}\right]$, (23) implies that

$$\underset{n\to \infty }{lim\; inf}{X}_n=\underset{n\to \infty }{lim\; sup}{X}_n\underset{n\to \infty }{=}\lim X_n=\overline{Y}.$$

□

Remark 2. 

Note that System (21) has a unique equilibrium point $E_0=\left[\begin{array}{c}0\\ 0\end{array}\right]$, for $0<a<1$, $0<b<1$, which is locally asymptotically stable. By using Lyapunov function $V:{\mathbb{R}}_{+}^2\to \mathbb{R}$ of the form $V\left(\left[\begin{array}{c}x\\ y\end{array}\right]\right)=x^2+y^2$ of the map $F=\left[\begin{array}{c}{\displaystyle \frac{ax}{1+c^{\left(11\right)}x+c^{\left(12\right)}y}}\\ {\displaystyle \frac{by}{1+c^{\left(21\right)}x+c^{\left(22\right)}y}}\end{array}\right]$, we can conclude that the equilibrium point $E_0$ is globally asymptotically stable for $0<a<1$ and $0<b<1$. Namely, if $x\ge 0$, $y\ge 0$, $\left(x,y\right)\ne \left(0,0\right)$ and $0<a<1$, $0<b<1$, we have that

$$\begin{array}{cc}\hfill \Delta V& =V\left(F\left(\left[\begin{array}{c}x\\ y\end{array}\right]\right)\right)-V\left(\left[\begin{array}{c}x\\ y\end{array}\right]\right)\hfill \\ \hfill & ={\left({\displaystyle \frac{ax}{1+c^{\left(11\right)}x+c^{\left(12\right)}y}}\right)}^2+{\left({\displaystyle \frac{by}{1+c^{\left(21\right)}x+c^{\left(22\right)}y}}\right)}^2-x^2-y^2\hfill \\ \hfill & =x^2\left({\left({\displaystyle \frac{a}{1+c^{\left(11\right)}x+c^{\left(12\right)}y}}\right)}^2-1\right)+y^2\left({\left({\displaystyle \frac{b}{1+c^{\left(21\right)}x+c^{\left(22\right)}y}}\right)}^2-1\right)\hfill \\ \hfill & <x^2\left(a^2-1\right)+y^2\left(b^2-1\right)<0.\hfill \end{array}$$

Since $V\left(\left[\begin{array}{c}x\\ y\end{array}\right]\right)=x^2+y^2\to \infty$, as $∥\left[\begin{array}{c}x\\ y\end{array}\right]∥\to \infty$, then equilibrium point $E_0=\left(0,0\right)$ is globally asymptotically stable.

Example 2. 

The competitive system considered in [14,15,16] was System

$$\left.\begin{array}{c}{x}_{n+1}={\displaystyle \frac{a+x_n}{b+y_n}}\\ y_{n+1}={\displaystyle \frac{d+y_n}{e+x_n}},\end{array}\right\}$$

(24)

$n=0,1,\dots$, for all positive values of parameters $a,b,d,e$, and non-negative initial conditions $x_0,y_0$, where the global dynamics was described. We found all values of parameters for which the unique equilibrium solution $(\overline{x},\overline{y})$ of (24) was globally asymptotically stable. Consider now the nonautonomous version of System (24):

$$\left.\begin{array}{c}{x}_{n+1}={\displaystyle \frac{a_n+x_n}{b_n+y_n}}\\ y_{n+1}={\displaystyle \frac{d_n+y_n}{e_n+x_n}},\end{array}\right\}$$

(25)

$n=0,1,\dots$, for non-negative initial conditions $x_0,y_0$, where each of positive valued sequences $a_n,b_n,d_n,e_n$ satisfies:

$$\underset{n\to \infty }{\lim }{a}_n=a,\underset{n\to \infty }{\lim }{b}_n=b,\underset{n\to \infty }{\lim }{d}_n=d,\underset{n\to \infty }{\lim }{e}_n=e.$$

The limiting system for (25) is System (24). So, for all values of parameters $a,b,d,e$ for which the unique equilibrium solution $(\overline{x},\overline{y})$ of System (24) is globally asymptotically stable, we have that

$$\underset{n\to \infty }{\lim }(x_n,y_n)=(\overline{x},\overline{y}),$$

for every solution $(x_n,y_n)$ of non-autonomous system (25).

Example 3. 

The competitive system considered in [17] was System

$$\left.\begin{array}{c}{x}_{n+1}={\displaystyle \frac{a{x}_n}{1+x_n+c_1{y}_n}}+h\\ y_{n+1}={\displaystyle \frac{b{y}_n}{1+c_2{x}_n+y_n}}\end{array}\right\}$$

(26)

$n=0,1,\dots$, for all positive values of parameters $a,b,c_1,c_2,h$, and non-negative initial conditions $x_0,y_0$, where the global dynamics was described. We found all values of parameters for which the unique equilibrium solution $(\overline{x},\overline{y})$ of (24) was globally asymptotically stable. Consider now the nonautonomous version of System (24):

$$\left.\begin{array}{c}{x}_{n+1}={\displaystyle \frac{a_n{x}_n}{1+x_n+c_1\left(n\right)y_n}}+h_n\\ y_{n+1}={\displaystyle \frac{b_n{y}_n}{1+c_2\left(n\right)x_n+y_n}}\end{array}\right\}$$

(27)

$n=0,1,\dots$, for non-negative initial conditions $x_0,y_0$, where each of the positive valued sequences $a_n,b_n,c_1\left(n\right),c_2\left(n\right),h_n$ satisfies:

$$\underset{n\to \infty }{\lim }{a}_n=a,\underset{n\to \infty }{\lim }{b}_n=b,\underset{n\to \infty }{\lim }{c}_1\left(n\right)=c_1,\underset{n\to \infty }{\lim }{c}_2\left(n\right)=c_2,\underset{n\to \infty }{\lim }{h}_n=h.$$

The limiting system for (27) is System (26). So, for all values of parameters for which the unique equilibrium solution $(\overline{x},\overline{y})$ of System (26) is globally asymptotically stable, we have that

$$\underset{n\to \infty }{\lim }(x_n,y_n)=(\overline{x},\overline{y}),$$

for every solution $(x_n,y_n)$ of non-autonomous system (27).

Example 4. 

The competitive system considered in [18] was System

$$\left.\begin{array}{c}{x}_{n+1}={\displaystyle \frac{b_1{x}_n}{1+x_n+c_1{y}_n}}+h_1\\ y_{n+1}={\displaystyle \frac{b_2{y}_n}{1+c_2{x}_n+y_n}}+h_2\end{array}\right\}$$

(28)

$n=0,1,\dots$, for all positive values of parameters $b_1,b_2,c_1,c_2,h_1,h_2$, and non-negative initial conditions $x_0,y_0$, where the global dynamics was described for all values of parameters. System (28) has between one and three equilibria, and the number of equilibria determines global behavior of this system. Here $h_1$ and $h_2$ are considered as constant stockings of two species which are in competition with Leslie–Gower type. We found in [18] that the unique equilibrium solution $(\overline{x},\overline{y})$ of (28) was globally asymptotically stable. We also found sufficient conditions for system (28) to have a unique equilibrium solution.

Consider now the nonautonomous version of System (28):

$$\left.\begin{array}{c}{x}_{n+1}={\displaystyle \frac{b_1{x}_n}{1+x_n+c_1{y}_n}}+h_1\left(n\right)\\ y_{n+1}={\displaystyle \frac{b_2{y}_n}{1+c_2{x}_n+y_n}}+h_2\left(n\right)\end{array}\right\}$$

(29)

$n=0,1,\dots$, for non-negative initial conditions $x_0,y_0$, where each of the positive valued sequences $h_1\left(n\right),h_2\left(n\right)$ satisfies:

$$\underset{n\to \infty }{\lim }{h}_1\left(n\right)=h_1,\underset{n\to \infty }{\lim }{h}_2\left(n\right)=h_2.$$

The limiting system for (29) is System (28). So for all values of parameters for which the unique equilibrium solution $(\overline{x},\overline{y})$ of System (28) is globally asymptotically stable we have that

$$\underset{n\to \infty }{\lim }(x_n,y_n)=(\overline{x},\overline{y}),$$

for every solution $(x_n,y_n)$ of non-autonomous system (29). For instance, as a consequence of Theorem 5 in [18], we have the following result:

Corollary 2. 

If at least one of the following conditions is satisfied,

$$1-b_1+h_1+c_1{h}_2\ge 0and1-b_2+h_2+c_2{h}_1\ge 0$$

(30)

or

$$c_1{c}_2\le 1,$$

(31)

then system (29) has a unique equilibrium, which is globally asymptotically stable.

Taking $h_1=h,h_2=0$ in Corollary 2, we get the global asymptotic stability result for system (26).

3. Examples of Competitive Evolutionary Models

In this section, we consider some competitive evolutionary models using the Beverton–Holt function and its modifications.

One of the reasons that model parameters can change in time is Darwinian evolution, which is a case that will be briefly explained here. The detailed explanation is given in [5,6,7,8,10,19]. Suppose v is a quantified, phenotypic trait of an individual that is subject to evolution. If we assume the per capita contribution to the population made by an individual depends on its trait v, then $f=f(x,v)$ depends on both x and v. It might happen that this contribution also depends on the traits of other individuals. We can model this situation by assuming that f also depends on the mean trait u in the population so that $f=f(x,v,u)$. A canonical way to model Darwinian evolution is to model the dynamics of $x_n$ and the mean trait $u_n$ by means of the equations

$$x_{n+1}=f(x_n,v,u_n){|}_{v=u_n}{x}_n$$

(32)

$$u_{n+1}=u_n+{\sigma }^2\frac{\partial F(x_n,v,u_n)}{\partial v}{|}_{v=u_n},$$

(33)

where $F(x,u,v)=lnf(x,u,v)$, see [19].

Equation (32) asserts that the population dynamics can be modeled by assuming the individual trait v is equal to the population mean. Equation (33) (called Lande’s or Fisher’s or the breeder’s equation) prescribes that the change in the mean trait is proportional to the fitness gradient, where fitness in this model is denoted by $F(x,v,u)$. The modeler decides on an appropriate measure of fitness, which is often taken to be f or $lnf$. The constant of proportionality ${\sigma }^2\ge 0$ is called the speed of evolution. It is related to the variance of the trait in the population, which is assumed to be constant in time. Thus, if ${\sigma }^2=0$, no evolution occurs (there is no variability) and one has a one-dimensional difference Equation (32) for just population dynamics. If evolution occurs ${\sigma }^2>0$, then the model is a two dimensional system of difference equations with state variable $[x_n,u_n]$. The term $x_n$ in Equation (32) can be vector. Similarly, mean trait $u_n$ can be vector as well. Also, $x_n$ can be scalar while $u_n$ can be vector—case when evolution depends on several traits.

Example 5. 

Now, we investigate the following competitive evolutionary model where the two growth coefficients a and b depend on two independent traits $u_1\left(n\right)$ and $u_2\left(n\right)$:

$$\begin{array}{ccc}\hfill x_{n+1}& =& a\left(u_1\left(n\right)\right)\frac{1}{1+y_n}{x}_n\hfill \\ \hfill y_{n+1}& =& b\left(u_2\left(n\right)\right)\frac{1}{1+x_n}{y}_n\hfill \\ \hfill u_1\left(n+1\right)& =& u_1\left(n\right)+{\sigma }_1^2\frac{a^{\prime }\left(u_1\left(n\right)\right)}{a\left(u_1\left(n\right)\right)}\hfill \\ \hfill u_2\left(n+1\right)& =& u_2\left(n\right)+{\sigma }_2^2\frac{b^{\prime }\left(u_2\left(n\right)\right)}{b\left(u_2\left(n\right)\right)},\hfill \end{array}$$

(34)

where $a\left(u_1\right)>0$ and $b\left(u_2\right)>0$ are twice differentiable functions on their domains. The third and fourth equations of system (34) are called Fisher’s or Lande’s equations, see [19].

The fixed points of the functions $u_1$ and $u_2$ are $u_1^{*}$ and $u_2^{*}$, respectively, where $u_1^{*}$ and $u_2^{*}$ are critical points of a and b.

If $u_1^{*}$ and $u_2^{*}$ are locally asymptotically stable, that is, if the following inequalities hold:

$$\frac{-2}{{\sigma }_1^2}<\frac{a^{″}\left(u_1^{*}\right)}{a\left(u_1^{*}\right)}<0\mathrm{and}\frac{-2}{{\sigma }_2^2}<\frac{b^{″}\left(u_2^{*}\right)}{b\left(u_2^{*}\right)}<0,$$

(35)

then there exist open neighborhoods ${\mathcal{U}}_1$ and ${\mathcal{U}}_2$ of $u_1^{*}$ and $u_2^{*}$, respectively, such that

$$\underset{n\to \infty }{\lim }{u}_1\left(n\right)=u_1^{*}\mathrm{and}\underset{n\to \infty }{\lim }{u}_2\left(n\right)=u_2^{*}.$$

This implies that the non-autonomous system formed by the first two equations in (34) is asymptotic to the following limiting system:

$$\left.\begin{array}{c}{x}_{n+1}=a\left(u_1^{*}\right){\displaystyle \frac{1}{1+y_n}}{x}_n\\ y_{n+1}=b\left(u_2^{*}\right){\displaystyle \frac{1}{1+x_n}}{y}_n\end{array}\right\}.$$

(36)

System (36) has a unique equilibrium point $E_0^{*}=\left[\begin{array}{c}0\\ 0\end{array}\right]$ for $0<a\left(u_1^{*}\right)<1$ and $0<b\left(u_2^{*}\right)<1$, which is locally asymptotically stable.

Based on Theorem 5 and using Example 1, we obtain the following result:

Theorem 9. 

If $0<a\left(u_1^{*}\right)<1$, $0<b\left(u_2^{*}\right)<1$, and the condition (35) holds, then all solutions of non-autonomous system (34) globally asymptotically converge to $\left(E_0^{*},u_1^{*},u_2^{*}\right)=\left[\begin{array}{c}0\\ 0\\ u_1^{*}\\ u_2^{*}\end{array}\right]\in {\mathbb{R}}_{+}^2\times {\mathcal{U}}_1\times {\mathcal{U}}_2$, for all points $x_0\ge 0$ and $y_0\ge 0$.

Example 6. 

Consider the following model, which is a special case of model (34),

$$\left.\begin{array}{c}{x}_{n+1}=\left(a+{\displaystyle \frac{u_1\left(n\right)-4}{{\left(u_1\left(n\right)\right)}^2}}\right){\displaystyle \frac{1}{1+y_n}}{x}_n\\ y_{n+1}=\left(b+{\displaystyle \frac{u_2\left(n\right)}{{\left(u_2\left(n\right)\right)}^2+4}}\right){\displaystyle \frac{1}{1+x_n}}{y}_n\\ u_1\left(n+1\right)=u_1\left(n\right)+{\sigma }_1^2{\displaystyle \frac{a^{\prime }\left(u_1\left(n\right)\right)}{a\left(u_1\left(n\right)\right)}}\\ u_2\left(n+1\right)=u_2\left(n\right)+{\sigma }_2^2{\displaystyle \frac{b^{\prime }\left(u_2\left(n\right)\right)}{b\left(u_2\left(n\right)\right)}},\end{array}\right\}$$

(37)

where $a\left(u_1\left(n\right)\right)=a+\frac{u_1\left(n\right)-4}{{\left(u_1\left(n\right)\right)}^2}$, $b\left(u_2\left(n\right)\right)=b+{\displaystyle \frac{u_2\left(n\right)}{{\left(u_2\left(n\right)\right)}^2+4}}$, $0<a<1$, and $0<b<1$.

From $a^{\prime }\left(u_1^{*}\right)={\displaystyle \frac{-u_1^{*}+8}{{\left(u_1^{*}\right)}^3}}=0$ and $b^{\prime }\left(u_2^{*}\right)={\displaystyle \frac{-{\left(u_2^{*}\right)}^2+4}{{\left({\left(u_2^{*}\right)}^2+4\right)}^2}}=0$, we obtain $u_1^{*}=8$ and ${\left(u_2^{*}\right)}_{\pm }=\pm 2$. In the following, we will use $u_2^{*}={\left(u_2^{*}\right)}_{+}=2$. Since $a^{″}\left(u_1^{*}\right)=a^{″}\left(8\right)=-\frac{1}{8^3}$, $b^{″}\left(u_2^{*}\right)=b^{″}\left(2\right)=-\frac{1}{16}$, $a\left(u_1^{*}\right)=a+\frac{1}{16}$, and $b\left(u_2^{*}\right)=b+\frac{1}{4}$, condition (35) is satisfied if

$${\sigma }_1^2<64(16a+1)and{\sigma }_2^2<8(4b+1).$$

Then, there exist open neighborhoods ${\mathcal{U}}_1$ and ${\mathcal{U}}_2$ of $u_1^{*}$ and $u_2^{*}$, respectively, such that

$$\underset{n\to \infty }{\lim }{u}_1\left(n\right)=u_1^{*}=8and\underset{n\to \infty }{\lim }{u}_2\left(n\right)=u_2^{*}=2.$$

Also, the non-autonomous system formed by the first two equations in (37) is asymptotic to the following limiting system:

$$\left.\begin{array}{c}{x}_{n+1}=\left(a+\frac{1}{16}\right){\displaystyle \frac{x_n}{1+y_n}}\\ y_{n+1}=\left(b+\frac{1}{4}\right){\displaystyle \frac{y_n}{1+x_n}}\end{array}\right\}.$$

(38)

Based on Theorem 9, we obtain the following two results.

1. If $0<a<\frac{15}{16}$ and $0<b<\frac{3}{4}$, then equilibrium point $E_0^{*}=\left(0,0\right)$ is globally asymptotically stable, i.e., every solution $\left\{\left(x_n,y_n\right)\right\}$ of (38) satisfies

$$\underset{n\to \infty }{\lim }{x}_n=\underset{n\to \infty }{\lim }{y}_n=0,$$

for all $x_0\ge 0$ and $y_0\ge 0$.

2. If ${\sigma }_1^2<64(16a+1),{\sigma }_2^2<8(4b+1)$, $0<a<\frac{15}{16}$, and $0<b<\frac{3}{4}$, then all solutions of non-autonomous system (37) globally asymptotically converge to $\left(E_0^{*},u_1^{*},u_2^{*}\right)=\left(0,0,u_1^{*},u_2^{*}\right)\in {\mathbb{R}}_{+}^2\times {\mathcal{U}}_1\times {\mathcal{U}}_2$, for all points $x_0\ge 0$ and $y_0\ge 0$.

This shows that ${\sigma }_1^2$ and ${\sigma }_2^2$ are bifurcation parameters in this model.

Example 7. 

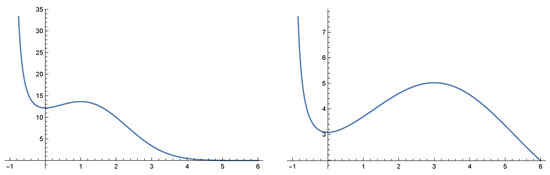
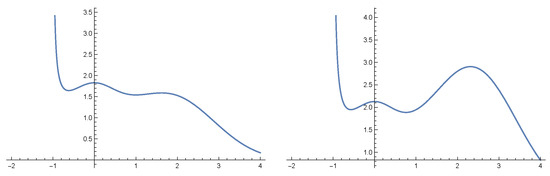
The coefficients of difference equations of state variable may depend on several traits. These traits might be decoupled or coupled. In the case when they are decoupled there will be a single Fisher’s equation for each trait.

For instance, consider the Leslie–Gower evolutionary model:

$$\left.\begin{array}{c}{x}_{n+1}={\displaystyle \frac{a\left(u_n\right)x_n}{1+x_n+c_1\left(u_n\right)y_n}}\\ y_{n+1}={\displaystyle \frac{b\left(w_n\right)y_n}{1+c_2\left(w_n\right)x_n+y_n}}\end{array}\right\}$$

(39)

with two Fisher’s equations

$$\left.\begin{array}{c}{\displaystyle u_{n+1}=p\frac{u_n}{1+u_n}}\\ {\displaystyle w_{n+1}=q\frac{w_n^2}{1+w_n^2},}\end{array}\right\}$$

(40)

$x_0>0,y_0>0,p>0,q>0,u_0\ge 0,w_0\ge 0$, with all positive coefficients for $n=0,1,\dots$. The dynamics of two equations in (40) follow from any of Theorems 2, 3 or 4.

The fitness functions for traits $u_n$ and $w_n$ are, respectively,

$${\displaystyle a\left(u\right)=\alpha e^{(1/2+p+pu-u^2/2)/{\sigma }_1^2}{(1+u)}^{-p/{\sigma }_1^2},\alpha >0}$$

(41)

and

$${\displaystyle b\left(w\right)=\beta e^{(qw-w^2/2-qarctan\left(w\right))/{\sigma }_2^2},\beta >0,}$$

(42)

see Figure 1 and Figure 2.

Based on known results for dynamics of Leslie–Gower model and Beverton–Holt’s equations, we get the following results.

Theorem 10. 

Consider System (39), where two traits $u_n$ and $w_n$ satisfy two Beverton–Holt’s equations (40).

(i) 

Assume that $p\le 1$ and $q\le 2$. If every solution of (39) converges to the zero equilibrium, which happens if $\alpha <e^{-\frac{1/2+p}{{\sigma }_1^2}}$ and $\beta <1$, then every solution of evolutionary model (39), (40) converges to the equilibrium $(0,0,0,0)$.

(ii) 

Assume that $p\le 1$ and $q>2$. If every solution of (39) converges to the zero equilibrium, which happens if $\alpha <e^{-\frac{1/2+p}{{\sigma }_1^2}}$ and $\beta <1$ or $\alpha <e^{-\frac{1/2+p}{{\sigma }_1^2}}$ and $\beta <e^{-\frac{q{\overline{w}}_{+}-{\overline{w}}_{+}^2/2-qarctan\left({\overline{w}}_{+}\right)}{{\sigma }_2^2}}$, then every solution of evolutionary model (39), (40) converges to the equilibrium $(0,0,0,0)$ or $(0,0,0,{\overline{w}}_{+})$, where ${\overline{w}}_{+}$ is a larger positive equilibrium of second equation in (40).

(iii) 

Assume that $p>1$ and $q\le 2$. If every solution of (39) converges to the zero equilibrium, which happens if $\alpha <e^{-\frac{p\left(p+2\right)}{2{\sigma }_1^2}}{p}^{p/{\sigma }_1^2}$ and $\beta <1$, then every solution of evolutionary model (39), (40) converges to the equilibrium $(0,0,p-1,0)$.

(iv) 

Assume that $p>1$ and $q>2$. If every solution of (39) converges to the zero equilibrium, which happens if $\alpha <e^{-\frac{p\left(p+2\right)}{2{\sigma }_1^2}}{p}^{p/{\sigma }_1^2}$, $\beta <e^{-\frac{q{\overline{w}}_{+}-{\overline{w}}_{+}^2/2-qarctan\left({\overline{w}}_{+}\right)}{{\sigma }_2^2}}$ or $\alpha <e^{-\frac{p\left(p+2\right)}{2{\sigma }_1^2}}{p}^{p/{\sigma }_1^2}$, $\beta <1$, then every solution of evolutionary model (39), (40) converges to the equilibrium $(0,0,p-1,{\overline{w}}_{+})$ or $(0,0,p-1,0)$, where ${\overline{w}}_{+}$ is larger positive equilibrium of second equation in (40).

(v) 

Assume that $p>1$ and $q>2$. If every solution of (39) converges to the interior positive equilibrium, which happens if

$$\alpha >e^{-\frac{p\left(p+2\right)}{2{\sigma }_1^2}}{p}^{p/{\sigma }_1^2},\beta >e^{-\frac{q{\overline{w}}_{+}-{\overline{w}}_{+}^2/2-qarctan\left({\overline{w}}_{+}\right)}{{\sigma }_2^2}},$$

$$\alpha e^{\frac{p\left(p+2\right)}{2{\sigma }_1^2}}{p}^{-p/{\sigma }_1^2}>1+c_1(p-1)(\beta e^{\frac{q{\overline{w}}_{+}-{\overline{w}}_{+}^2/2-qarctan\left({\overline{w}}_{+}\right)}{{\sigma }_2^2}}-1),$$

$$\beta e^{\frac{q{\overline{w}}_{+}-{\overline{w}}_{+}^2/2-qarctan\left({\overline{w}}_{+}\right)}{{\sigma }_2^2}}>1+c_2\left({\overline{w}}_{+}\right)(\alpha e^{\frac{p\left(p+2\right)}{2{\sigma }_1^2}}{p}^{-p/{\sigma }_1^2}-1)$$

or

$$\alpha >e^{-\frac{p\left(p+2\right)}{2{\sigma }_1^2}}{p}^{p/{\sigma }_1^2},\beta >1,$$

$$\alpha e^{\frac{p\left(p+2\right)}{2{\sigma }_1^2}}{p}^{-p/{\sigma }_1^2}>1+c_1(p-1)(\beta -1),$$

$$\beta >1+c_2\left(0\right)(\alpha e^{\frac{p\left(p+2\right)}{2{\sigma }_1^2}}{p}^{-p/{\sigma }_1^2}-1),$$

then every solution of evolutionary model (39), (40) converges to the equilibrium $(\overline{x},\overline{y},p-1,{\overline{w}}_{+})$ or $(\overline{x},\overline{y},p-1,0)$, where ${\overline{w}}_{+}$ is larger positive equilibrium of second equation in (40).

Proof. 

The proof is a consequence of the global dynamics of the first two equations of system (39) in [20] and global dynamics of (40) given in [2]. Notice that the global dynamics of (40) follows from Theorem 4. □

Example 8. 

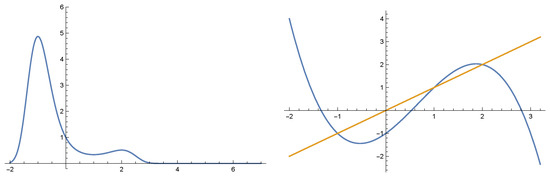
Consider the first two equations of System (34), where

$$a\left(u_1\right)=b\left(u_2\right)=e^{-\frac{u^4}{4}+\frac{2u^3}{3}+\frac{u^2}{2}-2u}$$

(see Figure 3) and Fisher’s equation has the form

$$u_{n+1}=u_n-{\sigma }^2(u_n+1)(u_n-1)(u_n-2),n=0,1,\dots .$$

(43)

Equation (43) has three equilibrium solutions ${\overline{u}}_1=-1,{\overline{u}}_2=1$ and ${\overline{u}}_3=2$. Straightforward local stability analysis implies that ${\overline{u}}_2=1$ is always a repeller, while ${\overline{u}}_1=-1$ is locally asymptotically stable when ${\sigma }^2<1/3$ and ${\overline{u}}_3=2$ is locally asymptotically stable when ${\sigma }^2<2/3$. In addition, the function $f\left(u\right)=u-{\sigma }^2(u+1)(u-1)(u-2)$ satisfies the negative feedback condition in the neighborhood of the equilibrium solutions ${\overline{u}}_1$ and ${\overline{u}}_3$, for the values of ${\sigma }^2$, which are less than $1/3$ and $2/3$ respectively. Finally the Schwarzian derivative given as

$$Sf\left(x\right)=-\frac{6{\sigma }^2\left({\sigma }^2\left(6x^2-8x+5\right)+1\right)}{{\left({\sigma }^2\left(3x^2-4x-1\right)-1\right)}^2}$$

is negative in all points. In view of Theorem 3, both equilibrium solutions are globally asymptotically stable within their immediate basins of attractions (part of basin of attraction which contains the equilibrium) which are given as:

$$B\left({\overline{u}}_1\right)=\left(\frac{\sigma -\sqrt{9{\sigma }^2+4}}{2},1\right),B\left({\overline{u}}_3\right)=\left(1,\frac{\sigma +\sqrt{9{\sigma }^2+4}}{2}\right)$$

(see Figure 3).

Since $b(-1)=e^{19/12}$ and $b\left(2\right)=e^{-2/3}$, we conclude that the equilibrium ${\overline{u}}_1=-1$ is ESS (evolutionary stable), since it is located at a global maximum of the fitness function, see [5,6,19].

An analysis of second and third iterate of a map f and a bifurcation diagram of trait equation (using the speed of evolution ${\sigma }^2$ as a bifurcation parameter) indicates that period three solutions exist and so period doubling route to chaos is possible. For instance, when $\sigma =1$ the Fisher’s equation has three period-two solutions and six period three solutions such as in

Table 1. Period-two and period-six solutions.

Period	Solutions
2	$\begin{array}{c}\\ \left\{-{1.4811943040920157}^{\prime },{2.675130870566657}^{\prime }\right\}\hfill \\ \left\{-{1.2143197433775346}^{\prime },{0.3111078174659819}^{\prime }\right\}\hfill \\ \left\{{1.539188872810899}^{\prime },{2.170086486626063}^{\prime }\right\}\hfill \end{array}$
6	$\begin{array}{c}\\ \left\{-{1.4744747878196507}^{\prime },{2.604821255408912}^{\prime },-{0.8941349225595812}^{\prime }\right\}\hfill \\ \left\{-{1.459059143004265}^{\prime },{2.4457148775318593}^{\prime },{0.22539345987688394}^{\prime }\right\}\hfill \\ \left\{-{1.2753075808869003}^{\prime },{0.7763759605752573}^{\prime },{0.2903030970553621}^{\prime }\right\}\hfill \\ \multicolumn{1}{c}{\left\{-{1.2260445983561825}^{\prime },{0.39725380515042014}^{\prime },-{0.9525620739512014}^{\prime }\right\}}\\ \left\{{1.2372751086979754}^{\prime },{1.642167387692556}^{\prime },{2.24931261120429}^{\prime }\right\}\hfill \\ \left\{{1.8314588915790713}^{\prime },{2.2282465032983643}^{\prime },{1.3232389577735175}^{\prime }\right\}\hfill \end{array}$

.

Assuming that ${\sigma }^2<1/3$ we have that

$$\underset{n\to \infty }{\lim }{u}_n=\overline{u_1}for{u}_0\in B\left({\overline{u}}_1\right)$$

which in turn implies that if $a\left({\overline{u}}_1\right),b\left({\overline{u}}_1\right)\in (0,1)$ every solution of system (36) converges to $(0,0,{\overline{u}}_1)$. Similarly, assuming that ${\sigma }^2<2/3$ we have that

$$\underset{n\to \infty }{\lim }{u}_n={\overline{u}}_{3}for{u}_0\in B\left({\overline{u}}_3\right),$$

which in turn implies that if $a\left({\overline{u}}_3\right),b\left({\overline{u}}_3\right)\in (0,1)$, every solution of system (34) converges to $(0,0,{\overline{u}}_3)$.

Example 9. 

Consider the Leslie–Gower evolutionary model:

$$\left.\begin{array}{c}{x}_{n+1}={\displaystyle \frac{a{x}_n}{1+x_n+c_1\left(u_n\right)y_n}}\\ y_{n+1}={\displaystyle \frac{b{y}_n}{1+c_2\left(u_n\right)x_n+y_n}}\end{array}\right\}$$

(44)

with a single Fisher’s equation

$${\displaystyle u_{n+1}=p\frac{u_n^3}{1+u_n^3}}$$

(45)

$x_0>0,y_0>0,u_0\ge 0$, with all positive coefficients $a,b,c_1\left(u_n\right),c_2\left(u_n\right)$ for $n=0,1,\dots$.

The equilibrium points of Fisher’s Equation (45) are solutions of the following equation:

$$u\left(u^3-p{u}^2+1\right)=0,$$

which implies that there exist one negative equilibrium point $E_1$, and zero equilibrium $E_0$. The critical points of the function $h\left(u\right)=u^3-p{u}^2+1$ are $u_1^{*}=0$ and $u_2^{*}=\frac{2p}{3}$, where h reaches the maximum $h\left(u_1^{*}\right)=1$, and reaches a minimum at $u_2^{*}$. Since

$$h\left(\frac{2p}{3}\right)=\frac{27-4p^3}{27}\left\{\begin{array}{ccc}>0\hfill & for\hfill & p<\frac{3}{\sqrt[3]{4}}\hfill \\ =0\hfill & for\hfill & p=\frac{3}{\sqrt[3]{4}}\hfill \\ <0\hfill & for\hfill & p>\frac{3}{\sqrt[3]{4}}\hfill \end{array}\right.$$

then the following claims hold:

(i) 

if $p<\frac{3}{\sqrt[3]{4}}$, then there exist two equilibrium points: $-1<E_1<0$ and $E_2=0$,

(ii) 

if $p=\frac{3}{\sqrt[3]{4}}$, then there exist three equilibrium points: $-1<E_1=-\frac{1}{\sqrt[3]{4}}<0$, $E_2=0$ and $E_3=E_4=\sqrt[3]{2}$,

(iii) 

if $p>\frac{3}{\sqrt[3]{4}}$, then there exist four equilibrium points: $-1<E_1<0$, $E_2=0$, $E_3$, and $E_4$, where $E_3<\frac{2p}{3}<E_4$.

The equilibrium points $E_2$ and $E_4$ are locally asymptotically stable and the equilibrium points $E_1$ and $E_3$ are locally repellers. By using Theorem 4, we see that $E_2$ and $E_4$ are globally asymptotically stable with the corresponding basins of attractions:

(i) 

if $p<\frac{3}{\sqrt[3]{4}}$, then $\mathcal{B}\left(E_2\right)=\left(E_1,\infty \right)$,

(ii) 

if $p=\frac{3}{\sqrt[3]{4}}$, then $\mathcal{B}\left(E_2\right)=\left(E_1,E_3\right)$ and $\mathcal{B}\left(E_3=E_4\right)=\left(E_3,\infty \right)$,

(iii) 

if $p>\frac{3}{\sqrt[3]{4}}$, then $\mathcal{B}\left(E_2\right)=\left(E_1,E_3\right)$ and $\mathcal{B}\left(E_4\right)=\left(E_3,\infty \right)$.

The fitness function is

$$c_1\left(x\right)=c_2\left(x\right)=exp\left(\frac{\frac{1}{6}plog\left(x^2-x+1\right)+px-\frac{1}{3}plog(x+1)-\frac{p{tan}^{-1}\left(\frac{2x-1}{\sqrt{3}}\right)}{\sqrt{3}}-\frac{x^2}{2}}{{\sigma }^2}\right).$$

(46)

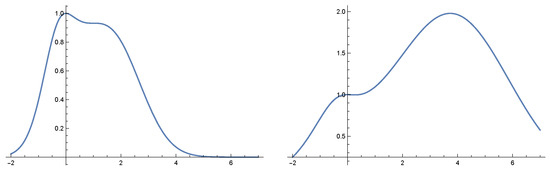
In view of Theorem 3, the equilibrium solutions $E_2$ and $E_4$ are globally asymptotically stable within their immediate basins of attractions. One of them is ESS (evolutionary stable) and that is the one located at a global maximum of the fitness function, see [5,6,19]. The second equilibrium is evolutionary convergent but is not an ESS since it does not yield a global maximum of the fitness function, see [5,6,19]. Figure 4 indicates that the position of the global maximum depends on parameter p.

4. Conclusions

In this paper, we give some global attractivity results for non-autonomous competitive systems of difference equations (1) where f is non-decreasing in the first variable and is non-increasing in the second variable, and g is non-increasing in the first variable and is non-decreasing in the second variable. Here, $a_n$ and $b_n$ are sequences that are assumed to be asymptotically constant. Such systems appear in many recent applications in evolutionary (Darwinian) dynamics, where, in addition to dynamics of state variables, we are interested in the dynamics of traits that affect the coefficients of state variables. Our techniques are based on the method of difference inequalities, and the obtained results hold when the limiting system of difference equations is in a hyperbolic case. We extend some asymptotic results from single species models to the case of two species competition models. We apply our results to evolutionary population competition models, which have been considered lately by Ackleh, Cushing, Elaydi, and others. We illustrate our results with Leslie–Gower evolutionary model where Fisher’s trait equation is a sigmoid Beverton–Holt equation, with up to four equilibrium points, only one of which is ESS (evolutionary stable) and that is, according to the theory in Vincent and Brown [19], exactly the equilibrium where the fitness function attains its global maximum, see Example 9.