Abstract
Intuitionistic Fuzzy Sets with Ordered Pairs (IFSOP) are the recent extension of intuitionistic fuzzy sets by incorporating functional and dysfunctional points of view into the definition of membership functions. This paper extends the Technique of Order Preference Similarity to the Ideal Solution (TOPSIS) method to the Intuitionistic Fuzzy TOPSIS (IF TOPSIS) with ordered pairs method and applies it to a multi-criteria risk-based supplier selection problem under fuzziness. IF TOPSIS with ordered pairs involves finding a positive ideal solution and a negative ideal solution, and measuring the distance between each alternative and these solutions. The final ranking of the alternatives is obtained based on the proportion of distances between the positive and negative ideal solutions. By asking functional and dysfunctional questions in this ranking process, the developed IF TOPSIS with ordered pairs method incorporates the accuracy and consistency of expert judgments, enhancing the decision-making process. A sensitivity analysis is also presented in order to show the robustness of the rankings obtained by IF TOPSIS with ordered pairs.
Keywords:
intuitionistic fuzzy sets; ordered pairs; TOPSIS; risk analysis; supplier selection problem MSC:
90-08; 03B52; 03E72
1. Introduction
Intuitionistic fuzzy sets (IFS) were introduced by Atanassov [1] in order to include the hesitancy degrees of experts in their assessments. Since membership and non-membership degrees are complementary to one another in ordinary fuzzy sets (OFS), it is assumed that an expert is not hesitant in assigning his/her judgments. The sum of the membership, non-membership, and hesitancy degrees is complementary to one in IFS, which makes IFS a superset of OFS. Two questions for each element in an IFS are enough to ask an expert to construct it. What is the membership degree of the considered element? And what is the non-membership degree of the considered element?
However, determining membership and non-membership degrees requires a deeper analysis since an assignment for membership or non-membership degrees may be a momentarily erroneous assignment. To determine these degrees, more questions composed of functional and dysfunctional questions can be asked by an expert, making the set of two sub-IFS components. Asking functional and dysfunctional questions is a common practice in various fields such as psychology, sociology, organizational development, and relationship counseling. These types of questions serve different purposes and can provide valuable insights into a person’s or a system’s functioning. It is essential to ask both functional and dysfunctional questions in a balanced manner, as focusing solely on either aspect may lead to an incomplete understanding of a situation or individual. By asking both types of questions, experts or groups gain a better understanding of their actions/preferences. This is the most important advantage of IFSOP [2,3]. The total number of questions becomes four since two for membership and non-membership degrees of functional question and two for membership and non-membership degrees of dysfunctional question are asked by an expert. Striking a balance between the two helps in the comprehensive analysis and development of effective solutions. For this, IFSOP has been introduced to the literature. Such a fuzzy set can be represented by . Since the sum in each component, or is at most equal to one, providing that where is the membership degree of element x with functional point of view; is the non-membership degree of element x with functional point of view; is the membership degree of element x with dysfunctional point of view; and is the non-membership degree of element x with dysfunctional point of view. IFSOP takes uncertainty into consideration based on questions with two perspectives. The aim of IFSOP is to increase the accuracy and consistency of the judgments assigned by experts through functional and dysfunctional questions. IFSOP should be especially preferred when experts’ knowledge is not highly reliable. Cebi et al. [2] used IFSOP in operational risk analysis in business processes in a more realistic and detailed way through functional and dysfunctional question-based membership functions. Cebi et al. [3] extended the analytic hierarchy process (AHP) method by using IFSOP, making pairwise comparisons in AHP more reliable by considering the individual answers given by experts to the reciprocal questions under vagueness and impreciseness. In the scope of this study, parallel to the newly published paper on the enlargement of IFSOP in MCDM methods, it aims to extend the TOPSIS (Technique of Order Preference Similarity to the Ideal Solution) method, which is widely used in the literature.
In this paper, the TOPSIS method is extended to the IF TOPSIS with the ordered pairs method and is applied to a multi-criteria supplier selection problem under fuzziness. As the name implies, the method is based on finding a positive ideal and a negative ideal solution and comparing the distance of each of the alternatives to these solutions. Then, based on a proportion of the distances of alternatives to the positive and negative ideal solutions, the final ranking is obtained. The developed IF TOPSIS with ordered pairs has the ability to take the accuracy and consistency of the assigned judgments by an expert into account.
The rest of this paper is organized as follows: Section 2 presents a literature review on intuitionistic fuzzy sets and their extensions. Section 3 presents the preliminaries of IFSOP. Section 4 includes the proposed IF TOPSIS with the ordered pairs method. Section 5 describes the application of the proposed IF TOPSIS with the ordered pairs method to a supplier selection problem. Section 6 concludes the paper.
2. Intuitionistic Fuzzy Sets and Their Extensions: Literature Review
Intuitionistic fuzzy sets (IFSs) were introduced by Atanassov in [1] as a generalization of ordinary fuzzy sets. In IFSs, the sum of degrees of membership and non-membership is not necessarily equal to one, allowing another complementary parameter to be incorporated into the membership function. This makes them more suitable for representing imprecise and vague information [4,5,6,7,8]. The degree of membership of an element in an IFS is defined as the degree to which the element belongs to a given set, while the degree of non-membership represents the degree to which the element does not belong to the set without a complementary feature requirement. Thus, the third parameter introduced in IFS is the degree of indeterminacy, which quantifies the degree of uncertainty associated with the membership and non-membership degrees.
IFS have been applied in a variety of fields, including decision-making, pattern recognition, and image processing, since IFS can handle situations where data are incomplete or uncertain, allowing for more robust decision making even in situations where the available information is limited. The inclusion of a degree of non-membership and a complementary degree of indeterminacy makes IFS more adaptable to situations where the degree of uncertainty is not clear-cut [9,10]. Intuitionistic Fuzzy Sets (IFS) have been extended based on different points of view by defining membership functions. These extensions of IFS are briefly described as follows.
Interval-valued intuitionistic fuzzy sets (IVIFSs): This type of IFS defines the membership and non-membership degrees as intervals rather than single numbers. This allows for more flexibility in representing uncertainty and imprecision in decision-making problems [5,8]. An IVIFS can be used to represent uncertain values that lie between two known values.
Hesitant intuitionistic fuzzy sets (HIFSs): HIFSs were introduced by Torra in 2010 [11] to represent hesitant or uncertain information in decision-making problems. In HIFSs, the degree of membership, non-membership, and hesitation are considered separately, allowing for a more accurate representation of the decision maker’s uncertainty.
Type-2 IFS: These sets let experts determine membership and non-membership degrees in a larger area. Atanassov’s [12] IFS of type-2 (IFS2), which were later called Pythagorean Fuzzy Sets by Yager [13], are characterized by membership and non-membership degrees, provided that their squared sum is at most equal to one. This gives a larger domain than IFS in order to determine membership and non-membership degrees by increasing the complexity, which also leads to a more accurate representation of uncertainty [13,14,15].
Picture Fuzzy Sets (PFSs): PFSs were introduced by Cuong and Kreinovich [16] in 2013 and can represent spatially related membership degrees. In PFSs, the degree of positive membership, the degree of neutral membership, and the degree of negative membership are represented. In addition, the degree of refusal membership is defined as the complement of the total value of the degree of positive membership, degree of neutral membership, and degree of negative membership [16]. PFSs have been used in various applications, including image processing, computer vision, and decision making. However, PFSs have been defined as inconsistent fuzzy sets by some researchers [17,18,19].
q-Rung orthopair FS (q-ROFS): The q-Rung orthopair FS was introduced by Yager [20]. q-ROFS is defined by a membership degree and a non-membership degree, which satisfy the condition that exponent of their sum is equal to or less than 1. Yager proposed q-ROFS to better model real-life decision-making processes, where the sum of the membership degree and non-membership degree of an alternative may be greater than 1, but their exponent sum is equal to or less than 1 [20].
Spherical Fuzzy Sets (SFS): Another addition to the literature on the generalization of IFS sets is the introduction of Spherical Fuzzy Sets (SFS) defined by three functions that express the degree of membership, degree of indeterminacy, and degree of non-membership. SFS allow participants a vast preference domain to assign membership functions, with the only constraint being that the squared sum of the spherical parameters cannot exceed 1.0. In the SFS, the degree of indeterminacy is presented separately, along with the degree of membership and non-membership [21,22].
Circular Intuitionistic Fuzzy Sets (CIFS): CIFS extend IFS by incorporating a circular membership function. In CIFS, each element is associated with three values: the degree of membership, the degree of non-membership, and the radius of the circle around each element. The membership function in CIFS is circular in shape, and it allows for a more flexible and natural representation of uncertainty compared to traditional IFS [23].
3. Intuitionistic Fuzzy Sets with Ordered Pairs
Intuitionistic Fuzzy Sets with Ordered Pairs (IFSOP) have been introduced in the literature to address the inconsistency in expert judgments by considering both functional and dysfunctional perspectives. IFSOP considers both the dysfunctional and functional perspectives of the decision makers on the subject under consideration. As a result, it computes the uncertainty in the decision environment by measuring the consistency of the decision maker’s judgments. The decision maker’s responses to the functional and dysfunctional questions are used for this. When the decision is made in confidence, the sum of these assessments is expected to equal one. However, due to the uncertainty in the decision-making environment, the sum of both judgments will not be exactly equal to 1.0 . In this case, the inconsistency of the decision maker is represented by . Figure 1 (inspired by [24]) presents the dysfunctional and functional views of decision makers on the percentage of dark balls. It is assumed the percentage of dark balls in the box cannot be determined precisely by human judgment. The functional view meaning of the percentage of dark balls is symbolized by , while the dysfunctional view meaning the percentage of light-colored balls is symbolized by . Although these functional and dysfunctional views on a given example are mathematically complementary to one another, they may not be fully complementary to one another in human sight. This section provides an explanation of the definitions and basics of IFSOP.
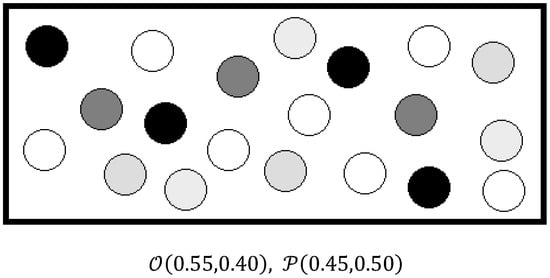
Figure 1.
Expression of the percentage of dark balls using IFSOP.
Definition 1.
Let X be a universe of discourse. An IFSOP
is an object having the form
where the functions
are the degrees of membership, non-membership of
to
and
, respectively, where
and
are functional and dysfunctional sets, satisfying the conditions
and inconsistency in the judgment is
where
and
. An IFSOP
has maximum inconsistency if
and an IFSOP
has maximum consistency if
[2,3].
Definition 2.
Let
,
, and
be IF numbers with ordered pairs. If none of them has maximum consistency or maximum inconsistency, the basic operators are as follows [2,3]:
Addition:
Multiplication:
Multiplication by a scalar:
power of :
:
Definition 3.
Let ,
, then
Definition 4.
Let
be a collection of IF-Weighted Arithmetic Mean with ordered pairs (IFWAMOP) with respect to
and
, IFWAMOP is defined as [2,3]
Definition 5.
Let
be a collection of IF-Weighted Geometric Mean with ordered pairs (IFWGMOP) with respect to
and
, IFWGMOP is defined as [2,3]
Definition 6.
The consistency index (CI) of IF number with ordered pairs
is defined as [2,3]
The closer the
is to 1, the more consistent the decision maker is.
Definition 7.
The score index
of an IF number with ordered pairs
is proposed as follows [2,3]
where
is the linguistic scale multiplier. If a standard linguistic scale is used in a study, where you pull fuzzy numbers from a standard table, the value
is obtained as follows:
4. Multi-Attribute Decision Making: A Novel IF TOPSIS with Ordered Pairs
In this section, we propose an extension version of the TOPSIS method for IFSOP. The steps of the IF TOPSIS with ordered pairs method are as follows.
Step 1. Obtain the IFSOP decision matrix in Equation (17) and weights of the criteria from each decision maker (k = 1,…,K) using the IF scale with ordered pairs given in Table 1.
where denotes the number of criteria (, denotes the number of alternatives (, and represents the number of experts .

Table 1.
Linguistic terms for functional and dysfunctional sets.
Step 2. Obtain the aggregated decision matrix using the IFWAMOP formula in Equation (12).
Step 3. Obtain the weighted aggregated decision matrix by using Equation (18).
Step 4. Determine the fuzzy positive ideal solution (, ) and fuzzy negative ideal solution (, ) for the weighted aggregated decision matrix by using the score index in Equation (15).
Let
where is the maximum intuitionistic fuzzy set among the alternatives’ values for jth criterion and is the minimum intuitionistic fuzzy set among the alternatives’ values for jth criterion. In order to determine the minimum and maximum values, the rating scale must be converted to a crisp value.
Step 5. Calculate the separation measure between the jth alternative and for each decision maker by using Equation (21).
Step 6. Calculate the separation measure between the jth alternative and for each decision maker by using Equation (22).
Step 7. Calculate the closeness coefficient of each alternative using Equation (23).
Step 8. Rank the preference order of all alternatives based on their closeness coefficients and choose the best one. To test the robustness of decisions, conduct a sensitivity analysis.
5. Case Study
5.1. Problem Definition
In this section, a risk analysis-based supplier selection problem (RSS) is handled. RSS refers to the process of considering and evaluating risks associated with potential suppliers during the supplier selection process. It involves identifying and assessing various risks that may impact the performance, reliability, and overall suitability of suppliers. In this context, risks can arise from various sources, such as financial instability, quality issues, delivery delays, and reputational risks. The goal of risk analysis-based supplier selection is to identify suppliers that not only meet the organization’s requirements but also demonstrate the ability to manage and mitigate potential risks effectively. The risk analysis-based supplier selection process typically involves risk identification, risk assessment, risk-mitigation strategies, supplier evaluation, and decision-making steps. By incorporating risk analysis into the supplier selection process, organizations can make more informed decisions and select suppliers that demonstrate resilience, proactive risk management, and the ability to handle potential disruptions. In this section, a supplier selection problem will be solved by the proposed approach, IF TOPSIS with ordered pairs. The proposed approach helps to mitigate supply chain risks, enhance business continuity, and build a more robust and sustainable supply chain network.
5.2. Application of IF TOPSIS with Ordered Pairs
In this RSS problem, four criteria, which are delivery time, financial instability, reputation, and quality, will be considered in the evaluation of eight supplier alternatives. The following decision matrixes are filled out by three experts. Three experts evaluate eight alternatives with respect to four criteria.
The linguistic evaluations are transformed into associated IF values with ordered pairs using the scale given in Table 1.
The IF linguistic terms with ordered pairs given in Table 2 are aggregated using Equation (12). The aggregated evaluations are represented in Table 3.

Table 2.
Expert linguistic evaluations.

Table 3.
Aggregated expert evaluations.
The weighted aggregated expert evaluations are calculated in Step 2. The criteria weights are defined by the experts as follows: C1. Delivery time: ((0.8,0.2),(0.2,0.8)); C2. Financial instability: ((0.95,0.05),(0.05,0.95)); C3. Reputation: ((0.8,0.2),(0.2,0.8)); and C4. Quality: ((0.95,0.05),(0.05,0.95)). The weighted aggregated expert evaluations are obtained using Equation (18) and are shown in Table 4.

Table 4.
Weighted aggregated expert evaluations.
The score index is computed as given in Step 4. Before obtaining the score index, the consistency index is calculated as given in Table 5.

Table 5.
Consistency index.
Using the consistency index and Equation (15), the score index for each IF value with ordered pairs in Table 5 is obtained.
The score index values are represented in Table 6.

Table 6.
Score index values.
The score index values are used to define the positive and ideal negative solutions as given in Table 7.

Table 7.
Positive and negative ideal solutions.
After the positive and negative ideal solutions are obtained, the distances of each alternative to the negative and positive ideal solutions are calculated by Steps 5 and 6 and given in Table 8.

Table 8.
Distances, CC indexes and rank of the alternatives.
The closeness coefficients of the alternatives are calculated using Equation (23).
According to the results, the alternative rankings are as follows: A6 > A8 > A4 > A5 > A2 > A7 > A3 > A1.
5.3. Comparative Analysis
In this section, the supplier selection problem is solved using the classical fuzzy TOPSIS approach proposed by Chen [25] and the results are compared with the results of the proposed IF TOPSIS with the ordered pairs method. In order to make the comparison, first the experts’ functional linguistic evaluations are used in classical fuzzy TOPSIS, and the alternatives are ranked based on functional evaluations. Then, similarly dysfunctional linguistic evaluations are used for ranking the alternatives. Table 9 shows the results of these comparative analyses.

Table 9.
Comparative analysis.
The findings demonstrate that, although functional and dysfunctional set results are similar, they are not identical. Using IF TOPSIS with ordered pairs, it is possible to capture this discrepancy in meaning.
5.4. Sensitivity Analysis
In order to show the robustness of the proposed methodology, one-at-a-time sensitivity analysis is applied. To this end, the weight of each main criterion is changed to each of the linguistic terms “AH/AL, VH/VL, H/L, M/M, L/H, VL/VH, AL/AH”, respectively, whereas the linguistic terms of other criteria are held fixed to their original values. The result of the closeness coefficient values for different weights is calculated and shown in Figure 2. In Figure 2a, the best alternative remains A6 until the weight of C1 becomes VL/VH or more, leaving its position to alternative A4. Moreover, the rankings of some alternatives, such as A1, A2, A7, and A8, are very sensitive to the changes in the weight of C1. In Figure 2b, the best alternative remains A6 until the weight of C2 becomes L/H or more, leaving its position to alternative A2. As the weight of C2 decreased, alternative A2 moved up from fourth place to first place after L/H. In Figure 2c, the best alternative remains A6, whatever the weight of C3 is. This means that A6 is quite robust to changes in the weights of C3. Alternative A8 leaves its place for alternative A2 when the weight of C3 becomes M/M or more. In Figure 2d, the sensitivity analysis of C4 shows that the ranking is quite sensitive to changes in the weight of C4. Ranking changes much earlier in the C4 criterion than others. The best alternative remains A6 until the weight of C4 becomes M/M or less, leaving its position to alternative A8.
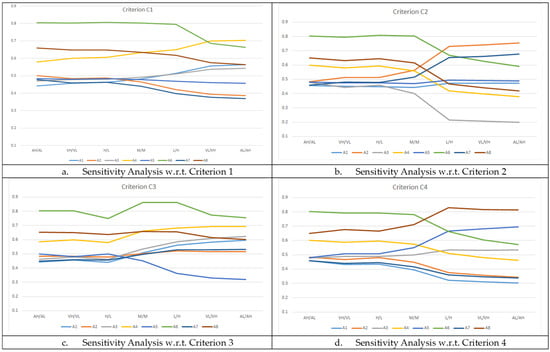
Figure 2.
One-at-a-time sensitivity analysis.
6. Conclusions
In this study, the IFSOP-based TOPSIS method was developed, and the proposed method was applied to a multi-criteria risk-based supplier selection problem under fuzziness. The objective of the proposed study was to enhance the decision-making process in scenarios where uncertainty and vagueness exist within the linguistic data. By incorporating the IF TOPSIS with ordered pairs method, we were able to address the limitations of the TOPSIS method in handling the accuracy and consistency of the assigned judgments by experts. The results of our case study demonstrated the effectiveness of the proposed IF TOPSIS with the ordered pairs method. Through the application of the IF TOPSIS with ordered pairs, the method successfully captured the inherent uncertainty in the data and allowed decision makers to make informed choices based on comprehensive assessments. One notable advantage of the proposed IF TOPSIS with ordered pairs is its ability to handle complex and ambiguous data sets by allowing the representation and analysis of fuzzy and vague information, providing decision makers with a clearer understanding of the decision space through functional and dysfunctional questions.
However, the limitation of the proposed study is that asking two-way questions makes the data collection process difficult since the method produces effective results in the collected data by asking functional and dysfunctional questions. In future studies, an interval valued IFSOP based TOPSIS method is planned to be developed to capture and represent the imprecision and uncertainty present in real-world data more effectively.
Author Contributions
Conceptualization, B.O.; Methodology, C.K., S.C., B.O. and S.C.O.; Software, S.C.O.; Validation, S.C.; Resources, S.C. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
No new data were created or analyzed in this study. Data sharing is not applicable to this article.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Atanassov, K. Intuitionistic fuzzy sets. Fuzzy Sets Syst. 1986, 20, 87–96. [Google Scholar] [CrossRef]
- Cebi, S.; Gündoğdu, F.K.; Kahraman, C. Operational risk analysis in business processes using decomposed fuzzy sets. J. Intell. Fuzzy Syst. 2022, 43, 2485–2502. [Google Scholar] [CrossRef]
- Cebi, S.; Kutlu Gündoğdu, F.; Kahraman, C. Consideration of reciprocal judgments through Decomposed Fuzzy Analytical Hierarchy Process: A case study in the pharmaceutical industry. Appl. Soft Comput. 2023, 134, 110000. [Google Scholar] [CrossRef]
- Atanassov, K.T. Research on intuitionistic fuzzy sets in Bulgaria. Fuzzy Sets Syst. 1987, 22, 93. [Google Scholar] [CrossRef]
- Atanassov, K.T.; Gargov, G. Interval-valued intuitionistic fuzzy sets. Fuzzy Sets Syst. 1989, 31, 343–349. [Google Scholar] [CrossRef]
- Atanassov, K.T. Remarks on the intuitionistic fuzzy sets. Fuzzy Sets Syst. 1992, 51, 117–118. [Google Scholar] [CrossRef]
- Atanassov, K.T. Research on intuitionistic fuzzy sets, 1990–1992. Fuzzy Sets Syst. 1993, 54, 363–364. [Google Scholar] [CrossRef]
- Atanassov, K.T. New operations defined over the intuitionistic fuzzy sets. Fuzzy Sets Syst. 1994, 61, 137–142. [Google Scholar] [CrossRef]
- Chen, S.M.; Chen, J.M. Intuitionistic fuzzy sets in decision making and decision support: An overview. J. Intell. Fuzzy Syst. 2014, 26, 635–647. [Google Scholar]
- Verma, A.; Singh, U. Intuitionistic fuzzy sets and their applications: A review. J. Intell. Fuzzy Syst. 2018, 34, 3863–3878. [Google Scholar]
- Torra, V. Hesitant fuzzy sets. Int. J. Intell. Syst. 2010, 25, 529–539. [Google Scholar] [CrossRef]
- Atanassov, K.T. Intuitionistic Fuzzy Sets; Springer: Berlin/Heidelberg, Germany, 1999. [Google Scholar]
- Yager, R.R. Pythagorean Fuzzy Subsets. In Proceedings of the 2013 Joint IFSA World Congress and NAFIPS Annual Meeting (IFSA/NAFIPS), Edmonton, AB, Canada, 24–28 June 2013; pp. 57–61. [Google Scholar]
- Atanassov, K.T. More on intuitionistic fuzzy sets. Fuzzy Sets Syst. 1989, 33, 37–45. [Google Scholar] [CrossRef]
- Zhao, T.; Xiao, J. Type-2 intuitionistic fuzzy sets. Control Theory Appl. 2012, 29, 1215–1222. [Google Scholar]
- Cuong, N.V.; Kreinovich, V. Picture fuzzy sets—A new concept for computational intelligence problems. In Proceedings of the 2013 3rd World Congress on Information and Communication Technologies, WICT, Hanoi, Vietnam, 15–18 December 2013; pp. 1–6. [Google Scholar]
- Hinde, C.J.; Patching, R.S.; McCoy, S.A. Inconsistent Intuitionistic Fuzzy Sets and Mass Assignment. In Developments in Fuzzy Sets, Intuitionistic Fuzzy Sets, Generalized Nets and Related Topics. Foundations; Polish Academy of Sciences: Warsaw, Poland, 2008; Volume 1, pp. 133–153. [Google Scholar]
- Vassilev, P.; Atanassov, K.T. Modifications and Extensions of Intuitionistic Fuzzy Sets; Prof. Marin Drinov Publishing House of Bulgarian Academy of Science: Sofia, Bulgaria, 2019. [Google Scholar]
- Atanassov, K.T.; Vassilev, P. Intuitionistic fuzzy sets and other fuzzy sets extensions representable by them. J. Intell. Fuzzy Syst. Appl. Eng. Technol. 2020, 38, 525–530. [Google Scholar] [CrossRef]
- Yager, R.R. Generalized orthopair fuzzy sets. IEEE Trans. Fuzzy Syst. 2017, 25, 1222–1230. [Google Scholar] [CrossRef]
- Kahraman, C.; Kutlu Gündoǧdu, F. From 1D to 3D membership: Spherical fuzzy sets. In Proceedings of the BOS/SOR 2018, Polish Operational and Systems Research Society, Warsaw, Poland, 24–26 September 2018. [Google Scholar]
- Kutlu Gündoǧdu, F.; Kahraman, C. Spherical fuzzy sets and spherical fuzzy TOPSIS method. J. Intell. Fuzzy Syst. 2019, 36, 337–352. [Google Scholar] [CrossRef]
- Atanassov, K.T. Circular intuitionistic fuzzy sets. J. Intell. Fuzzy Syst. 2020, 39, 5981–5986. [Google Scholar] [CrossRef]
- Wygralak, M. Intelligent Counting under Information Imprecision. In Applications to Intelligent Systems and Decision Support; Springer: Berlin/Heidelberg, Germany, 2013; ISBN 978-3-642-34684-2. [Google Scholar]
- Chen, C.-T. Extensions of the TOPSIS for group decision-making under fuzzy environment. Fuzzy Sets Syst. 2000, 114, 1–9. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).